A&A 437, 1135-1146 (2005)
DOI: 10.1051/0004-6361:20042426
J. I. B. Camargo - G. Daigne - C. Ducourant - P. Charlot
Observatoire Aquitain des Sciences de l'Univers, CNRS-UMR 5804, BP 89, 33270 Floirac, France
Received 23 November 2004 / Accepted 10 March 2005
Abstract
We present high quality astrometry, along with J, H, and ![]() photometry, for 30 southern ICRF
quasars observed with the ESO NTT/SOFI at La Silla. Our main purpose is to document the optical
counterpart of ICRF quasars, by reporting their position in a stellar reference frame and their
near-infrared photometry. Our investigation lies within the scope of extending the (radio) extragalactic
reference frame into the optical range. An internal precision generally better than 10 mas was
obtained in positioning the near-infrared counterpart of these quasars within their stellar surroundings.
The actual astrometric accuracy is estimated from the departure between the observed and the radio (VLBI)
positions of quasars, and is about 35 mas, mainly due to the statistical uncertainties of the
stellar reference catalogue (UCAC2). The positional accuracy was improved to 25 mas for a subset
of 14 quasars observed with extended fields of view, as obtained from mosaics of overlapping images.
The 3-band photometry was achieved with a precision most often better than 0.04 mag, based on
calibration with the 2MASS magnitudes. A spectral index
photometry, for 30 southern ICRF
quasars observed with the ESO NTT/SOFI at La Silla. Our main purpose is to document the optical
counterpart of ICRF quasars, by reporting their position in a stellar reference frame and their
near-infrared photometry. Our investigation lies within the scope of extending the (radio) extragalactic
reference frame into the optical range. An internal precision generally better than 10 mas was
obtained in positioning the near-infrared counterpart of these quasars within their stellar surroundings.
The actual astrometric accuracy is estimated from the departure between the observed and the radio (VLBI)
positions of quasars, and is about 35 mas, mainly due to the statistical uncertainties of the
stellar reference catalogue (UCAC2). The positional accuracy was improved to 25 mas for a subset
of 14 quasars observed with extended fields of view, as obtained from mosaics of overlapping images.
The 3-band photometry was achieved with a precision most often better than 0.04 mag, based on
calibration with the 2MASS magnitudes. A spectral index ![]() (
(
![]() )
was derived from the observed quasar fluxes in the near-infrared. With a mean value
)
was derived from the observed quasar fluxes in the near-infrared. With a mean value
![]() ,
this spectral index does not show any significant correlation with the radio
spectral index.
,
this spectral index does not show any significant correlation with the radio
spectral index.
Key words: astrometry - infrared: general - methods: numerical - reference systems
As of 1 January 1998, the International Celestial Reference Frame (ICRF) replaced the FK5 optical frame as the fundamental IAU celestial frame. The ICRF is a quasi-inertial reference frame based on the sub-milliarcsecond-accurate Very Long Baseline Interferometry (VLBI) positions of 212 extragalactic compact sources distributed over the entire sky (Ma et al. 1998). The ICRF is the prime realization of the IAU International Celestial Reference System (ICRS, Arias et al. 1995). In addition to these so called "defining'' sources, positions for 294 "candidate'' sources and 102 "other'' sources were also published. This categorization was based on the observational history and the astrometric suitability of the sources. "Candidate'' sources have the potential to be designated as defining sources in the future, as more observations or analysis improvements become available. "Other'' sources were included in order to densify the frame, or because they may be useful for radio-optical frame ties (see e.g. Lestrade et al. 1999). Recently, positions in the ICRF for an additional 109 new sources were reported, based on VLBI observations accumulated since 1995 (Fey et al. 2004). Intrinsic source structure is also continuously monitored from VLBI observations in order to determine their suitability for reference-frame use (Fey & Charlot 2000,1997; Ojha et al. 2004; Fey et al. 1996).
Realization of the ICRS at optical wavelengths is given by the HIPPARCOS Celestial Reference Frame
(HCRF), whose principal axes coincide with those of the ICRF at the level of ![]() 0.6 mas at J1991.25
with no global rotation at the level of
0.6 mas at J1991.25
with no global rotation at the level of ![]() 0.25 mas/year (Kovalevsky et al. 1997). Due to the relatively low
density of objects in the HCRF (about 3 objects per square degree), its densification is important to
make access to the frame easier. Many authors (e.g. Monet et al. 1998; Camargo et al. 2001; Urban et al. 1998; Monet et al. 2003; Camargo et al. 2003; Rapaport et al. 2001; Zacharias et al. 2000) have
contributed to this densification from ground-based astrometry. The most recent achievement is the
second US Naval Observatory (USNO) CCD Astrographic Catalogue (UCAC2) with positions
and proper motions of about 48 million objects in the declination range
0.25 mas/year (Kovalevsky et al. 1997). Due to the relatively low
density of objects in the HCRF (about 3 objects per square degree), its densification is important to
make access to the frame easier. Many authors (e.g. Monet et al. 1998; Camargo et al. 2001; Urban et al. 1998; Monet et al. 2003; Camargo et al. 2003; Rapaport et al. 2001; Zacharias et al. 2000) have
contributed to this densification from ground-based astrometry. The most recent achievement is the
second US Naval Observatory (USNO) CCD Astrographic Catalogue (UCAC2) with positions
and proper motions of about 48 million objects in the declination range
![]() to
to
![]() (Zacharias et al. 2004).
(Zacharias et al. 2004).
In the GAIA perspective, a prime realization of the ICRS at optical wavelengths may also be considered.
Within this scenario, the coincidence between the optical and radio frames is a natural concern.
Detailed imaging in the visible range of sources as faint as V=18-20, a magnitude range that includes a
large number of quasars, is out of reach for the ground-based optical interferometers that are being built.
The near-IR range is currently privileged for this task. With large optical telescopes and spatial
phase-referenced imaging, objects as faint as
![]() may be detectable in the future
(Daigne & Lestrade 2003; Glindemann et al. 2003), so that an image resolution of some few mas will be possible for these objects.
In this respect, single-dish astrometry of quasar fields in near-IR photometric bands
is important for evaluating the feasibility of imaging with near-IR interferometry and for selecting
initial candidates to the optical extension of the ICRF. Additionally, as compared to
observations in the visible range, near-IR ones benefit from less atmospheric disturbances
(scintillations, chromatic refraction) and lower Galactic extinction.
may be detectable in the future
(Daigne & Lestrade 2003; Glindemann et al. 2003), so that an image resolution of some few mas will be possible for these objects.
In this respect, single-dish astrometry of quasar fields in near-IR photometric bands
is important for evaluating the feasibility of imaging with near-IR interferometry and for selecting
initial candidates to the optical extension of the ICRF. Additionally, as compared to
observations in the visible range, near-IR ones benefit from less atmospheric disturbances
(scintillations, chromatic refraction) and lower Galactic extinction.
In this context, we conducted a pilot observing program of thirty ICRF quasars in the near-IR range with the ESO NTT in January 2003, as further described in the next section. Data processing and analysis are detailed in Sect. 3. Much effort was devoted to the astrometric reduction, first with an estimate of the camera field distortion and then with a global reduction of the observations in an extended-field mode (mosaics of overlapping images for fourteen ICRF quasars). Photometric results are given in Sect. 4 and astrometric results in Sect. 5. Discussion and concluding remarks are given in Sects. 6 and 7, respectively.
Our near-IR observations were carried out with the 3.5 m ESO NTT/SOFI located at La Silla,
![]() W
W
![]() S,
during a 3-night run from 8 to 11 January 2003. Overall, a total of thirty ICRF quasars were observed
generally when close to the local meridian, in order to minimize
all systematic effects due to large airmass. The targets were selected according to two criteria:
(i) the existence of a probable optical counterpart in the R band, as available in the USNOA-2.0
catalogue, and (ii) the existence of a sufficient number of UCAC reference stars in their
vicinity. The second criterion was achieved by observing at low Galactic latitudes; see the sky
distribution of the targets in Fig. 1. Furthermore, the declination range was limited to
S,
during a 3-night run from 8 to 11 January 2003. Overall, a total of thirty ICRF quasars were observed
generally when close to the local meridian, in order to minimize
all systematic effects due to large airmass. The targets were selected according to two criteria:
(i) the existence of a probable optical counterpart in the R band, as available in the USNOA-2.0
catalogue, and (ii) the existence of a sufficient number of UCAC reference stars in their
vicinity. The second criterion was achieved by observing at low Galactic latitudes; see the sky
distribution of the targets in Fig. 1. Furthermore, the declination range was limited to
![]() due to the sky coverage of the UCAC1 (Zacharias et al. 2000), since the UCAC2 was not
available at the time the proposal for these near-IR observations was submitted to the ESO.
due to the sky coverage of the UCAC1 (Zacharias et al. 2000), since the UCAC2 was not
available at the time the proposal for these near-IR observations was submitted to the ESO.
The SOFI instrument was used in its large field configuration with a resolution of 0.288''/pixel and an image size of
![]() .
All quasars
.
All quasars![]() were observed in a so-called "photometry'' mode, where single images
centered on the quasar positions were taken in each of the three near-IR photometric broad-band
filters J, H, and
were observed in a so-called "photometry'' mode, where single images
centered on the quasar positions were taken in each of the three near-IR photometric broad-band
filters J, H, and ![]() ,
the same as those of the Two Micron All-Sky Survey (2MASS),
thus permitting proper calibration of our photometric measurements.
,
the same as those of the Two Micron All-Sky Survey (2MASS),
thus permitting proper calibration of our photometric measurements.
Due to the limited duration of our observing run, only fourteen quasars were observed in a so-called
"astrometry'' mode, which consists in observing extended fields centered on the
quasar position. With a mosaic of 4 or 5 overlapping images, the field size was about twice that of a
single-image area. The number of reference stars was larger, so positioning an extragalactic
object in the UCAC2 stellar frame should be improved. Observations in the astrometry mode were
performed with a narrow H-band filter![]() (
(
![]() m) to
prevent saturation of the brightest reference stars. This filter is labelled "F'' hereafter.
m) to
prevent saturation of the brightest reference stars. This filter is labelled "F'' hereafter.
Additionally, a dense stellar field (labelled 21 in Fig. 1) was also observed to
determine the field distortion pattern (FDP) of the SOFI camera. This field comprised a mosaic of nine
overlapping frames in the F filter only at low Galactic latitude (
![]() and
and
![]() ). All fields were observed with jitter offsets
(see Hainaut et al. 2002, for further details) within a 10'' radius circle and an exposure
time of 30 s per frame. Observations in each of the three broad-band J, H, and
). All fields were observed with jitter offsets
(see Hainaut et al. 2002, for further details) within a 10'' radius circle and an exposure
time of 30 s per frame. Observations in each of the three broad-band J, H, and ![]() filters were
performed with seven jittered frames per image for a total exposure of 210 s. Observations in the
narrow-band filter F were performed with 10 jittered frames for a total exposure of 300 s.
filters were
performed with seven jittered frames per image for a total exposure of 210 s. Observations in the
narrow-band filter F were performed with 10 jittered frames for a total exposure of 300 s.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2426f1}
\end{figure}](/articles/aa/full/2005/27/aa2426-04/Timg18.gif) |
Figure 1: Sky distribution of the observed ICRF quasars in equatorial coordinates. Each quasar is identified by an internal identification number listed in Col. 11 of Table 2. The dotted line indicates the Galactic equator. |
The data analysis was carried out with the software ECLIPSE using the routine "jitter''
(Devillard 1999) to perform sky subtraction and co-addition of the jittered frames, in order to
obtain a final single-image in each filter. These single images were then treated with the
DAOPHOT II package, to determine instrumental magnitudes and coordinates (x, y)
for each detected object. The detection threshold was 7 times the rms value of background
fluctuations (sky and readout noise). The coordinates (x, y) were determined by fitting
a Moffat function of the form
![]() to the observed star profiles.
In this function,
to the observed star profiles.
In this function, ![]() and
and
![]() ,
as given by Stetson (2000). The three parameters
,
as given by Stetson (2000). The three parameters
![]() were adjusted in each image from a sub-sample of about 20 bright stars.
The estimated diameter (FWHM) of the model point-spread function was generally in the range
0.7''-0.8'' during the three nights. The
were adjusted in each image from a sub-sample of about 20 bright stars.
The estimated diameter (FWHM) of the model point-spread function was generally in the range
0.7''-0.8'' during the three nights. The ![]() value of the fit
obtained for each object, generally in the range 0.6-2.5, is further used as a weighing function in
the astrometric reduction (Sect. 3.2).
value of the fit
obtained for each object, generally in the range 0.6-2.5, is further used as a weighing function in
the astrometric reduction (Sect. 3.2).
The magnitudes were determined by finding the zero-points of each image for each filter. Each zero-point
was calculated as the weighted mean of the differences between the instrumental and 2MASS magnitudes.
An iterative procedure was used to eliminate 3-![]() discrepant data and
stopped when no further elimination was necessary.
discrepant data and
stopped when no further elimination was necessary.
The final precision of the magnitude is then given by
The initial astrometric reduction was carried out by using a linear model for the transformation
between the measured pixel coordinates (xi, yi) of the reference stars and their standard
coordinates (![]() ,
,
![]() ):
):
Coefficients (
a1,b1,c1) and (
a2,b2,c2) in Eq. (2) were derived from
a weighted least squares fit to the reference star coordinates. The weight for each star i was
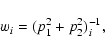 |
(3) |
The transformation given by Eq. (2) was a first approach to astrometric reduction of the
SOFI images. Clearly, corrections for an FDP have to be performed, in order to eliminate biases on the
image coordinates. The dependence on the position in the image of the Observed minus Calculated (![]() )
differences for the reference stars can be used to characterize the FDP. The effect of the FDP can
then be seen through such systematic
)
differences for the reference stars can be used to characterize the FDP. The effect of the FDP can
then be seen through such systematic ![]() deviations, as e.g. those shown in the upper right panel of Fig. 2.
deviations, as e.g. those shown in the upper right panel of Fig. 2.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{2426f3}
\end{figure}](/articles/aa/full/2005/27/aa2426-04/Timg36.gif) |
Figure 3:
Relative positions of the 9 mosaic images used for the FDP analysis. Each
image is identified with a number. The total area is
|
| 0.3487 | 0.2974 | 0.0830 | -0.0948 | -0.3280 |
| 0.2242 | 0.2672 | 0.1491 | -0.1421 | -0.2748 |
| 0.1527 | 0.2257 | 0.1972 | -0.1207 | -0.2411 |
| -0.0153 | 0.1485 | -0.0033 | -0.0612 | -0.2045 |
| -0.1166 | -0.0813 | 0.0865 | -0.0800 | -0.1114 |
| -0.4076 | -0.3691 | -0.2566 | -0.2334 | -0.2275 |
| -0.1874 | -0.2350 | -0.1902 | -0.0646 | -0.0284 |
| 0.0268 | 0.0805 | 0.0939 | 0.2191 | 0.2306 |
| -0.0196 | 0.0982 | 0.2612 | 0.3134 | 0.3001 |
| -0.0872 | -0.0415 | 0.0983 | 0.2134 | 0.2173 |
|
All values are expressed in pixel units, with the bottom leftmost elements of the matrices corresponding to the bottom leftmost corner of the image. |
The corrections for the FDP were determined from a mosaic of 9 overlapping images (see Fig. 3) observed in the F filter. The basic idea was to use the overlap to compare the positions of the same object as measured in different positions on the camera and then to determine systematic position shifts according to the location on the respective image area.
The initial astrometric reduction was first performed independently for each image as indicated above,
in order to have initial spherical coordinates for each star. Then, new standard coordinates
![]() were determined for every star i in image j, using the centre of Image 5 (see Fig. 3) as the tangential point of the gnomonic projection,
so that these new standard coordinates are on the plane given by the projection of Image 5. Relative
rotations between them were previously corrected. Relative corrections for each star position were
then derived as
were determined for every star i in image j, using the centre of Image 5 (see Fig. 3) as the tangential point of the gnomonic projection,
so that these new standard coordinates are on the plane given by the projection of Image 5. Relative
rotations between them were previously corrected. Relative corrections for each star position were
then derived as
The SOFI image was partitioned into a mosaic of ![]() tiles with
tiles with
![]() pixels each. The
average of the relative corrections in each tile defines the local FDP effect. In practice, the FDP is
represented by two
pixels each. The
average of the relative corrections in each tile defines the local FDP effect. In practice, the FDP is
represented by two ![]() matrices Mx and My with coefficients defined as
matrices Mx and My with coefficients defined as
| Literature data | Observational data | ||||||||||||||||||
| Magnitude | Flux | ||||||||||||||||||
| ICRF | c | z | 6 cm |
|
Type | MB | B | V | R | IntID | MJD | J | H | J | H |
|
|||
| name | |||||||||||||||||||
| 0312-770 | C | 0.223 | 0.56 | 0.3 | Gal | -24.5 | 15.93 | 16.1 | 15.3 | 01a | 52 648.02 | 14.67 | 14.04 | 13.06 | 2.22 | 2.55 | 3.97 | 0.26 | |
| 0431-512 | C | 0.557 | 0.59 | Quasar | -24.7 | 17.43 | 18.0 | 18.4 | 03p | 52 649.02 | 16.88 | 16.03 | 15.17 | 0.29 | 0.40 | 0.57 | 0.01 | ||
| 0511-220 | C | 1.296 | 0.87 | 0.1 | Quasar | -25.4 | 19.34 | 19.5 | 19.6 | 04p | 52 650.05 | 18.83 | 17.72 | 17.04 | 0.05 | 0.09 | 0.10 | 0.01 | |
| 0521-365 | D | 0.055 | 8.89 | BL Lac | - | 12.15 | 14.6 | 11.4 | 07p | 52 650.03 | 13.10 | 12.30 | 11.54 | 9.40 | 12.60 | 16.14 | 0.12 | ||
| 0530-727 | D | - | - | - | - | - | 18.85 | - | 18.0 | 08p | 52 648.05 | 16.39 | 15.41 | 14.47 | 0.46 | 0.72 | 1.08 | 0.01 | |
| 0528-250 | O | 2.765 | 0.85 | Quasar | -29.0 | 18.01 | 17.3 | 17.3 | 09a | 52 649.04 | 16.09 | 15.71 | 15.39 | 0.60 | 0.55 | 0.47 | 0.44 | 0.01 | |
| 0537-286 | D | 3.104 | 1.23 | 0.5 | Quasar | -27.7 | 19.72 | 20.0 | 19.0 | 10a | 52 650.07 | 17.76 | 16.94 | 16.24 | 0.13 | 0.18 | 0.21 | 0.01 | |
| 0614-349 | C | - | - | Other | - | 19.98 | 18.0 | 16.8 | 11p | 52 649.10 | 17.67 | 16.84 | 16.07 | 0.14 | 0.19 | 0.25 | 0.00 | ||
| 0622-441 | C | 0.688 | 0.89 | 0.2 | Quasar | -26.1 | 16.36 | 16.9 | 16.7 | 13p | 52 650.10 | 15.81 | 15.09 | 14.28 | 0.78 | 0.97 | 1.30 | 0.03 | |
| 0629-418 | D | 1.416 | 0.74 | 0.5 | Quasar | -26.0 | 18.18 | 19.3 | 18.2 | 14a | 52 649.11 | 17.55 | 16.72 | 16.41 | 0.16 | 0.22 | 0.18 | 0.03 | |
| 0637-752 | D | 0.654 | 6.19 | Gal | -27.0 | 16.00 | 15.8 | 15.8 | 15p | 52 650.12 | 14.82 | 14.31 | 13.60 | 1.92 | 1.98 | 2.43 | 0.11 | ||
| 0646-306 | C | 0.455 | * | 0.2 | Quasar | -24.2 | 19.10 | * | 18.8 | 17a | 52 648.09 | 16.90 | 15.93 | 15.02 | 0.28 | 0.44 | 0.66 | 0.00 | |
| 0700-465 | C | * | * | 0.3 | - | -24.3 | 18.57 | * | 19.4 | 19a | 52 649.15 | 15.67 | 14.82 | 13.94 | 0.88 | 1.23 | 1.76 | 0.02 | |
| 0700-465 | C | * | * | 0.3 | - | -24.3 | 18.57 | * | 19.4 | 19a | 52 650.19 | 16.10 | 15.27 | 14.36 | 0.59 | 0.82 | 1.20 | 0.02 | |
| 0743-673 | C | 1.510 | 1.96 | Quasar | -28.6 | 16.15 | 16.4 | 15.9 | 23a | 52 648.17 | 14.94 | 14.30 | 14.10 | 1.72 | 2.00 | 1.53 | 0.21 | 0.22 | |
| 0809-493 | C | - | - | - | - | 21.40 | - | - | 24p | 52 650.30 | 19.29 | 18.32 | 17.28 | 0.03 | 0.05 | 0.08 | 0.00 | ||
| 0823-500 | C | - | - | - | - | - | - | - | - | 25p | 52 648.20 | 18.14 | 17.06 | 16.30 | 0.09 | 0.16 | 0.20 | 0.02 | |
| 0823-223 | C | >0.910 | 0.78 | 0.5 | BL Lac | - | 15.88 | 16.2 | 15.8 | 26a | 52 649.18 | 14.22 | 13.31 | 12.47 | 3.35 | 4.98 | 6.87 | 0.09 | |
| 0834-201 | D | 2.752 | 3.42 | Quasar | -27.9 | 19.09 | 19.4 | 18.8 | 30p | 52 650.23 | 17.30 | 16.78 | 16.27 | 0.20 | 0.20 | 0.21 | 0.00 | ||
| 0842-754 | C | 0.524 | 1.38 | Gal | -24.2 | 18.03 | 18.9 | 17.0 | 31p | 52 650.32 | 16.76 | 15.94 | 15.16 | 0.32 | 0.44 | 0.58 | 0.00 | ||
| 0919-260 | O | 2.300 | 2.38 | 0.2 | Quasar | -27.7 | 18.63 | 18.4 | 18.0 | 32p | 52 650.24 | 16.45 | 15.89 | 15.16 | 0.43 | 0.46 | 0.58 | 0.02 | |
| 0920-397 | C | 0.591 | 1.51 | Quasar | -24.4 | 18.54 | 18.8 | 17.7 | 33p | 52 649.23 | 16.02 | 15.23 | 14.49 | 0.64 | 0.85 | 1.07 | 0.01 | ||
| 0925-203 | C | 0.348 | 0.69 | Gal | -25.3 | 16.34 | 16.4 | 16.0 | 34p | 52 649.21 | 15.48 | 14.74 | 14.02 | 1.04 | 1.33 | 1.64 | 0.01 | ||
| 1048-313 | C | * | * | - | -25.7 | - | * | - | 38p | 52 649.25 | 18.29 | 17.43 | 16.88 | 0.08 | 0.11 | 0.12 | 0.01 | ||
| 1101-325 | C | 0.354 | 0.73 | Gal | -25.5 | 17.11 | 16.3 | 15.5 | 39p | 52 649.27 | 14.74 | 14.09 | 13.18 | 2.07 | 2.43 | 3.57 | 0.18 | ||
| 1101-536 | C | - | - | - | Quasar | - | 17.82 | 17.9 | 16.4 | 40a | 52 648.22 | 14.84 | 13.83 | 12.82 | 1.90 | 3.09 | 4.96 | 0.01 | |
| 1104-445 | O | 1.598 | 2.03 | 0.1 | Quasar | -26.8 | 17.45 | 18.2 | 17.4 | 41a | 52 648.25 | 16.20 | 15.39 | 15.07 | 0.54 | 0.73 | 0.62 | 0.09 | |
| 1105-680 | C | 0.588 | 1.37 | 0.3 | Quasar | -23.6 | 17.89 | 18.4 | 17.9 | 42a | 52 648.28 | 16.24 | 15.50 | 14.77 | 0.52 | 0.66 | 0.82 | 0.00 | |
| 1116-462 | C | 0.713 | 1.31 | Quasar | -26.0 | 17.25 | 17.0 | 16.5 | 43a | 52 648.32 | 15.79 | 15.41 | 14.55 | 0.79 | 0.72 | 1.01 | 0.10 | ||
| 1116-462 | C | 0.713 | 1.31 | Quasar | -26.0 | 17.25 | 17.0 | 16.5 | 43a | 52 650.35 | 15.81 | 15.40 | 14.51 | 0.77 | 0.72 | 1.05 | 0.11 | ||
| 1129-580 | C | - | - | - | - | - | 18.92 | - | 17.7 | 44a | 52 649.33 | 15.73 | 15.01 | 14.39 | 0.83 | 1.04 | 1.17 | 0.03 | |
| 1144-379 | C | 1.048 | 2.22 | BL Lac | -27.7 | 17.23 | 16.2 | 16.7 | 46a | 52 649.29 | 15.97 | 15.14 | 14.14 | 0.67 | 0.92 | 1.47 | 0.05 | ||
|
Column 1: ICRF quasar identification; Col. 2: source category in the ICRF: Defining, Candidate or Other;
Col. 3: redshift as given either by Archinal et al. (1997) or by the Veron-Cetty & Veron catalogue
(Veron-Cetty & Veron 2003) (*); Col. 4: flux [Jy] at 6 cm as given either by Archinal et al. (1997) or by the Veron-Cetty & Veron
catalogue (*); Col. 5: radio spectral index as given by Archinal et al. (1997); Col. 6: object type as given by Archinal et al. (1997); Col. 7: absolute B magnitude as given by the Veron-Cetty & Veron catalogue; Col. 8: B magnitude
as given by the USNOB-1 catalogue (Monet et al. 2003); Col. 9: V magnitude as given either by Archinal et al. (1997) or by
the Veron-Cetty & Veron catalogue (*); Col. 10: R magnitude as given by the USNOB-1 catalogue;
Col. 11: internal identification - "p'' for photometry mode, and "a'' for astrometry mode; Col. 12:
Modified Julian Date of the observation; Cols. 13-15: Observed J, H, and |
As mentioned above, fourteen ICRF quasars were observed in the "astrometry'' mode, that is, with three or four additional images shifted with respect to the central one. The offsets are about half a single-image size, so that the extended field benefits from overlapping zones. This observing mode contributes to weakening the influence of positional errors of reference stars. It also brings some improvement when reference stars are not uniformly distributed over each image. With four offset images, the overall field is about twice as large as that of a single image.
The astrometric reduction of these extended fields was performed by using a global technique (Eichhorn 1960), also known as Block-Adjustment Method, similar to that used in the reduction of the Cape Photographic Catalogue plates (Zacharias 1988). Overall, this technique returns a set of positions in an essentially instrumental system, which should be aligned to the axes defined by a given reference frame afterwards. In this way, it is possible to benefit from a larger number of reference stars, while retaining the intrinsic imaging qualities of the instrument. This reduction method will not be explained further here, as it has been extensively described elsewhere (Teixeira et al. 1992,1998). The application of this technique to extend a CCD field of view is also discussed in Yu et al. (2004).
Table 2 presents the photometric results obtained for our thirty ICRF quasars,
along with further information available for these objects as retrieved from the literature. The detection
threshold in the three near-IR photometric bands was J=20.8, H=19.8 and
![]() .
All thirty
quasars were detected in the three bands, and their magnitude distribution is shown in Fig. 5.
With such a magnitude distribution, 17 quasars are not found in the 2MASS catalogue within a search radius
of 1'' around the ICRF position. This figure goes down to 10 with a 5'' search
radius.
The magnitude precision, as derived from Eq. (1), is plotted in Fig. 6.
The average precision is 0.037, 0.035, and 0.040 mag for the J, H, and
.
All thirty
quasars were detected in the three bands, and their magnitude distribution is shown in Fig. 5.
With such a magnitude distribution, 17 quasars are not found in the 2MASS catalogue within a search radius
of 1'' around the ICRF position. This figure goes down to 10 with a 5'' search
radius.
The magnitude precision, as derived from Eq. (1), is plotted in Fig. 6.
The average precision is 0.037, 0.035, and 0.040 mag for the J, H, and ![]() filters,
respectively.
filters,
respectively.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2426f5}
\end{figure}](/articles/aa/full/2005/27/aa2426-04/Timg53.gif) |
Figure 5:
Distribution of the observed quasar magnitudes in the three near-IR
bands (full line: J, dotted line: H, dashed line: |
Near-IR spectral indices ![]() ,
defined as
,
defined as
![]() ,
were inferred from the observed
fluxes in the J, H, and
,
were inferred from the observed
fluxes in the J, H, and ![]() filters. These range from -1.8 to +0.4 with a
mean value of about -1. We stress that these spectral indices do not refer to the emitted (rest-frame)
frequencies
filters. These range from -1.8 to +0.4 with a
mean value of about -1. We stress that these spectral indices do not refer to the emitted (rest-frame)
frequencies ![]() from the quasars.
The near-IR spectral indices are plotted in Fig. 7 as a function of the spectral indices in the
radio range for these objects (see Table 2). The absence of significant correlation between the
two sets of spectral indices has to be noticed.
from the quasars.
The near-IR spectral indices are plotted in Fig. 7 as a function of the spectral indices in the
radio range for these objects (see Table 2). The absence of significant correlation between the
two sets of spectral indices has to be noticed.
Spectral energy distribution (SED) was estimated from the data in Table 2, considering radio, near-IR, and visible measurements. When available, flux at 11 cm or 15 cm as given by Archinal et al. (1997) was also used. The SEDs for all objects are available in the electronic version of this paper (Figs. 12 to 26). They show large amounts of energy being emitted in radio, near-IR, and optical wavelengths, as one would expect for AGNs. We stress that the radio and visible flux information do not correspond to the same epochs as the near-IR ones.
| ICRF | MJD |
|
|
|
|
|
|
|
|
N |
| name | ||||||||||
| 0312-770 | 52 648.02 | -23 | 21 | 47 | 21 | 10 | 5 | 47 | 11 | 5 |
| 0431-512 | 52 649.02 | -238 | 183 | 333 | 174 | 24 | 11 | 0 | 0 | 3 |
| 0511-220 | 52 650.05 | -56 | 47 | 141 | 61 | 11 | 3 | 0 | 0 | 3 |
| 0521-365 | 52 650.03 | -36 | 27 | -21 | 27 | 10 | 12 | 9 | 35 | 5 |
| 0530-727 | 52 648.05 | 43 | 44 | 5 | 46 | 6 | 5 | 79 | 27 | 4 |
| 0528-250 | 52 649.04 | -7 | 10 | 5 | 10 | 4 | 4 | 24 | 38 | 6 |
| 0537-286 | 52 650.07 | 17 | 9 | -14 | 9 | 6 | 6 | 45 | 37 | 7 |
| 0614-349 | 52 649.10 | 107 | 20 | -190 | 19 | 18 | 15 | 11 | 105 | 4 |
| 0622-441 | 52 650.10 | 38 | 32 | 43 | 34 | 8 | 7 | 47 | 32 | 4 |
| 0629-418 | 52 649.11 | 1 | 22 | -8 | 18 | 18 | 12 | 13 | 9 | 4 |
| 0637-752 | 52 650.12 | -27 | 14 | 3 | 14 | 5 | 4 | 90 | 37 | 6 |
| 0646-306 | 52 648.09 | -99 | 10 | -21 | 10 | 4 | 3 | 154 | 33 | 6 |
| 0700-465 | 52 649.15 | 12 | 6 | -23 | 5 | 6 | 16 | 28 | 39 | 9 |
| 0700-465 | 52 650.19 | 12 | 6 | -23 | 5 | 6 | 16 | 31 | 26 | 10 |
| 0743-673 | 52 648.17 | 123 | 12 | -43 | 15 | 2 | 3 | 53 | 84 | 8 |
| 0809-493 | 52 650.30 | 24 | 8 | -34 | 8 | 5 | 16 | 52 | 48 | 14 |
| 0823-500 | 52 648.20 | 34 | 16 | -10 | 17 | 4 | 6 | 56 | 71 | 11 |
| 0823-223 | 52 649.18 | -25 | 11 | 21 | 11 | 5 | 8 | 60 | 122 | 18 |
| 0834-201 | 52 650.23 | 38 | 16 | 56 | 16 | 5 | 10 | 40 | 53 | 14 |
| 0842-754 | 52 650.32 | 18 | 12 | 31 | 13 | 8 | 5 | 50 | 43 | 15 |
| 0919-260 | 52 650.24 | 53 | 11 | -53 | 11 | 6 | 1 | 42 | 46 | 9 |
| 0920-397 | 52 649.23 | 45 | 7 | 27 | 6 | 13 | 4 | 56 | 61 | 18 |
| 0925-203 | 52 649.21 | -28 | 20 | 44 | 19 | 2 | 3 | 44 | 14 | 5 |
| 1048-313 | 52 649.25 | 41 | 12 | -41 | 12 | 8 | 14 | 58 | 28 | 6 |
| 1101-325 | 52 649.27 | -13 | 25 | -58 | 20 | 8 | 4 | 86 | 102 | 4 |
| 1101-536 | 52 648.22 | 52 | 6 | 9 | 6 | 2 | 6 | 60 | 65 | 27 |
| 1104-445 | 52 648.25 | -32 | 19 | 18 | 21 | 6 | 4 | 42 | 43 | 7 |
| 1105-680 | 52 648.28 | 25 | 5 | -10 | 5 | 3 | 7 | 51 | 50 | 33 |
| 1116-462 | 52 648.32 | 35 | 4 | -57 | 4 | 18 | 6 | 43 | 53 | 9 |
| 1116-462 | 52 650.35 | 35 | 4 | -57 | 4 | 18 | 6 | 48 | 50 | 13 |
| 1129-580 | 52 649.33 | -15 | 6 | -6 | 6 | 8 | 6 | 59 | 52 | 22 |
| 1144-379 | 52 649.29 | 4 | 16 | -49 | 15 | 7 | 7 | 53 | 30 | 6 |
|
All positional derived data are given in milliarcseconds [mas]. All ICRF positions are taken
from Ma et al. (1998).
|
| Single-image | Mosaic | |||||||||||||||||
|
|
||||||||||||||||||
| ICRF | MJD |
|
|
|
|
N |
|
|
|
|
N |
|
|
|
|
|||
| name | ||||||||||||||||||
| mas | mas | mas | ||||||||||||||||
| 0312-770 | 52 648.02 | -5 | 37 | 54 | 37 | 5 | -41 | 18 | 11 | 23 | 10 | 53 | 91 | 58 | 33 | 1.18 | 0.72 | |
| 0528-250 | 52 649.04 | -4 | 17 | -4 | 17 | 6 | 4 | 11 | -11 | 10 | 14 | 31 | 20 | 20 | 35 | 0.53 | 1.00 | |
| 0537-286 | 52 650.07 | 35 | 18 | 14 | 16 | 7 | 28 | 13 | 31 | 12 | 11 | 26 | 23 | 47 | 36 | 1.18 | 0.92 | |
| 0629-418 | 52 649.11 | 38 | 39 | 31 | 33 | 4 | 30 | 9 | -4 | 9 | 20 | 40 | 25 | 37 | 26 | 0.97 | 0.67 | |
| 0646-306 | 52 648.09 | -132 | 26 | 8 | 26 | 6 | -44 | 7 | 9 | 6 | 31 | 35 | 36 | 35 | 33 | 1.00 | 1.03 | |
| 0700-465 | 52 649.15 | 21 | 24 | -17 | 23 | 9 | -3 | 11 | -1 | 9 | 23 | 38 | 27 | 46 | 33 | 0.92 | 0.80 | |
| 0700-465 | 52 650.19 | 18 | 18 | -3 | 18 | 10 | 8 | 12 | -1 | 11 | 22 | 26 | 27 | 57 | 61 | 1.00 | 1.17 | |
| 0743-673 | 52 648.17 | 128 | 22 | -45 | 27 | 8 | 112 | 13 | 23 | 14 | 19 | 29 | 31 | 44 | 38 | 0.81 | 0.63 | |
| 0823-223 | 52 649.18 | -31 | 22 | 48 | 22 | 18 | -28 | 9 | 25 | 10 | 46 | 26 | 28 | 57 | 69 | 0.90 | 1.06 | |
| 1101-536 | 52 648.22 | 46 | 11 | 17 | 11 | 27 | 33 | 6 | 36 | 6 | 81 | 25 | 21 | 46 | 73 | 0.96 | 1.46 | |
| 1104-445 | 52 648.25 | -42 | 34 | 25 | 38 | 7 | 8 | 8 | 9 | 8 | 32 | 30 | 23 | 49 | 53 | 1.11 | 1.26 | |
| 1105-680 | 52 648.28 | 32 | 8 | 29 | 8 | 33 | 25 | 5 | 4 | 5 | 88 | 27 | 27 | 67 | 54 | 1.46 | 1.20 | |
| 1116-462 | 52 648.32 | 46 | 22 | -52 | 22 | 9 | 22 | 7 | -42 | 7 | 42 | 25 | 25 | 39 | 53 | 0.93 | 1.23 | |
| 1116-462 | 52 650.35 | 40 | 21 | -28 | 21 | 13 | 18 | 7 | -26 | 7 | 42 | 26 | 30 | 45 | 51 | 1.07 | 1.19 | |
| 1129-580 | 52 649.33 | -43 | 13 | 33 | 13 | 22 | -30 | 4 | 14 | 4 | 131 | 30 | 26 | 54 | 56 | 1.10 | 1.10 | |
| 1144-379 | 52 649.29 | 12 | 30 | -29 | 27 | 6 | 28 | 13 | -51 | 11 | 16 | 30 | 29 | 39 | 43 | 0.76 | 1.02 | |
|
All positional derived data are given in milliarcseconds [mas]. All ICRF positions are taken
from Ma et al. (1998). |
Our astrometric results are presented in Tables 3 and 4, respectively obtained with the single-image analysis of all observed quasar fields and with the mosaics of overlapping images of fourteen selected quasar fields, with two of them observed twice.
Table 3 summarizes the astrometric results obtained from the analysis of single images (photometry mode). Figure 8 plots positional differences before and after the correction for the FDP (left and right panels, respectively). A better agreement with ICRF positions is clearly obtained after the correction for the FDP with larger improvement in declination.
The rms of the FDP-corrected positional differences is 35 mas in right ascension and
34 mas in declination, not considering the Fields 3, 4, 11, and 23, which show large discrepancies.
The mean of these differences is ![]() mas and
mas and ![]() mas in right ascension and
declination, respectively. Thus, no significant overall shift is present. These results are
comparable to those presented in Assafin et al. (2003), obtained from the
observations of 172 ICRF quasar fields with the Cerro Tololo Inter-American Observatory (CTIO) 0.9 m
astrograph. The latter had
mas in right ascension and
declination, respectively. Thus, no significant overall shift is present. These results are
comparable to those presented in Assafin et al. (2003), obtained from the
observations of 172 ICRF quasar fields with the Cerro Tololo Inter-American Observatory (CTIO) 0.9 m
astrograph. The latter had
![]() fields, corresponding to four times the
area of a NTT/SOFI field. It will be shown that better results are obtained from the NTT/SOFI when
similar field sizes are involved.
fields, corresponding to four times the
area of a NTT/SOFI field. It will be shown that better results are obtained from the NTT/SOFI when
similar field sizes are involved.
Figure 9 shows the moduli of the positional differences as a function of the ![]() magnitude. It is found that positions of similar quality are obtained over the whole magnitude
range.
magnitude. It is found that positions of similar quality are obtained over the whole magnitude
range.
An important indicator of the achievable quality of the measurements is the internal coherence between the three photometric bands. As indicated in Cols. 7 and 8 of Table 3, this coherence is generally better than 10 mas. Thus, the NTT/SOFI appears to be an excellent instrument for narrow field astrometry.
Table 4 summarizes the astrometric results derived from analysis of the fields
observed in astrometry mode. As noticed in this table, improved quasar positions have been obtained, as compared to those from the single-image analysis (Cols. 3 and 5 versus Cols. 8 and 10).
This table also shows that external astrometric errors are dominated by the positional uncertainties of the reference stars (Cols. 17 and 18). A plot comparing the near-IR and ICRF positional
differences obtained from the two analyses is shown in Fig. 10. From the mosaics, the mean of
these differences is ![]() mas in right ascension and
mas in right ascension and ![]() mas in declination. These shifts are
smaller than those found in the single-image analysis.
mas in declination. These shifts are
smaller than those found in the single-image analysis.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{2426f8a}\hspace*{4mm}
\includegraphics[width=6.5cm,clip]{2426f8b}
\end{figure}](/articles/aa/full/2005/27/aa2426-04/Timg78.gif) |
Figure 8:
Differences in the sense near-IR minus ICRF, before ( left panel)
and after ( right panel) correcting for the FDP. The near-IR positions are the mean of
the J, H, and |
The rms of the differences between near-IR and ICRF positions is also printed in both panels of Fig. 10. As expected, these values are smaller for the mosaics, since they benefit from a larger number of reference stars than the single images. However, the gain factor is smaller than the square root of the increased number of reference stars (factors of 1.32 and 1.24 in right ascension and declination, respectively, instead of about 1.4). This may result from systematic offsets in the UCAC2.
Columns 13 to 16 of Table 4 show that the positional internal coherence of the measurements within the images is frequently better than the agreement with the UCAC2 at the observation epoch. The same conclusion is also inferred from Cols. 17 and 18 of the same table. This implies that the measurement uncertainties are smaller than the nominal uncertainties of the reference stars.
Bearing this in mind, we applied the astrometric analysis given by Eq. (2) only to the central images in the F filter of each of the fourteen fields observed in the astrometry mode. Reference star positions were previously modified according to the corrections obtained from analysis of the mosaics. The derived rms of the positional differences near-IR minus radio for the observed ICRF quasars were 27 and 28 mas in right ascension and declination, respectively, excluding Fields 17 and 23. As expected, these values are better than those previously obtained from the concerned single images (33 and 31 mas, respectively). This indicates good performance of the FDP model and also that the positions of the reference stars are improved on the average.
Taking these corrections into consideration, the dispersion of the ![]() differences is naturally
attenuated, and it becomes easier to visualise the FDP effects. This is illustrated in Fig. 11,
which shows the uncorrected and the FDP-corrected positional scatter in the same way as originally in
Figs. 2 and 4.
The pattern shown in the left panel of Fig. 11 is the intrinsic FDP effect. The right panel shows more clearly that most of its signature was eliminated.
differences is naturally
attenuated, and it becomes easier to visualise the FDP effects. This is illustrated in Fig. 11,
which shows the uncorrected and the FDP-corrected positional scatter in the same way as originally in
Figs. 2 and 4.
The pattern shown in the left panel of Fig. 11 is the intrinsic FDP effect. The right panel shows more clearly that most of its signature was eliminated.
0431-512 (03p) Only three reference stars. Quasar not detected in the F filter.
0511-220 (04p) Only three reference stars. Quasar not detected in the F filter.
0530-727 (08p) Only four reference stars.
0614-349 (11p) Only four reference stars. A high value obtained to the ![]() fit parameter
from DAOPHOT II indicates that the PSF profile fit to this source did not work well. This object is
classified as "Pair of Galaxies'' in the SIMBAD database. Its ICRF positional precision is 66 mas in
fit parameter
from DAOPHOT II indicates that the PSF profile fit to this source did not work well. This object is
classified as "Pair of Galaxies'' in the SIMBAD database. Its ICRF positional precision is 66 mas in
![]() and 39 mas in
and 39 mas in ![]() .
.
0622-441 (13p) Only four reference stars.
0646-306 (17a) The significant difference
![]() obtained from
the single-image reduction in the F filter (-132 mas) is clearly reduced with
the extended field reduction (-44 mas).
obtained from
the single-image reduction in the F filter (-132 mas) is clearly reduced with
the extended field reduction (-44 mas).
0743-673 (23a) The significant difference
![]() (128 mas) obtained from
the single-image reduction in the F filter persists in the extended field reduction (112 mas).
(128 mas) obtained from
the single-image reduction in the F filter persists in the extended field reduction (112 mas).
0809-493 (24p) A revised VLBI position of this source is given in Fey et al. (2004). As compared with
that given by Ma et al. (1998), a difference of 6 mas in right ascension is found, whereas Table 3,
Col. 3, shows a difference of 24 mas to this source. Although these differences are within the accuracies
of their radio and near-IR measurements, ![]() 8 mas and
8 mas and ![]() 35 mas respectively, it is interesting to
notice that both have the same sign.
35 mas respectively, it is interesting to
notice that both have the same sign.
1101-325 (39p) Only four reference stars.
In preparation for the next astrometric missions, visible/near-IR astrometry and photometry of ICRF quasars is important for identifying the best candidates for an extension of the ICRF in the optical range. Also worth emphasizing is its importance for checking the positional accuracy of extensions of the current stellar reference frame to fainter magnitudes, as well as for studies related to the radio-optical frame tie (da Silva Neto et al. 2002; Assafin et al. 2003). With less atmospheric disturbances than in the visible range, narrow-field astrometry of ICRF quasars in the near-IR reaches an internal precision generally better than 10 mas (see Table 3). However, the actual position accuracy is significantly worse, and mainly affected by two major uncertainties: (i) the quality of the image mapping and its FDP correction, and (ii) statistical errors due to the limited number of reference stars and their position uncertainties.
A model for the FDP has been obtained with overlapping fields in a narrow band filter at ![]() m. At
the epoch of our observations, the FDP reached 0.4 pixel (or 115 mas) in the cell corners, and sub-0.1
pixel effects may not have been completely corrected (see
m. At
the epoch of our observations, the FDP reached 0.4 pixel (or 115 mas) in the cell corners, and sub-0.1
pixel effects may not have been completely corrected (see ![]() residuals in Fig. 11).
Improvements in this domain should be possible in future observing runs, due to a re-alignment of the
SOFI camera (Billères 2004, private communication). Additionally, astrometry in the newly-implemented
residuals in Fig. 11).
Improvements in this domain should be possible in future observing runs, due to a re-alignment of the
SOFI camera (Billères 2004, private communication). Additionally, astrometry in the newly-implemented
![]() filter will be helpful for such modelling due to the larger dynamic range available in this
band and the adjustement of the (active) primary mirror in this same band.
filter will be helpful for such modelling due to the larger dynamic range available in this
band and the adjustement of the (active) primary mirror in this same band.
Positional accuracy is limited at first by the internal precision of the instrument used to perform the astrometric observations. While in an ideal situation it is the only limiting error, there are often systematic errors that dominate the reduction process in actual measurements. In our case, the internal positional precision of the quasars observed with the NTT/SOFI is generally better than 10 mas, but uncertainties in the reference stellar frame dominate the error budget. Enlarging the field of view by mosaics of overlapping images is one way to reduce such systematic effects, as presented in this paper. This effort should be pursued further with observations on even larger fields, in order to bring the error contribution from the reference stars down to a lower level than that of the internal astrometric precision of the NTT/SOFI. Also of interest is that the overlapping of images may be used to link closely ICRF sources and obtain improved stellar positions and proper motions from multi-epoch observations.
Enlarging the field of view to profit from a larger number of reference stars may represent a time-consuming
operation to the NTT/SOFI, so that one envisages the construction of a denser and more accurate stellar
frame as performed by a different instrument. This represents a twofold process that has long been common
practice in quasar optical astrometry, with traditionally wide field photographic plates, on the one hand,
and narrow field CCD image, on the other (see e.g. Zacharias et al. 1999). A similar densification process could
be now obtained with the Wide Field Imager (WFI) mounted at the Cassegrain focus of the
2.2-m MPG/ESO telescope. The WFI has a
![]() field area, enough to contain about
200 UCAC2 stars, therefore making a refined selection of reference stars for the astrometric analysis
possible. Although a more detailed investigation is needed, it is likely that the 10 mas internal precision
of the NTT/SOFI may be reached for the positional accuracy with this observing procedure in the future.
field area, enough to contain about
200 UCAC2 stars, therefore making a refined selection of reference stars for the astrometric analysis
possible. Although a more detailed investigation is needed, it is likely that the 10 mas internal precision
of the NTT/SOFI may be reached for the positional accuracy with this observing procedure in the future.
It is to be noted that a large departure (>100 mas) in right ascension between the near-IR and ICRF positions was found out to Field 23 from both single-image and extended field analyses. In the radio, the corresponding target (0743-673) now has a sub-milliarcsecond-accurate improved VLBI position (Fey et al. 2004) that differs only at the sub-mas level from the original ICRF position in Ma et al. (1998). Thus, it is unlikely that the ICRF positional error contributes significantly to the observed >100 mas discrepancy. While physical effects (different spatial location for the optical and radio emission) may play a role, we cannot go further in explaining this discrepancy with the present 25 mas accuracy of our near-IR observations. Future improved accuracies down to the 10 mas level, as discussed above, should provide deeper insight into this matter.
We have reported results of near-IR astrometry and photometry for 30 southern ICRF quasars. Based on single-image analysis, the positional accuracy of our measurements is about 35 mas, which compares favourably to the best ground-based visible/near-IR measurements published so far. When observing with the mosaic mode's larger field of view, the positional accuracy is improved to 25 mas. Because of the excellent metrological capabilities of the NTT/SOFI (10 mas internal positional precision), even better accuracy could be obtained if denser stellar frames were available around our targets.
Astrometric results derived from each of the three photometric filters were found to be equivalent within
the involved errors. Instrumental magnitudes were calibrated with the 2MASS catalogue and with
precision better than 0.04 mag. The magnitudes of our 30 quasars range from 11.5 to 17.3 in the
![]() band. Within this range, the uncertainty of the near-IR position and the difference
from the ICRF position are independent of the magnitude.
band. Within this range, the uncertainty of the near-IR position and the difference
from the ICRF position are independent of the magnitude.
Pursuing this investigation further would require improved stellar reference frames around ICRF quasars. Astrometric accuracies at the level of 10 mas in the optical range are foreseeable in the future, and would imply a more physical approach when comparing radio and optical positions, as this level of accuracy corresponds to the typical size of extended structures observed in quasar radio maps.
Acknowledgements
The authors acknowledge partial financial support from the (OASU/L3AB). The authors also acknowledge the suggestions from an anonymous referee. This publication makes use of data products from the Two Micron All-Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This research has also made use of the SIMBAD database operated at CDS, Strasbourg, France. This publication makes use of numerical codes from Numerical Recipes in FORTRAN 77. J. I. B. Camargo is supported by CNPq - Brazil.