1 - Astronomical Observatory of A. Mickiewicz University, S
2 - Grupo de Mecánica Espacial, Universidad de Zaragoza, 50009 Zaragoza, Spain
S. Breiter1 - B. Melendo2 - P. Bartczak1 - I. Wytrzyszczak1
1 - Astronomical Observatory of A. Mickiewicz University,
S![]() oneczna 36, 60-286 Poznan, Poland
oneczna 36, 60-286 Poznan, Poland
2 -
Grupo de Mecánica Espacial, Universidad de Zaragoza,
50009 Zaragoza, Spain
Received 9 March 2005 / Accepted 18 March 2005
Abstract
A Lie-Poisson integrator with Wisdom-Holman type splitting is constructed for the
problem of a rigid body
and a sphere (the Kinoshita problem). The algorithm propagates
not only the position, momentum and angular momentum vector of the system,
but also the tangent vector of "infinitesimal displacements''. The latter
allow to evaluate the maximum Lyapunov exponent or the MEGNO indicator
of Cincotta and Simó. Three exemplary cases are studied: the motion
of Hyperion, a fictitious binary asteroid with Hyperion as one of
the components,
and the binary asteroid 90 Antiope. In all cases the attitude instability
of the rotation state with spin vector normal to an equatorial orbit influences
stability of the system at lower rotation rates. The MEGNO maps with variations
restricted to the orbital plane for position and momentum, and
to the orbit normal direction
for the angular momentum resemble usual Poincaré sections. But if no restriction
is imposed on the variations, some stable zones turn into highly chaotic regions,
often retaining the shape of their boundaries.
Key words: chaos - methods: numerical - celestial mechanics - planets and satellites: individual: Hyperion - minor planets, asteroids
The dynamics of a system consisting of a triaxial rigid body and
a homogeneous sphere has a particular importance for celestial
mechanics. The problem is nonintegrable in general, but still much simpler than
the general problem of two rigid bodies and may serve as the first approximation
when one of the bodies is almost spherical. Probably the most comprehensive source
about the general problem of a rigid body
and a sphere in the absence of resonances is still the work due to Kinoshita (1972).
The author was obviously not the first one to discuss the problem,
but he provided a first order analytical theory of orbital and rotational motion
in the system. He also demonstrated that - without any approximation -
an appropriate choice of the reference frame leads to the constant separation (![]() )
between the ascending nodes of orbit and equator. We hope that naming
the "triaxial body + sphere'' problem after H. Kinoshita is a justified
abbreviation to be used in this paper and it should not be taken as a disrespect
to other authors who worked on this problem.
)
between the ascending nodes of orbit and equator. We hope that naming
the "triaxial body + sphere'' problem after H. Kinoshita is a justified
abbreviation to be used in this paper and it should not be taken as a disrespect
to other authors who worked on this problem.
There are two satellite-type
limit cases of the Kinoshita problem: when the mass of the sphere (![]() )
is negligibly small,
the system represents the motion of a point mass satellite around a freely rotating
planet with the mass
)
is negligibly small,
the system represents the motion of a point mass satellite around a freely rotating
planet with the mass
![]() ,
but in the opposite case, when
,
but in the opposite case, when
![]() ,
one obtains
the problem of a rotating satellite of a spherical planet. Both problems are quite common
in the natural and artificial satellites studies and were extensively studied,
but the discovery of binary asteroids calls for more interest in studying
the intermediate cases that fall half way between the two extremes.
Indeed, a significant part of binary systems,
like 90 Antiope or 617 Patroclus,
have components with comparable masses (Merline et al. 2002, Table 2).
,
one obtains
the problem of a rotating satellite of a spherical planet. Both problems are quite common
in the natural and artificial satellites studies and were extensively studied,
but the discovery of binary asteroids calls for more interest in studying
the intermediate cases that fall half way between the two extremes.
Indeed, a significant part of binary systems,
like 90 Antiope or 617 Patroclus,
have components with comparable masses (Merline et al. 2002, Table 2).
Even in the triaxial satellite limit case, however, one should observe that most of the studies were performed for the planar case, with the triaxial body rotating around the axis of the maximum moment of inertia normal to the orbital plane. This case is perfectly suited for the application of Poincaré surface of section method. On the other hand, Wisdom et al. (1984) pointed out the attitude instability phenomenon that makes such restriction unjustified in some situations. One of the objectives of the present paper is to compare the results obtained with and without the planar restriction.
The present paper actually describes our research on a special case of the Kinoshita problem: the triaxial body is an ellipsoid. The ellipsoid as a source of the gravity field is approximated by a model of two material segments and a central mass - a modification of the two segments model introduced by Bartczak & Breiter (2003). Sections 2 and 3 present the formalism and a Lie-Poisson numerical integration algorithm for the Kinoshita problem. The algorithm has many common points with the work of Touma & Wisdom (1994) hence we do not repeat their discussion of the conservation of Lie-Poisson structure and of approximate conservation of the Hamiltonian. We only recall that Lie-Poisson integrators integrate Hamiltonian equations of the Lie-Poisson type in a same manner that symplectic integrators numerically solve canonical Hamiltonian equations. In Sect. 4 we extend the integrator, providing the algorithm to propagate the associated tangent vector. For the Keplerian motion we incorporate the formulation of Mikkola & Innanen (1999) and we add the recipe for the rotational component of the problem. Tangent maps allow the application of the MEGNO (Mean Exponential Growth factor of Nearby Orbits) stability indicator invented by Cincotta & Simó (2000). Section 5 recalls basic facts about MEGNO and its relation to the maximum Lyapunov exponent. MEGNO is a reliable tool originally developed for the galactic dynamics studies (Cincotta et al. 2003; Cincotta & Simó 2000) but then successfully transplanted to the dynamics of planetary systems (Gozdziewski et al. 2001) and artificial satellite problem (Breiter et al. 2005). Gozdziewski (2003) originated combining the MEGNO computation with symplectic integration of equations of motion. In the rotational dynamics problems, the MEGNO indicator was successfully applied by Pavlov & Maciejewski (2003) who studied the 3:2 spin-orbit coupling of Mercury.
Finally, Sect. 6 presents the MEGNO analysis for three sample problems. First we revisit the classical problem of the Saturn's moon Hyperion. This is an example of the Kinoshita problem in the triaxial satellite limit. Two following examples treat the comparable masses case of the Kinoshita problem intended to shed light on the dynamics of binary asteroids. The rigid body and a sphere model was already used in this context as a first approximation (Scheeres 2002). In order to provide a direct comparison with the satellite limit, we first study a fictitious system composed of Hyperion and a spherical companion whose mass is only 5 times greater than Hyperion. Then we focus on a real problem of the binary system 90 Antiope.
We study the evolution of 9 variables
The reduced mass m is a function of the ellipsoid mass ![]() and
the sphere mass
and
the sphere mass ![]()
In order to integrate numerically Eq. (5), we construct
the algorithm based on a splitting method, using the
Wisdom-Holman strategy of partitioning Hamiltonian in a way that
introduces a small parameter as a multiplier of the truncation
error (Wisdom & Holman 1991). There are two small parameters in our problem:
![]() and
and
![]() ,
both
related to the deviation of the ellipsoid shape from the spherical
symmetry. Their magnitudes depend on the problem at hand, but
,
both
related to the deviation of the ellipsoid shape from the spherical
symmetry. Their magnitudes depend on the problem at hand, but
![]() implies
implies
![]() .
Thus, the potential V of the ellipsoid can be considered as the
sum of a purely Keplerian part
.
Thus, the potential V of the ellipsoid can be considered as the
sum of a purely Keplerian part
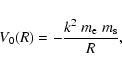 |
(10) |
The Hamiltonian (4) can be split into four separately
integrable parts
| |
= | 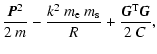 |
(12) |
| = | 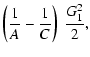 |
(13) | |
| = | 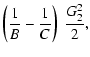 |
(14) | |
| = | 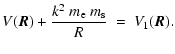 |
(15) |
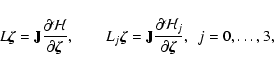
The main building block of the Yoshida-type integrators
(Yoshida 1993)
is a second order "leapfrog'' map ![]() .
If
.
If
![]() ,
it is defined as
,
it is defined as
| |
= | ![$\displaystyle \exp\left[\frac{h}{2}~L_0\right] \circ \exp\left[h~L_1\right]
\circ \exp\left[\frac{h}{2}~L_0\right]
~ \vec{\zeta}_0$](/articles/aa/full/2005/26/aa3031-05/img56.gif) |
|
| (17) |
In order to create the Lie-Poisson integrator, we have to find
the explicit form of the maps
![]() .
.
![]() describes the relative two-body problem in the reference
frame rotating with a constant angular rate around the axis determined
by
describes the relative two-body problem in the reference
frame rotating with a constant angular rate around the axis determined
by ![]() .
One may easily check that
.
One may easily check that
![]() and
and ![]() is a constant vector. Accordingly, we will only discuss the
motion in
is a constant vector. Accordingly, we will only discuss the
motion in ![]() and
and ![]() .
.
As a matter of fact, we can further split
![]() into
into
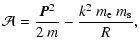 |
(20) | ||
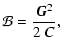 |
(21) |
| |
= | (22) | |
| = | 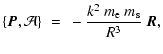 |
(23) |
| |
= | 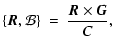 |
(24) |
| = | 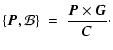 |
(25) |
The Keplerian motion
![]() can be most easily
implemented in terms of the Gaussian functions
can be most easily
implemented in terms of the Gaussian functions ![]() and
and ![]() (Mikkola & Innanen 1999)
(Mikkola & Innanen 1999)
| |
= | (26) | |
| = | (27) |
The Hamiltonian function
![]() generates the rotation around
the axis OX1 of the body frame
generates the rotation around
the axis OX1 of the body frame
| (31) |
| (35) |
The perturbing part of the ellipsoid's potential
![]() depends on the
depends on the ![]() vector only and it leads to trivial equations
vector only and it leads to trivial equations
In these circumstances we obtain the simple "kick map''
![]()
| l1 | = | 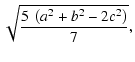 |
(48) |
| L3 | = | 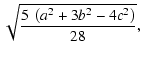 |
(49) |
| = | 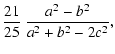 |
(50) | |
| = | 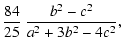 |
(51) | |
| = | (52) |
Using the straight segments approximation is by no means a crucial feature. One may consider using the exact potential of an ellipsoid in terms of elliptic integrals or the spherical harmonics series, as long as the former is fast enough or the latter reasonably convergent.
In many applications the knowledge of a trajectory
![]() alone is not
sufficient. The information how small variations of the initial conditions
alone is not
sufficient. The information how small variations of the initial conditions
![]() evolve in time is equally useful for the theoretical stability
analysis as well as for practical problem of adjusting the modeled trajectory
to observations.
In principle, infinitesimal variations obey differential equations of motion
and one might think about applying a splitting method to solve them. But
the equations, albeit linear, are explicitly time-dependent due to the
presence of the fiducial trajectory expressions
evolve in time is equally useful for the theoretical stability
analysis as well as for practical problem of adjusting the modeled trajectory
to observations.
In principle, infinitesimal variations obey differential equations of motion
and one might think about applying a splitting method to solve them. But
the equations, albeit linear, are explicitly time-dependent due to the
presence of the fiducial trajectory expressions
![]() in their
right-hand sides.
in their
right-hand sides.
A practical solution to the problem of finding
![]() is based on
the observation that symplectic (or Lie-Poisson) integration amounts to the
iteration of a map
is based on
the observation that symplectic (or Lie-Poisson) integration amounts to the
iteration of a map ![]() ,
generating a sequence of values
,
generating a sequence of values
Let us now examine the expressions of tangent maps associated with ![]() of our four-terms
leapfrog. According to the definition (18), the tangent map matrix
of our four-terms
leapfrog. According to the definition (18), the tangent map matrix
![]() is a product
is a product
Another important remark concerns the actual form of tangent maps. Tangent maps are linear transformations and as such they can always be written as matrix products. But the matrix form is often too cumbersome and then it is easier to use the formulas resulting from the direct differentiation of the original nonlinear map.
According to Sect. 3.1,
![]() ,
hence
,
hence
![]() .
The tangent map for the Keplerian
motion has been derived by Mikkola & Innanen (1999). Using their formulation in our
case, when
.
The tangent map for the Keplerian
motion has been derived by Mikkola & Innanen (1999). Using their formulation in our
case, when
Straightforward differentiation of
Eq. (29) leads to
![]() - the tangent map
for the rotation around
- the tangent map
for the rotation around
![]()
Tangent maps for the elementary rotations can be easily derived
through the differentiation of the respective rotation matrices.
Let
The kick map (39) leads to the tangent map
![]()
Knowing the evolution of the tangent vector
![]() ,
we may study the qualitative
properties of motion in the phase space
by evaluating the Maximum Lyapunov Characteristic Exponent (MLCE)
,
we may study the qualitative
properties of motion in the phase space
by evaluating the Maximum Lyapunov Characteristic Exponent (MLCE) ![]() .
For a continuous orbit
.
For a continuous orbit
![]() that satisfies the differential equation
that satisfies the differential equation
![]() ,
the MLCE is defined as
,
the MLCE is defined as
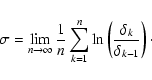 |
(70) |
Evaluating the MLCE by means of numerical integration, one has to rely on some finite
time estimate ![]() of
of ![]() .
The convergence of
.
The convergence of ![]() is
often slow and requires the integration on unreasonably long intervals.
The Mean Exponential Growth factor
of Nearby Orbits (MEGNO) function, invented by Cincotta & Simó (2000),
is a good remedy for this difficulty.
For a continuous orbit, the MEGNO function y(t)is defined as
is
often slow and requires the integration on unreasonably long intervals.
The Mean Exponential Growth factor
of Nearby Orbits (MEGNO) function, invented by Cincotta & Simó (2000),
is a good remedy for this difficulty.
For a continuous orbit, the MEGNO function y(t)is defined as
The information that we obtain from the MEGNO in a non-chaotic case is more rich than what we get from the MLCE. From the formal standpoint, Y(t)converges to 2 for all kinds of quasi-periodic orbits; but the convergence rate is different depending on the local phase space environment and this provides an additional depth to the finite time estimators Y(t). Quasi-periodic orbits close to a stable periodic orbit tend to approach 2 from the left: the closer they are to the periodic orbit, the more slowly their Y(t) approach 2. Similarly, the neighborhood of an unstable periodic orbits slows down the convergence of Y(t) to 2 from the right. In these circumstances, the finite time (or even "short time'') estimators reveal the presence of periodic orbits between the grid points of the studied initial conditions or parameters.
A fixed step integrator, like the one we present in this paper, is equivalent to a discrete time map, so we have applied the definition of the MEGNO from Eqs. (73) and (74). The practical implementation of the algorithm was initially the following:
But in the triaxial satellite limit of the Kinoshita problem
we faced the difficulty, that the random choice of
![]() components
in the
components
in the
![]() range did not lead to the removal
of low MEGNO artifacts. Observing that
range did not lead to the removal
of low MEGNO artifacts. Observing that
![]() is much smaller than
is much smaller than
![]() or
or
![]() ,
we realized, that even the random choice
of
,
we realized, that even the random choice
of
![]() with all components equally treated actually preferred the direction
of the slowest MEGNO growth. The problem was solved by the following device:
at the beginning
with all components equally treated actually preferred the direction
of the slowest MEGNO growth. The problem was solved by the following device:
at the beginning
![]() is randomly generated with all
components in the
is randomly generated with all
components in the
![]() range, then
one step of algorithm is performed propagating the values of
range, then
one step of algorithm is performed propagating the values of
![]() ;
finally the lengths of the so obtained
;
finally the lengths of the so obtained
![]() ,
,
![]() ,
and
,
and
![]() are used as the weighting factors to generate actual
are used as the weighting factors to generate actual
![]() with the components of
with the components of
![]() equal to
equal to
![]() times random numbers
from the
times random numbers
from the
![]() interval etc.
This device practically removed systematic patterns of small Y(t).
interval etc.
This device practically removed systematic patterns of small Y(t).
After completing the formal tests of our program based on the algorithms described
in previous sections, we chose the system of Saturn and its satellite Hyperion as
the first realistic problem to be investigated. Wisdom et al. (1984) predicted the chaotic
rotation of Hyperion by inspecting the phase space of the Kinoshita
problem in the
![]() limit. Their prediction was confirmed by the analysis of the photometric
observations undertaken by Klavetter (1989a). Wisdom et al. (1984) studied mainly
the planar case (
limit. Their prediction was confirmed by the analysis of the photometric
observations undertaken by Klavetter (1989a). Wisdom et al. (1984) studied mainly
the planar case (![]() normal to the orbital plane and aligned with the axis
of the maximum moment of inertia) that is perfectly suited for the analysis by means
of the Poincaré section maps and reducible to an almost paradigmatic
Beletsky equation (Beletsky 1965). But in the same paper, the authors
notice and discuss the attitude instability effect arising when the planar
restriction is suppressed. Due to this effect the widespread surface of section
plot for Hyperion is actually misleading, because some regular regions of this
plot prove to be chaotic in the spatial problem.
normal to the orbital plane and aligned with the axis
of the maximum moment of inertia) that is perfectly suited for the analysis by means
of the Poincaré section maps and reducible to an almost paradigmatic
Beletsky equation (Beletsky 1965). But in the same paper, the authors
notice and discuss the attitude instability effect arising when the planar
restriction is suppressed. Due to this effect the widespread surface of section
plot for Hyperion is actually misleading, because some regular regions of this
plot prove to be chaotic in the spatial problem.
In order to study the phase space of Hyperion-like objects the following set of
physical parameters was assumed (Klavetter 1989b): Hyperion's semi-axes
![]() ,
b=0.76316 a, c=0.6 a, its density
,
b=0.76316 a, c=0.6 a, its density
![]() ,
and
Saturn's mass
,
and
Saturn's mass
![]() .
Initial conditions
of Saturn in the Hyperion-fixed frame were derived from the Keplerian elements
.
Initial conditions
of Saturn in the Hyperion-fixed frame were derived from the Keplerian elements
For each orbit the MEGNO coefficient
was evaluated on the interval of 103 of orbital periods ![]() .
The computations were performed twice and the two simulations differed
only by the treatment of the tangent vectors.
First, the initial variations
.
The computations were performed twice and the two simulations differed
only by the treatment of the tangent vectors.
First, the initial variations
![]() were
selected with a planar restriction
were
selected with a planar restriction
In Fig. 1a we see the MEGNO map that exactly mimics the well know
Hyperion surface of section pictures that can be found in papers like
Wisdom et al. (1984), Klavetter (1989b),
Black et al. (1995), or Breiter & Buciora (2000), not to mention numerous popular science texts.
We recognize a chaotic sea with the main island of regular motion close to 1:1 spin-orbit
resonance at
![]() and
and
![]() ,
surrounded by a small archipelago of a
secondary resonance.
The small island of 1:2 resonance is visible at
,
surrounded by a small archipelago of a
secondary resonance.
The small island of 1:2 resonance is visible at
![]() and
and
![]() .
Other larger islands surround the 9:4 resonance (
.
Other larger islands surround the 9:4 resonance (
![]() ,
,
![]() )
and 2:1 spin-orbit coupling (
)
and 2:1 spin-orbit coupling (
![]() ,
,
![]() ).
The values of
).
The values of ![]() should not be confused with the resonant ratios p:q in question,
because the vertical
axes of all plots in this paper refer to instantaneous,
initial values of angular rate that can differ
from the mean angular rate by the current value of the sum of periodic terms. The best analogy at hand is the
difference between the orbital angular rate at pericentre and the mean motion.
should not be confused with the resonant ratios p:q in question,
because the vertical
axes of all plots in this paper refer to instantaneous,
initial values of angular rate that can differ
from the mean angular rate by the current value of the sum of periodic terms. The best analogy at hand is the
difference between the orbital angular rate at pericentre and the mean motion.
![\begin{figure}
\par\includegraphics[height=5.5cm]{3031f1a.eps}\includegraphics[height=5.5cm]{3031f1b.eps}\includegraphics[height=5.5cm]{3031leg1.eps}
\end{figure}](/articles/aa/full/2005/26/aa3031-05/Timg243.gif) |
Figure 1: MEGNO maps for Hyperion in RTM a) and ATM models b). |
| Open with DEXTER | |
According to Wisdom et al. (1984), the attitude instability brings chaos into the 1:1 and 1:2 resonance regions. Our MEGNO map in Fig. 1b confirms these results. Surprisingly, the 1:2 island is still visible, but now as a region of extremely high MEGNO (Y > 1000) with the Lyapunov times shorter than 10 days. The island has turned into an abyss. We also do not lose the trace of the 1:1 zone (including the small archipelago !) - this time as a "less chaotic'' region.
The stability of spin-orbit resonances depends on two factors: orbital eccentricity e and ![]() - a parameter that describes the departure of the primary's
matrix of inertia from the prolate spheorid with A=B (Wisdom et al. 1984).
For a homogeneous ellipsoid
- a parameter that describes the departure of the primary's
matrix of inertia from the prolate spheorid with A=B (Wisdom et al. 1984).
For a homogeneous ellipsoid
In order to demonstrate the dependence of resonant rotation states
on ![]() within RTM and ATM models, we
computed the MEGNO maps for 401 various rotation rates and 201
within RTM and ATM models, we
computed the MEGNO maps for 401 various rotation rates and 201
![]() values spanning the range from 0 up to 1.2. The latter
value is the limit obtained with b=c=0.6 a. Our simulations
were performed for two initial values of
values spanning the range from 0 up to 1.2. The latter
value is the limit obtained with b=c=0.6 a. Our simulations
were performed for two initial values of ![]() equal 0 and
equal 0 and
![]() .
Thus the plots of Figs. 2a and 2c
should be interpreted as a collection of the leftmost (or,
due to symmetry, the rightmost) columns of plots
similar to Fig. 1, but for different shapes of Hyperion.
Analogously, Figs. 2b and 2d collect the
middle columns of the plots similar to Fig. 1. Combining the
information from
.
Thus the plots of Figs. 2a and 2c
should be interpreted as a collection of the leftmost (or,
due to symmetry, the rightmost) columns of plots
similar to Fig. 1, but for different shapes of Hyperion.
Analogously, Figs. 2b and 2d collect the
middle columns of the plots similar to Fig. 1. Combining the
information from
![]() and
and
![]() one may
partially reconstruct the basic features of the whole phase space.
The figures can be compared with Wisdom et al. (1984, Fig. 3).
one may
partially reconstruct the basic features of the whole phase space.
The figures can be compared with Wisdom et al. (1984, Fig. 3).
Table 1: MEGNO map codes and Lyapunov time estimates for Hyperion.
![\begin{figure}
\par\includegraphics[height=5.5cm]{3031f2a.eps}\includegraphics[h...
...5.5cm]{3031f2d.eps}\includegraphics[height=5.5cm]{3031leg2.eps}\\\end{figure}](/articles/aa/full/2005/26/aa3031-05/Timg251.gif) |
Figure 2: MEGNO for different shapes of Hyperion; RTM ( top) and ATM ( bottom). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=5.5cm]{3031f3a.eps}\includegraphics[h...
...5.5cm]{3031f3d.eps}\includegraphics[height=5.5cm]{3031leg2.eps}\\\end{figure}](/articles/aa/full/2005/26/aa3031-05/Timg252.gif) |
Figure 3: MEGNO for different eccentricities of Hyperion orbit; RTM ( top) and ATM ( bottom). |
| Open with DEXTER | |
Figure 2 tells the story of bifurcations and resonance overlaps.
The stable resonance curves are seen as strings of low MEGNO values.
When they enter the chaotic sea, their width varies reflecting
the width of a stable zone that surrounds the periodic orbit
for a given value of ![]() .
From time to time the stable zone branches which is the evidence of
a periodic orbit bifurcation. The branches
terminate quickly because of the created secondary resonances overlap
(Lichtenberg & Lieberman 1992).
For a given p:q ratio, the resonance curve originates at
.
From time to time the stable zone branches which is the evidence of
a periodic orbit bifurcation. The branches
terminate quickly because of the created secondary resonances overlap
(Lichtenberg & Lieberman 1992).
For a given p:q ratio, the resonance curve originates at
![]() when
when
![]() ,
and extends first horizontally but then bending up or down
as
,
and extends first horizontally but then bending up or down
as ![]() grows. The robustness of the
9:4 resonance in Figs. 2b and 2d is spectacular:
it survives as long as the 1:2 case - up to
grows. The robustness of the
9:4 resonance in Figs. 2b and 2d is spectacular:
it survives as long as the 1:2 case - up to
![]() .
Confronting the planar case
(Figs. 2a,b) with the full problem (Figs. 2c,d),
we notice the effects known from Fig. 1: low
.
Confronting the planar case
(Figs. 2a,b) with the full problem (Figs. 2c,d),
we notice the effects known from Fig. 1: low ![]() and 1:2 zones
change their stable nature into an extreme chaos. There are also moderate
chaos (type G) streaks in upper-right regions of Figs. 2c
and 2d - apparently generated by some non-obvious resonance effect
and definitely deserving future studies.
and 1:2 zones
change their stable nature into an extreme chaos. There are also moderate
chaos (type G) streaks in upper-right regions of Figs. 2c
and 2d - apparently generated by some non-obvious resonance effect
and definitely deserving future studies.
Figure 3 is constructed and arranged similarly to Fig. 2, but
it shows the dependence of MEGNO at
![]() and
and
![]() as a function
of orbital eccentricity of Hyperion (more precisely - of Saturn in our Hyperion-based
reference frame). The value of
as a function
of orbital eccentricity of Hyperion (more precisely - of Saturn in our Hyperion-based
reference frame). The value of ![]() was set to 0.89 according to the adopted
ellipsoid of inertia. The maps at the top were computed with RTM; their counterparts at the bottom
were obtained using nonrestricted tangent vectors. A sample of 201 eccentricity values was used,
ranging from 0 to 0.4, allowing us to see the subsequent destruction of stable
resonance areas after the chain of bifurcations. The influence of attitude instability
is similar to previous cases. Interestingly, the 1:1 synchronicity becomes chaotic starting
from very low eccentricities, and the 1:2 state is extremely chaotic even for
the circular orbit.
was set to 0.89 according to the adopted
ellipsoid of inertia. The maps at the top were computed with RTM; their counterparts at the bottom
were obtained using nonrestricted tangent vectors. A sample of 201 eccentricity values was used,
ranging from 0 to 0.4, allowing us to see the subsequent destruction of stable
resonance areas after the chain of bifurcations. The influence of attitude instability
is similar to previous cases. Interestingly, the 1:1 synchronicity becomes chaotic starting
from very low eccentricities, and the 1:2 state is extremely chaotic even for
the circular orbit.
![\begin{figure}
\par\includegraphics[height=5.5cm]{3031f4a.eps}\includegraphics[height=5.5cm]{3031f4b.eps}\includegraphics[height=5.5cm]{3031leg1.eps}
\end{figure}](/articles/aa/full/2005/26/aa3031-05/Timg255.gif) |
Figure 4: MEGNO maps for a Hyperion-like binary asteroid computed with RTM a) and ATM b) models. |
| Open with DEXTER | |
Is the attitude instability phenomenon intrinsically related to the negligible
mass of the triaxial body? The simplest way to answer this question is
to consider a hypothetic system consisting of Hyperion and a sphere with
![]() of similar order of magnitude as
of similar order of magnitude as ![]() .
Decreasing
the Saturn's mass we appropriately shrunk the orbital radius to conserve the
the orbital mean motion. Thus we built a binary asteroid with a Hyperion-like
ellipsoid and a sphere with the Hyperion's density and the radius of
.
Decreasing
the Saturn's mass we appropriately shrunk the orbital radius to conserve the
the orbital mean motion. Thus we built a binary asteroid with a Hyperion-like
ellipsoid and a sphere with the Hyperion's density and the radius of
![]() (i.e.
(i.e.
![]() ). The orbital semi-axis
). The orbital semi-axis ![]() was
was
![]() .
Maintaining the mean motion, we can use directly the values
of Lyapunov times associated with MEGNO bins in Table 1.
.
Maintaining the mean motion, we can use directly the values
of Lyapunov times associated with MEGNO bins in Table 1.
Mapping MEGNO as a function of initial ![]() and
and ![]() ,
maintaining the eccentricity
e=0.1, we obtained the results presented in Fig. 4 - the analogues of
Fig. 1. Recognizing the characteristic 1:1 and 1:2 zones we notice that
the 1:2 spin-orbit resonance reacts on passing from RTM to ATM similarly to the
real Hyperion case and a similar chaotic wave is seen at low rotation rates.
But, interestingly, the 1:1 synchronicity is not destabilized completely. Thanks
to distinguishing different levels of chaoticity, we recognize a pattern resembling
a strongly perturbed Second Fundamental Model of resonance Henrard & Lemaitre (1983).
,
maintaining the eccentricity
e=0.1, we obtained the results presented in Fig. 4 - the analogues of
Fig. 1. Recognizing the characteristic 1:1 and 1:2 zones we notice that
the 1:2 spin-orbit resonance reacts on passing from RTM to ATM similarly to the
real Hyperion case and a similar chaotic wave is seen at low rotation rates.
But, interestingly, the 1:1 synchronicity is not destabilized completely. Thanks
to distinguishing different levels of chaoticity, we recognize a pattern resembling
a strongly perturbed Second Fundamental Model of resonance Henrard & Lemaitre (1983).
![\begin{figure}
\par\includegraphics[height=5.5cm]{3031f5a.eps}\includegraphics[height=5.5cm]{3031f5b.eps}\includegraphics[height=5.5cm]{3031leg1.eps}
\end{figure}](/articles/aa/full/2005/26/aa3031-05/Timg260.gif) |
Figure 5: MEGNO maps for 90 Antiope in RTM a) and ATM models b). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=5.5cm]{3031f6a.eps}\includegraphics[h...
...ght=5.5cm]{3031f6d.eps}\includegraphics[height=5.5cm]{3031leg2.eps}
\end{figure}](/articles/aa/full/2005/26/aa3031-05/Timg261.gif) |
Figure 6: MEGNO for different shapes of 90 Antiope; RTM ( top) and ATM ( bottom). |
| Open with DEXTER | |
Thanks to the Keck Adaptive Optics observations (Merline et al. 2000)
and extensive photometric data covering
5 oppositions (first 4 collected in Michaowski et al. 2004),
the asteroid 90 Antiope
is known to be an interesting example of a binary system with
two comparable components. According to the recent results
of Michaowski et al. (2004), Antiope is most likely an almost synchronous
system with the rotation period of the primary
![]() and the orbital period of the satellite
and the orbital period of the satellite
![]() .
These results were obtained
using a kinematic model with a spheroidal primary
having semi-axes
.
These results were obtained
using a kinematic model with a spheroidal primary
having semi-axes
![]() ,
b=c=0.9 a and a spherical satellite
with the radius of
,
b=c=0.9 a and a spherical satellite
with the radius of
![]() .
A common density of the components
was assumed as
.
A common density of the components
was assumed as
![]() and the circular orbit
of the satellite had the radius
and the circular orbit
of the satellite had the radius
![]() .
In spite of the successful prediction of the observed lightcurves
by means of the current model, its kinematic origin calls for a closer look from the
dynamical point of view.
.
In spite of the successful prediction of the observed lightcurves
by means of the current model, its kinematic origin calls for a closer look from the
dynamical point of view.
Figure 5 presents the dependence of MEGNO on the initial ![]() and
and ![]() for Antiope.
The values of MEGNO are coded according to Table 1, but to account for the
difference of orbital periods, the estimates of Lapunov times from Table 1 should be
divided by 30. The results obtained using RTM and ATM do not differ as significantly as in
the previous examples. The 1:1 synchronicity zone is wide and stable in both cases,
although the stochastic separatrix layer is quite thick. Few secondary resonances are
also visible at
for Antiope.
The values of MEGNO are coded according to Table 1, but to account for the
difference of orbital periods, the estimates of Lapunov times from Table 1 should be
divided by 30. The results obtained using RTM and ATM do not differ as significantly as in
the previous examples. The 1:1 synchronicity zone is wide and stable in both cases,
although the stochastic separatrix layer is quite thick. Few secondary resonances are
also visible at
![]() and
and ![]() between
between
![]() and
and
![]() .
Is it justified to claim that in a weakly spheroidal problem with comparable masses
the attitude instability does not play any significant role? The answer is negative if
we inspect Fig. 6. It is arranged similarly to Fig. 4:
columns refer to the initial
.
Is it justified to claim that in a weakly spheroidal problem with comparable masses
the attitude instability does not play any significant role? The answer is negative if
we inspect Fig. 6. It is arranged similarly to Fig. 4:
columns refer to the initial ![]() equal 0 (left) or
equal 0 (left) or
![]() (right),
and rows display RTM (top) or ATM (bottom). The appearance of secondary resonances
bifurcating from the main 1:1 state is seen as the sequence of branchings
in Fig. 6a.
But comparing them with ATM map in Fig. 6c
we see that three of the secondary resonances are attitude unstable -
notably the one close to
(right),
and rows display RTM (top) or ATM (bottom). The appearance of secondary resonances
bifurcating from the main 1:1 state is seen as the sequence of branchings
in Fig. 6a.
But comparing them with ATM map in Fig. 6c
we see that three of the secondary resonances are attitude unstable -
notably the one close to
![]() .
There is also the evidence of
the high MEGNO wave at small
.
There is also the evidence of
the high MEGNO wave at small ![]() and
and ![]() that shrinks when
the shape changes from a=b towards the b=c spheroid.
that shrinks when
the shape changes from a=b towards the b=c spheroid.
All previous examples discussed the planar Kinoshita problem. The last simulation
scanned the whole range of orbital inclinations (
![]() grid)
with respect to the equator of the
spheroidal component, assuming circular orbital motion. The rotation rates were
sampled in the
grid)
with respect to the equator of the
spheroidal component, assuming circular orbital motion. The rotation rates were
sampled in the
![]() range with a step of 0.01.
This time there was no reason to impose RTM, hence Fig. 7 consists of
two parts only: 7a was obtained with the initial
range with a step of 0.01.
This time there was no reason to impose RTM, hence Fig. 7 consists of
two parts only: 7a was obtained with the initial
![]() and argument of latitude
and argument of latitude
![]() ,
and 7b - with
,
and 7b - with
![]() and
and
![]() .
The former leads to
.
The former leads to
![]() and
the latter to
and
the latter to
![]() when the inclination is 0.
when the inclination is 0.
The symmetry of both pictures with respect to their central points is obvious and
it should be expected. The width of the 1:1 stable librations zone decreases with
growing inclination (Fig. 7a) but at the same time
the width of the 1:1 chaotic zone close to unstable equilibrium becomes smaller
(Fig. 7b). As usually, the 1:2 resonance is the most capricious we can
observe a sudden growth of the associated chaotic zone when inclination approaches
![]() .
Of course, the same is true for 1:(-2) and retrograde orbits. Generally,
there is a similarity between (
.
Of course, the same is true for 1:(-2) and retrograde orbits. Generally,
there is a similarity between (![]() )
and (
)
and (
![]() )
pairs.
Polar orbits are chaotic for a slowly rotating primary if the orbital plane is
perpendicular to the longest axis of the ellipsoid. If the orbital plane is
aligned with the longest axis, polar orbits are stable. Interestingly, there are
no vertical structures visible that might be attached to some critical inclination
type phenomena.
)
pairs.
Polar orbits are chaotic for a slowly rotating primary if the orbital plane is
perpendicular to the longest axis of the ellipsoid. If the orbital plane is
aligned with the longest axis, polar orbits are stable. Interestingly, there are
no vertical structures visible that might be attached to some critical inclination
type phenomena.
![\begin{figure}
\par\includegraphics[width=4cm,clip]{3031f7a.eps}\includegraphics[width=4.6cm,clip]{3031f7bl.eps}
\end{figure}](/articles/aa/full/2005/26/aa3031-05/Timg280.gif) |
Figure 7: MEGNO as a function of initial inclination and rotation rate of 90 Antiope. |
| Open with DEXTER | |
Combining the MEGNO method with a fast integration algorithm results in a convenient tool for the study of spin-orbit interactions. The efficiency is gained thanks to few factors: the Lie-Poisson integrator allows to use a low-order method with relatively large stepsize without the immediate penalty of artificial energy drift and orthogonality loss, and MEGNO indicator has a faster convergence compared to traditional MLCE computation methods.
Although the applications presented in this paper were selected rather to illustrate the performance of the numerical algorithm, yet they reveal few interesting aspects of the studied problems. The difference between the values of MEGNO obtained for the same trajectory with restricted and arbitrary tangent maps is both understandable and intriguing. Suppose, that the trajectory is investigated by means of some Fourier spectrum method like the Frequency Analysis (Laskar 1993) or autocorrelation function; the conclusion should be similar to the RTM - no chaos. But the same trajectory investigated with Lyapunov exponents related methods without restrictions on tangent vectors qualifies the motion as chaotic. In our opinion, the discrepancy of results is due to the important difference between the chaos detectors based on the study of an orbit alone (Fourier type) an those referring to the divergence of nearby orbits (Lyapunov type).
Revisiting the motion of Hyperion we confirmed the results of Wisdom et al. (1984) concerning location of spin-orbit resonance states. We have also shown how the width of their stable zones varies depending on the moon's shape and orbital eccentricity.
For binary asteroids with comparable mass of components we have shown that chaotic tumbling is as common feature of the phase space as it is in the case of planetary satellites (Wisdom 1987). Any scenario of the evolution of binary asteroids should take this phenomenon into account regardless of the spin-up or spin-down effects included.
Our results concerning 90 Antiope contribute two important features to the current model of the system. First, the width of the regular libration zone surrounding the 1:1 synchronicity is too large to agree with the kinematic model of the tiny constant difference between the mean motion and rotation rate. On the other hand, the fact that no chaos has been observed in the lightcurve of Antiope may help to put better constraints on the shape of the primary, because some ratios of the ellipsoid's axes should be excluded according to Fig. 6c.
Acknowledgements
We thank Dr. Krzysztof Gozdziewski for numerous stimulating discussions about the theory and practice of the MEGNO. The research was carried under the Polish State Committee of Scientific Research (KBN) grant 1 P03D 020 27.