A&A 437, 687-690 (2005)
DOI: 10.1051/0004-6361:20052714

Numerical simulations of fast magnetosonic waves in a curved coronal loop

K. Murawski1 - M. Selwa 1 - L. Nocera2


1 - Institute of Physics, UMCS, ul. Radziszewskiego 10, 20-031 Lublin, Poland
2 - Theoretical Plasma Physics, IPCF - CNR, via Moruzzi 1, 56124 Pisa, Italy

Received 17 January 2005 / Accepted 8 February 2005

Abstract
We consider an impulsive excitation of fast magnetosonic waves in a dense and highly magnetised curved loop that is embedded in a potential arcade. The results of our numerical simulations reveal that the period of the excited waves agrees with both the period of the fast kink mode in the arcade and with the observations by TRACE.

Key words: Sun: oscillations - Sun: corona - magnetohydrodynamics (MHD)

1 Introduction

Oscillations of solar coronal loops and arcades have been studied for a few decades. Body MHD waves propagating throughout an arcade structure attracted much interest because the highly inhomogeneous magnetic field background of the arcade modifies the linear spectrum of the waves (Oliver et al. 1993). Also the bearings of explosive flare events on the arcade were the subject of numerical investigations. The flare-driven short period oscillations were held responsible peculiar microwave signatures from the Sun (Oliver et al. 1998).

It is, however, dense, luminous, localised loop structures that provide better opportunity for comparing theory and observation. Such structures have already been advocated as the sites for peculiar radio signatures from the Sun (e.g. Roberts et al. 1983). An even greater interest in them has recently been kindled by observations by TRACE (e.g. Nakariakov et al. 1999).

Loops with a sufficiently small aspect ratio can be treated as rectilinear ducts. Surface waves propagating along the duct's edges (aptly named ducted waves) were studied by Roberts et al. (1983, 1984) who showed that, in the assumption of cold plasma (zero $\beta$), these waves can be classified as sausage and kink waves and are akin to waves in seismology.

Zero $\beta$ is a good assumption for a highly magnetised solar corona. In this limit the effects of energy leakage from ducts was investigated by Murawski & Roberts (1993b). The effect of a finite $\beta$ is the generation of slow magnetosonic waves propagating in the duct; and these were studied by Tsiklauri et al. (2004) and by Selwa et al. (2004) who also analysed the effects of dissipation and radiative losses.

The nonlinear properties of kink and sausage modes were investigated by Murawski & Roberts (1993a), who found them prone to wave breaking. The nonlinear propagation of ducted waves was studied by Nakariakov et al. (1997), who developed a model based upon the nonlinear Schrödinger equation, and by Ruderman (1993), who used an asymptotic relaxation method.

Murawski et al. (2005) found that high-order standing fast kink mode oscillations take place within a curved loop embedded in an unrealistically high $\beta$ potential arcade. Waves in curved ducts were also dealt with by Smith et al. (1997), who found that high frequency kink waves are affected by curvature induced energy leakage. Van Doorsselaere et al. (2004) found that continuum damping acts on curved duct quasi-modes (virtual global modes) and drew a connection with the damping of toroidal Alfvén eigenmodes of tokamak devices.

In this short note we give an interpretation of some oscillations recently observed by TRACE (Wang & Solanki 2004) as the ducted kink oscillations of a dense, highly magnetised, curved loop of a small aspect ratio embedded in a potential arcade and subject to impulsive perturbation. The dispersion relation for linear fast waves in rectilinear ducts (Roberts 1983) provides a good approximation of the oscillation period given by the simulations. The numerous effects outlined above may explain the difference between the two periods, the most prominent effect being the inhomogeneity of the duct along its longitudinal coordinate.

Our paper is organised as follows: the physical model is described in Sect. 2; the numerical results are presented in Sect. 3; conclusions and comparison with the work by other authors are drawn in Sect. 4.

  
2 Physical model

In the solar corona the sound speed attains small values in comparison to the Alfvén speed. Therefore we describe coronal plasma by the ideal MHD equations in which gas pressure terms are neglected in comparison to the magnetic terms. This "cold'' plasma approximation leads to the equations

   
    $\displaystyle {\partial\varrho\over \partial t}+\nabla\cdot \left(\varrho{\vec V}\right)=0,$ (1)
    $\displaystyle \varrho{\partial{\vec V}\over\partial t}+ \varrho\left({\vec V}\cdot\nabla\right){\vec V}= {1\over\mu}(\nabla\times{\vec B})\times{\vec B},$ (2)
    $\displaystyle {\partial{\vec B}\over\partial t}=\nabla\times \left({\vec V}\times {\vec B}\right).$ (3)

Here $\varrho $ is the mass density, ${\vec V}$ - the flow velocity, $\mu$ - the magnetic permeability, and ${\vec B}$ is the magnetic induction that satisfies the divergence-free condition $\nabla\cdot{\vec B} = 0$.

   
2.1 A potential arcade loop equilibrium

We use the coronal arcade model described by Oliver et al. (1993, 1998). In this model the coronal arcade is settled in a motionless environment ( ${\vec V}=0$). From the momentum Eq. (2) it follows that at equilibrium the Lorentz force must vanish, i.e.

 \begin{displaymath} (\nabla\times {\vec B})\times {\vec B} = 0 . \end{displaymath} (4)

This equation possesses a particular solution which corresponds to zero current,

 \begin{displaymath} \nabla\times {\vec B}=0 . \end{displaymath} (5)

We limit our discussion to a two-dimensional magnetically structured atmosphere for which the plasma quantities are independent of the spatial coordinate y, $\partial / \partial y = 0$. Additionally, we assume that the initial, unperturbed (i.e. equilibrium) magnetic field has two non-zero components, viz. ${\vec B_{\rm0}} = \left( B_{0x}(x,z),0,B_{0z}(x,z)\right )$ and Vy=By=0. In such a system we can express the equilibrium magnetic field by the vector magnetic potential ${\vec A}=A{\vec{\hat y}}$ as

 \begin{displaymath} {\vec B}= \nabla A\times{\vec{\hat y}} , \end{displaymath} (6)

where ${\vec{\hat y}}$ is a unit vector along the y-direction. Substituting this expression in Eq. (5) we obtain the Laplace equation, $\nabla^2 A=0$. We choose the following simple solution:

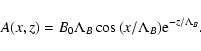\begin{displaymath}A(x,z) = B_0\Lambda_{B}\cos{(x/\Lambda_{B})}{\rm e}^{-z/\Lambda_{B}} . \end{displaymath} (7)

This choice leads to the equilibrium magnetic field components
                         Bx = $\displaystyle ~~~~ B_0 \cos{(x/\Lambda_{B})} {\rm e}^{-z/\Lambda_{B}} ,$ (8)
Bz = $\displaystyle -B_0 \sin{(x/\Lambda_{B})} {\rm e}^{-z/\Lambda_{B}} ,$ (9)

where B0 is the magnetic field at the level z=0 and $\Lambda_{B}$ - the magnetic scale height. We define the arcade width 2L at z=0 as the distance between two consecutive coordinates x at which Bx(x,0)=0, which gives

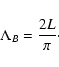\begin{displaymath}\Lambda_{B} = \frac{2L}{\pi}\cdot \end{displaymath} (10)

Since we neglected gravitational stratification we take a constant equilibrium density:

 \begin{displaymath} \varrho(x,z) = {\varrho}_0 = {\rm const} . \end{displaymath} (11)

For such a choice of the equilibrium quantities the squared Alfvén speed decays exponentially with height:

 \begin{displaymath}v_{\rm A}^{2}=\frac{B^{2}}{\mu \varrho}=v_{{\rm A}{\rm e}}^{2} {\rm e}^{-2z/\Lambda_{B}} , \end{displaymath} (12)

where $v_{{\rm A}{\rm e}}$ is the value of the Alfvén speed at z=0.

The scale parameters introduced above are shown in Table 1, and are chosen in such a way that our results agree with the observations (cf. Sect. 4).


  \begin{figure} \par\includegraphics[width=7cm,clip]{2714fg1.eps} \end{figure} Figure 1: Mass density profiles within the loop according to Eq. (13). Parameters are given in Table 2.
Open with DEXTER

Next we embed a loop in the arcade in such a way that its edges follow two specific magnetic field lines. We prescribe that the inner and outer field lines cross the base of the arcade at |x|=D-2d and |x|=D, respectively. D and d are given in Table 2: they uniquely specify the loop's length l, height h, and its width 2a at the top (cf. Table 2).

Table 1: Scale parameters.

Table 2: Parameters of the equilibrium.

Inside the loop we use the following density profile (cf. Fig. 1):

 \begin{displaymath}\varrho(x,z)=\varrho_{0}r \left[ H\left(\frac{A-A_{2}}{B_{0}\... ...)-H\left(\frac{A-A_{1}}{B_{0}\Lambda_{\rm B}}\right) \right] , \end{displaymath} (13)

where A1=A(D,0)<A2=A(D-2d,0) and H is the Heaviside function. In accordance with observations by Aschwanden et al. (1999), we choose the mass density ratio $r\gg1$ (cf. Table 2). Due to the enhanced density, the Alfvén speed within the loop will be smaller than its value outside the loop. We denote the Alfvén speed at the loop's foot points by $v_{{\rm A}{\rm i}}=r^{-1/2}v_{{\rm A}{\rm e}}$.

2.2 Perturbations

Perturbations in Eqs. (1)-(3) can be excited in the loop structure in numerous ways. As we are interested in impulsively excited waves, we launch a pulse in the mass density and velocity. This pulse has the following spatial form:
 
$\displaystyle \delta{q}(x,z,t=0)$ = $\displaystyle A_{q}{\rm e}^{-({x-x_{\rm0}})^2/w^2}{\rm e}^{-({z-z_{\rm0}})^2/w^2},$ (14)

where Aq, $(x_{\rm0},0,z_{\rm0})$ and w denote the relative amplitudes, position, and width of the initial pulse, respectively. The values of these parameters are given in Table 3 and correspond to a pulse launched just below the loop's apex.
  \begin{figure} \par {\bf a}\hskip12pt\includegraphics[width=6.8cm,clip]{2714fg2a... ...ar {\bf b}\hskip12pt\includegraphics[width=6.8cm,clip]{2714fg2b.eps}\end{figure} Figure 2: a) Time-signatures of mass density $\varrho $ profiles measured on the line x=0. b) The density at the loop's top $\varrho (x_d=0,z_d=0.9L)$ in time. Parameters of the simulations are given in Tables 2 and 3.
Open with DEXTER

Table 3: Parameters of the perturbation.

  
3 Numerical results

To study the development of the perturbed arcade we use a numerical code originally developed by DeVore (1991) and based on the Flux Corrected Transport scheme by Boris & Book (1973). We solve Eqs. (1)-(3) numerically in an Eulerian box with the x and z dimensions $(-L,L)\times(0,1.2L)$. At z=0 and $x=\pm L$ reflecting boundary conditions are set. At z=1.2L open boundary conditions are adopted. We use $500\times 400$ numerical cells to cover the whole simulation region.

As this loop is perturbed by the pulse it raises up initially and subsequently exhibits oscillations. These oscillations are discernible in Fig. 2a, which shows $\varrho(0,z,t)$, the profile of the mass density across the loop's apex as it develops in time. The development of mass density at the location xd=0, zd=0.9L is shown in Fig. 2. The spectra of the oscillations of Fig. 2 are displayed in Fig. 3. The peak in the wavelet spectrum agrees with the peak in the frequency spectrum and, using the values in Table 1, the main peaks in the spectra correspond to a wave period of $240{~\rm s}$ i.e. to a frequency of $4.2{~\rm mHz}$. The wavelet spectrum reveals a characteristic tadpole structure which shows that the instantaneous period of oscillation decreases with time. This behaviour is akin to that of fast magnetosonic waves in coronal loops (Nakariakov et al. 1993).


  \begin{figure} \par {\bf a}\hskip12pt\includegraphics[width=6.8cm,clip]{2714fg3a... ...] {\bf b}\hskip12pt\includegraphics[width=7.2cm,clip]{2714fg3b.eps} \end{figure} Figure 3: Power spectra of the signals of Fig. 2. a) Wavelet spectrum. b) Frequency spectrum: the continuous and dashed lines are drawn using the FFT and Maximum method respectively. Using the values in Table 1 the main peaks in the spectra correspond to a wave period of $240{~\rm s}$, i.e. to a frequency of $4.2{~\rm mHz}$.
Open with DEXTER

   
4 Summary and conclusions

In this paper we have numerically studied the impulsive excitation of oscillations of a highly magnetised ($\beta=0$) low aspect ratio solar coronal loop embedded in a two-dimensional magnetic arcade. We interpret these oscillations as kink modes propagating along the loop with a period of a few hundred seconds.

To prove this conjecture we approximate the thin loop of Sect. 2.1 by a rectilinear slab of width 2d and extension l. We denote the Alfvén speeds inside and outside the loop by $v_{{\rm A}{\rm i}}$ and $v_{{\rm A}{\rm e}}=r^{1/2}v_{{\rm A}{\rm i}}$, respectively, $r\gg1$ being the ratio of the density inside the loop to the density outside the loop. The dispersion relation for the fast mode kink oscillation of the slab is (Roberts et al. 1983, Eq. (2))

 \begin{displaymath}\tan\left[\left(\omega^{2}/v_{{\rm A}{\rm i}}^{2}-k^{2}\right... ...\rm A}{\rm e}}^{2}} {\omega^{2}/v_{{\rm A}{\rm i}}^{2}-k^{2}}, \end{displaymath} (15)

where $\omega$ and $k=n\pi/l$ are the angular frequency and wavenumber of the oscillation. To determine the mode number n we sampled the amplitude of the density oscillations at the position corresponding to a quarter of the loop's length starting from its right foot. We found that the amplitude there is much smaller than the amplitude at the loop's top. This shows that the oscillation has a node near one third loop position, antinode at the apex, and thus n=3. In this case the solution of the dispersion relation (15) gives $\omega=0.8396kv_{{\rm A}{\rm e}}$. Using the values of l given in Table 2 we find $\tau=2\pi/\omega\simeq2.0L/v_{{\rm A}{\rm e}}$ for the period of the kink oscillations, in agreement with the value $1.87L/v_{{\rm A}{\rm e}}$ provided by the simulations.

The most likely explanation for the $13\%$ mismatch is the inhomogeneity of the Alfvén speed in the arcade. Indeed the value of the Alfvén speed at the apex of the loop ( $z\simeq 0.9L$, cf. Fig. 1) is about $25\%$ of its value at the base (cf. Eq. (12)). If the loop is approximated by a rectilinear duct, then both $v_{{\rm A}{\rm i}}$ and $v_{{\rm A}{\rm e}}$ vary along the duct. Furthermore the width of the loop also varies with height. These effects were not accounted for in the derivation of the dispersion relation of Eq. (15).

We may conclude that the oscillations observed in our numerical simulations are compatible with kink oscillations of a curved magnetic arcade. A similar conclusion was reached by Murawski et al. (2005), who also report the onset of the n=3 kink oscillations, although for a different arcade model and for a finite value of the plasma $\beta$.

A match for the period of the oscillations found in the simulations with the value of $240{~\rm s}$given by TRACE (Wang & Solanki 2004) is attained if $L/v_{{\rm A}{\rm e}}\simeq130{~\rm s}$. For an Alfvén speed of $v_{{\rm A}{\rm e}}=10^{6}{~\rm m ~s}^{-1}$ we have $L\simeq1.3\times10^{8}{~\rm m}$. According to Table 2 for the loop's height and length we have $h\simeq1.2\times10^{8}{~\rm m}$ and $l\simeq3.4\times10^{8}{~\rm m}$, which agrees with the observed values (Wang & Solanki 2004).

Acknowledgements
The authors express their cordial thanks to Prof. Sami Solanki, Dr. Valery Nakariakov, and Dr. Jaume Terradas for their warm and encouraging comments. M.S.'s & K.M.'s work wasfinancially supported by the grant from the State Committee for Scientific Research Republic of Poland, with KBN grant No. 2 PO3D 016 25. LN is grateful to KBN for support during his visit to KFT-UMCS, Lublin. The magnetohydrodynamics code used in this study was authored by C. Richard DeVore and provided through the sponsorship of NASA's HPCC/ESS program. Wavelet software is disseminated by C. Torrence and G. Compo and is available at URL http://paos.colorado.edu/research/wavelets.

References

 
Copyright ESO 2005