We present a simple model of binary star formation based on the assumption that rotating prestellar cores collapse to form rings and these rings then fragment into protostars. We assume that each ring spawns a small number (
A&A 437, 113-125 (2005)
DOI: 10.1051/0004-6361:20042428
D. A. Hubber - A. P. Whitworth
School of Physics & Astronomy, Cardiff University, 5 The Parade, Cardiff CF24 3YB, UK
Received 24 November 2004 / Accepted 11 March 2005
Abstract
We present a simple model of binary star formation based on
the assumption that rotating prestellar cores collapse to
form rings and these rings then fragment into protostars.
We assume that each ring spawns a small number (
![]() )
of protostars, and that the
condensation of the protostars is sufficiently rapid
that they can subsequently be treated as point masses.
)
of protostars, and that the
condensation of the protostars is sufficiently rapid
that they can subsequently be treated as point masses.
The first part of the model
is therefore to simulate the dynamical evolution of a ring
of ![]() stars and record the properties of
the single stars, binaries and higher multiples that form
as a result of the dissolution of the ring. The masses of
the individual stars in a ring are drawn from a log-normal
distribution with dispersion
stars and record the properties of
the single stars, binaries and higher multiples that form
as a result of the dissolution of the ring. The masses of
the individual stars in a ring are drawn from a log-normal
distribution with dispersion
![]() .
This part of
the model is perfomed for many different realizations of
the ring, to obtain good statistics. It can be formulated
using dimensionless variables and immediately yields the
overall multiplicity.
.
This part of
the model is perfomed for many different realizations of
the ring, to obtain good statistics. It can be formulated
using dimensionless variables and immediately yields the
overall multiplicity.
The second part of the model is to convolve the results of these dimensionless simulations, first with the distribution of core masses, which yields the distributions of multiplicity, mass ratio and eccentricity, as a function of primary mass; and second with the distribution of core angular momenta, which yields the distributions of semi-major axis and period, again as a function of primary mass.
Using the observed distribution of core masses, and a
distribution of core angular momenta which is consistent with the
observations, our model is able to reproduce the observed IMF, the
observed high multiplicity frequency of pre-Main Sequence stars,
the observed distribution of separations, and - for
long-period systems - the observed distributions of eccentricity
and mass-ratio, provided we invoke
![]() and
and
![]() .
.
We presume that for short-period systems the distributions of eccentricity and mass-ratio are modified by the dissipative effects of subsequent tidal interaction and competitive accretion; and that the reduced multiplicity frequency in the field, compared with young clusters, is the result of dynamical interactions between stars formed in different cores but the same cluster, following ring dissolution. Further numerical experiments are required to explore the consequences of such interactions.
Key words: binaries: general - methods: N-body simulations - methods: statistical - stars: formation
One of the main problems in star formation is to explain
the wide range
of scales over which multiple systems form. The observed
distribution of binary separations (e.g. Duquennoy & Mayor 1991,
hereafter DM91; Fischer & Marcy 1992, hereafter FM92) extends
from
![]() to
to
![]() .
The explanation
for this large range of separations must lie in the details of
the star formation process. In the field, the multiplicity
of mature solar-mass stars is around
.
The explanation
for this large range of separations must lie in the details of
the star formation process. In the field, the multiplicity
of mature solar-mass stars is around ![]() (DM91); and in
some star formation regions, the multiplicity of
young solar-mass objects is at least
(DM91); and in
some star formation regions, the multiplicity of
young solar-mass objects is at least ![]() ,
and possibly higher
(Ghez et al. 1993; Reipurth & Zinnecker 1993; Simon et al. 1992;
Patience et al. 2002; Duch
,
and possibly higher
(Ghez et al. 1993; Reipurth & Zinnecker 1993; Simon et al. 1992;
Patience et al. 2002; Duch
![]() ne et al. 2004).
This implies that the genesis of multiple systems is an intrinsic
part of the star formation process. A prestellar core is presumed
to collapse and fragment to produce a dense ensemble of protostars.
Interactions between these protostars and the ambient gas then
determine their final masses, which ones end up in multiple
systems, and their orbital parameters.
ne et al. 2004).
This implies that the genesis of multiple systems is an intrinsic
part of the star formation process. A prestellar core is presumed
to collapse and fragment to produce a dense ensemble of protostars.
Interactions between these protostars and the ambient gas then
determine their final masses, which ones end up in multiple
systems, and their orbital parameters.
Understanding how cores fragment and how many objects are produced requires 3-D hydrodynamical simulations, which are (a) very computer intensive, and (b) highly dependent on the input physics and initial conditions of the cores (e.g. Tohline 2002). Few simulations can be performed, and the statistical properties of the resulting protostars are therefore poorly constrained. Also, such simulations are not able to follow star formation to completion, so the final fate of a star-forming core and the stars it produces is not completely resolved. In particular, the orbital parameters of the resulting multiple systems are unlikely to have reached their final values when a 3-D hydrodynamic simulation is terminated.
A complementary approach to hydrodynamic simulations is to use
an ![]() -body code to follow the ballistic evolution of a
system of protostars, treating them as point masses, and thereby
ignoring complicated gas-dynamical processes like fragmentation,
merger and accretion. This approach has been pioneered by Kroupa
and co-workers (Kroupa 1995a,b; Kroupa & Bouvier 2003a,b;
Kroupa et al. 2003), and by Sterzik & Durisen (1998, 2003), with
a view to explaining the observed statistics of binary stars.
The work of Sterzik & Durisen is similar to the present
study, in that it is mainly concerned with the origin of the
primordial binary properties in small-
-body code to follow the ballistic evolution of a
system of protostars, treating them as point masses, and thereby
ignoring complicated gas-dynamical processes like fragmentation,
merger and accretion. This approach has been pioneered by Kroupa
and co-workers (Kroupa 1995a,b; Kroupa & Bouvier 2003a,b;
Kroupa et al. 2003), and by Sterzik & Durisen (1998, 2003), with
a view to explaining the observed statistics of binary stars.
The work of Sterzik & Durisen is similar to the present
study, in that it is mainly concerned with the origin of the
primordial binary properties in small-![]() clusters (or
subclusters) of protostars. In Kroupa's work the emphasis is
more on how these primordial binary properties are altered
by subsequent dynamical interactions with other multiple systems
and single stars in a wider cluster environment.
clusters (or
subclusters) of protostars. In Kroupa's work the emphasis is
more on how these primordial binary properties are altered
by subsequent dynamical interactions with other multiple systems
and single stars in a wider cluster environment.
Sterzik & Durisen (1998) investigate the binary statistics
resulting from the dynamical dissolution of small-![]() clusters. They pick cluster masses from a power-law core mass
spectrum, and calculate cluster radii from a scaling law of the
form
clusters. They pick cluster masses from a power-law core mass
spectrum, and calculate cluster radii from a scaling law of the
form
![]() (
(
![]() ). Each cluster contains
). Each cluster contains ![]() stars
(
stars
(
![]() )
with masses picked from a
prescribed stellar mass spectrum. Initially the stars are
positioned randomly in the cluster volume, with zero velocity.
Their ballistic evolution is then followed for many crossing
times, using an
)
with masses picked from a
prescribed stellar mass spectrum. Initially the stars are
positioned randomly in the cluster volume, with zero velocity.
Their ballistic evolution is then followed for many crossing
times, using an ![]() -body code, and the properties of the
resulting multiple systems are recorded. However, this model is
unable to reproduce the broad distribution of binary semi-major
axes observed by DM91.
-body code, and the properties of the
resulting multiple systems are recorded. However, this model is
unable to reproduce the broad distribution of binary semi-major
axes observed by DM91.
In a second paper Sterzik & Durisen (2003) repeat these experiments,
but now with clusters which initially are oblate and have some
rotation about their short axis (specifically,
![]() ,
where
,
where ![]() is the ratio of rotational to gravitational energy). In addition,
they relax the assumption of constant
is the ratio of rotational to gravitational energy). In addition,
they relax the assumption of constant ![]() .
Instead stars are
chosen from a prescribed mass distribution until their total mass
adds up to the preordained mass of the cluster, and this then determines
.
Instead stars are
chosen from a prescribed mass distribution until their total mass
adds up to the preordained mass of the cluster, and this then determines
![]() for that cluster. They are able to reproduce the dependence
of multiplicity frequency on primary mass, but the distribution of
semi-major axes is still much narrower than that observed by DM91.
for that cluster. They are able to reproduce the dependence
of multiplicity frequency on primary mass, but the distribution of
semi-major axes is still much narrower than that observed by DM91.
Delgado-Donate et al. (2003) adopt a somewhat different approach,
designed to capture hydrodynamic effects. They model a uniform-density
core of isothermal gas using Smoothed Particle Hydrodynamics, and place
5 sink particles (representing protostellar embryos) at random
positions within the core. Initially each sink contains only ![]() of the total mass, but subsequently the sinks grow by competitive
accretion and interact dynamically with one another, to generate a
mass function which is a good fit to the observed Initial Mass
Function. The resulting binary systems also have the right distribution
of eccentricities. However, the distribution of semi-major axes is
again much narrower than that observed by DM91, and is more similar
to that observed in open clusters (Patience et al. 2002).
of the total mass, but subsequently the sinks grow by competitive
accretion and interact dynamically with one another, to generate a
mass function which is a good fit to the observed Initial Mass
Function. The resulting binary systems also have the right distribution
of eccentricities. However, the distribution of semi-major axes is
again much narrower than that observed by DM91, and is more similar
to that observed in open clusters (Patience et al. 2002).
Kroupa (1995a) explores the evolution of a cluster of binary systems,
and concludes that the properties of G-dwarf binaries in the field
can be reproduced by dynamical interactions between binaries in a
young cluster. Specifically he identifies a dominant mode cluster,
which starts off with 200 binaries formed by random pairings from the
field IMF, and with periods drawn randomly from a distribution covering
1 day to 109 days and having no correlation with primary mass.
Interactions amongst the binaries (termed stimulated evolution)
reduces the binary fraction to ![]()
![]() ,
by selectively removing
low-mass companions (i.e. dynamical biasing), and thereby reproduces
the distributions of period and mass ratio observed in field G-dwarf
binaries by DM91.
,
by selectively removing
low-mass companions (i.e. dynamical biasing), and thereby reproduces
the distributions of period and mass ratio observed in field G-dwarf
binaries by DM91.
In Kroupa (1995b), this model is extended to include the eigenevolution of short-period systems (for example, their tidal circularization). He shows that stimulated evolution does not change the distribution of orbital eccentricities significantly (so the observed distribution must be essentially primordial). In addition, stimulated evolution does not generate sufficient higher multiples by capture to match the observed numbers of triples and quadruples. However, it does produce a distribution of mass ratios for G-dwarf primaries which is in good agreement with the observations of DM91. Kroupa (1995b) also suggests that long-period binaries with large eccentricities are somewhat more likely to be disrupted tidally than long-period binaries with low eccentricities.
Kroupa & Burkert (2001) investigate the ballistic evolution of clusters comprising 100 or 1000 primordial binaries, with a narrow range of initial separations. They find that even under the most favourable conditions, dynamical interactions between binaries cannot produce a distribution of separations as broad as that observed by DM91. The observed separation distribution must therefore be set principally by the properties of primordial binaries.
Kroupa et al. (2001) show that the Pleiades may have evolved from a cluster like the Orion Nebula Cluster (ONC), following loss of residual gas and simultaneous stimulated evolution. They point out that the primordial binary population in the ONC could have been very similar to the pre-Main Sequence binary population that is currently observed in Taurus-Auriga. Subsequent dynamical interactions in the dense cluster environment then changed it into what we see today.
Kroupa & Bouvier (2003a) show that the basic model developed in Kroupa (1995a) can not only explain the high multiplicity fraction for pre-Main Sequence stars in Taurus-Auriga, but also the apparent paucity of brown dwarfs (relative to the ONC). However, the basic model is seemingly unable to explain the binary properties of brown dwarfs: it produces too many stars with brown dwarf companions, and too many wide star-BD and BD-BD systems (Kroupa et al. 2003). It is also unable to reproduce the number of brown dwarfs per star, unless brown dwarfs have different formation mechanisms from stars, and possibly even different formation mechanisms in different environments (e.g. embryo ejection, photoevaporation, etc.; Kroupa & Bouvier 2003b).
In simulations of core collapse which include rotation (e.g.
Bonnell & Bate 1994; Cha & Whitworth 2003; Hennebelle et al. 2004), in particular those where instability against collapse is triggered impulsively, the core may
overshoot centrifugal balance and then bounce to form a dense ring,
which subsequently fragments into multiple protostars. In this paper,
we investigate the consequences of assuming that this is the
dominant mechanism by which a core breaks up into individual protostars.
Specifically, we use an ![]() -body code to follow the ballistic
evolution of protostars which are initially distributed on a ring, and
record their final binary statistics. We scale the mass and radius of
the ring to match the observed distributions of core mass, core radius,
and core rotation; and we compare the resulting binary statistics
with observation. Our approach is similar to that adopted by
Sterzik & Durisen (1998, 2003). The main difference - and the reason
that we obtain a broader distribution of separations, comparable with
what is observed - is that we consider clusters having a distribution
of
-body code to follow the ballistic
evolution of protostars which are initially distributed on a ring, and
record their final binary statistics. We scale the mass and radius of
the ring to match the observed distributions of core mass, core radius,
and core rotation; and we compare the resulting binary statistics
with observation. Our approach is similar to that adopted by
Sterzik & Durisen (1998, 2003). The main difference - and the reason
that we obtain a broader distribution of separations, comparable with
what is observed - is that we consider clusters having a distribution
of ![]() -values (i.e. a range of rotation rates), whereas Sterzik &
Durisen (1998) considered clusters with no rotation, and Sterzik &
Durisen (2003) considered clusters with a universal
-values (i.e. a range of rotation rates), whereas Sterzik &
Durisen (1998) considered clusters with no rotation, and Sterzik &
Durisen (2003) considered clusters with a universal
![]() .
.
In Sect. 2, we review the observations of cores which provide the input parameters for our model. In Sect. 3 we review the observations of stars and binary systems which our model seeks to explain. In Sect. 4 we sketch the sequence of stages through which the model is developed. In Sect. 5, we present the results of dimensionless simulations of ring dissolution. In Sect. 6, we scale the dimensionless results by convolving them with the core mass spectrum and obtain the distributions of multiplicity, eccentricity and mass ratio as a function of primary mass. In Sect. 7, we scale the results, by convolving them with the distribution of core angular momenta, and obtain the distribution of semi-major axes, as a function of primary mass. In Sect. 8, we summarize our main conclusions.
In this section we review briefly the observations of cores which provide the input parameters for our model, namely the distribution of core masses (Sect. 2.1), the mass-radius relation for cores (Sect. 2.2), and the distribution of core rotation rates (Sect. 2.3).
Motte et al. (2001) have measured the core-mass spectrum in Orion B and fitted it with a two part power law:
We shall assume that the initial core radii are given by the
scaling relations
![\begin{figure}
\par\includegraphics[height=8cm,width=5.4cm,angle=270,clip]{2428logb.ps}\end{figure}](/articles/aa/full/2005/25/aa2428-04/Timg44.gif) |
Figure 1:
The histogram and the dotted curve represent the distribution
of observed |
| Open with DEXTER | |
![\begin{figure*}
\par\includegraphics[height=6.9cm,width=4.8cm,angle=270,clip]{24...
...cludegraphics[height=6.9cm,width=4.8cm,angle=270,clip]{2428IMF4.ps}\end{figure*}](/articles/aa/full/2005/25/aa2428-04/Timg46.gif) |
Figure 2:
a) The model IMF for
|
| Open with DEXTER | |
Goodman et al. (1993, hereafter G93) have measured the velocity
profiles across a sample of 43 pre-stellar cores. They find
statistically significant velocity gradients across many of the
cores, and from these velocity gradients they calculate the ratio
of rotational to gravitational potential energy, ![]() ,
on the
asumption of uniform global rotation, for 24 of the cores they
observe. The distribution of these
,
on the
asumption of uniform global rotation, for 24 of the cores they
observe. The distribution of these ![]() -values, normalized
to
-values, normalized
to
![]() ,
is represented by the histogram in
Fig. 1, and also by the dotted line. The dotted line
is obtained by smoothing the individual
,
is represented by the histogram in
Fig. 1, and also by the dotted line. The dotted line
is obtained by smoothing the individual ![]() values with a
Gaussian kernel having
values with a
Gaussian kernel having
![]() ,
,
![\begin{displaymath}%
\left. \frac{{\rm d}{\cal N}_{_{\rm CORE}}}{{\rm d}\log \be...
...eta_i - \log\beta)^2}{2 \sigma_{\log\beta}^2} \right]\right\},
\end{displaymath}](/articles/aa/full/2005/25/aa2428-04/img49.gif) |
(3) |
Burkert & Bodenheimer (2000) have pointed out that the velocity
gradients observed by G93 can also be explained by turbulent
motions in cores, rather than uniform global rotation. By
modelling the turbulence as a Gaussian random velocity field
with power spectrum
![]() with
with
![]() ,
they show that the resulting distribution of
,
they show that the resulting distribution of ![]() -values
fits the G93 observations well, and is approximately log-normal
(see their Fig. 3, lower left panel).
-values
fits the G93 observations well, and is approximately log-normal
(see their Fig. 3, lower left panel).
Therefore we assume a log-normal distribution of ![]() -values:
-values:
In Case A we adopt
![]() and
and
![]() (dashed curve in Fig. 1).
This is the less extreme possibility, in the sense that (a) it is
easily compatible with the constraint of containing the observed
distribution, and (b) it has most of the remaining
(dashed curve in Fig. 1).
This is the less extreme possibility, in the sense that (a) it is
easily compatible with the constraint of containing the observed
distribution, and (b) it has most of the remaining
![]() of
of ![]() values below, but only just below, the observed ones.
It is therefore also our preferred possibility. In Sect. 7
we show that it yields a distribution of separations similar to that of the
pre-Main Sequence binaries collated by Patience et al. (2002).
values below, but only just below, the observed ones.
It is therefore also our preferred possibility. In Sect. 7
we show that it yields a distribution of separations similar to that of the
pre-Main Sequence binaries collated by Patience et al. (2002).
In Case B we adopt
![]() and
and
![]() (dot-dash curve in Fig. 1).
This is the more extreme possibility, in the sense that (a) it is
only just compatible with the constraint of containing the observed
distribution and (b) it has most of the
remaining
(dot-dash curve in Fig. 1).
This is the more extreme possibility, in the sense that (a) it is
only just compatible with the constraint of containing the observed
distribution and (b) it has most of the
remaining ![]() of
of ![]() values not just below, but well below,
the observed ones. In Sect. 7 we show that it yields
a distribution of separations similar to that of the Main Sequence
G-dwarf binaries in the field.
values not just below, but well below,
the observed ones. In Sect. 7 we show that it yields
a distribution of separations similar to that of the Main Sequence
G-dwarf binaries in the field.
We assume that ![]() is not correlated with core mass, as indicated
by G93 (their Fig. 13b).
is not correlated with core mass, as indicated
by G93 (their Fig. 13b).
![\begin{figure}
\par\includegraphics[height=6.9cm,width=4.8cm,angle=270,clip]{242...
...includegraphics[height=6.9cm,width=4.8cm,angle=270,clip]{2428MF4.ps}\end{figure}](/articles/aa/full/2005/25/aa2428-04/Timg58.gif) |
Figure 3:
The multiplicty frequency as a function of primary mass for a)
|
| Open with DEXTER | |
In this section we review briefly the observations of stars and multiple systems which our model seeks to explain, namely the stellar Initial Mass Function (Sect. 3.1), stellar multiplicity (Sect. 3.2), the binary separation distribution (3.3), the binary eccentricity distribution (3.4) and the binary mass-ratio distribution (3.5). We stress that none of these distributions is used as input to the model. They are used solely for comparison with the predictions of the model.
We will adopt the IMF determined by Kroupa (2001), i.e.
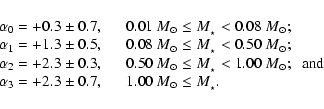 |
(6) |
There are many different measures of multiplicity in use (e.g.
Reipurth & Zinnecker 1993; Goodwin et al. 2004b), but we will
limit our discussion to the multiplicity frequency, ![]() .
If the total number of singles is S, the total number of
binaries is B, the total number of triples is T, the
total number of quadruples is Q, etc., then
.
If the total number of singles is S, the total number of
binaries is B, the total number of triples is T, the
total number of quadruples is Q, etc., then
Furthermore ![]() can be defined as a function of primary mass,
can be defined as a function of primary mass,
For Main Sequence stars, the observed values of
![]() are
are
![]() for primaries in the mass range
for primaries in the mass range
![]() (Martín et al. 2000),
(Martín et al. 2000),
![]() for primaries in the mass range
for primaries in the mass range
![]() (FM92),
(FM92),
![]() for primaries in the mass range
for primaries in the mass range
![]() (DM91) and
(DM91) and
![]() for primaries in the mass range
for primaries in the mass range
![]() (Shatsky &
Tokovinin 2002). These observational points are plotted with error bars
in Fig. 3.
(Shatsky &
Tokovinin 2002). These observational points are plotted with error bars
in Fig. 3.
![\begin{figure}
\par\includegraphics[height=6.9cm,width=4.9cm,angle=270,clip]{242...
...ncludegraphics[height=6.9cm,width=4.9cm,angle=270,clip]{2428Gsma.ps}\end{figure}](/articles/aa/full/2005/25/aa2428-04/Timg73.gif) |
Figure 4:
a) The histogram shows the observed distribution of semi-major
axes for pre-Main Sequence binaries in Taurus, as collated by Patience
et al. (2002), and the dashed line is their best fit to this
distribution. The dotted line shows the predictions of our model for
Case A (
|
| Open with DEXTER | |
For pre-Main Sequence (PMS) stars the situation is less clear,
because observations of PMS binaries only cover a limited range of
separations. However, in those separation ranges where PMS binaries
can be observed, the multiplicity frequency appears to be significantly
higher than for Main Sequence field stars in the same separation ranges.
The compilation of Patience et al. (2002) suggests that for PMS primaries in the mass range
![]() the multipilicity frequency is in the range
the multipilicity frequency is in the range
![]() .
This is shown as a hatched region in Fig. 3.
.
This is shown as a hatched region in Fig. 3.
DM91 have measured the binary properties of a complete sample of multiple systems in the solar
neighbourhood having Main Sequence G-dwarf primaries. They find
the distribution of periods to be approximately log-normal, i.e.
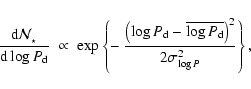 |
(9) |
FM92 find a similar log-normal distribution of periods and separations for multiple systems in the solar neighbourhood having Main Sequence M-dwarf primaries.
Pre-Main Sequence binaries (Simon et al. 1992; Ghez et al. 1993; Reipurth & Zinnecker 1993; Patience et al. 2002) have a distribution of separations that can again be approximated as log-normal over a limited range of separations, but it is
different from that for Main-Sequence binaries in being shifted to larger separations, and somewhat narrower, with
![]()
![]() 0.2 and
0.2 and
![]() (Patience et al. 2002), as illustrated in Fig. 4a.
(Patience et al. 2002), as illustrated in Fig. 4a.
DM91 find that for binaries with Main Sequence G-dwarf primaries,
the eccentricity distribution depends on the period. For long-period
systems (
![]() ,
,
![]() ), the eccentricty
distribution is approximately thermal (i.e.
), the eccentricty
distribution is approximately thermal (i.e.
![]() ,
Valtonen & Mikkola 1991); the DM91 results for long-period
binaries are shown in Fig. 8a. For short-period binaries with Main Sequence G-dwarf primaries (
,
Valtonen & Mikkola 1991); the DM91 results for long-period
binaries are shown in Fig. 8a. For short-period binaries with Main Sequence G-dwarf primaries (
![]() ), the eccentricities tend to be significantly
lower, with a distribution peaked around
), the eccentricities tend to be significantly
lower, with a distribution peaked around
![]() .
In addition,
there appears to be an upper limit on the eccentricity,
.
In addition,
there appears to be an upper limit on the eccentricity,
![]() ,
which decreases with decreasing P and approaches
zero for
,
which decreases with decreasing P and approaches
zero for
![]() .
.
The data available for binaries with Main Sequence primaries of other
spectral types (i.e. M dwarfs and K dwarfs) are limited, particularly
for systems with long periods, but the overall distribution of
eccentricity with period appears to be broadly similar to that for
binaries with G-dwarf Main Sequence primaries. In particular, the
upper limit on the eccentricity,
![]() ,
decreasing with
decreasing P and approaching zero for
,
decreasing with
decreasing P and approaching zero for
![]() ,
appears
to apply to all Main Sequence binaries. This upper limit on e is
normally attributed to tidal circularization of close orbits.
,
appears
to apply to all Main Sequence binaries. This upper limit on e is
normally attributed to tidal circularization of close orbits.
For Pre-Main Sequence binaries the data on eccentricity is limited
to short-period systems (
![]() ). Again there appears
to be an upper limit on the eccentricity,
). Again there appears
to be an upper limit on the eccentricity,
![]() ,
which
decreases with decreasing P (Mathieu 1994). However, this limit is
somewhat larger than that for binaries with G-dwarf Main Sequence primaries,
and it only approaches zero for
,
which
decreases with decreasing P (Mathieu 1994). However, this limit is
somewhat larger than that for binaries with G-dwarf Main Sequence primaries,
and it only approaches zero for
![]() .
Again, this is
consistent with a picture in which close systems are circularized
tidally; in pre-Main Sequence systems there has been less time
for the process to work.
.
Again, this is
consistent with a picture in which close systems are circularized
tidally; in pre-Main Sequence systems there has been less time
for the process to work.
The binary mass ratio, q, is defined by
q = M2 / M1,
where M1 is the primary mass, so necessarily ![]() .
.
DM91 find that for binaries having Main Sequence G-dwarf primaries,
the distribution of q-values is dependent on the period. For
long-period systems (
![]() ), the q-distribution
has a significant peak at around q = 0.3 (see Fig. 8b). For short-period systems, a much flatter distribution is observed, gently rising towards q = 1 (Mazeh et al. 1992).
), the q-distribution
has a significant peak at around q = 0.3 (see Fig. 8b). For short-period systems, a much flatter distribution is observed, gently rising towards q = 1 (Mazeh et al. 1992).
Mass ratios have also been determined for binaries having
Main Sequence M-dwarf primaries by FM92. However, there are too
few systems to reveal any clear dependence on period, and the
sample is incomplete for q < 0.4. For the whole sample,
the distribution of mass ratios is consistent with being flat
in the range ![]() ,
but there is the suggestion of a
decrease for lower q-values. We note that for M-dwarf
primaries these low q-values (
,
but there is the suggestion of a
decrease for lower q-values. We note that for M-dwarf
primaries these low q-values (![]() )
usually correspond
to brown dwarf companions.
)
usually correspond
to brown dwarf companions.
Woitas et al. (2001) have determined mass ratios for pre-Main
Sequence binaries with primary masses corresponding roughly to
G- and M-dwarf Main Sequence stars. The mass ratios depend
somewhat on whose evolutionary tracks are used to determine
individual masses, but again the results are consistent with
a flat distribution at large mass ratios (![]() ). There
appears to be a decrease for
). There
appears to be a decrease for ![]() ,
but this is probably due
to incompleteness.
,
but this is probably due
to incompleteness.
Our model of binary star formation is based on the assumption that all cores are rotating, that they collapse and fragment via ring formation, and that the resulting protostars then interact ballistically to form multiple systems. The aim of the paper is to investigate whether this simple model can explain the observed multiplicity of stars and their distributions of period, separation, eccentricity and mass-ratio.
Consider a rotating prestellar core of mass
![]() which
initially has radius
which
initially has radius
![]() and ratio of rotational to
gravitational energy
and ratio of rotational to
gravitational energy
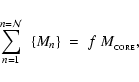 |
(12) |
For fixed ![]() and
and
![]() ,
we first formulate the
dynamical evolution in dimensionless form and simulate a large number
of cases to obtain statistically robust distributions of (a) multiplicity,
(b) orbital eccentricity, e, (c) component mass-ratio,
,
we first formulate the
dynamical evolution in dimensionless form and simulate a large number
of cases to obtain statistically robust distributions of (a) multiplicity,
(b) orbital eccentricity, e, (c) component mass-ratio,
![]() ,
and (d) ratio of orbital separation to ring radius,
,
and (d) ratio of orbital separation to ring radius,
![]() .
.
Then we convolve, first with the distribution of core masses,
to obtain the overall stellar initial mass function (IMF) and
the distributions of multiplicity, eccentricity and mass-ratio
as a function of primary mass; and second with the distribution
of core ![]() -values to obtain the distribution of separations
as a function of primary mass M1.
-values to obtain the distribution of separations
as a function of primary mass M1.
The core mass spectrum is fairly tightly constrained by observation
(Motte et al. 1998; Testi & Sargent 1998; Johnstone et al. 2000;
Motte et al. 2001; Johnstone et al. 2001), and therefore we do not
adjust it (Sect. 2.1). Likewise the relation between
core mass and core initial radius is constrained by
observations, and we do not adjust it (Sect. 2.2).
However, the distribution of ![]() -values is less well constrained,
and we consider two possible distributions (Sect. 2.3).
-values is less well constrained,
and we consider two possible distributions (Sect. 2.3).
![]() and
and
![]() are treated as free parameters.
are treated as free parameters.
The first stage in constructing the model is to perform dimensionless
simulations of low-![]() star clusters. The results of these
simulations can later be scaled up to any mass and size depending on
the given parameters of the core, i.e.
star clusters. The results of these
simulations can later be scaled up to any mass and size depending on
the given parameters of the core, i.e.
![]() and
and ![]() .
.
We assume that a collapsing core forms a centifugally supported ring
having radius
![]() given by Eq. (11).
However, for the dimensionless simulations we set
given by Eq. (11).
However, for the dimensionless simulations we set
![]() .
There are then two free parameters which must be explored in the
dimensionless simulations. First, we must specify the number of stars in
the ring,
.
There are then two free parameters which must be explored in the
dimensionless simulations. First, we must specify the number of stars in
the ring, ![]() .
Second, as posited in Sect. 4.2,
the stellar masses must be drawn at random from a log-normal distribution
having standard deviation
.
Second, as posited in Sect. 4.2,
the stellar masses must be drawn at random from a log-normal distribution
having standard deviation
![]() ,
,
Next, we must specify the initial positions and velocities of
the stars on the ring. If a ring having uniform line-density
fragments into ![]() stars, then each star n forms from
material in an "angular segment'',
stars, then each star n forms from
material in an "angular segment'',
![]() ,
proportional
to it's mass, i.e.
,
proportional
to it's mass, i.e.
| (15) |
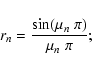 |
(17) |
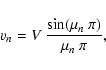 |
(18) |
The ring is then evolved balistically using an adapted version of NBODY3, supplied by Sverre Aarseth (e.g. Aarseth 1999). NBODY3 uses a fourth-order integrator, plus special regularisation routines, which are required for close encounters. 2-body regularisation is used to treat binaries and close encounters by transforming the co-ordinates of the binary components and calculating the motion separately from the rest of the system (e.g. Aarseth 2001). This technique reduces the error generated during close encounters and eliminates the need for extra terms such as gravity softening. Close interactions between three bodies or more can be treated using 3-body, 4-body and chain regularisation. Wider binaries and higher order multiple systems such as hierarchical triples and quadruples are identified by calculating the 2-body energies of all the pairs and selecting the most bound pair.
Simulations are performed for all possible combinations of
![]() ,
and
,
and
![]() ,
and the distributions of multiplicity, semi-major
axis (as a fraction of the radius of the ring), eccentricity,
and mass-ratio are recorded.
,
and the distributions of multiplicity, semi-major
axis (as a fraction of the radius of the ring), eccentricity,
and mass-ratio are recorded.
For each set of parameters (i.e. each pair of ![]() and
and
![]() values), a large number of runs is required to obtain statistically significant distributions.
Each set of runs treats 105 stars in total (e.g. for
values), a large number of runs is required to obtain statistically significant distributions.
Each set of runs treats 105 stars in total (e.g. for ![]() = 4, 2.5
= 4, 2.5 ![]() 104 runs are performed). Small-
104 runs are performed). Small-![]() systems usually dissolve in a few tens of crossing times (e.g. Van Albada 1968; Sterzik & Durisen 1998), so, to ensure that the majority of
systems have dissolved at the end of a simulation, each realisation is run for about 1000 crossing times. We choose a conservative tolerance parameter for the time step, to ensure
accurate integration. Specifically we require that energy is
conserved to 1 part in 105 over the entire integration.
systems usually dissolve in a few tens of crossing times (e.g. Van Albada 1968; Sterzik & Durisen 1998), so, to ensure that the majority of
systems have dissolved at the end of a simulation, each realisation is run for about 1000 crossing times. We choose a conservative tolerance parameter for the time step, to ensure
accurate integration. Specifically we require that energy is
conserved to 1 part in 105 over the entire integration.
Table 1: The numbers of different multiple systems produced in the dimensionless simulations.
![\begin{figure*}
\par\includegraphics[height=6.9cm,width=4.9cm,angle=270,clip]{24...
...ncludegraphics[height=6.9cm,width=4.9cm,angle=270,clip]{2428dlq.ps}\end{figure*}](/articles/aa/full/2005/25/aa2428-04/Timg127.gif) |
Figure 5:
The distributions of a) eccentricity and b) mass-ratio
resulting from the dimensionless simulations. The parameters used are
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=6.9cm,width=4.7cm,angle=270,clip]{242...
...ncludegraphics[height=6.9cm,width=4.7cm,angle=270,clip]{2428sma2.ps}\end{figure}](/articles/aa/full/2005/25/aa2428-04/Timg130.gif) |
Figure 6:
The dimensionless separation distribution for clusters with
a)
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=6.9cm,width=4.9cm,angle=270,clip]{242...
...ncludegraphics[height=6.9cm,width=4.9cm,angle=270,clip]{2428dis2.ps}\end{figure}](/articles/aa/full/2005/25/aa2428-04/Timg131.gif) |
Figure 7:
a) Dimensionless lifetimes of small- |
| Open with DEXTER | |
Typically a cluster dissolves after a few tens of dynamical
times (e.g. Van Albada 1968) leaving ejected singles and a variety
of multiple systems, i.e. binaries, triples and quadruples. In
the present context, we define the dynamical timescale of the initial
ring to be
![]() ;
this is roughly equivalent to the
crossing time for a cluster with isotropic velocity dispersion.
Figure 7a shows the dissolution times,
;
this is roughly equivalent to the
crossing time for a cluster with isotropic velocity dispersion.
Figure 7a shows the dissolution times,
![]() ,
as a function of
,
as a function of
![]() ,
for the
case
,
for the
case
![]() and
and
![]() .
About half of
the rings have dissolved after 20
.
About half of
the rings have dissolved after 20
![]() ,
in agreement
with previous numerical work.
,
in agreement
with previous numerical work.
Table 1 shows the total numbers of singles, binaries,
triples and quadruples produced and the multiplicity frequencies
for different values of ![]() and
and
![]() .
As
.
As
![]() is increased,
is increased, ![]() decreases. The reason for this
is that a small cluster relaxes by dynamically ejecting stars,
leaving a stable multiple system. For higher
decreases. The reason for this
is that a small cluster relaxes by dynamically ejecting stars,
leaving a stable multiple system. For higher ![]() ,
more stars
need to be ejected as singles before the cluster stabilizes, and this
increases S, thereby reducing
,
more stars
need to be ejected as singles before the cluster stabilizes, and this
increases S, thereby reducing ![]() .
We do not consider systems
with very large
.
We do not consider systems
with very large ![]() ,
since such systems are found to produce
too many singles to match the observations. Also hydrodynamical simulations suggest
that ring fragmentation produces only a small numbers of fragments
(e.g. Cha & Whitworth 2003). The effect of changing
,
since such systems are found to produce
too many singles to match the observations. Also hydrodynamical simulations suggest
that ring fragmentation produces only a small numbers of fragments
(e.g. Cha & Whitworth 2003). The effect of changing
![]() is quite small compared with changing
is quite small compared with changing ![]() ,
and is not monotonic.
,
and is not monotonic.
In Figs. 6a and b, we see that the separation distribution
has an approximately log-normal form, but for high-![]() there
is an asymmetric tail stretching to large-separations.
there
is an asymmetric tail stretching to large-separations.
If we fix
![]() and increase
and increase ![]() (Fig. 6a), the peak separation shifts to smaller values and the overall distribution becomes broader.
Increasing
(Fig. 6a), the peak separation shifts to smaller values and the overall distribution becomes broader.
Increasing ![]() tends to increase the number of 3-body interactions which must occur before a stable multiple is formed, and therefore it tends to increase the
binding energy of the surviving multiple, i.e. to decrease its semi-major axis.
The greater number of 3-body interactions also produces a wider logarithmic range of final separations because it is a stochastic process (i.e. one binary system may be stabilized by just two mild interactions and another by four violent interactions).
tends to increase the number of 3-body interactions which must occur before a stable multiple is formed, and therefore it tends to increase the
binding energy of the surviving multiple, i.e. to decrease its semi-major axis.
The greater number of 3-body interactions also produces a wider logarithmic range of final separations because it is a stochastic process (i.e. one binary system may be stabilized by just two mild interactions and another by four violent interactions).
If we now fix ![]() and increase
and increase
![]() (Fig. 6b), the separation distibution shifts to larger
separations and becomes somewhat broader. This is because the number
of 3-body interactions which occur before a stable multiple is
formed is fixed by
(Fig. 6b), the separation distibution shifts to larger
separations and becomes somewhat broader. This is because the number
of 3-body interactions which occur before a stable multiple is
formed is fixed by ![]() and is therefore the same.
However, for large
and is therefore the same.
However, for large
![]() ,
the two most massive stars
which form the final binary contain almost all the mass, and
the remaining stars are so lightweight, that their ejection does
not harden the binary much. Conversely, for small
,
the two most massive stars
which form the final binary contain almost all the mass, and
the remaining stars are so lightweight, that their ejection does
not harden the binary much. Conversely, for small
![]() the two stars which form the final binary are of comparable mass
to those which get ejected, and so their ejection hardens the
remaining binary considerably.
the two stars which form the final binary are of comparable mass
to those which get ejected, and so their ejection hardens the
remaining binary considerably.
The distribution of eccentricities depends strongly on the
value of
![]() ,
and much less on the value of
,
and much less on the value of ![]() .
For low
.
For low
![]() ,
there are few low-eccentricity binaries,
and the numbers increase monotonically with increasing eccentricity,
rising rapidly for very high eccentricities (e > 0.9). The
rise at high eccentricities is characteristic of the dissolution of
2D planar systems; in contrast, the dissolution of 3D systems results
in a thermal distribution of eccentricities (
,
there are few low-eccentricity binaries,
and the numbers increase monotonically with increasing eccentricity,
rising rapidly for very high eccentricities (e > 0.9). The
rise at high eccentricities is characteristic of the dissolution of
2D planar systems; in contrast, the dissolution of 3D systems results
in a thermal distribution of eccentricities (
![]() ,
e.g. Valtonen & Mikkola 1991). As we increase
,
e.g. Valtonen & Mikkola 1991). As we increase
![]() ,
the number of high eccentricity binaries decreases and the distribution becomes flatter (but not flat, see Fig. 5a).
,
the number of high eccentricity binaries decreases and the distribution becomes flatter (but not flat, see Fig. 5a).
The distribution of mass-ratio,
q = M2/M1, is found to be strongly
dependent on
![]() ,
and only lightly dependent on
,
and only lightly dependent on ![]() .
.
![]() controls the range of masses possible in a single core
and thus the possible masses of components in a binary. If there is
a low range of masses available, q cannot differ greatly from unity.
Figure 5b shows that for low
controls the range of masses possible in a single core
and thus the possible masses of components in a binary. If there is
a low range of masses available, q cannot differ greatly from unity.
Figure 5b shows that for low
![]() ,
most of the binaries have mass-ratios greater than 0.5 with a peak at
around q=0.8. As
,
most of the binaries have mass-ratios greater than 0.5 with a peak at
around q=0.8. As
![]() is increased, there are more
binaries with lower mass-ratios and the peak moves to a lower value
of q.
is increased, there are more
binaries with lower mass-ratios and the peak moves to a lower value
of q.
We can now convolve the dimensionless simulations with the core mass spectrum to produce an overall distribution of stellar masses (i.e. an IMF), the multiplicity as a function of primary mass M1, and the distributions of eccentricity e and mass-ratio q, as functions of M1.
First, we look at the IMFs generated by our model, and compare
them with the observed IMF. The model IMFs,
![]() ,
are given by folding together the core mass function,
,
are given by folding together the core mass function,
![]() (Eq. (1)),
and the dimensionless stellar mass spectrum,
(Eq. (1)),
and the dimensionless stellar mass spectrum,
![]() ,
as defined in Sect. 5.1,
,
as defined in Sect. 5.1,
Figure 3 shows the multiplicity frequency as a
function of stellar mass,
![]() ,
for all combination
of
,
for all combination
of
![]() and
and
![]() .
Overall, the model results have a similar trend to the
observations, with
.
Overall, the model results have a similar trend to the
observations, with ![]() increasing from near zero at the
lowest masses to near unity at the highest masses.
increasing from near zero at the
lowest masses to near unity at the highest masses.
As
![]() is increased,
is increased, ![]() increases at all
masses above the peak in the initial mass function. This is
because, as
increases at all
masses above the peak in the initial mass function. This is
because, as
![]() is increased, these masses are
increasingly likely to be the most massive star in the ring,
and hence increasingly likely to form part of a multiple system
due to dynamical biasing (McDonald & Clarke 1993).
is increased, these masses are
increasingly likely to be the most massive star in the ring,
and hence increasingly likely to form part of a multiple system
due to dynamical biasing (McDonald & Clarke 1993).
As ![]() is increased,
is increased, ![]() decreases at all masses.
This is because a small cluster evolves to a stable state (i.e. a binary), or a quasi-stable configuration (i.e. an hierarchical multiple), by ejecting stars. For higher
decreases at all masses.
This is because a small cluster evolves to a stable state (i.e. a binary), or a quasi-stable configuration (i.e. an hierarchical multiple), by ejecting stars. For higher ![]() ,
it is
necessary to eject more stars before stability, or quasi-stability,
is reached, and this decreases the overall multiplicity. If there
is a range of masses, the lower mass stars are ejected preferentially.
,
it is
necessary to eject more stars before stability, or quasi-stability,
is reached, and this decreases the overall multiplicity. If there
is a range of masses, the lower mass stars are ejected preferentially.
Figure 3 shows that for intermediate stellar masses
(
![]() )
)
![]() is almost independent of primary mass M1. This is a direct consequence of using a simple power-law
core mass function and convolving with a dimensionless distribution.
For stars of given mass
is almost independent of primary mass M1. This is a direct consequence of using a simple power-law
core mass function and convolving with a dimensionless distribution.
For stars of given mass
![]() in the range
in the range
![]() to
to
![]() ,
there is an approximately constant ratio
between the number of stars which have formed in a relatively
low-mass core (and are therefore probably the most massive stars
in that core and likely to end up as the primary in a multiple
system) and the number of stars which have formed in a relatively
high-mass core (and are therefore probably one of the less massive
stars in that core and unlikely to end up as a primary). This
approximately constant ratio translates into an approximately
constant
,
there is an approximately constant ratio
between the number of stars which have formed in a relatively
low-mass core (and are therefore probably the most massive stars
in that core and likely to end up as the primary in a multiple
system) and the number of stars which have formed in a relatively
high-mass core (and are therefore probably one of the less massive
stars in that core and unlikely to end up as a primary). This
approximately constant ratio translates into an approximately
constant ![]() .
.
For low masses (
![]() ),
), ![]() decreases rapidly with decreasing M. Low mass stars and brown dwarfs are therefore seldom found as primaries in binary
systems, in agreement with observations. This decrease of
decreases rapidly with decreasing M. Low mass stars and brown dwarfs are therefore seldom found as primaries in binary
systems, in agreement with observations. This decrease of ![]() below
below ![]()
![]() would be less severe if the core mass spectrum were not cut off abruptly below
would be less severe if the core mass spectrum were not cut off abruptly below
![]() (see Eq. (1)).
(see Eq. (1)).
If we consider the multiplicity of pre-Main Sequence stars,
a high multiplicity (>0.8) in the mass range
![]() can only be realised in our model if
can only be realised in our model if
![]() is large (
is large (![]() 0.6).
To obtain a good fit to the IMF, we require
0.6).
To obtain a good fit to the IMF, we require
![]() and
and
![]() (see Sect. 6.1). Therefore we can obtain a good fit to both the observed IMF,
and the observed high
(see Sect. 6.1). Therefore we can obtain a good fit to both the observed IMF,
and the observed high ![]() for PMS stars, with
for PMS stars, with
![]() and
and
![]() .
.
However, there exists no parameter set that results in a
satisfactory fit to the observed IMF, and reproduces the ![]() of mature field stars. For example, to obtain a
of mature field stars. For example, to obtain a ![]() of about 0.6 for G-dwarf primaries requires a low
of about 0.6 for G-dwarf primaries requires a low
![]() ,
but this produces a poor IMF which has too few brown dwarfs. This inconsistency can be resolved, if we retain
,
but this produces a poor IMF which has too few brown dwarfs. This inconsistency can be resolved, if we retain
![]() and the
and the
![]() for G-dwarf primaries is reduced, after ring dissolution, by the interactions which occur between binary systems formed in different rings. This is essentially what
Kroupa (1995a) calls stimulated evolution.
for G-dwarf primaries is reduced, after ring dissolution, by the interactions which occur between binary systems formed in different rings. This is essentially what
Kroupa (1995a) calls stimulated evolution.
![\begin{figure}
\par\includegraphics[height=6.9cm,width=4.9cm,angle=270,clip]{242...
...\includegraphics[height=6.9cm,width=4.9cm,angle=270,clip]{2428Gq.ps}\end{figure}](/articles/aa/full/2005/25/aa2428-04/Timg155.gif) |
Figure 8:
The distributions of a) eccentricity and b) mass-ratio for the long-period G-dwarf binaries observed by DM91 (dot-dashed histogram, are compared with our model results. The
model parameters used are
|
| Open with DEXTER | |
The eccentricity distribution of G dwarfs in our model is
consistent with the observed eccentricity distribution for
long-period systems (DM91; Fig. 8a). We expect that
the eccentricities of short-period systems are modified by tidal
forces between the two components and/or mass equalization by
accretion (e.g. Whitworth et al. 1995; Bate 2000),
neither of which processes is modelled in this work. Therefore
we only compare our model to the observed eccentricity distribution
for long-period systems. The observations are fitted best by
![]() and
and
![]() (see Fig. 8a).
(see Fig. 8a).
For all cases, there is an excess of binaries with very high eccentricity (e>0.9) compared to the observations. The simulations of Delgado et al. (2003) show that these systems would migrate to lower eccentricities if proper account were taken of gas dynamical processes at periastron during the protostellar stage (tidal interactions, mass exchange, etc.). High-eccentricity systems may also be more susceptible to tidal disruption, as noted by Kroupa (1995b).
The mass-ratio distribution from our model, with
![]() and
and
![]() ,
is very
similar to the mass-ratio distribution for G dwarfs observed by DM91 (as illustrated in Fig. 8b), but somewhat different from the mass ratio distribution observed in Taurus by Woitas et al. (2001). This difference may be attributable to
Taurus having an unusual IMF, and in particular a paucity of brown
dwarfs (Briceño et al. 2002; Luhman et al. 2003). However, the
evidence for an unusual IMF in Taurus has recently been called into
question (Luhman 2004; Kroupa et al. 2003), and it may be necessary
to seek another explanation for this difference.
,
is very
similar to the mass-ratio distribution for G dwarfs observed by DM91 (as illustrated in Fig. 8b), but somewhat different from the mass ratio distribution observed in Taurus by Woitas et al. (2001). This difference may be attributable to
Taurus having an unusual IMF, and in particular a paucity of brown
dwarfs (Briceño et al. 2002; Luhman et al. 2003). However, the
evidence for an unusual IMF in Taurus has recently been called into
question (Luhman 2004; Kroupa et al. 2003), and it may be necessary
to seek another explanation for this difference.
In order to obtain the distribution of separations, we must convolve
the dimensionless results with both the distribution of core masses
![]() ,
and the distribution of core
,
and the distribution of core ![]() -values.
-values.
![]() gives the core radius
gives the core radius
![]() through Eq. (2),
and
through Eq. (2),
and ![]() gives the ring radius
gives the ring radius
![]() through Eq. (11). Knowing
through Eq. (11). Knowing
![]() and
and
![]() ,
the dimensionless simulations can be scaled to give the distributions of a and P, as a function of primary mass M1. As explained
in Sect. 2.3 we consider two different
,
the dimensionless simulations can be scaled to give the distributions of a and P, as a function of primary mass M1. As explained
in Sect. 2.3 we consider two different ![]() distributions.
distributions.
Using Case A (
![]() ,
,
![]() ), our model gives the distribution of semi-major axes illustrated
in Fig. 4a (dotted line), where it is compared with the
observations of pre-Main Sequence binaries having primary mass in the
range
), our model gives the distribution of semi-major axes illustrated
in Fig. 4a (dotted line), where it is compared with the
observations of pre-Main Sequence binaries having primary mass in the
range
![]() collated
by Patience et al. (2002; dashed line and histogram). We see that there
is close corresondence between these two distributions. The implication
is that, if cores have a distribution of rotation rates similar
to the one adopted in Case A, then the dynamical dissolution of
small rings of protostars is able to reproduce the distribution
of binary periods observed for pre-Main Sequence stars like
those in Taurus and Ophiuchus.
collated
by Patience et al. (2002; dashed line and histogram). We see that there
is close corresondence between these two distributions. The implication
is that, if cores have a distribution of rotation rates similar
to the one adopted in Case A, then the dynamical dissolution of
small rings of protostars is able to reproduce the distribution
of binary periods observed for pre-Main Sequence stars like
those in Taurus and Ophiuchus.
Using Case B (
![]() ,
,
![]() ), our model gives the distribution of semi-major axes illustrated
in Fig. 4b (dotted line), where it is compared
with the observations of G Dwarf binaries in the field by DM91
(dashed line and histogram). We see that there is a very close
correspondence between the two distributions. The implication
is that, if cores have a distribution of rotation rates similar
to the one adopted in Case B, then the dynamical dissolution of
small rings of protostars is able to reproduce the distribution
of binary periods observed for G-Dwarf binaries in the field by DM91. The problem is that if we persist with the parameters
), our model gives the distribution of semi-major axes illustrated
in Fig. 4b (dotted line), where it is compared
with the observations of G Dwarf binaries in the field by DM91
(dashed line and histogram). We see that there is a very close
correspondence between the two distributions. The implication
is that, if cores have a distribution of rotation rates similar
to the one adopted in Case B, then the dynamical dissolution of
small rings of protostars is able to reproduce the distribution
of binary periods observed for G-Dwarf binaries in the field by DM91. The problem is that if we persist with the parameters
![]() and
and
![]() ,
the resulting
multiplicity fraction for G-dwarf binaries is much higher than
observed, as noted in Sect. 6.2.
,
the resulting
multiplicity fraction for G-dwarf binaries is much higher than
observed, as noted in Sect. 6.2.
However, if most of the stars in the field are formed in populous clusters, we must allow that their binary statistics continue to evolve dynamically after the dissolution of the rings in which they are formed. The cause of further dynamical evolution is that, following dissolution of the individual rings, the stars and binary systems formed in one ring interact with the stars and binary systems formed in other neighbouring rings. In other words, the individual rings are just subclusters within the larger cluster, and interactions on the scale of the cluster also influence the final binary statistics. Kroupa (1995a) has shown that interactions between binaries in clusters can widen the distribution of binary separations somewhat, and reduce the multiplicity from near unity to that observed in the field.
The dimensionless ring dissolution times,
![]() ,
derived in Sect. 5.4, can be converted
into physical times by combining Eqs. (2) and (11) with
,
derived in Sect. 5.4, can be converted
into physical times by combining Eqs. (2) and (11) with
![]() (Sect. 5.4) to obtain
(Sect. 5.4) to obtain
We have developed a model of binary star formation in which cores collapse and bounce to produce rings, and the rings then fragment into protostars. The dynamical evolution of the protostars is followed using Aarseth's NBODY3 code, for many different realizations, and the properties of the resulting multiple systems are recorded.
We adopt (i) the observed distribution of core masses;
(ii) the observed scaling relation between core mass and core
radius; and (iii) two possible log-normal distribution of core
rotation (Case A and Case B), which are consistent with
the limited observations of core rotation, but attempt to take
account of the selection effects which make the rotation of
some cores unmeasurable (see Fig. 1). Case A
(
![]() ,
,
![]() ),
which is our preferred option, assumes that the tendency to
detect higher rotation rates is small, i.e. most of the
undetected rotation rates are not much smaller than the
detected ones. In contrast, Case B (
),
which is our preferred option, assumes that the tendency to
detect higher rotation rates is small, i.e. most of the
undetected rotation rates are not much smaller than the
detected ones. In contrast, Case B (
![]() ,
,
![]() )
assumes that the tendency
to detect higher rotation rates is large, i.e. the
undetected rotation rates are usually much smaller than the
detected ones. We stress that this dichotomy of model rotation
rates is unavoidable, because of the incompleteness of the
observed rotation rates, but it only affects the
distribution of binary separations and the time-scale on
which ring dissolution takes place.
)
assumes that the tendency
to detect higher rotation rates is large, i.e. the
undetected rotation rates are usually much smaller than the
detected ones. We stress that this dichotomy of model rotation
rates is unavoidable, because of the incompleteness of the
observed rotation rates, but it only affects the
distribution of binary separations and the time-scale on
which ring dissolution takes place.
Irrespective of the distribution of core
rotation rates, our model reproduces the observed IMF
(Fig. 2), and the distributions of eccentricity
and mass ratio in long-period binary systems
(Fig. 8), provided only that (a) each ring
spawns
![]() protostars, and (b) the protostars
have a log-normal mass-distribution with standard deviation
protostars, and (b) the protostars
have a log-normal mass-distribution with standard deviation
![]() .
Thus
.
Thus
![]() and
and
![]() are our preferred choices for
these free parameters. The distributions of eccentricity
and mass ratio for short-period binary systems are not
reproduced by our model, but we presume that this is because
our model does not include tidal circularization or mass
equalization by accretion.
are our preferred choices for
these free parameters. The distributions of eccentricity
and mass ratio for short-period binary systems are not
reproduced by our model, but we presume that this is because
our model does not include tidal circularization or mass
equalization by accretion.
The model also reproduces the observed variation of multiplicity with primary mass for mature field stars (Fig. 3), but only if
![]() .
With our preferred values,
.
With our preferred values,
![]() and
and
![]() ,
the model
produces multiplicities which are higher than those observed for mature field stars, but are very similar to those observed for pre-Main Sequence stars, in the mass range
,
the model
produces multiplicities which are higher than those observed for mature field stars, but are very similar to those observed for pre-Main Sequence stars, in the mass range
![]() (this is the only mass range for which reliable pre-main Sequence multiplicities are available). We conclude that the multiplicities resulting from ring
dissolution represent the observed pre-main Sequence population well, and that the pre-main Sequence population then evolves into the observed Main Sequence population
through interactions between stars and binary systems from different
rings in the same cluster.
(this is the only mass range for which reliable pre-main Sequence multiplicities are available). We conclude that the multiplicities resulting from ring
dissolution represent the observed pre-main Sequence population well, and that the pre-main Sequence population then evolves into the observed Main Sequence population
through interactions between stars and binary systems from different
rings in the same cluster.
In a somewhat different context, Kroupa (1995a) has shown that such interactions can reduce the overall multiplicity from ![]() 1.0 to
1.0 to ![]() 0.6. Our model only requires
such interactions to destroy
0.6. Our model only requires
such interactions to destroy ![]()
![]() of pre-Main Sequence binaries,
but a concern with the model is then that binaries with low mass-ratio
will be destroyed preferentially (although not exclussively). This will skew
the distribution of mass-ratios somewhat, and may thereby degrade the agreement
with observations of mature G-dwarfs in the field. We are currently
conducting numerical experiments to explore the effect of interactions
between binary systems from different rings, in the cluster environment.
of pre-Main Sequence binaries,
but a concern with the model is then that binaries with low mass-ratio
will be destroyed preferentially (although not exclussively). This will skew
the distribution of mass-ratios somewhat, and may thereby degrade the agreement
with observations of mature G-dwarfs in the field. We are currently
conducting numerical experiments to explore the effect of interactions
between binary systems from different rings, in the cluster environment.
In order to predict the distribution of semi-major axes, we have to consider the distribution of core rotation rates. If we adopt Case A, our results match closely the distribution of semi-major axes obtained by Patience et al. (2002) for pre-Main Sequence stars (Fig. 4a), and we conclude that further dynamical evolution takes place - presumably involving interactions with protostars from other neighbouring rings - to convert this distribution into the one observed in the field.
Conversely, if we adopt Case B, our results match closely the
peak and width of the separation distribution obtained by DM91 for
field G Dwarfs (Fig. 4b). However, our results do not
match the observed multiplicity frequency for field G-dwarfs, in
the sense that our predicted ![]() -value is too high. It is
unlikely that further dynamical evolution, following
ring dissolution, can rectify this, since to preserve the peak
and width of the separation distribution would require dynamical
processes which destroy, with equal efficiency, binary systems
having widely different separations. Therefore Case A is our
preferred option.
-value is too high. It is
unlikely that further dynamical evolution, following
ring dissolution, can rectify this, since to preserve the peak
and width of the separation distribution would require dynamical
processes which destroy, with equal efficiency, binary systems
having widely different separations. Therefore Case A is our
preferred option.
Most rings have dissolved after
![]() and fewer than
and fewer than ![]() remain after
remain after
![]() .
.
Acknowledgements
We would like to thank Simon Goodwin for many helpful discussions during this work, Gary Fuller for useful comments on the rotation of cores, and Sverre Aarseth for his NBODY3 code and patient help with learning to use it. We also thank the referee for comments which helped to improve the original version of the paper. D.A.H. gratefully acknowledges the support of a PPARC postgraduate studentship, and A.P.W. acknowledges the support of a European Commission Research Training Network awarded under the Fifth Framework (Ref. HPRN-CT-2000-00155).
Stellar masses,
![]() are initially picked
randomly from a log-normal distribution which is symmetric in
are initially picked
randomly from a log-normal distribution which is symmetric in
![]() (Eq. (13)). These masses are then re-scaled by a factor g,
(Eq. (13)). These masses are then re-scaled by a factor g,
![]() ,
so that the total
mass is unity (Eq. (14)). After this re-scaling, the
minimum possible mass is 0, corresponding to
,
so that the total
mass is unity (Eq. (14)). After this re-scaling, the
minimum possible mass is 0, corresponding to
![]() ,
and the maximum possible mass is 1, corresponding to
,
and the maximum possible mass is 1, corresponding to
![]() .
It follows that the distribution can now only be symmetric in
.
It follows that the distribution can now only be symmetric in
![]() if its median lies at
if its median lies at
![]() ,
but this is clearly non-sensical. In fact the distribution is skewed, in the sense of having a tail to low values of
,
but this is clearly non-sensical. In fact the distribution is skewed, in the sense of having a tail to low values of ![]() ,
and the median
is of order
,
and the median
is of order
![]() .
.
The asymmetry arises because we are invoking a finite - indeed small - number of stars. For simplicity consider the case
![]() ,
and assume that the two stars do not have equal mass. If the more massive star is initially (pre re-scaling) exceptionally massive, it
has to be reduced to achieve
,
and assume that the two stars do not have equal mass. If the more massive star is initially (pre re-scaling) exceptionally massive, it
has to be reduced to achieve
![]() ,
and this inevitably decreases the mass of the lower mass star, even if it was already quite small. Conversely, if the less massive star is
initially of exceptionally low-mass, this has little or no influence
on the re-scaling, which is mainly influenced by the more massive star.
It is this asymmetry between the effects of exceptionally high-mass
and exceptionally low-mass stars on the re-scaling that causes the
re-scaled distribution to be skewed, particularly for small
,
and this inevitably decreases the mass of the lower mass star, even if it was already quite small. Conversely, if the less massive star is
initially of exceptionally low-mass, this has little or no influence
on the re-scaling, which is mainly influenced by the more massive star.
It is this asymmetry between the effects of exceptionally high-mass
and exceptionally low-mass stars on the re-scaling that causes the
re-scaled distribution to be skewed, particularly for small ![]() .
The effect disappears as
.
The effect disappears as
![]() .
.