R. van Boekel1,2 - M. Min1 - L. B. F. M. Waters1,3 - A. de Koter1 - C. Dominik1 - M. E. van den Ancker2 - J. Bouwman4
1 - Astronomical Institute "Anton Pannekoek'', University of
Amsterdam, Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
2 -
European Southern Observatory, Karl-Schwarzschildstrasse 2, 85748
Garching bei München, Germany
3 -
Instituut voor Sterrenkunde, Katholieke Universiteit Leuven,
Celestijnenlaan 200B, 3001 Heverlee, Belgium
4 -
Max-Planck-Institut für Astronomie, Königstuhl 17,
69117 Heidelberg, Germany
Received 9 November 2004 / Accepted 4 March 2005
Abstract
We present spectroscopic observations of a large sample of Herbig Ae
stars in the 10 ![]() m spectral region. We perform compositional fits
of the spectra based on properties of homogeneous as well as
inhomogeneous spherical particles,
and derive the mineralogy and typical grain sizes of the
dust responsible for the 10
m spectral region. We perform compositional fits
of the spectra based on properties of homogeneous as well as
inhomogeneous spherical particles,
and derive the mineralogy and typical grain sizes of the
dust responsible for the 10 ![]() m emission. Several trends are
reported that can constrain theoretical models of dust processing in
these systems: i) none of the sources consists of fully pristine dust
comparable to that found in the interstellar medium; ii) all sources
with a high fraction of crystalline silicates are dominated by large
grains; iii) the disks around more massive stars
(
m emission. Several trends are
reported that can constrain theoretical models of dust processing in
these systems: i) none of the sources consists of fully pristine dust
comparable to that found in the interstellar medium; ii) all sources
with a high fraction of crystalline silicates are dominated by large
grains; iii) the disks around more massive stars
(![]()
![]() ,
,
![]()
![]() )
have a higher fraction of crystalline silicates than those around
lower mass stars, iv) in the subset of lower mass stars
(
)
have a higher fraction of crystalline silicates than those around
lower mass stars, iv) in the subset of lower mass stars
(![]()
![]() )
there is no correlation between stellar
parameters and the derived crystallinity of the dust. The
correlation between the shape and strength of the 10 micron
silicate feature reported
by van Boekel et al. (2003) is reconfirmed with
this larger sample. The evidence presented in this paper is combined
with that of other studies to present a likely scenario of dust
processing in Herbig Ae systems. We conclude that the present
data favour a scenario in which the crystalline silicates
are produced in the innermost regions of the disk, close to the star,
and transported outward to the regions where they can be detected by
means of 10 micron spectroscopy. Additionally, we conclude that the final
crystallinity of these disks is reached very soon after active accretion
has stopped.
)
there is no correlation between stellar
parameters and the derived crystallinity of the dust. The
correlation between the shape and strength of the 10 micron
silicate feature reported
by van Boekel et al. (2003) is reconfirmed with
this larger sample. The evidence presented in this paper is combined
with that of other studies to present a likely scenario of dust
processing in Herbig Ae systems. We conclude that the present
data favour a scenario in which the crystalline silicates
are produced in the innermost regions of the disk, close to the star,
and transported outward to the regions where they can be detected by
means of 10 micron spectroscopy. Additionally, we conclude that the final
crystallinity of these disks is reached very soon after active accretion
has stopped.
Key words: stars: circumstellar matter - stars: pre-main sequence - infrared: ISM - ISM: lines and bands - dust, extinction
The interstellar dust which finds its way into a proto-planetary disk will undergo large changes in average size and chemical composition. These changes trace the process of disk dissipation and planet formation. Our solar system contains a precious record of the processes that took place during its formation. Comparison of this record to what is observed around young pre-main-sequence stars provides important insight into the history of our own solar system, and helps to constrain planet formation models.
The infrared spectral region is rich in vibrational resonances of
abundant dust species. Therefore, infrared spectroscopy can be used to
determine the composition of dust in proto-planetary disks,
as well as constrain the size and shape of the dust grains.
Analysis of the infrared (IR) dust emission features originating from the
disk surface layer can
be used
to establish to what extent the dust composition in the disk has
evolved away from that seen in the interstellar medium (ISM). For
instance, crystalline silicates appear absent in the ISM
(e.g. Kemper et al. 2004; Demyk et al. 2000)
but are a substantial component in (some) comets and in
interplanetary dust particles
(Bradley et al. 1992; MacKinnon & Rietmeijer 1987). Clearly, the
refractory material in the proto-solar cloud went through large changes
as the solar system was formed.
It should be kept in mind that spectroscopy in the 10 micron
region is sensitive to a
limited grain size range: large grains (with sizes above a few ![]() m,
depending on chemical composition and wavelength) show only weak
spectral structure and do not contribute significantly to the
infrared emission features.
m,
depending on chemical composition and wavelength) show only weak
spectral structure and do not contribute significantly to the
infrared emission features.
In this work we study the composition of dust in the circumstellar environment of Herbig Ae/Be stars (Herbig 1960), using infrared spectroscopy. We restrict our study to a sub-group of mostly late B and A-F type stars (hereafter HAe stars). These stars show little or no optical extinction and low mass accretion rates, as derived from radio analysis (Skinner et al. 1993), and the lack of significant veiling in optical spectra. For these lower mass members of the Herbig class, evidence for the disk hypothesis is compelling (e.g. Eisner et al. 2003; Grady et al. 2001; Mannings & Sargent 1997; Augereau et al. 2001).
The observed SEDs of these HAe stars can very well be explained with models for gas-rich, passively heated disks in hydrostatic equilibrium and a puffed-up inner rim (Dullemond et al. 2001). These models indicate that the emission observed at near-IR wavelengths is dominated by the inner rim, while the mid-IR spectrum has a large contribution from the dust grains in the warm surface layers of the disk, typically located between a few to several tens of Astronomical Units (AU) from the star. Therefore, mid-IR spectroscopy predominantly relates to the composition of the dust in this surface layer. Van Boekel et al. (2003) argue that due to the turbulent nature of the disks, the small grains observed at the disk surface are well coupled to those in the disk mid-plane, and so the observations of the surface layers likely bear relevance for the overall small grain population.
Observations of the dust composition in HAe disks have revealed a very
rich mineralogy, and strong source to source variations of the dust
composition (e.g. Bouwman et al. 2001).
Some stars show strong 9.7 and 18 ![]() m amorphous
silicate emission, with a band shape and strength very similar to that
seen in the interstellar medium. Other objects have only weak silicate
emission, with sub-structure at 9.2, 10.6 and 11.3
m amorphous
silicate emission, with a band shape and strength very similar to that
seen in the interstellar medium. Other objects have only weak silicate
emission, with sub-structure at 9.2, 10.6 and 11.3 ![]() m due to
crystalline silicates. At longer wavelengths, high-quality observations
only exist for a small number of stars, so far all obtained with the Infrared Space
Observatory (ISO). This situation is rapidly improving due to
ongoing observations with the Infrared Spectrograph
on board of the Spitzer Space Telescope.
The ISO spectra reveal a
mineralogy dominated by the crystalline silicates forsterite and
enstatite, i.e. Mg-rich, Fe-poor materials
(e.g. Meeus et al. 2001; Malfait et al. 1998b; , hereafter ME01). A small group of
stars lacks silicate emission, but shows prominent emission from
Polycyclic Aromatic Hydrocarbons (PAHs) at 3.3, 6.2, 7.7-7.9, 8.6 and 11.3
m due to
crystalline silicates. At longer wavelengths, high-quality observations
only exist for a small number of stars, so far all obtained with the Infrared Space
Observatory (ISO). This situation is rapidly improving due to
ongoing observations with the Infrared Spectrograph
on board of the Spitzer Space Telescope.
The ISO spectra reveal a
mineralogy dominated by the crystalline silicates forsterite and
enstatite, i.e. Mg-rich, Fe-poor materials
(e.g. Meeus et al. 2001; Malfait et al. 1998b; , hereafter ME01). A small group of
stars lacks silicate emission, but shows prominent emission from
Polycyclic Aromatic Hydrocarbons (PAHs) at 3.3, 6.2, 7.7-7.9, 8.6 and 11.3 ![]() m. Many stars show a combination
of silicates and PAHs.
m. Many stars show a combination
of silicates and PAHs.
In recent years, several investigators have attempted to find
correlations between the properties of the dust in the disk of Herbig
stars on the one hand, and global properties of the disk (e.g. disk
geometry) and/or the star (e.g. mass, luminosity, age, binarity) on
the other hand (ME01; Acke & van den Ancker 2004; Bouwman et al. 2001).
Perhaps the most
promising results so far are relations between the dust properties and
the shape of the SEDs of the disk; for instance, the PAH bands are on
average stronger in sources with SEDs that rise at far-IR wavelengths
(ME01).
This has been interpreted in terms of the disk geometry in the
following way. Relatively red SEDs correspond to flaring disks, that have a large
surface which is directly irradiated by the star. If PAHs are present
in this flaring disk surface layer, they will contribute to the
emission in the familiar PAH bands.
Van Boekel et al. (2004b) studied the spatial
distribution of the PAH emission in HD 97048, which was found to be
extended on a scale of 1-2 arcsec (![]() 250 AU)
but clearly associated with the
disk. It is likely that also in the other stars of our sample, the PAH
emission originates from the outer disk region.
Disks that lack a flaring outer
region will have much less prominent PAH emission. Acke & van den Ancker (2004)
confirm this relation between PAH band strength and SED shape using a
sample of about 50 Herbig Ae/Be stars. Acke et al. (2004) note that
stars with flat far-IR SEDs on average have flat millimeter spectral
slopes, suggesting that the cold mid-plane grains in these sources
have grown to larger size than the corresponding grains of stars with
rising far-IR SEDs.
250 AU)
but clearly associated with the
disk. It is likely that also in the other stars of our sample, the PAH
emission originates from the outer disk region.
Disks that lack a flaring outer
region will have much less prominent PAH emission. Acke & van den Ancker (2004)
confirm this relation between PAH band strength and SED shape using a
sample of about 50 Herbig Ae/Be stars. Acke et al. (2004) note that
stars with flat far-IR SEDs on average have flat millimeter spectral
slopes, suggesting that the cold mid-plane grains in these sources
have grown to larger size than the corresponding grains of stars with
rising far-IR SEDs.
Despite considerable efforts, it has proven difficult so far to
determine relations between stellar and dust parameters. This has
prompted us to carry out a comprehensive spectral survey at 10 ![]() m
of isolated HAe stars.
Our goal is to establish relations between star and dust
properties that are of relevance for our understanding of the
evolution of dusty disks around young stars, by
increasing the number of stars for which mid-IR spectra are available.
We have used the
Thermal Infrared Multi Mode Instrument 2
(TIMMI2, Reimann et al. 1998), attached to the 3.6 m
telescope of the European Southern Observatory for our spectral
survey. All known optically bright HAe stars accessible from the La
Silla observatory were included in our initial list of targets. In
practice, high quality data could be obtained for stars with
10
m
of isolated HAe stars.
Our goal is to establish relations between star and dust
properties that are of relevance for our understanding of the
evolution of dusty disks around young stars, by
increasing the number of stars for which mid-IR spectra are available.
We have used the
Thermal Infrared Multi Mode Instrument 2
(TIMMI2, Reimann et al. 1998), attached to the 3.6 m
telescope of the European Southern Observatory for our spectral
survey. All known optically bright HAe stars accessible from the La
Silla observatory were included in our initial list of targets. In
practice, high quality data could be obtained for stars with
10 ![]() m fluxes of about 3 Jy or more.
m fluxes of about 3 Jy or more.
Here we present the results of our spectroscopic survey at 10 ![]() m.
In total, we obtained high quality spectra of a sample of 24 HAe
stars, introduced in Sect. 2. We report on the
observations and data reduction in
Sect. 3. An overview of
the spectra is given in Sect. 4. In
Sect. 5 we present compositional fits to the
silicate feature observed in most of the sources, using the optical
properties of minerals commonly found in circumstellar disks. In
Sect. 6 we discuss the implications of our
results for our understanding of dust processing in HAe disks.
m.
In total, we obtained high quality spectra of a sample of 24 HAe
stars, introduced in Sect. 2. We report on the
observations and data reduction in
Sect. 3. An overview of
the spectra is given in Sect. 4. In
Sect. 5 we present compositional fits to the
silicate feature observed in most of the sources, using the optical
properties of minerals commonly found in circumstellar disks. In
Sect. 6 we discuss the implications of our
results for our understanding of dust processing in HAe disks.
Table 1: Basic parameters of the sample stars. In Cols. 1 and 2 we give the index number by which a star can be identified in tables and figures throughout this work, and the name of the star, respectively. The classification of the sources according to ME01 is listed in the third column. In Col. 5 the distances, derived from direct (Hipparcos) parallax measurements or by association to a star forming region (SFR, Col. 4), are given. For the stars where the distance is determined by association with a SFR we assume an error of 30% in the distance. The spectral type according to the MK classification, the effective temperature and the stellar luminosity are given in Cols. 6-8, respectively. Mass and age estimates for most stars, as derived by comparing their positions in the HR diagram to theoretical pre-main-sequence tracks, are given in Cols. 9 and 10. For HD 101412 we have no reliable distance estimate, and can therefore not determine its luminosity, mass and age.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2339fg1.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg32.gif) |
Figure 1:
The positions of our stars in the HR diagram. The solid
curves indicate the pre-main sequence evolutionary tracks of stars of
different masses; the dashed curve represents the birthline for an
accretion rate of 10 |
| Open with DEXTER | |
Our sample of stars was selected from a larger list of (candidate) Herbig Ae/Be stars studied by Malfait et al. (1998a). This list was constructed by comparing the positions of stars in the Smithsonian Astrophysical Observatory Star Catalog with positions in the Infrared Astronomical Satellite (IRAS) point source catalogue, and subsequent follow-up studies to find the Herbig star candidates. Clearly, such a way to select stars may introduce biases. Our sample does not contain stars that are heavily obscured due to e.g. on-going accretion or an edge-on dusty disk. Instead, our sample is dominated by stars with a relatively "clean'' environment, low optical extinction, and disk orientations that are not close to edge-on. An overview of the stars in the sample and their basic parameters is given in Table 1.
In order to select "genuine'' HAe stars, we applied the following selection criteria:
In order to identify if other selection effects may have entered our
sample, we determined the mass and age (calculated from the birthline,
for an accretion rate of 10-5
![]() )
of the stars by placing them in
the HR diagram (Fig. 1)
and comparing their positions to
PMS evolutionary tracks published by Palla & Stahler (1993).
Throughout this work "(PMS) age''
)
of the stars by placing them in
the HR diagram (Fig. 1)
and comparing their positions to
PMS evolutionary tracks published by Palla & Stahler (1993).
Throughout this work "(PMS) age'' ![]() is defined
as the time that past since the star was on the
birthline, which is when the star becomes optically
visible for the first time.
The luminosity is calculated from the observed photometry and the
measured distance to each star.
The uncertainties in the derived stellar masses and ages listed in
Table 1 and shown in Fig. 2 mainly reflect the uncertainty in the distances (see also van den Ancker et al. 1998).
A comparison of the stellar parameters derived using the
Palla & Stahler (1993) evolutionary tracks to those obtained using more
recent calculations (Palla & Stahler 1999; Siess et al. 2000), shows that
the particular choice of PMS tracks introduces an additional uncertainty in the
stellar ages that is of the same order as those implied by observational uncertainties in the position of the star in the HR diagram. This additional uncertainty is not taken into account.
In Fig. 2 we show the derived stellar
masses versus the PMS ages of the stars.
It is evident from this figure that our sample lacks "old'' (
is defined
as the time that past since the star was on the
birthline, which is when the star becomes optically
visible for the first time.
The luminosity is calculated from the observed photometry and the
measured distance to each star.
The uncertainties in the derived stellar masses and ages listed in
Table 1 and shown in Fig. 2 mainly reflect the uncertainty in the distances (see also van den Ancker et al. 1998).
A comparison of the stellar parameters derived using the
Palla & Stahler (1993) evolutionary tracks to those obtained using more
recent calculations (Palla & Stahler 1999; Siess et al. 2000), shows that
the particular choice of PMS tracks introduces an additional uncertainty in the
stellar ages that is of the same order as those implied by observational uncertainties in the position of the star in the HR diagram. This additional uncertainty is not taken into account.
In Fig. 2 we show the derived stellar
masses versus the PMS ages of the stars.
It is evident from this figure that our sample lacks "old'' (
![]() yr)
disks around 3-4
yr)
disks around 3-4 ![]() stars, and "young'' (
stars, and "young'' (
![]() yr)
disks around stars less massive than about 2.5
yr)
disks around stars less massive than about 2.5 ![]() .
The lack of "old'' disks around 3-4
.
The lack of "old'' disks around 3-4 ![]() stars is likely
caused by the shorter timescale on which the disks around more
massive stars are dispersed. It is therefore not a selection effect.
The lack of "young'' disks around the lower mass stars is
most likely
caused by the fact that these stars do not clear their environment
as rapidly as the more massive (more luminous) stars, and
consequently become optically bright later in their evolution.
Also, at a given age, lower mass PMS stars are less
luminous than more massive ones, and so more easily escape optical
detection.
This selection effect must be taken into account in any discussion
about the evolution of the dust in proto-planetary disks based on
optically selected samples.
stars is likely
caused by the shorter timescale on which the disks around more
massive stars are dispersed. It is therefore not a selection effect.
The lack of "young'' disks around the lower mass stars is
most likely
caused by the fact that these stars do not clear their environment
as rapidly as the more massive (more luminous) stars, and
consequently become optically bright later in their evolution.
Also, at a given age, lower mass PMS stars are less
luminous than more massive ones, and so more easily escape optical
detection.
This selection effect must be taken into account in any discussion
about the evolution of the dust in proto-planetary disks based on
optically selected samples.
ME01 empirically decomposed the infrared spectra of Herbig Ae/Be stars into
three components: a power law component, a cold black-body component,
and solid state emission bands (mainly at 10 and 20 ![]() m). They
found that some sources exhibit both the power law and cold black-body
component, and classified these sources as "group I''. Sources that
lack the cold black-body component were classified as "group II''. A
further division into subgroups "a'' and "b'' serves to indicate the
presence or absence, respectively, of silicate emission bands at 10
and 20
m). They
found that some sources exhibit both the power law and cold black-body
component, and classified these sources as "group I''. Sources that
lack the cold black-body component were classified as "group II''. A
further division into subgroups "a'' and "b'' serves to indicate the
presence or absence, respectively, of silicate emission bands at 10
and 20 ![]() m. It was proposed by ME01 that group I sources have a
large (several hundred AU) flared outer disk, whereas the group II
sources have a smaller, non-flaring outer disk.
m. It was proposed by ME01 that group I sources have a
large (several hundred AU) flared outer disk, whereas the group II
sources have a smaller, non-flaring outer disk.
We classify the sources for which we have newly measured N-band
(8-13.5 ![]() m)
spectra following ME01. Whereas ME01 had ISO spectra of their sources
at their disposal, our classification is based solely on broad-band
photometry. We find that the group I and group II sources are well
separated in an IRAS
m12-m60 color versus
m)
spectra following ME01. Whereas ME01 had ISO spectra of their sources
at their disposal, our classification is based solely on broad-band
photometry. We find that the group I and group II sources are well
separated in an IRAS
m12-m60 color versus
![]() diagram
(Fig. 3), where
diagram
(Fig. 3), where
![]() is the integrated luminosity as derived from the
J,H,K,L and M band photometry, and
is the integrated luminosity as derived from the
J,H,K,L and M band photometry, and
![]() is the
corresponding quantity derived from the IRAS 12, 25 and 60
is the
corresponding quantity derived from the IRAS 12, 25 and 60 ![]() m
points. For group I sources,
m
points. For group I sources,
![]() (
m12-m60)+1.5, group II sources have
(
m12-m60)+1.5, group II sources have
![]() (m12-m60)+1.5. The dashed line in
Fig. 3 indicates the boundary
between the two groups.
We
did not apply color correction to the IRAS data for the classification of the
sources.
(m12-m60)+1.5. The dashed line in
Fig. 3 indicates the boundary
between the two groups.
We
did not apply color correction to the IRAS data for the classification of the
sources.
By use of the
![]() /
/
![]() ratio
(van Boekel et al. 2003)
we compare the near-IR SED to the mid-IR SED.
The near-IR SED is found to be similar for all HAe stars
(Natta et al. 2001), while the major differences occur in
the mid-IR SED. The
ratio
(van Boekel et al. 2003)
we compare the near-IR SED to the mid-IR SED.
The near-IR SED is found to be similar for all HAe stars
(Natta et al. 2001), while the major differences occur in
the mid-IR SED. The
![]() ratio is smaller for group I than
for group II sources. The mid-IR SED of group I sources
is "double-peaked'' compared to the SED of a group II source.
Group I sources are redder than their group II counterparts. The IRAS
m12-m60 color index quantifies this difference in SED shape.
ratio is smaller for group I than
for group II sources. The mid-IR SED of group I sources
is "double-peaked'' compared to the SED of a group II source.
Group I sources are redder than their group II counterparts. The IRAS
m12-m60 color index quantifies this difference in SED shape.
Table 2:
Literature infrared photometry used in this work.
Columns 3-7 list the magnitudes in the J (1.25 ![]() m),
H (1.65
m),
H (1.65 ![]() m), K (2.2
m), K (2.2 ![]() m), L (3.6
m), L (3.6 ![]() m), and M (4.8
m), and M (4.8 ![]() m)
photometric bands, with references in Col. 8. The listed reference
codes are:
BO: Bouchet et al. (1991);
CA: Carter (1990);
CO: Cohen (1973);
CU: Cutri et al. (2003);
DW: de Winter et al. (2001);
DW2: de Winter et al. (1996);
EI: Eiroa et al. (2001);
FO: Fouque et al. (1992);
GL: Glass & Penston (1974);
HI: Hillenbrand et al. (1992);
LA: Lawrence et al. (1990);
MA: Malfait et al. (1998a);
ME: Mendoza (1967);
ST: Strom et al. (1990);
SY: Sylvester et al. (1996);
VR: Vrba et al. (1976);
WA: Waters et al. (1988).
Columns 9-12 contain the infrared fluxes in Jy from the IRAS Point Source
Catalogue (Joint IRAS Science Working Group 1988).
m)
photometric bands, with references in Col. 8. The listed reference
codes are:
BO: Bouchet et al. (1991);
CA: Carter (1990);
CO: Cohen (1973);
CU: Cutri et al. (2003);
DW: de Winter et al. (2001);
DW2: de Winter et al. (1996);
EI: Eiroa et al. (2001);
FO: Fouque et al. (1992);
GL: Glass & Penston (1974);
HI: Hillenbrand et al. (1992);
LA: Lawrence et al. (1990);
MA: Malfait et al. (1998a);
ME: Mendoza (1967);
ST: Strom et al. (1990);
SY: Sylvester et al. (1996);
VR: Vrba et al. (1976);
WA: Waters et al. (1988).
Columns 9-12 contain the infrared fluxes in Jy from the IRAS Point Source
Catalogue (Joint IRAS Science Working Group 1988).
Infrared spectra in the 10 ![]() m atmospheric window were taken in
December 2001 and March 2003 with the TIMMI2 instrument
mounted at the 3.60 m telescope at ESO La Silla observatory.
Conditions were clear during all nights. The low resolution
(
m atmospheric window were taken in
December 2001 and March 2003 with the TIMMI2 instrument
mounted at the 3.60 m telescope at ESO La Silla observatory.
Conditions were clear during all nights. The low resolution
(
![]() )
N band grism was used in combination with a 1.2 arcsec slit. The pixel scale in the spectroscopic mode of TIMMI2 is
0.45 arcsec. A log of our observations is given in
Table 3.
)
N band grism was used in combination with a 1.2 arcsec slit. The pixel scale in the spectroscopic mode of TIMMI2 is
0.45 arcsec. A log of our observations is given in
Table 3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2339fg2.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg44.gif) |
Figure 2:
The derived stellar mass estimates vs.
the pre-main-sequence age estimates derived from a comparison of the position
in the HR diagram to PMS evolutionary tracks of Palla & Stahler (1993).
Our sample shows a clear lack of disks around relatively old
stars of 3-4
|
| Open with DEXTER | |
To deal with the high background signal, we employed standard chopping and
nodding, using a +10 arcsec chop throw North-South, and a -10 arcsec nod throw North-South.
For the spectral calibration of our measurements we regularly observed standard
stars. These observations are used to determine both the
atmospheric extinction per unit airmass (![]() )
and the instrumental
response (
)
and the instrumental
response (![]() )
at all wavelengths. For each science observation, we
determine
)
at all wavelengths. For each science observation, we
determine ![]() and
and ![]() from two calibration measurements:
from two calibration measurements:
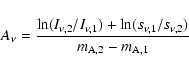 |
(2) |
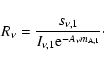 |
(3) |
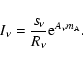 |
(4) |
![\begin{figure}
\par\includegraphics[angle=90,width=8.4cm,clip]{2339fg3.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg63.gif) |
Figure 3:
Classification of the sources based on global SED properties.
We plot the ratio of the near-infrared and infrared luminosity
(see Sect. 2.2) vs. the
IRAS
m12-m60 color (defined as
|
| Open with DEXTER | |
![\begin{displaymath}q\int_{\nu=0}^{\infty} I_{\nu}T_{\nu}{\rm d}\nu = \mathcal{F}...
... \times 10^{-10}
\ \ \ {\rm\left[erg \ s^{-1} cm^{-2}\right]},
\end{displaymath}](/articles/aa/full/2005/25/aa2339-04/img64.gif) |
(5) |
Table 3: Log of the TIMMI 2 observations. We list the observing date (defined as the day on which each observing night began), time (UT), airmass of the observation, and integration time in seconds (Cols. 3-6). The calibrators used for the atmospheric correction are also given, with the time and airmass of the measurements (Cols. 7-12).
ME01 and Acke & van den Ancker (2004) found that the SED correlates with the presence and/or strength of the PAH bands: group I sources tend to show (prominent) PAH emission, while group II sources do not. This trend is confirmed in our sample, but we note that there is considerable scatter. For instance, HD 95881 has little far-IR excess and is thus classified as group II, but, nonetheless, shows clear PAH emission bands.
The silicate band shows very large variations in shape and strength.
The bulk of the emission is in most cases due to amorphous silicates,
but almost all stars show some spectral structure near 11.3 ![]() m,
which can be attributed to forsterite. Note, however, that this
feature blends with the 11.3
m,
which can be attributed to forsterite. Note, however, that this
feature blends with the 11.3 ![]() m PAH band. There are also prominent narrow
emission bands near 9.2 and 10.6
m PAH band. There are also prominent narrow
emission bands near 9.2 and 10.6 ![]() m. These are due to crystalline
enstatite. The spectrum of HD 100546 is
dominated by crystalline forsterite, while that of HD 179218 is dominated
by crystalline enstatite. This latter star shows one of the richest
10
m. These are due to crystalline
enstatite. The spectrum of HD 100546 is
dominated by crystalline forsterite, while that of HD 179218 is dominated
by crystalline enstatite. This latter star shows one of the richest
10 ![]() m spectra observed to date (see
Fig. 5). The resonances of crystalline
enstatite are clearly visible in the spectrum of this source.
The ISO spectrum of
HD 179218 at longer wavelengths
also points to a relatively high abundance of crystalline
enstatite (Bouwman et al. 2001). It is obvious that the nature
of the crystalline dust in our sample shows very large variations,
both in terms of the fraction of the dust that is crystalline, and in
composition.
m spectra observed to date (see
Fig. 5). The resonances of crystalline
enstatite are clearly visible in the spectrum of this source.
The ISO spectrum of
HD 179218 at longer wavelengths
also points to a relatively high abundance of crystalline
enstatite (Bouwman et al. 2001). It is obvious that the nature
of the crystalline dust in our sample shows very large variations,
both in terms of the fraction of the dust that is crystalline, and in
composition.
Table 4: Spectral templates used for the calibrators (see Sect. 3.1).
There are four stars (HD 97048, HD 100453, HD 135344 and HD 169142),
all classified as group I, that show no detectable silicate emission.
Instead, their 10 ![]() m spectra are dominated by PAH emission. The
lack of silicate emission is most simply explained by assuming that
there are no small (<3-5
m spectra are dominated by PAH emission. The
lack of silicate emission is most simply explained by assuming that
there are no small (<3-5 ![]() m) silicate grains in the inner
10-20 AU of the disk. Meeus et al. (2002) derive limits on the
presence of small silicate grains in HD 100453, and argue that all
grains smaller than 4
m) silicate grains in the inner
10-20 AU of the disk. Meeus et al. (2002) derive limits on the
presence of small silicate grains in HD 100453, and argue that all
grains smaller than 4 ![]() m must have been removed. The most likely
cause for the removal of small silicate grains is grain growth, but
apparently this has not affected the population of small carbonaceous
grains to the same extent (van Boekel et al. 2004b).
Possibly, small grains
survive in the outer disk regions. At large distance from the star,
the silicate grains may be too cold to contribute to the 10
m must have been removed. The most likely
cause for the removal of small silicate grains is grain growth, but
apparently this has not affected the population of small carbonaceous
grains to the same extent (van Boekel et al. 2004b).
Possibly, small grains
survive in the outer disk regions. At large distance from the star,
the silicate grains may be too cold to contribute to the 10 ![]() m
spectrum, while the PAHs can still produce significant emission.
This can only occur if the PAHs have not been incorporated into
larger grains. Indeed, van Boekel et al. (2004a)
find evidence for a distance dependence of the typical silicate grain
size in the surface layers of HAe star disks: in the innermost regions
growth has proceeded further than in the outer disk regions.
m
spectrum, while the PAHs can still produce significant emission.
This can only occur if the PAHs have not been incorporated into
larger grains. Indeed, van Boekel et al. (2004a)
find evidence for a distance dependence of the typical silicate grain
size in the surface layers of HAe star disks: in the innermost regions
growth has proceeded further than in the outer disk regions.
![\begin{figure}
\par\includegraphics[angle=90,width=16.5cm,clip]{2339fg4a.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg73.gif) |
Figure 4: N-band spectra of the sources in our sample. The ISM silicate extinction efficiency, plotted in the upper left panel, was taken from Kemper et al. (2004). The AB Aur spectrum was taken by ISO (van den Ancker et al. 2000). Also plotted are the best fits to the spectra (grey curves, see Sect. 5.2). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=16.5cm,clip]{2339fg4b.ps} \end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg74.gif) |
Figure 4: continued. |
| Open with DEXTER | |
In Fig. 6 we show the
ratio of the normalized spectrum at 11.3 and 9.8 ![]() m,
against the silicate peak to continuum ratio
("feature strength'')
m,
against the silicate peak to continuum ratio
("feature strength'')![]() .
Group I sources are indicated with triangles,
group II sources with diamonds (the "outlier'' # 12 is
HD 100546). Sources with a low 11.3/9.8 ratio have a triangular
shaped emission feature, clearly peaked just shortward of 10
.
Group I sources are indicated with triangles,
group II sources with diamonds (the "outlier'' # 12 is
HD 100546). Sources with a low 11.3/9.8 ratio have a triangular
shaped emission feature, clearly peaked just shortward of 10 ![]() m
(e.g. UX Ori, in Fig. 4). Sources
with a high 11.3/9.8 generally have a broad, flat-topped emission
band, often showing substructure (e.g. HD 37806, HD 142527). There is
a clear correlation between the shape and strength of the silicate
feature; stars with a strong feature (i.e. a high peak/continuum
ratio) have a low 11.3/9.8 ratio, whereas stars with weaker silicate
features have higher 11.3/9.8 ratios. This correlation was first
demonstrated in Herbig Ae stars by van Boekel et al. (2003).
Meeus et al. (2003) and Przygodda et al. (2003) have
subsequently shown that the same trend is observed in the silicate
feature of T-Tauri stars.
m
(e.g. UX Ori, in Fig. 4). Sources
with a high 11.3/9.8 generally have a broad, flat-topped emission
band, often showing substructure (e.g. HD 37806, HD 142527). There is
a clear correlation between the shape and strength of the silicate
feature; stars with a strong feature (i.e. a high peak/continuum
ratio) have a low 11.3/9.8 ratio, whereas stars with weaker silicate
features have higher 11.3/9.8 ratios. This correlation was first
demonstrated in Herbig Ae stars by van Boekel et al. (2003).
Meeus et al. (2003) and Przygodda et al. (2003) have
subsequently shown that the same trend is observed in the silicate
feature of T-Tauri stars.
The shape of the emission bands with a low 11.3/9.8 ratio is similar to that of the ISM silicate absorption feature. Such 10 micron features are indicative of small, amorphous silicate grains, i.e. relatively "primitive'' dust. The emission bands with high 11.3/9.8 ratios can be explained with on average larger grains, and a higher degree of crystallinity, i.e. relatively "processed'' dust. Thus, the silicate feature 11.3/9.8 ratio is a measure of the amount of processing that the material has undergone (Bouwman et al. 2001).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2339fg5.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg81.gif) |
Figure 5:
The N-band spectrum of HD 179218 ( upper panel), and the measured mass
absorption coefficients of ortho enstatite taken from
Chihara et al. (2002) ( lower panel). The wavelengths of the most
prominent emission bands are indicated by the dotted lines.
In this object, enstatite grains are an important constituent
of the grain population that causes the 10 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2339fg6.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg82.gif) |
Figure 6: The flux ratio of the normalized spectra at 11.3 and 9.8 micron (a measure for the amount of processing that the material has undergone) versus the peak/continuum ratio of the silicate feature (a measure for the typical grain size). Group I sources are represented by triangles, group II sources by diamonds. In the upper right corner of the figure we have indicated the typical uncertainties in the displayed quantities. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2339fg7.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg83.gif) |
Figure 7:
The mass absorption coefficients of the various templates used
in the fitting procedure (upper 5 panels).
We use grains with volume equivalent radii of 0.1 |
| Open with DEXTER | |
Table 5: Characteristics of the various dust components used in the fitting procedure (see Sect. 5.1). The chemical formulae and assumed grain shapes have been indicated in the second and third column. In the fourth column, we give references for the refractive index data used.
To derive the composition of the silicate dust causing the 10 micron
feature, the observed spectra have been fitted using the most commonly found
dust species in circumstellar material that show spectral structure in
the 10 micron region (see Fig. 7).
These are amorphous and
crystalline olivine and pyroxene, and amorphous silica
(e.g. Bouwman et al. 2001). Amorphous
olivine (Mg2xFe2(1-x)SiO4, where
![]() denotes the magnesium
content of the material)
is the most commonly found
silicate in astrophysical environments. It dominates the 10 micron
extinction caused by dust grains in the ISM
(Kemper et al. 2004). The 10 micron emission spectrum of small
amorphous olivine grains is characterized by a rather broad feature
which peaks at 9.8
denotes the magnesium
content of the material)
is the most commonly found
silicate in astrophysical environments. It dominates the 10 micron
extinction caused by dust grains in the ISM
(Kemper et al. 2004). The 10 micron emission spectrum of small
amorphous olivine grains is characterized by a rather broad feature
which peaks at 9.8 ![]() m. Small amorphous pyroxene grains
(MgxFe1-xSiO3) show an emission feature very similar to
that of amorphous olivine grains, though shifted toward shorter wavelengths.
The emission spectra from small crystalline olivine and pyroxene grains show
strong, narrow resonances that are observed in
for example circumstellar disks (Waters & Waelkens 1998; Bouwman et al. 2001) and comets (Crovisier et al. 1997; Bouwman et al. 2003). From the positions of the resonances in the emission
spectra of these objects it is clear that the magnesium rich
components dominate the emission (see
e.g. Jäger et al. 1998). In our fitting procedure we therefore
use crystalline olivine and pyroxene with x=1, i.e. forsterite and
enstatite respectively. For the amorphous olivine and pyroxene we use
x=0.5.
m. Small amorphous pyroxene grains
(MgxFe1-xSiO3) show an emission feature very similar to
that of amorphous olivine grains, though shifted toward shorter wavelengths.
The emission spectra from small crystalline olivine and pyroxene grains show
strong, narrow resonances that are observed in
for example circumstellar disks (Waters & Waelkens 1998; Bouwman et al. 2001) and comets (Crovisier et al. 1997; Bouwman et al. 2003). From the positions of the resonances in the emission
spectra of these objects it is clear that the magnesium rich
components dominate the emission (see
e.g. Jäger et al. 1998). In our fitting procedure we therefore
use crystalline olivine and pyroxene with x=1, i.e. forsterite and
enstatite respectively. For the amorphous olivine and pyroxene we use
x=0.5.
Studies of interplanetary dust particles (Rietmeijer 1989)
have shown that some of these particles contain large inclusions of
silica (SiO2). Also, from laboratory experiments it is suggested
that when amorphous silicates are annealed to form forsterite, silica
will be formed (see e.g. Fabian et al. 2000). The emission
spectrum of silica in the 10 micron region has a distinct spectral
signature, with a strong feature peaking at 8.9 ![]() m. Therefore,
silica is included as one of the possible dust components.
m. Therefore,
silica is included as one of the possible dust components.
Many of our sources show emission bands at 7.9, 8.6, 11.3 and
12.7 ![]() m that are attributed to PAHs.
In order to include the PAH emission in our compositional fits, we
constructed a simple PAH template. This was done by taking our two highest
quality spectra of sources without a silicate feature
(HD 97048 and HD 169142),
subtracting the continuum emission, and averaging over the two spectra.
The resulting PAH emission spectrum was added as a fit component, and
is shown in the bottom panel of Fig. 7.
m that are attributed to PAHs.
In order to include the PAH emission in our compositional fits, we
constructed a simple PAH template. This was done by taking our two highest
quality spectra of sources without a silicate feature
(HD 97048 and HD 169142),
subtracting the continuum emission, and averaging over the two spectra.
The resulting PAH emission spectrum was added as a fit component, and
is shown in the bottom panel of Fig. 7.
Dust grains in circumstellar environments are most likely aggregates of many different dust species. However, in order to perform an analysis of the abundances of the various components in a large sample of sources, it is not (yet) feasible to do computations for such complex aggregates. If the aggregates are very fluffy, the constituents of which they are composed will interact with the incident radiation as separate entities. Molster et al. (2003) show that indeed a measurement of the infrared spectrum of a relatively large IDP still displays the spectral structure one would expect from much smaller particles. Therefore, we assume that the emission properties of an aggregated structure can be represented by the sum of the emission properties of the constituents (for a similar approach see e.g. Honda et al. 2004; Bouwman et al. 2001; Brucato et al. 1999).
All dust grains contributing to the 10![]() m region will in principle have
their own temperature depending on the grain size and composition as well as on
position in the disk. Consequently, the emission function of the dust will be a
(weighted) sum over blackbody curves of different temperatures. In order to
account for these effects one should use a disk model that self-consistently
describes the disk geometry and all relevant radiation processes. This is
beyond the scope of the analysis presented here. For state of the art disk
models we refer to Dullemond & Dominik (2004). We add that even these
sophisticated models still do not account for many relevant processes,
including the settling and (turbulent) mixing of grains leading to spatial
gradients in the dust properties. Such spatial gradients have been reported by
van Boekel et al. (2004a) to exist in Herbig Ae disks. One should also realize
that even if such a detailed modeling approach was attempted, the modest
wavelength interval provided by the TIMMI2 data would reveal only very limited
information on the temperature distribution. The continuum in the 10 micron
region is a very smooth, almost linear function of wavelength. We therefore
opted to represent the continuum by a single blackbody curve with a
temperature,
m region will in principle have
their own temperature depending on the grain size and composition as well as on
position in the disk. Consequently, the emission function of the dust will be a
(weighted) sum over blackbody curves of different temperatures. In order to
account for these effects one should use a disk model that self-consistently
describes the disk geometry and all relevant radiation processes. This is
beyond the scope of the analysis presented here. For state of the art disk
models we refer to Dullemond & Dominik (2004). We add that even these
sophisticated models still do not account for many relevant processes,
including the settling and (turbulent) mixing of grains leading to spatial
gradients in the dust properties. Such spatial gradients have been reported by
van Boekel et al. (2004a) to exist in Herbig Ae disks. One should also realize
that even if such a detailed modeling approach was attempted, the modest
wavelength interval provided by the TIMMI2 data would reveal only very limited
information on the temperature distribution. The continuum in the 10 micron
region is a very smooth, almost linear function of wavelength. We therefore
opted to represent the continuum by a single blackbody curve with a
temperature, ![]() that is characteristic for the dust emission as a
whole. Inherent in this approach is that we essentially assume that the
temperature of the individual grains is independent of composition and size,
and that there are no gradients in grain properties (per unit mass) throughout
the disk.
that is characteristic for the dust emission as a
whole. Inherent in this approach is that we essentially assume that the
temperature of the individual grains is independent of composition and size,
and that there are no gradients in grain properties (per unit mass) throughout
the disk.
The disk regions that we study are partially optically thick at
10![]() m. However, we assume that the disk surface layer from which the
observed flux originates is optically thin at this wavelength. This must be the
case since we see emission features.
The flux emitted by a distribution of dust grains is then given by
m. However, we assume that the disk surface layer from which the
observed flux originates is optically thin at this wavelength. This must be the
case since we see emission features.
The flux emitted by a distribution of dust grains is then given by
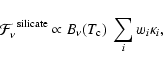 |
(6) |
The shape and structure of the dust grains are very important
parameters determining the feature shape of the emission
spectrum. Usually it is assumed that the grains are homogeneous and
spherical so that Mie theory can be applied to calculate the
![]() .
Another widely used assumption is that the grains are much
smaller than the wavelength of radiation ("Rayleigh limit'') in which
case it is mathematically straightforward to adopt a continuous
distribution of ellipsoids
(CDE Bohren & Huffman 1983; Bouwman et al. 2003).
Since micron sized silicate grains are not in the Rayleigh limit at a
wavelength of 10
.
Another widely used assumption is that the grains are much
smaller than the wavelength of radiation ("Rayleigh limit'') in which
case it is mathematically straightforward to adopt a continuous
distribution of ellipsoids
(CDE Bohren & Huffman 1983; Bouwman et al. 2003).
Since micron sized silicate grains are not in the Rayleigh limit at a
wavelength of 10 ![]() m, we cannot use CDE calculations
to study grain growth.
Furthermore, a comparison between calculations of the mass absorption
coefficients of small crystalline silicates with measurements shows
that we cannot get good agreement using homogeneous spherical
particles (see for example Fabian et al. 2001).
m, we cannot use CDE calculations
to study grain growth.
Furthermore, a comparison between calculations of the mass absorption
coefficients of small crystalline silicates with measurements shows
that we cannot get good agreement using homogeneous spherical
particles (see for example Fabian et al. 2001).
Adopting different grain shapes, Min et al. (2003) showed that the absorption properties can be divided in essentially two categories. One category contains the perfect homogeneous spheres; the other all other investigated shapes, including hollow spheres. Shape effects within the second category do exist, but they are small compared to the differences with homogeneous spheres. One could say that the difference between perfect homogeneous particles and those having other shapes is essentially a result of a breaking of perfect symmetry (see also Min et al. 2003). This implies that we have only very limited information on the true (likely irregular) shape of astrophysical dust grains from spectroscopic analysis. However, a practical implication of this result is that one may represent the absorption properties of irregular grains with sufficient accuracy by adopting the average properties of a distribution of shapes other than that of homogeneous spheres. For this purpose, a practical choice is a distribution of hollow spheres (DHS), simply averaging over the volume fraction occupied by the central inclusion, which ranges from 0 to 1. In this shape distribution, the material volume of the particle is kept constant, thus particles with a high value of f will have a large outer radius. This shape distribution has the advantage that it can be applied for all grain sizes using a simple extension of Mie theory. Min et al. (2003) showed that this indeed gives excellent results for small forsterite grains. Therefore, in this work, the mass absorption coefficients of all crystalline grains (forsterite, enstatite) and silica are calculated with a distribution of hollow spheres. For the amorphous olivine and pyroxene particles we use Mie theory since for these species the effects of shape on absorption properties are minor.
The ![]() are calculated using laboratory measurements of the
refractive index as a function of wavelength. References for the measurements used
for the various dust species are listed in Table 5.
are calculated using laboratory measurements of the
refractive index as a function of wavelength. References for the measurements used
for the various dust species are listed in Table 5.
The dust grains in circumstellar disks most likely have a rather broad size
distribution. In the 10 micron region the observational data are sensitive to
the dust grains with a volume equivalent radius up to a few micron in size.
Larger grains mainly contribute to the continuum. In order to minimize the
number of free parameters in the fitting procedure, we want to sample the size
distribution carefully. We find that the variety of spectral shapes can be best
covered using only two distinct particle sizes, a "small'' particle size with a
material volume equivalent sphere radius
![]() m and a "large'' particle
size with
m and a "large'' particle
size with
![]() m (for a similar approach
see Honda et al. 2004; Bouwman et al. 2001). We have extensively checked
that the results of the analysis using three, four or five particle sizes with
volume equivalent radii ranging up to
m (for a similar approach
see Honda et al. 2004; Bouwman et al. 2001). We have extensively checked
that the results of the analysis using three, four or five particle sizes with
volume equivalent radii ranging up to ![]() m do not change significantly.
The size of the large grain component, when using only two particle sizes, has
to be chosen with care. When it is too large, the difference in absolute value
of the mass absorption coefficients of the small and the large grain component
will be too big. If, for example, one adopts for the large grain size
m do not change significantly.
The size of the large grain component, when using only two particle sizes, has
to be chosen with care. When it is too large, the difference in absolute value
of the mass absorption coefficients of the small and the large grain component
will be too big. If, for example, one adopts for the large grain size
![]() m, one would overestimate the abundance of large grains. This is
especially so for the large crystalline grains and results in an overestimate
of the crystallinity.
The differences between the absolute values of the emissivities of a
0.1 and a 2
m, one would overestimate the abundance of large grains. This is
especially so for the large crystalline grains and results in an overestimate
of the crystallinity.
The differences between the absolute values of the emissivities of a
0.1 and a 2![]() m amorphous grain are not so big.
Actually, adopting 2
m amorphous grain are not so big.
Actually, adopting 2![]() m sized grains
is even slightly better for the large amorphous component
(see also Bouwman et al. 2001).
However, considering both the amorphous
and crystalline component,
m sized grains
is even slightly better for the large amorphous component
(see also Bouwman et al. 2001).
However, considering both the amorphous
and crystalline component, ![]() m is the best choice for the
large grains.
m is the best choice for the
large grains.
In order to keep the number of free parameters in the model small, only two grain sizes are used for every silicate dust type (as discussed above). We thus have contributions of five silicate species, of PAHs and of a blackbody continuum of which the absolute level and shape (characteristic temperature) can be varied. The emissivities of the silicates are multiplied by a blackbody spectrum with the same characteristic temperature as the continuum. This results in 13 free parameters. The silicate and PAH templates are shown in Fig. 7.
To fit the spectra we minimize the reduced ![]() of the entire 10
micron region given by
of the entire 10
micron region given by
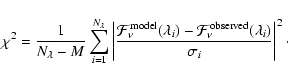 |
(7) |
The measurement errors (![]() )
used in the fitting procedure
represent the statistical noise in the spectra. The calibrator spectra
all have a very high signal to noise ratio (SNR)
and statistical noise of the calibration
observations is negligible. The SNR in our Herbig star spectra range from
)
used in the fitting procedure
represent the statistical noise in the spectra. The calibrator spectra
all have a very high signal to noise ratio (SNR)
and statistical noise of the calibration
observations is negligible. The SNR in our Herbig star spectra range from
![]() 18 in the faintest source (HD 135344) to approximately 60 in
the bright sources (e.g. HD 100546).
There are also systematic uncertainties,
arising from an imperfect calibration, and the uncertainty in the used
spectral templates for the calibrators. Some degree of systematic
error is inevitable, since the science target and calibrator cannot be
measured at the same time and in the same direction. Since we cannot
assess the systematic uncertainties we do not take these into
account. We note, however, that agreement between our ground based
spectra and high SNR ISO spectra is generally very good. For the faint
sources (such as UX Ori), the statistical noise dominates the error
budget. For bright sources (e.g. HD 144432) the systematic
uncertainties may be important, implying that we underestimate
the errors. This will evidently lead to higher
18 in the faintest source (HD 135344) to approximately 60 in
the bright sources (e.g. HD 100546).
There are also systematic uncertainties,
arising from an imperfect calibration, and the uncertainty in the used
spectral templates for the calibrators. Some degree of systematic
error is inevitable, since the science target and calibrator cannot be
measured at the same time and in the same direction. Since we cannot
assess the systematic uncertainties we do not take these into
account. We note, however, that agreement between our ground based
spectra and high SNR ISO spectra is generally very good. For the faint
sources (such as UX Ori), the statistical noise dominates the error
budget. For bright sources (e.g. HD 144432) the systematic
uncertainties may be important, implying that we underestimate
the errors. This will evidently lead to higher ![]() values in the
fit procedure.
values in the
fit procedure.
The errors on the fit parameters are calculated using a Monte Carlo
method. For every spectrum we generate 1000 synthetic spectra,
by randomly adding Gaussian noise to the spectrum with
a distribution of width ![]() at each wavelength point.
This yields 1000 spectra that are all consistent with our
data. On each of these, we perform the exact same compositional fit
procedure, yielding (slightly) different values of the fit
parameters. From the resulting distribution of all fit parameters, we
calculate the mean (which will be our "best fit'' value) and standard
deviation. Besides its simplicity, this method has the advantage that
degeneracies between fit parameters automatically show up as large
errors in these parameters.
at each wavelength point.
This yields 1000 spectra that are all consistent with our
data. On each of these, we perform the exact same compositional fit
procedure, yielding (slightly) different values of the fit
parameters. From the resulting distribution of all fit parameters, we
calculate the mean (which will be our "best fit'' value) and standard
deviation. Besides its simplicity, this method has the advantage that
degeneracies between fit parameters automatically show up as large
errors in these parameters.
Table 6:
The best fit values of the parameters in our compositional fits.
The abundances of small (0.1 ![]() m) and large (1.5
m) and large (1.5 ![]() m) grains of the
various dust species are given
as fractions of the total dust mass, excluding the dust responsible
for the continuum emission. If a species was not found, or unconstrained
by the spectra, this is indicated by a - symbol.
The PAH and continuum flux contributions
(the last two columns) are listed as percentages of the total integrated flux over the 10
m) grains of the
various dust species are given
as fractions of the total dust mass, excluding the dust responsible
for the continuum emission. If a species was not found, or unconstrained
by the spectra, this is indicated by a - symbol.
The PAH and continuum flux contributions
(the last two columns) are listed as percentages of the total integrated flux over the 10 ![]() m region, contained in these
components. These are measures for the relative flux contributions, but cannot be interpreted as relative dust masses.
m region, contained in these
components. These are measures for the relative flux contributions, but cannot be interpreted as relative dust masses.
Figure 4 shows the observed spectra together
with the best fit model spectra. For comparison we also fit the
interstellar extinction as observed towards the galactic center
(Kemper et al. 2004).
The resulting values of the fit
parameters are summarized in Table 6. The overall
quality of the model fits is very good and we thus conclude that the
diversity of the shapes of the observed spectra are well covered by
the choice of the spectral templates. We notice that in some sources
the model fits show slightly more spectral structure between 9 and
11 ![]() m than the observed spectra. This could be caused by the
choice of the shape distribution of the dust grains, which may be too
simple to represent the spectral details of realistic particles. We
also notice that in, for example, HD 179218 we cannot accurately
reproduce the detailed shape of the spectrum. Especially the feature
around 11.3
m than the observed spectra. This could be caused by the
choice of the shape distribution of the dust grains, which may be too
simple to represent the spectral details of realistic particles. We
also notice that in, for example, HD 179218 we cannot accurately
reproduce the detailed shape of the spectrum. Especially the feature
around 11.3 ![]() m is less sharply peaked in the observed spectrum
than in the model fit. This effect can also be seen in other sources,
albeit in a more modest form, and could be caused by a missing dust
component or by the choice of the shape distribution.
m is less sharply peaked in the observed spectrum
than in the model fit. This effect can also be seen in other sources,
albeit in a more modest form, and could be caused by a missing dust
component or by the choice of the shape distribution.
As an objective measure for the goodness of fit, the reduced ![]() of every fit is listed in Table 6. For a good fit
this parameter should be close to unity. The likely reason that we
have relatively high values of
of every fit is listed in Table 6. For a good fit
this parameter should be close to unity. The likely reason that we
have relatively high values of ![]() for about half of the sources
is that we do not take into account the uncertainties on the
for about half of the sources
is that we do not take into account the uncertainties on the
![]() .
These are mainly caused by uncertainties in
the shape, structure and size of the grains, and in the laboratory
measurements of the wavelength dependent refractive indices.
.
These are mainly caused by uncertainties in
the shape, structure and size of the grains, and in the laboratory
measurements of the wavelength dependent refractive indices.
To test whether we have degeneracies between the various templates used in the
fitting procedure we tried to fit each of the silicate templates using
a linear combination of all other templates. The results are shown
in Fig. 8 where we plot the mass
absorption coefficients together with the best fit using the other
templates (here the mass absorption coefficients have been normalized such
that the maximum value equals unity).
The figure shows that almost all of the templates used
have a unique spectral structure that cannot be reproduced by the
other templates.
Only the emission
from large pyroxene grains can be reproduced reasonably well by the
other templates, although significant differences still exist (e.g.
the 11.3 ![]() m feature that is present in the fit to the large
pyroxene opacity in Fig. 8).
The fit consists of 52% large olivine
grains, 43% small pyroxene grains and only 5% of crystalline
silicates. This could result in a slight change in the mass
fraction of large grains when this template is not used. The
crystalline fraction would not be affected significantly. Because
the small pyroxene grains are needed in order to reproduce the short
wavelength side of some of the spectra, we chose to include also the
large pyroxene grains for consistency.
The presence of
large pyroxene grains can be firmly established only in the highest
SNR spectra.
m feature that is present in the fit to the large
pyroxene opacity in Fig. 8).
The fit consists of 52% large olivine
grains, 43% small pyroxene grains and only 5% of crystalline
silicates. This could result in a slight change in the mass
fraction of large grains when this template is not used. The
crystalline fraction would not be affected significantly. Because
the small pyroxene grains are needed in order to reproduce the short
wavelength side of some of the spectra, we chose to include also the
large pyroxene grains for consistency.
The presence of
large pyroxene grains can be firmly established only in the highest
SNR spectra.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{2339fg8.eps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg247.gif) |
Figure 8:
The templates used in the fitting procedure (solid curves)
together with the resulting best fits using all other templates
(dotted curves). The spectra are all normalized such that the maximum
value of the template equals unity. In the left column we show the
templates for the small grains (0.1 |
| Open with DEXTER | |
There are a few points one has to keep in mind when interpreting the results of the analysis presented above.
We will now discuss the trends and correlations observed in the derived fit parameters.
In Fig. 9 we visualize the grain growth
and crystallinity, as implied by our compositional fits.
Horizontally we plot the mass in large (1.5 ![]() m) grains, as a
fraction of the total dust mass, excluding the dust responsible
for the continuum component, and the PAHs. Vertically, we
likewise plot the mass fraction contained in crystalline silicates
in small and large grains,
which is also referred to as the crystallinity of the material.
m) grains, as a
fraction of the total dust mass, excluding the dust responsible
for the continuum component, and the PAHs. Vertically, we
likewise plot the mass fraction contained in crystalline silicates
in small and large grains,
which is also referred to as the crystallinity of the material.
Upon inspection of the figure it is clear
that all disks show signs of substantial removal of small
grains. There are no sources with a mass fraction
in large grains below 30%.
This infers that none of the sources in our sample contains truly
"pristine'' dust. All sources have an appreciable amount of large
grains at their disk surface, compared to ISM conditions. In addition,
all sources have a crystallinity that is higher
than the value we derive for the ISM
(![]() 0.6%; Kemper et al. 2004
derive an even more stringent upper limit of 0.4%).
0.6%; Kemper et al. 2004
derive an even more stringent upper limit of 0.4%).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2339fg9_new.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg251.gif) |
Figure 9:
The relation between grain size and crystallinity found in
our spectral fits. Vertically, we plot the mass fraction of
crystalline grains (forsterite and enstatite). Horizontally,
the mass fraction of large (1.5 |
| Open with DEXTER | |
The derived mass fraction in large grains ranges from ![]() 30% to
30% to
![]() 100%, with most sources at high values.
All sources exhibiting a
high degree of crystallinity have a high mass fraction in large
grains. There are no highly crystalline sources (crystallinity
above 10%) with less than 85% of the dust mass in large grains.
100%, with most sources at high values.
All sources exhibiting a
high degree of crystallinity have a high mass fraction in large
grains. There are no highly crystalline sources (crystallinity
above 10%) with less than 85% of the dust mass in large grains.
There are no sources with a mass fraction of crystalline
material above 35%
(see also Table 6).
It should be kept in mind that the silicate emission we see likely
originates in the surface layer of the disk.
Van Boekel et al. (2003) argue that the disks are
well mixed in the vertical direction, and that therefore the observed
silicate emission should be representative of the whole micron and sub-micron
sized dust population of the disk. We point out that in this work, "crystallization''
refers to the process of crystallizing the material (by whatever
means), spreading it over a significant part of the disk region seen
at 10 ![]() m, and bringing it up to the disk surface where we can see
it spectroscopically. In a scenario where the crystalline silicates
are produced by thermal annealing in the innermost disk regions, and
transported outward by radial mixing, the degree of crystallization is
therefore a measure of the degree of mixing in the disk rather than
the actual process of annealing, which is effectively instantaneous at
the inner disk edge.
m, and bringing it up to the disk surface where we can see
it spectroscopically. In a scenario where the crystalline silicates
are produced by thermal annealing in the innermost disk regions, and
transported outward by radial mixing, the degree of crystallization is
therefore a measure of the degree of mixing in the disk rather than
the actual process of annealing, which is effectively instantaneous at
the inner disk edge.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2339fg10.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg253.gif) |
Figure 10: The fraction of the dust mass contained in silica grains vs. the mass fraction contained in forsterite grains. Following Bouwman et al. (2001) we also plot the theoretical annealing behavior of two different amorphous magnesium silicates, smectite dehydroxylate (SMD; Mg6Si8O22; upper dashed line) and serpentine dehydroxylate (SD; Mg3Si2O7; lower dashed line). The solid line represents the expected annealing behavior of a mixture of these two silicates, consisting of 4% SMD and 96% SD, which was found by Bouwman et al. (2001) to give the best fit to their data. Our data are in better agreement with a pure SMD initial composition. |
| Open with DEXTER | |
In Fig. 10 we plot the mass fraction of
dust contained in forsterite versus that contained in silica
grains. It is clear that these mass fractions are correlated.
Experiments show that when forsterite is created by annealing of an
amorphous silicate, silica is formed as a by-product
(Rietmeijer et al. 1986; Fabian et al. 2000; Hallenbeck & Nuth 1997).
The amount of silica that is created when forming a certain amount of
forsterite depends on the type of amorphous silicate one starts out
with. As already suggested by Bouwman et al. (2001), we can try
to constrain the composition of the amorphous material by measuring
the ratio of forsterite over silica. In the figure
we also plot the expected
annealing behaviour of smectite dehydroxylate (SMD;
Mg6Si8O22) and serpentine dehydroxylate (SD;
Mg3Si2O7). In low temperature condensation experiments, these
are the only magnesium silicates that are formed
(Rietmeijer et al. 1999). Whereas Bouwman et al. (2001)
found that a mixture of 4% of SMD and 96% of SD yielded the best fit
to their data, our results seem to favour an initial composition of
pure SMD. Possibly, the discrepancy between the results found by
Bouwman et al. (2001) and the results found here is connected to
the differences in the dust components used to fit the 10 ![]() m
spectra. Notably, Bouwman et al. (2001) do not include large
silica and forsterite particles.
m
spectra. Notably, Bouwman et al. (2001) do not include large
silica and forsterite particles.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2339fg11.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg254.gif) |
Figure 11: The mass fraction of crystalline material contained in enstatite vs. the total mass fraction of crystalline material. A value of 0 on the vertical axis indicates that all the crystalline silicates present in the disk are in the form of forsterite, while a value of 1 means all crystalline silicates are in the form of enstatite. |
| Open with DEXTER | |
In Fig. 11 we show the mass fraction of crystalline material contained in enstatite versus the total mass fraction of crystalline material. There is a correlation between the fraction of the total mass contained in crystalline silicates and the composition of these crystalline silicates. In general, for sources with a high degree of crystallinity most crystals are in the form of enstatite, while for the sources with a low crystallinity, forsterite is the dominant crystalline species. We will discuss this further in Sect. 6.3.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2339fg12.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg255.gif) |
Figure 12: The mass fraction of large grains in the crystalline grain population vs. the mass fraction of large grains in the amorphous component. When the average size of the amorphous grains is large, the majority of the crystalline material resides in large grains as well. |
| Open with DEXTER | |
The amount of growth that the crystalline material has experienced is compared to the growth in the amorphous component in Fig. 12. If the amorphous grains are large, also the crystalline grains are large, though the correlation is not tight. In all sources in which the amorphous component has more than 85% large grains, also the crystalline component is dominated by large grains. The sources that have less than 85% large grains in the amorphous component all have a low crystallinity (see Fig. 9). Therefore, the ratio of large and small crystals is poorly constrained in these sources, which is reflected in the large errorbars.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2339fg13.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg256.gif) |
Figure 13: The mass fraction of dust in crystalline grains vs. the stellar mass. Higher mass stars show an on average higher fraction of crystalline grains than do lower mass stars. |
| Open with DEXTER | |
The fraction of crystalline silicates is correlated with the mass and luminosity of the central star. This is visualized in Fig. 13. The higher mass (higher luminosity) stars have an on average higher crystallinity than the lower mass (lower luminosity) stars. This correlation will be discussed in Sect. 6.3.
All stars with a stellar mass above about 2.5
![]() (L>60
(L>60
![]() )
have a high fraction (
)
have a high fraction (![]() 85%)
of large grains (Fig. 14).
Possibly, conditions in the disks around more massive stars are more favourable
for growth than they are in the disks around lower mass stars. An alternative
explanation for the observed trend is that
the disks around the more massive stars, which are all relatively
young (Fig. 2), are more turbulent
than those around the less massive, older stars.
As a consequence the mixing in the
young disks will be more efficient. While in the older stars the large
grains decouple from the gas and settle to the midplane (and therefore
will not be detected in the 10 micron spectrum anymore), in the young
stars, larger grains may still reach the disk surface and cause the
observed average grain size to be higher.
85%)
of large grains (Fig. 14).
Possibly, conditions in the disks around more massive stars are more favourable
for growth than they are in the disks around lower mass stars. An alternative
explanation for the observed trend is that
the disks around the more massive stars, which are all relatively
young (Fig. 2), are more turbulent
than those around the less massive, older stars.
As a consequence the mixing in the
young disks will be more efficient. While in the older stars the large
grains decouple from the gas and settle to the midplane (and therefore
will not be detected in the 10 micron spectrum anymore), in the young
stars, larger grains may still reach the disk surface and cause the
observed average grain size to be higher.
We now discuss our fit results in terms of the processes that are
responsible for the dust evolution. We will first briefly outline the
expected conditions that prevailed during the active disk phase
(Sect. 6.1),
i.e. the phase prior to the passive disk phase. For a comprehensive
review of active disks, see e.g. Calvet et al. (2000). The disks of
all stars in our sample are in the passive disk phase. The
characteristics of this phase are discussed in
Sect. 6.2. In
Sect. 6.3 we summarize the constraints
put on dust processing by this work and previous studies. Lastly,
in Sect. 6.4 we sketch a scenario
that is consistent with the current knowledge of dust processing
and disk evolution.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2339fg14.ps}
\end{figure}](/articles/aa/full/2005/25/aa2339-04/Timg259.gif) |
Figure 14:
The mass fraction of dust residing in large grains vs.
the stellar mass. All stars with a mass
|
| Open with DEXTER | |
During this so-called active disk phase, gravitational energy
of the accreting material is dissipated in the disk, thereby heating
it. Accretion rates in the active phase may reach values up to
10
![]()
![]() (Calvet et al. 2000). Close to the central star
the main energy source of the disk is accretion luminosity, whereas
at larger radii irradiation by the star and hot inner disk regions is
expected to be the main heating source of the disk material.
(Calvet et al. 2000). Close to the central star
the main energy source of the disk is accretion luminosity, whereas
at larger radii irradiation by the star and hot inner disk regions is
expected to be the main heating source of the disk material.
The dust in the disk consists mainly of silicates (studied in this work), and carbon. The dust does not contribute significantly to the disk mass in this phase of the disk evolution (the gas over dust ratio is on the order of 102 by mass). However, the thermal radiation emitted by the dust is the dominant cooling process in the disk. In the outer disk regions where the main energy source is irradiation, the dust governs the heating of the disk as well. Therefore, the dust properties determine the disk temperature, except in the innermost disk region where the heating is dominated by viscous dissipation of gravitational energy of the accreting material. The gas, heated by the dust, provides the pressure support of the disk.
The densities in the disk are high, especially near the disk
mid-plane, and one may expect coagulation of small dust grains
into larger aggregates to occur. Already after ![]() 104 yr of
dynamical disk evolution the average mass of a grain can increase by a
factor 101 to 102, and close to the disk midplane the grains
may reach sizes of at least a few times 10
104 yr of
dynamical disk evolution the average mass of a grain can increase by a
factor 101 to 102, and close to the disk midplane the grains
may reach sizes of at least a few times 10 ![]() m up to millimeters
(Suttner & Yorke 2001). Close to the central star
the temperatures in the disk can reach values in excess of 1000 K. At
this temperature the (initially mostly amorphous) silicates are
annealed, to form crystalline silicates. Yet closer to the star,
temperatures reach values of about 1500 K, and crystalline silicates
may form by gas phase condensation of evaporated material.
m up to millimeters
(Suttner & Yorke 2001). Close to the central star
the temperatures in the disk can reach values in excess of 1000 K. At
this temperature the (initially mostly amorphous) silicates are
annealed, to form crystalline silicates. Yet closer to the star,
temperatures reach values of about 1500 K, and crystalline silicates
may form by gas phase condensation of evaporated material.
In some of the stars in our sample, the crystalline silicates appear
so prominent that it is unlikely that their emission arises from the
innermost disk region only; the abundance of crystalline silicates
must be high in a relatively large part of the region of the disk responsible for
the 10 ![]() m emission (the innermost 10-20 AU of the disk).
There are in essence two
possible ways to get crystalline material at
m emission (the innermost 10-20 AU of the disk).
There are in essence two
possible ways to get crystalline material at ![]() 10 AU distance from the
star: (1) thermal processing in the hot inner disk and subsequent
radial transport of this material outward, and (2) local production of
crystalline material at large distance from the star in transient
heating events caused by shocks (e.g. Harker & Desch 2002)
or lightning (e.g. Desch & Cuzzi 2000; Pilipp et al. 1998).
During the active disk phase the
accretion rate in the viscous disk is high and the disk will be
turbulent. This is expected to enable radial mixing of material
(Gail 2004; Bockelée-Morvan et al. 2002).
10 AU distance from the
star: (1) thermal processing in the hot inner disk and subsequent
radial transport of this material outward, and (2) local production of
crystalline material at large distance from the star in transient
heating events caused by shocks (e.g. Harker & Desch 2002)
or lightning (e.g. Desch & Cuzzi 2000; Pilipp et al. 1998).
During the active disk phase the
accretion rate in the viscous disk is high and the disk will be
turbulent. This is expected to enable radial mixing of material
(Gail 2004; Bockelée-Morvan et al. 2002).
The formation of planets and planetesimals is thought to occur during the
passive disk phase. As the disk dissipates on a timescale of
107 yr, the infrared excess fades. The inner disk regions become
devoid of gas and dust first. When the system has evolved into the
debris disk phase
(e.g. ![]() Pictoris, Aumann 1984; Smith & Terrile 1984)
excess emission can be seen above the stellar photospheric emission only
at wavelengths above
Pictoris, Aumann 1984; Smith & Terrile 1984)
excess emission can be seen above the stellar photospheric emission only
at wavelengths above ![]() 10
10 ![]() m.
m.
We first briefly repeat the results that follow directly from our spectral modeling:
When the stellar parameters of our sample stars (see Table 1) are taken into account, several additional conclusions can be drawn:
A number of previous studies have been concerned with the crystalline silicates in HAe star disks. Here we briefly recall some of the results that are of relevance for this study:
Crystallization is most efficient in the disks surrounding the more
massive, more luminous stars (![]()
![]() ,
,
![]()
![]() ). In these disks, the region in which thermal
annealing and chemical equilibrium processes can produce crystalline
silicates is larger than in the disks surrounding lower mass stars.
Additionally, the disks around the more massive stars may be more
turbulent, enabling more efficient radial mixing. It is unclear
whether the crystallization of the dust in the disks occurs
predominantly in the active disk phase, or in the passive phase that
follows. Our data do suggest that the disks reach their final
crystallinity relatively early in the passive phase
(
). In these disks, the region in which thermal
annealing and chemical equilibrium processes can produce crystalline
silicates is larger than in the disks surrounding lower mass stars.
Additionally, the disks around the more massive stars may be more
turbulent, enabling more efficient radial mixing. It is unclear
whether the crystallization of the dust in the disks occurs
predominantly in the active disk phase, or in the passive phase that
follows. Our data do suggest that the disks reach their final
crystallinity relatively early in the passive phase
(![]()
![]() 2 Myr). Therefore, crystallization happens during the active
and/or early passive phase.
2 Myr). Therefore, crystallization happens during the active
and/or early passive phase.
We find a trend between the mass fraction in large grains and the mass fraction in crystalline grains: all sources with a high crystallinity have a high mass fraction in large grains. There are no highly crystalline sources which are dominated by small grains. Most sources have a mass fraction in large grains of more than 80 percent.
We note that there is an important bias in our sample (and probably in
most samples of Herbig stars studied in the literature): the more
massive sample stars (![]() 3
3
![]() ,
"high mass'') are younger than
the less massive (
,
"high mass'') are younger than
the less massive (![]() 2.5
2.5
![]() ,
"low mass'') stars.
There are no low mass stars younger than 1 Myr in our sample. In
order to establish the disk conditions at the end of the active disk
phase, which precedes the passive phase, it is essential that
such very young, low mass stars are found and studied. Since these
stars may still be enshrouded in circumstellar material, they may
have to be selected using infrared data.
,
"low mass'') stars.
There are no low mass stars younger than 1 Myr in our sample. In
order to establish the disk conditions at the end of the active disk
phase, which precedes the passive phase, it is essential that
such very young, low mass stars are found and studied. Since these
stars may still be enshrouded in circumstellar material, they may
have to be selected using infrared data.
We find a trend between the derived crystallinity of the dust and the
mass (and luminosity) of the central star: the disks around stars with
a mass larger than 2.5
![]() (a luminosity above 60
(a luminosity above 60
![]() )
have
a higher crystallinity (
)
have
a higher crystallinity (![]() 20%) than the less massive, less
luminous stars. Within the subset of sources with a stellar mass
below 2.5
20%) than the less massive, less
luminous stars. Within the subset of sources with a stellar mass
below 2.5
![]() ,
no correlation between crystallinity and stellar
parameters (mass, luminosity, age) is seen. These lower mass stars in
our sample are all older than
,
no correlation between crystallinity and stellar
parameters (mass, luminosity, age) is seen. These lower mass stars in
our sample are all older than ![]() 2 Myr. Since in this subset there
is no correlation between age and crystallinity, we conclude that the
crystallization of the material predominantly happens in the active or
early passive disk phase (before 2 Myr).
2 Myr. Since in this subset there
is no correlation between age and crystallinity, we conclude that the
crystallization of the material predominantly happens in the active or
early passive disk phase (before 2 Myr).
The evidence presented in this paper combined with conclusions from other studies seems to favour a scenario in which crystalline silicates are produced in the innermost regions of the disk and transported outwards. Spatially resolved spectra of these disks, as can be obtained using for example the MIDI instrument on the Very Large Telescope Interferometer, will provide crucial information on the radial dependence of the mineralogy of the dust in these disks. In addition, measurements at longer wavelengths can probe colder regions (further out) in the disk which can provide further constraints on the temperature structure and spatial distribution of the dust.
Acknowledgements
We wish to thank the referee, John Mathis, for helpful comments and suggestions. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. We gratefully acknowledge J. W. Hovenier for thorough reading and valuable comments on an earlier version of the manuscript.