A&A 437, 375-381 (2005)
DOI: 10.1051/0004-6361:20042003
Catalogue of the orbital elements, masses, and luminosities for short-periodic RS CVn-type eclipsing systems![[*]](/icons/foot_motif.gif)
G. Dryomova
1 -
E. Perevozkina2 -
M. Svechnikov1
1 - Ural State University,
Lenin Street 51, K-83, Yekaterinburg, 620083, Russia
2 -
Ministry of Education of Sverdlovsk region,
Malysheva Street 33, Yekaterinburg, 620075, Russia
Received 13 September 2004 / Accepted 31 January 2005
Abstract
New data on the orbital elements, masses, and luminosities were collected
for 31 pre-contact binary systems of short-periodic RS CVn-type.
We treat the catalogued data statistically in order to accurately define the
properties and evolutionary status of each class system. The ages of pre-contact
systems were estimated by the isochrone method. Numerous comments and
bibliographic references to the catalogue are also included.
Key words: binaries: eclipsing - catalogs - stars: fundamental parameters
Our catalogue updates the section devoted to DW-type eclipsing variable stars
in the "Catalogue of the orbital elements, masses, and luminosities of close
binary systems'' by Svechnikov (1986). According to the
classification by Svechnikov (1985) specially developed for
close binaries, the DW abbreviation means
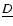 etached (components
far from the contact configuration) eclipsing binaries similar in their physical
characteristics to stars of
etached (components
far from the contact configuration) eclipsing binaries similar in their physical
characteristics to stars of
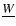
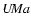 -type and with orbital periods
(
-type and with orbital periods
(
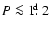 )
noticeably greater than those of W
)
noticeably greater than those of W 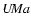 -type stars
(
-type stars
(
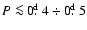 ). Another designation widely used in the
literature for DW eclipsing binaries is "short-periodic'' RS CVn-type systems.
). Another designation widely used in the
literature for DW eclipsing binaries is "short-periodic'' RS CVn-type systems.
The phenomenological class of RS CVn-type binaries was defined by
Hall (1972) to comprise all known sorts of anomalous objects with
various chromospheric activity levels. These may be single stars, as well as
binaries, consisting of far evolved components, subgiants, Main-Sequence (MS),
and pre-MS stars, the orbital periods of which vary in a huge range from
twelve hours to ten or more years. The large sample of such objects were
catalogued and studied by Strassmeier et al. (1989; 1993).
It is quite clear that an RS CVn-class that is so inhomogeneous in its
properties will be difficult to study. On the basis of intensive photometric
and spectroscopic analysis of observational data, therefore, it was advisable
to separate out the chromospherically active close binary systems with orbital
periods less than
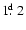 into an independent category of "short-periodic''
RS CVn-type systems (DW-stars). Also all binaries presented in the
DW-catalogue are eclipsing systems whose variability is rigorously established
from photometric light curves, whereas more than a half of the systems from
Strassmeier's catalogue (1993) are not eclipsing and their
variability is determined from the wave migration period. This past decade has
offered plentiful observational information about short-periodic RS CVn-type
stars.
into an independent category of "short-periodic''
RS CVn-type systems (DW-stars). Also all binaries presented in the
DW-catalogue are eclipsing systems whose variability is rigorously established
from photometric light curves, whereas more than a half of the systems from
Strassmeier's catalogue (1993) are not eclipsing and their
variability is determined from the wave migration period. This past decade has
offered plentiful observational information about short-periodic RS CVn-type
stars.
All DW-type systems presented in the new version of the catalogue are
characterized by well-studied photometric light curves and radial velocity
curves (in most cases). Therefore, we can consider absolute and relative
elements of spectroscopic and photometric orbits as reliable data, in contrast
to other earlier catalogues by Strassmeier et al. (1989,
1993) and Svechnikov & Kuznetsova (1990).
DW-type binaries have always attracted attention due to their solar-like
activity and been intensively studied in past years to understand the nature
of their activity. The principle observation features of the short-periodic
RS CVn-type systems are the following:
- obvious asymmetry and significant peculiarities inherent
in photometric light curves of DW systems;
- presence of the long-period regular constituent in a changing light
known as the photometric wave, or distortion wave, interpretation
of which is based on the hypothesis of a developed structure of photospheric
spots covering the stellar surface;
- existence of intensive emission lines such as the well-known doublet H and K Ca II, the resonance doublet Mg II, and the line He I
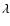 10 830 Å in the spectra of
components. It serves as evidence of chromospheric activity in these
systems;
10 830 Å in the spectra of
components. It serves as evidence of chromospheric activity in these
systems;
- irregular variations in the orbital period linked with the magnetic
stellar wind emanating from the star (to explain the orbital jumps, the
surface magnetic fields may not exceed a few hundred Gauss);
- powerful radio-, IR- and X-ray flashes;
The rich observations of this class of binaries deserve careful study and
explain why we have compiled a new catalogue of DW-binaries.
A lot of new data concerning the photometric and spectroscopic elements of
orbits of eclipsing systems have been gathered since the catalogue by Svechnikov
(1986) was published. Modern all-wave observations, the newest
instrumental capabilities of which include CCD arrays and multicoloured
photometers, considerably increase the accuracy of light curve definition
for eclipsing variables. Extra-atmospheric observations from satellites have
been carried out for some of these systems. A series of pre-contact binaries
was registered in the list of program variable stars of the main mission of the
HIPPARCOS satellite (1989-1996) in order to more precisely define
orbital periods, amplitudes, epochs, and variability types for all variable stars.
Using powerful computers to apply the up-to-date methods of light curve
simulation and spectra treatment, including the synthesis method of light
curve and direct methods of photometric elements estimation, will add to the
number of well-studied stars.
High-dispersion spectrograms that exclude blending effects for spectral lines
enable us to make reliable estimations of the mass ratio and proper masses for
each component. As a result, all the above-mentioned modernizations concerning
observations and data require periodic revision of catalogues and especially
of the catalogue for pre-contact systems. The new version of this catalogue
contains 31 DW-type systems, while only seven systems of this class
are presented in the previous version of the catalogue by Svechnikov (1986).
During 1986-2003 a series of photometric catalogues of the eclipsing variables
was published:
- "sixth catalogue of the orbits of visual double systems'' containing
information about 1660 orbits;
- the INCA catalogue containing 11 434 program double systems in the
framework of the
HIPPARCOS project was supplemented with 3000 newly
discovered doubles, among which 917 are eclipsing variables of EA,
EB, and EW types (347 newly discovered);
- a photometric catalogue of light curves constructed from 110 points for
each of 118 204 variable stars.
Thus taking into account the new observational data, and thanks to the Internet
for a rapid information and discussion (for some eclipsing variables the
photometric solutions were unmatched with each other), the updated catalogue
of pre-contact systems containing information about masses, radii, luminosities,
and other characteristics of a star has been compiled. The archive card catalogue
of relative and absolute elements of the close binary systems started as far
back as the 1961 by Svechnikov has served as a basis of this one.
For systems whose spectroscopic elements are unknown and whose absolute
characteristics are impossible to directly compute, the statistical relations
such as "mass-spectrum'' (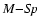 )
and "spectrum-effective temperature'' (
)
and "spectrum-effective temperature'' (
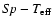 )
which were obtained and substantiated in Svechnikov (1985) were
employed here to estimate mass and effective temperature of the primary component
by its known spectrum. For the satellites the values of mass and effective
temperature are found from known photometric solutions based on mass ratio and
the surface brightness ratio of components, respectively. As for determining
the major semi-axis and absolute radii, the generalized third Kepler's law is
used along with simple geometrical proportions that connect relative radii known
from photometric solutions with absolute ones, for instance WZ And, RX Ari,
AE Cas, ST Cen, AR Dra, MT Her, CN Lac, and UU Lyn.
The percentage of similar binaries is approximately 25
)
which were obtained and substantiated in Svechnikov (1985) were
employed here to estimate mass and effective temperature of the primary component
by its known spectrum. For the satellites the values of mass and effective
temperature are found from known photometric solutions based on mass ratio and
the surface brightness ratio of components, respectively. As for determining
the major semi-axis and absolute radii, the generalized third Kepler's law is
used along with simple geometrical proportions that connect relative radii known
from photometric solutions with absolute ones, for instance WZ And, RX Ari,
AE Cas, ST Cen, AR Dra, MT Her, CN Lac, and UU Lyn.
The percentage of similar binaries is approximately 25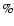 .
In rare cases of
lacking information on the relative radii of components, the "mass-radius''
(M-R) relation obtained by Svechnikov (1985) is employed when
calculating the absolute radii, at which point relative radii are deduced from
inverse geometrical proportions.
.
In rare cases of
lacking information on the relative radii of components, the "mass-radius''
(M-R) relation obtained by Svechnikov (1985) is employed when
calculating the absolute radii, at which point relative radii are deduced from
inverse geometrical proportions.
All stars are listed alphabetically according to Roman constellations:
- 1.
- the sequence number is indicated in the first column;
- 2.
- the pre-contact system name is given in the second column;
- 3.
- orbital period P (changeability of which is marked by
the asterisk "
 ''), the spectra, and luminosity classes of the
components are in the third column. If the satellite spectrum
''), the spectra, and luminosity classes of the
components are in the third column. If the satellite spectrum
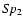 was derived from the known spectrum class of the
primary component
was derived from the known spectrum class of the
primary component
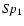 and surface brightness ratio
J1/J2, then it is enclosed in square brackets;
and surface brightness ratio
J1/J2, then it is enclosed in square brackets;
- 4.
- mass ratio q (
M2/M1) and major semi-axis A expressed in units of Sun radius
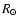 are placed into
the fourth column. If q is determined from the spectroscopy
via radial velocity curves known for both components ("double-lined
spectra'' case) then its value is underlined by a solid line; its value
is underlined by a dashed line when q is found via the mass
function derived from the radial velocity curve known for the more
massive component only ("single-lined spectrum'' case) under the
assumption that this component satisfies "mass-luminosity''
are placed into
the fourth column. If q is determined from the spectroscopy
via radial velocity curves known for both components ("double-lined
spectra'' case) then its value is underlined by a solid line; its value
is underlined by a dashed line when q is found via the mass
function derived from the radial velocity curve known for the more
massive component only ("single-lined spectrum'' case) under the
assumption that this component satisfies "mass-luminosity''
 dependence for MS stars (so-called
dependence for MS stars (so-called
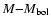 method developed
in detail by Svechnikov 1969); and if q is
photometrically estimated via light curves then its value is not
underlined.
method developed
in detail by Svechnikov 1969); and if q is
photometrically estimated via light curves then its value is not
underlined.
- 5.
- masses of more massive primary and less massive secondary components
M1 and M2 expressed in units of Sun mass
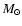 are presented in the fifth column;
are presented in the fifth column;
- 6.
- radii of primary R1 and secondary R2 components
expressed in units of Sun radius
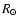 are contained in
the sixth column;
are contained in
the sixth column;
- 7.
- absolute bolometric stellar magnitudes of primary
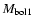 and secondary
and secondary
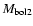 components estimated according to their
geometric sizes, spectra, and luminosity classes are given in the
seventh column. When calculating
components estimated according to their
geometric sizes, spectra, and luminosity classes are given in the
seventh column. When calculating
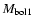 and
and
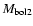 the Popper (1980) scale of effective temperatures was used.
The preferred temperature scale in all catalogues by Svechnikov
is Popper's. In order to maintain uniform treatment of the newly
obtained (as a result of revision) data the same scale was used;
the Popper (1980) scale of effective temperatures was used.
The preferred temperature scale in all catalogues by Svechnikov
is Popper's. In order to maintain uniform treatment of the newly
obtained (as a result of revision) data the same scale was used;
- 8.
- relative radii of both components r1 and r2 (average components radii) expressed in the units of a major semi-axis
of the orbit are given in the eighth column;
- 9.
- the relative luminosity of the primary component expressed in
relative units (
L1+L2=1) and surface brightness ratio
J1/J2 are in the ninth column, along with the effective
wave length
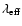 or the wave length close to V-band
pass in which these observations were performed;
or the wave length close to V-band
pass in which these observations were performed;
- 10.
- the orbit inclination of picture plane i and weight W,
characterizing the quality of the estimation of absolute and
photometric elements of the system on a ten-point scale, are included
in the tenth column; criteria for weight estimation are discussed in
detail by Svechnikov (1969);
- 11.
- the key papers, on the basis of which the photometric and
spectroscopic data were selected and, if needed, averaged over the
different sets of solutions, are presented in the eleventh column.
- 12.
- the symbol ":'' is used in any case when an element is determined
as unreliable.
The empirical coefficients of such relations as M-R, 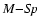 ,
,
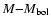 ,
and
,
and
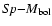 have been obtained for primary and secondary components by
summarizing data compiled for pre-contact systems. 31 systems of DW-type
were involved in this treatment; for a better fitting to the statistical
dependences for systems WZ And (2) and UV Leo (20),
we have taken photometric solutions under Number 1 (see Table 1).
have been obtained for primary and secondary components by
summarizing data compiled for pre-contact systems. 31 systems of DW-type
were involved in this treatment; for a better fitting to the statistical
dependences for systems WZ And (2) and UV Leo (20),
we have taken photometric solutions under Number 1 (see Table 1).
The empirical relation generalized for primary and secondary components
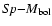 (see Appendix, Fig. A.1) may be written in the following form:
(see Appendix, Fig. A.1) may be written in the following form:
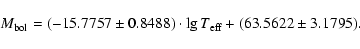 |
(1) |
For the mass range of both components
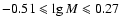 the
empirical relation M-R was found (Fig. A.2) in the linear form:
the
empirical relation M-R was found (Fig. A.2) in the linear form:
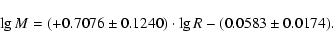 |
(2) |
The primary and secondary components of DW-type systems also satisfy
the linear empirical relations
 and
and
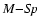 (see Figs. A.3
and A.4):
(see Figs. A.3
and A.4):
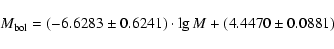 |
(3) |
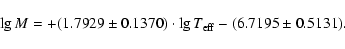 |
(4) |
It should be interesting to test the conclusions in Dryomova & Svechnikov
(1999) made after analyzing 153 DW-type binaries taken from
the "Catalogue of the approximate photometric and absolute elements of the
eclipsing variable stars'' by Svechnikov & Kuznetsova (1990)
and based on new data on the 31 pre-contact systems from the catalogue presented
here. As shown in Dryomova & Svechnikov (1999) the dependence of
the radius excess (as well as the luminosity excess) upon mass (or mass ratio),
constructed for the primary and secondary components of 153 DW-type
binaries, is almost constant. The faint radius and luminosity excesses reveal
themselves only in the range
 and q>0.8.
This means the binaries of DW-type have only evolved slightly from Zero
Age Main Sequence (ZAMS) and stay in the initial stage of the Roche
lobes filling; i.e. their evolutionary status is close to that of
and q>0.8.
This means the binaries of DW-type have only evolved slightly from Zero
Age Main Sequence (ZAMS) and stay in the initial stage of the Roche
lobes filling; i.e. their evolutionary status is close to that of
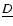 etached
etached
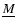 ain
ain
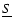 equence
(DMS-type) systems, both components of which are MS-stars not yet
filling their inner Roche lobes and so not interacting with each other. One
must emphasize that this abbreviation (DMS) adopted according to the
classification by Svechnikov (1985) is used in the General
Catalogue of the Variable Stars (see Kholopov et al. 1985). The
distinction between these two classes is the chromospheric and photospheric
activity (which reveal themselves in numerous spots), sharply expressed in the
case of DW-type binaries and barely noticeable (i.e. a thousand times
less by intensity) in the case of DMS-systems. Also, eclipsing binaries
with orbital periods less then
equence
(DMS-type) systems, both components of which are MS-stars not yet
filling their inner Roche lobes and so not interacting with each other. One
must emphasize that this abbreviation (DMS) adopted according to the
classification by Svechnikov (1985) is used in the General
Catalogue of the Variable Stars (see Kholopov et al. 1985). The
distinction between these two classes is the chromospheric and photospheric
activity (which reveal themselves in numerous spots), sharply expressed in the
case of DW-type binaries and barely noticeable (i.e. a thousand times
less by intensity) in the case of DMS-systems. Also, eclipsing binaries
with orbital periods less then
 do not occur among DMS-class, whereas
all DW-systems have orbital periods
do not occur among DMS-class, whereas
all DW-systems have orbital periods
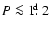 at the same
masses as for the DMS-class, as indicated in Svechnikov (1985).
The light curves of DW eclipsing variables possess significant pecularities
in contrast to DMS-systems.
at the same
masses as for the DMS-class, as indicated in Svechnikov (1985).
The light curves of DW eclipsing variables possess significant pecularities
in contrast to DMS-systems.
The excess of the radius of DW-satellites is defined as the difference between
the observed (calculated as
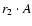 )
value and that found in accordance
with the empirical "mass-radius'' relation averaged for MS stars. The same
is true for the definition of luminosity excess with only one difference: the
empirical "mass-luminosity'' relation for MS stars is used. When calculating
radius and luminosity excesses we have used new
)
value and that found in accordance
with the empirical "mass-radius'' relation averaged for MS stars. The same
is true for the definition of luminosity excess with only one difference: the
empirical "mass-luminosity'' relation for MS stars is used. When calculating
radius and luminosity excesses we have used new
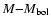 and M-R relations
obtained by Gorda & Svechnikov (1999) for detached MS eclipsing
variables with well-known absolute elements. These radius and luminosity excesses
indicate that the position of DW-binaries is close to Terminal Age Main
Sequence (
and M-R relations
obtained by Gorda & Svechnikov (1999) for detached MS eclipsing
variables with well-known absolute elements. These radius and luminosity excesses
indicate that the position of DW-binaries is close to Terminal Age Main
Sequence (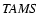 )
but is not a midpoint of the MS-band as is true for
DMS-systems.
)
but is not a midpoint of the MS-band as is true for
DMS-systems.
Actually analysis of the distributions depicted in Figs. A.5 and A.6 verifies
the presence of insignificant radius and luminosity excesses in a majority of
satellites in DW-type systems. The tendency of radius and luminosity excesses
to increase as the mass ratio of DW-binaries decreases (q< 0.6)
is noticed. As for the mass ratio range q> 0.6, the average statistical
scattering in values of radius and luminosity excesses should be noted.
The maximum radius of DW-satellites is two and a half times larger than that
of MS-stars, and the maximum luminosity excess is approximately two and a
half magnitudes at q= 0.25. These excesses are indeed quite small in
comparison with analogous radius and luminosity excesses for the satellites
of W 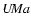 -type contact systems, which reach a maximum up to
-type contact systems, which reach a maximum up to 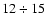 times
and
times
and 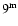 ,
respectively, at q= 0.15 as compared to MS stars
according to Svechnikov (1990). This comparison is important
because W
,
respectively, at q= 0.15 as compared to MS stars
according to Svechnikov (1990). This comparison is important
because W 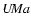 -type contact systems present the next evolutionary stage of
pre-contact short-periodic RS CVn-type binaries. The resulting radius and
luminosity excesses of DW-satellites are quite expected in the framework of
the formalism of magnetic braking.
-type contact systems present the next evolutionary stage of
pre-contact short-periodic RS CVn-type binaries. The resulting radius and
luminosity excesses of DW-satellites are quite expected in the framework of
the formalism of magnetic braking.
This approach explains the evolution of low-mass (
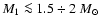 )
DMS-binaries, DW-stars, and W
)
DMS-binaries, DW-stars, and W 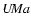 -type contact systems in terms
of orbital angular momentum loss (AML) and combines them into a common
evolutionary chain that in fact has already been confirmed from extensive
observational data by Svechnikov & Kuznetsova (1990) and from
the relations of statistics and lifetimes obtained by Tutukov et al. (2004).
The magnetic stellar wind in low-mass close binaries is a driving force in
the approach of the two components. But considering that the orbital
AML-timescale is shorter than the nuclear timescale, the mass loss process
in the binary may be initiated before the components fill up their Roche lobes.
It is very likely that such a process might lead to the appearance of excess
in radii and luminosities of DW-satellites. As for satellites of W
-type contact systems in terms
of orbital angular momentum loss (AML) and combines them into a common
evolutionary chain that in fact has already been confirmed from extensive
observational data by Svechnikov & Kuznetsova (1990) and from
the relations of statistics and lifetimes obtained by Tutukov et al. (2004).
The magnetic stellar wind in low-mass close binaries is a driving force in
the approach of the two components. But considering that the orbital
AML-timescale is shorter than the nuclear timescale, the mass loss process
in the binary may be initiated before the components fill up their Roche lobes.
It is very likely that such a process might lead to the appearance of excess
in radii and luminosities of DW-satellites. As for satellites of W 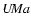 -type
contact systems, the question of radius and luminosity excesses was treated
in detail by Istomin (1986) with the assumption that the luminosity
increase of their satellites is due to gravitational energy release originating
from the matter flowing from the more massive component.
-type
contact systems, the question of radius and luminosity excesses was treated
in detail by Istomin (1986) with the assumption that the luminosity
increase of their satellites is due to gravitational energy release originating
from the matter flowing from the more massive component.
Analysis of the position of DW-systems relative to tracks constructed
from evolutionary stellar models by Maeder & Meynet (1988) in the
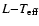 -diagram (Fig. A.7) showed that the primaries are well positioned within
the MS band in the Hertzsprung-Russel (H-R) diagram and justified their
status as slightly evolved stars, whereas the satellites demonstrate luminosity
excesses for their masses. The same conclusion can be made from Fig. A.9. The
M-R diagram (Fig. A.8) clearly shows that almost all DW-primaries
are strongly localized between the boundaries of
-diagram (Fig. A.7) showed that the primaries are well positioned within
the MS band in the Hertzsprung-Russel (H-R) diagram and justified their
status as slightly evolved stars, whereas the satellites demonstrate luminosity
excesses for their masses. The same conclusion can be made from Fig. A.9. The
M-R diagram (Fig. A.8) clearly shows that almost all DW-primaries
are strongly localized between the boundaries of 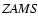 and
and 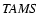 also taken
from models by Maeder & Meynet (1988); and yet at the same time
DW-satellites are oversized for their masses. Also the
also taken
from models by Maeder & Meynet (1988); and yet at the same time
DW-satellites are oversized for their masses. Also the 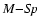 -diagram (Fig. A.10)
is of interest because of temperature excesses which are so evident for
secondary components of DW-systems.
-diagram (Fig. A.10)
is of interest because of temperature excesses which are so evident for
secondary components of DW-systems.
The ages and their errors, calculated by the isochrone method in M-R diagram
for primary components of DW-type systems and taken from the catalogue
presented here, are placed in Table 2. The isochrone
method is also based on the theoretical stellar evolution models by Maeder &
Meynet (1988), taking an overshooting into account along with mass
loss of components and developed for Population I stars with
(X,Y,Z)=0.70,
0.28, 0.02. This method was expounded in Dryomova & Svechnikov (2003).
The choice of these models with given abundances is explained by the fact that
all eclipsing binaries considered here are located in Sun neighbourhood and
therefore should have similar chemical composition.
The t1 ages and their errors are given in Gyr. Pre-contact
systems such as WY Cnc (10), VZ CVn (11), and
AE Cas (12) lay off the M-R desigh diagram so the
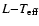 diagram was applied to estimate the ages of these systems
by the isochrone method as well. We obtained a fairly wide spread for an age
change; for example, the age of UV Psc (24) equals approximately 10 Gyr, while MT Her (18) and V 361 Lyr (22)
binaries are located near the ZAMS.
diagram was applied to estimate the ages of these systems
by the isochrone method as well. We obtained a fairly wide spread for an age
change; for example, the age of UV Psc (24) equals approximately 10 Gyr, while MT Her (18) and V 361 Lyr (22)
binaries are located near the ZAMS.
This new catalogue of short-periodic RS CVn-type systems gives information
about elements of spectroscopic and/or photometric orbits such as orbital
period, mass ratio, proper masses, orbital inclination, surface brightness
ratio, luminosities, absolute and relative radii. We have determined that 18 DW-systems correspond to the "double-lined spectra'' case, while only three
systems (UU Lyn, DD Mon, GR Tau) relate to the "single-lined spectrum''
case. In these instances the indicated DW-type systems are characterized by
well-studied radial velocity curves and photometric light curves. It is evident
from their high weights as mentioned in the catalogue. The remaining ten
pre-contact eclipsing binaries have no spectroscopic observations so may only
be described in photometric solution terms. Nevertheless this catalogue may
serve as a reliable data source with just an accent on those five systems
whose weights (W) do not exceed 2: AE Cas, RS Col, BZ Eri,
CN Lac, and GY Tel. This catalogue is useful for analyzing basic
empirical relations such as M-R, 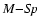 ,
,
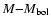 ,
and
,
and
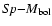 and
when studying properties of pre-contact DW-class which represents the intermediate
stage between the detached DMS-class and contact binaries of W
and
when studying properties of pre-contact DW-class which represents the intermediate
stage between the detached DMS-class and contact binaries of W 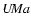 -type.
-type.
- Agerer, F., Berthold, T., & Kroll, P. 1999,
IBVS, N 4798
- Albayrak, B., Demircan, O., Djurasevic, G.,
Erkapic, S., & Ak, H. 2001, A&A, 376, 158
- Andersen 1991, A&AR, 3, 91
- Arevalo, M., Lazaro, C., & Claret, A. 1995,
AJ, 110, 1376
- Arevalo, M., & Lazaro, C. 1999,
AJ, 118, 1015
- Arevalo, M., Lazaro, C., Barrera, E., & Dominguez, R.
2002, IBVS, N 5222
- Bell, S., Rainger, P., Hill, G., & Hilditch, R. 1990,
MNRAS, 244, 328
- Biermann, P., & Hall, D. 1973, A&A, 27, 249
- Botsula, R. 1978, IzKaz, 43, 170
- Broglia, P., & Conconi, P. 1979, A&AS, 37, 487
- Buckley, D. 1984, Ap&SS, 99, 191
- Budding, E., & Zeilik, M. 1987, ApJ, 319, 827
- Budding, E., & Murad, I. 1982, IBVS, N 2207
- Budding, E., & Murad, I. 1989, Ap&SS, 153, 335
- Budding, E., Butler, C., Doyle, J., et al. 1996, Ap&SS, 236, 215
- Busch, H. 1985, IBVS, N 2788
- Cameron, A. 1997, MNRAS, 287, 556
- Cameron, A., & Hilditch, R. 1997, MNRAS, 287, 567
- Cellino, A., Scaltriti, F., & Busso, M. 1985,
A&A, 144, 315
- Cester, B., Mardirossian, F., & Pucillo, M. 1977,
A&A, 56, 75
- Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039
- CDS, http://simbad.u-strasbg.fr/sim_id.pl
- Cook, A. 1948, AJ, 1948, 53, 211
- Cook, S. 1992, J. Am. Assoc.
Var. Star Obs., 21, 119
- Chudovichev, N. 1952, Bull.
Engelhard's AO, 28
- Dapergolas, A., Kontizas, E., & Kontizas, M. 2000,
IBVS, N 5011
- Derman, E., Demircan, O., & Akalin, A. 1993,
Ap&SS, 205, 327
- Dryomova, G., & Svechnikov, M. 1999,
Odessa Astron. Publ., 12, 187
- Dryomova, G., & Svechnikov, M. 2003, Ap&SS, 283, 309
- Ekmekci, F., Ozeren, F., & Ak, H. 2002,
Astron. Nachr., 323, 31
- Frasca, A., Catalano, S., & Mantovani, D. 1996,
Bologna Astrophysics preprints, 22
- Frederic, M., & Etzel, P. 1996, AJ, 111, 2081
- Frigo, A., Piccolli, P., Setti, A., et al. 2002, IBVS, 5359
- Garcia-Sanchez, J., Paredes, J., & Ribo, M.
2003, A&A, 403, 613
- Gimenez., A., Ballester, J., Reclero, V.,
Fernandez-Figueroa, M., & de Castro, E. 1985, IBVS, N 2797
- Gimenez, A., Ballester, J., Reclero, V.,
Fernandez-Figueroa, M., & de Castro, E. 1986, AJ, 92, 131
- Gorda, S., & Svechnikov, M. 1999,
Astron. Rep., 43, 521
- Gunn, A., & Doyle, J. 1997, A&A, 318, 60
- Gulmen, O., Gudur, N., Sezer, C., et al. 1988, IBVS, N 3271
- Hall, D. 1972, PASP, 84, 323
- Heckert, P. 1994, IBVS, N 4127
- Heckert, P. 1999, IBVS, N 4806
- Heckert, P. 2001, AJ, 121, 1076
- Heckert, P. 2003, IBVS, N 5419
- Hilditch, R., & Bell, S. 1994, MNRAS, 267, 1081
- Hilditch, R., Cameron, A., Hil, G., Bell, S.,
& Harries, T. 1997, MNRAS, 291, 749
- Hill 1990, A&A, 238, 145
- HIPPARCOS, http://astro.estec.esa.nl/HIPPARCOS
- Hoffmeister, C. 1933,
Astron. Nachr., 247, 281
- Istomin, L. 1986, Ph.D. Thesis, Ural State University,
Yekaterinburg
- Jassur, D., Khalaj, A., & Kermani, M. 2000, IBVS, N 5006
- Kholopov, P. 1985, General Catalogue of Variable Stars,
Moscow, Sci., fourth edition, first volume
- King, D., & Hilditch, R. 1984, MNRAS, 209, 645
- Kjurkchieva, D., Marchev, D., & Ogloza, W. 2001,
A&A, 378, 102
- Kjurkchieva, D., Marchev, D., & Ogloza, W. 2002,
A&A, 386, 548
- Kjurkchieva, D., Marchev, D., & Ogloza, W. 2003,
A&A, 400, 623
- Kozhevnikova, A., & Alekseev, I.,
private communication
- Kreiner, J., Kim, C.-H., & Nha, I.-S. 2001,
An Atlas of OC-Diagrams of Eclipsing Binary stars
- Kyu-Dong, O. 1977, J. Korean
Astron. Society, 10, 23,
http://vsnet.kusastro.kyoto_u.ac.Sp/vsnet/gevs
- Lacy, C., Torres, G., & Guilbault, P. 2002, IBVS, N 5301
- Lavrov, M. 1955, IzKaz, N 31
- Lazaro, C., Niarchos, P., Rovithis, P.,
et al. 1995, AJ, 110, 1796
- Lipari, S., & Sistero, R. 1988, PASP, 100, N 625, 380
- Loktin, A., Gerasimenko, T., Malisheva, H.,
& Zakharova, P. 1997, Baltic Astron., 6, 316
- Lu, W.-X., Wang, Y.-R., & Wang, X.-M. 1991,
A&A, 15, 214
- Lu, W.-X., Wang, Y.-R., & Wang, X.-M. 1990,
Acta Astron. Sinica, 31, 319
- Lu, W.-X., Wang, Y.-R., & Wang, X.-M. 1990,
Acta Astron. Sinica, 10, 262
- Maeder, A., & Meynet, G. 1988, A&AS, 76, 411
- Marschall, L., Gauthier, C., Nations H.,
Taylor, B., & Huard, T. 1991, IBVS, N 3633,
- McCluskey, G. 1966, AJ, 71, 527
- McDonald, D. 1964, Publ. Mc Cormick Obs., 12, 21
- McFarlane, T., & Hilditch, R. 1987, MNRAS, 227, 381
- Metcalfe, T., Mathieu, R., Latham, D., & Torres, G.
1996, ApJ, 456, 356
- Milone, E., & Hrivnak, B. 1981, AJ, 86, 1546
- Milano, L., Mancuso, S., Vittone, A., Dórsi, A.,
& Marcozzi, S. 1986, Ap&SS, 124, 83
- Nelson, R. 2002, IBVS, N 5224
- Nekrasova, S. 1936, Variable stars, 5, 45
- Olah, K., Budding, E., Kim, H.-L., & Etzel, P. 1994,
A&A, 291, 110
- Patkos, L., & Hempelmann, A. 1994, A&A, 292, 119
- Pojmanski, G. 1998, Acta Astron., 48, 711
- Pokorny, Z. 1973, IBVS, N 772
- Popper, D. 1980, ARA&A,
18, 115
- Popper, D. 1988, AJ, 95, 190
- Popper, D. 1993, ApJ, 404, 67
- Popper, D. 1994, AJ, 108, 1091
- Popper, D. 1995, IBVS, N 4185
- Popper, D. 1996, ApJS, 106, 133
- Popper, D. 1997, AJ, 114, 1195
- Pribulla, T., Chochol, D., Milano, L., et al. 2000, A&A, 362, 169
- Rainger, P., Hilditch, R., & Edwin, R. 1991,
MNRAS, 248, 168
- Robb, R., Dean, F., & Scarfe, C. 1990, IBVS, N 3633
- Rucinski, S. 1983, A&A, 127, 84
- Rucinski, S. 1998, PASP,
110, 272
- Sarma, C., Sarma, M., & Sanwal, N. 1989, A&A,
10, 307
- Schiller, S., & Milone, E. 1988, AJ, N 5, 1466
- Shaw, J. 1994, Mem. Soc. Astron. Italian, 65, 95
- Shen, L., Jiang, Z., & Lu, W. 1990, Chinese A&A, 14, 273
- Shengbang, Q., Qingyao, L., Yulan, Y.,
Shenghong, G., & Zhangkui, H. 1996, IBVS, N 4387
- Shengbang, Q., Qingyao, L., Yulan, Y.,
Shenghong, G., & Zhangkui, H. 1997, A&AS, 125, 475
- Shenghong, G., Qingyao, L., Yulan, Y., Bi, W.,
& Zhangkui, H. 1994, IBVS, N 4060
- Srivastava, R., & Sinha, B., Uttar Pradesh State
Observatory, Manora peak, Naini Tal - 263129, India - IBVS, N 1919, 2806
- Srivastava, J., & Kandpal, C. 1984, Acta Astron.,
34, 281
- Srivastava, R. 1986, Ap&SS, 121, 317
- Srivastava, R., & Uddin, W. 1986, Ap&SS, 126, 105
- Strassmeier, K., Hall, D., Boyd, L., & Genet, R.
1989, AJS, 69, 141
- Strassmeier, K., Hall, D., Fekel, F., & Scheck, M.
1993, A&AS, 100, 173
- Svechnikov, M. 1969, Catalogue of orbital
elements, masses and luminosities of close binary stars, Scientific notes,
Yekaterinburg, Ural State University, N88, 179
- Svechnikov, M., & Snezhko, L. 1974, in book:
Nonstationary phenomena and stellar evolution (Moscow: Nauka), 181
- Svechnikov, M. 1985, Doctoral Thesis,
Chelyabinsk State University
- Svechnikov, M. 1986, Catalogue of orbital elements,
masses and luminosities of close binary stars, edition of Irkutsk University
- Svechnikov, M., & Kuznetsova, E. 1990,
Catalogue of approximate photometric and absolute elements of variable
stars, Ural State University, Yekaterinburg, 1-2, 454
- Svechnikov, M. 1990, Study of the interaction effects
in close binary systems with the non-relativistic components, Tallinn,
publisher Valgus, 26
- Tutukov, A., Dryomova, G., & Svechnikov, M. 2004,
Astron. Repor., 48, 219
- Vivekananda Rao, P., Sarma, M., & Prakash Rao, B.
1991, A&A, 12, 225
- Wachmann, A. 1933, Astron. Nachr.,
255, 341
- Wenzel, W., & Wicklein, A. 1991, Mitt. veranderl.
Sterne, 12, 89
- Wilson, R., & Rafert, J. 1980, A&AS, 42, 195
- Wood, D. 1978, WINK Status Report, N 9
- Wunder, E. 1995, IBVS, N 4179
- Yamasaki, A., Okazaki, A., & Kitamura, M. 1983, PASJ,
35, 131
- Yamasaki, A., Okazaki, A., & Kitamura, M. 1984, PASJ,
36, 175
- Yamasaki, A., Okazaki, A., & Kitamura, M. 1986,
A&SS, 118, 279
- Yamasaki, A., Okazaki, A., & Kitamura, M. 1990,
AJ, 99, 1218
- Zhai, D., Qiao, G., & Zhang, X. 1990, A&A, 237, 148
- Zhang, X., Zhang, R., & Fang, M. 2002, A&A, 395, 587
- Zeilik, M., Ledlow, M., Rhodes, M., Arevalo, M.,
& Budding, E. 1990, ApJ, 354, 352
- Zeilik, M., Gorgon, S., Jadelund, E., et al. 1994, ApJ, 421, 303
- Zeinali, F., & Edalati, M. 1995, IBVS, N 4190
- Zwitter, T., Munari, U., Marrese, P., et al. 2003, A&A, 404, 333
5 Online Material
- 1.
- RT And. All available photometric and spectroscopic
data have been reanalyzed in the same manner.
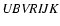 light curves
without maculation effects together with the radial velocities of both
components were analyzed with the Wilson-Devinney code by Pribulla et al.
(2000). The high orbital inclination was confirmed by photoelectric
observations of the secondary minimum. A small eccentricity found from
the light curve analysis cannot be ruled out. The face-to-face position of
the spots on the surface of both components (registered in 1971) indicates
the possibility of a mass transfer from the primary to the secondary
component through a magnetic bridge connecting both active regions.
Analysis of all available light curves suggests a random position of
starspots and does not confirm the idea of active longitudinal belts by
Arevalo et al. (1995). From the longitudinal spot motion
(between 1995 and 1998) it was inferred by Ekmerci et al. (2002)
that the migration period of the distortion wave has a value of 6.6 years.
This system was included in the main
HIPPARCOS mission (
light curves
without maculation effects together with the radial velocities of both
components were analyzed with the Wilson-Devinney code by Pribulla et al.
(2000). The high orbital inclination was confirmed by photoelectric
observations of the secondary minimum. A small eccentricity found from
the light curve analysis cannot be ruled out. The face-to-face position of
the spots on the surface of both components (registered in 1971) indicates
the possibility of a mass transfer from the primary to the secondary
component through a magnetic bridge connecting both active regions.
Analysis of all available light curves suggests a random position of
starspots and does not confirm the idea of active longitudinal belts by
Arevalo et al. (1995). From the longitudinal spot motion
(between 1995 and 1998) it was inferred by Ekmerci et al. (2002)
that the migration period of the distortion wave has a value of 6.6 years.
This system was included in the main
HIPPARCOS mission (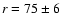 pc). Spectroscopic observations in the range 6500-6700
pc). Spectroscopic observations in the range 6500-6700  and
and
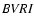 photometry were obtained by Kjurkchieva et al. (2001).
Both spectral and photometric data lead to the conclusion that the secondary
star is oversized for its mass. Spectral types were designated to both
components as averaged over data by Arevalo et al. (1995) and
Popper (1994). Preference was given to a photometric solution
by Popper (1994) averaged over nine sets of data by Zeilik
et al. (1994).
photometry were obtained by Kjurkchieva et al. (2001).
Both spectral and photometric data lead to the conclusion that the secondary
star is oversized for its mass. Spectral types were designated to both
components as averaged over data by Arevalo et al. (1995) and
Popper (1994). Preference was given to a photometric solution
by Popper (1994) averaged over nine sets of data by Zeilik
et al. (1994).
- 2.
- WZ And is an eclipsing binary without spectroscopic
elements. Two photometric solutions are presented according to the
visual-photometric observations by Chudovichev (1952) and to
the collected and analysed light curves, which were available in the
literature before 1977 (see Kyu-Dong 1977). The nature of the
variations of the orbital period and its abrupt jumps were theoretically
studied in the frame of a mass exchange model as applied to close binary
systems by Biermann and Hall (1973). Their calculation yielded a
mass flow of
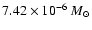 per year from the hotter
component to the colder one. At present it is impossible to favour either
one of the authors. The spectral type of the primary component has been
classified as F5 according to Wood (1978).
per year from the hotter
component to the colder one. At present it is impossible to favour either
one of the authors. The spectral type of the primary component has been
classified as F5 according to Wood (1978).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig1.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg176.gif) |
Figure A.1:
The generalized empirical "spectrum-luminosity'' dependence
for the primary (designated as circles) and the secondary (marked
by asterisks) components of DW-systems |
- 3.
- BX And is the brighter component of the visual binary
ADS 1671. The
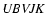 photometry of this system was thoroughly
studied by Bell et al. (1990) and Dermann et al. (1993). The
analysis of three V Algol-like light curves and infrared light
curves in the J and K pass-bands indicates marginal contact of the
binary with a hot spot (
photometry of this system was thoroughly
studied by Bell et al. (1990) and Dermann et al. (1993). The
analysis of three V Algol-like light curves and infrared light
curves in the J and K pass-bands indicates marginal contact of the
binary with a hot spot (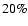 of the star surface) on the secondary
component, which is approximately 1200 K hotter than the surrounding
photosphere. It seems likely that variations in the period are due to
changes in the mass transfer rate. There is no asymmetry in the profiles
of the minima and no displacement in the secondary minimum, while the maxima
are equal according to Jassur et al. (2000). The series of
spectroscopic observations were carefully processed with the use of
cross-correlation functions CCF. The relatively narrow wavelength
range in this study precludes any attempt to make a spectral classification
for the binary under consideration. Comparative analysis of absolute elements
(masses, radii, luminosities) shows that the primary component is close to
the TAMS; but the secondary component is
of the star surface) on the secondary
component, which is approximately 1200 K hotter than the surrounding
photosphere. It seems likely that variations in the period are due to
changes in the mass transfer rate. There is no asymmetry in the profiles
of the minima and no displacement in the secondary minimum, while the maxima
are equal according to Jassur et al. (2000). The series of
spectroscopic observations were carefully processed with the use of
cross-correlation functions CCF. The relatively narrow wavelength
range in this study precludes any attempt to make a spectral classification
for the binary under consideration. Comparative analysis of absolute elements
(masses, radii, luminosities) shows that the primary component is close to
the TAMS; but the secondary component is 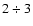 times larger
than is expected for its ZAMS mass, and it lies upwards and to the
right of the ZAMS line in the HR diagram as was noted by Bell
et al. (1990).
times larger
than is expected for its ZAMS mass, and it lies upwards and to the
right of the ZAMS line in the HR diagram as was noted by Bell
et al. (1990).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig2.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg180.gif) |
Figure A.2:
The generalized empirical "mass-radius'' relation for
DW-systems. The designations are the same. |
- 4.
- DS And is well covered by photometric and spectroscopic
observations by Schiller and Milone (1988). No sign of a period
variability is indicated over a 52 yr timespan covering the moments of
minimum light. Complete BVRI light curves and radial velocity
curves extracted from the photographic and Reticon spectra and analyzed with
the cross-correlation technique were solved compatibly with the generalized
Wilson-Devinney model. The primary component nearly fills its Roche lobe,
while the satellite is a slightly evolved solar-type star. The distance
modulus (
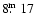 )
and the measured proper motion confirm that this binary
is a member of NGC 752 open cluster.
)
and the measured proper motion confirm that this binary
is a member of NGC 752 open cluster.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig3.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg182.gif) |
Figure A.3:
The generalized empirical "mass-luminosity'' relation for
DW-systems. The designations are the same. |
- 5.
- HS Aqr = HD 197010 is an X-ray emitting chromospherically
active binary system. A series of the photometric observations including
V-and R-bands was carried out by Robb et al. (1990). But
these data are insufficient to accurately compute orbital elements and so
approximate values of the relative radii r1, r2,
mass ratio q, temperatures of hot and cool stars, and orbit
inclination i were chosen by the best fit to the model light curve
in R-band. The large asymmetry in the brightness of the maxima is
generally attributed to stellar spots, which may also be the source of the
observed X-rays. 32 spectra at 1 Å resolution in the region
Mg B triplet were obtained and analyzed by Marschall et al.
(1991); but it gave no information about the mass ratio of the
system, while the spectroscopic observations performed by Popper (1995)
allowed calculation of the minimum values of masses
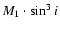 ,
,
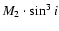 and of the mass ratio itself.
and of the mass ratio itself.
- 6.
- RX Ari. The light curves have been analyzed by Wilson
& Rafert (1980) using the differential corrections method. The
spectroscopic solution is absent. The spectral type of the primary component
has been classified as F2 by Kreiner et al. (2001) and its mass
estimated with the use of a "mass-spectrum'' relation by Popper (1980).
The satellite mass was determined using the "mass-luminosity'' dependence
for MS-stars and the photometric value of mass ratio
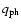 .
One
may conclude that this system is a MS-binary with an oversized secondary.
.
One
may conclude that this system is a MS-binary with an oversized secondary.
- 7.
- CV Boo was photographically discovered as an eclipsing
binary by Busch (1985) and is well covered by spectroscopic
observations. The sources for estimating the spectral types are the
intensities of NaD-lines; and since the inclination (
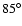 )
was
chosen arbitrarily by Popper (1993), it was recalculated with
the empirical dependence of the main minimum amplitude A1 upon
the orbital inclination derived for near-contact systems by Svechnikov
(1985). New photometric observations are needed for more
precise definition of the geometric elements such as relative radii of both
components r1, r2, and inclination i.
)
was
chosen arbitrarily by Popper (1993), it was recalculated with
the empirical dependence of the main minimum amplitude A1 upon
the orbital inclination derived for near-contact systems by Svechnikov
(1985). New photometric observations are needed for more
precise definition of the geometric elements such as relative radii of both
components r1, r2, and inclination i.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig4.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg187.gif) |
Figure A.4:
The generalized empirical "mass-spectrum'' relation for the
DW-systems. The designations are the same. |
- 8.
- SV Cam. 34 spectra were collected as a result of near
IR spectroscopic observations and analyzed by applying CCF-mapping (Pojmanski 1998). It is important to emphasize that
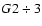 V photometry-based classification, as well as that
derived from the average equivalent width of the lines, would not correspond
to the stellar masses, if one does not suppose the primary surface is
covered with a large amount of dark spots or that curcumstellar matter is
present. Such explanation is plausible since some excess in the infrared flux
was observed by Cellino et al. (1985). Derived masses of the
components would fit the
V photometry-based classification, as well as that
derived from the average equivalent width of the lines, would not correspond
to the stellar masses, if one does not suppose the primary surface is
covered with a large amount of dark spots or that curcumstellar matter is
present. Such explanation is plausible since some excess in the infrared flux
was observed by Cellino et al. (1985). Derived masses of the
components would fit the
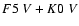 classification best. However
the model parameters for a circular orbit without spots obtained by the
Wilson-Devinney code in Frigo et al. (2002) indicate the lower
effective temperature of the satellite that corresponds to a
classification best. However
the model parameters for a circular orbit without spots obtained by the
Wilson-Devinney code in Frigo et al. (2002) indicate the lower
effective temperature of the satellite that corresponds to a 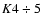 V spectral class. The spectroscopic observations performed by
Kjurkchieva et al. (2002) in the range 6500-6700 Å cover the whole orbital period. The absorption profiles of the line H
V spectral class. The spectroscopic observations performed by
Kjurkchieva et al. (2002) in the range 6500-6700 Å cover the whole orbital period. The absorption profiles of the line H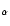 and Fe I 6678 Å are doubled out of the eclipses. Three sources
of the activity of this system have been found in Kjurkchieva et al. (2001):
(i) photospheric spots on the primary component; (ii) enhanced chromospheric
emission from the satellite; and (iii) some additional emission originating
from circumstellar gas. Relative orbit elements were taken from a more
general spot solution of the light curve by Patkos & Hempelmann (1994).
and Fe I 6678 Å are doubled out of the eclipses. Three sources
of the activity of this system have been found in Kjurkchieva et al. (2001):
(i) photospheric spots on the primary component; (ii) enhanced chromospheric
emission from the satellite; and (iii) some additional emission originating
from circumstellar gas. Relative orbit elements were taken from a more
general spot solution of the light curve by Patkos & Hempelmann (1994).
- 9.
- WX Cnc was found to be a detached binary whose light
curve asymmetry is due to a spot lying on the satellite surface, according
to Lu et al. (1990). The photoelectric light curves (V-, B-bands) and the radial velocity curves were solved compatibly using the
Wilson-Devinney method in Lu et al. (1991). The radial velocity curves
were also computed by the cross-correlation method in Lu et al. (1990).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fi5a.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg192.gif) |
Figure A.5:
The dependence of the radii excesses (designated as squares) and
their errors (denoted as bars) upon the mass ratio for DW-satellites
in comparison with MS stars. |
WY Cnc. The solution combines the near IR spectroscopic observations by Pojmanski (1998) applying
CCF-mapping and the new optical BVRI-photometry data by
Heckert (2003), which were modeled using the ILOT code
(Information Limit Optimization Technique) according to Budding & Zeilik
(1987) and cleaned from the effects of the distortion wave and
spots. Fits for each wavelength were done independently.
- 10.
- VZ CVn is a well-detached binary. The last photoelectric
light curves were observed by Shenghong et al. (1994) in B,V-bands. These data helped to evaluate the orbital period more
exactly. The new light curves showed some pulsation variations near the
maxima. The spectral types are based on the colour indices. The orbital
solution was found as a combination of the spectrographic observations of
this system by Popper (1988) and the photometric analysis by
Cester et al. (1977). The physical characteristics of this system
place its components well within the Main Sequence band in the
HR-diagram with the less massive, colder component lying near the
ZAMS and the more massive star slightly evolved. From analysis of
the colour indices one would conclude that the masses are too large for
the observed radiative properties. There is no clear evidence for any
variation in the period over an interval of 46 yr.
- 11.
- AE Cas. The photometric elements P, i,
r1, r2, and L1 were obtained by employing
the Kopal method of Fourier analysis of light curves in U, B,
and V filters in Srivastava & Kandpal (1984). The
spectroscopic data are absent and the spectra of both components were
estimated according to their colour indices. The absolute elements of the
system are restored with the use of a "mass-spectrum'' relation, third
Kepler's law, and the relative radii and luminosities. Information about
the period behaviour and its improved value is given by Nelson (2002).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fi5b.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg193.gif) |
Figure A.6:
The same as Fig. 5a but for the luminosity excesses. |
- 12.
- ST Cen was well covered by
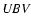 photometric
observations on the basis of which the synthetic light curve solution was
obtained by Milone & Hrivnak (1981) using the Wilson-Devinney
code. Spectral classifications for both components were derived from the
spectroscopy observations. The data on radial velocity curves are absent,
and there is no strong evidence for Ca II H and K emission or for light curve variability. The nature of the asymmetry is not
clear. Three stable photometric solutions were found for q=0.9,
0.62, and 0.46, but the theoretical light curves predicted with Solution I
(q= 0.9) showed better fit to the observed normal points. Further
photometry and high-resolution spectroscopy are needed for more accurate
calculation of the absolute elements of the binary.
photometric
observations on the basis of which the synthetic light curve solution was
obtained by Milone & Hrivnak (1981) using the Wilson-Devinney
code. Spectral classifications for both components were derived from the
spectroscopy observations. The data on radial velocity curves are absent,
and there is no strong evidence for Ca II H and K emission or for light curve variability. The nature of the asymmetry is not
clear. Three stable photometric solutions were found for q=0.9,
0.62, and 0.46, but the theoretical light curves predicted with Solution I
(q= 0.9) showed better fit to the observed normal points. Further
photometry and high-resolution spectroscopy are needed for more accurate
calculation of the absolute elements of the binary.
- 13.
- RS Col shows a W
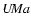 -like light curve,
although its classification by Agerer et al. (1999) as EW/DW may prove to be erroneous as it is thought. This binary is covered well by
ubvy observations analyzed by Rucinski (1983) and by
-like light curve,
although its classification by Agerer et al. (1999) as EW/DW may prove to be erroneous as it is thought. This binary is covered well by
ubvy observations analyzed by Rucinski (1983) and by
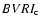 photometry observations performed by McFarlane &
Hilditch (1987). The photometric solutions have been found by
McFarlane & Hilditch (1987) using the WUNA3 code by
Rucinski. These solutions have proved very insensitive to mass ratio, that
tends toward the unity, which is rather unlikely. The absolute elements
have been predicted unreliably, so spectroscopic data are needed for more
accurate computation of absolute stellar characteristics for given system.
photometry observations performed by McFarlane &
Hilditch (1987). The photometric solutions have been found by
McFarlane & Hilditch (1987) using the WUNA3 code by
Rucinski. These solutions have proved very insensitive to mass ratio, that
tends toward the unity, which is rather unlikely. The absolute elements
have been predicted unreliably, so spectroscopic data are needed for more
accurate computation of absolute stellar characteristics for given system.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig6.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg197.gif) |
Figure A.7:
The location of the primaries and satellites of DW-systems
against a background of the evolutionary tracks by Maeder &
Meynet (1988) in the "
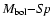 ''-diagram. The MS band
is marked between the ''-diagram. The MS band
is marked between the 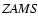 and
and 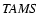 boundaries designated
by solid and dotted lines respectively. Denoted as crosses, the
errors of
boundaries designated
by solid and dotted lines respectively. Denoted as crosses, the
errors of
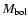 and
and 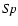 values for DW-components are
found from the proportions constructed on the basis of relationship
values for DW-components are
found from the proportions constructed on the basis of relationship
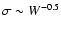 with the assumption of correspondence of the
average errors in (M, R) and (L,
with the assumption of correspondence of the
average errors in (M, R) and (L,
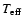 )
taken from
Andersen (1991) to the weight W=5. )
taken from
Andersen (1991) to the weight W=5. |
- 14.
- CG Cyg is the most peculiar system among the short-period
chromospherically active binary stars. From the copious data sets on this
system it seems that CG Cyg changes its spot structure rather rapidly.
Photometric observations were obtained by Heckert (1994),
Dapergolas et al. (2000) and Kozhevnikova et al. (2004).
But the preference was given to photometric elements averaged by Popper
(1994) over 29 sets of photometric data by Zeilik et al. (1994)
who analyzed these sets using procedures by Budding & Zeilik (1987)
to separate an eclipse, proximity, and spot effects in a light curve. As
noted by Dapergolas et al. (2000) the system presents
irregularities outside of the eclipses and depths of the minima change as
time advances. It is a complex system with changing active regions probably
due to photospheric activity. The spectroscopic observations were carried
out by Popper (1994) at Lick Observatory with the Hamilton
echelle-CCD spectrometer with high dispersion (0.4 km s-1 per pixel).
The latest spectroscopic data around the H
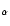 line were
obtained by Kjurkchieva et al. (2003). Masses and mass ratio
values of both components are averaged over spectroscopic data presented
by Popper (1994) and Kjurkchieva et al. (2003).
The values of mass ratio q found from the photometry and spectroscopy
differ from each other very strongly. This binary was included in the Tycho
HIPPARCOS mission.
line were
obtained by Kjurkchieva et al. (2003). Masses and mass ratio
values of both components are averaged over spectroscopic data presented
by Popper (1994) and Kjurkchieva et al. (2003).
The values of mass ratio q found from the photometry and spectroscopy
differ from each other very strongly. This binary was included in the Tycho
HIPPARCOS mission.
- 15.
- AR Dra = BV 226. Photometric solutions according
to Roche geometry were obtained by Broglia & Conconi (1979)
on the basis of the numerous B, V photoelectric observations
processed using the Wilson-Devinney light curve synthesis method. One should
note, however, a small seasonal change in the light curves. The spectroscopic
observations and data about mass ratio q are absent. The components
of this system are well inside the critical inner lobes corresponding to
assumed value q=0.75, and the system is most likely a detached one. The
presence of a gaseous material around the components or an intrinsic
variability of one of the stars are both possible. The spectral classes of
the components were assigned by the colour indices.
- 16.
- BZ Eri. First photoelectric photometry in three UBV colours has been analyzed in Srivastava & Sinha (1981).
The orbital period variations were registered by Srivastava (1986)
from 1976 to 1979 when the period slightly decreased, but from 1979 to 1980
it increased. The changes in depth, humps, and asymmetries in the branches
of minima noticed in U, B, V light curves may be
interpreted on the basis of the mass transfer between the components
according to Srivastava (1986). The secondary minimum, as
found by Srivastava & Uddin (1986), is subjected to
wave-like distortion that may be connected with a physical change in the
system. Current knowledge of this eclipsing binary is not satisfactory, as
noted by Srivastava & Uddin (1986), because the
spectroscopic and/or scanner observations are not very informative, but the
existing photometric data are insufficient for a reliable estimate of the
physical and geometrical elements of the orbit.
- 17.
- MT Her has a
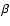 Lyrae-type light variation character
according to the first photoelectric observations by Budding and Murad
(1982). The ephemeris comes from Pokorny (1973). The
photometric elements were computed by modified Roche's model in the
NOPTS code by Budding & Murad (1989) using observational
data in B, V filters. The secondary effective temperature
(5500 K), mass ratio (0.6), and ratio of radii (0.75) were chosen as initial
approximations to find optimal curve fitting. The spectral type of the
primary component in accordance with the colour index is expected to be
somewhat later than F5-type classification as, for example, with
F8. This spectral estimate accords better with the derived
absolute radius. There is no convincing evidence of a period variation over
the last 12 000 orbital revolutions. More complete spectrographic study is
needed for accurate definition of the absolute parameters of this binary
system.
Lyrae-type light variation character
according to the first photoelectric observations by Budding and Murad
(1982). The ephemeris comes from Pokorny (1973). The
photometric elements were computed by modified Roche's model in the
NOPTS code by Budding & Murad (1989) using observational
data in B, V filters. The secondary effective temperature
(5500 K), mass ratio (0.6), and ratio of radii (0.75) were chosen as initial
approximations to find optimal curve fitting. The spectral type of the
primary component in accordance with the colour index is expected to be
somewhat later than F5-type classification as, for example, with
F8. This spectral estimate accords better with the derived
absolute radius. There is no convincing evidence of a period variation over
the last 12 000 orbital revolutions. More complete spectrographic study is
needed for accurate definition of the absolute parameters of this binary
system.
- 18.
- CN Lac is a poorly-studied binary in Nekrasova
(1936). The photometric elements were obtained on the basis of
187 photographic observations by Wachmann (1935), but
spectroscopic data are absent. The system is projected onto the
NGC 7209 region, but is not a member of the cluster. The estimates
of the orbital elements and absolute parameters are rough, so the weight W for this system was assigned as very low.
- 19.
- UV Leo. The intrinsic variability of the system light
linked with the spots on the components surfaces distorts the photometric
data whose "cleaning'' procedure nevertheless does not eliminate
the uncertainty in photometric solutions. Therefore two photometric
solutions are considered here:
- (a)
- The first evaluation of absolute stellar parameters is a combination
of the photometric analysis by Botsula (1978) with the spectroscopic
results obtained by Popper (1993). High-resolution CCD spectra and the cross-correlation function obtained by Popper (1993)
demonstrate that the hotter primary component is more luminous and larger
as opposed to the satellite. It corresponds well to the modern evolutionary
theory for coeval stars on the Main Sequence.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig7.eps}
\end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg199.gif) |
Figure A.8:
The location of the primaries and satellites of DW-systems
relative to the 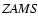 and
and 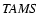 boundaries in the "M-R'' diagram
based on the evolutionary tracks by Maeder & Meynet (1988).
The designations are the same. If error in the component mass or
radius is comparable with the symbol size, its designation is
absent on the diagram.
boundaries in the "M-R'' diagram
based on the evolutionary tracks by Maeder & Meynet (1988).
The designations are the same. If error in the component mass or
radius is comparable with the symbol size, its designation is
absent on the diagram. |
- (b)
- The second solution is based on spectroscopic data obtained with
the use of the Hamilton echelle-CCD spectrometer by Popper (1997)
and the combination of HP, VT, and BT photometry
performed within the framework of the Hipparcos/Tycho mission and 8480-8740
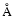 ground-based spectroscopy, as if mimicking GAIA observations
in Zwitter et al. (2003). Also the set of
ground-based spectroscopy, as if mimicking GAIA observations
in Zwitter et al. (2003). Also the set of
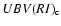 photometric data by Frederic & Etzel (1996) was used, the
analysis of which has showed that the hotter and more massive star is the
smaller and less luminous one; whereas for two MS stars the opposite
relationship is expected if one does not suppose the mass exchange.
photometric data by Frederic & Etzel (1996) was used, the
analysis of which has showed that the hotter and more massive star is the
smaller and less luminous one; whereas for two MS stars the opposite
relationship is expected if one does not suppose the mass exchange.
- 20.
- UU Lyn has Main Sequence components that do not make
contact but come very close to the corresponding Roche lobes. The period
change does not appear according to Yamasaki et al. (1983). The
symmetry of the light curve is also noted. Masses, absolute radii, and
major semi-axis were derived by Yamasaki et al. (1986)
combining results of spectroscopic ("single-lined spectrum'') and B,
V-bands photometric observations. There is excellent agreement between
the photometric mass ratio deduced from light curve analysis and the
spectroscopic one.
- 21.
- V 361 Lyr is quite well-studied both photometrically
and spectroscopically and has been identified as a true pre-contact binary.
From analysis of the new differential V-band light curves along
with V- and R-band light curves (see Hilditch et al. 1997),
which were computed by the synthetic code taking non-Keplerian corrections
into account, it follows that the primary component fills its Roche lobe
while the secondary component is detached and fills
 57
57 of the
Roche volume. These data confirm the stable nature of the asymmetric light
curve. The eclipse maps have also been built for both components to
illustrate the small changes in the cool spot structures for the primary
component. The spectroscopic observations carried out simultaneously in the
blue and red regions indicate the "double-lined spectra'' case. This is a
rare binary system that has very small orbital period but is not a contact.
of the
Roche volume. These data confirm the stable nature of the asymmetric light
curve. The eclipse maps have also been built for both components to
illustrate the small changes in the cool spot structures for the primary
component. The spectroscopic observations carried out simultaneously in the
blue and red regions indicate the "double-lined spectra'' case. This is a
rare binary system that has very small orbital period but is not a contact.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig8.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg202.gif) |
Figure A.9:
The same as Fig. 7 but in "the
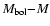 '' diagram. '' diagram. |
- 22.
- DD Mon is a single-lined spectroscopic binary, so it
is impossible to directly evaluate the mass ratio of components q.
The absolute and relative orbit elements were found as a combination of
photoelectric B-, V-band observations by Shengbang et al. (1996),
Shengbang et al. (1997) and from spectroscopic data including
39 spectrograms in the blue region made by Yamasaki et al. (1990).
No emission features have been detected either during eclipses or outside
them. All results show that the components of this binary have evolved away
from the ZAMS and through the mass-transfer process to the present
semi-detached state. The variation in the light curve shape may be caused
by the system evolution and by activity of the dark spots according to
Shengbang et al. (1997). The components are undermassive for
their radii and luminosities, which could be explained by their mass loss.
- 23.
- UV Psc. The high-dispersion spectrograms received with
the Hamilton CCD-spectrometer and covering 47 spectral regions along with
the radial velocity curves of Popper (1997) allowed estimation of
both the spectra and masses of components, respectively. 14 light curves
obtained by various observers were analyzed by Budding & Zeilik (1987)
and Budding et al. (1996), taking the properties of starspots
and distortion waves into account. The 14 photometric solutions agree quite
well. These data served to initiate the stellar parameters when running the
ILOT code, which seeks better fit of all parameters for the
photometric light curves simultaneously (Heckert 1999).
- 24.
- RS Sct is a
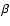 Lyrae type eclipsing binary that
possesses appreciable intrinsic variation in comparison with other
eclipsing binaries according to Cook (1992), while the effect of
the third light as a factor of such variation is excluded. The absolute and
relative orbital elements were obtained as a combination of spectroscopic
observations by King & Hilditch (1984) and photometric data by
Buckley (1984) taking the lack of coincidence between the values
of the photometric (
Lyrae type eclipsing binary that
possesses appreciable intrinsic variation in comparison with other
eclipsing binaries according to Cook (1992), while the effect of
the third light as a factor of such variation is excluded. The absolute and
relative orbital elements were obtained as a combination of spectroscopic
observations by King & Hilditch (1984) and photometric data by
Buckley (1984) taking the lack of coincidence between the values
of the photometric (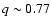 )
and spectroscopic(
)
and spectroscopic(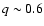 )
mass ratio
into account. The orbital parameters
)
mass ratio
into account. The orbital parameters
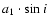 ,
,
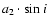 and minimum values of masses
and minimum values of masses
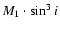 ,
,
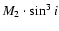 were calculated
from analysis of the radial velocity curves of both components based on the
Reticon spectroscopy. As computed by the Wilson-Devinney code the simultaneous
solution of BVR light curves results in a detached configuration,
although Buckley noted that the solution obtained by Wood (1978)
with the WINK-code indicates a tendency towards a semi-detached model.
were calculated
from analysis of the radial velocity curves of both components based on the
Reticon spectroscopy. As computed by the Wilson-Devinney code the simultaneous
solution of BVR light curves results in a detached configuration,
although Buckley noted that the solution obtained by Wood (1978)
with the WINK-code indicates a tendency towards a semi-detached model.
- 25.
- GR Tau is a near-contact detached system with both
components almost filling their critical Roche lobes, as follows from the
photometric solution obtained by the Wilson-Devinney code based on the
long-term photoelectric and CCD photometry of Zhang et al. (2002)
and on visual and infrared light curves by Lazaro et al. (1995).
The spectroscopic observations carried out by Yamasaki et al. (1984)
correspond to a "single-lined spectrum'' case, therefore no spectroscopic
mass ratio for the system is known. The direct spectra measurements are
not available, and the spectral classification of the components was performed
in accordance with the colour indices. More spectroscopic and photometric
observations are needed to clarify the spectral classification of the
stellar components and the current evolutionary status of the system.
- 26.
- GY Tel was included in the observational program of
southern eclipsing binaries and classified by Lipari & Sistero
(1988) as a near-contact short-period system showing EB-type
light curve. Extremely poor data, such as an orbital period, main and
second minima depths, and a primary spectrum assigned by the colour index,
were obtained by Shaw (1994) as a result of processing 400 UBV photoelectric observations. The rest orbital parameters and absolute elements
were reconstructed by relying on approximate statistical dependences of the
type "mass-spectrum'', "mass-radius'', "inclination-main minimum depth'',
and so on, derived by Svechnikov (1985). It explains such a
tiny evaluative weight. The large thermal decoupling of the components
should also be noted.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig9.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg207.gif) |
Figure A.10:
The same as Fig. 7 but in the " '' diagram. '' diagram. |
- 27.
- XY UMa The set of the system geometric parameters was
first obtained by Hilditch & Bell (1994) and then evaluated
more precisely by the eclipse mapping technique. This algorithm is based on
the maximum entropy method to recover the images of the distribution of
visual surface brightness for the primary component (Cameron & Hilditch
1997). The reconstructed images derived from V, I,
R-photometric light curves show the presence of time-variable star
spot activity in the eclipsed region of the primary. Processing of 42 spectra collected and computed by CCF-mapping as a result of near
IR spectroscopic observations reveals the faint satellite at the low
signal-to-noise ratio. It allows in fact to derive the absolute elements
of an orbit (see Pojmanski 1998).
- 28.
- BH Vir is an active binary system displaying vast
solar-type variability. Photometric visible light curves have been published
regularly since 1957 and are now supplemented by the J and K infrared
light curves of Arevalo et al. (2002) from which new geometrical
elements were determined with the use of the ILOT code developed by Budding
& Zeilik (1987). IR light curves show equal maxima,
especially in K filter. The infrared light curve solutions are in
good agreement with the calculations by Zeilik et al. (1990)
from the ILOT analysis of UBVRI light curves. The spectra
defined with the high-resolution Hamilton spectrometer and absolute
elements were obtained by Popper (1997).
- 29.
- CG Vir is a double-lined eclipsing binary, for which
the orbital solutions were found by Shen et al. (1990) from
photoelectric (1977, 1982) and spectroscopic observations (1985-86). The
yellow light curves were solved by the Russell-Merrill method. The solutions
of ten light curves computed by the Wilson-Devinney method assuming the
detached model gave smaller residuals than those obtained in the semi-detached
model. The system shares a number of properties with Algol-type
binaries, so it is likely that CG Vir might have left the
Algol-phase not so long ago.
- 30.
- ER Vul. The orbital solution is compiled on the basis
of UBVRI photometric data by Olah et al. (1994) and high-
resolution spectroscopic observations carried out by Hill (1990).
No firm spectroscopic evidence for the existence of extended material
around this binary was found by Gunn & Doyle (1997). The well-known
irregularities of this binary are interpreted largely in terms of the dark
maculae whose major characteristics (size, surface position) are quantified.
Very Large Array (VLA) continuous monitoring of this system
(X-band, 3.6 cm) has shown a pattern of variability with the dominant
slow hourly timescale variations (about 3 mJy), whereas the contemporaneous
Extreme Ultraviolet Explorer (EUE) in the 70-140 Å band did
not show any significant EUE flaring, which could correlate with the
radio emission, according to Rucinski (1998). VLA multifrequency observations were also carried out and discussed in Garcia-Sanchez et al. (2003).
The binary
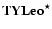 has led to only very unreliable
photometric data on the photographic plates of the Zonnenberg survey. This
system was also included by Popper (1996) in the spectroscopic
program of lower Main Sequence eclipsing binary stars (
has led to only very unreliable
photometric data on the photographic plates of the Zonnenberg survey. This
system was also included by Popper (1996) in the spectroscopic
program of lower Main Sequence eclipsing binary stars (
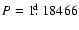 ,
,
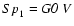 ). Assuming DW systems class-averaged
). Assuming DW systems class-averaged
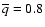 as an initial value for the mass ratio and using the
empiric relations of the type "spectrum-mass'', "mass-radius'', and
"main minimum amplitude-orbital inclination'', one might restore the elements
of the spectroscopic and photometric orbits (
as an initial value for the mass ratio and using the
empiric relations of the type "spectrum-mass'', "mass-radius'', and
"main minimum amplitude-orbital inclination'', one might restore the elements
of the spectroscopic and photometric orbits (
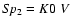 ,
,
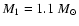 ,
M2=0.9:
,
M2=0.9:
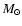 ,
,
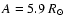 ,
,
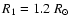 ,
,
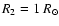 ,
,
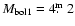 ,
,
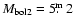 ,
r1=0.20,
r2=0.16,
,
r1=0.20,
r2=0.16,
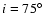 ,
(J1/J2)V=2,
(L1)V=0.75). But as the three spectrograms showed in
Popper (1996), there is no evidence for a second component in the
spectrum, although the phases are uncertain. In addition, analysis of the
modern photometric and spectroscopic observations carried out by Lacy et al.
(2002) leads to the conclusion that the above system is not an
eclipsing binary and that its classification was a mistake by
Hoffmeister (1933).
,
(J1/J2)V=2,
(L1)V=0.75). But as the three spectrograms showed in
Popper (1996), there is no evidence for a second component in the
spectrum, although the phases are uncertain. In addition, analysis of the
modern photometric and spectroscopic observations carried out by Lacy et al.
(2002) leads to the conclusion that the above system is not an
eclipsing binary and that its classification was a mistake by
Hoffmeister (1933).
Copyright ESO 2005
![]() etached (components
far from the contact configuration) eclipsing binaries similar in their physical
characteristics to stars of
etached (components
far from the contact configuration) eclipsing binaries similar in their physical
characteristics to stars of
![]()
![]() -type and with orbital periods
(
-type and with orbital periods
(
![]() )
noticeably greater than those of W
)
noticeably greater than those of W ![]() -type stars
(
-type stars
(
![]() ). Another designation widely used in the
literature for DW eclipsing binaries is "short-periodic'' RS CVn-type systems.
). Another designation widely used in the
literature for DW eclipsing binaries is "short-periodic'' RS CVn-type systems.
![]() into an independent category of "short-periodic''
RS CVn-type systems (DW-stars). Also all binaries presented in the
DW-catalogue are eclipsing systems whose variability is rigorously established
from photometric light curves, whereas more than a half of the systems from
Strassmeier's catalogue (1993) are not eclipsing and their
variability is determined from the wave migration period. This past decade has
offered plentiful observational information about short-periodic RS CVn-type
stars.
into an independent category of "short-periodic''
RS CVn-type systems (DW-stars). Also all binaries presented in the
DW-catalogue are eclipsing systems whose variability is rigorously established
from photometric light curves, whereas more than a half of the systems from
Strassmeier's catalogue (1993) are not eclipsing and their
variability is determined from the wave migration period. This past decade has
offered plentiful observational information about short-periodic RS CVn-type
stars.
![]() )
and "spectrum-effective temperature'' (
)
and "spectrum-effective temperature'' (
![]() )
which were obtained and substantiated in Svechnikov (1985) were
employed here to estimate mass and effective temperature of the primary component
by its known spectrum. For the satellites the values of mass and effective
temperature are found from known photometric solutions based on mass ratio and
the surface brightness ratio of components, respectively. As for determining
the major semi-axis and absolute radii, the generalized third Kepler's law is
used along with simple geometrical proportions that connect relative radii known
from photometric solutions with absolute ones, for instance WZ And, RX Ari,
AE Cas, ST Cen, AR Dra, MT Her, CN Lac, and UU Lyn.
The percentage of similar binaries is approximately 25
)
which were obtained and substantiated in Svechnikov (1985) were
employed here to estimate mass and effective temperature of the primary component
by its known spectrum. For the satellites the values of mass and effective
temperature are found from known photometric solutions based on mass ratio and
the surface brightness ratio of components, respectively. As for determining
the major semi-axis and absolute radii, the generalized third Kepler's law is
used along with simple geometrical proportions that connect relative radii known
from photometric solutions with absolute ones, for instance WZ And, RX Ari,
AE Cas, ST Cen, AR Dra, MT Her, CN Lac, and UU Lyn.
The percentage of similar binaries is approximately 25![]() .
In rare cases of
lacking information on the relative radii of components, the "mass-radius''
(M-R) relation obtained by Svechnikov (1985) is employed when
calculating the absolute radii, at which point relative radii are deduced from
inverse geometrical proportions.
.
In rare cases of
lacking information on the relative radii of components, the "mass-radius''
(M-R) relation obtained by Svechnikov (1985) is employed when
calculating the absolute radii, at which point relative radii are deduced from
inverse geometrical proportions.
![]() ,
,
![]() ,
and
,
and
![]() have been obtained for primary and secondary components by
summarizing data compiled for pre-contact systems. 31 systems of DW-type
were involved in this treatment; for a better fitting to the statistical
dependences for systems WZ And (2) and UV Leo (20),
we have taken photometric solutions under Number 1 (see Table 1).
have been obtained for primary and secondary components by
summarizing data compiled for pre-contact systems. 31 systems of DW-type
were involved in this treatment; for a better fitting to the statistical
dependences for systems WZ And (2) and UV Leo (20),
we have taken photometric solutions under Number 1 (see Table 1).
![]() (see Appendix, Fig. A.1) may be written in the following form:
(see Appendix, Fig. A.1) may be written in the following form:
![]() )
value and that found in accordance
with the empirical "mass-radius'' relation averaged for MS stars. The same
is true for the definition of luminosity excess with only one difference: the
empirical "mass-luminosity'' relation for MS stars is used. When calculating
radius and luminosity excesses we have used new
)
value and that found in accordance
with the empirical "mass-radius'' relation averaged for MS stars. The same
is true for the definition of luminosity excess with only one difference: the
empirical "mass-luminosity'' relation for MS stars is used. When calculating
radius and luminosity excesses we have used new
![]() and M-R relations
obtained by Gorda & Svechnikov (1999) for detached MS eclipsing
variables with well-known absolute elements. These radius and luminosity excesses
indicate that the position of DW-binaries is close to Terminal Age Main
Sequence (
and M-R relations
obtained by Gorda & Svechnikov (1999) for detached MS eclipsing
variables with well-known absolute elements. These radius and luminosity excesses
indicate that the position of DW-binaries is close to Terminal Age Main
Sequence (![]() )
but is not a midpoint of the MS-band as is true for
DMS-systems.
)
but is not a midpoint of the MS-band as is true for
DMS-systems.
![]() -type contact systems, which reach a maximum up to
-type contact systems, which reach a maximum up to ![]() times
and
times
and ![]() ,
respectively, at q= 0.15 as compared to MS stars
according to Svechnikov (1990). This comparison is important
because W
,
respectively, at q= 0.15 as compared to MS stars
according to Svechnikov (1990). This comparison is important
because W ![]() -type contact systems present the next evolutionary stage of
pre-contact short-periodic RS CVn-type binaries. The resulting radius and
luminosity excesses of DW-satellites are quite expected in the framework of
the formalism of magnetic braking.
-type contact systems present the next evolutionary stage of
pre-contact short-periodic RS CVn-type binaries. The resulting radius and
luminosity excesses of DW-satellites are quite expected in the framework of
the formalism of magnetic braking.
![]() )
DMS-binaries, DW-stars, and W
)
DMS-binaries, DW-stars, and W ![]() -type contact systems in terms
of orbital angular momentum loss (AML) and combines them into a common
evolutionary chain that in fact has already been confirmed from extensive
observational data by Svechnikov & Kuznetsova (1990) and from
the relations of statistics and lifetimes obtained by Tutukov et al. (2004).
The magnetic stellar wind in low-mass close binaries is a driving force in
the approach of the two components. But considering that the orbital
AML-timescale is shorter than the nuclear timescale, the mass loss process
in the binary may be initiated before the components fill up their Roche lobes.
It is very likely that such a process might lead to the appearance of excess
in radii and luminosities of DW-satellites. As for satellites of W
-type contact systems in terms
of orbital angular momentum loss (AML) and combines them into a common
evolutionary chain that in fact has already been confirmed from extensive
observational data by Svechnikov & Kuznetsova (1990) and from
the relations of statistics and lifetimes obtained by Tutukov et al. (2004).
The magnetic stellar wind in low-mass close binaries is a driving force in
the approach of the two components. But considering that the orbital
AML-timescale is shorter than the nuclear timescale, the mass loss process
in the binary may be initiated before the components fill up their Roche lobes.
It is very likely that such a process might lead to the appearance of excess
in radii and luminosities of DW-satellites. As for satellites of W ![]() -type
contact systems, the question of radius and luminosity excesses was treated
in detail by Istomin (1986) with the assumption that the luminosity
increase of their satellites is due to gravitational energy release originating
from the matter flowing from the more massive component.
-type
contact systems, the question of radius and luminosity excesses was treated
in detail by Istomin (1986) with the assumption that the luminosity
increase of their satellites is due to gravitational energy release originating
from the matter flowing from the more massive component.
![]() -diagram (Fig. A.7) showed that the primaries are well positioned within
the MS band in the Hertzsprung-Russel (H-R) diagram and justified their
status as slightly evolved stars, whereas the satellites demonstrate luminosity
excesses for their masses. The same conclusion can be made from Fig. A.9. The
M-R diagram (Fig. A.8) clearly shows that almost all DW-primaries
are strongly localized between the boundaries of
-diagram (Fig. A.7) showed that the primaries are well positioned within
the MS band in the Hertzsprung-Russel (H-R) diagram and justified their
status as slightly evolved stars, whereas the satellites demonstrate luminosity
excesses for their masses. The same conclusion can be made from Fig. A.9. The
M-R diagram (Fig. A.8) clearly shows that almost all DW-primaries
are strongly localized between the boundaries of ![]() and
and ![]() also taken
from models by Maeder & Meynet (1988); and yet at the same time
DW-satellites are oversized for their masses. Also the
also taken
from models by Maeder & Meynet (1988); and yet at the same time
DW-satellites are oversized for their masses. Also the ![]() -diagram (Fig. A.10)
is of interest because of temperature excesses which are so evident for
secondary components of DW-systems.
-diagram (Fig. A.10)
is of interest because of temperature excesses which are so evident for
secondary components of DW-systems.
![]() diagram was applied to estimate the ages of these systems
by the isochrone method as well. We obtained a fairly wide spread for an age
change; for example, the age of UV Psc (24) equals approximately 10 Gyr, while MT Her (18) and V 361 Lyr (22)
binaries are located near the ZAMS.
diagram was applied to estimate the ages of these systems
by the isochrone method as well. We obtained a fairly wide spread for an age
change; for example, the age of UV Psc (24) equals approximately 10 Gyr, while MT Her (18) and V 361 Lyr (22)
binaries are located near the ZAMS.
![]() ,
,
![]() ,
and
,
and
![]() and
when studying properties of pre-contact DW-class which represents the intermediate
stage between the detached DMS-class and contact binaries of W
and
when studying properties of pre-contact DW-class which represents the intermediate
stage between the detached DMS-class and contact binaries of W ![]() -type.
-type.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig1.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg176.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig2.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg180.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig3.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg182.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig4.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg187.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fi5a.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg192.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig6.eps} \end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg197.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2003Fig7.eps}
\end{figure}](/articles/aa/full/2005/25/aa2003-04/Timg199.gif)