A&A 437, 9-22 (2005)
DOI: 10.1051/0004-6361:20041046
G. Bodo1 - G. Chagelishvili3 - G. Murante1 - A. Tevzadze3 - P. Rossi 1 - A. Ferrari2
1 -
INAF Osservatorio Astronomico di Torino, Strada dell'Osservatorio
20, 10025 Pino Torinese, Italy
2 -
Dipartimento di Fisica Generale dell'Università,
via Pietro Giuria 1, 10125 Torino, Italy
3 -
Center for Plasma Astrophysics, Abastumani
Astrophysical Observatory, 2a Kazbegi Ave., Tbilisi 0160, Georgia
Received 7 April 2004 / Accepted 28 February 2005
Abstract
We perform a detailed analytical and numerical study of the dynamics
of perturbations (vortex/aperiodic mode, Rossby and spiral-density
waves) in 2D compressible disks with a Keplerian law of rotation. We
draw attention to the process of spiral-density wave generation
from vortices, discussing, in particular, the initial, most peculiar
stages of wave emission. We show that the linear phenomenon of
wave generation by vortices in smooth (without inflection points)
shear flows found by using the
so-called non-modal approach, is directly applicable to the present
case. After an analytical non-modal description of the physics and
characteristics of the spiral-density wave generation/propagation in
the local shearing-sheet model, we follow
the process of wave generation by small amplitude coherent circular
vortex structures, by direct global
numerical simulation, describing the main features of the generated
waves.
Key words: accretion, accretion disks - waves - hydrodynamics
The dynamics of vortices in astrophysical disks has recently received much interest both because vortices in protoplanetary disks can represent aggregation regions of solid particles for the eventual formation of planets (Barge & Sommeria 1995) and more generally for understanding accretion disk dynamics and the basic problem of angular momentum transport (Lovelace et al. 1999; Li et al. 2000). Several works have been devoted to the analysis of the possibility of forming and maintaining coherent vortex structures in the strongly sheared flow pertaining to a Keplerian disk, both in barotropic configurations, where the initial potential vorticity perturbation is conserved (Bracco et al. 1999; Godon & Livio 1999, 2000; Davis et al. 2000; Davis 2002) and in baroclinic situations where one can have vorticity generation (Klahr & Bodenheimer 2003; Klahr 2004). In the incompressible case it has been shown that coherent vortex structures can indeed form (under conservation of potential vorticity) and anticyclonic vortices can survive longer than cyclonic ones (Bracco et al. 1999) and give rise to the appearance of Rossby waves in the system (Davis et al. 2000). The effects of compressibility have not yet been fully analyzed and require rigorous study. Godon & Livio (1999) performed two-dimensional time-dependent numerical simulations of vortices in viscous compressible Keplerian disks. Vorticity waves are considered as one of the constituents of (anticyclonic) vortex dynamics, but without specification of the wave properties and any analysis of their genesis and dynamics (the subject of the study was the stability and lifetime of vortices). Davis (2002) performed fully compressible numerical simulations of the dynamics of a single vortical structure in a Keplerian disk flow and has reported the generation of outward-moving compressible waves by the coherent vortex (the generation was attributed to nonlinear processes) pointing out the potential importance of this phenomenon for vortex dynamics. Johansen et al. (2004) considered the dynamics of nonlinear vortices by numerical 3D simulations in the local shearing sheet approximation, also observing indications of wave generation. Klahr & Bodenheimer (2003), performing 2D and 3D hydrodynamical simulations of protoplanetary disks, found that a radial entropy gradient can generate Rossby waves which eventually break into vortices. Klahr (2004), by a linear stability analysis similar to the one presented in this paper, in fact showed that a radial entropy gradient leads to continuous generation of potential vorticity and to a transient swing-like amplification of the vortical/aperiodic mode, without the subsequent decay observed in the linear barotropic configuration.
The aim of this paper is to investigate the linear dynamics of initially-imposed vortical perturbations in 2D compressible Keplerian disks to understand the phenomena of spiral-density and Rossby wave generation and to study the initial, most peculiar stages of wave emission/propagation. In this repect, we want to stress that the origins of spiral-density and Rossby waves are absolutely different.
We base our understanding of spiral-density wave generation on the papers by Chagelishvili et al. (1997, 2000), where a completely linear phenomenon of acoustic wave generation by vortex mode perturbation in smooth shear flows was for the first time discussed. It was also shown that the generated acoustic waves are emitted as two symmetric packages in opposite directions from the parent coherent vortex perturbation. This wave generation phenomenon is directly applicable to the generation of spiral-density waves by vortices in disk flows (Sect. 3). The Rossby wave appearance from the vortex mode perturbations, on the contrary, is not connected to any generation process. The essence of the Rossby wave formation lies in the "breaking of degeneracy'' of vortex mode perturbations (Sect. 4).
Recently, much progress has been made by the hydrodynamic community in the analysis of the linear dynamics of smooth shear flows by recognising that the traditional normal mode approach does not represent the best tool for its study because of the non-normality of the linear operators in the flows (cf. Reddy et al. 1993; Henningson & Reddy 1994; Gustavsson 1991; Farrell & Ioannou 1993; Craik & Criminale 1986). This means that the corresponding eigenfunctions are not orthogonal and strongly interfere. The knowledge drawn from the analysis of separate eigenfunctions and eigenvalues is far from complete. A correct and full description of the shear flow phenomena needs knowledge of the interference processes which cannot be easily taken into account in the framework of modal analysis. These circumstances led to the development of the so-called non-modal approach that could reveal several unexpected phenomena, which were overlooked by the normal mode analysis. The non-modal analysis is a modification of the initial value problem. It involves the change of independent variables from the laboratory to a moving frame and the study of the temporal evolution of spatial Fourier harmonics (SFH) of perturbations without any spectral expansion in time. The resulting linear dynamics is much richer than that expected from the stability predictions of the modal approach and these linear processes may also play a fundamental role in the full dynamics of smooth shear flows. For example, it has been shown that vortical perturbations can have a phase of transient amplification, which is at the base of the so-called "bypass'' concept of the onset of turbulence in planar Couette flows (Baggett et al. 1995; Gebhardt & Grossman 1994; Farrell & Ioannou 1993; Henningson & Ready 1994; Grossmann 2000; Chagelishvili et al. 2002; Chapman 2002). Another phenomenon of interest here is the generation of waves by a vortex/aperiodic mode of perturbations, which has been discussed for the first time, as we saw above, by Chagelishvili et al. (1997) and analyzed by Chagelishvili et al. (2000) and Farrell & Ioannou (2000) in the simplest planar configuration. In this paper we extend the non-modal analysis of this process to the case of 2D Keplerian disk flow (that is a natural example of smooth shear flows) in the shearing sheet approximation, giving the theoretical basis to understand the results of simulations like those presented by Davis (2002). We also perform numerical simulations of the vortex dynamics in Keplerian disks: we consider a small amplitude (to include only linear processes), coherent circular vortex and focus on wave generation and emission, on the properties of density and vorticity fields and on the description of the wave propagation trajectories. Physical model and equations are presented in Sect. 2. The non-modal analysis of spiral-density wave generation/emission by vortex mode perturbation is presented in Sect. 3. The appearance of the Rossby wave from vortex mode perturbation is outlined in Sect. 4. Numerical simulations of wave emergence from a coherent circular vortex perturbation is presented in Sect. 5 and in the last section we summarize our results. In the Appendix we describe the method for the selection of initial values of pure vortex mode perturbations for our numerical study.
In cylindrical coordinates, the basic equations will
read as follows:
Our 2D model of a Keplerian disk retains the
dynamical effects of differential rotation, while discarding geometrical
and thermodynamic
![]() complications. The sound
speed is defined by:
complications. The sound
speed is defined by:
In a Keplerian disk the basic flow vorticity is (cf. Tagger
2001):
Here we study the linear dynamics of 2D small-scale perturbations
(i.e. with characteristic scales in radial and
azimuthal directions much less than the radial characteristic
scale of the background/disk flow) in the shearing sheet
approximation (e.g., Goldreich & Lynden-Bell 1965; Goldreich &
Tremaine 1978; Nakagawa & Sekiya 1992). In this case the dynamical
equations are written in the local co-moving Cartesian co-ordinate
system:
Introducing linear perturbations
Substitution of Eqs. (21), (22) into
Eqs. (17)-(20) yields the system of
ordinary differential equations that governs the linear dynamics of
SFH of perturbations in the described flow:
The latter system is characterized by the important time
invariant:
We can define the spectral density of the total energy in the ![]() -plane as:
-plane as:
The numerical study of SFH dynamics is governed by
Eqs. (27)-(30).
However, for the fundamental comprehension of the physical nature
of the perturbations and their linear dynamics in the flow, we
rewrite them in another form: from
Eqs. (27)-(30) one
can get the following second order inhomogeneous
differential equation for vy(t):
Equation (32) describes two different modes of perturbations:
Here we present a numerical and qualitative study of the linear
dynamics of an initially excited SFH of vortex mode perturbation.
The dynamics is defined by the value of the parameter:
| R(t) | ![$\displaystyle {2\vert A\vert \over {\sqrt {4\Omega_0(\Omega_0 + A) +
[k_x^2(t) + k_y^2] c_{\rm s}^2}}}$](/articles/aa/full/2005/25/aa1046-04/img68.gif) |
||
| = | ![$\displaystyle {3 \over 2\sqrt {1+[k_x^2(t) +
k_y^2]H^2 }},$](/articles/aa/full/2005/25/aa1046-04/img69.gif) |
(37) |
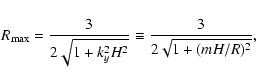 |
(38) |
We carried out numerical integration of
Eqs. (27)-(29) for an
initially imposed leading vortex mode SFH (
kx(0) / ky <0),
without mixture of waves. Initial vortex SFH perturbations are
defined by the equations presented in the Appendix. The
calculations show a fundamental difference in the dynamics of
vortices at low and moderate
![]() .
.
At
![]() all dynamics occurs at small R(t), at low shear
rates compressibility is negligible and only one phenomenon occurs,
i.e. transient growth of SFH of aperiodic vortices.
The leading SFH gains energy from the mean
flow and increases its amplitude; when the SFH becomes trailing, it gives
back the energy to the flow and decreases its amplitude. It is obvious that the
transient growth of vortex perturbations exists in the
spectrally/asymptotically stable flow system (the rotation curve
derived from Kepler's law is extremely stable based on the Rayleigh
criterion). The transient growth of two dimensional vortical/aperiodic
perturbations in an incompressible Keplerian flow was found by
Lominadze et al. (1988). Later on, the existence of transient
growth was confirmed by Fridman (1989) and Ioannou & Kakouris
(2001). The importance of transient growth for the onset of
hydrodynamic turbulence in Keplerian disks is discussed by
Chagelishvili et al. (2003) and Tevzadze et al. (2003).
all dynamics occurs at small R(t), at low shear
rates compressibility is negligible and only one phenomenon occurs,
i.e. transient growth of SFH of aperiodic vortices.
The leading SFH gains energy from the mean
flow and increases its amplitude; when the SFH becomes trailing, it gives
back the energy to the flow and decreases its amplitude. It is obvious that the
transient growth of vortex perturbations exists in the
spectrally/asymptotically stable flow system (the rotation curve
derived from Kepler's law is extremely stable based on the Rayleigh
criterion). The transient growth of two dimensional vortical/aperiodic
perturbations in an incompressible Keplerian flow was found by
Lominadze et al. (1988). Later on, the existence of transient
growth was confirmed by Fridman (1989) and Ioannou & Kakouris
(2001). The importance of transient growth for the onset of
hydrodynamic turbulence in Keplerian disks is discussed by
Chagelishvili et al. (2003) and Tevzadze et al. (2003).
At moderate/large
![]() ,
the dynamics are richer: our
calculations show the appearance of a conversion of vortices to
spiral-density waves at moderate shear rates. In Figs. 1-2 we present the results of
calculations at
,
the dynamics are richer: our
calculations show the appearance of a conversion of vortices to
spiral-density waves at moderate shear rates. In Figs. 1-2 we present the results of
calculations at
![]() (respectively m = R/H and
m = 0.5 R/H in terms of the azimuthal wavenumber) . We can start to notice the conversion
at about
(respectively m = R/H and
m = 0.5 R/H in terms of the azimuthal wavenumber) . We can start to notice the conversion
at about
![]() (i.e., at about
(i.e., at about
![]() ), but the overall behavior is still dominated by
the vortex transient growth, as is evident from the lower right
panel in Fig. 1 that shows the SFH energy growth and
decrease. The process already becomes dominant in the SFH dynamics
at
), but the overall behavior is still dominated by
the vortex transient growth, as is evident from the lower right
panel in Fig. 1 that shows the SFH energy growth and
decrease. The process already becomes dominant in the SFH dynamics
at
![]() (i.e., at about kyH<0.5).
(i.e., at about kyH<0.5).
In Fig. 2 we present the evolution of non-dimensional perturbed
quantities
![]() and of the normalized energy
and of the normalized energy
![]() of a SFH, for the case with
of a SFH, for the case with
![]() .
In this case, at the beginning
.
In this case, at the beginning ![]() (as
kx(0)/ky = - 15, i.e.,
(as
kx(0)/ky = - 15, i.e.,
![]() ), and the
initial stage of the evolution is incompressible. Evolving
in the shear flow, the vortex SFH gains energy from the mean flow
and amplifies, while retaining its aperiodic nature.
R(t) increases, becomes moderate and compressibility comes into
effect. As a result, we observe the appearance of an oscillating
part of SFH, i.e. we observe the appearance of spiral-density waves.
Thus, the linear dynamics of a vortex mode
perturbation is followed by the generation of a spiral-density wave.
When R(t) is moderate, the time scales of the vortex and wave SFH are comparable and the perturbations are not
separable/distinguishable, i.e. we have a mix of SFH of aperiodic
and oscillating modes. Subsequently, R(t) becomes small again,
the time scale of the wave SFH becomes much shorter than that of the
vortex SFH and the modes become clearly distinguishable again.
), and the
initial stage of the evolution is incompressible. Evolving
in the shear flow, the vortex SFH gains energy from the mean flow
and amplifies, while retaining its aperiodic nature.
R(t) increases, becomes moderate and compressibility comes into
effect. As a result, we observe the appearance of an oscillating
part of SFH, i.e. we observe the appearance of spiral-density waves.
Thus, the linear dynamics of a vortex mode
perturbation is followed by the generation of a spiral-density wave.
When R(t) is moderate, the time scales of the vortex and wave SFH are comparable and the perturbations are not
separable/distinguishable, i.e. we have a mix of SFH of aperiodic
and oscillating modes. Subsequently, R(t) becomes small again,
the time scale of the wave SFH becomes much shorter than that of the
vortex SFH and the modes become clearly distinguishable again.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1046fig1.eps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg84.gif) |
Figure 1:
The evolution of SFH normalized
velocity and density perturbations (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1046fig2.eps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg85.gif) |
Figure 2:
The evolution of SFH normalized
velocity and density perturbations
(
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1046fig3.eps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg90.gif) |
Figure 3:
The dynamics of
|
| Open with DEXTER | |
In spite of what was said above, we carry out a separation of the modes also in the vicinity of time t*, when kx(t*)=0 and R(t) is not small. The performed separation allows us to establish the initial characteristics of the generated wave SFH, that, in turn, determine the further dynamics/energetic of SFH, even quantitatively.
In Fig. 3 we present separately the dynamics of
![]()
![]() D and of their vortex
D and of their vortex
![]() and wave components
and wave components
![]() for a
pure vortex/aperiodic initial perturbation (
for a
pure vortex/aperiodic initial perturbation (
![]() ), with the same parameters
used for the case in Fig. 2. From Fig. 3
we notice:
), with the same parameters
used for the case in Fig. 2. From Fig. 3
we notice:
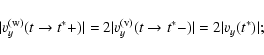 |
(39) |
In the previous section we found that the compressible shearing sheet approximation results in a third order system of ordinary differential equations (see Eqs. (27)-(29)), or, equivalently, in a second order inhomogeneous differential equation (see Eq. (32)). This reduction is connected to the conservation of potential vorticity and results in the fact that one of the perturbation modes is aperiodic/vortex. Consequently, the approximation involves two spiral-density waves propagating in opposite directions and one vortex mode. The vortex mode and spiral-density waves are no longer independent: they are coupled by the strong differential character of Keplerian rotation. As is shown in the previous section, the vortex mode unconditionally generates spiral-density waves, but the opposite does not occur, i.e. the waves do not a generate vortex/aperiodic mode.
A question arises: how does the picture change when the shearing
sheet approximation is not valid, especially, when the mean vorticity
gradient across the disk is at work? We consider this problem
qualitatively, borrowing some estimates from Tagger
(2001). At first, the linear dynamics of perturbations is
described by a third order system of ordinary differential
equations that, however, cannot be reduced to a second order
inhomogeneous differential equation, as in the previous case. In
this case all the perturbation modes are waves: two spiral-density
and one Rossby wave. The frequency of the first ones is given
by Eq. (35). We can get the frequency of the Rossby wave from Eq. (16)
of Tagger (2001):
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1046fig4.eps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg107.gif) |
Figure 4: Simple sketch of the relation between the Rossby wave and vortex mode perturbations in the wavenumber plane (Kx, Ky), see details in the text. |
| Open with DEXTER | |
We present a simple sketch of the "breaking of the
degeneracy'' in the wavenumber plane (kx,ky) (see Fig. 4).
The linear dynamics of a vortical perturbation may be described by
following each of its SFH in the wavenumber plane. We single out
a SFH that, initially, is located at point 1 in Fig. 4,
for which
kx/ky<0; ky < 1/r;
![]() ,
i.e.
a tightly leading vortical perturbation with large
azimuthal size. Formally, the perturbation represents a Rossby
wave SFH. However, according to Eq. (40), its frequency
is substantially smaller than
,
i.e.
a tightly leading vortical perturbation with large
azimuthal size. Formally, the perturbation represents a Rossby
wave SFH. However, according to Eq. (40), its frequency
is substantially smaller than ![]() .
Thus, the SFH is
aperiodic, i.e., it is degenerated to a vortex mode SFH. According
to Eq. (22), as kx(t) varies in time, the SFH drifts in the
direction marked by the arrows (we present the drift of the SFH only in the upper half-plane ky>0; since the perturbation is
real, there is a counterpart in the lower half-plane.)
Initially, as |kx(t)| decreases, the energy of the SFH grows
(see Figs. 1-3). Then, the SFH reaches the circled domain where
|ky|/(kx2+ky2)<r (point 2) and its frequency becomes no
longer negligible (the boundaries of the
domain, where breaking of degeneracy occurs, are indistinct, but
we fixed the domain to clarify the analysis). Thus, passing
this domain, the SFH acquires a wave nature, i.e., the
degeneration to a vortex mode is broken. At the same time, the
Rossby wave SFH continues its growth that lasts until it crosses the
line kx=0 (point 3). It then generates the related SFH of a
spiral-density wave (as it does the vortex mode SFH - see Sect. 3).
The drift after passing the line kx = 0 is shown by the double line
arrows to stress the appearance of the spiral-density wave SFH and
its further drift equal to the Rossby wave drift. At point 4,
the Rossby wave SFH leaves the circled domain and becomes tightly
trailing, again degenerating into an aperiodic/vortex SFH.
Thus, the Rossby wave appearance from a
vortex mode perturbation is not connected to a generation
process. The essence of the Rossby wave formation lies just in the
"breaking of degeneracy'' of the vortex mode perturbation. If we now choose
a vortex mode SFH with ky>1/r (e.g., at point
.
Thus, the SFH is
aperiodic, i.e., it is degenerated to a vortex mode SFH. According
to Eq. (22), as kx(t) varies in time, the SFH drifts in the
direction marked by the arrows (we present the drift of the SFH only in the upper half-plane ky>0; since the perturbation is
real, there is a counterpart in the lower half-plane.)
Initially, as |kx(t)| decreases, the energy of the SFH grows
(see Figs. 1-3). Then, the SFH reaches the circled domain where
|ky|/(kx2+ky2)<r (point 2) and its frequency becomes no
longer negligible (the boundaries of the
domain, where breaking of degeneracy occurs, are indistinct, but
we fixed the domain to clarify the analysis). Thus, passing
this domain, the SFH acquires a wave nature, i.e., the
degeneration to a vortex mode is broken. At the same time, the
Rossby wave SFH continues its growth that lasts until it crosses the
line kx=0 (point 3). It then generates the related SFH of a
spiral-density wave (as it does the vortex mode SFH - see Sect. 3).
The drift after passing the line kx = 0 is shown by the double line
arrows to stress the appearance of the spiral-density wave SFH and
its further drift equal to the Rossby wave drift. At point 4,
the Rossby wave SFH leaves the circled domain and becomes tightly
trailing, again degenerating into an aperiodic/vortex SFH.
Thus, the Rossby wave appearance from a
vortex mode perturbation is not connected to a generation
process. The essence of the Rossby wave formation lies just in the
"breaking of degeneracy'' of the vortex mode perturbation. If we now choose
a vortex mode SFH with ky>1/r (e.g., at point
![]() ), it is not
difficult to understand that the drifting SFH misses the circled
domain and the breaking of degeneration never occurs, but,
in crossing the line kx=0 (see point
), it is not
difficult to understand that the drifting SFH misses the circled
domain and the breaking of degeneration never occurs, but,
in crossing the line kx=0 (see point
![]() ), it
generates its related spiral density wave SFH.
), it
generates its related spiral density wave SFH.
A supposition about the coupling of Rossby and spiral-density waves
is expressed in Tagger (2001): "density waves generating Rossby
waves as they propagate, and reciprocally Rossby waves spawning
density waves as they are sheared by differential rotation''.
Chagelishvili & Chkhetiani (1995) investigated the linear dynamics
of planetary atmospheric Rossby waves in the ![]() -plane
approximation, in a case of zonal flow. They found and described
the generation of spiral-density waves by Rossby waves, but not the
opposite. It may be that this asymmetry of the wave coupling is
connected to the fact that in the system, we have only one Rossby
and two spiral-density waves (propagating in opposite directions).
The same asymmetry exists in case of wave and vortex mode coupling
(see Sect. 3 and Chagelishvili et al. 1997). In this
context it would be particularly interesting to consider the case
where a radial entropy gradient is present (Klahr 2004), since in
this case there are two independent Rossby waves. The
problem of Rossby wave generation by spiral-density waves in a given
disk model (containing both angular velocity and vorticity
gradients) will be the subject of a separate investigation.
-plane
approximation, in a case of zonal flow. They found and described
the generation of spiral-density waves by Rossby waves, but not the
opposite. It may be that this asymmetry of the wave coupling is
connected to the fact that in the system, we have only one Rossby
and two spiral-density waves (propagating in opposite directions).
The same asymmetry exists in case of wave and vortex mode coupling
(see Sect. 3 and Chagelishvili et al. 1997). In this
context it would be particularly interesting to consider the case
where a radial entropy gradient is present (Klahr 2004), since in
this case there are two independent Rossby waves. The
problem of Rossby wave generation by spiral-density waves in a given
disk model (containing both angular velocity and vorticity
gradients) will be the subject of a separate investigation.
In this section we present 2D numerical simulations of Eqs. (1)-(5) in case of an initial coherent circular vortex perturbation superimposed on an equilibrium Keplerian flow.
Since the emphasis of our numerical simulations is not only on the vortex dynamics itself but also on the process of wave generation, we need initial conditions corresponding to the vortex perturbations in a pure form.
One of the ways to select the initial conditions for the vortex would be to employ an equilibrium vortex configuration. A class of widely used exact steady analytic solutions for single vortex patches is given by Saffman (1992). These solutions were also used for the construction of an elliptic vortex in Keplerian shear flow in numerical simulations by Chavanis (2000). Another class of time-dependent vortex solutions in uniform shear flows is given by Kida (1981). Stability analysis of the Kida vortex revealed some aspects of its non-modal behavior - transient growth due to the background velocity shear (see Meacham et al. 1990). However, these vortex configurations are solutions for incompressible flows and cannot be directly used in the compressible setup initially preserving the no-wave condition.
An exact equilibrium vortex solution in Keplerian shear flow is given by Goodman et al. (1987). However, the specificity of this solution is that it has a non-divergent velocity field, yielding a particular enthalpy distribution to balance the compressibility effects. In this sense, this vortex is not purely kinematic by nature, but involves thermodynamic forces in the equilibrium configuration.
Our aim is to perform numerical simulations of vortex dynamics for a direct comparison and verification of results obtained within the non-modal analysis in the wave-number space. For this purpose, we need an initial vortex configuration which will persist in a medium with constant sound speed - a property which is not valid for the equilibrium vortex derived by Goodman et al. (1987). Hence, we provide the algorithm for the construction of a pure vortex structure in compressible shear flow.
For simplicity we chose the initial vortex to be circular in shape
having in mind that it will be sheared into an elliptical configuration
during the evolution in the shear flow. The compressibility
effects on vortex perturbations in flows with moderate shear
parameters (as in Keplerian disks) are appreciable at
![]() ,
while the circular vortex we want to construct contains SFH
from this domain of the wave-number space. Therefore, in this case
we need a refined procedure to construct pressure, density and
velocity fields that correspond to the vortex mode perturbations in
a pure form. For this purpose we use "pre-initial'' conditions for
the perturbations in as follows:
,
while the circular vortex we want to construct contains SFH
from this domain of the wave-number space. Therefore, in this case
we need a refined procedure to construct pressure, density and
velocity fields that correspond to the vortex mode perturbations in
a pure form. For this purpose we use "pre-initial'' conditions for
the perturbations in as follows:
![$\displaystyle v_x^{\prime}(x,y,0)= \pm \epsilon_r \frac{y}{a} \left( \frac{x^2 +
y^2}{a^2} \right)^n \exp \left[-(x^2+y^2)/a^2\right],$](/articles/aa/full/2005/25/aa1046-04/img113.gif) |
(41) | ||
![$\displaystyle v_y^{\prime}(x,y,0)= \mp \epsilon_r \frac{x}{a} \left( \frac{x^2 +
y^2}{a^2} \right)^n \exp \left[-(x^2+y^2)/a^2\right],$](/articles/aa/full/2005/25/aa1046-04/img114.gif) |
(42) | ||
| (43) |
Table 1: Parameters of the simulations and estimated values of other nondimensional parameters at the initial vortex position. For comparison we also give values of some parameters for Godon & Livio (1999) and Davis (2002) simulations.
We have then superimposed this perturbation on the equilibrium
Keplerian flow and have performed the simulations using our
implementation of the PPM scheme in its Eulerian version (Woodward
& Colella 1984; Mignone et al. 2004). The main characteristics of
the scheme are a parabolic reconstruction that gives third order
spatial accuracy in smooth regions of the flow, a nonlinear Riemann
solver and time advance based on a characteristic projection that is
second order accurate. We have not used an angular momentum
conserving form of the ![]() component of the momentum equation,
however, we have tested that the total angular momentum is
conserved by our code
during the simulations, with a relative accuracy of 10-5.
For long-term simulations, e.g. hundreds of orbits, one would have to use
a scheme that conserves the local angular momentum density (Kley 1998), but,
as we only study the evolution of 2.5 orbits and only impose a linear perturbation,
it is possible to neglect the precise angular momentum conservation.
Since in this problem there are no natural
units of length, we have arbitrarily chosen our unit of length as
the radius at which the vortex center is located. The unit of
velocity is then chosen as the Keplerian velocity vkv computed
at this radius, i.e. at r = 1, and the disk density is taken as
units of density. In these units the computational domain covers the
region
0.056 < r < 1.94 and
component of the momentum equation,
however, we have tested that the total angular momentum is
conserved by our code
during the simulations, with a relative accuracy of 10-5.
For long-term simulations, e.g. hundreds of orbits, one would have to use
a scheme that conserves the local angular momentum density (Kley 1998), but,
as we only study the evolution of 2.5 orbits and only impose a linear perturbation,
it is possible to neglect the precise angular momentum conservation.
Since in this problem there are no natural
units of length, we have arbitrarily chosen our unit of length as
the radius at which the vortex center is located. The unit of
velocity is then chosen as the Keplerian velocity vkv computed
at this radius, i.e. at r = 1, and the disk density is taken as
units of density. In these units the computational domain covers the
region
0.056 < r < 1.94 and
![]() ,
in polar
coordinates, with a uniform (both in r and in
,
in polar
coordinates, with a uniform (both in r and in ![]() )
grid
of
)
grid
of
![]() points. We had to use such a number of grid points in
order to have a good resolution on the vortex also covering
a large area of the disk. In this way, for example, in the case with a =
0.1, we cover the vortex with about 100 points.
The center of the vortex perturbation
is then located at r = 1 and
points. We had to use such a number of grid points in
order to have a good resolution on the vortex also covering
a large area of the disk. In this way, for example, in the case with a =
0.1, we cover the vortex with about 100 points.
The center of the vortex perturbation
is then located at r = 1 and
![]() .
In our units, the
rotation period at the location of the vortex is therefore
.
In our units, the
rotation period at the location of the vortex is therefore ![]() and
our simulations reach time t = 2.5 T. Boundary conditions are
periodic in the azimuthal direction and outflow in the radial
direction. More precisely, in the radial direction we impose the zero-derivative
of all the quantities, except the azimuthal velocity, for which we continue
the Keplerian profile and impose the zero-derivative on the perturbation.
These conditions do not ensure perfect transmission of perturbations
impinging on the boundaries, however the portions of perturbation that are
reflected at the boundaries become leading waves that are deamplified by
the shear and can influence only a small region close to the boundaries.
The main parameters of our system are then
and
our simulations reach time t = 2.5 T. Boundary conditions are
periodic in the azimuthal direction and outflow in the radial
direction. More precisely, in the radial direction we impose the zero-derivative
of all the quantities, except the azimuthal velocity, for which we continue
the Keplerian profile and impose the zero-derivative on the perturbation.
These conditions do not ensure perfect transmission of perturbations
impinging on the boundaries, however the portions of perturbation that are
reflected at the boundaries become leading waves that are deamplified by
the shear and can influence only a small region close to the boundaries.
The main parameters of our system are then ![]() ,
a,
,
a,
![]() and n (see Eqs. (41)-(43) above). We have considered two
values of the sound speed, two sizes of the vortex and two values
for n. In Table 1 we report the values of the
parameters used in our simulations together with some other nondimensional
parameters that may help
in comparing the importance of different effects on the vortex
dynamics. For comparison, in the table we reported the same
parameters for the simulation performed by Godon & Livio (1999)
and Davis (2002).
and n (see Eqs. (41)-(43) above). We have considered two
values of the sound speed, two sizes of the vortex and two values
for n. In Table 1 we report the values of the
parameters used in our simulations together with some other nondimensional
parameters that may help
in comparing the importance of different effects on the vortex
dynamics. For comparison, in the table we reported the same
parameters for the simulation performed by Godon & Livio (1999)
and Davis (2002).
The second column in Table 1 gives the value of the
sound speed (in units of the Keplerian velocity vkv at the
position of the center of the vortex) and, according to
Eq. (10) this is equivalent to the values of the ratio H/r between the disk thickness and the radius. Case B clearly represents
the case with the lowest value of H/r, however all the cases
help to gain more insight into the dependence of the vortex
dynamics on the parameters: a comparison between case A and case B
allows us to investigate the effect of the sound speed, case C allows us to
investigate the effect of the vortex size and case D allows us to
investigate the effect of a different vorticity distribution (a value
of n different from 0 gives a vorticity ring, while n = 0 gives a
filled distribution). Unlike what we said above, in case C
we made use of
![]() grid points covering the domain
0.5 < r < 1.5 and
grid points covering the domain
0.5 < r < 1.5 and
![]() and the final integration time is t = 3.5. With this
choice we could keep the same resolution on the vortex
that we have for the other cases. The amplitude of the perturbation
in all cases, except case C, is
and the final integration time is t = 3.5. With this
choice we could keep the same resolution on the vortex
that we have for the other cases. The amplitude of the perturbation
in all cases, except case C, is
![]() ,
and in case C it
is ten times smaller, in order to minimize the action of nonlinear
terms of Eqs. (1)-(4), since in this paper we want to address the linear
dynamics of the perturbation. We do this to prove the linear character
of the spiral-density wave generation process (the main aim of our
study) and to visualize the wave generation and propagation processes
clearly. In the linear case there is no difference between the dynamics of
cyclonic and anticyclonic vortices, so, without loss of generality we
took the vortex rotation to be anticyclonic.
,
and in case C it
is ten times smaller, in order to minimize the action of nonlinear
terms of Eqs. (1)-(4), since in this paper we want to address the linear
dynamics of the perturbation. We do this to prove the linear character
of the spiral-density wave generation process (the main aim of our
study) and to visualize the wave generation and propagation processes
clearly. In the linear case there is no difference between the dynamics of
cyclonic and anticyclonic vortices, so, without loss of generality we
took the vortex rotation to be anticyclonic.
The parameters
![]() and
and
![]() ,
as discussed in Sect. 4, giving the vortex core size
,
as discussed in Sect. 4, giving the vortex core size ![]() in units respectively of the
radius and of the disk thickness, measure the importance of the Rossby
waves. On the basis of Eq. (40) one can estimate the characteristic oscillation times of the Rossby waves in the simulated cases. These times significantly exceed the time
of our simulation - a few revolutions of the disk at the vortex location.
Consequently, Rossby waves do not manifest themselves in our
simulations, i.e., the real participants of the simulated dynamics are
the vortex mode and the (generated) spiral-density wave.
in units respectively of the
radius and of the disk thickness, measure the importance of the Rossby
waves. On the basis of Eq. (40) one can estimate the characteristic oscillation times of the Rossby waves in the simulated cases. These times significantly exceed the time
of our simulation - a few revolutions of the disk at the vortex location.
Consequently, Rossby waves do not manifest themselves in our
simulations, i.e., the real participants of the simulated dynamics are
the vortex mode and the (generated) spiral-density wave.
The parameter N in the last column of Table 1
measures the competition between the distortion by the shear flow (linear
phenomenon) and nonlinear phenomenona that might oppose this distorsion.
This competition may be estimated by the ratio between the vortex
maximum velocity ![]() and the local Keplerian velocity difference
across the vortex core radius (
and the local Keplerian velocity difference
across the vortex core radius (
![]() )
)
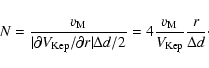 |
(44) |
| |
Figure 5: Images of the initial density ( left plot) and vorticity ( right plot) distributions with enlargements of the vortex area. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1046fig6.ps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg139.gif) |
Figure 6: Evolution of the vorticity distribution for case A. The six panels show the vorticity distributions at six different times. The times are respectively t = 0.31, 1, 2, 3.12, 4.5, 6.31. At late times the vorticity distribution in the inner region becomes quite noisy, however one has to take into account that the calculation of vorticity implies a numerical differentiation operation that amplifies the error, larger here due to the grid deformation |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1046fig7.ps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg140.gif) |
Figure 7: Evolution of the density distribution for case A. The six panels show the density distributions at six different times, t = 0.31, 1, 2, 3.12, 4.5, 6.31. |
| Open with DEXTER | |
In Fig. 5 we represent the initial conditions of our simulations (for
n = 0),
more precisely we show the vorticity (upper panel) and density (lower
panel) perturbation fields, with enlargements of the vortex region. The vorticity
field of the initial vortical perturbation has axial symmetry, as
expected, while the density field has a different structure resulting
from the balance of pressure and Coriolis forces. In Figs. 6 and 7,
we show the initial phases of the vortex evolution for case A, up to
![]() ,
that corresponds to one rotation period at the initial
vortex location. The figures show respectively images of vorticity
and density distributions at six different times. We see that the
vortex is stretched by the background Keplerian flow, but we can
also observe that, in agreement with the theory
presented in Sect. 3, two spiral-density waves are being generated by
the vortex. The stretching is well visualized in Fig. 6, that shows
the vorticity dynamics. The wave generation and propagation phenomena
are well traced by the two arms that are visible on the images of
Fig. 7. According to what we have shown in previous sections, a
vortex SFH generates a wave when the SFH crosses the ky axis,
i.e. when the wavenumber in the local radial direction becomes zero
(kx = 0, see Fig. 3 and points 3 and
,
that corresponds to one rotation period at the initial
vortex location. The figures show respectively images of vorticity
and density distributions at six different times. We see that the
vortex is stretched by the background Keplerian flow, but we can
also observe that, in agreement with the theory
presented in Sect. 3, two spiral-density waves are being generated by
the vortex. The stretching is well visualized in Fig. 6, that shows
the vorticity dynamics. The wave generation and propagation phenomena
are well traced by the two arms that are visible on the images of
Fig. 7. According to what we have shown in previous sections, a
vortex SFH generates a wave when the SFH crosses the ky axis,
i.e. when the wavenumber in the local radial direction becomes zero
(kx = 0, see Fig. 3 and points 3 and
![]() in
Fig. 4). Our vortex is composed of many SFH, and each of them,
crossing the ky axis, generates the corresponding spiral-density
wave SFH component. Therefore, since at the moment of generation
the wavenumber is along the azimuthal direction, we can observe the
two generated waves to be propagating in opposite azimuthal
directions. The waves, as they propagate, have their wavevectors
turned by the shear flow towards the radial direction, and in time
they are carried by the flow and become tightly trailing. The
appearance of two arms is related to the conservation of the
perturbation action, that initially is zero, since the vortex
perturbation does not propagate. The total action of the generated
wave arms should then be zero and therefore we have two arms with
opposite propagation directions.
in
Fig. 4). Our vortex is composed of many SFH, and each of them,
crossing the ky axis, generates the corresponding spiral-density
wave SFH component. Therefore, since at the moment of generation
the wavenumber is along the azimuthal direction, we can observe the
two generated waves to be propagating in opposite azimuthal
directions. The waves, as they propagate, have their wavevectors
turned by the shear flow towards the radial direction, and in time
they are carried by the flow and become tightly trailing. The
appearance of two arms is related to the conservation of the
perturbation action, that initially is zero, since the vortex
perturbation does not propagate. The total action of the generated
wave arms should then be zero and therefore we have two arms with
opposite propagation directions.
We now define and compute the trajectories of the excited
spiral-density waves by using the group velocity concept (of course,
trajectory, as wave group velocity, gains in importance only for
wave packages when the concept of ray is applicable). The trajectories
that we will compute will be global, but they will be based on the
local dispersion relation that can be obtained at each position in
the shearing-sheet approximation. The validity of the
trajectories that we will compute has therefore all the
limitations of this approximation. Due to this "half-globality''
we will indicate by kr(t) and
![]() (instead of kx(t) and ky that are used in the local reference frame) the components of
the wavenumber vector respectively in the local radial and
azimuthal directions. We rewrite the
dispersion relation of spiral-density waves from Eq. (34)
(instead of kx(t) and ky that are used in the local reference frame) the components of
the wavenumber vector respectively in the local radial and
azimuthal directions. We rewrite the
dispersion relation of spiral-density waves from Eq. (34)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1046fig8.ps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg151.gif) |
Figure 8:
Ray trajectories superimposed on the density distribution for
case A at time t = 2. The different rays correspond to different
values of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1046fig9.ps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg152.gif) |
Figure 9:
Ray trajectories superimposed on the density distribution for
case C at time t = 2. The different rays correspond to different
values of
|
| Open with DEXTER | |
In Fig. 10 we again plot trajectories and numerical simulation results for case A at a later time (t = 3.75), to show that the computed trajectories follow with a very good agreement the further perturbation evolution.
Figure 7 show a very regular structure of the emitted spiral-density
waves. Prima facie, they look like shocks, but this is not the
case. They have a linear origin and we can understand
the observed regular structure as described below. A wide spectrum
of wave SFH is generated at each moment of time, since the
intensity of generation is different from zero over a wide range of ky (see Sect. 3), and the panels in Fig. 7
represent an integral picture of the
generated and propagating wave interference. On the other hand,
according to the
graphs of
![]() in Fig. 3, the wave harmonics, at the moment of generation, have very
regular phases that are similar to each other (specifically, all
density perturbation SFH are excited with zero phase - see graph
of
in Fig. 3, the wave harmonics, at the moment of generation, have very
regular phases that are similar to each other (specifically, all
density perturbation SFH are excited with zero phase - see graph
of
![]() in Fig. 3). This phase regularity and
similarity are the roots of the regular interference picture
shown in Fig. 7.
in Fig. 3). This phase regularity and
similarity are the roots of the regular interference picture
shown in Fig. 7.
In vortical flows, potential perturbations acquire a vortical nature and
this is the case for the spiral-density waves that we are considering.
We can estimate the
wave vorticity by Eq. (29), rewritten in a
"half-global'' fashion (as was done defining trajectories). For
spiral density waves we have
![]() :
:
![\begin{displaymath}k_r(t) v_{\theta}^{\rm (w)}(t) - k_{\theta} v_r^{\rm (w)}(t)
+ 2[\Omega(r) + A(r)] D^{\rm (w)}(t) =0.
\end{displaymath}](/articles/aa/full/2005/25/aa1046-04/img155.gif) |
(49) |
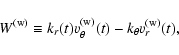 |
(50) |
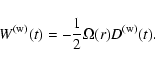 |
(51) |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1046f10.ps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg158.gif) |
Figure 10:
Ray trajectories superimposed on the density distribution for
case A at time t = 3.75. The different rays correspond to different
values of
|
| Open with DEXTER | |
In Fig. 11 we show grey-scale images of the density distribution at t=2 for the cases A, B, C, D. Cases A and D relate to equal sizes of parent vortex and sound speeds (see Table 1, they differ only for the values of n) and the wave propagation pictures are very similar. In case B, due to the small value of the sound speed, the wave arms are radially compressed and not strongly pronounced. In case C, due to the small size of the parent vortex, the generated wave SFH has large wavenumbers, their group and phase velocities are more or less the same (close to the sound speed) and the arms are more uniform (not diffuse).
Due to linearity, the described phenomena have a short life time (a few disk revolutions): in fact vortex distortion by the background shear flow cannot be prevented by velocity self-induction (a nonlinear phenomenon). The parent vortex is stretched, becomes tightly trailing (see Fig. 6) and, in accordance with Sect. 3, is not able to generate any more spiral-density waves. Also, the trailing vortex mode perturbations (kx(t)/ky>0) give back energy to the flow and disappear (also in accordance with Sect. 3). The disappearance of the parent vortex is evident in Fig. 12, where we show grey-scale images of density at later evolution times; the three panels are respectively at t=8.12, 11.25 ,14.5, i.e. up to two and a half revolutions. Spiral-density tightly trailing waves have extended to the whole disk region inside the vortex position, but their generation seems to have stopped and they have disappeared from the outer region.
Preliminary results show that nonlinearity makes the parent vortex long-lived and the wave generation process more permanent (Bodo et al. 2005). Indeed, prevention of parent vortex stretching should be the result of positive nonlinear feedback, i.e. nonlinear regeneration of the leading SFH in the vortex spectrum. These replenished leading SFH extract the disk flow energy and generate continuously spiral-density wave SFH. Consequently, they provide a permanent generation of waves. (The concept of replenishing of SFH - a root of the positive nonlinear feedback - is a theoretical concept, numerical investigation of which is under way).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1046f11.ps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg159.gif) |
Figure 11: Comparison of the four different cases at the same time. The four panels show images of the density distribution for cases A ( top left), B ( top right), C ( bottom right) and D ( bottom left) at t = 2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1046f12.ps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg160.gif) |
Figure 12: Longer time evolution for case A. The three panels show images of the density distributions at three different times; from top to bottom the times are respectively t = 8.12, 11.25, 14.5. |
| Open with DEXTER | |
The results for a single Fourier component, given in Sect. 3, show that the energy of the generated spiral density wave increases with time, i.e. trailing spiral density waves are capable of extracting energy from the mean flow. This wave amplification should also be visible in our numerical calculations; for this reason, in Fig. 13, we plot the perturbation energy (as defined in Eq. (31)) vs. time.
In the figure we can see the perturbation normalized energy (normalized to
the initial value) vs. time for the cases A, B and D (case A - solid
curve, case B - dotted curve, case D -
dashed-dotted curve).
The plots go up to one revolution time (
![]() ), when the
action of the parent vortex has not yet completely disappeared.
In this process of wave
generation, the vortex acts only as a mediator and the waves draw
their energy from the background flow, both at the beginning, when
they are generated, and in their propagation, when they are amplified
by the background shear flow. kr(t) of the generated wave
SFH increases with time and the dynamics of SFH becomes adiabatic,
therefore the energy of each SFH increases linearly with its
frequency:
), when the
action of the parent vortex has not yet completely disappeared.
In this process of wave
generation, the vortex acts only as a mediator and the waves draw
their energy from the background flow, both at the beginning, when
they are generated, and in their propagation, when they are amplified
by the background shear flow. kr(t) of the generated wave
SFH increases with time and the dynamics of SFH becomes adiabatic,
therefore the energy of each SFH increases linearly with its
frequency:
![]() .
Generally, according to Eq. (35)
.
Generally, according to Eq. (35)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{1046f13.ps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg167.gif) |
Figure 13: Energy normalized to the initial value versus time for the cases A, B and D (the solid line refers to case A, the dotted curve to case B and the dashed curve to case D). |
| Open with DEXTER | |
A feature of the generated spiral density waves that we have
discussed above is their regularity, i.e. perturbations associated
with the waves have a prominent sign and do not average to
zero. One consequence of this is that, in principle,
it may be possible to have a mass flux associated with them,
that would be therefore proportional to the wave amplitude.
We have tested this possibility by plotting the function:
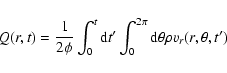 |
(53) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1046f14.eps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg170.gif) |
Figure 14: Plot of the total mass that has flown through radius r at time t versus time, for case A. This figure refers to radial positions that are immediately inside (r = 0.875, solid line) and immediately outside (r = 1.125, dashed line) the vortex. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1046f15.eps}
\end{figure}](/articles/aa/full/2005/25/aa1046-04/Timg171.gif) |
Figure 15: Total mass that has flown through radius r at time t versus time, for case A. This figure refers to r = 0.1. |
| Open with DEXTER | |
In this paper we present a linear, non-resonant phenomenon of
spiral-density wave generation by vortices in a Keplerian disk
flow that is closely related to the non-normality of linear dynamics of
perturbations in smooth (without inflection points) shear flows.
This phenomenon can be well interpreted by the use of the non-modal
approach, i.e. by following in time the linear dynamics of spatial
Fourier harmonics of the vortex mode perturbations. We have done this
in the shearing sheet model and we found that spiral-density wave
are generated only by the
leading vortex mode SFH that meet the condition
kx(0)/ky<0.
The generation takes place at relatively large wavelengths of SFH
- it becomes noticeable at about
![]() and it is
dominant in the SFH dynamics at kyH<0.5. At large
wavenumbers (small wavelength) all dynamics of SFH runs at low
shear rates and only one phenomenon occurs: transient growth of SFH of aperiodic vortices. At small
wavenumbers (large wavelength) when kyH<0.5, the dynamics in
addition to the transient growth involves conversion of vortices
to spiral-density waves. After their appearance, the energy of the
wave SFH increases and the wave SFH itself in time becomes tightly
trailing
and it is
dominant in the SFH dynamics at kyH<0.5. At large
wavenumbers (small wavelength) all dynamics of SFH runs at low
shear rates and only one phenomenon occurs: transient growth of SFH of aperiodic vortices. At small
wavenumbers (large wavelength) when kyH<0.5, the dynamics in
addition to the transient growth involves conversion of vortices
to spiral-density waves. After their appearance, the energy of the
wave SFH increases and the wave SFH itself in time becomes tightly
trailing
![]() .
.
Small amplitude (linear) circular vortex structures (that
represent a rich ensemble of leading and trailing SFH) generate
two oppositely propagating wave arms in accordance with the perturbation
action conservation law. They have very regular structure and
prima facie look like shocks, but this is not the case. They have
a linear origin and are the result of the interference of the
generated spiral-density waves. Their outward and inward propagating
arms are asymmetric due to the disk curved geometry and flow
asymmetry (![]() increases outward and decreases inward).
increases outward and decreases inward).
Since spiral-density wave generation is governed by linear forces, it does not depend on the sign of the vorticity of initial aperiodic perturbation and should be equal for cyclonic and anticyclonic vortices even in the nonlinear regime. Davis (2002) (whose simulations are in a nonlinear regime - see Table 2), reported that a coherent cyclonic vortex simultaneously emits a wave as does an anticyclonic one (nonlinear cyclonic and anticyclonic vortices differ by their lifetime - cyclonic vortices are destroyed in appreciably shorter times than anticyclonic ones). This result may be considered as circumstantial evidence for the linear origin of the wave.
The fact that the waves are generated by a linear mechanism (and not nonlinear ones, as was thought ) appreciably increases the significance of waves in the disk matter inflow/outflow processes and we showed that waves generated by anticyclonic vortices tend to collect matter in the vortex region, which may be important for protoplanetary disks, and tend to induce inflow of matter in the inner disk regions.
The described dynamics are short-lived due to the small amplitude of the parent vortex. One can speculate that the parent vortex could be long-lived and the dynamical picture more permanent at larger amplitudes, when nonlinear self-induction of the vortex velocity prevents its shear distortion. Indeed, nonlinear regeneration of the leading SFH ( (kx/ky<0)) in the vortex spectrum can prevent the vortex from stretching. These replenished leading SFH gain the disk flow energy and continuously generate spiral-density wave SFH. Thus, permanent nonlinear replenishment of leading SFH of the parent vortex could generate permanent disk flow energy extraction and wave generation. The effective efficiency of the feedback mechanism in permanently maintaing the vortex and overcoming the linear and nonlinear damping effects inherent to a Keplerian disk (Hawley et al. 1999) however has still to be proven by numerical simulations and analytical means.
The linear phenomenon of spiral-density wave generation by vortices investigated in this paper is quite universal; it occurs in disk flows with high shear rates and should be seen in different kind of astrophysical disks (protoplanetary disks; quasars; thin and thick galactic and binary system disks).
Acknowledgements
This work is supported by ISTC grant G-553 and GRDF grant 3315 and by MIUR grant 2002028843. G.D.C. and A.G.T. would like to acknowledge the hospitality of Osservatorio Asrtonomico di Torino. Numerical calculations were partly performed in CINECA (Bologna, Italy) thanks to the support by INAF. The authors would like to thank H. Klahr for helpful comments that improved the paper.
| |
= | (A.1a) | |
| = | (A.1b) | ||
| = | (A.1c) |
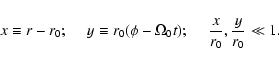 |
(A.2) |
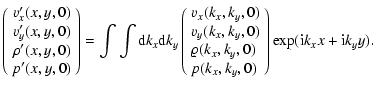 |
(A.3) |
![\begin{displaymath}{{{\rm d}^2 v_y(t)} \over {{\rm d} t^2}} +
\left[4\Omega_0(\O...
... k^2(t) c_{\rm s}^2\right]v_y(t)= k_x(t)c_{\rm s}^2
{\cal I} ,
\end{displaymath}](/articles/aa/full/2005/25/aa1046-04/img183.gif) |
(A.4) |
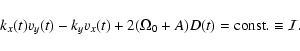 |
(A.5) |
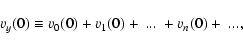 |
(A.6) |
![\begin{displaymath}v_0(0) \equiv [v_0(t)]_{t=0} \equiv \left[{k_x(t) \over
{\cal K}}\right]_{t=0} {\cal I}(k_x,k_y),
\end{displaymath}](/articles/aa/full/2005/25/aa1046-04/img187.gif) |
(A.7) |
![\begin{displaymath}v_n(0) \equiv [v_n(t)]_{t=0} \equiv - \left[{1\over {\cal
K} ...
...2}{{{\rm d}^2 v_{n-1}(t)}~ \over {{\rm d} t^2}}\right]_{t=0} ,
\end{displaymath}](/articles/aa/full/2005/25/aa1046-04/img188.gif) |
(A.8) |
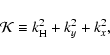 |
(A.9) |
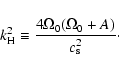 |
(A.10) |
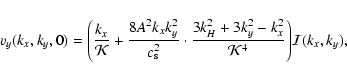 |
(A.11) |
| |
= | 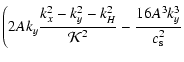 |
|
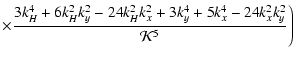 |
|||
| (A.12) |
![\begin{displaymath}v_y^\prime(k_x,k_y,0) = \left[ {{\rm d} \over {\rm d} t}
v_y(k_x(t),k_y,t) \right]_{t=0} .
\end{displaymath}](/articles/aa/full/2005/25/aa1046-04/img200.gif)
![$\displaystyle {p(k_x,k_y,0)\over c_{\rm s}^2}=\varrho(k_x,k_y,0)
= {{\rm i} \rh...
...+ A)} \Big[ k_x v_y(k_x,k_y,0) - k_y
v_x(k_x,k_y,0) - {\cal I}(k_x,k_y) \Big] .$](/articles/aa/full/2005/25/aa1046-04/img202.gif) |
(A.13) |