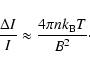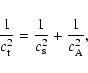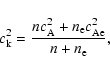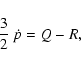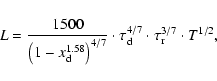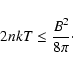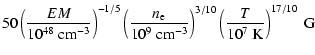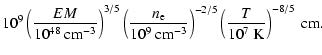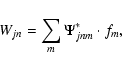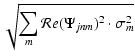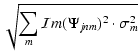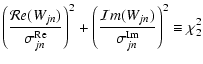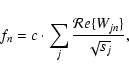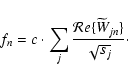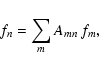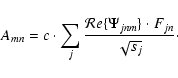A&A 436, 1041-1047 (2005)
DOI: 10.1051/0004-6361:20052834
The first observed stellar X-ray flare oscillation: Constraints on
the flare loop length and the magnetic field
U. Mitra-Kraev - L. K. Harra - D. R. Williams - E. Kraev
Mullard Space Science Laboratory, University College
London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
Received 7 February 2005 / Accepted 12 March 2005
Abstract
We present the first X-ray observation of an oscillation during a stellar
flare. The flare occurred on the active M-type dwarf AT Mic and
was observed with XMM-Newton. The soft X-ray light curve
(0.2-12 keV) is investigated with wavelet analysis. The flare's
extended, flat peak
shows clear evidence for a damped oscillation with a period of around
750 s, an exponential damping time of around 2000 s, and an initial,
relative peak-to-peak amplitude of around 15%.
We suggest that
the oscillation is
a standing magneto-acoustic wave tied to the
flare loop, and find that
the most likely interpretation is a longitudinal, slow-mode
wave, with a resulting loop length of
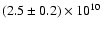 cm. The local
magnetic field strength is found to be 105
cm. The local
magnetic field strength is found to be 105 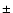 50 G. These values are
consistent with (oscillation-independent) flare cooling time models
and pressure balance scaling laws.
Such a flare oscillation provides an excellent opportunity to obtain
coronal properties like the size of a flare loop or the local magnetic
field strength for the otherwise spatially-unresolved star.
50 G. These values are
consistent with (oscillation-independent) flare cooling time models
and pressure balance scaling laws.
Such a flare oscillation provides an excellent opportunity to obtain
coronal properties like the size of a flare loop or the local magnetic
field strength for the otherwise spatially-unresolved star.
Key words: stars: coronae - stars: flare
- stars: magnetic fields - stars: oscillations
- X-rays: stars - stars: individual: AT Mic
1 Introduction
Oscillations in the solar corona have by now been observed for many
years. Wavelength regimes ranging from radio to hard X-rays have been
investigated in the search for evidence of waves. Table 1 in
Aschwanden et al. (1999) provides a summary and description of
the different periods found (0.02 to 1000 s). Most of these waves have been
explained by magneto-hydrodynamic (MHD) oscillations in coronal
loops, see Roberts (2000) for a detailed review of waves and oscillations
in the corona.
One of the most exciting aspects of "coronal seismology'' is
that it potentially provides us with the capability for determining the
magnetic field strength in the corona (Roberts et al. 1984), as well as, in the
stellar case, with information on otherwise unresolved spatial
scales, e.g., flare loop lengths.
It is notoriously difficult to measure
the magnetic field strength in the corona because of the very high speeds of
coronal electrons, which broaden spectral lines far beyond the width of Zeeman
splitting. Techniques using both near-infrared
emission lines and radio observations are successful, but have
poor spatial
resolution. Indirect methods are commonly used, such as the
extrapolations of the coronal magnetic field from the photospheric
magnetic field, which in turn can be measured using the Zeeman effect.
Many of the observations of waves have been determined from variations
in intensity.
However, a huge step forward was achieved in solar
coronal physics due to the high spatial resolution available with the
Transition Region and Coronal Explorer
(TRACE, Handy et al. 1999). Aschwanden et al. (1999) observed the
first spatial displacement oscillations of
coronal loops. It was suggested
that these oscillations were triggered by a fast-mode shock from a flare site,
and they were interpreted as standing fast kink-mode waves.
Nakariakov & Ofman (2001) made use of such flare-related spatial
oscillations to determine the magnetic field strength (13 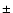 9 G), which in
the case of a
standing kink wave is related to the period of the oscillation, the
density of the loop, and the length of the loop.
Another model used to derive the magnetic field strength from loop
oscillations was
put forward by Zaitsev & Stepanov (1989), which assumes that the oscillation
is triggered by a centrifugal force, generated by the evaporating
chromospheric plasma moving upward along the magnetic field. In this case, the
magnetic field strength is given by the amplitude of the oscillation, as well
as the loop density and
temperature. The model also predicts loop lengths if collisional
damping is assumed. (Or vice versa, density and temperature, if the
loop length is known.)
9 G), which in
the case of a
standing kink wave is related to the period of the oscillation, the
density of the loop, and the length of the loop.
Another model used to derive the magnetic field strength from loop
oscillations was
put forward by Zaitsev & Stepanov (1989), which assumes that the oscillation
is triggered by a centrifugal force, generated by the evaporating
chromospheric plasma moving upward along the magnetic field. In this case, the
magnetic field strength is given by the amplitude of the oscillation, as well
as the loop density and
temperature. The model also predicts loop lengths if collisional
damping is assumed. (Or vice versa, density and temperature, if the
loop length is known.)
Although waves are observed across the electromagnetic spectrum on the
Sun, observations on other stars are rarer. The principal reason for
this is that the Sun can be spatially resolved, whereas on stars, the signal
for the wave must be strong enough to be observed above the full disk emission.
The first oscillation associated with a stellar flare was reported by
Rodonò (1974), who observed the flare star II Tau with
high-speed optical photometry, and found a long-lived oscillation
during flare decay with a mean period of 13 s.
In a series of papers in the late 1980's and early 1990's, Andrews and
coworkers (e.g., Andrews 1990) presented optical observations of dMe
flare stars, where
they observed quasi-periodicities with periods of a few tens of
seconds, and put forward the idea that these were coronal loop
oscillations.
Mullan et al. (1992) also
found optical oscillations (periods of the order of a few minutes) in
dMe stars, concluding that they more likely arise
from a coronal than from a photospheric origin.
In a later paper, Mullan & Johnson (1995) found oscillations in X-ray data
of dMe stars. These oscillations have periods in the range of several
tens to a few hundreds of seconds. They were not associated with any
flare, though they were interpreted as coronal loop oscillations.
Optical stellar flare oscillations have been observed
by Mathioudakis et al. (2003), who found a period of 220 s in
the decay phase of a white-light flare on the RS CVn binary II
Peg.
In this work, we investigate the first X-ray observation of an oscillation
during a stellar flare.
Section 2 describes the target, AT Mic, as well as the
observation.
In Sect. 3, we present the data analysis, determining
the period and amplitude of the oscillation through wavelet analysis.
In Sect. 4, we determine the magnetic field strength and the length of
the coronal loop by assuming that the oscillation is due to a
magneto-acoustic wave.
As a validity check, the value of loop length was compared to the
value determined from a radiative cooling model, as well as from
pressure balance scaling laws. The latter also gives an independent
estimate of the magnetic field strength.
Finally, we discuss the results and give conclusions (Sect. 5).
2 Target and observation
AT Mic (GJ 799A/B) is an M-type binary dwarf, with
both stars of the
same spectral type (dM4.5e+dM4.5e).
Both components of the binary flare frequently.
The radius of AT Mic given by Lim et al. (1987) is
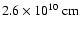 ,
using a stellar distance of 8.14 pc
(Gliese & Jahreiss 1991).
Correcting for the newer value for the distance from HIPPARCOS
(
,
using a stellar distance of 8.14 pc
(Gliese & Jahreiss 1991).
Correcting for the newer value for the distance from HIPPARCOS
(
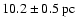 ,
Perryman et al. 1997), and using the fact
that the stellar
radius is proportional to the stellar distance for a given luminosity
and spectral class, we obtain a stellar
radius of
,
Perryman et al. 1997), and using the fact
that the stellar
radius is proportional to the stellar distance for a given luminosity
and spectral class, we obtain a stellar
radius of
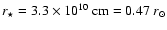 .
The mass
of AT Mic given by Lim et al. (1987) is
.
The mass
of AT Mic given by Lim et al. (1987) is
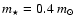 .
.
For our analysis we used the XMM-Newton (Jansen et al. 2001)
observations of AT Mic
on 16 October 2000 during revolution 156.
Raassen et al. (2003) have analysed this data spectroscopically,
obtaining elemental abundances, temperatures, densities and emission
measures, while a comparative flare analysis between X-ray and
simultaneously observed ultraviolet emissions can be found in
Mitra-Kraev et al. (2005).
Here, we solely used the 0.2-12 keV X-ray data from the pn-European Photon
Imaging Camera (EPIC-pn, Strüder et al. 2001).
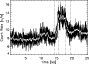 |
Figure 1:
The AT Mic 0.2-12 keV X-ray 10-s bin
light curve (shown in black). Overplotted in white is the same light
curve smoothed
with a sliding time window of 200 s. The time is in ks, starting
from the beginning of the observation (2000-10-16 00:42:00). The
vertical dotted lines mark the flare start, end of rise phase, end
of extended top phase and end of the flare. |
| Open with DEXTER |
The observation started at 00:42:00 and lasted for 25.1 ks ( 7 h).
Figure 1 shows the AT Mic light curve.
A large flare, starting
7 h).
Figure 1 shows the AT Mic light curve.
A large flare, starting  15 ks into the observation,
increases the count-rate from flare onset to flare peak by a factor
of 1.7, and lasts for 1 h 25 min.
It shows a steep rise (rise time
15 ks into the observation,
increases the count-rate from flare onset to flare peak by a factor
of 1.7, and lasts for 1 h 25 min.
It shows a steep rise (rise time
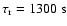 )
and decay
(decay time
)
and decay
(decay time
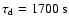 ). There is an extended peak to
this flare, which shows clear oscillatory behaviour.
Applying a multi-temperature model, Raassen et al. (2003)
obtain a best fit with a mean flare temperature
). There is an extended peak to
this flare, which shows clear oscillatory behaviour.
Applying a multi-temperature model, Raassen et al. (2003)
obtain a best fit with a mean flare temperature
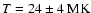 and a quiescent
temperature
and a quiescent
temperature
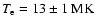 ,
and from the O VII line
ratio a flare and quiescent electron density of
,
and from the O VII line
ratio a flare and quiescent electron density of
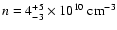 and
and
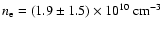 ,
respectively. The total flare and quiescent emission
measures are
,
respectively. The total flare and quiescent emission
measures are
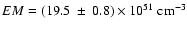 and
and
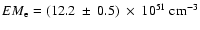 .
The total emitted energy in the 0.2-12 keV band of this flare is
.
The total emitted energy in the 0.2-12 keV band of this flare is
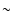
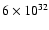 erg (Mitra-Kraev et al. 2005).
erg (Mitra-Kraev et al. 2005).
3 Analysis
For the extraction of the EPIC-pn light curve we used the XMM-Newton Science Analysis System (SAS) version 6.0. Light curves
with a cadence of 1 s were extracted for concentric regions around
the source (20:41:51.156, -32:26:11.02, ICRS 2000 coordinates), and
a background, off-set from the source on the same detector chip
(20:41:48.428, -32:29:00.66); both regions used a radius of
41.325 arcsec. The selected energy range is 0.2-12 keV
(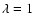 -62 Å).
The obtained errors for the count rates follow Poisson statistics for
all data points.
The background light curve is subtracted from the source light curve.
Data missing due to telemetry absences are identified by obtaining the
1-s light curve of the entire detector chip; they manifest as time
intervals with zero count rate.
At such times, the background-subtracted raw light curve is
interpolated.
This light curve is then re-binned to 10-s bins and used for further
analysis.
-62 Å).
The obtained errors for the count rates follow Poisson statistics for
all data points.
The background light curve is subtracted from the source light curve.
Data missing due to telemetry absences are identified by obtaining the
1-s light curve of the entire detector chip; they manifest as time
intervals with zero count rate.
At such times, the background-subtracted raw light curve is
interpolated.
This light curve is then re-binned to 10-s bins and used for further
analysis.
3.2 Continuous wavelet transform and frequency band
decomposition
We apply a continuous wavelet transform (CWT) to the
10-s light curve, following the approach laid out by
Torrence & Compo (1998).
For our analysis, we use the Morlet wavelet
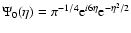 .
Figure 2 displays the CWT.
The vertical dotted lines denote the start (14.3 ks), the end of the
rise phase (15.6 ks), the beginning of the decay phase (17.9 ks) and
the end (19.6 ks) of the flare.
The contours give significance levels of 68%, 95% and 99.9%, respectively.
At flare rise, the power is enhanced at all timescales in the CWT.
The bold arrow points to the flare oscillation, which
causes a local maximum in the wavelet coefficient plane.
It has a period between 500 and 1200 s and occurs during flare
maximum, with a significance level of >99.9%.
Note that there is another local maximum of 68% significance at a
period of
.
Figure 2 displays the CWT.
The vertical dotted lines denote the start (14.3 ks), the end of the
rise phase (15.6 ks), the beginning of the decay phase (17.9 ks) and
the end (19.6 ks) of the flare.
The contours give significance levels of 68%, 95% and 99.9%, respectively.
At flare rise, the power is enhanced at all timescales in the CWT.
The bold arrow points to the flare oscillation, which
causes a local maximum in the wavelet coefficient plane.
It has a period between 500 and 1200 s and occurs during flare
maximum, with a significance level of >99.9%.
Note that there is another local maximum of 68% significance at a
period of 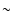 1000 s occurring during a weaker flare
at around
1000 s occurring during a weaker flare
at around
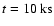 ,
which suggests that this earlier flare
might oscillate as well.
A third, minor flare at
,
which suggests that this earlier flare
might oscillate as well.
A third, minor flare at
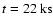 ,
on the other hand, shows no
oscillation.
Here, we investigate only the major oscillation during the largest
flare.
,
on the other hand, shows no
oscillation.
Here, we investigate only the major oscillation during the largest
flare.
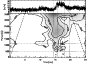 |
Figure 2:
The upper panel shows the 10-s bin light curve. The lower panel
displays the high-frequency wavelet coefficients of the continuous
wavelet transform of the above light curve, using a Morlet
wavelet (see Sect. 3.2). The contours give the
68%, 95% and 99.9% significance levels. The dashed lines
represent the cone of influence. The vertical dotted lines are the
same as in Fig. 1. The arrow points to the flare
oscillation in the wavelet domain and the horizontal dotted lines
mark the division between the high (noise), medium (oscillation) and low
frequency ranges. |
| Open with DEXTER |
We split the CWT into three frequency bands with periods of
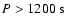 ,
,
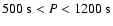 ,
and
,
and
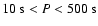 ,
so that
the middle band encompasses only the oscillation range.
The light curve is reconstructed for the three bands separately.
Figure 3 shows these decomposed light curves (upper three
panels), and their sum, the reconstructed light curve (lowest
panel). As the decomposition is a linear transform, it is easy to
derive the standard errors for the decomposed light curves (see
Appendix A for the error treatment in CWT analysis), they
are represented by the shaded areas around each light curve.
Figure 3 demonstrates how the oscillation has been separated
from the flare profile, allowing the oscillation to be analysed separately.
,
so that
the middle band encompasses only the oscillation range.
The light curve is reconstructed for the three bands separately.
Figure 3 shows these decomposed light curves (upper three
panels), and their sum, the reconstructed light curve (lowest
panel). As the decomposition is a linear transform, it is easy to
derive the standard errors for the decomposed light curves (see
Appendix A for the error treatment in CWT analysis), they
are represented by the shaded areas around each light curve.
Figure 3 demonstrates how the oscillation has been separated
from the flare profile, allowing the oscillation to be analysed separately.
 |
Figure 3:
The reconstructed light curve divided into three frequency
bands, low (
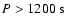 ), medium (500 s < P < 1200 s,
including the oscillation) and high (10 s < P < 500 s, mainly
noise); together they add up to the original data (lowest
panel). The shaded areas show the standard errors. The vertical dotted lines
are the same as in
Fig. 1. A coherent oscillation is easily identified during
flare peak. ), medium (500 s < P < 1200 s,
including the oscillation) and high (10 s < P < 500 s, mainly
noise); together they add up to the original data (lowest
panel). The shaded areas show the standard errors. The vertical dotted lines
are the same as in
Fig. 1. A coherent oscillation is easily identified during
flare peak. |
| Open with DEXTER |
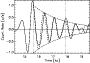 |
Figure 4:
The flare part of the
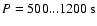 reconstructed
light curve (Fig. 3, second panel). The vertical dotted
lines bound the flare top. The solid line shows
the reconstructed light curve from the data, whereas the dashed line
is a damped sine curve (bounded by the exponential envelope,
dashed-dotted line) with an
oscillation period of P = 750 s and an exponential decay time of
reconstructed
light curve (Fig. 3, second panel). The vertical dotted
lines bound the flare top. The solid line shows
the reconstructed light curve from the data, whereas the dashed line
is a damped sine curve (bounded by the exponential envelope,
dashed-dotted line) with an
oscillation period of P = 750 s and an exponential decay time of
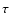 = 2000 s. The relative peak-to-peak amplitude is initially
15%. = 2000 s. The relative peak-to-peak amplitude is initially
15%. |
| Open with DEXTER |
Figure 4 shows the isolated oscillation (solid line) to which
we fit a damped sine curve (dashed line).
The fitted curve has an oscillation with a period of P=750 s, an exponential
decay (damping) time of 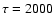 s, and an amplitude of 1 count s-1,
which gives, with an average count rate of 13 counts s-1during flare peak (from the low-frequency light curve), a peak-to-peak
amplitude of
s, and an amplitude of 1 count s-1,
which gives, with an average count rate of 13 counts s-1during flare peak (from the low-frequency light curve), a peak-to-peak
amplitude of
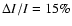 .
.
A continuous wavelet transform is able to provide us with all our aims
simultaneously: the wave is located in time and frequency (=1/period), it is
naturally isolated from the underlying flare profile and thus the
amplitude and damping are easily available from the fit parameters for
a damped sine wave. The low signal-to-noise ratio is dealt with by
disentangling the high frequencies from the lower oscillating frequency.
In particular, this provides us with a better estimate for the
amplitude. While the period derived from the smoothed light curve is
broadly the same as the period obtained from wavelet analysis, the
amplitude
![$\Delta I/I =
(I_{\max}-I_{\min})[(I_{\max}+I_{\min})/2]^{-1}=10\%$](/articles/aa/full/2005/24/aa2834-05/img34.gif) ,
with
,
with 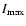 (
(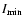 )
the intensity at the first peak (dip), is considerably
underestimated.
)
the intensity at the first peak (dip), is considerably
underestimated.
4 Results
Our analysis clearly shows that there is an oscillation during
the X-ray flare on AT Mic. The oscillation, which has a confidence
level >99.9%, starts when the flare reaches its maximum and
continues during the extended flare top. A damped sine curve with an
oscillation period of
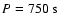 and an exponential decay time of
and an exponential decay time of
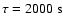 fits the data. The initial relative
amplitude is
fits the data. The initial relative
amplitude is
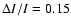 .
.
In the following, we investigate the different types of
magneto-acoustic loop oscillations. Comparing their various estimates
for the flare loop length with two other, independent methods for the
loop length, namely from radiative cooling times and from pressure
balance, we find the most likely oscillation mode. We also derive the
magnetic field strength.
Zaitsev & Stepanov (1989) introduced a model, where a hard X-ray oscillation is
excited by a centrifugal force, which the evaporating plasma exerts on
the flare loop, stretching the magnetic
field lines upward and triggering Alfvén oscillations. In this
scenario, the
relative amplitude of the oscillation is determined by the additional
energy from filling the magnetic flux tube with hot plasma
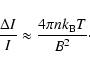 |
(1) |
With
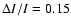 ,
,
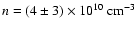 ,
,
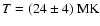 and
and 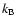 the Boltzmann constant, the magnetic
field then is B = (105
the Boltzmann constant, the magnetic
field then is B = (105 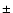 50) G.
50) G.
Roberts et al. (1984) showed that for a straight cylindrical geometry
several types of magneto-acoustic
wave modes in a magnetic loop are feasible, namely the slow
(acoustic), the fast kink and the fast sausage modes.
For a standing oscillation in a loop, the loop length L is given
by
with P the oscillation period, j the mode number and cthe appropriate wave speed. For slow modes, c is the tube speed
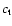 ,
with
,
with
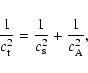 |
(3) |
whereas for the fast kink modes, c is the
kink speed 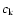 ,
with
,
with
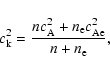 |
(4) |
with the sound speed
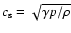 and the Alfvén
speed
and the Alfvén
speed
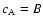 /
/
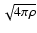 .
.
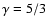 is the adiabatic constant for a
monatomic gas/plasma, p the gas pressure and
is the adiabatic constant for a
monatomic gas/plasma, p the gas pressure and 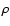 the plasma
density. For the fast sausage mode,
the plasma
density. For the fast sausage mode,
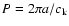 ,
where
a is the tube radius. We set j=1 for the fundamental mode, where
the loop apex has maximum displacement, in agreement with the
centrifugal model of Zaitsev & Stepanov (1989).
,
where
a is the tube radius. We set j=1 for the fundamental mode, where
the loop apex has maximum displacement, in agreement with the
centrifugal model of Zaitsev & Stepanov (1989).
The sound speed is
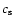 =
=
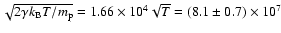 cm s-1.
Using the centrifugal model and inserting Eq. (1) into the
expression for the Alfvén speed, we obtain
cm s-1.
Using the centrifugal model and inserting Eq. (1) into the
expression for the Alfvén speed, we obtain
![$c_{\rm A}=(k_{\rm B} T)^{1/2}[m_{\rm p}(\Delta I/I)]^{-1/2}$](/articles/aa/full/2005/24/aa2834-05/img56.gif) =
=
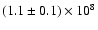 cm s-1.
We immediately see that, assuming the
centrifugal model, the ratio of Alfvén to sound speed is
determined by the relative oscillation amplitude and is
cm s-1.
We immediately see that, assuming the
centrifugal model, the ratio of Alfvén to sound speed is
determined by the relative oscillation amplitude and is
![$c_{\rm A}/c_{\rm s} =
[2\gamma(\Delta I/I)]^{-1/2}\approx 1.41$](/articles/aa/full/2005/24/aa2834-05/img58.gif) .
Using this last
relation, the tube speed then is
.
Using this last
relation, the tube speed then is
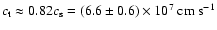 .
To obtain the kink speed, we also need to know
the Alfvén speed outside the loop,
.
To obtain the kink speed, we also need to know
the Alfvén speed outside the loop,
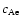 .
Assuming the same value
for the magnetic field strength inside and outside the loop,
.
Assuming the same value
for the magnetic field strength inside and outside the loop,
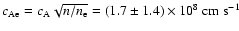 .
Note the large error because of the large density error. The
kink speed then is
.
Note the large error because of the large density error. The
kink speed then is
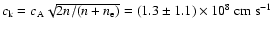 .
Thus, we have
.
Thus, we have
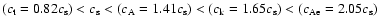 .
.
Assuming a standing slow-mode oscillation, the loop length is
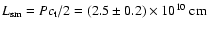 .
For a standing fast kink-mode
oscillation, a loop length of
.
For a standing fast kink-mode
oscillation, a loop length of
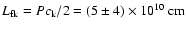 is derived. And assuming a fast sausage mode
oscillation,
is derived. And assuming a fast sausage mode
oscillation,
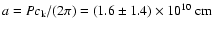 and
and
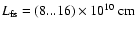 ,
assuming an aspect
ratio of
L/a=5...10.
,
assuming an aspect
ratio of
L/a=5...10.
4.2 Loop length from radiative cooling times
The loop length can also (and independently of any oscillation) be
estimated from rising and cooling times obtained from the temporal
shape of the flare, applying a flare heating/cooling model (see,
e.g., Cargill et al. 1995). We follow
the approach by Hawley et al. (1995) who investigated a flare on AD Leo
observed in the extreme ultraviolet. The shape of this flare is very
similar to our flare on AT Mic, but roughly 10 times larger,
and shows a flat top, too.
The flare loop energy equation for the spatial average is given by
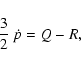 |
(5) |
with Q the volumetric flare heating rate, R the optically thin
cooling rate and 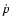 the time rate change of the loop
pressure. During the rise phase, strong evaporative
heating is dominant (
the time rate change of the loop
pressure. During the rise phase, strong evaporative
heating is dominant (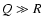 ), while the decay phase is dominated by
radiative cooling and strong condensation (
), while the decay phase is dominated by
radiative cooling and strong condensation (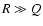 ).
At the loop top, there is an
equilibrium (R = Q). The loop length can be derived as
).
At the loop top, there is an
equilibrium (R = Q). The loop length can be derived as
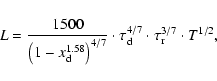 |
(6) |
where
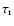 is the rise time,
is the rise time,
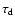 the flare decay time
(indicated in Fig. 2 with the vertical dotted lines), Tthe apex flare temperature and
the flare decay time
(indicated in Fig. 2 with the vertical dotted lines), Tthe apex flare temperature and
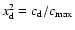 ,
with
,
with 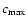 the peak count rate and
the peak count rate and 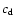 the count rate at the end of the
flare. Inserting these values, the loop length is found to be
the count rate at the end of the
flare. Inserting these values, the loop length is found to be
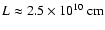 .
.
4.3 Pressure balance
To maintain stable flare loops, the gas pressure of the evaporated
plasma must be smaller than the magnetic pressure
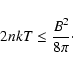 |
(7) |
Knowing the flare density and temperature, we get a lower limit for
the magnetic field strength
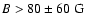 .
Again, there is a large error
because of the large uncertainty for the density. Shibata & Yokoyama (2002)
assume pressure balance and give equations for B and
L:
.
Again, there is a large error
because of the large uncertainty for the density. Shibata & Yokoyama (2002)
assume pressure balance and give equations for B and
L:
B = 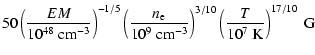 |
(8) |
L = 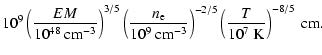 |
(9) |
Using these relations, we obtain a magnetic field strength of
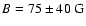 and a loop length of
and a loop length of
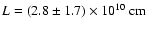 .
.
Combining the above results, we find that both pressure balance
considerations as well as the centrifugal oscillation model are
consistent.
The derived loop lengths from pressure balance and radiative cooling times are
consistent with each other
and in agreement with the loop length derived assuming a slow-mode oscillation
or a fast kink mode.
The fast sausage mode is much less likely to be the cause of this
oscillation, as its derived loop length is inconsistent with the other
independent methods. We further discuss the plausibility of the different
modes in the following section.
5 Discussion and conclusions
We have investigated an X-ray oscillation during a flare on AT Mic, observed by XMM-Newton. In order to locate the oscillation
in time and frequency, we applied a continuous wavelet transform to
the time series, and found that the oscillation, starting at flare
peak and continuing during the flare's flat-top phase, with a period
around P = 750 s, has a confidence level of >99.9%
(Fig. 2). We then reconstructed the light curve from the CWT
for three different frequency bands (Fig. 3). In particular, the
light curve passed through a low-pass filter (
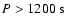 ,
first
panel), displays the overall shape of the light curve and picks out
the long-lasting flares, whereas the light curve reconstructed from wavelet
coefficients in the range around the oscillation period (
,
first
panel), displays the overall shape of the light curve and picks out
the long-lasting flares, whereas the light curve reconstructed from wavelet
coefficients in the range around the oscillation period (
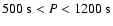 ,
second panel),
isolates the oscillation. The coherent oscillation during the large
flare can be fitted with a damped sine curve with a period of
,
second panel),
isolates the oscillation. The coherent oscillation during the large
flare can be fitted with a damped sine curve with a period of
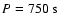 and an exponential decay time of
and an exponential decay time of
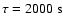 (Fig. 4). The initial, relative peak-to-peak amplitude of the
oscillation is found
to be
(Fig. 4). The initial, relative peak-to-peak amplitude of the
oscillation is found
to be
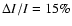 .
Decomposing a light curve in such a way
is a powerful tool for isolating an oscillation from a
flare, as well as disentangling the flare and the oscillation from
the high-frequency noise. Because the effect of noise can thus be greatly
reduced,
this method provides us with a more accurate value for the
oscillation amplitude than a value potentially obtained from a binned or
smoothed light curve, which is always underestimated, especially if the bins
are large.
.
Decomposing a light curve in such a way
is a powerful tool for isolating an oscillation from a
flare, as well as disentangling the flare and the oscillation from
the high-frequency noise. Because the effect of noise can thus be greatly
reduced,
this method provides us with a more accurate value for the
oscillation amplitude than a value potentially obtained from a binned or
smoothed light curve, which is always underestimated, especially if the bins
are large.
Interpreting this oscillation as a standing magneto-acoustic wave
in the flare loop, we infer that it is a longitudinal slow-mode
wave, oscillating at the fundamental frequency. This mode has an
anti-node (maximum disturbance) at the loop apex and is capable of causing the
largest global flux variations. Using the relations derived by
Roberts et al. (1984), we find a flare loop length of
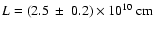 .
This value is consistent with
estimating the loop length from radiative cooling times of the flare
(Hawley et al. 1995) as well as from pressure balance considerations
(Shibata & Yokoyama 2002).
.
This value is consistent with
estimating the loop length from radiative cooling times of the flare
(Hawley et al. 1995) as well as from pressure balance considerations
(Shibata & Yokoyama 2002).
Table 1:
Comparison of values derived for the indicated models.
Table 1 provides a comparison of these results.
The derived loop length of a fast kink wave, which has a large error
due to a large error in density, is also consistent with the two
independent methods of radiative cooling times and pressure
balance. This mode, however, is basically incompressible
(Nakariakov et al. 2004), and it would be hard to
imagine how it could cause intensity perturbations in a spatially
unresolved light curve.
We discount fast sausage-mode waves, since they would
require either much longer loops (several times the stellar radius) for the
observed period, which is inconsistent with the loop length derived from the
radiative cooling as well as from pressure balance models, or a
loop aspect ratio (L/a) close to 1, in which case the
cylindrical geometry assumption breaks down.
In summary, we conclude that the observed oscillation is most
likely a standing longitudinal slow-mode wave.
To estimate the magnetic field strength, we apply the centrifugal force model
of
Zaitsev & Stepanov (1989), where the magnetic loop is stretched by a
centrifugal force which is caused by the upwardly evaporating plasma,
stretching the loop beyond equilibrium and thus exciting MHD waves. The flux
tube starts to oscillate up and down (i.e. in the plane of the
loop). Consequently,
the particle density inside the loop also
oscillates, causing an oscillation in the thermal
radiation (soft X-rays and extreme ultra-violet). Non-thermal
radiation, originating from gyro-synchrotron (radio) and bremsstrahlung
(hard X-rays and optical), caused by fast electrons trapped within the
loop and moving back and forth from one end of the loop to the other,
also oscillates: the speed of the trapped electrons, and hence the
non-thermal radiation, is modulated by the plasma density. This
picture is consistent with a slow-mode (acoustic) wave. The magnetic
field strength thus obtained is
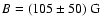 .
The large error results
from the large uncertainty in the particle density.
This value for the magnetic field strength is consistent with pressure balance
considerations (Shibata & Yokoyama 2002), where
.
The large error results
from the large uncertainty in the particle density.
This value for the magnetic field strength is consistent with pressure balance
considerations (Shibata & Yokoyama 2002), where
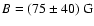 .
.
The observed rapid damping of the oscillation (a damping time comparable
to the oscillation period) is in agreement with other magneto-acoustic
wave observations (e.g., Verwichte et al. 2004; Ofman & Wang 2002). So far, various
models have been put forward to
explain the fast damping. In the case of slow-mode waves,
Ofman & Wang (2002) numerically find that thermal conduction is the
dominant dissipation mechanism in loops with 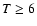 MK.
MK.
An alternative to the interpretation of a standing magneto-acoustic
wave causing the flare oscillation is that repeated and rapid
flaring is occurring. This might also explain the flat-top character of the
time profile of this flare, which differs from the usual shape of
solar flares, which shows a rapid rise from beginning to
peak, followed by a slow decay (see, e.g.,
Svestka 1989). However, repeated flaring should be random, rather than have
a periodic and exponentially-decaying nature, and would have difficulties
explaining the observation of what appears to be a damped oscillation.
The derived length of the flare loop is about the size of the stellar
radius and is comparable to loop lengths of large solar flares.
In particular, Svestka (1994) investigated solar X-ray
observations which showed periods close to 20 min. They associated
them with spatially resolved large-scale coronal loops with loop
lengths of
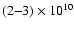 cm, and interpreted the oscillations as
slow-mode MHD waves.
Terekhov et al. (2002) observed an X-ray oscillation with P=143 s during
a solar flare, and derived a loop length of
cm, and interpreted the oscillations as
slow-mode MHD waves.
Terekhov et al. (2002) observed an X-ray oscillation with P=143 s during
a solar flare, and derived a loop length of
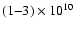 cm.
The centrifugal force model, originally derived for non-thermal X-rays
(Zaitsev & Stepanov 1989), has also been applied to millimetre-wave emission
(Stepanov et al. 1992), thermal X-rays (Terekhov et al. 2002), and, in the
stellar case, to optical emission
(Mathioudakis et al. 2003; Mullan et al. 1992).
cm.
The centrifugal force model, originally derived for non-thermal X-rays
(Zaitsev & Stepanov 1989), has also been applied to millimetre-wave emission
(Stepanov et al. 1992), thermal X-rays (Terekhov et al. 2002), and, in the
stellar case, to optical emission
(Mathioudakis et al. 2003; Mullan et al. 1992).
This is the first time that an oscillation has been
observed in X-rays in a stellar flare, and has been used to derive a flare loop
length and a local magnetic field strength.
Comparable loop dimensions and magnetic field
strengths indicate the similar natures of AT Mic's corona and
that of our Sun. Because of the smaller radius of these M-type stars (
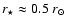 ), the loop length is in fact of the order of the
stellar radius, whereas the magnetic field strength is around the upper limit
for solar coronal values. This is consistent with this class of low mass stars
(dMe-type) being very X-ray active.
), the loop length is in fact of the order of the
stellar radius, whereas the magnetic field strength is around the upper limit
for solar coronal values. This is consistent with this class of low mass stars
(dMe-type) being very X-ray active.
Acknowledgements
We would like to thank the referee D. J. Mullan for calling to our
attention a missed reference and a couple of inconsistencies in the
text. We would also like to thank V. M. Nakariakov, B. Roberts,
M. Mathioudakis, N. Schartel, G. Peres, A. J. J. Raassen,
R. Erdélyi, E. Verwichte, and J. L. Culhane for
various helpful discussions and comments.
We acknowledge financial support from the UK Particle Physics and Astronomy
Research Council (PPARC).
Appendix A: CWT error analysis
The continuous wavelet transform of the signal f is given by
convolving the signal with a wavelet function 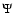
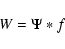 |
(A.1) |
or in components:
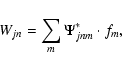 |
(A.2) |
with
Wjn = W(tn,sj),
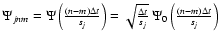 ,
fm = f(tm), the
,
fm = f(tm), the
 denoting the complex conjugate and the scale
denoting the complex conjugate and the scale
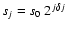 .
In our analysis, we set s0=1 and
.
In our analysis, we set s0=1 and
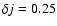 for the Morlet
wavelet.
Significance levels can be derived as
for the Morlet
wavelet.
Significance levels can be derived as
for
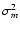 the variance of fm, and
the variance of fm, and 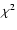 the
the
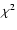 -distribution of Wjn.
The signal can be reconstructed by using
-distribution of Wjn.
The signal can be reconstructed by using
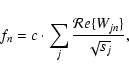 |
(A.6) |
with c the normalisation constant (see, e.g., Torrence & Compo 1998).
If a filter F is applied to the wavelet coefficients,
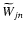 =
=
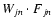 ,
the filter coefficients
being 0 or 1, the filtered signal is then given by
,
the filter coefficients
being 0 or 1, the filtered signal is then given by
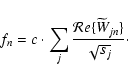 |
(A.7) |
Inserting Eqs. (A.2) into (A.7) and rearranging the
sums, we obtain
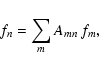 |
(A.8) |
with
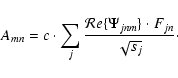 |
(A.9) |
Thus, the signal can be filtered and reconstructed using a linear
transform, which is determined by the wavelet function and the filter.
The variance of the reconstructed light curve is then given by
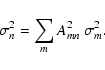 |
(A.10) |
The signal can be decomposed without loss, if the
sum of the different filters used is 1 for all filter components.
- Andrews,
A. D. 1990, A&A, 239, 235 [NASA ADS] (In the text)
-
Aschwanden, M. J., Fletcher, L., Schrijver, C. J., &
Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] (In the text)
- Cargill,
P. J., Mariska, J. T., & Antiochos, S. K. 1995,
ApJ, 439, 1034 [NASA ADS] [CrossRef] (In the text)
- Gliese, W.,
& Jahreiss, H. 1991, Preliminary Version of the Third Catalogue
of Nearby Stars, Astron. Rechen-Institut, Heidelberg
(In the text)
- Handy,
B. N., Acton, L. W., Kankelborg, C. C., et al.
1999, Sol. Phys., 187, 229 [NASA ADS] [CrossRef] (In the text)
- Hawley,
S. L., Fisher, G. H., Simon, T., et al. 1995, ApJ,
453, 464 [NASA ADS] [CrossRef] (In the text)
- Jansen, F.,
Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Lim, J., Nelson,
G. J., & Vaughan, A. E. 1987, Proc. ASA, 7, 2 (In the text)
-
Mathioudakis, M., Seiradakis, J. H., Williams, D. R.,
et al. 2003, A&A, 403, 1101 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Mitra-Kraev, U., Harra, L. K., Güdel, M., et al.
2005, A&A, 431, 679 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Mullan,
D. J., & Johnson, M. 1995, ApJ, 444, 350 [NASA ADS] [CrossRef] (In the text)
- Mullan,
D. J., Herr, R. B., & Bhattacharyya, S. 1992, ApJ,
391, 265 [NASA ADS] [CrossRef] (In the text)
-
Nakariakov, V. M., & Ofman, L. 2001, A&A, 372,
L53 [EDP Sciences] [NASA ADS] (In the text)
-
Nakariakov, V. M., Tsiklauri, D., Kelly, A., Arber,
T. D., & Aschwanden, M. J. 2004, A&A, 414,
L25 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Ofman, L., &
Wang, T. 2002, ApJ, 580, L85 [NASA ADS] [CrossRef]
- Perryman,
M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997,
A&A, 323, L49 [NASA ADS] (In the text)
- Raassen, A.
J. J., Mewe, R., Audard, M., & Güdel, M. 2003,
A&A, 411, 509 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Roberts, B.
2000, Sol. Phys., 193, 139 [NASA ADS] [CrossRef] (In the text)
- Roberts, B.,
Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef] (In the text)
- Rodonò, M.
1974, A&A, 32, 337 [NASA ADS] (In the text)
- Shibata, K.,
& Yokoyama, T. 2002, ApJ, 577, 422 [NASA ADS] [CrossRef] (In the text)
- Stepanov,
A. V., Urpo, S., & Zaitsev, V. 1992, Sol. Phys., 140,
139 [NASA ADS] [CrossRef] (In the text)
-
Strüder, L., Briel, U., Dennerl, K., et al. 2001,
A&A, 365, 18 [NASA ADS] [CrossRef] (In the text)
- Terekhov,
O. V., Shevchenko, A. V., Kuz'min, A. G.,
et al. 2002, Astron. Lett., 28, 397 [NASA ADS] [CrossRef] (In the text)
- Torrence,
C., & Compo, G. P. 1998, Bull. Amer. Meteor. Soc., 79,
61 [NASA ADS] (In the text)
-
Verwichte, E., Nakariakov, V. M., Ofman, L., & DeLuca,
E. E. 2004, Sol. Phys., 223, 77 [NASA ADS] [CrossRef]
- Svestka, Z.
1989, Sol. Phys., 121, 399 [NASA ADS] (In the text)
- Svestka, Z.
1994, Sol. Phys., 152, 505 [NASA ADS] [CrossRef] (In the text)
- Zaitsev,
V. V., & Stepanov, A. V. 1989, Sov. Astron. Lett.,
15, 66 [NASA ADS] (In the text)
Copyright ESO 2005