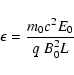 |
(1) |
A&A 436, 1103-1111 (2005)
DOI: 10.1051/0004-6361:20042589
S. Dalla - P. K. Browning
School of Physics and Astronomy, University of Manchester, PO Box 88, Manchester M60 1QD, UK
Received 21 December 2004 / Accepted 9 March 2005
Abstract
We study test particle trajectories in the vicinity of
a three-dimensional (3D) magnetic null point during spine
reconnection.
Particles are injected into the steady-state non-uniform
magnetic and electric fields derived by Priest & Titov (1996),
and the equations of motion numerically integrated.
We use input parameters typical of the solar corona, for which
reconnection has been suggested as the fundamental mechanism
responsible for particle acceleration in flare events.
We show that substantial acceleration is possible in the 3D spine
reconnection configuration, in the strong electric field regime.
The energy gain is strongly dependent on the location of
injection into the simulation box, as was the case in 2D X-point
configurations. In our 3D geometry, we first vary the location
of injection within a plane through the spine, and
derive an analytical value
for the injection angle for which maximum energy gain is achieved.
Secondly we vary the azimuthal location of particle injection
and show that as one moves away from the plane with maximum electric
field magnitude, higher final energies can be achieved, though this
requires substantially longer times.
Key words: acceleration of particles - Sun: flares - Sun: particle emission
Magnetic reconnection has been put forward as an efficient mechanism for particle acceleration in a wide variety of astrophysical contexts: including the solar corona, during flares, which is the primary interest here, but also the Earth's magnetotail and pulsars (de Gouveia et al. 2000). Ions accelerated by reconnection have also been recently observed in a high temperature laboratory plasma device (Helander et al. 2002). The presence and properties of such high energy particles constitute an important diagnostic of reconnection, and the energy of non-thermal particles is a significant component of solar flare energy balance. Recent observational evidence from the RHESSI spacecraft in particular, points towards reconnection playing a key role in solar flares (Sui et al. 2004).
For the purpose of investigating how an energetic particle population is created as a result of reconnection, the test particle approach has been widely adopted. Here the trajectories of charged particles (ions and electrons) are calculated in prescribed electromagnetic fields representative of magnetic reconnection scenarios. This then allows study of how the electric field generated during the reconnection process can energise particles, and how this process depends on the magnetic field and plasma properties. The collisionless test particle approach is valid for particles of velocity a few times larger than the thermal velocity, as they have long collisional mean free paths. It is also required that the population of such high energy particles is sufficiently small that its feedback on the electromagnetic fields can be neglected. The majority of test particle studies investigating particle acceleration during reconnection, have been carried out within a 2D framework. This involves assuming uniformity of all physical parameters along one spatial direction, which is also usually the direction of the electric field. Two-dimensional studies demonstrated that efficient acceleration can take place at X-point (also called 2D null) configurations and clarified the importance of the location of particle injection into the simulation box in determining a particle's final energy (Moses et al. 1993; Deeg et al. 1991; Vekstein & Browning 1997; Burkhart et al. 1990). The effect of adding a magnetic field component transverse to the X-point plane, parallel to the electric field, has also been widely studied (Hamilton et al. 2003; Bruhwiler & Zweibel 1992; Browning & Vekstein 2001; Mori et al. 1998; Bulanov 1980). This was a first step towards more realistic 3D geometries. Even a very weak transverse field component can have a significant effect. Other studies modelled acceleration in a current sheet configuration (Litvinenko & Somov 1993; Zharkova & Gordovskyy 2004).
In this paper we adopt a test particle approach to study
particle acceleration during reconnection at a 3D magnetic null.
It is useful to summarise some of the results for test particle motion in
2D X-point geometries, for comparison with the 3D results
presented here. It has been shown (Vekstein & Priest 1995; Vekstein & Browning 1997; Burkhart et al. 1990)
that particles are strongly
magnetised at global scale if the parameter:
Two-dimensional configurations are necessarily somewhat unrealistic, and three-dimensional reconnection has recently become a topic of intense investigation. This has significant qualitative differences from 2D reconnection (see, for example Priest & Forbes 2002, for a review of 3D reconnection). Particular attention has been devoted to developing magnetohydrodynamic models of the kinematics and dynamics of 3D reconnection. Reconnection in 3D does not necessarily require the presence of null points in the magnetic field, but from the point of view of particle acceleration these are the most interesting configurations. Three-dimensional magnetic null points are believed to occur frequently in the solar corona, for example during flares (Aulanier et al. 2000). Indeed, given the complex topology of the coronal field arising from photospheric flux sources of mixed polarity, null points are likely to be common.
Within a 2D model, the uniformity of the electric field along one spatial direction can lead to a very large energy gain during the time when the particle is in the low magnetic field region near the null or field reversal layer. In principle, since the region is of infinite extent in the invariant direction, particles can acquire arbitrarily large energies by moving in this direction. Here we address the question of whether 3D configurations, where the electric field has finite extent and is not spatially uniform, can also be efficient particle accelerators. There have as yet been few studies of particle acceleration in such 3D configurations. A study of trajectories in the fields output of a 3D reconnection MHD code has shown significant differences in the shape of electron spectra, compared with a 2D model (Schopper et al. 1999). Test particles in analytical model fields for 3D stationary reconnection (Craig et al. 1995) have been studied by Kobak et al. (2000), including also the effects of scattering due to turbulence in the vicinity of the null point. But the complexity of the field configurations in such studies means that a direct comparison with the better understood 2D case is difficult.
Studies of magnetic reconnection in 3D, have now clarified the structure of the plasma flow and fields in the vicinity of a 3D magnetic null (Priest & Titov 1996). Two types of reconnection have been shown to occur: spine and fan reconnection. In this paper we investigate particle acceleration in the vicinity of a 3D magnetic null for the spine reconnection scenario. A natural extension will be to consider also fan reconnection and this will indeed be done in future.
We use the 3D reconnection fields derived by Priest & Titov (1996) as the input to our calculation of test particle trajectories. These simple fields are not exact solutions of the resistive MHD equations, but are derived by means of several simplifications. Full solutions, valid both in 2D and 3D have been derived by Craig et al. (1996,1995). However it has been shown in a 2D geometry, that the simplified fields produce an energetic particle spectrum which is almost identical to the one obtained from the full reconnection solution field (Heerikhuisen et al. 2002). Hence the usage of simplified fields to study the particle acceleration problem appears to be a good first approximation. It also allows a most direct comparison with the widely studied 2D problem, so that we may understand the extent to which features of particle acceleration in 2D geometries carry over to 3D, or the extent to which 3D is fundamentally different. The aim at this stage is thus to develop a basic understanding of the trajectories of charged particles and particle acceleration in 3D reconnecting geometries, which can then be applied to more complex and realistic models in future.
Trajectories are obtained by numerical solution of the full equations of motion, as decribed in Sect. 2, for parameters typical of the solar corona. General characteristics of the 3D trajectories are described in Sects. 3 and 4, while in Sects. 5-8 we focus on the acceleration problem in a 3D scenario. Conclusions are presented in Sect. 10.
The nature of reconnection near a three-dimensional (3D) magnetic null was investigated by Priest & Titov (1996). They considered a potential 3D magnetic null, and discussed two types of reconnection which may take place in its vicinity: spine and fan reconnection. More general non-potential 3D nulls are discussed by Parnell et al. (1996) and Pontin et al. (2005).
In this study we focus on the potential 3D
magnetic null configuration, described in cylindrical coordinates
![]() by the equation (Priest & Titov 1996):
by the equation (Priest & Titov 1996):
By imposing continous footpoint motions on a cylindrical boundary
enclosing the null,
Priest & Titov (1996) were able to derive analytical expressions for the electric
field and flow velocity associated to 3D reconnection.
For spine reconnection, footpoint motions are imposed on the curved
surface of the cylindrical boundary, in such a way that field line motion
takes place in planes through the spine. A plane through the spine
can be characterised by the
azimuthal angles
![]() .
The field lines approach the null point moving within such a plane, break
and reconnect as the footpoints cross the plane z=0.
.
The field lines approach the null point moving within such a plane, break
and reconnect as the footpoints cross the plane z=0.
For fan reconnection, continuos footpoint motions are imposed on the two bases of the cylindrical boundary, causing a swirling motion of magnetic field lines at the fan.
In this paper we consider the spine reconnection scenario, for which
the electric field associated to reconnection takes the form (Priest & Titov 1996):
We obtain particle trajectories by numerically solving the equations
of motion of a particle in the magnetic and electric fields ![]() and
and ![]() :
:
| |
= | (4) | |
| = | 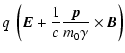 |
(5) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2589fig1.eps}
\end{figure}](/articles/aa/full/2005/24/aa2589-04/Timg30.gif) |
Figure 1: a) Magnetic field lines for the potential 3D magnetic null configuration. b) Diagram of the inflow and outflow regions for spine reconnection. |
| Open with DEXTER | |
The particle's equations of motion are solved numerically
by means of a variable-order variable-step Adams
method, as implemented in the subroutine D02CJF of the
NAG libraries (NAG Fortran Library 1999).
Distances are normalised by the characteristic length L,
the magnetic field by B0, and times by the nonrelativistic
gyroperiod associated
with a magnetic field of magnitude B0:
![]() .
.
To verify that the numerical integration is performed accurately, we monitor the sum of kinetic and potential energy, which is a constant of motion (as described in Sect. 4). In the runs of the code described in this paper, we find that this quantity is conserved up to the first 6 significant figures. We developed both a relativistic and non-relativistic version of the code, which give identical results for a particle which does not reach relativistic energy. We use the relativistic version of the code in the next sections as near-relativistic energies are reached in the strong electric field regime as discussed below.
A particle injected into the non-uniform fields given by Eqs. (2), (3) will follow a trajectory which depends on the field magnitudes and spatial variations, and on the initial particle position and velocity. We inject particles with a small initial energy, at a boundary of the reconnection site, i.e. at a distance L from the null point, corresponding to the dimensionless value R=1.
In regions where the particle is strongly magnetised, the motion can be described as the superposition of a rapid gyration about the local magnetic field direction and a drift motion of the guiding centre (adiabatic approximation). However near the null point this approximation breaks down as the particle becomes essentially unmagnetised (nonadiabatic region); this is where the particle can be most efficiently accelerated by the electric field.
In the adiabatic region, a particle is subject to drifts associated
with the magnetic field gradient and curvature, and to the electric
field drift, with velocity:
We observe that the electric field given by Eq. (3)
varies as
![]() ,
where
,
where ![]() is the azimuthal coordinate
in the cylindrical coordinate system chosen. Therefore in the
plane corresponding to the values
is the azimuthal coordinate
in the cylindrical coordinate system chosen. Therefore in the
plane corresponding to the values
![]() ,
270
,
270![]() ,
the
electric field magnitude is maximum. Thus, for our initial studies, we
focus on particles injected in this plane.
,
the
electric field magnitude is maximum. Thus, for our initial studies, we
focus on particles injected in this plane.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2589fig2.ps}
\end{figure}](/articles/aa/full/2005/24/aa2589-04/Timg37.gif) |
Figure 2: Trajectories for the weak electric field ( top panels) and strong electric field ( bottom panels) regimes. The particle's initial position is (x0,y0,z0)=(0, 0.8, 0.6), and input parameters are given in Table 1. Dotted lines indicate projections of magnetic field lines. |
| Open with DEXTER | |
Table 1: Input parameters to the trajectory code for runs of Fig. 2.
Figure 2 shows the trajectories of a proton for two
values of the electric field magnitude. For each case the trajectory
is described by its projections along the x-y plane (the fan
plane) and the y-z plane, the z axis being the spine.
Dotted lines represent projections of
magnetic field lines.
The top panels of Fig. 2 are for E0=30 V/m,
and the bottom panels for E0=1.5 kV/m.
In the former case
![]() and we are in the weak electric
field regime, in the latter case
and we are in the weak electric
field regime, in the latter case
![]() and we are just in the
strong electric field regime. The other input parameters
for the numerical integration are summarised in Table 1.
The magnetic field strength is typical of the solar corona. The
length scale is small compared with the observed size of coronal
structures (e.g. a flare region) because the model fields here are
supposed to apply to a localised reconnection site within a global
field configuration - thus the length L is the scale on which the
fields near a null can locally be approximated by
Eqs. (2), (3).
The electric field cannot be easily determined from observations.
Whilst the value for the "strong electric field'' regime might
appear large,
it should
be noted that this is only expected to exist in a localised region,
and indeed we expect such strong fields (giving values of
and we are just in the
strong electric field regime. The other input parameters
for the numerical integration are summarised in Table 1.
The magnetic field strength is typical of the solar corona. The
length scale is small compared with the observed size of coronal
structures (e.g. a flare region) because the model fields here are
supposed to apply to a localised reconnection site within a global
field configuration - thus the length L is the scale on which the
fields near a null can locally be approximated by
Eqs. (2), (3).
The electric field cannot be easily determined from observations.
Whilst the value for the "strong electric field'' regime might
appear large,
it should
be noted that this is only expected to exist in a localised region,
and indeed we expect such strong fields (giving values of
![]() near 1)
for fast reconnection with inflow speed a significant fraction of the
Alfvén speed.
The particle is injected at a position
(x0,y0,z0)=(0, 0.8, 0.6)
hence in
the plane where the electric field is maximum.
Thus for this choice of parameters the values of
near 1)
for fast reconnection with inflow speed a significant fraction of the
Alfvén speed.
The particle is injected at a position
(x0,y0,z0)=(0, 0.8, 0.6)
hence in
the plane where the electric field is maximum.
Thus for this choice of parameters the values of ![]() ,
as given by Eq. (1), are
,
as given by Eq. (1), are
![]() for the weak electric
field
regime and
for the weak electric
field
regime and
![]() for the strong electric field one.
for the strong electric field one.
In the weak electric field case, the particle is spiralling about the magnetic field line (this component of the motion not being visible in Fig. 2 as the gyroradius is much smaller than the lenght scale L), and its velocity reverses at mirror points as a result of the nonuniformity of the magnetic field. The simulation is run up to a final dimensionless time of 320 000 (gyroperiods), corresponding to a dimensional final time of 2 s. The particle is not accelerated, its final energy being 250 eV.
In the strong electric field case, however, a large acceleration
is observed, with the proton reaching 0.9 MeV after
a time of 10 000 (gyroperiods) corresponding to 65 ms.
The presence of two separate regimes of particle motion depending
on the value of the electric field and the corresponding
dimensionless parameter
![]() ,
as shown in Fig. 2, is similar to what is observed in 2D configurations (Vekstein & Browning 1997).
,
as shown in Fig. 2, is similar to what is observed in 2D configurations (Vekstein & Browning 1997).
We now introduce a potential for the electric field and calculate the sum of kinetic and potential energy for our system. This quantity remains constant during the motion.
A potential V such that
![]() can be obtained
from Eq. (3), and is given by:
can be obtained
from Eq. (3), and is given by:
| (8) |
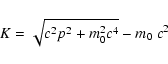 |
(10) |
Equation (9) implies that
2 q E0 L is the maximum
kinetic energy which can be gained by a particle in this configuration.
A particle may or may not gain this maximum energy, depending on
the details of its trajectory.
For a particle with initial kinetic energy negligible
compared to q E0 L, the kinetic energy at a time twill be given by:
![\begin{figure}
\par\includegraphics[width=6cm,clip]{2589fig3.ps}
\end{figure}](/articles/aa/full/2005/24/aa2589-04/Timg52.gif) |
Figure 3:
Dependence of energy gain on the particle's initial position.
Top panel: each line type represents a particle trajectory projected onto the
y-z plane. Bottom panel: time variation of the kinetic energy for the
trajectories shown in the top panel. Here time is normalised by the initial
particle gyroperiod. We consider a proton of initial energy 300 eV and
initial pitch-angle 92 |
| Open with DEXTER | |
We now focus on the strong electric field regime, and study how the energy gain depends on the particle's initial position. We will show that the energy gain strongly depends on the location where the particle is injected into the box, and that the largest energy gain is associated to locations where the electric field drift, with velocity given by Eq. (6), takes the particle very close to the magnetic null, where acceleration is most efficient.
In the case of spine reconnection, ![]() lies in planes through the
spine, hence we focus first on one such plane, the y-z plane.
Here
lies in planes through the
spine, hence we focus first on one such plane, the y-z plane.
Here
![]() and the electric field is maximum.
It might be expected that particles injected in this plane are most
strongly accelerated, though we shall see later in Sect. 8
that this is not in fact the case.
and the electric field is maximum.
It might be expected that particles injected in this plane are most
strongly accelerated, though we shall see later in Sect. 8
that this is not in fact the case.
The dependence of the final energy on initial positions in the y-z plane is shown in Fig. 3, where different line types correspond to different initial positions on the circle of radius R=1. Other parameters such as the particle's initial energy and pitch angle and the configuration of the fields are kept constant. For the dashed trajectory (a), the particle drifts quickly towards the spine, where the electric field is strong, and is efficiently accelerated. The solid trajectory (b) shows a particle going very close to the null and gaining large energy. The particle following the dash-dotted trajectory (c) however does not enter the region of strong electric field and has a much smaller energy gain.
If we introduce the angle ![]() ,
giving the angle in the y-z plane
between the y axis and the radius connecting the initial position to the origin,
we can plot the final energy versus
,
giving the angle in the y-z plane
between the y axis and the radius connecting the initial position to the origin,
we can plot the final energy versus ![]() ,
and obtain the plot
given in Fig. 4.
This shows the existence of an optimal angle
,
and obtain the plot
given in Fig. 4.
This shows the existence of an optimal angle
![]() for which
the particle gains the largest final energy. For angles smaller
than
for which
the particle gains the largest final energy. For angles smaller
than
![]() ,
the energy gain drops quickly, corresponding
qualitatively to the (c) trajectory of Fig. 3.
For angles larger than
,
the energy gain drops quickly, corresponding
qualitatively to the (c) trajectory of Fig. 3.
For angles larger than
![]() ,
large acceleration can
be obtained, corresponding to trajectories such as (a)
in Fig. 3.
,
large acceleration can
be obtained, corresponding to trajectories such as (a)
in Fig. 3.
The 3D result shown in Fig. 4 can be compared with
results previously obtained in a 2D X-point configuration (Vekstein & Browning 1997),
keeping in mind that the magnetic field lines in Fig. 1 of the
latter reference need to be rotated
by 45 degrees about the origin, to display a dependence similar to that of 3D field lines in a plane through the spine.
In a 2D configuration, the optimal angle of approach is 45![]() and
there is symmetry about the line of optimal approach. In a 3D geometry
we obtain a smaller optimal angle, and as shown in Fig. 4,
there is no symmetry about the line of optimal approach.
and
there is symmetry about the line of optimal approach. In a 3D geometry
we obtain a smaller optimal angle, and as shown in Fig. 4,
there is no symmetry about the line of optimal approach.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2589fig4.eps}
\end{figure}](/articles/aa/full/2005/24/aa2589-04/Timg55.gif) |
Figure 4:
Plot of the particle's final energy versus the angle |
| Open with DEXTER | |
The value of the angle
![]() can be obtained analytically
by calculating the expression of the flow lines of the velocity
can be obtained analytically
by calculating the expression of the flow lines of the velocity
![]() ,
from Eq. (6) combined with
Eqs. (2) and (3).
One obtains that flow lines are described by:
,
from Eq. (6) combined with
Eqs. (2) and (3).
One obtains that flow lines are described by:
| R2= 2 z2 + C | (12) |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{2589fig5.ps}
\end{figure}](/articles/aa/full/2005/24/aa2589-04/Timg60.gif) |
Figure 5:
Trajectories in the y-z plane for the same initial conditions
as trajectory (b) of Fig. 3, but different values of
the initial particle pitch-angle: (a) pitch-angle = 110 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.9cm,clip]{2589fig6.ps}
\end{figure}](/articles/aa/full/2005/24/aa2589-04/Timg61.gif) |
Figure 6:
Trajectory of a particle injected into a strong electric
field configuration, with the same initial parameters as the
solid-line trajectory of Fig. 3, except for the
fact that initial pitch-angle is 90 |
| Open with DEXTER | |
In the strong electric field regime, varying the value of the initial
particle pitch-angle will result in very different trajectories.
This is shown in Fig. 5, where the same initial conditions
as for trajectory (b) of Fig. 3 were used, apart from
the value of initial pitch-angle.
The solid trajectory corresponds to initial pitch-angle equal to 110![]() and the dash-dotted one to initial pitch angle 80
and the dash-dotted one to initial pitch angle 80![]() .
It is clear that varying the initial pitch angle by as little as 10
.
It is clear that varying the initial pitch angle by as little as 10![]() results in the particle following very different paths, and in
the case of pitch angle 80
results in the particle following very different paths, and in
the case of pitch angle 80![]() gaining much smaller energy,
for injection at this particular location.
A particle of pitch-angle 80
gaining much smaller energy,
for injection at this particular location.
A particle of pitch-angle 80![]() will however be able to gain large
energy if injected at a larger value of
will however be able to gain large
energy if injected at a larger value of ![]() ,
in such a way that it
passes close to the null point. In other words, a plot similar
to the one shown in Fig. 4 can be obtained for any
pitch angle, with the position of the peak (i.e. the optimal
injection angle) being different for different pitch angles.
,
in such a way that it
passes close to the null point. In other words, a plot similar
to the one shown in Fig. 4 can be obtained for any
pitch angle, with the position of the peak (i.e. the optimal
injection angle) being different for different pitch angles.
It is well known that magnetic null configurations can give rise
to chaotic orbits, since the Larmor radius
diverges where the magnetic field becomes zero (Nocera et al. 1996).
Figure 6 shows the trajectory
of a proton in the strong electric field regime, with the same
initial position and very similar initial velocity as the
solid-line trajectory of Fig. 3.
The only parameter that was changed in this run with respect to
the one in Fig. 3 is the initial pitch-angle,
which is here 90![]() rather than 92
rather than 92![]() .
Thus the particle moves directly towards the null, initially
along the drift streamline given by Eq. (13).
.
Thus the particle moves directly towards the null, initially
along the drift streamline given by Eq. (13).
This small change in the initial conditions results in the particle following a completely different trajectory, an indication of chaotic behaviour. This type of behavior is observed only for trajectories going very close to the magnetic null.
In Sects. 3 and 5 we injected particles
into the simulation box at various locations in the plane
![]() ,
where the value of the electric field at
a distance R=1 from the spine is largest.
,
where the value of the electric field at
a distance R=1 from the spine is largest.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2589fig7.ps}
\end{figure}](/articles/aa/full/2005/24/aa2589-04/Timg62.gif) |
Figure 7:
Top panels: trajectories for injections at different values of
|
| Open with DEXTER | |
We now consider trajectories with initial positions in other
planes, characterised by a value of ![]() different from 90
different from 90![]() and consequently electric fields at R=1 smaller than the values
previously considered.
and consequently electric fields at R=1 smaller than the values
previously considered.
In Fig. 7
the trajectory (a) is for a particle injected in the semiplane with
![]() where the electric field
is maximum, trajectory (b) for a particle injected
in the semiplane
where the electric field
is maximum, trajectory (b) for a particle injected
in the semiplane
![]() ,
with a smaller value of the
initial electric field, and (c) for
,
with a smaller value of the
initial electric field, and (c) for
![]() ,
where the initial electric field is 0.34 times the value in
the plane
,
where the initial electric field is 0.34 times the value in
the plane
![]() .
The bottom panel shows the variation of kinetic energy with time
for the three trajectories. We see that a particle moving
initially in a
plane with smaller electric field takes a longer time to reach the
region where acceleration is most efficient, as a result of the
electric drift speed being smaller. However,
it gains a larger final energy.
.
The bottom panel shows the variation of kinetic energy with time
for the three trajectories. We see that a particle moving
initially in a
plane with smaller electric field takes a longer time to reach the
region where acceleration is most efficient, as a result of the
electric drift speed being smaller. However,
it gains a larger final energy.
We therefore have the surprising result that the plane
with maximum electric field is not the one where the
largest kinetic energy is gained.
This fact can be understood in terms of the energy conservation
arguments presented in Sect. 4, in the sense that,
from Eq. (11),
the value of
![]() ,
where
,
where ![]() is the
azimuthal angle at t=0, influences the maximum energy
that can be reached by a particle.
For all three trajectories in Fig. 7,
particles exit the reconnection region near
is the
azimuthal angle at t=0, influences the maximum energy
that can be reached by a particle.
For all three trajectories in Fig. 7,
particles exit the reconnection region near
![]() ,
where
,
where
![]() ,
the second term on the rhs of Eq. (11),
is small.
For trajectory (b), the initial potential energy (first term on
the rhs of Eq. (11)), is
,
the second term on the rhs of Eq. (11),
is small.
For trajectory (b), the initial potential energy (first term on
the rhs of Eq. (11)), is
![]() eV, and this is approximately
the energy gained during the motion. A similar behaviour is seen for trajectory (c) for which initially
eV, and this is approximately
the energy gained during the motion. A similar behaviour is seen for trajectory (c) for which initially
![]() eV, allowing an even larger acceleration.
For the trajectory (a),
eV, allowing an even larger acceleration.
For the trajectory (a),
![]() ,
hence the magnitude of
the energy gain is determined by
,
hence the magnitude of
the energy gain is determined by
![]() at the time of exit from the acceleration region, and this is
about an order of magnitude smaller than in previous cases as
at the time of exit from the acceleration region, and this is
about an order of magnitude smaller than in previous cases as ![]() is close to 270
is close to 270![]() .
In all three cases motion in the region near the null is towards
decreasing values of
.
In all three cases motion in the region near the null is towards
decreasing values of
![]() ,
i.e. in the counterclockwise direction.
,
i.e. in the counterclockwise direction.
The plane with maximum electric field (
![]() )
is the one where a
particle takes the shortest time to arrive in the vicinity of
the null, as a result of
)
is the one where a
particle takes the shortest time to arrive in the vicinity of
the null, as a result of ![]() being large. In other words,
acceleration happens on the shortest time scales in this plane.
Figure 7 shows that as one moves to smaller values of
being large. In other words,
acceleration happens on the shortest time scales in this plane.
Figure 7 shows that as one moves to smaller values of ![]() ,
the time required for a particle to be strongly accelerated increases,
becoming for the plane
,
the time required for a particle to be strongly accelerated increases,
becoming for the plane
![]() more than 3 times larger than
for the plane
more than 3 times larger than
for the plane
![]() .
For values of
.
For values of ![]() below
below
![]() a situation is reached where
the electric drift velocity
a situation is reached where
the electric drift velocity ![]() becomes smaller than other drift velocities
and the particle does not reach the region near the null, inhibiting
efficient acceleration.
becomes smaller than other drift velocities
and the particle does not reach the region near the null, inhibiting
efficient acceleration.
As noted above, for all three trajectories in
Fig. 7
particles exit the region near the null at
an angle close to
![]() .
This shows a tendency of accelerated
particles to be focussed near the plane where the electric field
is maximum. It should be however pointed out that, for the parameters
considered in Fig. 7, particles moving away from the null
become trapped by the magnetic field, and start
bouncing back and forward in the way shown in Fig. 8,
which displays the trajectory (c) of Fig. 7 up to longer
times.
.
This shows a tendency of accelerated
particles to be focussed near the plane where the electric field
is maximum. It should be however pointed out that, for the parameters
considered in Fig. 7, particles moving away from the null
become trapped by the magnetic field, and start
bouncing back and forward in the way shown in Fig. 8,
which displays the trajectory (c) of Fig. 7 up to longer
times.
![\begin{figure}
\par\includegraphics[width=11.9cm,clip]{2589fig8.ps}
\end{figure}](/articles/aa/full/2005/24/aa2589-04/Timg71.gif) |
Figure 8:
Trajectory for injection in the plane
|
| Open with DEXTER | |
The behaviour shown in Fig. 8 is the result of the
particle having gained a large energy: once it exits the region near
the null, the value of
![]() ,
as defined by Eq. (7),
has now become very large, i.e. the electric field drift is not
the dominant component of the motion, as it was prior to passage by the
null point.
,
as defined by Eq. (7),
has now become very large, i.e. the electric field drift is not
the dominant component of the motion, as it was prior to passage by the
null point.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2589fig9.ps}
\end{figure}](/articles/aa/full/2005/24/aa2589-04/Timg72.gif) |
Figure 9:
Top panels: trajectories for injections into the electric field
given by Eq. (14), with three values of
|
| Open with DEXTER | |
The electric field and flow velocity given by Eqs. (3) and (6) respectively,
were derived by Priest & Titov (1996) within the ideal MHD description, and
are therefore valid outside the region close to the spine where
resistive effects need to be taken into account. As a result
the electric field displays a 1/R dependence, i.e. a singularity
at the spine. It was shown by Priest & Titov (1996) that resolution of
this singularity cannot be achieved within linear MHD theory, and that
a fully non-linear resistive treatment is required to eliminate it.
While a solution to the latter resistive MHD problem is being
worked out by scientists, the qualitative effect of the removal
of the singularity at spine on energetic particle trajectories
can be studied by considering a modified electric field of the
following form:
We injected particles into a configuration with modified electric field given by Eq. (14), and studied how the resolution of the singularity at the spine would impact the results on particle acceleration presented in the previous sections.
We considered two values of the dimensionless parameter
![]() ,
given by
,
given by
![]() and
and
![]() ,
and compared trajectories for these two
cases with the one obtained by using the original singular electric
field, i.e.
,
and compared trajectories for these two
cases with the one obtained by using the original singular electric
field, i.e.
![]() .
The corresponding trajectories are shown in Fig. 9.
One can observe that for
.
The corresponding trajectories are shown in Fig. 9.
One can observe that for
![]() ,
the trajectory and energy gain are very similar to the
,
the trajectory and energy gain are very similar to the
![]() case. However for a value
case. However for a value
![]() ,
there are large
differences in the trajectory and in the energy gained by a particle,
although the particle is still accelerated in this case.
,
there are large
differences in the trajectory and in the energy gained by a particle,
although the particle is still accelerated in this case.
We conclude that the size of the non-ideal region around the spine is an important parameter in determining the magnitude of the energy gained by a particle, and that quantitative application of the results described in this paper would require the size of the resistive region to be orders of magnitude smaller than the entire region under consideration.
We obtained trajectories of particles near a 3D magnetic null during spine reconnection, and studied the dependence of the energy gain on the field properties and the particle's initial position. Particles injected from the boundaries of a supposed localised reconnection site were investigated, with a range of injection positions.
We found that efficient particle acceleration can take place in
the strong electric field regime which is expected in fast magnetic
reconnection.
The energy gain is strongly dependent on the initial position of
the particle. Within a plane passing through the spine, an
optimal angle above (or below) the fan plane exists, for which
maximum acceleration is observed. This angle is found to
be
![]() ,
for a particle of
pitch angle 90
,
for a particle of
pitch angle 90![]() .
This is broadly consistent
with studies of 2D configurations, although the "symmetry breaking'' of
moving to 3D means that this optimal angle is no longer
a simple 45
.
This is broadly consistent
with studies of 2D configurations, although the "symmetry breaking'' of
moving to 3D means that this optimal angle is no longer
a simple 45![]() .
.
We also studied the acceleration of particles injected
in different planes through the spine, i.e. we considered
several values of the azimuthal coordinate ![]() for the initial
position, as the electric field in spine reconnection has a
for the initial
position, as the electric field in spine reconnection has a
![]() dependence. We found that
particles injected at an angle to the plane where the electric field is
maximum can also be very efficiently accelerated, though it takes a
longer time. Surprisingly, the initial position which gives
the greatest net kinetic energy gain is not that at which the electric
field is strongest. An interesting feature, which could be
significant in terms of interpreting observations of
accelerated particles, is that the particles do not leave
the reconnection site isotropically distributed in direction, but
tend to exit the reconnection region along a preferred direction.
dependence. We found that
particles injected at an angle to the plane where the electric field is
maximum can also be very efficiently accelerated, though it takes a
longer time. Surprisingly, the initial position which gives
the greatest net kinetic energy gain is not that at which the electric
field is strongest. An interesting feature, which could be
significant in terms of interpreting observations of
accelerated particles, is that the particles do not leave
the reconnection site isotropically distributed in direction, but
tend to exit the reconnection region along a preferred direction.
Since the study of particle trajectories in 3D null point configurations is quite novel, our work is quite preliminary and can be extended naturally in future in a number of ways. A first step, as previously mentioned, will be to investigate also fan reconnection. Furthermore, within the same configuration, the trajectories of electrons and ions can be quite different due to the different charge to mass ratio; this has been recently emphasised by Zharkova & Gordovskyy (2004), who provide an explanation of flare observations in terms of proton-electron separation due to acceleration in a 2D current sheet. Thus, in future we will analyse the dependence of trajectories on the charge to mass ratio of particles, considering electrons as well as different ion species. Energy spectra, and their dependence on the angle of the ejected particles, will be calculated. These results will be compared with observations e.g. from the RHESSI spacecraft. It is also important to note that the null point geometry considered here is only a special case, and in future more general 3D null points will be investigated (Parnell et al. 1996).
Our model does not include the effects of inductive electric fields generated by the strong transient currents likely to be present in many reconnection scenarios such as in solar flares, and this will be the subject of future study.
Acknowledgements
S.D. acknowledges support from the UK Particle Physics and Astronomy Research Council through a Post-Doctoral Fellowship.