A&A 436, 1123-1130 (2005)
DOI: 10.1051/0004-6361:20042025
M. Meléndez - M. A. Bautista
Centro de Física, Instituto Venezolano de Investigaciones Científicas (IVIC), PO Box 21827, Caracas 1020A, Venezuela
Received 17 September 2004 / Accepted 1 February 2005
Abstract
This paper reports on radiative transition
rates and electron impact excitation rate coefficients for levels of the
3d7 ground configuration of Ni IV.
The radiative data were computed using
the Thomas-Fermi-Dirac central potential method,
which allows for configuration interactions (CI) and relativistic effects
in the Breit-Pauli formalism.
Collision strengths in LS-coupling were calculated in the close coupling approximation
with the R-matrix
method. Then, fine structure collision strengths were obtained
by means of the intermediate-coupling frame transformation (ICFT) method
that accounts for spin-orbit coupling effects.
The collision strengths were integrated over
a Maxwellian distribution of electron
energies, and the resulting effective collision strengths are given for a
wide range of temperatures.
We build a multilevel model for the Ni IV system
and use it to identify the most important lines in optical and
infrared spectra and to compute line ratios as diagnostics of nebular
conditions. Finally, we test these data against recent observations
of the bipolar planetary nebula Mz 3.
Key words: atomic data - atomic processes - line: formation - ISM: HII regions - ISM: planetary nebulae: general - ISM: planetary nebulae: individual: Mz 3
Accurate atomic data for iron and other iron group elements is of major importance in astrophysics. Among these species, nickel is the second most abundant element; and under typical conditions of H II regions, Ni IV is the dominant ionization stage of that element. Ni IV is also important to the spectra of early supernova spectra.
The IRON Project is an international enterprise devoted to the computation of accurate atomic data for the iron group elements (Hummer et al. 1993). A complete list of publications from this project can be found at http://www.am.qub.uk/projects/iron/papers/. Within this project and following on previous efforts by A. Pradhan and his group at The Ohio State University, we have been systematically working on data for the low ionization stages of iron peak elements, e.g. radiative and collisional rates for Fe I-IV (Bautista & Pradhan 1998), Ni II (Bautista 1999, 2005), Ni III (Bautista 2001), and here we present a calculation for Ni IV. The first calculation of collisional data for Ni IV was presented by Sunderland et al. (2002), as a test case for a new parallel R-matrix program PRMAT. Nevertheless, this computation was wholly done in LS-coupling and is thus of limited practical use.
A recent spectroscopic study of the bipolar planetary nebula Mz 3
(Zhang & Liu 2002) found
five Ni IV lines from forbidden transitions among levels of the 3d7 ground configuration,
i.e.
![]() (
(
![]() ),
),
![]() (
(
![]() and
and
![]() ),
and
),
and
![]() (
(
![]() and
and
![]() ).
In the present work, we
build a multilevel model for the Ni IV ion, that can be
used to analyze this and other nebulae. In this sense, we find that Ni IV emissivity line ratios are useful as diagnostics
of electron densities between 106 and 108 cm-3, where lines of iron
ions and lighter species cannot be used.
).
In the present work, we
build a multilevel model for the Ni IV ion, that can be
used to analyze this and other nebulae. In this sense, we find that Ni IV emissivity line ratios are useful as diagnostics
of electron densities between 106 and 108 cm-3, where lines of iron
ions and lighter species cannot be used.
Table 1:
Spectroscopic and correlation configuration for Ni IV, and scaling parameters
![]() for each
spectroscopic orbital in the Thomas-Fermi-Dirac potential and
the
for each
spectroscopic orbital in the Thomas-Fermi-Dirac potential and
the
![]() pseudo-orbital in the Coulombpotential.
pseudo-orbital in the Coulombpotential.
Relativistic effects are included in the calculation by means of the Breit-Pauli operators in the form:
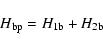 |
(3) |
Table 2: Calculated and observed term energies (in Ryd) for Ni IV. The second column shows the ab initio energies neglecting relativistic effects (no relat.); the third column shows the energies including the effects of mass, velocity, and Darwin relativistic effects (1-B relat.) but without two-body interactions; the fourth column gives the calculated energies allowing for all relativistic effects (2-B rel.); and the fifth column gives the experimental energies from NIST (2000).
The expansion considered here for the Ni IV system includes 36 LS terms.
Table 2 presents the complete list
of states included, as well as a comparison between the calculated target term energies and the observed
energies taken from NIST (2000), averaged over fine structure. Here
we show the LS-coupling energies without relativistic effects and
those that allow for one- and two-body relativistic corrections.
We find that the 2-body relativistic operators have only negligible
effects, less than 0.1%, on the averaged term energies. Mass, velocity, and
Darwin operators, on the other hand, lower the computed energies
between 1% and 2% for the
![]() and
and
![]() terms to bring them
closer to experimental values.
In our best target representation, the theoretical energies for
the lowest eight terms are typically within 5% of the experimental values, and for the higher terms the agreement is
within 2%.
terms to bring them
closer to experimental values.
In our best target representation, the theoretical energies for
the lowest eight terms are typically within 5% of the experimental values, and for the higher terms the agreement is
within 2%.
For calculating radiative rates,
fine tuning is performed with term energy corrections, where the improved
relativistic wavefunction
![]() is obtained in terms of
the non-relativistic functions
is obtained in terms of
the non-relativistic functions
For dipole allowed transitions, spontaneous decay rates are given by
Equations (7)-(9) show that the transition rates are sensitive to the energy levels accuracy, particularly for forbidden transitions between levels with small energy difference. Thus, we perform further adjustments to the transitions rates by correcting out best calculated energies to experimental values. Such corrections are called "Level Energy Corrections (LECs)''.
Table 3: Calculated and observed fine structure energy levels. (a) With neither 2-body relativistic operators nor TECs; (b) including 2-body relativistic effects, but without TECs; (c) with 2-body relativistic operators and TECs.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2025fig1.eps}\end{figure}](/articles/aa/full/2005/24/aa2025-04/Timg117.gif) |
Figure 1:
Log
|
| Open with DEXTER | |
In Fig. 1 we plot the gf-values for dipole allowed transitions
among fine structure levels computed
in the length gauge vs. those in the velocity gauge. The overall agreement
between the two gauges is around 20% for ![]() -values greater than -3, which offers a good indicator of the quality of the dipole allowed radiative
data.
-values greater than -3, which offers a good indicator of the quality of the dipole allowed radiative
data.
Table 4: Magnetic dipole transition rates (in s-1) for levels within 3d7 ground state configuration of Ni IV. The table shows results computed with neither TEC nor 2-body relativistic operators (w/o T + w/o 2-body), with 2-body relativistic operators (w/o T + 2-body), with TECs and 2-body relativistic operators (T + 2-body) and with TECs, LEVs and 2-body relativistic operators (T + L + 2-body). The rates previously reported by Hansen et al. (1984) and Garstang (1969) are also given.
Table 5: Electric quadrupole transition rates (in s-1) for levels within the 3d7 ground state configuration of Ni IV. The table shows the results computed with neither TEC nor 2-body relativistic operators (w/o T + w/o 2-body), with 2-body relativistic operators (w/o T + 2-body), with TECs and 2-body relativistic operators (T + 2-body) and with TECs, LEVs and 2-body relativistic operators (T + L + 2-body). The rates previously reported by Hansen et al. (1984) and Garstang (1969) are also given.
As regards forbidden transitions, Tables 4 and 5 present
transition probabilities for magnetic dipole and
electric quadrupole transitions rates for the ![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() levels within the 3d7 ground
configuration of Ni IV. Here we show the effects of TECs and 2-body relativistic
operators on the radiative rates for forbidden transitions. These effects
go from a few percent in most cases to several factors for some transitions
that involve highly mixed levels.
We also compare the present data with those
by Hansen et al. (1984) and Garstang (1968),
who used the method of parametric fitting to observed energy level structure.
Overall, there is good agreement between our best results
(TEC + 2-body) and the data of these authors, except for
a few weak transitions. From these comparisons, the observed accuracy in the
representation of the energy level structure of the ions and analysis of the completeness
of the configurations expansion used in the calculation we estimate that the
transition rates for forbidden transitions among lowly excited levels
have an accuracy of
levels within the 3d7 ground
configuration of Ni IV. Here we show the effects of TECs and 2-body relativistic
operators on the radiative rates for forbidden transitions. These effects
go from a few percent in most cases to several factors for some transitions
that involve highly mixed levels.
We also compare the present data with those
by Hansen et al. (1984) and Garstang (1968),
who used the method of parametric fitting to observed energy level structure.
Overall, there is good agreement between our best results
(TEC + 2-body) and the data of these authors, except for
a few weak transitions. From these comparisons, the observed accuracy in the
representation of the energy level structure of the ions and analysis of the completeness
of the configurations expansion used in the calculation we estimate that the
transition rates for forbidden transitions among lowly excited levels
have an accuracy of ![]()
![]() .
.
The variational procedure gives rise to a set of coupled integro-differential
equations that are solved by the R-matrix technique
(Burke et al. 1971; Berrington 1978, 1995) within a box of radios ![]() .
In
the asymptotic region r>a exchange between the outer electron and
the target ion can be neglected and if all long-range potentials beyond
Coulombic are also neglected, the reactance K-matrix and the scattering
S-matrix are obtained by matching the inner-radial functions at the boundary
to linear combinations of the outer-region Coulomb solutions.
Later, contributions of long-range potentials to the collision strengths
are included perturbatively (see Griffin et al. 1999).
.
In
the asymptotic region r>a exchange between the outer electron and
the target ion can be neglected and if all long-range potentials beyond
Coulombic are also neglected, the reactance K-matrix and the scattering
S-matrix are obtained by matching the inner-radial functions at the boundary
to linear combinations of the outer-region Coulomb solutions.
Later, contributions of long-range potentials to the collision strengths
are included perturbatively (see Griffin et al. 1999).
The S-matrix elements determine collision strength for a transition
from an
initial target state i to a final target state f
Table 6:
Comparison between the present effective collision
strengths in LS-coupling and
those of Sunderland et al. (2002). The data is for transitions
from the 3d7 ![]() ground state to other terms of the 3d7 configuration.
ground state to other terms of the 3d7 configuration.
To calculate collision strengths we used the same basic expansion
shown in Tables 1 and 2. Since our R-matrix calculations only include
the one-body relativistic operators,
the third column of Table 2
best represents the quality of the target for the present
collisional calculations.
One problem with the current target can be seing in the predicted
relative order of the terms
![]() and
and ![]() .
These two states
are difficult to represent because they are mixed at the fine structure
level. In theory, one should be very careful computing collision
strengths among states whose relative energy order is incorrect because
spin-orbit coupling of fine structure levels may affect the
resonance structures. However, in the present case we do not
expect to find major errors due to
reversed order of these terms, because the J values of the associated
levels are all very different and not coupled to each other.
.
These two states
are difficult to represent because they are mixed at the fine structure
level. In theory, one should be very careful computing collision
strengths among states whose relative energy order is incorrect because
spin-orbit coupling of fine structure levels may affect the
resonance structures. However, in the present case we do not
expect to find major errors due to
reversed order of these terms, because the J values of the associated
levels are all very different and not coupled to each other.
Collision strengths and effective collision strengths were calculated for all
transitions between the lowest 8 even parity terms that yield 19
levels.
The additional higher excitation terms shown in Table 2 were
also included in the CC calculation, yet the collision strengths involving these terms
may be inaccurate due to
the lack of correlation interaction. In the case of
the
![]() configuration there are also problems because
of the incomplete list of levels included, thus there maybe
collisional coupling effects that are unaccounted for.
The importance of including a large CC expansion, beyond the terms of the 3d7 configuration, was demonstrated by Sunderland et al. (2002). They showed that
the collision strengths for transitions within the 3d7 configuration were underestimated
by up to 40% when the calculation neglected states of
the
configuration there are also problems because
of the incomplete list of levels included, thus there maybe
collisional coupling effects that are unaccounted for.
The importance of including a large CC expansion, beyond the terms of the 3d7 configuration, was demonstrated by Sunderland et al. (2002). They showed that
the collision strengths for transitions within the 3d7 configuration were underestimated
by up to 40% when the calculation neglected states of
the
![]() and
and
![]() .
.
The computations were carried out with the RMATRX package of codes
(Berrington 1995). The set of (N+1)-electron
wavefunctions on the right hand of the CC expansion in
Eq. (10) includes all the configurations that result from adding
an additional electron to the target configurations.
Partial wave contributions are include from 104 ![]() total symmetries with angular momentum
L = 0-12, total multiplicities
(2S+1) = 1-7, and parities even and odd.
Additional contributions from partial waves up to L=60 were computed
without exchange, which is a good approximation for high partial waves.
Beyond this point the collision strengths were "topped up'' with estimates of high partial
waves contributions based on the Coulomb-Bethe
approximation (Burgess 1974).
For all transitions the contributions
from the high partial waves is less than
total symmetries with angular momentum
L = 0-12, total multiplicities
(2S+1) = 1-7, and parities even and odd.
Additional contributions from partial waves up to L=60 were computed
without exchange, which is a good approximation for high partial waves.
Beyond this point the collision strengths were "topped up'' with estimates of high partial
waves contributions based on the Coulomb-Bethe
approximation (Burgess 1974).
For all transitions the contributions
from the high partial waves is less than ![]() .
The collision strengths were calculated at 22 000 energy points from 0 to 12 Ry,
with a resolution of 10-5 Ry in the region with resonances and
.
The collision strengths were calculated at 22 000 energy points from 0 to 12 Ry,
with a resolution of 10-5 Ry in the region with resonances and
![]() Ry at higher energies.
This resolution was found
sufficient for accurate calculations of effective collision strengths.
Ry at higher energies.
This resolution was found
sufficient for accurate calculations of effective collision strengths.
A dimensionless thermally-averaged effective collision strength results from averaging the collision
strength over a Maxwellian distribution for electron velocities
In Table 6 we compare the present LS effective collision strengths with those of
Sunderland et al. (2002). Agreement between the two sets of data is
good (within ![]()
![]() ), with the exception of the effective collision
strengths for the
), with the exception of the effective collision
strengths for the
![]() transition, which differs by
transition, which differs by ![]()
![]() .
The
reasons for discrepancy seem related to the difference in the target
representations.
Our target representation yields reasonably accurate
energies, but the
.
The
reasons for discrepancy seem related to the difference in the target
representations.
Our target representation yields reasonably accurate
energies, but the
![]() and
and ![]() terms come out in reverse energy order. By contrast,
the target representation of Sunderland et al. (2002) does predict the
terms come out in reverse energy order. By contrast,
the target representation of Sunderland et al. (2002) does predict the
![]() and
and ![]() terms in the correct order; yet their computed energies
are considerably overestimated for all states of the 3d7 configuration,
perhaps due to missing configuration interaction.
terms in the correct order; yet their computed energies
are considerably overestimated for all states of the 3d7 configuration,
perhaps due to missing configuration interaction.
In order to investigate differences between the present results
and those of Sunderland et al. (2002), we carried out additional
calculations with reduced configuration expansions.
Here we tried to remove all configurations
with two-electron jumps
from the 3s and 3p orbitals from the CC expansion, but without major detriment to the
target. Thus we worked with two new configuration expansions: (a) a
10-configuration expansion that includes the correlation configurations
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() ;
(b)
a 12-configuration expansion that includes
;
(b)
a 12-configuration expansion that includes
![]() and
and
![]() in addition to the configurations in (a).
In all calculations we maintained the same number of LS terms
in the CC expansion. Table 6 shows a comparison between effective
collision strengths obtained from our calculations and the
results of Sunderland et al. (2002). This table offers a good
explanation for the discrepancies between our results
and those of Sunderland et al. One can see that the collision
strengths vary by up to 20% between our various calculations.
In particular, we find that the collision strength for the
in addition to the configurations in (a).
In all calculations we maintained the same number of LS terms
in the CC expansion. Table 6 shows a comparison between effective
collision strengths obtained from our calculations and the
results of Sunderland et al. (2002). This table offers a good
explanation for the discrepancies between our results
and those of Sunderland et al. One can see that the collision
strengths vary by up to 20% between our various calculations.
In particular, we find that the collision strength for the
![]() transition obtained from the 10-configuration expansion is
only
transition obtained from the 10-configuration expansion is
only ![]()
![]() higher than that of Sunderland et al. (2002), yet
this collision strength grows with the number of configurations
in the target representation.
higher than that of Sunderland et al. (2002), yet
this collision strength grows with the number of configurations
in the target representation.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2025fig2.eps}\end{figure}](/articles/aa/full/2005/24/aa2025-04/Timg151.gif) |
Figure 2:
Collision strengths for the Ni IV ion for transitions within
the 3d7 configuration: a)
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2025fig3.eps} \end{figure}](/articles/aa/full/2005/24/aa2025-04/Timg152.gif) |
Figure 3: Effective collision strengths for the Ni IV ion for the same transitions as in Fig. 2. |
| Open with DEXTER | |
Collision strengths for the fine-structure levels were obtained by re-coupling unphysical LS reactance matrices and then converting them to the physical matrices by means of multi-channel quantum defect theory. This is the so-called intermediate-coupling frame transformation (ICFT) method of Griffin et al. (1998), which accounts for the spin-orbit effects that are very important for the Ni IV system. Hence, we find differences of up to several factors between the ICFT results and fine structure collision strengths obtained from algebraic recoupling that reach up to several factors for many transitions.
Figure 2 shows the collision strength for a sample of transitions between levels of the lowest four multiplets. Consequently, Fig. 3 shows the effective collision strength for the same transitions over a wide range of temperatures.
Table 7:
Comparison between the effective collision
strengths at 10 000 K
in LS-coupling obtained from three different configuration
expansions for the target and
those of Sunderland et al. (2002). The data is for transitions
from the 3d7 ![]() ground state to other terms of the 3d7 configuration.
ground state to other terms of the 3d7 configuration.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2025fig4.eps} \end{figure}](/articles/aa/full/2005/24/aa2025-04/Timg154.gif) |
Figure 4:
Emissivity line ratios vs. Log
|
| Open with DEXTER | |
We build a collisional-radiative model of the Ni IV ion using the data described above. This model is used to study the emission spectrum of the system, identifying the most important lines and selecting line emissivity ratios useful as diagnostics of physical conditions in non-LTE plasmas.
For typical nebular temperatures between 7000 and 15 000 K, the strongest lines appear in the optical region.
For electron densities <106 cm-1 the dominant lines
are
![]() (
(
![]() )
and
)
and
![]() (
(
![]() ), but even these are rather weak. Higher densities
favor the appearance of several other lines and the likelihood that the
Ni IV spectrum can be observed. In this case, the strongest lines are
), but even these are rather weak. Higher densities
favor the appearance of several other lines and the likelihood that the
Ni IV spectrum can be observed. In this case, the strongest lines are
![]() (
(
![]() ),
),
![]() (
(
![]() ), and
), and
![]() (
(
![]() ). These lines were all
identified in the spectrum of the bipolar planetary nebula Mz 3 (Zhang & Liu
2002) together with the transitions
). These lines were all
identified in the spectrum of the bipolar planetary nebula Mz 3 (Zhang & Liu
2002) together with the transitions
![]() (
(
![]() )
and
)
and
![]() (
(
![]() ).
).
Figure 4 depicts the line emissivity ratios
![]() /
/
![]() and
and
![]() vs. the logarithm of the electron density for various
temperatures. These line ratios are sensitive to electron
density in the Log
vs. the logarithm of the electron density for various
temperatures. These line ratios are sensitive to electron
density in the Log
![]() (cm-3) range from 6 to 8.
The plots also show line ratios observed in the
spectra of Mz 3 (Zhang & Liu 2002), which indicate electron density
log
(cm-3) range from 6 to 8.
The plots also show line ratios observed in the
spectra of Mz 3 (Zhang & Liu 2002), which indicate electron density
log
![]() (cm
(cm
![]() .
This diagnostic agrees very closely
with the density derived from [Fe III] lines.
.
This diagnostic agrees very closely
with the density derived from [Fe III] lines.
We have computed radiative data, collision strengths, and effective collision strengths for transitions among 19 levels from the 3d7 ground configuration of Ni IV. The radiative data were calculated using the Thomas-Fermi-Dirac central potential and the rates for dipole forbidden transitions were found in good agreement with previous semi-empirical calculations by Hansen et al. (1984) and Garstang (1968). The collisional data for Ni IV obtained from the R-matrix method is presented for the first time. These collision strengths account for relativistic effects and contributions from extensive resonance structures.
The complete set of data obtained here allows us to build a non-LTE collisional-radiative model for Ni IV, which was then used to study the Ni IV emission from typical photoionized nebulae. Furthermore, we demonstrate the usefulness of various Ni IV emissivity line ratios as diagnostics of electron density between 106 and 108 cm-3, beyond the range of sensitivity of line ratios from iron ions and lighter species.
The whole set of data reported here can be obtained in electronic form from the CDS or by request to the authors.
Acknowledgements
We are grateful to N.R. Badnell, K. Butler, and W. Eissner for comments and corrections that led to substantial improvement of the manuscript.