A&A 436, 805-815 (2005)
DOI: 10.1051/0004-6361:20035593
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received 29 October 2003 / Accepted 24 February 2005
Abstract
We report on a calculation of the growth of the mass of
supermassive black holes at galactic centers from dark matter and
Eddington - limited baryonic accretion.
Assuming that
dark matter halos are made of fermions and harbor
compact degenerate Fermi balls
of masses from
![]() to
to
![]() ,
we find that dark matter accretion can boost the mass of
seed black holes from about
,
we find that dark matter accretion can boost the mass of
seed black holes from about ![]()
![]() to
to
![]() black holes, which then
grow by Eddington-limited baryonic accretion to
supermassive black holes of
black holes, which then
grow by Eddington-limited baryonic accretion to
supermassive black holes of
![]() .
We then show that the formation of the recently
detected supermassive black hole
of
.
We then show that the formation of the recently
detected supermassive black hole
of
![]() at a
redshift of z = 6.41 in the quasar SDSS J114816.64+525150.3
could be understood if the black hole completely consumes the
degenerate Fermi ball
and then grows by Eddington-limited baryonic accretion.
In the context of this model we constrain the dark matter particle masses
to be within the
range from 12
at a
redshift of z = 6.41 in the quasar SDSS J114816.64+525150.3
could be understood if the black hole completely consumes the
degenerate Fermi ball
and then grows by Eddington-limited baryonic accretion.
In the context of this model we constrain the dark matter particle masses
to be within the
range from 12
![]() to about 450
to about 450
![]() .
Finally we investigate the black hole growth dependence
on the formation time
and on the mass of the seed black hole. We find that in order to
fit the observed data point of
.
Finally we investigate the black hole growth dependence
on the formation time
and on the mass of the seed black hole. We find that in order to
fit the observed data point of
![]() and
and
![]() ,
dark matter accretion cannot start later
than about
,
dark matter accretion cannot start later
than about
![]() years and the seed BH cannot be
greater than about
years and the seed BH cannot be
greater than about
![]() .
Our results are in full agreement with the
WMAP observations that indicate that the first onset of
star formation might have occurred at a
redshift of
.
Our results are in full agreement with the
WMAP observations that indicate that the first onset of
star formation might have occurred at a
redshift of
![]() .
For other models of dark matter particle masses,
corresponding constraints may be derived from the growth of black holes in the
center of galaxies.
.
For other models of dark matter particle masses,
corresponding constraints may be derived from the growth of black holes in the
center of galaxies.
Key words: black holes physics - galaxies: nuclei - cosmology: dark matter - galaxies: quasars: general
It has been established that the mass of the central BH is tightly correlated with the velocity dispersion ![]() of its host bulge, where it is found that
of its host bulge, where it is found that
![]() (Faber et al. 1997; Magorrian et al. 1998;
Ferrarese & Merritt 2000; Gebhardt et al. 2000; Ferrarese 2002; Haering & Rix 2004). This tight relation between the masses of the BHs and the gravitational potential well that hosts them
suggests that the formation and evolution of supermassive BHs and the bulge of the
parent galaxy may be closely
related, e.g. Wang et al. (2000).
In addition, the recent discovery of high redshift quasars
with z > 6 (Fan et al. 2001)
implies that the formation of supermassive BHs
took place over fewer than 109 years. In spite of the vast and tantalizing work undertaken on BHs,
their genesis and evolution are not well understood (see Rees 1984, for a review).
Since the discovery of quasars in the early 1960s, it has
been suggested that these objects are powered by accretion of gas onto the supermassive BHs of masses
(Faber et al. 1997; Magorrian et al. 1998;
Ferrarese & Merritt 2000; Gebhardt et al. 2000; Ferrarese 2002; Haering & Rix 2004). This tight relation between the masses of the BHs and the gravitational potential well that hosts them
suggests that the formation and evolution of supermassive BHs and the bulge of the
parent galaxy may be closely
related, e.g. Wang et al. (2000).
In addition, the recent discovery of high redshift quasars
with z > 6 (Fan et al. 2001)
implies that the formation of supermassive BHs
took place over fewer than 109 years. In spite of the vast and tantalizing work undertaken on BHs,
their genesis and evolution are not well understood (see Rees 1984, for a review).
Since the discovery of quasars in the early 1960s, it has
been suggested that these objects are powered by accretion of gas onto the supermassive BHs of masses
![]() (Lynden-Bell 1969). Two scenarios have been discussed in modeling the growth of BHs. One is that BHs grow out of a low mass "seed'' BH through accretion (Rees 1984), and another one is that BHs grow by
merging (Barkana et al. 2001; Wang et al. 2000;
Gopal-Krishna et al. 2003,2004). In a recent paper, Duschl &
Strittmatter (2004) have investigated a model for the
formation of supermassive black
holes using a combination of merging and accretion mechanisms.
(Lynden-Bell 1969). Two scenarios have been discussed in modeling the growth of BHs. One is that BHs grow out of a low mass "seed'' BH through accretion (Rees 1984), and another one is that BHs grow by
merging (Barkana et al. 2001; Wang et al. 2000;
Gopal-Krishna et al. 2003,2004). In a recent paper, Duschl &
Strittmatter (2004) have investigated a model for the
formation of supermassive black
holes using a combination of merging and accretion mechanisms.
The purpose of this paper is to study
the growth of BHs from dark matter and Eddington-limited baryonic accretion.
Also, we would like to obtain some constraints on the DM particle masses.
In the past, self gravitating neutrino matter
has been suggested as a model
for quasars, with neutrino masses in the
range
![]() (Markov 1964).
Later, neutrino matter was suggested to describe DM in clusters of galaxies
and galactic halos with masses in the range of
(Markov 1964).
Later, neutrino matter was suggested to describe DM in clusters of galaxies
and galactic halos with masses in the range of
![]() (Cowsick & McClelland 1973; Ruffini
1980).
More recently, fermion balls (FBs) made of degenerate fermionic matter
of
(Cowsick & McClelland 1973; Ruffini
1980).
More recently, fermion balls (FBs) made of degenerate fermionic matter
of
![]() were
suggested as an alternative to supermassive BHs in galaxies
(Viollier 1994; Bilic et al. 1999;
Tsiklauri & Viollier 1998; Munyaneza & Viollier 2002).
It has been also suggested that if the Galaxy harbors a supermassive BH, then
there should be a density spike in which dark matter (DM) falling towards the
center could annihilate and the detection of these annihilation signals
could be used as a probe for the nature of DM (Bertone et al.
2002; Gondolo & Silk 1999; and Merritt et al.
2002).
The current belief is that DM particles are bosonic and very massive, i.e.
were
suggested as an alternative to supermassive BHs in galaxies
(Viollier 1994; Bilic et al. 1999;
Tsiklauri & Viollier 1998; Munyaneza & Viollier 2002).
It has been also suggested that if the Galaxy harbors a supermassive BH, then
there should be a density spike in which dark matter (DM) falling towards the
center could annihilate and the detection of these annihilation signals
could be used as a probe for the nature of DM (Bertone et al.
2002; Gondolo & Silk 1999; and Merritt et al.
2002).
The current belief is that DM particles are bosonic and very massive, i.e.
![]() .
However, the absence of experimental constraints on the weakly interacting
massive particles (WIMPs) that probably constitute DM leaves the door
open for further investigation of the hidden mass of the Universe.
.
However, the absence of experimental constraints on the weakly interacting
massive particles (WIMPs) that probably constitute DM leaves the door
open for further investigation of the hidden mass of the Universe.
In this paper, we will assume DM to be of fermionic matter and described by a Fermi-Dirac distribution with an energy cutoff in phase space (King 1966). We will then explore the limits for the DM particle masses in order to reproduce the mass distribution in the Galaxy (Wilkinson & Evans 1999) and then study the growth of a seed BH immersed at the center of the DM distribution in galaxies. We use degenerate FBs at the center of DM halos not as replacements for the BHs but as necessary ingredients to grow the BHs in galactic centers.
The resulting distribution of stars around a massive BH was studied in
detail in the 1970s and early 1980s in the context of
globular clusters (Hills 1975; Frank & Rees 1976;
Bahcall & Wolf 1976; Duncan & Shapiro 1982;
Shapiro 1985). Peebles (1972) studied the adiabatic
growth of a BH in an isothermal sphere and showed that the BH would alter the
matter density to an adiabatic cusp with
![]() .
A few years later,
Young (1980) constructed numerical models that confirmed Peebles' results and showed that the BH induces a tangential anisotropy in the velocity dispersion.
In this paper, we use the results of previous calculations on the
growth of BHs that are accreting stars
(Lightman & Shapiro 1978) to investigate the
growth of a BH that accretes DM.
Here we assume that the physics driving the formation of the power law cusp
in the star - star case is the same as in the case of DM particle
orbits being perturbed by molecular clouds. Julian (1967)
investigated a similar scenario in which the stellar orbits in our Galaxy were perturbed by
molecular clouds to explain the stellar velocity dispersion dependence on the star's age.
Moreover, Duncan & Wheeler (1980) investigated the anisotropy of the velocity dispersions of the stars
around the BH in M87.
.
A few years later,
Young (1980) constructed numerical models that confirmed Peebles' results and showed that the BH induces a tangential anisotropy in the velocity dispersion.
In this paper, we use the results of previous calculations on the
growth of BHs that are accreting stars
(Lightman & Shapiro 1978) to investigate the
growth of a BH that accretes DM.
Here we assume that the physics driving the formation of the power law cusp
in the star - star case is the same as in the case of DM particle
orbits being perturbed by molecular clouds. Julian (1967)
investigated a similar scenario in which the stellar orbits in our Galaxy were perturbed by
molecular clouds to explain the stellar velocity dispersion dependence on the star's age.
Moreover, Duncan & Wheeler (1980) investigated the anisotropy of the velocity dispersions of the stars
around the BH in M87.
Given the density distribution in DM halos, we are interested in
establishing how a seed BH would grow by accreting DM.
Moreover, the comparison of the growth of the BH from accretion of DM and
Eddington-limited baryonic matter would give us
another piece of information in the debate surrounding the nature of DM.
We therefore investigate how a BH
seed of
![]() could grow
to a
could grow
to a
![]() BH as
recently detected in quasar SDSS J1148+5251 at z=6.41 (Willot et al. 2003). Such a seed BH of a typical mass between 5 and 9
BH as
recently detected in quasar SDSS J1148+5251 at z=6.41 (Willot et al. 2003). Such a seed BH of a typical mass between 5 and 9 ![]() could have evolved in BH binaries (Podsiadlowski et al. 2003).
Here, we note that the seed BH could be an intermediate mass black hole
(IMBH)
of
could have evolved in BH binaries (Podsiadlowski et al. 2003).
Here, we note that the seed BH could be an intermediate mass black hole
(IMBH)
of
![]() that might have formed from collisions in dense
star-forming regions (Portegies Zwart & McMillan 2002; Coleman Miller
2003; and van der Marel 2003, for a review).
In fact, Wang & Biermann (1998) have established that a BH would
grow exponentially with time accreting baryonic matter as long as the supply lasts.
In addition, they were able to reproduce the observed correlation
that might have formed from collisions in dense
star-forming regions (Portegies Zwart & McMillan 2002; Coleman Miller
2003; and van der Marel 2003, for a review).
In fact, Wang & Biermann (1998) have established that a BH would
grow exponentially with time accreting baryonic matter as long as the supply lasts.
In addition, they were able to reproduce the observed correlation
![]() using standard disk galaxy parameters.
Assuming a cusp - like distribution of self-interacting DM (Spergel & Steinhardt 2000), Ostriker (2000) has estimated that BHs could grow to
using standard disk galaxy parameters.
Assuming a cusp - like distribution of self-interacting DM (Spergel & Steinhardt 2000), Ostriker (2000) has estimated that BHs could grow to
![]() from DM accretion.
For completeness, we note that accretion of DM particles by BHs has recently been
studied in Zhao et al. (2002)
and Read & Gilmore (2003).
from DM accretion.
For completeness, we note that accretion of DM particles by BHs has recently been
studied in Zhao et al. (2002)
and Read & Gilmore (2003).
Cosmological parameters of
![]() ,
,
![]() and
and
![]() are assumed throughout this paper.
In Sect. 2, we
establish the main equations to describe DM in galaxies.
We then discuss the growth of seed BHs from DM and Eddington-limited baryonic matter accretion in Sect. 3 and conclude
with a discussion in Sect. 4.
are assumed throughout this paper.
In Sect. 2, we
establish the main equations to describe DM in galaxies.
We then discuss the growth of seed BHs from DM and Eddington-limited baryonic matter accretion in Sect. 3 and conclude
with a discussion in Sect. 4.
We characterize DM by its mass density ![]() and
its velocity dispersion
and
its velocity dispersion ![]() .
DM is assumed to be collisionless and of fermionic matter and the mass of DM particles is denoted by
.
DM is assumed to be collisionless and of fermionic matter and the mass of DM particles is denoted by ![]() .
We will look for DM distributions with degenerate
cores at the center of the DM halos instead of a steep power law
.
We will look for DM distributions with degenerate
cores at the center of the DM halos instead of a steep power law
![]() with
with
![]() (e.g. Navarro et al. 1997) as we are assuming here that a central
cusp is a result of BH growth.
In order to obtain bound astrophysical solutions at
finite temperature, we follow King (1966) and
introduce an energy cutoff in phase space using the Fermi-Dirac distribution function.
We therefore adopt the following prescription for the distribution function
(e.g. Navarro et al. 1997) as we are assuming here that a central
cusp is a result of BH growth.
In order to obtain bound astrophysical solutions at
finite temperature, we follow King (1966) and
introduce an energy cutoff in phase space using the Fermi-Dirac distribution function.
We therefore adopt the following prescription for the distribution function
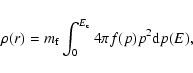 |
(3) |
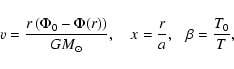 |
(5) |
![\begin{displaymath}a=\left[\frac{3\pi\hbar^{3}}{2^{5/2}m_{\rm f}^{4}g_{\rm f}G^{...
...right]^{2/3} ,
\; \; \; T_{0}=\frac{GM_{\odot}m_{\rm f}}{ak} ,
\end{displaymath}](/articles/aa/full/2005/24/aa0593-03/img73.gif) |
(6) |
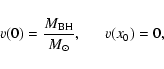 |
(9) |
| (13) |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0593f1.eps}
\end{figure}](/articles/aa/full/2005/24/aa0593-03/Timg91.gif) |
Figure 1:
The mass density and the mass enclosed within a radius r are
plotted in the upper and lower panels, respectively.
Near the center of the DM halo, the fermions are completely
degenerate and condensed in a FB of mass |
| Open with DEXTER | |
In Fig. 1, we plot the mass density and the mass enclosed
for solutions
with a
![]() mass and
a radius of 200 kpc, which corresponds to our Galaxy.
Throughout our paper, we will study solutions of type 3 which have
degenerate FBs in the center.
For the case of our galaxy,
in order to have a degenerate FB
of
mass and
a radius of 200 kpc, which corresponds to our Galaxy.
Throughout our paper, we will study solutions of type 3 which have
degenerate FBs in the center.
For the case of our galaxy,
in order to have a degenerate FB
of
![]() at the center and fit the rotation curve of the Galaxy, i.e.
reproduce the 1/r2 law,
the mass of fermions should be about
at the center and fit the rotation curve of the Galaxy, i.e.
reproduce the 1/r2 law,
the mass of fermions should be about
![]() .
For a FB of
.
For a FB of
![]() ,
one would need
a fermion mass of
,
one would need
a fermion mass of
![]() .
Thus under the assumption of a degenerate FB of
.
Thus under the assumption of a degenerate FB of
![]() to
to
![]() at the center of a DM halo of
at the center of a DM halo of
![]() with a density scaling as 1/r2 in the outer edge of the halo, the fermion mass
is constrained in the range
with a density scaling as 1/r2 in the outer edge of the halo, the fermion mass
is constrained in the range
The solutions shown in Fig. 1 have been obtained using the fact that at large distances the Fermi gas is
non degenerate. The degree of non-degeneracy is described by Eq. (7) which contains the
chemical potential ![]() .
Thus, the use of the chemical potential in the Fermi-Dirac ditribution allows
to constrain the DM particles in the range
from 12 to 450 keV, much below the Lee-Weinberg lower limit of about 2 GeV (Lee & Weinberg 1977) which was
established under the assumptions that
DM particles were in thermodynamic equilibrium at the freeze - out temperature.
We also note that a suitable candidate for the DM particle as defined by the range
given in Eq. (14)
could be either the gravitino, postulated in supergravity theories with a mass in the
.
Thus, the use of the chemical potential in the Fermi-Dirac ditribution allows
to constrain the DM particles in the range
from 12 to 450 keV, much below the Lee-Weinberg lower limit of about 2 GeV (Lee & Weinberg 1977) which was
established under the assumptions that
DM particles were in thermodynamic equilibrium at the freeze - out temperature.
We also note that a suitable candidate for the DM particle as defined by the range
given in Eq. (14)
could be either the gravitino, postulated in supergravity theories with a mass in the ![]()
![]() to
to ![]()
![]() range (Lyth 2000), or the axino, with a mass in the range between
range (Lyth 2000), or the axino, with a mass in the range between ![]() 10 and
10 and
![]()
![]() ,
as predicted by
supersymmetric extensions of the Peccei-Quinn solution to the strong CP problem (Goto & Yamaguchi 1992).
For a recent review on DM particle candidates, the reader is referred
to Bertone et al. (2005) and Baltz (2004).
,
as predicted by
supersymmetric extensions of the Peccei-Quinn solution to the strong CP problem (Goto & Yamaguchi 1992).
For a recent review on DM particle candidates, the reader is referred
to Bertone et al. (2005) and Baltz (2004).
We define the local dynamical (orbital) time scale
and the mass accretion flow as
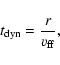 |
(15) |
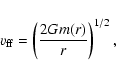 |
(17) |
Near the center of the DM halo, the core becomes
completely degenerate and the Pauli condition can be written as
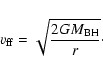 |
(19) |
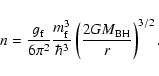 |
(20) |
Here we note that the mass ![]() of nonrelativistic
degenerate FBs scales with radius
of nonrelativistic
degenerate FBs scales with radius ![]() as
as
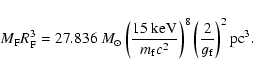 |
(22) |
In Fig. 2 we plot the mass-radius relation for FBs for
different values of the fermion mass. In the same plot we have
drawn the BH line and two horizontal lines that
correspond to a mass of
![]() and
and
![]() .
From this plot, we find an upper limit for the fermion mass of
.
From this plot, we find an upper limit for the fermion mass of
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0593f2.eps}
\end{figure}](/articles/aa/full/2005/24/aa0593-03/Timg116.gif) |
Figure 2:
The mass-radius relation for degenerate FBs.
The total mass scales as
|
| Open with DEXTER | |
The choice of the lowest value for the FB mass
is motivated by the fact that
once the BH has consumed a FB of
![]() ,
it would grow by Eddington-limited
baryonic matter accretion to
,
it would grow by Eddington-limited
baryonic matter accretion to
![]() as observed in
quasars at redshifts
as observed in
quasars at redshifts ![]() .
The choice of the second value of
.
The choice of the second value of
![]() ,
is due to increasing evidence for the existence of a BH of mass
,
is due to increasing evidence for the existence of a BH of mass
![]() at the
center of our galaxy. Thus we will assume throughout this
paper that galaxies which have BHs had
degenerate FBs of masses ranging from
at the
center of our galaxy. Thus we will assume throughout this
paper that galaxies which have BHs had
degenerate FBs of masses ranging from ![]()
![]() to
to ![]()
![]() .
The fermion mass range given by Eq. (14)
is of course
well below the upper limit for the fermion mass from Eq. (23).
.
The fermion mass range given by Eq. (14)
is of course
well below the upper limit for the fermion mass from Eq. (23).
For completeness we note here that stable degenerate FBs exist up
to a maximum mass also called the Oppenheimer Volkoff limit
From Eq. (24), the fermion mass needed to form a degenerate FB of
![]() at the OV limit is about
at the OV limit is about
![]() .
This value is in agreement with the lower limit on the mass of fermions obtained from fitting the
Galactic DM halo with a FB of
.
This value is in agreement with the lower limit on the mass of fermions obtained from fitting the
Galactic DM halo with a FB of
![]() at the center and 1/r2 density law from about 3 kpc.
The most compact supermassive object of
at the center and 1/r2 density law from about 3 kpc.
The most compact supermassive object of
![]() has been
identified as a BH at the center of M87 (Macchetto et al. 1997).
has been
identified as a BH at the center of M87 (Macchetto et al. 1997).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0593f3.eps}
\end{figure}](/articles/aa/full/2005/24/aa0593-03/Timg127.gif) |
Figure 3:
Fit of the rotation curve of dwarf galaxies DD0154. The data points can be
fitted by a non-degenerate Fermi-Dirac
distribution function for DM particles in the mass
range discussed in this paper, i.e. for
|
| Open with DEXTER | |
Apart from fermions as candidates of DM, bosons have also been considered
as an alternative to the DM constituents in galaxies. Self-gravitating bosons can form boson stars and they are prevented from complete gravitational collapse by the Heisenberg
uncertainty principle
![]() (Schunck & Liddle 1977).
Boson stars are described by Einstein's field equations coupled with the non-linear Klein Gordon equation
for a complex field
(Schunck & Liddle 1977).
Boson stars are described by Einstein's field equations coupled with the non-linear Klein Gordon equation
for a complex field ![]() with self-interaction of the form
with self-interaction of the form
![]() where
where ![]() is the boson mass
and
is the boson mass
and ![]() is a coupling constant.
It has been shown that boson stars have a maximum mass called the Kaup limit given by
is a coupling constant.
It has been shown that boson stars have a maximum mass called the Kaup limit given by
In Fig. 3, we fit the rotation curve of dwarf galaxies using a Fermi-Dirac
distribution. The rotation curve data points are well fitted in the outer
region. In the inner region, i.e. around 1 kpc, baryonic matter is perhaps
needed to get a better fit of the rotation curve. In order to fit the rotation curve of
dwarf galaxies, a non-degenerate FD distribution is needed.
The data points are taken from Carignan & Purton (1998) and the mass
of the dwarf galaxy DD0154 is taken to be
![]() with
a size of
with
a size of ![]()
![]() (Kravtsov et al. 1998).
The merging of dwarf galaxies would generate another galaxy with a degenerate
FB, and the BH would grow by the same mechanism considered in this
paper in the merged galaxy.
The
Fermi-Dirac distribution studied in this paper allows two types of
solutions: one which fits dwarf galaxies with a non-degenerate core
and the other solution with 1/r2 drop off in the outer edge
of the halo.
Degenerate FBs are consistent with data on the rotational
curves only in the second type of solution with a 1/r2 density profile at large
distances.
(Kravtsov et al. 1998).
The merging of dwarf galaxies would generate another galaxy with a degenerate
FB, and the BH would grow by the same mechanism considered in this
paper in the merged galaxy.
The
Fermi-Dirac distribution studied in this paper allows two types of
solutions: one which fits dwarf galaxies with a non-degenerate core
and the other solution with 1/r2 drop off in the outer edge
of the halo.
Degenerate FBs are consistent with data on the rotational
curves only in the second type of solution with a 1/r2 density profile at large
distances.
From Eq. (26), we can estimate the time
![]() needed for the BH mass to be infinite
to be
needed for the BH mass to be infinite
to be
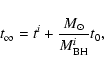 |
(28) |
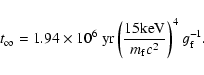 |
(29) |
The mechanism of consumption of DM particles by the BH can be understood using a quantum cascade mechanism. First, low angular momentum DM particles at the inner Fermi surface in phase space will be consumed by the BH. Due to a high degeneracy pressure, high angular momentum particles will be pushed to the inner Fermi surface and taken up by the BH. Outside the FB, fermions will hit the outer Fermi surface and for the FB to be hit continuously by DM particles, we use molecular clouds as perturbers of DM orbits. Thus, we have a three body interaction between the FB, the molecular clouds and DM particles. For our mechanism of consumption of DM by the BH to work, we will assume that the dark matter particles interact with the FB through inelastic collisions. In hitting the FB, some of the DM particles will be excited to a slightly higher energy level and get stuck in high momentum segments of phase space. This process will continue until the FB has been completely consumed by the BH and thereafter baryonic matter accretion will control the BH growth.
In this paper, we assume that there is a compact degenerate FB at
the center of galaxies that have BHs.
The seed BH first consumes the degenerate FB and grows to a mass of about
![]() and then grows by
Eddington-limited baryonic
matter accretion to higher masses of
and then grows by
Eddington-limited baryonic
matter accretion to higher masses of
![]() .
.
We will be mostly concerned with the calculation of the time needed to refill the BH loss cone using
molecular clouds as DM perturbers. To this effect, we
denote by r the radial distance from the BH to the DM particle position,
![]() the distance from the BH to the molecular clouds,
the distance from the BH to the molecular clouds,
![]() is the angle between the direction from the BH to the DM particle and
its projection in the disk and
is the angle between the direction from the BH to the DM particle and
its projection in the disk and ![]() is the angle
between the direction from the BH to the molecular clouds and to
the foot of the DM particle location in the disk. The diagram for the
geometry used is shown in Fig. 4.
is the angle
between the direction from the BH to the molecular clouds and to
the foot of the DM particle location in the disk. The diagram for the
geometry used is shown in Fig. 4.
In order to get the expression for the
time
![]() needed to refill the loss
cone
which is due to multiple small-angle
gravitational (Coulomb) encounters,
we evaluate the
random walk integral (Spitzer 1987)
needed to refill the loss
cone
which is due to multiple small-angle
gravitational (Coulomb) encounters,
we evaluate the
random walk integral (Spitzer 1987)
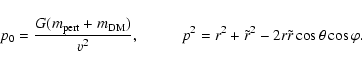 |
(31) |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{0593f4.eps}
\end{figure}](/articles/aa/full/2005/24/aa0593-03/Timg163.gif) |
Figure 4: Geometry for the system BH (BH), DM (DM) particles and molecular clouds (MC). FD stands for the foot (projection) of the DM particle in the disk. The angles BH-FD-DM and MC-FD-DM are both right angles. |
| Open with DEXTER | |
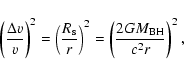 |
(34) |
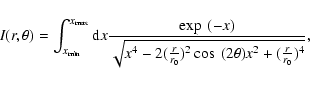 |
(35) |
The FB is consumed from inside by the BH with an accretion rate
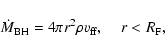 |
(36) |
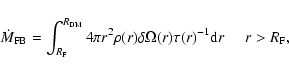 |
(37) |
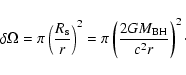 |
(38) |
In Fig. 5, we plot the dynamical and the refilling timescales as functions
of the radius. At small radii, i.e.
![]() ,
the time
,
the time
![]() to
refill the loss cone is too long for the DM to feed the BH.
Near the BH, we use the dynamical timescale to feed the BH.
For radii greater than the size of the FB, we will use the slowest of the two timescales
to feed the FB. Thus the FB feeds from the outside DM particles via the loss cone mechanism while the BH feeds
from DM inside the FB via the quantum cascade mechanism.
to
refill the loss cone is too long for the DM to feed the BH.
Near the BH, we use the dynamical timescale to feed the BH.
For radii greater than the size of the FB, we will use the slowest of the two timescales
to feed the FB. Thus the FB feeds from the outside DM particles via the loss cone mechanism while the BH feeds
from DM inside the FB via the quantum cascade mechanism.
In Fig. 6, we plot the mass flow as a function of the radius from the center.
To this end, we fix the mass of the FB to
![]() and
use a fermion mass of
and
use a fermion mass of
![]() .
Using the BH accretion rate Eq. (21), the
accretion rate becomes
.
Using the BH accretion rate Eq. (21), the
accretion rate becomes
![]() for a fermion mass of
for a fermion mass of
![]() and a
BH mass of
and a
BH mass of
![]() .
For fermions of mass
.
For fermions of mass
![]() and
a BH mass of
and
a BH mass of
![]() ,
the accretion rate is
,
the accretion rate is
![]() .
It is seen than the BH accretion rate is independent on the radius and drops
significantly when the size of the FB is reached. Thus the BH grows much faster from
the inner DM particles than the FB from the outer DM particles.
After the BH has reached a mass equal to that of the FB, i.e.
.
It is seen than the BH accretion rate is independent on the radius and drops
significantly when the size of the FB is reached. Thus the BH grows much faster from
the inner DM particles than the FB from the outer DM particles.
After the BH has reached a mass equal to that of the FB, i.e.
![]() ,
its growth is
controlled by Eddington baryonic matter accretion.
,
its growth is
controlled by Eddington baryonic matter accretion.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0593f5.eps}
\end{figure}](/articles/aa/full/2005/24/aa0593-03/Timg191.gif) |
Figure 5:
The refilling and orbital timescales plotted as a function of the radius from
the center of the DM halo. In this plot,
the mass of the FB
is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0593f6.eps}
\par\end{figure}](/articles/aa/full/2005/24/aa0593-03/Timg192.gif) |
Figure 6:
The mass accretion flow as a function of distance from the center.
For a given mass of the BH, the accretion rate is independent of the
radius until the Bondi radius where the BH dominates the gravitational
potential of the fermions. As the BH mass approaches that of the Fermion
ball, the BH accretion rate becomes constant until the radius of the FB and as the size of the FB is reached,
the DM accretion rate onto the FB drops dramatically. Thus the growth rate of the
FB is much lower than that of the BH which grows by feeding on DM from inside the FB.
Similarly to the last plot, we have used here a FB mass of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0593f7.eps}
\end{figure}](/articles/aa/full/2005/24/aa0593-03/Timg195.gif) |
Figure 7:
The black hole mass growth from only DM accretion. The fermion mass is varied as shown on the plot.
It can be seen that the BH mass can grow to
|
| Open with DEXTER | |
In Fig. 7, we plot the BH mass as a function of time for different values of
the fermion mass. The BH mass - time dependence is
given by Eq. (26). It is shown that for fermion masses lower than about 1 keV, it would take more
than 1010 years for the BH to grow to
![]() .
However, due to the Pauli principle used in
the derivation of Eq. (26),
if the fermion mass is constrained in the mass range between about 1 keV
and 1 MeV, a seed BH of 5
.
However, due to the Pauli principle used in
the derivation of Eq. (26),
if the fermion mass is constrained in the mass range between about 1 keV
and 1 MeV, a seed BH of 5 ![]() can
grow to a
can
grow to a
![]() BH in about
107-8 years, which would then
grow by Eddington-limited baryonic
accretion to
BH in about
107-8 years, which would then
grow by Eddington-limited baryonic
accretion to
![]() at a redshift of
at a redshift of
![]() (see next subsection).
Fermion masses greater than about 1 MeV would make the BH grow much faster and the BH could be as large as
(see next subsection).
Fermion masses greater than about 1 MeV would make the BH grow much faster and the BH could be as large as
![]() in less than
about one year after the beginning of the Universe.
in less than
about one year after the beginning of the Universe.
In the next section, we will discuss the Eddington baryonic matter accretion and discuss the plots of BH growth from both DM and Eddington baryonic matter accretion.
The details of Eddington-limited baryonic accretion have been studied by many authors,
here we
refer the reader to Wang & Biermann (1998) and provide just the main formulae:
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0593f8.eps}
\end{figure}](/articles/aa/full/2005/24/aa0593-03/Timg205.gif) |
Figure 8:
The mass
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0593f9.eps}
\end{figure}](/articles/aa/full/2005/24/aa0593-03/Timg206.gif) |
Figure 9:
The same as in the last figure but for a degenerate FB mass of
|
| Open with DEXTER | |
It is seen from Figs. 8 and 9 that
only baryonic matter accretion
cannot fit this data point and the
curve for the growth of the BH due to baryonic
matter lies on the right side of the data point.
Using
Eq. (41) the total mass
of the BH from Eddington-limited baryonic accretion at
![]() years
i.e. z=6.41 is
years
i.e. z=6.41 is
![]() which is about ten times less
than the inferred BH mass of
which is about ten times less
than the inferred BH mass of
![]() ,
clearly outside the error
range.
The growth of a seed BH from 5
,
clearly outside the error
range.
The growth of a seed BH from 5 ![]() to
to
![]() is accomplished in two steps:
First, the BH completely consumes the degenerate Fermi core with
masses between
is accomplished in two steps:
First, the BH completely consumes the degenerate Fermi core with
masses between
![]() and
and
![]() .
In the second step, the
.
In the second step, the
![]() BH feeds on
baryonic matter accretion to reach the mass
of
BH feeds on
baryonic matter accretion to reach the mass
of
![]() at a redshift of
at a redshift of
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0593f10.eps}
\end{figure}](/articles/aa/full/2005/24/aa0593-03/Timg212.gif) |
Figure 10:
The BH growth dependence on the
starting time of accretion. We find that starting DM accretion at
a time of
|
| Open with DEXTER | |
In Fig. 10, we investigate how the
growth of the mass of the BH depends on the accretion starting time.
To this effect, we fix the total mass of the FB to
![]() and the fermion mass to
and the fermion mass to
![]() and vary
the initial time when the DM accretion starts as shown on the
graph.
We find that the data point of
and vary
the initial time when the DM accretion starts as shown on the
graph.
We find that the data point of
![]() at
at
![]() is well fitted for an accretion starting time of
is well fitted for an accretion starting time of
![]() for any fermion greater
than
for any fermion greater
than
![]() .
Here we also note that Eddington baryonic matter accretion
could also allow the seed BH
to grow to a
.
Here we also note that Eddington baryonic matter accretion
could also allow the seed BH
to grow to a
![]() BH if the efficiency is
BH if the efficiency is
![]() .
The accretion starting time
of
.
The accretion starting time
of
![]() corresponds to a redshift
of reionization of
corresponds to a redshift
of reionization of
![]() as obtained by WMAP
observations (Krauss 2003).
as obtained by WMAP
observations (Krauss 2003).
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0593f11.eps}
\end{figure}](/articles/aa/full/2005/24/aa0593-03/Timg217.gif) |
Figure 11:
We investigate how the BH growth depends on the mass of the seed BH.
To fit the data point of mass
|
| Open with DEXTER | |
Finally in Fig. 11, we investigate how the growth of the BH is
affected by the mass of the seed BH at different
starting times of accretion.
In order to constrain the mass of the seed BH, we vary the mass of the
FB from
![]() to
to
![]() and also
the mass of the seed BH from
and also
the mass of the seed BH from
![]() to
to
![]() at initial times of
at initial times of
![]() and
and
![]() years.
These values
correspond to the earliest and latest plausible times
for the formation of the first stellar seed BHs in order to grow into
supermassive BHs at redshift
years.
These values
correspond to the earliest and latest plausible times
for the formation of the first stellar seed BHs in order to grow into
supermassive BHs at redshift
![]() .
From recent WMAP observations (Spergel et al. 2003), BHs of
masses
.
From recent WMAP observations (Spergel et al. 2003), BHs of
masses ![]()
![]() might have formed at a redshift
might have formed at a redshift ![]() .
In Fig. 11, we have
plotted only the limiting curves
which show that
the mass of the FB
should be
.
In Fig. 11, we have
plotted only the limiting curves
which show that
the mass of the FB
should be
![]() and the mass of
the seed BH cannot be greater than about
and the mass of
the seed BH cannot be greater than about
![]() .
The best fit is obtained for a BH formation time a reionization time
of
.
The best fit is obtained for a BH formation time a reionization time
of
![]() ,
i.e.
,
i.e.
![]() .
.
It is interesting to estimate the maximum
luminosity attainable by an accreting BH of this mass. This is usually
considered to be the Eddington luminosity at
which the outward radiation pressure equals the inward
gravitational attraction.
Using Eq. (42), the luminosity of a
![]() BH is of the order of a
few
BH is of the order of a
few
![]() and the corresponding accretion rate is
about
and the corresponding accretion rate is
about
![]() .
However, such high luminosity values (Fan et al. 2001) would be
obtained only for a standard efficiency of
.
However, such high luminosity values (Fan et al. 2001) would be
obtained only for a standard efficiency of
![]() which as seen
from Figs. 8 and 9 does not fit the data point for only
baryonic matter accretion.
which as seen
from Figs. 8 and 9 does not fit the data point for only
baryonic matter accretion.
A gravitational system in which molecular clouds provide the
interaction path between DM particles and feeding the BH leads to a strong
limit on the maximum mass of the BH.
For an initial distribution of DM in the halo
without a BH,
the
total energy of the system is given by
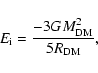 |
(43) |
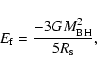 |
(44) |
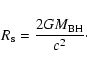 |
(45) |
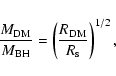 |
(46) |
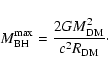 |
(47) |
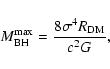 |
(48) |
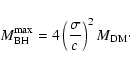 |
(49) |
If we use heavy fermions with masses of
about
![]() ,
then according to Eq. (24) the maximum mass allowed for the degenerate Fermi
core would only be of about
,
then according to Eq. (24) the maximum mass allowed for the degenerate Fermi
core would only be of about
![]() ,
which is not enough to grow a stellar mass BH
to
,
which is not enough to grow a stellar mass BH
to
![]() in about 108 years.
On the other hand, very light fermions i.e.
in about 108 years.
On the other hand, very light fermions i.e.
![]() would generate very massive degenerate FBs of masses greater than
would generate very massive degenerate FBs of masses greater than
![]() and the BH would grow to
and the BH would grow to
![]() in a very short time, i.e
in a very short time, i.e
![]() .
.
The growth of seed BHs from DM accretion is investigated using the
quantum cascade mechanism
upon which low angular momentum DM particles at the inner Fermi surface
are first consumed by the BH and then due to a high degeneracy pressure,
higher angular momentum particles are pushed inwards and the process
continues until the entire degenerate FB is consumed by the BH.
Moreover, molecular clouds have been used as perturbers of
DM particle orbits outside the FB
and we have shown that the BH grows faster than the FB.
After the BH has consumed the entire FB, it then grows by Eddington-limited baryonic
accretion to
higher masses of ![]()
![]() at redshifts
at redshifts
![]() .
We also point out that molecular clouds of mass
.
We also point out that molecular clouds of mass
![]() have also been
detected in the host galaxy of the same quasar at a redshift of
have also been
detected in the host galaxy of the same quasar at a redshift of
![]() (Walter et al. 2003).
(Walter et al. 2003).
We have also constrained the possible starting time of
accretion, i.e. the time of BH seed formation.
From our analysis, the mass of a
![]() BH in the
quasar SDSS sJ114816.64+525150.3 at a redshift of z=6.41 can be fitted
exactly if the accretion process starts at a time of about
BH in the
quasar SDSS sJ114816.64+525150.3 at a redshift of z=6.41 can be fitted
exactly if the accretion process starts at a time of about
![]() years, which corresponds to the reionization time.
years, which corresponds to the reionization time.
The seed BH mass is found to be in the range from a few solar masses up to an upper limit
of ![]()
![]() .
For a seed BH mass of
.
For a seed BH mass of
![]() ,
Eddington
baryonic matter accretion would be enough to cause the seed BH to grow into a
supermassive BH of
,
Eddington
baryonic matter accretion would be enough to cause the seed BH to grow into a
supermassive BH of
![]() mass.
The data point at a redshift of z=6.41 can be fitted by only
Eddington baryonic matter accretion with an efficiency of
mass.
The data point at a redshift of z=6.41 can be fitted by only
Eddington baryonic matter accretion with an efficiency of
![]() .
.
Our model provides a method to find the DM particles mass.
If it is found that there is a clear lower mass cut of
103 to
![]() in the distribution of BH masses, then
this mass can be used for the mass of the FB to find the corresponding mass
in the distribution of BH masses, then
this mass can be used for the mass of the FB to find the corresponding mass ![]() of the
fermions which will be in the range of 12 keV to 450 keV.
If on the other hand the BH mass distribution is a continuous function, then our model of BH
growth with DM will probably be ruled out.
of the
fermions which will be in the range of 12 keV to 450 keV.
If on the other hand the BH mass distribution is a continuous function, then our model of BH
growth with DM will probably be ruled out.
The postulated DM particles in this paper were non-relativistic at the decoupling time and
are usually called cold dark matter
particles (CDM). The latter have to be neutral, stable or quasi-stable and have to weakly interact with ordinary matter.
As mentioned in Sect. 2.1, these particles could be axions which have been investigated by DAMA/NAI (Bernabei et al.
2001). The heavier particles of mass above
![]() could also be of the class of DM
candidates named WIMPS (Weakly Interactive
Massive particles). However, in the standard model of particle physics, CDM cannot be
suitable candidates for particles.
Thus, a new window beyond the standard model of particle physics has to accommodate these particles
for our model of BH growth to work.
The DAMA/NAI experiment (see Bernabei et al. 2004, for a review) which aims at the verification of
the presence of DM particles in the Galactic halo,
will be able to confirm whether GeV WIMPS or axions of masses of 12 to 450 keV could exist in nature.
could also be of the class of DM
candidates named WIMPS (Weakly Interactive
Massive particles). However, in the standard model of particle physics, CDM cannot be
suitable candidates for particles.
Thus, a new window beyond the standard model of particle physics has to accommodate these particles
for our model of BH growth to work.
The DAMA/NAI experiment (see Bernabei et al. 2004, for a review) which aims at the verification of
the presence of DM particles in the Galactic halo,
will be able to confirm whether GeV WIMPS or axions of masses of 12 to 450 keV could exist in nature.
Observations have shown that the masses of
supermassive BHs at galactic centers correlate with the masses of the
host bulges, i.e.
![]() (Haering & Rix 2004). This result is obtained in our model as long as the
Eddington limited accretion dominates the final growth of the BH. This happens for BH
masses of more than about
(Haering & Rix 2004). This result is obtained in our model as long as the
Eddington limited accretion dominates the final growth of the BH. This happens for BH
masses of more than about
![]() (Wang et al. 2000).
(Wang et al. 2000).
Mergers of dwarf galaxies as well as the spinning of BHs would play an important role in the growth of the BHs. The consideration of these two effects will be the subject of further investigations. In addition, it would be of great interest to study the growth of BHs from boson DM particles. Although it has been shown that bosons could provide a good fit to the rotation curves in dwarf galaxies, it is not yet clear whether an analogous mechanism could work in galaxies with a 1/r2 density fall off.
While it takes only
![]() years to grow supermassive BHs in
most distant quasars, the Galactic center
might have grown to its current
mass of
years to grow supermassive BHs in
most distant quasars, the Galactic center
might have grown to its current
mass of ![]()
![]() with only DM accretion in a Hubble time.
In the following paper, we will address the growth of the Galactic center BH.
with only DM accretion in a Hubble time.
In the following paper, we will address the growth of the Galactic center BH.
Acknowledgements
We thank Yiping Wang for providing us with the data file for baryonic matter growth. We are also grateful to Heino Falcke and Rainer Spurzem for useful discussions. F.M. research is supported by the Alexander von Humboldt Foundation. Work with P.L.B. has been supported through the AUGER theory and membership grant 05 CU1ERA/3 through DESY/BMF (Germany). Further support for the work with PLB has come from the DFG, DAAD, Humboldt Foundation (all Germany), grant 2000/06695-0 from FAPESP (Brasil) through G. Medina-Tanco, a grant from KOSEF (Korea) through H. Kang and D. Ryu, a grant from ARC (Australia) through R. J. Protheroe, and European INTAS/ Erasmus/ Sokrates/Phare grants with partners V. Berezinsky, L. Gergely, M. Ostrowski, K. Petrovay, A. Petrusel, M. V. Rusu and S. Vidrih.