T. Leismann1 - L. Antón2 - M. A. Aloy1 - E. Müller1 - J. M. Martí2 - J. A. Miralles3 - J. M. Ibáñez2
1 - Max-Planck-Institut für Astrophysik,
Postfach 1312, 85741 Garching, Germany
2 - Departamento de Astronomía y Astrofísica,
Universidad de Valencia, 46100 Burjassot, Spain
3 - Departamento de Física Aplicada, Universidad de
Alicante, Ap. Correus 99, 03080 Alacant, Spain
Received 10 December 2004 / Accepted 5 March 2005
Abstract
We have performed a comprehensive parameter study of the morphology
and dynamics of axisymmetric, magnetized, relativistic jets by means
of numerical simulations. The simulations have been performed with
an upgraded version of the GENESIS code which is based on a
second-order accurate finite volume method involving an approximate
Riemann solver suitable for relativistic ideal magnetohydrodynamic
flows, and a method of lines. Starting from pure hydrodynamic
models we consider the effect of a magnetic field of increasing
strength (up to
![]() times the
equipartition value) and different topology (purely toroidal or
poloidal). We computed several series of models investigating the
dependence of the dynamics on the magnetic field in jets of
different beam Lorentz factor and adiabatic index.
We find that the inclusion of the magnetic field leads to diverse
effects which contrary to Newtonian magnetohydrodynamics models do
not always scale linearly with the (relative) strength of the
magnetic field. The relativistic models show, however, some clear
trends. Axisymmetric jets with toroidal magnetic fields produce a
cavity which consists of two parts: an inner one surrounding the
beam which is compressed by magnetic forces, and an adjacent outer
part which is inflated due to the action of the magnetic field. The
outer border of the outer part of the cavity is given by the
bow-shock where its interaction with the external medium takes
place. Toroidal magnetic fields well below equipartition (
times the
equipartition value) and different topology (purely toroidal or
poloidal). We computed several series of models investigating the
dependence of the dynamics on the magnetic field in jets of
different beam Lorentz factor and adiabatic index.
We find that the inclusion of the magnetic field leads to diverse
effects which contrary to Newtonian magnetohydrodynamics models do
not always scale linearly with the (relative) strength of the
magnetic field. The relativistic models show, however, some clear
trends. Axisymmetric jets with toroidal magnetic fields produce a
cavity which consists of two parts: an inner one surrounding the
beam which is compressed by magnetic forces, and an adjacent outer
part which is inflated due to the action of the magnetic field. The
outer border of the outer part of the cavity is given by the
bow-shock where its interaction with the external medium takes
place. Toroidal magnetic fields well below equipartition (
![]() )
combined with a value of the adiabatic index of 4/3 yield
extremely smooth jet cavities and stable beams.
Prominent nose cones form when jets are confined by toroidal fields
and carry a high Poynting flux (
)
combined with a value of the adiabatic index of 4/3 yield
extremely smooth jet cavities and stable beams.
Prominent nose cones form when jets are confined by toroidal fields
and carry a high Poynting flux (
![]() and
and
![]() ). In contrast, none of our models possessing a
poloidal field develops such a nose cone. The size of the nose cone
is correlated with the propagation speed of the Mach disc (the
smaller the speed the larger is the size). If two models differ
only by the adiabatic index, jets having smaller adiabatic indices
tend to develop smaller nose cones.
). In contrast, none of our models possessing a
poloidal field develops such a nose cone. The size of the nose cone
is correlated with the propagation speed of the Mach disc (the
smaller the speed the larger is the size). If two models differ
only by the adiabatic index, jets having smaller adiabatic indices
tend to develop smaller nose cones.
Key words: magnetohydrodynamics (MHD) - methods: numerical - relativity - galaxies: active - galaxies: jets
The presence of magnetic fields in relativistic fluids is ubiquitous among the most luminous objects in the universe like, e.g., active galactic nuclei (AGNs), quasars, gamma-ray bursts, X-ray binaries, core-collapse supernovae, etc. In the specific case of jets originating from AGNs, the observation of non-thermal synchrotron radiation (see, e.g., Ferrari 1998, for a review) requires the presence of a magnetic field in which relativistic electrons gyroradiate. The high degree of polarization observed in many AGN sources (e.g., Gabuzda et al. 2000) indicates that magnetic fields are not randomly oriented but posses some large scale structure (at least at parsec scales).
Disentangling the intrinsic structure of the magnetic field is still an observational challenge because of the finite spatial resolution of the interferometric beams used in observations of AGN jets. At parsec scales a variety of magnetic field configurations are observed including predominantly toroidal ones (e.g., 0954 + 658: Gabuzda & Cawthorne 1996; 1803 + 784: 0823 + 033 and 1749 + 701: Gabuzda & Pushkarev 2001), configurations with alternating orthogonal, alternating aligned and predominantly poloidal fields along the jet (e.g., OJ 287: Gabuzda & Gómez 2001; 1418 + 546: Gabuzda 2003), and even helical field configurations (1055 + 018: Attridge et al. 1999; 0820 + 225: Gabuzda et al. 2001; 0745 + 241: Pushkarev & Gabuzda 2001; 1652 + 398: Gabuzda 2003). Different magnetic field topologies are also observed at kiloparsec scales ranging from fields which are mostly aligned with the jet (e.g., 3C 120: Walker et al. 1987; NGC 4258: Krause & Löhr 2004) to fields which are oriented preferentially perpendicular (toroidal) to the jet axis (e.g., 3C 449: Kigure et al. 2004). Other more complex structures are observed, too (e.g., Laing & Bridle 2002). Furthermore, there are indications that the intergalactic and interstellar medium the AGN jets are propagating into can be threaded with large scale magnetic fields of some microgauss (e.g., Kim et al. 1990; Crusius-Waetzel et al. 1990; Taylor & Perley 1993). This variety of ordered magnetic field structures most likely reflects different formation and evolutionary processes. For example, magnetized jets with a dominant toroidal field component can be produced by winding up an initial field which has a significant longitudinal component due to the rotation of the central AGN engine (e.g., Nakamura et al. 2001; Lovelace et al. 2002; Tsinganos & Bogovalov 2002; Lynden-Bell 2003).
Relativistic magnetized jets from AGNs can be described in the
framework of ideal relativistic magnetohydrodynamics (RMHD). Among
the first attempts to simulate the corresponding nonlinear, time
dependent and multidimensional RMHD equations we mention here that of
Evans & Hawley (1988), who using a two-dimensional finite difference code
investigated several problems involving general relativistic
magnetohydrodynamic accretion flows onto a black hole. More
importantly, these authors also proposed a new numerical technique
called constrained transport (CT) for evolving the induction equation
while maintaining vanishing divergence of the magnetic field down to
machine roundoff error. Later on van Putten (1993, 1996)
performed the first axisymmetric simulations of RMHD jets having
moderately small Lorentz factors (![]() 3). Koide & coworkers
(Koide et al. 1996; Koide 1997) simulated 2D RMHD slab jets being
restricted, however, to rather low spatial resolution, short evolution
times, and small Lorentz factors (
3). Koide & coworkers
(Koide et al. 1996; Koide 1997) simulated 2D RMHD slab jets being
restricted, however, to rather low spatial resolution, short evolution
times, and small Lorentz factors (![]() 4.6). This study was extended
to 3D jets by Nishikawa & coworkers (Nishikawa et al. 1997, 1998). Komissarov developed a high-resolution,
shock-capturing, second-order accurate RMHD code (Komissarov 1999a) which
he used to simulate 2D jets possessing toroidal fields
(Komissarov 1999b) and the jet-torus structure observed in the Crab
nebula (Komissarov & Lyubarsky 2004, 2003, see also
Del Zanna et al. 2004). Jet formation
has been studied using general relativistic magnetohydrodynamic
(GRMHD) simulations based on a simplified Total Variation Diminishing
scheme ignoring the evolution of the constraint
4.6). This study was extended
to 3D jets by Nishikawa & coworkers (Nishikawa et al. 1997, 1998). Komissarov developed a high-resolution,
shock-capturing, second-order accurate RMHD code (Komissarov 1999a) which
he used to simulate 2D jets possessing toroidal fields
(Komissarov 1999b) and the jet-torus structure observed in the Crab
nebula (Komissarov & Lyubarsky 2004, 2003, see also
Del Zanna et al. 2004). Jet formation
has been studied using general relativistic magnetohydrodynamic
(GRMHD) simulations based on a simplified Total Variation Diminishing
scheme ignoring the evolution of the constraint ![]() .
Koide et al. (1999, 2000, 2002, 1998) and
Koide (2003) modeled the formation of axisymmetric jets in a system
consisting of an accretion disk and a rotating black hole. The simulations,
which cover a few rotational periods of the black hole, show the
formation of a relativistic outflow with a Lorentz factor
.
Koide et al. (1999, 2000, 2002, 1998) and
Koide (2003) modeled the formation of axisymmetric jets in a system
consisting of an accretion disk and a rotating black hole. The simulations,
which cover a few rotational periods of the black hole, show the
formation of a relativistic outflow with a Lorentz factor
![]() .
A similar study but without any symmetry restrictions was carried
by Nishikawa et al. (2002, 2003). Jet
formation in the context of gamma-ray burst progenitors was considered
by Mizuno et al. (2004a,b) using a GRMHD code (and no specific
measures to maintain
.
A similar study but without any symmetry restrictions was carried
by Nishikawa et al. (2002, 2003). Jet
formation in the context of gamma-ray burst progenitors was considered
by Mizuno et al. (2004a,b) using a GRMHD code (and no specific
measures to maintain ![]() ). The evolution of magnetized
accretion tori around rotating black holes was investigated in
axisymmetry by Gammie et al. (2003) and De Villiers & Hawley (2003); De Villiers & Hawley (2003) including a CT
algorithm to keep the magnetic field divergence-free. While
Gammie et al. (2003) used a Godunov-type conservative scheme, De Villiers & Hawley (2003)
employed a ZEUS-like (i.e., non conservative) scheme to integrate the
GRMHD equations.
). The evolution of magnetized
accretion tori around rotating black holes was investigated in
axisymmetry by Gammie et al. (2003) and De Villiers & Hawley (2003); De Villiers & Hawley (2003) including a CT
algorithm to keep the magnetic field divergence-free. While
Gammie et al. (2003) used a Godunov-type conservative scheme, De Villiers & Hawley (2003)
employed a ZEUS-like (i.e., non conservative) scheme to integrate the
GRMHD equations.
In previous 2D RMHD simulations relativistic jets only served the purpose of demonstrating the capabilities of the RMHD code (e.g., Komissarov 1999a, in slab geometry; Del Zanna et al. 2003, assuming axial symmetry and using cylindrical coordinates), or the simulations only covered a very limited range of jet parameters (e.g., in Komissarov 1999b, only two models were considered both involving only toroidal fields). In the following we present the first comprehensive parameter study of the morphology and dynamics of magnetized relativistic axisymmetric jets including both toroidal and poloidal field configurations of different strength, and beam plasmas of different adiabatic index. Preliminary results of our research can be found in Leismann et al. (2004).
The paper is organized as follows. The basic equations and the numerical algorithm used in the code are discussed in Sect. 2. As we assume cylindrical symmetry in our simulations of relativistic magnetized jets, we give the explicit form of the corresponding equations in the Appendix A. Various tests our code has passed successfully are described in Appendix B. In Sect. 3 we discuss the simulation setup and the model parameters, and in Sect. 4 we present the results of our study. Finally, in Sect. 5 we discuss and interpret our findings, and point out some limitations of our approach.
In this section we describe the details of the numerical algorithm which we used to integrate the equations of ideal relativistic magnetohydrodynamics (Sect. 2.1). The numerical method is implemented on an upgraded version of GENESIS (Aloy et al. 1999b) and relies on the modular structure of its predecessor. As GENESIS, it is based on a directional-splitting, Godunov-type, finite-volume method, a series of intercell reconstruction routines and a method of lines for the time advance. The new code is second order accurate both in space and time, and relies on a constrained transport method (mainly based on the developments of Ryu et al. 1998) in order to keep (to machine precision) the magnetic field divergence-free throughout a simulation. Unlike GENESIS, the numerical fluxes at the cell interfaces are computed employing an HLL-type solver (Sect. 2.3.1) which uses as the maximum and minimum signal speeds some accurate estimates which are given in Sect. 2.2.1 together with the generic spectral decomposition and properties of the RMHD system of conservation laws. The combination of an HLL-like solver along with a high order spatial reconstruction and a consistently high order method to keep the divergence-free property of the magnetic field was proven to be useful to build RMHD algorithm by Del Zanna et al. (2003). Finally, a new algorithm to recover the primitive variables from the conserved ones has been implemented (Sect. 2.3.3).
The equations that describe the evolution of an ideal relativistic
magneto-fluid can be written in the form of conservation laws (see,
e.g., Anile 1989, for a full derivation of the equations), the
conservation of mass,
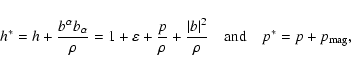 |
(4) |
Introducing the 3-velocity vector
vi=ui/u0 (Latin indices run
from 1 to 3, or x,y,z in Cartesian coordinates), the 4-velocity
![]() can be written as
can be written as
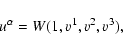 |
(6) |
| b0 | = | (7) | |
| bi | = | 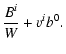 |
(8) |
The evolution of the magnetic field components is described by the
homogeneous Maxwell equation,
The time component of Eq. (9) becomes the usual
divergence constraint
Equations (1), (2) and (10), together with
the constraint (11) and the equation of state (EOS)
| (12) |
In the following we will use an ideal EOS with a constant adiabatic
index, ![]() :
:
The speed of sound, ![]() ,
can then be calculated from
(e.g. Landau & Lifshitz 1966)
,
can then be calculated from
(e.g. Landau & Lifshitz 1966)
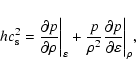 |
(16) |
The RMHD system of partial differential equations in a flat space-time
and in Cartesian coordinates can be cast in conservation form as
follows
Our method exploits a directional splitting algorithm to compute the
numerical fluxes across cell interfaces, i.e.,in each directional sweep
the changes of the variables due to fluxes in the orthogonal
directions are assumed to be zero. The fluxes along the sweep
direction are computed by solving a one dimensional system, e.g.,in the
x-sweep the system reads
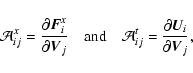 |
(25) |
Equation (24) yields a polynomial of degree seven, the
solution of which is non-trivial. Anile (1989) tackled the problem
using a fully covariant formulation of the RMHD system. The new
system, formed by ten evolution equations instead of seven, leads to
the appearance of three additional non-physical waves that have to be
discarded. The remaining seven waves are physical. The corresponding
eigenvalues can be found in, e.g., Anile (1989). The speeds
(eigenvalues) of the four magnetosonic (ms) waves (two slow and two
fast ones, sms and fms, respectively) are given by the roots of a
quartic polynomial in
![]() (C.1) which does not
have a simple analytic solution, i.e.,it has to be solved numerically
(Sect. 2.3.1).
(C.1) which does not
have a simple analytic solution, i.e.,it has to be solved numerically
(Sect. 2.3.1).
In RMHD there exist degeneracies where system (23) is
not strictly hyperbolic (for an extended discussion see, e.g.,
Komissarov 1999a). The two possible degenerate cases can be
characterized in terms of the components of the magnetic field
parallel (![]() )
and normal (
)
and normal (![]() )
to the Alfvén-wavefronts in the
fluid rest frame. Particularly, when
)
to the Alfvén-wavefronts in the
fluid rest frame. Particularly, when
![]() ,
the slow magnetosonic
and the waves propagate at the same speed as the entropy wave, it
is possible to find an analytic solution to the eigenvalue problem
Eq. (24) taking into account that, applied to the one
dimensional system (23),
,
the slow magnetosonic
and the waves propagate at the same speed as the entropy wave, it
is possible to find an analytic solution to the eigenvalue problem
Eq. (24) taking into account that, applied to the one
dimensional system (23),
![]() in the fluid rest
frame implies Bx = 0 in the laboratory frame, i.e.,the quartic
equation factors into two parts: a quadratic equation in
in the fluid rest
frame implies Bx = 0 in the laboratory frame, i.e.,the quartic
equation factors into two parts: a quadratic equation in ![]() whose
solutions are the two fast magnetosonic waves, and a trivial factor
whose
solutions are the two fast magnetosonic waves, and a trivial factor
![]() .
The complete set of eigenvalues is hence given by
.
The complete set of eigenvalues is hence given by
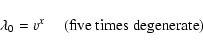 |
(26) |
In this section, we will describe the main ingredients of our numerical algorithm. We apply a method of lines (e.g., LeVeque 1991) to the equations written in conservation form. This method consists of a spatial discretization step during which the numerical fluxes (Sect. 2.3.1) and the source terms are computed using different types of inter cell reconstructions of the primitive variables (Sect. 2.3.2). Subsequently, the remaining system of semi-discrete ordinary differential equations is integrated in time using a multi-step Runge-Kutta algorithm developed by Shu & Osher (1988) which provides up to third order accuracy. Our implementation also includes a second order time accurate version of the algorithm. A set of test problems which have been successfully passed by the code are presented in Appendix B.
Numerical fluxes across cell interfaces are computed using the HLL
flux formula (Harten et al. 1983) similar as in Del Zanna et al. (2003) and
Gammie et al. (2003). The flux formula is based on the calculation of the
maximum speed of perturbations propagating into the states left and
right of the cell interface:
| (29) | |||
Although they are presently not implemented in our code, we have
explored several numerical and analytical methods (including the
method described in Abramowitz & Stegun 1965 and used by Del Zanna et al. 2003) to find
the four roots of the quartic Eq. (C.1). According
to our tests the best procedure is (1) to compute the two fast
magnetosonic wave speeds using a Newton-Raphson iteration scheme; then
(2) to reduce the quartic to a quadratic equation by polynomial
division; and finally (3) to obtain the two slow magnetosonic wave
speeds by a combination of Newton-Raphson iteration and bisection
schemes (Press et al. 1992). However, even this best procedure leads to
severe numerical problems for high Lorentz factors (
![]() ).
).
In the code we use the analytical solution for the left- and
right-propagating waves as given by Eq. (27)
(corresponding to the first degenerate case) for
![]() .
The resulting speeds are always smaller than the speed of light and
provide very good (i.e.,within
.
The resulting speeds are always smaller than the speed of light and
provide very good (i.e.,within ![]() )
lower and upper bounds to the
actual slowest and fastest magnetosonic wave speeds (as given by the
numerical solution of the quartic), respectively. Because of the
latter property (proved in Appendix C), the estimates
are ideally suited to be used in the HLL flux formula (28).
Our analytic estimates are more precise than
those reported by Gammie et al. (2003) obtained from the solution of an
approximate RMHD dispersion relation. The estimates of the maximum and
minimum eigenvalue are also used to compute the Courant time step
condition.
)
lower and upper bounds to the
actual slowest and fastest magnetosonic wave speeds (as given by the
numerical solution of the quartic), respectively. Because of the
latter property (proved in Appendix C), the estimates
are ideally suited to be used in the HLL flux formula (28).
Our analytic estimates are more precise than
those reported by Gammie et al. (2003) obtained from the solution of an
approximate RMHD dispersion relation. The estimates of the maximum and
minimum eigenvalue are also used to compute the Courant time step
condition.
The resulting HLL algorithm (as those of Del Zanna et al. 2003; and Gammie et al. 2003) is robust and very efficient computationally. The implementation of more refined Riemann solvers or flux formulas requiring the complete set of eigenvalues and eigenvectors (like, e.g., Balsara 2001; Komissarov 1999b; or Koldoba et al. 2002) is very difficult to realize because of the presence of the RMHD degeneracies discussed above. This may change once a consistent set of eigenvectors is found which can handle both non-degenerate and degenerate states.
In order to increase the spatial order of the accuracy of the code, we have implemented two algorithms for reconstructing variables within numerical cells.
We use a modified version of the minmod linear interpolation
algorithm (e.g., LeVeque 1991) for the one dimensional
reconstruction of the variables within cells. If a is one of the
variables to be reconstructed and ak is its value in zone k, we
construct the slopes ![]() :
:
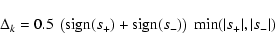 |
(30) |
| (32) | |||
| (33) |
In the x sweep the reconstruction procedure just described is
applied to the variables
![]() .
Interpolating the logarithms of density and pressure reduces
the magnitude of the jumps at cell interfaces with large gradients of
density and/or pressure. Finally, and here is where the modification
with respect to the standard minmod algorithm takes place, we limit
the absolute value of the slope to 2 when interpolating
.
Interpolating the logarithms of density and pressure reduces
the magnitude of the jumps at cell interfaces with large gradients of
density and/or pressure. Finally, and here is where the modification
with respect to the standard minmod algorithm takes place, we limit
the absolute value of the slope to 2 when interpolating ![]() and
and ![]() in those zones where the magnetization parameter
in those zones where the magnetization parameter ![]() (14)
is larger than a certain threshold (between 4 and 10
in our applications). Reconstruction of Bx is unnecessary in the
x sweep, as the magnetic field is originally defined on a staggered
grid (see Sect. 2.3.4). In the y and z sweep the
primitive variables are reconstructed in a similar way, but permuting
the indices (x,y,z) cyclically.
(14)
is larger than a certain threshold (between 4 and 10
in our applications). Reconstruction of Bx is unnecessary in the
x sweep, as the magnetic field is originally defined on a staggered
grid (see Sect. 2.3.4). In the y and z sweep the
primitive variables are reconstructed in a similar way, but permuting
the indices (x,y,z) cyclically.
From the original relativistic version of the PPM algorithm of Martí & Müller (1996) we only adopt the cell reconstruction in order to construct monotonic parabola. For each zone k the quartic polynomial is obtained, which has zone-averaged values ak-2, ak-1, ak, ak+1 and ak+2, where a is the variable to be reconstructed (the same as in the PLM algorithm). The polynomial interpolates the structure inside the zone, and provides the values at the left and right interface of the zone, aL,k and aR,k. These reconstructed values are then modified such that the parabolic profile defined by aL,k, aR,k and ak is monotonic inside the zone. The modified interpolated values at the zone interfaces define local Riemann problems which are solved by Eq. (28). Near contact discontinuities the interpolation procedure is slightly modified to produce narrower jumps. In the vicinity of shocks the scheme switches (locally) to a piecewise constant approximation in order to avoid spurious post shock oscillations (Appendix I in Martí & Müller 1996). The original relativistic hydrodynamic algorithms for the detection of contact discontinuities and shocks can also be used in RMHD provided the character of the discontinuity does not change in the presence of a magnetic field: in a shock there is a jump of the thermal pressure accompanied by a negative value of the divergence of the velocity field and, in a contact discontinuity there is a jump in density without change of normal velocity.
The code evolves the conserved quantities
![]() ,
but not the primitive variables
,
but not the primitive variables
![]() .
Therefore, an algorithm is required which computes the latter from the
zone-averaged values of the former set. Since the conserved quantities
can be written in terms of the primitives in an analytic closed form,
but not the other way around, one has to employ iterative algorithms
to compute the primitive variables.
.
Therefore, an algorithm is required which computes the latter from the
zone-averaged values of the former set. Since the conserved quantities
can be written in terms of the primitives in an analytic closed form,
but not the other way around, one has to employ iterative algorithms
to compute the primitive variables.
We use Eqs. (21) and (13) to construct two
functions
![]() and
and
![]() depending on the Lorentz
factor W and the variable
depending on the Lorentz
factor W and the variable
![]() (the
inertial rest mass density for an ideal gas),
(the
inertial rest mass density for an ideal gas),
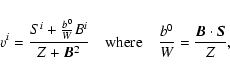 |
(36) |
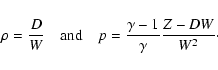 |
(37) |
This recovery scheme yields physical results for a wide range of
parameters. Using in FORTRAN double-precision arithmetics, for an
initial guess which differs from the solution by less than about
![]() ,
a tolerance of 10-8, and magnetic fields of the order of
10-5, the recovery provides physical solutions (expressed in code
units) for
10-10 < p < 108,
,
a tolerance of 10-8, and magnetic fields of the order of
10-5, the recovery provides physical solutions (expressed in code
units) for
10-10 < p < 108,
![]() ,
and
1
< W < 104. For stronger fields these intervals get smaller, while
for smaller fields they become larger. If no magnetic field is
present, the recovery works for density and pressure values as low as
10-17 up to W=104. It also works for strong magnetic fields,
if
,
and
1
< W < 104. For stronger fields these intervals get smaller, while
for smaller fields they become larger. If no magnetic field is
present, the recovery works for density and pressure values as low as
10-17 up to W=104. It also works for strong magnetic fields,
if ![]() ,
or in general if the magnetic energy density and the
Poynting flux do not much exceed the internal plus kinetic energy
density and the hydrodynamic momentum fluxes, respectively. The
parameter range where the recovery algorithm works properly widens
when better initial values are available for the iterative procedure.
,
or in general if the magnetic energy density and the
Poynting flux do not much exceed the internal plus kinetic energy
density and the hydrodynamic momentum fluxes, respectively. The
parameter range where the recovery algorithm works properly widens
when better initial values are available for the iterative procedure.
The equations for the rest mass, momentum and energy are integrated
using the numerical fluxes given in Eq. (28),
while the equations for the magnetic field are evolved in a different
way in order to keep ![]() during the simulation. The latter
constraint is not trivially fulfilled although it is implicitly
encoded in the RMHD Eqs. (19). To guarantee
the constraint also numerically, we use the constrained transport (CT)
method developed by Evans & Hawley (1988) and adapted to Godunov-type schemes
by Ryu et al. (1998), which keeps
during the simulation. The latter
constraint is not trivially fulfilled although it is implicitly
encoded in the RMHD Eqs. (19). To guarantee
the constraint also numerically, we use the constrained transport (CT)
method developed by Evans & Hawley (1988) and adapted to Godunov-type schemes
by Ryu et al. (1998), which keeps ![]() up to machine precision, but
which has the disadvantage that it is at most second order accurate in
space (see, Londrillo & Del Zanna (2004) for higher order implementations of the
divergence free condition).
up to machine precision, but
which has the disadvantage that it is at most second order accurate in
space (see, Londrillo & Del Zanna (2004) for higher order implementations of the
divergence free condition).
We define two sets of magnetic field vectors (for the sake of clarity we will restrict ourselves here to the algorithm for two dimensional problems):
The zone centered vector
![]() ,
which is required for setting the
boundary conditions, and for calculating the source terms and the
fluxes of the other variables, is computed in every sweep by a simple
interpolation from the staggered field components
,
which is required for setting the
boundary conditions, and for calculating the source terms and the
fluxes of the other variables, is computed in every sweep by a simple
interpolation from the staggered field components
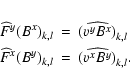
At the boundaries the computational grid is extended by up to four so-called ghost zones which serve to enforce the boundary conditions for the primitive variables before the spatial interpolation is performed. The number of ghost zones employed in this process depends on the order of the spatial interpolation algorithm (one for PLM, four in case for our implementation of PPM).
A second boundary routine is called after the dimensional sweeps to
set the boundary values for the fluxes associated to the magnetic
field components. These fluxes only need to be fixed in the first
ghost zone (see Eq. (42)), e.g.,when computing
![]() one has to prescribe both
one has to prescribe both
![]() and
and
![]() .
Usually fluxes at the ghost zone are
set in such a way that zero flux gradients are enforced.
.
Usually fluxes at the ghost zone are
set in such a way that zero flux gradients are enforced.
All jet simulations in this work are performed on a 2D equidistant grid in cylindrical coordinates, (r,z), assuming axisymmetry. The simulations themselves are 2.5-dimensional as we evolve all three spatial components of vectors using Eqs. (A.2)-(A.9), and thus include a toroidal magnetic field and flow velocity.
The simulated jets are produced by injecting beam matter into the grid
along the z axis through a nozzle of radius ![]() (the beam
radius) at z=0. Outside the nozzle, i.e.,for
(the beam
radius) at z=0. Outside the nozzle, i.e.,for
![]() and z=0 we
impose special reflecting boundary conditions assuming that the axial
and toroidal velocity and field components are mirrored. This is
justified by the presence of a twin counterjet in actual radio
galaxies, and eliminates the Lorentz force in the equatorial plane.
The assumed axisymmetry implies reflecting boundary conditions on the
symmetry axis at r = 0, where the radial and toroidal velocity and
magnetic field components are mirrored, i.e.,they are zero at zero
radius. At the two outer edges of the grid at
and z=0 we
impose special reflecting boundary conditions assuming that the axial
and toroidal velocity and field components are mirrored. This is
justified by the presence of a twin counterjet in actual radio
galaxies, and eliminates the Lorentz force in the equatorial plane.
The assumed axisymmetry implies reflecting boundary conditions on the
symmetry axis at r = 0, where the radial and toroidal velocity and
magnetic field components are mirrored, i.e.,they are zero at zero
radius. At the two outer edges of the grid at
![]() and
and
![]() ,
respectively, we impose zero gradient boundary
conditions. Material is allowed to freely leave the grid there.
,
respectively, we impose zero gradient boundary
conditions. Material is allowed to freely leave the grid there.
Initially the computational domain is filled with a uniform medium at rest having the same thermal pressure and adiabatic index as the jet. The initial magnetic field configuration depends on the type of simulation.
Every jet simulation is fully specified by setting the following independent parameters:
We point out here that there are three ways for a magnetized jet to be
relativistic. First, when the flow velocity is close to c, and
therefore the Lorentz factor of the flow is much larger than
one. Second, when the beam plasma is hot, i.e.,
![]() such
that
such
that
![]() and the sound speed (17) are relativistic
approaching the maximum value
and the sound speed (17) are relativistic
approaching the maximum value
![]() (
(![]() 0.58c for
0.58c for
![]() ,
and
,
and ![]() 0.83c for
0.83c for
![]() ). In this
case, the internal beam Mach number,
). In this
case, the internal beam Mach number, ![]() ,
approaches the minimum
value for a given
,
approaches the minimum
value for a given ![]() (
(
![]() for
for
![]() ,
and
,
and
![]() for
for
![]() ). Finally, when
). Finally, when
![]() such that
such that
![]() ,
and when
,
and when
![]() ,
the speed (18) is
close to c.
,
the speed (18) is
close to c.
When simulating a jet with a non-uniform magnetic field, the
magnetization parameter of the beam is given by the average value,
![]() ,
across the beam. In our simulations of jets with purely
toroidal magnetic fields presented below we have assumed the same
profile for the magnetic field as Lind et al. (1989) and Komissarov (1999b),
corresponding to a beam in transverse hydromagnetic equilibrium with a
core of uniform electric current with radius
,
across the beam. In our simulations of jets with purely
toroidal magnetic fields presented below we have assumed the same
profile for the magnetic field as Lind et al. (1989) and Komissarov (1999b),
corresponding to a beam in transverse hydromagnetic equilibrium with a
core of uniform electric current with radius ![]() - the
magnetization radius - and a shell without any current. The
(toroidal) magnetic field in the beam,
- the
magnetization radius - and a shell without any current. The
(toroidal) magnetic field in the beam,
![]() ,
is then given by
,
is then given by
Averaging (44) over the beam cross section at the
nozzle and dividing by the uniform thermal beam pressure, ![]() ,
yields
,
yields
In the simulations with purely poloidal magnetic fields we have chosen
a simpler initial setup. The grid is initially filled with a uniform
axial magnetic field,
![]() ,
which according to the definitions of
,
which according to the definitions of
![]() and
and ![]() is given by
is given by
Besides the analysis and comparison of the distributions of rest-mass density, flow velocity, magnetic field lines, etc. for the different models, we introduce a number of global quantities that are used to characterize some morphodynamical aspects of the models. These quantities are:
A one dimensional estimate for the head advance speed of a
non-magnetized, relativistic jet can be obtained by equating the
momentum flux of the beam and the ambient gas in the frame of the
working surface (Martí et al. 1997):
The evolution of 2D jets can be divided into two phases (Scheck et al. 2002): (1) a 1D phase where the velocity is constant and approximated by (47); and (2) a 2D phase where 2D effects become important and the jet decelerates. The 2D phase begins when the first major vortex shedding occurs at the terminal Mach disk.
We have selected three of the jet models of Martí et al. (1997) to study
the effects of magnetic fields on the dynamics and morphology of
relativistic jets. All three jets are light (![]() ), supersonic,
cold (
), supersonic,
cold (
![]() ), and the gas pressure is matched with that of the
ambient medium. In the toroidal field models the magnetization radius
is
), and the gas pressure is matched with that of the
ambient medium. In the toroidal field models the magnetization radius
is
![]() ,
and the magnetic field (44) is
injected with the beam into a uniform, non-magnetized medium. In the
poloidal field simulations, the whole grid is filled with a uniform,
purely axial magnetic field of the same strength as that injected with
the beam according to Eq. (46). The other parameters
of the external medium are identical to those of the toroidal field
models. The simulations are performed on a uniform grid of
,
and the magnetic field (44) is
injected with the beam into a uniform, non-magnetized medium. In the
poloidal field simulations, the whole grid is filled with a uniform,
purely axial magnetic field of the same strength as that injected with
the beam according to Eq. (46). The other parameters
of the external medium are identical to those of the toroidal field
models. The simulations are performed on a uniform grid of
![]() zones covering a domain of
zones covering a domain of
![]() beam radii, i.e.,the resolution is
beam radii, i.e.,the resolution is
![]() .
We point out that this numerical resolution is equivalent to that of
Martí et al. (1997), who used a third order algorithm (but only
.
We point out that this numerical resolution is equivalent to that of
Martí et al. (1997), who used a third order algorithm (but only
![]() ), while we only use a second order accurate one. Thus,
as in Martí et al. (1997), the most prominent supersonic structures are
properly resolved. Of course, even better numerical resolution would
be required to study problems like the mass entrainment in the jet or
the mixing of beam and ambient plasma in the cavity of the generated
jets. The purely hydrodynamic and the toroidal field models are
simulated with PLM spatial interpolation, while the poloidal field
runs employ PPM interpolation (although in both cases the two spatial
interpolations could have been used indistinctly; see Appendix B).
All models are evolved until the head of the jet reaches the opposite
edge of the computational domain.
), while we only use a second order accurate one. Thus,
as in Martí et al. (1997), the most prominent supersonic structures are
properly resolved. Of course, even better numerical resolution would
be required to study problems like the mass entrainment in the jet or
the mixing of beam and ambient plasma in the cavity of the generated
jets. The purely hydrodynamic and the toroidal field models are
simulated with PLM spatial interpolation, while the poloidal field
runs employ PPM interpolation (although in both cases the two spatial
interpolations could have been used indistinctly; see Appendix B).
All models are evolved until the head of the jet reaches the opposite
edge of the computational domain.
Table 1:
Overview of the simulated models: the columns give from
left to right the name of the model, the type of the
initial field configuration, the adiabatic index ![]() ,
the beam speed
,
the beam speed ![]() ,
the proper beam Mach number
,
the proper beam Mach number
![]() ,
the average magnetization parameter
,
the average magnetization parameter
![]() ,
and the ratio of the magnetic energy density and the rest
mass density
,
and the ratio of the magnetic energy density and the rest
mass density ![]() .
.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{2520fg01.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg192.gif) |
Figure 1:
Snapshots of the logarithm of the rest mass density of
models C2-0, C2-1/20, C2-1 and C2-10/3 at
|
| Open with DEXTER | |
For our models (see Table 1) we use the same
model names as Martí et al. (1997) extended by suffixes describing the
magnetic field strength. For example, the toroidal field model of
series C2 with an average magnetization of 1 (i.e.,the equipartition
model) is called C2-1, and the corresponding poloidal field model is
called C2-pol-1. The model corresponding to the pure hydrodynamic case
is named C2-0. All models have
![]() ,
i.e.,they have a low
Poynting flux. The models of series B1 and C2 only differ in the
adiabatic index
,
i.e.,they have a low
Poynting flux. The models of series B1 and C2 only differ in the
adiabatic index ![]() ,
and those of series C1 and C2 only in the
beam velocity
,
and those of series C1 and C2 only in the
beam velocity ![]() .
The toroidal velocity at injection is zero in all
models, which together with the chosen initial magnetic field
configurations prevent the models from generating additional
components of magnetic field and flow velocity in the course of
evolution.
.
The toroidal velocity at injection is zero in all
models, which together with the chosen initial magnetic field
configurations prevent the models from generating additional
components of magnetic field and flow velocity in the course of
evolution.
Our boundary condition at z=0 (reflecting outside the nozzle, see previous section) differs from that of Martí et al. (1997) (zero gradients outside the jet nozzle), as does the Riemann solver and the reconstruction procedure. Therefore, the results of our purely hydrodynamic reference simulations are slightly different from their results. We choose the reflecting boundary conditions in order to avoid that a large part of the energy contained in the back flow leaves the grid. This boundary condition is also consistent with that of more recent jet simulations, like e.g., Scheck et al. (2002) and Krause (2003).
![\begin{figure}
\par\includegraphics[width=11cm,clip]{2520fg02.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg194.gif) |
Figure 2: Same as Fig. 1 but showing snapshots of the Lorentz factor and the flow field. |
| Open with DEXTER | |
Besides the field topology the setup of the toroidal and the poloidal
field models differs in other aspects, too. In the toroidal field
models ![]() is injected together with the beam flow into a domain
filled with a non-magnetized medium. In the poloidal case, however,
the computational domain initially already contains a magnetic field
of the same strength as that injected with the beam. Hence, in the
poloidal field models both the total pressure p* (as in the
toroidal field models) and the thermal pressure p are matched at the
beam surface, p being uniform and the same inside the beam and in
the ambient medium. In contrast, the toroidal field models have a
negative radial gradient in p*, which is compensated by the
magnetic tension.
is injected together with the beam flow into a domain
filled with a non-magnetized medium. In the poloidal case, however,
the computational domain initially already contains a magnetic field
of the same strength as that injected with the beam. Hence, in the
poloidal field models both the total pressure p* (as in the
toroidal field models) and the thermal pressure p are matched at the
beam surface, p being uniform and the same inside the beam and in
the ambient medium. In contrast, the toroidal field models have a
negative radial gradient in p*, which is compensated by the
magnetic tension.
All jet simulations were carried out on an IBM p690 Regatta computer and required between 8 and 30 h on a shared memory node with 32 Power4 1300 MHz processors.
The most remarkable result we find is that different from classical MHD simulations (e.g., Lind et al. 1989) the inclusion of a magnetic field leads to diverse effects which do not always scale linearly with the relative strength of the field. There are, however, some clear trends which we will discuss in detail below.
Figures 1 and 2 show the rest mass
density and the Lorentz factor of the purely hydrodynamic model C2-0,
and those of the toroidal field models C2-1/20, C2-1 and C2-10/3 (from
top to bottom), respectively. Apart from differences in details, one
morphological feature is particularly noticeable: with growing
toroidal field strength, the supersonic part of the beam ends further
behind the leading edge of the bow shock (note the steep decline of
the Lorentz factor near the head of the jet in Fig. 2),
i.e.,the jet becomes transonic much closer to the origin. The high
density and pressure structure between the termination of the
supersonic beam at the Mach disk and the head of the jet is called
nose cone (Clarke et al. 1986) or plug (Lind et al. 1989) (e.g.,
the region around the axis between 28 and 46 beam radii in the bottom
panel of Fig. 1). The nose cone is made up of beam
material that it is not deflected backwards into the cocoon, and of
entrained ambient material near its rear end. Both the density and
the pressure in the nose cone are very high, and show indications of
turbulence. Moreover, the pressure in the nose cone is relatively
smooth and particularly high on the axis (due to magnetic confinement)
where it can reach values ![]() 103 times larger than that of the
external medium. The nose cone makes the head of the jet appear
narrower for larger values of
103 times larger than that of the
external medium. The nose cone makes the head of the jet appear
narrower for larger values of
![]() .
.
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{2520fg03.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg196.gif) |
Figure 3:
Snapshots of the magnetization parameter |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{2520fg04.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg199.gif) |
Figure 4:
Snapshots of the logarithm of the pressure for all the
models having a toroidal field with
|
| Open with DEXTER | |
In the cocoon, close to the head of the jet, a number of organized
structures appear as a result of the dynamic effects of the toroidal
field. The magnetic field confines and suppresses the development of
Kelvin-Helmholtz instabilities at the interface cocoon/shocked ambient
medium, and the material deflected into the cocoon after passing the
Mach disk starts to fill a low density bubble. With increasing
toroidal field strength the bubble grows larger in size. In model
C2-10/3 it roughly stretches from
![]() up to
up to
![]() ,
and
is confined by a shell of highly magnetized material
(Fig. 3). The Mach disk and the terminal shock of the
beam reside in the middle of the bubble. The beam flow is terminated
at the Mach disk, and matter has to flow around it to reach the head
of the jet (Fig. 2). In model C2-1 the shocked flow
around the Mach disk reaches relativistic speeds with Lorentz factors
of 3 and more. The average beam Lorentz factor decreases with
increasing magnetization of the beam.
,
and
is confined by a shell of highly magnetized material
(Fig. 3). The Mach disk and the terminal shock of the
beam reside in the middle of the bubble. The beam flow is terminated
at the Mach disk, and matter has to flow around it to reach the head
of the jet (Fig. 2). In model C2-1 the shocked flow
around the Mach disk reaches relativistic speeds with Lorentz factors
of 3 and more. The average beam Lorentz factor decreases with
increasing magnetization of the beam.
In models C2-1 and C2-10/3 the magnetization ![]() (Fig. 3) decreases drastically across the first cross
shock due to an increase in the thermal pressure
(Fig. 4). It remains low inside the beam up to the
terminal shock, increases downstream of this shock, and becomes even
larger when the shocked plasma begins to flow away radially from the
jet axis. The pinching force provided by the toroidal field in that
region suppresses any further sideways expansion of the jet, and
pushes a large fraction of the plasma into the nose cone. In model
C2-10/3 this pinching is strongest at
(Fig. 3) decreases drastically across the first cross
shock due to an increase in the thermal pressure
(Fig. 4). It remains low inside the beam up to the
terminal shock, increases downstream of this shock, and becomes even
larger when the shocked plasma begins to flow away radially from the
jet axis. The pinching force provided by the toroidal field in that
region suppresses any further sideways expansion of the jet, and
pushes a large fraction of the plasma into the nose cone. In model
C2-10/3 this pinching is strongest at
![]() (see the bottom
panel of Fig. 2). The nose cone contains primarily
highly magnetized plasma which leads to a strong pinching force
confining the flow close to the axis. The magnetic field accumulates
at the inside of the high density shell (the shroud of
Lind et al. 1989) of the jet, where the thermal pressure is low and
(see the bottom
panel of Fig. 2). The nose cone contains primarily
highly magnetized plasma which leads to a strong pinching force
confining the flow close to the axis. The magnetic field accumulates
at the inside of the high density shell (the shroud of
Lind et al. 1989) of the jet, where the thermal pressure is low and ![]() is large (Fig. 3). This magnetized shell
will influence the emission properties of the radio lobes in actual
sources, as it contains the largest and most ordered return current
(Fig. 4, top panel), which occurs because there is
no confining field in the ambient medium, and because this environment
behaves as a perfect conductor (Begelmann et al. 1984). However, the structure
of the return current becomes highly anisotropic throughout the cocoon
and at the surface of the jet. The magnetic field itself is largest
in the beam and in the nose cone (see the two bottom panels of
Fig. 3).
is large (Fig. 3). This magnetized shell
will influence the emission properties of the radio lobes in actual
sources, as it contains the largest and most ordered return current
(Fig. 4, top panel), which occurs because there is
no confining field in the ambient medium, and because this environment
behaves as a perfect conductor (Begelmann et al. 1984). However, the structure
of the return current becomes highly anisotropic throughout the cocoon
and at the surface of the jet. The magnetic field itself is largest
in the beam and in the nose cone (see the two bottom panels of
Fig. 3).
![\begin{figure}
\par\includegraphics[width=11cm,clip]{2520fg05.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg204.gif) |
Figure 5:
Snapshots of the poloidal field model C2-pol-1 at
|
| Open with DEXTER | |
Figure 5 shows the rest mass density, the Lorentz
factor with the flow field, the logarithm of the modulus of the
magnetic field with the field lines superimposed, and the
magnetization parameter ![]() for the poloidal field model
C2-pol-1. Although the overall morphology and structure of the jet and
the cocoon of this model are very similar to those of other models of
series C2, there are a number of striking differences. In particular,
we will compare model C2-pol-1 both with the hydrodynamic model C2-0
and the toroidal field model having the same magnetization (C2-1).
for the poloidal field model
C2-pol-1. Although the overall morphology and structure of the jet and
the cocoon of this model are very similar to those of other models of
series C2, there are a number of striking differences. In particular,
we will compare model C2-pol-1 both with the hydrodynamic model C2-0
and the toroidal field model having the same magnetization (C2-1).
First of all, instead of forming a narrow nose cone structure, the beam broadens close to its termination point giving the head of the jet a hammer-like appearance caused by the emission of vortices from the head of the jet. The beam plasma flows along the field lines up to the head of the jet, where it is deflected to form a cocoon (second panel of Fig. 5) dragging along the magnetic lines.
Model C2-pol-1 also differs from all the other models in the strength
of the cross shocks on the axis. While the first cross shock in model
C2-pol-1 occurs much nearer to the nozzle (at
![]() )
than in
model C2-0, it is also much weaker (the density contrast is
)
than in
model C2-0, it is also much weaker (the density contrast is ![]() 8
and
8
and ![]() 3 times smaller than in models C2-10/3 and C2-1,
respectively) and has the least extended post-shock region (in axial
direction) of all models. Downstream of this shock, the beam pressure
and density remain low (below
3 times smaller than in models C2-10/3 and C2-1,
respectively) and has the least extended post-shock region (in axial
direction) of all models. Downstream of this shock, the beam pressure
and density remain low (below ![]()
![]() )
until the flow reaches the
second cross shock, which is weak compared to those of the other
models, too. It is especially weak compared to the toroidal field
model with the same average
)
until the flow reaches the
second cross shock, which is weak compared to those of the other
models, too. It is especially weak compared to the toroidal field
model with the same average ![]() .
This behavior results from the
increase of the radially (outward) directed magnetic tension force
which straightens the poloidal field lines, which are bent towards the
axis due to external radial pressure forces and thereby repel waves
driven into the beam. Thus, during the whole evolution the beam
remains much less affected by shocks than in the models with toroidal
magnetic fields. The terminal shock, however, is as strong as in
model C2-1 or C2-0. Furthermore, the value of
.
This behavior results from the
increase of the radially (outward) directed magnetic tension force
which straightens the poloidal field lines, which are bent towards the
axis due to external radial pressure forces and thereby repel waves
driven into the beam. Thus, during the whole evolution the beam
remains much less affected by shocks than in the models with toroidal
magnetic fields. The terminal shock, however, is as strong as in
model C2-1 or C2-0. Furthermore, the value of ![]() decreases with
increasing axial distance along the beam in model C2-pol-1
(Fig. 5) while it is rather uniform in model C2-1.
decreases with
increasing axial distance along the beam in model C2-pol-1
(Fig. 5) while it is rather uniform in model C2-1.
The cocoon is also much more homogeneous in model C2-pol-1 than in the other models of series C2, which is especially apparent when comparing the rest mass density snapshots in Figs. 1 and 5. The poloidal field model shows much less turbulent structure, and the back flow of beam material through the cocoon is almost straight (Fig. 5, third panel) indicating that the poloidal magnetic field reduces or completely suppresses the development of Kelvin-Helmholtz instabilities at the surface between the cocoon and the shroud. This is very different in the toroidal field and purely hydrodynamic cases, where the back flow is less ordered.
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[angle=0, scale=0.31]{2...
...
\includegraphics[angle=0, scale=0.31]{2520f06f.eps} \end{tabular} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg212.gif) |
Figure 6:
Average thermal pressure
|
| Open with DEXTER | |
In model C2-pol-1 the magnetic field is almost completely expelled
from the cocoon. The third panel of Fig. 5 shows that
the absolute value of the field strength remains very low. The narrow
dark filaments in the cavity interior of model C2-pol-1
(Fig. 5, third panel from top) trace the magnetopauses,
i.e.,the surfaces where the magnetic field changes direction and hence
is zero. The magnetopauses are surrounded by areas of high magnetic
field strength giving rise to the extended, twisted filaments. The
magnetization parameter (Fig. 5, bottom panel) is
nearly zero everywhere within the jet, because the magnetic field is
advected out the cavity by the fluid flow, and accumulates in the
shroud with its large thermal pressure yielding a low value of ![]() (compared to e.g.,model C2-1). This differs from the behavior of
models with toroidal magnetic fields where the magnetic tension
prevents a strong reduction of the magnetic field in the cavity.
(compared to e.g.,model C2-1). This differs from the behavior of
models with toroidal magnetic fields where the magnetic tension
prevents a strong reduction of the magnetic field in the cavity.
![\begin{figure}
\par\includegraphics[angle=90, scale=1.0]{2520f07a.eps} \includeg...
...]{2520f07b.eps} \includegraphics[angle=90, scale=1.0]{2520f07c.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg213.gif) |
Figure 7: Motion of the head of the jet for all computed models. The solid lines correspond to the 1D velocity estimate given by Eq. (47). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90, scale=1.0]{2520f08a.eps} \includeg...
...]{2520f08b.eps} \includegraphics[angle=90, scale=1.0]{2520f08c.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg214.gif) |
Figure 8:
Temporal change of the cylindric aspect ratio |
| Open with DEXTER | |
The top panel of Fig. 7 displays the motion of the jet's head for all models of series C2 and a straight line corresponding to the 1D velocity estimate given by Eq. (47). Apart from model C2-10/3 the jet propagates at essentially the same speed in all models. The 1D estimate gives a very good approximation to the speed in the 1D phase, and becomes an upper bound in the 2D phase. The small differences between the analytic estimate for non-magnetized jets and the actual simulation values are due to the fact that the jets are cold. Even the equipartition magnetic energy density (model C2-1) is still very small compared to the ram pressure at the head of the jet. Remarkably, there is no simple dependence of the propagation speed on the magnetic field strength: in model C2-10/3 the jet propagates fastest, in model C2-1 slowest, in model C2-1/20 second fastest, and the remaining models fall in between. The propagation speed of magnetized jets is determined by a number of competing effects related to both the strength and the topology of the magnetic field. However, our simulations do not show a clear trend with these two parameters, i.e.,the speed depends on both parameters nonlinearly. The high speed of model C2-10/3 can be explained by its large nose cone.
The speed of propagation of the Mach disk, ![]() (which corresponds,
approximately, to the speed of propagation of the jet without
considering the nose cone) tends to decrease with increasing
magnetization (Table 2). In the hydrodynamic model C2-0,
(which corresponds,
approximately, to the speed of propagation of the jet without
considering the nose cone) tends to decrease with increasing
magnetization (Table 2). In the hydrodynamic model C2-0,
![]() is slightly smaller than in the weakly magnetized model. This
trend also holds for the models of series B1, but not for those of
series C1.
is slightly smaller than in the weakly magnetized model. This
trend also holds for the models of series B1, but not for those of
series C1.
Table 2:
Propagation velocity of the Mach disc (![]() )
for
models with a toroidal magnetic field.
)
for
models with a toroidal magnetic field.
Figure 8 shows the cylindrical aspect ratio of all models as a function of time. As the jet reaches the radial grid boundary in models C1 and C2 before the end of the simulation, the aspect ratio approaches that of the grid, which is about 5. This and the fact that the differences among the models are smaller than those for a computational domain containing the whole cavity, makes one to interpret these plots with caution. Nevertheless, our explanation for the high propagation speed of model C2-10/3 is further supported by its large aspect ratio. The other models do not show any trend.
The average thermal pressure
![]() (defined as
(defined as
![]() )
of the
more strongly magnetized models (poloidal or toroidal) of series C2 is
up to 4 times larger inside the beam at
)
of the
more strongly magnetized models (poloidal or toroidal) of series C2 is
up to 4 times larger inside the beam at
![]() than in
the corresponding hydrodynamic model C2-0 (Fig. 6).
The pressure distributions show a distinct maximum at the beam axis
instead of being flat there and leveling off at larger radii as
predicted by Begelmann et al. (1984). This difference arises because in our
simulations the magnetization radius
than in
the corresponding hydrodynamic model C2-0 (Fig. 6).
The pressure distributions show a distinct maximum at the beam axis
instead of being flat there and leveling off at larger radii as
predicted by Begelmann et al. (1984). This difference arises because in our
simulations the magnetization radius ![]() is smaller than the jet
radius (
is smaller than the jet
radius (
![]() ), while Begelmann et al. (1984) assume a jet with a
uniform current along the whole beam, i.e.,
), while Begelmann et al. (1984) assume a jet with a
uniform current along the whole beam, i.e.,
![]() .
Our
simulations further show that the average thermal pressure
.
Our
simulations further show that the average thermal pressure
![]() can be dominated by the contributions of the hotspot
and/or the nose cone, while Begelmann et al. (1984) exclude these regions from
their analysis. Just outside the beam (
can be dominated by the contributions of the hotspot
and/or the nose cone, while Begelmann et al. (1984) exclude these regions from
their analysis. Just outside the beam (
![]() )
the
radial distribution of
)
the
radial distribution of
![]() is quite flat in all models
of series C2 (except of model C2-10/3), and declines at larger radii
(
is quite flat in all models
of series C2 (except of model C2-10/3), and declines at larger radii
(
![]() ). Thus, the jets have a core-sheath structure in radial
direction. The radial pressure gradient is larger in model C2-10/3
than in any other model of series C2 and seems to decrease
monotonically with decreasing magnetization. Beyond some typical
radius (
). Thus, the jets have a core-sheath structure in radial
direction. The radial pressure gradient is larger in model C2-10/3
than in any other model of series C2 and seems to decrease
monotonically with decreasing magnetization. Beyond some typical
radius (![]()
![]() )
)
![]() as a function of rbecomes very similar (almost flat) for all the models. Also the
thermal pressure gradients (
as a function of rbecomes very similar (almost flat) for all the models. Also the
thermal pressure gradients (![]() )
approach to zero beyond
)
approach to zero beyond
![]()
![]() .
The behavior of model C2-pol-1 is different from
that of the models transporting toroidal fields. Its average thermal
pressure is smaller than that in the hydrodynamic model C2-0 at all
radii.
.
The behavior of model C2-pol-1 is different from
that of the models transporting toroidal fields. Its average thermal
pressure is smaller than that in the hydrodynamic model C2-0 at all
radii.
The high compression of the beam in models carrying a toroidal
magnetic field is the result of the imposed magnetic field structure
in the beam (Eq. (44)). Up to the magnetization
radius ![]() ,
,
![]() grows linearly with radius, i.e.,the pressure
necessary to keep hydromagnetic equilibrium for
grows linearly with radius, i.e.,the pressure
necessary to keep hydromagnetic equilibrium for
![]() is
(e.g. Lind et al. 1989)
is
(e.g. Lind et al. 1989)
![\begin{figure}
\par\includegraphics[width=11cm,clip]{2520fg09.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg228.gif) |
Figure 9:
Snapshots of the logarithm of the rest mass density of
models B1-0, B1-1/20, B1-1 and B1-10/3 at
|
| Open with DEXTER | |
Models C2-1/20, C2-1 and C2-10/3 which transport toroidal magnetic
fields are confined by the toroidal fields in the beam and in the
cocoon. In the cocoon the density profile rearranges itself in such a
way that the toroidal field decreases nearly linearly with radius
(note that this scaling does not hold inside the magnetization radius
![]() ). The radial distribution of the axial average of the net radial
force
). The radial distribution of the axial average of the net radial
force
![]() (Fig. 6) displays two distinct regions in case of
models with toroidal fields (for model C2-pol-1
(Fig. 6) displays two distinct regions in case of
models with toroidal fields (for model C2-pol-1
![]() ): (1) an internal (contractive region up to
): (1) an internal (contractive region up to ![]()
![]() )
where
)
where
![]() and where the gas in the beam
and its neighborhood is pinched; and (2) an external (expansive
region), where
and where the gas in the beam
and its neighborhood is pinched; and (2) an external (expansive
region), where
![]() because the thermal pressure
gradient dominates the magnetic tension force.
because the thermal pressure
gradient dominates the magnetic tension force.
![\begin{figure}
\par\includegraphics[width=11.2cm,clip]{2520fg10.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg232.gif) |
Figure 10: Same as Fig. 9 but showing snapshots of the Lorentz factor and the flow field. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.2cm,clip]{2520fg11.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg233.gif) |
Figure 11:
Snapshots of the magnetization parameter |
| Open with DEXTER | |
The results of the non-magnetized and toroidal field models of the series B1 are displayed in Figs. 9 and 10. The rest mass density (Fig. 9) shows some of the trends of series C2, however the effects caused by the toroidal magnetic field do not scale linearly with the magnetic field strength. The weakly magnetized model B1-1/20 behaves quite differently both from the equipartition model B1-1 and the strongly magnetized model B1-10/3. The more magnetized models develop nose cones preceded in the case of model B1-10/3 by a magnetically confined bubble. The rest mass density (Fig. 9) and the pressure (not shown) distributions show much more structure for these two more strongly magnetized models than that of the non-magnetized model. The corresponding distributions of model B1-1/20 are very smooth suggesting that its weak magnetic field inhibits the formation of structures (see Sect. 5).
The first recollimation shock shows the same trend as in series
C2. Due to magnetic pinching the shock is stronger and is located
closer to the nozzle for a stronger toroidal field. The strong
pinching of the beam in models B1-1 and B1-10/3 leads to a widening of
the beam downstream of the recollimation shocks and to smaller Lorentz
factors (![]() ;
Fig. 10). In model B1-1/20 the
pinching is very weak, and no difference to the non-magnetized model
can be recognized. Instead, it is even better collimated than model
B1-0, and the flow remains highly relativistic up to the terminal
shock of the beam, where the beam plasma is deflected and flows
backwards smoothly in a very thin layer around the beam. This
behavior explains why the jet of model B1-1/20 has propagated further
than those of the other models in the same time. These results imply,
that with the right combination of parameters, a small toroidal field
helps to collimate the beam without producing too much pinching, which
helps to keep the jet stable.
;
Fig. 10). In model B1-1/20 the
pinching is very weak, and no difference to the non-magnetized model
can be recognized. Instead, it is even better collimated than model
B1-0, and the flow remains highly relativistic up to the terminal
shock of the beam, where the beam plasma is deflected and flows
backwards smoothly in a very thin layer around the beam. This
behavior explains why the jet of model B1-1/20 has propagated further
than those of the other models in the same time. These results imply,
that with the right combination of parameters, a small toroidal field
helps to collimate the beam without producing too much pinching, which
helps to keep the jet stable.
Figure 11 shows the magnetization ![]() and
and ![]() for the two models B1-1 and B1-10/3, respectively. As for the
corresponding C2 models the initial magnetization of the beam is
reduced very much in the first cross shock. It is strongest near the
beam's terminal shock, where the plasma flows radially away from the
axis leading to the formation of the nose cone. Apart from the fact
that the structures are much narrower than in the models of series C2,
the overall distributions of
for the two models B1-1 and B1-10/3, respectively. As for the
corresponding C2 models the initial magnetization of the beam is
reduced very much in the first cross shock. It is strongest near the
beam's terminal shock, where the plasma flows radially away from the
axis leading to the formation of the nose cone. Apart from the fact
that the structures are much narrower than in the models of series C2,
the overall distributions of ![]() and
and ![]() are very similar
everywhere in the cavity.
are very similar
everywhere in the cavity. ![]() is lowest near the axis and then
increases until it reaches its maximum value in the magnetic shell
around the beam.
is lowest near the axis and then
increases until it reaches its maximum value in the magnetic shell
around the beam. ![]() remains largest inside the beam and the nose
cone. Different from series C2, an increase of the magnetic field
strength yields a more turbulent cocoon in case of the models of
series B1.
remains largest inside the beam and the nose
cone. Different from series C2, an increase of the magnetic field
strength yields a more turbulent cocoon in case of the models of
series B1.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{2520fg12.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg235.gif) |
Figure 12:
Snapshots of the poloidal field model B1-pol-1 at
|
| Open with DEXTER | |
Figure 12 shows snapshots of the rest mass density, the Lorentz factor, the magnetic field strength and the magnetization parameter of model B1-pol-1. Most of the features found in model C2-pol-1 are also present here: the jet as a whole is very smooth both in density and pressure, the cocoon showing only an indication of an eddy. The beam is almost undisturbed, and the cross shocks are very weak. The back flow is confined to a narrow region directly around the beam and is absolutely straight. The hammer-like structure at the head of the jet seen in model C2-pol-1, which is associated with the emission of vortices, is not present in model B1-pol-1.
The smoothness of the cocoon results from the presence of the poloidal
field (see the top panel of Fig. 12), which is smooth
throughout the cavity. The field is only twisted in the narrow low
density sheet around the beam, and even there, the twist is mostly
aligned with the axis. This does not favor the formation of eddies,
which could drive strong shocks into the beam. As in model C2-pol-1,
![]() in a large part of the cavity, which however,
does not diminish the effect of the poloidal field on the morphology
of the jet. Model B1-pol-1 shows a smoother cavity than model C2-pol-1
because the cocoon (even in the hydrodynamic case) is less prominent
in series B1 than in series C2 (see Sect. 4.2.3).
in a large part of the cavity, which however,
does not diminish the effect of the poloidal field on the morphology
of the jet. Model B1-pol-1 shows a smoother cavity than model C2-pol-1
because the cocoon (even in the hydrodynamic case) is less prominent
in series B1 than in series C2 (see Sect. 4.2.3).
![\begin{figure}
\par\includegraphics[width=11cm,clip]{2520fg13.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg238.gif) |
Figure 13:
Snapshots of the logarithm of the rest mass density of the
models C1-0, C1-1 and C1-10/3 at
|
| Open with DEXTER | |
Models C2-0 and B1-0 differ only by the adiabatic index (see
Table 1, yet the cavity of the latter is much
more elongated and the jet has a larger propagation speed. These
differences can be understood using the simple analytic model of
Begelman & Cioffi (1989). In their model, the cavity pressure ![]() determines the
sideways expansion of the cocoon. This pressure is related to
determines the
sideways expansion of the cocoon. This pressure is related to
![]() ,
the propagation velocity of the bow shock in the axial
direction (
,
the propagation velocity of the bow shock in the axial
direction (![]() ), the cavity cross section (
), the cavity cross section (![]() ), and the power
transported into the cocoon through the Mach disc (
), and the power
transported into the cocoon through the Mach disc (![]() )
by
)
by
![\begin{figure}
\par\includegraphics[width=11cm,clip]{2520fg14.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg246.gif) |
Figure 14: Same as Fig. 13 but showing snapshots of the Lorentz factor and the flow pattern. |
| Open with DEXTER | |
We now focus on the effects of the magnetic field on the propagation
of the jets in series B1. As discussed in the previous paragraph, the
1D estimate (Eq. (47)) is a lower bound of the
propagation velocity, and as for series C2, the propagation speed does
not depend linearly on the magnetic field strength
(Fig. 7). However, in contrast to the C2 jets, the jet
with the weakest toroidal field propagates fastest followed by the
hydro model and the poloidal field model. Consequently, due to their
larger propagation velocities, these models also exhibit larger aspect
ratios (Fig. 8). The poloidal field model B1-pol-1 is
more elongated than model B1-1/20, because the poloidal field
initially present in the ambient medium inhibits the sideways
expansion of the cavity. The jet of model B1-pol-1 propagates
![]()
![]() faster than that of model B1-1, which has a similar
degree of magnetization, because of the reduced transversal expansion
of the cocoon (according to the argument expressed above).
faster than that of model B1-1, which has a similar
degree of magnetization, because of the reduced transversal expansion
of the cocoon (according to the argument expressed above).
The average thermal pressure of the models of series B behaves
qualitatively similarly, but is slightly larger than that of the
corresponding models of series C2 (Fig. 6).
Furthermore, the distance at which all the models display a very
similar thermal pressure and pressure gradient (![]()
![]() )
is
slightly smaller than in the C2 series (with the exception of
B1-pol-1). The models of series B1 with a toroidal field develop a
region in the cocoon between the contractive and the expansive regions
(see above), where there is an almost perfect hydromagnetic
equilibrium the net force being almost zero
(Fig. 6). Model B1-pol-1 differs in its behavior,
because
)
is
slightly smaller than in the C2 series (with the exception of
B1-pol-1). The models of series B1 with a toroidal field develop a
region in the cocoon between the contractive and the expansive regions
(see above), where there is an almost perfect hydromagnetic
equilibrium the net force being almost zero
(Fig. 6). Model B1-pol-1 differs in its behavior,
because
![]() is everywhere smaller than in the hydrodynamic model
B1-0 and decreases almost exactly as r-1.
is everywhere smaller than in the hydrodynamic model
B1-0 and decreases almost exactly as r-1.
Figures 13 and 14 show the rest mass density and the Lorentz factor, respectively, of all the models of series C1 with toroidal magnetic fields. Many of the effects of the different magnetic field configurations described in the previous sections also hold for series C1, some of them being more enhanced.
The toroidal field models develop very large nose cones. In model
C1-10/3 the nose cone makes up 50% of the total length of the jet,
which has a high density (
![]() ), high pressure (
), high pressure (
![]() )
spine consisting of beam plasma preceded by a large low
density bubble filled up with beam material. The same structure is
visible in model C1-1, although the nose cone is only half as long as
in model C1-10/3 (Fig. 13).
)
spine consisting of beam plasma preceded by a large low
density bubble filled up with beam material. The same structure is
visible in model C1-1, although the nose cone is only half as long as
in model C1-10/3 (Fig. 13).
![\begin{figure}
\par\includegraphics[width=11cm,clip]{2520fg15.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg250.gif) |
Figure 15:
Snapshots of the magnetization parameter |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10.9cm,clip]{2520fg16.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg251.gif) |
Figure 16:
Snapshots of the poloidal field model C1-pol-1 at
|
| Open with DEXTER | |
As in series B1 and C2, the strength of the recollimation shocks increases with toroidal magnetic field, because most of the cocoon of models C1-1 and C1-10/3 is dominated by magnetic pressure (see upper two panels of Fig. 15). This also explains the high density of the nose cone of model C1-10/3 (Fig. 13), which is confined by strongly magnetized matter. The strong recollimation shocks reduce the Lorentz factor in the post-shock regions to values close to 1. In the most strongly magnetized model of the series (C1-10/3) some of the recollimation shocks are planar instead of conical shocks (Fig. 4, bottom panel), i.e.,the beam fluid is most effectively decelerated (Fig. 14). In the magnetized models the back flow of beam plasma through the cocoon is confined by the toroidal field, i.e.,it is slower and smoother than in model C1-0 (Fig. 14).
Model C1-pol-1 also shows the same, but enhanced features as model C2-pol-1. The density and pressure morphology look very similar to that of model C1-0, which has a similar propagation speed, too. However, the cross shocks are weaker than in the non-magnetized model, and the pressure in the cocoon is slightly more homogeneous. The flow pattern (second panel from top in Fig. 16) shows the same hammer-like head structure as observed in model C2-pol-1 (Sect. 4.1.2). Model C1-pol-1 has the same magnetization structure as model C2-pol-1, but the shell surrounding its beam is more strongly magnetized (bottom panel of Fig. 16). The magnetic field is almost completely expelled from the jet's cocoon, and is reduced by four to five orders of magnitude compared to the initial value (third panel from top in Fig. 16). Only twisted filaments of larger magnetic field strength survive inside the cocoon.
All models propagate at a speed very close to the 1D estimate
(Eq. (47)) up to an evolutionary time of
![]() (1D phase; see Fig. 7, top panel). Only model
C1-10/3 propagates faster from the very beginning of its evolution,
and shows no sign of slowing down during the whole simulation. The
other three models eventually leave the 1D phase and start slowing
down. Model C1-1 is still faster than model C1-pol-1 and the
non-magnetized models, the latter two following a similar evolutionary
track. We find that the toroidal magnetic field speeds up the jet by
almost 100% in the case of model C1-10/3 and by about 20% in the
case of model C1-1 as compared to model C1-0. However, this effect is
not seen for the velocities of the Mach disk (Table 2).
The poloidal field does not have a large effect on the propagation
speed of the jet. Model C1-pol-1 shows only a slightly stronger
deceleration compared to model C1-0 at the very end of the simulation.
(1D phase; see Fig. 7, top panel). Only model
C1-10/3 propagates faster from the very beginning of its evolution,
and shows no sign of slowing down during the whole simulation. The
other three models eventually leave the 1D phase and start slowing
down. Model C1-1 is still faster than model C1-pol-1 and the
non-magnetized models, the latter two following a similar evolutionary
track. We find that the toroidal magnetic field speeds up the jet by
almost 100% in the case of model C1-10/3 and by about 20% in the
case of model C1-1 as compared to model C1-0. However, this effect is
not seen for the velocities of the Mach disk (Table 2).
The poloidal field does not have a large effect on the propagation
speed of the jet. Model C1-pol-1 shows only a slightly stronger
deceleration compared to model C1-0 at the very end of the simulation.
The models of series C1 with a toroidal field develop larger nose cones than the equivalent models of series C2, because of the smaller propagation velocity of the former. For smaller propagation speeds there is a larger amount of mass crossing the Mach disk which ends up in the cavity, and hence there is also a larger amount of matter that is deflected forward and fills up a larger nose cone. In other words, the nose cone is larger in those models where the cocoon is larger (i.e.,in models where the speed of the head is smaller).
As with series C2 the cylindrical aspect ratio (bottom panel in
Fig. 8) has to be analyzed with caution, since in all
models the cavity reaches the edge of the grid in radial direction
quite early in the simulation. Nevertheless, the differences between
the models are larger than suggested by their propagation speeds
alone. While model C1-10/3 has a much larger aspect ratio than any of
the other models, because of its long nose cone, the two equipartition
models, C1-1 and C1-pol-1, have similar aspect ratios for
![]() .
Later model C1-1 evolves differently, and its aspect
ratio almost doubles until the end of the simulation. Model C1-pol-1,
however, maintains a constant aspect ratio of around 2.4 until it hits
the radial boundary of the grid at
.
Later model C1-1 evolves differently, and its aspect
ratio almost doubles until the end of the simulation. Model C1-pol-1,
however, maintains a constant aspect ratio of around 2.4 until it hits
the radial boundary of the grid at
![]() .
The aspect
ratio of model C1-0 is even smaller in the beginning, but starts to
grow earlier in the simulation.
.
The aspect
ratio of model C1-0 is even smaller in the beginning, but starts to
grow earlier in the simulation.
Although the thermal pressure of the gas injected through the nozzle
is quite similar in all three series, the averaged thermal pressure
along the beam of the models of series C1 is smaller than that of
series C2 or B1, if one compares models with the same ![]() (Fig. 6). The reason is that the averaged pressure
along the axis is dominated by the contribution of the hotspot or the
plug pressure, which is much smaller in series C1 than in series C2 or
B1. However, the relative increase of the averaged gas pressure of
models C1-1 and C1-10/3 relative to the hydrodynamic model C1-0 is
roughly twice times larger than in the other two series.
(Fig. 6). The reason is that the averaged pressure
along the axis is dominated by the contribution of the hotspot or the
plug pressure, which is much smaller in series C1 than in series C2 or
B1. However, the relative increase of the averaged gas pressure of
models C1-1 and C1-10/3 relative to the hydrodynamic model C1-0 is
roughly twice times larger than in the other two series.
Our results show that jets carrying a toroidal field are confined both
by the field transported inside the beam and by the field advected
into the cocoon by the back flow. The most prominent morphological
feature caused by the toroidal magnetic field is the nose cone. As
found in previous Newtonian (e.g. Clarke et al. 1986; Lind et al. 1989; Kössl et al. 1990) and
relativistic simulations (Komissarov 1999b) this structure occurs for
jets with toroidal fields close to equipartition strength or larger
and for
![]() .
The nose cone forms because of the
magnetic pinching by the Lorentz force which acts inwards radially
near the beam. The magnetized beam plasma (which in a non-magnetized
beam is deflected at the Mach disk shock and flows backwards inflating
the cocoon) is partially forced to flow around the Mach disk into the
nose cone. Only a smaller fraction of the beam plasma (namely the less
magnetized fraction for which the Lorentz force is not as strong)
flows backwards into bubble-like structures that reside upstream of
the nose cone forming a cocoon similar as in hydrodynamic jets. This
formation mechanism explains several properties of nose cones: (a) the
larger the magnetization of the beam plasma, the stronger is the
Lorentz force acting on the flow in the beam, i.e.,more of the shocked
beam plasma is forced into the nose cone which thereby grows larger
with larger magnetization of the beam; (b) nose cones contain stronger
magnetic fields than cocoons, because only the weakly magnetized
plasma flows into the cocoon. The high magnetic field in the nose cone
itself is the cause for the confinement to a narrow region, the high
pressure (approximately two orders of magnitude higher than the
external pressure in the
.
The nose cone forms because of the
magnetic pinching by the Lorentz force which acts inwards radially
near the beam. The magnetized beam plasma (which in a non-magnetized
beam is deflected at the Mach disk shock and flows backwards inflating
the cocoon) is partially forced to flow around the Mach disk into the
nose cone. Only a smaller fraction of the beam plasma (namely the less
magnetized fraction for which the Lorentz force is not as strong)
flows backwards into bubble-like structures that reside upstream of
the nose cone forming a cocoon similar as in hydrodynamic jets. This
formation mechanism explains several properties of nose cones: (a) the
larger the magnetization of the beam plasma, the stronger is the
Lorentz force acting on the flow in the beam, i.e.,more of the shocked
beam plasma is forced into the nose cone which thereby grows larger
with larger magnetization of the beam; (b) nose cones contain stronger
magnetic fields than cocoons, because only the weakly magnetized
plasma flows into the cocoon. The high magnetic field in the nose cone
itself is the cause for the confinement to a narrow region, the high
pressure (approximately two orders of magnitude higher than the
external pressure in the
![]() models) and high density
(
models) and high density
(![]()
![]() )
spine.
)
spine.
According to Komissarov (1999b) prominent nose cones should not form in
low Poynting flux jets even if the magnetization parameter is large.
Our results confirm this argument if we restrict ourselves to models
transporting toroidal magnetic fields: nose cones only form in those
models with toroidal magnetic field where
![]() and
and
![]() at injection. However, even if these requirements are fulfilled,
none of our poloidal field models develops a nose cone. On the other
hand, the formation of the nose cone in case of strong toroidal fields
resembles what happens in pulsar wind nebulae: the postshock velocity
cannot decrease fast enough to match the outer boundary condition.
Hence, the region expands mostly longitudinally (see,
e.g., Bucciantini et al. 2004). The size of the nose cone is correlated with the
propagation velocity of the Mach disc, but neither with
at injection. However, even if these requirements are fulfilled,
none of our poloidal field models develops a nose cone. On the other
hand, the formation of the nose cone in case of strong toroidal fields
resembles what happens in pulsar wind nebulae: the postshock velocity
cannot decrease fast enough to match the outer boundary condition.
Hence, the region expands mostly longitudinally (see,
e.g., Bucciantini et al. 2004). The size of the nose cone is correlated with the
propagation velocity of the Mach disc, but neither with ![]() nor
nor
![]() .
The most prominent nose cone exists in model C1-10/3
where the propagation velocity of the Mach disk is the smallest of all
models, and where
.
The most prominent nose cone exists in model C1-10/3
where the propagation velocity of the Mach disk is the smallest of all
models, and where ![]() is considerably smaller than in models
B1-10/3 or C2-10/3 which have the same
is considerably smaller than in models
B1-10/3 or C2-10/3 which have the same ![]() .
.
Since a considerable fraction of shocked beam plasma is locked in the
nose cone, it cannot flow back towards the nozzle and drive the radial
expansion of the cavity. However, most of the toroidal field models
are not narrower (i.e.,have a smaller aspect ratio) than their
corresponding hydrodynamic reference models. Considering the models of
series B1,
![]() the aspect ratio is smaller both in models B1-1 and B1-10/3 than in
model B1-0, which is possible because of the subtle relation between
the mass flux, the mass accumulated in the nose cone, and the force
balance in the radial direction. Let us assume that the pressure and
the Lorentz force scale differently with r. If
the aspect ratio is smaller both in models B1-1 and B1-10/3 than in
model B1-0, which is possible because of the subtle relation between
the mass flux, the mass accumulated in the nose cone, and the force
balance in the radial direction. Let us assume that the pressure and
the Lorentz force scale differently with r. If
![]() and
and
![]() ,
the net force will vary with radius as
,
the net force will vary with radius as
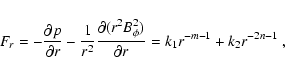 |
(50) |
In all models transporting toroidal field the aspect ratio of the
cavity is very similar to that of the hydrodynamic model B1-0, because
the pressure gradient causes an expansion for
![]() which
compensates for the smaller mass flux into the cocoon. As a rule of
thumb, the net force that contracts the beam and its immediate
neighborhood (contractive region) causes an expansion in the outer
layers of the cocoon and the cavity (expansive region). The increased
gas pressure, the formation of strong shocks in the beam, and the pull
of the expanding region limit the amount of the contraction. However,
as the balance between the pinch induced by the magnetic tension and
the total pressure is not perfect, a number of transient phenomena
arise. For example, magnetic bubbles form close to the head of the jet
around the Mach disk in models with stronger toroidal fields, because
the flow tries to establish hydromagnetic equilibrium in the
cocoon. In regions which are evacuated (e.g.,because of a strong back
flow) the gas pressure decrease tends to be balanced by the growth of
the magnetic field, i.e.,the reduced thermal pressure is compensated
for by an increase of the isotropic magnetic pressure. This mechanism
is similar to that described by Parker (1979) when considering an
isolated flux tube, but applied to extended regions of the jet
cavity. In actual radio sources, the magnetically confined bubbles
could be observed as spherical smooth radio lobes surrounding the hot
spot. One example of such a radio structure may be the hot spot
residing in the middle of the roughly spherical radio lobe associated
to the jet in 3C 353 (Swain et al. 1998). Interestingly, the counter jet of
the same source shows a striking bright annular feature which could be
associated with the flow around the beam terminal shock in a jet with
a dynamically important toroidal magnetic field.
which
compensates for the smaller mass flux into the cocoon. As a rule of
thumb, the net force that contracts the beam and its immediate
neighborhood (contractive region) causes an expansion in the outer
layers of the cocoon and the cavity (expansive region). The increased
gas pressure, the formation of strong shocks in the beam, and the pull
of the expanding region limit the amount of the contraction. However,
as the balance between the pinch induced by the magnetic tension and
the total pressure is not perfect, a number of transient phenomena
arise. For example, magnetic bubbles form close to the head of the jet
around the Mach disk in models with stronger toroidal fields, because
the flow tries to establish hydromagnetic equilibrium in the
cocoon. In regions which are evacuated (e.g.,because of a strong back
flow) the gas pressure decrease tends to be balanced by the growth of
the magnetic field, i.e.,the reduced thermal pressure is compensated
for by an increase of the isotropic magnetic pressure. This mechanism
is similar to that described by Parker (1979) when considering an
isolated flux tube, but applied to extended regions of the jet
cavity. In actual radio sources, the magnetically confined bubbles
could be observed as spherical smooth radio lobes surrounding the hot
spot. One example of such a radio structure may be the hot spot
residing in the middle of the roughly spherical radio lobe associated
to the jet in 3C 353 (Swain et al. 1998). Interestingly, the counter jet of
the same source shows a striking bright annular feature which could be
associated with the flow around the beam terminal shock in a jet with
a dynamically important toroidal magnetic field.
Opposite trends are observed for the evolution of the aspect ratios of models C1-10/3 and C2-10/3 on the one hand, and model B1-10/3 on the other hand. While all three models have the same strong magnetic field, the nose cone of models C1-10/3 and C2-10/3 are much larger than that of model B1-10/3 leaving a much smaller fraction of high pressure plasma to drive the radial expansion of the cavity.
Owing to the same inward directed Lorentz force which produces the nose cones, the internal cross shocks are stronger in the toroidal field models than in the corresponding hydrodynamic models. In the poloidal field case, however, the effect is opposite: the magnetic field makes the jet less susceptible to shock waves driven into the beam perpendicular to the field lines as the magnetic tension on the beam repels shock waves. While the cross shocks in hydrodynamic jets are produced mainly by compression waves driven into the beam from the outside (e.g.,by eddies in the cavity), the cross shocks in the toroidal field models are of different nature. They are created intrinsically by the inwards pointing magnetic stress even in models having smooth cocoons, like e.g.,model B1-1/20.
The strengthening of the cross shocks with increasing toroidal magnetic field may cause a more knotty appearance of kpc-scale magnetic jets compared to hydrodynamic ones. The extra pinching provided by the toroidal field leads to a decrease of the beam Lorentz factor with increasing beam magnetization. This effect is less important in models having poloidal fields. Still, in all models except B1-pol-1 the mean magnetization in the beam drops below its initial value after the plasma has passed through successive recollimation shocks in the beam (in model B1-pol-1 the beam remains almost unperturbed). Even in the most strongly magnetized models the field never reaches equipartition values neither in the cross shocks nor in the hot spot. However, there might exist magnetic field configurations which lead to equipartition values at large distances from the nozzle, although this hypothesis has to be tested by simulations combining poloidal and toroidal fields.
If the magnetic field energy is indeed in equipartition with the
internal energy of the plasma in the hotspot and other bright emission
features of radio sources, then our results imply that the magnetic
field triggering such features is either not mainly of toroidal nature
or the initial magnetic field strength (at distances ![]() 1 kpc
from the AGN central engine) is well above equipartition (namely,
1 kpc
from the AGN central engine) is well above equipartition (namely,
![]() ). Otherwise, if observations point towards a
toroidal structure of the magnetic field in bright radio features, the
magnetic field energy might be more than one order of magnitude below
equipartition in these features (if the magnetic field energy at
distances
). Otherwise, if observations point towards a
toroidal structure of the magnetic field in bright radio features, the
magnetic field energy might be more than one order of magnitude below
equipartition in these features (if the magnetic field energy at
distances ![]() 1 kpc from the AGN core is in rough equipartition
with the thermal energy). Both conclusions can explain the current
estimates for the magnetic field strength in the hot spots of several
radio galaxies which has values between a factor of 25 below
equipartition and slightly above equipartition
(e.g. Wilson et al. 2000; Hardcastle et al. 2002, 1998; Donahue et al. 2003; Harris et al. 1994).
1 kpc from the AGN core is in rough equipartition
with the thermal energy). Both conclusions can explain the current
estimates for the magnetic field strength in the hot spots of several
radio galaxies which has values between a factor of 25 below
equipartition and slightly above equipartition
(e.g. Wilson et al. 2000; Hardcastle et al. 2002, 1998; Donahue et al. 2003; Harris et al. 1994).
The morphology and dynamics of relativistic jets can be substantially
influenced by toroidal magnetic fields of a strength far below
equipartition. This is demonstrated by model B1-1/20 which has a
featureless cocoon as well as an optimal propagation efficiency and
collimation. Since this behavior is not found in model C2-1/20 (and we
have not simulated model C1-1/20), noticeable morphodynamical changes
in jets carrying weak toroidal magnetic fields seem to require the
concourse of several circumstances. Models B1-1/20 and C2-1/20 differ
by the value of ![]() (Table 1). As we
have argued in Sect. 4.2.3 a smaller
(Table 1). As we
have argued in Sect. 4.2.3 a smaller ![]() yields
a reduced lateral expansion of the cavity blown by the jet, which in
turn increases the propagation speed of the head of the jet, and hence
also increases the aspect ratio. If the jet propagates faster, the
mass flux of the backflow is reduced. As the back flow is mainly
responsible for exciting the Kelvin-Helmholtz modes in the surface of
the beam, the reduced back flow in models having a relativistic
(small)
yields
a reduced lateral expansion of the cavity blown by the jet, which in
turn increases the propagation speed of the head of the jet, and hence
also increases the aspect ratio. If the jet propagates faster, the
mass flux of the backflow is reduced. As the back flow is mainly
responsible for exciting the Kelvin-Helmholtz modes in the surface of
the beam, the reduced back flow in models having a relativistic
(small) ![]() reduces the amount of perturbations of the beam. A
weak toroidal magnetic field in the beam helps to increase the
collimation and propagation efficiency of the jet, because a small
part of the mass that should flow backwards after crossing the Mach
disk is forced into the nose cone and does not contribute to the
upstream pinching of the beam. In model B1-1/20 the nose cone is
reduced to a little plug in front of the Mach disk because the Lorentz
force is small due to the small value of the field strength. The
resulting tiny nose cone does not affect the propagation efficiency of
the jet.
reduces the amount of perturbations of the beam. A
weak toroidal magnetic field in the beam helps to increase the
collimation and propagation efficiency of the jet, because a small
part of the mass that should flow backwards after crossing the Mach
disk is forced into the nose cone and does not contribute to the
upstream pinching of the beam. In model B1-1/20 the nose cone is
reduced to a little plug in front of the Mach disk because the Lorentz
force is small due to the small value of the field strength. The
resulting tiny nose cone does not affect the propagation efficiency of
the jet.
According to Begelman (1998) a cylindric jet carrying a purely
toroidal magnetic field should be stable against pinching
instabilities if
The smaller value of the adiabatic index also explains why the nose
cones of the models of series B1 (
![]() )
are smaller than those
of the models of series C1 or C2 (
)
are smaller than those
of the models of series C1 or C2 (
![]() ). The magnetization
downstream of a strong shock depends on the adiabatic index through
(Komissarov 1999b)
). The magnetization
downstream of a strong shock depends on the adiabatic index through
(Komissarov 1999b)
The evolution of axisymmetric jets can be divided into a 1D phase and
a 2D phase. During the initial 1D phase the evolution is almost linear
in time, and the propagation velocity matches almost exactly the 1D
estimate (Eq. (47)). This holds for the models of
the series C1 and C2 despite their p* over-pressured beams (the 1D
estimate is obtained for pressure matched hydrodynamic jets!), or
their different working surface topologies. All models of series B1
propagate faster than estimated by Eq. (47) because
of their adiabatic index is smaller
![]() .
The 2D phase is
characterized by the ejection of vortices from the head of the jet,
and by the non-linear, multidimensional interaction between the beam
and the cocoon. Usually during the 2D phase the propagation speed of
the jet is reduced, because the head of the jet widens and the thrust
is exerted onto a larger cross sectional area. The models of series B1
do not reach the 2D phase in our simulations. Their propagation
velocity remains constant until the jets reach the end of the
computational domain (Fig. 7). Models of series C1 and C2 reach,
however, the 2D phase sufficiently early in their evolution.
Especially in the models of series C1 the evolutionary times are very
large, and the different phases are clearly distinguishable: the
propagation velocities are constant and coincide with the estimated 1D
velocity (Eq. (47)) up to
.
The 2D phase is
characterized by the ejection of vortices from the head of the jet,
and by the non-linear, multidimensional interaction between the beam
and the cocoon. Usually during the 2D phase the propagation speed of
the jet is reduced, because the head of the jet widens and the thrust
is exerted onto a larger cross sectional area. The models of series B1
do not reach the 2D phase in our simulations. Their propagation
velocity remains constant until the jets reach the end of the
computational domain (Fig. 7). Models of series C1 and C2 reach,
however, the 2D phase sufficiently early in their evolution.
Especially in the models of series C1 the evolutionary times are very
large, and the different phases are clearly distinguishable: the
propagation velocities are constant and coincide with the estimated 1D
velocity (Eq. (47)) up to
![]() ,
where
the jets start to decelerate. The aspect ratios become nearly constant
at about the same time (Fig. 8, all models but
C1-10/3). A similar behavior is observed for all models of series
C2. Model C1-10/3 behaves differently, because its dynamics is
completely dominated by the high density nose cone.
,
where
the jets start to decelerate. The aspect ratios become nearly constant
at about the same time (Fig. 8, all models but
C1-10/3). A similar behavior is observed for all models of series
C2. Model C1-10/3 behaves differently, because its dynamics is
completely dominated by the high density nose cone.
Models with poloidal fields develop remarkably smooth cocoons and jet
cavities as well as very stable beams. Due to the configuration of the
magnetic field no nose cones are formed. Instead, the beam plasma
flows along the field lines which are bent sidewards by the expansion
of the leading bow shock yielding overdense, hammer-like structures at
the head of the jet (in models of series C). The cross shocks in the
beam of jets threaded by poloidal fields are weaker than those having
toroidal fields of the same average magnetization or even models
without any magnetic field. This behavior is due to the magnetic
tension in the beam that acts as a restoring force repelling waves
driven into the beam. Owing to the smoothness of their beams
relativistic jets with a dominant poloidal magnetic field component
may have a brightness distribution along the beam which will be rather
uniform in contrast to the very knotty distribution that we predict
for jets with predominantly toroidal fields. However, the hot spot
associated with the terminal shock of the jet might be similarly
bright since the strength of the terminal shock is almost the same in
the case of toroidal or poloidal field configurations. In jets with
poloidal fields there is a substantial radial component of the
magnetic field (directed towards the axis) at the bow shock (most
evident in the models of series C; Figs. 5 and 16),
which should manifest itself in radio maps of the
polarized intensity. This feature might help to discriminate poloidal
and toroidal magnetic field structures. The magnetic field is almost
completely expelled from the cocoon of models with a poloidal field,
but not from that of models with toroidal fields. Indeed,
![]() in most of the cavities of models having poloidal
fields.
in most of the cavities of models having poloidal
fields.
Our present approach has several limitations which prevent us from
extracting more solid conclusions from our simulations. The
evolutionary times covered in the simulations are very short (assuming
![]() kpc the longest evolutionary time is
kpc the longest evolutionary time is
![]() y corresponding to the series C1) compared to the
typical lifetimes of extragalactic radio sources (
y corresponding to the series C1) compared to the
typical lifetimes of extragalactic radio sources (![]() 107 -
108 y). The size of the domain in the direction perpendicular to
the jet axis is not sufficiently large as to contain the complete
cocoon in some of the simulations. Both technical limitations will be
overcome in a forthcoming paper where we will consider the long-term
evolution of kiloparsec scale jets transporting toroidal fields in a
sufficiently large computational box. Furthermore, three-dimensional
(3D) simulations are necessary in order to include all the possible
destabilizing properties of the magnetic field and to study the
stability properties of relativistic magnetized jets. This will be
addressed in a future investigation. As 3D simulations are obviously
very costly, our present comprehensive parameter study of axisymmetric
RMHD jets serves to identify and to select the most significant cases
to be simulated later in 3D without any symmetry restriction.
107 -
108 y). The size of the domain in the direction perpendicular to
the jet axis is not sufficiently large as to contain the complete
cocoon in some of the simulations. Both technical limitations will be
overcome in a forthcoming paper where we will consider the long-term
evolution of kiloparsec scale jets transporting toroidal fields in a
sufficiently large computational box. Furthermore, three-dimensional
(3D) simulations are necessary in order to include all the possible
destabilizing properties of the magnetic field and to study the
stability properties of relativistic magnetized jets. This will be
addressed in a future investigation. As 3D simulations are obviously
very costly, our present comprehensive parameter study of axisymmetric
RMHD jets serves to identify and to select the most significant cases
to be simulated later in 3D without any symmetry restriction.
Finally, we point out that we have presented a new high-order numerical algorithm to integrate the RMHD equations in several spatial dimensions for flows of astrophysical interest. The verification and robustness of the algorithm has been proven with several one- and two-dimensional tests the results being qualitatively the same as those produced with other existing numerical codes.
Acknowledgements
The numerical simulations presented here were carried out on the IBM p690 Regatta computer of the Rechenzentrum Garching (RZG), and we gratefully acknowledge the RZG for providing that computer time. M.A.A. acknowledges support through an agreement between the Max-Planck-Gesellschaft and the Consejo Superior de Investigaciones Científicas. L.A. acknowledges the support received by the Spanish DGES through grant PB97-1432. This research was supported in part by the Spanish Dirección General de Enseñanza Superior grants AYA-2001-3490-C02-01 and AYA-2001-3490-C02-02.
For jet applications where axisymmetry is assumed,
Eqs. (1), (2)
and (10) have to be written in cylindrical coordinates,
i.e.,the corresponding vector of geometrical source terms has be added
to the right hand side of the equations, ![]() ,
and the appropriate
geometrical factors have to be considered.
,
and the appropriate
geometrical factors have to be considered.
Using cylindrical coordinates
![]() the metric becomes
the metric becomes
Table B.1: Parameters for the 1D Riemann problems.
Before a numerical simulation code is used to solve a physical problem, it is necessary to verify its results by comparing them with known solutions of test problems. To this end one sets up several Riemann problems in one or more dimensions and checks whether the code can resolve all the waves that result from the breakup of the initial discontinuity. Ideal test cases would be those where an analytical solution to the problem is known. However, in RMHD there are not too many tests with known solutions mainly because a closed solution for the general RMHD Riemann problem has not yet been found. An alternative way of testing a code is to cross-check its test results against those obtained by other authors for the same test problems. With this aim in mind we have verified our code against the 1D test problems from Balsara (2001) which are also reproduced by Del Zanna et al. (2003). In 2D we have used the results of Komissarov (1999a).
Table B.1 lists the parameters of the five 1D Riemann
problems described in Balsara (2001). The first four were also
considered by Del Zanna et al. (2003). Every test involves a discontinuity
placed in the center of a 1D computational domain of 1600 grid zones.
We ran each of the five problems twice: (1) using PLM interpolation
with a threshold of ![]() for the slope limiting (see
Sect. 2.3.2); and (2) using PPM. A Courant number of
0.5 was used in all of the test runs. For the sake of conciseness,
and considering that our results are of the same quality as those of
Balsara (2001) and Del Zanna et al. (2003) we only show here tests 3 and 4 of
Table B.1.
for the slope limiting (see
Sect. 2.3.2); and (2) using PPM. A Courant number of
0.5 was used in all of the test runs. For the sake of conciseness,
and considering that our results are of the same quality as those of
Balsara (2001) and Del Zanna et al. (2003) we only show here tests 3 and 4 of
Table B.1.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{2520fg18.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg309.gif) |
Figure B.2: Fourth 1D test problem. Shock reflection test. The black crosses are the results obtained with PPM interpolation, the grey dots those computed with PLM interpolation. |
The results of the blast wave test problems 3 is displayed in Fig. B.1. Again the resulting waves are the same as in Balsara (2001). Test 3 is a strong blast wave with a large initial pressure difference. It develops two rarefaction waves propagating to the left, for example displayed in the density and pressure panels of Fig. B.1, which are both captured equally well by PPM and PLM. However, the high density structure on the right is neither resolved in our runs nor in Balsara (2001). Nevertheless, using PLM and PPM we obtain the same maximum Lorentz factor of about 3.4 as Balsara (2001). This illustrates that despite the numerical viscosity of the algorithm we can obtain the physically correct overall structure for this test problem. The comparison with Del Zanna et al. (2003) shows that our PPM results are again slightly better resolved in test No. 2 (not shown in this paper), while we get slightly worse results for the stronger blast wave test No. 3. This is visible from the height of the high density shell which is 40% larger for PPM than for PLM, but approximately 2% smaller than in Del Zanna et al. (2003).
Figure B.2 shows the results of test No. 4, a strong relativistic shock reflection test with two streams approaching each other at a Lorentz factors of 22.366. This setup produces two fast and two slow shocks. Both PPM and PLM handle this test very well, but PLM requires more zones to resolve the slow shocks. At the initial collision point (x=0) a certain amount of "wall heating'' occurs, which is a numerical pathology of approximate Riemann solvers (e.g. Donat & Marquina 1996). The problem arises because an excess of entropy is generated at the collision point at t=0. This can diffuse numerically only slowly, because the fluid is at rest at that point. Higher order reconstruction schemes help to confine the problem to a small number of points initially, but generate less diffusion. Hence the "hole'' in the rest mass density is larger with PPM (confined to only three grid zones with a relative error of about 10%) than with PLM (the "hole'' is much more spread out with an error of 5%). In this test our PLM results are of similar quality than those of Balsara (2001) and Del Zanna et al. (2003), while our PPM implementation requires less zones to resolve the slow shocks.
In summary, our code solves all test problems presented in Balsara (2001) correctly. As a rule of thumb, the PPM runs require less zones to resolve structures (in particular those of slowly moving waves) than the methods described in Balsara (2001) and Del Zanna et al. (2003), which are closer to our PLM results.
While the 1D tests have shown that our code can resolve all the waves appearing in RMHD reasonably well, 2D calculations introduce further complexities related with the constraint that the divergence of the magnetic field should remain zero (Sect. 2.3.4), which is trivially fulfilled in 1D tests. Furthermore, in Sect. B.2.2 we include an standard convergence test in 2D which shows that our algorithm converges at global second order accuracy.
The cylindrical explosion test consists of a strong shock propagating into a magnetically dominated medium. Although there is no analytic solution to verify against, this test still has very useful properties which make it a standard test of multidimensional numerical schemes for gas dynamics and MHD. For example, it encompasses all the degeneracies of the RMHD eigensystem (Sect. 2.2.1). Its simple setting makes it easy to spot bugs or weaknesses of a scheme which might not be seen so clearly in more complicated problems. Results for different cylindrical explosion problems in RMHD have been published (1) by Dubal (1991) indicating severe problems with his scheme; (2) by van Putten (1995) reaching a maximum velocity of v=0.35; (3) by Komissarov (1999a); and (4) by Del Zanna et al. (2003).
We have chosen a setup very similar to that in Komissarov (1999a): a
cylinder of high pressure and density is located in the center of a
square Cartesian grid, which initially contains a uniform, strong
magnetic field. The grid has 200 by 200 zones spanning 12 by 12 units
of distance. In the center of the grid there is a circle of radius 0.8
where
![]() and p=1. Between a radius of 0.8 and 1.0 the
values smoothly decrease to those of the homogeneous ambient medium
(
and p=1. Between a radius of 0.8 and 1.0 the
values smoothly decrease to those of the homogeneous ambient medium
(
![]() and
and
![]() ). Initially, the magnetic
field is Bx = 0.1, and the velocity is zero everywhere. The
simulations were carried out on an IBM Power4 processor and required
about 300 s of CPU time.
). Initially, the magnetic
field is Bx = 0.1, and the velocity is zero everywhere. The
simulations were carried out on an IBM Power4 processor and required
about 300 s of CPU time.
Figure B.3 shows the results of this test at time
t=4.0 using PLM. One recognizes an outer fast shock, which is
almost circular, because the fast magnetosonic speed varies little
across the grid. The innermost region is also circular and bounded by
a reverse fast shock. The expansion of this region is almost
circular, because the Lorentz force is small there. In between these
two shocks there are two more discontinuities bounded on the outside
by the compressed magnetic field (see the field lines in the Lorentz
factor panel of Fig. B.3). The CT method works in both
cases as demonstrated by the plot of ![]() (the non-zero values are
consistent with machine accuracy in double precision FORTRAN
arithmetics).
(the non-zero values are
consistent with machine accuracy in double precision FORTRAN
arithmetics).
The PPM results exhibit oscillations on a 5% level which are largely reduced by increasing the resolution. Figure B.4 shows plots of the thermal pressure along x=0 for two different resolutions: 200 by 200 zones (upper panel) and 800 by 800 zones (lower panel). While PPM (black crosses) requires less points than PLM (grey dots) in discontinuities in the higher resolution run, there is no such trend in the lower resolution run. At both resolutions PPM produces small oscillations.
In order to show that our algorithm, specially in the multidimensional
case, is able to preserve global second order accuracy, we include a
convergence test that has been also used in previous RMHD algorithms
for the same purpose (Del Zanna et al. 2003). The test consists on the
propagation of relativistic circularly polarized waves. Our set
up coincides with that of Del Zanna et al. (2003), i.e., after one period T we
evaluate the L1 norm of the numerical solution, compared to the
initial values,
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{2520fg21.eps} \end{figure}](/articles/aa/full/2005/23/aa2520-04/Timg317.gif) |
Figure B.5: Convergence test for the propagation of circularly polarized waves in 2D. The relative L1 errors (Eq. B.1) are shown in logarithmic scale (solid line) as a function of the resolution per dimension (N=Nx=Ny). The PLM reconstruction has been used. As a reference, the perfect second order convergence slope is also shown (dashed line). |
The quartic equation that yields the magnetosonic eigenvalues can be
cast in the following form
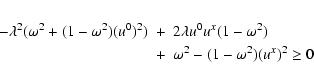
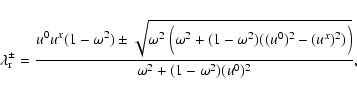
It turns out that the fast magnetosonic eigenvalues for the degenerate
case Bx=0 and b0=0 are exactly equal to
![]() (see Eq. (27)), and therefore
(see Eq. (27)), and therefore
![]() .
.