A&A 436, 549-567 (2005)
DOI: 10.1051/0004-6361:20042447
F. Sabbadin 1 - S. Benetti 1 - E. Cappellaro 2 - R. Ragazzoni 3 - M. Turatto 1
1 - INAF - Osservatorio Astronomico di Padova, vicolo dell'Osservatorio 5, 35122 Padova, Italy
2 -
INAF - Osservatorio Astronomico di Capodimonte, via Moiariello 11,
80131 Napoli, Italy
3 - INAF - Osservatorio
Astrofisico di Arcetri, Largo E. Fermi 5, 50125, Italy
Received 29 November 2004 / Accepted 17 January 2005
Abstract
We infer the gas kinematics, diagnostics and ionic radial profiles, distance and central
star parameters, nebular photo-ionization model, spatial
structure and evolutionary phase of the Planetary Nebula NGC 6741 by means of long-slit ESO NTT+EMMI high-resolution
spectra at nine position angles, reduced and analysed according to the tomographic and 3-D methodologies developed at the Astronomical Observatory
of Padua (Italy).
NGC 6741 (
![]() kpc,
kpc,
![]() yr,
ionized mass
yr,
ionized mass
![]() )
is a dense (electron density up to 12 000 cm-3), high-excitation, almost-prolate ellipsoid
(
)
is a dense (electron density up to 12 000 cm-3), high-excitation, almost-prolate ellipsoid
(
![]() pc, major, intermediate and minor semi-axes, respectively), surrounded by a sharp low-excitation skin (the ionization
front), and embedded in a spherical (
pc, major, intermediate and minor semi-axes, respectively), surrounded by a sharp low-excitation skin (the ionization
front), and embedded in a spherical (
![]() pc), almost-neutral, high-density (
pc), almost-neutral, high-density (
![]() atoms cm-3) halo
containing a large fraction of the nebular mass (
atoms cm-3) halo
containing a large fraction of the nebular mass (
![]() ).
The kinematics, physical conditions and ionic structure indicate that NGC 6741 is in a deep recombination
phase, started about 200 years ago, and caused by the rapid luminosity drop of the massive (
).
The kinematics, physical conditions and ionic structure indicate that NGC 6741 is in a deep recombination
phase, started about 200 years ago, and caused by the rapid luminosity drop of the massive (
![]() ), hot (log
), hot (log
![]() )
and faint (log
)
and faint (log
![]() )
post-AGB star, which has exhausted the hydrogen-shell nuclear
burning and is moving along the white dwarf cooling sequence. The general expansion law of the ionized gas in NGC 6741,
)
post-AGB star, which has exhausted the hydrogen-shell nuclear
burning and is moving along the white dwarf cooling sequence. The general expansion law of the ionized gas in NGC 6741,
![]() (km s
(km s
![]() ,
fails in the innermost, highest-excitation
layers, which move slower than expected. The observed deceleration is ascribable to the luminosity drop of the central star (the decreasing
pressure of the hot-bubble no longer balances the pressure of the ionized gas), and appears in striking contrast to recent reports inferring that
acceleration is a common property of the Planetary Nebulae innermost layers. A detailed comparative analysis proves that the
"U''-shaped expansion velocity field is a spurious,
incorrect result due to a
combination of: (a) simplistic assumptions (spherical shell hypothesis for the nebula); (b) unfit reduction method (emission profiles integrated
along the slit); and (c) inappropriate diagnostic choice (
,
fails in the innermost, highest-excitation
layers, which move slower than expected. The observed deceleration is ascribable to the luminosity drop of the central star (the decreasing
pressure of the hot-bubble no longer balances the pressure of the ionized gas), and appears in striking contrast to recent reports inferring that
acceleration is a common property of the Planetary Nebulae innermost layers. A detailed comparative analysis proves that the
"U''-shaped expansion velocity field is a spurious,
incorrect result due to a
combination of: (a) simplistic assumptions (spherical shell hypothesis for the nebula); (b) unfit reduction method (emission profiles integrated
along the slit); and (c) inappropriate diagnostic choice (![]() 4686
4686 ![]() of He II, i.e. a thirteen fine-structure components
recombination line). Some general implications for the shaping mechanisms of Planetary Nebulae are discussed.
of He II, i.e. a thirteen fine-structure components
recombination line). Some general implications for the shaping mechanisms of Planetary Nebulae are discussed.
Key words: planetary nebulae: individual: NGC 6741- ISM: kinematics and dynamics
The sentence by the late Professor Lawrence H. Aller (1994): "A nebula is a three-dimensional structure for which we obtain a
two-dimensional projection'' fully synthesizes the many, so far unsolved, observational limitations and interpretation problems connected to
Planetary Nebula (PN) research, leading to: (a) rough spatio-kinematical reconstruction; (b) unrealistic assumptions for the gas
parameters (in particular, electron
temperature (![]() )
and electron density (
)
and electron density (![]() )
constant all across the nebula); and (c) proliferation of kinematical,
physical and evolutional models, frequently based on the mere nebular morphology (i.e. appearance).
)
constant all across the nebula); and (c) proliferation of kinematical,
physical and evolutional models, frequently based on the mere nebular morphology (i.e. appearance).
The tomographic and 3-D analyses developed at the Astronomical Observatory of Padua (Sabbadin et al. 2004, and references therein) have overcome the stumbling block of nebular de-projection, rebuilding the ionic spatial structure, and allow us a direct comparison of each real, true PN with the current theoretical evolutionary models (Schönberner et al. 1997; Steffen et al. 1998; Marigo et al. 2001), the detailed hydro-dynamical simulations (Icke et al. 1992; Frank 1994; Mellema 1997; Perinotto et al. 2004a) and the updated photo-ionization codes (Ferland et al. 1998; Ercolano et al. 2003).
Though the observational starting point is common - i.e. long-slit spectra -, the "philosophy'' of tomography is just opposite of the
conventional method. The latter compacts the spectrum along the slit (in practice, it restricts
the nebula to a point), and gives mean, integrated results (line flux, expansion velocity, ![]() ,
,
![]() ,
ionization etc.). Vice versa, tomography is based on a pixel-to-pixel analysis of both flux and velocity, and furnishes
the bi-dimensional structure (in different ions) of the radial slice of the nebula intercepted by the spectrograph slit.
Later on, a 3-D rendering procedure combines all
tomographic slices and provides the true spatial distribution of the kinematics, physical
conditions (
,
ionization etc.). Vice versa, tomography is based on a pixel-to-pixel analysis of both flux and velocity, and furnishes
the bi-dimensional structure (in different ions) of the radial slice of the nebula intercepted by the spectrograph slit.
Later on, a 3-D rendering procedure combines all
tomographic slices and provides the true spatial distribution of the kinematics, physical
conditions (![]() and
and ![]() )
and ionic and chemical abundances with unprecedented accuracy.
Tomography needs spectra at high "relative'' spatial (SS) and spectral (RR) resolutions (S
)
and ionic and chemical abundances with unprecedented accuracy.
Tomography needs spectra at high "relative'' spatial (SS) and spectral (RR) resolutions (S
![]() ,
,
![]() radius,
radius,
![]() ;
;
![]() /
/![]() ,
,
![]() spectral resolution). It is based on the simple consideration that the position,
depth and density of each elementary volume within an extended,
regularly expanding nebula can be, in principle, derived from the radial velocity, FWHM and flux, respectively, of the corresponding
emission.
spectral resolution). It is based on the simple consideration that the position,
depth and density of each elementary volume within an extended,
regularly expanding nebula can be, in principle, derived from the radial velocity, FWHM and flux, respectively, of the corresponding
emission.
So far we have studied NGC 40 (Sabbadin et al. 2000a), NGC 1501 (Sabbadin et al. 2000b; Ragazzoni et al. 2001), NGC 6565 (Turatto et al. 2002), NGC 6818 (Benetti et al. 2003) and NGC 7009 (Sabbadin et al. 2004). Here we present the results for NGC 6741.
NGC 6741 (PN G033.8-02.6, Acker et al. 1992) is a compact (main
![]() ,
halo
,
halo
![]() ;
Curtis 1918;
Schwarz et al. 1992),
high-surface brightness, high-excitation (class 8, Hyung & Aller 1997) PN with a large degree of stratification of the
radiation. The powering star is very hot (log
;
Curtis 1918;
Schwarz et al. 1992),
high-surface brightness, high-excitation (class 8, Hyung & Aller 1997) PN with a large degree of stratification of the
radiation. The powering star is very hot (log
![]() ,
Pottasch 1981; Pottasch & Preite-Martinez 1983; Heap et al. 1989; Tylenda et al. 1989; Kaler & Jacoby 1989) and faint (
,
Pottasch 1981; Pottasch & Preite-Martinez 1983; Heap et al. 1989; Tylenda et al. 1989; Kaler & Jacoby 1989) and faint (
![]() ;
Pottasch 1981; Tylenda et al. 1989; Kaler & Jacoby 1989; Hyung & Aller
1997).
;
Pottasch 1981; Tylenda et al. 1989; Kaler & Jacoby 1989; Hyung & Aller
1997).
The [O III] and [N II] apparent morphology of NGC 6741 (sometimes called "Phantom Streak Nebula'') is shown in Figs. 1 and 2 (HST-WFPC2 frames retrieved from NASA public archives). Note the vertical (equatorial?) inhomogeneous strip of absorbing knots in the [O III] image of Fig. 1, and in Fig. 2 the roundish halo and the series of weak, radial [O III] rays penetrating into the [N II] skin along and close to the apparent major axis. A multi-color HST reproduction of the nebula is given by Hajian & Terzian at http://ad.usno.navy.mil/pne/gallery.html
The optical appearance of NGC 6741, the co-existence of
ionic species with a large range of ionization potential, IP (from [O I
![]() eV to [Ne V
eV to [Ne V
![]() eV; Aller et al. 1985; Hyung & Aller 1997)
and the characteristics of the central star (hot and faint) are suggestive of a recombining PN, i.e. the star has exhausted
the hydrogen-shell nuclear burning and is rapidly fading in luminosity (and temperature); the UV flux being unable to fully ionize the
gas, the outer nebular regions recombine, producing the faint halo (Tylenda 1986; Phillips 2000). In many respects NGC 6741
is very much like NGC 6565 (Turatto et al. 2002).
eV; Aller et al. 1985; Hyung & Aller 1997)
and the characteristics of the central star (hot and faint) are suggestive of a recombining PN, i.e. the star has exhausted
the hydrogen-shell nuclear burning and is rapidly fading in luminosity (and temperature); the UV flux being unable to fully ionize the
gas, the outer nebular regions recombine, producing the faint halo (Tylenda 1986; Phillips 2000). In many respects NGC 6741
is very much like NGC 6565 (Turatto et al. 2002).
To deepen our knowledge of the kinematics, physical conditions, ionic and spatial
structure, distance and evolutionary status
of NGC 6741, we have secured long-slit ESO NTT+EMMI echellograms (spectral range
![]() 3900-7900
3900-7900 ![]() ,
spectral resolution
,
spectral resolution ![]() /
/![]()
![]() )
at nine position angles (PA). The spectra were reduced and analysed using our 3-D
reconstruction technique (Turatto et al. 2002; Benetti et al. 2003).
)
at nine position angles (PA). The spectra were reduced and analysed using our 3-D
reconstruction technique (Turatto et al. 2002; Benetti et al. 2003).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2447f1.ps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg48.gif) |
Figure 1:
Apparent morphology of NGC 6741 in the medium-excitation line |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2447f2.ps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg49.gif) |
Figure 2: Apparent I([N II])/I([O III]) distribution over NGC 6741 (same WFPC2 images as Fig. 1). The sharp, inhomogeneous layer at low-excitation ([N II]) framing the main nebula is punched, along and close to the apparent major axis, by a series of radial [O III] rays or jets penetrating into the faint, roundish halo. |
| Open with DEXTER | |
NGC 6741 was observed with ESO NTT + EMMI (echelle mode; grating ![]() 14,
grism
14,
grism ![]() )
at nine equally spaced PA, under photometric
sky conditions and seeing ranging between 0.50
)
at nine equally spaced PA, under photometric
sky conditions and seeing ranging between 0.50
![]() and 0.70
and 0.70
![]() .
The spectrograph slit (1.0
.
The spectrograph slit (1.0
![]() wide
and 30
wide
and 30
![]() long) was
centered on the nebular image, the exciting star being invisible in the slit-viewer.
The echellograms (exposure time 600 s) cover the spectral range
long) was
centered on the nebular image, the exciting star being invisible in the slit-viewer.
The echellograms (exposure time 600 s) cover the spectral range ![]()
![]() 900-7900
900-7900 ![]() with resolution
with resolution
![]() ,
and provide
the kinematical structure of the main ionic species within the nebular slices covered by the slit.
Bias, zero-order flat field and distortion corrections and wavelength and flux calibrations were performed according
to the straightforward procedure fully described by Turatto et al. (2002).
,
and provide
the kinematical structure of the main ionic species within the nebular slices covered by the slit.
Bias, zero-order flat field and distortion corrections and wavelength and flux calibrations were performed according
to the straightforward procedure fully described by Turatto et al. (2002).
We stress the fundamental difference between our frames, covering 80 echelle orders, and the observing procedure usually adopted for extended objects, inserting an interference filter to isolate a single order. The same is valid for the reduction and investigation methods: so far long-slit echellograms have been used to obtain, either the kinematics in a few ions (in general, [O III], H I and [N II]), or the "average'' nebular properties (physical conditions, ionic and chemical abundances) integrated over the whole slit length. On the contrary, we perform a detailed, pixel-to-pixel, flux and velocity determination for a number of nebular lines, thus inferring the spatial distribution of the kinematics, diagnostics, ionic and total abundances at the same time.
The richness of physical information contained in the echellograms is illustrated in Figs. 3 and 4, presenting the spectral structure
of twelve ionic species (from [O I], ![]() eV to [Ar V],
eV to [Ar V],
![]() eV) at
eV) at
![]() and 75
and 75
![]() (close to the apparent minor and major axes
of NGC 6741, respectively).
(close to the apparent minor and major axes
of NGC 6741, respectively).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2447f3.ps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg56.gif) |
Figure 3:
Detailed spectral image of twelve ionic species in NGC 6741 at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2447f4.ps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg57.gif) |
Figure 4:
Same as Fig. 3, but for
|
| Open with DEXTER | |
These figures show the spectral characteristics common at all PA, in particular: (a) large stratification of both the radiation and kinematics (compare, e.g., the ionic sequences [O I]-[O II]-[O III] and [Ar III]-[Ar IV]-[Ar V]); and (b) blurred appearance of recombination lines (of H I, He I and He II), due to a combination of thermal motions, fine-structure and expansion velocity gradient. At the same time, they highlight the kinematical and physical differences at the two PA:
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2447f5.ps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg59.gif) |
Figure 5:
De-blending procedure for the [O II]
|
| Open with DEXTER | |
The "relative'' spectral and spatial resolutions of our echellograms are similar to each other:
![]() /
/
![]() to
to
![]() .
This means that the spatial information of NGC 6741 is as accurate as
the kinematical information,
and both are close to the lower limit for tomographic analysis (Ragazzoni et al. 2001). Thus, the spectral images in Figs. 3 and 4 are
affected by non-negligible blurring agents.
.
This means that the spatial information of NGC 6741 is as accurate as
the kinematical information,
and both are close to the lower limit for tomographic analysis (Ragazzoni et al. 2001). Thus, the spectral images in Figs. 3 and 4 are
affected by non-negligible blurring agents.
Seeing and guiding are broadening components
along the spatial (i.e. vertical) axis; in our case the full-width at half maximum, W(spat)
![]() ,
is 0.60
,
is 0.60
![]() for
for
![]() (Fig. 3), and 0.65
(Fig. 3), and 0.65
![]() for
for
![]() (Fig. 4). The true, "intrinsic'' profile of the
nebula has:
(Fig. 4). The true, "intrinsic'' profile of the
nebula has:
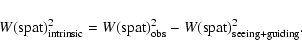 |
(1) |
The final broadening along the velocity axis is:
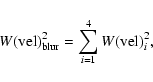 |
(2) |
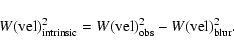 |
(3) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2447f6.ps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg78.gif) |
Figure 6:
High-contrast [O III] and [N II] line profiles (in logarithmic scale) of NGC 6741 close to the apparent minor and major
axes (
|
| Open with DEXTER | |
Let us consider, for example, the spectral images at
![]() (Fig. 3). The intrinsic FWHM in both the zvpc and cspl (as defined at the
opening of
Sect. 3) is 0.52
(Fig. 3). The intrinsic FWHM in both the zvpc and cspl (as defined at the
opening of
Sect. 3) is 0.52
![]() to 0.72
to 0.72
![]() (forbidden lines), 0.77
(forbidden lines), 0.77
![]() to 0.95
to 0.95
![]() (He I), 1.00
(He I), 1.00
![]() to 1.15
to 1.15
![]() (He II), and 1.35
(He II), and 1.35
![]() to 1.45
to 1.45
![]() (H I), thus confirming that:
(H I), thus confirming that:
This preliminary, qualitative description enhances the complexity of NGC 6741 (a common characteristic of all PNe analysed at adequate spatial and spectral resolutions). Before starting a thorough investigation of the kinematical and physical information contained in the spectra, we underline that the general characteristics of NGC 6741 - in particular: (a) nebular compactness and (b) star weakness (the stellar continuum, generally used as a position marker, is absent in the echellograms) - make this nebula the ideal target to test the reliability limits of our 3-D reconstruction procedure.
According to Sabbadin et al. (2004, and references therein), the overall spatio-kinematical properties of a regularly expanding nebula can be derived by combining the kinematics of the gas projected at the apparent position of the star (the "central star pixel line'', cspl, of the echellograms, common at all PA) with the spatial profile at the systemic radial velocity (the "zero velocity pixel column'', zvpc, at each PA).
Although the stellar continuum is absent in the echellograms of NGC 6741,
we obtain a satisfactory cspl-location and zvpc-alignement (within ![]() 0.1
0.1
![]() )
of the echelle orders
thanks to: (a) the central, symmetrical position of the star in the broad-band HST-WFPC2 nebular images; (b) the cspl- and zvpc-calibration
given by the continuum spectrum of the central star of NGC 7009 (observed in the same night, and with the same instrumental
configuration).
)
of the echelle orders
thanks to: (a) the central, symmetrical position of the star in the broad-band HST-WFPC2 nebular images; (b) the cspl- and zvpc-calibration
given by the continuum spectrum of the central star of NGC 7009 (observed in the same night, and with the same instrumental
configuration).
Table 1: Peak separation in the cspl of NGC 6741.
The peak separations in the cspl of NGC 6741, 2
![]() ,
are contained in Table 1 (last column), where
ions are put in order of increasing IP.
Typical errors are 1.0 km s-1 for the strongest forbidden emissions (like
,
are contained in Table 1 (last column), where
ions are put in order of increasing IP.
Typical errors are 1.0 km s-1 for the strongest forbidden emissions (like
![]() 4959-5007
4959-5007 ![]() of [O III] and
of [O III] and ![]() 6548-6584
6548-6584 ![]() of [N II])
to 2.0 km s-1 for the faintest ones (in particular,
of [N II])
to 2.0 km s-1 for the faintest ones (in particular,
![]() 6312
6312 ![]() of [S III],
of [S III], ![]() 4711-4740
4711-4740 ![]() of [Ar IV] and
of [Ar IV] and ![]() 6435-7005
6435-7005 ![]() of [Ar V]).
The uncertainties for recombination lines
are: 2.0 km s-1 for
of [Ar V]).
The uncertainties for recombination lines
are: 2.0 km s-1 for ![]() 4861-6563
4861-6563 ![]() of H I,
of H I, ![]() 4686-6560
4686-6560 ![]() of He II and
of He II and ![]() 4640
4640 ![]() of N III, and 1.5 km s-1 for
of N III, and 1.5 km s-1 for ![]() 5876-6678
5876-6678 ![]() of He I.
of He I.
The agreement with the kinematical results given in the literature (also contained in Table 1) is quite poor, probably due to the
compactness of NGC 6741, combined with image rotation on the slit (long-exposure Coudé spectra by Wilson 1950) or inadequate spatial
resolution (circular aperture 18
![]() in diameter by Robinson et al. 1982).
in diameter by Robinson et al. 1982).
Table 2: Peak separation in the zvpc at the nine PA of NGC 6741.
Concerning the zvpc at the nine PA of NGC 6741, the intensity peak separations, 2
![]() ,
in the different ionic species are listed in Table 2.
,
in the different ionic species are listed in Table 2.
To assemble the kinematical results of Table 1 and the spatial results of Table 2 we can follow two ways:
![\begin{figure}
\par\includegraphics[width=14cm,clip]{h2447f7.ps}\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg92.gif) |
Figure 7:
Nebular tomography vs. spectral image connection. In this example we use the [O III] spectral images of NGC 6741 at
|
| Open with DEXTER | |
In practice, and reversing the foregoing procedure, we compress the [O III] spectral image of NGC 6741 at
![]() (Fig. 7, central panel) by a factor 1.60 along the x axis, thus correcting for the spectral deformation introduced by NTT+EMMI
on the nebular slice intercepted by the slit, and obtaining:
(Fig. 7, central panel) by a factor 1.60 along the x axis, thus correcting for the spectral deformation introduced by NTT+EMMI
on the nebular slice intercepted by the slit, and obtaining:
This is the same law given by method (I).
The compression factor along the x axis being the same at all PA, we can repeat the procedure for the [O III] spectral image of NGC 6741
at
![]() (close to the apparent minor axis; Fig. 3), thus recovering the tomographic map shown in the right panel of Fig. 7, i.e.
an almost
circular ring with
(close to the apparent minor axis; Fig. 3), thus recovering the tomographic map shown in the right panel of Fig. 7, i.e.
an almost
circular ring with
![]() ,
QED
,
QED![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{h2447f8.eps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg96.gif) |
Figure 8:
The cspl-zvpc relation for NGC 6741 at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{h2447f9.eps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg97.gif) |
Figure 9:
Selected emission line profiles integrated along the slit for NGC 6741 at PA=15
|
| Open with DEXTER | |
We believe that NGC 6741 is the first PN showing clear evidence of deceleration in the highest ionization layers (the second candidate being IC 418: a preliminary analysis of our NTT+EMMI echellograms, taken at six PA, suggests the presence of infalling gas).
Vice versa, recent results by Gesicki & Zijlstra (2003, 3 PNe) and Gesicki et al. (2003, 14 PNe) - based on high-resolution emission
profiles integrated
along the slit, and spherical shell hypothesis for the emitting gas - indicate
that acceleration is a quite common property in the PN innermost layers (i.e. "U''-shaped expansion profile), due to the dynamical contribution
by the shocked, hot wind
from the central star. Gesicki & Zijlstra (2003)
adopted ![]() 4686
4686 ![]() of He II as diagnostic of the high-ionization kinematics,
whereas Gesicki et al. (2003) used
of He II as diagnostic of the high-ionization kinematics,
whereas Gesicki et al. (2003) used ![]() 5007
5007 ![]() of [O III]
(in a few cases
of [O III]
(in a few cases ![]() 6560
6560 ![]() of He II).
of He II).
The following
![]() are in order:
are in order:
To further test this point, let us consider the emission line profiles integrated along the slit of NGC 6741 at
![]() .
The results for
.
The results for ![]() 4686
4686 ![]() and
and ![]() 6560
6560 ![]() of He II, and the ionic sequence of argon - [Ar III] at
of He II, and the ionic sequence of argon - [Ar III] at ![]() 7135
7135 ![]() ,
[Ar IV] at
,
[Ar IV] at ![]() 4740
4740 ![]() and [Ar V] at
and [Ar V] at ![]() 7005
7005 ![]() - are shown in Fig. 9; they confirm that:
- are shown in Fig. 9; they confirm that:
A direct confirmation of the misleading kinematical results - in particular, the high-velocity of the innermost layers - provided by the
combination (spectral profile of recombination lines integrated
along the slit) + (spherical symmetry assumption) comes from a comparative analysis of the emission line profiles contained in
Gesicki & Zijlstra
(2003) and Gesicki et al. (2003): in all cases (17 PNe) the forbidden lines of the ionic species with the highest IP also show the
sharpest emission profile (as expected for a simple, positive
![]() vs. radius relation).
vs. radius relation).
All this questions the general validity of the spatio-kinematical studies based on the spherical symmetry assumption and/or spectral profiles of recombination lines integrated along the slit, and weakens (or even cancels) the reliability of their results on turbulence, radial kinematics, matter distribution and ionization, whose quantification needs detailed studies at high spatial and spectral resolutions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2447f10.eps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg104.gif) |
Figure 10:
Combined position-velocity maps in the nine observed PA of NGC 6741 at high (He II), medium ([O III]) and low ([N II]) excitation
(multi-color maps in the electronic version of the paper; blue = He II, green = [O III], and red = [N II]), scaled according to the relation
|
| Open with DEXTER | |
Figure 10 (multi-color in the electronic version) shows the complete velocity field at
the nine
observed PA of NGC 6741. We select He II, [O III] and [N II] as markers of
the high, medium and low-excitation regions, respectively.
These position-velocity (P-V) maps are relative to the systemic heliocentric velocity
of the nebula,
![]() ) km s-1, corresponding
to
) km s-1, corresponding
to
![]() km s-1, and are scaled (along the x axis) according to
km s-1, and are scaled (along the x axis) according to
![]() (km s
(km s
![]() ,
i.e. they reproduce the tomographic maps of the nebular slices covered by the spectrograph slit.
,
i.e. they reproduce the tomographic maps of the nebular slices covered by the spectrograph slit.
Figure 10 highlights the kinematical complexity and large stratification of the radiation within NGC 6741. The main nebula consists
of an almost-prolate ellipsoid (
![]() ,
,
![]() ,
,
![]() ), whose major axis (projected at
), whose major axis (projected at
![]() )
forms an angle of 55(
)
forms an angle of 55(![]() 3)
3)
![]() with the line of sight: on the whole, the eastern part of the nebula is approaching the observer, and the
western part receding.
with the line of sight: on the whole, the eastern part of the nebula is approaching the observer, and the
western part receding.
All this throws new light on two specific fields: (I) nature of the curious skip of absorbing knots present in Fig. 1 (upper panel), and (II) turbulent motion.
(I) Skip of absorbing knots: the central location, orientation (vertical) and light curvature (concavity towards East) are suggestive of an inhomogeneous belt of neutral matter (gas + molecules + dust) embedding the dense ionized gas of the equatorial regions. The amount of circum-nebular neutral gas can be estimated from the [O III] flux-depletion suffered by the underlying ionized nebula, being:
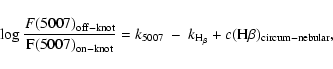 |
(4) |
Intensity scans in the neighbourhood of the deepest knots provide
![]() up to 1.4 (
up to 1.4 (![]() 0.1), i.e.
c(
0.1), i.e.
c(
![]() up to 0.18 (
up to 0.18 (![]() 0.03). Assuming a "normal'' gas-to-dust ratio (Spitzer 1978; Bohlin et al. 1978) and
c(
0.03). Assuming a "normal'' gas-to-dust ratio (Spitzer 1978; Bohlin et al. 1978) and
c(
![]() (Acker 1978), we have:
(Acker 1978), we have:
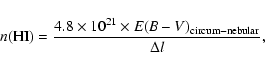 |
(5) |
(II) Turbulent motion. In Fig. 10, the tomographic map close to the apparent minor axis (i.e. at
![]() )
being almost circular
and quite homogeneous, we can assume W(spat
)
being almost circular
and quite homogeneous, we can assume W(spat
![]() (zvpc at
(zvpc at
![]() (cspl), thus inferring W(vel)
(cspl), thus inferring W(vel)
![]() (through Eqs. (1) to (3),
(through Eqs. (1) to (3),
![]() (km s
(km s
![]() ,
and the
,
and the ![]() radial profile given in Sect. 7.1). We overlook
the recombination lines of hydrogen and helium (dominated by thermal motion and/or fine-structure), and consider the strongest
forbidden lines. The analysis of
radial profile given in Sect. 7.1). We overlook
the recombination lines of hydrogen and helium (dominated by thermal motion and/or fine-structure), and consider the strongest
forbidden lines. The analysis of ![]() 6300
6300 ![]() ([O I]),
([O I]), ![]() 6731
6731 ![]() ([S II]),
([S II]), ![]() 6584
6584 ![]() ([N II]),
([N II]),
![]() 7135
7135 ![]() ([Ar III]), and
([Ar III]), and ![]() 5007
5007 ![]() ([O III]) provides
([O III]) provides
![]() 2.0) km s-1,
with no evident relation to the ionization degree. Thus, in spite of the crude assumptions and wide uncertainties, we conclude
that the turbulent motion in NGC 6741 is quite modest.
2.0) km s-1,
with no evident relation to the ionization degree. Thus, in spite of the crude assumptions and wide uncertainties, we conclude
that the turbulent motion in NGC 6741 is quite modest.
In general, the observed line intensities must be corrected for absorption according to:
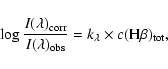 |
(6) |
| (7) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2447f11.ps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg130.gif) |
Figure 11:
F(H |
| Open with DEXTER | |
The extinction estimates reported in the literature (mean values along the nebular slice covered by the spectrograph slit) cluster
around
![]() (Kaler & Lutz 1985; Kaler & Jacoby 1989; Cahn et al. 1992; Hyung & Aller 1997).
(Kaler & Lutz 1985; Kaler & Jacoby 1989; Cahn et al. 1992; Hyung & Aller 1997).
To disentangle the complex absorption over NGC 6741, we apply the
H![]() /H
/H![]() analysis of the whole spectral image, as introduced by Turatto et al. (2002). Figure 11 shows the F(H
analysis of the whole spectral image, as introduced by Turatto et al. (2002). Figure 11 shows the F(H![]() )/F(H
)/F(H![]() )
isophotal contours superimposed on the H
)
isophotal contours superimposed on the H![]() spectral image for three representative PA of NGC 6741:
at
spectral image for three representative PA of NGC 6741:
at
![]() (close to the apparent minor axis; untilted H
(close to the apparent minor axis; untilted H![]() spectral image) F(H
spectral image) F(H![]() )/F(H
)/F(H![]() )
increases outwards along the
spatial (i.e. y) axis, peaking beyond the top of the H
)
increases outwards along the
spatial (i.e. y) axis, peaking beyond the top of the H![]() flux.
At
flux.
At
![]() (intermediate PA; tilted H
(intermediate PA; tilted H![]() spectral image) the F(H
spectral image) the F(H![]() )/F(H
)/F(H![]() )
rise along the y axis is overwhelmed by the
broad maximum to the S-W of the nebular centre (at the expected position of the absorbing belt visible in Fig. 1, upper
panel). The same occurs at
)
rise along the y axis is overwhelmed by the
broad maximum to the S-W of the nebular centre (at the expected position of the absorbing belt visible in Fig. 1, upper
panel). The same occurs at
![]() (close to the apparent major axis; tilted H
(close to the apparent major axis; tilted H![]() spectral image), where F(H
spectral image), where F(H![]() )/F(H
)/F(H![]() )
peaks W-SW of the centre, corresponding to the equatorial absorbing belt.
)
peaks W-SW of the centre, corresponding to the equatorial absorbing belt.
Summing up the H![]() /H
/H![]() intensity distribution at the nine observed PA of NGC 6741, we infer that:
intensity distribution at the nine observed PA of NGC 6741, we infer that:
Last, an indicative value of the total neutral mass embedding the ionized nebula (through Eq. (5) and using simple geometrical considerations)
is
![]() (
(![]() 0.05)
0.05) ![]() .
.
Although the small angular size prevents a deeper analysis, these results do represent the umpteenth sign of the complex structure and peculiar evolutionary phase of NGC 6741, and will be a precious support in the determination of the topical parameter, i.e. distance.
Individual values reported in the literature are: 1300 pc (nebular radial velocity combined with the circular law of galactic rotation;
Acker 1978), 2100 pc (Acker 1978) and 1400 pc (Pottasch 1983) (both based on the large-scale galactic interstellar absorption map by Lucke 1978),
and 1500 pc (color-excess vs. distance relation for early-type stars within 1.5
![]() of the nebula; Kaler & Lutz 1985).
of the nebula; Kaler & Lutz 1985).
We tried to determine the nebular parallax by combining the expansion velocity field with the angular expansion measured in first- and second-epoch HST-WFPC2 frames. The NASA public archives contain 21 images of NGC 6741, taken at two epochs separated by 2.97 years (programs GO 7501 and GO 8773; P. I. Arsen Hajian). The [O III] and [N II] multiple exposures (WFPC2 central planetary camera, PC; pixel size = 0.0455 arcsec) were co-added, corrected for optical distortions, aligned and rotated using IRAF packages (Reed et al. 1999; Palen et al. 2002).
No apparent image-shift is detected, i.e. image-
![]() pixel, and
pixel, and
![]() arcsec yr-1.
For an optically thin, fully ionized PN this implies
arcsec yr-1.
For an optically thin, fully ionized PN this implies ![]() pc, being:
pc, being:
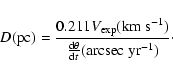 |
(8) |
We decided to enrich (and sharpen, if possible) the broad color-excess vs. D relation given by Kaler & Lutz (1985) with recent bibliographic reports. Scanning the NGC 6741 neighbourhood with the SIMBAD facilities of CDS (Centre de Données astronomiques de Strasbourg) gave two dozen (low-weight) field stars with accurate photometry and spectral type (in most cases the luminosity class is absent; we assume a luminosity class V), and two important distance markers:
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{h2447f12.eps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg149.gif) |
Figure 12: Color-excess vs. distance relation in the direction of NGC 6741. Symbols: small dots = field stars; filled square = open cluster OCL 88; large dot = classical Cepheid V336 Aql. |
| Open with DEXTER | |
To test this point, we consider the four more PNe projected within the Aquila-Scutum cloud (at an apparent distance from
NGC 6741 less than 90'). They are CBSS 3, K 3-19, M 1-66 and K 3-20 (we reject a fifth object, Sp 2-151, because of the unreliable line
intensities - in particular F(H![]() )/F(H
)/F(H
![]() - and peculiar spectral-type A for the exciting star reported by Acker et al.
1992, probably due to the partial blending with a relatively bright,
- and peculiar spectral-type A for the exciting star reported by Acker et al.
1992, probably due to the partial blending with a relatively bright,
![]() ,
field star). The four selected PNe in the
Aquila-Scutum cloud have
,
field star). The four selected PNe in the
Aquila-Scutum cloud have ![]() (
(
![]() (line intensities by Acker et al. 1992; and Cappellaro et al. 1994, for
(line intensities by Acker et al. 1992; and Cappellaro et al. 1994, for
![]() K and
K and
![]() cm-3), i.e.
cm-3), i.e.
![]() ,
and, using the obscuration law by Forbes
(1985), D> 6000 pc for all four nebulae.
,
and, using the obscuration law by Forbes
(1985), D> 6000 pc for all four nebulae.
The last result appears quite improbable. Thus, in the following we will adopt the
color-excess vs.
distance relation shown in Fig. 12 and D(NGC 6741) = 2000 (![]() 300) pc.
300) pc.
The linear size of the main nebula is
![]() pc (major, intermediate and minor semi-axes, respectively), whereas both
the spherical recombining halo and the [O III] rays punching the [N II] skin close to the apparent major axis extend up to 0.080 pc.
pc (major, intermediate and minor semi-axes, respectively), whereas both
the spherical recombining halo and the [O III] rays punching the [N II] skin close to the apparent major axis extend up to 0.080 pc.
The "kinematical'' age of NGC 6741,
![]() ,
is about 750 years and the "true'' age
,
is about 750 years and the "true'' age
![]() / [
/ [
![]() today
today
![]() AGB)
AGB)
![]() years.
years.
Summing up: NGC 6741 is a very young, compact, high surface brightness (i.e. dense) PN. The combination of (a) high excitation (up to [Ne V]) of the innermost layers; (b) a low ionization skin; and (c) an almost neutral, large density halo, is indicative of a very hot central star at low luminosity. A deep analysis of the powering engine is needed.
The HST-WFPC2 frames of NGC 6741 taken through the broad-band filter F555W
(central
![]() ,
,
![]() )
provide
mV=20.09 (
)
provide
mV=20.09 (![]() 0.05), where the unknown star color is the main source of inaccuracy. Previous ground-based estimates reported
in the
literature are: 19.5 (Pottasch 1981), 17.6 (Tylenda et al. 1989), 19.16 (Kaler & Jacoby 1989) and 19.26 (Hyung & Aller 1997) for mV, and >20.2 (Gathier & Pottasch 1988) and 18.2 (Tylenda et al. 1989) for mB.
0.05), where the unknown star color is the main source of inaccuracy. Previous ground-based estimates reported
in the
literature are: 19.5 (Pottasch 1981), 17.6 (Tylenda et al. 1989), 19.16 (Kaler & Jacoby 1989) and 19.26 (Hyung & Aller 1997) for mV, and >20.2 (Gathier & Pottasch 1988) and 18.2 (Tylenda et al. 1989) for mB.
The H I and He II Zanstra temperatures are given by the stellar magnitude, combined with both the total H![]() nebular flux,
log F(H
nebular flux,
log F(H![]() )
)
![]() (
(![]() ) mW
) mW![]() m-2 (Kaler & Lutz 1985; Kaler & Jacoby 1989; Acker et al. 1991;
Cahn et al. 1992; this paper), and the flux ratio F(
m-2 (Kaler & Lutz 1985; Kaler & Jacoby 1989; Acker et al. 1991;
Cahn et al. 1992; this paper), and the flux ratio F(![]() 4686
4686 ![]() )/F(H
)/F(H
![]() (
(![]() )
(Aller et al. 1985; Kaler & Jacoby 1989; Hyung & Aller 1997; this paper).
)
(Aller et al. 1985; Kaler & Jacoby 1989; Hyung & Aller 1997; this paper).
We obtain
log(![]() H I
H I
![]() )
and log(
)
and log(![]() He II
He II
![]() ),
thus confirming the peculiarity already reported by Heap et al. (1989) and Hyung & Aller (1997), i.e. the Zanstra discrepancy is reversed.
),
thus confirming the peculiarity already reported by Heap et al. (1989) and Hyung & Aller (1997), i.e. the Zanstra discrepancy is reversed.
![]() He II is a typical signature of recombining PNe, e.g. NGC 6565 (Turatto et al. 2002), where the
ionization and thermal structure are out of equilibrium, and the recombination processes dominate. These are faster for the
higher-ionization species (Tylenda 1986; Stasinska 1989; Marten & Szczerba 1997); thus, in the following, we will adopt
He II is a typical signature of recombining PNe, e.g. NGC 6565 (Turatto et al. 2002), where the
ionization and thermal structure are out of equilibrium, and the recombination processes dominate. These are faster for the
higher-ionization species (Tylenda 1986; Stasinska 1989; Marten & Szczerba 1997); thus, in the following, we will adopt
![]() H I.
H I.
The stellar luminosity (using D=2000 pc, and the bolometric corrections by Schönberner 1981) is log L*/
![]() (
(![]() ).
).
The high temperature and low luminosity of the star, added to the low nebular age, suggest that the stellar mass,
M*, is larger
than the average value (![]() 0.60
0.60 ![]() )
of the PNe nuclei. According to the evolutionary tracks by
Schönberner (1981, 1983), Iben (1984),
Wood & Faulkner (1986), Blöcker & Schönberner (1990), Vassiliadis & Wood (1994) and Blöcker (1995), the 0.66-0.68
)
of the PNe nuclei. According to the evolutionary tracks by
Schönberner (1981, 1983), Iben (1984),
Wood & Faulkner (1986), Blöcker & Schönberner (1990), Vassiliadis & Wood (1994) and Blöcker (1995), the 0.66-0.68 ![]() post-AGB star of NGC 6741 has recently (a few hundreds years ago) exhausted the hydrogen-shell nuclear burning, and is fading
along the white dwarf cooling sequence.
post-AGB star of NGC 6741 has recently (a few hundreds years ago) exhausted the hydrogen-shell nuclear burning, and is fading
along the white dwarf cooling sequence.
The early luminosity decline of the star was very fast (and caused the nebular recombination), but later
it gradually slowed, so that
we cannot exclude that, at present, the gas has reached (or even passed) the contraction-expansion equilibrium condition,
(1/3)![]() (d(lnL*)/d
(d(lnL*)/d
![]() in the classical Strömgren model, thanks to matter dilution due to expansion.
in the classical Strömgren model, thanks to matter dilution due to expansion.
New input will come from the nebular physical conditions, radial ionization structure and photo-ionization model.
The main limitation is connected to the NGC 6741 compactness, large stratification of the radiation and weakness of the [N II] auroral line and
the [S II] and [Ar IV] doublets: ![]() [N II],
[N II], ![]() [S II] and
[S II] and ![]() [Ar IV] can be derived only at (or close to) the
intensity peak of the corresponding emission.
[Ar IV] can be derived only at (or close to) the
intensity peak of the corresponding emission.
Moreover, the large H![]() broadening implies a complex deconvolution for instrumental resolution plus thermal motion plus fine-structure
(see Sect. 2), lowering the accuracy of the F(H
broadening implies a complex deconvolution for instrumental resolution plus thermal motion plus fine-structure
(see Sect. 2), lowering the accuracy of the F(H
![]() and
and ![]() (H
(H![]() )
profiles. Thus, according to Benetti et al. (2003),
F(H
)
profiles. Thus, according to Benetti et al. (2003),
F(H
![]() and
and ![]() (H
(H![]() )
are also obtained from the radial ionization structure relative to O++ (Sect. 7.2) and the fair assumption
)
are also obtained from the radial ionization structure relative to O++ (Sect. 7.2) and the fair assumption
![]() across the nebula; at each position:
across the nebula; at each position:
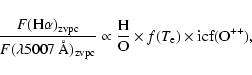 |
(9) |
For the internal, high-excitation regions
![]() comes from the ionization structure of helium (Seaton 1968; Benetti et al. 2003):
comes from the ionization structure of helium (Seaton 1968; Benetti et al. 2003):
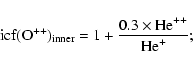 |
(10) |
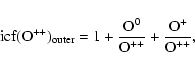 |
(11) |
Moreover (Sabbadin et al. 2004),
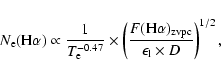 |
(12) |
A comparative analysis gives quite satisfactory results: the ![]() (H
(H![]() )
profiles obtained in the two ways
differ by less than 5
)
profiles obtained in the two ways
differ by less than 5![]() everywhere, except in the faint, innermost regions, where the discrepancy rises up to 10
everywhere, except in the faint, innermost regions, where the discrepancy rises up to 10![]() .
In the following we
will adopt
.
In the following we
will adopt ![]() (H
(H![]() )
given by F(
)
given by F(![]() 5007
5007 ![]() )
)
![]() and Eqs. (9) to (12).
and Eqs. (9) to (12).
![\begin{figure}
\par\includegraphics[width=8cm,height=8.9cm,clip]{h2447f13.eps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg191.gif) |
Figure 13:
Radial distribution of the physical conditions ( |
| Open with DEXTER | |
Figure 13 shows the resulting radial distribution of the physical conditions in NGC 6741 at
![]() and
and
![]() (close to the apparent
minor and major axes, respectively).
(close to the apparent
minor and major axes, respectively).
The radial trend of ![]() [O III] is common at all PA:
[O III] is common at all PA: ![]() 15 000 K in the
weak innermost regions, rapidly decreasing outward to 12 000 K in the densest layers, and
more or less constant further (uncertain).
15 000 K in the
weak innermost regions, rapidly decreasing outward to 12 000 K in the densest layers, and
more or less constant further (uncertain). ![]() [N II] is systematically lower than
[N II] is systematically lower than ![]() [O III]. All this is in quantitative
agreement with the results by Hyung & Aller (1997) and Pottasch et al. (2001).
[O III]. All this is in quantitative
agreement with the results by Hyung & Aller (1997) and Pottasch et al. (2001).
![]() presents a broad, asymmetric bell-shape profile with peaks up to 12 000 (
presents a broad, asymmetric bell-shape profile with peaks up to 12 000 (![]() 1000) cm-3 close to the minor axis,
and 6000-8000 (
1000) cm-3 close to the minor axis,
and 6000-8000 (![]() 800) cm-3 close to the major axis.
Note that, in spite of the high density peaks - causing strong collisional de-excitation of the [S II]
800) cm-3 close to the major axis.
Note that, in spite of the high density peaks - causing strong collisional de-excitation of the [S II] ![]() 6717
6717 ![]() line -
we have
line -
we have
![]() S II
S II
![]() (H
(H![]() ), i.e. the local filling factor is
), i.e. the local filling factor is
![]() ,
with
,
with
![]() S II
S II
![]() (H
(H![]() (Aller 1984; Pottasch 1984;
Osterbrock 1989).
(Aller 1984; Pottasch 1984;
Osterbrock 1989).
![]() [Ar IV] is systematically lower than
[Ar IV] is systematically lower than ![]() [S II] adopting the electron impact excitation rates
by Keenan et al. (1997), whereas
[S II] adopting the electron impact excitation rates
by Keenan et al. (1997), whereas
![]() Ar IV
Ar IV
![]() S II] for earlier collisional rates (for example, Aller 1984).
S II] for earlier collisional rates (for example, Aller 1984).
Concerning the halo, ![]() peaks at the inner edge (
peaks at the inner edge (![]() 1000-1500 cm-3), and decreases outwards.
1000-1500 cm-3), and decreases outwards.
Recent density determinations (mean values integrated over the slit) reported in the literature for NGC 6741 are:
![]() (different ions)=6300 cm-3 by Hyung & Aller (1997),
(different ions)=6300 cm-3 by Hyung & Aller (1997), ![]() [S II]=6000 cm-3,
[S II]=6000 cm-3, ![]() [O II]=8500 cm-3,
[O II]=8500 cm-3,
![]() [Cl III]=9000 cm-3 and
[Cl III]=9000 cm-3 and ![]() [Ar IV]=5500 cm-3 by Pottasch et al. (2001), and
[Ar IV]=5500 cm-3 by Pottasch et al. (2001), and ![]() [Cl III]=4470 cm-3,
[Cl III]=4470 cm-3,
![]() [Ar IV]=6610 cm-3 and
[Ar IV]=6610 cm-3 and ![]() [52
[52 ![]() m/88
m/88 ![]() m]=2880 cm-3 by Liu et al. (2001).
m]=2880 cm-3 by Liu et al. (2001).
The ionized mass of NGC 6741, obtainable from the observed ![]() spatial distribution, the H
spatial distribution, the H![]() flux, and
the radio flux (Aller 1984; Pottasch 1984; Osterbrock 1989; and Turatto et al. 2002), results to be
flux, and
the radio flux (Aller 1984; Pottasch 1984; Osterbrock 1989; and Turatto et al. 2002), results to be
![]() (
(![]() 0.02)
0.02) ![]() ,
i.e. much lower than the mass of the external, neutral cocoon,
,
i.e. much lower than the mass of the external, neutral cocoon,
![]() (
(![]() 0.05)
0.05) ![]() (see Sect. 4),
thus confirming the peculiar evolutionary phase of our nebula.
(see Sect. 4),
thus confirming the peculiar evolutionary phase of our nebula.
The relatively high ![]() of the halo implies a quite recent recombination start, no more
that 200 years ago. In fact, the
of the halo implies a quite recent recombination start, no more
that 200 years ago. In fact, the ![]() depletion rate for
recombination is:
depletion rate for
recombination is:
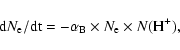 |
(13) |
![\begin{displaymath}N_{\rm e}(0) = N_{\rm e}({t})/[1{-}8.2\times10^{-6}\times{t}\times N_{\rm e}{(t)}],
\end{displaymath}](/articles/aa/full/2005/23/aa2447-04/img204.gif) |
(14) |
All this, combined with the short nebular age (![]() 1400 years), agrees with the theoretical evolutionary
times of a 0.66-0.68
1400 years), agrees with the theoretical evolutionary
times of a 0.66-0.68 ![]() post-AGB star. According to Blöcker (1995, and references therein), in the interval
post-AGB star. According to Blöcker (1995, and references therein), in the interval
![]() (end of the superwind ejection) to
(end of the superwind ejection) to
![]() yr the hydrogen-burning star horizontaly crosses
the H-R diagram (at log L*/
yr the hydrogen-burning star horizontaly crosses
the H-R diagram (at log L*/
![]() )
becoming hotter and hotter (up to log
)
becoming hotter and hotter (up to log
![]() K). At
K). At
![]() yr the nuclear fuelling becomes insufficient, and
in a century the luminosity
declines to log L*/
yr the nuclear fuelling becomes insufficient, and
in a century the luminosity
declines to log L*/
![]() (whereas T* reaches its maximum, log
(whereas T* reaches its maximum, log
![]() K). At
K). At
![]() yr the
hydrogen-shell burning ceases,
the stellar evolution drastically accelerates untill
yr the
hydrogen-shell burning ceases,
the stellar evolution drastically accelerates untill
![]() yr (log L*/
yr (log L*/
![]() ;
log
;
log
![]() K), and later
slows down (for example, at
K), and later
slows down (for example, at
![]() yr we have log L*/
yr we have log L*/
![]() and log
and log
![]() K).
K).
Thus, NGC 6741 is close to (or has even passed) the recombination-reionization transition.
![\begin{figure}
\par\includegraphics[width=8cm,height=9.8cm,clip]{h2447f14.eps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg223.gif) |
Figure 14:
The
|
| Open with DEXTER | |
Table 3: NGC 6741: chemical abundances (relative to log H = 12).
The zvpc of the different emissions furnishes the detailed radial ionization structure of NGC 6741. Since the blurred H![]() appearance
lowers the accuracy of the
F(H
appearance
lowers the accuracy of the
F(H
![]() distribution, we adopt
distribution, we adopt ![]() 5007
5007 ![]() as the reference emission, thus
inferring the radial ionization structure relative to O++ (for details, see Benetti et al. 2003). The
as the reference emission, thus
inferring the radial ionization structure relative to O++ (for details, see Benetti et al. 2003). The
![]() profiles
of NGC 6741 at
profiles
of NGC 6741 at
![]() and
and
![]() (close to the apparent minor and major axes, respectively), presented in Fig. 14,
confirm that the nebula is optically thick in all directions.
(close to the apparent minor and major axes, respectively), presented in Fig. 14,
confirm that the nebula is optically thick in all directions.
Within this scenario, the [O III] rays punching the [N II] skin (Fig. 2) identify a few radial directions along and close to the true
major axis of the nebula with "low'' ![]() peaks (
peaks (
![]() peak
peak![]() cm-3 according to the photo-ionization model
presented in this section): in these directions (barely visible in our spectral images at
cm-3 according to the photo-ionization model
presented in this section): in these directions (barely visible in our spectral images at
![]() ,
95
,
95
![]() and 115
and 115
![]() ;
see Figs. 4 and 10) recombination processes are less efficient and the gas can be (partially) ionized by the UV stellar flux at larger
distances.
;
see Figs. 4 and 10) recombination processes are less efficient and the gas can be (partially) ionized by the UV stellar flux at larger
distances.
When combined with the results in the previous sections, the overall, complex structure of NGC 6741, fully driven by the fast evolving central star, can be divided into three distinct zones showing quite different physical characteristics: the internal, high-to-medium excitation nebula directly ionized by the stellar radiation ends in a sharp transition zone at medium-to-low excitation marking the present edge of the ionization front. It is surrounded by the gas no longer reached by the fading UV flux (i.e. the halo), dominated by recombination processes. A similar onion-like radial structure (ionization-transition-recombination) is observed in NGC 6565 (Turatto et al. 2002).
Although the ionization and thermal structure of NGC 6741 are out of equilibrium, the large ![]() of the ionized gas (peaks
up to 12 000 cm-3) assures a rapid nebular response to the variable stellar flux. In particular, the delay in the "transition zone''
is short, the recombination time,
of the ionized gas (peaks
up to 12 000 cm-3) assures a rapid nebular response to the variable stellar flux. In particular, the delay in the "transition zone''
is short, the recombination time,
![]() ), being a few years for hydrogen (even shorter
for higher ionization species).
), being a few years for hydrogen (even shorter
for higher ionization species).
Thus, NGC 6741 is nearly in equilibrium. This allows us to neglect (to a first approximation) the time dependance, and estimate the total chemical abundances of the ionized gas with the classical method valid for "static'' nebulae.
We follow a two-step procedure:
I (broad approach): according to the critical analyses by Alexander & Balick (1997) and Perinotto et al. (1998), the mean ionic abundances are obtained from the line fluxes integrated over the spatial profile and the expansion velocity field; later on, we correct for the unobserved ionic stages by means of the ionization correcting factors, derived both empirically (Barker 1983, 1986) and from interpolation of theoretical nebular models (Shields et al. 1981; Aller & Czyzak 1983; Aller 1984; Osterbrock 1989). The resulting mean chemical abundances are listed in Table 3 (second row); recent estimates reported in the literature are also given in the table.
Table 4: Input parameters for the model nebula (CLOUDY).
II (refining): we apply the photo-ionization code CLOUDY (Ferland et al. 1998) to a model nebula characterized by the same
distance, gas distribution, mean chemical composition and exciting star parameters as NGC 6741 and combine the model-line profiles
(convolved for a seeing+guiding of 0.60
![]() )
with the line profiles observed in the true nebula.
)
with the line profiles observed in the true nebula.
Let us focus on the zvpc of the S-SW sector at
![]() (close to the apparent minor axis of NGC 6741). The input parameters of the model-nebula
are given in Table 4, and Fig. 15 shows the physical conditions in the model nebula (to be compared with Fig. 13), and the absolute
radial flux distribution of the main emission in both the model nebula and NGC 6741.
(close to the apparent minor axis of NGC 6741). The input parameters of the model-nebula
are given in Table 4, and Fig. 15 shows the physical conditions in the model nebula (to be compared with Fig. 13), and the absolute
radial flux distribution of the main emission in both the model nebula and NGC 6741.
Figure 15 provides a satisfactory model nebula vs. true nebula agreement for the internal, high-to-medium excitation regions and the transition zone. Further, the weak recombining halo appears in NGC 6741, whereas emission is absent in the static model nebula. The same is observed at the other PA.
In more detail, some disturbing drifts arise in Fig. 15. Two minor discrepacies are:
![\begin{figure}
\par\includegraphics[width=8cm,height=10.6cm,clip]{h2447f15.eps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg228.gif) |
Figure 15:
Model-nebula (CLOUDY) vs. true-nebula (NGC 6741,
|
| Open with DEXTER | |
Unfortunately, the large number of parameters involved (density profile, chemical abundances, dust, temperature and luminosity of the star) and assumptions (distance, black-body distribution, seeing convolution), added to the nebular compactness and peculiar evolutionary phase, greatly complicate the analysis, whose definitive solution needs detailed observations at even higher spatial and spectral resolutions.
According to the reconstruction method introduced by Sabbadin et al. (1985, 1987) and deepened by Sabbadin et al. (2000a,b),
we select ![]() 4686
4686 ![]() of He II,
of He II, ![]() 5007
5007 ![]() of [O III] and
of [O III] and ![]() 6584
6584 ![]() of [N II] as markers of the high, medium and low-ionization regions of NGC 6741, respectively. The spectral images are:
of [N II] as markers of the high, medium and low-ionization regions of NGC 6741, respectively. The spectral images are:
The projection of NGC 6741 for a rotation around the N-S direction (almost perpendicular to the major axis) is presented in Fig. 18 (multi-color images in the electronic version), providing a representative sample of the nebular appearance when changing the line of sight. The left panel, (0, 0), corresponds to NGC 6741 as seen from Earth (North is up and East to the left), to be compared with Fig. 1 and the HST image by Hajian & Terzian at http://ad.usno.navy.mil/pne/gallery.html
The overall characteristics of NGC 6741 (a hot and faint star at the centre of a dense, inhomogeneous, equatorial torus merging into a closed, ellipsoidal structure embedded in a large cocoon of almost neutral matter) closely resemble NGC 6565, a compact, recombining PN projected pole-on (Turatto et al. 2002), and show remarkable affinities with NGC 7027, the PNe prototype (Cox et al. 2002; Bains et al. 2003). Very likely, all three objects represent "middle-aged'' snapshots of a massive, fast evolving post-AGB star.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2447f16.eps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg237.gif) |
Figure 16:
Stereoscopic structure of NGC 6741 for a rotation around the
North-South axis centered on the exciting star. Opaque reconstruction at high flux-cut for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2447f17.eps}
\end{figure}](/articles/aa/full/2005/23/aa2447-04/Timg238.gif) |
Figure 17: Same as Fig. 16, but at low flux-cut. |
| Open with DEXTER | |
In spite of the nebula compactness, we have quite successfully applied tomographic and 3-D analyses to NGC 6741, covered at high spatial and spectral resolution with ESO NTT+EMMI.
NGC 6741 is a young (
![]() years) PN at a distance of 2000 pc; it consists of a high-excitation, almost-prolate ellipsoid
(
years) PN at a distance of 2000 pc; it consists of a high-excitation, almost-prolate ellipsoid
(
![]() pc; major, intermediate
and minor semi-axes, respectively) denser at the equator than at the poles
(
pc; major, intermediate
and minor semi-axes, respectively) denser at the equator than at the poles
(![]() peaks at 12 000 and 7000 cm-3, respectively), surrounded by a thin skin of low-excitation (the transition zone,
corresponding to the present ionization front), and embedded
in an extended, spherical (
peaks at 12 000 and 7000 cm-3, respectively), surrounded by a thin skin of low-excitation (the transition zone,
corresponding to the present ionization front), and embedded
in an extended, spherical (
![]() pc), almost neutral recombining halo containing a large fraction of the nebular mass
(
pc), almost neutral recombining halo containing a large fraction of the nebular mass
(
![]() versus
versus
![]() ).
).
The complex ionization structure of NGC 6741 is fully driven by the fast evolution of the central star, a massive (0.66-0.68 ![]() ),
hot (log
),
hot (log
![]() K) and faint (log L*/
K) and faint (log L*/
![]() )
post-AGB star fading towards the white-dwarf region (after exhaustion
of the hydrogen-shell nuclear burning).
)
post-AGB star fading towards the white-dwarf region (after exhaustion
of the hydrogen-shell nuclear burning).
The ionized gas of NGC 6741 follows the general expansion law
![]() (km s
(km s
![]() ,
except the innermost,
highest-excitation layers, showing clear evidence of deceleration. This peculiar kinematical behaviour can be qualitatively ascribed to the
luminosity drop of the central star (Schönberner et al. 1997; Steffen et al. 1998; Marigo et al. 2001; Perinotto et al. 2004a): in this
evolutionary phase
the stellar mass-loss quickly decreases, and the falling hot-bubble's pressure
no longer balances the
pressure of the ionized gas, so that the contact discontinuity and the
adjacent, high-excitation nebular layers accelerate inwards.
,
except the innermost,
highest-excitation layers, showing clear evidence of deceleration. This peculiar kinematical behaviour can be qualitatively ascribed to the
luminosity drop of the central star (Schönberner et al. 1997; Steffen et al. 1998; Marigo et al. 2001; Perinotto et al. 2004a): in this
evolutionary phase
the stellar mass-loss quickly decreases, and the falling hot-bubble's pressure
no longer balances the
pressure of the ionized gas, so that the contact discontinuity and the
adjacent, high-excitation nebular layers accelerate inwards.
The argument is poorly known, and deserves more attention, the kinematical properties of the innermost layers being an excellent diagnostic of the star-nebula interaction. A search for more "decelerated'' candidates, a high-resolution spectroscopic survey in ionic species at large IP and a detailed comparison with current hydro-dynamical simulations are highly desired.
Note that the opposite situation (i.e. acceleration) is expected for the external, recombining layers of NGC 6741, whose de-pressuring gives
rise to Rayleigh-Taylor instability at the ionization edge. Although the knotty and filamentary [N II] nebular appearance (Fig. 1, lower panel)
qualitatively agrees with this scenario, its confirmation needs very-high spectral resolution (
![]() )
echellograms detecting the
increase of expansion velocity (and turbulence) at the ionization edge.
)
echellograms detecting the
increase of expansion velocity (and turbulence) at the ionization edge.
A further interesting point concerns the wide radial matter distribution of NGC 6741 (much wider than the ![]() profile given in
Fig. 13, due to the presence of the dense, almost-neutral recombining halo). This indicates a modest contribution of wind interaction to the
nebular shaping
(it essentially supports the innermost layers, avoiding gas infall), whereas most occurs ionization: the thermal pressure
of the ionized gas accelerates the matter outwards and decelerates inwards, creating the density and velocity distributions observed in NGC 6741 (more general comments are given towards the end of this section).
profile given in
Fig. 13, due to the presence of the dense, almost-neutral recombining halo). This indicates a modest contribution of wind interaction to the
nebular shaping
(it essentially supports the innermost layers, avoiding gas infall), whereas most occurs ionization: the thermal pressure
of the ionized gas accelerates the matter outwards and decelerates inwards, creating the density and velocity distributions observed in NGC 6741 (more general comments are given towards the end of this section).
| |
Figure 18:
Optical appearance of NGC 6741 (multi-color in the electronic version of the paper; blue = He II, green = [O III], red = [N II]) for a rotation
through the N-S axis centered on the exciting star. The left panel, (0, 0), corresponds to the re-built
nebula as seen from the Earth (North is up and East to the left);
projection(
|
| Open with DEXTER | |
Although the precise radial profile of the matter remains unknown - a large fraction of NGC 6741 being neutral -, the
outer radius
of the main nebula extends well beyond the present ionization edge. This is supported by the absence of any extended, diffuse, faint and round
AGB-halo emission in the Palomar Sky Survey plates, deep imaging by
Schwarz et al. (1992), and HST frames. This is confirmed by our spectra:
no kinematical signature of an AGB-halo (i.e. external, faint, un-tilted and un-split emission) appears.
Since the low-density gas of an AGB-halo (usually
![]() to 200 cm-3; Chu et al. 1987; Corradi et al. 2003) is little affected by
recombination
(from Eq. (14),
to 200 cm-3; Chu et al. 1987; Corradi et al. 2003) is little affected by
recombination
(from Eq. (14),
![]() to 200 cm-3 implies
to 200 cm-3 implies ![]() (200 yr)=47 to 162 cm-3), we infer that:
(200 yr)=47 to 162 cm-3), we infer that:
Thanks to the unprecedented accuracy achieved by tomography and 3-D recovery, we have obtained observational evidence supporting the recombination hypothesis for NGC 6741:
| (15) |
The Strasbourg-ESO Catalogue of Galactic PNe (Acker et al. 1992) allowed us to select some fifty targets satisfying
Eq. (15). Half of them (e.g. NGC 2440, Hb 4, NGC 6565, NGC 6537, NGC 6620, NGC 6741, NGC 6886, NGC 6881, NGC 7027, Hu 1-2, NGC 6302, and NGC 6563) are compact
(sometimes with butterfly-like extentions) at high surface brightness, and represent young recombining PNe ejected and
excited by a massive (
![]() )
fast evolving star beyong the turn-around point in the H-R diagram. The remaining candidates
are mean-to-low surface brightness, extended (often bipolar) nebulae (e.g. NGC 6445,
NGC 6439, A 55, NGC 6772, A 53, NGC 6818, NGC 6894, NGC 7048, NGC 2438, NGC 2818, and IC 4406),
corresponding to aged, evolved PNe, optically thick (at least in some directions) to the fading UV radiation of a moderately-massive (0.60 to 0.64
)
fast evolving star beyong the turn-around point in the H-R diagram. The remaining candidates
are mean-to-low surface brightness, extended (often bipolar) nebulae (e.g. NGC 6445,
NGC 6439, A 55, NGC 6772, A 53, NGC 6818, NGC 6894, NGC 7048, NGC 2438, NGC 2818, and IC 4406),
corresponding to aged, evolved PNe, optically thick (at least in some directions) to the fading UV radiation of a moderately-massive (0.60 to 0.64 ![]() )
post-AGB star in the white dwarf cooling sequence.
)
post-AGB star in the white dwarf cooling sequence.
Further support for the "massive'' nature of the central stars of PNe satisfying Eq. (15) is that:
Thus, recombination represents a not un-common evolutionary phase in PNe; it becomes inescapable for massive nebulae ejected and excited by a massive, fast-evolving post-AGB star (also see Tylenda 1986; Szczerba 1990; Phillips 2000; Marigo et al. 2001; Turatto et al. 2002; Benetti et al. 2003; and Perinotto et al. 2004a).
We end with some general considerations on the kinematics of the whole PN class. The comparative analysis performed in Sect. 3 - rejecting the kinematical results based on spherical symmetry assumption and/or emission profiles of recombination lines integrated along the slit - demonstrates the rarity of real nebulae showing a "U'-shaped expansion velocity field.
We stress that:
Wind interaction being the main cause of the "V''-shaped expansion profile in double-shell model-PNe, as well of the increasing inwards velocity field in single-shell model-PNe, we infer that all current radiation-hydrodynamics simulations tend to overestimate the dynamical effects of fast stellar wind on the nebular gas (we suspect that post-AGB mass-loss rates adopted by theoretical simulations are systematically too high). Although the same finding arose in the study of NGC 6565 (Turatto et al. 2002), NGC 6818 (Benetti et al. 2003) and NGC 7009 (Sabbadin et al. 2004), a quantitative answer (also including (a) the temporal evolution of mass-loss in the superwind phase, Schönberner et al. 2005, and (b) the binarity and the possible role of magnetic fields, Garcia-Segura & Lopez 2000; Blackman et al. 2001) will come from a detailed analysis performed on a representative sample of PNe in both hemispheres, covered with ESO NTT+EMMI and TNG+SARG (work in preparation).
We investigated gas kinematics, galactic and circum-nebular absorptions, nebular distance, mass and age. We also discussed the stellar properties, nebular physical conditions, ionization structure and photo-ionization model, image de-projection, and multi-color and opaque reconstructions of the nebula.
The results:
Acknowledgements
We wish to thank the support staff of the NTT (in particular, Olivier Hainaut) for the excellent assistance during the observations.
 n6741he2_high.avi
n6741he2_high.avi