A&A 436, 479-492 (2005)
DOI: 10.1051/0004-6361:20041887
O. Moreau1 - C. Libbrecht1 - D.-W. Lee1,2 - J. Surdej1,![]()
1 - Institut d'Astrophysique et de Géophysique, Université de Liège, Allée du 6 août 17, B5c, 4000 Sart Tilman, Belgium
2 -
ARCSEC, Dept. of Astronomy, Sejong University, Goonja-dong, Kwangjin-gu, Seoul, Republic of Korea
Received 24 August 2004 / Accepted 3 March 2005
Abstract
Using an optimal image subtraction technique, we have derived the V and R light curves of the four lensed QSO components of Q2237+0305 from the monitoring CCD frames obtained by the GLITP collaboration with the 2.6 m NOT telescope in 1999/2000 (Alcalde et al. 2002). We give here a detailed account of the data reduction and analysis and of the error estimates. In agreement with Wozniak et al. (2000b,a), the good derived photometric accuracy of the GLITP data allows to discuss the possible interpretation of the light curve of component A as due to a microlensing event taking place in the deflecting galaxy. This interpretation is strengthened by the colour dependence of the early rise of the light curve of component A, as it probably corresponds to a caustics crossing by the QSO source.
Key words: gravitational lensing - quasars: individual: Q2237+0305 - techniques: photometric - techniques: image processing
First discovered by Huchra and collaborators (Huchra et al. 1985), the gravitational lens system Q2237+0305 (so-called the Einstein Cross) is a very interesting case where the quadruple image of the quasar at z=1.7 is mixed with that of the nucleus of the very nearby (z=0.039) deflecting galaxy. Due to the symmetry of the system and to the small angular separation of its components (1 arcsec, typically), a time delay of approximately 1 day is expected between the four quasar images (Schneider et al. 1988). Because of the proximity of the intervening galaxy and because the lines of sight of the four components are very close to its centre, microlensing by stars - or at least compact objects - is highly probable (Kayser & Refsdal 1989). Since the discovery by Irwin et al. (1989) of the first event in the light curve of the brightest component (i.e. A), it has been recognized that Q2237+0305 represents an ideal system to study extragalactic microlensing.
This lens is known, however, to be one of the most complex cases for accurate photometry because of the blending of the four quasar images and the high apparent brightness of the deflecting galaxy core, polluting the components A, B, C and D with a strong and non-uniform background. As pointed out by Burud et al. (1998), the study of this peculiar object requires that one applies the best photometric methods; these authors compared deconvolution with two different profile fitting techniques and concluded that the achieved accuracy is dramatically dependent on the model used to describe the galaxy photometric profile.
Thus, a very good strategy for an accurate monitoring of the four lensed components of Q2237+0305 appears to be the implementation of an image subtraction technique designed to remove the galaxy contribution without any modeling of its photometric profile. Wozniak et al. (2000b,a) made the first use of that method to obtain accurate light curves of the Einstein Cross components from monitoring CCD frames taken in the V band using the 1.3 m Warsaw telescope located on Las Campanas (Chile), with a pixel size of 0.42''. As a matter of fact, a method for optimal image subtraction using convolution by space-varying kernels has been provided by Alard (2000) who implemented the ISIS software![]() , mainly in order to search for galactic microlensing events in highly crowded fields.
, mainly in order to search for galactic microlensing events in highly crowded fields.
In a paper published a few years ago (Alcalde et al. 2002), we analyzed the set of data available from the GLITP (Gravitational Lenses International Time Project) monitoring of Q2237+0305, using an adapted and completed version of the ISIS image subtraction technique, and compared the light curves with those derived by our IAC (Instituto de Astrofísica de Canarias) colleagues through PSF![]() -fitting direct photometry. In the present paper, we give a detailed account of the data reduction and analysis that we performed using a modified and completed version of ISIS and of our estimates of the photometric uncertainties. We also report on the colour effects displayed in the light curves of components A, B, C and D of Q2237+0305.
-fitting direct photometry. In the present paper, we give a detailed account of the data reduction and analysis that we performed using a modified and completed version of ISIS and of our estimates of the photometric uncertainties. We also report on the colour effects displayed in the light curves of components A, B, C and D of Q2237+0305.
We present in Sect. 2 the set of data available from the GLITP monitoring of Q2237+0305 that was obtained in the V and R bands at the 2.6 m NOT telescope (La Palma, Canary Islands) with a very good angular sampling (0.18'' per pixel). In Sect. 3, we describe the differential photometric technique that we used, based on a modified version of the ISIS software that we implemented in Liège to properly analyze the restricted field available around Q2237+0305. We also present the original software that we designed for differential photometry on the ISIS-subtracted CCD frames. We detail in Sect. 4 how we derived the magnitude zero-points necessary to calculate from differential photometry the final photometric light curves. We describe in Sect. 5 the analysis of simulated CCD frames that we have performed in order to estimate realistic error bars.
We display in Sect. 6 the light curves of components A, B, C and D that we derived in the V and R bands as well as the resulting V-R colour measurements. We also mention the results of several photometric tests validating the obtained results. Finally, we discuss in Sect. 7 the interpretation of the light curve of component A as due to a strong microlensing event in the intervening galaxy.
In the framework of the GLITP collaboration, a monitoring program of Q2237+0305 was conducted (Alcalde et al. 2002). We detail in this paper the photometric measurements of the data taken between October 1999 and February 2000 with the 2.6 m NOT telescope. A total of 56 CCD frames in the V band and 55 in the R one is available for accurate photometry of the lensed components A, B, C and D of this particular object during the considered period (see Table 1).
These good-quality frames have all been taken with an exposure time of 300 s and, for the majority of them, obtained using the StanCam
![]() detector, characterized by a pixel size of 0.176'' on the sky, a gain of 1.68 electrons/ADU and a read-out noise of 6.5 electrons. However, a few of them (8 in each band) were obtained using the ALFOSC
detector, characterized by a pixel size of 0.176'' on the sky, a gain of 1.68 electrons/ADU and a read-out noise of 6.5 electrons. However, a few of them (8 in each band) were obtained using the ALFOSC
![]() detector, i.e. with a pixel size of 0.189'', a gain of 1.05 electrons/ADU and a read-out noise of 5.5 electrons. In order to include these particular frames in the same photometric process as the other ones, we made them compatible in sampling and field of view. To do that, we rebinned these images to a common scale of 0.176''/pixel and selected from them only the central
detector, i.e. with a pixel size of 0.189'', a gain of 1.05 electrons/ADU and a read-out noise of 5.5 electrons. In order to include these particular frames in the same photometric process as the other ones, we made them compatible in sampling and field of view. To do that, we rebinned these images to a common scale of 0.176''/pixel and selected from them only the central
![]() -pixel part of the field. We also note that some images were flipped east to west and for these, we merely transposed their pixels (without rebinning). Moreover, we observed in a few frames a field rotation of up to 45
-pixel part of the field. We also note that some images were flipped east to west and for these, we merely transposed their pixels (without rebinning). Moreover, we observed in a few frames a field rotation of up to 45
![]() ,
that we also corrected in order to reduce the total set of data to a frame series as homogeneous as possible; for that correction, we clearly had to rebin the images. All this preliminary image processing was made using the IRAF package.
,
that we also corrected in order to reduce the total set of data to a frame series as homogeneous as possible; for that correction, we clearly had to rebin the images. All this preliminary image processing was made using the IRAF package.
The standard field of view of the frames, i.e. 3', is quite small and, as the star density in this high galactic region of the sky is low, only a few field stars could be observed. Furthermore, the frames are usually shifted by tens of pixels from one night to another so that the field of view common to the whole frame set is even narrower... As we shall see, the optimal subtraction technique involves the building of a stacked reference frame from which all individual images will be subtracted; it requires that they are aligned on the same coordinate grid. Only the field common to the different frames is then usable for kernel fitting and we may get problems if there are too few stars lying in this common field. So, we recommend that any future monitoring data be taken with proper attention to the centring of the field of view and also to the field rotation.
We received from IAC the CCD frames already flat-fielded and corrected for bias (see Alcalde et al. 2002) so that we were able to go directly to photometry. The set of data is described in detail in Table 1: one finds in Col. 1 the date and universal time at the beginning of the exposure, in Col. 2 the corresponding heliocentric Julian Day and finally in Cols. 3 and 4 the seeing and mean sky background values, respectively, that we estimated using IRAF commands. From that list, we were constrained to exclude two frames from the analysis process: one (Dec. 13, V) because of a detector line problem exactly located on the image of Q2237+0305 and another one (Feb. 3, R) showing an excessive elongation of the images. Finally, 55 frames remained available in the V band and 54 in the R one. However, for the sake of accuracy, we decided to exclude from the following photometric process all frames characterized by a seeing equal to, or greater than 1.8'' such that a total of 53 frames in V and 51 in R were actually analyzed.
Table 1: CCD frames of the gravitational lens system Q2237+0305 taken with the 2.6 m NOT telescope in 1999/2000 for the GLITP collaboration (Bgnd stands for mean sky background level).
Image subtraction appears to be one of the best suited techniques to derive accurate photometry of the four lensed components of Q2237+0305 because it does not require any modeling of the lensing galaxy profile. Differential photometry performed on the residual images is free from systematic uncertainties due to the unknown lensing galaxy model; only a possible systematic error from the zero-point calibration is expected to affect the light curves obtained using this method.
First of all, we rebinned all the CCD frames available in each of the V and R bands so that they match a common sampling pixel grid. We modified routines from the public ISIS package (Alard 2000) to perform astrometric calibration of the images to a reference coordinate system, arbitrarily chosen to be that of the Nov. 3 frame. A first-order two-dimensional polynomial fit to the positions of the few field stars was used to correct for offsets and field rotation; then, all the images were resampled on the same pixel grid using bicubic spline interpolation. These rebinned images (53 frames in V and 51 R ones) are generically denoted I in the following.
At this step, stacking or subtracting CCD frames becomes possible for a strictly astrometric application but for an optimal co-addition, we must take into account the disparities in seeing, sky background level and possibly PSF shape from one image to another. For both the V and R bands, we actually built a reference frame from the average stacking of eight selected frames with very good seeing, that were first convolved with a two-dimensional optimal kernel in order to match a common PSF shape and similar observing conditions. We explicitly describe hereafter the procedure that we have adopted.
One given base CCD frame Base was selected among these eight images. We then determined for each of the remaining seven frames
![]() ,
the convolution kernel Ker that makes it fit Base optimally. For any pixel at position (i,j), it writes,
,
the convolution kernel Ker that makes it fit Base optimally. For any pixel at position (i,j), it writes,
![\begin{displaymath}\chi^{2} = \sum_{(i, j)} \frac{[{\it Base} (i, j) - [I_{\rm S...
... - \Delta {\it SB}(i, j)]^{2}}{\sigma_{{\it Base}} (i, j)^{2}}
\end{displaymath}](/articles/aa/full/2005/23/aa1887-04/img11.gif)
Table 2: Kernel parameters for both the V and R bands.
In both the V and R bands, we then co-added Base with all the convolved
frames
![]() and built, by average stacking, a deep and quasi-noiseless reference frame which we denote Ref in the remainder. Note that before performing the average stacking, we first rejected for each pixel, the values which differed by more than
and built, by average stacking, a deep and quasi-noiseless reference frame which we denote Ref in the remainder. Note that before performing the average stacking, we first rejected for each pixel, the values which differed by more than ![]() from the median value.
from the median value.
This reference frame was subtracted subsequently from each of the frames I available in the field after proper alignment (with seeing <1.8'', i.e. 53 epochs in V and 51 in R) in order to obtain difference frames, where the only residuals expected to appear lie at the positions of the variable objects (see the bottom
picture in Fig. 1). The subtraction operation was also optimized in the sense that the reference frame Ref was successively convolved with an adapted kernel Ker - obtained as above by least-squares fitting of its space-varying model coefficients - in order to match at best each frame I:
![\begin{displaymath}{\it Sub} (i, j) = \frac{[{\it Ref} * {\it Ker}] (i, j) + \Delta {\it SB} (i, j) - I (i, j)} {{\it Sum}\_{\it Ker}}
\end{displaymath}](/articles/aa/full/2005/23/aa1887-04/img22.gif)
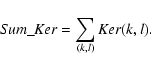
![\begin{figure}
\par\includegraphics[width=13cm,clip]{1887Fig1.eps}\par\end{figure}](/articles/aa/full/2005/23/aa1887-04/Timg25.gif) |
Figure 1:
For a given observing date (Oct. 29, V), we show aligned CCD frames Ref ( top left), I ( top right) and Sub ( bottom left). The image Sub is the result of the subtraction of the frame I from the reference frame Ref convolved with an optimal kernel. In these frames, north is up and east is to the right. Field of view is approximately
|
| Open with DEXTER | |
We performed a four-PSF fitting photometry of all difference frames Sub obtained by optimal subtraction in order to measure for each of the four lensed quasar images the respective flux differences observed between the frames I and the reference frame Ref. In order to do so, we have implemented an original dedicated software which enables simultaneous fitting of four PSF models to the residual images at the exact positions of the components of Q2237+0305. As the flux differences may either be positive or negative, the fitting must of course be capable of matching negative PSF profiles on the subtracted images.
The photometry process begins with the determination of a representative PSF model in the reference frame Ref. We used for that a routine provided in the public ISIS package that builds a normalized composite PSF out of a few bright-star profiles. It selects in fact small sub-images around a certain number of bright stars distributed all over the field, removes local sky-background from them and finally divides them by the integrated flux of the selected star for normalization. These sub-images are then co-added pixel by pixel so that we obtain by median stacking a sub-frame containing the image of a typical PSF, that is divided once more by its integrated flux in order to finally ensure flux normalization. Let us denote
![]() the pixel values of this sub-frame.
We are now able to model the zone Z of the reference frame Ref surrounding any isolated star-like (i.e. unresolved) object with flux
the pixel values of this sub-frame.
We are now able to model the zone Z of the reference frame Ref surrounding any isolated star-like (i.e. unresolved) object with flux
![]() above the local value of the sky background
above the local value of the sky background
![]() and assumed to be exactly centred on pixel
and assumed to be exactly centred on pixel
![]() :
:
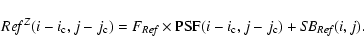
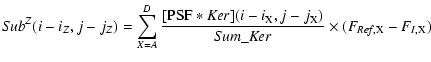 |
![\begin{displaymath}\chi^{2} = \sum_{Z} \frac{[{\it Sub} (i, j) - {\it Sub}^Z (i-i_Z, j-j_Z)]^{2}} {\sigma_{\it Sub} (i, j)^{2}}
\end{displaymath}](/articles/aa/full/2005/23/aa1887-04/img44.gif)
So, fitting simultaneously four adapted PSF models into every subtracted frame Sub, we measured for each of the A, B, C and D components of Q2237+0305 a flux difference between each frame I and the reference frame Ref; we did so for both the V and R bands, successively. As we performed differential photometry, we did not need to assume any light-distribution model for the galaxy and therefore avoided related (cf. possible systematic) errors. But of course, we need as the next step to do absolute photometry of the reference frame Ref in order to get, from the measured flux differences, the absolute fluxes at all epochs, i.e. for each frame I.
Let us note that the non-independent fitting of four PSFs at such nearby positions could possibly lead to strong correlation effects between the flux measurements of the lensed components A, B, C and D, especially at observing epochs characterized by a bad or poor seeing. We double checked whether the changing observing conditions (seeing, sky background, characteristics of the CCD camera, ...) from frame to frame could change the level of correlation between the flux measurements of components A, B, C and D and therefore affect the consistency of these flux measurements from one epoch to another and thus the reliability of the produced light curves. No significant effect has been found.
Absolute photometry of the four lensed QSO components of Q2237+0305 was performed in each band using the so-called General software (Østensen et al. 1996; Remy 1996). We fitted the central part of both the V and R reference frames Ref with a global model of the gravitational lens system composed of one PSF for each of the four lensed components plus a model for the lensing galaxy photometric profile.
Using a public HST image (dataset U2LG0401T) taken in 1995 with the Wide Field Planetary Camera 2 (the Einstein Cross being the target for the planetary camera PC), during 800 s through the filter F555W (centre 540.7 nm), we accurately measured (using the MIDAS command "center/Gauss'') the positions of the four lensed components and the galaxy centre and also that of a faint field star (denoted star #4 in Sect. 6.2).
Now, in order to determine as accurately as possible the (x,y) positions of the four
lensed components and the galaxy centre in the reference coordinate system that we
defined in Sect. 3.1, we "oversampled'' the reference frames Ref following
the procedure detailed hereafter. Using IRAF, we replicated by blocks of 2 by
2 pixels the frames
![]() selected to build Ref (meaning that
every pixel of a single frame
selected to build Ref (meaning that
every pixel of a single frame
![]() is replicated into a square block
of 4 identical pixels and correlatively that the frames are enlarged by a
factor 4) and then smoothing them by convolution with a 2D circular
Gaussian function of sigma 0.8 pixel. In both V and R bands, the
"oversampled'' frames
is replicated into a square block
of 4 identical pixels and correlatively that the frames are enlarged by a
factor 4) and then smoothing them by convolution with a 2D circular
Gaussian function of sigma 0.8 pixel. In both V and R bands, the
"oversampled'' frames
![]() entered the same process as detailed
in Sect. 3.1 to produce two new "oversampled'' Ref frames. In
both bands, we measured (still using "center/Gauss'') on these oversampled
reference frames the positions of the A, B, C and D components as well as
that of the field star and determined the coordinate transformation between
the HST positions and the oversampled Ref ones. The coefficients
(enlargement factor and rotation angle) of this first-order transformation
were computed as the mean values of those of the respective transformations
determined from the following couples of
positions (A - star), (B - star), (C - star), (D - star).
The object positions (four components and galaxy centre), obtained
from the HST image and adapted in each band via the coordinate
transformation that we determined, were given to the General software
as input values and we performed a fit of the Q2237+0305 system on the
"oversampled'' reference frames. The free parameters of the fit were
all the fluxes and the positions of component A; the relative positions
from component A of the galaxy centre and of components B, C, D were
imposed in order to preserve the geometry of the system as determined from the HST frame.
entered the same process as detailed
in Sect. 3.1 to produce two new "oversampled'' Ref frames. In
both bands, we measured (still using "center/Gauss'') on these oversampled
reference frames the positions of the A, B, C and D components as well as
that of the field star and determined the coordinate transformation between
the HST positions and the oversampled Ref ones. The coefficients
(enlargement factor and rotation angle) of this first-order transformation
were computed as the mean values of those of the respective transformations
determined from the following couples of
positions (A - star), (B - star), (C - star), (D - star).
The object positions (four components and galaxy centre), obtained
from the HST image and adapted in each band via the coordinate
transformation that we determined, were given to the General software
as input values and we performed a fit of the Q2237+0305 system on the
"oversampled'' reference frames. The free parameters of the fit were
all the fluxes and the positions of component A; the relative positions
from component A of the galaxy centre and of components B, C, D were
imposed in order to preserve the geometry of the system as determined from the HST frame.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1887Simu.eps} \end{figure}](/articles/aa/full/2005/23/aa1887-04/Timg46.gif) |
Figure 2: An example of CCD frame simulated for the statistical determination of the photometric error bars: the frame corresponds to the same observing date as Fig. 1 (Oct. 29, V). |
| Open with DEXTER | |
Coming back to the original (non-oversampled) pixel grid, we thus obtained in both the V and R bands the accurate (x,y) coordinates of the galaxy centre and the four components of Q2237+0305 on the original-sized V and R Ref frames and all the aligned frames that we analyzed in Sect. 3.2. These last positions were given to the General software as input values for the further respective fits we performed, on the V and R original Ref frames now. Using these starting values and running General, while still preserving the geometry of the system (i.e. free parameters being again the position of component A and all fluxes), we finally obtained the best-fitted position for A and the fluxes of the A, B, C and D lensed components.
About the galaxy model, we noticed on the HST image that the galaxy core may be approximated by a point-like, PSF model and for this reason, we adopted the combination of a PSF plus several Gaussian functions. Of course, we also tested other galaxy models but we noted in the case of the V band observations that a model made of a central PSF plus two Gaussians leads to very faint and acceptable residuals. In the R band, the galaxy model turned out to be more complex and we therefore fitted the reference image using several different possible galaxy models. We tried a de Vaucouleurs profile, an exponential disk, the sum of a PSF and several Gaussians and many combinations of the three previous models. As we did not find a model clearly better than another one, we averaged the photometric measurements derived for the four lensed components only taking into account the best galaxy models (de Vaucouleurs profile + exponential disk, de Vaucouleurs profile +3 Gaussians) which led to the faintest residuals.
![\begin{figure}
\par\includegraphics[angle=-90,width=13cm,clip]{1887Vban.eps} \end{figure}](/articles/aa/full/2005/23/aa1887-04/Timg47.gif) |
Figure 3: Light curves of the lensed components A, B, C and D of Q2237+0305 in the V band. Magnitude is plotted with error bars as a function of time (heliocentric Julian Days -2 450 000). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=13cm,clip]{1887Rban.eps} \end{figure}](/articles/aa/full/2005/23/aa1887-04/Timg48.gif) |
Figure 4: Light curves of the components A, B, C and D of Q2237+0305 in the R band. Magnitude is plotted with error bars as a function of time (heliocentric Julian Days -2 450 000). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=13.5cm,clip]{1887ind.eps} \end{figure}](/articles/aa/full/2005/23/aa1887-04/Timg49.gif) |
Figure 5: Resulting V-R colour curves of the components A, B, C and D of Q2237+0305 plotted as a function of time (heliocentric Julian Days - 2 450 000). |
| Open with DEXTER | |
As results from the General fit, we finally obtained the following measurements:
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
The accurate component positions were used for the differential photometry described in Sect. 3.2, while the reference fluxes
.
The accurate component positions were used for the differential photometry described in Sect. 3.2, while the reference fluxes
![]() yielded zero points for the relative photometry, allowing one to compute the respective absolute fluxes
yielded zero points for the relative photometry, allowing one to compute the respective absolute fluxes
![]() corresponding to each epoch of observation. The flux
corresponding to each epoch of observation. The flux
![]() (assumed to be constant) of a photometric standard star with known apparent magnitude
(assumed to be constant) of a photometric standard star with known apparent magnitude ![]() was also derived from the reference frame by single-PSF fitting and we thus obtained magnitude calibration in both the V and R bands. Finally, the magnitude of component X of Q2237+0305 measured at the epoch of observation is, for a given band,
was also derived from the reference frame by single-PSF fitting and we thus obtained magnitude calibration in both the V and R bands. Finally, the magnitude of component X of Q2237+0305 measured at the epoch of observation is, for a given band,
| |
= | ||
| = | 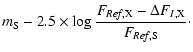 |
While it is possible theoretically to infer statistical error bars from the photometry process, we consider that such purely internal values are generally underestimated. We prefered to derive realistic 1-sigma error bars in magnitudes, on the basis of simulated frames precisely mimicking the field of Q2237+0305 and taking into account the actual observing conditions (seeing, sky background) at each epoch, as well as the magnitude of the field stars and those of the lensed components derived in Sect. 4.2. For each observing date, we simulated one hundred frames (including photon noise and CCD read-out noise) and we shifted them by a random fractional pixel in order to simulate different independent samplings. A Gaussian profile has been used for the stars and for the four lensed components; the galaxy has been generated using the sum of an exponential disk and a de Vaucouleurs profile (Yee 1988). We present in Fig. 2 an example of frame simulation, mimicking the (Oct. 29, V) observation displayed in Fig. 1.
We applied the image subtraction method to our simulated frames, in the same way as for the real ones. For a given component X considered in a given band at the observing date correponding to frame I, ISIS returned hundred values of
![]() that we converted into fluxes by means of the relation
that we converted into fluxes by means of the relation
![]() ,
where
,
where
![]() is the flux value measured on the real Ref frame (i.e. that measured in Sect. 4.2) and not from simulations. We must say that the use of the General software is not automatic and it would have been very time consuming to run it hundred times in V and hundred times in R! In both the V and R bands, we were thus led to assume that the
is the flux value measured on the real Ref frame (i.e. that measured in Sect. 4.2) and not from simulations. We must say that the use of the General software is not automatic and it would have been very time consuming to run it hundred times in V and hundred times in R! In both the V and R bands, we were thus led to assume that the
![]() on the hundred reference frames built from the simulated series of observations are statistically equal to that measured on the real reference image Ref.
on the hundred reference frames built from the simulated series of observations are statistically equal to that measured on the real reference image Ref.
Then, we derived the standard deviation
![]() of the hundred flux values
of the hundred flux values
![]() computed as detailed above and obtained the error bars shown in Figs. 3-5 using the following relations which give the upper and lower magnitude limits of the asymetric error bar plotted at the measurement point corresponding to component X on frame I:
computed as detailed above and obtained the error bars shown in Figs. 3-5 using the following relations which give the upper and lower magnitude limits of the asymetric error bar plotted at the measurement point corresponding to component X on frame I:
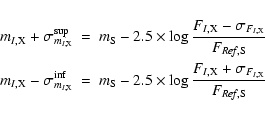
We have displayed in Figs. 3 and 4 the light curves derived for the four lensed components of Q2237+0305 in both the V and R bands and Table 3 lists the photometric results.
Table 3: Photometric results in the V and R bands.
In Fig. 5, we have illustrated the corresponding V-R colour curves. Thanks to the brighter average magnitude of the lensed component A, its resulting V and R lightcurves, as well as its V-R colour curve, are characterized by a better S/N ratio. The trend of the flux variations observed for A is definitely different from those characterizing the other components.
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{1887sta1.eps} \includegraphics[angle=-90,width=15cm,clip]{1887sta2.eps} \end{figure}](/articles/aa/full/2005/23/aa1887-04/Timg67.gif) |
Figure 6: Light curves of four field stars in the V band ( left) and in the R band ( right). Magnitude is plotted with error bars as a function of time (heliocentric Julian Days - 2 450 000). NB: in a few CCD frames (Oct. 16, V; Oct. 16, R; Oct. 19, V; Oct. 19, R; Oct. 21, V; Oct. 21, R; Oct. 23, V; Oct. 23, R; Oct. 30, R; Dec. 9, V), no photometry of star#1 could be derived because its image is truncated by the field border. Moreover, an aberrant point on Nov. 8, R (mag 15.35) does not appear in the star#1 plot. |
| Open with DEXTER | |
In order to test the quality of the produced lightcurves, we measured using the same method as above the V and R magnitudes of four selected field stars covering a wide range in magnitude (exceeding the range of magnitudes covered by the four lensed components of Q2237+0305). We selected for this test the following four stars:
| |
= | ![$\displaystyle \sum_{Z} \frac{[{\it Sub} (i, j) - {\it Sub}^Z (i-i_{\rm c}, j-j_{\rm c})]^{2}}
{\sigma_{\it Sub} (i, j)^{2}}$](/articles/aa/full/2005/23/aa1887-04/img73.gif) |
|
![$\displaystyle \sum_{Z} \frac{[{\it Sub} (i, j) - {\it Sub}^Z (i-i_{\rm c}, j-j_{\rm c})]^{2}}
{\sigma_{I} (i, j)^{2}}\cdot$](/articles/aa/full/2005/23/aa1887-04/img75.gif) |
Then, using a locally implemented software made out of blocks extracted from the public ISIS routines, we defined the flux zero-points through direct photometry on the V and R reference frames Ref. To do that, we independently measured the respective fluxes
![]() of the four stars by successive single-PSF fittings. Then, to derive magnitude measurements, we measured as well on the V and R reference frames the fluxes
of the four stars by successive single-PSF fittings. Then, to derive magnitude measurements, we measured as well on the V and R reference frames the fluxes ![]() of the same
of the same ![]() standard star as we used for calibration in Sect. 4.2, and we finally computed in both V and R bands
standard star as we used for calibration in Sect. 4.2, and we finally computed in both V and R bands
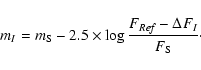
![\begin{figure}
\par\includegraphics[angle=-90,width=13cm,clip]{1887fit.eps} \end{figure}](/articles/aa/full/2005/23/aa1887-04/Timg79.gif) |
Figure 7: For both the V ( left) and R ( right) bands, results of the fitted straight line through the B, C and D light curves, after subtraction of their respective mean magnitude ( top). The results of subtracting this average straight line from the previous B, C and D light curves are shown in the middle diagrams. Finally we show in the bottom diagrams the results of subtracting the same straight line from the A light curve. |
| Open with DEXTER | |
One can see that down to the levels of magnitude characteristic of component D
(![]() 18.4 in V and
18.4 in V and ![]() 17.7 in R), the photometric method yields quite flat light curves for all field stars assumed to be non variable. This represents according to us a valuable global check of the photometric chain that we used to derive the Q2237+0305 light curves displayed in Sect. 6.1.
17.7 in R), the photometric method yields quite flat light curves for all field stars assumed to be non variable. This represents according to us a valuable global check of the photometric chain that we used to derive the Q2237+0305 light curves displayed in Sect. 6.1.
Given the very different trends observed between the lightcurves of component A and those of components B, C and D, we proceeded as follows.
For each band, we first derived the mean magnitude of the B, C and D components of Q2237+0305 and we subtracted this average value from the respective light curves. We then fitted a straight line through these light curves of the B, C and D components and we show the results of this fitting procedure for both the V and R bands in Fig. 7 (top row). Let us note that two dates (Dec. 23, R and Jan. 25, V) were rejected because of their very important shift relatively to the trends of the other dates. Then, we subtracted this fitted straight line from the light curves of components B, C and D and we note that the
new light curves are not perfectly flat (Fig. 7, middle row), which would be the case if only intrinsic photometric variations of the quasar were reflected in the individual lightcurves, with time delays typically less than a day. The residual lightcurves of B, C and D individually show linear trends characterized by very weak slopes included within the interval
![]() (Fig. 7). The bottom row in Fig. 7 represents the results of subtracting the above linear trend assumed to possibly reflect intrinsic variations of the QSO from the lightcurves of component A. It thus seems that the lensed component A is very much affected by a microlensing event induced by stars in the lensing galaxy, but that at the epoch of the GLITP observations, components B, C and D are also possibly affected by independent, although much less significant, microlensing events.
Plots of the V-R colour versus time (Fig. 5) and
versus the V magnitude (Fig. 8) show possible distinct trends of colour variations as well as correlations between V-R and V for the different components A, B, C and D. Colour variations such as those conspicuously observed for the A, and possibly D, components are reminiscent of microlensing effects during a caustics crossing by the QSO source (Wambsganss & Paczynski 1991).
(Fig. 7). The bottom row in Fig. 7 represents the results of subtracting the above linear trend assumed to possibly reflect intrinsic variations of the QSO from the lightcurves of component A. It thus seems that the lensed component A is very much affected by a microlensing event induced by stars in the lensing galaxy, but that at the epoch of the GLITP observations, components B, C and D are also possibly affected by independent, although much less significant, microlensing events.
Plots of the V-R colour versus time (Fig. 5) and
versus the V magnitude (Fig. 8) show possible distinct trends of colour variations as well as correlations between V-R and V for the different components A, B, C and D. Colour variations such as those conspicuously observed for the A, and possibly D, components are reminiscent of microlensing effects during a caustics crossing by the QSO source (Wambsganss & Paczynski 1991).
![\begin{figure}
\par\includegraphics[angle=-90,width=13cm]{1887VR.eps} \end{figure}](/articles/aa/full/2005/23/aa1887-04/Timg82.gif) |
Figure 8: V-R colour curves for the components A, B, C and D of Q2237+0305 plotted as a function of the V magnitude. |
| Open with DEXTER | |
Contrary to the lensed component A of Q2237+0305, we observe in both the V and R bands that the light curves of the lensed components B, C and D have faded by about one tenth of a magnitude in V and R during the observing period (see Figs. 3 and 4). In Fig. 7 (top row), the fitted straight lines reflect a common variation of about +0.15 mag in V and +0.10 mag in R for the B, C and D lensed images, with additional independent but weak trends (cf. Fig. 7, middle row). We interpret these observations as possibly due to intrinsic flux variations of the QSO itself, the time delay between the lensed components being only of the order of 1 day (Schneider et al. 1988), plus some additional and independent weak microlensing effects taking place for these three images. These assumptions are supported by the fact that the slopes of the V-R colour variations observed for components B, C and D are somewhat different between each other, although the amplitudes of the colour variations never exceed 0.1 mag (see Figs. 5 and 8).
The light curves of component A show a quite different pattern (see Figs. 3, 4 and 7). We interpret these light curves as due to a strong microlensing effect arising from stars in the deflecting galaxy (see below). The significant colour dependence during the early rise of light amplification that we see in Fig. 5 reinforces that interpretation, as it probably corresponds to a caustics crossing by the QSO source (Wambsganss & Paczynski 1991). The error bar estimates (about 0.01 mag in V and about 0.02 mag in V-R) confirm the significance of the microlensing signal detected in the V and R light curves of component A of Q2237+0305. The trends of the V-R colour observed for the lensed components A, B, C and D as a function of V (see Fig. 8) are reminiscent of those reported over longer time scales by Vakulik et al. (2004). These authors also interpret the observed colour trends as being caused by microlensing effects.
Recently, Lee et al. (2005) have proposed a possible microlensing model to account for the OGLE data (Wozniak et al. 2000b) as well as the present GLITP monitoring data for the high amplification event (HAE) observed in the lightcurves of images A and C. The complete set of observations covers more than 3 years and a very detailed interpretation is given in that paper. The whole set of data has been analyzed through a new N-body microlensing analysis method, the Local HAE Caustic Modeling (LOHCAM). By applying this method to the V light curve of the lensed component A in the Einstein Cross, Lee et al. (2005) have found that a torus source model may easily account for the observed light curve of component A, especially for the double peak present in the GLITP data. So far, Shalyapin et al. (2002) and Goicoechea et al. (2003) have also investigated this observed HAE in terms of a Newtonian geometrically thin and optically thick accretion disk. They used the same GLITP data, but the results derived from the PSF fitting photometry, not those obtained by the ISIS image subtraction technique presented in this paper. Therefore, they did not recognize the double peak feature in the lightcurve of A, because they used the GLITP-PSF results affected by relatively large error bars, compared to the GLITP-ISIS results. Furthermore, Shalyapin et al. (2002) and Yonehara (2001) have analyzed the HAE only for selected parts of the OGLE data. On the contrary, the proposed LOHCAM produces a remarkably good fitting over the entire data points covered by the OGLE and GLITP observations (Lee et al. 2005). Lee et al. (2005) noticed that the observed double peak feature probably constitutes an important microlensing signature induced by the torus structure of the continuum source of QSO2237+0305. A detailed and complete description of our HAE analysis method and its results (size of the torus, masses of the microlenses) may be found in Lee et al. (2005). We only have presented here the fitting results for component A obtained by Lee et al. (2005) using the complete set of OGLE+GLITP data, altogether with the GLITP-ISIS data (Alcalde et al. 2002) being superimposed. Let us however be careful that at this moment, there is no proof about the unicity of the proposed model and therefore, a more speculative discussion is probably premature at this moment. We refer to Lee et al. (2005) for a more detailed presentation of the possible microlens model.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1887Mod.eps} \end{figure}](/articles/aa/full/2005/23/aa1887-04/Timg83.gif) |
Figure 9: The GLITP-ISIS data (Alcalde et al. 2002) in the V band are shown altogether with the simulated light curve (solid line) using a torus source model (Lee et al. 2005). The logarithmic magnitude scale has been transformed into linear flux units (mJy). |
| Open with DEXTER | |
Acknowledgements
We thank C. Alard and P. R. Wozniak for some fruitful interactions. This work was supported in part by PRODEX (Gravitational lens studies with HST), by contract IUAP P5/36 "Pôle d'Attraction Interuniversitaire'' (OSTC, Belgium) and by the "Fonds National de la Recherche Scientifique'' (Belgium), including a two-year research position for O.M. (1999-2001). D.W.L. would like to acknowledge the support from the "Astrophysical Research Center for the Structure and Evolution of the COSMOS (ARCSEC)'' in Sejong university (Korea), for a post-doc position. Last, but not least, we would like to thank the anonymous referee for very helpful comments.