A&A 436, 209-230 (2005)
DOI: 10.1051/0004-6361:20042484
B. Acke1 - M. E. van den Ancker2,![]() -
C. P. Dullemond3
-
C. P. Dullemond3
1 - Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200B,
3001 Leuven, Belgium
2 -
European Southern Observatory, Karl-Schwarzschild Strasse 2, 85748
Garching bei München, Germany
3 -
Max-Planck-Institut für Astrophysik, Karl-Schwarzschildstrasse 1,
Postfach 1317, 85748 Garching bei München, Germany
Received 6 December 2004 / Accepted 21 February 2005
Abstract
We present high spectral-resolution optical spectra of 49 Herbig Ae/Be
stars in a search for the [O I]6300 Å line. The vast
majority of the stars in our sample show narrow (
![]() km s-1)
emission lines, centered on the stellar radial velocity. In only
three sources is the feature much broader (
km s-1)
emission lines, centered on the stellar radial velocity. In only
three sources is the feature much broader (![]() 400 km s-1),
and strongly blueshifted (-200 km s-1) compared to the stellar
radial velocity. Some stars in our sample show double-peaked line
profiles, with peak-to-peak separations of
400 km s-1),
and strongly blueshifted (-200 km s-1) compared to the stellar
radial velocity. Some stars in our sample show double-peaked line
profiles, with peak-to-peak separations of ![]() 10 km s-1.
The presence and strength of the [O I]line emission appears
to be correlated with the far-infrared energy distribution of
each source: stars with a strong excess at 60
10 km s-1.
The presence and strength of the [O I]line emission appears
to be correlated with the far-infrared energy distribution of
each source: stars with a strong excess at 60 ![]() m have in general
stronger [O I] emission than stars with weaker 60
m have in general
stronger [O I] emission than stars with weaker 60 ![]() m excesses.
We interpret these narrow [O I]6300 Å line profiles as
arising in the surface layers of the protoplanetary disks surrounding
Herbig Ae/Be stars. A simple model for [O I]6300 Å line
emission due to the photodissociation of OH molecules shows that our
results are in quantitative agreement with that expected from the
emission of a flared disk if the fractional OH abundance is
m excesses.
We interpret these narrow [O I]6300 Å line profiles as
arising in the surface layers of the protoplanetary disks surrounding
Herbig Ae/Be stars. A simple model for [O I]6300 Å line
emission due to the photodissociation of OH molecules shows that our
results are in quantitative agreement with that expected from the
emission of a flared disk if the fractional OH abundance is
![]()
![]() .
.
Key words: circumstellar matter - stars: pre-main-sequence - planetary systems: protoplanetary disks
Herbig Ae/Be (HAEBE) stars are intermediate-mass pre-main-sequence objects. The spectral energy distribution (SED) of these sources is characterized by the presence of an infrared excess, due to thermal emission of circumstellar dust. For HAEBE stars of spectral type F, A and late-B, the evidence for a disk-like geometry of this circumstellar dust (e.g. Fuente et al. 2003; Mannings & Sargent 1997; Natta et al. 2004; Piétu et al. 2003; Testi et al. 2003) is generally accepted. The spatial distribution of the circumstellar matter around early-B-type stars is less clear (e.g. Natta et al. 2000). Early-B stars have dissipation time scales for the circumstellar spherical envelope of the order of their pre-main-sequence life time. Nevertheless observations seem to indicate that at least some of these sources have disks (Vink et al. 2002). Both disk-like and spherical geometries might be present around these sources.
Meeus et al. (2001, henceforth M01) have classified the 14 isolated
HAEBE stars in their sample based on the
shape of the mid-IR (20-100 ![]() m) SED. Group I contains the
sources which have a rising mid-IR flux excess (double-peaked
SED). Group II sources display more modest IR excesses. M01
suggest phenomenologically that the difference in SED shape reflects a
different disk geometry: group I sources have flared disks, while
group II objects have geometrically flat disks.
m) SED. Group I contains the
sources which have a rising mid-IR flux excess (double-peaked
SED). Group II sources display more modest IR excesses. M01
suggest phenomenologically that the difference in SED shape reflects a
different disk geometry: group I sources have flared disks, while
group II objects have geometrically flat disks.
Dullemond (2002), Dullemond et al. (2002) and
Dullemond & Dominik (2004) have modeled circumstellar
disks with a self-consistent model based on 2D-radiative transfer
coupled to the equations of vertical hydrostatics. The model is
composed of a disk with an inner hole (![]() 0.5 AU), a puffed-up
inner rim and an outer part. The inner rim, which is located at the dust
sublimation temperature, is puffed-up due to the direct head-on stellar
radiation and the consequent increase of the local gas temperature.
The models show that the outer part of the disk can either be flared
(as in the models of Chiang & Goldreich 1997), or lie completely in
the shadow of
the puffed-up inner rim. The SED of a flared disk displays a strong
mid-IR excess, comparable to that of the M01 group I
sources. Self-shadowed disk models have SEDs with a steeper decline
towards longer wavelengths, like the SEDs of group II sources. The
Dullemond (2002) models hence connect the M01 classification to the
disk geometry: group I sources have flared disks, group II objects
self-shadowed disks.
0.5 AU), a puffed-up
inner rim and an outer part. The inner rim, which is located at the dust
sublimation temperature, is puffed-up due to the direct head-on stellar
radiation and the consequent increase of the local gas temperature.
The models show that the outer part of the disk can either be flared
(as in the models of Chiang & Goldreich 1997), or lie completely in
the shadow of
the puffed-up inner rim. The SED of a flared disk displays a strong
mid-IR excess, comparable to that of the M01 group I
sources. Self-shadowed disk models have SEDs with a steeper decline
towards longer wavelengths, like the SEDs of group II sources. The
Dullemond (2002) models hence connect the M01 classification to the
disk geometry: group I sources have flared disks, group II objects
self-shadowed disks.
Acke & van den Ancker (2004, henceforth AV04) have investigated all available
near-infrared Infrared Space Observatory
(ISO, Kessler et al. 1996) spectra of HAEBE
stars. In their paper, the emission bands at 3.3, 6.2, "7.7'', 8.6
and 11.3 ![]() m were studied qualitatively. These emission
features are attributed to polycyclic aromatic hydrocarbons
(PAHs, Allamandola et al. 1989; Léger & Puget 1984). The latter, carbonaceous
molecules, are thought to be
excited by ultraviolet (UV) photons, and radiate in the near-infrared in
bands linked to the vibrational modes of the CC and CH bonds.
AV04 have found a correlation between the strength of the PAH
features and the shape of the SED:
group I sources display significant PAH emission in their spectra.
Group II members on the other hand show much
weaker PAH bands, indicating the lack of excited PAH molecules in
these systems. Following the remark of M01, AV04 suggest this is due
to the geometry of the circumstellar disk. In self-shadowed
geometries, the stellar UV
flux needed to excite the PAH molecules cannot reach the disk surface,
while in flared disks this surface is directly exposed to the radiation
field of the central star. Theoretical modeling of the PAH emission in flared
circumstellar disks (Habart et al. 2004) is in agreement with the observations.
m were studied qualitatively. These emission
features are attributed to polycyclic aromatic hydrocarbons
(PAHs, Allamandola et al. 1989; Léger & Puget 1984). The latter, carbonaceous
molecules, are thought to be
excited by ultraviolet (UV) photons, and radiate in the near-infrared in
bands linked to the vibrational modes of the CC and CH bonds.
AV04 have found a correlation between the strength of the PAH
features and the shape of the SED:
group I sources display significant PAH emission in their spectra.
Group II members on the other hand show much
weaker PAH bands, indicating the lack of excited PAH molecules in
these systems. Following the remark of M01, AV04 suggest this is due
to the geometry of the circumstellar disk. In self-shadowed
geometries, the stellar UV
flux needed to excite the PAH molecules cannot reach the disk surface,
while in flared disks this surface is directly exposed to the radiation
field of the central star. Theoretical modeling of the PAH emission in flared
circumstellar disks (Habart et al. 2004) is in agreement with the observations.
Forbidden-line emission from different elements (C
I, N II, O I, O II, S II, Ca II, Cr
II, Fe II, Ni II; see e.g., Hamann 1994) in the
optical part of the spectrum has been
observed in a considerable amount of HAEBEs. In the present paper we
focus on the [O I]features at 6300 and 6363 Å . The circumstellar region from
which these lines emanate has been the subject of a long-standing
debate in the literature (e.g., Hirth et al. 1994; Hernández et al. 2004; Böhm & Catala 1994; Finkenzeller 1985; Corcoran & Ray 1997,1998; Böhm & Hirth 1997; Hamann 1994). There is agreement
that the blueshifted high-velocity (a few 100
![]() )
wing observed in a
few sources is formed in an outflow whose redshifted part is obscured
by the circumstellar disk. The origin of low-velocity symmetric [O I]
emission profile is less clear. Kwan & Tademaru (1988) have provided a
qualitative explanation for the observed [O I] profiles in T Tauri stars. Their model consists of a low- and a high-velocity component,
the first due to a slow disk wind, the latter emanating from a
collimated jet. Previously published suggestions for the
forbidden-line emitting region in HAEBE stars are based on this model
and include a low-velocity disk wind (Corcoran & Ray 1997; Hirth et al. 1994)
and a spherically
symmetric stellar wind (without an obscuring
circumstellar disk, Böhm & Catala 1994). In the latter explanation, the
authors suggest that the [O I] line is formed in the outermost parts of
the stellar wind.
)
wing observed in a
few sources is formed in an outflow whose redshifted part is obscured
by the circumstellar disk. The origin of low-velocity symmetric [O I]
emission profile is less clear. Kwan & Tademaru (1988) have provided a
qualitative explanation for the observed [O I] profiles in T Tauri stars. Their model consists of a low- and a high-velocity component,
the first due to a slow disk wind, the latter emanating from a
collimated jet. Previously published suggestions for the
forbidden-line emitting region in HAEBE stars are based on this model
and include a low-velocity disk wind (Corcoran & Ray 1997; Hirth et al. 1994)
and a spherically
symmetric stellar wind (without an obscuring
circumstellar disk, Böhm & Catala 1994). In the latter explanation, the
authors suggest that the [O I] line is formed in the outermost parts of
the stellar wind.
With the present paper, we intend to contribute to this discussion, and try to explain the observed low-velocity component in a broader framework. In Sect. 2, the composition of the sample is presented. First, we investigate the observational data and perform a quantitative analysis. We search for correlations between parameters describing the forbidden-line emission and the SED. We have also checked the possible connection between the presence and strength of PAH features and the forbidden-line emission (Sects. 3, 4). Second, we propose a simple model for the forbidden-line emission region, and compare the model results to the observations (Sect. 5).
We have observed 49 Herbig Ae/Be stars in the wavelength region around the forbidden oxygen line at 6300 Å. Since we intend to compare the results of the ISO study of HAEBE stars by AV04 to the present [O I]-emission-line analysis, we have compiled our [O I]sample in order to have as large as possible an overlap with their sample. Additional HAEBE stars from the catalogues of Thé et al. (1994, Tables 1 and 2, in their article) and Malfait et al. (1998) were observed when possible to enlarge the sample.
Optical spectra of the sample stars were obtained with four different instruments on five different telescopes: the Coudé Echelle Spectrometer (CES) on the Coudé Auxiliary Telescope (CAT) and on the ESO 3.6 m telescope, the Fiber-fed Extended Range Optical Spectrograph (FEROS) on the ESO 1.5 m telescope, the CCD Echelle Spectrograph on the Mayall 4 m telescope at Kitt Peak National Observatory (KPNO) and the Utrecht Echelle Spectrograph (UES) on the William Herschel Telescope (WHT). The first three telescopes are located at the ESO site La Silla (Chile), KPNO is in Arizona (USA) and the WHT is situated on La Palma (Canary Islands, Spain). The FEROS and WHT measurements were made by Gwendolyn Meeus. The spectra were obtained at different periods during the past 10 years. In Table 1, we have summarized the sample stars and spectra included in this analysis. For 10 sources, two or more spectra were obtained.
Table 1: The sample of HAEBEs used in this analysis, based on Thé et al. (1994) and Malfait et al. (1998). For each object, the available optical spectra are indicated. Furthermore, the SIMBAD values for right ascension (RA) and declination (Dec) are given, as well as the date, start time and integration time T of the observation.
In order to extract the spectra from the raw data, a standard echelle-data reduction was applied. This includes background subtraction, cosmic-hit removal, flatfielding and wavelength calibration. The spectra were normalized to unity by fitting a spline function through continuum points and dividing by it. The reduction and normalization was performed using the ESO program MIDAS.
The spectral resolution
![]() at 6300 Å
is instrument-dependent. The resolution for the KPNO data is
at 6300 Å
is instrument-dependent. The resolution for the KPNO data is ![]() 30 000, for
the FEROS and WHT spectra
30 000, for
the FEROS and WHT spectra ![]() 45 000, and
45 000, and ![]() 65 000 for the CAT data.
The highest spectral resolution is reached in the ESO 3.6 m
spectra with
65 000 for the CAT data.
The highest spectral resolution is reached in the ESO 3.6 m
spectra with
![]() .
The FEROS and WHT data cover a large
fraction of the optical wavelength range (3700-8860 Å and
5220-9110 Å respectively), which allows us to accurately determine the radial
velocity of the central star (
.
The FEROS and WHT data cover a large
fraction of the optical wavelength range (3700-8860 Å and
5220-9110 Å respectively), which allows us to accurately determine the radial
velocity of the central star (
![]() )
based on many
photospheric absorption lines
throughout the spectrum. The KPNO data cover the wavelength range
between 5630 and 6640 Å. We have used the Fe II absorption line at
5780.128 Å to estimate the stellar radial velocity in these spectra. The CES
spectra (CAT and ESO 3.6 m) are limited to one order around the [O I]line at 6300 Å. No
stellar radial velocities could be determined from these spectra.
For a few sources, Ca II K 3934 Å spectra are at our disposal. When no
photospheric-line spectra were available to us, we estimated the radial velocity
based on these circumstellar lines.
An estimate of
)
based on many
photospheric absorption lines
throughout the spectrum. The KPNO data cover the wavelength range
between 5630 and 6640 Å. We have used the Fe II absorption line at
5780.128 Å to estimate the stellar radial velocity in these spectra. The CES
spectra (CAT and ESO 3.6 m) are limited to one order around the [O I]line at 6300 Å. No
stellar radial velocities could be determined from these spectra.
For a few sources, Ca II K 3934 Å spectra are at our disposal. When no
photospheric-line spectra were available to us, we estimated the radial velocity
based on these circumstellar lines.
An estimate of
![]() was retrieved from the literature in case we
could not determine it from any of our spectra. When no literature
estimate exists, we have computed an average
was retrieved from the literature in case we
could not determine it from any of our spectra. When no literature
estimate exists, we have computed an average
![]() of stars in
the area on the sky (radius 2
of stars in
the area on the sky (radius 2![]() )
around the source.
The radial velocities are included in Table 4 (see later).
)
around the source.
The radial velocities are included in Table 4 (see later).
The spectra were velocity-rebinned and, after applying a heliocentric correction, centered around the stellar radial velocity. In this way we can compare the measured velocities, independently of the intrinsic radial velocity of the entire system.
In this analysis, we focus on the [O I]emission line at
6300 Å. For the sample stars with FEROS, KPNO and WHT spectra, the
extended spectral range allows us to include the [O I] line at
6363 Å as well. Furthermore, these spectra contain the H![]() line at
6550 Å.
line at
6550 Å.
Before analysing the [O I]6300 Å line, we have removed the telluric absorption lines from the spectrum by cutting out these wavelength regions and replacing them by a spline approximation based on all the other data points in the spectrum. The airglow feature ([O I] emission from the Earth's atmosphere) was suppressed in the same way.
In ten of our sample sources, the 6300 Å region is rich in photospheric absorption lines. This hampers the detection of possible superimposed [O I] emission. Of the other 39 stars, 29 objects display a pure-emission shape (i.e. no underlying absorption features). The ten remaining sources have no detected [O I] line.
We have measured the equivalent width
(EW) in Å and centroid position![]() in
in
![]() .
Following tradition, the EW is negative when the
feature is in emission. The EW in
absorption-rich 6300 Å spectra is determined in a fixed interval
(
.
Following tradition, the EW is negative when the
feature is in emission. The EW in
absorption-rich 6300 Å spectra is determined in a fixed interval
(![]() 50
50
![]() )
around the stellar radial velocity. We remind the
reader that the centroid position is
given with respect to the reference frame of the central star: a
positive (negative) centroid position indicates that the feature is
redshifted (blueshifted) compared to the stellar radial velocity. For
the detected emission lines, we have also
determined the full width at half maximum (FWHM) by fitting a Gaussian
function to the feature. This estimate of the FWHM is corrupted
by the instrumental profile of the spectrograph.
Since the telluric lines in the spectra are intrinsicly very narrow,
the FWHM of these absorption features is a good estimate for the
instrumental width. The measured FWHM of the [O I]lines is corrected for
this instrumental broadening. All detected
features in this sample are spectrally resolved (i.e. have a corrected
FWHM several times larger than the instrumental width).
Finally, we have defined an asymmetry
parameter
)
around the stellar radial velocity. We remind the
reader that the centroid position is
given with respect to the reference frame of the central star: a
positive (negative) centroid position indicates that the feature is
redshifted (blueshifted) compared to the stellar radial velocity. For
the detected emission lines, we have also
determined the full width at half maximum (FWHM) by fitting a Gaussian
function to the feature. This estimate of the FWHM is corrupted
by the instrumental profile of the spectrograph.
Since the telluric lines in the spectra are intrinsicly very narrow,
the FWHM of these absorption features is a good estimate for the
instrumental width. The measured FWHM of the [O I]lines is corrected for
this instrumental broadening. All detected
features in this sample are spectrally resolved (i.e. have a corrected
FWHM several times larger than the instrumental width).
Finally, we have defined an asymmetry
parameter
![]() based on the centroid position and the extreme
blue (
based on the centroid position and the extreme
blue (
![]() )
and red (
)
and red (
![]() )
ends of the emission
profile:
)
ends of the emission
profile:
![]() .
When
.
When
![]() is larger (smaller) than 1, the
centroid position lies closer to the red (blue) end of the emission line,
hence indicating a stronger red (blue) wing compared to the center
is larger (smaller) than 1, the
centroid position lies closer to the red (blue) end of the emission line,
hence indicating a stronger red (blue) wing compared to the center
![]() of the
line
of the
line![]() . Note that the
line profile can be completely blueshifted compared to the stellar radial
velocity, while having
. Note that the
line profile can be completely blueshifted compared to the stellar radial
velocity, while having
![]() .
The only [O I] line parameter
that is sensitive to (errors on) the stellar radial velocity is the
centroid position.
.
The only [O I] line parameter
that is sensitive to (errors on) the stellar radial velocity is the
centroid position.
Errors on the [O I]parameter values have been estimated based on the noise in the spectrum. In the figures that are presented in this paper, we have chosen to show a representative error bar instead of plotting the individual error bars on each measurement. This was done for the sake of clarity. The plotted error bar, which indicates the errors on a mean entry in the figure, is refered to in the captions of the figures as the typical error bar.
When no [O I]feature was detected, we have computed an upper limit for the
EW from the noise on the data (![]() ). We assume that the strongest
feature that remains undetected is a rectangular
emission line with a height of 5 times the noise on the data and a
width of 1 Å (=47
). We assume that the strongest
feature that remains undetected is a rectangular
emission line with a height of 5 times the noise on the data and a
width of 1 Å (=47
![]() ). The equivalent width of this hypothetical
feature thus is
). The equivalent width of this hypothetical
feature thus is
![]() .
The latter
value was used as the upper limit for the undetected line.
.
The latter
value was used as the upper limit for the undetected line.
For the 10 sources for which we have more than one optical spectrum at our
disposal, we have measured the [O I]6300 Å feature in all spectra
separately. Afterwards the parameter values
were compared. No significant differences were noted, except for
Z CMa (for which the
![]() increased with
increased with ![]() 40% in 6 years) and MWC 297 (decrease of
40% in 6 years) and MWC 297 (decrease of
![]() with
with ![]() 25% in
3 months). This suggests that for most stars in our
sample the [O I]emission is constant in time, although variations
- either in the continuum flux or in the line emission itself - do
occur in some objects. The final data consist of one measurement for
each source, which is a weighted average when two or more spectra are
available. The centroid positions of the features in the
different spectra of the same source agree well within the error bar,
except again for MWC 297, where the difference in centroid
position adds up to 20
25% in
3 months). This suggests that for most stars in our
sample the [O I]emission is constant in time, although variations
- either in the continuum flux or in the line emission itself - do
occur in some objects. The final data consist of one measurement for
each source, which is a weighted average when two or more spectra are
available. The centroid positions of the features in the
different spectra of the same source agree well within the error bar,
except again for MWC 297, where the difference in centroid
position adds up to 20
![]() .
The forbidden-line emission region of
this source apparently rotates as a whole around the central
star.
.
The forbidden-line emission region of
this source apparently rotates as a whole around the central
star.
Thanks to the large wavelength coverage of the FEROS, KPNO and WHT
spectra, also the wavelength region around the forbidden
[O I]6363 Å emission line was observed for 30 objects.
When present in these spectra, we have determined the EW
and FWHM of the [O I]6363 Å emission line. Otherwise, an upper limit
for the EW was determined. The EW of the H![]() line was measured as well. When no H
line was measured as well. When no H![]() spectrum was available to us,
we have included literature values.
spectrum was available to us,
we have included literature values.
To characterize the spectral energy distribution (SED) of the
central star, several quantities were determined, based on
UV-to-millimeter photometry from the literature. For each source, a
Kurucz (1991) model with effective temperature
![]() and surface
gravity
and surface
gravity ![]() corresponding to the
spectral type of the source was fitted to the de-reddened photometry. From this
model, parameters like total
luminosity L and UV luminosity
corresponding to the
spectral type of the source was fitted to the de-reddened photometry. From this
model, parameters like total
luminosity L and UV luminosity
![]() (2-13.6 eV) can be
determined. By subtracting the Kurucz model
from the infrared photometry, the flux excesses at 2.2
(i.e. K band), 60, 850 and 1300 micron can be determined. Other
parameters used in this analysis are the
the observed bolometric luminosity
(2-13.6 eV) can be
determined. By subtracting the Kurucz model
from the infrared photometry, the flux excesses at 2.2
(i.e. K band), 60, 850 and 1300 micron can be determined. Other
parameters used in this analysis are the
the observed bolometric luminosity
![]() (not corrected for
extinction) and the distance d to the source.
(not corrected for
extinction) and the distance d to the source.
To convert the measured EW of the [O I]lines to [O I]
luminosities, we have computed the theoretical 6300 Å continuum flux from
the Kurucz model. The relationship between the [O I]luminosity L([O I]) and the EW is
![\begin{displaymath}L(\rm {[O~{\mathsc i}]}) = 4 \pi d^2~~ 2.5 \times 10^2~ \vert{\it EW}\vert \times
\mathcal{F}\left(6300~\r{A} \right)
\end{displaymath}](/articles/aa/full/2005/22/aa2484-04/img55.gif) |
(1) |
The sample sources were classified into the M01 groups, based on the
shape of their IR excess. In accordance with van Boekel et al. (2003), we
characterize the SED using the following quantities: the ratio of
![]() (the integrated luminosity derived from broad-band J, H, K, L and M photometry) and L(IR) (the corresponding
quantity derived from IRAS 12, 25 and 60 micron points), and the
non-color-corrected
IRAS [12]-[60] color. These quantities naturally
separate sources with a strong mid-IR excess (group I) from
more modest mid-IR emitters (group II). In Fig. 1,
the classification is visualized in a diagram. The dashed line
represents
(the integrated luminosity derived from broad-band J, H, K, L and M photometry) and L(IR) (the corresponding
quantity derived from IRAS 12, 25 and 60 micron points), and the
non-color-corrected
IRAS [12]-[60] color. These quantities naturally
separate sources with a strong mid-IR excess (group I) from
more modest mid-IR emitters (group II). In Fig. 1,
the classification is visualized in a diagram. The dashed line
represents
![]() ,
which empirically
provides the best separation between both groups. This classification
method has also been used in Dullemond et al. (2003) and AV04 and has
been described more thoroughly in Acke et al. (2004). The quantities
,
which empirically
provides the best separation between both groups. This classification
method has also been used in Dullemond et al. (2003) and AV04 and has
been described more thoroughly in Acke et al. (2004). The quantities
![]() and [12]-[60] are listed in Table 2.
and [12]-[60] are listed in Table 2.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2484fig01.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg63.gif) |
Figure 1:
Classification diagram, based on van Boekel et al. (2003).
Objects in the upper left corner are classified as group
II sources (open diamonds), sources on the lower right side are
either group I (filled diamonds) or group III (squares) members. The
dashed line represents the empirical separation between group I and
II:
|
| Open with DEXTER | |
Table 2:
The non-color-corrected
IRAS [12]-[60] color and the
near-to-mid IR luminosity ratio
![]() of the sample
sources.
of the sample
sources.
Five sources in this sample display the amorphous 10 micron silicate feature in absorption (AV04). Considering the presence of an outflow and CO bandhead emission, strong veiling and a UV excess, these objects are thought to have disks whose luminosity is dominated by viscous dissipation of energy due to accretion, and are deeply embedded sources. This idea is supported by their very red IR spectral energy distribution. They are likely fundamentally different from the other sample stars. We therefore classify them in a different group: group III.
BD+40![]() 4124, R CrA and LkH
4124, R CrA and LkH![]() 224 have not been
classified based on their location in the diagram in
Fig. 1. Confusion with background sources in the IRASphotometry made it impossible to derive the desired quantities
224 have not been
classified based on their location in the diagram in
Fig. 1. Confusion with background sources in the IRASphotometry made it impossible to derive the desired quantities
![]() and [12]-[60]. BD+40
and [12]-[60]. BD+40![]() 4124 has been classified
as a group I source, because its SED resembles that of HD 200775. R CrA and LkH
4124 has been classified
as a group I source, because its SED resembles that of HD 200775. R CrA and LkH![]() 224 are both UX Orionis
stars. According to Dullemond et al. (2003), these sources are group II
sources. Hence we have classified them as members of the latter group.
224 are both UX Orionis
stars. According to Dullemond et al. (2003), these sources are group II
sources. Hence we have classified them as members of the latter group.
In Figs. 2-4, the velocity-rebinned spectra of the [O I] 6300 Å emission lines are presented. The first plot contains the detected emission profiles. Figure 3 shows the spectra in which the possible detection of [O I]emission is confused by underlying photospheric absorption lines. Sample sources with undetected 6300 Å emission are displayed in Fig. 4. In each plot, the targets are listed according to group.
The forbidden oxygen 6300 Å emission line in Herbig Ae/Be stars has
been studied in previous articles
(Corcoran & Ray 1997; Finkenzeller 1985; Hamann 1994; Böhm & Hirth 1997; Corcoran & Ray 1998; Hernández et al. 2004; Böhm & Catala 1994).
We have compared the equivalent widths measured in our
spectra to published literature values in Fig. 5. The error on
our EWs is computed from the noise on the data, multiplied with the
average FWHM of the feature. Few previous authors indicate the errors on their
measurements, hence we cannot set an error bar on the literature
numbers. Nevertheless we are convinced that our data set, consisting of
high-resolution, high-signal-to-noise spectra (![]() -375), are
of better quality than the data studied in previous papers. We
believe that our error bars are a reliable estimate for the scatter on
our determinations, and a lower limit to the literature errors.
The observed scatter in Fig. 5 is
quite large. This might be due to intrinsicly variable [O I] emission
(e.g. Z CMa, van den Ancker et al. 2004)
or variable continuum emission (e.g. in UX Orionis
stars). A possible extrinsic explanation is the uncorrected airglow
emission in previous articles. Since we have removed the telluric
lines and airglow wavelength regions from our data, our measurements
are less affected by these features. Low spectral resolution does not
allow for removal of the latter. Most of the literature EW values in
Fig. 5 - especially those of the weak lines - appear to
be larger than our values, suggesting that the airglow effect indeed
corrupts these measurements.
-375), are
of better quality than the data studied in previous papers. We
believe that our error bars are a reliable estimate for the scatter on
our determinations, and a lower limit to the literature errors.
The observed scatter in Fig. 5 is
quite large. This might be due to intrinsicly variable [O I] emission
(e.g. Z CMa, van den Ancker et al. 2004)
or variable continuum emission (e.g. in UX Orionis
stars). A possible extrinsic explanation is the uncorrected airglow
emission in previous articles. Since we have removed the telluric
lines and airglow wavelength regions from our data, our measurements
are less affected by these features. Low spectral resolution does not
allow for removal of the latter. Most of the literature EW values in
Fig. 5 - especially those of the weak lines - appear to
be larger than our values, suggesting that the airglow effect indeed
corrupts these measurements.
In Sect. 2.2, we have categorized the profiles based on the
presence of absorption features underlying the [O I] emission line at
6300 Å. The latter features are photosperic absorption
lines, which have no direct relation with the [O I] emission. This idea
is supported by the fact that all 10 sources which display absorption
features in the 6300 Å region have late spectral types (i.e. low
effective temperatures;
![]() ). Such
objects display photosperic absorption lines in this
wavelength region, contrary to early-type stars which have flat
continua around 6300 Å.
). Such
objects display photosperic absorption lines in this
wavelength region, contrary to early-type stars which have flat
continua around 6300 Å.
In Fig. 6, the measured EWs of the line
profiles is plotted versus the effective temperature. In the left part
of the figure, the targets with detected [O I]emission are
plotted. These appear to be the early-type sources.
For stars in which the possible [O I]6300 Å emission is confused by
photospheric lines (right part of the plot), the EWs increase
with decreasing
![]() .
This is probably the combined effect of
the increasing strength of the photospheric absorption lines on one
hand, and the decreasing UV luminosity in late-type stars on the
other (see later). Because of the difficulty to distinguish between
the possible [O I] emission line and the underlying photospheric absorption spectrum, no
accurate measurements of the FWHM and centroid position could be
made for these objects. Therefore, these determinations have been left
out of the further analysis.
.
This is probably the combined effect of
the increasing strength of the photospheric absorption lines on one
hand, and the decreasing UV luminosity in late-type stars on the
other (see later). Because of the difficulty to distinguish between
the possible [O I] emission line and the underlying photospheric absorption spectrum, no
accurate measurements of the FWHM and centroid position could be
made for these objects. Therefore, these determinations have been left
out of the further analysis.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2484fig02.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg66.gif) |
Figure 2:
The detected [O I]6300 Å emission line spectra. Along the x-axis, the velocity
in
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{2484fig03.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg67.gif) |
Figure 3: The 6300 Å spectra of the sample stars for which the detection of [O I]emission is confused by photospheric absorption lines. Legend see Fig. 2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{2484fig04.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg68.gif) |
Figure 4: The 6300 Å spectra of the sample stars with undetected [O I] emission. Legend see Fig. 2. |
| Open with DEXTER | |
The other sample sources display no absorption lines in the [O I]
wavelength range. 10 objects do not display any significant
features and will be included in the figures as upper limits. The
majority of our sample sources (29/49) have a clear [O I] emission
profile in their spectra. In
Figs. 7 to 10, the parameters that
describe the emission [O I]profile are plotted against each
other. The mean
parameters describing the emission line profile are
![]() FWHM
FWHM
![]()
![]() ,
,
![]() centroid position
centroid position
![]() 4
4
![]() and
and
![]() .
The median
values of these quantities in this sample
are 47
.
The median
values of these quantities in this sample
are 47
![]() ,
-7
,
-7
![]() and 0.95 respectively. It is striking
that, when excluding the three outliers (PV Cep, V645
Cyg and Z CMa;
and 0.95 respectively. It is striking
that, when excluding the three outliers (PV Cep, V645
Cyg and Z CMa; ![]() in the plots) which will
be discussed later, most of
the sample sources with pure-emission [O I]profiles lie
close to these average values. The objects seem to have quite
uniform [O I] emission line profiles. The EW of the feature
is not correlated to its width (FWHM), indicating that the broadening
mechanism of the line does not depend on the amount of [O I] emission. Nevertheless, a difference in FWHM is observed between
group I (mean: 36
in the plots) which will
be discussed later, most of
the sample sources with pure-emission [O I]profiles lie
close to these average values. The objects seem to have quite
uniform [O I] emission line profiles. The EW of the feature
is not correlated to its width (FWHM), indicating that the broadening
mechanism of the line does not depend on the amount of [O I] emission. Nevertheless, a difference in FWHM is observed between
group I (mean: 36
![]() ;
median: 34
;
median: 34
![]() )
and group II (mean: 67
)
and group II (mean: 67
![]() ;
median: 55
;
median: 55
![]() ). The centroid position is also independent of the EW
(Fig. 8).
). The centroid position is also independent of the EW
(Fig. 8).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2484fig05.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg75.gif) |
Figure 5:
Comparison between published values for the equivalent width
of the [O I]6300 Å line and our determinations. The different plotting
symbols refer to data obtained by different authors. The typical error
bar is plotted
in the upper left corner. The error bar on the literature values is
expected to be larger than the indicated error, which is equal to our
estimate for the error bar. The dashed line represents
|
| Open with DEXTER | |
Böhm & Catala (1994) note that the [O I]6300 Å
profiles in their sample are not blueshifted with respect to the
stellar radial velocity. Corcoran & Ray (1997) on the other hand report
that most of the HAEBEs in their sample show low-velocity blueshifted
centroid positions. We look into this more carefully.
Figure 9 displays the distribution of the centroid
positions of the pure-emission [O I] profiles in a histogram. The group III sources have been excluded from the diagram. The width of the
bins is 10
![]() .
The estimated error on the measured centroid positions,
including the error on the stellar-radial-velocity determination, is
.
The estimated error on the measured centroid positions,
including the error on the stellar-radial-velocity determination, is
![]()
![]() .
We assume that the errors on the centroid
positions are distributed following a standard-normal distribution
.
We assume that the errors on the centroid
positions are distributed following a standard-normal distribution
![]() .
We check whether the observed distribution
.
We check whether the observed distribution
![]() is
representative for the expected normal distribution
is
representative for the expected normal distribution
![]() .
The possibility that the centroid position of a
feature is >
.
The possibility that the centroid position of a
feature is >![]() under the hypothesis of the
under the hypothesis of the
![]() distribution is 16%. Five sources display
redshifted centroid
positions larger than 15
distribution is 16%. Five sources display
redshifted centroid
positions larger than 15
![]() .
This is not a statistically significant deviation
from
.
This is not a statistically significant deviation
from
![]() for a sample of 24 stars. Nevertheless, on the
blue side, nine sources display centroid positions <-15
for a sample of 24 stars. Nevertheless, on the
blue side, nine sources display centroid positions <-15
![]() .
The
possibility for this to happen under the current hypothesis is less
than 1%. We conclude that, although the majority of stars in our
sample have centroid positions that are compatible with the stellar
radial velocity, there appear to be some objects that indeed show
low-velocity blueshifted centroid positions as reported by
Corcoran & Ray (1997). The Gaussian fit (full line in
Fig. 9) to the observed
histogram is centered around -7
.
The
possibility for this to happen under the current hypothesis is less
than 1%. We conclude that, although the majority of stars in our
sample have centroid positions that are compatible with the stellar
radial velocity, there appear to be some objects that indeed show
low-velocity blueshifted centroid positions as reported by
Corcoran & Ray (1997). The Gaussian fit (full line in
Fig. 9) to the observed
histogram is centered around -7
![]() and has
and has
![]()
![]() .
Notice that for the five sources with detected [O I]6300 Å emission for
which we
have spectra covering a large part of the optical wavelength region
(i.e. AB Aur, HD 245185, HD 97048,
HD 100546 and Z CMa), the error on the centroid
determination is much smaller than 15 km s-1. Of these objects, only
group III member Z CMa shows evidence for a blueshifted
feature. In particular the small error (
.
Notice that for the five sources with detected [O I]6300 Å emission for
which we
have spectra covering a large part of the optical wavelength region
(i.e. AB Aur, HD 245185, HD 97048,
HD 100546 and Z CMa), the error on the centroid
determination is much smaller than 15 km s-1. Of these objects, only
group III member Z CMa shows evidence for a blueshifted
feature. In particular the small error (![]() 2
2
![]() )
for HD
100546 proves that at least some sources are definitely not
blueshifted.
)
for HD
100546 proves that at least some sources are definitely not
blueshifted.
Even though some sources display blueshifted emission, there does not
seem to be a strong deviation from asymmetry. In
Fig. 10 the FWHM of the [O I]feature is
plotted versus the asymmetry parameter
![]() .
No correlation
between the two parameters is noted.
.
No correlation
between the two parameters is noted.
Three group III sources (PV Cep, V645 Cyg and Z CMa)
have radically different [O I]emission profiles from the other sources
in our sample. The shape of these
features is double-peaked, with one peak close to the radial velocity
of the central star (v = 0
![]() )
and the other at high blueshift
(
)
and the other at high blueshift
(
![]()
![]() ). The red wing (v > 0
). The red wing (v > 0
![]() )
of the
feature extends up to
)
of the
feature extends up to ![]()
![]() ,
while the blue wing (v < 0
,
while the blue wing (v < 0
![]() )
is much stronger and expands
as far as
)
is much stronger and expands
as far as
![]() to -730
to -730
![]() .
This makes the [O I]6300 Å line
in these sources
outliers in Figs. 7 and 8.
Because of the obvious differences, the parameters describing the
[O I] profiles of these three sources are not included in the
computation of the average [O I] parameters. The asymmetry parameter on
the other hand is close to 1 for all three sources. Indeed, the
features are quite symmetric around the (strongly blueshifted)
centroid position. This is due to the fact that the blueshifted
emission peak in these features is of comparable strength to the
emission peak near 0
.
This makes the [O I]6300 Å line
in these sources
outliers in Figs. 7 and 8.
Because of the obvious differences, the parameters describing the
[O I] profiles of these three sources are not included in the
computation of the average [O I] parameters. The asymmetry parameter on
the other hand is close to 1 for all three sources. Indeed, the
features are quite symmetric around the (strongly blueshifted)
centroid position. This is due to the fact that the blueshifted
emission peak in these features is of comparable strength to the
emission peak near 0
![]() .
.
For 30 objects, the 6363 Å line region is covered by our spectra. In
15 sample sources, where the [O I]6300 Å line was detected, the [O I]6363 Å line was detected as
well. The profile of the [O I] line in these objects is
pure-emission. Six sources for which the [O I]6300 Å line was detected,
did not display the 6363 Å line. In the remaining 9 objects, no [O I] lines were detected. This includes all 5 sources with an
absorption-line-rich 6300 Å wavelength region, for which we have data
around 6363 Å. The mean ratio of the EWs of the 6300 Å and 6363 Å lines
![]() is
is ![]() ,
which is within
the error equal to the ratio of the Einstein transition rates
of the lines (
A6300/A6363 = 3.0). The lower limits derived
for the sources with an undetected 6363 Å line are also consistent with
this value. The mean difference between the FWHMs of both lines is
close to 0
,
which is within
the error equal to the ratio of the Einstein transition rates
of the lines (
A6300/A6363 = 3.0). The lower limits derived
for the sources with an undetected 6363 Å line are also consistent with
this value. The mean difference between the FWHMs of both lines is
close to 0
![]() ,
FWHM(6300 Å) - FWHM(6363 Å) =
,
FWHM(6300 Å) - FWHM(6363 Å) = ![]()
![]() .
The [O I]6363 Å emission line has the same origin as
the [O I]6300 Å line, as one would expect for two lines that
originate from the same upper energy level (
.
The [O I]6363 Å emission line has the same origin as
the [O I]6300 Å line, as one would expect for two lines that
originate from the same upper energy level (
![]() ). The spectral
information in one line is exactly the same as in the other. The only
parameter that can influence the EW ratio of both lines is
differential extinction. Using a standard interstellar
extinction law (Fluks et al. 1994) and the error bar on the EW ratio
(
). The spectral
information in one line is exactly the same as in the other. The only
parameter that can influence the EW ratio of both lines is
differential extinction. Using a standard interstellar
extinction law (Fluks et al. 1994) and the error bar on the EW ratio
(![]() 30%), one can derive that the visual
extinction towards the emission region must be less than 30.
Also for Z CMa - in which the profile is very broad, and we
have a sufficient S/N in both the 6300 and 6363 Å line to allow an
accurate comparison - the two [O I]lines have comparable profiles.
The [S II] emission line at 6731 Å - which is
present in the WHT spectrum of Z CMa - has a
similar shape as the [O I] lines, be it with a much weaker blue wing.
This forbidden line is undetected (<0.01 Å) in the other FEROS
and WHT spectra.
30%), one can derive that the visual
extinction towards the emission region must be less than 30.
Also for Z CMa - in which the profile is very broad, and we
have a sufficient S/N in both the 6300 and 6363 Å line to allow an
accurate comparison - the two [O I]lines have comparable profiles.
The [S II] emission line at 6731 Å - which is
present in the WHT spectrum of Z CMa - has a
similar shape as the [O I] lines, be it with a much weaker blue wing.
This forbidden line is undetected (<0.01 Å) in the other FEROS
and WHT spectra.
![\begin{figure}
\par\includegraphics[width=17.7cm,clip]{2484fig06.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg86.gif) |
Figure 6:
The EWs of the [O I]emission lines versus the effective
temperature of the central star. Filled diamonds refer to group I
sources, open diamonds to
group II. Squares are group III sources, with the |
| Open with DEXTER | |
The wavelength region around the forbidden oxygen line at 5577 Å is
covered by the FEROS and WHT spectra. No features where detected, with
upper limits of 0.01 Å. Assuming that the emission of
both the 5577 Å and 6300 Å line are thermal, one can estimate the
theoretical Saha-Boltzmann 5577/6300 intensity ratio. In our
sample we measure upper limits for this ratio of the order of
![]() 1/20. The observations hence exclude that the oxygen lines are
produced by thermal emission of oxygen atoms at temperatures above
1/20. The observations hence exclude that the oxygen lines are
produced by thermal emission of oxygen atoms at temperatures above
![]() 3000 K. This is a strong
indication that the source of the [O I] emission at 6300 Å in HAEBEs
cannot be found in thermal excitation of oxygen in a "super-heated''
surface layer, as is the case for T Tauri stars (see later).
3000 K. This is a strong
indication that the source of the [O I] emission at 6300 Å in HAEBEs
cannot be found in thermal excitation of oxygen in a "super-heated''
surface layer, as is the case for T Tauri stars (see later).
The H![]() features in our sample were classified based on the observed
profile: single-peaked, double-peaked, P Cyg-like or inversed P Cyg-like. Despite the object's name, in our spectrum of
LkH
features in our sample were classified based on the observed
profile: single-peaked, double-peaked, P Cyg-like or inversed P Cyg-like. Despite the object's name, in our spectrum of
LkH![]() 225 no H
225 no H![]() feature was detected. Since this
spectral feature has previously been observed in emission in both
components of this binary system (Magakyan & Movsesyan 1997), the absence of the line
in our spectrum suggests H
feature was detected. Since this
spectral feature has previously been observed in emission in both
components of this binary system (Magakyan & Movsesyan 1997), the absence of the line
in our spectrum suggests H![]() variability.
10 of the 49 sample sources (20%) display single-peaked, 25 (51%)
double-peaked and 12 (24%) P Cyg-like H
variability.
10 of the 49 sample sources (20%) display single-peaked, 25 (51%)
double-peaked and 12 (24%) P Cyg-like H![]() emission
profiles. In SV Cep, an inversed P
Cyg-profile is observed. This is in good agreement with the H
emission
profiles. In SV Cep, an inversed P
Cyg-profile is observed. This is in good agreement with the H![]() distribution in the samples of Finkenzeller & Mundt (1984) and
Böhm & Catala (1994): 50% double-peaked, 25% single-peaked and 20% P
Cyg-like. In Table 3 the different categories of the
H
distribution in the samples of Finkenzeller & Mundt (1984) and
Böhm & Catala (1994): 50% double-peaked, 25% single-peaked and 20% P
Cyg-like. In Table 3 the different categories of the
H![]() profile are listed versus the types of the [O I] profile.
When plotting the [O I] luminosities of the sample stars versus the H
profile are listed versus the types of the [O I] profile.
When plotting the [O I] luminosities of the sample stars versus the H![]() luminosities, regardless of the type of profile, a clear correlation
is noted (Fig. 11). Z CMa, PV Cep
and V645 Cyg seem to have significantly more [O I]-to-H
luminosities, regardless of the type of profile, a clear correlation
is noted (Fig. 11). Z CMa, PV Cep
and V645 Cyg seem to have significantly more [O I]-to-H![]() luminosity than other sources. No significant differences
between the other groups are noted. The average luminosity ratio
L([O I])
luminosity than other sources. No significant differences
between the other groups are noted. The average luminosity ratio
L([O I])
![]() is
is
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2484fig07.ps} %\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg89.gif) |
Figure 7:
The EW of the detected [O I]emission lines versus the FWHM. Filled
diamonds represent group I, open diamonds group II and
squares group III sources. The |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2484fig08.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg90.gif) |
Figure 8:
The EW of the detected [O I]emission lines versus the centroid
position of the feature. The plotting symbols are as in
Fig. 7. The vast majority of the features is
centered around the stellar radial velocity within the error
bars. The dashed line represents the average centroid position (-4
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2484fig09.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg91.gif) |
Figure 9:
The histogram of the centroid positions of the 12 group I and
12 group II sample sources with a detected [O I]6300 Å feature. The bin
size is 10
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2484fig10.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg92.gif) |
Figure 10:
The FWHM of the detected [O I]emission lines versus the asymmetry
parameter of the feature. The plotting symbols are as in
Fig. 7. The dashed horizontal line represents the mean value (1.04)
for
|
| Open with DEXTER | |
Table 3:
The different categories of H![]() profiles versus the types
of [O I]profiles. The entries of the table are the number of
stars belonging to the corresponding category. U: undetected
feature, E: pure-emission profile, A: 6300 Å region rich in
photospheric absorption lines, S: single-peaked profile, D: double-peaked
profile, P: P Cyg-like profile, inv. P: inversed P
Cyg-like profile.
profiles versus the types
of [O I]profiles. The entries of the table are the number of
stars belonging to the corresponding category. U: undetected
feature, E: pure-emission profile, A: 6300 Å region rich in
photospheric absorption lines, S: single-peaked profile, D: double-peaked
profile, P: P Cyg-like profile, inv. P: inversed P
Cyg-like profile.
In this section we compare the parameters describing the [O I]6300 Å
emission line to the SED parameters. In Fig. 12 the [O I] luminosity is plotted versus the UV luminosity of the central
star. The dashed line represents the median [O I]-over-UV
luminosity ratio (
![]() )
of the detected lines, while
the average
value is
)
of the detected lines, while
the average
value is ![]()
![]() .
In general, the [O I]luminosity
increases with increasing
.
In general, the [O I]luminosity
increases with increasing
![]() .
The different plotting symbols
represent the three groups of HAEBE stars in our sample.
Note that there is a considerable number of (almost all group II)
sources with an undetected [O I] 6300 Å feature. The upper limits
clearly deviate from the average.
.
The different plotting symbols
represent the three groups of HAEBE stars in our sample.
Note that there is a considerable number of (almost all group II)
sources with an undetected [O I] 6300 Å feature. The upper limits
clearly deviate from the average.
The group III sources display the strongest [O I]
emission. All 5 sources in this group have high L([O I]) in the range
between
![]() and
and
![]() .
The median [O I]6300 Å
luminosity is
.
The median [O I]6300 Å
luminosity is
![]() .
Of the 12 group I objects
in the plot, only one source does
not show a detected [O I]6300 Å emission line. The median [O I]luminosity of
the detected features in this group is
.
Of the 12 group I objects
in the plot, only one source does
not show a detected [O I]6300 Å emission line. The median [O I]luminosity of
the detected features in this group is
![]() .
About 43% of the
group II sources in this sample (excluding
those with absorption-polluted spectra) do not
have a detected [O I] emission line. Moreover, even the median
luminosity of the detected features in group II (
.
About 43% of the
group II sources in this sample (excluding
those with absorption-polluted spectra) do not
have a detected [O I] emission line. Moreover, even the median
luminosity of the detected features in group II (
![]() )
is smaller than in the other two groups.
Figure 13 shows the histogram of the EWs of the group I and II sources. The group I sources have slightly stronger [O I]
intensities than group II sources. Also the typical width of the features
differs between group I and II. The latter is illustrated in
Fig. 14. The group II profile is
)
is smaller than in the other two groups.
Figure 13 shows the histogram of the EWs of the group I and II sources. The group I sources have slightly stronger [O I]
intensities than group II sources. Also the typical width of the features
differs between group I and II. The latter is illustrated in
Fig. 14. The group II profile is ![]() 20
20
![]() broader than the group I profile.
We conclude that there is a clear correlation between the IR-SED
classification of the sources and the strength and shape of the [O I] emission line.
broader than the group I profile.
We conclude that there is a clear correlation between the IR-SED
classification of the sources and the strength and shape of the [O I] emission line.
In Table 4 we have summarized the parameters describing the [O I] emission lines. The sample sources are listed according to their classification.
In this section we look for correlations between the PAH parameters and the [O I]6300 Å parameters for the 40 sample objects which were included in the analysis of AV04.
Figure 15 shows the estimated PAH luminosity versus the [O I]6300 Å luminosity. The 31 objects that are included in this plot have a pure-emission [O I]profile. A clear positive correlation is seen for the 14 stars that have detected PAH as well as [O I]6300 Å emission. The PAH luminosity is on average 350 times larger than the [O I] luminosity. All group III sources in this sample have strong [O I] luminosity, but weak or undetected PAH emission. The PAH and [O I] luminosities of the group II sources are weak or undetected in most cases, while a typical group I source displays strong PAH and [O I] emission.
Table 4:
The [O I]parameters for each sample source. The objects are
listed according to their IR-SED classification. The distance to the
source, the effective temperature, UV luminosity and bolometric
(= integrated observed) luminosity are given. References
for the first two values can be found in Table 6 of AV04, unless
otherwise indicated: A de Zeeuw et al. (1999); B Finkenzeller (1985); C Gray & Corbally (1993); D Gray & Corbally (1998);
E Houk (1978); F Mora et al. (2001); G Vieira et al. (2003);
H van den Ancker et al. (1998). The type of [O I]
6300 Å emission profile observed in each object has been indicated;
E: pure-emission profile, A: 6300 Å region rich in photospheric
absorption lines, U: undetected feature (upper limit). n.s.: no spectrum
available. The typical errors on the FWHM and centroid position are
![]() 8 and
8 and ![]() 15
15
![]() respectively.
The thirth column contains the stellar radial velocity employed in
this study. This value is estimated from the
available spectra, unless otherwise indicated: a Arce & Goodman (2002);
b Arellano Ferro & Giridhar (2003); c Barbier-Brossat & Figon (2000); d Dunkin et al. (1997a); e Piétu et al. (2003); f Reipurth et al. (1996); g Yonekura et al. (1997, based on CO lines).
respectively.
The thirth column contains the stellar radial velocity employed in
this study. This value is estimated from the
available spectra, unless otherwise indicated: a Arce & Goodman (2002);
b Arellano Ferro & Giridhar (2003); c Barbier-Brossat & Figon (2000); d Dunkin et al. (1997a); e Piétu et al. (2003); f Reipurth et al. (1996); g Yonekura et al. (1997, based on CO lines). ![]() Based on Ca II
lines.
Based on Ca II
lines.
![]() Average of radial velocities of
stars in the same field (radius
Average of radial velocities of
stars in the same field (radius![]() 2
2![]() ).
The last two columns of the table give the type and EW of the
observed H
).
The last two columns of the table give the type and EW of the
observed H![]() profile; S: single-peaked; D: double-peaked; P: P
Cygni-like; inv. P: inversed P Cyg-like. When no spectrum was
available, literature
values were used: h Arellano Ferro & Giridhar (2003); i de Winter & Thé (1990);
j Dunkin et al. (1997a); k Dunkin et al. (1997b); l Finkenzeller & Mundt (1984); m Merín et al. (2004); n Pérez & Grady (1997).
profile; S: single-peaked; D: double-peaked; P: P
Cygni-like; inv. P: inversed P Cyg-like. When no spectrum was
available, literature
values were used: h Arellano Ferro & Giridhar (2003); i de Winter & Thé (1990);
j Dunkin et al. (1997a); k Dunkin et al. (1997b); l Finkenzeller & Mundt (1984); m Merín et al. (2004); n Pérez & Grady (1997).
When comparing the luminosity of the amorphous 10 micron silicate feature to the [O I] 6300 Å luminosity (Fig. 16), no clear correlation is seen. The arrows which indicate upper limits support this non-correlation.
A few sources like the group III outliers Z CMa, PV
Cep and V645 Cyg, but also group I source HD 200775
and group II source HD 141569 have broad features
(FWHM > 100
![]() )
with
pronounced blue wings. A few more sources have low-velocity
blueshifted centroids. Nevertheless, the majority of observed [O I]
6300 Å emission lines have narrow (
)
with
pronounced blue wings. A few more sources have low-velocity
blueshifted centroids. Nevertheless, the majority of observed [O I]
6300 Å emission lines have narrow (
![]()
![]() )
symmetric
profiles, centered around the stellar radial velocity. Some of the
high-resolution spectra display double-peaked profiles with a
peak-to-peak distance of
)
symmetric
profiles, centered around the stellar radial velocity. Some of the
high-resolution spectra display double-peaked profiles with a
peak-to-peak distance of ![]() 10
10
![]() .
The low velocities,
symmetry of the feature and the peak-to-peak separation correspond to
what one would expect from an emission-line region at the
circumstellar-disk surface. We interpret the observed
[O I]lines in the majority of our sample as being circumstellar-disk emission
features. The forbidden-line emission region is located in the disk's
atmosphere; a warm layer, directly irradiated by the central star and
corotating with the disk. The
blue wing which is present in a minority of the cases is most probably
emanating from an outflow, with the red wing eclipsed by the
circumstellar disk. In this section we will discuss the arguments
for this interpretation.
.
The low velocities,
symmetry of the feature and the peak-to-peak separation correspond to
what one would expect from an emission-line region at the
circumstellar-disk surface. We interpret the observed
[O I]lines in the majority of our sample as being circumstellar-disk emission
features. The forbidden-line emission region is located in the disk's
atmosphere; a warm layer, directly irradiated by the central star and
corotating with the disk. The
blue wing which is present in a minority of the cases is most probably
emanating from an outflow, with the red wing eclipsed by the
circumstellar disk. In this section we will discuss the arguments
for this interpretation.
When investigating the narrow profiles of the non-blueshifted
features in the high-resolution ESO 3.6 m spectra, a double-peaked
profile is seen in a some cases. In Fig. 17 this
specific shape in the spectrum of HD 100546 (group I) is
shown. The two peaks are located at equal distance (![]()
![]() 6
6
![]() )
from the centroid position. Similar profiles have been observed in CO
emission lines (e.g. Chandler et al. 1993; Thi et al. 2001) and have been attributed to the
Keplerian rotation of the circumstellar gas disk. Also in group I
sources HD 97048, HD 135344 and T CrA, for
which we have ESO spectra, this double-peaked shape is clearly
seen. The other spectra have a lower spectral resolution, and thus the
double peaks are less clear. Considering the latter, more sources with
symmetrical low-velocity profiles, like AB Aur, might have a
double-peaked line shape. In Sect. 5 we model the
spectral profiles of some of these features.
)
from the centroid position. Similar profiles have been observed in CO
emission lines (e.g. Chandler et al. 1993; Thi et al. 2001) and have been attributed to the
Keplerian rotation of the circumstellar gas disk. Also in group I
sources HD 97048, HD 135344 and T CrA, for
which we have ESO spectra, this double-peaked shape is clearly
seen. The other spectra have a lower spectral resolution, and thus the
double peaks are less clear. Considering the latter, more sources with
symmetrical low-velocity profiles, like AB Aur, might have a
double-peaked line shape. In Sect. 5 we model the
spectral profiles of some of these features.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2484fig11.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg143.gif) |
Figure 11:
The [O I]-versus-H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2484fig12.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg144.gif) |
Figure 12:
The [O I]6300 Å luminosity versus the stellar UV
luminosity. The plotting symbols are as in
Fig. 7. The typical error bar is indicated in the
upper left corner. The dotted line represents the median luminosity
ratio L([O I])
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2484fig13.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg145.gif) |
Figure 13: Histogram of the EWs containing the 13 group I and 24 group II members for which we have a measurement of, or an upper limit to the EW of the [O I]6300 Å emission line. The filled part of the bars represents group I sources, the open part group II members. The bin size is 0.05 Å. The group I sources have slightly higher EW values than their group II counterparts. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2484fig14.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg146.gif) |
Figure 14:
The average [O I]6300 Å profiles for
group I and group II. The horizontal dotted lines are plotted at 0 and 0.5, while the vertical dotted line represents the centroid position
of the feature. The 12 group I and 12 group II sources which
display [O I] emission are included. The profile of each source was
shifted to its centroid position, continuum-subtracted and
normalized by dividing by its peak-flux. The group II profile
(dashed line) is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2484fig15.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg147.gif) |
Figure 15: The PAH luminosity versus the [O I]6300 Å luminosity. The plot includes the 12 group I, 14 group II and 5 group III sources for which (an upper limit of) both measurements was available. The dotted line represents the median PAH-over-[O I]luminosity ratio L(PAH)/L([O I]) = 130. Plotting symbols are as in Fig. 7. The typical error bar is indicated in the upper left corner. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2484fig16.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg148.gif) |
Figure 16:
The luminosity of the amorphous 10 micron silicate feature
versus the [O I]6300 Å luminosity. The
plot includes the 12 group I and 15 group II sources for which (an
upper limit of) both measurements was available. The group III
sources are left out since they display silicate absorption at
10 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2484fig17.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg149.gif) |
Figure 17:
The [O I]6300 Å emission line in the spectra of HD
100546. The double-peaked profile is clearly seen in the ESO 3.6 m
and CAT spectrum. Due to the lower spectral resolution, the profile
remains unresolved in the FEROS spectrum. The horizontal dotted
lines represent the continuum levels of the three spectra. The
vertical line is the mean centroid position of the feature at 3
|
| Open with DEXTER | |
A second indication that the forbidden-line emission region is connected to the circumstellar disk lies in the correlation between the strength of the [O I] line and the SED classification of the sources. As explained before, group I sources are suggested to have a flared-disk geometry, while it is believed that group II members have self-shadowed disks. The disk geometry can play an important role in the amount of neutral oxygen in the upper level of the 6300 Å line. Apart from thermal excitation, photodissociation of OH and H2O molecules by UV photons can significantly increase the number of excited oxygen atoms (van Dishoeck & Dalgarno 1984). When these molecules are exposed to high UV fluxes, e.g. at the surface of a flared disk, the non-thermal population of the upper level of the 6300 Å line occurs very efficiently. The outer parts of self-shadowed disks lie completely in the shade of the puffed-up inner rim. Consequently, the UV radiation of the central star cannot reach the disk surface and no significant photodissociation of OH and H2O molecules will take place. This would result in weaker [O I]emission for group II sources. The absence of the feature in 40% of the group II sources and Fig. 13 indeed show that the correlation between [O I]6300 Å luminosity and M01 classification exists, as described in Sect. 3.2.
Furthermore, the [O I]luminosity is also correlated to the PAH luminosity of the source (see Fig. 15). These molecules need stellar UV photons to get excited. In flared disks, significantly more PAH emission is observed than in self-shadowed disks (AV04). The observed correlation between the [O I]and PAH luminosity suggests that both the oxygen atoms and the PAH molecules radiate from the same location: the disk's atmosphere. This low-density, UV-photon-immersed region at the disk's surface offers the ideal locus for the photodissociation of OH and H2O and the consequent 6300 Å forbidden-line emission.
The non-correlation of the [O I]6300 Å luminosity with the luminosity of the amorphous 10 micron band is also expected under the present hypothesis. The small silicate grains that cause this emission feature are thermally excited and do not need direct stellar flux. The observed lack of correlation is similar to the non-correlation between the PAH luminosity and the luminosity of the 10 micron feature as described by AV04.
In this section we model the [O I]emission in the atmosphere of a flared disk. We have computed the structure of a flared disk (Chiang & Goldreich 1997) and determined the layer from which the [O I]emission emanates. In this layer, the density is low and the UV flux abundant. We calculate the intensity of the [O I] emission for different stellar and disk parameters. In order to model the line profiles observed in the spectra, the theoretical emission-line profile was determined by convolving the computed intensities with a Keplerian-rotation profile.
We have implemented the flared-disk model of Chiang & Goldreich (1997) with some
improvements described by Dullemond et al. (2001, their Sects. 2.1.1 and 2.1.2). The
input values of the model consist of the stellar parameters
(![]() ,
,
![]() and
and ![]() ), dust opacities
), dust opacities
![]() and
the surface density
and
the surface density ![]() .
The latter quantity is
assumed to be a power-law function of the radius R to the star:
.
The latter quantity is
assumed to be a power-law function of the radius R to the star:
![]() .
The surface
density at 1 AU (
.
The surface
density at 1 AU (![]() )
and the power (
)
and the power (![]() )
can be
chosen freely. The structure of the disk's interior is then calculated
iteratively by demanding vertical hydrostatic equilibrium at each
radius. The output quantities (in the nomenclature
of Dullemond et al. 2001) include the pressure scale height
)
can be
chosen freely. The structure of the disk's interior is then calculated
iteratively by demanding vertical hydrostatic equilibrium at each
radius. The output quantities (in the nomenclature
of Dullemond et al. 2001) include the pressure scale height
![]() ,
the
disk surface height
,
the
disk surface height
![]() ,
the midplane temperature Ti and the surface
temperature
,
the midplane temperature Ti and the surface
temperature ![]() .
These are all a function of the radius R. The
density
.
These are all a function of the radius R. The
density ![]() is a Gaussian
function in the vertical (i.e. z) direction, centered around the midplane
(z=0). Its half-width depends on the pressure scale height
is a Gaussian
function in the vertical (i.e. z) direction, centered around the midplane
(z=0). Its half-width depends on the pressure scale height
![]() ,
which is a function of the midplane temperature Ti.
,
which is a function of the midplane temperature Ti.
The temperature distribution in the disk is calculated more precise
than described in Chiang & Goldreich (1997) and Dullemond et al. (2001). These authors assume a
two-temperature model which is determined by the midplane temperature Tiand the temperature at the optically thin surface layer ![]() .
Inspired by the full-fledged, computationally demanding models
of Dullemond (2002) and Dullemond & Dominik (2004), we allowed for a
temperature gradient
in vertical direction. The stellar flux penetrates the disk, directly
heating the circumstellar matter. At a certain radius R from the
star and height z above the midplane, the temperature T(R,z) can be
determined using
.
Inspired by the full-fledged, computationally demanding models
of Dullemond (2002) and Dullemond & Dominik (2004), we allowed for a
temperature gradient
in vertical direction. The stellar flux penetrates the disk, directly
heating the circumstellar matter. At a certain radius R from the
star and height z above the midplane, the temperature T(R,z) can be
determined using
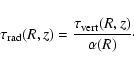 |
(3) |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2484fig18color.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg165.gif) |
Figure 18:
The temperature structure of a flared-disk model. On the
x-axis the radial distance R to the star is plotted, on the y-axis the
ratio of the height above the midplane z over R. The color
scale is linear and ranges from 0 to 3500 K. The dashed line
represents the disk surface height
|
| Open with DEXTER | |
We note that the temperature stratification in the
disk and the density function are not computed self-consistently.
The temperature gradient is calculated a posteriori;
the effect of the higher temperatures in the upper layers of the
disk is not included in the determination of ![]() .
The deviation
from the self-consistent calculation is however very small.
.
The deviation
from the self-consistent calculation is however very small.
To determine the [O I]6300 Å emission emanating from a flared circumstellar disk, we have implemented the model of Störzer & Hollenbach (2000) for [O I] emission. They have modelled the optical forbidden-line emission from a plane-parallel semi-infinite photodissociation region (PDR). Both thermal and non-thermal emission are included. Slight changes were applied to the method to adapt it to our specific case.
Following Störzer & Hollenbach (2000), a five-level oxygen atom is assumed. The
atomic data and references can be found in their paper
(Table 1 of the Appendix). Since we are only interested in modeling the 6300 Å
line, the relevant transitions for the present paper are
![]() (63.2
(63.2 ![]() m),
m),
![]() (44.2
(44.2 ![]() m),
m),
![]() (6300.3 Å) and
(6300.3 Å) and
![]() (5577.4 Å). Collisions with free electrons and atomic hydrogen are
considered. From PDR models (e.g. Hollenbach & Tielens 1999, and references
therein), one derives that the transition region from
the atomic-H dominated upper layers to the disk interior where H2is abundant occurs at about
(5577.4 Å). Collisions with free electrons and atomic hydrogen are
considered. From PDR models (e.g. Hollenbach & Tielens 1999, and references
therein), one derives that the transition region from
the atomic-H dominated upper layers to the disk interior where H2is abundant occurs at about
![]() .
Based on the latter, we assume
that only at
.
Based on the latter, we assume
that only at
![]() free electrons and H atoms are important
collisional partners for the O I atom. In optically thick
regions, the collisional rate is set to zero.
free electrons and H atoms are important
collisional partners for the O I atom. In optically thick
regions, the collisional rate is set to zero.
The proton number density ![]() depends on the radial and vertical
position (R,z) in the disk and the input surface density
depends on the radial and vertical
position (R,z) in the disk and the input surface density ![]() .
It
is computed from the flared-disk model. The oxygen number density is
the product of the proton density and the fractional oxygen abundance
.
It
is computed from the flared-disk model. The oxygen number density is
the product of the proton density and the fractional oxygen abundance
![\begin{displaymath}n(O) = n_{\rm p} \left[\frac{\rm O}{\rm H}\right]\cdot
\end{displaymath}](/articles/aa/full/2005/22/aa2484-04/img173.gif) |
(4) |
![\begin{displaymath}n_{\rm e^-} = n_{\rm C^+} = n_{\rm p} \left[ \frac{\rm C}{\rm H} \right]\cdot
\end{displaymath}](/articles/aa/full/2005/22/aa2484-04/img175.gif) |
(5) |
To determine the thermal [O I]6300 Å emission, the population of the upper
level of this line (![]() )
needs to be known. Using the formula of
thermal equilibrium (see Appendix), one can determine the relative
population of two levels a and b for a temperature T. From the latter ratios,
the relative fraction F of O I atoms in the
)
needs to be known. Using the formula of
thermal equilibrium (see Appendix), one can determine the relative
population of two levels a and b for a temperature T. From the latter ratios,
the relative fraction F of O I atoms in the ![]() state can be
calculated. The number density of the thermally populated upper level
of the 6300 Å line is
state can be
calculated. The number density of the thermally populated upper level
of the 6300 Å line is
![]() .
.
Since the typical temperature range (10-1500 K) in our disk models is rather low to thermally excite the oxygen atoms, the emanating [O I]6300 Å emission is very weak. The intensity of the thermal emission is more than a million times smaller than the non-thermal [O I]emission, which is discussed in the next section.
Following Störzer & Hollenbach (2000), the dominant non-thermal excitation
mechanism for neutral oxygen atoms is the photodissociation of OH
molecules. This results in a hydrogen atom and an excited oxygen
atom. A fraction of the latter (![]() 55%, van Dishoeck & Dalgarno 1984)
find themselves in the upper state (
55%, van Dishoeck & Dalgarno 1984)
find themselves in the upper state (![]() )
of the 6300 Å line.
This mechanism hence produces strong non-thermal [O I] emission in
regions where the photodissociating UV flux is abundant and the
densities high enough to have a sufficient amount of emitting oxygen
atoms.
)
of the 6300 Å line.
This mechanism hence produces strong non-thermal [O I] emission in
regions where the photodissociating UV flux is abundant and the
densities high enough to have a sufficient amount of emitting oxygen
atoms.
In our simple model for non-thermal emission, we assume that the
fractional OH abundance
![]() is constant throughout the
disk. In reality, this may not be the case, as the optically thick disk
interior will have a much higher
is constant throughout the
disk. In reality, this may not be the case, as the optically thick disk
interior will have a much higher
![]() than the
photon-immersed surface layers. Nevertheless this assumption needs not
to be valid for the entire disk, but only for the [O I] emission
region. The latter will be located close to the
than the
photon-immersed surface layers. Nevertheless this assumption needs not
to be valid for the entire disk, but only for the [O I] emission
region. The latter will be located close to the ![]() surface and
is geometrically quite thin, because the proton density drops off rapidly
when moving away from the disk midplane while the high optical depth
in the disk interior prohibits photodissociation of the OH
molecules. From the OH number density
surface and
is geometrically quite thin, because the proton density drops off rapidly
when moving away from the disk midplane while the high optical depth
in the disk interior prohibits photodissociation of the OH
molecules. From the OH number density
![]() ,
the density of non-thermally-excited oxygen
atoms can be determined (Störzer & Hollenbach 1998, adapted to the UMIST rate
coefficients):
,
the density of non-thermally-excited oxygen
atoms can be determined (Störzer & Hollenbach 1998, adapted to the UMIST rate
coefficients):
The local [O I]6300 Å emissivity j(R,z) (in erg s-1 cm-3 sr-1) is given by
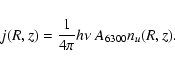 |
(7) |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2484fig19color.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg186.gif) |
Figure 19:
The [O I]6300 Å emissivity in the flared-disk
model. The x-axis gives the radial distance R to the central star in
AU, the y-axis plots z/R, the ratio of the vertical height and the
radial distance. The colors represent the local [O I]6300 Å emissivity
on a log-scale which covers 10 orders of magnitude. On the color
bar, the emissivity is given in [erg s-1 cm-3 sr-1]. The disk region sampled by the model
ranges from roughly 0.6 to 1.5 times the disk surface height
|
| Open with DEXTER | |
Integrating the emissivity over the vertical direction, considering the
optical depth
![]() at 6300 Å, one extracts the surface intensity I(R)at each radius R:
at 6300 Å, one extracts the surface intensity I(R)at each radius R:
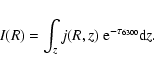 |
(8) |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2484fig20.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg189.gif) |
Figure 20:
Pictogram of a flat rotating circumstellar disk, seen under
an inclination of
|
| Open with DEXTER | |
To convert the intensity-versus-radius function I(R) to an
intensity-versus-velocity profile, we assume that the rotation
of the disk is Keplerian![]() .
We anticipate this to be a fairly accurate assumption, since the disk mass
is expected to be much smaller than the mass of the central star
(e.g., Acke et al. 2004).
Additionally we adopt that the Keplerian rotation velocity of matter in
the upper layers of a flared disk is the same as the rotational
velocity in the midplane.
Figure 20 illustrates how the profile is
computed. The light-grey band in the pictogram
represents a circular orbit in the inclined - geometrically flat -
disk where the [O I] intensity is constant. The
disk's matter in this band rotates around the central star with a
Keplerian velocity
.
We anticipate this to be a fairly accurate assumption, since the disk mass
is expected to be much smaller than the mass of the central star
(e.g., Acke et al. 2004).
Additionally we adopt that the Keplerian rotation velocity of matter in
the upper layers of a flared disk is the same as the rotational
velocity in the midplane.
Figure 20 illustrates how the profile is
computed. The light-grey band in the pictogram
represents a circular orbit in the inclined - geometrically flat -
disk where the [O I] intensity is constant. The
disk's matter in this band rotates around the central star with a
Keplerian velocity
![]() in which
in which
![]() is the radius of
the orbit and
is the radius of
the orbit and ![]() is the mass of the central star. The
narrow darker-grey band represents the parts of the disk that move
towards (or away from) the observer with the same projected velocity
is the mass of the central star. The
narrow darker-grey band represents the parts of the disk that move
towards (or away from) the observer with the same projected velocity
![]() .
This area is the region where
.
This area is the region where
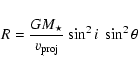 |
(9) |
The computed theoretical profile is then convolved with a Gaussian
function![]() .
This function mimics the effect of instrumental
broadening. The width of the - unresolved - telluric lines in each
type of spectrum were used as the width of the instrumental Gaussian
profile.
.
This function mimics the effect of instrumental
broadening. The width of the - unresolved - telluric lines in each
type of spectrum were used as the width of the instrumental Gaussian
profile.
The input parameters for our model that calculates the non-thermal
emission consist of some
stellar parameters (
![]() )
which are
derived from the photometric data. Furthermore, a dust opacity table
and dust-to-gas mass ratio are needed. Following the
Dullemond et al. (2001) model for AB Aur, we assume
that the dust consists of olivines and represents 1% of the total
disk mass. The stellar parameters are
)
which are
derived from the photometric data. Furthermore, a dust opacity table
and dust-to-gas mass ratio are needed. Following the
Dullemond et al. (2001) model for AB Aur, we assume
that the dust consists of olivines and represents 1% of the total
disk mass. The stellar parameters are
![]() ,
,
![]() ,
,
![]() and
and
![]() K.
The free parameters in our [O I] emission model are the surface density
K.
The free parameters in our [O I] emission model are the surface density
![]() ,
the fractional OH abundance
,
the fractional OH abundance
![]() and the disk's inclination i. In the template model,
we take
and the disk's inclination i. In the template model,
we take
![]() g cm-2,
g cm-2, ![]() ,
,
![]() and
and
![]() .
The inner and outer radius of the
disk,
.
The inner and outer radius of the
disk,
![]() and
and
![]() ,
are 0.1 AU and 100 AU respectively.
We discuss the influence of the four free input parameters on the
shape of the emission profile, starting with the surface density.
,
are 0.1 AU and 100 AU respectively.
We discuss the influence of the four free input parameters on the
shape of the emission profile, starting with the surface density.
The two parameters ![]() and
and ![]() describing the power-law
surface density are coupled when the disk mass is known:
describing the power-law
surface density are coupled when the disk mass is known:
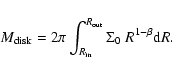 |
(10) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2484fig21color.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg210.gif) |
Figure 21:
The intensity-versus-radius distribution I(R) for four
template models, with different values for the surface-density
parameters. From top to bottom, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2484fig22color.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg211.gif) |
Figure 22:
The line profiles I(v) corresponding to the
intensity-versus-radius distribution in Fig. 21. From
top to bottom, |
| Open with DEXTER | |
The fractional OH abundance
![]() scales linearly with the
total intensity of the profile. It does not alter the
shape, as we assume it is constant throughout the [O I] emission
region.
scales linearly with the
total intensity of the profile. It does not alter the
shape, as we assume it is constant throughout the [O I] emission
region.
Observations of Doppler-broadened spectral lines do not observe the
real, but the projected velocities in the system. In the present
flared-disk model, the inclination i is a free parameter which alters
the shape as well as the intensity of the computed profile. The total
integrated intensity
![]() is proportional to
is proportional to ![]() ,
while
the position of the two typical peaks of the line changes with
,
while
the position of the two typical peaks of the line changes with ![]() .
Fig. 23 shows the line profiles of the template model as seen
under different inclinations. Note that inclinations larger than
about
.
Fig. 23 shows the line profiles of the template model as seen
under different inclinations. Note that inclinations larger than
about ![]() are not relevant in flared disks, since at such
high i, the outer parts of the disk would occult most of the disk
surface.
are not relevant in flared disks, since at such
high i, the outer parts of the disk would occult most of the disk
surface.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2484fig23color.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg215.gif) |
Figure 23:
The line profiles I(v) of the template model seen under
different inclinations. From top to bottom, the inclination is
|
| Open with DEXTER | |
In this section we compare our model results to the observations. We
focus on the sample stars which display a narrow, symmetric and
centered profile. Since the thermal emission is weak compared to the
non-thermal emission for the relatively cool disks studied in this
paper, we will only consider the non-thermal emission component in the
following discussion.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2484fig24.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg216.gif) |
Figure 24:
Similar plot as Fig. 12. The filled diamonds
are the observed [O I]intensities for the group I sources. The open
circles represent model results. The typical error bar for the
observations is given in the upper left corner. The models differ
from each other
in stellar parameters; from the lower left to the upper right, the
model [O I]-versus-UV luminosity for a
typical F0V, A3V, A0V, B8V, B5V and B0V star are plotted
respectively. The error bars on the model determinations represent
the spread in results when simultaneously varying the surface
density |
| Open with DEXTER | |
We compare the observed [O I]6300 Å emission luminosity and its
theoretical counterpart to the UV luminosity in
Fig. 24. Our model
applies for flared-disk geometries, therefore only the group I sources
have been plotted in the figure. The model results and the
observations agree nicely for an acceptable range of the free
parameters ![]() ,
i and
,
i and
![]() .
Note that all models in
the figure have the same disk mass as the template model. Varying the
disk mass affects the [O I]6300 Å emission in a comparable manner as
when the surface density is altered. Figure 25
compares the [O I] luminosity to the effective temperature of the group
I objects and the models. Again, reasonable values for the free
parameters lead to theoretical [O I] luminosities close to the observed
values.
.
Note that all models in
the figure have the same disk mass as the template model. Varying the
disk mass affects the [O I]6300 Å emission in a comparable manner as
when the surface density is altered. Figure 25
compares the [O I] luminosity to the effective temperature of the group
I objects and the models. Again, reasonable values for the free
parameters lead to theoretical [O I] luminosities close to the observed
values.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2484fig25.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg217.gif) |
Figure 25: The [O I]6300 Å luminosity versus the effective temperature of the group I sources (filled diamonds). The open circles and dotted lines plotted in this figure represent the same models as in Fig. 24. |
| Open with DEXTER | |
Not only the strength of the [O I]6300 Å emission can be reproduced
with our model. After scaling the total theoretical to the observed
intensity, the typical FWHM and double-peaked shape of the narrow centered
features can be explained by assuming Keplerian rotation of
the flared disk. In Fig. 26 we have overplotted observed
profiles with theoretical ones. For each star, we have used the
stellar parameters (
![]() )
as input
parameters. The remaining parameters were set to the template values,
unless otherwise indicated in the plots. Note that the theoretical
profiles are not fitted to the data, but are just overplotted
model profiles, rebinned to the spectral resolution of the observed
spectrum. The similarity between theory and observation is
nevertheless striking. For AB Aur and HD 100546, the
inclination of the disk have been determined to be
)
as input
parameters. The remaining parameters were set to the template values,
unless otherwise indicated in the plots. Note that the theoretical
profiles are not fitted to the data, but are just overplotted
model profiles, rebinned to the spectral resolution of the observed
spectrum. The similarity between theory and observation is
nevertheless striking. For AB Aur and HD 100546, the
inclination of the disk have been determined to be
![]() (Mannings & Sargent 1997) and
(Mannings & Sargent 1997) and
![]() (Augereau et al. 2001)
respectively. The observed profiles of the [O I]6300 Å line can be
approximated by theoretical line profiles for these inclinations when
using
(Augereau et al. 2001)
respectively. The observed profiles of the [O I]6300 Å line can be
approximated by theoretical line profiles for these inclinations when
using
![]() and
and
![]() for
AB Aur and
for
AB Aur and
![]() and
and
![]() for HD 100546.
for HD 100546.
The flaring of the disk is due to the dust opacities, while the gas
opacities are negligible. Since dust evaporates above the dust
sublimation temperature
![]() K, we
have shifted the inner edge of the flared-disk from
K, we
have shifted the inner edge of the flared-disk from
![]() AU
to the radius where the surface temperature
AU
to the radius where the surface temperature ![]() equals
equals
![]() .
For a typical F0V, A0V and B0V star, the
inner radius hence becomes 0.2, 0.8 and 30 AU respectively. As a
consequence, the high-velocity (
.
For a typical F0V, A0V and B0V star, the
inner radius hence becomes 0.2, 0.8 and 30 AU respectively. As a
consequence, the high-velocity (
![]()
![]() )
wings of the
theoretical [O I] emission line profile disappear, in agreement with the
observed spectra of narrow 6300 Å features which do not display
extended wings (e.g., AB Aur, HD 97048,
HD 100546, HD 135344, HD 169142, R CrA,
T CrA, HD 179218, HD 190073). Furthermore,
the models of Dullemond (2002) suggest
that the inner rim of the disk is puffed-up and casts its shadow of
the first few AU in a flared geometry. This effect could be mimicked
in our flared-disk model by shifting the inner radius
)
wings of the
theoretical [O I] emission line profile disappear, in agreement with the
observed spectra of narrow 6300 Å features which do not display
extended wings (e.g., AB Aur, HD 97048,
HD 100546, HD 135344, HD 169142, R CrA,
T CrA, HD 179218, HD 190073). Furthermore,
the models of Dullemond (2002) suggest
that the inner rim of the disk is puffed-up and casts its shadow of
the first few AU in a flared geometry. This effect could be mimicked
in our flared-disk model by shifting the inner radius
![]() even
further out (up to
even
further out (up to ![]() 5 AU). The effect of the latter on the
theoretical line profile would be mostly a decrease of the
wings, without reducing the total intensity much.
5 AU). The effect of the latter on the
theoretical line profile would be mostly a decrease of the
wings, without reducing the total intensity much.
The innermost parts of the circumstellar disk, where no dust can survive
due to the high temperatures, are relatively small in spatial
dimensions. Nevertheless, we cannot exclude that the contribution of these
parts to the total [O I] emission strength is significant. Specifically,
a few group II sources (e.g., VX Cas, V586 Ori,
HD 95881, HD 98922, HD 101412, WW
Vul, SV Cep) display broader, but relatively
weaker [O I]profiles. In our current interpretation and with no external
bright UV source near, this [O I] emission cannot emanate from the disk
surface for the self-shadowing prohibits direct stellar flux to reach
this area. In the latter cases, the emission might come from a
rotating gaseous disk inside the dust-sublimation radius.
The modeling of this inner gaseous region is however beyond the scope
of the present paper. We refer to the recent paper of
Muzerolle et al. (2004) for a more elaborate discussion on this subject.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2484fig26color.ps}
\end{figure}](/articles/aa/full/2005/22/aa2484-04/Timg229.gif) |
Figure 26:
The observed spectra of group I sources AB Aur,
HD 97048, HD 100546 and T CrA overplotted
with the model results. The parameters of the model are adapted to
the stellar parameters of each source combined with the template
parameters, unless otherwise indicated in the upper right
corner. We have shifted the theoretical profile to the centroid
position of the
observed feature. For HD 100546 two models with different parameter
sets have been displayed to illustrate the difficulty to distinguish
between models.
The theoretical profiles extracted from our flared-disk model fit
the observed features strikingly well for a range of reasonable
model parameters. a(-b) represents
|
| Open with DEXTER | |
The observed [O I]6300 Å emission line in many HAEBE stars in our sample shows evidence for a rotating forbidden-line emission region. In this paper we suggest that the surface of the flared circumstellar disk around the group I objects is the perfect location to harbor this emission region. The combination of the direct stellar UV flux and the relatively high densities in this region give rise to strong non-thermal [O I] emission, which can explain the observed luminosities reasonably well. Furthermore, the shape of the spectrally resolved 6300 Å profile in the observations and the profile produced by our simple model indicate that Keplerian rotation indeed is the broadening mechanism for (at least the narrow component of) this line. The observed 6300 Å spectra of the group I members in our sample can be reproduced strikingly well.
In the group of self-shadowed-disk sources, significantly more targets do not display the [O I] 6300 Å emission line (43% versus 8% in group I). The line profiles of the detected [O I]6300 Å emission feature in group II are twice as weak as, and somewhat broader than the lines observed in group I spectra. In our current interpretation, the surface of a self-shadowed disk's outer parts is not directly irradiated by the central star. However, the non-thermal [O I] line formation mechanism - photodissociation of OH and H2O - may produce the observed group II emission lines as well. Assuming that the [O I] emission emanates from the inner gaseous disk naturally explaines the weaker emission and the higher-velocity wings of the feature: the inner gaseous disk provides a smaller emission volume and is located closer to the central star, where the Keplerian velocities are larger.
In T Tauri stars, the less massive counterparts of HAEBE stars, the
observed [O I] emission profile can be explained using the model of
Kwan & Tademaru (1988) (e.g. Hartigan et al. 1995). However, this model assumes
that a "super-heated'' disk atmosphere, fed by accretion, is present,
in which the temperatures are sufficiently high (![]() 104 K) to
produce thermal [O I] emission. The absence of a strong UV excess and strong photospheric
veiling, the relatively weak IR recombination lines and CO emission,
and the presence of 10 micron silicate emission (AV04) in the majority
of the group I and II sources in our sample all indicate that these
disks are passive. Furthermore, the observed upper limits for the
5577/6300 [O I] ratio indicate that the observed emission
cannot be thermal. Each model which models the [O I] emission based on
thermal processes - including the disk wind model - will have
difficulties reproducing the strength of the [O I] 6300 Å line in HAEBE
stars. The non-detections of the [S II] 6731 Å line in the spectra of
group I and II sources in our sample confirm this picture. Moreover,
amongst the late-type
sample sources no strong [O I]emitters are present. In the T Tauri
model the forbidden line emission is dependent on accretion rate
and thus the model cannot explain the absence of strong late-type [O I] sources. The
OH photodissociation model suggested in the present paper
naturally predicts that passive disks around weak UV sources will not
produce strong [O I]6300 Å emission.
104 K) to
produce thermal [O I] emission. The absence of a strong UV excess and strong photospheric
veiling, the relatively weak IR recombination lines and CO emission,
and the presence of 10 micron silicate emission (AV04) in the majority
of the group I and II sources in our sample all indicate that these
disks are passive. Furthermore, the observed upper limits for the
5577/6300 [O I] ratio indicate that the observed emission
cannot be thermal. Each model which models the [O I] emission based on
thermal processes - including the disk wind model - will have
difficulties reproducing the strength of the [O I] 6300 Å line in HAEBE
stars. The non-detections of the [S II] 6731 Å line in the spectra of
group I and II sources in our sample confirm this picture. Moreover,
amongst the late-type
sample sources no strong [O I]emitters are present. In the T Tauri
model the forbidden line emission is dependent on accretion rate
and thus the model cannot explain the absence of strong late-type [O I] sources. The
OH photodissociation model suggested in the present paper
naturally predicts that passive disks around weak UV sources will not
produce strong [O I]6300 Å emission.
The high-velocity blue wings in the [O I]6300 Å line of a small minority of our sample stars cannot be accounted for by an emitting passive Keplerian disk. This emission feature is suggested to emanate from an outflow, of which the redshifted part is occulted by the circumstellar disk. Note however that this pronounced blue wing is often accompanied by a symmetric peak at low velocities (e.g., Z CMa, PV Cep, V645 Cyg, HD 200775). The latter might again be formed in the surface layers of the rotating disk. Alternatively, the model of Kwan & Tademaru (1988) for T Tauri stars may be valid for these objects: since the assumption of passivity is likely not to be valid for the disks of the group III members, these sources might resemble classical accreting T Tauri stars. As noted before, accretion is needed to create the right settings for the T Tauri model to work. This idea is supported by the detection of the [S II] 6731 Å line in Z CMa, which is exclusive to this target in the present sample. We note however that this behaviour seems to be rather exceptional for HAEBE stars.
The values for the fractional OH abundance
![]() needed to
explain the observed [O I] 6300 Å luminosities are
needed to
explain the observed [O I] 6300 Å luminosities are ![]() 10
-7-10-6.
Observations of diffuse interstellar clouds show that
relative OH abundances of this magnitude (
10
-7-10-6.
Observations of diffuse interstellar clouds show that
relative OH abundances of this magnitude (![]() 10-7) occur in the
interstellar medium (e.g., Crutcher 1979, and references therein).
Nevertheless, these values are two orders larger than
the abundances computed in
recent models including a full treatment of disk chemistry
(e.g., Kamp & Dullemond 2004; Markwick et al. 2002). A possible reason for this
discrepancy may be the exact location of the [O I]emission region in our
models: a shift to higher densities (i.e. to a lower vertical height z) would reduce the fractional OH abundance required to fit the
observed [O I]intensity, since the latter is
inversely proportional to the first. This effect can potentially be
induced by the input dust opacities, which define the disk's flaring,
but also the UMIST coefficients determine the exact location of the
[O I] emitting region through formula (6). Alternatively,
the chemical models may be wrong due to uncertainties in the
reaction rate coefficients or the incompleteness of the
network.
10-7) occur in the
interstellar medium (e.g., Crutcher 1979, and references therein).
Nevertheless, these values are two orders larger than
the abundances computed in
recent models including a full treatment of disk chemistry
(e.g., Kamp & Dullemond 2004; Markwick et al. 2002). A possible reason for this
discrepancy may be the exact location of the [O I]emission region in our
models: a shift to higher densities (i.e. to a lower vertical height z) would reduce the fractional OH abundance required to fit the
observed [O I]intensity, since the latter is
inversely proportional to the first. This effect can potentially be
induced by the input dust opacities, which define the disk's flaring,
but also the UMIST coefficients determine the exact location of the
[O I] emitting region through formula (6). Alternatively,
the chemical models may be wrong due to uncertainties in the
reaction rate coefficients or the incompleteness of the
network.
Böhm & Hirth (1997) have stated that the forbidden-line emission region
in Hillenbrand et al. (1992) group
I sources![]() cannot be located at the
surface of the circumstellar disk, because the suggested accretion
disk would cover most of the forbidden-line emission region.
The authors suggest that, even when the stellar light is able to reach
the disk surface, a problem remains: the upper layer would be
geometrically very thin and the outer radius of the disk
would need to be much larger than 100 AU in order to create enough
emission volume to explain the observed [O I]intensities. Both problems
are countered when considering a flared disk with a puffed-up inner
rim. Hillenbrand et al. have invoked a circumstellar accretion disk
model to explain the observed near-IR (
cannot be located at the
surface of the circumstellar disk, because the suggested accretion
disk would cover most of the forbidden-line emission region.
The authors suggest that, even when the stellar light is able to reach
the disk surface, a problem remains: the upper layer would be
geometrically very thin and the outer radius of the disk
would need to be much larger than 100 AU in order to create enough
emission volume to explain the observed [O I]intensities. Both problems
are countered when considering a flared disk with a puffed-up inner
rim. Hillenbrand et al. have invoked a circumstellar accretion disk
model to explain the observed near-IR (![]() 2
2 ![]() m) bump
which is typical for Hillenbrand group I sources. The puffed-up inner
rim in the Dullemond et al. (2001) model naturally
explains this excess. In other words, no dynamically active model is
needed to explain this bump. Furthermore, the outer parts of
the disk can be flared, hence increasing the angle
m) bump
which is typical for Hillenbrand group I sources. The puffed-up inner
rim in the Dullemond et al. (2001) model naturally
explains this excess. In other words, no dynamically active model is
needed to explain this bump. Furthermore, the outer parts of
the disk can be flared, hence increasing the angle ![]() under
which the stellar light impinges onto the disk surface. The UV flux
can penetrate deeper into the disk, thus increasing the geometrical
thickness of the [O I] emission layer. As we have shown in the present
paper, the observed [O I] 6300 Å emission profile can be explained as
being due to the photodissociation of OH molecules and the subsequent
non-thermal excitation of oxygen atoms in the atmosphere of a rotating
flared disk.
under
which the stellar light impinges onto the disk surface. The UV flux
can penetrate deeper into the disk, thus increasing the geometrical
thickness of the [O I] emission layer. As we have shown in the present
paper, the observed [O I] 6300 Å emission profile can be explained as
being due to the photodissociation of OH molecules and the subsequent
non-thermal excitation of oxygen atoms in the atmosphere of a rotating
flared disk.
The fractional level population of two levels a and b of an atom in thermal
equilibrium at a temperature T[K] is given by
To determine the fraction F of neutral oxygen in the ![]() state in the
five-level model assuming thermal excitation, one applies
state in the
five-level model assuming thermal excitation, one applies
 |
(12) |
 |
(13) |
Acknowledgements
The authors would like to thank the support staff at La Silla and Kitt Peak observatories for their excellent support during the observing runs on which this paper is based. Especially the expertise of G. Lo Curto (ESO La Silla) and D. Willmarth (KPNO) proved invaluable in completing our project succesfully. We thank the anonymous referee for insightful comments which improved both contents and presentation of the manuscript. B.A. would like to thank I. Kamp for the useful discussions concerning chemical modeling.