A&A 436, 171-185 (2005)
DOI: 10.1051/0004-6361:20042454
The lives and deaths of positrons in the interstellar medium
N. Guessoum1 - P. Jean2 - W. Gillard2
1 - American University of Sharjah, College of Arts & Sciences,
Physics Department, PO Box 26666, Sharjah, UAE
2 -
CESR, CNRS/UPS, BP 4346, 31028 Toulouse Cedex 4, France
Received 30 November 2004 / Accepted 25 January 2005
Abstract
We reexamine in detail the various processes undergone by positrons
in the interstellar medium (ISM) from their birth to their
annihilation using the most recent results of positron interaction cross
sections with atomic and molecular hydrogen, as well as helium.
The positrons' lives are divided into two phases: the "in-flight'' phase
(between 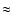 1 MeV and tens of eV) and the thermal phase.
The first phase is treated with a Monte Carlo simulation that
allows us to determine the fraction of positrons that form positronium
and annihilate as well as the characteristics of the annihilation
emission as a function of the medium conditions. The second phase is
treated with a binary reaction rate approach, with cross sections adopted
from experimental measurement or theoretical calculations. An extensive
search and update of the knowledge of positron processes was thus
undertaken. New reaction rates and line widths have been obtained.
1 MeV and tens of eV) and the thermal phase.
The first phase is treated with a Monte Carlo simulation that
allows us to determine the fraction of positrons that form positronium
and annihilate as well as the characteristics of the annihilation
emission as a function of the medium conditions. The second phase is
treated with a binary reaction rate approach, with cross sections adopted
from experimental measurement or theoretical calculations. An extensive
search and update of the knowledge of positron processes was thus
undertaken. New reaction rates and line widths have been obtained.
We investigate the treatment of the
complicated interactions between positrons and interstellar dust grains.
Fully relevant data were not always available, but we were nonetheless
able to reach satisfactory understanding of positron annihilation
on grains, both qualitatively
and quantitatively. All factors of the problem have been considered,
including the grain size distribution and composition, the electric charge
of the grains, the backscattering, positronium formation and ejection from
the grain, the pick-off annihilation inside them and the partial
destruction of dust in the hot regions of the ISM. New reaction rates
and widths of the line resulting from the annihilation inside and outside
of the grain have been obtained. The final results of our calculations
(reaction rates and spectra) showed that dust is only important in the
hot phase of the ISM, where it dominates all other processes.
Combining the new calculations, we have constructed annihilation
spectra for each phase of the ISM, considering various grain contents,
as well as an overall combined spectrum for the ISM as a whole.
Key words: gamma rays: theory - line: formation - line: profiles - ISM: general
1 Introduction
Positrons are produced at tremendous rates in the Galaxy. This has been
firmly established by a long series of balloon and satellite detections of
the positrons' landmark signature, the gamma-ray line at 511 keV produced
in their annihilation with electrons. A rate of 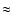
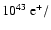 s is
usually inferred from such detections (Purcell et al. 1997; Milne et al.
2000).
Surprisingly, despite three
decades of (indirect) detections of positrons, the origin and galactic
distribution of these huge amounts of antiparticles is still puzzling
astrophysicists. There are several major reasons for this problem: 1) our
understanding of the positron production processes in astrophysical media
is plagued by significant uncertainties; 2) the galactic map of the 511 keV
annihilation line, which is supposed to lead us to the positrons, has yet
to be determined with any reasonable accuracy; 3) the physics of the
annihilation processes, which have until now been believed to be well
understood, may need to be improved to a certain extent; 4) our lack of
knowledge of the extent of diffusion/propagation of positrons between
their production sites and their annihilation places.
s is
usually inferred from such detections (Purcell et al. 1997; Milne et al.
2000).
Surprisingly, despite three
decades of (indirect) detections of positrons, the origin and galactic
distribution of these huge amounts of antiparticles is still puzzling
astrophysicists. There are several major reasons for this problem: 1) our
understanding of the positron production processes in astrophysical media
is plagued by significant uncertainties; 2) the galactic map of the 511 keV
annihilation line, which is supposed to lead us to the positrons, has yet
to be determined with any reasonable accuracy; 3) the physics of the
annihilation processes, which have until now been believed to be well
understood, may need to be improved to a certain extent; 4) our lack of
knowledge of the extent of diffusion/propagation of positrons between
their production sites and their annihilation places.
In nature, positrons can be produced by one of the following main
processes: a) 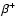 decay of radioactive nuclei; b)
decay of radioactive nuclei; b) 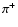 decay into
decay into 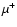 ,
which decays and gives off a positron; c) pair
(electron-positron) production through photon-photon interactions; d) pair
production by the interaction of an electron with a strong magnetic field.
All these processes can be found in astrophysical settings, provided that
the physical conditions for them are fulfilled. For example, the first
process (the
,
which decays and gives off a positron; c) pair
(electron-positron) production through photon-photon interactions; d) pair
production by the interaction of an electron with a strong magnetic field.
All these processes can be found in astrophysical settings, provided that
the physical conditions for them are fulfilled. For example, the first
process (the 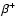 decay of a radioactive nucleus) is widespread in
the
explosive and/or hydrostatic nucleosynthesis environments of novae,
supernovae, Wolf-Rayet and Asymptotic Giant Branch stars. The second
process (
decay of a radioactive nucleus) is widespread in
the
explosive and/or hydrostatic nucleosynthesis environments of novae,
supernovae, Wolf-Rayet and Asymptotic Giant Branch stars. The second
process (
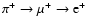 )
takes place where the
pion is produced in collisions of highly energetic (more than
)
takes place where the
pion is produced in collisions of highly energetic (more than 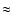 200 MeV)
cosmic rays with interstellar material (mostly protons). The third process
(photon-photon pair production) requires photons of high energies and is
known to occur in the environment of luminous compact objects (black hole
candidates, micro-quasars, active galactic nuclei, etc.). The fourth
process requires intense magnetic fields and is rather common in the
environments of pulsars/neutron stars.
200 MeV)
cosmic rays with interstellar material (mostly protons). The third process
(photon-photon pair production) requires photons of high energies and is
known to occur in the environment of luminous compact objects (black hole
candidates, micro-quasars, active galactic nuclei, etc.). The fourth
process requires intense magnetic fields and is rather common in the
environments of pulsars/neutron stars.
On the scale of the whole Galaxy, as we are interested in here, the main
positron generators are, in order of decreasing importance: supernovae
(SNe), novae (Ne), compact objects (microquasars, pulsars, etc.), cosmic
rays and possibly gamma ray bursts. However, substantial uncertainties
over the specific factors involved in each case have made the precise
identification of the positron sources very difficult. For instance, for
the main candidates for galactic positrons (supernovae), depending
on their type, the specific positron production process and the escape
fraction from the expanding shell into the interstellar medium (ISM),
the amount of positrons contributed by supernovae may vary significantly.
The issue of the origin of positrons responsible for the observed
annihilation in the Galaxy will be investigated in another work, in
relation to the new 511 keV map(s) obtained by INTEGRAL/SPI (Knodlseder
et al. 2005). For a recent review of some of the issues pertaining to this
topic, see the paper by Paul (2004) or Jean et al. (2004).
We will address here only the physics
of the annihilation as it leads to the spectra observed by high
energy-resolution instruments.
Since the discovery of the 511 keV annihilation radiation emanating
from the Galactic center in 1970 (Johnson et al. 1972),
interest in this radiation, from the observational viewpoint as well as
from the theoretical stance, has been very high.
On the observational side, dozens of balloon and, more recently,
satellite missions have been conducted over the past 2 or 3 decades. We
will cite only high energy-resolution (germanium) instruments that allowed
for the extraction of a detailed line spectrum, because
the physics of the annihilation produces a spectrum that can only be
compared to one obtained by such instruments. In 1977 the Ge-detector
(high energy resolution) balloon mission
(Leventhal et al. 1978), established the electron-positron
annihilation nature of the radiation by accurately measuring the line
centroid energy at 511 keV. The Gamma-Ray Imaging Spectrometer (GRIS)
balloon missions (Gehrels et al. 1991; Leventhal
et al. 1993) firmly established the narrow width of the line (FWHM less
than about 3 keV) and separated the extended, diffuse emission in the
interstellar medium (ISM) from that of the Galactic center region. The
HEXAGONE balloon-borne spectrometer mission (Chapuis et al. 1991;
Durouchoux et al. 1993) also detected a narrow line (FWHM less than about 3 keV). The Transient Gamma-Ray Spectrometer (TGRS), onboard the WIND
satellite, rather strongly disproved the two-component, time-variability (of
the Galactic Center emission) paradigm (Teegarden et al. 1996; Harris et al. 1998; Harris 2000) and showed an even narrower line (
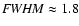 keV). The most recent analysis of the data from the on-going
INTEGRAL/SPI detection of the annihilation line shows the line to have a
width of
keV). The most recent analysis of the data from the on-going
INTEGRAL/SPI detection of the annihilation line shows the line to have a
width of 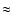 2.3 keV (Knodlseder et al. 2005).
2.3 keV (Knodlseder et al. 2005).
In parallel, theoretical modeling and data analyses of the emission have
proceeded in an attempt to understand both the physical
processes behind the emission and the physical conditions prevailing in
the regions where the annihilation is taking place.
Detailed theoretical investigations of the annihilation processes behind
the observed radiation go back to Crannell et al. (1976) who, while
interested in the line produced specifically in solar flares, investigated
most of the processes involved in electron-positron interactions. Other
researchers, i.e. Steigman (1968),
Stecker (1969) and Leventhal (1973) had pointed out the importance of the
Positronium in astrophysical settings. Positronium (Ps) is the bound state
of a positron with an electron, and depending on whether the two have
parallel or anti-parallel spins, this "atom'' will be in the long-lifetime
(t = 140 ns) ortho-Ps state or the short-lifetime (t = 0.125 ns) para-Ps
state. The latter decays into 2 photons of 511 keV (plus or minus some
small amount of energy corresponding to the relative momenta of the bound
particles), while the former (ortho-Ps) state decays into 3 photons of
energies totaling 1022 keV. The distribution of photon energies resulting
from the decay of ortho-Ps was first calculated by Ore & Powell (1949)
and more recently by Adkins (1983).
Subsequent work on the positron processes focused on the conditions of the
interstellar medium. Bussard et al. (1979 - hereafter
BRD79)
calculated the rates of the various processes undergone by low-energy
positrons and obtained the resulting annihilation spectrum; Ramaty &
Meszaros (1981) considered the processes and the resulting radiation
in the conditions of a relativistic, hot (high-temperature) plasma.
Zurek (1985) emphasized the
role of dust grains and showed their potentially important modification of
the annihilation spectrum, especially in the hot/warm/ionized phases of
the ISM. Guessoum et al. (1991) reconsidered the
problem in light of earlier developments (new calculations of reaction
rates by Gould 1989, recent observational data, more precise treatment of
dust grains, etc.), performed detailed theoretical spectroscopy of the
annihilation line, and produced spectra for various conditions of the ISM;
one of the ideas emphasized in that work was that the FWHM value was not
an accurate descriptor of the line, as the line cannot always be simply
represented or fitted by a Gaussian function. Guessoum et al.
(1997) updated the knowledge of positron processes (reaction rates and
line widths), adding molecular hydrogen and helium. Most recently, Dermer
& Murphy (2001) reviewed the positron production and annihilation
mechanisms, dealing with both the sources of positrons and the line
profile depending on the annihilation environment.
Positron annihilation models for astrophysical settings also rely heavily
on many laboratory measurements and theoretical calculations of positron
interactions with atoms and molecules. We mention the pioneering work of:
Bhatia et al. (1977) for early theoretical
calculations of annihilation in positron-hydrogen collisions; Brown et al.
(1984, 1986), Brown & Leventhal (1986) for
measurements of line widths and Positronium formation fractions in gases
(H2, He) relevant to the ISM conditions; see Charlton & Humberston
(2001) for a general review of positron work in gases (particularly H,
H2, He), Puska & Nieminen (1994) for the theory of positrons in solids
and on solid surfaces, and the body of work by Iwata, Surko and
collaborators (Iwata et al. 1996, 1997b, 2000)
on laboratory measurements of cross sections and annihilation line widths
of positrons colliding with atoms and molecules (up to and including
large
complex alcohol and/or aromatic molecules, some of which may exist in
galactic molecular clouds). We would draw attention to the significant
amount of relevant "non-astrophysical'' work currently being
performed by atomic and condensed
matter researchers in positron physics![[*]](/icons/foot_motif.gif) .
.
In order to determine the overall
spectrum of the line produced by the galactic positrons, one must consider
a model of the ISM, i.e. distributions and characteristics (temperature,
ionization, etc.) of the gas (H, H2, He) and dust. Guessoum et al. (1991) based their work on the model of McKee & Ostriker
(1977); Gillard (pers. comm.) use the models of Ferriere
(1998a,b, 2001), deeming them more detailed and more conveniently
described by analytical expressions.
Taking all the above physical information (processes, cross sections, line
widths, gas distributions, etc.) into account, one can attempt to
reproduce the observational data (from GRIS, HEXAGONE, TGRS, INTEGRAL/SPI)
and infer useful knowledge about the environment where the annihilation is
predominantly taking place. This kind of approach was adopted by Wallyn et al. (1993) for the HEXAGONE data and by Guessoum et al. (2004) for the SPI
and the TGRS data.
The latest such analysis (Guessoum et al. 2004)
partly led us to revisit the subject of positron processes and annihilation.
Analysis of the SPI data (for which the FWHM was then
(
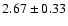 ) keV - Lonjou et al. 2004), unlike that of TGRS (for which
the FWHM was
(
) keV - Lonjou et al. 2004), unlike that of TGRS (for which
the FWHM was
(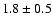 ) keV - Harris et al. 1998) tended to imply a very large
amount (or
reaction rate) of dust grains, simply because the interaction of positrons
with grains resulted (in the treatments done until now) in a line made up
of two Gaussians, one with
) keV - Harris et al. 1998) tended to imply a very large
amount (or
reaction rate) of dust grains, simply because the interaction of positrons
with grains resulted (in the treatments done until now) in a line made up
of two Gaussians, one with
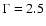 keV and one with
keV and one with
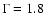 keV. Similarly, the cross section for positron-hydrogen charge
exchange had been known to be extremely important, because this reaction
dominates all other processes in the cold phases of the ISM, and because
it leads to both a wide line (6.4 keV in the old treatments) and a large
Ps fraction (f1, the fraction of the positrons that annihilate via
Positronium formation). We thus realized that a detailed and refined
treatment of positron processes was needed before one can attempt to
analyze the high-quality data and draw astrophysical conclusions from it.
keV. Similarly, the cross section for positron-hydrogen charge
exchange had been known to be extremely important, because this reaction
dominates all other processes in the cold phases of the ISM, and because
it leads to both a wide line (6.4 keV in the old treatments) and a large
Ps fraction (f1, the fraction of the positrons that annihilate via
Positronium formation). We thus realized that a detailed and refined
treatment of positron processes was needed before one can attempt to
analyze the high-quality data and draw astrophysical conclusions from it.
In the next section, we review
the processes that take place "in flight'', i.e. before the positrons
thermalize with the medium of the given ISM phase; this applies for
positron energies between 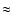 1 MeV (their kinetic energies when
they come out of beta decay) and a few tens of eV, when Positronium
formation through
charge exchange starts to occur. This regime includes Coulomb energy
losses (with free electrons), excitation and ionization of atoms (H,
H2, He), and Ps formation by charge exchange with H, H2 and He. We
review the cross sections for all the relevant processes and perform a
Monte Carlo simulation to determine the width of the line produced in this
regime. This is done with utmost care
because of the importance of the charge exchange process as explained
above. In Sect. 3, we review the positron processes after
thermalization; these comprise: charge exchange with H, H2, He, direct
annihilation with bound electrons, direct annihilation with free
electrons and radiative combination (with free electrons). We discuss
the dust grains and the processes that positrons
undergo with them. We also
present up-to-date line widths for all processes. In Sect. 4, we use the
knowledge compiled and presented here to obtain annihilation spectra in
standard ISM situations. In the final section, we summarize the most
important new information and discuss the application of this revision to
the 511 keV SPI data analysis that we intend to perform.
1 MeV (their kinetic energies when
they come out of beta decay) and a few tens of eV, when Positronium
formation through
charge exchange starts to occur. This regime includes Coulomb energy
losses (with free electrons), excitation and ionization of atoms (H,
H2, He), and Ps formation by charge exchange with H, H2 and He. We
review the cross sections for all the relevant processes and perform a
Monte Carlo simulation to determine the width of the line produced in this
regime. This is done with utmost care
because of the importance of the charge exchange process as explained
above. In Sect. 3, we review the positron processes after
thermalization; these comprise: charge exchange with H, H2, He, direct
annihilation with bound electrons, direct annihilation with free
electrons and radiative combination (with free electrons). We discuss
the dust grains and the processes that positrons
undergo with them. We also
present up-to-date line widths for all processes. In Sect. 4, we use the
knowledge compiled and presented here to obtain annihilation spectra in
standard ISM situations. In the final section, we summarize the most
important new information and discuss the application of this revision to
the 511 keV SPI data analysis that we intend to perform.
2 In-flight processes
When, after being slowed down by Coulomb collisions in the ISM,
the positron has an energy less than a few tens of eV, it starts to pick
up
an electron from an atom or a molecule by charge exchange, thus forming
a positronium. This process is endoenergetic; it can happen as long as
the kinetic energy of the positron is above the charge exchange threshold
energy of Ps formation with the given atom or the molecule. We calculate
the probability for such an event to occur using the Monte Carlo method,
similarly to the method presented in BRD79. In the following sections we
present the cross sections we used for the calculation and the results of
the simulation for positrons in atomic and molecular hydrogen and helium.
In a partially ionized medium, the positron loses its energy by collisions
with electrons and by interaction with plasma waves, excitation and
ionization of atoms and molecules. The energy loss in the plasma is
a continuous process. Its rate, which depends on the energy of the
positron, the electron temperature and density in the plasma, is
given by Book & Ali (1975). The other processes require a collision
with an individual atom or molecule. In
this case the amount of the energy lost by the positron depends on the
positron energy and on the type of collision: excitation or ionization.
The thresholds for all these processes are presented in Table 1. Figures 1a,b and c
show the cross sections we used for excitation, ionization and charge
exchange in H, H2 and He respectively.
Table 1:
Energy threshold of reactions induced by positrons.
The various cross section measurements for positron-impact ionization of H we have found in the literature (Jones et al. 1993; Hofmann et al. 1997; and Kara 1999) are in agreement, except those of Spicher et al. (1990)
which are thought to have a systematic normalisation error (Charlton &
Humberston 2001 - hereafter CH2001). On the theoretical side, the results
of calculations by Janev & Solov'ev (1998) fit the previous measurements
below 40 eV, whereas those of Ratnavelu (1991) are in good accord with the
data above 30 eV but slightly overestimate the cross-section in the
150-300 eV range.
We have thus reconstructed the cross section dependence on the positron
kinetic energy by using the calculations of Janev & Solov'ev (1998)
below 40 eV and averages of the experimental data above this value. The
energy loss by positrons in such a collision has been approximated by
BRD79 to be distributed as a Gaussian with a mean of one-fourth of the
binding energy and a standard deviation of 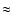 2 eV. We adopt this
approximation, which was inspired by the calculations by Omidvar (1965)
of the ejected electron velocities in electron-hydrogen ionization
collision.
2 eV. We adopt this
approximation, which was inspired by the calculations by Omidvar (1965)
of the ejected electron velocities in electron-hydrogen ionization
collision.
Concerning the positron-induced excitation of H we used the calculated
cross sections of Walters (1988) and Kernoghan et al. (1996) for 1s-2s and 1s-2p excitations. The cross section for excitation of
higher energy levels is taken from Fig. 3 of Stein et al. (1998). The
latter has been deduced by subtracting the elastic, ionization,
1s-2s and 1s-2p excitation and Ps formation cross sections calculated
by Kernoghan et al. (1996) from their total calculated cross section.
The positron energy lost in an excitation to the 2s or 2p levels
of H is 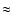 10.2 eV. We assume the energy loss in excitation of
the highest levels to be identical to the one for the n=3 level (12.1 eV).
10.2 eV. We assume the energy loss in excitation of
the highest levels to be identical to the one for the n=3 level (12.1 eV).
Among the recent measurements of Ps formation cross sections (Sperber et al. 1992; Zhou et al. 1997; Kara et al. 1999), the results of Sperber
et al. (1992), which were the first to be performed, differ significantly
(a factor of 4/3) from the others and are thought to be incorrect
(Hoffman et al. 1997). Ps formation cross sections calculated by
Kernoghan et al. (1996) are in good accord with the experimental
results of Zhou et al. (1997) and Kara et al. (1999). We thus use
this calculation's results in modelling the cross section. Since
the excitation and ionization processes dominate above 100 eV,
measurements of the Ps formation cross section are subject to
large uncertainties. For the same reasons, the extrapolation of
the charge exchange cross section by a power law or by an exponential
cut does not affect the results of the fraction of Ps formation
in-flight significantly.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2454fi1a.eps}\par\includeg...
...]{2454fi1b.eps}\par\includegraphics[width=8.8cm,clip]{2454fi1c.eps}
\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg20.gif) |
Figure 1:
Cross sections for positronium formation, ionization and
excitation in positron collision with a) atomic hydrogen; b) molecular
hydrogen; and c) helium as a function of the kinetic energy. |
| Open with DEXTER |
Experiments for the measurement of the single ionization of helium by
positron
impact (Fromme et al. 1986; Knudsen et al. 1990; Jacobsen et al. 1995;
Moxom et al. 1996) yield general agreement, except for
the results of Fromme et al. (1986) which slightly overestimate the cross
section below 50 eV and underestimate it (by 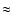 12%) in the
100-200 eV range. The calculation for positron kinetic energies below
150 eV made by Campbell et al. (1998) fits the data quite well
(see also CH2001 p. 241). We use this theoretical result for energies
less than 150 eV and
the average of the measurements above this value. The energy distribution
of the ejected electron is taken from Goruganthu et al. (1985), who
calculated the single differential cross section of secondary
electron production for electron-impact ionization in helium. These
distributions can be approximated by an exponential law with an energy
scale of
12%) in the
100-200 eV range. The calculation for positron kinetic energies below
150 eV made by Campbell et al. (1998) fits the data quite well
(see also CH2001 p. 241). We use this theoretical result for energies
less than 150 eV and
the average of the measurements above this value. The energy distribution
of the ejected electron is taken from Goruganthu et al. (1985), who
calculated the single differential cross section of secondary
electron production for electron-impact ionization in helium. These
distributions can be approximated by an exponential law with an energy
scale of 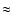 18.5 eV. We neglected the He double ionization by a
positron since its cross section is
18.5 eV. We neglected the He double ionization by a
positron since its cross section is 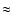
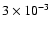 lower than that for single ionization (Charlton et al. 1988; CH2001).
lower than that for single ionization (Charlton et al. 1988; CH2001).
The cross section for the excitation of He by positrons is not well
determined, either by measurements or by calculations. Chapuis et al.
(1994) deduced it from the difference between the total cross section and
those of the charge exchange and ionization cross sections. However, the
excitation cross-section for positron-He scattering evaluated with this
method overestimates by a factor of 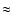 4 the experimental
measurements
(Coleman et al. 1982; Mori & Suoeka 1994) and theoretical calculations
(Parcell et al. 1987; Hewitt et al. 1992; Ficocelli Varrachio & Parcell 1992; Campbell et al. 1998; see also Fig. 5.4
of CH2001). We used the cross section curve of Chapuis et al. (1994)
scaled to fit the most recent experimental results of Mori & Suoeka
(1994).
4 the experimental
measurements
(Coleman et al. 1982; Mori & Suoeka 1994) and theoretical calculations
(Parcell et al. 1987; Hewitt et al. 1992; Ficocelli Varrachio & Parcell 1992; Campbell et al. 1998; see also Fig. 5.4
of CH2001). We used the cross section curve of Chapuis et al. (1994)
scaled to fit the most recent experimental results of Mori & Suoeka
(1994).
While the measurements of the cross section for positronium formation
in positron collisions with helium (Fornari et al. 1983;
Diana et al. 1986; Fromme et al. 1986; Moxom et al. 1993; Overton et al. 1993) are in good agreement below 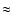 80 eV, large
discrepancies occur above this value. These discrepancies may be due
to experimental errors (CH2001), and the most recent results
of Overton et al. (1993), which are lower than the other measurements
above 80 eV, are in better accord with theoretical calculations of
McAlinden & Walters (1992) and Campbell et al. (1998). We have used the
results of the latter authors to model the cross section for charge
exchange in helium.
80 eV, large
discrepancies occur above this value. These discrepancies may be due
to experimental errors (CH2001), and the most recent results
of Overton et al. (1993), which are lower than the other measurements
above 80 eV, are in better accord with theoretical calculations of
McAlinden & Walters (1992) and Campbell et al. (1998). We have used the
results of the latter authors to model the cross section for charge
exchange in helium.
The four cross section measurements by Fromme et al. (1988), Knudsen
et al. (1990), Jacobsen et al. (1995) and Moxom et al. (1996)
of the positron-impact single ionization of molecular hydrogen provide
very different results for energies less than 200 eV (see also CH2001).
The latest results of Moxom et al. (1996) seem more appropriate since
they are not far from the results of Fromme et al. (1988) and Knudsen
et al. (1990).
However, data of Jacobsen et al. (1995), which underestimate the
results of previous experiments by 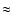 40% at 80 eV, are the
closest
to the theoretical evaluations performed by Chen et al. (1992).
So by chosing to use the cross section of Moxom et al. (1996), we
ran the risk of making a systematic error in the calculation
of the fraction of positronium formation in flight in molecular hydrogen.
But, as presented in the next section, the results of this assumption
provide a fraction in agreement with measurements of Brown & Leventhal
(1986).
40% at 80 eV, are the
closest
to the theoretical evaluations performed by Chen et al. (1992).
So by chosing to use the cross section of Moxom et al. (1996), we
ran the risk of making a systematic error in the calculation
of the fraction of positronium formation in flight in molecular hydrogen.
But, as presented in the next section, the results of this assumption
provide a fraction in agreement with measurements of Brown & Leventhal
(1986).
There are few measurements and studies on the energy distribution of the
ejected electrons in ionisation collision of H2 by positrons.
Köver & Laricchia (1998), Berakdar (1998) and Köver et al. (2002) provide such a distribution, but only for forward
electrons and specific positron energies. As for helium we approximate
the distribution of the ejected electrons by an exponential law.
According to the few existing measurements, the energy scale of this
distribution is approximately 15 eV. Since the cross section for the
dissociative ionization of molecular hydrogen by electrons contributes
only to 6% of the ionization cross section
(Rapp et al. 1965), we neglect this
process in the simulation.
Measurements of the charge exchange cross section in molecular
hydrogen are mostly in agreement (Fornari et al. 1983; Diana et al.
1986; Fromme et al. 1988; Zhou et al. 1997 - see also Kwan et al. 1998).
However, the Fromme et al. (1988) results are above the upper
limit derived by Zhou et al. (1997) for energies less than 10 eV.
Therefore we have used the cross section measured by Fornari
et al. (1983) and Diana et al. (1986) for the low (E<100 eV) and high
(E>100 eV) energies, respectively. It should be noted that the
cross section derived by BRD79 fits the data of Fornari et al. (1983) quite well in the 15-50 eV range.
Very little is known from either theory or experiment concerning the
excitation of molecules by positrons.
We thus estimate the excitation cross section of positrons colliding with
molecular hydrogen by subtracting the charge
exchange, ionization and elastic cross sections from the total cross
section, which has been measured by Hoffman et al. (1982). The elastic
cross section was evaluated by Wallyn et al. (1994).
We simulate the interactions of positrons with atoms and molecules
by Monte-Carlo methods on the basis of the cross sections and energy loss
mechanisms
presented previously. For any value of the positron's kinetic energy (that
is at any stage of the simulation), the interaction process is chosen
randomly according to the values of the cross sections of all the possible
processes. The particular interaction then specifies the energy lost at
that stage. The positron is "dropped'' either when it forms a positronium
or when its kinetic energy falls below the threshold of charge exchange;
in the latter case, the positron is assumed to start thermalizing with the
ambient medium.
The fraction f1 of positrons forming a positronium in flight is then
obtained simply by counting the number of positrons undergoing a
charge exchange. When such a process occurs, the kinetic energy value of
the positronium (i.e. the kinetic energy of the positron minus the
energy required to form the positronium) is stored. The set of kinetic
energies
obtained from the simulation is then used to
calculate the spectral shape of the annihilation emission by
accounting for the Doppler broadening due to the motion of
the positronium. The shapes of the annihilation line differ somewhat from
a simple Gaussian, but we parametrize them with FWHMs by fitting Gaussian
functions to the
spectra (see Sect. 3.2). We also record the time spent by positrons to
slow down and reach the charge exchange threshold or form a
positronium. The resulting mean duration deduced from a large number
of positrons allows us to calculate the slowing down time of positrons
before thermalization.
We tested our Monte Carlo simulation by reproducing the results
obtained by BRD79 (see Fig. 2). They
calculated the fraction of positrons undergoing charge exchange with
atomic hydrogen before thermalization as a function of the ionization
fraction. Similarly our calculation has been performed for two cases
of media characterized by their electron density and temperature. The
first is representative of a warm component of the ISM (
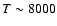 K)
and the second of solar flares (
K)
and the second of solar flares (
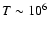 K).
K).
![\begin{figure}
\par\includegraphics[width=8.cm,height=8.cm,clip]{2454fig2.eps}
\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg24.gif) |
Figure 2:
Fraction of positrons forming positronium in flight
(f1) by charge exchange with atomic hydrogen as a function of the
ionization fraction (y) in a warm component of the interstellar medium
(electron density:
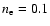 cm-3, electron temperature: cm-3, electron temperature:
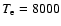 K) and
in solar flare ( K) and
in solar flare (
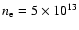 cm-3, cm-3,
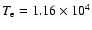 K). The results presented in Fig. 2 of BRD79
are shown for comparison. K). The results presented in Fig. 2 of BRD79
are shown for comparison. |
| Open with DEXTER |
Values of f1 for a totally neutral medium are summarized in Table 2 where they are compared with results of previous
measurements (Brown & Leventhal 1984, 1986) and calculations
(BRD79; Wallyn et al. 1994; Chapuis et al. 1994).
Table 2:
Fraction (in %) of positrons forming positronium in flight,
in a completely neutral medium.
After they have lost the bulk of their energies during the "in-flight''
phase, the positrons thermalize with the ambient medium and undergo a
series of processes leading to their annihilation, either directly
or via positronium formation.
In thermal conditions, the reaction rate for non-relativistic binary
collisions is easy to calculate; we use the usual
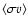 formula,
where the averaging is done over the interacting particles' (Maxwellian)
energy distributions:
formula,
where the averaging is done over the interacting particles' (Maxwellian)
energy distributions:
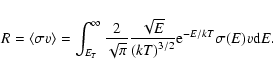 |
(1) |
![\begin{figure}
\par\includegraphics[width=1.0\linewidth ,height=9.0cm,width=8.5cm,clip]{2454fig3.eps}
\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg28.gif) |
Figure 3:
Positron reaction rates as a function of temperature. |
| Open with DEXTER |
The cross sections for these reactions were discussed in the previous
section. The calculated rate is shown in Fig. 3 along with
the rates of the other processes. These rates are significant only above
a few times 104 K, when the high-energy tail of the Maxwellian
distribution is above the threshold of Ps formation. Also, although
few atoms remain neutral at such a high temperatures, we present the
charge exchange rate up to
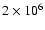 K.
K.
The cross section for this process (
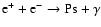 )
is so small (10-20 cm2 at 1 eV and decreasing fast at
higher energies) that it cannot be measured in the laboratory. We must
thus rely on theoretical calculations. Various attempts and approaches
have been made over the past several decades, going back to 1930, the most
recent and accurate of which is that of Gould (1989), who obtained the
reaction rate for both the ground state and the first excited state of Ps
directly from first principles. The earlier calculation of Crannell et al.
(1976) used the similarity between this process and the radiative
recombination of hydrogen (
)
is so small (10-20 cm2 at 1 eV and decreasing fast at
higher energies) that it cannot be measured in the laboratory. We must
thus rely on theoretical calculations. Various attempts and approaches
have been made over the past several decades, going back to 1930, the most
recent and accurate of which is that of Gould (1989), who obtained the
reaction rate for both the ground state and the first excited state of Ps
directly from first principles. The earlier calculation of Crannell et al.
(1976) used the similarity between this process and the radiative
recombination of hydrogen (
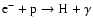 )
for
which the cross section was already known.
)
for
which the cross section was already known.
This process (
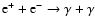 )
has a very
small cross section (about an order of magnitude less than that of
radiative
combination at temperature less than 105 K - Heitler 1954;
Crannell et al. 1976; BRD79). It is therefore only relevant in the hot
phase
of the ISM and can be ignored in all other conditions, as can be see in
Fig. 3.
)
has a very
small cross section (about an order of magnitude less than that of
radiative
combination at temperature less than 105 K - Heitler 1954;
Crannell et al. 1976; BRD79). It is therefore only relevant in the hot
phase
of the ISM and can be ignored in all other conditions, as can be see in
Fig. 3.
This process (
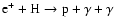 ,
or e+ on
H2 or on He) has the lowest
cross section of all the positron processes, more
than an order of magnitude less than the second slowest process, direct
annihilation with free electrons, and more than two orders of magnitude
weaker than radiative combination. Direct
annihilation with bound electrons applies only at the lowest temperatures
(less than a few thousand degrees) where charge exchange does not proceed
because the positrons then do not have the threshold energy needed
and there are no free electrons for the other two processes - radiative
combination and direct annihilation with free electrons - to take place.
Due to the weakness of its cross section, this process cannot be
investigated in the laboratory, and again one must rely on theoretical
calculations. The work of Bhatia et al. (1977) has not been
corrected or updated by any later works, so we still use the rate they
obtained for direct
annihilation with H. For He and H2 the method is similar, except that
we calculated the cross section using estimates of the dependence of
,
or e+ on
H2 or on He) has the lowest
cross section of all the positron processes, more
than an order of magnitude less than the second slowest process, direct
annihilation with free electrons, and more than two orders of magnitude
weaker than radiative combination. Direct
annihilation with bound electrons applies only at the lowest temperatures
(less than a few thousand degrees) where charge exchange does not proceed
because the positrons then do not have the threshold energy needed
and there are no free electrons for the other two processes - radiative
combination and direct annihilation with free electrons - to take place.
Due to the weakness of its cross section, this process cannot be
investigated in the laboratory, and again one must rely on theoretical
calculations. The work of Bhatia et al. (1977) has not been
corrected or updated by any later works, so we still use the rate they
obtained for direct
annihilation with H. For He and H2 the method is similar, except that
we calculated the cross section using estimates of the dependence of
 ,
the effective charge
,
the effective charge![[*]](/icons/foot_motif.gif) ,
on the kinetic energy from Campeanu & Humberston (1977) and
Armour et al. (1990), respectively.
,
on the kinetic energy from Campeanu & Humberston (1977) and
Armour et al. (1990), respectively.
The measured
 in H2 at room
temperature is
in H2 at room
temperature is 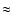 45% larger than the theoretical evaluation
(CH2001). This may turn out to be a source of systematic error in the
annihilation rate we will be using.
45% larger than the theoretical evaluation
(CH2001). This may turn out to be a source of systematic error in the
annihilation rate we will be using.
The widths of the annihilation line resulting from charge exchange in
flight with H, H2, and He have been calculated as a result of the
Monte Carlo simulation we presented in the previous section.
We have found 5.8 keV, 6.4 keV and 7.4 keV for H, H2 and He respectively in a neutral medium. These widths are in quite good
agreement with previous measurements and calculations (BRD79; Brown
& Leventhal 1984; Brown & Leventhal 1986). The width of the
511 keV line does not vary with the ionisation fraction of the ambient
medium although its shape is slightly "flattened'' (the top of the
spectral distribution is less peaked). This flattening is
due to the loss of low energy positrons which are quickly slowed down
below the Ps threshold by way of Coulomb collisions with electrons.
The widths of the annihilation line resulting from the direct annihilation
with H, H2, and He have all been measured experimentally: Brown &
Leventhal (1986) obtained 1.56 keV for H; and Iwata et al.
(1997a) obtained 1.71 keV and 2.50 keV for H2 and He, respectively.
These widths depend very weakly on the temperature in our range of
interest.
The widths of both the radiative combination and direct annihilation with
free electrons were calculated by Crannell et al. (1976) using a simple
argument of thermal broadening due to the motion of the center of mass of
the e+-e- pair; this calculation gives the same following simple
expression for both widths:
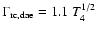 keV,
where T4 is the temperature in units of 104 K.
keV,
where T4 is the temperature in units of 104 K.
The importance of positron capture and annihilation on interstellar dust
grains was first pointed out by Zurek (1985), who estimated the rate for
the process and concluded that dust can play a crucial role in the warm
ionized phase of the ISM, leading to drastic modifications of the Ps
formation fraction depending on the value of the cross section of the
positron capture on the dust grains. Guessoum et al.
(1991) added spectral considerations to the positron-dust process but kept
a simplified picture of the dust and showed that unless the abundance of
dust in the annihilation regions is increased many times compared to
"normal'' quantities, grains change the spectrum of the line mostly in the
hot phase. Astrophysical knowledge of grains has since increased
considerably (see the reviews by Draine 2003, 2004; Li 2004; and Krugel
2003) and although a huge body of work exists on positron interactions
with solids and solid surfaces (Nieminen & Oliva 1980; Huttunen et al.
1990; Dannefaer et al. 1996; Dupasquier & Mills 1995; Puska & Nieminen
1994; Weiss et al. 1994; Suzuki et al. 2003; Mills et al. 1989; Mokrushin
et al. 2003; Pi et al. 2003; Weber & Lynn 2000), experiments
dealing with positrons and dust like materials remain
scarce. We here summarize our best understanding of the
relevant information we have collected on dust grains in our context.
The total amount of dust in the Galaxy is estimated at
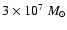 ,
which represents 0.6% of the total mass of gas (Krugel 2003),
although Ferriere (2003) indicates that there is a large uncertainty on
this fraction,
which could range from 0.5 to 1%. The abundance
of dust grains is found to correlate approximately with hydrogen,
particularly in the cold and neutral phases; there is also some evidence
(Herter et al. 1989; Krugel 2003) for partial dust destruction in the HII regions.
,
which represents 0.6% of the total mass of gas (Krugel 2003),
although Ferriere (2003) indicates that there is a large uncertainty on
this fraction,
which could range from 0.5 to 1%. The abundance
of dust grains is found to correlate approximately with hydrogen,
particularly in the cold and neutral phases; there is also some evidence
(Herter et al. 1989; Krugel 2003) for partial dust destruction in the HII regions.
Several species of dust (composition, size) exist in the ISM. Dust is
often
divided into 3 categories as follows:
- large grains, of radii ranging between 20 nm and 0.3
 m, made
of either silicate particles (Mg2SiO4 or Fe2SiO4) or amorphous
carbon;
m, made
of either silicate particles (Mg2SiO4 or Fe2SiO4) or amorphous
carbon;
- very small grains, of radii ranging between 1 nm and 10 nm, made
mostly
of graphite, and representing about 10% of the amorphous carbons;
- PAH (polycyclic aromatic hydrocarbons), which are big molecules and
make up 3 to 6% of the large grains (in abundance).
We have ignored the PAHs in the present treatment due to their negligible
contribution; in fact, we have found that the "very small grains'' can be
neglected as well, as their abundance and small sizes (small geometric
cross sections) give extremely low positron capture rates.
Grain sizes follow a power-law distribution: d
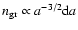 ,
where a is the radius of the grain, which ranges between
,
where a is the radius of the grain, which ranges between
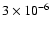 cm and
cm and
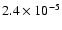 cm for the large carbonaceous grains
and between
cm for the large carbonaceous grains
and between
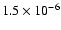 cm and
cm and
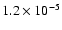 cm for the
large silicate grains (Krugel 2003). Other distributions and grain size
ranges that distinguish between grain types have also been proposed
(Weingartner & Draine 2001; Li & Draine 2001), but we will adopt the
simple unified expression of Krugel (2003).
The distributions and grain size ranges given by Weingartner & Draine
(2001) or Li & Draine (2001) lead to reaction rates that are several
times higher than those we obtain with the "conservative'' values of
Krugel (2003). This factor (the sizes and distribution law of the grains)
is the fundamental uncertainty in the determination of the reaction rate
of positron interaction with the dust. Secondary factors include the
amount of dust in the ISM (as stated previously) and the electric charge
of the grains in the cold phase. We have combined these uncertainties
into one parameter, denoted by
cm for the
large silicate grains (Krugel 2003). Other distributions and grain size
ranges that distinguish between grain types have also been proposed
(Weingartner & Draine 2001; Li & Draine 2001), but we will adopt the
simple unified expression of Krugel (2003).
The distributions and grain size ranges given by Weingartner & Draine
(2001) or Li & Draine (2001) lead to reaction rates that are several
times higher than those we obtain with the "conservative'' values of
Krugel (2003). This factor (the sizes and distribution law of the grains)
is the fundamental uncertainty in the determination of the reaction rate
of positron interaction with the dust. Secondary factors include the
amount of dust in the ISM (as stated previously) and the electric charge
of the grains in the cold phase. We have combined these uncertainties
into one parameter, denoted by
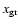 (similar to that of Guessoum et al. 1991), where
(similar to that of Guessoum et al. 1991), where
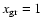 represents our
"standard'' rate, obtained on the basis of the Krugel (2003)
parametrization of dust;
represents our
"standard'' rate, obtained on the basis of the Krugel (2003)
parametrization of dust;
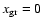 represents a total absence of dust
in a given region;
represents a total absence of dust
in a given region;
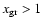 represents an overabundance of dust and/or
grain characteristics (sizes and composition) that are especially
favorable for positron capture. We emphasize however, that these factors do
not affect our conclusions, namely that the reaction rates for
positron capture on dust are, even in the most extreme assumptions,
negligible compared to other processes' in all but the warm-ionized and
hot ISM phase: in the latter environment the dust dominates all other
processes under all assumptions, and in the other case the dust becomes
comparable or dominant only when the grain capture rate
(or equivalently
represents an overabundance of dust and/or
grain characteristics (sizes and composition) that are especially
favorable for positron capture. We emphasize however, that these factors do
not affect our conclusions, namely that the reaction rates for
positron capture on dust are, even in the most extreme assumptions,
negligible compared to other processes' in all but the warm-ionized and
hot ISM phase: in the latter environment the dust dominates all other
processes under all assumptions, and in the other case the dust becomes
comparable or dominant only when the grain capture rate
(or equivalently
 )
is increased by a large factor.
)
is increased by a large factor.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{2454fig4.eps}
\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg48.gif) |
Figure 4:
Collisions and subsequent annihilation of positrons with grains
(of various sizes and types) - a) positron re-emission; b) positron
backscattering; c) positronium in grain, d) positronium ejection. |
| Open with DEXTER |
Positron collisions with dust grains can be treated along the same lines
as Zurek (1985) and Guessoum et al. (1991) did, namely
that the cross section is essentially a geometric one ( a2) with
the electric charge effect (attraction or repulsion with the positron
depending on the local conditions) and the positron escape (backscattering
and re-emission from the dust grain) taken into account:
a2) with
the electric charge effect (attraction or repulsion with the positron
depending on the local conditions) and the positron escape (backscattering
and re-emission from the dust grain) taken into account:
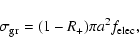 |
(2) |
where a is the radius of the grain and R+ is the probability
that the positron is either backscattered by the grain or re-emitted after
being captured.
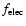 is given by (
1 - Ze2/akT) or
exp(-Ze2/akT)
depending on whether the grain is negatively or positively charged,
respectively; Z is the grain charge, and T is the temperature of the
medium. Grains are expected to be negatively charged in the hot and
ionized phases of the ISM and possibly positively charged in the cold and
neutral phases (being slightly ionized themselves by the UV radiation of
nearby stars if applicable). It can be shown (Krugel 2003) that the
electric potential of a grain is 2.5 kT/e, so that the quantity
Ze2/akT
= 2.5 is independent of the temperature of the medium or the size of the
grain.
is given by (
1 - Ze2/akT) or
exp(-Ze2/akT)
depending on whether the grain is negatively or positively charged,
respectively; Z is the grain charge, and T is the temperature of the
medium. Grains are expected to be negatively charged in the hot and
ionized phases of the ISM and possibly positively charged in the cold and
neutral phases (being slightly ionized themselves by the UV radiation of
nearby stars if applicable). It can be shown (Krugel 2003) that the
electric potential of a grain is 2.5 kT/e, so that the quantity
Ze2/akT
= 2.5 is independent of the temperature of the medium or the size of the
grain.
The positrons that are captured will diffuse and thermalize quickly with
the grain molecules; infra-red emission of the ISM dust shows that the
temperature of the grains varies between 15 K and 100 K depending on
the conditions of the ISM medium (15 K in the coldest phases, and between 50 K and 100 K in the ionized and hot conditions). Once thermalized, the
positrons in the grains will form a positronium atom, which will either
readily be in the para-state or be formed in the ortho-state but undergo a
"pick-off'' annihilation reaction as a para-state (giving 2 photons) when
the positron (bound in the Ps) "picks off'' an electron from the
surrounding valence electrons. Most of the positrons
that diffuse inside the grain will reach the surface, the diffusion length
being greater than the diameter of most of the grains, but upon reaching
the surface the positron will be captured in a "surface state'' and form
Ps there or be ejected, if the "positron work function'' of the
material is negative, which is the case for our dust grains
(Rosenberg et al. 1987). A
fraction of the Ps atoms formed at or near the surface will also be
ejected if the "Positronium work function'' for the material is negative,
which is also the case for our dust (Hodges & Stott 1973; Nieminem
& Oliva 1980; Eldrup et al. 1985; Rice-Evans & Rao 1988; Puska &
Nieminem 1994).
Aside from the backscattering probability measured and simulated for Si
and a few other elements (Makinen et al. 1992), we have found no specific
measurements of e+ and Ps probabilities for the materials that
constitute our dust grains in the conditions that we deal with (slow
positrons, etc.). There are some experiments (and a few calculations) that
deal with metals (Huttunen et al. 1990; Nieminen & Oliva 1990) and
polymers (Mukherjee et al. 1998) or conduct studies
(probing) of defects in semi-conductors by positrons (Britton et al. 2001; van Veen et al. 2004), but none that consider materials
of the dust type.
We have adopted the value of 10% of positron backscattering probability
obtained by Makinen et al. (1992) when they extrapolate to the lowest
positron energies (less than 1 keV), a value that seems to apply for all
the materials they investigated (including Si).
For the rest of the parameters, we can only use measurements
for materials that have similar chemical behavior (positron and
Positronium negative work functions), and the closest we could find were
copper and aluminum. For instance, the probability of re-emission of
positrons from copper varies linearly with T from 0 to 15% between 0 and 150 K, the temperature of the metal, which we will take as the temperature
of the dust, in our case. (Nieminen & Oliva's
theoretical treatment predicted that this probability would tend to zero
at very low temperatures.) The probability of ejection of Ps from the
surface of the grain is found to be very similar for Cu and Al, taking the
following approximate values: 0 at 0 K, 5% at 25 K, 9% at 50 K, 14%
at 100 K, 17% at 150 K and 20% at 200 K.
If these measurements are used for our dust grains (whose temperature
ranges between 15 and 100 K), it would imply that the bulk (65 to 80%)
of the positrons colliding with grains will annihilate inside (giving two
photons), a small fraction (5 to 15%) will form Ps, be ejected
and annihilate outside (giving two/three photons in the usual 25/75% proportions), while 15 to 20% of the positrons will simply fly back out
after hitting a grain.
Figure 4 gives a schematic description of the main processes
that a positron can undergo during its interaction(s) with dust grains.
The rate
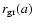 of positron capture by grains of size a is obtained from the
effective cross section of positron capture by grains and the thermal
speed of positrons in the medium:
of positron capture by grains of size a is obtained from the
effective cross section of positron capture by grains and the thermal
speed of positrons in the medium:
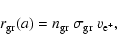 |
(3) |
where
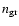 is the number density of dust grains in the
ISM,
is the number density of dust grains in the
ISM,
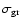 is the cross section of positron-capture
by grains (Eq. (2), and
is the cross section of positron-capture
by grains (Eq. (2), and
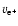 is the average thermal
speed of positrons in the given ISM phase:
is the average thermal
speed of positrons in the given ISM phase:
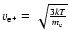 .
.
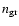 is obtained from the overall mass of dust in the galaxy (0.6%
of
the total gass mass) as well as the the grain size distribution
is obtained from the overall mass of dust in the galaxy (0.6%
of
the total gass mass) as well as the the grain size distribution
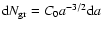 ,
which yields the mean value of the
grain's mass (
,
which yields the mean value of the
grain's mass (
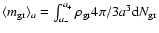 ).
The constant C0 is inferred from the normalization condition
).
The constant C0 is inferred from the normalization condition
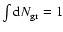 .
For the carbonaceous dust, the density is
.
For the carbonaceous dust, the density is
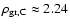 g cm-3; for the silicate dust,
g cm-3; for the silicate dust,
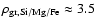 g cm-3. A simple calculation,
assuming the total dust mass to be equally divided into the two main
types, then gives:
g cm-3. A simple calculation,
assuming the total dust mass to be equally divided into the two main
types, then gives:
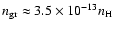 for the
carbonaceous dust and
for the
carbonaceous dust and
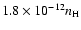 for the silicate dust.
for the silicate dust.
Replacing
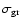 by its expression (Eq. (2))
in Eq. (3) allows one to show explicitly the factors
that influence
the value of the positron capture rate: the reflection factor R+ of positrons
backscattered or ejected from the dust grain as explained above, the
electrostatic enhancement of inhibition of positron-grain collision
by its expression (Eq. (2))
in Eq. (3) allows one to show explicitly the factors
that influence
the value of the positron capture rate: the reflection factor R+ of positrons
backscattered or ejected from the dust grain as explained above, the
electrostatic enhancement of inhibition of positron-grain collision
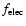 .
We add an additional factor
.
We add an additional factor
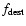 to take into account
the potential destruction of dust grains, most likely
in the hot environments. Averaging over the grain size distribution,
the rate then becomes:
to take into account
the potential destruction of dust grains, most likely
in the hot environments. Averaging over the grain size distribution,
the rate then becomes:
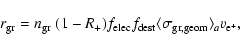 |
(4) |
where
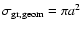 is the geometric cross-section
and
is the geometric cross-section
and
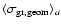 the mean value of the geometric cross section.
As stated previously, dust is likely to be
partially destroyed only in the hot phase of the ISM, so we take
the mean value of the geometric cross section.
As stated previously, dust is likely to be
partially destroyed only in the hot phase of the ISM, so we take
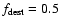 in that case, and
in that case, and
 in all other
conditions. In the hot and warm-ionized phases, grains are widely
considered to be negatively charged, with a potential such that
in all other
conditions. In the hot and warm-ionized phases, grains are widely
considered to be negatively charged, with a potential such that
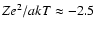 ,
so that
,
so that
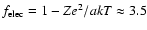 ;
in the cold and neutral phases, however, the grains are assumed
to be positively charged, but their electrostaic potential
depends on local conditions (proximity of an
ionizing UV radiation from a neighboring hot star, etc.), so that the
potential can vary between 0 and 2.5 V; in these cases, and considering the
de facto impossibility of pinpointing such a value we take
;
in the cold and neutral phases, however, the grains are assumed
to be positively charged, but their electrostaic potential
depends on local conditions (proximity of an
ionizing UV radiation from a neighboring hot star, etc.), so that the
potential can vary between 0 and 2.5 V; in these cases, and considering the
de facto impossibility of pinpointing such a value we take
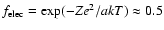 ,
keeping in mind that such a factor is in
effect irrelevant in the cold phase since the dust has no effect on the
annihilation there.
,
keeping in mind that such a factor is in
effect irrelevant in the cold phase since the dust has no effect on the
annihilation there.
Taking all these factors into account then yields final values for
the positron capture rates by the carbonaceous and the silicate dust
for the various ISM phase conditions, as reported in Table 3.
Table 3:
Reaction rates (in cm3/s) for the various processes
after thermalization in the
different ISM phases.
The rates obtained and reported here are in most cases essentially the
same as those of Guessoum et al. (1991), but in some
cases and due to the use of new data, the rates are substantially
different. The differences are found in the rates of charge exchange with H in the warm neutral phase, where our new value is greater than the
previous one by about 33%; direct annihilation with H in the warm
neutral phase, where our rate is greater than the old one by about 16%;
capture by grains, where our rates are about a factor of 10 lower, a factor
of 3 lower and a factor of 1.5 greater than the old values in the cold,
warm neutral and hot phases respectively.
The width of the annihilation line resulting from the decay of the Ps produced inside the grain is an important quantity. There are actually two
widths, corresponding to the annihilation of the Ps atoms that escape and
those that remain and die in the grains. Nieminen & Oliva (1980) state
that the kinetic energy of the Ps ejected by the grain is equal to the
absolute value of the "Ps work function''
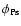 of the material.
This implies a width
of the material.
This implies a width
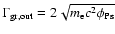 of
about 1.4 keV, taking
of
about 1.4 keV, taking
 eV. (Note that the value used
for
eV. (Note that the value used
for
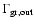 since Guessoum et al. 1991, was
2.5 keV.) Moreover, the fraction of Ps escaping from the grain is now taken
to be 5-15%, compared to the previously held 1/3 value. This will have
some significant impact on the shape of the annihilation line, at least in
the hot and ionized phases.) The width of the line produced by para-Ps
decaying inside the grain cannot be estimated via other physical
quantities and needs to be measured in the laboratory. Again, there have
been no measurements for the kinds of materials that make up our grains,
but typical ACAR (angular correlation of the annihilation radiation)
measurements of the two emitted photons give values
since Guessoum et al. 1991, was
2.5 keV.) Moreover, the fraction of Ps escaping from the grain is now taken
to be 5-15%, compared to the previously held 1/3 value. This will have
some significant impact on the shape of the annihilation line, at least in
the hot and ionized phases.) The width of the line produced by para-Ps
decaying inside the grain cannot be estimated via other physical
quantities and needs to be measured in the laboratory. Again, there have
been no measurements for the kinds of materials that make up our grains,
but typical ACAR (angular correlation of the annihilation radiation)
measurements of the two emitted photons give values
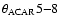 mrad (Biasini et al. 2000; Sasaki et al. 2003), which would translate
into
mrad (Biasini et al. 2000; Sasaki et al. 2003), which would translate
into
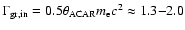 keV.
We note, however, that the measurements of
keV.
We note, however, that the measurements of
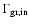 by Iwata et al. (1997a) for many atoms and molecules (including complex
alcohols) shows the width to be always between 2.0 keV and 3.0 keV. We
have thus adopted the higher value of the ACAR measurements, which
corresponds to the lowest value of the annihilation on molecules:
by Iwata et al. (1997a) for many atoms and molecules (including complex
alcohols) shows the width to be always between 2.0 keV and 3.0 keV. We
have thus adopted the higher value of the ACAR measurements, which
corresponds to the lowest value of the annihilation on molecules:
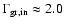 keV.
keV.
4 Annihilation spectra
Table 4:
Line widths (in keV) for various positron annihilation
processes.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{2454fi5a.eps}\hspace*{4mm}...
...m}
\includegraphics[width=8.3cm,clip]{2454fi5e.eps}\hspace*{8.8cm}\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg84.gif) |
Figure 5:
Annihilation spectra for the 5 ISM phases separately (see text):
a) cold, molecular hydrogen medium;
b) cold, atomic hydrogen medium; c) warm, neutral medium; d) warm,
ionized medium; e) hot medium. |
| Open with DEXTER |
Having reviewed and recalculated the various processes' reaction rates
and line widths, we can construct the standard spectra of the annihilation
radiation for each phase of the ISM as well as an overall "global''
or "diffuse'' radiation spectrum, one that includes contributions from
the various regions; the latter "global'' spectrum requires knowledge
about the relative distribution of the ISM phases and their volume
contributions to the emitted radiation.
The emission processes are spectroscopically modeled as either a pure
two-photon direct annihilation represented by a Gaussian with a given
FWHM or a combined two-photon-line/three-photon-continuum when the
annihilation proceeds via formation of a positronium atom; in this
latter case, the two-photon line is represented by a Gaussian with
its characteristic FWHM, while the continuum part is represented by
the usual Ore & Powell (1949) function
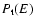 that describes
the probability of the emitted photon being emitted with an energy E between 0 and 511 keV (Eq. (10) of Guessoum et al.
1991).
that describes
the probability of the emitted photon being emitted with an energy E between 0 and 511 keV (Eq. (10) of Guessoum et al.
1991).
Table 4 summarizes the line widths for various processes.
For several processes the Gaussian function with a given
FWHM represents a slight simplification of the real spectrum, but the
annihilation spectra obtained in the end, and their eventual comparison
with the data, are insensitive to this level of precision.
However, several values of the various processes'
FWHM have now changed to some extent (by about 10% in most cases, but
sometimes more) compared to the values used in previous modeling.
In particular, the width of the line produced in the decay of Ps formed
"in-flight'' with H is now 5.8 keV instead of the 6.4 keV used for over
two decades. (The difference is due to the accurate experimental cross
sections now available for positron excitation, ionization and charge
exchange with H.) Likewise the lines resulting from positron annihilation
after capture by a grain (either two-photon annihilation inside the grain
or decay of the Ps ejected from the grain) have widths of 2.0 keV and 1.4 keV respectively, compared to 1.8 keV and 2.5 keV previously.
References and discussions of the various FWHMs are given in the
Sects. 3.2 and 3.3.
The following formula then allows us to construct the theoretical
spectrum for a given ISM phase:
where X and Y are the relative abundances of H/H2 and He (90% and 10% respectively),
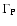 refers to the FWHM of the line
produced by a given process P (if, ce, dae, daH, gr refer to in-flight,
charge exchange, direct annihilation with free electrons, direct
annihilation with H, annihilation with grains - inside or outside -,
etc.);
refers to the FWHM of the line
produced by a given process P (if, ce, dae, daH, gr refer to in-flight,
charge exchange, direct annihilation with free electrons, direct
annihilation with H, annihilation with grains - inside or outside -,
etc.);
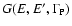 is the Gaussian function of variable E',
centered on E, and of
is the Gaussian function of variable E',
centered on E, and of
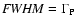 ,
normalized to 1; the
factors
,
normalized to 1; the
factors 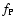 are the relative probabilities for each process:
are the relative probabilities for each process:
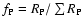 ,
,
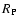 denoting the rates of various processes (Table 3) weighted by the relative abundance of each element.
denoting the rates of various processes (Table 3) weighted by the relative abundance of each element.
Figures 5a-d, and e show the annihilation spectrum in
the molecular,
cold (atomic), warm neutral, warm ionized and hot phases, respectively.
In each case the solid curve shows the spectrum assuming a "standard
grain model'' (in terms of grain abundance, size distribution, composition,
etc., as adopted in Sect. 3.3) in the given phase, i.e. a factor
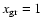 ;
dashed curves represent the spectra in the case of grains
greatly amenable to positron capture (
;
dashed curves represent the spectra in the case of grains
greatly amenable to positron capture (
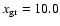 ); dotted
curves represent the spectra when dust is removed from the phase.
The spectra confirm that unless dust is overabundant in the warm
ionized or hot phases (or the rates of capture are greater than
we have adopted - as explained in Sect. 3.3), it has a negligible
effect on the annihilation radiation emitted in the ISM.
); dotted
curves represent the spectra when dust is removed from the phase.
The spectra confirm that unless dust is overabundant in the warm
ionized or hot phases (or the rates of capture are greater than
we have adopted - as explained in Sect. 3.3), it has a negligible
effect on the annihilation radiation emitted in the ISM.
In order to construct the "global'' spectrum of 511 keV annihilation from
the ISM as a whole, one simple approach is to combine the previous phase
spectra on the basis of the relative contributions (densities and filling
factors) of each phase. For this, filling factors such as those used in
the ISM model of McKee & Ostriker (1977) can be adopted: 2.4% for the
cold phase(s), 23% for each of the warm phases and 52% for the hot
phase. In the same model, the densities of each phase are: 42 cm-3,
0.37 cm-3, 0.25 cm-3,
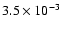 cm-3 in the
cold, warm neutral, warm ionized and hot phases, respectively.
cm-3 in the
cold, warm neutral, warm ionized and hot phases, respectively.
Figure 6 shows the result of combining the
individual-phase spectra using the McKee & Ostriker
simple prescription as well as the spectra obtained when
the positrons are excluded from the cold regions (both
the molecular and atomic phases); this we do for comparative
purposes with the results obtained in the treatment of
Guessoum et al. (1991). In the first
case (annihilation in all phases according to the description
of McKee & Ostriker), we see that the dust makes no
difference to the line profile. In the second case, the
profile of the overall emission spectrum is substantially
different from the "uniform'' case, and the dust does
make a non-negligible difference.
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{2454fig6.eps}
\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg106.gif) |
Figure 6:
Combined ("global'') ISM annihilation spectra, obtained
under two assumptions: 1) positrons annihilating in all phases
according to the filling factors and densities given in the
McKee & Ostriker (1977) model, either with or without the effect
of the grains (solid, blue dashed and red dotted curves);
2) positrons not annihilating in the cold phases, with/without
grain effect (solid and dotted narrower purple curves). |
| Open with DEXTER |
A more physically realistic approach would be to adopt an analytic ISM model such as Ferriere's, which gives the densities of each species
(H, H2, free electrons, etc.) in each volume element (defined by
its galactocentric coordinates r and z) of the ISM. This latter approach
we save for a future, more physical treatment of annihilation in the
ISM, one that will consider the change in the annihilation spectrum and
profile when emanating from different directions and regions of the
Galaxy.
Table 5 displays the FWHMs of the lines obtained in each
phase as well as in the "global'' case. These allow us to compare
our results with earlier ones and serve to give us a rough idea
about the physical properties of the annihilation region(s),
although we must emphasize that the FWHM parameter is not a
sufficient parameter in characterize such spectra.
Until the full follow-up modeling and interpretation
work is performed, these values are used for comparison and indication
purposes. Our present results are largely consistent with the older
ones, but our line widths tend to
be slightly larger than the older ones in all phases. In the
warm neutral phase the line appears to be substantially broader
than the result of Guessoum et al. (1991), but
only because in that treatment the warm neutral phase has a 15%
ionization fraction, whereas in the present treatment the warm
neutral phase is completely neutral. Moreover
the rate for charge exchange with H has increased (by about 20%)
in this work, which increases the contribution of the broad line;
indeed the in-flight process, for which the line widths are always
large ( 6 keV), has now become more dominant overall.
6 keV), has now become more dominant overall.
Table 5:
Values of FWHMs obtained (in keV) in each ISM phase separately
and in the "global'' case; the values are given for the "standard grain
model'' (
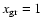 ), for
), for
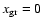 (no dust) and for
(no dust) and for
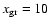 (overabundant and/or grain characteristics especially favorable for
positron capture - see text), respectively. For the "global (combined)''
spectrum we give FWHM values in two cases: the McKee & Ostriker
model with its phase densities and filling fractions, and the
situation (results in parentheses) when the positrons are excluded
from the cold phases.
(overabundant and/or grain characteristics especially favorable for
positron capture - see text), respectively. For the "global (combined)''
spectrum we give FWHM values in two cases: the McKee & Ostriker
model with its phase densities and filling fractions, and the
situation (results in parentheses) when the positrons are excluded
from the cold phases.
The main conclusions from this "phase'' treatment are first that the
"global'' spectra obtained here (on the basis of the McKee & Ostriker
1977, ISM model) are consistent with the observed widths reported
by the various missions (including SPI and TGRS) and second that unless
specific physical assumptions are made regarding whether the positrons
annihilate prefentially in some regions (say the hot and/or ionized phases),
the dust will in general play a negligible role. A careful analysis and
interpretation of the observational data in the light of our new
modelling
of the positron processes will be performed in a follow-up work, and we
do not exclude a priori the possibility that positrons may show a preference
for some phases and/or for grain capture.
5 Summary and conclusions
The aim of this work was to carefully reexamine all the processes that
positrons undergo in the ISM, including the complicated interactions
with dust grains, and to try to determine as precisely as possible
all the quantitative factors in the problem, particularly the
various reaction rates and the widths of the lines emitted in the process.
We also included all aspects of positron interactions with molecular
hydrogen, in addition to atomic hydrogen, as well as helium (excitation,
ionization, charge exchange, direct annihilation with the bound electron,
etc.). For this we undertook a major review of the literature (cross
section measurements and calculations, etc.) and performed a detailed
Monte Carlo simulation that allowed us to obtain new, accurate results
on the fraction of positrons that form positronium in flight, the profile
and width of the line emitted in the process, the lifetimes of the
positrons in such conditions, etc. We also investigated in detail
the interstellar dust and its effect on positron annihilation.
The final results of our calculations (reaction rates and spectra) showed
that dust is only important in the hot phase of the ISM (where it
dominates
all other processes), but previous modelling efforts
(e.g. Guessoum et al. 2004) stressed the importance of this process.
There are still some pieces of the puzzle missing in this regard, for
example the widths of the lines emitted in the annihilation of
positrons/positroniums inside/outside a dust grain, the extent of
the destruction of grains in the hot/warm regions of the ISM and
also the electrostatic charge carried by dust in various conditions.
We aimed to provide solid basis for modelling the detailed
annihilation data currently being obtained by INTEGRAL-SPI
(Knodlseder et al. 2005) as well as future observations,
e.g. spectroscopic explorations of regions of the Galaxy other than the
central regions (galactic plane, compact objects / LMXBs, etc.).
Indeed, with the positron processes now much more firmly understood
and quantified, it becomes possible to compare the annihilation model
outlined here and the spectra obtained by our calculations
with the SPI data and infer useful information regarding the
regions where the annihilation is predominantly taking place. It
will also become possible to model and interpret data obtained for
more local and specific places. Finally, with the microscopic
processes now fully examined and more precisely parametrized,
it becomes possible to perform a time-dependent investigation of
the lives of positrons from their births to their ultimate
deaths/annihilations. This would then constitute a major step
towards the resolution of the "origin of positrons
in the Galaxy'' puzzle.
Acknowledgements
N. Guessoum would like to acknowledge the support of the INTEGRAL project.
The researchers and staff of the Centre d'Étude Spatiale des Rayonnements
(Toulouse, France) are thanked for their kind hospitality during the
various times when much of this work was conducted. Cliff Surko is thanked
for helpful discussions and for providing us with useful references.
- Armour, E. A.
G., Baker, D. J., & Plummer, M. 1990, J. Phys. B, 23, 3057 [NASA ADS] (In the text)
- Berakdar,
J. 1998, Phys. Rev. Lett., 81, 1393 [NASA ADS] [CrossRef] (In the text)
- Bhatia, A. K.,
Drachman, R. J., & Temkin, A. 1977, Phys. Rev. A, 16, 1719 [NASA ADS] [CrossRef] (In the text)
- Biasini, M.,
et al. 2000, J. Phys. Cond. Matter, 12, 5961 [NASA ADS] [CrossRef] (In the text)
- Book, D. L., &
Ali, A. W. 1975, NRL Memorandum Rep. 2898
(In the text)
- Britton, D.
T., Hempel, A., & Triftshauser, W. 2001, Phys. Rev. Lett., 87,
217401 [NASA ADS] [CrossRef] (In the text)
- Brown, B. L.,
Leventhal, M., Mills, A. P., Jr., & Gidley, D. W. 1984, Phys.
Rev. Lett., 53, 2347 [NASA ADS] [CrossRef] (In the text)
- Brown, B. L.,
& Leventhal, M. 1986, Phys. Rev. Lett., 57, 1651 [NASA ADS] [CrossRef] (In the text)
- Brown, B. L.,
Leventhal, M., & Mills, A. P., Jr. 1986, Phys. Rev. A, 33,
2281 [NASA ADS] [CrossRef] (In the text)
- Bussard, R.
W., Ramaty, R., & Drachman, R. J. 1979, ApJ, 228, 928 [NASA ADS] [CrossRef] (In the text)
- Campbell,
C. P., McAlinden, M. T., Kernoghan, A. A., & Walters, H. R. J.
1998, Nucl. Inst. Meth. B, 143, 41 [NASA ADS] (In the text)
- Campeanu,
R. I., & Humberston, J. W. 1977, J. Phys. B, 10, L153 [NASA ADS] (In the text)
- Chapuis, C.,
Wallyn, P., & Durouchoux, Ph. 1991, Gamma-Ray Line
Astrophysics, Proc. of the Int. Symp., Paris, France, Dec. 10-13,
1990, ed. P. Durouchoux, & N. Prantzos (New York: American
Institute of Physics), AIP Conf. Proc., 232, 54
(In the text)
- Chapuis, C.,
Wallyn, P., & Durouchoux, P. 1994, ApJS, 92, 545 [NASA ADS] [CrossRef] (In the text)
- Charlton,
M., et al. 1988, J. Phys. B, 21, L545 [NASA ADS] (In the text)
- Charlton,
M., & Humberston, J. W. 2001, Positron Physics (Cambridge
University Press)
(In the text)
- Chen, X. X., Chen,
J., & Kuang, J. 1992, J. Phys. B, 25, L5489 [NASA ADS] (In the text)
- Coleman, P.
G., et al. 1982, Can. J. Phys., 60, 584 [NASA ADS] (In the text)
- Crannell,
C. J., Joyce, G., Ramaty, R., & Werntz, C. 1976, ApJ, 210,
582 [NASA ADS] [CrossRef] (In the text)
-
Dannefaer, S., et al. 1996, J. Appl. Phys., 79, 12 (In the text)
- Dermer, C. D.,
& Murphy, R. J. 2001, in Exploring the gamma-ray universe,
Proc. of the Fourth INTEGRAL Workshop, 4-8 September 2000,
Alicante, Spain, ed. B. Battrick, Scientific editors: A. Gimenez,
V. Reglero & C. Winkler, ESA SP-459 (Noordwijk: ESA
Publications Division), 115
(In the text)
- Diana, L. M.,
Coleman, P. G., Brooks, D. L., Pendleton, P. K., & Norman, D.
M. 1986, Phys. Rev. A, 34, 2731 [NASA ADS] [CrossRef] (In the text)
- Draine, B. T.
2003, ARA&A, 41, 241 [NASA ADS] (In the text)
- Draine, B. T.
2004, Carnegie Observatories Astrophysics Series, ed. A. McWilliam,
& M. Rauch, 320
(In the text)
-
Dupasquier, A., & Mills, A. P. Jr. 1995, Positrons Solid-State
Physics, Proc. Internat. School of Physics "Enrico Fermi'', Course
CXXV, Varenna 1993 (Amsterdam: IOS Press)
(In the text)
-
Durouchoux, P., Wallyn, P., Chapuis, C., & Matteson, J. 1993,
A&AS, 97, 185 [NASA ADS] (In the text)
- Eldrup, M., et
al. 1985, Phys. Rev. B, 32, 7048 [NASA ADS] [CrossRef] (In the text)
- Ferriere,
K. 1998a, ApJ, 497, 759 [NASA ADS] [CrossRef]
- Ferriere,
K. 1998b, ApJ, 503, 700 [NASA ADS] [CrossRef]
- Ferriere,
K. M. 2001, Rev. Mod. Phys., 73, 1031 [NASA ADS] [CrossRef]
- Ferriere,
K. M. 2003, in Physique et Astrophysique du Rayonnement Cosmique,
Proc. of École de Goutelas, held 2-6 June 2003, Goutelas,
France, ed. E. Parizot, A. Marcowith, V. Tatischeff, G. Pelletier,
& P. Salati (Observatoire Astronomique de Strasbourg &
SF2A), 7
(In the text)
- Ficocelli
Varrachio, E., & Parcell, L. A. 1992, J. Phys. B, 25, 3037 [NASA ADS] (In the text)
- Fornari, L.
S., Diana, L. M., & Coleman, P. G. 1983, Phys. Rev. A, 51,
2276 [NASA ADS] (In the text)
- Fromme, D.,
Kruse, G., Raith, W., & Sinapius, G. 1986, Phys. Rev. Lett.,
57, 3031 [NASA ADS] [CrossRef] (In the text)
- Fromme, D., et
al. 1988, J. Phys. B, 21, 262 (In the text)
- Gehrels, N.,
Barthelmy, S. D., Teegarden, B. J., et al. 1991, ApJ, 375, L13 [NASA ADS] [CrossRef] (In the text)
-
Goruganthu, R. R., et al. 1985, Phys. Rev. A., 34, 103 [NASA ADS] [CrossRef] (In the text)
- Gould, R. J.
1989, ApJ, 344, 232 [NASA ADS] [CrossRef] (In the text)
- Guessoum,
N., Ramaty, R., & Lingenfelter, R. E. 1991, ApJ, 378, 170 [NASA ADS] [CrossRef] (In the text)
- Guessoum,
N., Ramaty, R., & Skibo, J. G. 1997, in The Transparent
Universe, Proc. of the 2nd INTEGRAL Workshop held 16-20 September
1996, St. Malo, France, ed. C. Winkler, T. J.-L. Courvoisier, &
Ph. Durouchoux (European Space Agency), 113
(In the text)
- Guessoum,
N., et al. 2004, in The Integral Universe, Proc. of the 5th
INTEGRAL Workshop held 16-20 February 2004, Munich, Germany, in
press
(In the text)
- Harris, M. J.,
Teegarden, B. J., Cline, T. L.,et al. 1998, ApJ, 501, L55 [NASA ADS] [CrossRef] (In the text)
- Harris, M. J.,
Teegarden, B. J., Cline, T. L., et al. 2000, Proc. of the fifth
Compton Symposium, held in Portsmouth, NH, USA, September 1999, ed.
L. Mark McConnell, & M. James Ryan (Melville, NY: American
Institute of Physics), AIP Conf. Proc., 510, 31
(In the text)
- Heitler, W.
1954, Quantum theory of radiation, International Series of
Monographs on Physics (Oxford: Clarendon), 3rd ed.
(In the text)
- Herter, T.,
Gull, G. E., Megeath, S. T., Rowlands, N., & Houck, J. R. 1989,
ApJ, 343, 696 [NASA ADS] [CrossRef] (In the text)
- Hewitt, R. N.,
Noble, C. J., & Bransden, B. H. 1992, J. Phys. B, 25, 2683 [NASA ADS] (In the text)
- Hodges, C. H.,
& Stott, M. J. 1973, Phys. Rev. B, 7, 73 [NASA ADS] [CrossRef] (In the text)
- Hofmann, et
al. 1997, J. Phys. B., 30, 3297 [NASA ADS] (In the text)
- Huttunen,
P. A., et al. 1990, Phys. Rev. B, 42, 1560 [NASA ADS] [CrossRef] (In the text)
- Iwata, K.,
Greaves, R. G., & Surko, C. M. 1996, Can J. Phys., 74, 407 [NASA ADS] (In the text)
- Iwata, K.,
Greaves, R. G., & Surko, C. M. 1997a, Phys. Rev. A, 55,
3586 [NASA ADS] [CrossRef] (In the text)
- Iwata, K., et al.
1997b, Phys. Rev. Lett., 79, 39 [NASA ADS] [CrossRef] (In the text)
- Iwata, K., et al.
2000, Phys. Rev. A, 61, 2719 [NASA ADS] (In the text)
- Jacobsen,
et al. 1995, J. Phys. B., 28, 4691 [NASA ADS] (In the text)
- Janev, R. K.,
& Solov'ev, E. A. 1998, J. Phys. B, 32, 3215 [NASA ADS] (In the text)
- Jean, P., et al.
2004, in The Integral Universe, Proc. of the 5th INTEGRAL Workshop
held 16-20 February 2004, Munich, Germany, in press
(In the text)
- Johnson, W.
N., Harnden, F. R., & Haymes, R. C. 1972, ApJ, 172, 1 [NASA ADS] [CrossRef] (In the text)
- Jones, G. O., et
al. 1993, J. Phys. B, 26, 483 [NASA ADS] (In the text)
- Kara, V. 1999,
Ph.D. Thesis, University of London
(In the text)
-
Kernoghan, A. A., et al. 1996, J. Phys. B, 29, 2089 [NASA ADS] (In the text)
- Köver, A.,
& Laricchia, G. 1998, Phys. Rev. Lett., 80, 5309 [NASA ADS] [CrossRef] (In the text)
- Köver, A.,
Paludan, K., & Laricchia, G. 2002, Nucl. Inst. Meth. B, 192,
167 [NASA ADS] (In the text)
-
Knodlseder, J., et al. 2004, A&A, in preparation
- Knudsen, H.,
et al. 1990, J. Phys. B, 23, 3955 [NASA ADS] (In the text)
- Krugel, E.
2003, The Physics of Interstellar Dust (London: The Institute of
Physics)
(In the text)
- Kwan, C. K., et al.
1998, Nucl. Inst. Meth. B, 143, 61 [NASA ADS] (In the text)
-
Leventhal, M. 1973, ApJ, 183, L147 [NASA ADS] [CrossRef] (In the text)
-
Leventhal, M., MacCallum, C. J., & Stang, P. D. 1978, ApJ, 225,
L11 [NASA ADS] [CrossRef] (In the text)
-
Leventhal, M., Barthelmy, S. D., Gehrels, N., et al. 1993, ApJ,
405, L25 [NASA ADS] [CrossRef] (In the text)
- Li, A. 2004,
Astrophysics of Dust, ed. A. N. Witt, C. Clayton, & B. T.
Draine, ASP Conf. Ser., 309
(In the text)
- Li, A., & Draine,
B. T. 2001, ApJ, 554, 778 [NASA ADS] [CrossRef] (In the text)
- Lonjou, V., et
al. 2004, in The Integral Universe, Proc. of the 5th INTEGRAL
Workshop held 16-20 February 2004, Munich, Germany, in press
(In the text)
- Makinen, J.,
et al. 1992, JPCM Lett., 4, 503 [NASA ADS] (In the text)
-
McAlinden, M. T., & Walters, H. R. J. 1992, Hyperfine
Interactions, 73, 65 (In the text)
- McKee, C. F.,
& Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] (In the text)
- Mills, A. P., et
al. 1989, Phys. Rev. B, 40, 8616 [NASA ADS] [CrossRef] (In the text)
- Milne, P. A., et
al. 2000, American Astronomical Society, HEAD Meeting #5, #40.06;
BAAS, 32, 1253
(In the text)
-
Mokrushin, A., et al. 2003, Phys. Stat. Sol., 197, 212 [NASA ADS] [CrossRef] (In the text)
- Mori, S., &
Suoeka, O. 1994, J. Phys. B., 17, 3295 (In the text)
- Moxom, J., et al.
1993, J. Phys. B, 26, 367 [NASA ADS] (In the text)
- Moxom, J.,
Ashley, P., & Laricchia, G. 1996, Can. J. Phys., 74, 367 [NASA ADS] (In the text)
-
Mukherjee, M., Chakravorty, D., & Nambissan, P. M. G. 1998,
Phys. Rev. B, 57, 848 [NASA ADS] [CrossRef] (In the text)
- Nieminen,
R. M., & Oliva, J. 1980, Phys. Rev. B, 22, 2226 [NASA ADS] [CrossRef] (In the text)
- Omidvar, K.
1965, Phys. Rev., 140, 38 [NASA ADS] [CrossRef] (In the text)
- Ore, A., &
Powell, J. L. 1949, Phys. Rev., 75, 1963 [NASA ADS] (In the text)
- Overton, N.,
Mills, R. J., & Coleman, P. G. 1993, J. Phys. B, 26, 3951 [NASA ADS] (In the text)
- Parcell, L.
A., Cheng, L.-X., Dixon, D. D., et al. 1987, J. Phys. B, 20,
2307 [NASA ADS] (In the text)
- Paul, J. 2004,
Nucl. Inst. Meth. B, 221, 215 [NASA ADS] (In the text)
- Pi, X. D., et al. 2003,
Physica B, 340, 1094 [NASA ADS] (In the text)
- Purcell, W.
R., et al. 1997, ApJ, 491, 725 [NASA ADS] [CrossRef] (In the text)
- Puska, M. J.,
& Nieminen, R. M. 1994, Rev. Mod. Phys., 66, 841 [NASA ADS] [CrossRef] (In the text)
- Ramaty, R.,
& Meszaros, P. 1981, ApJ, 25, 384 [NASA ADS] (In the text)
- Rapp, D.,
Englander-Golden, P., & Briglia, D. D. 1965, J. Chem. Phys.,
42, 4081 [CrossRef] (In the text)
-
Ratnavelu, K. 1991, Austr. J. Phys., 44, 265 [NASA ADS] (In the text)
- Rice-Evans, P.,
& Rao, K. U. 1988, Phys. Rev. Lett., 61, 581 [NASA ADS] [CrossRef] (In the text)
-
Rosenberg, I. J., Howell, R. H., & Fluss, M. J. 1987, Phys.
Rev. B, 35, 2083 [NASA ADS] [CrossRef] (In the text)
- Sasaki, et al.
2003, Radiat. Phys. Chem., 68, 569 [NASA ADS] [CrossRef] (In the text)
- Sperber, W.,
Becker, D., Lynn, K. G., et al. 1992, Phys. Rev. Lett., 68,
3690 [NASA ADS] [CrossRef] (In the text)
- Spicher, G.,
Olsson, B., Raith, W., Sinapius, G., Sperber, W. 1990, Phys. Rev.
Lett., 64, 1019 [NASA ADS] [CrossRef] (In the text)
- Stecker, F.
W. 1969, Ap&SS, 3, 579 [NASA ADS] (In the text)
- Steigman,
G. 1968, Ph.D. Thesis - New York University. Source: Dissertation
Abstracts International, 30, 01, 0324
(In the text)
- Stein, T. S., et
al. 1998, Nucl. Inst. Meth. B, 143, 68 [NASA ADS] (In the text)
- Surko, C. M., et
al. 2000, Nucl. Inst. Meth. B, 171, 2 [NASA ADS]
- Suzuki, R., et
al. 2003, Radiat. Phys. & Chem., 68, 339 [NASA ADS] (In the text)
-
Teegarden, B. J., Cline, T. L., Gehrels, N., et al. 1996, ApJ, 463,
L75 [NASA ADS] [CrossRef] (In the text)
- van Veen, A., et
al. 2004, Materials Science Forum, 445, 254 [NASA ADS] (In the text)
- Wallyn, P.,
Durouchoux, Ph., Chapuis, C., et al. 1993, ApJ, 403, 621 [NASA ADS] [CrossRef] (In the text)
- Wallyn, P.,
Durouchoux, Ph., Chapuis, C., & Leventhal, M. 1994, ApJ, 422,
610 [NASA ADS] [CrossRef] (In the text)
- Walters, H.
R. J. 1988, J. Phys. B, 21, 1893 [NASA ADS] (In the text)
- Weber, M. H.,
& Lynn, K. G. 2000, Radiat. Phys. & Chem., 58, 2000 (In the text)
-
Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] (In the text)
- Weiss, A. H., et
al. 1994, Radiat. Phys. Chem., 44, 665 [NASA ADS] [CrossRef] (In the text)
- Zhou, S., et al.
1997, Phys. Rev. A, 55, 361 [NASA ADS] [CrossRef] (In the text)
- Zurek, W. H.
1985, ApJ, 289, 603 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2454fi1a.eps}\par\includeg...
...]{2454fi1b.eps}\par\includegraphics[width=8.8cm,clip]{2454fi1c.eps}
\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg20.gif)
![\begin{figure}
\par\includegraphics[width=8.cm,height=8.cm,clip]{2454fig2.eps}
\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg24.gif)
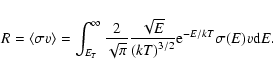
![\begin{figure}
\par\includegraphics[width=1.0\linewidth ,height=9.0cm,width=8.5cm,clip]{2454fig3.eps}
\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=11cm,clip]{2454fig4.eps}
\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg48.gif)
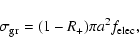
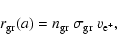
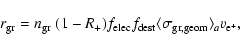
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{2454fi5a.eps}\hspace*{4mm}...
...m}
\includegraphics[width=8.3cm,clip]{2454fi5e.eps}\hspace*{8.8cm}\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg84.gif)
![$\displaystyle \int {\rm d}E' \left[ 3 \times {3 \over 4} P_{\rm t}(E') + 2 \times {1 \over 4} \delta(E'-E_0) \right]$](/articles/aa/full/2005/22/aa2454-04/img86.gif)
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{2454fig6.eps}
\end{figure}](/articles/aa/full/2005/22/aa2454-04/Timg106.gif)