A&A 436, 325-331 (2005)
DOI: 10.1051/0004-6361:20042214
A. López Ariste 1 - R. Casini 2
1 - THEMIS. C/ Vía Láctea s/n, 38200 La Laguna, Tenerife,
Spain
2 -
High Altitude Observatory, National Center for Atmospheric
Research![]() ,
PO Box 3000, Boulder, CO 80307-3000, USA
,
PO Box 3000, Boulder, CO 80307-3000, USA
Received 20 October 2004 / Accepted 28 January 2005
Abstract
We present observations of spicules in the He I D3line with
full-Stokes spectropolarimetry, which were done with the Advanced
Stokes Polarimeter at the Dunn Solar Telescope of the Sacramento Peak
Observatory. The line profiles appear to be significantly broadened
by non-thermal processes, which we interpret using the hypothesis
of a distribution of velocities inside the spicule. The possibility of
inferring the magnetic field in those conditions is tested on
synthetic data, and the results are generalized to the interpretation of
the observed data. We conclude that the magnetic field is aligned with
the visible structure of the spicule, with strengths above
![]() in some cases (for heights between 3000 and
in some cases (for heights between 3000 and
![]() above the
photosphere).
above the
photosphere).
Key words: Sun: chromosphere - Sun: magnetic fields
Spicules are extremely interesting features for several reasons. From the point of view of MHD theory, they almost certainly can be considered quasi-1D systems (De Pontieu et al. 2004; Sterling 2000), for which numerical solutions can easily be derived and then tested against observations. Spicules are also a visibly organized atmospheric structure in a region where the Sun's global field has probably rid itself of most of the local magnetic disturbances originating in the photosphere. In fact, spicules are generally organized in patterns that seem to reproduce the global distribution of magnetic field observed in the photospheric network. Whatever the mechanism driving the plasma ejection in the spicules, however, it is evident that they must be one of the main (if not the most important) contributors to the refueling of gas in the corona. Athay (2000) among others attributes to them a predominant role in the dynamics of the whole solar atmosphere, pointing also to the fact that the amount of matter ejected by spicules is so large that it ought to be compensated for by some kind of coronal rain, perhaps filling in the process other magnetic structures, like prominences. Finally, spicules are also interesting because they present a true observational challenge. The sub-arcsec size pushes the instrument capabilities to their limit, as one struggles to improve image quality while adversely affected by the high level of scattered light from the solar disk. This is particularly true if one is interested in acquiring spectropolarimetric data of these objects.
In this paper, we present spectropolarimetric observations of spicules done with the Advanced Stokes Polarimeter (ASP, Elmore et al. 1992) at the Dunn Solar Telescope (DST) of the Sacramento Peak Observatory (New Mexico). Spectropolarimetry requirements forced us to abandon any hope for image quality, so we lack, for instance, adequate control over distance to the limb. The limited spatial resolution also makes it difficult to disentangle the contributions by different spicules to the observed spectra. Despite these drawbacks, the observed spicules do show a strong signal in the He I D3 line, both in intensity and in linear polarization. Circular polarization, even when present, is always close to the noise level. The height from the limb at which we placed the spectrograph slit had to be chosen in such a way that the solar disk would never fall onto the slit because of seeing-induced image motions. For this reason, we could not observe any lower than about 5 arcsec above the limb. As limb trackers become increasingly available to stabilize the solar image along the radial direction, we should, in the near future, be able to observe spicules closer to the solar limb. Observing with an unocculted telescope that was not designed for high control of scattered light (as opposed to coronagraphs) means that we never see the upper parts of spicules.
The most obvious feature of the observed spectra in spicules, as described in Sect. 2, is the very large width of the line profiles. Any attempt to infer the magnetic field in spicules must necessarily be based on some assumption regarding the origin of such a linewidth. In this paper, we adopt the hypothesis that the only non-thermal broadening mechanism is the macroscopic distribution of velocities within the spicule. The possibility of applying our inversion procedure using this hypothesis is tested in Sects. 3 and 4. First, a database of synthetic Stokes profiles for He I D3, created by a numerical code for polarized resonance scattering in the presence of magnetic fields (López Ariste & Casini 2002), is convoluted with a Gaussian with width comparable to that of the observed profiles. Next we apply our inversion code to this broadened dataset to verify that some information on the magnetic field can still be recovered. Finally, in Sect. 5 we apply our inversion procedure to the real data.
Figure 6 shows one of the slit-jaw images in
H![]() with the slit across the spicules and the hairlines.
On the visible part of the
chromosphere a bright patch may indicate a plage region with possibly
enhanced photospheric magnetic fields. The spatial resolution does not
allow us to tell the individual spicules apart, and we are also unable
to differentiate the spicules in the plane of the sky from those
in the background or in the foreground. However, we can affirm that
most of them are inclined at about
with the slit across the spicules and the hairlines.
On the visible part of the
chromosphere a bright patch may indicate a plage region with possibly
enhanced photospheric magnetic fields. The spatial resolution does not
allow us to tell the individual spicules apart, and we are also unable
to differentiate the spicules in the plane of the sky from those
in the background or in the foreground. However, we can affirm that
most of them are inclined at about ![]() from the radial direction,
in a fashion that is well described by wheat field pattern
(Lippincot 1957; cf. Beckers 1968). The brightest feature visible in the image
was more likely a jet, since it was seen ejecting during the time
series, still following the general direction at
from the radial direction,
in a fashion that is well described by wheat field pattern
(Lippincot 1957; cf. Beckers 1968). The brightest feature visible in the image
was more likely a jet, since it was seen ejecting during the time
series, still following the general direction at ![]() from the
local vertical.
from the
local vertical.
The ASP was used in the configuration described by Casini et al. (2003), adopting a camera lens with a shorter focal length than the nominal one (Elmore et al. 1992). This setup allowed us to observe the Na I D1 and D2 lines simultaneously, along with the He I D3 line. In this paper we will describe only the D3 data. The position of the slit at approximately 5 arcsecs above the limb was set in response to a concern with image motion and in the hope of avoiding an excess of scattered light from the disk into the spectrograph, which greatly compromises the quality of the Stokes profiles during off-limb observations.
The observed profiles of He I D3 can be characterized in the first place by their significant broadening, much larger than the typical thermal broadening, which we can tentatively attribute to macroscopic velocity distributions within the spatial resolution element. The broadening also appears to be slightly asymmetric, being larger in the red wing of the line. This is likely due to the intrinsic asymmetry of the D3 multiplet, which has a larger blue component and a smaller red component (in the ratio 8:1, at the limit of optically thin plasmas). When this asymmetry is combined with the macroscopic velocity distribution of the spicules, the resulting profile will show the kind of asymmetric broadening that we see in our data. We will further discuss this broadening in the following sections.
The polarization signal is evident in Stokes Q and U![]() , whereas circular polarization
(Stokes V) is present but not very significant. In the following
sections we will discuss the possibility of extracting all possible
information on the magnetic fields of spicules from the analysis of
these polarization signals.
, whereas circular polarization
(Stokes V) is present but not very significant. In the following
sections we will discuss the possibility of extracting all possible
information on the magnetic fields of spicules from the analysis of
these polarization signals.
Before attempting an interpretation of the observed polarization signals
we must first provide a mathematical description of this broadening. We
first noticed that all the observed profiles in the collected data are
similarly broadened. In order to determine this we used a
characteristic, thermally-broadened profile with a Doppler width equivalent to
a temperature of 7500 K (as in the profile database used in López Ariste & Casini (2002)
for the inversion of prominence data). This characteristic profile,
![]() ,
was broadened according to the following algorithm,
,
was broadened according to the following algorithm,
We did not include radiative transfer effects here, so the only
account of those effects comes through the use of a convolution with
the two Gaussian velocity distributions, according to
Eq. (1). A database of broadened
synthetic profiles was then built by computing the profiles for different
Gaussian widths ![]() and
and ![]() .
These two parameters were the only
free parameters in the problem of finding an empirical fit to the observed
Stokes I profiles. We solved that inversion problem by a simple code
based on Principal
Component Analysis (PCA) (Rees et al. 2000).
The observed intensity profiles were reproduced by the
broadened profiles in a very satisfactory way. In Fig. 1 we
present a histogram of the results for the two parameters
.
These two parameters were the only
free parameters in the problem of finding an empirical fit to the observed
Stokes I profiles. We solved that inversion problem by a simple code
based on Principal
Component Analysis (PCA) (Rees et al. 2000).
The observed intensity profiles were reproduced by the
broadened profiles in a very satisfactory way. In Fig. 1 we
present a histogram of the results for the two parameters ![]() and
and ![]() that were allowed to vary in the inversion and
see that both histograms peak very nicely at around a
FWHM of the Gaussian of roughly 50 km s-1.
that were allowed to vary in the inversion and
see that both histograms peak very nicely at around a
FWHM of the Gaussian of roughly 50 km s-1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2214fig1.ps}
\end{figure}](/articles/aa/full/2005/22/aa2214-04/Timg17.gif) |
Figure 1: Histograms of the FWHM of the two Gaussians weighting the blue- (thick line) and red-shifted (thin line) contributions as inferred from inversion of the observed He D3 intensity profiles. |
The equations of the polarized emission of the He I D3 line, following the single-scattering approximation used for our inversion, are given, e.g., by López Ariste & Casini (2002), where we also discuss the limits of neglecting radiative transfer for magnetic inversion. For this problem, we created a database of Stokes profiles of He I D3 that covers all possible directions of the magnetic field vector and a range of field strengths up to 100 G. The number of free parameters entering the database creation is 6:3 for the vector field, 2 for the scattering geometry, and 1 for the velocity parameter introduced in the previous section. As discussed by López Ariste & Casini (2002), adopting a regular grid over the parameter space to build a database of Stokes profiles is not efficient. First of all, the resulting database would be unmanageably large. At the same time, many models would be redundant because of intrinsic ambiguities of the Hanle and Zeeman effect and because of the reduced sensitivity of the Stokes profiles in certain ranges of the model parameters. The solution proposed in that paper is to create the database through a Montecarlo iterative procedure, in which models with randomly selected parameters are first proposed and the corresponding synthetic Stokes profiles are then compared with those already accumulated in the database. If the last computed set of Stokes profiles is too similar to one already existing in the database, then it is rejected. Otherwise it is added to the database. The similarity criterium is based on PCA considerations (López Ariste & Casini 2002). A database thus built does not contain redundant models and, at the same time, keeps typically a manageable size.
For the particular problem of this paper, the selected database from the
inversion of
prominences was broadened using Eq. (1) with
![]() ;
and we attempted to
invert this modified database with the original, unbroadened
database. This is the best case possible, since the actual models for
each individual case are present in the original database.
Figures 2 and 3 show the results of this
inversion for the azimuth and inclination in the line-of-sight (LOS)
reference frame
;
and we attempted to
invert this modified database with the original, unbroadened
database. This is the best case possible, since the actual models for
each individual case are present in the original database.
Figures 2 and 3 show the results of this
inversion for the azimuth and inclination in the line-of-sight (LOS)
reference frame![]() ,
and for the field strength.
,
and for the field strength.
From the inversion histograms we see that the azimuth in the LOS
reference frame is still fairly well recovered, in spite of the increased
inversion errors that are in most cases below ![]() from the
true solution (the
from the
true solution (the ![]() ambiguity is easily distinguished in
the histogram as a secondary peak). Information on the inclination
of the magnetic field, instead, is almost completely lost in the
broadening process, with error bars around
ambiguity is easily distinguished in
the histogram as a secondary peak). Information on the inclination
of the magnetic field, instead, is almost completely lost in the
broadening process, with error bars around ![]() .
The
field-strength information also seems to be lost at first glance.
However, error increases with the field
strength (right plot in Fig. 3), which allows us to
conclude that the inversion should still
be able to tell the presence of weak fields in spicules, as they would
be inverted with comparably weak (or at most average) fields. As an
example, for a true field-strength of
.
The
field-strength information also seems to be lost at first glance.
However, error increases with the field
strength (right plot in Fig. 3), which allows us to
conclude that the inversion should still
be able to tell the presence of weak fields in spicules, as they would
be inverted with comparably weak (or at most average) fields. As an
example, for a true field-strength of ![]() ,
the inversion code will
not, on average, retrieve solutions above
,
the inversion code will
not, on average, retrieve solutions above ![]() .
On the other
hand, the inversion solution corresponding to a true strong field
could fall anywhere within the magnetic field range accessible to the
inversion code.
.
On the other
hand, the inversion solution corresponding to a true strong field
could fall anywhere within the magnetic field range accessible to the
inversion code.
From the previous tests we can expect the inversion code to
provide information on the azimuth of the field in the LOS reference
frame. We can also expect to tell the following two cases apart: those in
which only weak fields
(under ![]() )
are present in spicules and those in which strong fields
can also be found. If strong fields are
retrieved, however, we cannot say much about the possible presence of
weak fields.
)
are present in spicules and those in which strong fields
can also be found. If strong fields are
retrieved, however, we cannot say much about the possible presence of
weak fields.
Before applying the inversion code to real data, we want to comment
on the results of another test performed on the broadened, synthetic
profiles. A common feature of our real data is that the Stokes-Vsignals have small amplitudes compared to observation noise, and
they also appear very distorted. As a consequence, one can expect that
these signals will not contribute significantly to the inversion
process. It is well known (López Ariste & Casini 2002; Brown et al. 2003) that neglecting Stokes V in
the polarization analysis of He I D3 increases the inversion
errors for both field strength and geometry. However, we also find
that this introduces new ambiguities into the inversion results.
Specifically, we find ![]() ambiguity in the inverted values of
the field azimuth in the LOS reference frame (Casini et al. 2005).
ambiguity in the inverted values of
the field azimuth in the LOS reference frame (Casini et al. 2005).
In Fig. 4 we see that this ambiguity is not as prominent in
the inversion error histograms as the one at ![]() ,
but it still
can determine perpendicular solutions for the direction of the magnetic
field in the plane of the sky, whenever Stokes V is not significant.
,
but it still
can determine perpendicular solutions for the direction of the magnetic
field in the plane of the sky, whenever Stokes V is not significant.
For the azimuth of the field in the LOS frame of reference, we limited
the possible range between ![]() and
and ![]() ,
thus avoiding the
problem of
,
thus avoiding the
problem of ![]() ambiguity. Because of this ambiguity, the azimuth
values will only indicate direction of the projection of the field
on the plane of the sky, but not its polarity.
ambiguity. Because of this ambiguity, the azimuth
values will only indicate direction of the projection of the field
on the plane of the sky, but not its polarity.
We also observe the presence of the additional ![]() ambiguity in
our results, which we attribute to the small significance of Stokes Vin our data (see previous section). Therefore, the field is either
aligned with the projected axis of the spicule on the plane of the sky, or
perpendicular to it.
ambiguity in
our results, which we attribute to the small significance of Stokes Vin our data (see previous section). Therefore, the field is either
aligned with the projected axis of the spicule on the plane of the sky, or
perpendicular to it.
Figure 5 shows the distribution of inclination ![]() and azimuth
and azimuth ![]() of the magnetic field in the LOS reference frame for the inverted data.
We opted for the LOS reference frame, because in it the 90
of the magnetic field in the LOS reference frame for the inverted data.
We opted for the LOS reference frame, because in it the 90![]() ambiguity is more easily grasped (see the appendix), and in fact we
notice the presence of two groups of solutions
roughly centered at
ambiguity is more easily grasped (see the appendix), and in fact we
notice the presence of two groups of solutions
roughly centered at
![]() in
Fig. 5.
In the appendix, we show the regions of the
in
Fig. 5.
In the appendix, we show the regions of the
![]() plane
that can be subject to the
plane
that can be subject to the ![]() ambiguity. We then see that the
dense cluster around
ambiguity. We then see that the
dense cluster around
![]() corresponds
to solutions that are mostly unambiguous. This is not the case for the
cluster around
corresponds
to solutions that are mostly unambiguous. This is not the case for the
cluster around
![]() ,
which instead
is mapped via the
,
which instead
is mapped via the ![]() ambiguity onto the lower part of the
leftmost group of solutions.
For the
ambiguity onto the lower part of the
leftmost group of solutions.
For the ![]() ambiguous solutions, we arbitrarily selected the
value of
ambiguous solutions, we arbitrarily selected the
value of ![]() that approximately aligns the projection of the magnetic
field on the plane of the sky with the observed spicule. However, we must
keep in mind that an ambiguous solution giving a field
approximately perpendicular to the axis of the spicule cannot be
excluded a priori on the basis of the observations.
that approximately aligns the projection of the magnetic
field on the plane of the sky with the observed spicule. However, we must
keep in mind that an ambiguous solution giving a field
approximately perpendicular to the axis of the spicule cannot be
excluded a priori on the basis of the observations.
Figure 6 shows Exposure # 19 as a sample of our data. We
plotted the inverted solution for the plane-of-the-sky projection of the magnetic
field over a slit-jaw image in H![]() .
Each solution vector field
corresponds to the spicular feature behind the slit at the same
horizontal position. The brightness of each segment
is proportional to the intensity brightness of the feature in the core
of the He I D3 line, thus
makin identification of the various structures easier. The
length of the segments is proportional to the inverted field strength.
Inclination of the segments with respect to the vertical
(perpendicular to the slit) is the azimuth
.
Each solution vector field
corresponds to the spicular feature behind the slit at the same
horizontal position. The brightness of each segment
is proportional to the intensity brightness of the feature in the core
of the He I D3 line, thus
makin identification of the various structures easier. The
length of the segments is proportional to the inverted field strength.
Inclination of the segments with respect to the vertical
(perpendicular to the slit) is the azimuth
![]() .
Because the error bars in the inverted values of
.
Because the error bars in the inverted values of ![]() are well below
10 degrees, we can conclude that the presence of magnetic fields roughly
aligned with the observed structures (or perpendicular to them!) is the
most reliable conclusion drawn from our data.
are well below
10 degrees, we can conclude that the presence of magnetic fields roughly
aligned with the observed structures (or perpendicular to them!) is the
most reliable conclusion drawn from our data.
As anticipated, the error bars on the magnetic strength are much larger, as they grow proportionally to the strength, so the inferred values cannot be considered very significant. A better picture of the distribution of magnetic strengths in our inverted data is shown in Fig. 7. Retrieval of strong fields in our inversion indicates that such fields must actually be present at a statistically significant level, because weaker fields, which are affected by proportionally smaller errors, cannot produce the polarization signature that the inversion algorithm attributes to the stronger fields. Statistically, strong fields above 30 G (and probably 40 G too) must therefore be present in spicules, although they may happen to occur only in a minority of cases. In particular, because of the large error bars, we cannot tell if, for any specific point in our data, a large value of the inverted strength actually corresponds to the presence of such strong field at that point. In contrast, small values of inverted strengths are more reliable.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2214fig7.ps} %\end{figure}](/articles/aa/full/2005/22/aa2214-04/Timg35.gif) |
Figure 7: Distribution of field strengths from inversion of the Stokes parameters plotted in 5 G bins. |
To compare the range of magnetic field strengths in spicules determined from our observations with typical field strengths adopted in MHD simulations of these structures we considered two of the most recent papers, among the few references in the literature on spicule modeling that report on the field strength values adopted for the numerical model. In the paper by De Pontieu et al. (2004), the magnetic field decreases from 1600 G in the photosphere to 120 G in the corona, above the spicules. Despite the title of that paper, it is clear that the authors refer mostly to fibrils that arise from active regions, rather than to quiet sun spicules. It is not clear to us if the model would lead to formation of spicules even for the weaker magnetic strengths inferred from our observations.
In James et al. (2003) on the numerical simulation of Alfvén waves generating and supporting spicules, the authors compute maximum spicule heights for different magnetic fields in the corona, and for several different wave periods from 2 to 10 s. Our inferred field strengths hardly allow coronal field strengths that reach a 20 G value, which seems right at the limit of what those authors would need to reproduce spicule heights. On the other hand, the spicule heights that they compute for 10 G coronal fields, which seems a more appropriate value for the range of field strengths in spicules that we inferred, appear to be too low compared to observed spicular heights.
Finally, all these works mostly assume magnetic fields aligned with the
spicular structures. However, from our
observations of He I D3 in spicules and because of the ![]() ambiguity,
we cannot exclude the possibility of a magnetic field
transversal to the spicule axis. Such transversal fields could be of
interest to explain those velocity fields we needed to introduce in order to
reproduce the anomalous broadening of the observed profiles.
ambiguity,
we cannot exclude the possibility of a magnetic field
transversal to the spicule axis. Such transversal fields could be of
interest to explain those velocity fields we needed to introduce in order to
reproduce the anomalous broadening of the observed profiles.
The validity of the second hypothesis is not tested, but is
equivalent to assuming that the magnetic topology and irradiation
conditions are identical in the emitting plasma independently of its
velocity, which is questionable for plasma that is frozen onto the
magnetic field lines. Tests run with synthetically broadened data
show that, despite broadening, the inversion code is still able
to infer the direction of the projection
of the field on the plane of the sky with relatively good precision,
apart from the ![]() ambiguity that can affect particular magnetic inclinations. Tests also
show that, although the field strength information is lost because of
the very large line broadening, the maximum inversion errors appear to be
proportional to the true field strength. Therefore, if only weak fields
are present in the spicules, the inversion code will on average retrieve the
correct order of magnitude of the field. If instead
strong fields are also present, statistically the inversion code will
invert them with both small and large inverted values of the field
strength.
ambiguity that can affect particular magnetic inclinations. Tests also
show that, although the field strength information is lost because of
the very large line broadening, the maximum inversion errors appear to be
proportional to the true field strength. Therefore, if only weak fields
are present in the spicules, the inversion code will on average retrieve the
correct order of magnitude of the field. If instead
strong fields are also present, statistically the inversion code will
invert them with both small and large inverted values of the field
strength.
We analyzed the data of 35 exposures of spicules at an approximate
height of 5 arcsec above the limb taken with the ASP at the DST of the
Sacramento Peak Observatory. The results suggest that the magnetic field
in spicules is aligned with the axis of the observable structures in
intensity. A ![]() ambiguity
that cannot be resolved with the present data also allows for solutions
presenting a magnetic field transversal to those structures. We chose the
first set of solutions with an aligned magnetic field with which
theoretical models
may agree better, but we stress that from the point of view of
spectropolarimetry the transversal solution is also valid.
Finally, we could infer that fields of the order of 40 G are likely to be
present in spicules, although weaker fields (10 G) are probably more
common. The inferred fields seem to be on the lower boundary of the
acceptable range of field strengths for most of the present spicule models.
ambiguity
that cannot be resolved with the present data also allows for solutions
presenting a magnetic field transversal to those structures. We chose the
first set of solutions with an aligned magnetic field with which
theoretical models
may agree better, but we stress that from the point of view of
spectropolarimetry the transversal solution is also valid.
Finally, we could infer that fields of the order of 40 G are likely to be
present in spicules, although weaker fields (10 G) are probably more
common. The inferred fields seem to be on the lower boundary of the
acceptable range of field strengths for most of the present spicule models.
Equations (A1a-d) in Casini (2002) give explicit expressions
of the emission in the four Stokes parameters for the case under study.
The saturated regime of the Hanle effect is defined by the condition
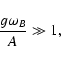 |
(A.1) |
| |
(A.2) | ||
| (A.3) |
In this regime, the 180![]() ambiguity appears naturally in the
factor 2 that multiplies the azimuth
ambiguity appears naturally in the
factor 2 that multiplies the azimuth ![]() in all the expressions.
We further realize that a 90
in all the expressions.
We further realize that a 90![]() change in
change in ![]() introduces only
a change of sign in all expressions, which can be masked
by a sign change of the factor
introduces only
a change of sign in all expressions, which can be masked
by a sign change of the factor
![]() ,
which
may occur for a different geometry of the magnetic field. One realizes
that this is not possible for all azimuths. Figure A.1 shows
the domain
,
which
may occur for a different geometry of the magnetic field. One realizes
that this is not possible for all azimuths. Figure A.1 shows
the domain
![]() where the ambiguity can occur. Two solutions
that are
where the ambiguity can occur. Two solutions
that are ![]() apart in
apart in ![]() are ambiguous (in the sense of the
are ambiguous (in the sense of the
![]() ambiguity) only if the corresponding value of the Z function is the same
(i.e., identical color in the contour plot).
ambiguity) only if the corresponding value of the Z function is the same
(i.e., identical color in the contour plot).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2214fig8.ps}
\end{figure}](/articles/aa/full/2005/22/aa2214-04/Timg49.gif) |
Figure A.1:
Contour plot of function
|
This ambiguity is inevitable if there is no independent manner of
determining the sign of the
![]() factor.
In principle, in the case of the saturated regime of the Hanle effect,
this is achieved by means of full spectropolarimetric observations,
therefore acquiring data in all four Stokes parameters I, Q, U,
and V. If Stokes V is not observed, the 90
factor.
In principle, in the case of the saturated regime of the Hanle effect,
this is achieved by means of full spectropolarimetric observations,
therefore acquiring data in all four Stokes parameters I, Q, U,
and V. If Stokes V is not observed, the 90![]() ambiguity
becomes inevitable. In fact, since in practice we never model the
true amplitude of Stokes I (i.e., with relative, rather than
absolute, spectropolarimetry), the full Stokes vector of one line is not
sufficient to completely avoid 90
ambiguity
becomes inevitable. In fact, since in practice we never model the
true amplitude of Stokes I (i.e., with relative, rather than
absolute, spectropolarimetry), the full Stokes vector of one line is not
sufficient to completely avoid 90![]() ambiguity.
In the depolarization regime of the Hanle effect, when the
field strength is such that
ambiguity.
In the depolarization regime of the Hanle effect, when the
field strength is such that
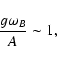 |
(A.4) |
After extrapolating these results to the case of the He D3 line, we
conclude that the presence of the two components and
observation of Stokes V typically mean one is able to resolve this
90![]() ambiguity (e.g., in quiescent prominences; see
López Ariste & Casini 2002 and Casini et al. 2003). In the case of spicules, however,
the broadening of the observed profiles implies that the two
components of the line are indistinguishable. At the same time,
Stokes V profiles are
driven too near to noise level in almost any configuration, thus
diminishing their relevance to the problem. It is thus not
surprising that we see the 90
ambiguity (e.g., in quiescent prominences; see
López Ariste & Casini 2002 and Casini et al. 2003). In the case of spicules, however,
the broadening of the observed profiles implies that the two
components of the line are indistinguishable. At the same time,
Stokes V profiles are
driven too near to noise level in almost any configuration, thus
diminishing their relevance to the problem. It is thus not
surprising that we see the 90![]() ambiguity affecting the
inversion of our data under these conditions.
ambiguity affecting the
inversion of our data under these conditions.