A&A 436, 47-56 (2005)
DOI: 10.1051/0004-6361:20041763

Clumpy tori around active galactic nuclei

C. P. Dullemond - I. M. van Bemmel[*]


1 - Max Planck Institut für Astrophysik, PO Box 1317, 85741 Garching, Germany
2 - Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA

Received 30 July 2004 / Accepted 18 January 2005

Abstract
We discuss the question whether the matter in dusty tori around active galactic nuclei has a smooth or a clumpy structure. Nenkova et al. (2002, ApJ, 570, L9) have argued that the lack of emission feature in the SEDs of type 1 AGN galaxies combined with a clear absorption feature in type 2 AGN can be explained if the circumnuclear dust is distributed in discrete clumps. Our aim is to verify this. We use multi-dimensional radiative transfer models of smooth and clumpy tori, and compare the SEDs of equivalent smooth and clumpy models. We find that the 10 $\mu $m emission feature of the clumpy models, when seen almost face-on, is not appreciably reduced compared to the equivalent smooth models. Some of the clumpy models have a weak or even absent 10 $\mu $m feature, but so do some of the smooth models. On the whole the SEDs of clumpy and smooth tori are similar, but some details are different. The absorption feature seen at edge-on inclinations appears to be less deep in the clumpy models than in the smooth models, and the average flux in the near-infrared regime is stronger in the clumpy models. Moreover, at these inclinations the clumpy models have a slightly wider SED. Whether these differences are unique enough to be used as a diagnostic for clumpiness of AGN tori is not yet clear.

Key words: galaxies: active - galaxies: nuclei - galaxies: Seyfert

1 Introduction

According to the unification principle of active galactic nuclei (AGN), the intrinsic difference between a Seyfert 1 and a Seyfert 2 galaxy (for the radio-quiet AGN) or between a narrow-line radio galaxy and a radio quasar (for radio-loud AGN) is merely a question of orientation (Antonucci & Miller 1985; Barthel 1989; see review by Antonucci 1993). The leading hypothesis is that the central engine, an accreting super-massive black hole, is surrounded by a geometrically and optically thick torus of dust and gas with an equatorial visual optical depth much larger than unity. When viewed face-on, the source would look like a type 1 active galaxy, e.g. a Seyfert 1 or a quasar, and when viewed edge-on, it would have the characteristics of a type 2 active galaxy, e.g. a Seyfert 2 or a narrow-line radio galaxy. From this unification model it follows that the dust in the circumnuclear torus emits strongly in the infrared, due to the irradiation by the central source. Indeed, the predicted infrared emission from multi-dimensional continuum radiative transfer models for such tori is reasonably well in agreement with the observed infrared radiation from such active nuclei (Pier & Krolik 1993; Efsthathiou & Rowan-Robinson 1995; Granato, Danese & Francheschini 1997; van Bemmel & Dullemond 2003, henceforth vBD03). Moreover, various other differences between Seyfert 1/Seyfert 2 and between quasar/radio galaxy can be explained in terms of such a torus model. For instance, the measured polarized (i.e. reflected) nuclear emission in type 2 sources proves that an active nucleus is present even though no direct emission is observed (Antonucci & Miller 1985; Pier et al. 1994).

In spite of the success of the obscuring torus model, there are a number of unsolved problems with this scenario. The most troubling problem originates from the fact that, in order to have a hydrostatically supported geometrically thick torus around a supermassive black hole, the temperature of the torus must be of the order of 106 K or more. Dust in such a hot torus would not survive long, yet dust signatures are observed to be present, such as a pronounced mid- to far-infrared thermal bump and 10 $\mu $m Si-O stretching band of silicate in absorption in type 2 sources. Various solutions have been proposed in the past. Pier & Krolik (1992, henceforth PK92) suggested that radiation pressure within the torus may be enough to support it. Dopita et al. (1998), on the other hand, put forward the scenario that the torus is a slowly rotating free-falling "envelope'', that circularizes at the centrifugal radius where it feeds the accretion disk around the black hole. Another scenario, first suggested by Krolik & Begelman (1988), is that the torus in fact consist of a large number of optically thick clumps orbiting around the central engine and experiencing regular collisions with other clumps. More recently it was shown that a nuclear starburst could provide enough energy input into the torus via supernovae, that the torus can keep up its scale height and has a "sponge'' like structure (Wada & Norman 2002). All of these scenarios have their strengths and problems, and the issue is still subject of debate (e.g. Vollmer et al. 2004).

In spite of lack of detailed knowledge about the structure of the torus, several studies have tried to describe its emission properties, using radiative transfer modeling of smooth tori (PK02; Efsthathiou & Rowan-Robinson 1995, henceforth ERR95; Granato & Danese 1994, henceforth GD94; vBD03). They encountered two major problems in matching the torus emission models to the observations. First, many of the model spectral energy distributions (SEDs) were too narrow to fit the observed broad mid- and far-infrared SEDs in active galaxies. This can either be related to the presence of alternative infrared emission mechanisms, but it has also been shown that the adopted radius of the torus affects the width of the resulting SED (vBD03).

A second, and still largely unsolved, issue is that the 10 $\mu $m silicate feature is often observed in absorption in type 2 sources, but has never been observed in emission in either type 1 or 2 sources. Radiative transfer models of smooth tori tend to predict a clearly measurable 10 $\mu $m feature in emission for type 1 sources (PK92, GD94, ERR95). However, Laor & Draine (1993) and vBD03 have shown that with larger grains dominating the grain-size distribution the 10 $\mu $m feature is absent in type 1's. Recently, Nenkova et al. (2002, henceforth NIE02) proposed a different explanation: they suggest that clumpy tori - and only clumpy tori - naturally have these desired properties. Their claim is based on a model for a single clump irradiated by the central engine and by neighboring clumps. A statistical generalization of this single-clump model to a clumpy torus is made, and the SED computed. The clump optical depth is taken as a global parameter. They find that if their clump optical depth exceeds 60, and the typical distance between clumps increases proportionally to radius, then the behaviour of their clumpy model is in better agreement with the observations than smooth torus models when it comes to the 10 $\mu $m feature. Relatively few clumps (typically $\sim$5) are needed in the line of sight. In addition to this, they find that the SED of such a configuration is relatively wide, in accordance with observations.

While the properties of the clumpy torus model of NIE02 are attractive, their model is highly approximative. First of all, their single-clump model was computed using a 1-D radiative transfer code, even though the main source of irradiation of the clumps near the dust evaporation radius is clearly one-sided and requires at least a 2-D axisymmetric approach. Secondly, their statistical approach to the generalization from one clump to an ensemble of clumps may be correct, but remains unproven.

Table 1: Overview of parameters and results of the smooth models. Columns from left to right: model number, powerlaw index pfor $\rho (R)\propto R^p$, grain size distribution (either $0.25~\mu$m or MRN distribution), temperature decoupling between silicate and carbon grains, inclusion of scattering opacity, the resulting SED widths \ensuremath {{\cal W}_1} (for $i=20^{{\rm o}}$) and \ensuremath {{\cal W}_2} (for $i=90^{{\rm o}}$), the resulting 10 $\mu $m feature strengths \ensuremath {{\cal S}_1} (for $i=20^{{\rm o}}$) and \ensuremath {{\cal S}_2} (for $i=90^{{\rm o}}$) and the resulting anisotropy parameter \ensuremath {{\cal I}}. See text for definition of \ensuremath {{\cal W}_1}, \ensuremath {{\cal W}_2}, \ensuremath {{\cal S}_1}, \ensuremath {{\cal S}_2} and \ensuremath {{\cal I}}.

In this paper we take a first step toward a more self-consistent model and we will test the claim by NIE02 that infrared observations of active galaxies point to a clumpy torus. In order to do so, we model the clumpy torus as a whole, using a multi-dimensional Monte-Carlo radiative transfer program called RADMC. Since RADMC can only handle axisymmetric problems (i.e. 2-D problems in R and $\Theta$), our "clumps'' are in reality rings around the polar axis. While this setup does not constitute a realistic 3-D clumpy torus, it does have many of the characteristics of such a torus: clumps can cool by radiating in all directions, radiation can move freely between clumps and there are high density constrasts. We therefore believe that this is a good first step toward an understanding of the properties of clumpy tori.

Our goal is to make a direct comparison between smooth models and clumpy models with the same global physical parameters. If clumpiness has a profound influence on the SED of a torus, this comparison should yield distinct differences between the 10 $\mu $m feature and overall width of smooth and clumpy torus models. The distribution of the clumps is random, but on average the distribution of matter of the clumpy torus is the same as in the smooth torus. Following NIE02 we assume that all clumps have the same optical depth.

2 Model setup

We solve the problem of continuum radiative transfer through a dust density distribution around an active nucleus of luminosity $L_{{\rm agn}}=1\times 10^{11}~L_{\odot}$. The spectral shape of the nuclear emission is taken to be that used in the models of GD94, but the precise spectral shape does not have a major effect on the results of model. The distribution of dusty matter around the nucleus is modeled on a computational grid based on spherical (polar) coordinates R, $\Theta$ and $\Phi$. Since our radiative transfer program RADMC can only handle axially symmetric density distributions, the model setup depends only on R and $\Theta$. In addition to this, we assume mirror symmetry in the equatorial plane located at $\Theta=\pi/2$, i.e. we only model the domain $0\le \Theta \le \pi/2$. The radial grid is logarithmically spaced, i.e. it has a constant  $\Delta R/R$. Such a grid ensures proper spatial resolution over a wide range of radii, so that a torus with large ratio of outer over inner radius can be modeled without resolution problems. The $\Theta$ grid is linearly spaced. In order to properly resolve the clumps we need a high spatial resolution of our grid. We have 356 R-grid points from the inner to the outer radius and we have 120 $\Theta$-grid points from pole to equatorial plane.

Our global torus setup is kept very simple. The density  $\rho_{{\rm s}}(R,\Theta)$ for the smooth torus setup is a powerlaw function of R, and is constant with $\Theta$ within a certain domain:

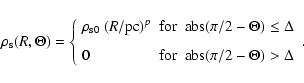\begin{displaymath}\rho_{{\rm s}}(R,\Theta) = \left\{\begin{array}{ll} \rho_{{\r... ...r} ~~ {\rm abs}(\pi/2-\Theta)> \Delta \\ \end{array}\right. . \end{displaymath} (1)

The quantity $\Delta$ is the geometric thickness of the torus. This parameter determines the overall luminosity of the infrared emission of the torus, but it has only weak effect on the shape of the SED. In this paper we shall take it fixed at $\Delta=\pi/4$, corresponding to an opening angle of 45 degrees. As inner- and outer radius we take, rather arbitrarily, 0.3 and 10 parsec respectively. The effect of varying inner and outer radius is described in detail in vBD03. Choosing these values differently will affect the width of the SED, but not so much the 10 $\mu $m feature. After optimizing the other model parameters, the inner and outer radius can be adjusted to tune the width of the SED and $\Delta$to tune to luminosity, in order to match observations. Many of the additional effects of the geometry of the torus have been described already by vBD03 and by others (e.g. ERR95; GD04), so we do not need to repeat all of them here.

We present four smooth torus and sixteen clumpy models in this paper. For each smooth model there are four clumpy models with the same global physical parameters. Two of the clumpy models have 40 clumps, and two have 20 clumps. The only difference between the pairs of clumpy models with identical number of clumps are the random positions of the clumps in $R,\Theta$. The smooth models will be used as benchmarks against which the clumpy models can be compared. In this paper we will focus on the effect of the radial powerlaw p of the density distribution ( $\rho\propto R^p$), and study the effect of thermal decoupling between silicate and graphite grains.

2.1 Smooth torus description

An overview of the smooth models is given in Table 1. All models assume a 50% carbon and 50% graphite mixture for the dust. For the silicate opacity we use the optical constants of Laor & Draine (1993). The optical constants for amorphous carbon were taken from Preibisch et al. (1993). All models have a total dust mass in the torus of $2\times 10^6~M_{\odot}$. We vary p between 0 and -1. We also vary the dust properties: on the one hand we use thermally coupled 0.25 $\mu $m sized silicate and carbon grains without scattering (the scattering opacity taken to be zero); on the other hand we use a distribution of Galactic (MRN) dust between 0.005 and 1 $\mu $m with a treatment of scattering (albeit in isotropic approximation). A standard MRN distribution only extends up to 0.25 $\mu $m, but we chose to extend it to 1 $\mu $m to maximize any possible effects of such a distribution compared to the single-grain-size models. It should be noted that we have only introduced a thermal decoupling between the carbon and silicate grains, but not between the different sizes of the MRN distribution, since the latter would be very computationally expensive, in particular for the high spatial grid resolution required for the clumpy models described below. We do not expect this to have much effect, since grains up to 1 $\mu $m size all have the same 10 $\mu $m feature shape. But future modeling will have to verify this.

Table 2: Overview of the model parameters and results of the clumpy models. Columns from left to right: model number, powerlaw index p for $\rho (R)\propto R^p$, number of clumps, grain size distribution (either $0.25~\mu$m or MRN distribution), temperature decoupling between silicate and carbon grains, inclusion of scattering opacity, optical depth of the clumps, the resulting width \ensuremath {{\cal W}_1} of the face-on SED, \ensuremath {{\cal W}_2} for the edge-on SED, the resulting 10 $\mu $m feature strength \ensuremath {{\cal S}_1} for the face-on SED and \ensuremath {{\cal S}_2} for the edge-on SED and the resulting anisotropy parameter \ensuremath {{\cal I}}. See text for definition of \ensuremath {{\cal W}_1}, \ensuremath {{\cal W}_2}, \ensuremath {{\cal S}_1}, \ensuremath {{\cal S}_2} and \ensuremath {{\cal I}}. The optical depth of the clumps follows from the number of clumps, the distribution of clumps and the total mass of the torus, and is therefore not an independent parameter of the model, hence the separated column for the optical depth.

2.2 Clumpy torus description

An overview of the clumpy models is given in Table 2. For the clumpy torus models we start from the smooth torus models S1$\cdots$S4, and contract the matter into discrete annular clumps randomly positioned on the R,$\Theta$ computational grid. The random positions are distributed such that on average the density is the same as that of the equivalent smooth torus. Following NIE02 we take the optical depth of the clumps to be a global parameter of the model. Another global parameter is the relative size of the clumps compared to R, i.e.  $\sigma\equiv {\rm size}/R$. This means that the size of the clumps scales with distance from the black hole. For the models presented in this paper we take this constant to be $\sigma=0.025$. Ideally we would wish to model smaller clumps (and more of them), but technical limitations of the resolution of our computational domain also limit the minimum size of our clumps, since it is important that all clumps are well resolved by the grid.

We present two pairs of clumpy models to match each smooth torus model, the clumpy models are numbered accordingly, i.e. C1 equals S1, etc. Between the pairs of clumpy models, only the number of clumps is varied, which we denote with suffices a and b, the a-series always having 40 clumps and the b-series having 20. Within the pairs we vary the random distribution of the clumps, allowing us to also study the effect of randomness on the resulting SED. This is denoted with the number following suffix a or b.

The matter within each individual clumps is distributed as follows:

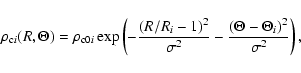\begin{displaymath}\rho_{{\rm c}i}(R,\Theta) = \rho_{{\rm c0}i} \exp\left(-\fra... ...-1)^2}{\sigma^2}-\frac{(\Theta-\Theta_i)^2}{\sigma^2}\right) , \end{displaymath} (2)

where i stands for clump number i.

2.3 SED generation

Once the clumps are put onto the computational domain, and the density distribution $\rho(R,\Theta)$ is set up, the continuum radiative transfer problem is solved using a Monte-Carlo program called RADMC (Dullemond & Dominik 2004), which uses an improved version of the original algorithm of Bjorkman & Wood (2001). This program solves the transport of continuum radiation and the local thermal equilibrium of the dust grains, thus obtaining the temperature of the dust everywhere on the grid. The SED at inclinations of 20, 70, and 90 degrees are then computed using a ray tracing code. We choose $i=20^{{\rm o}}$ to be the representative inclination for type 1 (face-on) AGN since with our sharp inner edge setup a perfect $i=0^{{\rm o}}$ inclination would produce an artificially low near-infrared flux because one would look perfectly along the inner edge. The representative inclination for type 2 (edge-on) AGN is chosen to be $i=90^{{\rm o}}$.

3 Results and analysis

In this section we present the results of the model calculations. We present figures of the SEDs at different inclination angles. We analyze our results using quantitative numbers for the width  \ensuremath{{\cal W}} of the SED ( \ensuremath {{\cal W}_1} for face-on and \ensuremath {{\cal W}_2} for edge-on), the strength \ensuremath{{\cal S}} of the 10 $\mu $m feature ( \ensuremath {{\cal S}_1} for face-on and \ensuremath {{\cal S}_2} for edge-on) and the anisotropy parameter \ensuremath {{\cal I}}. Following PK92 and GD94 we define the width \ensuremath{{\cal W}} (i.e.  \ensuremath {{\cal W}_1} and \ensuremath {{\cal W}_2}) of the SED as the 10-log of the frequency range in which the spectrum is more than 1/3 of its peak value. In $\nu F_{\nu }$; for a pure blackbody spectrum this value is \ensuremath{{\cal W}} =0.686, but observations indicate that the SED of active galaxies is generally much wider.

The feature strength \ensuremath{{\cal S}} (i.e.  \ensuremath {{\cal S}_1} and \ensuremath {{\cal S}_2}) is defined as the e-log of the peak-over-continuum ratio of the feature for face-on inclinations. Here an e-log is used, allowing a direct comparison to previous studies (GD94, Laor & Draine 1993). Following GD94 the continuum is defined by a powerlaw connecting the fluxes at 6.8 and 13.9 $\mu $m. A positive value of \ensuremath{{\cal S}} means the 10 $\mu $m feature is in emission, a negative value means absorption.

Finally we define the isotropy parameter \ensuremath {{\cal I}} as the linear ratio of the total integrated infrared flux at $90^{{\rm o}}$ inclination over the total integrated infrared flux at $20^{{\rm o}}$ inclination. This implies that for larger values of \ensuremath {{\cal I}} there is more isotropy, \ensuremath {{\cal I}} =1 indicating perfect isotropy.

3.1 Smooth models

The results of the smooth torus models S1$\cdots$S4 are shown in Fig. 1. We show the density distribution on the left, the total SED at different inclination angles in the middle, and on the right a zoom-in on the 10 $\mu $m region for face-on inclination.


  \begin{figure} \par {\includegraphics[width=13.8cm,clip]{NEWFIG/1763f1.eps} }\end{figure} Figure 1: The results of the smooth torus models. Each row represents one model. The leftmost column represents the density distribution. The middle column is the SED of the system at three inclinations: 20$^{\circ }$, 70$^{\circ }$ and 90$^{\circ }$ (where 20$^{\circ }$ is effectively face-on, i.e. corresponding to a perfect type 1 source and 90$^{\circ }$ is edge-on, i.e. corresponding to a perfect type 2 source.). The vertical axis represents $^{10}\log(\nu F_\nu)$ as seen at a distance of d=107 pc. The SED includes the emission from the torus as well as the emission from the illuminating star, though the latter is only marginally visible in this figure. The right column is a linear plot of the face-on ( $i=20^{\circ }$) spectrum in the 10 $\mu $m regime, again $\nu F_{\nu }$ at d=107pc.
Open with DEXTER

For model S1 we have taken a constant density throughout the torus, because according to GD94 such models fit better the observed SEDs of AGN. We find that the SED has a width of \ensuremath {{\cal W}_1} =1.17 (see Table 1). The model produces a quite strong 10 micron emission feature for face-on tori ( \ensuremath {{\cal S}_1} =0.314), which is inconsistent with observations. This strong emission feature is not entirely surprising, because the torus is not very optically thick. At R=1pc the 10 $\mu $m vertical optical depth through the torus is 2.9, and just shortward of the feature at 7 $\mu $m it is 1.0. In fact, the nuclear radiation impinging on the inner rim of the torus only reaches its $\tau=1$surface (at $\lambda\sim 1~\mu$m) at a radius of about R=0.42 pc which is about 1.5 times the radius of the inner rim. Therefore, the inner regions of the torus are relatively optically thin, and expected to produce a strong emission feature.

Model S2 is identical to S1 except for changing p=-1. Effectively, this puts more mass in the innermost regions of the disk, making these regions more optically thick. As a result of this, the 10 micron emission feature virtually disappears ( \ensuremath {{\cal S}_1} =-0.016). The SED also becomes a tiny bit narrower ( \ensuremath {{\cal W}_1} =1.13). These effects are similar to what was already found by PK92: compact tori with very high optical depth can have a very weak emission feature, but produce narrower SEDs (see also discussions in GD94). In the present case our torus is still relatively large and hence not really compact. The large outer radius ensures that there is a large reservoir of cool dust, which is relatively unaffected by the change in p. This is why the width is not strongly affected when varying p. The 10 $\mu $m feature, on the other hand, comes from the warm inner regions (i.e. small radius), which are very optically thick, hence the disappearance of the 10 $\mu $m feature.

It should be noted, however, that the disappearance of the 10 $\mu $m feature for highly optically thick inner regions of the torus is not obvious. It depends strongly on the geometry of these inner regions. In our conical torus model the edges are very sharp and straight. There is only one surface of the torus that is directly irradiated, which is the inner rim. When this irradiated hot inner rim is seen under an inclination of only $i=20^{{\rm o}}$, as in the figures, then the line of sight toward a surface element of the rim has a high inclination ( $i\sim 70^{{\rm o}}$) with respect to the normal vector on the rims surface, i.e. almost parallel to the surface. This weakens the emission feature. Moreover, the emission from the near side of the rim is partly re-absorbed again by the rim material itself. Additionally, a significant fraction of the 10 $\mu $m flux comes from larger radii than the inner rim radius. That emission has (if anything) an absorption feature. The end effect is that if our torus is optically thick near the inner rim, the emission feature is very weak. The total flux from the torus (including the regions at larger radii) may even have a slight absorption feature, even for $i=20^{{\rm o}}$, as can be seen in model S2 with \ensuremath {{\cal S}_1} =-0.016.

Models S3 and S4 are like model S1 and S2 respectively, but now with decoupling the temperatures for graphite and silicate grains, introducing an MRN grain size distribution and including isotropic scattering. We find that the 10 $\mu $m emission feature is significantly weakened in S3 compared to model S1 ( \ensuremath {{\cal S}_1} =0.137 instead of \ensuremath {{\cal S}_1} =0.314), but still clearly present. The reason for the weakening is that the graphite has a higher opacity at visual wavelengths than silicate. Therefore the graphite becomes hotter than the silicate, and produces more continuum emission in the 10 $\mu $m wavelength region. In model S4 we see the silicate feature slightly in absorption ( \ensuremath {{\cal S}_1} =-0.083) for $i=20^{{\rm o}}$ again. The width of the SED is virtually unaffected by changing to a proper dust grain size distribution. If anything, S3 is somewhat wider than S1, but no difference is found between S4 and S2. The same goes for the anisotropy: S3 is slightly more anisotropic than S1, but S4 and S2 do not differ.

3.2 Clumpy models

The clumpy models C1$\cdots$C4 are the clumpy generalizations of models S1$\cdots$S4. The results for the quantities \ensuremath {{\cal W}_1}, \ensuremath {{\cal W}_2}, \ensuremath {{\cal S}_1}, \ensuremath {{\cal S}_2} and \ensuremath {{\cal I}} are given in Table 2. The SEDs are shown in Fig. 2 for models C1 and C2, and in Fig. 3 for models C3 and C4. Again, on the left the density distribution, middle the total SED at different inclination angles, and on the right a zoom-in on the 10 $\mu $m region.
  \begin{figure} \par {\includegraphics[width=13.8cm,clip]{NEWFIG/1763f2.eps} } \end{figure} Figure 2: The results of the clumpy torus models C1 and C2. See Fig. 1 for explanation. In contrast to Fig. 1, however, the left panel shows $\rho \cdot R$ instead of $\rho $, so that all clumps have the same grey depth.
Open with DEXTER


  \begin{figure} \par {\includegraphics[width=14cm,clip]{NEWFIG/1763f3.eps} } \end{figure} Figure 3: As Fig. 2, but for models C3 and C4.
Open with DEXTER

Figures 2 and 3 show that with the still relatively large size of the clumps ( $\sigma=0.025$) and the number of clumps used in these models, the distance between clumps is not always very much larger than the size of the clumps themselves. The NIE02 definition of a clumpy torus requires that the clumps are very small compared to the mean free path between the clumps. In this respect our model is not a true representation of clumpy tori as defined by NIE02. However, as mentioned above, technical limitations prevent us at present from modeling smaller and more clumps. We use the a- and b-series to understand the effect of the inter-clump distance, which is larger in the b-series.

The values of \ensuremath {{\cal W}_1} do not seem to follow a major trend, except perhaps that models C2 and C4 produce marginally broader SEDs than models C1 and C3. This is the opposite effect of what we observe in the smooth models, where S2 and S4 generate narrower SEDs than S1 and S3. The isotropy \ensuremath {{\cal I}} has a somewhat stronger trend with the p=-1 ("b'') models being more isotropic than the p=0 ("a'') models, and the models C1 and C3 being more isotropic than models C2 and C4.

The random location of the clumps can have a reasonably strong effect on the values of \ensuremath {{\cal W}_1}, \ensuremath {{\cal W}_2} and \ensuremath {{\cal I}} and even more so on the values of \ensuremath {{\cal S}_1} and \ensuremath {{\cal S}_2}. The reason for these trends is more difficult to understand than for the smooth models.

3.3 Comparison between smooth and clumpy models

The face-on SED of models C1 are clearly less wide ( $0.77 < \ensuremath{{\cal W}_1} {} < 0.91$) than for model S1 ( \ensuremath {{\cal W}_1} =1.17), despite the same global parameters. The same is true for model C3 compared to S3. The difference in \ensuremath {{\cal W}_1} between C2-S2 and C4-S4 is less pronounced, but still present. For edge-on inclinations the clumpy models have clearly wider SED than the smooth models with e.g. model S1 having \ensuremath {{\cal W}_2} =0.44 and the C1 models having \ensuremath {{\cal W}_2} ranging between 0.57 and 0.66.

The clumpy models have a more isotropic emission, as can be seen from the values of \ensuremath {{\cal I}}. For instance, the model S3 has \ensuremath {{\cal I}} =0.09 while the models C3 have values ranging between \ensuremath {{\cal I}} =0.16 and \ensuremath {{\cal I}} =0.29.

The strength of the 10 $\mu $m emission feature for the $i=20^{{\rm o}}$inclination does not seem to be decreased in the clumpy models. In fact, on average the value of \ensuremath {{\cal S}_1} is somewhat larger for the clumpy models than for the smooth models. It is striking that while the S2 and S4 models have the feature slightly in absorption ( \ensuremath {{\cal S}_1} =-0.016 and \ensuremath {{\cal S}_1} =-0.083 respectively), the corresponding clumpy models C2_xx and C4_xx have it consistently in emission: for the case C2_b1 even strongly in emission ( \ensuremath {{\cal S}_1} =0.32). So the clumpiness apparently does little to suppress the emission feature. It does, however, appear to weaken the absorbtion feature for the high inclinations (type 2 AGN). For example, the model S3 has \ensuremath {{\cal S}_2} =-2.03, which is a strong absorption feature, while the models C3_xx have values ranging between -0.95 and -0.03.

4 Discussion

4.1 Silicate feature strength in clumpy tori

The results of our models indicate that clumpiness does not seem to have the effect of suppressing the 10 $\mu $m silicate feature. In fact, the smooth models appear to do better in this respect than the clumpy models. Some of our clumpy models do have a suppressed 10 $\mu $m feature (e.g. model C4_a2 with \ensuremath {{\cal S}_1} =0.06), but that seems to be strongly influenced by the random location of the clumps (model C4_a1 has \ensuremath {{\cal S}_1} =0.13). One reason why the C2 and C4 clumpy tori have on average stronger 10 $\mu $m emission features in their face-on SEDs than the smooth models S2 and S4 (which have no emission feature) is that the clumps have a "fluffy'' photosphere while the smooth models have sharp edges. Emission features are best produced if a photosphere is irradiated under a reasonably small angle, which is the case for a significant portion of the fluffy photosphere of the clumps. Another reason is that in the smooth models a part of the emission from the inner rim (in particular the emission from the near side) is re-absorped by the torus, producing an absorption feature there. For the clumpy tori this effect is weaker.

The weaker absorption feature for edge-on clumpy tori compared to the edge-on smooth tori appears to be due to the fact that for clumpy tori one can see at least partly between the clumps deeper into the torus where the 10 $\mu $m emission is produced. Moreover, each of the clumps in the outer regions of the torus, having a higher density than the equivalent smooth torus, either blocks the light from the inner regions entirely (if it is in the line of sight) or does not block any light (if it is out of the line of sight). Only in few cases does one look just through the fluffy photosphere of the clump, causing a 10 $\mu $m absorption feature. In other words: the line-of-sight extinction caused by a collection of clumps is more "grey'' than that of smoothly distributed matter.

It should be kept in mind that our results may depend on the opacity we use. To allow a direct comparison with the NIE02 models, we have chosen a Galactic grain size distribution and do not use larger grains than 1 $\mu $m. Grain sizes and distribution can have a profound effect on the silicate feature, as shown by Laor & Draine (1993) and vBD03. There is convincing observational evidence that the dust in active galaxies does not have Galactic properties (Maiolino et al. 2001). Also, in radio galaxy NGC 4261 the near-infrared colours of the observed 300 pc scalee disk cannot be modeled with standard Galactic dust (Martel et al. 2000). Therefore, it is quite conceivable that the silicate feature is in reality weakened by opacity effects. On the other hand, it is also important to ask the question whether our simplification of thermally coupling the different grain sizes would perhaps artificially suppress the feature.

  
4.2 Width of the SEDs

As mentioned above, the width of the face-on SED \ensuremath {{\cal W}_1} is slightly smaller for the clumpy models than for the smooth models, in particular for the p=0 models (S1, S3, C1, C3). This effect can be explained by the fact that for p=0 the typical number of clumps per $\delta \log R$is not constant. For these models the clumps are typically more concentrated to the outer regions of the torus. Since the number of clumps is relatively moderate, the chance is then high that there will be few (if any) clumps in the inner regions. The real inner radius of the torus is determined by the location of the clumps. Therefore this deficiency of clumps effectively shifts the inner radius of the clumpy torus outward. If models would be made with p<-1, the same reasoning would be applicable for the outer radius of the torus. Since the width of the face-on SED depends largely on the ratio of the outer to the inner radius (see e.g. GD94, vBD03), the effect of this shift will be to narrow the SED. For the case of p>-1 the short-wavelength part of the SED will be suppressed and for the case of p<-1 the long-wavelength part of the SED will be suppressed.

On the other hand, for the edge-on SED one would expect that clumpy tori have less absorption of the near-IR flux because emission from the inner regions of the torus can travel between clumps toward the edge-on observer. This effect is indeed seen in the models, which have larger \ensuremath {{\cal W}_2} values for the clumpy models than for the smooth models.

4.3 Isotropy of infrared emission

Like a smooth torus, the bolometric infrared flux of a clumpy torus is stronger in the polar direction than in equatorial directions. This is because in both cases the emission from the hotter inner regions cannot be directly observed for edge-on systems due to the obscuration by the cooler outer regions. This anisotropy of the infrared emission is typical for all disk- or torus-like configurations. Our models of clumpy tori show that their SEDs are generally more isotropic than their smooth counterparts. Some models show this stronger than others. In particular we find this effect to be very strong for models C1 compared to model S1, while the effect is much less pronounced for models C2 compared to model S2. The reason for the increased isotropy of clumpy models is that radiation can freely move in between clumps. In a way, the inter-clump distance acts as a new kind of mean-free-path, and since there are not so many clumps in the model, the new effective optical depth for the clumpy torus is therefore smaller (even though the actual optical depth along individual lines-of-sight may be still high). This effect is also reflected in the fact that the edge-on mid-infrared flux for the clumpy models is significantly higher than for the smooth models.

The increased isotropy in clumpy models C1 and C3 compared to C2 and C4 is for a large part due to the fact that there were not so many clumps at small radii, and therefore the inner radius was effectively moved outward (as discussed in Sect. 4.2 above). Since the total mass of the torus was kept constant (at $10^6~M_{\odot}$) and the number of clumps was kept the same (N=40 resp. N=20), the optical depth of the clumps is lower for the models C1 and C3 (p=0) than for the models C2 and C4 (p=-1). A lower optical depth increases the isotropy of the torus (a perfectly optically thin torus being perfectly isotropic). The generally higher isotropy of the N=20 models versus the N=40 models (in spite of the lower clump optical depth of the latter) is because for fewer clumps the inter-clump distance is larger and the effective optical depth of the torus is decreased.

4.4 A criterion for clumpiness?

It is interesting to ask if, instead of the 10 $\mu $m silicate emission feature, some of the other aspects of the infrared spectra of tori could give clear indications for clumpiness. For example, for edge-on inclinations (type 2 AGN) the width of the SED, the mid- over far-infrared flux ratio and the depth of the absorption feature do show some trend with clumpiness: the clumpy models having a slightly wider SED, higher mid-infrared flux and shallower absorption feature. Unfortunately the current study is not comprehensive enough to assure that these effects could not be reproduced by other properties of the torus, such as the opacity properties or the torus geometry. One has to scan a large parameter space of smooth models to make sure that some property of the spectra of clumpy tori is really unique to clumpy tori. This is, however, beyond the scope of this paper.

4.5 The nature of clumps and clumpiness

The models presented in this paper are meant to verify what is the effect of clumpiness on the SED of torus models for active galaxies. Yet how representative are our models for clumpy tori? Our clumps are not real 3-D clumps due to our 2-D approximation, but we have argued that this should not have a major effect on our conclusions. Aside from the 2-D issue, is our description of the clumps realistic? Very little is known about the structure of the dusty circumnuclear matter in active galactic nuclei. Arguments for clumpiness have so far been rather indirect, but it seems reasonable to assume that the circumnuclear matter is distributed in an irregular and chaotic way rather than in a smooth and ordered manner.

The kind of clumpiness would depend much on the mechanism causing the clumps. According to the model of Krolik & Begelman (1988) these clumps are individual dynamically independent objects orbiting the black hole, and experiencing regular semi-elastic collisions. These clumps must be very compact, self-gravitating, and must be supported by strong interal magnetic fields to provide sufficient elasticity upon collisions with other clumps. On the other hand, a supersonically turbulent medium of the kind described by Wada & Norman (2002) would produce filamentary (sponge) structures rather than isolated clumps. These different structures of clumpiness may have very different infrared emission properties. For instance, a filametary medium is likely to have more matter in a marginally optically thin state than a medium consisting of very compact clumps. Since an emission feature comes from marginally optically thin regions, such an emission feature is expected to be stronger for the filametary medium than for the compact clumpy medium.

In the light of this, it is interesting to question what the effect is of the "fluffiness'' of the clumps in our simulation. In contrast to NIE02 we assume our clumps to have a Gaussian density profile. If we would take constant density clumps with a sharp edge, like NIE02, these clumps may have less marginally optically thin material at their surface, perhaps suppressing thereby the 10 $\mu $m emission feature where our models exhibit this feature clearly in emission. On the other hand, even for a perfectly sharp edge of an optically thick clump, it is not guaranteed that the feature vanishes because the surface of such a clump may be super-heated with respect to the clump interior by the irradiation, yielding a hot optically thin emission-feature-producing layer similar to what was described for flared circumstellar disks by Chiang & Goldreich (1997). It is, unfortunately, not possible for us to investigate this with our current models because this would require us to increase the resolution of our computational grid by a large factor in order to make sure to sample the photosphere of the clumps properly. This would be prohibitively computationally expensive at present. We can therefore only draw conclusions about clumpy media with Gaussian clumps.

Another issue related to this is the assumption, made by both NIE02 and ourselves, that all the clumps have equal optical depth. According to Krolik & Begelman (1988) the clumps in a circumnuclear torus get regularly tidally disrupted, forming smaller clumps which subsequently merge to form bigger ones. In effect an equilibrium distribution of clump sizes will result, with clumps of various sizes (and optical depths) coexisting within the same torus. Some of these clumps may easily be optically thin, or at least have low optical depth. Such clumps may again provide a reservoir of marginally optically thin material which could produce a 10 $\mu $m feature in emission. How strong this effect will be depends on the equilibrium distribution function of clump sizes.

Finally it is important to mention that due to technical limitations we could only model a rather limited number of clumps, each with a rather large size. It cannot be excluded that some results may change if we would be able to model problems with a much higher number of clumps, all of which being much smaller than we have assumed in the models we presented here. It is hard to estimate how big these effects are. In the limit of increasingly many ever smaller clumps, while keeping the total mass of the torus and the clump filling factor (the average number of clumps along the line of sight toward the center) constant, the clump optical depth eventually drops below unity. In this case the SED would become identical to that of the smooth version. If one, on the other hand, keeps the optical depth of the clumps constant while increasing the number of clumps, the average number of clumps along the line of sight drops below unity, which would be against the whole idea of obscuring circumnuclear tori. One would have to increase the total mass of the torus to compensate for this. Since it poses technical problems to model much smaller clumps than we have done in this paper, we cannot be certain what the effect of such an increase of the number of clumps would be. But by comparing the models with N=40 and N=20 (the a-series to the b-series) we find very little differences, so we expect this to remain this way for very high N.

5 Conclusion

We present the first global simulations of clumpy tori around AGN using a axisymmetric, multi-dimensional radiative transfer model. From our analysis and comparison between smooth and clumpy tori models we conclude that the 10 $\mu $m feature can both be strengthened and weakened when clumpiness is introduced. The width of the SED is largely determined by the inner and outer radius and the main effect of clumpiness is to increase the effective inner radius and/or decrease the effective inner/outer radius due to statistical fluctuations in the positioning of the clumps. This results in a slightly narrower face-on SED. The edge-on SED for clumpy tori is slightly wider than for smooth tori, because radiation can move freely between the clumps and emission from the inner regions of the clumpy torus can more easily reach the observer even foredge-on inclinations. We find that the isotropy of the infrared emission is significantly affected by clumpiness for similar reasons. Unfortunately this is a quantity that cannot be directly observed in an individual source. It requires studies of large samples of sources at different inclinations with comparable physical properties.

We do confirm that for the particular parameters of clumpiness mentioned in NIE02 the 10 $\mu $m feature can be rather weak, but this is even more pronounced for a smooth torus with the same global parameters and average density. A stronger effect is the depth of the 10 $\mu $m absorption feature for edge-on tori: for clumpy tori it is clearly less deep than for smooth tori.

Although we use clumps with a slightly different structure than NIE02, and although the clumps in our 2-D models are annuli around the symmetry axis instead of real 3-D clumps, we believe that our models produce at least qualitatively the correct results for clumpy media. We therefore cast doubt on the idea that the properties of the 10 $\mu $m feature of type 1 and type 2 active galaxies point unequivocally to clumpy tori. It should be clear, though, that we do not claim that the circumnuclear matter is smooth. We merely call for caution in interpreting the properties of the SEDs in the context of clumpiness of the dusty tori in active galaxies.

Acknowledgements
We wish to thank the referee, Ari Laor, for helpful comments. C.P.D. thanks Marc Schartmann for useful discussions.

References

 
Copyright ESO 2005