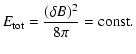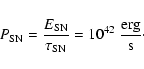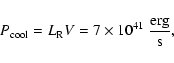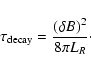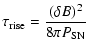A&A 436, 9-16 (2005)
DOI: 10.1051/0004-6361:20040364
Damping and wave energy dissipation in the
interstellar medium
II. Fast magnetosonic waves
F. Spanier - R. Schlickeiser
Institut für Theoretische Physik, Lehrstuhl IV:
Weltraum- und Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
Received 1 March 2004 / Accepted 12 February 2005
Abstract
The heating rate of the interstellar medium, especially the
warm ionized medium, is calculated considering damping of fast
magnetosonic waves. Starting with an anisotropic spectrum the energy
dissipation rate is derived from the damping rates. The results
show that the damping of fast magnetosonic waves is an
extraordinarily strong source of heat. The ion-neutral
and viscous damping contribute largely to the heating. Furthermore it is
shown that one would expect a strong parallelization of the spectrum
with exponents well above
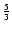 .
.
Key words: magnetohydrodynamics (MHD) - plasmas -
turbulence - waves - ISM: general - ISM: magnetic fields
The calculation of interstellar cosmic ray transport parameters,
like the parallel and perpendicular spatial diffusion
coefficients, the rate of adiabatic deceleration and the momentum
diffusion coefficient of cosmic ray particles, requires the
knowledge of the power spectra of magnetic and electric
fluctuations in the interstellar medium at frequencies below the
non-relativistic proton gyrofrequency
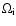 .
Adopting the
plasma wave viewpoint, in which one models the turbulent
electromagnetic fields as a superposition of low-frequency
magnetohydrodynamic plasma modes (shear Alfvén waves, fast
magnetosonic waves and slow magnetosonic waves), the electric
power spectrum is related to the magnetic power spectrum through
the Faraday induction law via the dispersion relation of the
individual plasma modes.
.
Adopting the
plasma wave viewpoint, in which one models the turbulent
electromagnetic fields as a superposition of low-frequency
magnetohydrodynamic plasma modes (shear Alfvén waves, fast
magnetosonic waves and slow magnetosonic waves), the electric
power spectrum is related to the magnetic power spectrum through
the Faraday induction law via the dispersion relation of the
individual plasma modes.
A problem arises because interstellar magnetic power spectra
cannot be measured directly. Only the power spectrum of
interstellar electron density fluctuations is accessible via radio
scintillation and dispersion measure studies (e.g. Armstrong et al. 1995).
Therefore, the relation between magnetic field fluctuations and
electron density fluctuations has to be investigated. According to
classical MHD theory, shear Alfven waves are incompressible
whereas fast magnetosonic waves for low-beta plasmas exhibit a
direct correspondence
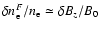 between electron density fluctuations and the fluctuations in the
parallel magnetic field. In a full kinetic description of the
turbulence (Schlickeiser & Lerche 2002), shear Alfvén waves
become compressible with the wavenumber-dependent relation
between electron density fluctuations and the fluctuations in the
parallel magnetic field. In a full kinetic description of the
turbulence (Schlickeiser & Lerche 2002), shear Alfvén waves
become compressible with the wavenumber-dependent relation
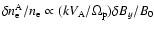 .
.
An additional constraint on interstellar magnetic power spectra is
provided by considering the heating of the interstellar medium by
plasma wave damping. In the first paper of this series, Lerche &
Schlickeiser (2001 - hereafter referred to as Paper I)
have calculated the heating rate of the ISM by collisionless
Landau damping of fast magnetosonic waves. They demonstrated that
the energy loss rate for this process agrees well with the cooling
rate of the diffuse interstellar medium if one considers an
anisotropic power spectrum and large spatial scales, especially
without strong spatial inhomogeneities so that to a first
approximation a simple balance of heating and cooling rates
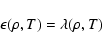 |
(1) |
holds. In the second paper of this series, Lazar et al. (2003 - hereafter referred to as Paper II)
calculated the influence of Alfvén wave damping on plasma
heating. Here the authors demonstrated that besides collisionless
Landau damping additional damping mechanisms related to gas
collisions are important. It is the purpose of the present
investigation to consider these additional collisional heating
processes also for fast magnetosonic waves because they were not
considered in Paper I. As we will show, this modifies the
conclusions of Paper I because these additional heating processes
are more important than the collisionless Landau damping of fast
magnetosonic waves considered there. Throughout this manuscript we
use the same notation as in Papers I and II.
As before, we distinguish between three different phases of the
interstellar medium coexisting in pressure equilibrium: cold
clouds, a warm intercloud medium (also: warm ionized medium) and
hot coronal gas, which is generated by supernova explosions. The
temperature of the warm medium can be determined by 21 cm
radio studies. These indicate a temperature range from 6000 to 104 K. Also, from radio studies we can infer the mean HII-density, which is about 0.08 cm-3, and the neutral (HI)
hydrogen density that ranges between 0.1-0.2 cm-3. The warm intercloud medium provides the dominant contribution to interstellar electron density fluctuations because its filling
factor and its degree of ionization are much higher than that of cold clouds, while the coronal gas, having approximately the same filling factor and degree of ionisation, has a much lower electron
density.
As in Paper I we adopt a power spectrum of electron density fluctuation in the form
![\begin{displaymath}%
P_n(\vec {k})=C_n^2~ \left[k_{\parallel}^2+\Lambda
k_{\perp}^2\right]^{-(2+s)/2}.
\end{displaymath}](/articles/aa/full/2005/22/aa0364-04/img8.gif) |
(2) |
As mentioned above for fast magnetic waves, magnetic fluctuations are
directly proportional to density fluctuations so we can write:
![\begin{displaymath}%
P_B(\vec {k})=C_B^2~ \left[k_{\parallel}^2+\Lambda
k_{\perp}^2\right]^{-(2+s)/2}.
\end{displaymath}](/articles/aa/full/2005/22/aa0364-04/img9.gif) |
(3) |
Here
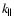 (
(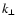 )
is the component of the wavenumber
vector parallel (perpendicular) to the ambient magnetic field; s is
the spectral index;
)
is the component of the wavenumber
vector parallel (perpendicular) to the ambient magnetic field; s is
the spectral index; 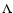 is the anisotropy parameter. Isotropy
corresponds to
is the anisotropy parameter. Isotropy
corresponds to
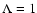 ,
whereas if the wave turbulence is aligned
more along the lines of thin "platelets'' paralleling the ambient
field, as suggested by Goldreich & Sridhar (1995), then
,
whereas if the wave turbulence is aligned
more along the lines of thin "platelets'' paralleling the ambient
field, as suggested by Goldreich & Sridhar (1995), then
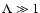 .
The constant CB2 is such that
.
The constant CB2 is such that
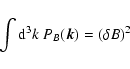 |
(4) |
where 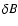 denotes the total magnetic fluctuation. The form
of the wave spectrum given by Eq. (3) is assumed
to hold between some small wavenumber,
denotes the total magnetic fluctuation. The form
of the wave spectrum given by Eq. (3) is assumed
to hold between some small wavenumber,
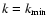 ,
and a
large wavenumber,
,
and a
large wavenumber,
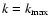 ,
with
,
with
![$k=\vert\vec{k}\vert=[k_{\parallel}^2+k_{\perp}^2]^{1/2}$](/articles/aa/full/2005/22/aa0364-04/img19.gif) .
Spangler
(1991) suggests that these wavenumbers are related to
outer and inner scale lengths,
.
Spangler
(1991) suggests that these wavenumbers are related to
outer and inner scale lengths,
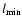 and
and
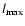 ,
respectively, with
,
respectively, with
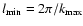 ,
,
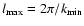 .
The physical bounds of
.
The physical bounds of
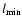 and
and
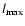 are not precisely known, but are probably related to the Whistler wave resonance limit of the interstellar electrons
and the physical size of the warm intercloud medium, i.e. the
mean cloud distance. The inner scale is estimated by Spangler
(1991) to be of the general order of
are not precisely known, but are probably related to the Whistler wave resonance limit of the interstellar electrons
and the physical size of the warm intercloud medium, i.e. the
mean cloud distance. The inner scale is estimated by Spangler
(1991) to be of the general order of
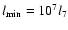 cm, (l7=1), with the outer scale of order
cm, (l7=1), with the outer scale of order
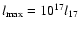 cm with l17=1 in hot,
ionized regions, and l17=30 in the diffuse phase of the
interstellar medium. In our study we assume that the power
spectrum (3) holds in the warm intercloud medium,
which is assumed to be stationary and homogenous.
cm with l17=1 in hot,
ionized regions, and l17=30 in the diffuse phase of the
interstellar medium. In our study we assume that the power
spectrum (3) holds in the warm intercloud medium,
which is assumed to be stationary and homogenous.
In this work we use a wavenumber-independent anisotropy factor 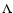 ,
while Goldreich & Sridhar (1995) predict it to be wavenumber dependent. This approximation is used for two reasons: first, it allows a direct comparison of our calculations
with the earlier results of Paper I for fast magnetosonic waves,
which were based on the power spectrum (3), and
secondly, the mathematically simple form of (3)
allows an exact analytical calculation of the wave dissipation
rates, which is not possible for more complicated power spectra.
,
while Goldreich & Sridhar (1995) predict it to be wavenumber dependent. This approximation is used for two reasons: first, it allows a direct comparison of our calculations
with the earlier results of Paper I for fast magnetosonic waves,
which were based on the power spectrum (3), and
secondly, the mathematically simple form of (3)
allows an exact analytical calculation of the wave dissipation
rates, which is not possible for more complicated power spectra.
The power spectrum itself results from the balance of all wave
damping and driving processes, although a detailed theory and
explanation is not available at present. Therefore, our
calculations are limited in the sense that we assume a given and
fixed power spectrum to determine the heating rate of the
interstellar medium, but we do not self-consistently investigate
the effect of this energy loss rate on the form of the power
spectrum, nor do we investigate the formation of real turbulence
spectra in wavenumber space. Although highly needed, such a
self-consistent theory lies beyond the scope of the present investigation.
2 Physical parameters
For our calculations we describe the warm intercloud medium with the
following set of parameters:
The minimum and maximum wavenumbers given by Spangler are
| |
|
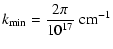 |
(11) |
| |
|
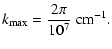 |
(12) |
From these parameters one can derive the following set of additional parameters
- a)
- Ion gyrofrequency
![$\displaystyle %
\Omega_{\rm i} = \frac{e B}{m_{\rm i} c} = 9.58 \times 10^3
B[{\rm G}]~{\rm Hz} =3.6 \times 10^{-2}\frac{{B}}{4~\mu{\rm G}}\cdot$](/articles/aa/full/2005/22/aa0364-04/img34.gif) |
|
|
(13) |
- b)
- Coulomb logarithm
![$\displaystyle %
L \approx 23.4 -1.15\log n[{\rm cm}^{-3}]
+ 3.45 \log T[{\rm eV}]\; {\rm for}\; T< 50~{\rm eV}= 24.0.$](/articles/aa/full/2005/22/aa0364-04/img35.gif) |
|
|
(14) |
- c)
- Ion-ion collision time
- d)
- Electron-electron collision time
- e)
- Alfvén speed
3 Relation between density and magnetic fluctuations
As we can see from Schlickeiser & Lerche (2002), we have the
following relation between electron density (Pnn) and magnetic
fluctuation (
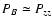 as the z-component of the magnetic
field is dominant) spectra for fast magnetosonic waves in a low
as the z-component of the magnetic
field is dominant) spectra for fast magnetosonic waves in a low
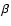 -plasma
-plasma
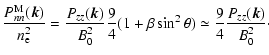 |
|
|
(18) |
So for small plasma 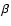 there holds a direct proportionality
between the both spectra. We will only have to normalize our
spectrum via the total fluctuating power. In order to derive the
constant CB we solve Eq. (4).
there holds a direct proportionality
between the both spectra. We will only have to normalize our
spectrum via the total fluctuating power. In order to derive the
constant CB we solve Eq. (4).
where F denotes the confluent hypergeometric function
2 F1(a,b;c;x).
For waves damping at a rate
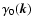 the energy loss
rate
the energy loss
rate
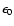 is conventionally written in the form (Spangler
1991)
is conventionally written in the form (Spangler
1991)
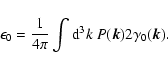 |
(22) |
The warm phase of the interstellar medium is a partially ionised
plasma. The fast magnetosonic waves undergo different types of
dissipation in this low-temperature plasma: besides collisionless
Landau damping (
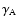 )
there is damping connected with the
collision-effects associated with Joule dissipation (
)
there is damping connected with the
collision-effects associated with Joule dissipation (
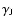 ),
ion viscosity (
),
ion viscosity (
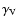 )
(Braginskii 1965; Hollweg
1985) and ion-neutral friction (
)
(Braginskii 1965; Hollweg
1985) and ion-neutral friction (
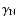 )
(Kulsrud &
Pearce 1969). All individual damping rates are taken from Tsap
(2000). The total damping rate for the fast magnetosonic
waves then is
)
(Kulsrud &
Pearce 1969). All individual damping rates are taken from Tsap
(2000). The total damping rate for the fast magnetosonic
waves then is
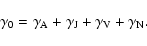 |
(23) |
We discuss each contribution in turn. With the respective damping rates
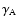 ,
,
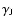 ,
,
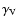 and
and
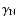 it is then straightforward to determine the respective energy loss rates by evaluating the integral of damping rate times
wave energy spectrum
it is then straightforward to determine the respective energy loss rates by evaluating the integral of damping rate times
wave energy spectrum
![\begin{displaymath}%
\epsilon _{\rm i}=C_B^2\int_{{k_{{\rm min}}}}^{{k_{{\rm max...
...eft[\mu
^2+\Lambda \left(1-\mu ^2\right)\right]^\frac{2+s}{2}}
\end{displaymath}](/articles/aa/full/2005/22/aa0364-04/img63.gif) |
(24) |
with
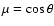 .
The total energy loss rate is then given by
the sum
.
The total energy loss rate is then given by
the sum
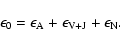 |
(25) |
As already described in Paper I the wave damping rate for
collisionless Landau damping may be written as
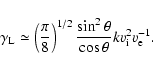 |
(26) |
Compared to the classical formula given by Ginzburg (1961) terms of order
 are neglected as the Alfvén speed is much higher than the ion speed in the
interstellar setting.
are neglected as the Alfvén speed is much higher than the ion speed in the
interstellar setting.
Lerche & Schlickeiser (2001) found an energy
dissipation rate
The variable
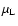 is the lower limit (
is the lower limit (
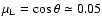 )
of the validity range of the approximation for the Landau
damping that we have used in Eq. (26).
)
of the validity range of the approximation for the Landau
damping that we have used in Eq. (26).
There exist approximations for the anisotropy term in the limit
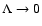 and
and
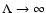 .
.
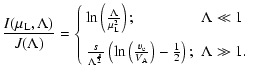 |
|
|
(30) |
The complete derivation can be found in Paper I. Numerical values for our given physical setting are
| |
|
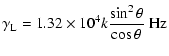 |
(31) |
| |
|
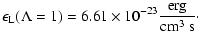 |
(32) |
Tsap (2000) gives the following damping rate for Joule
dissipation
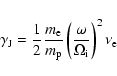 |
(33) |
where
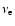 denotes the electron-electron-collision frequency.
Considering the dispersion relation for the fast magnetosonic
waves
denotes the electron-electron-collision frequency.
Considering the dispersion relation for the fast magnetosonic
waves
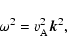 |
(34) |
we can write the damping rate as follows
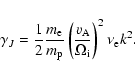 |
(35) |
This corresponds exactly to the damping rate given by Braginskii
(1965).
The Joule energy dissipation is then calculated as
If we use the value of CB from Eq. (4) we finally find
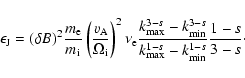 |
(37) |
Obviously this result is independent of the anisotropy factor 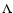 ,
which is easy to understand as we actually have no angular dependence of the Joule damping rate (35).
,
which is easy to understand as we actually have no angular dependence of the Joule damping rate (35).
For our given parameters we have the numerical values
| |
|
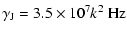 |
(38) |
| |
|
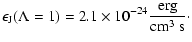 |
(39) |
From Braginskii (1965) we know that viscosity dissipation is
given by
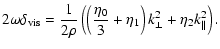 |
|
|
(40) |
So that
where
denote the viscosity coefficients for the ions. As 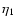 and
and 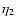 scale with
scale with
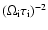 which in the ISM is much smaller than unity (
which in the ISM is much smaller than unity (
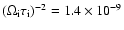 ), at least
), at least 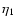 can be neglected for
can be neglected for 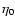 .
Therefore
.
Therefore
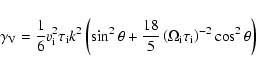 |
(45) |
where 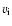 is the ion thermal velocity, which is supposed to be Maxwellian distributed.
is the ion thermal velocity, which is supposed to be Maxwellian distributed.
This damping rate is now multiplied again with the power spectrum
in order to get the energy dissipation rate
Again we use Eq. (21) and derive
With the given numerical values
| |
|
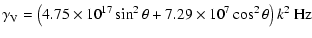 |
(50) |
| |
|
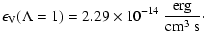 |
(51) |
This dissipation rate (51) for an isotropic spectrum
(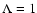 )
is far too large (15 orders of magnitude) compared
to the cooling rate (59), so we have to consider
either strong anisotropy or a wave number exponent other than
)
is far too large (15 orders of magnitude) compared
to the cooling rate (59), so we have to consider
either strong anisotropy or a wave number exponent other than
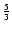 or a different spectral range. We expect to have waves mostly parallel to the ambient magnetic field, as
or a different spectral range. We expect to have waves mostly parallel to the ambient magnetic field, as 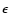 is decreasing with increasing
is decreasing with increasing 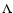 ,
which means
,
which means
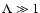 .
In Sect. 5 we try to find the exact parameters of the wave spectrum that yield the correct total dissipation rate.
.
In Sect. 5 we try to find the exact parameters of the wave spectrum that yield the correct total dissipation rate.
Kulsrud & Pearce (1969) have given the following damping
rate for ion-neutral collisions
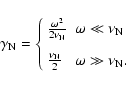 |
(52) |
The ion-neutral collision frequency
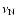 has an approximate
value of 4
has an approximate
value of 4 
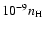 Hz, so we are in the high frequency
limit and can consider the damping rate as an angle-independent constant.
Hz, so we are in the high frequency
limit and can consider the damping rate as an angle-independent constant.
We note that this rate depends only on the total strength of the
magnetic turbulence and not on the extent of the turbulence spectrum.
After inserting Eq. (21) we have the simple and
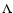 -indepedent expression
-indepedent expression
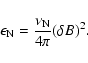 |
(56) |
The numerical values are given by
| |
|
 |
(57) |
| |
|
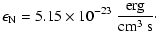 |
(58) |
This dissipation rate is also two orders of magnitude too high
compared to the cooling rate, indepedent of the form of the
spectrum. To change the magnitude of ion-neutral heating, the
total power of fluctuations has to be changed.
The dissipation rates for all damping processes are shown in Fig. 1.
5 Understanding the wave power spectrum
From Minter & Spangler (1997) we know that the
cooling rate of the diffuse interstellar medium is
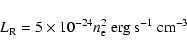 |
(59) |
with the electron density of the interstellar medium of
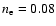 cm-3 we have a cooling rate of 3.2
cm-3 we have a cooling rate of 3.2 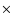 10-26 erg s-1 cm-3. Obviously, our
heating rates (compare Eqs. (51) and (58) with
Eq. (59)) are much higher than the cooling rate if we
adopt Kolmogorov scaling (s=5/3) and an isotropic spectrum
(
10-26 erg s-1 cm-3. Obviously, our
heating rates (compare Eqs. (51) and (58) with
Eq. (59)) are much higher than the cooling rate if we
adopt Kolmogorov scaling (s=5/3) and an isotropic spectrum
(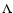 = 1).
= 1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0364fig1.eps}\end{figure}](/articles/aa/full/2005/22/aa0364-04/Timg133.gif) |
Figure 1:
Anisotropy dependence of different energy dissipation processes. |
| Open with DEXTER |
Within the current hypothesis of a steady-state configuration of
heating and cooling, in order to achieve agreement of the wave
turbulence spectrum with the constraints from the cooling rate we have
two options: we can either modify
- 1.
- the parameters s (spectral index) and
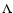 (anisotropy)
of our turbulence spectrum or
(anisotropy)
of our turbulence spectrum or
- 2.
- the maximum wavenumber
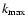 of the fast magnetosonic
waves because an early cutoff of the spectrum can be expected with the
dominant damping process (viscous damping) scaling as
of the fast magnetosonic
waves because an early cutoff of the spectrum can be expected with the
dominant damping process (viscous damping) scaling as 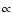 k2(see Eq. (41)).
k2(see Eq. (41)).
First we consider different cases for which we calculate the spectral
index s starting with an isotropic spectrum, and then we gradually
increase the parameter 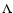 with the limit of a fully parallel spectrum.
with the limit of a fully parallel spectrum.
As the ion-neutral damping is only determined by the collision
frequency between ions and neutrals and the fluctuating magnetic power
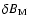 ,
the heaiting rate by ion-neutral friction can be used to fit the fluctuating magnetic power as it is the only parameter here. We attribute 50% of the heating to ion-neutral damping,
i.e.
,
the heaiting rate by ion-neutral friction can be used to fit the fluctuating magnetic power as it is the only parameter here. We attribute 50% of the heating to ion-neutral damping,
i.e.
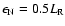 ,
so that Eqs. (58) and (59) yield
,
so that Eqs. (58) and (59) yield
| |
|
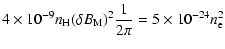 |
(60) |
| |
|
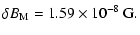 |
(61) |
Although this is a very small fluctuation power, it seems to be a
plausible starting point. Fast magnetosonic waves are strongly
damped, so that energy in that kind of wave dissipates very fast,
leading to the fact, that there cannot be much fluctuation energy
stored in the fast magnetosonic waces. This conclusion is in
contradiction to Paper I, where only collisionless Landau damping
was considered. The argument is still the same; in Paper I the
damping rate almost fitted the cooling rate, but our new results
contradict that earlier result: for FMS-dominated turbulence,
heating and cooling are not in balance.
As mentioned above we have fixed the value of
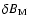 by demanding
by demanding
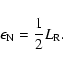 |
(62) |
The remaining parameters s and
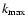 may be calculated by
attributing the remaining 50% heating to viscous damping, i.e.
may be calculated by
attributing the remaining 50% heating to viscous damping, i.e.
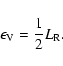 |
(63) |
We leave the parameter
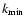 unchanged as it has only a
minor influence on the total dissipation rate. We will determine
the values of s and
unchanged as it has only a
minor influence on the total dissipation rate. We will determine
the values of s and
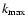 in the following way: we
will assume an isotropic spectrum
in the following way: we
will assume an isotropic spectrum 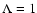 keeping the value
for
keeping the value
for
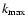 fixed (with the value given by Spangler 1991) to calculate s. In a second calculation we will do this vice versa assuming a Kolmogorov-like spectrum
(s=5/3) to calculate
fixed (with the value given by Spangler 1991) to calculate s. In a second calculation we will do this vice versa assuming a Kolmogorov-like spectrum
(s=5/3) to calculate
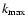 .
In the end we will derive the
general relation between s and
.
In the end we will derive the
general relation between s and
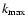 to identify all possible
parameter sets for isotropic spectra.
to identify all possible
parameter sets for isotropic spectra.
The first method of fixing
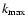 and varying s yields from
and varying s yields from
| |
|
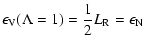 |
(64) |
| |
|
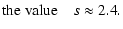 |
(65) |
This result shows that we have to assume a very high spectral
index s (much higher than the Kolmogorov value 5/3) and very
low fluctuating power to justify the chosen
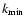 and
and
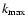 of Spangler.
of Spangler.
The second modification of fixing s=5/3 and varying
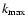 yields
from Eq. (64)
yields
from Eq. (64)
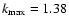
 10-12 cm-1,
which is five orders of magnitude smaller than the values of Spangler.
10-12 cm-1,
which is five orders of magnitude smaller than the values of Spangler.
Varying both the spectral index s and
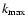 yields the relation
yields the relation
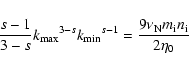 |
(66) |
in the approximation
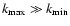 from Eq. (64). For given numerical values and different values of s we calculate the wavenumber of the wave spectrum cutoff.
The results are shown in Fig. 2.
from Eq. (64). For given numerical values and different values of s we calculate the wavenumber of the wave spectrum cutoff.
The results are shown in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0364fig2.eps}\end{figure}](/articles/aa/full/2005/22/aa0364-04/Timg146.gif) |
Figure 2:
Relation between cutoff wavenumber
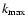 and spectral index s for isotropic turbulence. The dotted line shows Spangler's
and spectral index s for isotropic turbulence. The dotted line shows Spangler's
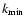 while the dashed shows his
while the dashed shows his
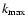 . . |
| Open with DEXTER |
As Fig. 1 shows, a small value of
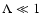 does
not modify the viscous damping rate. However, large values of
does
not modify the viscous damping rate. However, large values of
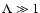 have a strong influence on the damping. Therefore, only for values of
have a strong influence on the damping. Therefore, only for values of
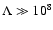 giving a fully parallel
spectrum are we able to justify s=5/3.
giving a fully parallel
spectrum are we able to justify s=5/3.
We have calculated the main damping processes of fast magnetosonic
waves in the interstellar medium. Using numerical parameters
derived from observations we found that for isotropic turbulence
ion viscosity and ion-neutral damping in particular lead to a much
higher energy dissipation than the cooling rate allows in a steady
state case. This leads to two conclusions:
- 1.
- Fluctuations of the ISM consist predominantly of shear Alfvén waves. Fast magnetosonic waves are damped instantaneously, so that the power ratio (
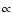
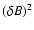 )
of fast magnetosonic waves to Alfvén waves is well below 0.1%
)
of fast magnetosonic waves to Alfvén waves is well below 0.1%
- 2.
- The assumed standard wave spectrum (3) implies either
- (a)
- values of
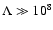 for s=5/3 (i.e. extremely
parallel fast magnetosonic turbulence);
for s=5/3 (i.e. extremely
parallel fast magnetosonic turbulence);
- (b)
- steep spectral indices s>2.4 for isotropic turbulence and perpendicular turbulence;
- (c)
- the existence of a high wavenumber cutoff for isotropic turbulence with a spectral index s=5/3, five orders below the standard cutoff attributed to gyroresonant damping.
The main question arising from our results is the physical plausibility of the proposed modifications (steeper spectra, low cutoff, parallel spectra). The main issue of all three
modifications proposed above is the very small fluctuating power of fast magnetosonic waves, which is a result quite different from Paper I. Observational results cannot clarify this point as they
do not allow us to distinguish between different wave types in the ISM.
We will initially analyze the energy conservation in the ISM turbulence to justify our model. Our basic assumption was the steady state model
As the outgoing power (
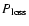 )
has clearly been identified as the plasma wave damping, we will now try to justify supernovae as the main input (
)
has clearly been identified as the plasma wave damping, we will now try to justify supernovae as the main input (
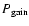 ) process.
) process.
As a simplified model we assume a cylindrical galaxy (r=50 000 Ly, h=3000 Ly) completely filled with diffuse ionized gas, which is heated by supernovae (the typical energy output for supernovae
is E=1051 erg and the mean time between two supernovae is approx.
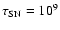 s =30 years).
s =30 years).
First, we calculate the average input power from supernovae for the
total Galaxy
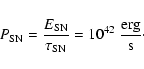 |
(70) |
This is in reasonable agreement with the total cooling rate
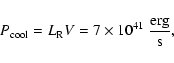 |
(71) |
which is 70% of the input supernova power.
The energy of the supernovae is approximately sufficient to
sustain the energy balance. But still one question remains: is it
likely that such a high fraction of the heating power from the
supernovae is ultimately dissipated by ISM heating, probably via
the formation of supernova shock waves, which are important for
the generation of turbulence? Thus the input power is almost fully
available as wave energy. On the other hand, the alternative
energy-consuming process, which is according to Schlickeiser
(2002) the acceleration of cosmic rays, only needs an
average power of 1040 erg/s. As it seems there are no other
processes in an interstellar phase at rest (no convective motions
like galactic winds) which could possibly consume the available
energy and as the input power and the heating fit remarkably well
(though we used a very rough model) it is reasonable to argue that
ISM heating is a stationary process driven by supernovae. It
should be noted, however, that the given figures are only rough
approximations, the supernova-frequency especially cannot be
treated as a constant and a strong deviation from the average
would lead to a cooling of the ISM.
One may also derive time scales from the total energy E instead of
the power 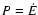 ,
but these time scales are not suitable for the
dynamical thermal equilibrium, which we examine, as there is no
intrinsic relation between E and
,
but these time scales are not suitable for the
dynamical thermal equilibrium, which we examine, as there is no
intrinsic relation between E and 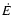 .
Those time scales can
only give estimates for the time the turbulent field would need to
build or decay when either the input or output power would be turned off.
.
Those time scales can
only give estimates for the time the turbulent field would need to
build or decay when either the input or output power would be turned off.
The "decay time scale'' is the ratio of field energy and loss power
(the plasma wave heating rate).
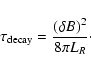 |
(72) |
We evaluate this time scale for both fast magnetosonic and
Alfvén waves.
| |
|
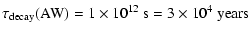 |
(73) |
| |
|
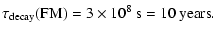 |
(74) |
These results show that Alfvénic turbulence would persist much
longer than fast mode waves after turning off supernovae, but it
also shows that the decay of energy in fast magnetosonic waves is
three times shorter than the typical input rate from supernovae
(
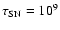 s).
s).
This could mean that fast magnetosonic waves can only be found in
the vicinity of supernovae and are damped completely after a
supernova occurs.
Another possibility is the nonlinear interaction of Alfvén waves
as a generation mechanism for the fast magnetosonic waves (see
e.g. Chin & Wentzel 1972). Particularly the production rate of fast waves
by Alfvén waves could help our understanding of the energy
transfer in the ISM.
Also the time scale of field creation should be analyzed. This
time scale is derived from turbulent electromagnetic energy and
input power. Again we differentiate between Alfvén and fast
magnetosonic waves. These "rise time scales'' are given by
These timescales differ by nearly three orders of magnitude, which
may support the physical model that the two wave types have
different origins. The fast magnetosonic wave timescale is again
of the order of
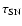 while Alfvénic turbulence
needs much longer to develop. It should be noted, however, that
the order of
while Alfvénic turbulence
needs much longer to develop. It should be noted, however, that
the order of
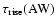 is not in
contradiction to our assumption of supernova heating. If we start
in a cold, not ionized gas there is no cooling function
is not in
contradiction to our assumption of supernova heating. If we start
in a cold, not ionized gas there is no cooling function 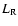 (which is proportional to the electron density) so that in the
beginning exponential heating of the ISM is possible.
(which is proportional to the electron density) so that in the
beginning exponential heating of the ISM is possible.
The next point concerning the physical plausibility is the
possibility of a nearly parallel spectrum. For Alfvén waves this
matter has been addressed by Goldreich & Sridhar
(1995), but their (disputed) process is not applicable to
fast magnetosonic waves. Nonetheless the ISM is marked by strong
anisotropies, which may result in anisotropic spectra. Again
further insight into the production processes of FMS waves would
be helpful, but in contrast to the question of input power of the
spectrum, the anisotropy may only be explained by the damping
itself. If we imagine an isotropic input spectrum, we may see
after short times that with increasing wavenumber the anisotropy
increases, as the damping of perpendicular waves is dominant. This
may be modelled by wavenumber dependent anisotropy factors 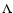 ,
which for reasons of simplicity are not included in our model.
,
which for reasons of simplicity are not included in our model.
The last point to be discussed is the possibility of very steep
spectra. If we stick to the Kolmogorov (1941) or
Kraichnan-Iroshnikov (1965) theory we should expect a 5/3or 3/2 spectrum, but one point in the derivation of those
theories seems not to be fulfilled in our case: The K41 (i.e.
turbulence with an inertial range power law s=5/3) and KI (i.e.
s=3/2) theories consider an inertial range, where the form of
the turbulence spectrum is given by the local transport in
wavenumber space, with damping being neglected in that range. But
as we already pointed out, the ISM has strong damping features.
This does not mean that there is no inertial range but there could
be additional effects due to the dispersion range studied by
Stawicki et al. (2001), an intermediate regime between the inertial and
dissipation range. Thus our findings are not in contradiction to
Kolmogorov theory but they seem to indicate that the inertial
range of the ISM turbulence is negligible.
Acknowledgements
We thank the anonymous referee for the very constructive and helpful report. We acknowledge partial support by the Deutsche Forschungsgemeinschaft through Sonderforschungsbereich 591. We would also like to thank Urs Schaefer-Rolffs for providing the figures.
- Abramowitz, M., &
Stegun, I. A. 1972, Handbook of Mathematical Functions, National
Bureau of Standards, Washington
- Armstrong, J. W.,
Rickett, B. J., & Spangler, S. R. 1995, ApJ, 443, 209 [NASA ADS] [CrossRef] (In the text)
- Braginskii, S. I. 1965, Rev.
Plasma Phys., 1, 205 [NASA ADS] (In the text)
- Chin, Y., & Wentzel, D.
G. 1972, Ap&SS, 16, 465 [NASA ADS] (In the text)
- Gary, S. P. 1986, J. Plasma
Phys., 35, 431 [NASA ADS]
- Ginzburg, V. I.
1961, Propagation of Electromagnetic Waves in Plasma (New York:
Pergamon Press)
(In the text)
- Goldreich, P., &
Sridhar, S. 1995, ApJ, 438, 763 [NASA ADS] [CrossRef] (In the text)
- Hollweg, J. V. 1985, J.
Geophys. Res., 90, 7620 [NASA ADS] (In the text)
- Kolmogorov, A. N. 1941, Dokl.
Akad. Nauk. SSSR, 30, 301 (In the text)
- Kraichnan, R. 1965, Phys.
Fluids, 8, 1835 (In the text)
- Kulsrud, R. M., &
Pearce, W. P. 1969, ApJ, 156, 445 [NASA ADS] [CrossRef] (In the text)
- Lazar, M., Spanier, F.,
& Schlickeiser, R. 2003, A&A, 410, 415 [EDP Sciences] [NASA ADS] [CrossRef] (Paper II)
(In the text)
- Lerche, I., &
Schlickeiser, R. 2001, A&A, 366, 1008 [EDP Sciences] [NASA ADS] [CrossRef] (Paper I)
(In the text)
- Lerche, I., &
Schlickeiser, R. 1982, MNRAS, 201, 1041 [NASA ADS]
- Minter, A. H.,
& Spangler, S. R. 1997, ApJ, 485, 182 [NASA ADS] [CrossRef] (In the text)
- Schlickeiser, R., &
Lerche, I. 2002, J. Plasma Phys., 68, 191 [NASA ADS] [CrossRef] (In the text)
- Schlickeiser, R. 2002,
Cosmic Ray Astrophysics (Berlin: Springer)
(In the text)
- Spangler, S. R.
1991, ApJ, 376, 540 [NASA ADS] [CrossRef] (In the text)
- Stawicki, O., Gary, S.
P., & Li, H. 2001, JGR, 106, 8273 [NASA ADS] [CrossRef] (In the text)
- Tsap, Y. T. 2000, Sol.
Phys., 194, 131 [NASA ADS] [CrossRef] (In the text)
- Sturrock, P. A. 1994,
Plasma Physics (Cambridge University Press)
Copyright ESO 2005
![\begin{displaymath}%
P_n(\vec {k})=C_n^2~ \left[k_{\parallel}^2+\Lambda
k_{\perp}^2\right]^{-(2+s)/2}.
\end{displaymath}](/articles/aa/full/2005/22/aa0364-04/img8.gif)
![\begin{displaymath}%
P_B(\vec {k})=C_B^2~ \left[k_{\parallel}^2+\Lambda
k_{\perp}^2\right]^{-(2+s)/2}.
\end{displaymath}](/articles/aa/full/2005/22/aa0364-04/img9.gif)
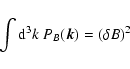
![$\displaystyle \frac{3\sqrt{m_{\rm i}}T_{\rm i}[{\rm eV}]^{3/2}}{4\sqrt{\pi} L
e^4 n_{\rm i}}$](/articles/aa/full/2005/22/aa0364-04/img37.gif)
![$\displaystyle 2.12 \times
10^7\frac{T_{\rm i}[{\rm eV}]^{3/2}}{n L}~{\rm s}= 3.5 \times 10^6~{\rm s}.$](/articles/aa/full/2005/22/aa0364-04/img39.gif)
![$\displaystyle \frac{3\sqrt{m_{\rm e}}T_{\rm e}[{\rm eV}]^{3/2}}{4\sqrt{2 \pi}
L e^4 n_{\rm i}}$](/articles/aa/full/2005/22/aa0364-04/img41.gif)
![$\displaystyle 3.43 \times 10^5\frac{T_{\rm e}[{\rm eV}]^{3/2}}{n L}~{\rm s}=5.7 \times 10^4~{\rm s}.$](/articles/aa/full/2005/22/aa0364-04/img42.gif)
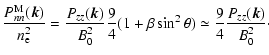
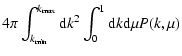
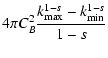
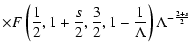
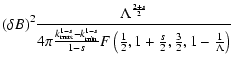
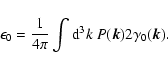
![\begin{displaymath}%
\epsilon _{\rm i}=C_B^2\int_{{k_{{\rm min}}}}^{{k_{{\rm max...
...eft[\mu
^2+\Lambda \left(1-\mu ^2\right)\right]^\frac{2+s}{2}}
\end{displaymath}](/articles/aa/full/2005/22/aa0364-04/img63.gif)
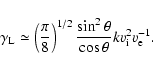
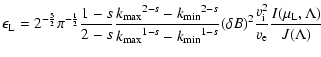
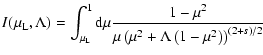
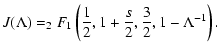
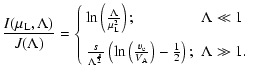
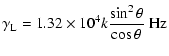
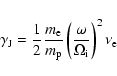
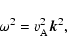
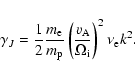
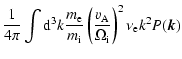
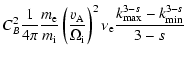
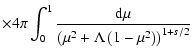
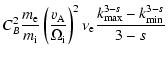
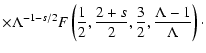
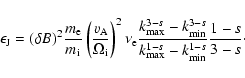
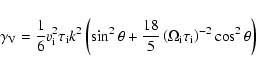
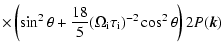
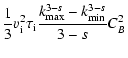
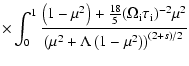
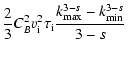
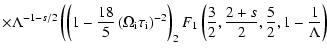
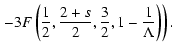
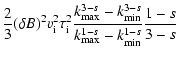
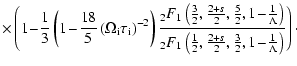
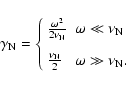
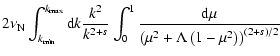
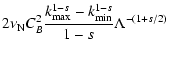
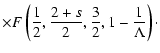
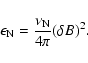
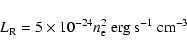
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0364fig1.eps}\end{figure}](/articles/aa/full/2005/22/aa0364-04/Timg133.gif)
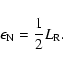
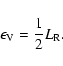
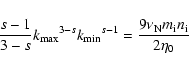
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0364fig2.eps}\end{figure}](/articles/aa/full/2005/22/aa0364-04/Timg146.gif)