A&A 435, 1013-1030 (2005)
DOI: 10.1051/0004-6361:20042368
Constraining the mass transfer in massive binaries through progenitor
evolution models of Wolf-Rayet+O binaries
J. Petrovic1,2
-
N. Langer1 -
K. A. van der Hucht3,4
1 - Sterrenkundig Instituut,
Universiteit Utrecht,
Princetonplein 5, 3584 CC Utrecht,
The Netherlands
2 -
Astronomical Institute,
Radboud Universiteit Nijmegen,
Toernooiveld 1, 6525 ED,
Nijmegen, The Netherlands
3 -
SRON, Nationaal Instituut voor Ruimte Onderzoek,
Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
4 -
Sterrenkundig Instituut Anton Pannekoek, Universiteit van Amsterdam,
Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
Received 15 November 2004 / Accepted 18 February 2005
Abstract
Since close WR+O binaries are the result of a strong interaction
of both stars in
massive close binary systems, they can be used to constrain
the highly uncertain mass and angular momentum budget
during the major mass transfer phase.
We explore the progenitor evolution of the three
best suited WR+O binaries HD 90657, HD 186943 and HD 211853,
which are characterized by
a WR/O mass ratio of  0.5 and periods of 6...10 days.
We are doing so at three different levels of approximation:
predicting the massive binary evolution through
simple mass loss and angular momentum loss estimates, through
full binary evolution models with parametrized mass transfer
efficiency, and through binary evolution models including rotation
of both components and a physical model which allows to
compute mass and angular momentum loss from the binary system
as function of time during the mass transfer process.
All three methods give consistently the same answers.
Our results show that, if these systems formed through stable mass transfer,
their initial periods were smaller than their current ones,
which implies that mass transfer has started during the
core hydrogen burning phase of the initially more massive star.
Furthermore, the mass transfer in all three cases must have
been highly non-conservative, with on average only
0.5 and periods of 6...10 days.
We are doing so at three different levels of approximation:
predicting the massive binary evolution through
simple mass loss and angular momentum loss estimates, through
full binary evolution models with parametrized mass transfer
efficiency, and through binary evolution models including rotation
of both components and a physical model which allows to
compute mass and angular momentum loss from the binary system
as function of time during the mass transfer process.
All three methods give consistently the same answers.
Our results show that, if these systems formed through stable mass transfer,
their initial periods were smaller than their current ones,
which implies that mass transfer has started during the
core hydrogen burning phase of the initially more massive star.
Furthermore, the mass transfer in all three cases must have
been highly non-conservative, with on average only  10%
of the transferred mass being retained by the mass receiving star.
This result gives support to our system mass and angular momentum
loss model, which predicts that, in the considered systems,
about 90% of the overflowing matter is expelled by the
rapid rotation of the mass receiver close to the
10%
of the transferred mass being retained by the mass receiving star.
This result gives support to our system mass and angular momentum
loss model, which predicts that, in the considered systems,
about 90% of the overflowing matter is expelled by the
rapid rotation of the mass receiver close to the 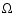 -limit,
which is reached through the accretion of the remaining 10%.
-limit,
which is reached through the accretion of the remaining 10%.
Key words: stars: binaries: close - stars: evolution - stars: fundamental parameters - stars: rotation -
stars: Wolf-Rayet
1 Introduction
The evolution of a star in a binary system can differ significantly
from that of an isolated one
with the same mass and chemical composition. The physical processes that enter
binary evolution are the gravitational and
radiation field from the companion, as well as the centrifugal force
arising from the rotation of the system. But, most important, it is the
evolution of the
more massive component that will influence dramatically the evolution of
the system. In certain evolutionary phases, mass transfer
from one star to another can occur, changing the fundamental properties
of both stars as well as their future evolution.
The rotational properties of binary components may play a key role
in this respect.
The evolution of massive single stars can be strongly influenced by
rotation
(Heger & Langer 2000; Meynet & Maeder 2000),
and evolutionary models of rotating stars are
now available for many masses and metallicities.
While the treatment of the rotational processes in these models
is not yet in a final stage
(magnetic dynamo processes are just being included Maeder & Meynet 2003; Heger et al. 2004), they provide
first ideas of what rotation can really do to a star.
Effects of rotation, as important they are in single stars,
can be much stronger in the components of close binary systems:
Estimates of the angular momentum gain of the accreting star
in mass transferring binaries show that critical rotation
may be reached quickly (Langer et al. 2000; Yoon & Langer 2004b; Packet 1981).
In order to investigate this, we need binary evolution models
which include a detailed treatment of rotation in the stellar interior,
as in recent single star models. However, in binaries, tidal
processes as well as angular momentum and accretion need to be considered
at the same time. Some first such models are now available and
are discussed below.
Angular momentum accretion and the subsequent rapid rotation
of the mass gainer may be essential for some of the most exciting cosmic
phenomena, which may occur exclusively in binaries: type Ia supernovae,
the main producers of iron and cosmic yardsticks to measure the
accelerated expansion of the universe (Yoon & Langer 2004b,a),
and gamma-ray bursts from collapsars,
which the most recent stellar models with rotation and magnetic fields
preclude to occur in single stars
(Heger et al. 2004; Woosley 2004; Petrovic et al. 2004).
For both, the type Ia supernova progenitors and the gamma-ray burst
progenitors, it is essential to understand how efficient the
mass transfer process is and on which physical properties it depends.
Further exciting astrophysical objects
whose understanding is affected by our understanding of mass transfer comprise
X-ray binaries (Chevalier & Ilovaisky 1998) and type Ib and Ic supernovae
(Podsiadlowski et al. 1992).
How much matter can stars accrete from a binary companion?
As mentioned above, non-magnetic accretion, i.e. accretion via a
viscous disk or via ballistic impact, transports angular momentum and can lead to a strong
spin-up of the mass gaining star. For disk accretion, it appears plausible that
the specific angular momentum of the accreted matter corresponds to
Kepler-rotation at the stellar equator; this leads to a spin-up of
the whole star to critical rotation when its initial mass is increased
by about 20% (Packet 1981).
It appears possible that mass accretion continues in this situation,
as viscous processes may transport angular momentum
outward through the star, the boundary layer, and the accretion
disk (Paczynski 1991).
However, as the star is rotating very rapidly, its wind mass
loss may dramatically increase (Langer 1998,1997), which may render
the mass transfer process inefficient.
Observations of massive post-mass transfer binary systems constrain this
effect. Langer et al. (2003) and Langer et al. (2004) points out that there is
evidence for both extremes occurring in massive close binaries, i.e. for
quasi-conservative evolution as well as for highly non-conservative evolution.
In the present study, we are interested in those binaries that contain a
Wolf-Rayet and a main sequence O star.
We have chosen to focus on three WN+O systems (HD 186943, HD 90657 and HD 211853)
which have similar mass ratios (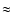 0.5) and orbital periods (6...10 days).
As clearly the two stars in these systems must have undergone
a strong interaction in the past, an understanding of their
progenitor evolution may be the key to constrain the mass transfer
efficiency in massive binaries: which fraction of the mass leaving
the primary star is accumulated by the secondary star during a mass
transfer event?
0.5) and orbital periods (6...10 days).
As clearly the two stars in these systems must have undergone
a strong interaction in the past, an understanding of their
progenitor evolution may be the key to constrain the mass transfer
efficiency in massive binaries: which fraction of the mass leaving
the primary star is accumulated by the secondary star during a mass
transfer event?
Evolutionary calculations of massive close binaries were performed by various authors.
General ideas about the formation of WR+O binary systems were given by
Paczynski (1967), Kippenhahn et al. (1967), van den Heuvel & Heise (1972).
Vanbeveren et al. (1979) modelled the evolution of massive Case B binaries
with different assumptions for mass and angular momentum loss from the binary system.
Vanbeveren (1982) computed evolutionary models of massive close Case B binaries with primary
masses between
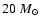 and
and
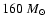 .
He concluded that most of the
WR primaries are remnants of stars initially larger than
.
He concluded that most of the
WR primaries are remnants of stars initially larger than
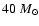 and
that the accretion efficiency in these systems should be very below 0.3
in order to fit the observations.
de Loore & de Greve (1992) computed detailed models of massive Case B binary
systems
for initial mass ratios of 0.6 and 0.9, assuming
an accretion efficiency of 0.5.
Wellstein & Langer (1999) and Wellstein et al. (2001) modelled
massive binary systems mass range 12...60
and
that the accretion efficiency in these systems should be very below 0.3
in order to fit the observations.
de Loore & de Greve (1992) computed detailed models of massive Case B binary
systems
for initial mass ratios of 0.6 and 0.9, assuming
an accretion efficiency of 0.5.
Wellstein & Langer (1999) and Wellstein et al. (2001) modelled
massive binary systems mass range 12...60
 assuming conservative evolution,
and Wellstein (2001) presented the first rotating binary evolution
models for initial masses of
assuming conservative evolution,
and Wellstein (2001) presented the first rotating binary evolution
models for initial masses of 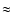
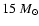 and initial mass ratios
and initial mass ratios
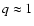 .
.
While it was realized through these models that different mass accretion
may be needed to explain different observations, these efforts did not
have the potential to explore the physical reasons for non-conservative
evolution. I.e., there is no reason to expect that the mass transfer efficiency
remains constant during the mass transfer process in a given binary system,
nor that its time-averaged value is constant for whole binary populations.
It is not yet known which physical processes can expel matter from a binary system.
Vanbeveren (1991) proposed that if a binary component is more
massive than 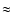 40-50
40-50
 it will go through an LBV phase of enhanced
mass loss, which will prevent the occurrence of RLOF.
Dessart et al. (2003) investigated the possibility that radiation pressure from the
secondary prevents the accretion. They found that even for moderate mass transfer rates
(
it will go through an LBV phase of enhanced
mass loss, which will prevent the occurrence of RLOF.
Dessart et al. (2003) investigated the possibility that radiation pressure from the
secondary prevents the accretion. They found that even for moderate mass transfer rates
(
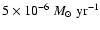 )
the wind and photon momenta
which emerge from the accretion star can not alter the
dynamics of the accretion stream. Here, we follow the suggestion
that the effective mass accretion rate can be significantly decreased
due to the spin-up of the mass receiving star (Petrovic & Langer 2004; Wellstein 2001; Langer et al. 2003,2004).
)
the wind and photon momenta
which emerge from the accretion star can not alter the
dynamics of the accretion stream. Here, we follow the suggestion
that the effective mass accretion rate can be significantly decreased
due to the spin-up of the mass receiving star (Petrovic & Langer 2004; Wellstein 2001; Langer et al. 2003,2004).
The remainder of this paper is organized as follows.
In Sect. 2 we briefly discuss the observational data
available for WR+O binary systems. In Sect. 3
we derive estimates for the masses of both stars in WR+O systems
for given initial masses and accretion efficiencies.
In Sect. 4 we present the
physics used to compute our detailed evolutionary models.
Non-rotating binary evolution models with an adopted constant mass accretion efficiency are presented in Sect. 5. Our
rotating models in which the mass accretion efficiency is obtained
selfconsistently are discussed in Sect. 6.
We briefly compare our models with observations in
Sect. 7.
Conclusions are given in Sect. 8.
2 Observational data
There are about 20 observed Wolf-Rayet+O binary systems with known masses
of components in the catalogue of van der Hucht (2001).
We have chosen to model three spectroscopic double-lined systems:
HD 186943 (WN3), HD 90657 (WN5) and GP Cep (WN6/WCE) have, since
they have similar mass ratios (
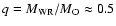 )
and orbital periods
(6...10 days).
)
and orbital periods
(6...10 days).
WN+O systems that also have short orbital periods are V444 Cyg, CX Cep,
CQ Cep, HD 94546, HD 320102 and HD 311884.
V444 Cyg has period of 4.2 days
and can be result of stable mass transfer evolution, but since mass ratio
of this
system is  0.3 we did not include it in this paper.
Orbital periods of CX Cep and CQ Cep
are very short (
0.3 we did not include it in this paper.
Orbital periods of CX Cep and CQ Cep
are very short ( 2 days) and these systems
are probably the result of a contact evolution.
HD 94546 and HD 320102 are systems with very low masses of WR and O components
(4
2 days) and these systems
are probably the result of a contact evolution.
HD 94546 and HD 320102 are systems with very low masses of WR and O components
(4
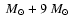 and 2.3
and 2.3
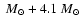 respectively)
and HD 311884 is extremely massive WR+O binary system
(51
respectively)
and HD 311884 is extremely massive WR+O binary system
(51
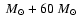 ). Recently, an even more massive WR+O system has been observed 83
). Recently, an even more massive WR+O system has been observed 83
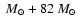 (Bonanos et al. 2004; Rauw et al. 2004).
(Bonanos et al. 2004; Rauw et al. 2004).
Table 1:
Basic parameters of selected WN+O SB2 binaries.
The mass ratio of a binary system is determined from its radial velocity
solution, with an error of 5-10%. However, to determine the exact value
of the masses of the binary components, the value of the inclination of the
system has to be known. Without knowledge of the inclination, only minimum
masses of the components can be determined, i.e., M sin3i.
Massey (1981) determined the minimum mass for the WR star in
HD 186943 to be 9-11
 .
Niemela & Moffat (1982)
determined the masses of the components of HD 90657 in the range
11-14
.
Niemela & Moffat (1982)
determined the masses of the components of HD 90657 in the range
11-14
 for the WN4 component and 21-28
for the WN4 component and 21-28
 for the O-type component. The masses of the WR components in HD 186943
and HD 90657 given in Table 1 have been determined by
Lamontagne et al. (1996) on the basis of improved values for the
inclination of these systems. Demers et al. (2002) determined
minimum masses of the components of the system GP Cep. Previously,
Lamontagne et al. (1996) suggested values of
for the O-type component. The masses of the WR components in HD 186943
and HD 90657 given in Table 1 have been determined by
Lamontagne et al. (1996) on the basis of improved values for the
inclination of these systems. Demers et al. (2002) determined
minimum masses of the components of the system GP Cep. Previously,
Lamontagne et al. (1996) suggested values of
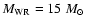 and
and
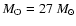 for this system.
for this system.
There is no obvious hydrogen contribution in the WR spectrum in any of
these systems (Niemela & Moffat 1982; Massey 1981).
Massey (1981) showed that hydrogen absorption lines are
fairly broad in the spectrum of HD 186943, equivalent to
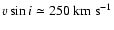 ,
thus the O-type star is rotating much faster
than synchronously.
,
thus the O-type star is rotating much faster
than synchronously.
Beside the fact that the binary system GP Cep has a similar mass ratio and
period as the other two systems, it has some very different properties as
well. The spectral type of the WR component in GP Cep is a combination of
WN and WC (WN6/WCE Demers et al. 2002). Also,
Massey (1981) showed that, next to the main period of
 6.69 days of the binary system GP Cep, radial velocities of
absorption lines vary also with a period of 3.4698 days. He proposed that
GP Cep is a quadruple system, consisting of two pairs of stars, WR+O and O+O.
Panov & Seggewiss (1990) suggested that in both pairs one component is a
WR star. However, Demers et al. (2002) showed that there is only
one WR star in this quadruple system.
6.69 days of the binary system GP Cep, radial velocities of
absorption lines vary also with a period of 3.4698 days. He proposed that
GP Cep is a quadruple system, consisting of two pairs of stars, WR+O and O+O.
Panov & Seggewiss (1990) suggested that in both pairs one component is a
WR star. However, Demers et al. (2002) showed that there is only
one WR star in this quadruple system.
3 The simple approach
If the initial binary system is very close (an initial period is of the order of few
days), RLOF occurs while the primary is still in the core hydrogen burning phase and Case A
mass transfer takes place (fast and slow phase).
When the primary expands due to shell hydrogen burning, it
fills its Roche lobe and Case AB mass transfer starts. During this mass transfer the primary
star loses the major part of its hydrogen envelope. After Case AB mass transfer,
the primary is a helium core burning Wolf-Rayet star.
During all this time, the secondary is still a main sequence star, but with an increased mass
due to mass transfer.
When the initial binary period is of the order of one to few weeks, the primary fills its Roche lobe for the
first time during shell hydrogen burning and Case B mass transfer takes place. The primary
loses most of its hydrogen envelope, becomes a WR star and the secondary is an O star with
an increased mass.
Case C mass transfer occurs when initial period is of the order of years.
The primary fills its Roche lobe during helium shell burning and mass transfer
takes place on the dynamical time scale.
This scenario is not likely for chosen systems,
since some of the secondary stars in WR+O systems have been observed to rotate faster than
synchronously. This means that they have accreted some matter which increased their spin angular
momentum.
We constructed a simple method to quickly estimate the
post-mass transfer parameters for a large number of binary systems
for a given accretion efficiency 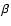 .
This allows us to narrow the space of possible initial
parameters (primary mass, secondary mass and orbital period)
that allows the evolution into a specific observed WR+O systems.
.
This allows us to narrow the space of possible initial
parameters (primary mass, secondary mass and orbital period)
that allows the evolution into a specific observed WR+O systems.
We considered binary systems with
initial primary masses
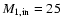 ...100
...100
 and secondaries masses
and secondaries masses
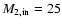 /1.7...100
/1.7...100
 with an initial period of 3 days. We assumed that the primary is transferring matter
to the secondary until it reaches the mass of its initial helium core (Eq. (1)).
with an initial period of 3 days. We assumed that the primary is transferring matter
to the secondary until it reaches the mass of its initial helium core (Eq. (1)).
Matter that is not accreted on the secondary leaves the system with
the specific angular momentum which corresponds to the secondary's orbital
angular momentum (King et al. 2001), which is consistent with
our approach for mass loss from the binary system (cf. Sect. 4).
Stellar wind mass loss is neglected.
More massive initial primaries produce more massive WR stars (helium cores) in general,
but if the star is in a binary system that goes through mass transfer during hydrogen
core burning of the primary (Case A), this depends also on other parameters:
- If the initial period is longer,
mass transfer starts later in the primary evolution and the initial helium core of the
primary is more massive.
- If the initial mass ratio is further from unity,
the mass transfer rate from the primary reaches higher values and the initial helium core mass
is smaller.
We initially want to restrict ourselves to systems that undergo stable mass transfer, i.e. avoid
contact situations. Wellstein et al. (2001) found that the limiting initial mass ratio for
conservative Case A binary system is
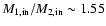 and for conservative Case B
systems
and for conservative Case B
systems  1.25. Since we allow non-conservative evolution,
we consider initial mass ratio
1.25. Since we allow non-conservative evolution,
we consider initial mass ratio 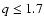 for Case A and
for Case A and 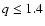 for Case B.
The observed WR+O systems (HD 186943, HD 90657 and HD 211853) all have very short orbital
periods, between 6 and 10 days. Since, the net effect of the Case A+Case AB,
or Case B is a widening of the orbit (if there is no contact), we have to assume that
the initial periods need to be shorter than, or approximatively equal to the observed ones.
We adopted a minimum initial orbital period of
3 days to avoid that the primary fills its Roche lobe on the ZAMS.
for Case B.
The observed WR+O systems (HD 186943, HD 90657 and HD 211853) all have very short orbital
periods, between 6 and 10 days. Since, the net effect of the Case A+Case AB,
or Case B is a widening of the orbit (if there is no contact), we have to assume that
the initial periods need to be shorter than, or approximatively equal to the observed ones.
We adopted a minimum initial orbital period of
3 days to avoid that the primary fills its Roche lobe on the ZAMS.
We estimated the minimum initial helium core masses, which are obtained
by the earliest Case A systems, for systems
with a mass ratio of
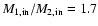 and an initial period of
3 days (
and an initial period of
3 days (
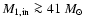 )
from the detailed
evolutionary models shown later in this paper
(Sect. 5):
)
from the detailed
evolutionary models shown later in this paper
(Sect. 5):
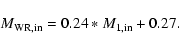 |
(1) |
In this linear approximation, we neglected the influence of the initial mass ratio on
the initial WR mass. It is shown in Sect. 5.2 that this dependence becomes
important only for initial mass ratios above 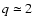 .
.
For Case B binaries, the initial WR mass does not depend on the initial period
and the initial mass ratio of the system, since during core hydrogen burning, the primary evolves as a single
star, without any interaction with the secondary.
We estimated the relation between initial main sequence mass and initial WR mass
as a linear fit from the Case B binary systems with initial primaries
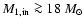 (Wellstein & Langer 1999):
(Wellstein & Langer 1999):
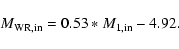 |
(2) |
The minimum initial period for a system to evolve through Case B mass transfer depends on the initial primary mass and
the mass ratio. We can estimate, based on the radii of the primaries at the end
of the main sequence evolution, what would be the initial orbital separation necessary to avoid the primary filling its
Roche lobe before shell hydrogen burning.
From Kepler's law follows that the orbital separation is proportional to the mass ratio
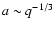 and the initial primary mass
and the initial primary mass
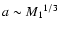 .
Since
.
Since 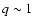 we can neglect this dependence and estimate the initial period for which the
radius of the primary at the end of MS is equal to its Roche radius.
For this estimate we do not take into account stellar wind that will widen the orbit and decrease
the masses.
We conclude that the Case B limiting initial orbital period
for 40
we can neglect this dependence and estimate the initial period for which the
radius of the primary at the end of MS is equal to its Roche radius.
For this estimate we do not take into account stellar wind that will widen the orbit and decrease
the masses.
We conclude that the Case B limiting initial orbital period
for 40
 is
is  10 days, for 45
10 days, for 45
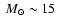 days and for
75
days and for
75
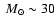 days. Since the result of stable Case B mass transfer is widening
of the orbit, it follows that (stable mass transfer)
Case B binary systems can not be progenitors of
the observed systems HD 186943, HD 90657 and HD 211853 whose orbital periods are shorter than
10 days. However, WR star masses resulting from Case B evolution are practically the same as those from
very late Case A evolution, which is still considered in our analysis.
days. Since the result of stable Case B mass transfer is widening
of the orbit, it follows that (stable mass transfer)
Case B binary systems can not be progenitors of
the observed systems HD 186943, HD 90657 and HD 211853 whose orbital periods are shorter than
10 days. However, WR star masses resulting from Case B evolution are practically the same as those from
very late Case A evolution, which is still considered in our analysis.
We calculate binary systems for early Case A (
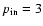 days) and for late Case A
(
days) and for late Case A
(
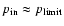 ).
).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig1.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg86.gif) |
Figure 1:
Masses of both components of post-Case A mass transfer WR+O binary
systems resulting from our simple approach, for
initial primary masses in the range 25...100
 and an initial
period of
and an initial
period of
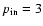 days, for four different assumed accretion
efficiencies days, for four different assumed accretion
efficiencies 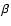 ( a)- d)). The solid line represents a mass ratio of ( a)- d)). The solid line represents a mass ratio of
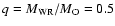 .
For an increasing .
For an increasing 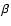 ,
the O stars in WR+O systems
become more massive and the WR/O-mass ratio decreases. ,
the O stars in WR+O systems
become more massive and the WR/O-mass ratio decreases. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig2.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg87.gif) |
Figure 2:
Masses of both components of post-Case A mass transfer WR+O binary
systems resulting from our simple approach, for
initial primary masses in the range 25...100
 and
for early (
and
for early (
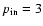 days) Case A and late Case A respective Case B evolution.
The assumed accretion efficiency is days) Case A and late Case A respective Case B evolution.
The assumed accretion efficiency is
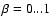 .
The solid line represents a mass ratio of .
The solid line represents a mass ratio of
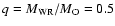 . .
|
| Open with DEXTER |
The results are shown in Fig. 1 for four different
accretion efficiencies (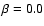 ,
0.1, 0.5, 1.0 respectively) for early Case A evolution
(p=3 days). Figure 2 shows the results for early Case A systems (p=3 days) for
all values of
,
0.1, 0.5, 1.0 respectively) for early Case A evolution
(p=3 days). Figure 2 shows the results for early Case A systems (p=3 days) for
all values of 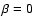 ...1 and for Case B/late Case A, also for all
...1 and for Case B/late Case A, also for all 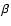 .
.
We notice from Fig. 1, that when the assumed 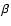 is larger,
the resulting WR+O systems lie further from the line defined by q=0.5. The reason is clear:
if the accretion efficiency is higher, the secondary will become
more massive while the initial mass of the WR star stays the same.
Conservative evolution (Fig. 1d) produces WR+O systems that have
small mass ratios,
q=1/5...1/6.
is larger,
the resulting WR+O systems lie further from the line defined by q=0.5. The reason is clear:
if the accretion efficiency is higher, the secondary will become
more massive while the initial mass of the WR star stays the same.
Conservative evolution (Fig. 1d) produces WR+O systems that have
small mass ratios,
q=1/5...1/6.
We conclude that if the considered three observed WR+O binary systems evolved through a
stable mass transfer,
a large amount of matter must have left the system. On the other hand,
since some of the secondary
stars in WR+O binaries have been observed to rotate faster than synchronously
(Underhill et al. 1988; Massey 1981), a certain amount of accretion
may be required.
Figure 2 shows the resulting WR+O masses in Case A and Case B (latest Case A) for accretion
efficiency 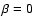 ...1. If the primary star does not lose
mass in a mass transfer during core hydrogen burning (
...1. If the primary star does not lose
mass in a mass transfer during core hydrogen burning (
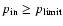 ),
it will form a more massive WR star, as we already explained.
There will be less mass to transfer from the primary to the secondary, and for fixed
),
it will form a more massive WR star, as we already explained.
There will be less mass to transfer from the primary to the secondary, and for fixed 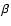 the corresponding O star will become less massive.
However, since the observed periods of HD 186943, HD 90657 and HD 211853 are shorter than
10 days and Case A+Case AB widens the binary orbit, the initial orbital period should be shorter
than observed, so we can conclude roughly that
the corresponding O star will become less massive.
However, since the observed periods of HD 186943, HD 90657 and HD 211853 are shorter than
10 days and Case A+Case AB widens the binary orbit, the initial orbital period should be shorter
than observed, so we can conclude roughly that
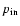 is between 3 and 10 days.
is between 3 and 10 days.
The orbital period of WR+O systems depends on their initial orbital period,
their initial mass ratio and on the parameter 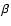 .
If the initial period increases and there is no contact during the evolution,
the orbital period in the WR+O stage will also increase.
However, the orbital period of WR+O systems will be shorter if the initial mass ratio is larger.
If the initial masses are very similar, the primary will become less massive than the
secondary very early during the mass transfer, and afterward matter is
transfered from the less to the more massive star, which results in a widening of the orbit.
Conversely, the final period is shorter for a larger difference in initial masses in the
binary system.
.
If the initial period increases and there is no contact during the evolution,
the orbital period in the WR+O stage will also increase.
However, the orbital period of WR+O systems will be shorter if the initial mass ratio is larger.
If the initial masses are very similar, the primary will become less massive than the
secondary very early during the mass transfer, and afterward matter is
transfered from the less to the more massive star, which results in a widening of the orbit.
Conversely, the final period is shorter for a larger difference in initial masses in the
binary system.
We can draw the following conclusions:
- The accretion efficiency during the major mass transfer phase
in the progenitor evolution of the three observed WR+O binaries is small, i.e.
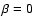 ...0.1, as for larger
...0.1, as for larger 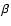 the O stars during the WR+O phase are more massive
and the WR/O-mass rations smaller than observed.
However, we note that it is unlikely that the secondaries did not accrete at all (
the O stars during the WR+O phase are more massive
and the WR/O-mass rations smaller than observed.
However, we note that it is unlikely that the secondaries did not accrete at all (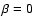 ),
since some O stars are found to rotate faster than synchronously.
),
since some O stars are found to rotate faster than synchronously.
- The initial orbital period needs to be larger than
 3 days,
to avoid contact at the beginning of hydrogen burning.
3 days,
to avoid contact at the beginning of hydrogen burning.
- The initial orbital period should be larger than
 3 days, in order to
obtain massive enough WR stars.
3 days, in order to
obtain massive enough WR stars.
- The initial orbital periods should be shorter than the observed orbital periods in the
three WR+O systems, i.e. shorter than
 10 days. This excludes Case B
mass transfer.
10 days. This excludes Case B
mass transfer.
- While the initial mass ratio
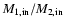 should not be too far from unity
so contact is avoided, it should be close to the contact limit, since this leads
to the shortest orbital periods and largest WR/O mass ratios in WR+O systems, as needed
for the three observed systems.
should not be too far from unity
so contact is avoided, it should be close to the contact limit, since this leads
to the shortest orbital periods and largest WR/O mass ratios in WR+O systems, as needed
for the three observed systems.
4 Numerical code and physical assumptions
We showed in Sect. 3 that we can roughly estimate the parameters
of the progenitor systems of observed WR+O binaries HD 186943, HD 90657 and HD 211853.
However, detailed numerical models are required in order to verify that
the assumption of contact-free evolution can in fact be justified.
And finally, we want to check whether the required mass and angular momentum
loss can be reproduced by our detailed selfconsistent approach.
We are using a binary evolutionary code which was originally
developed by Braun (1998) on the
basis of an implicit hydrodynamic stellar evolution code for single stars
(Langer 1998,1991).
It calculates simultaneous evolution of the two stellar
components of a binary system in a circular orbit
and the mass transfer within the Roche approximation
(Kopal 1978).
Mass loss from the Roche lobe filling component through the first Lagrangian point
is given by Ritter (1988) as:
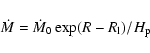 |
(3) |
with
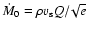 ,
where
,
where 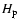 is the photospheric pressure scale height,
is the photospheric pressure scale height, 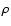 is the density,
is the density, 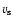 the velocity of sound and Q the effective cross-section of the stream through
the first Lagrangian point according to Meyer & Meyer-Hofmeister (1983).
the velocity of sound and Q the effective cross-section of the stream through
the first Lagrangian point according to Meyer & Meyer-Hofmeister (1983).
Stellar wind mass loss for O stars on the main sequence is calculated according to
Kudritzki et al. (1989).
For hydrogen-poor stars (
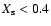 )
we assume mass loss based on the empirical
mass loss rates for Wolf-Rayet stars derived by Hamann et al. (1995):
)
we assume mass loss based on the empirical
mass loss rates for Wolf-Rayet stars derived by Hamann et al. (1995):
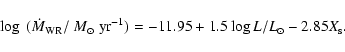 |
(4) |
Since Hamann & Koesterke (1998) suggested that these mass loss rates may be
overestimated, we calculated evolutionary models with mass loss rate given by Eq. (4)
multiplied by factors 1/2, 1/3 and 1/6.
The treatment of a convection and a semiconvection which is applied here is
described in Langer (1991) and Braun & Langer (1995).
Changes in chemical composition are computed using a nuclear network including pp chains,
the CNO-cycle, and the major helium, carbon, neon and oxygen burning reactions.
More details are given in Wellstein & Langer (1999) and Wellstein et al. (2001).
We use the OPAL Rosseland-mean opacities of (Iglesias & Rogers 1996).
For all models, a metallicity of Z=0.02 is adopted. The abundance ratios of
the isotopes for a given element are chosen to have the solar meteoritic abundance ratios
according to Grevesse & Noels (1993).
The change of the orbital period (orbital angular momentum loss) due to the mass transfer and
stellar wind mass loss is computed according to Podsiadlowski et al. (1992),
with the specific angular momentum of the stellar wind material calculated by
Brookshaw & Tavani (1993).
The influence of the centrifugal force in the rotating models
is implemented according to Kippenhahn & Thomas (1970).
The stellar spin vectors are assumed to be perpendicular to the
orbital plane. Synchronization due to tidal
spin-orbit coupling is included with a time scale given by Zahn (1977).
Rotationally enhanced mass loss is included as follows:
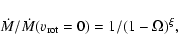 |
(5) |
where 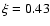 ,
,
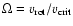 and
and
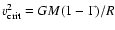 with
with
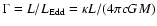 is Eddington factor,
G is gravitational constant, Mis mass, R radius,
is Eddington factor,
G is gravitational constant, Mis mass, R radius, 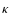 opacity,
opacity,
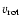 rotating velocity and
rotating velocity and
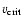 critical rotational velocity (Langer 1998).
critical rotational velocity (Langer 1998).
When the star approaches 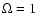 ,
the mass loss rate is increased according
to the previous equation. However, mass loss also causes a spin-down of the star
and equilibrium mass loss rate
,
the mass loss rate is increased according
to the previous equation. However, mass loss also causes a spin-down of the star
and equilibrium mass loss rate
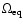 results (Langer 1998).
If
results (Langer 1998).
If
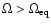 ,
the corresponding angular momentum loss is so large
that the star evolves away from the
,
the corresponding angular momentum loss is so large
that the star evolves away from the 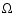 -limit.
-limit.
The transport of angular momentum through the stellar interiour is formulated as a diffusive process:
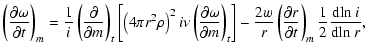 |
|
|
(6) |
where 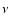 is the turbulent viscosity and i is the specific angular
momentum of a shell at mass coordinate m.
is the turbulent viscosity and i is the specific angular
momentum of a shell at mass coordinate m.
The specific angular momentum of the accreted matter is determined by integrating the
equation of motion of a test particle in the Roche potential in case the
accretion stream
impacts directly on the secondary star, and is assumed Keplerian otherwise Wellstein (2001).
Rotationally induced mixing processes and angular momentum transport through
stellar interior are described by Heger et al. (2000).
Magnetic fields generated due to differential rotation in the stellar interior
(Spruit 2002) are not included here (however, see Petrovic et al. 2004).
We calculated the evolution of the binary systems in detail until Case AB
mass transfer starts. Then we estimated the outcome of this mass transfer
by assuming that it ends when WR star has  5% of the hydrogen left at the surface.
For this purpose we calculate the Kelvin-Helmholtz time scale of the primary:
5% of the hydrogen left at the surface.
For this purpose we calculate the Kelvin-Helmholtz time scale of the primary:
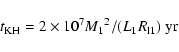 |
(7) |
where 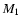 ,
,
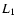 and
and
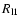 are mass, luminosity and Roche radius
(in Solar units) of the primary star at the onset of Case AB mass transfer.
The mass transfer rate is then assumed as:
are mass, luminosity and Roche radius
(in Solar units) of the primary star at the onset of Case AB mass transfer.
The mass transfer rate is then assumed as:
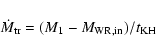 |
(8) |
where
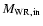 is the mass of the WR star that has a hydrogen surface abundance of 5%; all quantities are
taken at the beginning of the mass transfer.
We calculate the change of the orbital period orbit using
constant value of
is the mass of the WR star that has a hydrogen surface abundance of 5%; all quantities are
taken at the beginning of the mass transfer.
We calculate the change of the orbital period orbit using
constant value of 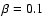 for non-rotating and
for non-rotating and 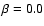 for rotating models
(Wellstein 2001).
Matter that is not retained by the secondary is assumed to leave the system with
a specific angular momentum which corresponds to the secondary's orbital
angular momentum (King et al. 2001).
for rotating models
(Wellstein 2001).
Matter that is not retained by the secondary is assumed to leave the system with
a specific angular momentum which corresponds to the secondary's orbital
angular momentum (King et al. 2001).
5 Non-rotating models
We concluded in Sect. 3 that massive O+O binaries can result in
WR+O systems similar to observed the (HD 186943,
HD 90657 and HD 211853) if accretion efficiency 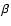 is low.
Since some O stars in WR+O binaries have been observed to rotate faster than synchronously,
we concluded that
is low.
Since some O stars in WR+O binaries have been observed to rotate faster than synchronously,
we concluded that
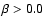 and assumed a constant value of
and assumed a constant value of
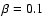 in our detailed evolutionary models.
We already mentioned that the orbital periods of the observed systems are between 6 and 10 days. Since the net effect of Case A+Case AB mass transfer is a widening
of the orbit, the initial periods should be shorter than the observed ones, so
we modelled binary systems with initial orbital periods of 3 and 6 days.
in our detailed evolutionary models.
We already mentioned that the orbital periods of the observed systems are between 6 and 10 days. Since the net effect of Case A+Case AB mass transfer is a widening
of the orbit, the initial periods should be shorter than the observed ones, so
we modelled binary systems with initial orbital periods of 3 and 6 days.
Table 2:
Non-rotating WR+O progenitor models for 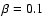 .
N is the number of the model,
.
N is the number of the model,
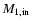 and
and
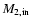 are initial masses of the primary and
the secondary,
are initial masses of the primary and
the secondary,
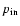 is the initial orbital period and
is the initial orbital period and
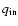 is the initial mass ratio of
the binary system.
is the initial mass ratio of
the binary system. 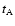 is time when Case A mass transfer starts,
is time when Case A mass transfer starts,
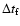 is the duration of the fast phase of Case A mass transfer,
is the duration of the fast phase of Case A mass transfer,
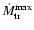 is the maximum mass
transfer rate,
is the maximum mass
transfer rate,
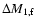 and
and
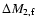 are mass loss of the primary and mass gain
of the secondary (respectively) during fast Case A,
are mass loss of the primary and mass gain
of the secondary (respectively) during fast Case A,
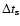 is the duration of slow Case A mass
transfer,
is the duration of slow Case A mass
transfer,
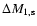 and
and
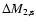 are mass loss of the primary and mass gain
of the secondary (respectively) during the slow Case A,
are mass loss of the primary and mass gain
of the secondary (respectively) during the slow Case A,
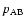 is the orbital period at the onset of Case
AB,
is the orbital period at the onset of Case
AB,
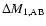 is the mass loss of the primary during Case AB (mass gain of the secondary is
1/10 of this, see Sect. 4),
is the mass loss of the primary during Case AB (mass gain of the secondary is
1/10 of this, see Sect. 4),
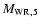 is the WR mass when the hydrogen surface abundance
is
is the WR mass when the hydrogen surface abundance
is
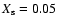 ,
the WR mass at
,
the WR mass at
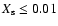 is given in brackets,
is given in brackets,
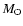 is the mass of the corresponding O star, q is the mass ratio
is the mass of the corresponding O star, q is the mass ratio
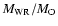 ,
and p is the orbital period of the WR+O system.
The models are computed with a stellar wind mass loss of Hamann/6, except
,
and p is the orbital period of the WR+O system.
The models are computed with a stellar wind mass loss of Hamann/6, except 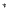 Hamann/3,
Hamann/3, 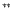 Hamann/2.
Hamann/2.
c indicates a contact phase that occurs
for low masses due to a mass ratio too far from unity, for high masses
due to the secondary expansion during slow phase of Case A.
We chose initial primary masses to be in the range 41...75
 .
The masses of the secondaries are chosen so that the initial mass
ratio (
.
The masses of the secondaries are chosen so that the initial mass
ratio (
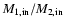 )
is
)
is
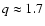 -2.0.
An initial mass ratio of
-2.0.
An initial mass ratio of 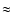 1.55 is estimated to be the limiting value
for the occurrence of contact between the components
in Case A systems by Wellstein et al. (2001) for conservative mass transfer.
Contact occurs when the accretion time scale of the secondary (
1.55 is estimated to be the limiting value
for the occurrence of contact between the components
in Case A systems by Wellstein et al. (2001) for conservative mass transfer.
Contact occurs when the accretion time scale of the secondary (
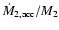 )
is much longer than the thermal (Kelvin-Helmholtz) time scale of the primary
(
)
is much longer than the thermal (Kelvin-Helmholtz) time scale of the primary
(
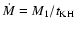 ), so the secondary expands
and fills its Roche lobe. In our models, only 10% of matter lost by the primary
is accreted on the secondary star, so it reaches hydrostatic equilibrium faster
and expands
less than in the case of larger
), so the secondary expands
and fills its Roche lobe. In our models, only 10% of matter lost by the primary
is accreted on the secondary star, so it reaches hydrostatic equilibrium faster
and expands
less than in the case of larger 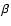 .
This is the reason why we adopted a weaker condition for contact formation and
calculate models with mass ratios
.
This is the reason why we adopted a weaker condition for contact formation and
calculate models with mass ratios
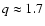 ...2.0.
...2.0.
All modelled systems (except the ones that enter contact) go
through Case A and Case AB mass transfer.
Details of the evolution of all calculated binary systems are given in Table 2.
We discuss the details of the binary evolution taking the system number 11 as an example.
Figure 3 shows the evolutionary tracks of the primary and the secondary in the HR
diagram until the onset of Case AB mass transfer.
This system begins its evolution with the initial parameters
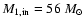 ,
,
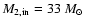 ,
,
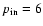 days.
Both stars are core hydrogen burning stars (dashed line, Fig. 3), but since the primary is more
massive, it evolves faster and fills its Roche lobe, so
the system enters Case A mass transfer (solid line, Fig. 3)
days.
Both stars are core hydrogen burning stars (dashed line, Fig. 3), but since the primary is more
massive, it evolves faster and fills its Roche lobe, so
the system enters Case A mass transfer (solid line, Fig. 3)

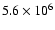 years after the beginning of core hydrogen burning.
The first phase of Case A is fast process and takes place on the Kelvin-Helmholtz (thermal) time
scale (
years after the beginning of core hydrogen burning.
The first phase of Case A is fast process and takes place on the Kelvin-Helmholtz (thermal) time
scale (
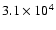 years). The primary loses matter quickly and
continuously with a high mass transfer rate
(
years). The primary loses matter quickly and
continuously with a high mass transfer rate
(
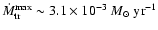 ).
In order to retain hydrostatic equilibrium, the envelope
expands, which requires energy
and causes a decrease in luminosity (Fig. 3). At the same time the secondary is
accreting matter and is expanding.
Due to this, its luminosity increases and the effective temperature decreases (Fig. 3).
During fast phase of Case A mass transfer the primary loses
).
In order to retain hydrostatic equilibrium, the envelope
expands, which requires energy
and causes a decrease in luminosity (Fig. 3). At the same time the secondary is
accreting matter and is expanding.
Due to this, its luminosity increases and the effective temperature decreases (Fig. 3).
During fast phase of Case A mass transfer the primary loses  19
19
 and the secondary
accretes 1/10 of that matter.
After the fast process of mass transfer,
the primary is still burning hydrogen in
its core and is still expanding, so
slow phase of Case A mass transfer takes place on a nuclear time scale (
and the secondary
accretes 1/10 of that matter.
After the fast process of mass transfer,
the primary is still burning hydrogen in
its core and is still expanding, so
slow phase of Case A mass transfer takes place on a nuclear time scale (
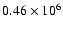 years)
with a mass transfer rate of
years)
with a mass transfer rate of
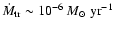 .
After this, the primary is the less massive star,
with decreased hydrogen surface abundance.
Stellar wind mass loss of the primary increases when its surface becomes hydrogen poor
(
.
After this, the primary is the less massive star,
with decreased hydrogen surface abundance.
Stellar wind mass loss of the primary increases when its surface becomes hydrogen poor
(
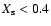 ).
At the end of core hydrogen burning the primary contracts (effective temperature increases)
and thus RLOF stops (Fig. 3 dotted line).
When the primary starts
shell hydrogen burning it expands (dash-dotted line, Fig. 3),
fills its Roche lobe and Case AB mass transfer starts.
).
At the end of core hydrogen burning the primary contracts (effective temperature increases)
and thus RLOF stops (Fig. 3 dotted line).
When the primary starts
shell hydrogen burning it expands (dash-dotted line, Fig. 3),
fills its Roche lobe and Case AB mass transfer starts.
Figures 4 and 5 show the evolution of the interior of the primary and the secondary until
Case AB mass transfer.
The primary loses huge amounts of matter during fast Case A mass transfer and its convective core becomes less than a half of its original mass. At the same time, the
secondary accretes matter from the primary and the heavier elements are being relocated by thermohaline
mixing.
In Figs. 6 and 7 we see the mass transfer rate and
the surface abundances of hydrogen, carbon, nitrogen and oxygen.
During Case AB mass transfer the primary
star loses the major part of its hydrogen envelope. After Case AB mass transfer,
the primary is a helium core burning star (WR) and the secondary is still
a core hydrogen burning O star.
The masses of the modelled WR stars are in the range from  8...18.5
8...18.5
 The orbital periods of the modelled WR+O systems vary
from
The orbital periods of the modelled WR+O systems vary
from  9.5 to
9.5 to  20 days, and the mass ratios are between 0.33 and 0.53.
20 days, and the mass ratios are between 0.33 and 0.53.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2368fig3.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg135.gif) |
Figure 3:
HR diagram of the initial system
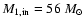 , ,
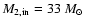 , ,
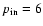 days.
Both stars are core hydrogen burning (dashed line) until Case A mass transfer starts (solid line).
The primary is losing mass and its luminosity and effective temperature decrease. At the same
time the secondary is accreting matter and expanding, becoming more luminous and cooler.
After Case A mass transfer is finished, the primary is losing mass by stellar wind and contracting
at the end of core hydrogen burning (dotted line). After this the primary starts with shell hydrogen
burning and expands (dash-dotted line). days.
Both stars are core hydrogen burning (dashed line) until Case A mass transfer starts (solid line).
The primary is losing mass and its luminosity and effective temperature decrease. At the same
time the secondary is accreting matter and expanding, becoming more luminous and cooler.
After Case A mass transfer is finished, the primary is losing mass by stellar wind and contracting
at the end of core hydrogen burning (dotted line). After this the primary starts with shell hydrogen
burning and expands (dash-dotted line).
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2368fig4.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg136.gif) |
Figure 4:
The evolution of the internal structure of the 56
 primary during the
core hydrogen
burning. Convection is indicated with diagonal hatching and semiconvection with crossed hatching.
The hatched area at the bottom indicates nuclear burning.
The topmost solid line corresponds to the surface of the star.
primary during the
core hydrogen
burning. Convection is indicated with diagonal hatching and semiconvection with crossed hatching.
The hatched area at the bottom indicates nuclear burning.
The topmost solid line corresponds to the surface of the star. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig5.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg137.gif) |
Figure 5:
The evolution of the internal structure of the 33
 secondary during core hydrogen
burning of the primary. Convection is indicated with diagonal hatching, semiconvection with
crossed hatching and thermohaline mixing with
straight crossed hatching.
The hatched area at the bottom indicates nuclear burning.
The topmost solid line corresponds to the surface of the star.
secondary during core hydrogen
burning of the primary. Convection is indicated with diagonal hatching, semiconvection with
crossed hatching and thermohaline mixing with
straight crossed hatching.
The hatched area at the bottom indicates nuclear burning.
The topmost solid line corresponds to the surface of the star. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2368fig6.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg138.gif) |
Figure 6:
Upper plot: mass transfer rate during Case A mass transfer in the binary system
with
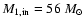 , ,
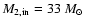 , ,
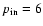 days.
Lower plot: the hydrogen surface abundance of the primary (solid line) is decreasing during mass transfer
and further due to stellar wind mass loss. The secondary (dashed
line) recovered its original surface hydrogen abundance through thermohaline mixing. The primary
starts losing mass with WR stellar wind mass loss when its hydrogen surface abundance falls beneath days.
Lower plot: the hydrogen surface abundance of the primary (solid line) is decreasing during mass transfer
and further due to stellar wind mass loss. The secondary (dashed
line) recovered its original surface hydrogen abundance through thermohaline mixing. The primary
starts losing mass with WR stellar wind mass loss when its hydrogen surface abundance falls beneath
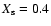 ,
represented by the dotted line. ,
represented by the dotted line. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig7.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg139.gif) |
Figure 7:
Surface abundance of carbon (solid line), nitrogen (dotted line) and
oxygen (dashed line) of the primary ( upper plot)
and the secondary ( lower plot) in the system with
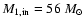 , ,
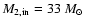 , ,
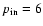 days. days. |
| Open with DEXTER |
5.1 Relation between initial and WR mass
The initial mass of helium core of the primary in the binary system depends on a
few parameters: initial primary mass, initial period, initial mass ratio and
stellar wind mass loss rate.
If the primary loses matter due to the mass transfer or stellar wind during core hydrogen
burning,
it will form a helium core that is less massive than if
there was no mass loss.
If the initial period is very short, Case A mass transfer will take place
very early in the evolution of the primary, so the star will not have time to
develop a larger core before it starts losing mass due to Roche lobe overflow.
If the initial mass ratio (
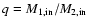 )
increases,
the mass transfer
rate from the primary star increases too and
this results in less massive primaries that will
evolve into less massive WR stars.
)
increases,
the mass transfer
rate from the primary star increases too and
this results in less massive primaries that will
evolve into less massive WR stars.
In our models the primary starts losing mass by stellar wind as WR star when its hydrogen surface
abundance goes below
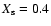 .
However, the observed WR stars in HD 186943, HD 90657 and HD 211853 do not have
obvious hydrogen on the surface, so we
assume that these WR stars are the result of Case AB mass transfer, with
a hydrogen surface abundance of
.
However, the observed WR stars in HD 186943, HD 90657 and HD 211853 do not have
obvious hydrogen on the surface, so we
assume that these WR stars are the result of Case AB mass transfer, with
a hydrogen surface abundance of
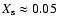 .
We also calculated the
corresponding WR masses with
.
We also calculated the
corresponding WR masses with
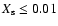 .
We plotted in Fig. 8 the initial WR masses (
.
We plotted in Fig. 8 the initial WR masses (
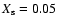 and
and
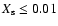 )
versus the initial primary (progenitor)
masses. With "star'' symbols we indicated WR stars that originate from binary
systems with an initial mass ratio of
)
versus the initial primary (progenitor)
masses. With "star'' symbols we indicated WR stars that originate from binary
systems with an initial mass ratio of
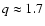 and an initial period
p=3 days (Table 2: N 4, 8, 9, 13, 14). Large "star'' symbols represent
WR stars with 5% of hydrogen at the
surface and small symbols indicate WR stars that
have a hydrogen surface abundance of less than 1%.
and an initial period
p=3 days (Table 2: N 4, 8, 9, 13, 14). Large "star'' symbols represent
WR stars with 5% of hydrogen at the
surface and small symbols indicate WR stars that
have a hydrogen surface abundance of less than 1%.
We derive a relation between the initial primary mass and the
initial WR mass (derived as a linear fit)
for p=3 days and
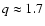 ,
(
,
(
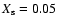 ):
):
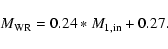 |
(9) |
We use this relation to estimate the initial parameters of the possible
progenitors of the observed WR+O binary systems, as already explained in Sect. 3.
In the same way, the relation between the initial primary mass and the
initial WR mass (
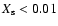 )
for the same systems is:
)
for the same systems is:
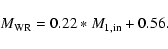 |
(10) |
We also show in Fig. 8 the initial WR masses (
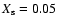 for binary systems
N 5, 10, 11, 12, Table 2)
for an initial mass ratio of
for binary systems
N 5, 10, 11, 12, Table 2)
for an initial mass ratio of  1.7 and an initial orbital period
of 6 days (diamond symbols). We notice that the resulting WR masses are higher than
the ones that come out from systems with an initial
orbital period of 3 days (see Sect. 5.3).
Different "diamond'' symbols for the initial primary 56
1.7 and an initial orbital period
of 6 days (diamond symbols). We notice that the resulting WR masses are higher than
the ones that come out from systems with an initial
orbital period of 3 days (see Sect. 5.3).
Different "diamond'' symbols for the initial primary 56
 are for different mass
loss rates (see Sect. 5.4).
Triangle symbols in Fig. 8 show the initial WR masses for constant initial primary mass,
are for different mass
loss rates (see Sect. 5.4).
Triangle symbols in Fig. 8 show the initial WR masses for constant initial primary mass,
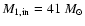 ,
but for different initial mass ratios (see Sect. 5.2).
,
but for different initial mass ratios (see Sect. 5.2).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig8.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg146.gif) |
Figure 8:
Initial WR mass as a function of initial (progenitor) mass.
Large and small symbols indicate WR stars with hydrogen surface abundance of
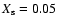 and
and
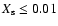 ,
respectively.
Systems with an initial orbital period of ,
respectively.
Systems with an initial orbital period of
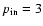 days and a mass ratio of
days and a mass ratio of 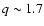 are indicated with star symbols, systems with an initial period of 6 days and
are indicated with star symbols, systems with an initial period of 6 days and 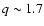 with diamond symbols,
systems with an initial primary 41
with diamond symbols,
systems with an initial primary 41
 and initial period of 3 days with triangle symbols.
The dashed line represents a linear fit for systems with an initial period of 3 days and
with
and initial period of 3 days with triangle symbols.
The dashed line represents a linear fit for systems with an initial period of 3 days and
with
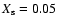 ,
and the dotted line
represents linear fit for systems with an initial period of 3 days and ,
and the dotted line
represents linear fit for systems with an initial period of 3 days and
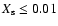 . .
|
| Open with DEXTER |
Note that the WR masses that are the result of early Case A progenitor evolution
are significantly lower than ones that are the result
of Case B evolution (Wellstein & Langer 1999), because of the mass transfer
from the primary during the core hydrogen burning phase.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig9.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg147.gif) |
Figure 9:
Mass transfer rate ( upper plot) and orbital period ( lower plot) during Case A
mass transfer as a function of the change of the primary mass for
systems with the initial primary
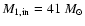 ,
initial orbital period ,
initial orbital period
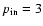 days and four different initial mass ratios: 2.00 (dotted line),
1.71 (solid line), 1.52 (dashed line) and 1.37 (dash-dotted line).
(Table 2: N 3, 4, 6, 7) days and four different initial mass ratios: 2.00 (dotted line),
1.71 (solid line), 1.52 (dashed line) and 1.37 (dash-dotted line).
(Table 2: N 3, 4, 6, 7) |
| Open with DEXTER |
5.2 Influence of the initial mass ratio on the WR mass and orbital period
During the mass transfer phase, the mass transfer rate increases roughly until the
masses of both components are equal.
The maximum mass transfer rate during Case A increases with the increase of the initial mass ratio
(
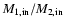 )
and the resulting WR star is less massive.
To analyse the influence of the initial mass ratio on the evolution of the binary system, we compared
systems with an initial primary mass of
)
and the resulting WR star is less massive.
To analyse the influence of the initial mass ratio on the evolution of the binary system, we compared
systems with an initial primary mass of
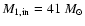 ,
an initial
orbital period of
,
an initial
orbital period of
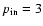 days for five different initial mass ratios: 2.05, 2.00, 1.71, 1.52 and 1.37.
(Table 2 N 1, 3, 4, 6, 7, Fig. 9).
The system with
days for five different initial mass ratios: 2.05, 2.00, 1.71, 1.52 and 1.37.
(Table 2 N 1, 3, 4, 6, 7, Fig. 9).
The system with
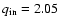 enters contact during fast Case A mass transfer. The
mass transfer rate
in this case is very high (
enters contact during fast Case A mass transfer. The
mass transfer rate
in this case is very high (
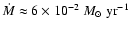 ),
the secondary expands, fills its Roche lobe and the system enters a contact phase.
The system with an
initial mass ratio of
),
the secondary expands, fills its Roche lobe and the system enters a contact phase.
The system with an
initial mass ratio of
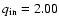 loses
loses 
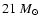 during the fast phase of Case A. The maximum mass transfer rate of this system is
during the fast phase of Case A. The maximum mass transfer rate of this system is
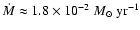 .
The helium surface abundance of the primary
after this mass transfer is 65%, so the
primary shrinks, loses mass through a WR stellar wind
and there is no slow phase of Case A mass transfer (
.
The helium surface abundance of the primary
after this mass transfer is 65%, so the
primary shrinks, loses mass through a WR stellar wind
and there is no slow phase of Case A mass transfer (
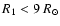 ).
For the other three models q=1.71, 1.52, 1.37, the primaries lose less mass
(
).
For the other three models q=1.71, 1.52, 1.37, the primaries lose less mass
( 15, 14, 13
15, 14, 13
 respectively) during the fast phase of Case
A mass transfer. The helium surface abundances in these systems after fast Case A mass transfer
are
respectively) during the fast phase of Case
A mass transfer. The helium surface abundances in these systems after fast Case A mass transfer
are  30-35%. The primaries
expand (
30-35%. The primaries
expand (
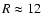 -15
-15
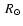 )
on a nuclear time scale and transfer
mass to the secondaries (slow phase of Case A).
)
on a nuclear time scale and transfer
mass to the secondaries (slow phase of Case A).
We can conclude the following:
first, if the initial mass ratio is larger, the mass transfer rate from the primary during fast phase
Case A mass transfer is higher.
Second, if the mass transfer rate is higher, the helium surface abundance of the star
increases faster and if it reaches 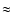 58%, the primary starts losing mass with
a higher (WR) mass loss rate and slow Case A mass transfer can be avoided.
58%, the primary starts losing mass with
a higher (WR) mass loss rate and slow Case A mass transfer can be avoided.
We also show in Fig. 9 (lower plot) how the period changes during
Case A mass transfer for binary systems N 3, 4, 6, 7.
Roughly, when the mass is transfered from the more to the less massive star, the
binary orbit shrinks, and when the mass is transfered from the less to the more massive
star, the orbit widens.
If the initial period is close to unity,
the absolute difference between stellar masses is small, and more mass is
transfered from the less to the more massive star during the evolution of the system.
This results in a longer final period after Case A mass transfer.
Systems with initial mass ratios of 2.00, 1.71, 1.52 and 1.37 enter Case AB mass
transfer with orbital periods of 2.9, 3.9, 4.4 and 5.2 days respectively.
However, the final period is also (more significantly)
influenced by the stellar wind mass loss rate and the amount of matter lost
from the primary during Case AB mass transfer (see
Sect. 5.4).
5.3 Influence of the initial period on the WR mass
Depending on the initial orbital period of a binary system, Case A mass transfer phase will
start earlier or later in the evolution. If the period is larger, the primary
will develop a larger core, before it starts transferring mass onto the secondary,
and the resulting WR star will be more massive.
To investigate the influence of the initial period, we compare binary systems
41
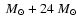 and
56
and
56
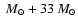 with p=3 days and p=6 days (Table 2: N 4, 5, 9, 10).
with p=3 days and p=6 days (Table 2: N 4, 5, 9, 10).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg10.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg158.gif) |
Figure 10:
Mass transfer rate during Case A mass transfer for systems
41
 +24 +24
 ( upper plot) and 56
( upper plot) and 56
 +33 +33
 ( lower plot)
and an initial orbital period of
( lower plot)
and an initial orbital period of
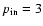 days (solid line) and days (solid line) and
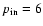 days (dashed line).
Case A mass transfer starts later in initially wider binary systems, the primary has more time to
increase mass of its core and the initial WR star is more massive (Table 2: N 4, 5, 9, 10). days (dashed line).
Case A mass transfer starts later in initially wider binary systems, the primary has more time to
increase mass of its core and the initial WR star is more massive (Table 2: N 4, 5, 9, 10). |
| Open with DEXTER |
If the initial orbital period increases for 3 days, a 41
 star will
enter Case A mass transfer
star will
enter Case A mass transfer 
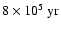 later and a 56
later and a 56
 star
star 
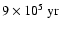 later.
So, there are two things to point out:
first, the more massive star (56
later.
So, there are two things to point out:
first, the more massive star (56
 )
evolves faster, and second,
a 3 days longer
initial period postpones Case A mass transfer, for this star, by about 10
)
evolves faster, and second,
a 3 days longer
initial period postpones Case A mass transfer, for this star, by about 10
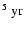 more than for a 41
more than for a 41
 star.
The net effect is a more significant increase of the convective
core (i.e. initial helium core, i.e. initial WR mass),
for more massive star, due to the initial orbit widening.
star.
The net effect is a more significant increase of the convective
core (i.e. initial helium core, i.e. initial WR mass),
for more massive star, due to the initial orbit widening.
5.4 Influence of WR mass loss rate on masses and final period
In our models, we assume that
when the star has less than 40% of hydrogen at the surface,
it starts losing mass according to the Hamann et al. (1995) WR mass loss rate,
multiplied by factors: 1/6, 1/3 and 1/2 (Table 2: N 10, 11, 12).
If the primary is losing more mass by stellar wind during core hydrogen burning,
it will develop a less massive helium core. At the same time there will be less matter
to be transfered during Roche lobe overflow, so the secondary will accrete less.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2368fg11.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg162.gif) |
Figure 11:
Primary mass ( first plot), mass transfer rate ( second plot) and stellar wind
mass loss rate from the primary (third plot) until the onset of Case AB mass transfer for the
system
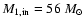 , ,
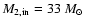 , ,
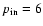 days and three different stellar wind mass loss rates (from
days and three different stellar wind mass loss rates (from
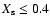 ): 1/6 (solid line),
1/3 (dotted line) and 1/2 (dashed line) of mass loss rate proposed by Hamann et al. (1995)
(Table 2: N 10, 11, 12). ): 1/6 (solid line),
1/3 (dotted line) and 1/2 (dashed line) of mass loss rate proposed by Hamann et al. (1995)
(Table 2: N 10, 11, 12). |
| Open with DEXTER |
We show in Fig. 11 the influence of the stellar wind mass loss (Plot c) on the primary mass
(Plot a) and mass transfer rate (Plot b) of
systems with
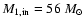 ,
,
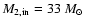 ,
,
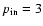 and three different stellar wind mass loss rates (from
and three different stellar wind mass loss rates (from
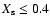 ): 1/6 (solid line),
1/3 (dotted line) and 1/2 (dashed line) of the mass loss proposed by Hamann et al. (1995).
We notice that for higher mass loss rates, the slow phase of Case A
stops earlier, due to the decrease of the stellar radius.
The orbit is widening due to the stellar wind mass loss and
the final period increases with the increasing mass loss rate.
However, the orbit is more significantly widening during Case AB mass transfer.
The more mass there is to
transfer from the primary to the secondary during Case AB mass transfer,
the larger the final orbital period.
So, if the stellar wind removes most of the hydrogen envelope of the primary,
there will be less mass to transfer during Case AB and
the net effect of a higher mass loss rate is a shorter orbital period of the WR+O system.
): 1/6 (solid line),
1/3 (dotted line) and 1/2 (dashed line) of the mass loss proposed by Hamann et al. (1995).
We notice that for higher mass loss rates, the slow phase of Case A
stops earlier, due to the decrease of the stellar radius.
The orbit is widening due to the stellar wind mass loss and
the final period increases with the increasing mass loss rate.
However, the orbit is more significantly widening during Case AB mass transfer.
The more mass there is to
transfer from the primary to the secondary during Case AB mass transfer,
the larger the final orbital period.
So, if the stellar wind removes most of the hydrogen envelope of the primary,
there will be less mass to transfer during Case AB and
the net effect of a higher mass loss rate is a shorter orbital period of the WR+O system.
6 Rotating models
When mass transfer in a binary system starts, the primary loses matter through the first Lagrangian
point (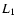 ). This matter carries a certain angular momentum that will be transfered to the
secondary. If there is an accretion disk, the angular momentum of the transfered matter is assumed to
be Keplerian. If there is a direct impact accretion, like in our models, we calculate the angular
momentum following a test particle moving through
). This matter carries a certain angular momentum that will be transfered to the
secondary. If there is an accretion disk, the angular momentum of the transfered matter is assumed to
be Keplerian. If there is a direct impact accretion, like in our models, we calculate the angular
momentum following a test particle moving through 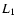 .
This angular momentum spins up the top layers of the secondary star, and
angular momentum is transfered further into the star due to rotationally induced mixing processes.
Every time the secondary spins up to close to critical rotation it starts losing
more mass due to the influence of centrifugal force (Eq. (5)). High mass loss decreases the net
accretion efficiency and
also removes angular momentum from the secondary star. The secondary star is also spun down by tidal
forces that tend to synchronize it with the orbital motion. Wellstein (2001)
investigated these processes in binary systems with
initial mass ratios close to unity and concluded that
the accretion efficiency does not decrease significantly for Case A mass transfer, but in
the Case B the parameter
.
This angular momentum spins up the top layers of the secondary star, and
angular momentum is transfered further into the star due to rotationally induced mixing processes.
Every time the secondary spins up to close to critical rotation it starts losing
more mass due to the influence of centrifugal force (Eq. (5)). High mass loss decreases the net
accretion efficiency and
also removes angular momentum from the secondary star. The secondary star is also spun down by tidal
forces that tend to synchronize it with the orbital motion. Wellstein (2001)
investigated these processes in binary systems with
initial mass ratios close to unity and concluded that
the accretion efficiency does not decrease significantly for Case A mass transfer, but in
the Case B the parameter 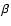 can be significantly decreased by rotation.
We present Case A rotating models with larger mass ratio
can be significantly decreased by rotation.
We present Case A rotating models with larger mass ratio
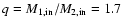 ...2 and
find
that accretion can be significantly decreased during Case A mass transfer. The reason is the following:
if the initial mass ratio increases, so does the maximum mass transfer rate (
...2 and
find
that accretion can be significantly decreased during Case A mass transfer. The reason is the following:
if the initial mass ratio increases, so does the maximum mass transfer rate (
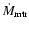 increases roughly until the masses in binary system are equal). If there is more mass
transfered from the primary to the secondary, the rotational velocity of the secondary is higher
as well as its mass loss, which leads to a smaller accretion efficiency.
increases roughly until the masses in binary system are equal). If there is more mass
transfered from the primary to the secondary, the rotational velocity of the secondary is higher
as well as its mass loss, which leads to a smaller accretion efficiency.
We compare the evolution of non-rotating and
rotating binary systems on the example
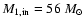
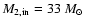 ,
an initial orbital period of p=6 days,
and Hamann/3 WR mass loss stellar wind rate (Table 3: N 6).
The rotating binary system is synchronized as it starts core hydrogen burning and it stays that way until
mass transfer starts. The radius of the primary increases during the main sequence phase
(from
,
an initial orbital period of p=6 days,
and Hamann/3 WR mass loss stellar wind rate (Table 3: N 6).
The rotating binary system is synchronized as it starts core hydrogen burning and it stays that way until
mass transfer starts. The radius of the primary increases during the main sequence phase
(from  10 to
10 to  25
25
 ,
Fig. 19b),
but the rotation of the primary stays synchronized with the orbital
period. This is why the rotational velocity of the primary also increases from
,
Fig. 19b),
but the rotation of the primary stays synchronized with the orbital
period. This is why the rotational velocity of the primary also increases from  100 to
100 to
 200
200
 (Fig. 19d). The radius of the rotating primary increases faster
than the radius of the non-rotating primary due to the influence of the centrifugal force.
The result is that Case A mass transfer starts earlier for the rotating binary system
(
(Fig. 19d). The radius of the rotating primary increases faster
than the radius of the non-rotating primary due to the influence of the centrifugal force.
The result is that Case A mass transfer starts earlier for the rotating binary system
(
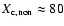 %) then for the corresponding nonrotating one(
%) then for the corresponding nonrotating one(
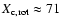 %,
Fig. 15).
%,
Fig. 15).
When the fast phase of Case A starts, the secondary spins up (Fig. 20d)
and stellar wind mass loss rapidly increases
(
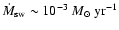 ,
Fig. 20c).
The accretion efficiency during this phase in the rotating system is
,
Fig. 20c).
The accretion efficiency during this phase in the rotating system is
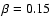 (Table 3).
We see in Fig. 15 that the orbital period after Case A mass transfer of the
rotating binary system is
shorter than for the non-rotating system (4.5 compared with 6.6 days).
The orbital angular momentum of the binary is changing due to mass transfer,
mass loss from the system and spin-orbit coupling. The rotating binary system loses more angular
momentum and the final orbital period is shorter than in the corresponding non-rotating system.
Angular momentum loss in our systems is calculated according to Podsiadlowski et al. (1992)
as already mentioned
in Sect. 4, and parameter
(Table 3).
We see in Fig. 15 that the orbital period after Case A mass transfer of the
rotating binary system is
shorter than for the non-rotating system (4.5 compared with 6.6 days).
The orbital angular momentum of the binary is changing due to mass transfer,
mass loss from the system and spin-orbit coupling. The rotating binary system loses more angular
momentum and the final orbital period is shorter than in the corresponding non-rotating system.
Angular momentum loss in our systems is calculated according to Podsiadlowski et al. (1992)
as already mentioned
in Sect. 4, and parameter 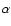 that determines the efficiency of angular momentum loss is
calculated according to Brookshaw & Tavani (1993). It increases with the mass ratio
that determines the efficiency of angular momentum loss is
calculated according to Brookshaw & Tavani (1993). It increases with the mass ratio
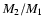 and
the ratio between the secondary radius and its Roche radius
and
the ratio between the secondary radius and its Roche radius
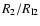 .
In rotating system the secondary
accretes slightly more matter (
.
In rotating system the secondary
accretes slightly more matter (
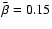 )
compared to
)
compared to 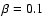 in non-rotating systems,
so the mass ratio
in non-rotating systems,
so the mass ratio
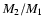 is larger in the rotating system. Second, the secondary is spinning fast and its
radius is larger than in the non-rotating case, and so is the ratio
is larger in the rotating system. Second, the secondary is spinning fast and its
radius is larger than in the non-rotating case, and so is the ratio
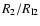 .
The result is that the angular
momentum is more efficiently removed from the system in the rotating binary system.
After the fast phase of Case A mass transfer, the two primaries, non-rotating and rotating, have almost the same
mass
.
The result is that the angular
momentum is more efficiently removed from the system in the rotating binary system.
After the fast phase of Case A mass transfer, the two primaries, non-rotating and rotating, have almost the same
mass  34
34
 and helium surfa- ce abundance
and helium surfa- ce abundance
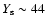 %. However, since the orbital periods are
%. However, since the orbital periods are
Table 3:
Rotating WR+O progenitor models.
N is the number of the model,
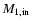 and
and
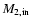 are initial masses of the primary and
the secondary,
are initial masses of the primary and
the secondary,
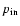 is the initial orbital period and
is the initial orbital period and
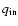 is the initial mass ratio of
the binary system.
is the initial mass ratio of
the binary system. 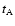 is the time when Case A mass transfer starts,
is the time when Case A mass transfer starts,
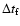 is the duration of the the fast phase of Case A mass transfer,
is the duration of the the fast phase of Case A mass transfer,
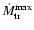 is the maximum mass
transfer rate,
is the maximum mass
transfer rate,
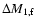 and
and
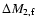 are mass loss of the primary and mass gain
of the secondary (respectively) during the fast Case A,
are mass loss of the primary and mass gain
of the secondary (respectively) during the fast Case A,
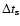 is the duration of slow Case A mass
transfer,
is the duration of slow Case A mass
transfer,
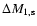 and
and
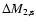 are mass loss of the primary and mass gain
of the secondary (respectively) during the slow Case A,
are mass loss of the primary and mass gain
of the secondary (respectively) during the slow Case A,
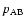 is the orbital period at the onset of Case
AB,
is the orbital period at the onset of Case
AB,
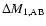 is the mass loss of the primary during Case AB (mass gain of the secondary is
1/10 of this, see Sect. 4),
is the mass loss of the primary during Case AB (mass gain of the secondary is
1/10 of this, see Sect. 4),
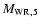 is the WR mass when the hydrogen surface abundance is
is the WR mass when the hydrogen surface abundance is
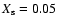 ,
,
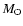 is the mass of the corresponding O star, q is the
mass ratio
is the mass of the corresponding O star, q is the
mass ratio
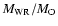 ,
p is the orbital period of the WR+O system and
,
p is the orbital period of the WR+O system and
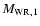 is WR mass with
is WR mass with
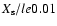 .
The models are computed with a stellar wind mass loss of Hamann/6 except :
.
The models are computed with a stellar wind mass loss of Hamann/6 except : Hamann/3,
Hamann/3,
 Hamann/2.
Hamann/2.
c indicates a contact phase.
different, so are the radii of the
primaries ( 18
18
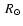 for the rotating and
for the rotating and
 23
23
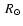 for the non-rotating
case).
for the non-rotating
case).
Table 4:
Comparison of resulting WR masses and orbital periods from
non-rotating and rotating binary systems with the same initial parameters.
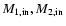 are
initial primary and secondary mass,
are
initial primary and secondary mass,
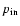 is the initial orbital period,
is the initial orbital period,
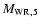 ,
,
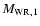 are WR masses at
are WR masses at
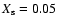 and
and
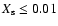 respectively
and p is the orbital period in the initial WR+O system where the hydrogen surface abundance of WR star is
respectively
and p is the orbital period in the initial WR+O system where the hydrogen surface abundance of WR star is
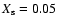 .
Systems are modelled with WR stellar wind mass loss H/6 except
.
Systems are modelled with WR stellar wind mass loss H/6 except  which are done with H/3,
which are done with H/3, 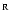 indicates rotating models.
indicates rotating models.
When the fast phase of Case A is finished, the non-rotating primary has still  20% of
hydrogen to burn (
20% of
hydrogen to burn (
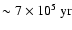 ), and the rotating primary has
), and the rotating primary has
 10% more than
that (
10% more than
that (
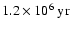 ). When the surface hydrogen abundance is less than 40%,
the primaries start losing mass as WR stars, i.e., their stellar wind mass loss rate increases.
Since the rotating primary has more time to spend on the main sequence, it also has more time to lose
mass by WR stellar wind mass loss (
). When the surface hydrogen abundance is less than 40%,
the primaries start losing mass as WR stars, i.e., their stellar wind mass loss rate increases.
Since the rotating primary has more time to spend on the main sequence, it also has more time to lose
mass by WR stellar wind mass loss (
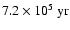 compared with
compared with
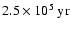 for non-rotating system).The result is that the non-rotating primary enters Case AB
mass transfer as a
for non-rotating system).The result is that the non-rotating primary enters Case AB
mass transfer as a
 26
26
 star with
star with
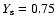 ,
while the rotating one is a
,
while the rotating one is a  17
17
 star
with
star
with
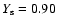 .
Clearly, the rotating primary has less hydrogen in its envelope, i.e. less mass to
transfer to the secondary during Case AB mass transfer, and the orbit widens less than in the non-rotating
system.
We can draw the conclusion that if rotation is included in our calculations,
the initial WR mass is smaller and the orbital period of the WR+O system is
shorter than in the corresponding non-rotating system (Table 4).
.
Clearly, the rotating primary has less hydrogen in its envelope, i.e. less mass to
transfer to the secondary during Case AB mass transfer, and the orbit widens less than in the non-rotating
system.
We can draw the conclusion that if rotation is included in our calculations,
the initial WR mass is smaller and the orbital period of the WR+O system is
shorter than in the corresponding non-rotating system (Table 4).
We present in Fig. 12 the evolutionary tracks of the rotating primary and secondary in the
HR diagram.
Both stars are core hydrogen burning stars (dashed line, Fig. 12),
but since the primary is more
massive, it evolves faster and fills its Roche lobe, so
the system enters Case A mass transfer (solid line, Fig. 12).
The primary loses matter quickly with a high mass transfer rate
(
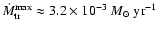 )
and its luminosity decreases (Fig. 12).
At the same time
the secondary accretes matter and its luminosity increases, but due to
change in rotational velocity (Fig. 20d) its radius and effective temperature are changing
as well (Figs. 12d, 20a,b).
During fast Case A mass transfer the primary lost
)
and its luminosity decreases (Fig. 12).
At the same time
the secondary accretes matter and its luminosity increases, but due to
change in rotational velocity (Fig. 20d) its radius and effective temperature are changing
as well (Figs. 12d, 20a,b).
During fast Case A mass transfer the primary lost  19
19
 and the secondary
accreted 15% of that matter.
After the fast mass transfer,
the primary is still burning hydrogen in
its core and is still expanding, so
slow Case A mass transfer takes place. After the primary starts losing mass with a WR
stellar wind mass loss rate (
and the secondary
accreted 15% of that matter.
After the fast mass transfer,
the primary is still burning hydrogen in
its core and is still expanding, so
slow Case A mass transfer takes place. After the primary starts losing mass with a WR
stellar wind mass loss rate (
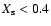 )
its radius will decrease and the slow phase of
Case A stops (Fig. 19c).
However, the primary continues expanding on the nuclear time scale (Fig. 19b)
and it fills its Roche lobe once again (Fig. 15, upper plot).
At the end of core hydrogen burning the primary contracts (effective temperature increases)
and thus RLOF stops. This phase is presented in Fig. 12 with a dotted line.
When hydrogen starts burning in
a shell, the primary star expands (dash-dotted line, Fig. 12),
fills its Roche lobe and Case AB mass transfer starts.
)
its radius will decrease and the slow phase of
Case A stops (Fig. 19c).
However, the primary continues expanding on the nuclear time scale (Fig. 19b)
and it fills its Roche lobe once again (Fig. 15, upper plot).
At the end of core hydrogen burning the primary contracts (effective temperature increases)
and thus RLOF stops. This phase is presented in Fig. 12 with a dotted line.
When hydrogen starts burning in
a shell, the primary star expands (dash-dotted line, Fig. 12),
fills its Roche lobe and Case AB mass transfer starts.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2368fg12.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg193.gif) |
Figure 12:
HR diagram of the initial system
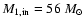 , ,
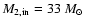 , ,
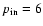 days with rotation.
Both stars are core hydrogen burning (dashed line) until Case A mass transfer starts (solid line).
The primary is losing mass and its luminosity decreases. At the same
time the secondary is accreting matter and expanding, becoming more luminous.
After Case A mass transfer is finished, the primary is losing mass by stellar wind and contracting
at the end of core hydrogen burning (dotted line). After this the primary starts shell hydrogen
burning and expands (dash-dotted line). days with rotation.
Both stars are core hydrogen burning (dashed line) until Case A mass transfer starts (solid line).
The primary is losing mass and its luminosity decreases. At the same
time the secondary is accreting matter and expanding, becoming more luminous.
After Case A mass transfer is finished, the primary is losing mass by stellar wind and contracting
at the end of core hydrogen burning (dotted line). After this the primary starts shell hydrogen
burning and expands (dash-dotted line). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg13.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg194.gif) |
Figure 13:
The evolution of the internal structure of the rotating 56
 primary during core hydrogen
burning. Convection is indicated with diagonal hatching and semiconvection with crossed hatching.
The hatched area
at the bottom indicates nuclear burning.
Gray shaded areas represent regions with rotationally induced
mixing (intensity is indicated with different shades, the darker the colour, the stronger rotational
mixing). The topmost solid line corresponds to the surface of the star.
primary during core hydrogen
burning. Convection is indicated with diagonal hatching and semiconvection with crossed hatching.
The hatched area
at the bottom indicates nuclear burning.
Gray shaded areas represent regions with rotationally induced
mixing (intensity is indicated with different shades, the darker the colour, the stronger rotational
mixing). The topmost solid line corresponds to the surface of the star. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg14.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg195.gif) |
Figure 14:
The evolution of the internal structure of the rotating 33
 secondary during core hydrogen
burning of the primary. Convection is indicated with diagonal hatching, semiconvection with
crossed hatching and thermohaline mixing with straight crossed hatching.
The hatched area
at the bottom indicates nuclear burning.
Gray shaded areas represent regions with rotationally induced
mixing (intensity is indicated with different shades, the darker the colour, the stronger rotational
mixing). The topmost solid line corresponds to the surface of the star.
secondary during core hydrogen
burning of the primary. Convection is indicated with diagonal hatching, semiconvection with
crossed hatching and thermohaline mixing with straight crossed hatching.
The hatched area
at the bottom indicates nuclear burning.
Gray shaded areas represent regions with rotationally induced
mixing (intensity is indicated with different shades, the darker the colour, the stronger rotational
mixing). The topmost solid line corresponds to the surface of the star. |
| Open with DEXTER |
The initial helium core masses are 18.6
 for the non-rotating and 14.8
for the non-rotating and 14.8
 for
the rotating primary. When Case AB mass transfer starts, the orbital periods are 7.9 d and 6.6 d
for the non-rotating and the rotating system respectively (Fig. 15, lower plot).
The non-rotating primary loses
for
the rotating primary. When Case AB mass transfer starts, the orbital periods are 7.9 d and 6.6 d
for the non-rotating and the rotating system respectively (Fig. 15, lower plot).
The non-rotating primary loses  7
7
 and the rotating one
and the rotating one  2
2
 during Case AB. When there is more mass to be transfered from the less to the more massive star in a binary
system, the orbit widens more and the final orbital period is longer.
during Case AB. When there is more mass to be transfered from the less to the more massive star in a binary
system, the orbit widens more and the final orbital period is longer.
Figures 13 and 14 show the structure of the primary and the secondary
before Case AB mass transfer.
The primary loses large amounts of matter during the fast phase of Case A mass transfer ( 20
20
 ),
and its convective core becomes less than half of its original mass. At the same time, the
secondary accretes matter from the primary and the heavier elements are being relocated by thermohaline
mixing.
Figures 16 and 17
show surface abundances of the primary and the secondary.
The secondary is accreting material from the primary and its surface abundances
change due to this, but also due to thermohaline and rotational mixing.
),
and its convective core becomes less than half of its original mass. At the same time, the
secondary accretes matter from the primary and the heavier elements are being relocated by thermohaline
mixing.
Figures 16 and 17
show surface abundances of the primary and the secondary.
The secondary is accreting material from the primary and its surface abundances
change due to this, but also due to thermohaline and rotational mixing.
Figure 18 shows the orbital angular momentum of the system and the spin periods
of both components. The orbital angular momentum of the system
decreases rapidly due to mass loss from the system during fast Case A mass transfer, and then further due
to stellar wind mass loss.
The primary slows down rapidly during fast Case A and
further due to stellar wind mass loss. The secondary spins up due to the accretion from the primary
during fast Case A mass transfer and then slows down due to stellar wind mass loss. It
spins up again during slow Case A mass transfer.
The masses of modelled WR stars are in the range from  11
11
 to
to  15.7
15.7
 .
Period of modelled WR+O systems vary
from
.
Period of modelled WR+O systems vary
from  7.6 to
7.6 to
 12.7 days and mass ratios are between 0.35 and 0.46 (Table 3).
12.7 days and mass ratios are between 0.35 and 0.46 (Table 3).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2368fg15.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg196.gif) |
Figure 15:
Upper plot: the mass transfer rate during
Case A mass transfer in the binary systems with
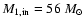 , ,
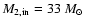 , ,
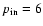 days with (solid line)
and without rotation (dotted line).
Lower plot: orbital period evolution in rotating and non-rotating system. days with (solid line)
and without rotation (dotted line).
Lower plot: orbital period evolution in rotating and non-rotating system. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg16.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg197.gif) |
Figure 16:
The hydrogen surface abundance (solid line) in the primary in system
with
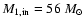 , ,
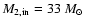 , ,
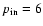 days
is decreasing during mass transfer
and further due to stellar wind mass loss. The secondary (dashed
line) decreases its hydrogen surface abundance due to mass transfer. The
dotted line indicates a hydrogen abundance of 0.4, where
the primary starts losing mass with a WR stellar wind. days
is decreasing during mass transfer
and further due to stellar wind mass loss. The secondary (dashed
line) decreases its hydrogen surface abundance due to mass transfer. The
dotted line indicates a hydrogen abundance of 0.4, where
the primary starts losing mass with a WR stellar wind. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg17.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg198.gif) |
Figure 17:
Surface abundance of carbon (solid line), nitrogen (dotted line) and
oxygen (dashed line) in the primary ( upper plot)
and the secondary ( lower plot), in the system with
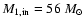 , ,
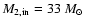 , ,
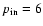 days.
The secondary abundances are changed due to mass transfer of matter from the primary,
thermohaline mixing and rotational mixing. days.
The secondary abundances are changed due to mass transfer of matter from the primary,
thermohaline mixing and rotational mixing. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg18.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg199.gif) |
Figure 18:
The orbital angular momentum ( upper plot) of
the non-rotating (dotted line) and the rotating (solid line) binary systems with
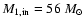 , ,
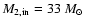 , ,
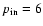 days, decreases
rapidly due to mass loss from the system during fast Case A mass transfer and then further due
to stellar wind mass loss.
Spin period ( lower plot) of the primary (dashed line) and the secondary (dash-dotted line)
in the above mentioned rotating binary system. days, decreases
rapidly due to mass loss from the system during fast Case A mass transfer and then further due
to stellar wind mass loss.
Spin period ( lower plot) of the primary (dashed line) and the secondary (dash-dotted line)
in the above mentioned rotating binary system. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg19.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg200.gif) |
Figure 19:
Effective temperature (plot a)), stellar radius (plot b)), stellar wind mass
loss rate (plot c)) and rotational velocity (plot d)) of the primary star
in the non-rotating (dotted line) and
rotating (solid line) binary system with
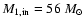 , ,
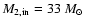 , ,
 days. days. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg20.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg201.gif) |
Figure 20:
Effective temperature (plot a)), stellar radius (plot b)), stellar wind mass
loss rate (plot c)) and rotational velocity (plot d)) of the secondary star
in the non-rotating (dotted line) and
rotating (solid line) binary system with
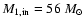 , ,
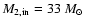 , ,
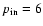 days. days. |
| Open with DEXTER |
6.1 Influence of rotation on the accretion efficiency
We show in Table 5 average accretion efficiencies of rotating binary systems during different
mass transfer phases, and total average values with and without stellar wind mass loss from the primary
included.
During fast Case A mass transfer, the primary stars are losing matter with very high mass transfer rates
(3...
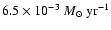 ). The angular momentum of surface layers in the secondary
increases fast, they spin up to close to the critical rotation and start losing mass
with high mass loss rate
(
). The angular momentum of surface layers in the secondary
increases fast, they spin up to close to the critical rotation and start losing mass
with high mass loss rate
( 10
10
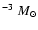 ). The average accretion efficiency during fast Case A in our
models is 15-20%. Since this phase takes place on the thermal time scale, stellar wind mass loss from the
primary is negligible during this phase.
). The average accretion efficiency during fast Case A in our
models is 15-20%. Since this phase takes place on the thermal time scale, stellar wind mass loss from the
primary is negligible during this phase.
Slow Case A mass transfer takes place on the nuclear time scale. The primary stars start losing
their mass due to a WR stellar wind when their surfaces become hydrogen deficient (
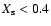 ).
The WR stellar wind mass
loss rates are of the order of:
).
The WR stellar wind mass
loss rates are of the order of:
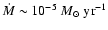 ,
and
we have to take into account stellar wind mass loss of the primary during slow Case A.
We calculate the mass loss of the primary only due to mass transfer and total mass loss including stellar
wind mass loss, and the two corresponding average accretion efficiencies.
If we calculate
,
and
we have to take into account stellar wind mass loss of the primary during slow Case A.
We calculate the mass loss of the primary only due to mass transfer and total mass loss including stellar
wind mass loss, and the two corresponding average accretion efficiencies.
If we calculate
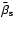 only for mass transfer, we notice that the slow Case A is
almost
a conservative process. The average mass transfer rates are
only for mass transfer, we notice that the slow Case A is
almost
a conservative process. The average mass transfer rates are  10
10
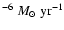 and the secondary stars are able to accrete almost everything without spinning up to critical
rotation.
and the secondary stars are able to accrete almost everything without spinning up to critical
rotation.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg21.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg207.gif) |
Figure 21:
Upper plot: mass transfer (solid line) and accretion rate (dotted line) of the rotating
initial system
56
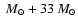 ,
p=6 days. Dashed line represent mass transfer rate in the corresponding
non-rotating binary.
Lower plot: accretion efficiency of the secondary taking into
account matter lost by the primary only due to mass transfer. ,
p=6 days. Dashed line represent mass transfer rate in the corresponding
non-rotating binary.
Lower plot: accretion efficiency of the secondary taking into
account matter lost by the primary only due to mass transfer. |
| Open with DEXTER |
Figure 21 shows how mass transfer rate, accretion rate and 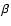 change in the rotating model with 56
change in the rotating model with 56
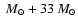 ,
,
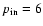 days
(WR mass loss Hamann/3) depending on the amount of matter lost by the primary.
We also see in this figure the mass transfer rate from the primary in the non-rotating case.
We can notice in the upper plot, what we previously discussed,
that during most of the fast Case A mass transfer,
the mass accretion rate of the secondary is about
one order of magnitude lower than the mass loss rate of the primary.
The primary loses
days
(WR mass loss Hamann/3) depending on the amount of matter lost by the primary.
We also see in this figure the mass transfer rate from the primary in the non-rotating case.
We can notice in the upper plot, what we previously discussed,
that during most of the fast Case A mass transfer,
the mass accretion rate of the secondary is about
one order of magnitude lower than the mass loss rate of the primary.
The primary loses  19.3
19.3
 during the fast phase and the secondary gains
during the fast phase and the secondary gains
 2.9
2.9
 ,
which means that on
average
,
which means that on
average  15% of the mass has been accreted.
However, the mass loss of the primary due to mass transfer during the slow phase is
15% of the mass has been accreted.
However, the mass loss of the primary due to mass transfer during the slow phase is
 4.5
4.5
 ,
and the secondary accretes
,
and the secondary accretes  3.9
3.9
 which means that
which means that
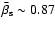 .
If we take into account stellar wind mass loss of the primary stars,
the average accretion efficiencies are lower.
For example, the total mass loss of the
primary during slow Case A mass transfer, including the stellar wind, in the previous example is
.
If we take into account stellar wind mass loss of the primary stars,
the average accretion efficiencies are lower.
For example, the total mass loss of the
primary during slow Case A mass transfer, including the stellar wind, in the previous example is
 10.9
10.9
 ,
which means that
,
which means that
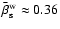 .
We neglected accretion during Case AB mass transfer since Wellstein (2001) showed that
it is inefficient, and since the primary stars in the modelled systems
have relatively low mass hydrogen envelopes, and masses of secondary stars will not
significantly change due to this mass transfer.
(However, let us not forget that even the accretion of very small amounts of matter
can be important for spinning up the secondary's surface layers and making it rotate
faster than synchronously in a WR + O binary system.)
Also, since this mass transfer
takes place on the thermal time scale, stellar wind mass loss can be neglected.
.
We neglected accretion during Case AB mass transfer since Wellstein (2001) showed that
it is inefficient, and since the primary stars in the modelled systems
have relatively low mass hydrogen envelopes, and masses of secondary stars will not
significantly change due to this mass transfer.
(However, let us not forget that even the accretion of very small amounts of matter
can be important for spinning up the secondary's surface layers and making it rotate
faster than synchronously in a WR + O binary system.)
Also, since this mass transfer
takes place on the thermal time scale, stellar wind mass loss can be neglected.
Finally, we can estimate the total mass loss from the binary systems including stellar wind,
or only due to mass
transfer, and calculate corresponding values of 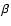 .
In the binary systems we modelled, the primary stars lose between 30
.
In the binary systems we modelled, the primary stars lose between 30
 and 45
and 45
 due to mass
transfer and stellar wind, until they
ignite helium in their core. The amount of lost mass increases with initial mass. At the same time
the secondaries accrete 3...10
due to mass
transfer and stellar wind, until they
ignite helium in their core. The amount of lost mass increases with initial mass. At the same time
the secondaries accrete 3...10
 .
This means that in most cases 80...90% of the mass lost by the primary leaves the binary system.
On the other hand, the primary stars lose
.
This means that in most cases 80...90% of the mass lost by the primary leaves the binary system.
On the other hand, the primary stars lose  20...30
20...30
 only due to mass transfer, so
the average accretion of secondary stars in our models is between 15 and 30%.
only due to mass transfer, so
the average accretion of secondary stars in our models is between 15 and 30%.
Table 5:
Mass loss from binary systems. N is number of the model corresponding to
Table 3.
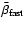 is the average accretion efficiency of the secondary during the
fast phase of
Case A mass transfer.
is the average accretion efficiency of the secondary during the
fast phase of
Case A mass transfer.
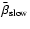 is the accretion efficiency of the secondary during the
slow phase of
Case A mass transfer taking into account matter lost by the primary only due to the mass transfer.
is the accretion efficiency of the secondary during the
slow phase of
Case A mass transfer taking into account matter lost by the primary only due to the mass transfer.
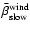 is the average accretion efficiency of the secondary during the slow phase of
Case A mass transfer taking into account matter lost by the primary due to the mass transfer and stellar
wind.
is the average accretion efficiency of the secondary during the slow phase of
Case A mass transfer taking into account matter lost by the primary due to the mass transfer and stellar
wind.
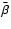 is the average accretion efficiency of the secondary during the
progenitor evolution of WR+O binary
system taking into account matter lost by the primary only due to the mass transfer and
is the average accretion efficiency of the secondary during the
progenitor evolution of WR+O binary
system taking into account matter lost by the primary only due to the mass transfer and
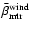 taking also into account stellar wind mass loss of the primary.
taking also into account stellar wind mass loss of the primary.
7 Comparison with observations
Our rotating models give generally similar results as our non-rotating models
for 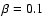 .
.
The rotating binary systems R6 (56
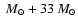 ,
p=6 days,
Hamann/3 WR mass loss) and R1 and R2
(41
,
p=6 days,
Hamann/3 WR mass loss) and R1 and R2
(41
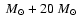 ,
p=6 days) agree quite well with the observed
systems HD 186943 and HD 90657,
as well as the non-rotating systems N11 and N12
(56
,
p=6 days) agree quite well with the observed
systems HD 186943 and HD 90657,
as well as the non-rotating systems N11 and N12
(56
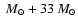 ,
p=6 days; WR mass loss rate Hamann/2 and
Hamann/3).
The system R6
evolves into a WR+O configuration with
15
,
p=6 days; WR mass loss rate Hamann/2 and
Hamann/3).
The system R6
evolves into a WR+O configuration with
15
 +39
+39
 and p=8.5 days.
I.e., its masses and period are close to those found in HD 186943 and HD 90657,
even though its mass ratio of 0.38 is somewhat smaller than what is observed.
Systems R1 and R2
evolve into a
11
and p=8.5 days.
I.e., its masses and period are close to those found in HD 186943 and HD 90657,
even though its mass ratio of 0.38 is somewhat smaller than what is observed.
Systems R1 and R2
evolve into a
11
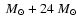 WR+O system with a 9.8 day orbital period.
I.e., period and mass ratio (0.46) agree well with the observed systems,
but the stellar masses are somewhat smaller than observed (cf. Sect. 2).
Systems N11 and N12 evolve into a WR+O system of
19
WR+O system with a 9.8 day orbital period.
I.e., period and mass ratio (0.46) agree well with the observed systems,
but the stellar masses are somewhat smaller than observed (cf. Sect. 2).
Systems N11 and N12 evolve into a WR+O system of
19
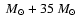 with an orbital period of 12...14 days.
In this case, both masses and the mass ratio (0.53) agree well with the observed
ones, but the orbital period is slightly too large.
I.e., although none of our models is a perfect match of HD 186943 or HD 90657
- which to find would require many more models, however, might not teach us
very much - it is clear form these results that both systems can in fact be well
explained through highly inefficient Case A mass transfer.
with an orbital period of 12...14 days.
In this case, both masses and the mass ratio (0.53) agree well with the observed
ones, but the orbital period is slightly too large.
I.e., although none of our models is a perfect match of HD 186943 or HD 90657
- which to find would require many more models, however, might not teach us
very much - it is clear form these results that both systems can in fact be well
explained through highly inefficient Case A mass transfer.
The situation is more difficult with HD 211853 (GP Cep):
neither the models with nor those without rotation reproduce it satisfactory.
HD 211853 has the shortest period (6.7 d) and largest mass ratio (0.54) of the three
chosen Galactic WR+O binaries. While we can not exclude that
a Case A model of the kind presented here can reproduce this systems,
especially the small period makes it appear more likely that this
system has gone through a contact phase: contact would reduce the orbital angular momentum,
and increase the mass loss from the system, i.e. result in a larger WR/O mass ratio
(Wellstein et al. 2001).
This reasoning is strengthened by the consideration that, in contrast to HD 186943 or HD 90657,
the WR star in HD 211853 is of spectral type WN6/WNC. I.e., as this spectroscopic
signature is not interpreted in terms of a binary nature of the WR component,
but rather by assuming that the WR star is in the transition phase from the WN to the
WC stage (Langer 1991; Massey & Grove 1989). This implies that the WR star
in HD 211853 must have already lost several solar masses of helium-rich matter,
which causes the orbit to widen.
For example, system R6, which evolved into a
14.8
 +39.0
+39.0
 WR+O system with p=8.53 days,
evolves into a WC+O system
after losing
WR+O system with p=8.53 days,
evolves into a WC+O system
after losing  5
5
 more from the Wolf-Rayet star,
which increases its orbital period by
more from the Wolf-Rayet star,
which increases its orbital period by  3 days.
I.e., HD 211853 might have entered the WR+O stage with an orbital period of about
4 days, which would put it together with the shortest period WR binaries like
CX Cep or CQ Cep whose periods are 2.1 and 1.64 days respectively.
3 days.
I.e., HD 211853 might have entered the WR+O stage with an orbital period of about
4 days, which would put it together with the shortest period WR binaries like
CX Cep or CQ Cep whose periods are 2.1 and 1.64 days respectively.
During the evolution of WR+O binary system, the primary loses
mass due to WR stellar wind mass loss.
WR stellar wind mass loss of the primary
decreases mass ratio of the system and increases the orbital period, which means
that, for example, WC+O binary system HD 63099 (
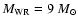 ,
,
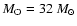 and p=14 days) could have evolved into present state
through a WN+O binary system with q=0.5.
and p=14 days) could have evolved into present state
through a WN+O binary system with q=0.5.
8 Conclusions
In an effort to constrain the progenitor evolution of the three WN+O
binaries HD 186943, HD 90657, and HD 211853,
we calculated the evolution of non-conservative Case A binary systems with
primaries
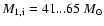 and initial mass ratios
between 1.7 and 2 until the WN+O stage.
We performed binary evolution calculations neglecting rotational processes in the
two stellar components, and assuming a constant mass accretion efficiency of 10% for all three phases of the mass transfer, fast Case A, slow Case A, and Case AB.
Those models could match two of the three systems reasonably well,
while HD 211853, which has the shortest orbital period, the largest mass ratio, and
a WN/WC Wolf-Rayet component, was found to be not well explained by contact-free
evolutionary models: While models with shorter initial orbital periods result in short periods
during the WR+O stage, the initial WR mass is decreasing at the same time, which
leads to smaller initial WR/O mass ratios.
and initial mass ratios
between 1.7 and 2 until the WN+O stage.
We performed binary evolution calculations neglecting rotational processes in the
two stellar components, and assuming a constant mass accretion efficiency of 10% for all three phases of the mass transfer, fast Case A, slow Case A, and Case AB.
Those models could match two of the three systems reasonably well,
while HD 211853, which has the shortest orbital period, the largest mass ratio, and
a WN/WC Wolf-Rayet component, was found to be not well explained by contact-free
evolutionary models: While models with shorter initial orbital periods result in short periods
during the WR+O stage, the initial WR mass is decreasing at the same time, which
leads to smaller initial WR/O mass ratios.
We then computed binary evolution models including the physics of rotation in
both stellar components as well as the spin-up process of the mass gainer due
to angular momentum accretion. In these models, the surface of the accreting star
is continuously spun-up by accretion, while at the same time angular momentum
is transported from the outer layers into the stellar interior by rotationally
induced mixing processes. By employing a simple model for the mass loss of
rapidly rotating luminous stars - the so called  -limit, which
was actually worked out to describe the mass loss processes in Luminous Blue Variables
(Langer 1997) - accretion is drastically reduced once the star reaches
critical rotation at its surface. The mass accretion rate is then controlled
by the time scale of internal angular momentum transport.
-limit, which
was actually worked out to describe the mass loss processes in Luminous Blue Variables
(Langer 1997) - accretion is drastically reduced once the star reaches
critical rotation at its surface. The mass accretion rate is then controlled
by the time scale of internal angular momentum transport.
Some first such model for Case A and early Case B have been computed
by Wellstein (Langer et al. 2003,2004) for a primary mass of 15
 and
a mass ratio close to one. The result was that rather high mass accretion efficiencies
(
and
a mass ratio close to one. The result was that rather high mass accretion efficiencies
(
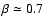 )
could be obtained for initial periods shorter than about 8 days.
Here we find that, with the same physical assumptions although at higher system mass,
the accretion efficiency drops to about 10% at an initial mass ratio of 1.7.
As Wellstein (2001) computed one early Case A model for a 26
)
could be obtained for initial periods shorter than about 8 days.
Here we find that, with the same physical assumptions although at higher system mass,
the accretion efficiency drops to about 10% at an initial mass ratio of 1.7.
As Wellstein (2001) computed one early Case A model for a 26
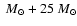 system which gave
system which gave
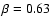 ,
it is like the high initial mass ratio
in our models which is responsible for the low accretion efficiency:
larger initial mass ratios lead to larger mass transfer rates and, as the time scale
of internal angular momentum transport in the accreting star is rather unaffected,
to smaller accretion efficiencies.
,
it is like the high initial mass ratio
in our models which is responsible for the low accretion efficiency:
larger initial mass ratios lead to larger mass transfer rates and, as the time scale
of internal angular momentum transport in the accreting star is rather unaffected,
to smaller accretion efficiencies.
Our rotating models - in which the accretion efficiency is no free
parameter any more but is computed selfconsistent and time-dependent -
reproduce the observed WR+O binaries quite well, i.e. as good as our
models without rotation physics, where the accretion efficiency is a free
parameter. Our simplified considerations in Sect. 3 have shown that this
is unlikely attributable to the freedom in the choice of the initial parameter
of the binary system, i.e. initial masses and period - at least under the
assumption that contact was avoided. In case of contact, various new parameters
enter the model, similar to the case of common envelope evolution.
And indeed, also our rotating models can not reproduce HD 211853
very well, mostly because it currently has a too short orbital period, which was
likely even significantly shorter at the beginning of its WR+O stage.
However, this of course only confirms the result of the simpler approaches
that a contact-free approach does not work well for this system.
In summary we can say that the system mass and angular momentum loss model used here
- which is the first detailed approach to tackle the long-standing angular
momentum problem in mass transferring binaries - has passed the test
of WR+O binaries. However, it still needs to be explored over which
part of the space spanned by the initial binary parameters this model
works well, and to what extent its results are sensitive to future
improvements in the stellar interior physics. The inclusion of magnetic
fields generated by differential rotation (Spruit 2002) will be the next
step in this direction (Petrovic et al. 2004).
- Bonanos, A. Z.,
Stanek, K. Z., Udalski, A., et al. 2004, ApJ, 611,
L33 [NASA ADS] [CrossRef]
- Braun, A. 1998,
Ph.D. Thesis
- Braun, H., &
Langer, N. 1995, A&A, 297, 483 [NASA ADS]
- Brookshaw, L., &
Tavani, M. 1993, ApJ, 410, 719 [NASA ADS] [CrossRef]
- Chevalier, C., &
Ilovaisky, S. A. 1998, A&A, 330, 201 [NASA ADS]
- de Loore, C., &
de Greve, J. P. 1992, A&AS, 94, 453 [NASA ADS]
- Demers, H., Moffat,
A. F. J., Marchenko, S. V., Gayley, K. G.,
& Morel, T. 2002, ApJ, 577, 409 [NASA ADS] [CrossRef]
- Dessart, L., Langer,
N., & Petrovic, J. 2003, A&A, 404, 991 [EDP Sciences] [NASA ADS]
- Hamann, W.-R., &
Koesterke, L. 1998, A&A, 335, 1003 [NASA ADS]
- Hamann, W.-R.,
Koesterke, L., & Wessolowski, U. 1995, A&A, 299, 151 [NASA ADS]
- Heger, A., &
Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef]
- Heger, A., Langer, N.,
& Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef]
- Heger, A., Woosley,
S. E., Langer, N., & Spruit, H. C. 2004, in IAU
Symp., 215, 591
- Iglesias, C. A.,
& Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef]
- King, A. R.,
Schenker, K., Kolb, U., & Davies, M. B. 2001, MNRAS, 321,
327 [NASA ADS] [CrossRef]
- Kippenhahn, R., &
Thomas, H.-C. 1970, in Stellar Rotation, IAU Coll., 4, 20
- Kippenhahn, R., Kohl,
K., & Weigert, A. 1967, Z. Astrophys., 66, 58 [NASA ADS]
- Kopal, Z., ed. 1978,
Dynamics of Close Binary Systems
- Kudritzki,
R. P., Pauldrach, A., Puls, J., & Abbott, D. C. 1989,
A&A, 219, 205 [NASA ADS]
- Lamontagne, R.,
Moffat, A. F. J., Drissen, L., Robert, C., &
Matthews, J. M. 1996, AJ, 112, 2227 [NASA ADS]
- Langer, N. 1991,
A&A, 252, 669 [NASA ADS]
- Langer, N. 1997, in
Luminous Blue Variables: Massive Stars in Transition, ASP Conf.
Ser., 120, 83
- Langer, N. 1998,
A&A, 329, 551 [NASA ADS]
- Langer, N.,
Deutschmann, A., Wellstein, S., & Höflich, P. 2000,
A&A, 362, 1046 [NASA ADS]
- Langer, N., Wellstein,
S., & Petrovic, J. 2003, in IAU Symp., 212, 275
- Langer, N., Yoon, S.-C.,
Petrovic, J., & Heger, A. 2004, in IAU Symp., 215, 535
- Maeder, A., &
Meynet, G. 2003, A&A, 411, 543 [EDP Sciences] [NASA ADS]
- Massey, P. 1981, ApJ,
244, 157 [NASA ADS] [CrossRef]
- Massey, P., &
Grove, K. 1989, ApJ, 344, 870 [NASA ADS] [CrossRef]
- Meyer, F., &
Meyer-Hofmeister, E. 1983, A&A, 121, 29 [NASA ADS]
- Meynet, G., &
Maeder, A. 2000, A&A, 361, 101 [NASA ADS]
- Niemela, V. S.,
& Moffat, A. F. J. 1982, ApJ, 259, 213 [NASA ADS] [CrossRef]
- Packet, W. 1981,
A&A, 102, 17 [NASA ADS]
- Paczynski, B. 1967,
Acta Astron., 17, 355 [NASA ADS]
- Paczynski, B. 1991,
ApJ, 370, 597 [NASA ADS] [CrossRef]
- Panov, K. P.,
& Seggewiss, W. 1990, A&A, 227, 117 [NASA ADS]
- Petrovic, J., &
Langer, N. 2004, in Rev. Mex. Astron. Astrofis. Conf. Ser.,
231
- Petrovic, J.,
Langer, N., Yoon, S.-C., & Heger, A. 2004, A&A,
accepted
- Podsiadlowski, P.,
Joss, P. C., & Hsu, J. J. L. 1992, ApJ, 391,
246 [NASA ADS] [CrossRef]
- Rauw, G., De Becker,
M., Nazé, Y., et al. 2004, A&A, 420, L9 [EDP Sciences] [NASA ADS]
- Ritter, H. 1988,
A&A, 202, 93 [NASA ADS]
- Spruit, H. C.
2002, A&A, 381, 923 [EDP Sciences] [NASA ADS]
- Underhill, A. B.,
Yang, S., & Hill, G. M. 1988, PASP, 100, 1256 [NASA ADS]
- van den Heuvel,
E. P. J., & Heise, J. 1972, Nature Phys. Sci., 239,
67 [NASA ADS]
-
van der Hucht, K. A. 2001, New Astron. Rev., 45,
135 [NASA ADS]
- Vanbeveren, D. 1982,
A&A, 105, 260 [NASA ADS]
- Vanbeveren, D. 1991,
A&A, 252, 159 [NASA ADS]
- Vanbeveren, D., de
Greve, J. P., de Loore, C., & van Dessel, E. L.
1979, A&A, 73, 19 [NASA ADS]
- Wellstein,
S. 2001, Ph.D. Thesis
(In the text)
- Wellstein, S., &
Langer, N. 1999, A&A, 350, 148 [NASA ADS]
- Wellstein, S.,
Langer, N., & Braun, H. 2001, A&A, 369, 939 [EDP Sciences] [NASA ADS]
- Woosley, S. E., Heger,
A. 2004, in IAU Symp., 215, 601
- Yoon, S.-C., &
Langer, N. 2004a, A&A, 419, 645 [EDP Sciences] [NASA ADS]
- Yoon, S.-C., &
Langer, N. 2004b, A&A, 419, 623 [EDP Sciences] [NASA ADS]
- Zahn, J.-P. 1977,
A&A, 57, 383 [NASA ADS]
Copyright ESO 2005
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig1.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig2.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg87.gif)
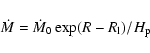
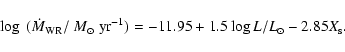
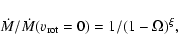
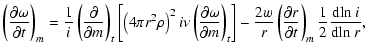
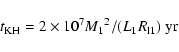
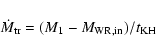
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2368fig3.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg135.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2368fig4.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg136.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig5.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg137.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2368fig6.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg138.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig7.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg139.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig8.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg146.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fig9.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg147.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg10.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg158.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2368fg11.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg162.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2368fg12.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg193.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg13.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg194.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg14.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg195.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2368fg15.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg196.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg16.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg197.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg17.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg198.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg18.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg199.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg19.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg200.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg20.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg201.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2368fg21.eps}
\end{figure}](/articles/aa/full/2005/21/aa2368-04/Timg207.gif)