A&A 435, 885-899 (2005)
DOI: 10.1051/0004-6361:20041170

Are PAHs precursors of small hydrocarbons in photo-dissociation regions? The Horsehead case

J. Pety 1,2 - D. Teyssier 3,4 - D. Fossé 1 - M. Gerin 1 - E. Roueff 5 - A. Abergel 6 - E. Habart 7 - J. Cernicharo 3


1 - LERMA, UMR 8112, CNRS, Observatoire de Paris and Ecole Normale Supérieure, 24 rue Lhomond, 75231 Paris Cedex 05, France
2 - IRAM, 300 rue de la Piscine, 38406 Grenoble Cedex, France
3 - Instituto de Estructura de la Materia, CSIC, Serrano 121, 28006 Madrid, Spain
4 - Space Research Organization Netherlands, PO Box 800, 9700 AV Groningen, The Netherlands
5 - LUTH UMR 8102, CNRS and Observatoire de Paris, Place J. Janssen 92195 Meudon Cedex, France
6 - IAS, Université Paris-Sud, Bât. 121, 91405 Orsay Cedex, France
7 - Osservatorio Astrofisico di Arcetri, L.go E. Fermi 5, 50125 Firenze, Italy

Received 27 April 2004 / Accepted 11 January 2005

Abstract
We present maps at high spatial and spectral resolution in emission lines of CCH, c-C3H2, C4H, 12CO and C18O of the edge of the Horsehead nebula obtained with the IRAM Plateau de Bure Interferometer (PdBI). The edge of the Horsehead nebula is a one-dimensional Photo-Dissociation Region (PDR) viewed almost edge-on. All hydrocarbons are detected at high signal-to-noise ratio in the PDR where intense emission is seen both in the H2 ro-vibrational lines and in the PAH mid-infrared bands. C18O peaks farther away from the cloud edge. Our observations demonstrate that CCH, c-C3H2 and C4H are present in UV-irradiated molecular gas, with abundances nearly as high as in dense, well-shielded molecular cores.
PDR models i) need a large density gradient at the PDR edge to correctly reproduce the offset between the hydrocarbons and H2 peaks; and ii) fail to reproduce the hydrocarbon abundances. We propose that a new formation path of carbon chains, in addition to gas phase chemistry, should be considered in PDRs: because of intense UV-irradiation, large aromatic molecules and small carbon grains may fragment and feed the interstellar medium with small carbon clusters and molecules in significant amounts.

Key words: ISM: clouds - ISM: molecules - ISM: individual object: Horsehead nebula - radio lines: ISM

   
1 Introduction

Due to the ISO mission, the knowledge of interstellar dust has significantly progressed in the recent years. With its instruments sensitive in the mid-infrared, ISO revealed the spatial distribution and line profile of the Aromatic Infrared Bands (AIBs at 3.3, 6.2, 7.7, 8.6 and 11.3 $\mu$m features), which have shed light on the emission mechanism and their possible carriers (Rapacioli et al. 2005; Boulanger et al. 2000). However, no definite identification of individual species has been possible yet because the bands are not specific for individual molecules. The most likely carriers are large polycyclic aromatic hydrocarbons (PAHs) with about 50 carbon atoms (Allain et al. 1996b; Le Page et al. 2003). The ubiquity of the aromatic band emission in the interstellar medium has triggered a wealth of theoretical and laboratory work in the past two decades, which has led to a revision of astrophysical models. PAHs are now suspected to play a major role in both interstellar medium physics and chemistry. With their small size, they are the most efficient particles for the photo-electric effect (Bakes & Tielens 1994; Habart et al. 2001; Weingartner & Draine 2001). Their presence also affects the ionization balance (Flower & Pineau des Forêts 2003; Wolfire et al. 2003), and possibly the formation of H2 (Habart et al. 2004). The role of PAHs in the neutralization of atomic ions in the diffuse interstellar medium has been recently reconsidered by Liszt (2003), following previous work by Lepp et al. (1988). As emphasized soon after their discovery (Lepp & Dalgarno 1988; Omont 1986), PAHs also play a role in gas chemistry: some laboratory experiments and theoretical calculations suggest that PAHs may fragment into small carbon clusters and molecules under photon impact (C2, C3, C2H2, etc.) (Allain et al. 1996b; Leger et al. 1989; Allain et al. 1996a; Scott et al. 1997; Joblin 2003; Le Page et al. 2003). In addition, investigation of the lifetimes of interstellar PAHs implies that photo-dissociation may be the main limiting process for their life in the interstellar medium (Verstraete et al. 2001).

It is therefore appropriate to wonder whether PAHs could fragment continuously and feed the interstellar medium with small hydrocarbons and carbon clusters. This hypothesis is attractive for the following reasons:

i)
Cyclopropenylidene (c-C3H2) is widely distributed in the interstellar medium (Matthews & Irvine 1985; Cox et al. 1988; Lucas & Liszt 2000; Matthews et al. 1986).
ii)
Recent works have shown that the diffuse interstellar medium is more chemically active than previously thought with molecules as large as C3 (Maier et al. 2001; Goicoechea et al. 2004; Ádámkovics et al. 2003; Roueff et al. 2002; Oka et al. 2003) and c-C3H2 (Lucas & Liszt 2000) widely distributed. The abundances of C3 and c-C3H2 are tightly connected to those of smaller molecules, C2 and CCH respectively, with abundance ratios of [C2]/[C3 $] \sim 10{-}40$ (Oka et al. 2003) and [CCH]/[c-C3H2 $] \sim 27.7 \pm 8$ (Lucas & Liszt 2000).
iii)
Thorburn et al. (2003) have found a correlation between the abundance of C2 and the strength of some (weak) Diffuse Interstellar Bands (DIBs).
As PAHs are present in the diffuse interstellar medium, could they contribute to form both the small carbon clusters (C2, C3) and larger hydrocarbon molecules which could be the DIB carriers?

Unfortunately, studies of the PAH emission bands in the diffuse interstellar clouds where the carbon clusters have been detected is extremely difficult because of the low column densities, and also because the bright background stars used for visible spectroscopy prohibit the use of sensitive IR cameras which would be saturated. Photo-Dissociation regions (PDRs) are the first interstellar sources in which AIBs have been found and for which the PAH hypothesis has been proposed (Sellgren 1984; Leger & Puget 1984). It is therefore interesting to investigate the carbon chemistry in these sources. Fossé et al. (2000) and Teyssier et al. (2004) have discussed medium spatial resolution (30'') observations of various hydrocarbons in nearby PDRs. They show that CCH, c-C3H2 and C4H are ubiquitous in these regions, with abundances almost as high as in dark, well shielded clouds, despite the strong UV radiation. Fuente et al. (2003) also report high abundances of c-C3H2 in NGC 7023 and the Orion Bar. Heavier molecules may be present in PDRs as Teyssier et al. (2004) report a tentative detection of C6H in the Horsehead nebula. PDRs and diffuse clouds therefore seem to share the same carbon chemistry, but because of their larger H2 column density and gas density, PDRs offer more opportunities to detect rare species.

Teyssier et al. (2004) and Fuente et al. (2003) propose that the presence of carbon chains is in favor of a causal link between small hydrocarbons and PAHs, but they lack the spatial resolution to draw firm conclusions. In the present work, we present high spatial resolution observations of one source studied by Teyssier et al. (2004), the Horsehead nebula, obtained with the Plateau de Bure interferometer. We describe the observations in Sect. 2. We show the interferometer maps in Sect. 3. Section 4 presents a comparison with chemical models.

   
2 Observations and data reduction

2.1 The Horsehead nebula

The Horsehead nebula, also called Barnard 33, appears as a dark patch of $\sim$5' extent against the bright HII region IC 434. Emission from the gas and dust associated with this globule has been detected from mid-IR to millimeter wavelengths (Teyssier et al. 2004; Abergel et al. 2003,2002; Pound et al. 2003). From the analysis of the ISOCAM images, Abergel et al. (2003) conclude that the Horsehead nebula is a PDR viewed edge-on and illuminated by the O9.5V star $\sigma $Ori at a projected distance of 0.5 \ensuremath {^\circ } (3.5 \ensuremath{~ \ensuremath{{\rm pc}}} for a distance of 400 \ensuremath{~ \ensuremath{{\rm pc}}}, Anthony-Twarog 1982). The far-UV intensity of the incident radiation field is G0 = 60relative to the average interstellar radiation field in Draine units (Draine 1978). The gas density, derived from the excitation of molecular lines and from the penetration depth of the UV-radiation, is a few $10^4\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $ (Abergel et al. 2003). From a combined analysis of maps of both CO and atomic carbon, Lis & Guesten (2005) obtain similar figures for the gas density. Habart et al. (2004,2005) have modeled the emission of H2 (from narrow band images of the H2 ro-vibrational line), PAHs and CO, and conclude that i) the gas density follows a steep gradient at the cloud edge, rising to $n_\ensuremath{{\rm H}} = 10^5\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $ in less than 10'' (i.e. 0.02 \ensuremath{~ \ensuremath{{\rm pc}}}); and ii) this density gradient model is essentially a constant pressure model (with $P = 4 ~\times~ 10^6\ensuremath{~ \ensuremath{{\rm K~km~s^{-1}}}} $).

The edge of the Horsehead nebula is particularly well delineated by the mid-IR emission due to PAHs, with a bright 7.7  \ensuremath{~ \ensuremath{{\rm\mu m}}}-peak (hereafter named the "IR peak'') reaching 25 MJy/sr at $\rm\alpha_{2000} = 05^h40^m53.70^s , \delta_{2000} = -02^\circ 28' 04''$. Figure 1 shows the region observed with the IRAM PdBI centered near the "IR peak''. Two mosaics (one for hydrocarbon lines and the other for the CO lines) have been observed. Their set-ups are detailed in Table 1.

Table 1: Observation parameters.


  \begin{figure} \includegraphics[height=8.8cm,angle=270,clip]{1170f1} \end{figure} Figure 1: The field of view covered when mapping small hydrocarbons at 3.4 \ensuremath{~ \ensuremath{{\rm mm}}} with the Plateau de Bure Interferometer (PdBI) is shown as a square over this ESO-VLT composite image (B, V and R bands) of the Horsehead nebula. Each circle indicates the 3.4 \ensuremath{~ \ensuremath{{\rm mm}}} primary beam of the PdBI at one of the 7 observed positions. Those positions are largely oversampled at the hydrocarbon wavelength (3.4 \ensuremath{~ \ensuremath{{\rm mm}}}) to ensure simultaneous Nyquist-sampling at 1.4 \ensuremath{~ \ensuremath{{\rm mm}}} used to observe C18O. A linear combination of the 7 pointed observation is done to obtain the final dirty image.
Open with DEXTER

2.2 Observations

2.2.1 c-C3H2 and C4H

First PdBI observations dedicated to this project were carried out with 6 antennae in the CD configuration (baseline lengths from 24 to 229 m) during March-April 2002. The 580 \ensuremath{~ \ensuremath{{\rm MHz}}} instantaneous IF-bandwidth allowed us to simultaneously observe c-C3H2 and C4H at 3 \ensuremath{~ \ensuremath{{\rm mm}}} using 3 different 20 \ensuremath{~ \ensuremath{{\rm MHz}}}-wide correlator windows. One other window was centered on the C18O (J=2-1) frequency. The full IF bandwidth was also covered by continuum windows both at 3.4 and 1.4 \ensuremath{~ \ensuremath{{\rm mm}}}. c-C3H2 and C4H were detected but the weather quality precluded use of 1.4 \ensuremath{~ \ensuremath{{\rm mm}}} data.

We observed a seven-field mosaic in a compact hexagonal pattern with full Nyquist sampling at 1.4 mm and large oversampling at 3.4 mm. This mosaic, centered on the IR peak, was observed for about 6h of on-source observing time per configuration. The rms phase noises were between 15 and 40 \ensuremath {^\circ } at 3.4 \ensuremath{~ \ensuremath{{\rm mm}}}, which introduced position errors <0.5''. Typical 3.4 \ensuremath{~ \ensuremath{{\rm mm}}} resolution was 6''.

2.2.2 CCH and C18O

As a follow-up, we carried out observations of CCH at PdBI with 6 antennae in CD configuration during December 2002 and March 2003. We used a similar correlator setup: three 20 \ensuremath{~ \ensuremath{{\rm MHz}}}-wide windows were centered so as to get the four 3.4 \ensuremath{~ \ensuremath{{\rm mm}}} hyperfine components of CCH; one 20 \ensuremath{~ \ensuremath{{\rm MHz}}}-wide window was centered on the C18O (J=2-1) frequency; the remaining windows were used to observe continuum at 3.4 and 1.4 \ensuremath{~ \ensuremath{{\rm mm}}}.

Exactly the same mosaic (center and field-pattern) and approximately the same on-source observing time per configuration ($\sim$6 h) as before were used. The rms phase noises were between 10 and 40 \ensuremath {^\circ } except during 4 h in D configuration where they were between 8 and 20 \ensuremath {^\circ } at 3.4 \ensuremath{~ \ensuremath{{\rm mm}}}. The data of those 4 h have been used to build the C18O map as the 1 \ensuremath{~ \ensuremath{{\rm mm}}} phase noises were then low enough (between 20 to 45 \ensuremath {^\circ }). We thus ended up with a 6'' typical resolution both at 3.4 \ensuremath{~ \ensuremath{{\rm mm}}} and 1.4 \ensuremath{~ \ensuremath{{\rm mm}}}. Both CCH and C18O were easily mapped while no continuum was detected at a level of 2 mJy/beam in a 6''-beam.

2.2.3 12CO

As part of another project (A. Abergel, private communication), the 12CO (J=1-0) and 12CO (J=2-1) lines were simultaneously observed during 6h on-source at PdBI in November 1999 (only 5 antennae were then available) in configuration C (baseline lengths from 24 to 82 m). The observation consisted of a 4-field mosaic, fully sampled at 1.3 \ensuremath{~ \ensuremath{{\rm mm}}}. The mosaic center is slightly shifted compared to the two other observations. The weather was excellent with phase noise from 3 to 5 \ensuremath {^\circ } and 6 to 10 \ensuremath {^\circ } at 2.6 \ensuremath{~ \ensuremath{{\rm mm}}} and 1.3 \ensuremath{~ \ensuremath{{\rm mm}}}, respectively. Typical resolutions were 5'' at 2.6 \ensuremath{~ \ensuremath{{\rm mm}}} and 2.5'' at 1.3 \ensuremath{~ \ensuremath{{\rm mm}}}.

2.2.4 Other data: H2, ISO-LW2 and 1.2 mm dust continuum

Table 2: Calibrator fluxes in Jy.

The H2 v=1-0 S(1) map shown here is a small part of Horsehead observations obtained at the NTT using SOFI. The resolution is $\sim$1''. Extensive explanations of the data reduction and analysis are discussed elsewhere (Habart et al. 2004,2005). The ISO-LW2 map (published by Abergel et al. 2003) shows aromatic features at $7.7~\mu$m with a resolution of $\sim$6''. The 1.2 \ensuremath{~ \ensuremath{{\rm mm}}} dust continuum was obtained at the IRAM-30 m telescope with a resolution of $\sim$11'' and has already been presented by Teyssier et al. (2004).

2.3 PdBI data processing

All data reduction was done with the GILDAS[*] softwares supported at IRAM. Standard calibration methods using close calibrators were applied to all the PdBI data. The calibrator fluxes used for the absolute flux calibration are summarized in Table 2.

Following Gueth et al. (1996), single-dish, fully sampled maps obtained with the IRAM-30 m telescope (Teyssier et al. 2004; Abergel et al. 2003) were used to produce the short-spacing visibilities filtered out by each mm-interferometer (e.g. spatial frequencies between 0 and 15 \ensuremath{~ \ensuremath{{\rm m}}} for PdBI). Those pseudo-visibilities were merged with the observed, interferometric ones. Each mosaic field were then imaged and a dirty mosaic was built combining those fields in the following optimal way in terms of signal-to-noise ratio (Gueth 2001):

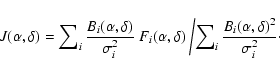
\begin{displaymath}\displaystyle % J(\alpha,\delta) = \sum\nolimits_i \frac{B_i(... ...imits_i \frac{B_i(\alpha,\delta)^2}{\sigma_i^2}\cdot \right. \end{displaymath}

In this equation, $J(\alpha,\delta)$ is the brightness distribution in the dirty mosaic image, Bi are the response functions of the primary antenna beams, Fi are the brightness distributions of the individual dirty maps, and $\sigma_i$ are the corresponding noise values. As may be seen in this equation, the dirty intensity distribution is corrected for primary beam attenuation. This implies that noise is inhomogeneous. In particular, noise strongly increases near the edges of the field of view. To limit this effect, both the primary beams used in the above formula and the resulting dirty mosaics are truncated. The standard level of truncation is set at 20% of the maximum in GILDAS. In our case, the intensity distribution does not drop to zero at all field edges. Hence, we used a much lower level of truncation of the beam (i.e. 5%) to ensure a better deconvolution of the side lobes of the sources sitting just at the field edges. We then use the standard adaptation to mosaics of the Högbom CLEAN algorithm to deconvolve (Gueth 2001). The sharp edge of the H2 emission defines a boundary that may be used as a priori knowledge in the deconvolution of the PdBI images: we use this boundary as a numerical support (in the language of signal processing) to exclude the search for CLEAN components outside the PDR front (i.e. in the direction of the exciting star). We finally truncated the noisy clean mosaic edges using the standard truncation level. The C4H maps are particularly difficult to deconvolve due to their low signal-to-noise ratio, S/N < 10 to 15.
  \begin{figure}\includegraphics[width=14cm,clip]{1170f2} \end{figure} Figure 2: Integrated emission maps obtained with the Plateau de Bure Interferometer. Maps of i) the H2 v=1-0 S(1) emission (Habart et al. 2004,2005); ii) the mid-IR emission (Abergel et al. 2003, labeled ISO-LW2); and iii) the 1.2 \ensuremath{~ \ensuremath{{\rm mm}}} dust continuum (Teyssier et al. 2004, labeled 1.2mm) are also shown for comparison. The center of all maps has been set to the mosaic 1 phase center: RA(2000 $)\rm = 05h40m54.27s$, Dec(2000 $) = -02\ensuremath {^\circ } {}28'00''$. The map size is $110'' \times 110''$, with ticks drawn every 10''. Either the synthesized beam or the single dish beam is plotted in the bottom left corner. The emission of all the lines observed at PdBI is integrated between 10.1 and 11.1  \ensuremath{~ \ensuremath{{\rm km~s^{-1}}}}. Values of contour level are shown on each image wedge (contours of the H2 image have been computed on an image smoothed to 5'' resolution). The sharp edge of the H2 emission ( upper right panel) defines a boundary, which is used as a numerical support (in the language of signal processing) for deconvolution of the other images. This deconvolution support is overplotted in red on each panel.
Open with DEXTER


  \begin{figure}\includegraphics[width=14cm,clip]{1170f3} \end{figure} Figure 3: Same as Fig. 2 except that maps have been rotated by 14 \ensuremath {^\circ } counter-clockwise around the image center to bring the exciting star direction in the horizontal direction as this eases the comparison of the PDR tracer stratifications. Maps have also been horizontally shifted by 20'' to set the horizontal zero at the PDR edge delineated as the vertical red line. Horizontal red lines delimit the two lanes that have been vertically averaged to produce the two series of cuts shown in Fig. 5.
Open with DEXTER


  \begin{figure}\includegraphics[width=6.5cm,clip]{1170f4} \end{figure} Figure 4: Joint histogram of the integrated emission of i) the second brightest CCH line ( top); ii) c-C3H2 ( middle); and iii) one C4H line ( bottom) vs. the main CCH line. The value at a given position of this joint histogram is the percentage of pixels of the input images whose intensities lies in the respective vertical and horizontal bins. Only image pixels lying inside the deconvolution support (shown in Fig. 2) have been used in the histogram computation. Contour levels are set to 0.125, 0.25, 0.5, 1, 2, 4 and 8% of points per pixel.
Open with DEXTER

   
3 Results

3.1 Maps

The PdBI maps are shown in Figs. 2 and 3 together with the 7  \ensuremath{~ \ensuremath{{\rm\mu m}}} ISOCAM image (Abergel et al. 2003), the 1.2 \ensuremath{~ \ensuremath{{\rm mm}}} dust emission map (Teyssier et al. 2004) and the map of the H2 2.1  \ensuremath{~ \ensuremath{{\rm\mu m}}}  line emission (Habart et al. 2004,2005) for comparison. For all lines, we obtained excellent spatial resolutions, similar to or even better than the ISOCAM pixel size of 6'' (see Table 1). Figure 2 shows the maps in the natural Equatorial coordinate system while Fig. 3 shows the maps in a coordinate system where the x-axis is in the direction of the exciting star and the y-axis defines an empirical PDR edge that corresponds to the sharp boundary of the H2 emission (i.e. the maps have been rotated by 14 \ensuremath {^\circ } counter-clockwise and horizontally shifted by 20''). The latter presentation enables a much better comparison of the PDR stratification.

The main structure in all hydrocarbon maps is an approximatively N-S filament, following nicely the cloud edge and corresponding closely to the mid-IR filament on the ISO-LW2 image. A weaker and more extended emission is also detected, which has no counterpart in the ISO-LW2 image and can be attributed to the bulk of the cloud. It is interesting to note that the hydrocarbon emission presents a minimum behind the main filament, and a weaker secondary maximum within the extended emission. The hydrocarbon emission is stronger on the edges of the dust 1.2 \ensuremath{~ \ensuremath{{\rm mm}}} emission and avoids the region of maximum dust emission where the gas is likely denser. This confirms a tendency revealed by chemical surveys of dense cores (study of TMC-1 by Pratap et al. 1997 and L134N by Fossé 2003; Dickens et al. 2000): i.e. carbon chains (CCH, C4H,...) generally avoid the densest and more depleted cores.

Even at the high spatial resolution provided by the plateau de Bure Interferometer, the maps of all hydrocarbons remain very similar. Detailed inspection of the maps shows small differences between CCH and c-C3H2, but these do not affect the overall similarity. Indeed, the joint histogram describing the correlation of line maps for i) the two most intense CCH lines; ii) c-C3H2 and CCH; and iii) C4H and CCH are displayed in Fig. 4. As expected the two CCH lines are extremely well correlated as illustrated by the elongated shape (approaching a straight line) of the joint histogram. The correlations between c-C3H2 and CCH, and between C4H and CCH are excellent too, although the signal-to-noise ratio is not as good for C4H. For this plot, we have used all points lying inside the support used for the deconvolution.

The high resolution c-C3H2 map appears to show more structure than the CCH maps, particularly in the well-shielded cloud interior (on the left hand side of the main filament). This effect seems real since it does not appear for the satellite CCH line maps, which have similar intensities and signal-to-noise ratio as the c-C3H2 map. The C4H maps are too noisy for a detailed analysis but are nevertheless very well correlated with the CCH map. The correlations found at low spatial resolution (Teyssier et al. 2004) are not an artifact but persist at high spatial resolution.

The correspondence of hydrocarbons with CO and C18O is not as good. The C18O (J=2-1) map presents two maxima, located on either side of the CCH peak along the N-S direction: the CCH peak is associated with a local minimum of C18O emission. Also, the C18O emission peak is displaced farther inside the cloud (East) compared to CCH and the other hydrocarbons.

To illustrate further the differences in the spatial distribution of CO, C18O and the hydrocarbons, we show two series of cuts across the PDR in Fig. 5. The UV radiation comes from $\sigma $ Ori far to the right side of Fig. 3. The cuts have been taken along the $\sigma $ Ori direction (i.e. $\rm PA = -104\ensuremath {^\circ } {}$). The main peak for all hydrocarbons is located near an offset of $\delta x \simeq 12{-}15\hbox{$^{\prime\prime}$ }$ at less than 5'' of the H2 peak. The ISO-LW2 peak is located half-way between hydrocarbons and H2 peaks. Intense 12CO emission in both the J=1-0 and J=2-1 lines is also detected in the same region, while the C18O (J=2-1) emission arises farther (at least 5'') inside the cloud.

As shown in Fig. 6, the 12CO (J=2-1) emission (convolved at the same angular resolution as the 12CO J=1-0 transition) is very bright ($\geq$ $50\ensuremath{~ \ensuremath{{\rm K}}} {}$ at $10.6\ensuremath{~ \ensuremath{{\rm km~s^{-1}}}} $, the line peak velocity) and more intense than 12CO (J=1-0) in the most external layers of the PDRs, directly facing $\sigma $Ori. The line intensity ratio $T_{\rm b}(1{-}0)/T_{\rm b}(2{-}1)$ rises from $\sim$0.3 to $\sim$0.8 from West to East. Combined with the high brightness temperature detected for both lines, the higher brightness temperature of the 12CO(2-1) line is a clear sign of the presence of warm and dense gas. We have estimated the kinetic temperature using an LVG model. We assumed that the emission is resolved and fills the beam. We explored the kinetic temperature dependence upon the density by solving for 5 different proton densities going from $1.6\times10^4\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $ to $10^5\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $. Under these hypotheses, the 12CO line intensity ratio and brightness temperature constrain the kinetic temperature to increase from $60\ensuremath{~ \ensuremath{{\rm K}}} $ in the inner PDR ( $15''= 0.03\ensuremath{~ \ensuremath{{\rm pc}}} $ from the PDR edge) to more than $100\ensuremath{~ \ensuremath{{\rm K}}} $ in the outer layers for proton densities larger than $4\times10^4\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $. For lower proton densities, the kinetic temperature still starts from $60\ensuremath{~ \ensuremath{{\rm K}}} $ in the inner PDR but increases much more stiffly. The kinetic temperature derived from single dish observations (Abergel et al. 2003) is lower, in the $30{-}40\ensuremath{~ \ensuremath{{\rm K}}} $ range and corresponds to the bulk of the cloud, rather than to the warm UV-illuminated edge.

3.2 Abundances

We have computed the CO and hydrocarbon column densities at three representative positions in the maps: the "IR peak'' where the PAH and hydrocarbon emission is the largest, the "IR edge'' 10'' West which represents the region with the most intense UV-radiation and a "Cloud'' position behind the IR filament. Table 3 lists the derived column densities and abundances relative to the total number of protons for these 3 positions. We have used a LVG model with different uniform total hydrogen density[*] (from $10^4\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $ to $10^5\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $) and a kinetic temperature of 40 \ensuremath{~ \ensuremath{{\rm K}}} for the "cloud'' position, and between 60 and 100 \ensuremath{~ \ensuremath{{\rm K}}} for the IR positions. The variance of the column densities therefore reflects both the systematic effect due to the imperfect knowledge of the physical conditions, and the random noise of the data. In most cases, the former contribution is the largest. The H2 column densities are derived from the dust 1.2 \ensuremath{~ \ensuremath{{\rm mm}}} emission assuming the same dust properties for all positions but a dust temperature range of 20 to 40 \ensuremath{~ \ensuremath{{\rm K}}} for the "Cloud'' position and 40 to 80 \ensuremath{~ \ensuremath{{\rm K}}} for the IR positions.

The LVG solution implies a typical 12CO column density of $2 \times 10^{17}\ensuremath{~ \ensuremath{{\rm cm^{-2}}}} $. This is inconsistent with the derived column density of C18O and the local ISM 16O/18O element ratio (560, Wilson & Rood 1994). Figure 7 shows clear indications of self-absorption of the 12CO spectra (asymmetries and dips in the top of the line profiles) while the C18O spectra are Gaussian. The same behaviour is seen in the single dish data discussed by Abergel et al. (2003) (cf. their Fig. 5). This explains why the LVG solution does not succeed in correctly inferring the 12CO column density. Conversely, the C18O abundance relative to H is fairly constant for all positions at $[\mbox{C$^{18}$ O}] = 1.0 \times 10^{-7}$. Assuming a local ISM 16O/18O element ratio, this corresponds to a CO abundance relative to the total number of hydrogen atoms of $[\mbox{CO}] = 5.6 \times 10^{-5}$, in rather good agreement with the gas phase abundance of carbon derived from CO in warm molecular clouds, and to the carbon abundance in diffuse clouds (Lacy et al. 1994; Sofia & Meyer 2001). In addition, using IRAM-30 m spectra of 13CO and C18O published by Abergel et al. (2003), we found $[\mbox{$^{13}$ CO}]/[\mbox{C$^{18}$ O}] \sim 7$. This good agreement with the local ISM isotopic ratio make us confident that we can use our LVG analysis on the PdBI C18O spectra to estimate the CO density. According to Lis & Guesten (2005), atomic carbon is less abundant than CO in the PDR. The peak column density of neutral carbon, observed with a 15'' beam, is $\sim$ $1.6 \times 10^{17}$ cm-2corresponding to a carbon abundance of $[\mbox{C}] = 5 \times 10^{-6}$. Even if we take into account the difference in linear resolution, we do not expect an increase of the column density larger than a factor of two based on the comparison of the low resolution single dish data with the interferometer maps of other tracers. Finally, although the H2 column densities are fairly similar at the "IR peak'' and "cloud'' positions, the abundances of hydrocarbons are larger by a factor of at least 5.0 at the "IR peak''. The abundances seem to be even larger at the "IR edge'' than at the cloud position.

  \begin{figure}\includegraphics[width=7.5cm,clip]{1170f5a}\hspace*{4mm} \includegraphics[width=7.5cm,clip]{1170f5b} \end{figure} Figure 5: Emission profiles along the exciting star direction ( $\rm PA = -104\ensuremath {^\circ } {}$ in the equatorial coordinate system). To improve the signal-to-noise ratio, those emission profiles have been integrated along the perpendicular direction between $-15'' < \delta y < 0''$ ( left column) and $0'' < \delta y < +15''$ ( right column). The comparison of those two series of mean cuts gives an idea of the influence of the local conditions (either excitation effects or chemical differentiation). We show from top to bottom, H2 v=1-0 S(1) (full resolution in black, smoothed at a 5''-resolution in red), 12CO J=2-1, 12CO J=1-0, C18O J=2-1, CCH lines (1 black, 2 green, 3 red and 4 blue, respectively following the ratios 1:0.5:0.5:0.25), c-C3H2, C4H lines (1 black, 2 red), ISO-LW2 and the 1.2 \ensuremath{~ \ensuremath{{\rm mm}}} dust continuum. For the PdBI data, the 3-$\sigma $ noise level is indicated by the dashed lines. It rises at the cut edges due to the primary beam correction. Note that the fields of view of the 12CO and C18O data are smaller than the field of view of the hydrocarbon data because of the smaller mosaic size and/or the higher frequency. The blue vertical lines are guidelines to localize the hydrocarbon peaks. They have been drawn at $\delta x =+12''$ ( left column) and $\delta x =+15''$ ( right column). Note that the bumps at $\delta x = -20''$ in the ISO-LW2 cut ( left column) and at $\delta x =70''$ in the H2 cut ( right column) are due to field stars.
Open with DEXTER

   
4 Discussion

4.1 Comparison with models


  \begin{figure}\includegraphics[width=7cm,clip]{1170f6} \end{figure} Figure 6: Spatial variation along the direction of the exciting star of a) the 12CO J=2-1 brightness temperature (convolved at the same angular resolution as the J=1-0 transition); b) 1-0/2-1 ratio and c), d), e) the kinetic temperature. $(\delta x, \delta y)$ offsets refer to the coordinate system defined in Fig. 3. The cuts at $\delta y = +10''$ are drawn in blue, those at $\delta y = +5''$ in green and those $\delta y = +0''$ in red. The data cuts have been taken from the 10.6 \ensuremath{~ \ensuremath{{\rm km~s^{-1}}}} velocity channel corresponding to the 12CO line peak. The kinetic temperature is derived from an LVG model assuming i) unity beam filling factor; and ii) uniform total hydrogen density of $n_\ensuremath{{\rm H}} = 1.6\times10^4\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $ (dashed lines), $2\times10^4\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $ (full lines), $4\times10^4\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $ (dotted lines) and $10^5\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $ (dotted-dashed lines). Arrows indicate lower limits.
Open with DEXTER

Table 3: Molecular column densities and abundances at 3 different positions of the PDR named "Cloud'', "IR peak'' and "IR edge''. Equatorial offsets refer to the Mosaic 2 map center given in Table 1. $(\delta x, \delta y)$ offsets refer to the coordinate system defined in Fig. 3. H2 column densities have been derived from the 1.2 \ensuremath{~ \ensuremath{{\rm mm}}} dust continuum emission using a dust temperature range of 20 to 40 \ensuremath{~ \ensuremath{{\rm K}}} for the "Cloud'' position and 40 to 80 \ensuremath{~ \ensuremath{{\rm K}}} for the IR positions. Others column densities used LVG models with a representative set of densities and kinetic temperature. 1-$\sigma $ uncertainties thus reflect the systematics due to the approximate knowledge of density and kinetic temperature. Abundances are computed with respect to the number of protons, i.e. $[{\rm X}] = 0.5~N({\rm X})/N(\mbox{H$_2$ })$.

We have used a monodimensional PDR code (Le Petit et al. 2002, http://aristote.obspm.fr/MIS/) to model the observations of the Horsehead nebula. The slab geometry is locally appropriate as seen in Fig. 3. We did not take into account projection effects as the source is viewed almost edge-on. Indeed, Habart et al. (2005) show that the main effect of the PDR possible small inclination (< $6\ensuremath{^\circ} $) is to enlarge the peak profiles and to shift them all compared to the model edge. The model includes a detailed treatment of the photo-dissociation of H2 and the CO isotopes as well as the statistical equilibrium of their rovibrational (rotational, respectively) states in a steady state approach. The parameters of the model include the element abundances, the cosmic ray ionization rate, the scaling factor of the interstellar ultraviolet radiation field (ISRF) measured in Draine units, the density profile and the grain parameters. As the observations involve complex carbon molecules, we have used the so-called "new standard model'' chemical rate file of Herbst and collaborators (Lee et al. 1998), available on the web site[*]. In a previous paper (Teyssier et al. 2004), we have found that the other extensive chemical rate file provided by the UMIST group (Le Teuff et al. 2000) gave close results for the carbon chain molecules. As C18O observations are reported, we have added to this reaction set the main isotopic molecules involving 18O and introduced the corresponding fractionation reactions (Graedel et al. 1982). We have also introduced the photo-dissociation rates given by van Dishoeck (1988), when available, which have been calculated specifically with the Draine ISRF and which were different from the values reported in the chemical rate file. The resulting chemical network involves about 450 chemical species and 5000 reactions. Only the most stable isomeric forms of hydrocarbons are considered here.

We define a reference model (hereafter named model A) of the Horsehead nebula as a uniform sheet of gas and dust of total hydrogen density $n_\ensuremath{{\rm H}} = 10^5\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $ exposed to a ISRF of 100 measured in Draine units.

  \begin{figure}\includegraphics[angle=270,width=16cm,clip]{1170f7} \end{figure} Figure 7: CO spectra (convolved at the same angular resolution) along the direction of the exciting star at $\delta y = -2.5''$. In the cuts, the label $\delta x = 13''$ indicates the IR peak position (cf. Table 3). Note that 12CO J=2-1 peak intensity decreases at positions $\delta x = 13''$ and 15'' while 12CO J=1-0 increases even reaching its maximum at $\delta x = 15''$. In addition, both 12CO lines show a small but clear dip (i.e. the center channel intensity is lower than its first neighbours) at $\delta x = 15''$. Finally, while C18O spectra are very close to Gaussian, 12CO spectra show asymmetric profiles. Spectra cuts at other close $\delta y$ values show the same trends.
Open with DEXTER

The cosmic ray ionization rate has a value of $5\times10^{-17}~\mbox{s}^{-1}$ and the elemental abundances are as follows: $\rm C/H = 1.38\times10^{-4}$, $\rm O/H = 3.02\times10^{-4}$, $^{18}\rm O/H = 6\times10^{-7}$, $\rm N/H = 7.95\times10^{-5}$, $\rm S/H = 5.8\times 10^{-8}$, $\rm Cl/H = 1.86\times10^{-9}$, $\rm P/H = 9.3\times10^{-10}$, $\rm Fe/H = 1.7\times10^{-9}$, $\rm Mg/H = 10^{-8}$, $\rm Na/H = 2.3\times10^{-9}$. The properties of the grains are the same as described in Le Petit et al. (2002), i.e. the size distribution law is taken from Mathis et al. (1977) with an exponent of -3.5 and we describe the attenuation of grains from the far-UV to the visible via the galactic extinction curve given as an analytic function of 1/$\lambda$ by including the coefficients derived by Fitzpatrick & Massa (1988). Charge exchange reactions between C+ and PAHs are not taken into account. The gas to dust mass ratio is 100.

Figure 8 shows i) the abundance of the H2 rovibrationally excited in the v=1, J=3 level at the origin of the 2.12  \ensuremath{~ \ensuremath{{\rm\mu m}}} line (this abundance is hereafter referred to as [H$_2^\star ]$); and ii) the C, CO and hydrocarbon abundances for this reference model and 5 variants. We ensure that the [H$_2^\star ]$ peak position is set at $\delta x = 10''$ as in the observations. Our reference model correctly reproduces the observed 3 to 5'' offset between the hydrocarbon and H2 peaks. The C18O also peaks behind the hydrocarbons at $\delta x = 20{-}25''$. However, the H2 profile is not correctly modeled here.

In model B, we replaced the Galactic extinction curve by one more representative of molecular gas. We have chosen HD 147889 in Ophiuchus. Its extinction curve has a rather strong far-UV rise ( EB-V = 1.09, Fitzpatrick & Massa 1988). Its ratio between the total and selective extinctions, \ensuremath{R_V}, is 4.2 a figure typical of molecular gas (Cardelli et al. 1989; Gordon et al. 2003). The PDR stratification does not qualitatively change compared to model A: It is just compressed. In model C, we added reactions of charge exchange between C+ and PAHs. This enhances the neutral atomic carbon abundance but does not have a large effect on the hydrocarbons: only CCH peaks closer to the H2 peak compared to model A. Neither model B nor C improves the modeling of the H2 profile.

  \begin{figure}\includegraphics[width=16cm,clip]{1170f8} \end{figure} Figure 8: Predictions of the spatial variation of the abundance relative to H2, using a unidimensional PDR code. For each model, the abundance of the population of the the upper level of the 2.12  \ensuremath{~ \ensuremath{{\rm\mu m}}} H2 line (i.e. v=1, J=3), written [H$_2^\star ]$, is shown on a linear scale ( top). The C, CO and hydrocarbon abundances are shown on a logarithmic scale ( bottom). The modeled cloud is illuminated from the right-hand side. The $\delta x$-axis origin has been set so that [H$_2^\star ]$ peaks at the position of the observed H2 peak (i.e. $\delta x = 10''$). The vertical dotted blue line indicates the peak of the c-C3H2 and C4H abundances. Each model is described in 4 lines: i) the density structure; ii) the UV-field properties; iii) the chemical network used; and iv) the gaseous sulfur abundance. 6 different models are compared here. Our reference model is labeled A. The total hydrogen density is kept uniform at a value of $n_\ensuremath{{\rm H}} = 10^5\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $. The far-UV intensity of the radiation field is G0=100 (in Draine units) and the extinction curve is the mean Galactic one. The chemical network rate file is the New Standard Model one with minor modifications described in the text. Charge exchange reactions between C+ and PAHs are not taken into account. The gaseous sulfur abundance is low compared to solar (i.e. $\rm S/H = 5.8\times 10^{-8}$). The parameters varied in other models are emphasized in red. Model B uses a different extinction curve. Model C adds reactions of charge exchange between C+ and PAHs. Model D decreases the uniform total hydrogen density. Models E and F use the density profile derived from the model of the H2 observations (Habart et al. 2004,2005). Model F uses a solar gaseous sulfur abundance (i.e. $\rm S/H = 10^{-5}$).
Open with DEXTER

As shown by model D, E and F, the density structure has a major impact on the PDR structure. Figure 9 shows the density profiles associated with each model. When keeping the total hydrogen density uniform but decreasing its value to $2\times10^4\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $ (as in model D), the carbon and hydrocarbon abundance peaks are highly broadened and shifted inward by more than 20'', a prediction clearly violated by the high resolution PdBI data. Models E and F use a density profile provided by Habart et al. (2004,2005) to fit the 2.12  \ensuremath{~ \ensuremath{{\rm\mu m}}}-H2 emission. Indeed, the [H$_2^\star ]$ profile qualitatively changes (it is now a peak rising from zero at the PDR edge) but it also reproduces the H2 filament width. Those two models, which impose a steep total hydrogen density gradient at the PDR edge, are the only ones that succeed in correctly reproducing the offset between the hydrocarbon and H2 peaks as well as the form of the H2 peak. The only difference between models E and F is the gaseous sulfur abundance: sulfur is depleted from the gas phase in model E ( $\rm S/H = 5.8\times 10^{-8}$) while the gaseous sulfur abundance is solar in model F ( $\rm S/H = 10^{-5}$).

Figure 10 is a zoom in our two best models (i.e. E and F) of the spatial variations of the abundances of hydrocarbons relative to i) total hydrogen density (top panel); and ii) CCH (bottom panel). The observed abundances are overplotted with their error bars. The dashed vertical line separates the zone where the proton gas density is constant from the zone where the proton gas density rapidly decreases outward. This latter zone is associated with the PDR. The sulfur element abundance has different effects in the two regions. In the region of moderate visual extinction (i.e. the "IR edge'' and the "IR peak'' where $\ensuremath{A_V} {} \la 1$), the charge transfer reaction between C+ and S leading to S+ and C reinforces the abundance of neutral carbon and thus enables the formation of carbon chains via the rapid neutral-carbon atom reactions. However this effect is small. Indeed this is in the dark region where the sulfur elemental abundance has a large effect. When the sulfur abundance is solar, the small carbon chains $\rm C_2$, CCH, $\rm C_2H_2$, $\rm C_3H$, $\rm C_3H_2$ and $\rm C_4H$ react with $\rm S^+$ to give $\rm C_2S^+$, $\rm CCS^+$, $\rm HC_2S^+$, $\rm C_3S^+$, $\rm HC_3S^+$ and $\rm C_4S^+$. In this main destruction path of the small carbon chains, one hydrogen atom is released impairing the reformation of the carbon chains. When S is higly depleted as in Model E, this destruction mechanism is superseded by other pathways involving C+. Those pathways form carbon chain ions which in turn contribute to the formation of other carbon chains. Overall, model E (i.e. low S/H) performs better in the comparison with observed abundances. The only exception is the $n(\mbox{c-C$_3$ H$_2$ })/n(\mbox{CCH})$ ratio at the "cloud'' position. We will thus use model E only for comparison with the observations. At the IR peak (median point at $\delta x = 15.5''$), the CCH abundance is correctly reproduced while c-C3H2 and C4H abundances are underestimated by at least a factor of 3. Discrepancies are much higher both at the "cloud'' (point to the right at $\delta x = 27''$) and the "IR edge'' (point to the left at $\delta x = 9''$) positions. In the UV-illuminated edge, the modeled $[\mbox{CCH}]$ has a quite shallow increase with $\delta x$ while the modeled $[\mbox{c-C$_3$ H$_2$ }]$ and $[\mbox{C$_4$ H}]$ share the same steep abundance profile. In contrast, the observed ("IR edge'') abundances are very similar for the 3 species, reflecting the very good spatial correlation between the different hydrocarbons (see Fig. 4). This discrepancy is independent of our knowledge of the total hydrogen density as it is also seen when comparing abundances relative to CCH.

  \begin{figure}\includegraphics[height=7cm,angle=270,clip]{1170f9} \end{figure} Figure 9: Spatial variation of the total hydrogen density in models A to F. In model E and F, the density increases as a power law of scaling exponent 4 in the first 10'' and then is kept constant at a value of $2\times10^5\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $. As in Fig. 8, the x-axis origin has been set so that [H$_2^\star ]$ peaks at the position of the observed 2.12  \ensuremath{~ \ensuremath{{\rm\mu m}}}, H2 line peak (i.e. $\delta x = 10''$).
Open with DEXTER


  \begin{figure} \includegraphics[height=8.8cm,angle=270,clip]{1170f10a} \includegraphics[height=8.8cm,angle=270,clip]{1170f10b} \end{figure} Figure 10: Comparison between our two best models (curves) and observed (points with error bars) abundances of the small hydrocarbons. CCH is shown as a green solid line, c-C3H2 as a dashed red line and C4H as a blue dotted line. The top and bottom panels respectively show abundances relative to the total hydrogen density and CCH. The dashed vertical line shows the position where the total hydrogen density profile changes from a steep gradient to a constant.
Open with DEXTER

In summary, none of our models is able to correctly reproduce the relative stratification of H2 and small hydrocarbons. Comparison of model A and C shows that to reproduce the observed offset between hydrocarbon and H2 peaks, we need a high total hydrogen density ( $10^5\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $). By varying the profile density (model E and F), a shallow total hydrogen density increase at the PDR edge is needed to reproduce the profile of the 2.12  \ensuremath{~ \ensuremath{{\rm\mu m}}} H2 line. However, the shallower the total hydrogen density increase, the larger the modeled offset between H2 and the hydrocarbons. A good compromise is provided by a total hydrogen density profile increasing as a power law with a scaling exponent 4 on the first 10'' and then constant at a value of  $2\times10^5\ensuremath{~ \ensuremath{{\rm cm^{-3}}}} $. Habart et al. (2005) show that this model essentially corresponds to a constant pressure model (with $P = 4 ~\times~ 10^6~\ensuremath{~ \ensuremath{{\rm K~km~s^{-1}}}} $). Model E with low sulfur elemental abundance performs better than model F with solar abundance. Nonetheless, even model E does not succeed in reproducing the good hydrocarbon correlation seen in the illuminated part of the PDR: while CCH is correctly predicted to have a smooth abundance increase, modeled c-C3H2 and C4H abundances show a much too steep increase.

4.2 Can the fragmentation of PAHs contribute to the synthesis of small hydrocarbons?

Examining the model predictions in more detail, three hypotheses can be proposed to explain the discrepancies between model calculations and observations:

i)
The photo-dissociation rates used in the models may be incorrect. As the main destruction process near the cloud edge is photo-dissociation, the actual values of the photo-dissociation rates are critical for an accurate prediction. However, similar results are obtained with the UMIST95 and NSM rate files. The photo-dissociation rates for c-C3H2, C3H and C4H are 10-9 s-1 for both rate files, and differ by a factor of two for CCH (i.e. $0.51 \times 10^{-9}$ s-1 for UMIST95 and 10-9 s-1 for NSM). The photo-dissociation rates of larger chains are similar. In most cases, except for CCH and acetylene, the numbers given in the rate files are not well documented. For instance, van Dishoeck (1988) discusses the photo-dissociation rate of c-C3H2 and concludes that it is accurate within an order of magnitude. More accurate photo-dissociation rates are clearly needed for the carbon chains and cycles. Recent calculations have been performed for C4H showing that the photo-dissociation threshold is 5.74 eV, but that efficient photo-dissociation requires more energetic photons, typically above 6.5 eV (Graf et al. 2001). However, it is unlikely that the rates are low enough to explain the large discrepancies between the models and the data since these molecules are known to be sensitive to UV-radiation (Song et al. 1994; Jackson et al. 1991).
ii)
Another possibility is that the chemical networks are missing important reactions for the synthesis of hydrocarbons. Neutral-neutral reactions are progressively included in the rate files, but still are much less numerous than ion-molecule reactions. It is now known that atomic carbon, diatomic carbon and CCH may react with hydrocarbons (Stahl et al. 2002; Mebel & Kaiser 2002; Kaiser et al. 2003). More work remains to be done. However, preliminary tests using a more extended data base of chemical reactions have not led to significant improvement.
iii)
The excellent spatial correlation between the mid-IR emission due to PAHs and the distribution of carbon chains suggests a last hypothesis: the fragmentation of PAHs due to the intense far UV-radiation could seed the interstellar medium with a variety of carbon clusters, chains and rings (Joblin 2003; Verstraete et al. 2001; Scott et al. 1997; Le Page et al. 2003, and references therein). These species would then further react with gas phase species (C, C+, H, H2, etc.) and participate in the synthesis of the observed hydrocarbons. Fuente et al. (2003) also favor this explanation to explain the abundance of c-C3H2 they observed in other PDRs.
A correct exploration of this third hypothesis needs a good qualitative and quantitative description of both the fragmentation and reformation of PAHs, which is out of the scope of this paper. We here give only a few indications. Omont (1986) pioneered attempts to understand the role of PAHs in interstellar chemistry. Elaborating on this work, Lepp & Dalgarno (1988) suggested that the participation of PAHs in the ion chemistry of dense clouds leads to large increases in the abundances of small hydrocarbons. Indeed, when the PAH fractional abundance exceeds $\sim$10-7, the formation of PAH- triggers mutual neutralization of the positive atomic and molecular ions and introduces new pathways for the formation of complex molecules. The equilibrium abundances of neutral atomic carbon C, CCH and c-C3H2 may thus be enhanced by two orders of magnitude. By comparison, our model C which includes charge exchange between C+ and PAHs, shows a decrease of C4H and c-C3H2 abundances by at least an order of magnitude in the dark region. Introduction of mutual neutralization between C+ and PAH- could be an interesting alternative to our "artificial'' lowering of the sulfur abundance. We are currently acquiring CS data at PdBI to constrain the S chemistry independently.

Lepp et al. (1988) suggested that the ion chemistry of diffuse clouds has little impact on the CH, OH and HD abundance, but can lead to a large increase in the abundance of other species (H2, NH3 and most noticeably $\rm CH_4$ and  $\rm C_2H_2$) by successive reactions of PAH and PAH- with carbon and hydrogen atoms. Talbi et al. (1993) suggested that Coulombic explosion of doubly ionized PAH could create c-C3H2 through the electronic dissociative recombination of  $\rm C_3H_3^+$. Laboratory experiments by Jochims et al. (1994) suggested that PAHs with less than 30-40 carbon atoms will be UV-photodissociated in HI regions while larger ones will be stable. Based on those results, models by Allain et al. (1996b,a) indicate that only PAHs with more than 50 carbon atoms survive the high UV radiation field of the diffuse interstellar medium, whereas smaller PAHs such as coronene or ovalene are destroyed by the loss of acetylenic groups. Destruction timescales are a few years for neutral species and typically five time shorter for the corresponding cations. All those reactions start from neutral or cation PAHs. They will be in competition with charge exchange and mutual neutralization discussed above. Mutual neutralization has a maximal effect in the transition region where the gas is molecular but the electronic abundance is significant. This region corresponds more or less to the region of maximum emission from the PAHs or slightly deeper in the molecular cloud. All other cited reactions are more efficient toward the illuminated edge where PAHs are mainly neutral. Recently, Le Page et al. (2003) discussed the possibility of addition reactions with ionized carbon, starting from the high reaction rate between C+ and anthracene measured by Canosa et al. (1995). If similar reaction rates persist for heavier PAHs, addition reactions with carbon would be very efficient in counteracting the destruction by far-UV photons.

From the observational point of view, the mid-IR emission due to PAHs is extended in interstellar clouds. On the other hand, a detailed analysis of the mid and far-IR images obtained by IRAS led Boulanger et al. (1990) and Bernard et al. (1993) to conclude that PAHs disappear in the dense cold cloud interiors, probably because they coagulate and/or condense. Stepnik et al. (2003) describe a convincing case for such a process in a small filament of the Taurus cloud. Rapacioli et al. (2005) have found clear evidence for spatial variations of the aromatic infrared band profiles, likely due to the spatial variation of the nature of their carriers. A sophisticated analysis of ISOCAM-CVF data allowed them to separate the mid-IR spectra of the ionized and neutral PAHs from the spectra of carbonaceous very small grains (possibly PAH aggregates). The very small grains are located at a larger distance from the illuminating stars than the PAHs, lending support to the idea that PAHs are produced from the photo-evaporation of these very small grains. While more examples are needed to understand the origin and fate of interstellar PAHs, it appears nonetheless that these macro molecules are released in the gas phase in the UV-illuminated regions of the interstellar medium, i.e. in the diffuse clouds, in PDRs, etc. In those regions, the destruction of the carbon skeleton is the main process limiting the smallest possible PAH size. It is likely that some carbon-bearing molecules are released in the gas phase in the UV-illuminated regions, either as a secondary product of the evaporation of the dust particles giving rise to PAHs, or as products of the destruction of the PAH carbon skeleton.

   
5 Summary and conclusions

We have presented maps of the edge of the Horsehead nebula in rotational lines of excited H2, CO, C18O and simple hydrocarbon molecules, CCH, c-C3H2 and C4H with 6'' resolution. All the hydrocarbon maps are strikingly similar to each other, and to the mid-IR emission mapped by ISOCAM (Abergel et al. 2003) while we measured a 3 to 5'' offset between the hydrocarbon and H2 peaks. State-of-the-art chemical models fail to reproduce both the PDR hydrocarbon stratification and the absolute abundances of 2 of 3 observed hydrocarbons. We have examined three hypotheses to improve the models, and we conclude that the most likely explanation is that we are witnessing the fragmentation of PAHs in the intense far-UV radiation due to $\sigma $Ori.

A detailed modeling of the chemistry including this new mechanism is beyond the scope of this paper. Indeed, such a modeling requires rates for both the growth (by addition of molecules or of carbon and hydrogen atoms) and the fragmentation of PAHs. This last item requires an accurate description of the fragmentation cascade of PAHs, in all their possible equilibrium states (ionized, neutral, partially or totally dehydrogenated, ...). Laboratory experiments such as the ion cyclotronic resonance cell PIRENEA (Joblin 2003) are key instruments to provide such information. In addition, the rate files used by the model need to be updated, especially the photo-dissociation rates of the simple carbon chains. A critical review of the role of neutral-neutral reactions in interstellar chemistry is also warranted.

Acknowledgements
We are grateful to the IRAM staff at Plateau de Bure, Grenoble and Pico Veleta for competent help with the observations and data reduction. IRAM is supported by the INSU/CNRS (France), MPG (Germany) and IGN (Spain). This work has benefited from many discussions with C. Joblin and C.M. Walmsley. We thank D. Lis for the communication of the (CI) map of the Horsehead nebula in advance of publication. We also thank E. Herbst for providing an updated chemical rate file. M.G. is grateful to the CSO for the hospitality of its office in Hilo where she worked on this paper. We acknowledge funding by the French CNRS/PCMI program. We thank the referee, J. Black, for insightful comments which improved the presentation and the discussion of our results.

References

 
Copyright ESO 2005