D. Urosevic1,2 - T. G. Pannuti3 - N. Duric4,5 - A. Theodorou4
1 - Department of Astronomy, Faculty of Mathematics,
University of Belgrade, Studentski trg 16, PO 550, 11000
Belgrade, Serbia and Montenegro
2 -
Isaac Newton Institute of
Chile, Yugoslavia Branch, Yugoslavia
3 -
Spitzer Science Center, Jet
Propulsion Laboratory/California Institute of Technology, Mailstop
220-6, Pasadena, CA 91125, USA
4 -
Institute for Astrophysics,
Department of Physics and Astronomy, University of New Mexico, 800
Yale Blvd., N.E., Albuquerque, NM 87131, USA
5 -
Karmanos Cancer
Institute, Department of Radiation Oncology, Wayne State
University, 4100 John R Street, Detroit, MI 48201, USA
Received 14 December 2004 / Accepted 20 December 2004
Abstract
This paper examines relations between the radio surface
brightness ![]() and the diameter D (also known as
and the diameter D (also known as ![]() relations) for a sample of extragalactic supernova remnants (SNRs)
as constructed from a combination of published data and data from
our own surveys. Our sample of extragalactic SNRs is the largest
ever devised for the purpose of analyzing
relations) for a sample of extragalactic supernova remnants (SNRs)
as constructed from a combination of published data and data from
our own surveys. Our sample of extragalactic SNRs is the largest
ever devised for the purpose of analyzing ![]() relations.
The main results of this paper may be summarized as follows:
(i) the empirical relations for SNRs in 10 of the 11 nearby
galaxies studied have the approximately trivial
relations.
The main results of this paper may be summarized as follows:
(i) the empirical relations for SNRs in 10 of the 11 nearby
galaxies studied have the approximately trivial
![]() form, therefore limiting their interpretation as physically
meaningful relations. In addition, these relations are subject to
selection effects rendering them even less useful. Further Monte
Carlo simulations suggest that the effect of survey sensitivity
has the opposite effect of volume selection (e.g. Malmquist bias,
a volume selection effect that shapes the Galactic sample) by
tending to flatten the slopes toward a trivial relation. In this
case, the true slopes may be steeper than the observed slopes;
(ii) compact M 82 SNRs appear to follow a uniquely different
form, therefore limiting their interpretation as physically
meaningful relations. In addition, these relations are subject to
selection effects rendering them even less useful. Further Monte
Carlo simulations suggest that the effect of survey sensitivity
has the opposite effect of volume selection (e.g. Malmquist bias,
a volume selection effect that shapes the Galactic sample) by
tending to flatten the slopes toward a trivial relation. In this
case, the true slopes may be steeper than the observed slopes;
(ii) compact M 82 SNRs appear to follow a uniquely different
![]() relation in comparison to the larger, older SNRs in the
other 10 galaxies. Monte Carlo simulations suggest that the
probability of this difference arising by chance is
relation in comparison to the larger, older SNRs in the
other 10 galaxies. Monte Carlo simulations suggest that the
probability of this difference arising by chance is ![]() 1%
to 10%, depending on what is assumed regarding the underlying SNR
population; (iii) three candidate hypernova remnants were identified in our
sample of 11 nearby galaxies.
1%
to 10%, depending on what is assumed regarding the underlying SNR
population; (iii) three candidate hypernova remnants were identified in our
sample of 11 nearby galaxies.
Key words: ISM: supernova remnants - methods: statistical - radio continuum: galaxies
The relation between surface brightness ![]() and diameter Dfor supernova remnants (SNRs) - known as the
and diameter Dfor supernova remnants (SNRs) - known as the ![]() relation
- presents a possible avenue for investigating the radio
brightness evolution of these sources. Shklovsky (1960a)
theoretically analyzed the synchrotron radiation for a spherical
expanding nebula and finds a
relation
- presents a possible avenue for investigating the radio
brightness evolution of these sources. Shklovsky (1960a)
theoretically analyzed the synchrotron radiation for a spherical
expanding nebula and finds a ![]() relation of the form
relation of the form
| (1) |
Early observations supported the existence of a ![]() relation in the form that the Shklovsky theory had predicted. The
first empirical
relation in the form that the Shklovsky theory had predicted. The
first empirical ![]() relation was determined by Poveda &
Woltjer (1968). Using the
relation was determined by Poveda &
Woltjer (1968). Using the ![]() relation, Shklovsky (1960b)
presented a way to determine distances to SNRs based on their
surface brightnesses. This method of distance determination for
SNRs has a significant advantage over other methods in that the
surface brightness of a radio SNR does not depend on its distance.
relation, Shklovsky (1960b)
presented a way to determine distances to SNRs based on their
surface brightnesses. This method of distance determination for
SNRs has a significant advantage over other methods in that the
surface brightness of a radio SNR does not depend on its distance.
Milne (1970) derived an empirical ![]() relation and
calculated distances to all of the observed SNRs in our Galaxy (97 in total). This relation was the subject of many investigations in
an attempt to precisely determine a specific set of calibrators to
achieve an improved
relation and
calculated distances to all of the observed SNRs in our Galaxy (97 in total). This relation was the subject of many investigations in
an attempt to precisely determine a specific set of calibrators to
achieve an improved ![]() relation. The basic criterion for
the choice of calibrators is a reliable distance to the SNR. Most
studies of the
relation. The basic criterion for
the choice of calibrators is a reliable distance to the SNR. Most
studies of the ![]() relation that were conducted during the 1970s and the early 1980s are of this type.
More sensitive observations
enabled more precise calculations of the distances to the
calibrators, and thus the number of quality calibrators increased.
During this time, Galactic
relation that were conducted during the 1970s and the early 1980s are of this type.
More sensitive observations
enabled more precise calculations of the distances to the
calibrators, and thus the number of quality calibrators increased.
During this time, Galactic ![]() relations were studied by
Downes (1971), Ilovaisky & Lequeux (1972),
Woltjer (1972),
Berkhuijsen (1973),
Clark & Caswell (1976), Sabbadin (1977),
Milne (1979), Caswell & Lerche (1979), Göbel et al.
(1981), Lozinskaya (1981) and Sakhibov & Smirnov (1982).
Critical analysis of this relation began with Allakhverdiyev et al. (1983a,b) and continued with the research of Green
(1984), Allakhverdiyev et al. (1986a), and
Allakhverdiyev et al. (1986b). Inaccurate calculations of the
distances to certain calibrators is the basic deficiency of the
relations derived in this manner, i.e. there are not as many SNRs
with precisely calculated distances as are needed to derive the
proper
relations were studied by
Downes (1971), Ilovaisky & Lequeux (1972),
Woltjer (1972),
Berkhuijsen (1973),
Clark & Caswell (1976), Sabbadin (1977),
Milne (1979), Caswell & Lerche (1979), Göbel et al.
(1981), Lozinskaya (1981) and Sakhibov & Smirnov (1982).
Critical analysis of this relation began with Allakhverdiyev et al. (1983a,b) and continued with the research of Green
(1984), Allakhverdiyev et al. (1986a), and
Allakhverdiyev et al. (1986b). Inaccurate calculations of the
distances to certain calibrators is the basic deficiency of the
relations derived in this manner, i.e. there are not as many SNRs
with precisely calculated distances as are needed to derive the
proper ![]() relation (Green 1984). Also, the ambient
interstellar medium where supernovae explode must be taken into
consideration. Allakhverdiyev et al. (1983a, 1983b,
1986a, 1986b)
argued that the
relation (Green 1984). Also, the ambient
interstellar medium where supernovae explode must be taken into
consideration. Allakhverdiyev et al. (1983a, 1983b,
1986a, 1986b)
argued that the ![]() relation was only applicable to
shell-type SNRs. Other significant works on the relation were
conducted by Li & Wheeler (1984), Huang & Thaddeus (1985) and
Berkhuijsen (1986).
relation was only applicable to
shell-type SNRs. Other significant works on the relation were
conducted by Li & Wheeler (1984), Huang & Thaddeus (1985) and
Berkhuijsen (1986).
Initial studies of the ![]() relation yielded significant
differences between theoretical models and empirical results.
Green (1991) argued that too much scatter exists among the
calibrators used for studies of the
relation yielded significant
differences between theoretical models and empirical results.
Green (1991) argued that too much scatter exists among the
calibrators used for studies of the ![]() relation and
therefore no valid relation can be derived. However, this view was
challenged by Case & Bhattacharya (1998, hereafter C&B) who
presented calculations of distances to 37 calibrators with the
help of new Galactic constants. Using these new distances, C&B
obtained a much flatter slope for the
relation and
therefore no valid relation can be derived. However, this view was
challenged by Case & Bhattacharya (1998, hereafter C&B) who
presented calculations of distances to 37 calibrators with the
help of new Galactic constants. Using these new distances, C&B
obtained a much flatter slope for the ![]() relation and
emphasized the inconsistency between the empirical and the
theoretical
relation and
emphasized the inconsistency between the empirical and the
theoretical ![]() relations. Finally, C&B also updated the
Galactic empirical relation and determined distances for all
identified shell-type SNRs. After nearly four decades of research,
our understanding of the
relations. Finally, C&B also updated the
Galactic empirical relation and determined distances for all
identified shell-type SNRs. After nearly four decades of research,
our understanding of the ![]() relation continues to evolve
from both theoretical and empirical perspectives.
relation continues to evolve
from both theoretical and empirical perspectives.
The construction of extragalactic ![]() relations are both
possible and straightforward because all of the calibrators are at
approximately the same distance. Therefore, the distance
determination problem is reduced once we know the distance to the
galaxy. If we identify a radio SNR, we may consider that source to
be a calibrator; furthermore, a set of extragalactic radio SNRs
does not suffer from Malmquist bias, i.e., distance dependent
selection effects. However, sensitivity becomes an issue with
increasing distance to target galaxies, and for that reason most
extragalactic radio SNRs have been detected in nearby Local Group
galaxies, such as the Large Magellanic Cloud (LMC), the Small
Magellanic Cloud (SMC), M 31, and M 33. The first empirical
extragalactic
relations are both
possible and straightforward because all of the calibrators are at
approximately the same distance. Therefore, the distance
determination problem is reduced once we know the distance to the
galaxy. If we identify a radio SNR, we may consider that source to
be a calibrator; furthermore, a set of extragalactic radio SNRs
does not suffer from Malmquist bias, i.e., distance dependent
selection effects. However, sensitivity becomes an issue with
increasing distance to target galaxies, and for that reason most
extragalactic radio SNRs have been detected in nearby Local Group
galaxies, such as the Large Magellanic Cloud (LMC), the Small
Magellanic Cloud (SMC), M 31, and M 33. The first empirical
extragalactic ![]() relation was constructed by Mathewson &
Clarke (1973b) for the LMC with 15 identified SNRs, followed by
the work of Milne et al. (1980) with 19 SNRs in the LMC,
Mathewson et al. (1983) with 31 SNRs (25 from the LMC and 6 from
the SMC), and finally Mills et al. (1984) with 38 SNRs (27 in the
LMC and 11 SNRs in the SMC).
relation was constructed by Mathewson &
Clarke (1973b) for the LMC with 15 identified SNRs, followed by
the work of Milne et al. (1980) with 19 SNRs in the LMC,
Mathewson et al. (1983) with 31 SNRs (25 from the LMC and 6 from
the SMC), and finally Mills et al. (1984) with 38 SNRs (27 in the
LMC and 11 SNRs in the SMC).
The ![]() relations for radio SNRs in the nearby spiral
galaxies M 31 and M 33 were investigated by Berkhuijsen (1983).
Observations conducted by Braun & Walterbos (1993) detected radio
emission from 24 radio SNRs in M 31 using observations made with
the Very Large Array (VLA) at an observing frequency of 1465 MHz.
Similarly, Duric et al. (1995) identified 53 SNRs in M 33 using the
VLA at approximately the same frequency. In general, the
relations for radio SNRs in the nearby spiral
galaxies M 31 and M 33 were investigated by Berkhuijsen (1983).
Observations conducted by Braun & Walterbos (1993) detected radio
emission from 24 radio SNRs in M 31 using observations made with
the Very Large Array (VLA) at an observing frequency of 1465 MHz.
Similarly, Duric et al. (1995) identified 53 SNRs in M 33 using the
VLA at approximately the same frequency. In general, the
![]() relations for radio SNRs in these two galaxies were
found to be flatter than the Galactic
relations for radio SNRs in these two galaxies were
found to be flatter than the Galactic ![]() relation.
relation.
A growing number of rather compact radio SNRs have been recently
detected in several nearby starburst galaxies. An example of such
a galaxy is M 82, which is known to harbor a particularly large
number of these SNRs (Huang et al. 1994). These compact SNRs are
presumably young, so at the opposite evolutionary extreme to the
old SNRs, e.g. the Galactic radio loops (Urosevic 2002,
2003). Including these young SNRs with the older SNRs in an
analysis of the ![]() relation provides an opportunity to
explore this relation beyond the parameters normally considered in
earlier studies, as well as to seek out unique evolutionary
signatures in the data.
relation provides an opportunity to
explore this relation beyond the parameters normally considered in
earlier studies, as well as to seek out unique evolutionary
signatures in the data.
Theory predicts that the evolution of young SNRs (![]() 10 pc
diameter) is different enough to define a measurably distinct
10 pc
diameter) is different enough to define a measurably distinct
![]() relation. For example, in the theory of D&S, the
youngest SNRs should follow a relation with
relation. For example, in the theory of D&S, the
youngest SNRs should follow a relation with ![]() ,
while the
older SNRs should exhibit
,
while the
older SNRs should exhibit ![]() .
To test this theoretical
prediction, we have included 21 of the young radio SNRs within M 82
as identified by Huang et al. (1994) in our analysis. A comparison
of these young radio SNRs with other extragalactic and Galactic
radio SNRs is presented in Sects. 2 and 3.
.
To test this theoretical
prediction, we have included 21 of the young radio SNRs within M 82
as identified by Huang et al. (1994) in our analysis. A comparison
of these young radio SNRs with other extragalactic and Galactic
radio SNRs is presented in Sects. 2 and 3.
This paper examines the ![]() relations of extragalactic SNRs
for the purpose of:
relations of extragalactic SNRs
for the purpose of:
Table 1: General properties of the nearby galaxies with radio SNRs.
Data sets of Galactic SNRs suffer from a severe Malmquist bias; i.e., intrinsically bright SNRs are favored because they are sampled from a larger spatial volume compared to any given flux limited survey. The result is a bias against low surface-brightness remnants such as highly evolved old SNRs. On the other hand, data sets made up of extragalactic SNRs do not suffer from Malmquist bias because all SNRs are at the same distance and are therefore sampled from the same volume. Though extragalactic data sets are generally better behaved compared to Galactic samples, they do suffer from other selection effects from limitations in sensitivity and resolution, as well as from source confusion. These selection effects cause samples of extragalactic radio SNRs to span a shorter range of both diameters and surface brightness.
Table 2: Resolution and sensitivity for searches for radio SNRs in nearby galaxies.
To prepare the sample of sources considered in this paper, we
performed a detailed literature search for candidate radio SNRs
detected in nearby galaxies and added them to our own data.
Properties of the 11 galaxies considered in this paper are listed
in Table 1 and include Hubble type, major and minor axes (in
arcmin), distance (in Mpc), inclination angle (in degrees) and a
number of known radio SNRs. For our study, we selected only those
SNRs both with a flux density at approximately 1.4 GHz (for M 82 we
used 8.4 GHz data).
When available, we adopted the given diameters for
these SNRs as measured by radio observations; however, in most
cases radio diameters were available for only the nearest
extra-galactic SNRs (e.g. sources in the LMC and the SMC) or those
sources observed at extremely high angular resolution with such
instruments as MERLIN (e.g. sources in NGC 1569 and NGC 2146). In
other cases where a radio diameter was not available, diameters
measured for the optical counterparts to the radio SNRs were
adopted. Finally, where available, we adopted published values for
the spectral index
![]() of these
sources; if no spectral index was given, a value of 0.5 was
assumed. For almost every radio SNR in our sample, we have
calculated a surface brightness at 1 GHz using a published flux
density at
of these
sources; if no spectral index was given, a value of 0.5 was
assumed. For almost every radio SNR in our sample, we have
calculated a surface brightness at 1 GHz using a published flux
density at ![]() 1.4 GHz (8.4 GHz for M 82) and a published (or
assumed) spectral index. Below we give some comments about each
galaxy in our study and their corresponding set of radio SNRs.
1.4 GHz (8.4 GHz for M 82) and a published (or
assumed) spectral index. Below we give some comments about each
galaxy in our study and their corresponding set of radio SNRs.
In Table A.1, for each extragalactic radio SNR in our sample we
list the name of the source, the host galaxy, the diameter D (in
parsecs), the flux density S1.4 at 1.4 GHz (in mJy), the
spectral index ![]() ,
and the surface brightness
,
and the surface brightness ![]()
![]() at 1 GHz (in W m-2 Hz-1 sr-1). In Table 2,
we list the resolution and sensitivity data (observing frequency
at 1 GHz (in W m-2 Hz-1 sr-1). In Table 2,
we list the resolution and sensitivity data (observing frequency ![]() ,
angular resolution, linear resolution, root-mean-square
noise, and limiting radio luminosity L
,
angular resolution, linear resolution, root-mean-square
noise, and limiting radio luminosity L![]() )
for the radio
SNR searches conducted in each galaxy. We have used the
least-squares method to derive
)
for the radio
SNR searches conducted in each galaxy. We have used the
least-squares method to derive ![]() relations for samples of
radio SNRs in individual galaxies (such as the LMC, the SMC, M 31,
M 33 and M 82), as well as for the entire sample of radio SNRs in
all of the galaxies. In Table 3 we list the derived values for
relations for samples of
radio SNRs in individual galaxies (such as the LMC, the SMC, M 31,
M 33 and M 82), as well as for the entire sample of radio SNRs in
all of the galaxies. In Table 3 we list the derived values for
![]() for each case; and to quantify the goodness of each fit,
we also give the corresponding values for the correlation
coefficient between log A and
for each case; and to quantify the goodness of each fit,
we also give the corresponding values for the correlation
coefficient between log A and ![]() (see Relation 1) and for
the fit quality based on the value of minimum Chi squared (scatter
of residuals relative to the best fit line). All of the
calibrators used to define these
(see Relation 1) and for
the fit quality based on the value of minimum Chi squared (scatter
of residuals relative to the best fit line). All of the
calibrators used to define these ![]() relations are assumed
to have equal statistical weight. Finally, all errors are formal
standard errors as derived by the least-squares method.
relations are assumed
to have equal statistical weight. Finally, all errors are formal
standard errors as derived by the least-squares method.
Table 3:
Fit characteristics of ![]() relations at 1 GHz
for SNRs in nearby galaxies.
relations at 1 GHz
for SNRs in nearby galaxies.
The LMC and the SMC, the two closest galaxies to the Milky Way,
are excellent choices for a survey of a nearby galaxy's candidate
radio SNR population. At distances of only 55 kpc and 65 kpc
(Filipovic 2002), respectively, the SNRs in these galaxies are
close enough to be resolved for detailed study at many wavelengths
(including radio); yet observations of these SNRs can be made
without the observational biases that affect studies of Galactic
radio SNRs. The first study of SNRs in the LMC was provided by
Westerlund & Mathewson (1966), who used radio and optical
observations to identify three SNRs in the LMC - N49, N63A, and
N132D. Since that work, numerous additional radio studies of the
SNRs in these two galaxies have been conducted (Mathewson &
Clarke 1972, 1973a,b; Mathewson et al. 1983, 1984, 1985; Dickel et al. 1993, 1994, 1995; Filipovic et al. 1998a,b). For the
present work, we have considered 25 of the best-studied radio SNRs
in the LMC and 7 in the SMC. Flux densities and spectral indices
for these sources have been extracted from the work of
Filipovic et al. (1998b). We calculated diameters for these
sources using our assumed distances to these two galaxies and the
optical diameters (in arcseconds) listed by the Magellanic Cloud
Emission-Line Survey (MCELS![]() ).
).
The
![]() relations for the 25 LMC and 7 SMC SNRs are:
relations for the 25 LMC and 7 SMC SNRs are:
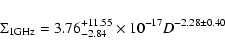 |
(2) |
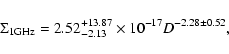 |
(3) |
The radio SNR population in M 31, the nearest major galaxy at a
distance of 0.75 Mpc (Freedman et al. 2001), has been the subject
of several studies, but its very steep inclination angle and its
large angular size have made a thorough analysis of this SNR
population very difficult. A total of 221 SNRs have been
identified in this galaxy by optical surveys (D'Odorico et al. 1980; Braun & Walterbos 1993; Magnier et al. 1995);
of these optically-identified SNRs, 30 have radio counterparts
(Dickel et al. 1982; Dickel & D'Odorico 1984; Braun & Walterbos
1993) and fifteen have X-ray counterparts (Supper et al. 2001). In
our sample, we calculated the diameters for the radio SNRs using
the optical axes for each SNR as given by Braun & Walterbos
(1993). Flux densities were extracted from the list presented by
Braun & Walterbos (1993; measured at 1.465 GHz) with two
exceptions. In the case of the optically-identified SNR K527A, the
flux density given by Braun & Walterbos (1993) does not
correspond to a 3![]() detection, so it was excluded. In the
case of the optically-identified SNR DDB-7, we used the flux
density given by Dickel & D'Odorico (1984) instead of the value
given by Braun & Walterbos (1993). We took the names for the SNRs
from both the lists of D'Odorico et al. (1980) and Braun &
Walterbos (1993), with an emphasis on the former work.
detection, so it was excluded. In the
case of the optically-identified SNR DDB-7, we used the flux
density given by Dickel & D'Odorico (1984) instead of the value
given by Braun & Walterbos (1993). We took the names for the SNRs
from both the lists of D'Odorico et al. (1980) and Braun &
Walterbos (1993), with an emphasis on the former work.
For the 30 selected radio SNRs in M 31, we obtained the relation
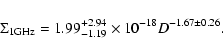 |
(4) |
Like M 31, M 33 has been the subject of many SNR studies given its proximity (0.82 Mpc - Freedman et al. 2001), but unlike M 31 the face-on orientation of M 33 is far more conducive to detailed studies of these sources at multiple wavelengths: e.g., Duric et al. (1995) and Gordon et al. (1999) at radio (6 and 20 cm), Long et al. (1996) at X-ray, and Gordon et al. (1998) at optical wavelengths. Based on radio observations, a total of 53 radio SNRs in M 33 have now been identified, and 51 are included here. For diameters of the sources, we adopted the values listed by Gordon et al. (1999), who assumed a slightly greater distance (to M 33 of 0.84 Mpc) than the present work. We recalculated the diameters accordingly to find, in all cases, a very slightly difference. Spectral indices and flux densities at 1.4 GHz for the radio SNRs were also taken from Gordon et al. (1999). Two radio SNRs from that survey (namely their sources 44 and 83) are not included in our analysis because confusing emission from adjacent HII regions prevented accurate measurement of flux densities for those two radio SNRs.
We derived a ![]() relation for the 51 radio SNRs, adopting
relation for the 51 radio SNRs, adopting
![]() for the 9 SNRs that had no spectral index
information. The corresponding relation has the form
for the 9 SNRs that had no spectral index
information. The corresponding relation has the form
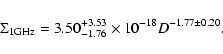 |
(5) |
The radio SNR in IC 1613 was first cataloged as an HII region
("S8'') by Sandage (1971) and identified as an SNR by D'Odorico
et al. (1980). Additional radio and optical observations and analysis
of this source were presented by Dickel et al.
(1985) and Peimbert et al. (1988). A
thorough multi-wavelength study (X-ray, optical and radio) of this
SNR was described by Lozinskaya et al. (1998), who measured a flux
density of
![]() mJy at 1.4 GHz and a spectral index of
mJy at 1.4 GHz and a spectral index of
![]() ,
which we used to calculate the
surface brightness for this SNR at 1 GHz. Lozinskaya et al. (1998)
also measured a diameter of 3 arcsec
,
which we used to calculate the
surface brightness for this SNR at 1 GHz. Lozinskaya et al. (1998)
also measured a diameter of 3 arcsec ![]() 2 arcsec for
this source using both radio and optical data; assuming a distance
to IC 1613 of 0.69 Mpc (Freedman et al. 2001), this corresponds to
a linear diameter of 8.4 pc.
2 arcsec for
this source using both radio and optical data; assuming a distance
to IC 1613 of 0.69 Mpc (Freedman et al. 2001), this corresponds to
a linear diameter of 8.4 pc.
NGC 300 and NGC 7793 are nearby, nearly face-on Sd galaxies located in the Sculptor Group (Puche & Carignan 1988). An optical search for SNRs by Blair & Long (1997) identified a total of 56 SNRs in these two galaxies. Subsequently, Pannuti et al. (2000) and Pannuti et al. (2002) detected radio counterparts to five of these SNRs - N300-S10, N300-S11, N300-S26, N7793-S11 and N7793-S26 - and provided both flux densities at 1.4 GHz and spectral indices for these sources. We adopted the optical diameters for these sources as given by Blair & Long (1997) who assumed distances of 2.1 Mpc for NGC 300 and 3.38 Mpc for NGC 7793 (Freedman et al. 1992; Puche & Carignan 1988). Radio properties for these SNRs were taken from the works of Pannuti et al. (2000, 2002). Note that N7793-S26 has a peculiar morphology; in both optical and radio images, this source appears to be more filamentary (about 450 pc long) than circular (Blair & Long 1997; Pannuti et al. 2002). This source is considered to be a candidate HNR; in Sects. 2.3.2 and 3.3, we will discuss other candidate HNRs in our sample in more detail.
This galaxy has been the subject of both optical and radio searches for SNRs (Matonick & Fesen 1997; Lacey et al. 1997). Though both searches detected a large number of sources (27 and 35, respectively), only two were in common (Lacey & Duric 2001): MF9 and MF16, using the notation from Matonick & Fesen (1997). MF16 is known to be an extremely luminous X-ray source with luminosity of approximately 1039 erg per second: the true nature of this X-ray emission is still not known (Dunne et al. 2000; Schlegel et al. 2000). We adopted the optical diameters for these sources as listed by Matonick & Fesen (1997), assuming a distance to the galaxy of 5.5 Mpc (Tully 1988). We also adopted the spectral indices and flux densities at 1.4 GHz for these two sources as given by Lacey & Duric (2001).
Starburst galaxies are expected to be excellent targets when
searching for SNRs, given the extensive amount of star formation
activity throughout their galactic disks. As mentioned previously, the
starburst galaxy M 82 is known to have a large population of young
radio SNRs. Huang et al. (1994) detected 50 radio SNRs in this
galaxy, all of which were less than six parsecs in diameter. These
authors also constructed a ![]() relation for these remnants
at 8.4 GHz, obtaining a fit with a slope of
relation for these remnants
at 8.4 GHz, obtaining a fit with a slope of
![]() ,
and
used 39 SNRs with precisely determined angular diameters and flux
densities. Another relation for 28 calibrators with angular
diameters less than or equal to the beam size was derived,
yielding a slope of
,
and
used 39 SNRs with precisely determined angular diameters and flux
densities. Another relation for 28 calibrators with angular
diameters less than or equal to the beam size was derived,
yielding a slope of
![]() .
For the 21 SNRs with both
reliable diameters and calculated spectral indices from the
parsec-scale study by McDonald et al. (2002) - which measured the
spectral indices of compact radio sources in this galaxy - we
obtained the relation
.
For the 21 SNRs with both
reliable diameters and calculated spectral indices from the
parsec-scale study by McDonald et al. (2002) - which measured the
spectral indices of compact radio sources in this galaxy - we
obtained the relation
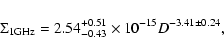 |
(6) |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{2535fig1.eps}
\end{figure}](/articles/aa/full/2005/20/aa2535/Timg45.gif) |
Figure 1:
The |
| Open with DEXTER | |
NGC 1569 and NGC 2146 are two other starburst galaxies like M 82, which are located at distances of 2.2 Mpc (Israel 1988) and 14.5 Mpc (Tarchi et al. 2000), respectively. Searches for radio supernovae and radio SNRs in these galaxies using observations made with MERLIN and the VLA are presented by Greve et al. (2002) and Tarchi et al. (2000), respectively. Greve et al. (2002) identified three radio SNRs in NGC 1569 (denoted in their work as VLA-8, VLA-16 and M-6), while the search presented by Tarchi et al. (2000) detected three radio SNRs in NGC 2146 (denoted in their work as 37.6+24.2, 38.9+22.5 and 41.4+15.0). Both papers gave radio diameters and spectral indices for the SNRs, while Tarchi et al. (2000) gave flux densities at 1.6 GHz for their sources, and Greve et al. (2002) gave flux densities for all three SNRs at 1.4 GHz. We incorporated all of these values into our analysis.
We now consider properties of the data for all of the radio SNRs
in the 11 galaxies discussed so far. This ensemble contains a
total of 148 SNRs, and the ![]() relation for the ensemble
may be expressed as
relation for the ensemble
may be expressed as
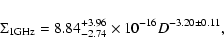 |
(7) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2535fig2.eps}
\end{figure}](/articles/aa/full/2005/20/aa2535/Timg47.gif) |
Figure 2:
The |
| Open with DEXTER | |
Three of the radio SNRs in our sample - N7793-S26 in the galaxy
NGC 7793, as well as the SNRs 37.6+24.2 and 38.9+42.5 in the
galaxy NGC 2146 - place in the right part of the ![]() diagram (Fig. 2), indicating that these SNRs are more
radio-luminous than expected for sources with their diameters. All
three are considered HNRs based on their extreme radio
luminosities. To test their effects on our derived fits, we
re-derived a
diagram (Fig. 2), indicating that these SNRs are more
radio-luminous than expected for sources with their diameters. All
three are considered HNRs based on their extreme radio
luminosities. To test their effects on our derived fits, we
re-derived a ![]() relation for the SNRs in our master
ensemble after excluding the three HNRs. As shown in Table 3, the
slope for this sample of 145 SNRs did not change within the
statistical errors (
relation for the SNRs in our master
ensemble after excluding the three HNRs. As shown in Table 3, the
slope for this sample of 145 SNRs did not change within the
statistical errors (
![]() ). To further test the
effects of extreme points, we again re-derived the relation after
excluding the three HNRs once again along with ten other radio
SNRs located toward the middle of the
). To further test the
effects of extreme points, we again re-derived the relation after
excluding the three HNRs once again along with ten other radio
SNRs located toward the middle of the ![]() vs. D plot. These
ten particular SNRs are located in galaxies which lie outside of
the Local Group (that is, located in the galaxies NGC 300, NGC 1569, NGC 2146, NGC 6946 and NGC 7793, with M 82 excluded). The
corresponding
vs. D plot. These
ten particular SNRs are located in galaxies which lie outside of
the Local Group (that is, located in the galaxies NGC 300, NGC 1569, NGC 2146, NGC 6946 and NGC 7793, with M 82 excluded). The
corresponding ![]() relation is
relation is
![]() (for the sample of 135 remaining SNRs). This
relation is very similar to the one derived for the whole sample
if the 3 HNRs are excluded. We therefore argue that including the
"outlier'' sources in our sample - either HNRs or other extreme
SNRs - does not dramatically affect our relations.
(for the sample of 135 remaining SNRs). This
relation is very similar to the one derived for the whole sample
if the 3 HNRs are excluded. We therefore argue that including the
"outlier'' sources in our sample - either HNRs or other extreme
SNRs - does not dramatically affect our relations.
In order to check whether the apparently anomalous M 82 could arise
by chance, we performed a series of Monte Carlo simulations with
the null hypothesis of no relation between ![]() and D. We
generated random SNR populations (10 000 SNRs) according to
various functional forms of
and D. We
generated random SNR populations (10 000 SNRs) according to
various functional forms of ![]() .
Then for each measured
value of log D we randomly selected one of the artificially
generated
.
Then for each measured
value of log D we randomly selected one of the artificially
generated ![]() values. If the pair fell within the
sensitivity cutoffs, we kept it; otherwise we randomly selected
another
values. If the pair fell within the
sensitivity cutoffs, we kept it; otherwise we randomly selected
another ![]() value until the pair did fall within the
sensitivity cutoffs. This procedure was repeated until we matched
up all the measured values of log D with artificially generated
log
value until the pair did fall within the
sensitivity cutoffs. This procedure was repeated until we matched
up all the measured values of log D with artificially generated
log ![]() 's. Then we fit a line through the points and measured
the slope. The process was repeated 1000 times, leading to a
histogram of 1000 slopes. A total of 7 different distributions
were used, leading to 7 such histograms. The results from two
representative distributions (a power law distribution with slope
of -3 and a Gaussian) are shown in Table 4.
's. Then we fit a line through the points and measured
the slope. The process was repeated 1000 times, leading to a
histogram of 1000 slopes. A total of 7 different distributions
were used, leading to 7 such histograms. The results from two
representative distributions (a power law distribution with slope
of -3 and a Gaussian) are shown in Table 4.
Table 4: Parameters from the Monte Carlo simulation for the M 82 slope.
Inspection of Table 4 shows that the probability of obtaining a
slope equal to the measured slope, or greater, is the range of 1%
to 9.6% depending on the assumed SNR population and the
uncertainties in the measured slope. It therefore seems likely
that the M 82 relation is statistically different from the other 10 galaxies, at a confidence level of ![]() 90-99%.
90-99%.
The "master'' relation does not appear useful for defining unique evolutionary tracks but does combine one potentially useful relation (M 82) and a number of non-useful relations (for SNRs from the other 10 nearby galaxies).
The Galactic relation (C&B) probably also has the trivial
![]() form and therefore does not represent a
physically meaningful relation. We concluded that the previously
reported Galactic relations were subject to severe selection
effects, the impact of which (e.g. volume dependent selection) is
to make the slope of the relation appear steeper than it really
is. These results suggest that even the modestly steep relation of
C&B may be too steep, possibly a result of Malmquist bias and
favor the interpretation of Green (1991).
form and therefore does not represent a
physically meaningful relation. We concluded that the previously
reported Galactic relations were subject to severe selection
effects, the impact of which (e.g. volume dependent selection) is
to make the slope of the relation appear steeper than it really
is. These results suggest that even the modestly steep relation of
C&B may be too steep, possibly a result of Malmquist bias and
favor the interpretation of Green (1991).
It is apparent that the ![]() relations within individual
galaxies have the trivial form (except for M 82). Selection effects
may explain the slight systematic differences between the
Magellanic clouds on the one hand, and M 31 and M 33 on the other.
The surveys of M 31 and M 33 were performed at better linear
resolution and with greater sensitivity than those of the LMC and
the SMC (see Table 2). These differences may give rise to
different levels of confusion and to a systematic shaping of the
relations. In any case, the effect is not great and relations
among the four galaxies are generally consistent with each other.
relations within individual
galaxies have the trivial form (except for M 82). Selection effects
may explain the slight systematic differences between the
Magellanic clouds on the one hand, and M 31 and M 33 on the other.
The surveys of M 31 and M 33 were performed at better linear
resolution and with greater sensitivity than those of the LMC and
the SMC (see Table 2). These differences may give rise to
different levels of confusion and to a systematic shaping of the
relations. In any case, the effect is not great and relations
among the four galaxies are generally consistent with each other.
Beyond the Local Group galaxies, we still do not have a very large
sample of radio SNRs with well-defined diameters, spectral indices
and flux densities. The greater distances to these galaxies,
combined with selection effects (related to sensitivity,
resolution and source confusion), are the major difficulties in
detecting radio SNRs in these galaxies. Thus, only the most
luminous radio SNRs were detected in the more distant galaxies in
our sample. The detection limitations for the nearby galaxies in
terms of sensitivity and resolution are presented in Table 2. In
Fig. 3, we present a plot in the
![]() plane that
illustrates limits in both
plane that
illustrates limits in both ![]() and D for the surveys
considered in this paper. Notice that only SNRs located above and
to the right of each line would be detected by the radio searches.
and D for the surveys
considered in this paper. Notice that only SNRs located above and
to the right of each line would be detected by the radio searches.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2535fig3.eps}
\end{figure}](/articles/aa/full/2005/20/aa2535/Timg52.gif) |
Figure 3:
Sensitivity lines in the |
| Open with DEXTER | |
To test the significance of our statistical results we performed a new Monte Carlo simulation as described below.
For a particular galaxy, we measured the standard deviation in
log ![]() of the real data from the best fit line, assuming that
log D is the independent variable. We then selected an interval
in log D 5 times as long as that of the real data. We sprinkled
this interval randomly with points with the same density in log Das the real data. Then we projected these points that lie on the
log D axis onto a series of lines of different slopes (1 to 5),
each passing through the extreme upper left hand end of the best
fit line to the real data. Then we added Gaussian noise in
log
of the real data from the best fit line, assuming that
log D is the independent variable. We then selected an interval
in log D 5 times as long as that of the real data. We sprinkled
this interval randomly with points with the same density in log Das the real data. Then we projected these points that lie on the
log D axis onto a series of lines of different slopes (1 to 5),
each passing through the extreme upper left hand end of the best
fit line to the real data. Then we added Gaussian noise in
log ![]() .
The noise is related to the scatter of the real data
by a parameter called "scatter''. A scatter of "1'' corresponds to
the same standard deviation as that of the real data. We applied
the appropriate sensitivity cutoff to the simulated datapoints and
generated a least squares best fit line from the selected points.
We did this 100 times and calculated the mean and standard
deviation of the best fit slopes.
.
The noise is related to the scatter of the real data
by a parameter called "scatter''. A scatter of "1'' corresponds to
the same standard deviation as that of the real data. We applied
the appropriate sensitivity cutoff to the simulated datapoints and
generated a least squares best fit line from the selected points.
We did this 100 times and calculated the mean and standard
deviation of the best fit slopes.
Table 5: Parameters from the second Monte Carlo simulation for LMC.
Table 6: Parameters from the second Monte Carlo simulation for M 33.
Table 7: Parameters from the second Monte Carlo simulation for M 82.
The results for LMC, M 33, and the M 82 are summarized in Tables 5-7, and reveal the following trends:
Investigation of Fig. 3 shows that for all galaxies, except M 82
and NGC 2146, the D-2 sensitivity lines are bunched in a
relatively narrow band in the ![]() plane. Consequently any
fits made to the collective data are affected by this
observational selection effect. This explains, in part, the slope
of the master relation, which is consistent with 2
plane. Consequently any
fits made to the collective data are affected by this
observational selection effect. This explains, in part, the slope
of the master relation, which is consistent with 2![]() when M 82 is excluded, although NGC 2146 does not play a
significant role statistically because there are only three data
points associated with it. Addition of M 82 steepens the slope
because its sensitivity line is shifted significantly to the right
in Fig. 3, partly explaining the steeper value obtained when all
data are used in the fit. In the case of M 82 by itself, the only
major observational effect is its own D-2 sensitivity line,
which by itself cannot account for the steep slope of 3.4 obtained
when only the M 82 data are fit, as shown in Sects. 3.1 and 3.2.
when M 82 is excluded, although NGC 2146 does not play a
significant role statistically because there are only three data
points associated with it. Addition of M 82 steepens the slope
because its sensitivity line is shifted significantly to the right
in Fig. 3, partly explaining the steeper value obtained when all
data are used in the fit. In the case of M 82 by itself, the only
major observational effect is its own D-2 sensitivity line,
which by itself cannot account for the steep slope of 3.4 obtained
when only the M 82 data are fit, as shown in Sects. 3.1 and 3.2.
The two sets of Monte Carlo simulations, the first relating to the
probability of a particular slope arising by chance and the second
investigating the effect of selection effects, both suggest that
the ![]() relation for M 82 is anomalously steep relative to
the relations of the other galaxies in our sample. At the same
time, the SNR diameters are uniquely small compared to the other
SNRs in the master sample. The measured slope for the M 82 SNRs is
relation for M 82 is anomalously steep relative to
the relations of the other galaxies in our sample. At the same
time, the SNR diameters are uniquely small compared to the other
SNRs in the master sample. The measured slope for the M 82 SNRs is
![]() ,
while that of the remaining SNRs in the master
relation is
,
while that of the remaining SNRs in the master
relation is
![]() .
The latter slope does not have
a physical origin, but is consistent with the luminosity-diameter
scattering artifact (see Arbutina et al. 2004). According to
theory, the surface brightness of the SNR is a function of the
density of the gas of the medium the SNR is interacting with. One
particular model (e.g. Bell 1978a,b) predicts the surface
brightness to have form
.
The latter slope does not have
a physical origin, but is consistent with the luminosity-diameter
scattering artifact (see Arbutina et al. 2004). According to
theory, the surface brightness of the SNR is a function of the
density of the gas of the medium the SNR is interacting with. One
particular model (e.g. Bell 1978a,b) predicts the surface
brightness to have form
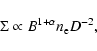 |
(8) |
According to the D&S theory, only coefficient A in Eq. (1)
depends on ![]() ,
also obvious from Eq. (8). From the same
theory, coefficient
,
also obvious from Eq. (8). From the same
theory, coefficient ![]() explicitly does not depend on
explicitly does not depend on ![]() .
Therefore the slopes of potential shallower (or steeper)
components are the same for all SNRs, and evolutionary tracks are
parallel. The breaks exist and, for all evolutionary tracks are
located at different points in the
.
Therefore the slopes of potential shallower (or steeper)
components are the same for all SNRs, and evolutionary tracks are
parallel. The breaks exist and, for all evolutionary tracks are
located at different points in the ![]() plane. We probably
identified one steep evolutionary track for SNRs in M 82 at higher
density, without the corresponding shallower part that is probably
hidden by the selection effects. Nevertheless, for other
(generally closer) galaxies we did not identify a unique shallower
track; we just proposed possible shallower tracks for the SNRs
that probably evolve in more dilute media without the
corresponding very young SNR tracks. These galaxies are
non-starburst, so we do not expect to see enough very young SNRs
to define the steeper track.
plane. We probably
identified one steep evolutionary track for SNRs in M 82 at higher
density, without the corresponding shallower part that is probably
hidden by the selection effects. Nevertheless, for other
(generally closer) galaxies we did not identify a unique shallower
track; we just proposed possible shallower tracks for the SNRs
that probably evolve in more dilute media without the
corresponding very young SNR tracks. These galaxies are
non-starburst, so we do not expect to see enough very young SNRs
to define the steeper track.
Despite the apparent effect of environmental differences, the M 82
result supports previous observations that the SNRs in M 82 are
younger and follow a different evolutionary track in the ![]() plane. Furthermore, the steep slope of the M 82 relation
is not caused by selection effects, because the difference in
slopes is greater (by a factor of over two) than the difference
that can be replicated by known selection effects in the Galaxy or
in the data-sets for radio SNRs in M 31 and M 33 (Urosevic
2003).
plane. Furthermore, the steep slope of the M 82 relation
is not caused by selection effects, because the difference in
slopes is greater (by a factor of over two) than the difference
that can be replicated by known selection effects in the Galaxy or
in the data-sets for radio SNRs in M 31 and M 33 (Urosevic
2003).
To investigate the break in the relation further, we examined the
locations of the SNRs in the ![]() plane from other starburst
galaxies. In the case of NGC 2146, the result was as expected.
However, in the case of NGC 1569, the SNRs were found to belong to
the shallower sample. This result suggests that the SNRs in that
galaxy are possibly more evolved, consistent with the hypothesis
that NGC 1569 is currently in a post starburst stage of evolution
(Greve et al. 2002). Also, it indicates that the location on a
plane from other starburst
galaxies. In the case of NGC 2146, the result was as expected.
However, in the case of NGC 1569, the SNRs were found to belong to
the shallower sample. This result suggests that the SNRs in that
galaxy are possibly more evolved, consistent with the hypothesis
that NGC 1569 is currently in a post starburst stage of evolution
(Greve et al. 2002). Also, it indicates that the location on a
![]() plot for a candidate radio SNR in a starburst galaxy
(that is, in the shallower or steeper part of the plot) may
originate from purely a "physical'' evolutionary effect predicted
by D&S.
plot for a candidate radio SNR in a starburst galaxy
(that is, in the shallower or steeper part of the plot) may
originate from purely a "physical'' evolutionary effect predicted
by D&S.
In the absence of knowledge about true scatter in the ![]() plane, we tentatively conclude:
plane, we tentatively conclude:
We briefly comment on properties of the three candidate HNRs included in our sample of extragalactic SNRs. In a separate study, we calculated the minimum energies required to power these sources through synchrotron radiation: we found that the minimum energies for all three SNRs exceeded 1051 ergs (Pannuti et al. 2005, in preparation). This result suggests that these three sources may have indeed been produced by extremely luminous supernova explosions known as hypernovae (e.g., Wang 1999), though the true nature of these sources is still the subject of intense debate (Snowden et al. 2001; Chen et al. 2002). It is interesting to note that both of the host galaxies for these three SNRs exhibit characteristics of starburst activity; NGC 2146 has a disturbed morphology and extensive star formation throughout its disk (Hutchings et al. 1990), while NGC 7793 - though more regular in appearance than NGC 2146 - still shows extensive massive star formation activity, as evidenced by large amounts of photo-ionized gas permeating the disk of this galaxy (Blair & Long 1997). Lastly, we note that Chevalier & Fransson (2001) discussed the high radio luminosity of SNRs located in starburst galaxies and argued that these elevated radio luminosities are correlated with the higher average molecular cloud densities with which these radio SNRs are interacting in these galaxies. Additional radio observations of more galaxies (both normal and starburst) are necessary in order to learn more about these very luminous radio SNRs, their environments, and their host galaxies.
The three major results of this paper may be summarized as follows:
Acknowledgements
We thank the referee L. Rudnick for many helpful comments that improved the quality of this paper, and especially those connected with the Monte Carlo simulations. We also acknowledge useful discussions with Miroslav Filipovic. D.U. would like to acknowledge Jelena Milogradov-Turin without whom his interest in supernova remnants would never have developed. This work is a part of the projects "Structure, Kinematics and Dynamics of the Milky Way'' (No. 1468) supported by the Ministry of Science and Environmental Protection of the Republic of Serbia. N.D. would like to thank the faculty and students of the Department of Astronomy of the University of Belgrade for their generous hospitality under very trying circumstances. This research made use of the NASA/IPAC Extragalactic Database (NED) operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
Table A.1:
The basic quantities for 148 SNRs in nearby galaxies
used in this paper for deriving of the updated ![]() relations.
relations.