A&A 435, 385-395 (2005)
DOI: 10.1051/0004-6361:20042451

Self-gravitational adaptive mesh magnetohydrodynamics with the NIRVANA code

U. Ziegler

Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany

Received 29 November 2004 / Accepted 21 January 2005

Abstract
I present a new version of the NIRVANA code capable for the simulation of multi-scale self-gravitational magnetohydrodynamics problems in three space dimensions employing the technique of adaptive mesh refinement. The building blocks of NIRVANA are (i) a fully conservative, divergence-free Godunov-type central scheme for the solution of the equations of magnetohydrodynamics; (ii) a block-structured mesh refinement algorithm which automatically adds and removes elementary grid blocks whenever necessary to achieve adequate resolution and; (iii) an adaptive mesh Poisson solver based on multigrid philosophy which incorporates the so-called elliptic matching condition to keep the gradient of the gravitational potential continous at fine/coarse mesh interfaces. In this paper I give an overview of the basic numerical ideas standing behind NIRVANA and apply the code to the problem of protostellar core collaps and fragmentation.

Key words: magnetohydrodynamics (MHD) - stars: formation - methods: numerical - ISM: magnetic fields

1 Introduction

From analysis of observational data there comes strong evidence that stars are preferably formed as a binary system or even higher-order multiple systems (Reipurth & Zinnecker 1993; Bodenheimer et al. 2000; Tokovinin & Smekhov 2002; Patience et al. 2002). From theory, the most plausible explanation for this is fragmentation of an unstable cloud core into smaller condensations (pre-stellar cores) during gravitational collapse. Fragmentation is usually studied through numerical simulations since the underlying equations are too complex to solve by analytical techniques. However, on several reasons, numerical investigations also require highly sophisticated codes. First, the problem of fragmentation is intrinsically three-dimensional. Second, it involves a large dynamic range in length scales which must be well resolved numerically to follow the collapse and to obtain useful solutions at all. Codes based on fixed resolution schemes are ruled out because these would need tremendous computer resources not available today. Moreover, such methods would be very inefficient since regions which actually need no high numerical resolution are yet fully resolved. Third, there are different physical effects involved described by different types of mathematical equations requiring different numerical methods. As an example, the conservation laws of ideal hydrodynamics are of hyperbolic type whereas the Poisson equation for the gravitational potential is elliptic.

An issue of particular interest in the fragmentation process is the likely role of magnetic fields. This is because there is striking evidence that dense cloud cores are partly supported - besides internal turbulent motions and ordered rotation - by magnetic fields against collapse (Crutcher 1999; Caselli et al. 2002). To study fragmentation of magnetized clouds the full nonlinear equations of gravitomagnetohydrodynamics (GMHD) must be solved in a multi-scale fashion.

Solutions of the G(M)HD equations for the collpase problem are either based on smoothed particle (magneto)hydrodynamics (SP(M)H) or finite-difference/finite-volume schemes with adaptive mesh refinement (AMR) each in combination with a solver for the Poisson equation. SPH is a Lagrangian approach where "smoothed particles'' carrying fluid properties are integrated forward in time subject to mutual gravitational attraction. Usually, the number of particles in a SPH simulation is fixed providing a variable spatial resolution through the movement of the particles itself but keeping the mass in a "smoothing sphere'' constant (Monaghan 1992). Variable mass resolution can be obtained to some extend by a new technique called particle splitting (Kitsionas & Whitworth 2002) in which a particle is subdivided into a number of child particles having accordingly lower masses.

In order to account for the large scale variations typical in collapse scenarios grid-based codes make use of AMR - the counterpart to particle splitting in SPH. Several approaches have been employed here. Boss (2002), for instance, applied a spherical code in which only the radial coordinate is adaptive. This is a useful procedure when structures near the coordinate origin are produced but it is less suited if such structures form further away from the center. Another approach which has been used by some workers is the nested-grid method in Cartesian geometry (see e.g. Burkert & Bodenheimer 1993). In this method a sequence of finer-spaced smaller grids is hierarchically nested and placed around the coordinate origin from the beginning of the simulation. Like in a r-adaptive spherical grid code a nested-grid scheme may underresolve structures not captured by the finest level of refinement. In a more sophisticated variant as that used by Truelove et al. (1997) the mesh is fully adaptive adding and removing finer grid units locally according to specific refinement criteria during the course of simulation.

Most numerical calculations on protostellar fragmentation so far focused on non-magnetic configurations (Truelove et al. 1998; Boss et al. 2000; Bate et al. 2002a,b; Bate et al. 2003; Klein et al. 2003; Goodwin et al. 2004a,b). Only just recently the magnetic regime has begun to be explored. Balsara & Burkert (2001) were the first using a fully adaptive GMHD scheme to study examplary the collapse of a magnetized cloud core. Boss (2002, 2004) in a more systematic way investigated the possible role of magnetic fields during collapse, however, neglecting the important effect of magnetic braking in the governing equations. Machida et al. (2004) constructed a fragmentation model based on a nested-grid GMHD code. Finally, Hosking & Whitworth (2004a,b) applied a recently developed two-fluid SPMH method to the problem of protostellar core collaps in the presence of a magnetic field including the effect of ambipolar diffusion. The major pitfall I see with this approach, however, is the severe violation of the divergence constraint for the magnetic field of up to 100% maximum relative error. Such large errors produce unphysical forces leading to wrong dynamics and generate wrong field topologies.

In this paper I present a new version of the NIRVANA code - a fully-conservative, divergence-free grid-based code for the equations of GMHD able to treat multi-scale problems employing AMR techniques. Section 2 will give an overview of the basic numerical algorithms implemented in the NIRVANA code. First results of an application of the code to the fragmentation problem in non-magnetic and magnetic cloud cores are then presented in Sect. 3 of this paper.

2 Algorithms

2.1 Equations

The algorithms described in the following aim to find numerical solutions to the equations of ideal magnetohydrodynamics including the effects of selfgravity:

                                               $\displaystyle \partial_t\varrho +\nabla\cdot(\varrho {\vec v}) = 0,$ (1)
    $\displaystyle \partial_t e +\nabla\cdot\left[\left(e+p+\frac{1}{2\mu}\vert{\vec... ...{\mu}({\vec v}\cdot{\vec B}){\vec B}\right] =-\varrho \nabla \Phi\cdot{\vec v},$ (2)
    $\displaystyle \partial_t(\varrho{\vec v}) +\nabla\cdot\left[\varrho\vec{vv} +\l... ...ert{\vec B}\vert^2\right)I-\frac{1}{\mu}\vec{BB}\right] = -\varrho \nabla \Phi,$ (3)
    $\displaystyle \partial_t {\vec B} -\nabla\times({\vec v}\times{\vec B}) = 0,$ (4)
    $\displaystyle \nabla^2 \Phi = 4\pi G\varrho$ (5)

where $\varrho$ is the mass density, e is the total energy density excluding gravitational energy, ${\vec v}$ is the velocity, ${\vec B}$ is the magnetic field, $\Phi$ is the gravitational potential, $\mu$ is the magnetic permeability and G is the gravitational constant. The equations are supplemented by the zero divergence condition for the magnetic field,

\begin{displaymath}\nabla\cdot{\vec B}=0, \end{displaymath}

and the ideal gas equation of state

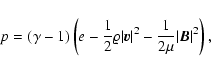\begin{displaymath}p=(\gamma -1)\left(e-\frac{1}{2}\varrho\vert{\vec v}\vert^2-\frac{1}{2\mu}\vert {\vec B}\vert^2\right), \end{displaymath} (6)

where $\gamma$ is the ratio of specific heats.

2.2 MHD solver

The first building block of the NIRVANA code is the numerical method for the solution of the ideal MHD equations on a fixed-resolution Cartesian grid. Here, I present a compact overview of the basic ideas standing behind the MHD scheme. More details can be found in Ziegler (2004).

Space discretization. Equations (1)-(3) excluding the gravity source terms but including the Lorentz force are solved with help of the Godunov-type central scheme for conservation laws developed by Kurganov et al. (2001). The scheme has been slightly modified for the MHD case and combined with the constraint transport to solve the induction equation for a divergence-free evolution of the magnetic field. I apply a semi-discrete approach where the equations are first discretized in flux conservation form in space leaving open the time discretization. The 3D Cartesian grid is indexed $\{ijk\}$with constant cell width $\delta x$ ($\delta y$, $\delta z$) in x(y,z)-direction. A numerical cell spans the index range $[i-{\scriptscriptstyle 1\over \scriptscriptstyle 2},i+{\scriptscriptstyle 1\ove... ...\over \scriptscriptstyle 2},k+{\scriptscriptstyle 1\over \scriptscriptstyle 2}]$ i.e. the cell center is located at [ijk].

Denoting $\overline{\vec u}_{ijk}$ as the numerical approximation to the cell-averaged solution vector ${\vec u}=(\varrho, e, {\vec m}=\varrho {\vec v})$the second-order version of the scheme reads:

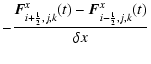                $\displaystyle \frac{{\rm d}}{{\rm d}t}\overline{\vec u}_{i,j,k}(t)$ = $\displaystyle -\frac{{\vec F}^x_{i+{\scriptscriptstyle 1\over \scriptscriptstyl... ...vec F}^x_{i-{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k}(t)}{\delta x}$  
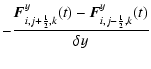    $\displaystyle -\frac{{\vec F}^y_{i,j+{\scriptscriptstyle 1\over \scriptscriptst... ...vec F}^y_{i,j-{\scriptscriptstyle 1\over \scriptscriptstyle 2},k}(t)}{\delta y}$  
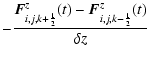    $\displaystyle -\frac{{\vec F}^z_{i,j,k+{\scriptscriptstyle 1\over \scriptscript... ...vec F}^z_{i,j,k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}(t)}{\delta z}$ (7)

where the numerical flux in x-direction, for example, is given by
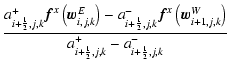                        $\displaystyle {\vec F}^x_{i+{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k}$ = $\displaystyle \frac{a^+_{i+{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k... ...riptstyle 2},j,k}-a^-_{i+{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k}}$  
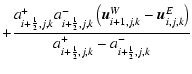    $\displaystyle +\frac{a^+_{i+{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,... ...riptstyle 2},j,k}-a^-_{i+{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k}}$  

with the flux function

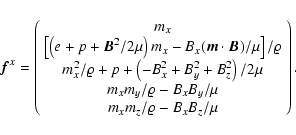
\begin{displaymath}{\vec f}^x = \left(\begin{array}{c} m_x \\ \left[\left(e+p+{... ...o-B_xB_y/\mu \\ m_xm_z/\varrho-B_xB_z/\mu \end{array}\right). \end{displaymath}

Expressions ${\vec F}^y_{i,j+{\scriptscriptstyle 1\over \scriptscriptstyle 2},k}$, ${\vec F}^z_{i,j,k+{\scriptscriptstyle 1\over \scriptscriptstyle 2}}$, ${\vec f}^y$ and ${\vec f}^z$ for the other coordinate directions look quite similar and can be found in Ziegler (2004). The quantities ${\vec w}^{W,E}_{ijk}$={ ${\vec u}^{W,E}_{ijk}$, ${\vec B}^{W,E}_{ijk}$} represent the reconstructed variables at the $i-{\scriptscriptstyle 1\over \scriptscriptstyle 2}$ cell face (W) and $i+{\scriptscriptstyle 1\over \scriptscriptstyle 2}$ cell face (E) of cell [ijk] at time t (notice that all quantities are functions of time since no time discretization is given yet). $a^{\pm}$ denotes the maximum (plus sign) and minimum (minus sign) local characteristic speed in x-direction at a cell interface i.e.
                              $\displaystyle a^+_{i+{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k}$ = $\displaystyle \max\left\{(v_x+c_{\rm f})^W_{i+1,j,k},(v_x+c_{\rm f})^E_{i,j,k},0\right\},$  
$\displaystyle a^-_{i+{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k}$ = $\displaystyle \min\left\{(v_x-c_{\rm f})^W_{i+1,j,k},(v_x-c_{\rm f})^E_{i,j,k},0\right\}$  

where $c_{\rm f}$ is the fast magnetosonic speed. The applied reconstruction procedure is linear in space and makes use of the van Leer (1977) slope limiter. Notice that the only information required to compute the numerical flux is the one-sided minimum and maximum propagation speed and no further details about the eigenstructure of the system is needed contrary to Riemann solver based schemes.

The induction Eq. (4) is solved separately with the constraint transport (CT) method (see e.g. Evans & Hawley 1988; Tóth 2000). Utilizing the staggered collocation of the magnetic field components on cell faces (see Fig. 1) renders the numerical divergence of curl operator to vanish exactely. CT thus ensures that an initially divergence-free magnetic field evolves divergence-free up to machine accuracy i.e. $(\nabla\cdot{\overline{\vec B}})_{ijk}=0$ where $\overline{B}_{x i-{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k}$, $\overline{B}_{y i,j-{\scriptscriptstyle 1\over \scriptscriptstyle 2},k}$and $\overline{B}_{z i,j,k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}$are numerical approximations to the face-averaged solution $\{B_x,B_y,B_z\}$.

As before, a semi-discrete ansatz is adopted. The scheme reads

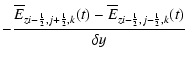                      $\displaystyle \frac{{\rm d}}{{\rm d}t}\overline{B}_{x i-{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k}(t)$ = $\displaystyle -\frac{\overline{E}_{z i-{\scriptscriptstyle 1\over \scriptscript... ...iptstyle 2},j-{\scriptscriptstyle 1\over \scriptscriptstyle 2},k}(t)}{\delta y}$  
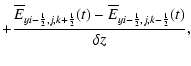    $\displaystyle +\frac{\overline{E}_{y i-{\scriptscriptstyle 1\over \scriptscript... ...ptstyle 2},j,k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}(t)}{\delta z},$ (8)
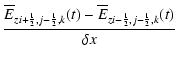$\displaystyle \frac{{\rm d}}{{\rm d}t}\overline{B}_{y i,j-{\scriptscriptstyle 1\over \scriptscriptstyle 2},k}(t)$ = $\displaystyle \frac{\overline{E}_{z i+{\scriptscriptstyle 1\over \scriptscripts... ...iptstyle 2},j-{\scriptscriptstyle 1\over \scriptscriptstyle 2},k}(t)}{\delta x}$  
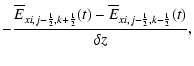    $\displaystyle -\frac{\overline{E}_{x i,j-{\scriptscriptstyle 1\over \scriptscri... ...riptstyle 2},k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}(t)}{\delta z},$ (9)
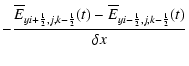$\displaystyle \frac{{\rm d}}{{\rm d}t}\overline{B}_{z i,j,k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}(t)$ = $\displaystyle -\frac{\overline{E}_{y i+{\scriptscriptstyle 1\over \scriptscript... ...iptstyle 2},j,k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}(t)}{\delta x}$  
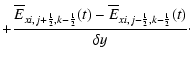    $\displaystyle +\frac{\overline{E}_{x i,j+{\scriptscriptstyle 1\over \scriptscri... ...style 2},k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}(t)}{\delta y}\cdot$ (10)

The edge-centered numerical components of the electric field, ${\vec E}=-{\vec v}\times{\vec B}$, are given by the compositions
                $\displaystyle \overline{E}_{x i,j-{\scriptscriptstyle 1\over \scriptscriptstyle 2},k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}$ = $\displaystyle \frac{1}{4}\big( -{E}^y_{z i,j-{\scriptscriptstyle 1\over \script... ...tstyle 2},k}-{E}^y_{z i,j-{\scriptscriptstyle 1\over \scriptscriptstyle 2},k-1}$  
    $\displaystyle +{E}^z_{y i,j,k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}+{E}^z_{y i,j-1,k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}\big),$  
$\displaystyle \overline{E}_{y i-{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}$ = $\displaystyle \frac{1}{4}\big( {E}^x_{z i-{\scriptscriptstyle 1\over \scriptscr... ...tyle 2},j,k}+{E}^x_{z i-{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k-1}$  
    $\displaystyle -{E}^z_{x i,j,k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}-{E}^z_{x i-1,j,k-{\scriptscriptstyle 1\over \scriptscriptstyle 2}}\big),$  
$\displaystyle \overline{E}_{z i-{\scriptscriptstyle 1\over \scriptscriptstyle 2},j-{\scriptscriptstyle 1\over \scriptscriptstyle 2},k}$ = $\displaystyle \frac{1}{4}\big( -{E}^x_{y i-{\scriptscriptstyle 1\over \scriptsc... ...tyle 2},j,k}-{E}^x_{y i-{\scriptscriptstyle 1\over \scriptscriptstyle 2},j-1,k}$  
    $\displaystyle +{E}^y_{x i,j-{\scriptscriptstyle 1\over \scriptscriptstyle 2},k}+{E}^y_{x i-1,j-{\scriptscriptstyle 1\over \scriptscriptstyle 2},k}\big),$  

i.e. by suitable face-to-edge interpolations of the face-centered electric field fluxes (see also Fig. 1). The latter are computed with help of the base central scheme applying the two-speed flux formula. It is this close relation to the central base scheme providing the CT algorithm with properly upwinded numerical electric field components which ultimately gives the full MHD scheme its stability and robustness as demonstrated in a variety of test problems (see Ziegler 2004). For example, for the x-flux
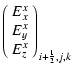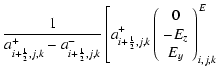                          $\displaystyle \left(\begin{array}{c} E^x_x\\ E^x_y\\ E^x_z \end{array}\right)_{i+{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k}$ = $\displaystyle \frac{1}{a^+_{i+{\scriptscriptstyle 1\over \scriptscriptstyle 2},... ...,j,k}\left(\begin{array}{c}0\\ -E_z\\ E_y\end{array}\right)^E_{i,j,k} \right.$  
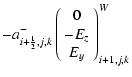    $\displaystyle -a^-_{i+{\scriptscriptstyle 1\over \scriptscriptstyle 2},j,k}\left(\begin{array}{c}0\\ -E_z\\ E_y\end{array}\right)^W_{i+1,j,k}$  
    $\displaystyle \left.\begin{array}{c} \end{array}+a^+_{i+{\scriptscriptstyle 1\o... ...riptstyle 2},j,k} \left({\vec B}^W_{i+1,j,k}-{\vec B}^E_{i,j,k}\right) \right].$  

and similar expressions exist for the y- and z-fluxes

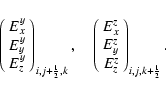
\begin{displaymath}\left(\begin{array}{c} E^y_x\\ E^y_y\\ E^y_z \end{array}\righ... ...ght)_{i,j,k+{\scriptscriptstyle 1\over \scriptscriptstyle 2}}. \end{displaymath}

The complete electric field flux tensor can be found in Ziegler (2004). Note that the electric field x-flux requires the reconstructed magnetic field ${\vec B}^{W,E}$ at cell faces W,E. Due to the staggered collocation of the magnetic field components, however, reconstruction slighly differs from the reconstruction of u-variables. In particular, no reconstruction of Bx is nessessary for the x-flux computation since that component is already at right position. The transverse magnetic field components are first reconstructed in x-direction and then averaged to W,E-locations.


  \begin{figure} \par\includegraphics[width=8cm,clip]{2451f1.eps}\end{figure} Figure 1: Left: collocation of the MHD variables in a cell [ ijk]. Right: locations of the electric field components and components of the electric field flux tensor.
Open with DEXTER

In the final GMHD scheme gravity source terms containing the gradient of the gravitational potential $\Phi$ appear on the rhs. of the energy equation and momentum equation. With $\Phi$ defined at cell centers as the u's, $(\nabla\Phi)_{i,j,k}$ to second-order is computed in straightforward manner by

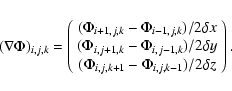
\begin{displaymath}(\nabla\Phi)_{i,j,k}=\left(\begin{array}{c} (\Phi_{i+1,j,k}-\... ... (\Phi_{i,j,k+1}-\Phi_{i,j,k-1})/2\delta z \end{array}\right). \end{displaymath}

Time discretization. The semi-discrete MHD scheme described above is discretized in time with a standard 2-step Runge-Kutta method. Denoting the rhs. of Eq. (7) as ${F}[\overline{\vec u},\overline{\vec B}]$, the rhs. of Eqs. (8)-(10) as ${E}[\overline{\vec u},\overline{\vec B}]$ and introducing the gravity source term ${S}_{\vec u}[{\vec u},\Phi]=(0,-{\vec m}\cdot\nabla\Phi, -\varrho \nabla\Phi)$ the set of resulting ODE's is solved in the following way. First, the solution at the new time level n+1 with $t_{n+1}=t_n+\delta t$where $\delta t$ is the usual CFL time-step is predicted to first-order accuracy according to
                $\displaystyle \overline{\vec u}^{n+1\star}$ = $\displaystyle \overline{\vec u}^n+\delta t\cdot{F} \left[\overline{\vec u}^n,\overline{\vec B}^n\right],$  
$\displaystyle \overline{\vec B}^{n+1\star}$ = $\displaystyle \overline{\vec B}^n+\delta t\cdot{E} \left[\overline{\vec u}^n,\overline{\vec B}^n\right].$  

In a second step temporal means are calculated which serve as approximations at time $t_{n+{\scriptscriptstyle 1\over \scriptscriptstyle 2}}$, and the time-averaged gravitational potential is determined from the Poisson equation using the time-averaged density $\varrho^{n+{\scriptscriptstyle 1\over \scriptscriptstyle 2}\star}$:
             $\displaystyle \overline{\vec u}^{n+{\scriptscriptstyle 1\over \scriptscriptstyle 2}\star}$ = $\displaystyle \frac{1}{2}\left(\overline{\vec u}^n +\overline{\vec u}^{n+1\star}\right),$  
$\displaystyle \overline{\vec B}^{n+{\scriptscriptstyle 1\over \scriptscriptstyle 2}\star}$ = $\displaystyle \frac{1}{2}\left(\overline{\vec B}^n +\overline{\vec B}^{n+1\star}\right),$  


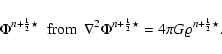
\begin{displaymath}\Phi^{n+{\scriptscriptstyle 1\over \scriptscriptstyle 2}\star... ...rho^{n+{\scriptscriptstyle 1\over \scriptscriptstyle 2}\star}. \end{displaymath}

Finally, second-order accuracy is achieved by a corrector flux term and by using time-averaged quantities in the gravitational source term update:
                                   $\displaystyle \overline{\vec u}^{n+1}$ = $\displaystyle \overline{\vec u}^{n+{\scriptscriptstyle 1\over \scriptscriptstyl... ...}\star},\Phi^{n+{\scriptscriptstyle 1\over \scriptscriptstyle 2}\star}\right] ,$  
$\displaystyle \overline{\vec B}^{n+1}$ = $\displaystyle \overline{\vec B}^{n+{\scriptscriptstyle 1\over \scriptscriptstyl... ...cdot{E}\left[\overline{\vec u}^{n+1\star}, \overline{\vec B}^{n+1\star}\right].$  

2.3 Adaptive mesh refinement

The second building block of the NIRVANA code is its AMR facility. The basic ideas of the algorithm are reviewed here, and the reader is refered to Ziegler (2005) for more details.

Refinement principle. AMR in the NIRVANA code as well as many other codes (e.g. AMRVAC, see Keppens et al. 2003) is based on a block-structured ansatz as described in the fundamental work of Berger & Oliger (1984) and Berger & Collela (1989). In this ansatz grid blocks of finer resolution and with variable size are overlain respective parent grids in a recursive procedure till the required resolution is reached. Major differences to the original approach comes about because in NIRVANA (i) blocks have a fixed size of 4 cells per coordinate direction; (ii) the base level itself consists out of such elementary blocks i.e. there is no single base grid (in contrast to previous code versions); (iii) the parent-to-child block refinement ratio is always two and; (iv), elementary blocks are clustered temporarily to larger grid objects (called superblocks, see below) on which numerical integration of the equations take place followed by a remap step. The set of blocks builds an oct-tree data structure similar to the PARAMESH package of MacNeice et al. (2000) used in the FLASH code. Each block with given resolution belongs to a refinement level l starting with l=0 for the base level up to some maximum level L specified by the user. Technically, a block has to be understood as a logical grid unit storing not only the variables (without ghost zones for boundary conditions) and cell positions but also all necessary informations about its mesh environment realized by a set of pointers to its parent block, block neighbors and child blocks.

Refinement criteria. Mesh refinement is controlled according to some refinement criteria. On the base level the criterion is based on evaluating normalized gradients in all variables. If any of these exceeds a prescribed threshold the mesh is locally refined by inserting a new block. On higher levels l>0, refinement is controlled by comparing the known solutions on levels l and l-1. Apart from that standard refinement criteria, in self-gravitational flows Truelove et al. (1997) demonstrated that it is an absolute necessity to sufficiently resolve the local Jeans length  $\lambda_{\rm J}$,

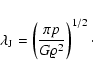
\begin{displaymath}\lambda_{\rm J}=\left(\frac{\pi p}{G\varrho^2}\right)^{1/2}\cdot \end{displaymath}

According to this, in order to avoid that grid-scale numerical perturbations grow into artificial fragments

\begin{displaymath}\lambda_{\rm J}>5\delta x \end{displaymath}

is used as additional criterion to trigger mesh refinement. In general, all criteria - standard and Jeans-based - are evaluated in a buffer zone around the point of refinement to ensure smart capturing of structures.

Block initialisation. Variables on a newly generated block are initialised by interpolation from the underlying coarser level. In doing so, the procedure of limited reconstruction is used as in the central-constraint transport MHD scheme. Conservation properties of the MHD scheme are maintained this way. In particular, the magnetic field is reconstructed in a divergence-free manner as described in Ziegler (2005).

Block clustering and time integration. The equations are not solved on individual blocks but on superblocks. Superblocks are larger rectangular grids which temporarily coexist with the blocks. Each refinement level made up of generic blocks is mapped onto a set of superblocks representing that refinement level for time integration. I call this mechanism block clustering. The number of superblocks associated with a refinement level depends on the degree of fragmentation of the grid structure. In generating superblocks generic blocks are clustered such that the resulting superblock has maximal possible dimension in x-direction. Ghost zones needed by the solver to take up boundary conditions are automatically added. After a time step is complete the advanced solution on superblocks is transfered back to generic blocks and superblocks are destroyed. Notice that when the grid structure changes the superblock distribution changes as well. The purpose of block clustering is to increase efficiency: the use of small blocks allow a very flexible mesh adaptation i.e. regions which are refined but actually need no refinement are sparse. On the other hand, solving the equations on lots of small blocks would be associated with an overwhelming amount of overhead due to the large number of interfaces. Block clustering combines mesh flexibility with performance because, by experience, the overhead due to the block clustering algorithm itself is much smaller than the overhead without block clustering[*]. For problems involving self-gravity each refinement level is integrated with the same time-step dictated by the CFL-related minimum time-step over the grid hierarchy.

Consistency. Several mechanism in an AMR simulation ensure that the solution remains consistent on the block-structured grid hierarchy. First, to restore conservation fixup steps in the hydrodynamical fluxes and the electric field at fine-coarse grid interfaces are necessary. More precisely, the numerical flux at coarse cell faces matching a coarse-fine interface has to be replaced by the corresponding fine cell numerical fluxes. Similarly, the numerical electric field at coarse cell edges matching a coarse-fine interface must be replaced by the corresponding fine cell numerical electric fields to ensure solenoidality of the magnetic field. The use of a multi-stage time integration scheme demands that the fixup steps are carried out after each substep. Here, in the 2-step Runge-Kutta method fixup steps are carried out after the predictor step and after the corrector step. Moreover, synchronization of boundary values along superblock interfaces is required after the predictor step to avoid time mismatching of the solution.

2.4 Poisson solver

The third building block of the NIRVANA code is the adaptive mesh solver for the Poisson equation

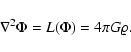
\begin{displaymath}\nabla^2\Phi={\it L}(\Phi)=4\pi G \varrho. \end{displaymath}

The algorithm used here is a modification of the node-centered algorithm of Almgren et al. (1994) adapted to the cell-centered terminology of the Godunov-type central scheme of the NIRVANA code. A similar approach to solve the Poisson equation in conjunction with AMR can be found in Martin & Cartwright (1996). The method resembles the basic idea of a V-cycle multigrid relaxation scheme: it is started with the finest level, then progressively coarsened and relaxed down the V-cycle, solved (or relaxed) on the base level, and interpolated and relaxed back up the V-cycle to complete one iteration step. The main difference is that within the AMR framework relaxation is restricted to the grid levels and may not encompass the entire domain spanned by the base level. Also, in the AMR multigrid solver matching of the solution at coarse-fine grid interfaces requires special attention. More precisely, to avoid artificial forces at interfaces one must enforce both Dirichlet matching (continuity of $\Phi$) and Neumann matching (continuity of $\partial \Phi/\partial n)$ at those locations.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{2451f2.eps} \end{figure} Figure 2: Principle of the AMR V-cycle.
Open with DEXTER

In the AMR multigrid approach the Poisson equation is solved simultaneously on all grid levels rather than level by level. Consequently, in a V-cycle iteration step relaxation takes place on the full grid hierarchy. Iteration is then stopped if the residual $R=s-L(\Phi)$ with $s=4\pi G\varrho$becomes small enough, i.e. if

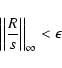
\begin{displaymath}\left\vert\left\vert\frac{R}{s}\right\vert\right\vert _{\infty}<\epsilon \end{displaymath}

where $\vert\vert\cdot\vert\vert _{\infty}$ means the maximum value over all superblocks of all levels $l=0,...,{\rm L}$, and the tolerance $\epsilon =10^{-5}$.

The procedure is as follows (see also Fig. 2). For reasons of clearness grid indices are dropped. The V-cycle starts on the finest level ${\rm L}$. First, save the current potential $\Phi^{\rm L}_{\rm save}$ for later update when going up the V-cycle. Then, perform one Gauß-Seidel relaxation step for the correction $\delta\Phi^{\rm L}$, i.e.

\begin{displaymath}{\rm GS}(\delta \Phi^{\rm L},R^{\rm L}):\quad \delta\Phi^{\rm... ...hi^{\rm L}+\alpha\left[ L(\delta\Phi^{\rm L})-R^{\rm L}\right] \end{displaymath}

where $\alpha=1/2(\delta x^{-2}+\delta y^{-2}+\delta z^{-2})$ is the relaxation parameter, and taking $\delta\Phi^{{\rm L}-1}=0$ as boundary condition when evaluating the L-operator. Define the corrected potential $\tilde{\Phi}^{\rm L}=\Phi^{\rm L}+\delta\Phi^{\rm L}$ needed later to ensure elliptic matching at grid interfaces. Next, perform a Gauß-Seidel relaxation step on the coarser level ${\rm L}-1$ using the residual

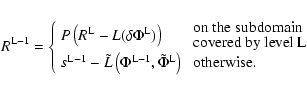
\begin{displaymath}R^{{\rm L}-1}=\left\{\begin{array}{ll} {P}\left(R^{\rm L}-L(\... ...hi}^{\rm L}\right) & \mbox{ otherwise}. \\ \end{array}\right. \end{displaymath}

P is the projection operator which averages the (by the current  $\delta\Phi^{\rm L}$ corrected) residual of level ${\rm L}$ down to level ${\rm L}-1$. $\tilde{L}$ is the usual (second-order) Laplacian operator except at grid interfaces where it is modified in such a way that the elliptic matching condition is fulfilled. For that the previously defined  $\tilde{\Phi}^{\rm L}$ is necessary to evaluate $\tilde{L}$. Now, repeat this process until the base level is reached. On the base level 5 SOR iteration steps - ${\rm SOR}(\delta\Phi^0,R^0)$ - instead of one Gauß-Seidel step are carried out. This gives the updated solution $\Phi^0\rightarrow \Phi^0+\delta\Phi^0$. On the following way up the V-cycle the current correction $\delta\Phi^1$ on level 1 is first updated by the known correction on the base level, i.e. $\delta\Phi^1\rightarrow \delta\Phi^1+{I}(\delta\Phi^0)$ where Iis an interpolation operator. Next, a Gauß-Seidel relaxation step is performed on level 1 using the given, now non-vanishing, coarser grid correction  $\delta\Phi^0$as boundary condition for evaluation of the Laplacian. Then, update the gravitational potential using the saved value:

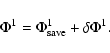
\begin{displaymath}\Phi^1=\Phi^1_{\rm save}+\delta\Phi^1. \end{displaymath}

Continue this process up to the finest level of the grid hierarchy to complete the V-cycle.

Note that, of course, synchronization work is needed during a V-cycle along superblock interfaces to achieve global convergence. For instance, internal boundary values of the correction  $\delta\Phi^l$ must be exchanged among adjacent superblocks since level l is relaxed sucessively superblock by superblock. Note also that, without AMR, the method reduces to a pure SOR scheme. Thats why SOR is used as relaxation scheme for the base level.

Boundary conditions on the base level are

\begin{displaymath}\frac{\partial\Phi}{\partial n}=0 \end{displaymath}

at symmetry planes and

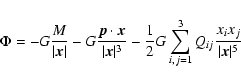
\begin{displaymath}\Phi=-G\frac{M}{\vert{\vec x}\vert}-G\frac{{\vec p}\cdot{\vec... ...{1}{2}G\sum_{i,j=1}^3Q_{ij}\frac{x_ix_j}{\vert{\vec x}\vert^5} \end{displaymath}

at open boundaries where the mono-, di- and quadrupole is given by
                                     M = $\displaystyle \int\varrho({\vec x}^{\prime})~{\rm d}V^{\prime},$  
$\displaystyle {\vec p}$ = $\displaystyle \int\varrho({\vec x}^{\prime}) {\vec x}^{\prime}~{\rm d}V^{\prime},$  
Qij = $\displaystyle \int\varrho({\vec x}^{\prime}) (3x_i^{\prime}x_j^{\prime} -\vert{\vec x}^{\prime}\vert^2\delta_{ij})~{\rm d}V^{\prime}.$  

3 Application to cloud collapse and fragmentation

As "tests'' of the GMHD scheme I consider a suite of collapse simulations of an initially uniform solar-mass cloud subject to various conditions, namely, with and without rigid rotation of the cloud, with and without attached azimuthal mode perturbation, with and without magnetic field and, finally, with different gas equation of states. In all simulations the computational domain is a cubic box with length four times the cloud radius and is spanned by 643 grid cells. From the beginning there is a first permanent refinement level in a spherical region covering the full cloud i.e. the cloud radius is effectively resolved by 32 grid cells. It may also be of interest for the reader to learn that the following adaptive mesh calculations do not require a supercomputer but were performed on a Linux PC with computing times of roughly 1 day for the isothermal simulations and up to 5 days for the barotropic simulations.

3.1 Isothermal collapse

In one class of simulations a quasi-isothermal equation of state is considered. Quasi-isothermal in this context means that the energy equation is retained but an adiabatic index $\gamma =1.001$ close to unity is adopted.

3.1.1 Non-rotating cloud


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{2451f3.ps} \end{figure} Figure 3: Non-rotating collaps: grey-scale representation of the density structure ( $\log\varrho_{\rm min}=-13.91$, $\log\varrho_{\rm max}=-9.28$) and velocity field in the x-y plane.
Open with DEXTER

The first case of a non-rotating uniform cloud is identical to the model described in Truelove et al. (1998) (hereafter T98) and for which analytical predictions exist. The cloud of radius $R_{\rm cl}=7.8\times 10^{13}$ m has density $\varrho_{\rm cl}=10^{-12}$ kg/m3, temperature T=3.63 K and is in pressure balance with the surrounding medium having a density $10^{-2}\cdot \varrho_{\rm cl}$. The analytic solution consists of a rarefaction wave propagating inwards from the cloud surface superimposed on a self-similar collapse solution. The central part of the cloud which at a time is still unaffected by the inward moving rarefaction wave collapses in free-fall time $t_{\rm ff}=(3\pi/32 G\varrho_{\rm cl})^{1/2}=6.645\times 10^{10}$ s towards a singular state according to

\begin{displaymath}\frac{t_{\varrho}}{t_{\rm ff}}=\frac{2}{\pi}\left[ \xi +\frac{1}{2}\sin (2\xi) \right] \end{displaymath}

where $t_{\varrho}$ is the time to reach density $\varrho$ and

\begin{displaymath}\xi=\arccos \left[\left(\frac{\varrho}{\varrho_{\rm cl}}\right)^{-1/6} \right]\cdot \end{displaymath}

The initial parameters of the problem have been chosen in such a way that the cloud collapses to a singularity before the rarefaction front can reach the cloud center.

Figure 3 illustrates the solution at time $t=6.501\times 10^{10}=0.978 t_{\rm ff}$ when the density has reached a maximum value $\log\varrho_{\rm max}=-9.28$. Figure 4 shows a cut of $\log\varrho$ along the x-axis. The horizontal line in Fig. 4 indicates the analytic solution for the collapsing portion not yet reached by the rarefaction wave at the given time. The extend of the plateau is computed using the formula for the rarefaction front radius as a function of density taken from T98. The maximum density fits very well whereas there are somewhat larger deviations from the analytic result at the edges of the plateau. About 45% of the mass is within the plateau region. As expected from theory the radial velocity to a good approximation grows linearly from the cloud center to the rarefaction front and then falls off in the surrounding medium.

When comparing the NIRVANA code result with the T98 result there is one obvious difference, that is, the T98 solution possesses a time delay also with respect to the analytic solution: Fig. 5 of T98 shows a snapshot at a time $t>t_{\rm ff}$ associated with a maximum density $\log\varrho_{\rm max}=-9.58$ which is even lower than in the state presented in Fig. 3 corresponding to a time  $t<t_{\rm ff}$. As reported in T98 this time delay might be mainly due to the periodic boundary conditions faking neighboring clouds. These image clouds act as inhibitors to collapse because of their attractive force on the real cloud. Here, Dirichlet boundary conditions for the gravitational potential are used which are computed from a multipole expansion of the density distribution. This is an excellent approximation for the almost spherically symmetric configuration and explains the very insignificant time shift to the analytic solution.


  \begin{figure} \par\includegraphics[width=8cm,clip]{2451f4.ps} \end{figure} Figure 4: Non-rotating collaps: cut of $\log\varrho$ along the x-axis.
Open with DEXTER

3.1.2 Rotating cloud

The second case of a rotating uniform cloud again is taken from T98 but has originally been described in Norman et al. (1980). A solar-mass cloud with density $\varrho_{\rm cl}=1.26\times 10^{-15}$ kg/m3, radius $R_{\rm cl}=7.01\times 10^{14}$ m and temperature T=5 K is initially set in uniform rotation with $\Omega =3.04\times 10^{-13}$ 1/s. In terms of characteristic energy ratios $\alpha =0.54$ (thermal energy to gravitational energy) and $\beta =0.08$ (rotational energy to gravitational energy).

The main purpose of this collapse problem is to check the quality of angular momentum conservation by the numerical method. As pointed out by Norman et al. (1980) good numerical advection of angular momentum is necessary in order to achieve the correct answer to the problem, namely, the production of a disk which in the isothermal case evolves towards a singular state. Bad advection of angular momentum, on the other hand, may generate a ring-like structure due to artifical transport effects.

As in T98 the collapse is followed over roughly 6 decades in density increase. The result is shown in Fig. 5 representing the density in logarithmic scale in the x-y plane (upper panel) and x-z plane (lower panel) at time $t=2.1753\times 10^{12}$ s where $\log\varrho_{\rm max}=-8.98$. The solution is throughout comparable to the findings of T98 of a rotating disk structure. There is no visible tendency to build rings indicating that the NIRVANA code, albeit solving for the linear momentum, can handle angular momentum advection in an acceptable manner.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{2451f5a.ps}\par\vspace*{2mm} \hspace*{6mm}\includegraphics[width=7cm,clip]{2451f5b.ps} \end{figure} Figure 5: Rotating collapse: grey-scale representation of the density structure in the x-y plane ( top) and x-z plane ( bottom).
Open with DEXTER

3.1.3 Rotating cloud with azimuthal perturbation

  \begin{figure} \par\includegraphics[width=5cm,clip]{2451f6a.ps}\hspace*{2mm} \in... ...f6b.ps}\hspace*{2mm} \includegraphics[width=5.5cm,clip]{2451f6c.ps} \end{figure} Figure 6: Isothermal collapse: snapshots at different evolutionary stages showing the density structure, velocity field ( only left panel) and block distribution ( middle and right panels). Evolution times in units of the free-fall time are: t=1.008,1.0647,1.0657.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=5cm,clip]{2451f7a.ps}\hspace*{2mm} \in... ...f7b.ps}\hspace*{2mm} \includegraphics[width=5.3cm,clip]{2451f7c.ps} \end{figure} Figure 7: Isothermal collapse with vertical magnetic field. Evolution times in units of the free-fall time are: t=1.145,1.2479,1.2482.
Open with DEXTER

Next, I consider a cloud with azimuthal m=2 mode perturbation i.e.

\begin{displaymath}\varrho_{\rm cl} \longrightarrow \left[1+0.1\cos (2\phi)\right]\varrho_{\rm cl} \end{displaymath}

where the angle $\phi$ is measured from the x-axis. Initial parameters are taken from Hosking & Whitworth (2004b) hereafter abbreviated HW. In HW  $\varrho_{\rm cl}=4.8\times 10^{-15}$ kg/m3, $R_{\rm cl}=4.65\times 10^{14}$ m, T=10 K and $\Omega=4.25\times 10^{-13}$ 1/s. The corresponding energy ratios are $\alpha =0.35$ and $\beta =0.05$. No magnetic field is present. The density of the outer medium is  $\varrho_{\rm cl}/100$. Similar problems of perturbed uniform clouds have been studied with a grid-based code by Boss & Bodenheimer (1979), Burkert & Bodenheimer (1993), Truelove et al. (1997), Truelove et al.(1998) and with SPH by Kitsionas & Whitworth (2002), for example.

Figure 6 shows a sequence of snapshots illustrating the result of this collapse problem after the density has increased by 2.2 decades, 6.3 decades and 9.43 decades, respectively. The last value corresponds to a time $1.066 t_{\rm ff}$ where $t_{\rm ff}=9.59\times 10^{11}$ s. Fourteen levels of refinement have been introduced at this latest stage so that the finest resolution is equivalent to a 1 048 5763 uniform grid simulation. The overdense regions of the cloud seeded by the initial perturbation stimulate binary fragmentation. When $\log(\varrho_{\rm max})=-8.02$ two density maxima have clearly been produced (Fig. 6, middle panel) which appear as elongated structures. These high-density regions are connected by a bar and have rotated in a clockwise sense around the cloud center a little bit less than 90 degress measured from its initial orientation in the x-z plane. At this stage each density peak is resolved by grid blocks of refinement level 9, the bar in between by grid blocks of refinement level 8. In the subsequent evolution each of the fragments approach a singular filamentary state consistent with the analytical predictions by Inutsuka & Miyama (1997) working on inviscid filament formation under the assumption of an isothermal gas equation of state. Figure 6 (right panel) presenting a close-up view (zooming factor is 4000) around the upper filament when $\log(\varrho_{\rm max})=-4.89$ apparently give support for such a scenario.

The situation is similar, though not identical, if a vertical magnetic field is present. Figure 7 illustrates the corresponding result for the magnetic case adopting an initial field strength which corresponds to a mass-to-flux ratio twice the critical value $(M/\Psi)_{\rm crit}$ i.e. the magnetic field is supercritical. From HW

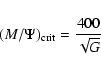
\begin{displaymath}(M/\Psi)_{\rm crit}=\frac{400}{\sqrt{G}} \end{displaymath}

and the initial magnetic field strength $B_{z0}=3\times 10^{-8}$ T. The presence of the magnetic field leads to a delay of the whole evolution which is due to the partial magnetic support against gravitational collapse. At a comparable stage to the non-magnetic case when $\log(\varrho_{\rm max})=-7.96$ ( $t=1.2479 t_{\rm ff}$; Fig. 7, middle panel) again two lengthy density peaks have emerged which possess a somewhat larger separation. At this time the binary fragment is oriented by $\approx$ $70^{\circ}$ relative to the x-axis which is less than before. This difference results from the effect of magnetic braking which serves to remove angular momentum from the cloud spinning down to the outer medium spinning up. As before, the final outcome are two very thin filaments which would continue to collapse if the simulation were not stopped at a time  $t=1.2482 t_{\rm ff}$ where the maximum density has reached a value $\log(\varrho_{\rm max})=-5.05$ (see Fig. 7, right panel).


  \begin{figure} \par\includegraphics[width=5cm,clip]{2451f8a.ps}\hspace*{2mm} \in... ...51f8b.ps}\hspace*{2mm} \includegraphics[width=5cm,clip]{2451f8c.ps} \end{figure} Figure 8: Barotropic collaps without magnetic field: snaphots of the density structure and velocity illustrating the evolution at times t=1.0855,1.112,1.119in units of the free-fall time ( from left to right).
Open with DEXTER

3.2 Barotropic collapse of perturbed clouds

The other class of simulations applies a barotropic equation of state given by

\begin{displaymath}p=c_s^2\varrho\cdot\left[1+\left(\frac{\varrho}{\varrho_{\rm crit}} \right)^{4/3}\right]^{1/2} \end{displaymath}

where the critical density $\varrho_{\rm crit}=10^{-10}$ kg/m3 and the isothermal sound speed $c_{\rm s}=200$ m/s. Here, the energy equation is redundant. The barotropic model describes more realistically the astrophysical cloud collaps problem because it mimics the transition from a low-density isothermal state to a high-density adiabatic state which is assumed to occur around $\varrho_{\rm crit}$.

For the following collapse problems the same initial conditions as in the isothermal perturbed case are adopted i.e. the configuration is identical to that used in the SPH simulations of HW. Therefore, a direct comparison of SPH and AMR-GMHD results is accessible. The main difference between the two models lies in the treatment of the cloud environment. In SPH there are no particles outside the cloud whereas in the grid case density is set to 1/50 of the initial cloud density to avoid vacuum conditions. Note by the way that due to the choice of equation of state the cloud surface is not in pressure equilibrium with the surroundings. This is in contrast to the quasi-isothermal calculations in which exact pressure balance were initially achieved. The resulting outwards directed acceleration is, however, relatively small and is a transient effect which plays no role in the late callapse phase.

I start with a simulation without magnetic field. As long as the system remains nearly isothermal runaway collapse occurs. Later on, when the density approches the critical density  $\varrho_{\rm crit}$ the collapse phase gradually turns into an accretion phase where scales no longer change drastically. Figure 8 presents a sequence of snapshots illustrating the structure of the system at such later evolutionary stages. The density in logarithmic scale and coded in black-white is shown in the x-y coordinate plane overlain by the velocity field. Only a subset of the entire domain is visualized by zooming in with a factor 50 around the coodinate origin. At time $t=1.0855 t_{\rm ff}$(recall that $t_{\rm ff}=9.59\times 10^{11}$ s) accompanied by a maximum density $\log(\varrho_{\rm max})=-8.82$ a filamentary structure has developed (Fig. 8, left panel). At this time the adiabatic regime has clearly reached expressed by the fact that only one filament appeared instead of two as in the quasi-isothermal case starting with same initial conditions. This is because the overdense regions generated early during the collaps by the imposed azimuthal perturbation have fallen towards the center and merged. In the non-magnetic SPH model of HW the same observation has been made (see their Fig. 2, top left).

  \begin{figure} \par\includegraphics[width=7cm,clip]{2451f9.ps} \end{figure} Figure 9: Barotropic collaps without magnetic field: density structure in the coordinate planes (shifted for the x-z and y-z planes) and block distribution in the x-y coordinate plane at time $t=1.119 t_{\rm ff}$.
Open with DEXTER

However, notice the difference of order 5% in evolution time between the grid solution and the HW result with the former lagging somewhat behind the latter. The filament is in rotational motion because a substantial fraction of initial angular momentum is still present. As a consequence, by $t=1.112 t_{\rm ff}$ ( $\log(\varrho_{\rm max})=-7.71$) the filamentary structure transforms into a bar-like structure with two leading spiral arms attached at the ends of the bar. In the center of the bar a core starts to condense out. For the purpose of comparison with the SPH simulations of HW consult their Fig. 2 with our snapshot lying in evolution somewhere between the bottom left and bottom right panel. The simulation has been stopped after a time $t=1.119 t_{\rm ff}$ where the maximum density has reached a value of $\log(\varrho_{\rm max})=-7.69$. Meanwhile, the spiral structure has evolved to a mini-spiral with central core surrounded by a ring-like object.
  \begin{figure} \par\mbox{\includegraphics[width=8.8cm,clip]{2451f10a.ps}\hspace*{4mm} \includegraphics[width=8.8cm,clip]{2451f10b.ps} }\end{figure} Figure 10: Barotropic collaps with magnetic field: resulting structure for $(M/\Psi )=2\cdot (M/\Psi )_{\rm crit}$ ( left) and $(M/\Psi )=1.2\cdot (M/\Psi )_{\rm crit}$ ( right). Corresponding evolution times are t=1.444 and t=2.057 in units of the free-fall time.
Open with DEXTER

The ring is formed from the collision of the spiral arms with the bar. In this context HW report the formation of further Jeans-unstable dense knots which is not seen here. Furthermore, the NIRVANA code solution provides an almost perfect point symmetry whereas in the SPH simulations of HW point-symmetry is clearly violated in the later course of evolution. Viewed edge-on the resulting structure appears rather flat in vertical direction with a rather sharp transition to the surrounding accretion flow. The disk scale height is of the order of the local Jeans length resolved by 5 grid cells. This can be seen in the color-coded representation of Fig. 9 showing density contours along the coordinate directions (the x-z plane and y-z plane is shifted) together with the block distribution of grid levels 5-7 in the x-y plane.

The situation is quite different if a magnetic field is present. Here, I consider only the case of a vertical magnetic field of uniform strength i.e. the magnetic field is oriented along the rotation axis. The initial magnetic field strength is chosen like in the isothermal case with a mass-to-flux ratio twice the critical mass-to-flux ratio and the magnetic field is supercritical from the beginning. The final outcome at $t=1.444 t_{\rm ff}$ with $\log(\varrho_{\rm max})=-7.73$is illustrated in the color-coded representation of Fig. 10 (left panel) similar to Fig. 9. In the very beginning of the collaps the overdense regions initiated by the initial perturbation again fall towards the center and merge. In contrast to the non-magnetic case, however, there is a rebound leading again to two separate overdensed objects. These objects are the seed for binary formation. Indeed a binary system is formed. The oblate cores separated a distance $\approx$ $0.06\cdot R_{\rm cl}$from each other are connected by a less dense bar. Each core is surrounded by a thin disk-like structure with a gap tied up by the bar. As expected the magnetic field is dragged with the infall and builds a hour-glass morphology around each of the density cores. The magnetic field lines in Fig. 10 show a perceptible amount of twist emanating from a differentially rotating flow field along the vertical direction.

For a stronger magnetic field with mass-to-flux ratio $1.2\cdot (M/\Psi)_{\rm crit}$ the situation again drastically changes. The solution at $t=2.057 t_{\rm ff}$ and $\log(\varrho_{\rm max})=-8.55$is illustrated in Fig. 10 (right panel). In this case only one core has been formed embedded in an extended disk. The magnetic field near the core again has a hour-glass structure but is significantly less twisted than in the previous case. This can be explained by efficient magnetic braking which removes angular momentum from the collapsing material and which tends to equalize differential rotation. The effect gets more pronounced as the magnetic field gets stronger.

4 Conclusions

I have presented a powerful new version of the NIRVANA code suitable for the simulation of multi-scale gravitomagnetohydrodynamics problems in three space dimensions. A state-of-the-art Godunov-type central scheme for divergence-free MHD has been combined with a multigrid-type Poisson solver both operating within an adaptive mesh refinement framework. This new code has then been applied to the gravitational collapse of a solar-mass uniform cloud subject to different gas equation of states and for various initial conditions: isothermal and barotropic, non-magnetic and magnetic, non-rotating and rotating, with and without binary perturbation. In particular, it has been demonstrated that the code was able to robustly model the magnetodydrodynamical collapse and the related issue of fragmentation - a problem of high complexity which just begins to become explored in more depth. It has been shown that in the models with barotropic equation of state and an initial m=2 mode perturbation fragmentation is controlled by magnetic fields. Without magnetic field the final outcome is a single core surrounded by a ring-like structure. In case of a strong vertical field with mass-to-flux ratio close to the critical value again a single core is formed but embedded in an extended disk. For a weaker field with mass-to-flux ratio twice the critical one a binary system is produced connected by a bar.

The results presented in this paper are very encouraging and give strong motivation for further studies in this research field. To get more insight in the fragmentation process during protostellar core collapse the effects of ambipolar diffusion and probably radiation transport should be included. It would also be very fruitful to compare such AMR-GMHD models with models based on using SPH.

References

 
Copyright ESO 2005