A&A 435, 379-384 (2005)
DOI: 10.1051/0004-6361:20042424
Combination of nulling interferometer
and modified pupil for observations of exo-planets
J. Nishikawa 1 -
T. Kotani 2,3 -
N. Murakami 4 -
N. Baba 4 -
Y. Itoh 5
-
M. Tamura 6
1 - MIRA project, National Astronomical Observatory of Japan,
Osawa, Mitaka, Tokyo 181-8588, Japan
2 -
LESIA, Observatoire de Paris, section Meudon, France
3 -
Department of Astronomy, Graduate School of Science,
University of Tokyo, Bunkyo-ku, Tokyo 113-0033, Japan
4 -
Department of Applied Physics, Graduate School of Engineering,
Hokkaido University, Sapporo 060-8628, Japan
5 -
Graduate School of Science and Technology,
Kobe University, Nada, Kobe 657-8501, Japan
6 -
Optical and Infrared Division,
National Astronomical Observatory of Japan,
Mitaka, Tokyo 181-8588, Japan
Received 26 August 2002 / Accepted 25 November 2004
Abstract
We consider a combination of two techniques, namely the nulling interferometer and
halo suppression by modified pupil such as shaped pupils
and apodized square apertures,
which achieves very high dynamic range, in order to
detect faint extra-solar planets around nearby stars.
The effects of the nulling interferometer and
the modified pupil are independent and in combination hence multiplied.
We show that
one can achieve higher dynamic range in the case of a resolved star
than with either method alone.
By numerical simulations, we show that the combination method
can achieve dynamic range levels of 10-10 at 3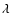 /D.
Used alone, the two-telescope interferometer would give the nulling depth of 10-3
whilst the halo suppression by a shaped aperture would do 10-7,
with a point-spread-function core radius less than 3
/D.
Used alone, the two-telescope interferometer would give the nulling depth of 10-3
whilst the halo suppression by a shaped aperture would do 10-7,
with a point-spread-function core radius less than 3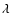 /D
for a shaped aperture.
The introduction of the modified pupil has the same effect
whether it is made at the entrance apertures of the interferometer or
at a re-imaged common pupil plane after the nulling interferometry.
From another point of view,
a nulling interferometer works as pre-optics
in front of any single telescope methods,
which reduces the intensity of a resolved source
transmitting some uniform wavefront residuals.
/D
for a shaped aperture.
The introduction of the modified pupil has the same effect
whether it is made at the entrance apertures of the interferometer or
at a re-imaged common pupil plane after the nulling interferometry.
From another point of view,
a nulling interferometer works as pre-optics
in front of any single telescope methods,
which reduces the intensity of a resolved source
transmitting some uniform wavefront residuals.
Key words: instrumentation: high angular resolution -
techniques: interferometric - techniques: high angular resolution -
telescopes - stars: planetary systems
Nulling interferometry (Bracewell 1978) is one of the useful methods
of achieving high dynamic range observations especially for the
direct detection of extra-solar planets (e.g. Woolf & Angel 1998).
Darwin (Fridlund 2000) and Terrestrial Planet Finder
(Beichman et al. 1999) originally have been based
on this concept at mid-infrared wavelengths.
Another method of achieving high dynamic range is
the advanced coronagraph, which extinguishes
the central star light within a single telescope optics.
The nulling coronagraph is a particular implementation using an
interferometric null for the star by putting a phase mask at the
center of the image plane
(Roddier & Roddier 1997; Rouan et al. 2000).
The third method is
the modified pupil,
which suppresses the halo of the point spread function (PSF)
relative to the core intensity.
Shaped apertures
(Jacquinot & Roizen-Dossier 1964;
Spergel 2001)
and apodized square or rectangular apertures
(Nisenson & Papaliolios 2001)
are examples.
Various modifications of the method are seen in recent studies
(e.g. Kasdin et al. 2003;
Guyon 2003).
The coronagraph and the modified pupil method are typically used
at optical and near infrared wavelengths.
The advanced coronagraph has many variations
(Baudoz et al. 2000;
Baba et al. 2002;
Guyon & Roddier 2002;
Kuchner & Traub 2002;
Soummer et al. 2003),
and some of the nulling coronagraph designs can provide
total extinction for an on-axis point source
(Rouan et al. 2002;
Abe et al. 2003).
Another kind of nulling coronagraph was also able
to achieve this
when combined with entrance aperture apodization
(Aime et al. 2002;
Soummer et al. 2003).
But considerable residual light from off-axis rays remains an issue
(Guyon et al. 1999;
Rouan et al. 2000;
Riaud et al. 2003).
The nulling interferometer is, in principle, able to extinguish
an on-axis point source perfectly, even for wide-band light
(Bracewell 1978).
Several teams are working to achieve high performance with
nulling interferometry, for example,
wide-band nullers
(Shao & Colavita 1992;
Serabyn et al. 1999;
Baba et al. 2001;
Ollivier et al. 2001)
or
differential wavelength techniques
(Danchi et al. 2003).
On the other hand, the two-telescope Bracewell interferometer
remains limited by residual light from off-axis rays.
In order to reach better null for resolved stars,
a nulling interferometer with more than two telescopes
and their various configurations were studied
(Angel & Woolf 1997;
Mennesson & Marriotti 1997),
but the combination with a
nulling coronagraph has not been studied yet,
nor the combination with a modified pupil.
If one look at a Sun-Earth-like system at a distance of 5 pc,
the planet is found at 200 milliarcsec (mas) separation
from the central star,
which has a 2 mas resolvable apparent diameter,
producing significant leakage intensities
for the nulling interferometer and
also for the nulling coronagraph,
which would
be a hindrance to the direct detection of the planet.
In the present paper, in order to reduce the off-axis
leakage light from resolved stars,
we study the combination of
the nulling interferometer and the modified pupil method.
The combination is effective in those cases where
the point-spread-function core radius
of each element telescope is a few times smaller than the
separation angle between a target exo-planet and the central star.
For example, 600 nm observations by an interferometer of two 3 m-apertures
which can be extracted as sub-apertures of a single 6 m telescope, or
observations by a telescope with LBT-like parameters
(Hinz et al. 2003)
at 1.6 microns.
In Sect. 2, the theoretical principle of the combination is described, and its
performance is confirmed by a simple numerical simulation in Sect. 3.
A nulling interferometer is shown to work as pre-optics
reducing the source intensity by a fixed amount,
independent of the modified pupil method.
It is convenient to put the nulling interferometer
in front of any other optics, since it keeps the wavefront flat.
A discussions of the performance of the combination
and of other possible combinations, for instance with the nulling coronagraph
or the modified Lyot stop, are given in Sect. 4.
![\begin{figure}
\par\includegraphics[height=4cm,width=8cm,clip]{2424fig1.eps} \end{figure}](/articles/aa/full/2005/19/aa2424/Timg15.gif) |
Figure 1:
Description of the proposed
combination of the nulling interferometer and the modified pupil method.
As described in Sect. 2, the on- or off-axis star light wavefront
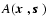 is extracted by two apertures at
is extracted by two apertures at
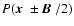 ,
shown as ,
shown as
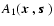 and
and
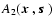 ,
and combined into ,
and combined into
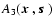 with phase difference
with phase difference 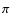 at an optical axis where an equivalent pupil is seen as
at an optical axis where an equivalent pupil is seen as
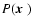 . .
|
| Open with DEXTER |
A general description of the combination concept is shown below
and in Fig. 1.
The complex amplitude of the wavefront from a source at the entrance
pupil plane of a nulling interferometer can be expressed as
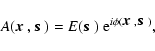 |
(1) |
where
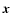 is a two-dimensional coordinate system in the
pupil plane, and
is a two-dimensional coordinate system in the
pupil plane, and
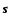 is the projected component of the unit pointing vector
to a source onto this plane.
Therefore,
is the projected component of the unit pointing vector
to a source onto this plane.
Therefore,
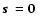 denotes the wavefront from an on-axis
unresolved star whose
pointing direction is perpendicular to the pupil plane.
denotes the wavefront from an on-axis
unresolved star whose
pointing direction is perpendicular to the pupil plane.
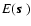 is the real positive amplitude of the electric field,
and the phase
is the real positive amplitude of the electric field,
and the phase
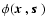 is given by
is given by
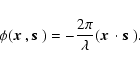 |
(2) |
Here, 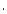 denotes inner product and
denotes inner product and 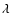 is the wavelength.
The wavefronts received by the two telescopes of
the nulling interferometer at positions
is the wavelength.
The wavefronts received by the two telescopes of
the nulling interferometer at positions
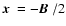 and
and
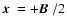 are described by
are described by
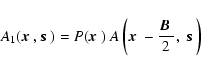 |
(3) |
and
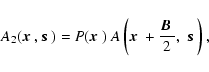 |
(4) |
respectively, here the
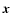 coordinates for A1 and A2
are considered after the beams are combined.
coordinates for A1 and A2
are considered after the beams are combined.
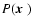 is the pupil function used for both telescopes
which is an arbitrary shape and apodization, written as
is the pupil function used for both telescopes
which is an arbitrary shape and apodization, written as
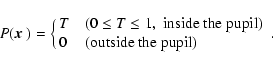 |
(5) |
The wavefronts from the two telescopes are combined with
an achromatic phase
difference 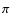 for an on-axis source
and interfere destructively.
Then, the electric field in the combined pupil plane
is given by
for an on-axis source
and interfere destructively.
Then, the electric field in the combined pupil plane
is given by
where
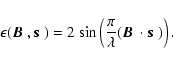 |
(7) |
Here, we assume that the effect of diffraction due to
the propagation of the light beams can be neglected,
which is possible by re-imaging the pupil plane.
Total extinction occurs when
(
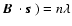 (n: integer),
therefore only when
(n: integer),
therefore only when
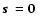 for white light.
Consequently, the output wavefront from the nulling interferometer
has an amplitude reduced by
for white light.
Consequently, the output wavefront from the nulling interferometer
has an amplitude reduced by 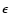 ,
a function of the baseline
,
a function of the baseline
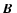 and
the source position
and
the source position
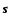 ,
with the wavefront remaining flat.
Note in Eq. (6) that the modified pupil function
operating at the entrance telescopes is identical to that
at the corresponding pupil plane after the nulling combiner.
,
with the wavefront remaining flat.
Note in Eq. (6) that the modified pupil function
operating at the entrance telescopes is identical to that
at the corresponding pupil plane after the nulling combiner.
![\begin{figure}
\par\includegraphics[height=4.2cm,width=11cm,clip]{2424fig2.eps} \end{figure}](/articles/aa/full/2005/19/aa2424/Timg36.gif) |
Figure 2:
Schematic of
a possible optical implementation of the concept
and the simulation parameters.
In the collimated beam of a single telescope, two contacted entrance apertures of
an equivalent diameter D are extracted. The two beams are combined
destructively with a nulling interferometric combiner.
Then a modified pupil telescope is applied
to produce a high dynamic range image which is
followed by an occulting mask hiding the bright core,
a collimator, Lyot stop, a focusing lens, and a camera,
suitably adjusted to avoid saturation.
|
| Open with DEXTER |
The intensity distribution in the focal plane is given by the
squared absolute value of the Fourier transform of A3(x,s).
By using the notation of the Fourier optics of a scaled transform
(Goodman 1996), Eqs. (1) and (2),
this can be described as follows.
where
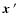 is an image plane two-dimensional coordinate defined as
is an image plane two-dimensional coordinate defined as
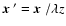 ,
,
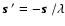 ,
z is the focal length of the imaging system,
and
,
z is the focal length of the imaging system,
and 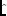 denotes the Fourier transform operation.
We re-use the notations E and
denotes the Fourier transform operation.
We re-use the notations E and 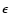 after
after
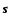 is transferred to
is transferred to
 .
.
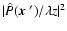 is the PSF of the
modified pupil function
is the PSF of the
modified pupil function
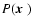 .
Equation (8) shows that the image of a point source
with this modified-pupil nulling interferometer
is the PSF of the modified pupil function
.
Equation (8) shows that the image of a point source
with this modified-pupil nulling interferometer
is the PSF of the modified pupil function
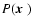 with an intensity of E2 reduced by
with an intensity of E2 reduced by
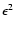 ,
the so-called transmission map, a function of
,
the so-called transmission map, a function of
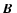 and
and
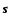 (or
(or
 ).
Thus the effect of the nulling interferometer
and the modified pupil imaging are independent, and multiplied.
).
Thus the effect of the nulling interferometer
and the modified pupil imaging are independent, and multiplied.
From Eq. (8),
the final image of an extended source like a
resolved star is given by
Here, the integral S is taken over the surface of the stellar disk.
The final image of the resolved star
is generated by a convolution of the modified pupil PSF
with the nulling-interferometrically dimmed source intensity
distribution E2
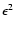 .
In our simulation results in the next section,
the dimming of the shaped-pupil PSF profiles is obvious.
.
In our simulation results in the next section,
the dimming of the shaped-pupil PSF profiles is obvious.
In this section we investigate the performance of the
combination of the nulling interferometer and the modified pupils,
using numerical simulations.
The simulation parameters that we used for the concept are as
can be seen in Fig. 2:
we assume a two-telescope interferometer with an entrance pupil
of diameter D. Setting the baseline B equal to D, at an observing
wavelength
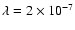 D we get
D we get
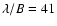 mas.
The observed star is a uniform disk of 0.05
mas.
The observed star is a uniform disk of 0.05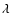 /D
apparent diameter. This parameter set corresponds to a 3 m baseline
optical interferometer with two 3 m telescopes observing
a Sun-like star at a distance of 5 pc, of 2 mas apparent diameter
at a wavelength of 600 nm.
A planet at a distance of 1 AU, of <10-9 contrast at optical wavelengths
is seen at 200 mas corresponding to 5
/D
apparent diameter. This parameter set corresponds to a 3 m baseline
optical interferometer with two 3 m telescopes observing
a Sun-like star at a distance of 5 pc, of 2 mas apparent diameter
at a wavelength of 600 nm.
A planet at a distance of 1 AU, of <10-9 contrast at optical wavelengths
is seen at 200 mas corresponding to 5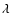 /D. We illustrate
the case where the two apertures are extracted from a primary mirror,
the nulling instruments
being more stable than in a separate telescope system.
For each point of the star and for each telescope a wavefront electric
field is generated on 800-by-800-point two-dimensional grids. The
wavefront from one of the two telescopes is modified by a phase shift of
/D. We illustrate
the case where the two apertures are extracted from a primary mirror,
the nulling instruments
being more stable than in a separate telescope system.
For each point of the star and for each telescope a wavefront electric
field is generated on 800-by-800-point two-dimensional grids. The
wavefront from one of the two telescopes is modified by a phase shift of
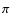 and summed with the other wavefront, which yields destructive
interference, the result of which is pasted on a section of the 8192 by
8192 array used for the pupil. A constructive result with zero phase
shift is calculated to normalize the performance of the nulling optics.
When we consider the wave front errors, they are added
for each aperture wavefront before the summation.
and summed with the other wavefront, which yields destructive
interference, the result of which is pasted on a section of the 8192 by
8192 array used for the pupil. A constructive result with zero phase
shift is calculated to normalize the performance of the nulling optics.
When we consider the wave front errors, they are added
for each aperture wavefront before the summation.
Either a circular or a modified pupil stop is applied to the
array. Three kinds of modified pupil are provided here.
The boundary curve for the shaped aperture with the Kaiser-Bessel window function
(cf. Harris 1978),
approximating a prolate-spheroidal wave function
(cf. Kasdin et al. 2003)
is given by
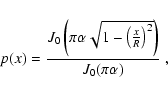 |
(10) |
where J0 is the zero-order modified Bessel function
of the first kind,
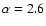 ,
R = 400, and
,
R = 400, and
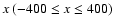 is the pixel number in the
pupil array along the axis in the image plane where the intensity profile
has the highest contrast.
The pupil function
is the pixel number in the
pupil array along the axis in the image plane where the intensity profile
has the highest contrast.
The pupil function
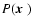 is unity when the pixel is entirely
inside the area
is unity when the pixel is entirely
inside the area
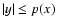 ,
zero when outside it,
and the appropriate fraction for boundary pixels.
Here y is an axis perpendicular to x in the array.
,
zero when outside it,
and the appropriate fraction for boundary pixels.
Here y is an axis perpendicular to x in the array.
Another boundary curve for a sonine-windowed Gaussian aperture
is given by
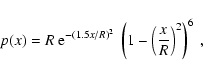 |
(11) |
and the pupil function is defined as previously.
Finally, we evaluate
a square aperture whose diagonal length is 800 pixels, rotated
by 45 degrees and with apodization function within the square pupil
(cf. Nisenson & Papaliolios 2001) for
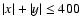 given by
given by
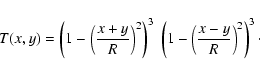 |
(12) |
FFT is used to calculate the intensity distribution in
the image plane. The star diameter is sampled on a 100 pixels square
grid and the image profiles corresponding to each pixel are summed.
In Fig. 3a we compare the intensity profiles for the nulling
interferometer combined with modified pupils to those with
circular pupils. In this case both constructive and destructive
conditions are represented. At a distance of 5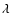 /D, the effect of
the modified pupil is a halo suppression of about 10-7,
for each of the three cases given by Eqs. (10)-(12)
while the interferometer nulling depth is
/D, the effect of
the modified pupil is a halo suppression of about 10-7,
for each of the three cases given by Eqs. (10)-(12)
while the interferometer nulling depth is
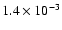 ,
yielding a combined dynamic range enhancement of about
,
yielding a combined dynamic range enhancement of about
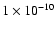 .
In this case the image core radius along the high-contrast axis
for the Kaiser-Bessel window shaped aperture
of Eq. (10)
could become less than 3
.
In this case the image core radius along the high-contrast axis
for the Kaiser-Bessel window shaped aperture
of Eq. (10)
could become less than 3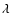 /D.
When
/D.
When 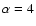 for the aperture,
the dynamic range reaches
for the aperture,
the dynamic range reaches
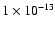 at 5
at 5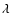 /D
combined with the nulling interferometer,
while the image core radius
becomes about 4
/D
combined with the nulling interferometer,
while the image core radius
becomes about 4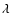 /D.
/D.
In Fig. 3b, the
same profiles are shown but this time including 0.01 wavelength rms
normally distributed wavefront errors. At a distance of >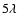 /D,
the effects of the modified pupils and the nulling interferometer are
wavefront error noise limited at
/D,
the effects of the modified pupils and the nulling interferometer are
wavefront error noise limited at
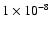 ,
while the combination method proves effective for <
,
while the combination method proves effective for <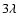 /D.
The halo noise is found as the background in the case of
constructive interference.
A noise level of
/D.
The halo noise is found as the background in the case of
constructive interference.
A noise level of
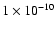 is obtained for 0.001 wavelength rms
errors.
The combination of a nulling interferometer and
a modified pupil does not reduce the wavefront error noise.
is obtained for 0.001 wavelength rms
errors.
The combination of a nulling interferometer and
a modified pupil does not reduce the wavefront error noise.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{2424fig3.eps}\\ \vspace*{2mm}
\includegraphics[width=7.8cm]{2424fig4.eps} \end{figure}](/articles/aa/full/2005/19/aa2424/Timg66.gif) |
Figure 3:
Intensity profiles along the high-contrast axis for
combinations of nulling interferometer with modified pupils. The profile
for the Kaiser-Bessel window shaped pupil of
Eq. (10) under
nulling interferometer destructive conditions is shown (1: bold line),
the sonine windowed Gaussian of
Eq. (11) by the dashed line 2,
and the apodized square of
Eq. (12) by the dot-dashed line 3.
In the case of the circular aperture we show both constructive
conditions (4: solid line) and destructive nulling conditions (5: dotted
line). a) is the ideal case of zero wavefront errors, and b) includes
normally distributed 0.01 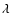 rms wavefront errors.
rms wavefront errors.
|
| Open with DEXTER |
The nulling interferometer can achieve total extinction for an on-axis source,
but off-axis residual intensity is observed depending on the transmission map
of the interferometer.
The combination of the nulling interferometer and
the modified pupil is shown to be more effective for resolved stars
in terms of off-axis light reduction than either method by itself,
because the effects of the two methods are multiplied.
It is possible to adopt here a multiple-aperture nulling interferometer
with a better null for a resolved star
than that achieved with the Bracewell two-aperture design,
for example one with four 3 m sub-apertures extracted from an 8 m telescope.
When the nulling performance of the interferometer is
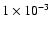 for a resolved star,
the modified pupil telescope is only required to suppress the halo
intensity at
for a resolved star,
the modified pupil telescope is only required to suppress the halo
intensity at
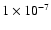 to get a combined intensity
of
to get a combined intensity
of
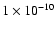 at the position of the planet.
The low dynamic range requirement for the modified pupil method
would favor a design with higher performance,
such as a small PSF core radius and a high throughput.
Various modified pupil telescope designs
(e.g. Kasdin et al. 2003; Guyon 2003)
are available for the combination.
at the position of the planet.
The low dynamic range requirement for the modified pupil method
would favor a design with higher performance,
such as a small PSF core radius and a high throughput.
Various modified pupil telescope designs
(e.g. Kasdin et al. 2003; Guyon 2003)
are available for the combination.
Equation (6) shows that the modification of
the two entrance pupils
of the nulling interferometer is equivalent to that of a
corresponding pupil plane after the nulling beam combiner.
Therefore the front nulling interferometer is considered to be
independent pre-optics of a back-side modified pupil single telescope,
which simply reduces the source intensity according to the transmission map.
Note that the planet intensity is also affected by the map and
rotation of the interferometer is required to get a sensitivity
for the whole field of view (Bracewell 1978).
The upstream nulling interferometer can be conveniently
put in front of any other optics without wavefront change.
This implies that an additional nulling operation is applicable
when the wavefront electric field in the output pupil plane
has a non-random and simple distribution
after any previous nulling interferometric or coronagraphic operation.
Consequently the nulling coronagraph method for a single telescope optics,
instead of the modified pupil method,
is considered to be effective as the back optics of the
nulling interferometer.
In Fig. 2,
a schematic of a possible optical layout for the concept
with a camera optics is shown.
In the collimated beam of a single telescope,
after the nulling interferometer,
a modified pupil telescope is placed
to produce a high dynamic range image,
which is followed by an occulting mask to hide the bright core,
a collimator, Lyot stop, a focusing lens, and a camera
suitably adjusted to avoid saturation.
The only stop actually needed is the one at
the common location of the modified pupil telescope,
i.e. after the combiner.
The nulling coronagraph method has various designs using
a simple circular (elliptical) or square (rectangular) pupil,
an image plane (phase) mask, and a Lyot stop.
Some nulling coronagraph methods without pupil modification
can achieve the complete extinction of an on-axis point source
(Rouan et al. 2002; Abe et al. 2003),
and some designs work when combined with apodized entrance apertures
(Aime et al. 2002; Soummer et al. 2003).
For any nulling coronagraph, however,
as well as for the nulling interferometer,
an off-axis source remains un-nulled.
The final image intensities including tip-tilt errors
were estimated for some coronagraphs
(Guyon et al. 1999; Rouan et al. 2000).
It was not estimated whether the residual intensity of a resolved star
was below
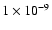 .
The rejection factor of stellar light within a radius of 0.012
.
The rejection factor of stellar light within a radius of 0.012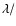 D
for a four-quadrant phase-mask coronagraph
is shown to be limited to 16 100
(Riaud et al. 2003).
In any case, the residual off-axis light for
the nulling coronagraph
can be suppressed by the upstream nulling interferometer,
yielding a combination concept of the nulling interferometer
and the nulling coronagraph methods
with/without modified entrance pupil.
In Fig. 2,
when the nulling coronagraph is used after the nulling interferometer,
only the occulting mask should be replaced by a suitable phase mask,
with/without modification of the common pupil.
D
for a four-quadrant phase-mask coronagraph
is shown to be limited to 16 100
(Riaud et al. 2003).
In any case, the residual off-axis light for
the nulling coronagraph
can be suppressed by the upstream nulling interferometer,
yielding a combination concept of the nulling interferometer
and the nulling coronagraph methods
with/without modified entrance pupil.
In Fig. 2,
when the nulling coronagraph is used after the nulling interferometer,
only the occulting mask should be replaced by a suitable phase mask,
with/without modification of the common pupil.
Though an apodized Lyot stop showed halo intensity suppression
for the classical coronagraph method
(Itoh et al. 1998),
all of the apodization has been done at the entrance pupil
for the nulling coronagraphy, achieving
total extinction for an on-axis point source
(Aime et al. 2002; Soummer et al. 2003).
However, it is not proved that the modified Lyot stop is ineffective
especially for the case of a resolved star.
When there is a significant residual amplitude of
partially-extinct off-axis regular light from a resolved star surface,
if the residual wavefront has a large uniform component,
the additional application of a modified Lyot stop
might suppress the halo intensity in the final image plane.
Eventual off-axis light from a star in the presence of tip-tilt errors
would be in a similar situation.
Some combinations of the nulling
interferometer, the modified entrance pupil,
the advanced coronagraph, and
the modified Lyot stop
might have the potential to achieve a higher dynamic range for realistic
resolved star observations
than that obtained by presently known methods.
Again looking at Fig. 2 in this case, the pupil,
the occulting mask, and the Lyot stop would be respectively replaced by
a modified pupil, an image plane (phase) mask, and modified Lyot stop
by using a variation of the modified pupil telescopes
(e.g. Kasdin et al. 2003; Guyon 2003).
The study of a combination of the
nulling coronagraph with a modified Lyot stop
in the case of a resolved star will be published in a future paper
(Murakami et al. in preparation).
Achromatic interfero-coronagraphy (AIC)
is another kind of interferometric nulling coronagraph
(Baudoz et al. 2000),
which might be used as back optics of the nulling interferometer.
Because the AIC output wave after recombination is similar to that of
a nulling interferometer, it might be used
as pre-optics of another nulling coronagraph,
though it produces axi-symmetric duplicated images.
As seen in Fig. 3,
wavefront errors limit the halo suppression level,
therefore the nulling interferometer and the modified pupil method are
only effective with sufficiently high-quality optics.
In the telescope optics, there are many parts producing wave front
errors and scattered light: mirror surfaces, apodization filters,
phase shifters, beam splitters, phase masks, dust, and so on.
A theoretically high performance method might become impossible
experimentally because of these difficulties.
The use of polarization characteristics
(e.g. Baba & Murakami 2003)
or differential wavelength techniques
(e.g. Danchi et al. 2003)
is one of the candidates
to develop high dynamic range optics insensitive to such disturbances.
To search realistically possible high performance nulling setup
for resolved star observations
especially in optical coronagraphs requiring very high dynamic range
is as important
as theoretical and numerical studies.
We have presented a combination of a nulling interferometer
in front of a modified pupil telescope
as a candidate for the high dynamic range optics for
direct observation of exo-planets.
The nulling interferometer can produce the total extinction for an
on-axis point source but it transmits leakage light for a resolved star
with off-axis rays.
With the combination presented here,
the effects of the nulling interferometer and
the modified pupil are independent and they are multiplied,
resulting in higher dynamic range than either method by itself.
For the source intensity reduction effect of the nulling
interferometer (e.g. 10-3)
in the combination methods
to reach the desired total dynamic range of 10-10,
the modified pupil is required to provide a lower contrast
halo suppression (e.g. 10-7)
which is a welcome situation for helping exo-planet-finding telescopes
to reduce the modified-pupil PSF core radius
(e.g. 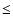
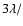 D) and to increase throughput.
The present combination is useful for the case where
the point-spread-function core radius
of each element telescope is a few times smaller than the
separation angle of the target exo-planet from the central star.
An example of the condition is a 600 nm wavelength observation
of a Sun-Earth-like system at a distance of 5 pc,
with an apparent stellar diameter of 2 mas and
a separation between the star and the planet of 200 mas,
using a 3 m baseline interferometer
which is composed of two 3 m sub-apertures with a diffraction limit
of 41 mas extracted from a 6 m telescope.
The introduction of a modified pupil has the same effect
whether it is made at the entrance aperture of the interferometer or
at a re-imaged common pupil plane after the nulling interferometry.
From another point of view,
a nulling interferometer is shown to work as pre-optics which
reduces the source intensity
in front of any single telescope optics, just like the modified pupil method.
An additional nulling operation is applicable
when the wavefront at the output pupil plane
for each point of the resolved source
has a uniform distribution
after any previous nulling operation.
Then, after the nulling interferometer, instead of the modified pupil,
the nulling coronagraph method for a single telescope optics
is considered to be effective for extinguishing off-axis light,
and further operations yielding a high dynamic range would be possible
if there remained some uniform wavefront residuals after the two nulling methods.
In analogy with the present concept,
it is important to investigate various optical designs and combinations
which have not yet been explored but
have the potential to achieve higher dynamic range than
that obtained by presently known methods and combinations.
We are interested in making modifications to known
methods including the proposals of the present paper
in order to achieve
high dynamic range with available optical components.
D) and to increase throughput.
The present combination is useful for the case where
the point-spread-function core radius
of each element telescope is a few times smaller than the
separation angle of the target exo-planet from the central star.
An example of the condition is a 600 nm wavelength observation
of a Sun-Earth-like system at a distance of 5 pc,
with an apparent stellar diameter of 2 mas and
a separation between the star and the planet of 200 mas,
using a 3 m baseline interferometer
which is composed of two 3 m sub-apertures with a diffraction limit
of 41 mas extracted from a 6 m telescope.
The introduction of a modified pupil has the same effect
whether it is made at the entrance aperture of the interferometer or
at a re-imaged common pupil plane after the nulling interferometry.
From another point of view,
a nulling interferometer is shown to work as pre-optics which
reduces the source intensity
in front of any single telescope optics, just like the modified pupil method.
An additional nulling operation is applicable
when the wavefront at the output pupil plane
for each point of the resolved source
has a uniform distribution
after any previous nulling operation.
Then, after the nulling interferometer, instead of the modified pupil,
the nulling coronagraph method for a single telescope optics
is considered to be effective for extinguishing off-axis light,
and further operations yielding a high dynamic range would be possible
if there remained some uniform wavefront residuals after the two nulling methods.
In analogy with the present concept,
it is important to investigate various optical designs and combinations
which have not yet been explored but
have the potential to achieve higher dynamic range than
that obtained by presently known methods and combinations.
We are interested in making modifications to known
methods including the proposals of the present paper
in order to achieve
high dynamic range with available optical components.
Acknowledgements
The authors acknowledge Prof. M. Yoshizawa, members of Mitaka optical and
InfraRed Array (MIRA) project, and members of Japanese TPF working group
for stimulating discussions and their constant encouragement with this work.
We are grateful to Dr. C. Aime, the referee, for helpful advice on
improving the manuscript.
Y.I. is supported by a Grant-in-Aid for Scientific Research No. 16740256
of the MEXT.
- Abe, L., Domiciano de
Souza, A., Jr., Vakili, F., & Gay, J. 2003, A&A, 400,
385 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Aime, C., Soummer,
R., & Ferrari, A. 2002, A&A, 389, 334 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Angel, J. R. P.,
& Woolf, N. J. 1997, ApJ, 475, 373 [NASA ADS] [CrossRef] (In the text)
- Baba, N., Murakami,
N., & Ishigaki, T. 2001, Opt. Lett., 26, 1167 [NASA ADS] (In the text)
- Baba, N., Murakami,
N., Ishigaki, T., & Hashimoto, N. 2002, Opt. Lett., 27,
1373 (In the text)
- Baba, N., &
Murakami, N. 2003, PASP, 115, 1363 [NASA ADS] [CrossRef] (In the text)
- Baudoz, P.,
Rabbia, Y., & Gay, J. 2000, A&AS, 141, 319 [NASA ADS] (In the text)
- Beichman,
C. A., Woolf, N. J., & Lindensmith, C. A. 1999, The Terrestrial
Planet Finder, JPL Publication 99-3 (Pasadena: JPL)
(In the text)
-
Bracewell, R. N. 1978, Nature, 274, 780 [NASA ADS] (In the text)
- Danchi, W. C.,
Deming, D., Kuchner, M. J., & Seager, S. 2003, ApJ, 597,
L57 [NASA ADS] [CrossRef] (In the text)
- Fridlund,
M. 2000, DARWIN, The Infrared Space Interferometer, The Search for
Terrestrial Exoplanets and High Resolution Imaging of the Universe,
ESA SCI-12 (Noordwijk: ESA)
(In the text)
- Goodman, J.
W. 1996, Introduction to Fourier Optics, 2nd ed. (McGraw-Hill)
(In the text)
- Guyon, O. 2003,
A&A 404, 379
(In the text)
- Guyon, O., &
Roddier, F. 2002, A&A 391, 379
(In the text)
- Guyon, O.,
Roddier, C., Graves, J. E., et al. 1999, PASP, 111, 1321 [NASA ADS] [CrossRef] (In the text)
- Harris, F.J.
1978, Proc. IEEE, 66, 51 (In the text)
- Hinz, P. M., Angel,
J. R. P., McCarthy, D. W., Jr., Hoffman, W. F., & Peng, C. Y.
2003, Proc. SPIE, 4838, 108 [NASA ADS] (In the text)
- Itoh, Y., Takato,
N., Takami, H., & Tamura, M. 1998, PASJ, 50, 55 [NASA ADS] (In the text)
-
Jacquinot, P., & Roizen-Dossier, M. B. 1964, Progress in
Optics, 3, 29 (In the text)
- Kasdin, J. N.,
Vanderbei, R. J., Spergel, D. N., & Littman, M. G. 2003, ApJ,
582, 1147 [NASA ADS] [CrossRef] (In the text)
- Kuchner, M.
J., & Traub, W. A. 2002, ApJ, 570, 900 [NASA ADS] [CrossRef] (In the text)
-
Mennesson, B., & Mariotti, J. M. 1997, Icarus, 128, 202 [NASA ADS] [CrossRef] (In the text)
- Nisenson,
P., & Papaliolios, C. 2001, ApJ, 548, L201 [NASA ADS] [CrossRef] (In the text)
- Ollivier,
M., Mariotti, J. -M., Léger, A., et al. 2001, A&A 370,
1128
(In the text)
- Riaud, P.,
Boccaletti, A., Baudrand, J., & Rouan, D. 2003, PASP, 115,
712 [NASA ADS] [CrossRef] (In the text)
- Roddier, F.,
& Roddier, C. 1997, PASP, 109, 815 [NASA ADS] [CrossRef] (In the text)
- Rouan, D., Riaud,
P., Boccaletti, A., Clenet, Y., & Labeyrie, A. 2000, PASP, 112,
1479 [NASA ADS] [CrossRef] (In the text)
- Rouan, D., Riaud,
P., & Baudrand, J. 2002, in Beyond Conventional Adaptive
Optics, ed. E. Vernet, R. Ragazzoni, S. Esposito, & N. Hubin
(Garching ESO), Proc. ESO Conf. 58, 193
(In the text)
- Shao, M., &
Colavita, M. 1992, ARA&A, 30, 457 [NASA ADS] (In the text)
- Serabyn, E.,
Wallace, J. K., Hardy, G. J., Schmidtlin, E. G. H., & Nguyen,
H. T. 1999, Appl. Opt. 38, 7128
(In the text)
-
Soummer, R., Aime, C., & Falloon, E. P. 2003, A&A, 397,
1116 (In the text)
- Soummer, R.,
Dohlen, K., & Aime, C. 2003, A&A, 403, 369 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Spergel, D.
N. 2001, preprint [arXiv:astro-ph/0101142]
(In the text)
- Woolf, N. J.,
& Angel, J. R. P. 1998, ARA&A, 36, 507 [NASA ADS] (In the text)
Copyright ESO 2005
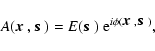
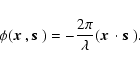
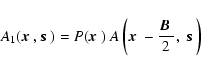
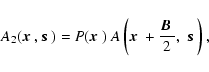
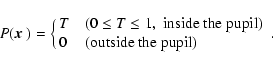
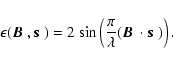
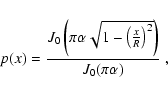
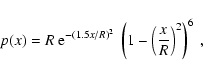
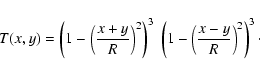
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{2424fig3.eps}\\ \vspace*{2mm}
\includegraphics[width=7.8cm]{2424fig4.eps} \end{figure}](/articles/aa/full/2005/19/aa2424/Timg66.gif)