1 - Departament de Física Aplicada, Escola Politécnica Superior de Castelldefels, Universitat Politècnica de Catalunya, Avda. del Canal Olímpic s/n, 08860 Castelldefels, Spain
2 - Departament d'Astronomia i Meteorologia, Universitat de Barcelona, Facultat de Física, Martí i Franquès 1, 08028 Barcelona, Spain
3 - Institute for Space Studies of Catalonia, c/Gran Capità 2-4, Edif. Nexus 104, 08034 Barcelona, Spain
4 - Special Research Center in Astrophysics, Particle Physics and Cosmology, University of Barcelona, Martí i Franquès 1, 08028 Barcelona, Spain

Abstract
The final stages of the evolution of electron-degenerate ONe cores, resulting from carbon burning in "heavy weight'' intermediate-mass stars ( $8 ~ M_{\odot}\la M \la 11 ~ M_{\odot}$ ) and growing in mass, either from carbon burning in a shell or from accretion of matter in a close binary system, are examined in the light of their detailed chemical composition. In particular, we have modelled the evolution taking into account the abundances of the following minor nuclear species, which result from the previous evolutionary history: ¹²C, ²³Na, ²⁴Mg, and ²⁵Mg. Both ²³Na and ²⁵Mg give rise to Urca processes, which are found to be unimportant for the final outcome of the evolution. ²⁴Mg was formerly considered a major component of ONe cores (hence called ONeMg cores), but updated evolutionary calculations in this mass range have severely reduced its abundance. Nevertheless, we have parameterized it and we have found that the minimum amount of ²⁴Mg required to produce NeO burning at moderate densities is $\sim$ 23%, a value exceedingly high in the light of recent evolutionary models. Finally, we have determined that models with relatively small abundances of unburnt carbon ( $X(^{12}\rm C)\sim 0.015$ ) could be a channel to explosion at low to moderate density ( $\sim$ $1\times 10^9$ g cm^-3). This is clearly below the current estimate for the explosion/collapse threshold and would have interesting consequences.

Key words: nuclear reactions, nucleosynthesis, abundances - stars: evolution - stars: interiors - white dwarfs - supernovae: general

The final evolution of electron-degenerate cores made of oxygen and neon (hereafter ONe) has received little attention in the last few years despite its potential importance for supernova theory. One of the reasons for this lack of accurate models is that there are very few realistic evolutionary calculations leading to the formation of such cores. This, in turn, is due to the fact that for stars with masses ranging from 8 to $11~ M_{\odot}$ , carbon-burning is ignited off-center and proceeds through a series of mild flashes in partially degenerate conditions, a situation especially difficult to simulate, which requires very short time-steps and careful zoning, leading to a heavy computational demand.

Up to now, no detailed multidimensional calculations of the evolution of high-end intermediate mass stars in this phase exist. Nevertheless, there are several possible effects, such as rotation-induced mixing and overshooting, and, more importantly, the possibilty of off-center ignitions (García-Senz & Woosley 1995; Woosley et al. 2004; Wunsch & Woosley 2004) that should be modeled and discussed using multi-dimensional hydrodynamics - see, however, Höflich & Stein (2002). Some multidimensional stellar models already exist, but they are in an early stage of development. Spherically-symmetric models include a degree of detail that current two- and three-dimensional simulations are still far from reaching. A discussion of this kind of effect is beyond the scope of this paper. However, although multidimensional evolutionary calculations of stars in this mass range do not exist yet, Hirschi et al. (2004) have studied the evolution of rotating stars with masses $M\geq 12~M_{\odot}$ - slightly larger than those considered here - and have found that most of the differences between the presupernova structures obtained from rotating and non-rotating stellar models have their origin in the effects of rotation during the core hydrogen and helium burning phases. Additionally, they explicitly mention that the advanced stellar evolutionary stages appear too short in time to allow the rotational instabilities to have a significant impact during the late stages. Hence, given the lack of accurate multidimensional calculations for this phase of the evolution of heavy-weight intermediate mass stars, one should conclude, in principle, that spherically-symmetric evolutionary calculations can still provide a reasonable approximation to the real behavior - see the recent review of Maeder & Meynet (2000) for a thorough discussion of this topic.

These objects were long ago proposed as clear candidates for the so-called accretion-induced collapse - a process first described by Canal & Schatzman (1976). Currently, it is widely accepted that ONe electron-degenerate objects do collapse to form a neutron star when the central density is driven beyond a certain threshold - see, for instance, Gutiérrez et al. (1966, 1997), or Canal & Gutiérrez (1997), and references therein. In particular, in the pioneering work of Miyaji et al. (1980) it was shown that all stars in the mass interval $8 ~ M_{\odot}\la M\la 12 ~ M_{\odot}$ would develop electron-degenerate ONeMg cores during carbon shell burning. These cores would undergo a phase of electron capture on ²⁴Mg and ²⁴Na first, and later on ²⁰Ne and ²⁰F, to finally ignite Ne and O explosively at central densities higher than $\sim$ $2\times10^{10}$ g cm^-3. At these very high central densities, fast electron captures occuring on the nuclear statistical equilibrium (NSE) material would rapidly drive the Chandrasekhar mass below the actual mass of the degenerate core and, consequently, gravitational collapse would ensue. Later, Woosley et al. (1980) and Nomoto (1984) reduced the above mass range to $8 ~ M_{\odot} \la M\la 10 ~ M_{\odot}$ . Stars more massive than $\sim$ $10 ~ M_{\odot}$ would ignite Ne in a series of non-explosive flashes and ultimately proceed through the O-burning and Si-burning stages in a way similar to more massive stars. Subsequently, Timmes & Woosley (1992, 1994) found that the density threshold for an ONe core to collapse to neutron star dimensions was around $\sim$ $4\times 10^9$ g cm^-3. On the contrary, if NSE was reached at densities below this critical density, the degenerate object would be completely disrupted. Finally, Gutiérrez et al. (1996) analyzed the role of Coulomb corrections, both in the equation of state and in the electron-capture threshold energies, and found that explosive NeO ignition takes place at densities high enough to ensure gravitational collapse to nuclear matter densities. The previously described scenario should apply not only to the cores of Super-Asymptotic Giant Branch (SAGB) stars (García-Berro & Iben 1994) but also to ONeMg white dwarfs accreting material from a companion in a close binary system (Miyaji et al. 1980; Nomoto 1984, 1987).

Most of the studies done so far for this mass range had considered ²⁴Mg as a major constituent of the core. However, the detailed studies of Ritossa et al. (1996), García-Berro et al. (1997), Iben et al. (1997) and Ritossa et al. (1999) have clearly shown that the mass fraction of ²⁴Mg is much smaller than previously thought. Following the trends shown by these modern evolutionary calculations for the stars in this mass range, in this paper we investigate the effects of the chemical composition of the degenerate core on the possible outcome of these objects. In particular, we analyze the impact of the abundance of ²⁴Mg, the presence of ²³Na and ²⁵Mg, and the presence of unburnt ¹²C, which appears to be a specific characteristic of current evolutionary models. The paper is organized as follows. In Sect. 2 we describe the most relevant input physics and the initial model. Section 3 is devoted to the effects of an increasing ²⁴Mg abundance, while in Sect. 4 we analyze the role played by the previously unburnt ¹²C. The role of the minor chemical species (²³Na and ²⁵Mg) is analyzed in Sect. 5. In Sect. 6 we discuss our results and we draw our conclusions.

2 Input physics and initial model

For the sake of conciseness, and given that the numerical code and most of the physical inputs employed in the calculations discussed in this paper have already been described in previous papers - see Gutiérrez et al. (1996) and references therein - we will not present them here in detail. Instead, in this section we only summarize the most relevant physical ingredients which are relevant for the discussion of the evolutionary sequences analyzed below. These are the electron capture rates, Coulomb corrections and the prescription adopted for convective transport.

Electron capture rates have been taken from Oda et al. (1994), which provides the most up-to-date, and physically consistent determinations. This point seems already fixed, as the rates for sd-shell nuclei have remained almost unchanged since the work of Takahara et al. (1989). However, the data of Oda et al. (1994) are much richer for ²⁴Mg, ²⁰Ne and other sd-shell nuclei relevant for this work, such as ²³Na and ²⁵Mg.

Coulomb corrections to the electron capture threshold have been included as in Couch & Loumos (1974). The net effect on the Coulomb interaction energy is to lower it, hence reducing the Fermi energy and increasing the capture density threshold. The exact expression to compute the energy shift is

$\displaystyle \mu(Z)$ = $\displaystyle -k_{\rm B}T\left(\frac{Z}{{\bar Z}}\right) \Bigg\{ \Gamma \left[ ... ...eft(\frac{Z}{\bar Z}\right)^{1/3} + c_2 \Big(\frac{Z}{\bar Z}\Big)^{2/3}\right]$ $\displaystyle +\left[d_0 + d_1 \left(\frac{Z}{\bar Z}\right)^{1/3} + ... \right] + O(1/\Gamma) \Bigg\}$

(2)

Another very important issue is what convective criterion must be adopted. In the paper of Miyaji et al. (1980), convection was assumed to set in according to the Schwarzschild criterion: a convective core started to develop at the onset of the electron captures on ²⁴Mg. Convective heat transport contributed to keep the temperature below that of explosive Ne ignition ( $\sim$ $2\times 10^{9}$ K) along core contraction until a central density $\rho \ga 2\times 10^{10}$ g cm^-3 was reached. That was questioned by Mochkovitch (1984), who argued that the steep gradient of the electron mole number, $Y_{\rm e}$ , produced by the same electron captures that create the superadiabatic temperature gradient, should stabilize the fluid against convective motion and a semiconvective region would form. Miyaji & Nomoto (1987) tested this situation by assuming semiconvective mixing to be negligible. They found that explosive NeO burning was ignited at a central density $\sim$ $9.5\times 10^{9}$ g cm^-3: heating by the electron captures and cooling by thermal neutrinos was then purely local. Thus, convective criteria are essential in ascertaining the final outcome of the evolution of compact ONe objects. In this paper we adopt a rather pragmatic approach. That is, we first consider the classical Schwarzschild criterion $\nabla \le \nabla_{\rm ad}$ . However, since this stability criterion assumes complete chemical homogeneity and this is not the case when electron-captures start, we also use the Ledoux criterion: $\nabla \le \nabla_{\rm L}$ , where:

$\begin{displaymath}\nabla_{\rm L} \equiv \nabla_{\rm ad} - \left[ \left(\frac{\p... ...\partial \ln T}\right)_{Y_{\rm e}} \right] \nabla_{Y_{\rm e}}. \end{displaymath}$

(3)

Our initial model, used in all the calculations, is a $1.375 ~ M_{\odot}$ electron-degenerate object, whose main chemical constituents are ¹⁶O and ²⁰Ne, with the distribution obtained by Ritossa et al. (1996). Its central density and temperature are, respectively, $\rho_{\rm c} \simeq 1.0 \times 10^9$ g cm^-3 and $T_{\rm c} \simeq 2.0\times 10^8$ K. The core is discretized in up to 1000 mass shells by an adaptive algorithm, which ensures good resolution both in chemical composition and in entropy throughout the structure. The ONe object is slowly contracting due to spherical accretion at a rate of $\sim$ $10^{-6}~ M_{\odot}$ yr ^-1. Its mass is consistent with the mass of ONe white dwarfs, and is close to the Chandrasekhar mass, making this object prone to experience sudden instability leading to either disruption or collapse.

3 The effects of the abundance of ²⁴Mg

Since the pioneering work of Miyaji et al. (1980), the astrophysical nuclear reaction rates have undergone significant changes. In particular, the amount of ²⁴Mg present in typical ONe cores has been reduced by almost an order of magnitude (Ritossa et al. 1996). Currently, it seems that the most important rates are already reasonably well known but, nonetheless, it would be interesting to ascertain the minimum abundance of ²⁴Mg required to cause an early explosion of the degenerate core. For this, we have parameterized the abundance of ²⁴Mg while keeping constant the ratio O/Ne. While this is not truly consistent, it serves well the point relevant here: how much ²⁴Mg is the minimum to engage a explosion at about $4\times 10^9$ g cm^-3, which would possibly lead to the complete disruption of the degenerate object. With the currently accepted abundances of ²⁴Mg ( $\sim$ 3% by mass), the maximum temperature attained during the electron captures is only $3.8\times 10^8$ K (Gutiérrez et al. 1996), very far below the minimum needed to initiate the explosive oxygen burning and to drive the matter to NSE. The goal of this section is to determine the minimum abundance of ²⁴Mg required to produce a central temperature of about $1.5 \times 10^9$ K.

In Fig. 1 several evolutionary sequences with increasing abundances (3%, 10%, 15% and 25%) of ²⁴Mg are shown. We have restricted our study to the Ledoux case because the preclusion of convection implies a stronger heating of the central region, due to the relative inefficiency of the radiative-conductive transport of energy. Evolutionary calculations performed with the Schwarzschild criterion (Fig. 2) confirm this point, even taking into account the mixing induced by the convective transport. As it can be seen in Fig. 1, the higher the abundance of ²⁴Mg, the higher the central temperature achieved during the phase of electron capture on this isotope.

$\begin{figure} \par\includegraphics[width=8.1cm,clip]{fig01.eps} % \end{figure}$	Figure 1: Evolutionary sequences of an ONe electron-degenerate object for increasing abundances of ²⁴Mg. The abundances of ²⁴Mg are, respectively, 3%, 10%, 15% and 25% by mass. The model with $X(^{24}\rm Mg)=0.15$ undergoes an off-center explosion and the model with $X(^{24}\rm Mg)=0.25$ produces a low density explosion, leading to the complete disruption of the degenerate core.
Open with DEXTER

Table 1: Ignition density and maximum central temperature reached during the captures on ²⁴Mg and ²⁴Na, for several initial abundances of ²⁴Mg. The cases whose central densities are marked with an asterisk correspond to off-centre explosions. In all the calculations, the Ledoux convective criterion has been adopted.

Table 1 shows the net effect of increasing the abundance of ²⁴Mg, both for the maximum central temperature and for the central density at ignition. The first trend obviously appearing in Table 1 is that failed explosions lead to higher collapse densities - see Fig. 1. This is due to the fact that electron captures proceed in conditions of constant $\rho Y_{\rm e} \sim n_{\rm e}$ , and hence higher amounts of ²⁴Mg imply larger reductions of $Y_{\rm e}$ . Consequently, the collapse density increases from $9.41\times 10^9$ g cm^-3, when there is no ²⁴Mg in the degenerate core, to about $10.409 \times 10^9$ g cm^-3, when the amount of ²⁴Mg is 10%. The minimum abundance of ²⁴Mg for which NSE develops during the electron capture phase is about 15%, and the explosion is clearly off-center. The reason is simple: during the phase of electron capture, part of the energy generated is released on the mass shells above that in which the electron capture reactions are proceeding; thus, the temperature of these shells is constantly increasing. There is also a second effect: a reduction in $Y_{\rm e}$ increases the rate of contraction and, thus, the gravitational enery release, leading to a still higher temperature of the material. This can be readily seen in Fig. 1, in which the slope of the evolutionary track in the $\log (\rho_{\rm c})-\log (T_{\rm c})$ plane becomes steeper with increasing abundances of ²⁴Mg. Eventually, the energy generation in one of these preheated shells is able to drive the temperature to the point at which oxygen burning can be self-sustained, and, in fact, accelerated to produce the transition to NSE. For even larger amounts of ²⁴Mg the mass shell in which the off-center explosion ensues is located closer to the center. The explanation is, again, rather straightforward, as the preheating for increasing abundances of ²⁴Mg is more extreme and the change in temperature caused by the electron captures on ²⁴Mg is also correspondingly higher.

$\begin{figure} \par\includegraphics[width=8.1cm,clip]{fig02.eps} % \end{figure}$

Figure 2: Evolution of an ONe object with the Schwarzschild criterion (solid line). The dotted line corresponds to a case in which convective mixing is inhibited. In the case with mixing, the effects of a convective Urca shell are evident. The peak corresponds to the point where the nuclides of mass 24 able to capture electrons (namely ²⁴Mg and ²⁴Na) are exhausted throughout the convective core.

Open with DEXTER

A central explosion occurs only when the amount of ²⁴Mg approaches $\sim$ 25%, which is not credible given the current nuclear reaction rates relevant for the production of ²⁴Mg during the carbon burning phase. The same can be said about the minimum abundance needed to produce off-center explosions: it is extremely unlikely - and many things would need to change significantly, in particular the rates of nuclear reactions during carbon burning - that ²⁴Mg could by itself induce the heating to NSE in a electron degenerate core at low density.

4 Explosions induced by ¹²C

$\begin{figure} \par\includegraphics[width=8.1cm,clip]{fig03.eps} % \end{figure}$	Figure 3: Evolution on the log( $\rho _{\rm c}$ )-log(T $_{\rm c}$ ) plane for the models incorporating abundances of ¹²C ranging from 0.01 to 0.06. The only model that fails to produce an explosion at moderate densities is that corresponding to $X(^{12}\rm C)=0.01$ . For all these calculations, the Ledoux criterion has been adopted.
Open with DEXTER

Recent models (Domínguez et al. 1993; Ritossa et al. 1996; Gil-Pons & García-Berro 2001, 2002) have convincingly shown that carbon burning can be incomplete in degenerate cores. The amount of remaining carbon depends somewhat on the detail of the calculations but is typically of the order of $\la$ 1%. Nevertheless, Domínguez et al. (1993) found a central region of $\sim$ $0.2~ M_{\odot}$ with a high carbon content, of the order of 25%, that may eventually lead to an early explosion, and hence to a disruption of the electron-degenerate core. More specifically, Domínguez et al. (1993) followed the evolution of a $10 ~ M_{\odot}$ star in a binary system. The extreme dependence of neutrino cooling on density was able to cool down the center of the star to temperatures low enough to preclude the onset of central carbon burning. Although it has been claimed that this result could be to due the roughness of the numerical procedure adopted in Domínguez et al. (1993) - in particular to the poor spatial resolution of their mesh - or to the very high mass-loss rate adopted, this is a point that undoubtely deserves more attention, since carbon burning in degenerate conditions is prone to develop into the explosive regime, even when this element is found in only relatively small amounts. Woosley (1986) has estimated that, in the interval T₈=2.5-7.5, for each 0.12% of carbon burned the temperature increases by 10⁸ K.

$\begin{figure} \par\includegraphics[width=8.1cm,clip]{fig04.eps} % \end{figure}$	Figure 4: Same as Fig. 3, but using the Schwarzschild convective criterion. Only the model with $X(^{12}\rm C)=0.01$ fails to trigger an explosion at moderate densities.
Open with DEXTER

In this case, given that there is a difference on the atomic mass of ¹²C and its daughter nuclei (namely, ¹⁶O, ²⁰Ne and ²⁴Mg), the Ledoux criterion must include an additional term to take it into account. The expression employed throughout this work is then

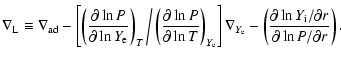$\displaystyle \nabla_{\rm L} \equiv \nabla_{\rm ad} - \left[ \left(\frac{\parti... ...\frac{\partial \ln Y_{\rm i} /\partial r} {\partial \ln P / \partial r}\right).$

(5)

Table 2: Models with variable ¹²C abundance. In the table, "L'' stands for the Ledoux criterion, while "S'' stands for the Schwarzschild criterion; "C'' denotes collapse and "E'' disruption. For carbon abundances over 2%, all realistic models imply the complete disruption of the star. The case with a 4% abundance of carbon, and with the convection artificially inhibited (marked by an asterisk) corresponds to an off-center explosion.

In order to determine the minimum amount of remaining carbon needed to completely disrupt the core at low densities, we have parameterized its abundance from 1% to 6%, a broad enough range. We have adopted both the Ledoux and the Schwarzschild criteria. Also, to investigate the worst possible case, we have artificially inhibited the convective motion and energy transport. In this case carbon burning proceeds in a strictly local mode, making the onset of NSE more difficult. This could be similar to what would happen if the thermonuclear timescale were much shorter than the convective turnover and evolutionary timescales.

The first set of calculations is shown in Fig. 3, for which the Ledoux criterion was used. As it can be seen, the only model for which an early explosion is avoided is that with carbon abundance $X(^{12}\rm C)\sim 0.01$ . In Fig. 4 the evolution in the $\log (\rho_{\rm c})-\log (T_{\rm c})$ plane is shown for the set of models in which the Swarzschild criterion was adopted. Again, only the models with $X(^{12}\rm C)\la 0.01$ do not lead to an early explosion. Finally, in Fig. 5 the results obtained when convection was artificially inhibited are shown. In this case, those models in which the carbon abundance is $\ga$ 2% give an explosion at moderate densities. For completeness, our results are summarized in Table 2, where the maximum temperature attained during carbon burning (fourth column), the ignition density (fith column) and the outcome of the evolution (sixth column) are shown as a function of the carbon abundance and the convective criterion. Table 2 shows that in the cases where convection is taken into account, the minimum abundance of ¹²C should be as high as 1.5%, only a factor of 2 higher than the abundance presently found in most calculations. Even when the convective processes are artificially inhibited, the amount of ¹²C required to achieve NSE at low densities increases to 4% - and the explosion occurs slightly off-center. It is clear that the presence of small amounts of unburned ¹²C could be a possible channel for the complete disruption of ONe degenerate objects at very low density unless non-physically consistent situations are artificially forced. It is also not surprising that a model adopting the ¹²C distribution obtained by Domínguez et al. (1993) results in an explosion at low density. Nevertheless, Rayleigh-Taylor instabilities would rapidly mix the ¹²C-rich matter with the rest of the core. In this case, the abundance of ¹²C is already within the range studied in the present work (about a 4.5%).

Given the low density at which NSE proceeds, it is likely that some of the reactions will be rapidly quenched, thus producing an incomplete burning and a corresponding lower fraction of Fe-peak elements. While this is not compatible with classical type Ia SNe nucleosynthesis, it could be an alternative explanation for subluminous type Ia SNe, like SN1991bg (Ruiz-Lapuente et al. 1993). Clearly, this outcome deserves further consideration, which is beyond the scope of this paper.

5 Effects of the Urca pairs ²³Na-²³Ne and ²⁵Mg-²⁵Na

Recent evolutionary calculations including detailed nuclear reaction networks have found that noticeable amounts of ²³Na and ²⁵Mg appear after the carbon burning phase - see, for example, Gil-Pons & García-Berro (2001). These nuclides have low electron-capture energy thresholds (Q=4.376 MeV and Q=3.833 MeV, respectively) and so they will start captures even before ²⁴Mg, which has a higher energy threshold. The Urca processes for these nuclides are ²³Na(e, $\nu)^{23}$ Na(e, $\nu)^{23}$ Ne and ²⁵Mg(e, $\nu)^{25}$ Na(e, $\nu)^{25}$ Mg, occurring at densities of $1.68\times 10^9$ g cm^-3 for ²³Na and $1.17\times 10^9$ g cm^-3 for ²⁵Mg. The rates for these Urca pairs have also been taken from Oda et al. (1994). Note that throughout the calculations presented in this section Coulomb corrections were applied to the rates, as was done previously. The chemical composition of the ONe core was $X(^{16}\rm O)=0.625$ , $X(^{20}\rm Ne)=0.262$ , $X(^{23}\rm Na)=0.052$ , $X(^{24}\rm Mg)=0.045$ , and $X(^{25}\rm Mg)=0.015$ as derived from Ritossa et al. (1996). Also note that for simplicity we have excluded the small abundance of unburnt ¹²C and renormalized the resulting abundances.

$\begin{figure} \par\includegraphics[width=8.1cm,clip]{fig05.eps} % \end{figure}$	Figure 5: Same as Figs. 3 and 4, but with convection artificially inhibited. In this case, even a 2% abundance of ¹²C fails to trigger a moderate density explosion.
Open with DEXTER

As it can be seen in Fig. 6, the main effect of the Urca pairs consist of small decreases in $T_{\rm c}$ and in $Y_{\rm e}$ . The later effect is the only lasting one. These Urca pairs are never in equilibrium, as the core is slowly contracting and, hence, increasing the Fermi energy of the electrons. Some 10⁹ s after formation of the Urca pairs, the rates for electron-capture on the involved nuclides are much higher than the $\beta$ -decay rates. Eventually, all the ²³Na becomes ²³Ne, and the ²⁵Mg becomes ²⁵Na, with a total reduction on $Y_{\rm e}$ of 0.00286, which translates into a slightly higher ignition density for NeO burning.

$\begin{figure} \par\includegraphics[width=8.1cm,clip]{fig06.eps} % \end{figure}$	Figure 6: Evolution in the $\log(\rho_{\rm c})-\log(T_{\rm c}$ ) plane of an ONe electron-degenerate object with the abundances given by Ritossa et al. (1994). The effect of the Urca pairs involving ²³Na and ²⁵Mg is apparent as a sudden decrease in $T_{\rm c}$ near $\log\rho_{\rm c}=9.2$ . The convective criterion adopted was that of Ledoux.
Open with DEXTER

When using the Schwarzschild criterion, convection appears during the electron captures on the nuclides of mass 24 (²⁴Mg and ²⁴Na). Due to the limited extent of the convective region, there is no convective Urca for ²³Ne nor for ²⁵Na, since the upper layer of the convective region is well above the density for significant rates of $\beta$ decay from these nuclides. Thus, the only durable effect of ²³Na and ²⁵Mg on the evolution of our objects is a small reduction in $Y_{\rm e}$ (from the original value of 0.4981 to 0.4952). Hence, due to this slight reduction in $Y_{\rm e}$ , the ignition density for NeO burning is $9.493\times 10^9$ g cm^-3, clearly above the collapse threshold given by Timmes & Woosley (1992, 1994).

6 Conclusions

The final fate of pure ONe electron degenerate objects seems at present well established: they will collapse to a neutron star after electron captures on ²⁰Ne at a density of about $9\times 10^9$ g cm^-3. The main goal of this work has been to elucidate whether the minor species present in ONe cores - namely, ¹²C, ²³Na, ²⁴Mg and ²⁵Mg - can open a channel to produce an explosion at moderate densities (about 10⁹ g cm^-3) which would lead to the complete disruption of the star.

We have found that the amount of ²⁴Mg required to produce a low density explosion is about one order of magnitude above the results of current, state-of-the-art evolutionary calculations. Hence, it is very unlikely that electron captures proceeding on ²⁴Mg (and its daughter nucleus ²⁴Na) can drive the temperature of the star to the point of igniting the NeO burning at $\rho \sim 4.5\times10^9$ g cm^-3. Even in the (improbable) case that this actually happened, this density is near the current accepted threshold for gravitational collapse (Timmes & Woosley 1992, 1994). Consequently, if there is not a very significant change in the reaction rates leading to the production of ²⁴Mg, this nuclide can be discarded as a possible trigger of a moderate density explosion.

On the contrary, even small amounts of unburned ¹²C are enough to drive a moderate to low density explosion. The reason is twofold. First, the energy yield is much higher for carbon burning than for electron captures on the A=24 nuclei. Secondly, there is much more ¹²C available, since the ignition is very local and can induce convective motion that leads to mixing that carries fresh ¹²C into the burning region. In this way, even seemingly small abundances of ¹²C (about a 1.5%) can produce an explosion at $\rho_{\rm c} \sim 1\times10^9$ g cm^-3, which would lead to the complete disruption of the star. This potential channel to complete disruption would give rise to a thermonuclear supernova. The characteristics of such a kind of thermonuclear supernova are beyond the scope of this work, but could explain in part why there seems to be a correlation between spiral arms and Type Ia supernovae (Bartsunov et al. 1994; McMillan & Ciardullo 1996). Finally, the effects of the Urca pairs generated by ²³Na and ²⁵Mg are minor. Apart from a small reduction in the temperature, the only lasting effect is a small decrease in the electron mole number $Y_{\rm e}$ . This will result in a slightly higher density for the electron captures on the nuclei of A=24 and A=20.

We note that multidimensional simulations of convection indicate a tendency to increase the amount of convective mixing and to induce rotational mixing to an extent that could slightly modify our conclusions. Many efforts are currently being invested in modeling carbon burning under strongly degenerate conditions using multidimensional codes - see, for instance, Reinecke et al. (2003) and Röpke et al. (2004a,b) for recent developments in this field. A time-dependent numerical procedure for mixing (necessary for coupling core contraction and convection) could slightly change the details of our conclusions, but it is unlikely to cause a qualitative change - that is, transforming a collapse into an explosion or vice versa. Until a complete treatment of multidimensional convection and burning is available, our results can be regarded as a fair approximation to the real evolution of this type of star.

The gravitational collapse of ONe electron-degenerate cores and white dwarfs: The role of ²⁴Mg and ¹²C revisited

1 Introduction

2 Input physics and initial model

3 The effects of the abundance of ²⁴Mg

4 Explosions induced by ¹²C

5 Effects of the Urca pairs ²³Na-²³Ne and ²⁵Mg-²⁵Na

6 Conclusions

References

The gravitational collapse of ONe electron-degenerate cores and white dwarfs: The role of 24Mg and 12C revisited

1 Introduction

2 Input physics and initial model

3 The effects of the abundance of 24Mg

4 Explosions induced by 12C

5 Effects of the Urca pairs 23Na-23Ne and 25Mg-25Na

6 Conclusions

References

The gravitational collapse of ONe electron-degenerate cores and white dwarfs: The role of ²⁴Mg and ¹²C revisited

3 The effects of the abundance of ²⁴Mg

4 Explosions induced by ¹²C

5 Effects of the Urca pairs ²³Na-²³Ne and ²⁵Mg-²⁵Na