A&A 434, 1191-1200 (2005)
DOI: 10.1051/0004-6361:20041680

Stellar wind regimes of close-in extrasolar planets

S. Preusse 1 - A. Kopp1 - J. Büchner 1 - U. Motschmann 2


1 - Max-Planck-Institut für Sonnensystemforschung[*], Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
2 - Institut für Theoretische Physik, Technische Universität Braunschweig, Mendelssohnstrasse 3, 38106 Braunschweig, Germany

Received 16 July 2004 / Accepted 26 December 2004

Abstract
Close-in extrasolar planets of Sun-like stars are exposed to stellar wind conditions that differ considerably from those for planets in the solar system. Unfortunately, these stellar winds belong to the still unknown parameters of these planetary systems. On the other hand, they play a crucial role in a number of star-planet interaction processes that may lead to observable radiation events. In order to lay a foundation for the investigation of such interaction processes, we estimate stellar wind parameters on the basis of the solar wind model by Weber & Davis and study the implications of the stellar magnetic fields. Our results suggest that in contrast to the solar system planets, some close-in extrasolar planets may be obstacles in a sub-Alfvénic stellar wind flow. In this case, the stellar wind magnetic pressure is comparable to or even larger than the dynamic flow pressure. We discuss possible consequences of these findings for the wind-exoplanet interactions. Further, we derive upper limit estimates for the energies such stellar winds can deposit in the exoplanetary magnetospheres. We finally discuss the implications the sub-Alfvénic environment may have on the star-planet interaction.

Key words: stars: winds, outflows - stars: magnetic fields - magnetohydrodynamics (MHD) - stars: planetary systems

1 Introduction

Among the extrasolar planets detected since 1995 many have been found in close vicinity to their star. OGLE-TR-56 b is an extreme but not unusual example. Its orbital distance of 0.0225 AU will be approx. 20 times closer than Mercury is to the Sun, if the orbital eccentricity is taken into account.

The implications of this extreme vicinity to the stars for the star-planet systems are expected to be manifold. A variety of phenomena resulting from interaction between the star and its close-in planet are expected. Though both components are involved in such interaction, the theories and observations can be sorted according to whether the physical processes are associated with the star or the planet.

From the stellar point of view, gravitational interaction may come into play in terms of spin up by planetary migration towards the star if counteracting processes are neglected as is discussed by Paetzold et al. (2004). Furthermore, it may lead to heating and an increase of stellar activity as pointed out by Cuntz et al. (2000) who also give estimates of the magnetic interaction for several planetary systems. Shkolnik et al. (2003) present observational evidence for a hot spot in the chromosphere of one of these stars, HD 179949, which they attribute to magnetic interaction of the star with its close-in planet. Rubenstein & Schaefer (2000), who discuss superflares on single solar-like stars, suggest that these flares might occur due to a RS CVn binary-like interaction between star and planet.

Strong radiation events are also expected to occur on the planets. Farrell et al. (1999) and Zarka et al. (2001) expect strong radio emission due to the interaction of the stellar wind with planetary magnetospheres. It should be noted that so far the only observational hint of a planetary magnetic field is given by the observations of Shkolnik et al. (2003). Bastian et al. (2000) report on a search for radio emission which, however, was not successful. The possibility of success with state-of-the-art instrumentation is discussed by Rucker (2002).

Paetzold et al. (2004) also studied the influence of the gravitational interplay between star and planet on the rotational evolution of the planets, and Grießmeier et al. (2004) extend these effects to the possible magnetospheric configuration of OGLE-TR-56 b and HD 209458 b. Further, they discuss the possibility of atmospheric erosion due to the stellar wind during the evolution of these planets which is supported by Vidal-Madjar et al. (2004) who observed an escaping atmosphere for the planet HD 209458 b. The first results of modelling of the star-exoplanet magnetosphere interaction numerically with a magnetohydrodynamical description are presented by Ip et al. (2004).

Table 1: Planetary parameters as given by J. Schneider (http://www.obspm.fr/encycl/catalog.html). Listed (in units of Jupiter's mass and radius) are the projected planetary mass, the planetary mass and radius if determined by observation. The orbital semi-major axis and eccentricity are given as well as the inclination. These are followed by the calculated distances in AU and stellar radii. The last column gives the orbital period.

All these models have in common that at some point they need information about the structure of the stellar wind either at the planetary orbit or in between. Up to now, there are no observations available of winds for the stars in question, so that alternative approaches have to be used. Grießmeier et al. (2004) for example use densities and velocities of the solar wind at 1 AU which are well determined due to a long history of measurements. They adopt these as quantities at the planetary orbits and derive changes due to the evolution of the star on the basis of indirect observations of stellar winds from Wood et al. (2002).

In this paper, we attempt to fill this gap using the wind model derived by Weber & Davis (1967). In order to estimate velocities and densities for a range of stellar parameters, some are taken directly from observations while others are varied within intervals as they are less well known. In Sect. 2, we discuss the well-known parameters of the planets and stars of interest. We then introduce the Weber & Davis model with its limits in Sect. 3.1 and discuss the model winds and the influence of magnetic field and stellar rotation period on the stellar wind velocity in Sect. 3.2. With the results from Sect. 3 the stand-off distances and energy deposition onto the magnetospheres are estimated in Sect. 4 before we conclude our study in Sect. 5.

Table 2: Stellar parameters taken from Allende Prieto & Lambert (1999). The first column gives the name of the planet followed by the stellar HD and HIP numbers. The other columns list the apparent visual magnitude, the parallax, the absolute magnitude, the colour B-V and the stellar mass, radius, bolometric correction and effective temperature. The rms errors are given below the parameter values except for the radius. Note that Allende Prieto & Lambert (1999) originally gave the radius as $\log R$. Hence, the error stated below the calculated radius is the maximum deviation of the calculated value obtained by applying the rms error to the $\log R$ value.

  
2 Planetary and stellar parameters

In order to make our derivations as realistic as possible, we use estimates from typical upper and lower limits of the required input parameters based on the diverse observed quantities.

At the beginning of 2004, 120 extrasolar planets in 105 stellar systems, of which 13 are multiple planetary systems, were listed in J. Schneider's web-page (http://www.obspm.fr/encycl/catalog.html). From radial velocity measurements, which is currently the most potent observation method, the semi-major axis a, the orbital period  $P_{\rm {orb}}$, the eccentricity e and the projected mass $M\sin i$, where i is the angle of inclination of the planetary orbit with respect to the observer, are available for all planets. The two planets HD 209458 b and OGLE-TR-56 b were also observed in transits across the stellar disk. Since this method allows one to determine the planetary radius, they are the only planets for which radii $R_{\rm p}$ and orbital inclinations and thus the planetary masses $M_{\rm p}$ are known from observations.

Almost all stars hosting extrasolar planets are listed in the Hipparcos Catalogue and approx. 80% are contained in the "Catalogue of Fundamental Parameters of Stars'' compiled by Allende Prieto & Lambert (1999) hereafter called APL. The latter derive basic stellar parameters such as stellar mass $M_\star$ and radius $R_\star$ by isochrone interpolation on the basis of the Hipparcos Catalogue. For stars with metallicities within 0.4 and 2.5 times the solar metallicity  $(-0.4<[{\rm Fe/H}]<0.4)$ they achieve an overall accuracy within $\sim$6% for the stellar radii and 8% for the masses. On the basis of these stellar radii, the condition that the star-planet distance d=a(1+e) is less than 10 $R_\star$ yields a subset of 12 planets. Table 1 summarises the planetary parameters $M\sin i$ and $M_{\rm p}$ in Jupiter masses $M_{\rm J}$, $R_{\rm p}$ in Jupiter radii $R_{\rm J}$, a, e, i and  $P_{\rm {orb}}$(rounded) as given by Schneider. Our computed distances d in AU and $R_\star$ are listed as well. OGLE-TR-56 was not surveyed by Hipparcos and is not contained in APL. Hence, the stellar mass and radius are taken from Konacki et al. (2003).

The condition of d<10 $R_\star$ puts a limit on the star-planet distance of 0.06 AU. Thus, BD-103166 is added to the list for completeness although it is neither included in the Hipparcos catalogue, nor is its radius specified in Butler et al. (2000) due to the parallax being unknown.

The stellar parameters, as given by APL are shown in Table 2. The first column gives for each planet the name of the planet in the first line, the stellar designation in the Henry Draper Catalogue (HD number) in the second line and the Hipparcos Catalogue (HIP number) in the third line. The apparent visual magnitude  $V{\rm mag}$, the parallax plx, the absolute magnitude  $V{\rm MAG}$, the B-V colour as well as the mass, the radius (calculated from the $\log R_\star$ values given in the catalogue), the bolometric correction BC and the effective temperature are given in the columns. The rms errors are printed below the parameter values except for the radius, for which the deviation of $R_\star$ obtained by applying the rms error to the $\log R_\star$ value of Allende Prieto & Lambert (1999) is given.

APL offer the most coherent set of stellar data for the 13 stars of interest. For comparison, Table 3 lists the stellar masses, radii, ages and rotation periods  $P_{\rm {rot}}$ as given by the authors listed beneath the table. The parameter columns give the minimum and maximum values. Each column is followed by a list of the individual references, sorted in ascending order according to the parameter value they provide. Laws et al. (2003) and Barnes (2001) derive the age with two different approaches each. If these differ within the paper, they are referred to twice in ascending order of the parameter value.

Table 3: Summarized stellar parameters taken from the references listed below. The columns show the lower and upper limits of the stellar masses, radii, ages and rotation periods. Each column is followed by a column listing the references, which are sorted in ascending order according to the parameter value the authors give.

  
3 Model stellar wind regimes

A basic hydrodynamic description of the plasma environment of the extrasolar planets must assume the mass m of the relevant particle species, their number density n or mass density $\rho=nm$, their temperature T and flow velocity $\vec v$. For a magnetohydrodynamic model we need the magnetic flux density $\vec B$. Which of these parameters can be estimated depends on the chosen model and on the availability of the input parameters.

A simple hydrodynamic approach for a non-rotating and unmagnetised star was first derived by Parker (1958). Weber & Davis (1967) added rotation and a magnetic field to approach a self-consistent magnetohydrodynamic stellar wind description. As the latter yields the Parker model in the limit of no rotation and no magnetic field, we restrict ourselves to the Weber & Davis model while discussing how both models are related.

  
3.1 Magnetised wind of a rotating star

Since the temperature variations in the stellar coronae are unknown, the coronae are assumed to be isothermal. The plasma is taken to be quasineutral, i.e. $n_{\rm e}=n_{\rm p}=n$, were $n_{\rm e}$ and $n_{\rm p}$ are the electron and proton number densities, respectively. Hence the pressure p is given by

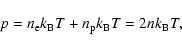\begin{displaymath}% p=n_{\rm e}k_{\rm B}T+n_{\rm p}k_{\rm B}T=2nk_{\rm B}T, \end{displaymath} (1)

where $k_{\rm B}$ is the Boltzmann constant and T the constant temperature. Generally, we restrict ourselves to the equatorial plane $\vartheta=\pi/2$ of a spherical coordinate system $r,\vartheta,\varphi$. Thus velocity and magnetic field have radial and azimuthal components

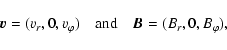\begin{displaymath}% {\vec v}=(v_r,0,v_{\varphi}) \quad {\rm and}\quad {\vec B}=(B_r,0,B_{\varphi}), \end{displaymath} (2)

which due to rotational symmetry depend only on the radial distance. Following Lamers & Cassinelli (1999, Chap. 9) the radial momentum equation is given by
 
$\displaystyle % \frac{r}{v_r}\left(\underbrace{v_r^2-v_{{\rm c}}^2}_1- \underbr... ..._1 +\underbrace{v_\varphi^2+2\frac{A_rA_\varphi v_r v_\varphi}{v_r^2-A_r^2}}_2,$     (3)

where

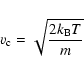\begin{displaymath}% v_{{\rm c}}=\sqrt{\frac{2k_{\rm B}T}{m}} \end{displaymath} (4)

is the thermal velocity, $M_\star$ the stellar mass and G the gravitational constant. Ar and $A_\varphi$ are the radial and azimuthal components of the Alfvén velocity

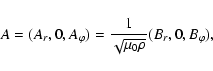\begin{displaymath}% A=(A_r,0,A_{\varphi})=\frac{1}{\sqrt{\mu_0 \rho}}(B_r,0,B_{\varphi}), \end{displaymath} (5)

where $\mu_0$ is the magnetic field constant.

For a non-rotating star without a magnetic field the components (2) in Eq. (3) vanish and the equation is equal to Parker's solar wind solution for a purely hydrodynamical expansion (Parker 1958). For rotating stars without magnetic fields the dynamics have been studied previously by e.g. Weidelt (1973) and Mufson & Liszt (1975). If the centrifugal forces due to an increased stellar rotation and magnetic field dominate term (1), Eq. (3) will turn into the fast magnetic rotator approximation as described by Belcher & MacGregor (1976).

Due to solenoidality the magnetic flux is

 \begin{displaymath}% F_{\rm B} = r^2B_r= {\rm const.} \end{displaymath} (6)

Integration of Eq. (3) yields

 \begin{displaymath}% v_r^2+v_{\varphi}^2-2v_{\rm c}^2\ln\left(\frac{v_r}{A_r}\ri... ...+2\frac{\Omega r}{\mu_0}\frac{F_B}{F_m}B_{\varphi}+C_{\rm WD}, \end{displaymath} (7)

where $v_{\varphi}$ and $B_\varphi $ are given by

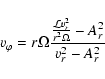\begin{displaymath}% v_{\varphi}=r\Omega \frac{\frac{\mathcal{L}v_r^2}{r^2\Omega}-A_r^2}{v_r^2-A_r^2} \end{displaymath} (8)

and

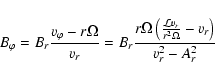\begin{displaymath}% B_{\varphi}=B_r\frac{v_{\varphi}-r\Omega}{v_r}=B_r\frac{r\O... ...left(\frac{\mathcal{L}v_r}{r^2\Omega}-v_r\right)}{v_r^2-A_r^2} \end{displaymath} (9)

respectively, with $\mathcal{L}=r_{\rm A}^2\Omega$ being the constant angular momentum per unit mass. This implies that the wind behaves as if corotating with the star out to the Alfvén point $r_{\rm A}$. $C_{\rm {WD}}$ is the integration constant.

If the fluid reaches radial Alfvén velocity Ar, the corresponding position will be called the Alfvén point $r_{\rm A}$. If the wind velocity equals the slow or fast magnetosonic wave speed, the bracket in Eq. (3) will vanish. This defines the two critical points, the slow and fast magnetosonic points $r_{\rm s}$ and $r_{\rm f}$, which are necessary for the existence of a stellar wind solution as e.g. shown by Goldreich & Julian (1970). They are defined as the radial distances at which the wind reaches the phase velocity of the slow magnetosonic wave

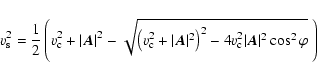\begin{displaymath}% v_{\rm s}^2=\frac{1}{2}\left(v_{\rm c}^2+\vert\vec{A}\vert^... ...right)^2-4v_{\rm c}^2\vert\vec{A}\vert^2\cos^2\varphi}~\right) \end{displaymath} (10)

and the velocity of the fast magnetosonic wave

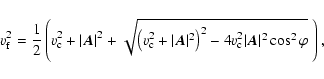\begin{displaymath}% v_{\rm f}^2=\frac{1}{2}\left(v_{\rm c}^2+\vert\vec{A}\vert^... ...ight)^2-4v_{\rm c}^2\vert\vec{A}\vert^2\cos^2\varphi}~\right), \end{displaymath} (11)

respectively. The constant $C_{\rm {WD}}$ is determined by the condition that the solution passes through both critical points for the same  $C_{\rm {WD}}$. This solution necessarily passes through the Alfvén point (Goldreich & Julian 1970).

For the calculation of the radial velocity profile, the Alfvén point $r_{\rm A}$ and velocity Ar have to be known a priori. As we are interested in the dependence of the wind parameters on changes of stellar parameters, we define the wind parameters at the base of the corona and search for the resulting Alfvén point $r_{\rm A}$ and Alfvén velocity Ar. For this we define

    $\displaystyle \mathcal{U} = \frac{GM_{\star}}{r_{\rm A}A_r^2},$ (12)
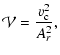    $\displaystyle \mathcal{V} = \frac{v_{\rm c}^2}{A_r^2},$ (13)
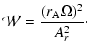    $\displaystyle \mathcal{W} = \frac{(r_{\rm A}\Omega)^2}{A_r^2}\cdot$ (14)

Furthermore, we use the constant mass flux at the Alfvén point $r_{\rm A}$

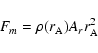\begin{displaymath}% F_m=\rho(r_{\rm A})A_rr_{\rm A}^2 \end{displaymath} (15)

and the constant magnetic flux

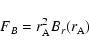\begin{displaymath}% F_B= r_{\rm A}^2B_r(r_{\rm A}) \end{displaymath} (16)

at the same location. Hence the Alfvén radius $r_{\rm A}$ can be eliminated and the parameters  $\mathcal{U}$ and  $\mathcal{V}$ can be expressed in terms of mass and magnetic fluxes as
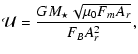    $\displaystyle \mathcal{U} = \frac{GM_{\star}\sqrt{\mu_0F_mA_r}}{F_BA_r^2},$ (17)
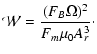    $\displaystyle \mathcal{W} = \frac{(F_B\Omega)^2}{F_m\mu_0A_r^3}\cdot$ (18)

We now vary $\mathcal{V}$ and solve for each $\mathcal{V}$ Eq. (3) for the critical points for which the constant of integration  $C_{\rm {WD}}$in Eq. (7) is then calculated. The correct solution for the parameters Fm, FB, $R_\star$, $M_\star$, T and $\Omega$ will be found if  $C_{\rm {WD}}$ is identical for both critical radii.

  
3.2 Model stellar winds

For all calculations we use the present day solar mass flux of $F_m=m\cdot6.3$ $\times $ 1034 s -1=1.05 $\times $ 108 kg s-1, with m the mass of the protons, following Mann et al. (1999). The density at the base of the corona thus varies according to the wind solution for the given parameters. Hence, increasing the rotation rate while keeping the temperature constant, the densities at the base of the corona are smaller when the wind speeds are higher. For the Sun the assumed mass flux is equivalent, with an averaged wind speed of 425 km s-1 at 1 AU. Combining this with the solar equatorial rotation period of 25.5 d and a radial magnetic field density of $\sim$3.1 nT at 1 AU, the corresponding Weber & Davis solution is found for a temperature of 0.8132 $\times $ 106 K and a magnetic field strength of 1.435 $\times $ 10-4 T at the base of the corona with $r_{\rm A}=0.08$ AU ($\approx$ $18~R_{\odot}$). Keeping these values fixed, we calculate the solution for the set of stars given in Table 3 for rotation periods of 3 and 30 d. The results for both rotation periods are presented as functions of the distance from the star in Fig. 1. The hatched curve indicates the ranges over which the radial velocity profiles vary. The locations of the planets are indicated by the dotted rectangle that extends along the whole y-axis. The other two rectangles indicate the locations of the Alfvén points (dark) and fast magnetosonic points (light), while their extension along the y-axis shows the range of the corresponding velocities. The overlap is due to the different stellar parameters. In the solutions the critical points are clearly distinguishable. For $P_{\rm {rot}}=3$ d the slow magnetosonic points are located between 0.0239 and 0.0314 AU with critical velocities of 110 to 112 km s-1 and for $P_{\rm {rot}}=30$ d the critical velocity of 116 km s-1 is reached between 0.0296 and 0.0449 AU. Two specific velocity profiles are given for $\upsilon $ And (thick line) and for HD 46375 (dash-dotted line). At 1 AU velocities between 406 and 431 km s-1 (Sun 425 km s-1) are reached for $P_{\rm {rot}}=30$ d and 501 and 594 km s-1 (Sun 501 km s-1) for $P_{\rm {rot}}=3$ d, respectively. For slow rotation rates the fastest wind is reached by the smallest and lightest star in terms of radius and mass, currently HD 46375, whereas the fastest by the largest and heaviest, currently $\upsilon $ And. For high rotation rates this is still valid at the location of the planets but further out, the situation changes. The fastest wind at 1 AU is now obtained for the largest star, and the slowest wind does not belong to the smallest and lightest but to the heavier one with the same radius, currently HD 83443.


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{1680fig1.eps}\hspace*{4mm} \includegraphics[width=8.3cm,clip]{1680fig2.eps}\end{figure} Figure 1: Stellar wind velocities obtained with the Weber & Davis model for the stars given in Table 3. The hatched curves indicate the velocity ranges over which the solutions vary for $P_{\rm {rot}}=30$ d ( left panel) and $P_{\rm {rot}}=3$ d ( right panel). The planets are located within the dotted rectangle. The Alfvén points lie within the dark grey rectangle and the fast magnetosonic point within the light grey one. The sizes of the rectangles are defined by the location and velocity ranges. The locations of the slow magnetosonic points are given in the text.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{1680fig3.eps}\hspace*{4mm} \includegraphics[width=8.3cm,clip]{1680fig4.eps}\end{figure} Figure 2: Radial velocity profiles for $\upsilon $ And and HD 46375 calculated with the Weber & Davis model. The results are compared with the Parker limits for all stars listed in Table 3 which are indicated by the dotted patches. The left panel shows the changes due to inclusion of a rotation period of 30 d and the right one for 3 d. Again, the upper velocity profiles belong to T=2.0 $\times $ 106 K and and the lower to T=0.5 $\times $ 106 K. The magnetic field at the base of the corona was set to 1 $\times $ 10-4 T (dots) and 10 $\times $ 10-4 T (triangles). For slow rotation, hardly any differences at all are observed with respect to the Parker limit solutions. For the faster rotation, the velocity changes significantly. These changes are larger for the lower temperature as well as for the star with the bigger mass and radius ($\upsilon $ And) which yields the slower velocity. The grey patch indicates the spatial distribution of the planetary orbits.
Open with DEXTER

In order to study the influence of magnetic field strength and coronal temperature on the stellar wind velocities, the magnetic flux FB is varied at the base of the corona, where we assume a magnetic flux density B0 of 1 to 10 $\times $ 10-4 T. The low value of 1 $\times $ 10-4 T is obtained from $F_B={\rm const.}$ with $B_r\sim 3.1$ nT at 1 AU, which was measured e.g. by Ulysses (see Banaszkiewicz et al. 1998). 10 $\times $ 10-4 T is an approximate mean value for the field strength at the base of the solar corona in a coronal hole, following Banaszkiewicz et al. (1998), who used an analytic model for the coronal magnetic field of the Sun. The difference between both values results from the additional expansion of magnetic flux tubes emanating from the coronal hole and then expanding into the equatorial plane.

In Fig. 2 we show the solutions for $P_{\rm {rot}}=30$ d (left panel) and 3 d (right panel) obtained with the Weber & Davis model for T=0.5 $\times $ 106 K and 2.0 $\times $ 106 K in comparison to the velocity profiles obtained in the Parker limit. The lower curves belong to the cool corona, the upper to the hot one. The magnetic field at the base of the corona was set to 1 $\times $ 10-4 T (dots) and 10 $\times $ 10-4 T (triangles). For the long rotation period, the Weber & Davis velocity profiles are almost equal to those calculated with the Parker model. The increase of rotation to 3 d shows a strong effect on the velocity profile while the influence of the magnetic field on the velocity becomes apparent. The velocity changes are larger for $\upsilon $ And, whose radius is larger than that of HD 46375 and which is the star with the slowest wind in the Parker limit. The locations of all planets of interest are indicated by the grey patch.

As we have calculated the velocity profiles for parameters which are specified either at the stellar surface (T, B0, $P_{\rm {rot}}$) or at 1 AU (Fm), we obtain the critical points as functions of these parameters and hence the Alfvén points $r_{\rm A}$ as functions of these parameters as well. In Table 4 the different locations of the Alfvén points $r_{\rm A}$ in AU, the corresponding Alfvén velocities Ar and the radial velocities  $v_{r,{\rm 1~AU}}$ reached at 1 AU in km s-1 are listed with respect to the parameters T=[0.5,2.0] $\times $ 106 K, B0=[1,10] $\times $ 10-4 K and $P_{{\rm rot}}=[3,30]$ d for the two stars HD 46375 and $\upsilon $ And. The values should be considered relative to the planetary locations, which are 0.041 AU and 0.0597 AU for HD 46375 b and $\upsilon $ And b, respectively. We can see that both planets are located within the Alfvén radius for all stellar winds that were modelled for their central stars. The velocities at 1 AU $v_{r,{\rm 1~AU}}$ should be compared to the velocities that are obtained in the Parker limit. The latter yields 310 to 313 km s-1 for T=0.5 $\times $ 106 K and 759 to 764 km s-1 for T=2.0 $\times $ 106 K.

Table 4: Alfvén radii $r_{\rm A}$ and velocities Ar obtained with the Weber & Davis model for the two stars HD 46375 and $\upsilon $ And. The stellar winds were modeled for different magnetic field strengths B0at the coronal base, rotation periods  $P_{\rm {rot}}$ and coronal temperatures T as given in the table. In addition, the wind velocities at 1 AU $v_{r,{\rm 1~AU}}$ are given.

The Alfvén Mach numbers $M_{\rm A}$, i.e. the ratios of the radial velocities vr at the planetary location to the radial Alfvén velocities Ar at the same location, are listed in Table 5 for both planets and the same parameters as above. They are complemented by two additional Alfvén Mach numbers, which were obtained relative to the planetary movements around their stars. Such the planets effectively see the wind moving with the relative velocity of their own movement with respect to the expanding stellar corona. We thus define an effective velocity  $v_{\rm {eff}}$, where

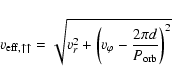\begin{displaymath}% v_{\rm {eff},\uparrow\uparrow}=\sqrt{v_r^2+\left(v_{\varphi}-\frac{2\pi d}{P_{\rm {orb}}}\right)^2} \end{displaymath} (19)

is the effective velocity at the parallel direction of planetary movement and stellar rotation and

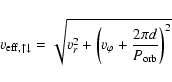\begin{displaymath}% v_{\rm {eff},\uparrow\downarrow}=\sqrt{v_r^2+\left(v_{\varphi}+\frac{2\pi d}{P_{\rm {orb}}}\right)^2} \end{displaymath} (20)

for antiparallel movement. The values for the planetary orbital period  $P_{\rm {orb}}$ are taken from Table 1. The results are listed in Table 5 in terms of the Mach numbers $M_{\rm A\uparrow\uparrow}$ and $M_{\rm A\uparrow\downarrow}$. For the parallel movement the effective velocity does not change the Mach numbers significantly except for the case of 30 d stellar rotation, where the planetary orbital velocity is large with respect to the azimuthal velocity component $v_{\varphi}$ of the stellar wind and the radial Alfvén velocity Ar of the wind is small, as is the case especially for the cool wind. For the antiparallel movement the Mach number may change from values less than one to about one.

Table 5: Alfvén Mach numbers $M_{\rm A}=v_r/A_r$ at the locations of HD 46375 b and $\upsilon $ And b for parallel and antiparallel directions of stellar rotation and planetary movement. The values were derived for different magnetic field strengths B0 at the coronal base as well as different stellar rotation periods  $P_{\rm {rot}}$ and coronal temperatures T as given in the table.

Figure 3 shows the absolute values of the magnetic field components obtained with the Weber & Davis model for $\upsilon $ And with T=2.0 $\times $ 106 K and B0=10 $\times $ 10-4 T for the two rotation periods. The magnetic field is scaled logarithmically. The radial components are identical as they are independent of the rotation period and are plotted as solid line. For the azimuthal component the dashed line is used for a rotation period of 30 d and the dash-dotted for 3 d. The vertical dotted line marks the location of the planet.


  \begin{figure} \par\includegraphics[width=8cm,clip]{1680fig5.eps}\end{figure} Figure 3: Absolute magnetic field components obtained with the Weber & Davis model for $\upsilon $ And with T=2.0 $\times $ 106 K and B0=10 $\times $ 10-4 T for different rotation periods. The radial component is plotted with a solid line and is independent of the rotation period. The dashed and the dash-dotted lines represent the azimuthal component for a rotation period of $P_{\rm {rot}}=30$ d and $P_{\rm {rot}}=3$ d respectively. The location of the planet is indicated by the dotted vertical line.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{1680fig6.eps}\end{figure} Figure 4: Components of stellar wind pressure for $\upsilon $ And with temperature of 2.0 $\times $ 106 K on the basis of the Weber & Davis model. The solid line is the dynamic flow pressure splitting at slightly higher values for $P_{\rm {rot}}=3$ d and B0=10 $\times $ 10-4 T. The lines present the magnetic pressure for B0=10 $\times $ 10-4 T and the symbols for B0=1 $\times $ 10-4 T. The rotation period of 30 d is shown with a dotted line and circles and the rotation period of 3 d as dashed line and triangles. The vertical line marks the location of the planet.
Open with DEXTER

The role of the magnetic field can be assessed by comparing the magnetic pressure and the dynamic flow pressure. The dynamic flow pressure $p_{\rm {d,sw}}$ can be expressed by $p_{\rm {d,sw}}=\rho v^2$, where the mass density $\rho$ at the planetary orbit is again estimated with Fm=1.05 $\times $ 108 kg s-1. The magnetic pressure  $p_{B\rm {,sw}}$ of the stellar wind is given by

 \begin{displaymath}% p_{B\rm {,sw}}=\frac{{{\vec B}_{\rm {sw}}}^2}{2\mu_0}=\frac{B_r^2+B_{\varphi}^2}{2\mu_0}\cdot \end{displaymath} (21)

In Fig. 4 the results for $\upsilon $ And with T=2.0 $\times $ 106 K, B0=1 $\times $ 10-4 T and 10 $\times $ 10-4 T and the rotation periods of 3 and 30 d on the basis of the Weber & Davis model are presented. The solid line is the dynamic flow pressure. The line splits at higher pressures for a rotation period of 3 d and B0=10 $\times $ 10-4 T yielding a wind about twice as fast at a distance of 1 AU compared to the winds obtained with the other parameters. The lines are used for a magnetic field at the base of the corona of 10 $\times $ 10-4 T and the symbols for B0=1 $\times $ 10-4 T. The rotation period of 30 d is shown as circles and the dotted line. For the rotation period of 3 d triangles and a dashed line are used. The vertical dotted line marks the location of the planet.

These results indicate that even for weak magnetic fields the magnetic pressure may be comparable to or even higher than the dynamic flow pressure at the planetary location. This should be taken into account if the interaction of the stellar wind with the planet is considered.

  
4 Estimation of the Poynting flux in the planetary magnetospheres

In order to estimate the energetics of a possible interaction between stellar wind and planet, we first derive an estimate for the magnetospheric stand-off distance as a characteristic length describing the size of the magnetosphere.

The location of the stand-off distance Rm of the planetary magnetosphere is defined by the pressure balance between dynamic flow and magnetic pressure  $p_{\rm {d,sw}}$ and  $p_{B\rm {,sw}}$ of the stellar wind and the magnetic pressure due to the planetary magnetic field  ${{\vec B}_{\rm p}}$ and the magnetic field component  ${{\vec B}_{\rm {mc}}}$, which is induced by magnetopause currents

 \begin{displaymath}% p_{\rm {d,sw}}+p_{B\rm {,sw}}=\frac{1}{2\mu_0}\left({{\vec B}_{\rm p}}+ {{\vec B}_{\rm {mc}}}\right)^2, \end{displaymath} (22)

where we follow Grießmeier et al. (2004) for the atmosphereless magnetosphere but consider the magnetic pressure of the stellar wind. Thus, since the planet lacks an atmosphere, the planetary plasma pressure is not taken into account in Eq. (22). Grießmeier et al. (2004) argue that a description of  ${{\vec B}_{\rm {mc}}}$ with spherical harmonics at the substellar point can be approximated with the planetary magnetic field. Hence, they find

 \begin{displaymath}% {{\vec B}_{\rm p}}+{{\vec B}_{\rm {mc}}}= 2 f_0 {{\vec B}_{\rm p}}, \end{displaymath} (23)

where ${{\vec B}_{\rm p}}$ is the dipolar magnetic field of the planet. f0 is a form factor describing the shape of the magnetosphere. Contrary to Grießmeier et al. (2004), who use f0=1.16 for a non-spherical magnetopause, we use f0=1.5 assuming a spherical magnetospheric shape. At the magnetopause the total value of the planetary magnetic field is given by

 \begin{displaymath}% {{\vec B}_{\rm p}}=\frac{\mu_0}{4\pi}\frac{{{\vec M}}}{R_m^3}, \end{displaymath} (24)

with ${\vec M}$ being the planetary magnetic dipole moment and Rm the stand-off distance. The planetary magnetic dipole moments ${\vec M}$ are calculated according to the scaling laws given in Eqs. (1) to (6) of Grießmeier et al. (2004) assuming in a first approximation that the planetary radius equals the radius of Jupiter.

Table 6: Results for $\upsilon $ And b and HD 46375 b obtained with the Weber & Davis model with coronal temperatures T, magnetic field strengths B0 and rotation periods $P_{\rm {rot}}$ as given as general parameters. For the two planets the radial and azimuthal velocity components  $(v_r,v_\varphi )$ and the azimuthal magnetic field components $B_\varphi $ at the location of the planets are listed. With these, the magnetospheric stand-off distances $R_{\rm m}$ and magnetic moments ${\vec M}$ were estimated, followed by the power P that can be deposited by the stellar wind into the magnetosphere. For comparison the stand-off distance and the power input into the magnetosphere for the same planet located at 1 AU are also given.

Inserting Eqs. (21), (24) and (23) into Eq. (22) yields

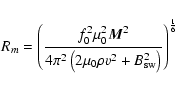\begin{displaymath}% R_m=\left(\frac{f_0^2\mu_0^2 {\vec M}^2}{4\pi^2\left(2\mu_0\rho v^2+B_{\rm {sw}}^2\right)}\right)^{\frac{1}{6}} \end{displaymath} (25)

for the stand-off distance.

Similar to Perreault & Akasofu (1978) and D'Angelo & Goertz (1979) we calculate the Poynting flux of the stellar wind by

 \begin{displaymath}% {\vec S}=\frac{1}{\mu_0}{\vec E}\times {\vec B}, \end{displaymath} (26)

where the frozen-in assumption yields the electric field ${\vec E}=-{\vec v}\times {\vec B}$. With ${\vec v}=(v_r,0,v_{\varphi})^T$ and ${\vec B}=(B_r,0,B_{\varphi})^T$ from the Weber & Davis model,

 \begin{displaymath}% S_r=\frac{1}{\mu_0}\left(v_rB_{\varphi}^2-v_{\varphi}B_rB_{\varphi}\right) \end{displaymath} (27)

follows from Eq. (26) for the radial component.

In order to estimate the energy flux through the cross section of the planetary magnetosphere given by $\pi R_m^2$, we assume that the stellar wind parameters obtained for the equatorial plane with the Weber & Davis model do not vary perpendicular to it. The multiplication of Poynting flux and magnetospheric cross section yields

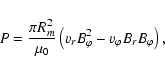\begin{displaymath}% P=\frac{\pi R_m^2}{\mu_0}\left(v_rB_{\varphi}^2-v_{\varphi}B_rB_{\varphi}\right), \end{displaymath} (28)

which is an upper limit for the power P that can be deposited by the stellar wind in the magnetosphere as the coherence with the relative orientation of the magnetic fields with respect to each other is neglected.

The detailed results for the planets $\upsilon $ And b and HD 46375 b are given in Table 6. At the top the model parameters such as temperature, magnetic field strength at the stellar surface and rotation period are given. Beneath, after the name of the planet, the specific parameters such as radial and azimuthal velocity components and the azimuthal magnetic field component are given at the location of the planet. These are followed by the planetary magnetic moments, for which we used the maximum value obtained as described above. They are given in  ${{\vec M}_{\rm J}}$, where the subscript J stands for Jupiter. With these, the stand-off distances are obtained, which were used for the estimation of the power that is deposited in the magnetosphere. Furthermore, the stand-off distance and the power are given for the same planet, but this time located at 1 AU. Due to the much higher velocities and lower densities, the stand-off distances are much larger. On the other hand, the magnetic field strengths decrease significantly, so that the upper limit of the power input is much smaller.

For the Earth's magnetosphere two processes are discernible in which the energy is dissipated, see e.g. Baker et al. (1986), Rostoker et al. (1987), Lu et al. (1998) and Sun et al. (1998). The first is characterised by direct ohmic or convective dissipation of energy in the ionosphere, the ring current and elsewhere. The second process is characterised by energy storage in the magnetotail (loading process) and its sudden dissipation during an unloading process. The time  $t_{{\rm load}}$ during which energy is stored in the magnetotail is typically $\sim$1 h before it is dissipated in the ionosphere and the ring current. Comparing the results obtained for the same planet at its true orbit and at an assumed Earth-like orbit of 1 AU two to three orders of magnitude are gained with respect to the energy input. Hence, radiation events due to energy dissipation may be much more intense than known from the Earth.

   
5 Conclusions

We consider the stellar wind conditions for extrasolar planets closer to their star than 10 stellar radii. For these planets, we modelled the stellar wind parameters on the basis of the stellar wind model of Weber & Davis. Due to the lack of exact input parameters we consider limits, i.e. we vary the less well-known parameters within probable parameter ranges. The models suggest that the exoplanets at least for isothermal stellar coronae are most probably not located in the quasi asymptotic wind velocity regime outside the fast magnetosonic point typical for solar system planets. Thus, compared to the solar system and the solar wind at 1 AU, the radial velocity of the stellar winds may be much lower and therefore, the densities of the stellar winds may be much higher then the solar wind at the Earth's orbit.

For slowly rotating stars the Weber & Davis model shows that the hydrodynamic Parker limit without rotation seems to yield a good first approximation for the slow rotating stars representing the majority of stars among the sample with planets within 10 $R_\star$. In this limit, the magnetic field does not introduce an additional acceleration of the stellar wind. However, the radial velocity is changed significantly if the stellar rotation period is decreased from 30 to 3 d due to the coupling of velocity and magnetic field.

As a major result, the magnetohydrodynamic approach suggests that the close-in extrasolar planets observed so far may lie within the Alfvén critical radius. Hence, the stellar wind velocities at the planetary orbit may be sub-Alfvénic and the winds behave as if corotating with the star. In such a case, the expansion speed of the corona is smaller than the local Alfvén speed in any place between the planet and the star. Because of this, information about the planet can be carried back to the star with Alfvén waves possibly allowing for a "magnetic communication'' between star and planet. Furthermore, the magnetic pressure may not be neglected in the estimation of the size of the magnetosphere and no bow shocks are formed. In the solar system, Io embedded within the magnetosphere of Jupiter is situated in a similar plasma regime. The resulting Io-Jupiter interaction with Alfvén waves is discussed e.g. by Neubauer (1980). It may be a speculative scenario for the observed chromospheric activity on HD 179949 by Shkolnik et al. (2003). The consequences of a sub-Alfvénic wind velocity on the interaction between stellar wind and possible planetary magnetospheres will be part of our future studies.

We estimated an upper limit for the energy flux deposited in the magnetospheres by the stellar wind for two planets at their true location and at a distance of 1 AU from their star. For the close-in planets the flux is two to three orders of magnitude higher than at the Earth-like orbital distance for the same stellar winds. Hence, we suggest that much more energy will be available for dissipation processes as e.g. aurorae. As these processes will probably depend on the specific shape of the planetary magnetospheres this question is strongly linked to our future studies mentioned above.

We expect the stellar wind regime to differ significantly from what is observed for planets in the solar system at the orbit of close-in extrasolar planets. The possibly sub-Alfvénic velocity regime raises questions about the interaction of the stellar wind with the planet and its influence on the planetary magnetosphere and magnetospheric energetics.

Acknowledgements
The authors acknowledge the fellowship of S. Preusse from the International Max Planck Research School on Physical Processes in the Solar System and Beyond of the Max Planck Society and at the Universities of Braunschweig and Göttingen. We further thank E. Marsch and J.-M. Grießmeier for inspiring discussions and the referee for clarifying and helpful comments.

References

 
Copyright ESO 2005