R. Vio1,2 - J. Nagy3 - W. Wamsteker4
1 - Chip Computers Consulting s.r.l., Viale Don L. Sturzo 82,
S.Liberale di Marcon, 30020 Venice, Italy
2 -
ESA-VILSPA, Apartado 50727, 28080 Madrid, Spain
3 -
Department of Mathematics and Computer Science, Emory University,
Atlanta, GA 30322, USA
4 -
ESA-VILSPA, Apartado 50727, 28080 Madrid, Spain
Received 27 November 2003 / Accepted 3 January 2005
Abstract
We generalize a reliable and efficient algorithm, to deal with
the case of spatially-variant PSFs. The algorithm was developed in the
context of a least-square (LS) approach, to estimate the image corresponding
to a given object when a set of observed images are available with
different and spatially-invariant PSFs. Noise is assumed additive and
Gaussian. The proposed algorithm allows the use of the classical LS single-image deblurring techniques
for the simultaneous deblurring of the observed images, with obvious advantages both for computational
cost and ease of implementation. Its performance and limitations, also in the case of Poissonian noise, are
analyzed through numerical simulations. In an appendix we also present
a novel, computationally efficient deblurring algorithm
that is based on a Singular Value Decomposition (SVD) approximation of the variant PSF,
and which is usable with any standard space-invariant direct deblurring algorithm.
The corresponding Matlab code is made available.
Key words: methods: data analysis - methods: statistical - techniques: image processing
Vio et al. (2004) presented a computationally efficient solution for the problem of simultaneous deblurring of a set of observed images (of a fixed object), where each observed image is degraded by a different spatially-invariant point spread function (PSF) and the noise is additive and Gaussian. The most serious limitation of the other techniques available in the literature is the use of algorithms that work cyclically on one image at a time (see Bertero & Boccacci 2000). For this reason they are computationally expensive and demanding of computer memory. The main idea of Vio et al. (2004) is to combine the observed images in a single one containing all the relevant information. In this way, apart from the obvious benefit concerning the memory requirements, it is possible to improve the convergence rate of Least-Squares (LS) iterative algorithms. Moreover, there is the additional benefit that standard algorithms (and software) for image restoration can be used.
There are important fields where potentially this methodology can be exploited. An example is the multi-frequency observations of the Cosmic Microwave Background (CMB) obtained from satellites such as PLANCK. Although some other physical components are present at the microwave frequencies, the images taken at high galactic latitudes are expected to be almost entirely dominated by the CMB contribution over a large range of observing frequencies (e.g., see Stolyarov et al. 2002). Since the PSFs corresponding to the images obtained at the various frequencies can be quite dissimilar, simultaneous deblurring can be useful to improve the extraction of CMB information from the data. Unfortunately, since the PSF of PLANCK's instruments is expected to be non-circular and, because of the observational strategy, to rotate during the observations (Burigana & Saez 2003; Arnau et al. 2002), the computational advantages provided by the methodology of Vio et al. (2004) cannot be exploited.
A similar situation can also hold for the restoration of images that will be obtained by the
Large Binocular Telescope (LBT). This instrument consists of two
![]() mirrors on a
common mount with a spacing of
mirrors on a
common mount with a spacing of
![]() between the centers
(Angel et al. 1998). For a given orientation of the telescope, the
diffraction-limited resolution along the center-to-center baseline is
equivalent to that of a
between the centers
(Angel et al. 1998). For a given orientation of the telescope, the
diffraction-limited resolution along the center-to-center baseline is
equivalent to that of a
![]() mirror, while the resolution
along the perpendicular direction is that of a single
mirror, while the resolution
along the perpendicular direction is that of a single ![]() mirror. A possible way to obtain an image with an improved and uniform
spatial resolution is to simultaneously deconvolve the images taken
with different orientations of the telescope. However, because of the
different corrections of the adaptive optics across the image domain,
the PSF for LBT can be space-variant (Carbillet et al. 2002; Bertero & Boccacci 2000).
mirror. A possible way to obtain an image with an improved and uniform
spatial resolution is to simultaneously deconvolve the images taken
with different orientations of the telescope. However, because of the
different corrections of the adaptive optics across the image domain,
the PSF for LBT can be space-variant (Carbillet et al. 2002; Bertero & Boccacci 2000).
To our knowledge, multiple-image deblurring in the case of a spatially-variant PSF has not been considered in the current literature. Given that the single-image technique undoubtedly offers some important benefits, in the present paper we extend it to deal with the case of PSFs that change across the images. In particular, in Sect. 2 we formalize the problem and propose an efficient solution in Sect. 3. In Sect. 4 its performance is studied through numerical experiments. In Sect. 5 we close with final comments and conclusions.
Suppose one has p observed images, gj(x,y),
![]() ,
,
![]() ,
of a fixed two-dimensional object f0(x,y), each of which is
degraded by a different blurring operator.
In the case of a generic blurring operator, gj(x,y) can
be modeled as
,
of a fixed two-dimensional object f0(x,y), each of which is
degraded by a different blurring operator.
In the case of a generic blurring operator, gj(x,y) can
be modeled as
In practice, the experimental images are discrete
![]() arrays
of pixels (for simplicity, we assume square images) contaminated by noise. Therefore
model (1) has to be recast in the form
arrays
of pixels (for simplicity, we assume square images) contaminated by noise. Therefore
model (1) has to be recast in the form
In the case of a spatially-invariant PSF, with a support much smaller than the image,
model (2) can be well approximated by a cyclic convolution
The classical unbiased LS estimate given by the inverse DFT of
In order to avoid this problem, Vio et al. (2004) proposed to use the normal
Eq. (8) in the form
![\begin{displaymath}\widehat K_{j_0}(m,n) = \max [ \widehat K_1(m,n), \widehat K_2(m,n), \ldots, \widehat K_p(m,n) ].
\end{displaymath}](/articles/aa/full/2005/17/aa0754/img44.gif) |
(12) |
From Eq. (11) it is evident that the single-image
![]() is obtained
in the Fourier domain. From the computational point of view, this is quite advantageous since
it permits us to exploit fast implementations of the DFT.
However, in the case of spatially-variant PSFs
some problems arise because model (2) has no representation
in the Fourier domain.
Consequently, model (11) has to be modified in such a way to take
into account the changes of the PSF across the images. In the next section, a possible solution
is provided.
is obtained
in the Fourier domain. From the computational point of view, this is quite advantageous since
it permits us to exploit fast implementations of the DFT.
However, in the case of spatially-variant PSFs
some problems arise because model (2) has no representation
in the Fourier domain.
Consequently, model (11) has to be modified in such a way to take
into account the changes of the PSF across the images. In the next section, a possible solution
is provided.
If ![]() is an image,
is an image,
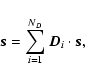 |
(13) |
| (14) |
![\begin{displaymath}\vec{\widehat{s}}= \textrm{DFT}\left[\sum_{i=1}^{N_D} \vec{D}...
...i \cdot \vec{s}\right] = \sum_{i=1}^{N_D} \vec{\widehat{s}}_i,
\end{displaymath}](/articles/aa/full/2005/17/aa0754/img53.gif) |
(15) |
The simplest form for Di(m,n) is obtained through piecewise
constant interpolation, when the permitted values are either 0 or 1. In this case, the non-zero entries constitute a partitioning of
the image domain. Although in many situations such a choice provides
satisfactory results, sometimes the resulting
![]() suffers from
blocking artifacts that are problematic for the deblurring
operation. A more sophisticated alternative, able to avoid this kind
of problem, is based on a linear interpolation approach (see Nagy & O'Leary 1998).
The basic idea is simpler to understand in the
one-dimensional case.
suffers from
blocking artifacts that are problematic for the deblurring
operation. A more sophisticated alternative, able to avoid this kind
of problem, is based on a linear interpolation approach (see Nagy & O'Leary 1998).
The basic idea is simpler to understand in the
one-dimensional case.
If a one-dimensional domain is partitioned into NDsubregions with dimension Ns, a useful set of overlapping masks,
with dimension
![]() ,
is shown in
Fig. 1. In fact, since they go smoothly to zero, the
boundary artifacts that affect each of the
,
is shown in
Fig. 1. In fact, since they go smoothly to zero, the
boundary artifacts that affect each of the
![]() are strongly
weakened. Moreover, the overlap works in such a way as to further reduce
these effects. The only exception is represented by the regions on the
border of the domain.
are strongly
weakened. Moreover, the overlap works in such a way as to further reduce
these effects. The only exception is represented by the regions on the
border of the domain.
In the two-dimensional case the argument is similar although made slightly more difficult by the larger number of masks that overlap at a given point of the image domain, and by the fact that there are two different situations for the subregions on the border of the frame. However, it is not difficult to see that, independent of the partitioning of the image domain, the resulting masks must have fixed values at the points marked in Fig. 1. Computationally, they can be obtained by interpolating these points through a bilinear interpolation (Press et al. 1992).
So far we have assumed that the noise level is the same in all of the images (
![]() ),
a condition that allows the combination of different images
to provide the most interesting results. Moreover, this requirement is often satisfied in practice.
The extension of the method to images with different noise levels is straightforward (Vio et al. 2004).
If the different
),
a condition that allows the combination of different images
to provide the most interesting results. Moreover, this requirement is often satisfied in practice.
The extension of the method to images with different noise levels is straightforward (Vio et al. 2004).
If the different
![]() are known, one may account for the different variabilities by
substituting Eq. (17) with
are known, one may account for the different variabilities by
substituting Eq. (17) with
A last question regards the images that present features close to their boundaries. This causes
the appearance of edge effects. In the present context, the situation is made more troublesome by the fact that
the masks Di(m,n) can overlap, thus causing a propagation of
artifacts to the central regions of
![]() .
For this reason, as explained in Vio et al. (2004) (see
also Von der Lühe 1993), before the calculation of
.
For this reason, as explained in Vio et al. (2004) (see
also Von der Lühe 1993), before the calculation of
![]() ,
all the images gj(m,n) should be windowed
through the matrix
,
all the images gj(m,n) should be windowed
through the matrix
We present results of some numerical experiments to show the
reliability and the good performance of the single-image approach for the multiple-image
deblurring in case of spatially-variant PSF. As claimed in the previous sections, in principle
the deblurring of the
image
![]() can be carried out by using any available algorithm
able to deal with PSFs that are not constant across the images. Here we use two particular
techniques. The first is based on an iterative method, which is a modified residual
norm steepest descent (MRNSD) method that minimizes a least
squares fit to data, using an exponential function reparameterization
to enforce a non-negativity constraint; see
Nagy & Strakos (2000) for details. The MRNSD method is
equivalent to an approach studied by Kaufman (1993), but the
numerical results reported here are obtained using the implementation
described by Nagy & Strakos (2000), which views the approach as a
preconditioned steepest descent method. In many respects
(such as computational cost per iteration)
MRNSD is similar to the Richardson-Lucy algorithm (Vogel 2002).
The difference between the two methods is that MRNSD is based
on a least squares criteria, where as Richardson-Lucy is
based on a maximum likelihood criteria. Furthermore,
MRNSD typically converges much more quickly than the
Richardson-Lucy method.
In either case, the main cost of the algorithm is
matrix vector multiplications at each iteration.
Efficient matrix
vector multiplications of the space variant PSF, using the sectioning
ideas given above, is described in Nagy & O'Leary (1998).
The second approach uses standard Tikhonov regularization (Vogel 2002),
efficiently implemented as a filtering-based method
(Vio et al. 2003a), using a novel
Singular Value Decomposition (SVD) approximation of the variant
PSF (see Appendix A). In this last case, the use of the
single-image
can be carried out by using any available algorithm
able to deal with PSFs that are not constant across the images. Here we use two particular
techniques. The first is based on an iterative method, which is a modified residual
norm steepest descent (MRNSD) method that minimizes a least
squares fit to data, using an exponential function reparameterization
to enforce a non-negativity constraint; see
Nagy & Strakos (2000) for details. The MRNSD method is
equivalent to an approach studied by Kaufman (1993), but the
numerical results reported here are obtained using the implementation
described by Nagy & Strakos (2000), which views the approach as a
preconditioned steepest descent method. In many respects
(such as computational cost per iteration)
MRNSD is similar to the Richardson-Lucy algorithm (Vogel 2002).
The difference between the two methods is that MRNSD is based
on a least squares criteria, where as Richardson-Lucy is
based on a maximum likelihood criteria. Furthermore,
MRNSD typically converges much more quickly than the
Richardson-Lucy method.
In either case, the main cost of the algorithm is
matrix vector multiplications at each iteration.
Efficient matrix
vector multiplications of the space variant PSF, using the sectioning
ideas given above, is described in Nagy & O'Leary (1998).
The second approach uses standard Tikhonov regularization (Vogel 2002),
efficiently implemented as a filtering-based method
(Vio et al. 2003a), using a novel
Singular Value Decomposition (SVD) approximation of the variant
PSF (see Appendix A). In this last case, the use of the
single-image
![]() has no effect on the efficiency of the
algorithm, but it makes coding the scheme much easier.
As is well known, direct methods are often
much more efficient than iterative methods. However, given the difficulty
concerning the incorporation of constraints on the solution (e.g., nonnegativity),
they have to be expected to provide results of inferior quality.
has no effect on the efficiency of the
algorithm, but it makes coding the scheme much easier.
As is well known, direct methods are often
much more efficient than iterative methods. However, given the difficulty
concerning the incorporation of constraints on the solution (e.g., nonnegativity),
they have to be expected to provide results of inferior quality.
For each experiment we use a set of eight images of
![]() pixels. Figure 2 shows the PSF corresponding
to a set of pixels uniformly distributed across the first image.
All the displayed PSFs are bidimensional Gaussian with dispersion along
the major axis set to twelve pixels, and to four pixels along the minor axis.
For the remaining pixels, the PSF is given by a bilinear interpolation
of the displayed pattern. The PSF of the other figures is obtained by rotating this PSF
by
pixels. Figure 2 shows the PSF corresponding
to a set of pixels uniformly distributed across the first image.
All the displayed PSFs are bidimensional Gaussian with dispersion along
the major axis set to twelve pixels, and to four pixels along the minor axis.
For the remaining pixels, the PSF is given by a bilinear interpolation
of the displayed pattern. The PSF of the other figures is obtained by rotating this PSF
by
![]() degrees, respectively. The
non-stationary pattern of the PSF has been deliberately chosen
quite peculiar in order to test the capabilities of the algorithm in
extreme situations. The images
degrees, respectively. The
non-stationary pattern of the PSF has been deliberately chosen
quite peculiar in order to test the capabilities of the algorithm in
extreme situations. The images ![]() have been obtained by the
direct computation of the discrete model (2).
have been obtained by the
direct computation of the discrete model (2).
Figures 3 and 4 show the
deblurring results for a set of 169 identical point-like objects
uniformly distributed across the image. Noise is additive and
Gaussian with a standard deviation of ![]() of the maximum value of
the blurred images. We have chosen these particular examples since,
the sources being of non-smooth functions, deblurring is a difficult
problem. The image
of the maximum value of
the blurred images. We have chosen these particular examples since,
the sources being of non-smooth functions, deblurring is a difficult
problem. The image
![]() has been calculated by
partitioning the observed images in 25 square subregions
(i.e., ND=25), and by using piecewise constant interpolation
for Di(m,n). For comparison, the deblurring of the first image of the set
(that with the PSF shown in Fig. 2) is also
presented; an MRNSD algorithm for spatially-invariant PSF has been used.
In each case the improvement due to the use of the eight
images is evident. The superiority of the results provided by the
MRNSD approach is due to the fact that the Tikhonov method does not
enforce a non-negativity constraint on the solution.
has been calculated by
partitioning the observed images in 25 square subregions
(i.e., ND=25), and by using piecewise constant interpolation
for Di(m,n). For comparison, the deblurring of the first image of the set
(that with the PSF shown in Fig. 2) is also
presented; an MRNSD algorithm for spatially-invariant PSF has been used.
In each case the improvement due to the use of the eight
images is evident. The superiority of the results provided by the
MRNSD approach is due to the fact that the Tikhonov method does not
enforce a non-negativity constraint on the solution.
Although the use of piecewise constant interpolation for Di(m,n) can provide reasonable results, very often the linearly interpolated version is able to remarkably improve them. Figures 5-7 show the results of an experiment, carried out under the same conditions as the previous one, that confirms the superiority of the interpolated method (here Ns=80).
In various situations the choice of the linear interpolation mask
is a necessity. When the constant interpolation mask
is applied to the object shown in Fig. 8
(NB. here noise is additive and Gaussian with a standard deviation of ![]() ,
the standard deviation of the dispersion of the blurred images),
the results are not so good since
,
the standard deviation of the dispersion of the blurred images),
the results are not so good since
![]() contains blocking
artifacts that later are magnified by the deblurring
operation. Consequently, the use of the linearly interpolated mask
becomes necessary. Although this approach produces
better results, some problems still remain in the form of fringes
that contaminate
contains blocking
artifacts that later are magnified by the deblurring
operation. Consequently, the use of the linearly interpolated mask
becomes necessary. Although this approach produces
better results, some problems still remain in the form of fringes
that contaminate
![]() .
This is linked to edge effects
because the original image contains significant features close to its
boundaries. For this reason, before the calculation of
.
This is linked to edge effects
because the original image contains significant features close to its
boundaries. For this reason, before the calculation of
![]() ,
all the images gj(m,n) should be windowed as explained at the end
of Sect. 3.1.
Figure 9 shows the results obtained after this
operation with Ns=80 and Nw=40. A border of 40 pixels was
removed by the windowing operation (see Vio et al. 2004).
Again, the improvement due to the use of the eight images
is evident. In this specific case, since the non-negativity of the
solution is not as critical as in the experiments presented above,
Tikhonov regularization is able to provide results as good as those
provided by MRNSD, but at a much lower computational cost (and thus
much more quickly).
,
all the images gj(m,n) should be windowed as explained at the end
of Sect. 3.1.
Figure 9 shows the results obtained after this
operation with Ns=80 and Nw=40. A border of 40 pixels was
removed by the windowing operation (see Vio et al. 2004).
Again, the improvement due to the use of the eight images
is evident. In this specific case, since the non-negativity of the
solution is not as critical as in the experiments presented above,
Tikhonov regularization is able to provide results as good as those
provided by MRNSD, but at a much lower computational cost (and thus
much more quickly).
Figures 10 and 11 show the results
that can be obtained in presence of Poissonian noise. Here the simulated images are the same
as those shown in Figs. 6 and 9. The only difference is that
the Gaussian noise is not added to the blurred images, but to non-stationary Poissonian processes with the
local mean given by the values of the pixels in the blurred images themselves
(peak signal to noise ratio = 40![]() ). In this way it is possible to get an idea of the degradation
in the quality of deblurring operation due to the presence of non-Gaussian noise.
The visual inspection of these figures, as well as the rms of
the true residuals (i.e.,
). In this way it is possible to get an idea of the degradation
in the quality of deblurring operation due to the presence of non-Gaussian noise.
The visual inspection of these figures, as well as the rms of
the true residuals (i.e.,
![]() ), clearly indicate that, if present, such degradation
is very small. This conclusion is not unexpected; various works have already shown that LS methods are able to
provide results very similar (and often almost identical) to those
obtainable with Maximum Likelihood techniques that take into account the Poissonian nature of the noise
(e.g., see Bertero & Boccacci 2000). However, the possible worsening of the
quality of the results is not due to the use of the mean image
), clearly indicate that, if present, such degradation
is very small. This conclusion is not unexpected; various works have already shown that LS methods are able to
provide results very similar (and often almost identical) to those
obtainable with Maximum Likelihood techniques that take into account the Poissonian nature of the noise
(e.g., see Bertero & Boccacci 2000). However, the possible worsening of the
quality of the results is not due to the use of the mean image
![]() ,
but is
intrinsic to the adoption of a LS model with non-Gaussian noise.
,
but is
intrinsic to the adoption of a LS model with non-Gaussian noise.
Figure 12 shows the results obtainable when the
proposed deblurring method is applied to simulated observations of the PLANCK Low
Frequency Instrument (LFI). The images have been computed as explained in
Vio et al. (2003a). The region we consider is a square patch of
![]() pixels with a side of
about
pixels with a side of
about
![]() centered at
centered at
![]() ,
,
![]() (Galactic coordinates).
The latitude is high enough that the Cosmic Microwave Background (CMB)
dominates over the foreground.
The PLANCK-LFI instrument works at frequencies 30, 44, 70, and
(Galactic coordinates).
The latitude is high enough that the Cosmic Microwave Background (CMB)
dominates over the foreground.
The PLANCK-LFI instrument works at frequencies 30, 44, 70, and
![]() ,
but we consider only the last three since
at these frequencies the contamination by the foreground is negligible.
We assume nominal noise and angular resolution
,
but we consider only the last three since
at these frequencies the contamination by the foreground is negligible.
We assume nominal noise and angular resolution![]() .
The maps are blurred through Gaussian PSFs with elliptical symmetry (axial ratio 1:1.3) and
appropriate FWHMs (i.e., for the major axis,
.
The maps are blurred through Gaussian PSFs with elliptical symmetry (axial ratio 1:1.3) and
appropriate FWHMs (i.e., for the major axis,
![]()
![]() at
at
![]() ,
,
![]()
![]() at
at
![]() ,
,
![]()
![]() at
at
![]() ).
Although the PSFs are not expected to change their shape during the
observations, it is not improbable that
they may suffer a rotation. Since the importance of such a phenomenon is not yet well determined,
for all the frequencies we assume a spatially-variant PSF similar to
that shown in Fig. 2,
which certainly represents a worst-possible-case scenario. Finally, each map is summed together
with simulated white noise with a rms level as expected for the considered channels.
Since we choose to work with a pixel size of about 3.5 arcmin, the noise
rms are .049, .042 and .043 mK in antenna temperature at 44, 70,
).
Although the PSFs are not expected to change their shape during the
observations, it is not improbable that
they may suffer a rotation. Since the importance of such a phenomenon is not yet well determined,
for all the frequencies we assume a spatially-variant PSF similar to
that shown in Fig. 2,
which certainly represents a worst-possible-case scenario. Finally, each map is summed together
with simulated white noise with a rms level as expected for the considered channels.
Since we choose to work with a pixel size of about 3.5 arcmin, the noise
rms are .049, .042 and .043 mK in antenna temperature at 44, 70,
![]() ,
respectively. The assumption of white noise is common in this kind of experiment
(e.g., see Vio et al. 2003a; Hobson et al. 1998; Stolyarov et al. 2002).
The CMB maps can have negative values, and this prevents the use of methods exploiting the
non-negativity constraint of the solution. For this reason, only the Tikhonov deblurring method
has been used. Because of the edge effects, the image
,
respectively. The assumption of white noise is common in this kind of experiment
(e.g., see Vio et al. 2003a; Hobson et al. 1998; Stolyarov et al. 2002).
The CMB maps can have negative values, and this prevents the use of methods exploiting the
non-negativity constraint of the solution. For this reason, only the Tikhonov deblurring method
has been used. Because of the edge effects, the image
![]() has been obtained
through the windowing procedure indicated above with Ns=60 and Nw=30.
Using the three maps instead of only the one with the highest resolution
provided final results whose rms of the true residuals is
improved by about
has been obtained
through the windowing procedure indicated above with Ns=60 and Nw=30.
Using the three maps instead of only the one with the highest resolution
provided final results whose rms of the true residuals is
improved by about ![]() .
.
We have considered the problem of simultaneously deblurring a set of images of a fixed object when the corresponding PSFs are space-variant and different from each other. We have developed a method, based on a LS approach, to efficiently transform a multi-image deblurring problem into a single-image one. This approach provides substantial savings in computational requirements, and can be implemented using numerical LS algorithms for single-image problems. These conclusions are confirmed by our numerical experiments. We have also presented a novel, computationally efficient, direct deblurring algorithm, which is based on a Singular Value Decomposition (SVD) approximation of the space variant PSF coupled with Tikhonov regularization.
Specific implementations used for the
experiments are available in the Matlab package RestoreTools
(Nagy et al. 2004b)![]() .
.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0754Fg1.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg93.gif) |
Figure 1:
One- and two-dimensional bases for the computation of the masks
using the linear interpolation approach. In the one-dimensional case the
dashed line indicates the limits of each subregion, whereas in the
two-dimensional case they indicate the limits of the masks.
Symbols |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0754Fg2.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg94.gif) |
Figure 2: Spatial variation of the PSF across the first image of the set used in the numerical experiments (see text). The pair of numbers in the header of each panel indicates the coordinates of the pixels to which the displayed PSF corresponds. In the intermediate pixels the PSFs are obtained through a linear interpolation of the displayed ones. Each PSF is given by a two-dimensional Gaussian function with a dispersion of 12 pixels along the major axis and 4 pixels along the minor axis. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0754Fg3.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg95.gif) |
Figure 3:
Original image, blurred version and
blurred + noise version of the first image of the set (see text), and corresponding mean PSF. The
images are
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0754Fg4.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg96.gif) |
Figure 4:
Mean image
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0754Fg5.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg97.gif) |
Figure 5:
Original image, blurred version and
blurred + noise version of the first image of the set (see text), and corresponding mean PSF. The
images are
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0754Fg6.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg98.gif) |
Figure 6:
Mean image
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0754Fg7.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg99.gif) |
Figure 7:
Mean image
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0754Fg8.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg100.gif) |
Figure 8:
Original image, blurred version and
blurred + noise version of the first image of the set (see text), and corresponding mean PSF. The
images are
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0754Fg9.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg101.gif) |
Figure 9:
Mean image
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0754Fg10.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg103.gif) |
Figure 10:
Mean image
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0754Fg11.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg104.gif) |
Figure 11:
Mean image
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0754Fg12.eps}
\end{figure}](/articles/aa/full/2005/17/aa0754/Timg105.gif) |
Figure 12:
Original image, observed image at
|
| Open with DEXTER | |
In matrix notation, model (2) can be written in the form
| (A.1) |
In Vio et al. (2003a,b) it has been shown that
for spatially-invariant blurs, spectral decompositions using fast transforms
(such as DFT and the Discrete Cosine Transform) can sometimes be used in place of the SVD,
but this depends
on the PSF and the boundary condition. If
it is not appropriate to use fast transforms, then another approach
we considered was to
compute an approximation of the SVD from a Kronecker product
factorization of
![]() .
.
For spatially-variant blurs, the situation is a bit more difficult since
the fast transform-based decomposition methods are no
longer a viable approach. However, here we show that
the SVD approximation based on a Kronecker product factorization
of
![]() can be extended to the case of space variant blurs.
This work builds on ideas initially proposed by Kamm & Nagy (1998).
can be extended to the case of space variant blurs.
This work builds on ideas initially proposed by Kamm & Nagy (1998).
Suppose the blur is spatially-invariant, and let ![]() be an image representing
the PSF. Then it can be shown that if
be an image representing
the PSF. Then it can be shown that if ![]() is decomposed as:
is decomposed as:
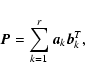 |
(A.2) |
![\begin{displaymath}\vec{A}\otimes \vec{B}
= \left[ \begin{array}{cccc}
a_{11} ...
...& a_{n2}\vec{B}& \cdots & a_{nn}\vec{B}
\end{array} \right] .
\end{displaymath}](/articles/aa/full/2005/17/aa0754/img112.gif) |
(A.4) |
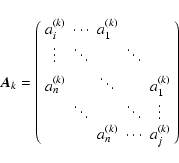
 |
(A.5) |
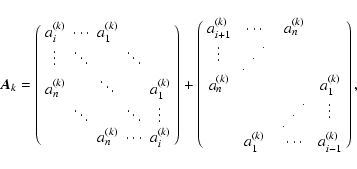 |
(A.6) |
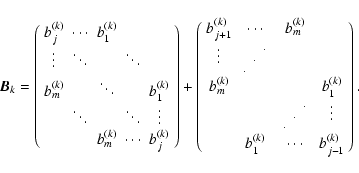 |
(A.7) |
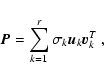 |
(A.8) |
| |
= | ||
| = | (A.9) |
The above remarks suggest that an SVD approximation can be obtained by
computing the SVD of
![]() .
It is possible, though, to
incorporate some information from
.
It is possible, though, to
incorporate some information from
![]() and
and
![]() .
Following an approach outlined in Nagy et al. (2004a); Kamm & Nagy (2000), this can be
done as follows:
.
Following an approach outlined in Nagy et al. (2004a); Kamm & Nagy (2000), this can be
done as follows:
| |
= | ||
| = | ![$\displaystyle \mbox{diag}\left[ (\vec{U}_a \otimes \vec{U}_b)^T
\left( \sum_{k=1}^r (\vec{A}_k \otimes \vec{B}_k) \right)
(\vec{V}_a \otimes \vec{V}_b) \right]$](/articles/aa/full/2005/17/aa0754/img142.gif) |
||
| = | ![$\displaystyle \mbox{diag}\left[
\sum_{k=1}^r (\vec{U}_a \otimes \vec{U}_b)^T(\vec{A}_k \otimes \vec{B}_k)
(\vec{V}_a \otimes \vec{V}_b)
\right]$](/articles/aa/full/2005/17/aa0754/img143.gif) |
||
| = | ![$\displaystyle \mbox{diag}\left[
\sum_{k=1}^r (\vec{U}_a^T \vec{A}_k \vec{V}_a) \otimes
(\vec{U}_b^T \vec{B}_k \vec{V}_b)
\right]$](/articles/aa/full/2005/17/aa0754/img144.gif) |
||
| = | 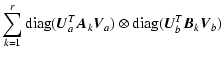 |
(A.10) |
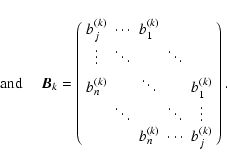
In the case of space variant blurs, a single PSF does not provide enough information
to obtain a complete representation of the matrix,
![]() .
One PSF provides
only information about one column (or row) of
.
One PSF provides
only information about one column (or row) of
![]() .
In order to get all N2 columns,
we would need N2 PSFs, each one centered at a different pixel location.
It would be extremely expensive to to find all of these PSFs. So instead, we
consider a simplifying assumption that the blur is locally spatially-invariant
(this approach has been used in Faisal et al. 1995; Boden et al. 1996; Nagy & O'Leary 1998).
Specifically, suppose that the image domain is partitioned into
.
In order to get all N2 columns,
we would need N2 PSFs, each one centered at a different pixel location.
It would be extremely expensive to to find all of these PSFs. So instead, we
consider a simplifying assumption that the blur is locally spatially-invariant
(this approach has been used in Faisal et al. 1995; Boden et al. 1996; Nagy & O'Leary 1998).
Specifically, suppose that the image domain is partitioned into
![]() rectangular
regions, each with a PSF,
rectangular
regions, each with a PSF,
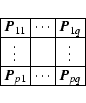
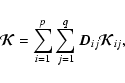 |
(A.11) |
Now using the Kronecker product factorization for spatially-invariant blurs
described in the previous section, we obtain (without loss of generality, we
assume each of the PSFs has rank equal to r):
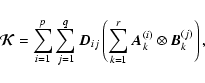 |
(A.12) |
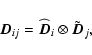 |
(A.13) |
 |
(A.14) |
| |
= | 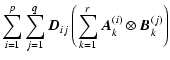 |
|
| = | 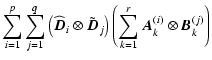 |
||
| = | 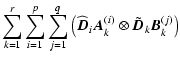 |
||
| = | ![$\displaystyle \sum_{k=1}^r \left[ \left(\sum_{i=1}^p \widehat{\vec{D}}_i \vec{A...
...t) \otimes
\left(\sum_{j=1}^q \tilde{\vec{D}}_j \vec{B}_k^{(j)} \right) \right]$](/articles/aa/full/2005/17/aa0754/img166.gif) |
||
| = | 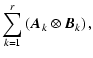 |
(A.15) |
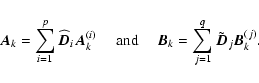 |
(A.16) |