A&A 434, 247-256 (2005)
DOI: 10.1051/0004-6361:20042184

Stability of the mixed phase in hybrid stars

O. Benhar 1,2 - R. Rubino2


1 - INFN, Sezione di Roma, Piazzale Aldo Moro, 2, 00185 Roma, Italy
2 - Dipartimento di Fisica, Università "La Sapienza", Piazzale Aldo Moro, 2, 00185 Roma, Italy

Received 15 October 2004 / Accepted 14 December 2004

Abstract
The transition from hadronic matter to quark matter in the core of neutron stars is likely to be associated with the appearance of a mixed phase, leading to a smooth variation of the star density profile. We discuss the results of a systematic study of the properties of the mixed phase on Coulomb and surface effects. A state-of-the-art nonrelativistic equation of state of nuclear matter has been used for the low density phase, while quark matter has been described within the MIT bag model, including the effect of perturbative one-gluon exchange interactions. The implications for neutron star structure are discussed.

Key words: dense matter - equation of state - stars: neutron

   
1 Introduction

The possible occurrence of a core of deconfined quark matter in the interior of neutron stars has been investigated by a number of authors over the past three decades (for a recent review see, e.g., Weber 2004). Due to the complexity of the underlying dynamics, theoretical approaches to the study of hybrid stars largely rely on models to describe the equation of state (EOS) of strongly interacting matter, in both the hadronic and quark sector, as well as on a set of assumptions on the nature of the phase transition.

Most calculations have been carried out using nuclear EOS obtained from either nonrelativistic nuclear many body theory (NMBT) or relativistic mean field theory (RMFT), while the deconfined phase is usually described within the MIT bag model (Chodos et al. 1974).

In their pioneering work, Baym & Chin (1976a) employed the familiar Maxwell double tangent construction (see, e.g., Huang 1963), which amounts to assuming that the transition occurs at constant pressure. Within this picture, charge-neutral nuclear matter at energy density $\epsilon_{\rm NM}$ coexists with charge-neutral quark matter at energy density $\epsilon_{\rm QM}$, the two phases being separated by a sharp interface.

In the early 90s Glendenning (Glendenning 1992,1997) first pointed out that the requirement that the two phases be individually charge-neutral is in fact too restrictive. In a more general scenario charged nuclear and quark matter may share a common lepton background, thus giving rise to a mixed phase extending in space over a sizable fraction of the star.

The appearance of a mixed phase strongly affects the macroscopic properties of the star. A transition at constant pressure necessarily leads to the appearance of a discontinuity in the density profile, i.e. to a star consisting of a inner core of quark matter at energy density $\epsilon_{\rm QM}$ surrounded by nuclear matter at energy density $\epsilon_{\rm NM}$. On the other hand, the mixed phase allows for a smooth variation of the energy density, leading in turn to a smooth variation of the star density profile.

Whether the transition proceeds at constant pressure or according to Glendenning's picture depends upon i) the value of the Debye screening length, driving charge separation, and ii) the amount of electrostatic and surface energy needed for the formation of the structures of quark and nuclear matter in the mixed phase. If screening is too strong to allow for a uniform lepton density, or if the energy loss due to Coulomb and surface effects exceeds the gain in bulk energy, the standard scenario predicted by Maxwell construction turns out to be favorable.

The results of a detailed study carried out by Heiselberg et al. (1993) suggest that the mixed phase is energetically favored over a sizable density range if the surface tension is less that $\sim $70 MeV/fm2. In their calculations these authors adopted the MIT bag model (Chodos et al. 1974) for the quark matter EOS, while nuclear matter was described using a somewhat oversimplified model in which the energy-density included a quadratic compressional term and a symmetry term taken from a previous work of Lattimer et al. (1991).

Over the past decade, the availability of new nucleon-nucleon potentials, resulting from accurate fits to nucleon-nucleon scattering data, and the improvement of the computational schemes made it possible to obtain a new generation of EOS within the framework of NMBT (Akmal & Pandharipande 1997; Akmal et al. 1998). In view of the fact that NMBT is a parameter-free approach whose dynamics is strongly constrained by nuclear data and has been shown to possess a highly remarkable predictive power in theoretical studies of few nucleon systems (Pieper & Wiringa 1995), it provides a natural candidate to describe neutron star matter in the nuclear phase.

In this paper we extend the work of Heiselberg et al. (1993) carrying out a systematic study of the stabilty of the mixed phase. We adopt the state-of-the-art EOS of nuclear matter, obtained by Akmal et al. (1998) within NMBT, and analyze the dependence of the results on i) the parameters entering the MIT bag model EOS, employed to describe quark matter, and ii) the value of the surface tension, driving both Coulomb and surface effects.

In Sect. 2 we summarize the main features of the model EOS of both nuclear and quark matter, while the implementation of Gibbs conditions in the case of two chemical potentials, leading to the appearance of the mixed phase, is discussed in Sect. 3. Our main results are presented in Sect. 4, devoted to the role of Coulomb and surface energy. The implication of the appearance of the mixed phase for neutron star structure are outlined in Sect. 5. The conclusions of our work are stated in Sect. 6.

   
2 Models of neutron star matter EOS

In this section we summarize the main features of the EOS employed in our work, focusing on the region of nuclear and supranuclear density ( $n_{\rm B} \ga0.1$ fm-3). For the lower density region, corresponding to the outer and inner crust of the star, we have used the EOS of Baym et al. (1971) and Pethick et al. (1995), respectively. However, our results are largely unaffected by the details of the EOS at subnuclear density, as the fraction of star mass in the crust is only about 2%.

The theoretical descriptions of nuclear and quark matter are both based on the standard assumptions that the system is at zero temperature and transparent to neutrinos produced in weak interaction processes (see, e.g., Shapiro & Teukolski 1997).

   
2.1 Nuclear matter

Within NMBT, nuclear matter is viewed as a collection of pointlike protons and neutrons, whose dynamics are described by the Hamiltonian

 \begin{displaymath}H = \sum_{i} \frac{ \vec{p}_i^2 }{ 2 M } + \sum_{j>i} v_{ij} + \sum_{k>j>i} V_{ijk} \ , \end{displaymath} (1)

M and $\vec{p}_i$ being the nucleon mass and the momentum of the ith particle, respectively. The nucleon-nucleon (NN) potential vijreduces to the well-known Yukawa one-pion exchange potential at large distances, while its short and intermediate range behavior is determined by fitting the available experimental data on the two-nucleon system (deuteron properties and $\sim $4000 NN scattering phase shifts) (Wiringa et al. 1995). The three-nucleon potential Vijk, whose inclusion is needed to reproduce the observed binding energies of the three-nucleon system, consists of the Fujita-Miyazawa two-pion exchange potential supplemented by a purely phenomenological repulsive interaction ( Pudliner et al. 1995).

The many-body Schrödinger equation associated with the Hamiltonian of Eq. (1) can be solved exactly, using stochastic methods, for nuclei of mass number $A \le 10$. The resulting energies of the ground and low-lying excited states are in excellent agreement with experimental data (Wiringa & Pieper 1995). Exploiting translational invariance, accurate calculations can also be carried out for uniform nuclear matter (Wiringa et al. 1988; Akmal & Pandharipande 1997).

Akmal & Pandharipande (1997) have used cluster expansions and chain summation techniques to obtain the energy per particle of both pure neutron matter (PNM) and symmetric nuclear matter (SNM). In their approach the Argonne v18 potential of Wiringa et al. (1995) is modified to take into account the fact that NN potentials fitted to scattering data describe interactions between nucleons in their center of mass frame, in which the total momentum $\vec{P}$ vanishes. Within the approach of Akmal & Pandharipande, relativistic corrections arising from the boost to a frame in which $\vec{P} \neq 0$, are included up to order $\vec{P}^2/M^2$.

Interpolating between the PNM and SNM results of Akmal & Pandharipande (1997), Akmal et al. (1998) have determined the energy of matter with arbitrary ptoton fraction needed to obtain the EOS of $\beta $-stable matter, consisting of neutrons, protons, electrons and muons. Their calculations span a range of baryon number density $n_{\rm B}$ extending up to $\sim $8 n0, n0 = 0.16 fm-3 being the empirical saturation density of symmetric nuclear matter.

At any given value of $n_{\rm B}$, proton and lepton densities are determined by the requirements of charge neutrality,

\begin{displaymath}n_{\rm p} = n_{\rm e} + n_\mu , \end{displaymath} (2)

and $\beta $-stability,

\begin{displaymath}\mu_{\rm n} = \mu_{\rm p} + \mu_{\rm e} , \end{displaymath} (3)


\begin{displaymath}\mu_{\rm e} = \mu_\mu . \end{displaymath} (4)

In the above equations ni and $\mu_i$ denote the number density and chemical potential of the particle of type i $(i=n,\rm p,e,\mu)$, respectively.

The EOS $P = P(\epsilon)$, where P and $\epsilon$ denote pressure and energy density is obtained from the density dependence of the binding energy per baryon, $E = E(n_{\rm B})$, through

 \begin{displaymath}P = - \frac{1}{n_{\rm B}^2}\frac{\partial E}{\partial n_{\rm B}} , \end{displaymath} (5)

and

 \begin{displaymath}\epsilon = n_{\rm B} ( E + M ) . \end{displaymath} (6)


  \begin{figure} \par\includegraphics[width=7.5cm]{2184fig1.eps}\end{figure} Figure 1: Energy per baryon of nuclear matter calculated by Akmal et al. (1998), plotted as a function of baryon number density. The dashed, dotdash and solid lines correspond to pure neutron matter, symmetrical nuclear metter and $\beta $-stable matter, respectively. The box represents the equilibrium properties of symmetrical nuclear matter obtained from extrapolation of empirical data.
Open with DEXTER

The results discussed in the following sections have been obtained using the EOS of Akmal et al. (1998), hereafter referred to as APR, to describe the nuclear phase of neutron star matter. The corresponding energy per baryon of PNM, SNM and $\beta $-stable matter is displayed in Fig. 1 as a function of density.

   
2.2 Quark matter

Due to the complexity of the fundamental theory of strong interactions (Quantum Chromo-Dynamics, or QCD) a first principle description of the EOS of quark matter at high density and low temperature is out of reach of the existing computational approaches. To describe the quark matter phase, we have used the simple MIT bag model (Chodos et al. 1974), in which the main features of QCD are implemented through the assumptions that: i) quarks occur in colour neutral clusters confined to a finite region of space (the bag), whose volume is limited by the pressure of the QCD vacuum (the bag constant B), and ii) residual interactions between quarks are weak, and can be treated using low order perturbation theory.

Within the MIT bag model the thermodynamic potential $\Omega$ can be written as

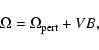\begin{displaymath}\Omega = \Omega_{\rm pert} + VB, \end{displaymath} (7)

where $\Omega_{\rm pert}$ and VB, V being the normalization volume, denote the perturbative and nonperturbative contribution, respectively, and

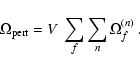\begin{displaymath}\Omega_{\rm pert} = V\ \sum_f \sum_n \Omega^{(n)}_f\ . \end{displaymath} (8)

In the above equation, the index f specifies the quark flavor, while $\Omega^{(n)}_f$ is the nth order term of the perturbative expansion in powers of the strong coupling constant, $\alpha_{\rm s}$.

The EOS of quark matter can be obtained from the relations linking pressure and energy density to $\Omega$:

 \begin{displaymath}P = - \frac{\Omega}{V} = - B - \sum_f \sum_n \Omega^{(n)}_f\ . \end{displaymath} (9)


 \begin{displaymath}\epsilon = \frac{\Omega}{V} - \sum_f \left( \frac{\partial \Omega}{\partial \mu_f} \right) = -P + \sum_f \mu_f n_f\ , \end{displaymath} (10)

nf and $\mu_f$ being the density and chemical potential of the quarks of flavor f.

The lowest order perturbative contributions to the thermodynamic potential, corresponding to $\Omega^{(n)}_f$ with n = 0 and 1, are (see, e.g., Tamagaki & Tatsumi 1993)

 
$\displaystyle \Omega_0^f = -\frac{1}{\pi^2} \left[ \frac{1}{4}\mu_f\sqrt{\mu_f^... ...right) + \frac{3}{8} m_f^4 \ln \frac{\mu_f-\sqrt{\mu_f^2-m_f^2}}{m_f} \right] ,$     (11)


 
$\displaystyle \Omega_1^f = \frac{2\alpha_{\rm s}}{\pi^3} \left [ \frac{3}{4} \l... ...mu_f^2-m_f^2}}{m_f}\ \right)^2 - \frac{1}{2} \Bigg. (\mu_f^2-m_f^2)^2 \right] .$     (12)

The chemical potentials appearing in Eqs. (11) and (12) can be written

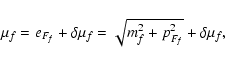\begin{displaymath}\mu_f = e_{F_f} + \delta\mu_f = \sqrt{ m_f^ 2 + p_{F_f}^2 } + \delta\mu_f, \end{displaymath} (13)

where the first term is the Fermi energy of a gas of noninteracting quarks of mass mf at density $n_f = p_{F_f}^3/\pi^2$, whereas the second term is a perturbative correction of order $\alpha_{\rm s}$, whose explicit expression is (Baym & Chin 1976b)

\begin{displaymath}\delta\mu_f = \frac{2\alpha_{\rm s}}{3 \pi^2} \left[ p_{F_f} ... ... \left( \frac{ e_{F_f} + p_{F_f} }{m_f} \right) } \right]\cdot \end{displaymath} (14)

In the case of massless quarks Eqs. (9) and (10) reduce to the simple form

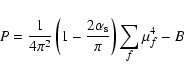\begin{displaymath}P = \frac{1}{4\pi^2} \left( 1 - \frac{2\alpha_{\rm s}}{\pi} \right) \sum_f \mu_f^4 - B \end{displaymath} (15)


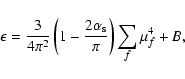\begin{displaymath}\epsilon = \frac{3}{4\pi^2} \left( 1 - \frac{2\alpha_{\rm s}}{\pi} \right) \sum_f \mu_f^4 + B , \end{displaymath} (16)

implying the relationship

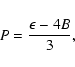\begin{displaymath}P = \frac{\epsilon - 4B}{3} , \end{displaymath} (17)

reminiscent of the EOS of noninteracting quarks.

For any baryon desity, quark densities are dictated by the requirements of baryon number conservation, charge neutrality and weak equilibrium. In the case of two flavors, in which only the light up and down quarks are present, we have

 \begin{displaymath}n_{\rm B} = \frac{1}{3} (n_u + n_d) , \end{displaymath} (18)


 \begin{displaymath}\frac{2}{3} n_u - \frac{1}{3}n_d - n_{\rm e} = 0 \end{displaymath} (19)


 \begin{displaymath}\mu_d = \mu_u + \mu_{\rm e} , \end{displaymath} (20)

where $n_{\rm e}$ and $\mu_{\rm e}$ denote the density and chemical potential of the electrons produced through $d \rightarrow u + {\rm e}^- + {\overline \nu}_{\rm e}$. Note that we have not taken into account the possible appearance of muons, as in the relevant density region $\mu_{\rm e}$ never exceeds the muon mass.

As the baryon density increases, the d-quark chemical potential reaches the value $\mu_d = m_{\rm s}$, $m_{\rm s}$ being the mass of the strange quark. The energy of quark matter can then be lowered turning d-quarks into s-quarks through $d + u \rightarrow u + s$. In presence of three flavors, Eqs.(18)-(20) become

 \begin{displaymath}n_{\rm B} = \frac{1}{3} (n_u + n_d + n_{\rm s})\ , \end{displaymath} (21)


 \begin{displaymath}\frac{2}{3} n_u - \frac{1}{3}n_d - \frac{1}{3}n_{\rm s} - n_{\rm e} = 0 \end{displaymath} (22)


 \begin{displaymath}\mu_d = \mu_{\rm s} = \mu_u + \mu_{\rm e} . \end{displaymath} (23)

Unfortunately, the parameters entering the bag model EOS are only loosely constrained by phenomenology and their choice is somewhat arbitrary.

As quarks are confined and not observable as individual particles, their masses are not directly measurable and must be inferred from hadron properties. The Particle Data Group (Hagiwara et al. 2000) report masses of a few MeV for up and down quarks and 60 to 170 MeV for the strange quark. We have set mu=md=0 and $m_{\rm s} = 150$ MeV for the up, down and strange quark, respectively. In the density region relevant to our work heavier quarks do not play a role.

The strong coupling constant $\alpha_{\rm s}$ can be obtained from the renormalization group equation, yielding

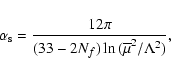\begin{displaymath}\alpha_{\rm s} = \frac{12 \pi}{ (33-2N_f) \ln{ ({\overline \mu^2}/\Lambda^2) } } , \end{displaymath} (24)

where Nf = 3 is the number of active flavors, $\Lambda$ is the QCD scale parameter and ${\overline \mu}$ is an energy scale typical of the relevant density region (e.g. the average quark chemical potential). Using $\Lambda \sim 100 \div 200$ MeV (see, e.g., Ellis et al. 1996) and setting ${\overline \mu} = \mu_d \sim \mu_u$ at a typical baryon density $n_{\rm B} \sim 4n_0$ one gets $\alpha_{\rm s} \sim 0.4 \div 0.6$. The results discussed in this paper have been obtained with $\alpha _{\rm s} = 0.5$.

The values of the bag constant resulting from fits of the hadron spectrum range between $\sim $57 MeV/fm3, with $\Lambda = 220$ MeV, (De Grand et al. 1975) and $\sim $350 MeV/fm3, with $\Lambda = 172$ MeV (Carlson et al. 1983). However, the requirement that the deconfinement transition does not occur at density $\sim $n0 constrains B to be larger than $\sim $120-150 MeV/fm3, and lattice results suggest a value of $\sim $210 MeV/fm3(Satz 1982). In order to gauge the dependence of the results on the value of B, we have carried out our calculations setting B = 120 and 200 MeV/fm3.


  \begin{figure} \par\includegraphics[width=7.cm]{2184fig2.eps}\end{figure} Figure 2: Energy density of neutral quark matter in weak equilibrium as a function of baryon number density. The solid and dashed lines have been obtained setting $\alpha _{\rm s} = 0.5$ and B = 200 and 120 MeV/fm3, respectively, while the dashdot line corresponds to $\alpha _{\rm s} = 0$ and B = 200 MeV/fm3. The quark masses are mu = md = 0, $m_{\rm s} = 150$ MeV.
Open with DEXTER

Figure 2 shows the energy density of neutral quark matter in weak equilibrium as a function of baryon density for different values of Band $\alpha_{\rm s}$. The solid and dashed lines have been obtained setting $\alpha _{\rm s} = 0.5$ and B = 200 and 120 MeV/fm3, respectively, while the dashdot line corresponds to $\alpha _{\rm s} = 0$ and B = 200 MeV/fm3. Comparison between the dotdash line and those corresponding to $\alpha_{\rm s} \neq 0$ suggests that, contrary to what is stated by many authors (see, e.g., Steiner et al. 2000), perturbative gluon exchange, whose inclusion produces a sizable change of slope, cannot be simulated by adjusting the value of the bag constant and must be explicitly taken into account.

   
3 From nuclear matter to quark matter

Early works on the possible occurrence of quark matter in neutron stars (e.g. Baym & Chin 1976a) were based on the assumption that nuclear and quark matter were both charge neutral. As a consequence, the transition was described using the Maxwell construction (see, e.g., Huang 1963) and the resulting picture of the star consisted of a quark matter core surrounded by a mantle of nuclear matter, the two phases being separated by a sharp interface.

Glendenning (1992,1997) pointed out that this assumption is too restrictive. More generally, the transition can proceed through the formation of a mixed phase of charged nuclear and quark matter, global neutrality being guaranteed by a uniform lepton background.

Equilibrium between charged phases of nuclear matter (NM) and quark matter (QM) at T=0 requires the fulfillment of Gibbs conditions (see, e.g., Huang 1963)

 \begin{displaymath}P_{\rm NM}\left(\mu_{\rm NM}^B,\mu_{\rm NM}^Q\right) = P_{\rm QM}\left(\mu_{\rm QM}^B,\mu_{\rm QM}^Q\right) , \end{displaymath} (25)


 \begin{displaymath}\mu_{\rm NM}^B=\mu_{\rm QM}^B , \ \ \ \ \mu_{\rm NM}^Q=\mu_{\rm QM}^Q , \end{displaymath} (26)

where P denotes the pressure, while $\mu^B$ and $\mu^Q$ are the chemical potentials associated with the two conserved quantities, namely baryonic number B and electric charge Q.

The above equations imply that, for any pressure ${\bar P}$, the projection of the surfaces $P_{\rm NM}(\mu^B,\mu^Q)$ and $P_{\rm QM}(\mu^B,\mu^Q)$ onto the $P={\bar P}$ plane defines two curves, whose intersection corresponds to the equilibrium values of the chemical potentials. As the chemical potentials determine the charge densities of the two phases, the volume fraction occupied by quark matter, $\chi$, can then be obtained exploiting the requirement of global neutrality

 \begin{displaymath}\chi Q_{\rm QM} + (1-\chi) Q_{\rm NM} + \sum_\ell Q_\ell = 0 , \end{displaymath} (27)

where $Q_{\rm QM}$, $Q_{\rm NM}$ and ${Q_\ell}$ denote the electric charge carried by nuclear matter, quark matter and leptons, respectively. From Eq. (27) it follows that

 \begin{displaymath}\chi = \frac{Q_{\rm NM} + \sum_\ell Q_\ell}{Q_{\rm NM} - Q_{\rm QM}} , \end{displaymath} (28)

with $0 \leq \chi \leq 1$. Finally, the total energy density $\epsilon$ can be calculated using

 \begin{displaymath}\epsilon = \chi \epsilon_{\rm QM} + (1-\chi) \epsilon_{\rm NM} , \end{displaymath} (29)

and the EOS of state of the mixed phase can be cast in the standard form $P = P(\epsilon)$.

Requiring that the two phases be individually neutral, as in the pioneering work of Baym & Chin (1976a), reduces the number of chemical potentials to one, thus leading to the equilibrium conditions

 \begin{displaymath}P_{\rm NM}(\mu_{\rm NM}^B) = P_{\rm QM}\left(\mu_{\rm QM}^B\right) , \end{displaymath} (30)


 \begin{displaymath}\mu_{\rm NM}^B=\mu_{\rm QM}^B . \end{displaymath} (31)

Within this scenario, charge-neutral nuclear matter at baryon number density $n_{\rm B}^{\rm NM}$ coexists with charge-neutral quark matter at density $n_{\rm B}^{\rm QM}$, $n_{\rm B}^{\rm NM}$ and $n_{\rm B}^{\rm QM}$ being determined by the requirements

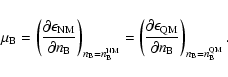\begin{displaymath}\mu_{\rm B} = \left( \frac{\partial \epsilon_{\rm NM}} {\part... ...} {\partial n_{\rm B}} \right)_{n_{\rm B}=n^{\rm QM}_{\rm B}}. \end{displaymath} (32)

At $n^{\rm NM}_{\rm B} < n_{\rm B} < n^{\rm QM}_{\rm B}$ pressure and chemical potential remain constant, the energy density is given by

 \begin{displaymath}\epsilon = \mu_{\rm B} n_{\rm B} - P , \end{displaymath} (33)

and the volume fraction occupied by quark matter grows linearly with density according to

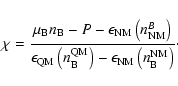\begin{displaymath}\chi = \frac{ \mu_{\rm B} n_{\rm B} - P - \epsilon_{\rm NM}\l... ...ght) - \epsilon_{\rm NM}\left(n^{\rm NM}_{\rm B}\right)}\cdot \end{displaymath} (34)

Note that the above equation obviously implies that $0 \leq \chi \leq 1$, with $\chi(n^{\rm NM}_{\rm B})=0$ and $\chi(n^{\rm QM}_{\rm B})=1$.


  \begin{figure} \par\includegraphics[width=7.0cm]{2184fig3A.eps}\par\includegraphics[width=7.0cm]{2184fig3B.eps}\end{figure} Figure 3: Isobars $P(\mu _{\rm n},\mu _{\rm p})=200$ MeV/fm3 ( upper panel) and 350 MeV/fm3 ( lower panel) obtained using the APR EOS of nuclear matter (solid lines) and the MIT bag model of quark matter, with $\alpha _{\rm s} = 0.5$ and B = 200 MeV/fm3 (dashed lines). The intersections determine the values of the chemical potentials corresponding to equilibrium of the two phases according to Gibbs rules.
Open with DEXTER

In the present work the intersection between the surfaces describing the pressure of nuclear and quark matter has been determined numerically, choosing as independent variables, instead of $\mu^B$ and $\mu^Q$, the proton and neutron chemical potentials $\mu_{\rm p}$ and $\mu_{\rm n}$. In nuclear matter they are simply related to the lepton chemical potential through the $\beta $-stability condition $\mu_{\rm n} - \mu_{\rm p} = \mu_\ell$. In quark matter the chemical potentials of up and down quarks can be obtained from $\mu_{\rm p}$ and $\mu_{\rm n}$, inverting the relations

 \begin{displaymath}\mu_{\rm p} = 2\mu_u + \mu_d \end{displaymath} (35)


 \begin{displaymath}\mu_{\rm n} = 2\mu_d + \mu_u , \end{displaymath} (36)

while the strange quark and lepton chemical potentials are dictated by the conditions of weak equilibrium

\begin{displaymath}\mu_{\rm s} = \mu_d , \end{displaymath} (37)


\begin{displaymath}\mu_d - \mu_u = \mu_\ell . \end{displaymath} (38)

Figure 3 illustrates the construction we have employed to determine the values of $\mu_{\rm p}$ and $\mu_{\rm n}$ corresponding to equilibrium between nuclear matter, described by the APR EOS, and quark matter, described by by the MIT bag model EOS with $\alpha _{\rm s} = 0.5$ and B = 200 MeV/fm3. The region $P_{\min} < P < P_{\max}$ in which the isobars of nuclear and quark matter intersect defines the range of densities $n_{\min} < n_{\rm B} < n_{\max}$ in which the mixed phase is energetically favored. At $n_{\rm B} < n_{\min}$ and $n_{\rm B} > n_{\max}$ the ground state consists of pure nuclear and quark matter, respectively.

The phase transition between nuclear and quark matter, obtained setting B = 200 MeV/fm3 and $\alpha _{\rm s} = 0.5$, is illustrated in Fig. 4. Dashed and dotdash lines show the dependence on $n_{\rm B}$ of the energy density of charge neutral nuclear and quark matter in weak equilibrium, respectively, while the solid line corresponds to the mixed phase. The latter turns out to be the ground state of neutron star matter at densities $.7 \la n_{\rm B} \la1.7$ fm-3.


  \begin{figure} \par\includegraphics[width=7.0cm]{2184fig4.eps}\end{figure} Figure 4: Dashed and dotdash lines show the energy density of charge neutral nuclear and quark matter in weak equilibrium, respectively. The bag model parameters have been set to B = 200 MeV/fm3 and $\alpha _{\rm s} = 0.5$. The solid line corresponds to the mixed phase, obtained from Gibbs equilibrium conditions.
Open with DEXTER

The dependence of our results on the MIT bag model parameters can be gauged from the upper panel of Fig. 5. It clearly appears that a lower value of the bag constant, corresponding to a softer quark matter EOS, leads to the appearance of the mixed phase at lower density. Keeping $\alpha _{\rm s} = 0.5$ and setting B = 120 MeV/fm3 one finds that the mixed phase is energetically favored in the range $.6 \la n_{\rm B} \la1.4$ fm-3. An even larger effect, illustrated by the lower panel of Fig. 5 is obtained with B = 120 MeV/fm3 and $\alpha _{\rm s} = 0$, i.e. neglecting perturbative gluon exchange altogether. For this case we also show the results obtained from the Maxwell construction, leading to the coexistence of charge-neutral nuclear matter at $n_{\rm B} = .42$ fm-3 and charge-neutral quark matter at $n_{\rm B} = .57$ fm-3. This cohexistence region is to be compared to the region of stability of the mixed phase, corresponding to $0.22 \la n_{\rm B} \la0.75$ fm-3.


  \begin{figure} \par\includegraphics[width=7.0cm]{2184fig5A.eps}\par\includegraphics[width=7.0cm]{2184fig5B.eps}\end{figure} Figure 5: As in Fig. 4, but with the EOS of quark matter obtained using different values of the MIT bag model parameters. Upper panel: B = 120 MeV/fm3 and $\alpha _{\rm s} = 0.5$; lower panel: B = 120 MeV/fm3 and $\alpha _{\rm s} = 0$. The straight line in the lower panel is the double tangent resulting from the Maxwell construction, while the open circles show the extrema of the coexistence region.
Open with DEXTER

   
4 Structure and stability of the mixed phase

The results of the previous section suggest that, irrespective of the details of the EOS, the transition from nuclear to quark matter proceed through the formation of a mixed phase. However, two issues relevant to both the appearance and the stability of the mixed phase, not taken into account in the discussion of Sect. 3, need to be further analyzed.

Consider a mixed phase consisting of droplets of quark matter immersed in $\beta $-stable nuclear matter, global charge neutrality being guaranteed by a lepton background. This picture is obvioulsy based on the assumption that the appearance of the charged droplets do not significantly affect the space distribution of the leptons, i.e. that the Debye screening length $\lambda_{\rm D}$ is large compared to both the typical size of the droplets and their separation distance (Heiselberg et al. 1993; Heiselberg & Hjort-Jensen 2000). If this condition is not satisfied the lepton background is distorted in such a way as to screen electrostastic interactions.

The estimates of $\lambda_{\rm D}$ reported by Heiselberg et al. (1993) suggest that screening effects can be disregarded if the structures appearing in the mixed phase of quark and nuclear matters have typical size and separation distance of $\sim $10 fm. The results of our calculations, that will be discussed discussed later in this section, show that this appears indeed to be the case.

The second issue deserving consideration is the stability of the mixed phase, i.e. the question of whether or not its energy is lower than the energy of the coexisting phases of nuclear and quark matter.

Formation of a spherical droplet of quark matter requires the energy

 \begin{displaymath}{\mathcal E}_{\rm D} = {\mathcal E}_{\rm C}+{\mathcal E}_{\rm S}, \end{displaymath} (39)

where the surface contribution ${\mathcal E}_{\rm S}$ is parametrized in terms of the surface tension $\sigma$ according to

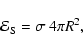\begin{displaymath}{\mathcal E}_{\rm S} = \sigma \ 4 \pi R^2 , \end{displaymath} (40)

R being the droplet radius. The electrostatic energy ${\mathcal E}_{\rm C}$ can be cast in the form (Ravenhall et al. 1983; Pethick et al. 1995)

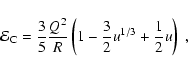\begin{displaymath}{\mathcal E}_{\rm C} = \frac{3}{5} \frac{Q^2}{R} \left( 1 - \frac{3}{2} u^{1/3} + \frac{1}{2} u \right)\ , \end{displaymath} (41)

with $u=(R/R_{\rm c})^3$, $R_{\rm c}$ being the radius of the Wigner-Seitz cell. Note that the first term on the right hand side of the above equation is the self energy of a droplet of radius R and charge Q obtained from Gauss law. The electric charge Q is given by

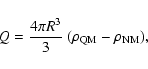\begin{displaymath}Q = \frac{4 \pi R^3}{3}\ (\rho_{\rm QM} - \rho_{\rm NM}) , \end{displaymath} (42)

$\rho_{\rm QM}$ and $\rho_{\rm NM}$ being the charge densities of quark matter and nuclear matter, respectively. Minimization of the energy density $\epsilon = 3{\mathcal E}_{\rm D}/4\pi R_{\rm c}^3$ with respect to the droplet radius yields

\begin{displaymath}{\mathcal E}_{\rm S} = 2 {\mathcal E}_{\rm C} \end{displaymath} (43)

and

 \begin{displaymath}R = \left[ \frac{4 \pi (\rho_{\rm QM} - \rho_{\rm NM})^2}{3 \sigma}\ f_3(u) \right]^{-1/3} \ , \end{displaymath} (44)

where

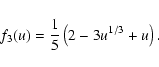\begin{displaymath}f_3(u) = \frac{1}{5} \left( 2 - 3u^{1/3} + u \right) . \end{displaymath} (45)

As the density increases, the droplets begin to merge and give rise to structures of variable dimensionality, changing first from spheres into rods (spaghetti) and eventually into slabs (lasagna). At larger densities the volume fraction occupied by quark matter exceeds 1/2, and the role of the two phases is reversed. Nuclear matter, initially arranged in slabs, turns into rods and spheres that finally dissolve in uniform charge-neutral quark matter.

The energy density needed for the formation of the structures appearing in the mixed phase has been obtained by Ravenhall et al. (1983) in the context of a study of matter in the neutron star inner crust. It can be written in the concise form

 \begin{displaymath}\epsilon_{\rm C} + \epsilon_{\rm S} = 6 \pi u \left[ \frac{\a... ...m B}^{\rm NM} - n_{\rm B}^{\rm QM} \right)^2 f_d(u) \right]\ , \end{displaymath} (46)

where $\alpha$ is the fine structure constant, u is the volume fraction occupied by the less abundant phase (i.e. $u = \chi$ for $\chi < 1/2$, $u=1-\chi$ for $\chi \geq 1/2$) and

 \begin{displaymath}f_d(u) = \frac{1}{d+2} \left[ \frac{1}{d-2} \left( 2 - d u ^{1-2/d} \right) + u \right]\ . \end{displaymath} (47)

For d=1,2 and 3 Eqs. (46) and (47) provide the correct energy density for the case of slabs, rods and spheres, respectively.

For $\sigma = 0$ both surface and Coulomb energies vanish, and the energy density of the mixed phase is given by Eq. (29), while for $\sigma \neq 0$

 \begin{displaymath}\epsilon(\sigma) = \epsilon(\sigma=0) + \epsilon_{\rm C} + \epsilon_{\rm S} . \end{displaymath} (48)

The mixed phase is energetically favorable if $\epsilon(\sigma)$ is less than the energy density obtained from the Maxwell construction, given by Eq. (33).

The value of the surface tension at the interface between nuclear and quark matter is not known. It has been estimated using the MIT bag model and ignoring gluon exchange (Berger & Jaffe 1987, 1991). Assuming that a strange quark has mass of $\sim $150 MeV, Berger & Jaffe predict $\sigma \sim 10$ MeV/fm2. To quantitatively investigate the stability of the mixed phase, we have calculated $\Delta _\epsilon = \epsilon (\sigma ) - \epsilon (0)$ for different values of $\sigma$, ranging from 2 MeV/fm2 to 10 MeV/fm2.

For any given value of the baryon number density $n_{\rm B}$, the energy density of Eqs. (46)-(47) has been calculated using the nuclear and quark matter densities determined according to the procedure described in Sect. 3 and carrying out a numerical minimization with respect to the value of the dimensionality parameter d. As $n_{\rm B}$ increases, the resulting values of d change initially from $\sim $3 to $\sim $2 and $\sim $1 and then again to $\sim $2 and finally to $\sim $3. For example, in the case illustrated by Fig. 6, and corresponding to $\sigma = 10$ MeV/fm2, we find that spherical droplets of quark matter ($d \sim 3$) appear at $n_{\rm B} \sim .75$ fm-3 and turn into rods ($d \sim 2$) and slabs ($d \sim 1$) at $n_{\rm B} \sim .95$ and $\sim $1.2 fm-3, respectively. For larger densities, quark matter becomes the dominant phase (i.e. $\chi > 1/2$): at $n_{\rm B} \sim 1.5$ and $\sim $1.7 fm-3 the mixed phase features rods ($d \sim 2$) and droplets ($d \sim 3$) of nuclear matter that eventually dissolve in the quark matter background.


  \begin{figure} \par\includegraphics[width=7.0cm]{2184fig6.eps}\end{figure} Figure 6: The solid lines correspond to the difference $\Delta _\epsilon = \epsilon (\sigma ) - \epsilon (0)$ (see Eq. (48)), evaluated for $\sigma = 10$, 5 and 2 MeV/fm3. The dashed line shows the difference $\widetilde{\Delta}$ between the energy density resulting from the Maxwell conatruction and $\epsilon (0)$. The arrows mark the limits of the cohexistence region. Nuclear and quark matter are described by the APR EOS and the MIT bag model EOS, with $\alpha _{\rm s} = 0.5$and B = 200 MeV/fm3, respectively.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.0cm]{2184fig7.eps}\end{figure} Figure 7: Same as in Fig. 6, but with $\alpha _{\rm s} = 0$ and B = 120 MeV/fm3. The solid lines show to the difference $\Delta _\epsilon = \epsilon (\sigma ) - \epsilon (0)$ (see Eq. (48)), evaluated for $\sigma = 5$ and 2 MeV/fm3, respectively.
Open with DEXTER

Our results are summarized in Figs. 6 and 7, that correspond to different choices of the MIT bag model parameters. The solid lines show the $n_{\rm B}$ dependence of the calculated $\Delta_\epsilon$ for different values of the surface tension $\sigma$. The dashed line represents the difference $\widetilde{\Delta}_\epsilon = \epsilon_{\rm M} - \epsilon(0)$, where $\epsilon_{\rm M}$ is the energy density obtained from Maxwell construction. For any given value of the surface tension, the mixed phase is favorable if the corresponding solid line lies below the dashed line.

The results of Fig. 6, corresponding to B=200 MeV/fm3 and $\alpha _{\rm s} = 0.5$, show that the mixed phase, while being always the lowest energy phase for $\sigma=2$ MeV/fm2, becomes energetically unfavorable at some densities for $\sigma \ga5$ MeV/fm2. For $\sigma = 10$ MeV/fm2 coexistence of charge neutral phases of nuclear and quark matter turn out to favorable over the whole density range.

To gauge the dependence upon the MIT bag model parameters we have repeated the calculations setting B=120 MeV/fm3 and $\alpha _{\rm s} = 0$. The results of Fig. 7 show that for $\sigma$ in the range 2-5 MeV/fm2 the mixed phase is energetically favorable over a density region larger than the coexistence region predicted by the Maxwell construction.

Finally, we return to the problem of the comparison between the Debye screening length and the typical size of the structures appearing in the mixed phase. Our results suggest that the condition outlined in the work of Heiselberg et al. (1993) are indeed fulfilled. For example, in the case B=200 MeV/fm3 and $\alpha _{\rm s} = 0.5$ we find that in the region of $\chi \ll 1$, corresponding to formation of droplets of quark matter, the droplets radius given by Eq. (44) is $\sim $2-3 fm.

   
5 Implications for star structure

Plugging the EOS $P = P(\epsilon)$ into the Tolman Oppenheimer Volkoff (TOV) equations (Tolman 1934; Oppenheimer & Volkoff 1939)

 \begin{displaymath}\frac{{\rm d}P(r)}{{\rm d}r} = - G\ \frac{ \left[ \epsilon(r)... ...pi r^2 P(r) \right] } { r^2 \left[ 1 - 2 G M(r) /r \right] } , \end{displaymath} (49)

where G denotes the gravitational constant, and

 \begin{displaymath}M(r) = 4 \pi \int_0^r {r^\prime}^2 {\rm d}{r^\prime} \epsilon({r^\prime}) , \end{displaymath} (50)

one can obtain the properties of the stable configurations of a nonrotating neutron star. Eqs. (49) and (50) are solved by integrating outwards with the initial condition $\epsilon(r=0) = \epsilon_{\rm c}$. For any given value of the central density, $\epsilon_{\rm c}$, the star radius R is determined by the condition P(R)=0 and its mass M=M(R) is given by Eq. (50).

The occurrence of the transition to quark matter makes the EOS softer, thus leading to a lower value of the maximum mass. In Fig. 8 we compare the mass-central energy density relations obtained using the APR EOS only to that obtained allowing for a transition to quark matter with $\alpha _{\rm s} = 0.5$ and B= 120 and 200 MeV/fm3. The transition is described according to Gibbs conditions, neglecting surface and Coulomb effects. We find $M_{\max} = 2.20 ~M_\odot$ for the star made of nuclear matter oly and $M_{\max} =$ 1.89 and 2.03 $M_\odot $ for the hybrid stars corresponding to B= 120 and 200 MeV/fm3, respectively.

In Fig. 8 we also compare the $M(\epsilon_{\rm c})$ curves obtained setting B= 120 MeV/fm3 and $\alpha _{\rm s} = 0$ and adopting either the Gibbs or Maxwell picture. Whether the phase transition proceeds through the appearance of a mixed phase or charge-neutral coexisting phases does not appear to significantly affect the mass-central energy density relation. On the other hand, neglecting perturbative gluon exchange results in a rather low maximum mass, $M_{\max} \sim 1.4 ~M_\odot$, barely compatible with the measured neutron star masses.


  \begin{figure} \par\includegraphics[width=7.0cm]{2184fig8.eps}\end{figure} Figure 8: Relation between neutron star mass and central energy density for different EOS. Dotdash line: pure nuclear matter (APR EOS); dotted lines: nuclear matter (APR EOS) and quark matter (MIT bag model with B= 120 and 200 MeV/fm3 and $\alpha _{\rm s} = 0.5$). The phase transition is described according to Gibbs rules. Solid line: same as the dotted line, but with B= 120 MeV/fm3 and $\alpha _{\rm s} = 0$; dashed line: same as the solid line, but with the phase transition described using Maxwell construction.
Open with DEXTER

The neutron star mass-radius relations associated with the $M(\epsilon_{\rm c})$ curves of Fig. 8, displayed in Fig. 9, show that in this case using the Maxwell construction instead of Gibbs rules produces a visible effect. All EOS predict the existence of stable star configurations with masses in the range allowed by observation (Thorsett & Chakrabarty 1999; Qaintrell et al. 2003), as well as a M(R) relation compatible with that resulting from the gravitational red shift measurement of Cottam et al. (2002).


  \begin{figure} \par\includegraphics[width=7.0cm]{2184fig9.eps}\end{figure} Figure 9: Mass radius relation for different EOS. The meaning of the curves is the same as in Fig. 8. The horizontal lines correspond to the observational limits on neutron star mass, whereas the third straight line is the mass-radius relation resulting from the gravitational redshift measurement of Cottam et al. (2002).
Open with DEXTER

Figure 10 shows that different descriptions of the phase transition lead to remarkably different star density profiles. While in the presence of the mixed phase the density is a smooth function of the distance from the star center, the Maxwell construction leads to the appearance of a disontinuity. For comparison, we also show the profile of a star of the same mass, $\sim $1.4 $M_\odot $, made of pure nuclear matter described by the APR EOS.

The discontinuous behavior can be easily understood noting that TOV Eqs. (49) and (50) require that the pressure P(r) be a monotonically decreasing function. It follows that if the pressure is the same for two different values of density, as in the phase transition in the Maxwell construction, they must necessarily correspond to the same value of r.


  \begin{figure} \par\includegraphics[width=7.0cm]{2184fig10.eps}\end{figure} Figure 10: Density profiles of a neutron star of mass $\sim $1.4 $M_\odot $ resulting from different models. Dashed line: APR EOS and MIT bag model EOS with $\alpha _{\rm s} = 0$ and B = 120 MeV/fm3. Phase transition described allowing for the presence of the mixed phase. Solid line: same as the solid line, but with the phase transition described according to Maxwell construction. Dotdash line: pure nuclear matter with APR EOS.
Open with DEXTER

In the coexisting phases scenario, the transition only takes place in stars whose central density exceeds the density of the quark matter phase. These star configurations turn out to be marginally stable, their mass being close to the maximum mass. For example, setting B= 200 MeV/fm3 and $\alpha _{\rm s} = 0.5$ we find that the transition only occurs in stars having mass $\sim $2.0 $M_\odot $. The radius of the quark matter core is small ($\sim $1 Km), while the density jump is large, going from $1.8\times10^{15}$ g/cm3 to $3.9\times10^{15}$ g/cm3. These results are to be compared with those obtained in the mixed phase scenario when Coulomb and surface effects are neglected. In this case there is no jump and the density varies smoothly. At the center of a star of mass $\sim $2.0 $M_\odot $, corresponding to energy-density $\sim $ $2.4\times10^{15}$ g/cm3 the volume fraction occupied by quark matter reaches $\chi \sim 30$%.

   
6 Conclusions

We have carried out a study of the transition from nuclear matter to quark matter in the inner core of neutron stars, aimed at assessing whether the appearance of a mixed phase is energetically favorable and how the emerging picture depends upon the parameters entering the MIT bag model EOS.

In order to minimize the uncertainty associated with the description of the nuclear matter phase, we have adopted a EOS obtained from an ab initio calculation, based on a dynamical model stongly contrained by experimental data and not involving any adjustable parameters (Akmal et al. 1998).

Our results show that the effect of perturbative gluon exchange on the MIT bag model EOS is large and cannot be accounted for adjusting the value of the bag constant B. Neglecting interactions between quarks leads to a considerable softening of the EOS, resulting in a drastically lower transition density.

The fact that the setting $\alpha _{\rm s} = 0$ lead to a much softer EOS is reflected by the rather small value of the maximum neutron star mass, barely exceeding the canonical value of 1.4 $M_\odot $.

The stability of the mixed phase turns out to be strongly affected by surface and Coulomb effects. Using the softer quark matter EOS ( $\alpha _{\rm s} = 0$, B=120 MeV/fm3) we find that even a very small value of the surface tension, $\sigma=2$ MeV/fm3, produces a narrowing of the density region spanned by the mixed phase. With the harder EOS ( $\alpha _{\rm s} = 0.5$, B=200 MeV/fm3) the coexistence of neutral phases of nuclear and quark matter is energetically favored at all densities for $\sigma = 10$ MeV/fm3.

Comparison with the results of Heiselberg et al. suggests that surface and Coulomb effects become larger when a realistic EOS is employed to describe the nuclear matter phase.

While the mass-central density relation appears to be largely unaffected by the occurrence of the mixed phase, its effect can be clearly seen in the M(R) curve. However, as measurements of neutron star radii are plagued by large uncertainties, this feature is not likely to be exploitable to extract clearcut information from observations.

The most striking difference between the Maxwell and Gibbs picture of the phase transition appears in the neutron star density profile, which in the case of transition at constant pressure exhibits a sharp discontinuity.

The presence of a density jump is known to affect neutron star dynamics, leading to the appearance of a class of nonradial oscillation modes, called g-modes, associated with emission of gravitational radiation.

Early investigations of the g-modes focused on the discontinuities produced by the changes of chemical composition in the low density region of the neutron star crust, corresponding to a fractional distance from the surface $\la$10% (Finn 1987; McDermott 1990). These studies have been recently extended to the case of g-modes produced by a discontinuity located at much larger density and involving a much larger density jump, such as those associated with the transition to quark matter (Miniutti et al. 2003). Based on the results of calculations carried out using a simple polytropic EOS, Miniutti et al. (2003) argue that a simultaneous measurements of the frequencies of the fundamental f-mode and the g-mode would provide information on both size and location of the discontinuity.

Although it is unlikely that the first generation of laser interferometric antennae will detect gravitational waves emitted by an oscillating neutron star, the new detectors currently under investigation (see, e.g., the EURO proposal (2000)) are expected to be much more sensitive at the relevant frequencies above 1-2 kHz. Hopefully, information on the neutron star matter EOS and the nature of the transition to quark matter may be provided by gravitational wave astronomy.

Acknowledgements
The authors are deeply indebted to Ignazio Bombaci, Adelchi Fabrocini, Stefano Fantoni, Valeria Ferrari and Vijay Pandharipande for a number of usefuls discussions on issues related to the subjet of this paper.

References

 
Copyright ESO 2005