A&A 434, 355-364 (2005)
DOI: 10.1051/0004-6361:20040238
Stability of planetary orbits in binary systems
Z. E. Musielak 1,2 - M. Cuntz 2,1 - E. A. Marshall 2 -
T. D. Stuit 3
1 - Institut für Theoretische Astrophysik, Universität Heidelberg, Albert Überle Straße 2, 69120 Heidelberg, Germany
2 -
Department of Physics, University of Texas at Arlington, Arlington, TX 76019-0059, USA
3 -
Center for Space Plasma and Aeronomic Research, University of Alabama in Huntsville, Huntsville, AL 35899, USA
Received 10 February 2004 / Accepted 23 December 2004
Abstract
Stability of S-type and P-type planetary orbits in binary systems of
different mass and separation ratios is investigated. Criteria for
stable, marginally stable and unstable planetary orbits are specified.
These criteria are used to determine regions of stability of planetary
orbits in different binary systems with Jupiter-type planets. The
obtained results show that the regions of stability for S-type orbits
depend on the distance ratio between the star and planet, and the
stellar companions, in the range of 0.22 and 0.46, depending on the
mass ratio. For P-type orbits, the regions of stability also depend
on that distance ratio, in the range of 1.75 and 2.45, again depending
on the the mass ratio. Applications of these results to three observed
binary systems with giant planets, namely, 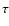 Boo, HD 195019 and
GJ 86, show that the orbits of the giant planets in those systems can
be classified as stable, as expected.
Boo, HD 195019 and
GJ 86, show that the orbits of the giant planets in those systems can
be classified as stable, as expected.
Key words: stars: binaries: general - celestial mechanics - stars: planetary systems - stars:
individual: 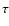 Boo - stars: individual: HD 195019 - stars: individual: GJ 86
Boo - stars: individual: HD 195019 - stars: individual: GJ 86
The existence of planets around single solar-type stars
has been demonstrated by observing the cyclic Doppler shift
in photospheric spectral lines. Since this technique favors
massive planets with small orbits, all discovered planets are
Jupiter-size planets with orbits close to their host stars,
although a few planets with sub-Saturn masses have also been
recently identified (e.g., Marcy & Butler 1998, 2000; Marcy
et al. 2000; Butler et al. 2002; Marcy et al. 2003; Fischer
& Valenti 2003; McArthur et al. 2004). There has been much
theoretical work done in the area of stability of planetary
orbits in habitable zones of these newly discovered systems
(e.g., Jones et al. 2001; Noble et al. 2002). These studies
have shown that terrestrial planets are likely to have stable
orbits in many of these systems, largely depending on the
location of planetary orbits relative to the stellar
habitable zones.
Interestingly, the long-standing question of whether planets
can also exist in multiple stellar systems has been
answered by observations as arguably at least ten binary
and five triple systems with Jupiter-like planets have been
identified (e.g., Patience et al. 2002; Eggenberger et al. 2004,
and references therein). These systems encompass a broad range
of planetary distances and masses, and a very large range of
distances of the binary components, with the closest system
20 AU (GJ 86), and the widest system 6400 AU apart (HD 40979).
Another binary system hosting a Jupiter-type planet not included
in the list by Eggenberger et al. (2004) is HD 168443 (Marcy et al. 2001), in which one of the main components is a brown dwarf. The solar-type star HD 178911B, according Zucker et al. (2002), constitutes the distant component of the system HD 178911 Aa+b
(Tokovinin et al. 2000), indicating that it hosts the first extra-solar planet in a triple system. Zucker et al. also discussed the status of 16 Cyg, which is also identified as
constituting a triple stellar system with a planet (Lloyd et al. 2002).
The number of known binary or triple stellar systems with planets may actually be larger as some single stars, known to host planets, exhibit a drift in the 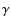 -velocity,
which indicates the presence of a distant companion (Fischer et al. 2001). There is also support for the existence of terrestrial planets in multiple stellar systems based on
recent theoretical studies, which show that Earth-mass planets
can successfully form in binary (and possibly multiple) stellar
systems depending on the stellar masses and separation distances
(e.g., Whitmire et al. 1998; Nelson 2000; Kley 2001; Quintana et al. 2002), even though the predominant effect of a companion on the efficiency of planet formation is a negative one. This work, mainly based on ab-initio simulations of planetary accretion,
supersedes earlier findings which implied that terrestrial planets would only exist around single stars (e.g., Heppenheimer 1974).
-velocity,
which indicates the presence of a distant companion (Fischer et al. 2001). There is also support for the existence of terrestrial planets in multiple stellar systems based on
recent theoretical studies, which show that Earth-mass planets
can successfully form in binary (and possibly multiple) stellar
systems depending on the stellar masses and separation distances
(e.g., Whitmire et al. 1998; Nelson 2000; Kley 2001; Quintana et al. 2002), even though the predominant effect of a companion on the efficiency of planet formation is a negative one. This work, mainly based on ab-initio simulations of planetary accretion,
supersedes earlier findings which implied that terrestrial planets would only exist around single stars (e.g., Heppenheimer 1974).
Multiple stellar systems are in fact very common. According to Abt
& Levy (1976), who studied the stellar multiplicity in a sample
of 135 F3-G2 IV or V stars, the frequency of these systems is
about 65%, with binary systems dominating. This number was
revised by Duquennoy & Mayor (1991) who used a CORAVEL spectroscopic
survey. They obtained 43% or 49% depending on whether a correction
for the presence of spurious binaries was applied. In any case, many
of these multiple (especially binary) systems are currently observed
(or are to be observed in the near future) as the extended search
for planets continues. The main goal of this paper is to investigate
stability of planetary orbits in binary systems of different mass
and separation ratios. The study will help to determine the best
candidates for hosting Jupiter-like and Earth-like planets in binary systems.
Planetary orbits in binary systems can be separated into three different categories. Following Dvorak (1986), the first category
includes orbits well outside the binary, where the planet essentially
orbits the center of mass of both stars (P-type orbit). The second
type of orbit is near one of the stars, with the second star to
be considered a perturbing agent (S-type orbits). The third type
refers to orbits near the triangular Lagrangian points L4 or L5,
which are of little interest here and will not be further discussed,
except in conjunction with test simulations (see Sect. 2). An
extensive body of literature is devoted to the stability of the P
and S-type orbits in binary systems (e.g., Henon & Guyot 1970;
Szebehely & McKenzie 1981; Dvorak 1984, 1986; Dvorak et al. 1989; Benest 1988, 1989, 1993, 1996; Kubala et al. 1993; Holman & Wiegert 1999). Specifically, in the work of Holman and Wiegert, binaries with different eccentricities and mass ratios were considered and
regions of stability of both S-type and P-type orbits were identified.
More recently, David et al. (2003) investigated the orbital stability
of an Earth-mass planet around a solar-mass star in the presence of
a companion star considering a range of companion masses between 0.001 and 0.5 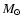 .
Their work covers a significant portion of the parameter space for S-type orbits studied in this paper, however, they do not consider P-type orbits. David et al. determined the
planet's ejection time for systems with different orbital eccentricities
and semimajor axes. For fixed companion masses, the ejection time
was found to be a steep function of the periastron distance (or orbital
radius for circular orbits) to the primary star, a prediction to be
compared with the results obtained in this paper.
.
Their work covers a significant portion of the parameter space for S-type orbits studied in this paper, however, they do not consider P-type orbits. David et al. determined the
planet's ejection time for systems with different orbital eccentricities
and semimajor axes. For fixed companion masses, the ejection time
was found to be a steep function of the periastron distance (or orbital
radius for circular orbits) to the primary star, a prediction to be
compared with the results obtained in this paper.
Further work focused on the study of orbital stability of terrestrial
planets in the habitable zone of binary systems. Simulations have
been performed for 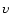 And,
And, 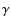 Cep, GJ 86, and 61 Cyg
(Norwood & Haghighipour 2002; Dvorak et al. 2003; Solovaya &
Pittich 2004; Haghighipour 2005). Models were also
given for the systems of 55 Cnc (von Bloh et al. 2003) and
GJ 777A (Asghari et al. 2004). In those cases, however, the effect
of the binary component on the orbital stability of the terrestrial
planet was neglected, owing to the very large separation distances
in those systems of 1065 and 3000 AU, respectively.
Cep, GJ 86, and 61 Cyg
(Norwood & Haghighipour 2002; Dvorak et al. 2003; Solovaya &
Pittich 2004; Haghighipour 2005). Models were also
given for the systems of 55 Cnc (von Bloh et al. 2003) and
GJ 777A (Asghari et al. 2004). In those cases, however, the effect
of the binary component on the orbital stability of the terrestrial
planet was neglected, owing to the very large separation distances
in those systems of 1065 and 3000 AU, respectively.
In this paper, we investigate the stability of both S and P-type orbits
in binary systems of different mass ratios and separation ratios. All
our calculations are performed for circular orbits. The problem of the
existence of habitable zones in the considered binary systems is not
within the scope of this work and will be addressed in a later paper
(Cuntz & Musielak 2005). Our method and criteria for stable, marginally
stable and unstable orbits are described in Sect. 2. Case studies and
general results for the stability of the S and P-type orbits given as
functions of mass and separation ratios are presented and discussed
in Sect. 3 and Sect. 4, respectively. Applications of our results to
specific binary systems that host Jupiter-like planets are described
in Sect. 5. Our conclusions are given in Sect. 6.
To investigate the stability of S and P-type orbits in binary systems,
we developed a numerical code based on the Runge-Kutta-Fehlberg
integration scheme that runs two algorithms simultaneously, i.e., one
of fourth-order accuracy and the other of fifth-order accuracy. The
difference between each element of the two sets of results are then
compared to a user-defined tolerance limit; if any of these differences
are larger than the tolerance limit, the step size is reduced and the
step is repeated until the differences are acceptable. These differences
are approximations of the local truncation error of the fifth-order
results of the integration, and provide a measure of error accumulated
over the time of simulation. By limiting these accumulated errors
to small fractions of their respective elements (position, velocity,
and acceleration), the validity of the simulation is guaranteed to
fifth-order accuracy. The automatic adjustment of step size is
especially useful for orbits that change shape unexpectedly.
In order to validate the code, several tests were performed, namely,
two-body and restricted three-body tests. In the two-body test,
simulations were performed with a central mass of one solar mass unit (MU) with zero absolute velocity and an orbiting mass of 1  10-6 MU at a distance of 2 astronomical units (AU) from the central mass with a velocity of 0.707 AU/TU, where TU is the time
unit that equals 5.0114019
10-6 MU at a distance of 2 astronomical units (AU) from the central mass with a velocity of 0.707 AU/TU, where TU is the time
unit that equals 5.0114019  106 s for a near-circular
orbit. The analytical solution for this configuration results in
an orbital period of 2.8218 years. The numerical solution after a
simulation time of 1600 years resulted in an approximate orbital
period of 2.8194
106 s for a near-circular
orbit. The analytical solution for this configuration results in
an orbital period of 2.8218 years. The numerical solution after a
simulation time of 1600 years resulted in an approximate orbital
period of 2.8194 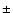 0.0024 years, which is within 0.17% of
the analytical solution for the maximal error bar.
0.0024 years, which is within 0.17% of
the analytical solution for the maximal error bar.
In the first restricted three-body case, the following input parameters
were considered: central body with m1 = 0.75 MU, secondary body with
m2 = 0.25 MU and a body with m3 = 1 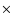 10-3 MU. In the
first test, the smallest body was placed at either the L4 or L5 Lagrangian stable point and its stability was studied for distances
1 AU, 2 AU and 5 AU between the central and secondary bodies. Numerical
simulations showed that the third body slowly moved away from the stable
points after three or more orbits. Decreasing the truncation tolerance
from 10-10 to 10-20 extended the valid results by approximately
20%. The second restricted three-body test was a straight-line, equal-spacing
configuration of three equal masses. The input parameters were chosen such
that the masses of all three bodies were 1 MU each, with the central mass
having zero velocity and the other two masses on opposite sides separated
by 1 AU with velocities of 1 AU/TU in opposite directions, perpendicular
to the line connecting the masses. The comparison between the analytical and
numerical results of these two tests provided a good basis for the truncation
tolerance selection.
10-3 MU. In the
first test, the smallest body was placed at either the L4 or L5 Lagrangian stable point and its stability was studied for distances
1 AU, 2 AU and 5 AU between the central and secondary bodies. Numerical
simulations showed that the third body slowly moved away from the stable
points after three or more orbits. Decreasing the truncation tolerance
from 10-10 to 10-20 extended the valid results by approximately
20%. The second restricted three-body test was a straight-line, equal-spacing
configuration of three equal masses. The input parameters were chosen such
that the masses of all three bodies were 1 MU each, with the central mass
having zero velocity and the other two masses on opposite sides separated
by 1 AU with velocities of 1 AU/TU in opposite directions, perpendicular
to the line connecting the masses. The comparison between the analytical and
numerical results of these two tests provided a good basis for the truncation
tolerance selection.
In addition to testing the code against known analytical solutions,
we also compared some of our results to those obtained by another numerical
code that was independently developed and tested by Noble et al. (2002).
Good agreement was found between orbits computed by these two different
numerical codes.
Typical initial conditions for calculating the inner (S-type) and
outer (P-type) planetary orbits in binary systems are presented in
Fig. 1. The considered configurations are such that the resulting
planetary orbits are always circular; this will simplify our
consideration of orbital stability in theoretical binary systems.
Since the initial positions of both stars and the giant planet are
specified, the initial velocity 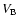 of the
secondary star relative to the primary star and the initial velocity
of the
secondary star relative to the primary star and the initial velocity 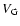 of the giant planet relative to the primary star must be determined.
of the giant planet relative to the primary star must be determined.
These velocities are computed using the energy equation for circular
orbits (e.g., Danby 1988) given as
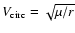 ,
where
,
where
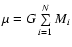 with G as universal
gravitational constant, Mi as masses, and r as orbital radius
of the center of mass. In units MU, AU, and TU, we have G = 1 and
with G as universal
gravitational constant, Mi as masses, and r as orbital radius
of the center of mass. In units MU, AU, and TU, we have G = 1 and
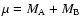 ,
with both
,
with both 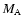 and
and 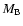 given in MU. The velocity
given in MU. The velocity 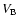 is calculated using the above
given equation with
is calculated using the above
given equation with
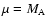 and
and
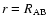 ,
where
,
where
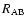 is the distance between the primary and secondary star. This two-body system is simulated by the numerical code for a short time to find the initial position and velocity of the center of mass
relative to the reference frame fixed to the primary star.
is the distance between the primary and secondary star. This two-body system is simulated by the numerical code for a short time to find the initial position and velocity of the center of mass
relative to the reference frame fixed to the primary star.
For the inner orbits, the velocity 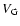 is computed taking
is computed taking
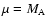 ,
since the primary star is the only body enclosed
by the orbit of the planet, and
,
since the primary star is the only body enclosed
by the orbit of the planet, and
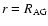 ,
where
,
where
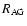 is the distance between the primary star and the planet. The result
is then added to the velocity of the center of mass of the stars to
cancel out the relative motion to produce a near-circular planetary
orbit. For the outer orbits, the velocity
is the distance between the primary star and the planet. The result
is then added to the velocity of the center of mass of the stars to
cancel out the relative motion to produce a near-circular planetary
orbit. For the outer orbits, the velocity 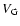 is again
computed using the same equation, but unlike the inner orbit
calculation, we have
is again
computed using the same equation, but unlike the inner orbit
calculation, we have
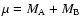 ,
since now the
planet's orbit encloses both stars. The result is again added to
the velocity of the center of mass of the stars to cancel out the
relative motion. In addition, the initial position of the planet
is adjusted by vectorially adding to it the position of the center
of mass of the stars relative to the primary star. This places the
initial position of the planet at the same x-axis position as the
system center-of-mass (see Fig. 1).
,
since now the
planet's orbit encloses both stars. The result is again added to
the velocity of the center of mass of the stars to cancel out the
relative motion. In addition, the initial position of the planet
is adjusted by vectorially adding to it the position of the center
of mass of the stars relative to the primary star. This places the
initial position of the planet at the same x-axis position as the
system center-of-mass (see Fig. 1).
These initial conditions were used in all simulations presented in
this paper. Of course, initial conditions often have a significant
effect on a system that is marginally stable (see below); therefore,
our results are by no means absolute in those cases. However, the
results showing undeniably stable or unstable orbits are definitely
significant in establishing the stability of a given configuration.
![\begin{figure}
\par\includegraphics[height=3.5cm,width=8.8cm,clip]{0238fig1.eps}\end{figure}](/articles/aa/full/2005/16/aa0238-04/Timg20.gif) |
Figure 1:
Initial position of a giant planet with mass 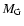 relative to the reference frame centered at the primary star with
mass
relative to the reference frame centered at the primary star with
mass 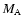 .
The secondary star has mass .
The secondary star has mass 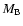 and
the center of mass is denoted by CM. Note that the initial position of the giant planet is different for inner (S-type) and outer (P-type) planetary orbits. The choice of the initial
velocities
and
the center of mass is denoted by CM. Note that the initial position of the giant planet is different for inner (S-type) and outer (P-type) planetary orbits. The choice of the initial
velocities 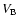 and
and 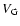 is described in the main text.
is described in the main text. |
| Open with DEXTER |
The main reason for considering circular orbits is that formal
criteria of stability can easily be determined (e.g., Danby 1988).
In this paper, orbital stability is determined based on the following
criterion: stable (S) 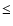
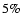 ,
marginally stable (MS), given as
,
marginally stable (MS), given as
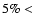 (MS)
(MS) 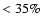 ,
and unstable (U)
,
and unstable (U) 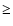
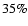 ,
where the percentage
refers to the orbital variability with respect to the initial distance
between the primary star and the giant planet specified at the begin of the
calculations (see Fig. 1). The variability is averaged over the number
of computed planetary orbits and thereafter the stability criterion is
applied. The stability limit of 5% is motivated by studies of Earth,
which seem to indicate that such a stability limit is required for Earth
to remain within the conservative habitable zone around the Sun
(e.g., Kasting et al. 1993; Underwood et al. 2003), a likely precondition
for the evolution of sophisticated forms of life (e.g., Bennett et al. 2003).
The limit of 35% between marginally stable and unstable orbits is based
on our own investigations which show that test planets outside that limit
are typically not orbitally confined to the respective binary system.
,
where the percentage
refers to the orbital variability with respect to the initial distance
between the primary star and the giant planet specified at the begin of the
calculations (see Fig. 1). The variability is averaged over the number
of computed planetary orbits and thereafter the stability criterion is
applied. The stability limit of 5% is motivated by studies of Earth,
which seem to indicate that such a stability limit is required for Earth
to remain within the conservative habitable zone around the Sun
(e.g., Kasting et al. 1993; Underwood et al. 2003), a likely precondition
for the evolution of sophisticated forms of life (e.g., Bennett et al. 2003).
The limit of 35% between marginally stable and unstable orbits is based
on our own investigations which show that test planets outside that limit
are typically not orbitally confined to the respective binary system.
Examples of stable, marginally stable and unstable planetary
orbits are shown in Figs. 2-4, respectively. The presented results
were obtained for a binary systems with 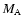 = 1
= 1 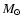 ,
,
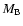 = 0.6
= 0.6 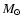 ,
,
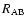 = 8 AU and
= 8 AU and 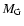 = 1
= 1
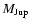 .
Stable, marginally stable and unstable orbits were
calculated by varying the distance between the primary star and the
planet, and the following cases were considered:
.
Stable, marginally stable and unstable orbits were
calculated by varying the distance between the primary star and the
planet, and the following cases were considered:
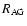 = 1.60 AU
for stable orbits (Fig. 2),
= 1.60 AU
for stable orbits (Fig. 2),
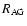 = 2.56 AU for marginally stable
orbits (Fig. 3), and finally
= 2.56 AU for marginally stable
orbits (Fig. 3), and finally
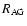 = 2.60 AU for unstable orbits
(Fig. 4). The results of these simulations are summarized in Table 2.
The same stability criteria were applied to both S-type and P-type orbits;
for details see Sects. 4.1 and 4.2.
= 2.60 AU for unstable orbits
(Fig. 4). The results of these simulations are summarized in Table 2.
The same stability criteria were applied to both S-type and P-type orbits;
for details see Sects. 4.1 and 4.2.
![\begin{figure}
\par\includegraphics[height=6.7cm,width=7cm,clip]{0238fig2.eps}\end{figure}](/articles/aa/full/2005/16/aa0238-04/Timg28.gif) |
Figure 2:
Stable planetary orbit obtained for the binary system 3 given in Table 1. The criterion for stable orbits is given in the main text. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[height=6.7cm,width=7cm,clip]{0238fig3.eps}\end{figure}](/articles/aa/full/2005/16/aa0238-04/Timg29.gif) |
Figure 3:
Marginally stable planetary orbit obtained for the binary
system 3 given in Table 1. The criterion for marginally stable
orbits is given in the main text. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[height=6.7cm,width=7cm,clip]{0238fig4.eps}\end{figure}](/articles/aa/full/2005/16/aa0238-04/Timg30.gif) |
Figure 4:
Unstable planetary orbit obtained for the binary system 3 given in Table 1. The criterion for unstable orbits is given in the main text. |
| Open with DEXTER |
We consider four different theoretical binary systems with the
physical properties summarized in Table 1. A Jupiter-type planet
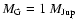 is included in each system and its distance
to the primary star is varied to obtain orbits of different stability.
Two of these systems (1 and 2) have the same masses, but different
separations
is included in each system and its distance
to the primary star is varied to obtain orbits of different stability.
Two of these systems (1 and 2) have the same masses, but different
separations
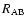 between the primary and secondary star.
The binary system 3 has different masses
between the primary and secondary star.
The binary system 3 has different masses 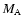 and
and 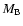 as well as different
as well as different
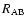 than the systems 1 and 2. However,
the mass ratio
than the systems 1 and 2. However,
the mass ratio
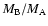 is the same in all three
systems. The binary system 4 differs in both mass and separation
ratios from the other systems. The stability of planetary S-type
and P-type orbits in these systems is studied using the
numerical code described in Sect. 2. Typical timespans for the
numerical simulation were 1000 planetary orbital periods. However,
in some cases (see below) additional calculations were performed
with the simulation time increased to 150 000 and 40 000 orbital
periods for S-type and P-type orbits, respectively. In our calculations of observed binary systems, we used up to 105 orbital periods (see Sect. 5).
is the same in all three
systems. The binary system 4 differs in both mass and separation
ratios from the other systems. The stability of planetary S-type
and P-type orbits in these systems is studied using the
numerical code described in Sect. 2. Typical timespans for the
numerical simulation were 1000 planetary orbital periods. However,
in some cases (see below) additional calculations were performed
with the simulation time increased to 150 000 and 40 000 orbital
periods for S-type and P-type orbits, respectively. In our calculations of observed binary systems, we used up to 105 orbital periods (see Sect. 5).
Table 1:
Theoretical binary systems.
Table 2:
Stability of S-type orbits in binary systems.
Various different cases have been studied and the most important
results obtained for inner (S-type) orbits are summarized in Tables 2
and 3. According to Table 2, orbital stability is the same for the
binary systems 1, 2 and 3, which have the same mass ratios
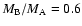 ,
but different masses
,
but different masses 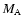 ,
,
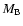 and separation distances
and separation distances
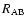 .
Different
separation ratios of
.
Different
separation ratios of
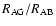 between 0.200 and 0.325
result in stable, marginally stable and unstable planetary orbits,
respectively. However, the orbital stability
behavior becomes different when the mass ratio is changed and the
separation ratio remains the same compared to the previous systems
(see binary system 4 of Table 2). This can be shown even more clearly
by taking the separation ratio to be constant and changing the mass
ratio by varying the mass of the secondary star (see Table 3).
Hereby we assumed
between 0.200 and 0.325
result in stable, marginally stable and unstable planetary orbits,
respectively. However, the orbital stability
behavior becomes different when the mass ratio is changed and the
separation ratio remains the same compared to the previous systems
(see binary system 4 of Table 2). This can be shown even more clearly
by taking the separation ratio to be constant and changing the mass
ratio by varying the mass of the secondary star (see Table 3).
Hereby we assumed
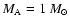 and
and
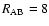 AU.
Now the orbits change from stable to unstable when the mass ratio
is increased from 0.2 to 0.8. These results suggest that the regions of stability of planetary orbits in binary systems are determined both by the mass and separation ratio.
AU.
Now the orbits change from stable to unstable when the mass ratio
is increased from 0.2 to 0.8. These results suggest that the regions of stability of planetary orbits in binary systems are determined both by the mass and separation ratio.
Table 3:
Dependence of orbital stability on mass of secondary star.
Table 4:
Time development of orbital variability near stability boundary
for S-type orbits.
The next step is to compute the boundaries separating
planetary orbits of different stability for binary systems of
different mass and separation ratios. These boundaries are plotted
in Fig. 5, which shows that the inner orbits can be divided into
two distinct classes, namely, stable and unstable (given by the
two solid curves in Fig. 5). According to our stability criteria
(see Sect. 3), orbits in the region between the two curves can be
classified as marginally stable. It is interesting that the region
of stable orbits decreases with increasing mass ratio. In addition, the
region of marginally stable orbits reaches its maximum for the lowest
mass ratio of 0.05, indicative that the classification is sensitive
to the considered stability criteria (see Figs. 2 to 4) and the adopted
initial conditions (see Fig. 1). The boundary separating stable
orbits from marginally stable orbits changes from a distance ratio
of 0.22 for a stellar mass ratio of 1.0 to 0.46 for a mass ratio of 0.05.
![\begin{figure}
\par\includegraphics[height=6.5cm,width=7cm,clip]{0238fig5.eps}\end{figure}](/articles/aa/full/2005/16/aa0238-04/Timg38.gif) |
Figure 5:
Range of mass ratios and separation ratios corresponding
to stable, marginally stable and unstable inner (S-type) planetary
orbits in binary systems. The simulations are based on 1000 orbits. |
| Open with DEXTER |
Furthermore, we tested the stability of the simulations over more
extended runs, by inspecting the degree of orbital stability for
mass ratio/distance ratio points just inside the domain of orbital
stability. We found that for 150 000 planetary orbits corresponding
to 0.6 to 1.4  106 years, depending on the system, the
range of orbital variability stays between 5.11 to 6.02% compared
to 5.12 to 6.00% for the baseline models of 1000 planetary orbits
(see Table 4). This approach allows us to highlight the time development,
if any, of small variations. The results obtained for mass ratios
106 years, depending on the system, the
range of orbital variability stays between 5.11 to 6.02% compared
to 5.12 to 6.00% for the baseline models of 1000 planetary orbits
(see Table 4). This approach allows us to highlight the time development,
if any, of small variations. The results obtained for mass ratios
 between 0.1 and 0.9 seem to indicate that the domain of stability is essentially independent on the length of the model run pursued, at least if the time of simulation exceeds
1000 planetary orbits.
between 0.1 and 0.9 seem to indicate that the domain of stability is essentially independent on the length of the model run pursued, at least if the time of simulation exceeds
1000 planetary orbits.
These results reconfirm that regions of stability for S-type orbits
exist in binary systems, in agreement with previous results. For
example, Benest (1993, 1996) showed that nearly circular orbits on the
order of a quarter of the periastron separation between two stars are
stable in the 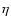 Coronae Borealis,
Coronae Borealis, 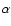 Centauri and Sirius systems.
The mass ratios of these systems are in the range of 0.45 to 0.66, which
is consistent with stable orbits presented in Fig. 5. Further
comparisons with the more recent work by David et al. (2003) will be given
in Sect. 4.3. The latter authors investigated a similar range of companion
masses, but assumed an Earth-mass rather than a Jupiter-mass planet
for their orbital stability analyses.
Centauri and Sirius systems.
The mass ratios of these systems are in the range of 0.45 to 0.66, which
is consistent with stable orbits presented in Fig. 5. Further
comparisons with the more recent work by David et al. (2003) will be given
in Sect. 4.3. The latter authors investigated a similar range of companion
masses, but assumed an Earth-mass rather than a Jupiter-mass planet
for their orbital stability analyses.
The location of the boundaries shown in Fig. 5 also depends on 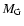 ,
to a certain extent. To assess this dependency, we increased
,
to a certain extent. To assess this dependency, we increased 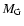 to 5
to 5
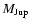 and computed the resulting shift of the boundaries.
Now the region of stability of each S-type system is increased on the order
of 10% (i.e., between 8.5 and 13.6%). In addition, the boundary between
the stable and marginally stable zone is shifted toward larger distance
ratios, but only on the order of 2%. Consequently, the region of stable
S-type orbits in Fig. 5 becomes larger when the mass of the giant planet
and computed the resulting shift of the boundaries.
Now the region of stability of each S-type system is increased on the order
of 10% (i.e., between 8.5 and 13.6%). In addition, the boundary between
the stable and marginally stable zone is shifted toward larger distance
ratios, but only on the order of 2%. Consequently, the region of stable
S-type orbits in Fig. 5 becomes larger when the mass of the giant planet 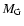 is increased while the masses
is increased while the masses 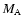 and
and 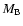 remain unchanged.
remain unchanged.
We also investigated the stability of outer (P-type) orbits for all
binary systems given in Table 1. The main conclusion from these
studies is similar to that obtained for the inner (S-type) orbits,
namely, that the region of stability of P-type orbits is determined by
the mass and separation ratios. Selected results are given in
Table 5. The orbits can be classified as either
stable, marginally stable, or unstable. Our simulations
show that all outer orbits classified as marginally stable
after the simulation time of 10 planetary orbital periods became
unstable after the time of simulations has been extended (see Table 6).
Interestingly, test simulation for binary system 2 showed that the point
in time for this transition critically depends on the distance
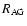 .
For
.
For
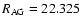 AU, this transition occurred after 20 orbital periods, whereas for
AU, this transition occurred after 20 orbital periods, whereas for
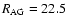 AU, the transition happened after 105 orbital periods. For some distances
AU, the transition happened after 105 orbital periods. For some distances
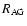 ,
even orbits originally classified as stable became unstable. Nevertheless, we always found a distance
,
even orbits originally classified as stable became unstable. Nevertheless, we always found a distance
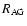 ,
for which the orbit remains stable even after
long simulation times such as 4
,
for which the orbit remains stable even after
long simulation times such as 4  104 orbital periods.
104 orbital periods.
Table 5:
Stability of P-type orbits in binary systems.
Table 6:
Dependence of orbital stability on simulation time.
Figure 6 shows the boundaries between stable, marginally stable,
and unstable P-type orbits. Selected results are given in Table 6.
The results depicted in Fig. 6 demonstrate that the minimum radius
of stable circular orbits increases from a distance ratio of 1.75
to 2.45, when the mass ratio is increased (due to increasing
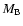 ), although it remains about constant for mass ratios
larger than 0.4. The existence of this "critical'' mass ratio of
approximately 0.4 is an interesting result as it shows that changes
in the sphere of influence of a binary system resulting from the
increasing
), although it remains about constant for mass ratios
larger than 0.4. The existence of this "critical'' mass ratio of
approximately 0.4 is an interesting result as it shows that changes
in the sphere of influence of a binary system resulting from the
increasing 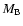 do not influence orbital stability of a
giant planet as long as the mass ratio is beyond that value. The
comparison between Figs. 5 and 6 also shows that this result is
only valid for the P-type orbits.
do not influence orbital stability of a
giant planet as long as the mass ratio is beyond that value. The
comparison between Figs. 5 and 6 also shows that this result is
only valid for the P-type orbits.
We again explored the stability of the simulations over a more
extended time frame. Therefore, we chose time periods of 30 000
or 40 000 planetary orbits corresponding to 2.7 to 3.3  106 years, depending on the system, compared to the baseline of 1000 orbits. The distance points were again chosen just inside the domain of stable orbits. We found that the orbital variability
stays between 4.04 to 4.99% compared to 4.16 to 5.00% for the
baseline models of 1000 planetary orbits (see Table 7). These
results again confirm that the domains of stability are essentially
independent of the lengths of the simulation - at least beyond a
minimal time of simulation.
106 years, depending on the system, compared to the baseline of 1000 orbits. The distance points were again chosen just inside the domain of stable orbits. We found that the orbital variability
stays between 4.04 to 4.99% compared to 4.16 to 5.00% for the
baseline models of 1000 planetary orbits (see Table 7). These
results again confirm that the domains of stability are essentially
independent of the lengths of the simulation - at least beyond a
minimal time of simulation.
![\begin{figure}
\par\includegraphics[height=6.5cm,width=7cm,clip]{0238fig6.eps}\end{figure}](/articles/aa/full/2005/16/aa0238-04/Timg43.gif) |
Figure 6:
Range of mass ratios and sparation ratios corresponding to
stable, marginally stable and unstable outer (P-type) planetary orbits
in binary systems. The simulations are based on 1000 orbits. |
| Open with DEXTER |
Table 7:
Time development of orbital variability near stability boundary
for P-type orbits.
The results shown in Fig. 6 have counterparts in Kubala et al.
(1993). Here, two plots can be used for comparison - a plot of
Hill's critical orbital radii and a plot combining the critical radii
of Graziani & Black (1981) using a Laplace method and a Hill's
method approach (e.g., Danby 1988). It should be noted that
Kubala et al. (1993) used a different definition of mass ratio than used
here. They defined
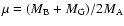 as the mass ratio. The
plot of Hill's critical orbit radii shows a peak at a radius of about 2.4 at approximately
as the mass ratio. The
plot of Hill's critical orbit radii shows a peak at a radius of about 2.4 at approximately 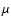 = 0.4 (which corresponds to a mass ratio
= 0.4 (which corresponds to a mass ratio
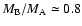 ).
The combination plot, in which the lower critical radius is used so that both stability criteria are satisfied, peaks at a radius of about 2.4 at
).
The combination plot, in which the lower critical radius is used so that both stability criteria are satisfied, peaks at a radius of about 2.4 at 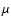 = 0.25 (which corresponds to
a mass ratio
= 0.25 (which corresponds to
a mass ratio
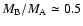 ). The curve representing
the boundary between stable and marginally stable orbits in Fig. 6 peaks at a radius just near 2.45 at a mass ratio of about 0.4 in agreement with the results described here.
). The curve representing
the boundary between stable and marginally stable orbits in Fig. 6 peaks at a radius just near 2.45 at a mass ratio of about 0.4 in agreement with the results described here.
Dvorak et al. (1989) also considered P-type planetary
orbits. They compared their results with the results from two other papers,
Henon & Guyot (1970) and Szebehely & McKenzie (1981) in tabular form for
mass ratios of 0.1 to 0.5, defined in the same way as by Kubala et al. (1993).
While these authors defined only a single stability boundary, Dvorak et al.
(1989) defined an upper and lower critical orbit. Their lower critical orbit
ranges from 1.7 at a 0.1 mass ratio to 1.9 at a 0.5 mass ratio. The upper
critical orbit ranges from 2.15 at 0.1 to 2.3 at 0.5 mass ratio, with a peak
of 2.4 at a mass ratio of 0.2. Henon & Guyot showed almost no variation with
mass ratio and the critical orbit radius is about 2.14; the general shape of
the curves presented by these authors is very similar to our results shown in
Fig. 6. Szebehely & McKenzie's critical orbits ranges from 2.27 at a mass
ratio of 0.1, to a peak of 2.45 at 0.25 mass ratio, to 2.17 at 0.5 mass ratio.
All these data are in the vicinity of the results of this paper, even though
the peaks appear at lower mass ratios. Dvorak et al. (1989) concluded that
the stability regions are independent of the mass ratio. The results presented
in this paper show that there is indeed a range of mass ratios for which
this conclusion is correct.
The results of this investigation indicate that domains of stability exist
for planetary orbits in various theoretical stellar binary systems and that
these domains can be generalized to any binary system based
on the mass and distance ratios of the various components involved -
a result in agreement with previous investigations.
In fact, only the mass ratio is relevant for defining the zones of stability,
not the individual masses of the stars themselves, which is a key point in the
characterization of the dynamics of stellar binary systems.
The boundary curves for stable orbits in Figs. 5 and 6 define
limits for the periods of stable planetary orbits in binary systems. The
leftmost curve in Fig. 5 (S-type orbits) corresponds to maximal separation
ratios between 0.22 and 0.46, depending on the mass ratio of the stellar
components, whereas the rightmost curve in Fig. 6 (P-type orbits) corresponds
to minimal separation ratios between 1.75 and 2.45, again given by the
stellar mass ratio. This information can be incorporated into Kepler's
third law to obtain a relation for a conservative maximum (minimum) period
for the stable inner (outer) orbits of planets in binary systems.
Table 8:
Comparison with results by David et al.
These findings can be compared to other results in the literature,
particularly the work by David et al. (2003). They studied the orbital
stability of an Earth-mass planet around a solar-mass star in the presence
of a companion star for a range of companion masses between 0.001 and 0.5 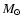 .
In fact, they considered both circular and elliptical orbits, and derived expressions for the expected ejection time of the planet from the system. For fixed companion masses, the ejection time
was found to be a steep function of the periastron distance (or orbital
radius for circular orbits) to the primary star.
David et al. predict that the domain of orbital stability gets progressively
smaller over time according to the logarithm of the time of simulation.
Table 4 depicting the possible time evolution of planetary instability
for S-type orbits, however, does not indicate this type of behavior,
as the domain of stability does not change noticeably beyond 1000 planetary
orbits (at least not within the time frame of up to 150 000 planetary orbits).
Nonetheless, we were able to estimate the consistency of the boundary between
stable and marginally stable orbits based on the formula for the planetary
ejection times by David et al. (2003) for simulations of up to
106 years. We found full consistency for the mass ratio
.
In fact, they considered both circular and elliptical orbits, and derived expressions for the expected ejection time of the planet from the system. For fixed companion masses, the ejection time
was found to be a steep function of the periastron distance (or orbital
radius for circular orbits) to the primary star.
David et al. predict that the domain of orbital stability gets progressively
smaller over time according to the logarithm of the time of simulation.
Table 4 depicting the possible time evolution of planetary instability
for S-type orbits, however, does not indicate this type of behavior,
as the domain of stability does not change noticeably beyond 1000 planetary
orbits (at least not within the time frame of up to 150 000 planetary orbits).
Nonetheless, we were able to estimate the consistency of the boundary between
stable and marginally stable orbits based on the formula for the planetary
ejection times by David et al. (2003) for simulations of up to
106 years. We found full consistency for the mass ratio
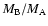 = 0.5, but no consistency for the lower mass ratio of
= 0.5, but no consistency for the lower mass ratio of
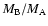 = 0.1 (see Table 8). A possible reason for this
disagreement might be that David et al. considered Earth-mass planets
rather than Jupiter-mass planets in their simulations, which may have an
increased impact for models involving a companion star with a relatively low mass.
= 0.1 (see Table 8). A possible reason for this
disagreement might be that David et al. considered Earth-mass planets
rather than Jupiter-mass planets in their simulations, which may have an
increased impact for models involving a companion star with a relatively low mass.
Table 9:
Stability of S-type orbits in binary systems with
observed giant planets.
Finally, we should also comment on the uncertainty bar assigned to the
planetary ejection times deduced in the simulations by David et al. (2003).
Here it should be noted that these authors studied a large variety of models
involving planets at different angular starting positions, whereas in our work
both the companion star and the giant planet were placed at the 3 o'clock
position in all simulations. David et al. found that the ejection critically
depends on those starting positions in the cases of orbital instability - a result in full agreement with our previous work (Noble et al. 2002).
A significantly reduced uncertainty bar is implied if the model
simulations would have been restricted to a distinct starting position
as in the present work.
Here we explore the orbital stability of planets
in realistic binary systems. As stated in Sect. 1, there are
at least 10 binary systems with known Jupiter-type planets
(Patience et al. 2002; Eggenberger et al. 2004, and references
therein). In all these systems, the Jupiter-type planets are
located on inner (S-type) orbits as so far no systems with
giant planets located on outer (P-type) orbits have been found.
In this work, we consider only cases in which the planet is orbiting
its host star in a circular or quasi-circular orbit. Therefore,
the permissible planetary eccentricity is assumed to be
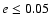 .
This condition limits the number of target systems to
three, namely,
.
This condition limits the number of target systems to
three, namely, 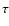 Boo, HD 195019, and GJ 86. Their physical
properties are briefly described below and summarized in Table 9.
Boo, HD 195019, and GJ 86. Their physical
properties are briefly described below and summarized in Table 9.
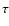 Boo (F7 V) is a well-studied star with a very massive
Jupiter-type planet with a minimum mass of 3.87
Boo (F7 V) is a well-studied star with a very massive
Jupiter-type planet with a minimum mass of 3.87
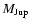 .
The orbital distance of the planet is 0.0462 AU (Butler
et al. 1997), allowing the planet to be classified as one of 20 or
so close-in giant planets discovered to date. Incidentally, the
planet has also been suspected to increase the activity level of
its host star, as first pointed out by Cuntz et al. (2000) and
recently verified observationally by Shkolnik
et al. (2003). The orbital eccentricity of the planet is given as
e = 0.018
.
The orbital distance of the planet is 0.0462 AU (Butler
et al. 1997), allowing the planet to be classified as one of 20 or
so close-in giant planets discovered to date. Incidentally, the
planet has also been suspected to increase the activity level of
its host star, as first pointed out by Cuntz et al. (2000) and
recently verified observationally by Shkolnik
et al. (2003). The orbital eccentricity of the planet is given as
e = 0.018 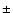 0.016 (Butler et al. 1997). Patience et al. (2002)
pointed out that
0.016 (Butler et al. 1997). Patience et al. (2002)
pointed out that  Boo constitutes an eccentric binary system
with
Boo constitutes an eccentric binary system
with  Boo A
Boo A  1.3
1.3 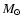 ,
,
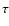 Boo B
Boo B 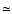 0.4
0.4 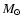 and a semi-major axis of 225 AU. Even though our method so far has only been proposed for systems with circular orbits for both the planets and the binary components, we included
and a semi-major axis of 225 AU. Even though our method so far has only been proposed for systems with circular orbits for both the planets and the binary components, we included 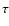 Boo
as a general illustration.
Boo
as a general illustration.
HD 195019 is a G3 IV-V star that is orbited by a Jupiter-type planet.
Based on the analysis of Doppler measurements obtained at Lick
Observatory, Fischer et al. (1999) identified Keplerian velocity
variations with a period of 18.27 days, an orbital eccentricity
of e = 0.03 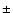 0.03, indicative of a minimum planet mass of
0.03, indicative of a minimum planet mass of
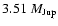 .
The semi-major axis of the orbit was determined as a=0.14 AU. HD 195019 was later identified as a
member of a wide binary system with a separation distance of 157 AU
(Allen et al. 2000). The secondary star is a mid-type K dwarf star with
a likely mass of about 0.7
.
The semi-major axis of the orbit was determined as a=0.14 AU. HD 195019 was later identified as a
member of a wide binary system with a separation distance of 157 AU
(Allen et al. 2000). The secondary star is a mid-type K dwarf star with
a likely mass of about 0.7 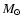 (Gray 1992). The mass of the
primary star was estimated as 0.98
(Gray 1992). The mass of the
primary star was estimated as 0.98 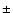
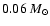 based on its
spectral type (Allen et al. 2000).
based on its
spectral type (Allen et al. 2000).
GJ 86 (=HD 13445) is an example of a system where a brown dwarf
constitutes a companion to a star that is orbited by a
planet. Queloz et al. (2000) reported a 4
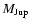 planet
(minimum mass) with a 15.8 day orbital period and a 0.11 AU semi-major
axis around GJ 86A, a K dwarf star. The inferred eccentricity is
e= 0.046
planet
(minimum mass) with a 15.8 day orbital period and a 0.11 AU semi-major
axis around GJ 86A, a K dwarf star. The inferred eccentricity is
e= 0.046 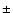 0.004. The planet detection has been made through
very precise radial velocity measurements with the CORALIE echelle
spectrograph. Els et al. (2001) concluded that GJ 86A has an
additional companion GJ 86B in an orbit with a semi-major axis
somewhat larger than 20 AU, also previously suggested by Queloz
et al. (2000). GJ 86B has been identified to be at the transition
from L to T dwarfs with a mass of 40-70
0.004. The planet detection has been made through
very precise radial velocity measurements with the CORALIE echelle
spectrograph. Els et al. (2001) concluded that GJ 86A has an
additional companion GJ 86B in an orbit with a semi-major axis
somewhat larger than 20 AU, also previously suggested by Queloz
et al. (2000). GJ 86B has been identified to be at the transition
from L to T dwarfs with a mass of 40-70
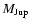 based on
atmospheric temperature models (Burrows et al. 1997). Here we
assume 50
based on
atmospheric temperature models (Burrows et al. 1997). Here we
assume 50
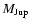 for simplicity.
for simplicity.
Table 10:
Time development of orbital variability in binary systems with
observed giant planets.
The results regarding the orbital stability of the planets in our
three target systems are given in Tables 9 and 10. It is found that
in all three systems, the planets are identified as stable
(S), as expected. The mass ratios
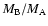 for the
stellar components in the systems
for the
stellar components in the systems 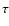 Boo, HD 195019, and GJ 86
are given as 0.3, 0.7, and 0.06, respectively. Furthermore, the
ratios of the separation distances between the stellar components
and the stars and planets
Boo, HD 195019, and GJ 86
are given as 0.3, 0.7, and 0.06, respectively. Furthermore, the
ratios of the separation distances between the stellar components
and the stars and planets
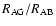 (see Sect. 4.1) are
2.1
(see Sect. 4.1) are
2.1  10-4, 8.9
10-4, 8.9  10-4, and 5.5
10-4, and 5.5  10-3,
respectively. Therefore, in all these cases, the Jupiter-type planets
are well within the stable parameter domain, and are far away
from the stable/marginally stable separation line (see Fig. 5).
In fact, the range of orbital variability, inspected in simulations
of up to 150 000 planetary orbits, remains close to 0.28% for
10-3,
respectively. Therefore, in all these cases, the Jupiter-type planets
are well within the stable parameter domain, and are far away
from the stable/marginally stable separation line (see Fig. 5).
In fact, the range of orbital variability, inspected in simulations
of up to 150 000 planetary orbits, remains close to 0.28% for
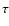 Boo, 0.34% for HD 195019, and 0.47% for GJ 86 (see Table 10).
Thus, the fact that in reality those planetary orbits are slightly
elliptical does not appear to be relevant here as no significant
modifications are expected to occur.
Boo, 0.34% for HD 195019, and 0.47% for GJ 86 (see Table 10).
Thus, the fact that in reality those planetary orbits are slightly
elliptical does not appear to be relevant here as no significant
modifications are expected to occur.
We investigated the stability of S and P-type planetary orbits
in binary systems of different mass and separation ratios using
a numerical code based on a Runge-Kutta-Fehlberg integration
scheme. The integration scheme is based on the simultaneous
computation of two algorithms, i.e., one of fourth-order and one
of fifth-order accuracy, allowing the choice of the integration
time step to attain optimal accuracy. Base line calculations are
pursued for 1000 planetary orbits to distinguish different cases
of stability, but a large number of runs extend to more than 105 planetary orbits.
In the study of S-type and P-type planetary orbits, we specified
criteria for stable, marginally stable and unstable circular
planetary orbits. We found that the separation lines between
the different stability regimes depend both on the mass and
separation ratios of the stellar system components. For S-type
planetary orbits, stable orbits are obtained for distance ratios
between 0.22 and 0.46, depending on the mass ratio. For P-type
planetary orbits, stable orbits are obtained for distance ratios
between 1.75 and 2.45, again depending on the the mass ratio.
The results were compared to those previously obtained, including
work by Holman & Wiegert (1999) and David et al. (2003), and we
found our results largely consistent with those earlier findings.
An interesting result was found for P-type orbits. Our results
demonstrate that the minimum radius of stable circular orbits
remains practically constant for all mass ratios larger than 0.4.
The existence of this "critical'' mass ratio clearly shows that
changes in the sphere of influence of a binary system resulting
from increasing the companion star mass 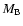 do not
influence orbital stability of a giant planet as long as the
mass ratio remains beyond that value.
do not
influence orbital stability of a giant planet as long as the
mass ratio remains beyond that value.
Finally, our studies of the stability of planetary orbits in three
observed binary systems with giant planets, namely, 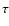 Boo,
HD 195019 and GJ 86, were based on simulations extending up to
150 000 planetary orbits. They showed that the orbits of the
giant planets in those systems remained well within the stable
domain during the time of simulations, as expected.
Boo,
HD 195019 and GJ 86, were based on simulations extending up to
150 000 planetary orbits. They showed that the orbits of the
giant planets in those systems remained well within the stable
domain during the time of simulations, as expected.
Acknowledgements
This work has been supported by the Alexander von Humboldt Foundation
(Z.E.M.) and the University of Texas at Arlington through its
Research Enhancement Program (M.C.).
- Abt, H. A., & Levy,
S. G. 1976, ApJS, 30, 273 [NASA ADS] [CrossRef] (In the text)
- Allen, C., Poveda, A.,
& Herrera, M. A. 2000, A&A, 356, 529 [NASA ADS] (In the text)
- Asghari, N., Broeg, C.,
Carone, L., et al. 2004, A&A, 426, 353 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Benest, D. 1988,
Celest. Mech. Dyn. Astron., 43, 47 (In the text)
- Benest, D. 1989,
A&A, 223, 361 [NASA ADS] (In the text)
- Benest, D. 1993,
Celest. Mech. Dyn. Astron., 56, 45 [NASA ADS] [CrossRef] (In the text)
- Benest, D. 1996,
A&A, 314, 983 [NASA ADS] (In the text)
- Bennett, J., Shostak,
S., & Jakosky, B. 2003, Life in the Universe (San Francisco:
Addison Wesley)
(In the text)
- Burrows, A., Marley,
M., Hubbard, W. B., et al. 1997, ApJ, 491, 856 [NASA ADS] [CrossRef] (In the text)
- Butler, R. P., Marcy,
G. W., Fischer, D. A., et al. 2002, in Planetary Systems in the
Universe: Observation, Formation and Evolution, ed. A. Penny, P.
Artymowicz, A.-M. Lagrange, & S. Russell (San Francisco: ASP),
IAU Symp., 202, in press
(In the text)
- Butler, R. P., Marcy,
G. W., Williams, E., Hauser, H., & Shirts, P. 1997, ApJ, 474,
L115 [NASA ADS] [CrossRef] (In the text)
- Cochran, W. D., Hatzes,
A. P., Butler, R. P., & Marcy, G. W. 1997, ApJ, 483, 457 [NASA ADS] [CrossRef]
- Cuntz, M., Saar, S. H.,
& Musielak, Z. E. 2000, ApJ, 533, L151 [NASA ADS] [CrossRef] (In the text)
- Cuntz, M., &
Musielak, Z. E. 2005, Icarus, in preparation
(In the text)
- Danby, J. M. A. 1988,
Fundamentals of Celestial Mechanics (Richmond: Willmann-Bell,
Inc.)
(In the text)
- David, E.-M., Quintana,
E. V., Fatuzzo, M., & Adams, F. C. 2003, PASP, 115, 825 [NASA ADS] [CrossRef] (In the text)
- Duquennoy, A., &
Mayor, M. 1991, A&A, 248, 485 [NASA ADS] (In the text)
- Dvorak, R. 1984,
Celest. Mech. Dyn. Astron., 34, 369 (In the text)
- Dvorak, R. 1986,
A&A, 167, 379 [NASA ADS] (In the text)
- Dvorak, R., Froeschle,
Ch., & Froeschle, Cl. 1989, A&A, 226, 335 [NASA ADS] (In the text)
- Dvorak, R.,
Pilat-Lohinger, E., Funk, B., & Freistetter, F. 2003, A&A,
398, L1 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Eggenberger, A.,
Udry, S., & Mayor, M. 2004, A&A, 417, 353 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Els, S. G., Sterzik, M.
F., Marchis, F., et al. 2001, A&A, 370, L1 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Fischer, D. A., Marcy,
G. W., Butler, R. P., Vogt, S. S., & Apps, K. 1999, PASP, 111,
50 [NASA ADS] [CrossRef] (In the text)
- Fischer, D. A., Marcy,
G. W., Butler, R. P., et al. 2001, ApJ, 551, 1107 [NASA ADS] [CrossRef] (In the text)
- Fischer, D. A., &
Valenti, J. A. 2003, in Scientific Frontiers in Research on
Extrasolar Planets, ed. D. Deming, & S. Seager, ASP Conf. Ser.,
294, 117
(In the text)
- Gray, D. F. 1992, The
Observation and Analysis of Stellar Photospheres, Cambridge
Astrophys. Ser., 20 (Cambridge: Cambridge Univ. Press)
(In the text)
- Graziani, F., &
Black, D. C. 1981, ApJ, 251, 337 [NASA ADS] [CrossRef] (In the text)
- Haghighipour, N. 2005,
ApJ, submitted
(In the text)
- Henon, M., & Guyot,
M. 1970, Periodic Orbits, Stability and Resonances, ed. G. E. O.
Giacaglia (Dordrecht: Reidel), 349
(In the text)
- Heppenheimer, T. A.
1974, Icarus, 22, 436 [NASA ADS] [CrossRef] (In the text)
- Holman, M. J., &
Wiegert, P. A. 1999, AJ, 117, 621 [NASA ADS] [CrossRef] (In the text)
- Jones, B. W., Sleep, P.
N., & Chambers, J. E. 2001, A&A, 366, 254 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kasting, J. F.,
Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] (In the text)
- Kley, W. 2001, in The
Formation of Binary Stars, ed. H. Zinnecker, & R. D. Mathieu
(San Francisco: ASP), IAU Symp., 200, 511
(In the text)
- Kubala, A., Black, D.,
& Szebehely, V. G. 1993, Celest. Mech. Dyn. Astron., 56,
51 [NASA ADS] [CrossRef] (In the text)
- Lloyd, J. P., et al.
2002, in Planetary Systems in the Universe: Observation, Formation
and Evolution, ed. A. Penny, P. Artymowicz, A.-M. Lagrange, &
S. Russell (San Francisco: ASP), IAU Symp., 202, in press
(In the text)
- Marcy, G. W., &
Butler, R. P. 1998, ARA&A, 36, 57 [NASA ADS] (In the text)
- Marcy, G. W., &
Butler, R. P. 2000, PASP, 112, 137 [NASA ADS] [CrossRef] (In the text)
- Marcy, G. W.,
Cochran, W. D., & Mayor, M. 2000, in Protostars and Planets IV,
ed. V. Mannings, A. P. Boss, & S. S. Russell (Tucson: Univ. of
Arizona Press), 1285
(In the text)
- Marcy, G. W., Butler,
R. P., Fischer, D. A., & Vogt, S. S. 2003, in Scientific
Frontiers in Research on Extrasolar Planets, ed. D. Deming, &
S. Seager, ASP Conf. Ser., 294, 1
(In the text)
- Marcy, G. W., Butler,
R. P., Vogt, S. S., et al. 2001, ApJ, 555, 418 [NASA ADS] [CrossRef] (In the text)
- McArthur, B. E., Endl,
M., Cochran, W. D., et al. 2004, ApJ, 614, L81 [NASA ADS] [CrossRef] (In the text)
- Nelson, A. F. 2000,
ApJ, 537, L65 [NASA ADS] [CrossRef] (In the text)
- Noble, M., Musielak, Z.
E., & Cuntz, M. 2002, ApJ, 572, 1024 [NASA ADS] [CrossRef] (In the text)
- Norwood, J., &
Haghighipour, N. 2002, BAAS, 34, 892 [NASA ADS] (In the text)
- Patience, J., White,
R. J., Ghez, A. M., et al. 2002, ApJ, 581, 654 [NASA ADS] [CrossRef] (In the text)
- Queloz, D., Mayor, M.,
Weber, L., et al. 2000, A&A, 354, 99 [NASA ADS] (In the text)
- Quintana, E. V.,
Lissauer, J. J., Chambers, J. E., & Duncan, M. J. 2002, ApJ,
576, 982 [NASA ADS] [CrossRef] (In the text)
- Shkolnik, E., Walker,
G. A. H., & Bohlender, D. A. 2003, ApJ, 597, 1092 [NASA ADS] [CrossRef] (Erratum:
2004, ApJ, 609, 1197 [CrossRef])
(In the text)
- Solovaya, N. A., &
Pittich, E. M. 2004, Contributions of the Astronomical Observatory
Skalnaté Pleso, 34, 105 [NASA ADS] (In the text)
- Szebehely, V. G., &
McKenzie, R. 1981, Celest. Mech. Dyn. Astron., 23, 3 (In the text)
- Tokovinin, A. A.,
Griffin, R. F., Balega, Yu. Yu., Pluzhnik, E. A., & Udry, S.
2000, Astron. Let., 26, 116 [NASA ADS] (translated from Astr. Zh., 26,
146)
(In the text)
- Underwood, D. R.,
Jones, B. W., & Sleep, P. N. 2003, Int. J. Astrobiology, 2,
289 (In the text)
- von Bloh, W., Cuntz, M.,
Franck, S., & Bounama, C. 2003, Astrobiology, 3, 681 [NASA ADS] [CrossRef] (In the text)
- Whitmire, D. P.,
Matese, J. J., Criswell, L., & Mikkola, S. 1998, Icarus, 132,
196 [NASA ADS] [CrossRef] (In the text)
- Zucker, S., Naef, D.,
Latham, D. W., et al. 2002, ApJ, 568, 363 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
![\begin{figure}
\par\includegraphics[height=6.7cm,width=7cm,clip]{0238fig2.eps}\end{figure}](/articles/aa/full/2005/16/aa0238-04/Timg28.gif)
![\begin{figure}
\par\includegraphics[height=6.7cm,width=7cm,clip]{0238fig3.eps}\end{figure}](/articles/aa/full/2005/16/aa0238-04/Timg29.gif)
![\begin{figure}
\par\includegraphics[height=6.7cm,width=7cm,clip]{0238fig4.eps}\end{figure}](/articles/aa/full/2005/16/aa0238-04/Timg30.gif)
![\begin{figure}
\par\includegraphics[height=6.5cm,width=7cm,clip]{0238fig5.eps}\end{figure}](/articles/aa/full/2005/16/aa0238-04/Timg38.gif)
![\begin{figure}
\par\includegraphics[height=6.5cm,width=7cm,clip]{0238fig6.eps}\end{figure}](/articles/aa/full/2005/16/aa0238-04/Timg43.gif)