- ... rings
![[*]](/icons/foot_motif.gif)
- The distinction between tori, discs and rings usually implies some hierarchy in the aspect ratio (thickness to radius ratio) and axis ratio (outer edge to inner edge ratio) of systems. Here, it is employed only to outline that the application range of the present method encompasses these three kinds of systems.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... time
![[*]](/icons/foot_motif.gif)
- It is worthwhile to revise or to clarify this kind of argument. The "large'' computing time i) is based on the assumption that the number of source points needed to perform the volume integral equals the number of field points, as imposed in finite-different methods; ii) does not account for the determination of boundary conditions; and iii) does not consider the accuracy (see Sect. 6.3).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tri-dimensional
![[*]](/icons/foot_motif.gif)
- In the paper, "tri-dimensional'' only means that matter occupies a volume. Regarding the axial symmetry, the problem can however be viewed as a "bi-dimensional'' problem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kinds
![[*]](/icons/foot_motif.gif)
- For nominal accuracy, special functions must be computed from numerical libraries. It is possible to use approximations in the form of truncated k-expansions (e.g. Byrd & Freeman 1971) or from fitting functions (Abramowitz & Stegun 1964; Bonazzola & Schneider 1974). This enables a significant reduction of the execution time, but high accuracy can generally not be reached on field and potential values.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... surface
![[*]](/icons/foot_motif.gif)
- The additional symmetry with respect to the mid-plane Z=0 is introduced for convenience only. Two equations can be considered: z+(a) for the top surface and z-(a) for the bottom. Here, we have set
z+=-z-=H(a).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... value
![[*]](/icons/foot_motif.gif)
- There can be sub-domains where H=0 (for instance, to model discs with gaps). In such a case, the method must be applied to each sub-domain.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cylinder
![[*]](/icons/foot_motif.gif)
- By cylinder, we mean a topologically bi-dimensional object with zero radial extent. To be rigorous (i.e. for dimensional reasons), we should introduce a lateral surface density
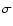 to refer to the field due to a topologically bi-dimensional object, and perform the conversion
to refer to the field due to a topologically bi-dimensional object, and perform the conversion
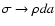 at the level of the radial integration.
at the level of the radial integration.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... high-order
![[*]](/icons/foot_motif.gif)
- This scheme is 5-order accurate for irregular spacing, and 6-order accurate for regular spacing.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... model
![[*]](/icons/foot_motif.gif)
- Note that
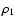 cannot represent any physical situation since the density depends on the field point. This is not crucial at this level since we need an exact solution.
cannot represent any physical situation since the density depends on the field point. This is not crucial at this level since we need an exact solution.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cylinder
![[*]](/icons/foot_motif.gif)
- For non-coincident cylinders, the Poisson kernel is regular suggesting that the splitting methods must be applied only to cases where k=1. This is not true. For field points located very close to the coincident cylinder, kernel components both exhibit a sharp peak at
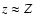 .
Such peaks are expected and have finite amplitude, but it is difficult to reach high accuracy from a straightforward computation of Eq. (12). This difficulty can be circumvented by using the splitting method for nearby cylinders, as will be done here.
.
Such peaks are expected and have finite amplitude, but it is difficult to reach high accuracy from a straightforward computation of Eq. (12). This difficulty can be circumvented by using the splitting method for nearby cylinders, as will be done here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... components
![[*]](/icons/foot_motif.gif)
- Note that
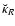 is discontinuous when going through the coincident cylinder, as soon as
is discontinuous when going through the coincident cylinder, as soon as
 at the field point (see for instance Fig. 7), but the amplitude of the discontinuity is known. Thus, each radial integration must numerically be separated into two parts, according to
at the field point (see for instance Fig. 7), but the amplitude of the discontinuity is known. Thus, each radial integration must numerically be separated into two parts, according to
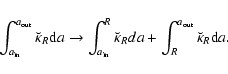 |
(30) |
Such an integral splitting must also be considered for
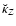 (as well as for
(as well as for
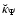 ;
see Sect. 5).
;
see Sect. 5).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... discs
![[*]](/icons/foot_motif.gif)
- The diameter of discs in active galaxies reach typically the parsec, and for circumstellar discs, it can be as large as 103 AU. In both cases, one finds
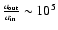 .
Further, there is evidence that such discs flare and have a decreasing density profile.
.
Further, there is evidence that such discs flare and have a decreasing density profile.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... technique
![[*]](/icons/foot_motif.gif)
- In Hachisu's paper,
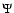 was computed from the Green function with a systematic cutoff in the series, and the polar-type grid contained at least
was computed from the Green function with a systematic cutoff in the series, and the polar-type grid contained at least
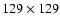 points in the half-plane
points in the half-plane 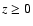 .
Here, we do not take advantage of the mid-plane symmetry, points being distributed vertically in the range [-H,H].
.
Here, we do not take advantage of the mid-plane symmetry, points being distributed vertically in the range [-H,H].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... method
![[*]](/icons/foot_motif.gif)
- To get a computer-independent quantity,
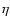 should be multiplied by the "speed'' of the actual computer. Values reported in the following are obtained with a 1 GHz personal computer.
should be multiplied by the "speed'' of the actual computer. Values reported in the following are obtained with a 1 GHz personal computer.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... experimentally
![[*]](/icons/foot_motif.gif)
- For this comparative study, we use the simple precision NETLB library HWSCYL(R3.10) routine which finds the solution
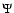 of the axi-symmetric Poisson equation from cyclic reduction based on a 5-point finite differences (Adams et al. 1980). Boundary conditions are computed from the double splitting method with maximum accuracy.
of the axi-symmetric Poisson equation from cyclic reduction based on a 5-point finite differences (Adams et al. 1980). Boundary conditions are computed from the double splitting method with maximum accuracy.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
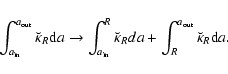
![]() (as well as for
(as well as for
![]() ;
see Sect. 5).
;
see Sect. 5).