A&A 433, 765-776 (2005)
DOI: 10.1051/0004-6361:20042161

Spectral and temporal signatures of ultrarelativistic protons in compact sources

I. Effects of Bethe-Heitler pair production

A. Mastichiadis1 - R. J. Protheroe2 - J. G. Kirk3


1 - Department of Physics, University of Athens, Panepistimiopolis, 15783, Zografos, Greece
2 - Department of Physics and Mathematical Physics, University of Adelaide, North Terrace, Adelaide, SA 5005, Australia
3 - Max-Planck-Institut für Kernphysik, Postfach 103980, 69029 Heidelberg, Germany

Received 12 October 2004 / Accepted 15 December 2004

Abstract
We present calculations of the spectral and temporal radiative signatures expected from ultrarelativistic protons in compact sources. The coupling between the protons and the leptonic component is assumed to occur via Bethe-Heitler pair production. This process is treated by modeling the results of Monte-Carlo simulations and incorporating them in a time-dependent kinetic equation, that we subsequently solve numerically. Thus, the present work is, in many respects, an extension of the leptonic "one-zone'' models to include hadrons. Several examples of astrophysical importance are presented, such as the signature resulting from the cooling of relativistic protons on an external black-body field and that of their cooling in the presence of radiation from injected electrons. We also investigate and refine the threshold conditions for the "Pair Production/Synchrotron'' feedback loop which operates when relativistic protons cool efficiently on the synchrotron radiation of the internally produced Bethe-Heitler pairs. We demonstrate that an additional component of injected electrons lowers the threshold for this instability.

Key words: radiation mechanisms: non-thermal - radiative transfer - galaxies: active

1 Introduction

The spectral energy distribution (SED) of powerful AGN such as flat-spectrum radio quasars and blazars has a double humped appearance with the low energy part extending from the radio to UV (or in extreme cases to X-rays), and a high energy part extending from X-rays to $\gamma$-rays. In AGN with relativistic jets closely aligned to the line of sight the emission is dominated by non-thermal radiation, with the low energy hump being mainly synchrotron radiation. If the alignment is not so close, a thermal component of UV radiation from an accretion disk may dominate. The non-thermal components can be strongly variable, probably originating in the jet.

These observations indicate that the jets of blazars act as efficient particle accelerators. Furthermore the gamma-ray observations in the GeV (Hartman et al. 1999) and TeV regime (Horan & Weekes 2004) imply that the accelerated particles can reach very high energies. Models involving electron radiation can adequately explain both this high energy emission and the coordinated multiwavelength campaigns (Tavecchio et al. 2001; Mastichiadis & Kirk 1997; Krawczynski et al. 2002). The usual assumption is then that the high energy part of the SED is due to inverse Compton scattering of the low energy part of the SED (synchrotron self-Compton model) possibly supplemented by inverse Compton scattering of external photons (external Compton models) for example from the disk, either directly or scattered by clouds. Despite these successes, the question of the role of a possible relativistic hadronic component remains an open one.

In principle, sites of electron acceleration may accelerate protons as well. Consequently, models in which the high energy part, and some fraction of the low energy part, of the SED is due to acceleration and interaction of protons in the jet have also been proposed. Some of these models invoke interactions with ambient matter (Beall & Bednarek 1999; Pohl & Schlickeiser 2000; Schuster et al. 2002) but they require high mass densities in the jet to be viable. Here we concentrate on hadronic models in which the protons interact with low energy photons via Bethe-Heitler pair production.

As with leptonic models, the target photons may be produced inside the emission region in the jet or may originate from outside of the jet, e.g., from an accretion disk (Atoyan & Dermer 2001; Bednarek & Protheroe 1999; Protheroe 1997; Neronov & Semikoz 2002). For internally produced target photons, synchrotron emission by a co-accelerated population of electrons is assumed (Mannheim 1993,1995; Mannheim & Biermann 1992). The high energy hump of the SED then results from electromagnetic cascading of gamma-rays from $\pi^0$ decay and electrons from Bethe-Heitler pair production and $\pi^\pm \to \mu^\pm \to e^\pm$ decay in the radiation and magnetic field of the blob. Neutrinos and cosmic rays would also be emitted as a result of the neutrinos from the $\pi^\pm$ and $\mu^\pm$ decays, and neutrons produced in $p\gamma \to n \pi^+$ interactions if the threshold for pion photoproduction is exceeded (Protheroe & Szabo 1992; Kirk & Mastichiadis 1989; Eichler & Wiita 1978; Sikora et al. 1989; Begelman et al. 1990; Waxman & Bahcall 1999; Atoyan & Dermer 2003; Sikora et al. 1987; Protheroe 2004; Mannheim et al. 2001; Giovanoni & Kazanas 1990; Szabo & Protheroe 1994). For protons to be accelerated to energies sufficient to exceed the Bethe-Heitler and photo-pion-production thresholds, relatively high magnetic fields are required. In proton synchrotron blazar models the magnetic field is sufficiently high such that the high energy part of the SED has a major contribution also due to synchrotron radiation by protons (Aharonian 2000; Mücke & Protheroe 2001; Reimer et al. 2004; Mücke & Protheroe 2000). All of the work described above assumes the emission has reached a steady state, and that the target photon fields are steady. In reality, the strong variability displayed by these sources mandates a time-dependent calculation, that, ideally, should be done self-consistently, with internally produced radiation fields contributing alongside external ones to the target radiation field.

Time-dependent codes that solve the kinetic equations describing electrons and photons and their interactions have been developed and successfully applied to AGN (Mastichiadis & Kirk 1997; Krawczynski et al. 2002). However, codes of this type that also account for hadronic interactions have been neglected. One reason for this is that whereas the modeling of leptonic processes is relatively straightforward (e.g., Lightman & Zdziarski 1987; Coppi & Blandford 1990), photo-hadronic and hadron-hadron interactions are much more complex. To date, all attempts have used approximations of uncertain accuracy (e.g., Stern & Svensson 1991) but the use of Monte-Carlo event generators which model in detail electromagnetic (Protheroe & Johnson 1996; Szabo & Protheroe 1994) and hadronic interactions (Mücke et al. 2000) opens up the possibility of extracting accurate descriptions of the fundamental interactions suitable for incorporation into a kinetic code.

Motivated by these developments we investigate the consequences of the presence of relativistic hadrons in compact sources by incorporating new results from Monte-Carlo simulations into a time-dependent code which follows the evolution of relativistic hadrons, electrons and photons by solving the appropriate kinetic equations. In the present paper we investigate as a first step, the case in which the only channel of coupling between hadrons and leptons is the Bethe-Heitler pair-production process, leaving the investigation of photo-meson production for a future paper. Although this is not a complete description of hadronic models it nevertheless enables one to draw useful and interesting new results.

The present paper is structured as follows: in Sect. 2 we present the numerical code that solves simultaneously in a self-consistent manner the coupled, time-dependent kinetic equations for each species, i.e. protons, electrons and photons. In Sect. 3 we present the Monte-Carlo results for the Bethe-Heitler process and show how these can be incorporated in the kinetic equations. In Sect. 4 we present some results for the case in which relativistic protons interact with an external black-body radiation field. In Sect. 5, we present a numerical analysis of the "Pair-Production/Synchrotron'' instability. The case of simultaneous injection of relativistic protons and electrons is examined in Sect. 6 and the main conclusions are summarized in Sect. 7.

2 The kinetic equations for electrons, protons and photons

The kinetic equations describing a homogeneous source region containing protons, electrons and photons were formulated and solved numerically by Mastichiadis & Kirk (1995, henceforth MK95). We follow the same method, using an improved description of the microscopic processes. The equations to be solved can be written in the generic form

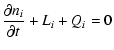$\displaystyle {{\partial n_i}\over{\partial t}} + L_i +Q_i=0$     (1)

where the index i can be any one of the subscripts "p'', "e'' or "$\gamma$'' referring to protons, electrons or photons respectively. The operators Li denote losses and escape from the system while Qi denote injection and source terms. These are defined below.

The unknown functions ni are the differential number densities of the three species, normalised as follows:

                                        $\displaystyle {\rm protons:}$  
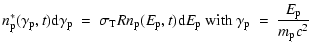    $\displaystyle n_{\rm p}^*(\gamma_{\rm p},t){\rm d}\gamma_{\rm p}~=~\sigma_{\rm ... ...m d}E_{\rm p} \ {\rm with } \ \gamma_{\rm p}~=~{{E_{\rm p}}\over{m_{\rm p}c^2}}$ (2)
    $\displaystyle {\rm electrons:}$  
    $\displaystyle n_{\rm e}^*(\gamma_{\rm e},t){\rm d}\gamma_{\rm e}=\sigma_{\rm T}... ... d}E_{\rm e}\ \textrm{with }\ \gamma_{\rm e}~=~{{E_{\rm e}}\over{m_{\rm e}c^2}}$ (3)
    $\displaystyle {{\rm photons:}}$  
    $\displaystyle n_\gamma^*(x,t){\rm d}x~=~\sigma_{\rm T}Rn_\gamma(\epsilon_\gamma... ...\rm d}\epsilon_\gamma \ {\rm with }~ x~=~{{\epsilon_\gamma}\over{m_{\rm e}c^2}}$ (4)

and the time t has been normalised in all equations to the light-crossing time of the source $t_{\rm cr}=R/c$.

The physical processes to be included in the kinetic equations are:

1.
Proton-photon (Bethe-Heitler) pair production which acts as a loss term for the protons ( $L_{\rm p}^{\rm BH}$) and an injection term for the electrons ( $Q_{\rm e}^{\rm BH}$).
2.
Synchrotron radiation which acts as an energy loss term for electrons ( $L_{\rm e}^{\rm syn}$) and as a source term for photons ( $Q_{\gamma}^{\rm syn}$).
3.
Synchrotron self absorption which acts as an absorption term for photons ( $L_{\gamma}^{\rm ssa}$).
4.
Inverse Compton scattering (in both the Thomson and Klein-Nishina regimes) which acts as an energy loss term for electrons ( $L_{\rm e}^{\rm ics}$) and as a source term for high energy photons and a loss term for low energy photons, both effects included in $Q_{\gamma}^{\rm ics}$.
5.
Photon-photon pair production which acts as an injection term for electrons ( $Q_{\rm e}^{\gamma\gamma}$) and as an absorption term for photons ( $L_{\gamma}^{\gamma\gamma}$).
6.
Electron-positron annihilation which acts as a sink term for electrons ( $L_{\rm e}^{\rm ann}$) and as a source term for photons ( $Q_{\gamma}^{\rm ann}$).
7.
Compton scattering of radiation on the cool pairs, which impede the free escape of photons from the system. This effect is treated approximately by multiplying the photon escape term by the factor $(1+H(1-x)\tau_{\rm T}/3)^{-1}$, where $\tau_{\rm T}$ the Thomson optical depth, while H(1-x) is the step-function. (Lightman & Zdziarski 1987).
With the inclusion of the above terms the kinetic equations become, for each species (from now on we refer only to normalised quantities and, for convenience, drop the asterisks) We note the following regarding the above equations
1.
When the various terms above are written explicitly, Eqs. (5)-(7) form a non-linear system of coupled integro-differential equations.
2.
The various rates conserve the energy exchange between the species - for example, the amount of energy lost per second by electrons at each instant due to synchrotron radiation is equal to the power radiated in synchrotron photons, (for details see MK95)
3.
In the absence of the Bethe-Heitler pair-production term $Q_{\rm e}^{\rm BH}$, Eqs. (6) and (7) decouple from the protons (Eq. (5)) and the system becomes identical to the "one-zone'' time-dependent leptonic models
4.
Protons are injected via the term $Q_{\rm p}$ with a prescribed distribution in energy. Thus, in contrast to MK95, we do not investigate the effects of particle acceleration.
5.
Electrons may also be injected externally through the prescribed term $Q_{\rm e}^{\rm ext}$. However the two other injection terms in the electron equation ( $Q_{\rm e}^{\rm BH}$ and $Q_{\rm e}^{\gamma\gamma}$) are determined self-consistently from the proton and photon distributions.
6.
Both protons and electrons (we make no distinction between electrons and positrons in the present treatment) escape from the source region on the timescales $t_{\rm p,esc}$ and $t_{\rm e,esc}$ respectively (given in units of  $t_{\rm cr}$).
We can also define various compactnesses related to the most important of the above quantities. So we define the photon compactness as (see MK95)
 
$\displaystyle \ell_{\gamma}={{1}\over{3}}\int {\rm d}x x {n_\gamma(x,t)\over {t_{\rm cr}(1+H(1-x)\tau_{\rm T}/3)}}$     (8)

while the scaled to electron rest-mass compactness of externally injected protons is
 
$\displaystyle \ell_{\rm p}={m_{\rm p}\over3m_{\rm e}} \int {\rm d}\gamma(\gamma-1)Q_{\rm p}(\gamma).$     (9)

In analogous fashion we can also define the compactness of the externally injected electrons
 
$\displaystyle \ell_{\rm e}^{\rm ext}={1\over 3} \int {\rm d}\gamma(\gamma-1)Q_{\rm e}^{\rm ext}(\gamma).$     (10)

Finally in order to calculate the Thomson optical depth of the cool pairs we use
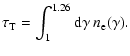$\displaystyle \tau_{\rm T}=\int_1^{1.26} {\rm d}\gamma~n_{\rm e}(\gamma).$     (11)

Closing this section we note that the treatment of synchrotron and inverse Compton scattering has been improved over that described by MK95 in that the full emissivities are incorporated, rather than delta-function approximations. However, the main improvement is in the treatment of the Bethe-Heitler pair-production process, using Monte-Carlo simulations, as described in the following section.

3 Bethe-Heitler pair production

3.1 Monte-Carlo simulations

For an isotropic target comprising monoenergetic photons of energy $\varepsilon=xm_{\rm e}c^2$ the effective cross-section for interaction of a proton of energy $E=\gamma_{\rm p}m_{\rm p}c^2$ is given by


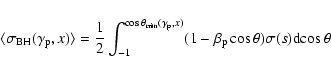\begin{displaymath}\langle \sigma_{\rm BH}(\gamma_{\rm p},x)\rangle = {1 \over 2... ...} (1 - \beta_{\rm p} \cos \theta)\sigma(s){\rm d}\!\cos\theta \end{displaymath} (12)

where $\theta$ is the angle between the proton and photon directions, $\theta_{\rm min}(\gamma_{\rm p},x)$ is the minimum value of this angle consistent with the threshold,

 \begin{displaymath}s=m_{\rm p}^2 c^4 + 2 \varepsilon E(1 - \beta_{\rm p} \cos \theta) \end{displaymath} (13)

is the centre of momentum (CM) frame energy squared, $\beta_{\rm p} c$ is the proton's velocity, and $\sigma_{\rm BH}$ the total cross-section for which we use the Racah formula as parameterized by Maximon (1968) (see Formula 3D-0000 in Motz et al. 1969). Changing variables, one obtains the angle-averaged cross-section

 \begin{displaymath}\langle \sigma_{\rm BH}(\gamma_{\rm p},x)\rangle = {1 \over 8... ...rm p},x)} \sigma(s) \left (s-m_{\rm p}^2 c^4\right){\rm d}s, \end{displaymath} (14)

where

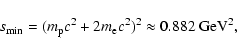\begin{displaymath}s_{\rm min}= (m_{\rm p}c^2 + 2 m_{\rm e}c^2)^2 \approx 0.882 \; \rm GeV^2, \end{displaymath} (15)

and

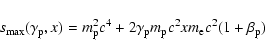\begin{displaymath}s_{\rm max}(\gamma_{\rm p},x) = m_{\rm p}^2c^4+2\gamma_{\rm p}m_{\rm p}c^2 xm_{\rm e}c^2 (1+\beta_{\rm p}) \end{displaymath} (16)

corresponding to a head-on collision. The angle-averaged cross-section is plotted as a function of the product of photon energy and proton energy in Fig. 1. For $x \ll 1$, the threshold condition implies $\gamma_{\rm p}\gg1$ and $\beta_{\rm p}\approx1$, so that to a first approximation, the cross-section is a function of $x\gamma_{\rm p}$, rather than of x and $\gamma_{\rm p}$ separately.
  \begin{figure} \par\includegraphics[width=6.1cm,clip]{2161fg1.ps} \end{figure} Figure 1: The angle-averaged Bethe-Heitler pair-production cross section $\langle \sigma_{\rm BH}(\gamma_{\rm p},x)\rangle$ (solid curve), the angle-averaged Bethe-Heitler pair-production inelasticity $\xi _{\rm BH}(\gamma _{\rm p},x)$ (dashed curve), and $\xi_{\rm BH}(\gamma_{\rm p},x)\langle \sigma_{\rm BH}(\gamma_{\rm p},x)\rangle$ (dotted curve) are plotted as a function of $\gamma _{\rm p} x$ for $x \ll 1$.
Open with DEXTER

Examination of the integrand in Eq. (14) shows that the square of the total CM frame energy is distributed as

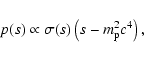\begin{displaymath}p(s) \propto \sigma(s)\left(s-m_{\rm p}^2c^4\right), \end{displaymath} (17)

in the range $s_{\rm min}\leq s\leq s_{\rm max}$. The Monte Carlo rejection technique is used to sample s, and Eq. (13) is used to find $\theta$. We then Lorentz transform the interacting particles to the proton rest frame and sample the positron's energy from the single-differential cross-section, d $ \sigma / {\rm d} E_+$, for which we use the Bethe-Heitler formula for an unscreened point nucleus (Formula 3D-1000 in Motz et al. 1969). Finally, the positron's direction is sampled from the double-differential cross-section, d $ \sigma / {\rm d} E_+ {\rm d} \Omega_+$for which we use the Sauter-Gluckstern-Hull formula for an unscreened point nucleus (Formula 3D-2000 in Motz et al. 1969), and its laboratory frame energy is obtained by a Lorentz transformation. For a range of proton energies, the simulation is repeated a large number of times to build up distributions in energy of positrons produced in BH pair production.

The distribution in energy $\gamma_{\rm e} m_{\rm e}c^2$ of electrons (of either charge),

 \begin{displaymath}f(\gamma_{\rm e}; \gamma_{\rm p},x) \equiv {{\rm d} N_{\rm e} \over {\rm d} \gamma_{\rm e}}, \end{displaymath} (18)

is taken to be twice that for positrons, as discussed in Protheroe & Johnson (1996), and is plotted in Fig. 2 for x=10-6 and three $\gamma_{\rm p}$values. In a similar calculation using black-body target photons (Protheroe & Johnson 1996), the mean inelasticity was found to be in excellent agreement with those calculated analytically (Rachen & Biermann 1993; Chodorowski et al. 1992; Blumenthal 1970). The mean inelasticity, given by

 \begin{displaymath}\xi(\gamma_{\rm p},x) = {m_{\rm e} \over m_{\rm p}} \int {\rm... ...rm e} \over \gamma_{\rm p}}f(\gamma_{\rm e}; \gamma_{\rm p},x) \end{displaymath} (19)

is plotted as a function of the product of photon energy and proton energy in Fig. 1 (dashed line) together with its product (dotted curve) with the cross-section, to show how the proton energy loss rate depends on energy.
  \begin{figure} \par\includegraphics[width=5.8cm,clip]{2161fg2.ps} \end{figure} Figure 2: The distribution of electron energies is shown for x=10-6 and $\gamma _{\rm p}=10^{6.3}$ (dashed histogram), 107 (solid histogram) and 109 (dotted histogram).
Open with DEXTER

3.2 Numerical modeling

3.2.1 Electron/positron pair production

The pair-production spectra were calculated using the results of the Monte Carlo code described in Sect. 2.1. Protons of a specific energy were allowed to interact with isotropic monoenergetic target photons and the energies of the products were tabulated. The photon target energies used were x0=10-6, 10-4, 10-2 and 1 (in units of electron rest mass). Proton energies ranged from $\gamma_{\rm p}=x_0^{-1}$ (so the threshold requirement could be met) up to $\gamma_{\rm p}=10^4x_0^{-1}$ in logarithmic steps of 0.1.

The pair-creation rate is then given

$\displaystyle Q_{\rm e}^{\rm BH}(\gamma_{\rm e},t)= \int {\rm d}\gamma_{\rm p}~... ...gamma_{\rm p},\gamma_{\rm e},x) \langle\sigma_{\rm BH}(\gamma_{\rm p},x)\rangle$     (20)

where $f(\gamma_{\rm p},\gamma_{\rm e},x)$ is the distribution found from the Monte-Carlo modelling (see Eq. (18)), normalised such that
$\displaystyle \int {\rm d}\gamma_{\rm e}f(\gamma_{\rm p},\gamma_{\rm e},x)=2.$     (21)

As simple parameterisations of these curves do not give acceptable fits, we tabulated the spectra and used interpolations to derive the produced pair-injection spectrum from a particular proton-photon collision.

We note that MK95 used the approximation $f(\gamma_{\rm p},\gamma_{\rm e},x)=2\delta(\gamma_{\rm e}-\gamma_{\rm p})$ corresponding to $\xi=m_{\rm e}/m_{\rm p}$. For a proton distribution $n_{\rm p}(\gamma_{\rm p})$ which decreases as  $\gamma_{\rm p}$ increases, this overestimates the production rate of electrons of a given energy.

3.2.2 Proton losses

Since the proton loses a small amount of energy (typically given by $\Delta\gamma_{\rm p}\sim m_{\rm e}/m_{\rm p}$ in each pair-producing collision we can treat the losses as a continuous process and write

 
$\displaystyle L_{\rm p}^{\rm BH}={{\partial}\over{\partial\gamma_{\rm p}}}\left[\gamma_{\rm p}n_{\rm p}(\gamma_{\rm p},t) Y(\gamma_{\rm p},t)\right]$     (22)

where
$\displaystyle Y(\gamma_{\rm p},t)=\int {\rm d}x n_{\rm\gamma}(x,t) \langle \sigma_{\rm BH}(\gamma_{\rm p},x)\rangle \xi(\gamma_{\rm p},x)$     (23)

is the convolution of the normalised collision rate with the inelasticity $\xi$ given by Eq. (19).

4 Proton injection and black-body photon field

As a first example, we examine the case of relativistic proton injection and subsequent cooling on a black-body photon field. We assume, as usual in astrophysical cases, a power-law proton injection of the form
 
$\displaystyle Q_{\rm p}(\gamma)=Q_{\rm {p,0}} \gamma^{-\beta}H(\gamma-\gamma_{\rm p,min})H(\gamma_{\rm p,max}-\gamma)$     (24)

where $\gamma_{\rm p,min}$ and $\gamma _{\rm p,max}$ are respectively the lower and upper cutoff of the proton distribution. We also assume that the protons can escape at a rate $t_{\rm p,esc}^{-1}$ from the source region, taken to be a sphere of radius R. Then the stationary solution, in the absence of proton losses is simply
 
$\displaystyle n_{\rm p}(\gamma)={Q_{\rm {p,0}}t_{\rm p,esc}} \gamma^{-\beta}H(\gamma-\gamma_{\rm p,min})H(\gamma_{\rm p,max}-\gamma).$     (25)

We assume next that a significant number of external photons is present and that these have a black-body distribution of temperature $T_{\rm BB}$. The energy density  $U_{\rm BB}$of these photons in the source can be parameterised in terms of the black-body compactness  $\ell_{\rm BB}$, defined by the relation
$\displaystyle \ell_{\rm BB}={{U_{\rm BB}\sigma_{\rm T}R}\over{m_{\rm e}c^2}}\cdot$     (26)

This emission can arise, for example, from the surface of an accretion disk located close to the source. In general, if the source is irradiated by a black body at temperature $T_{\rm BB}$ whose surface occupies a solid angle of $\Delta\Omega$ as seen from the source, then
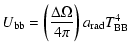$\displaystyle U_{\rm bb}=\left({\Delta\Omega\over 4 \pi}\right) a_{\rm rad}T_{\rm BB}^4$     (27)

where $a_{\rm rad}$ is the radiation density constant. In terms of compactness:
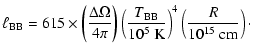$\displaystyle \ell_{\rm BB}= 615\times\left({\Delta\Omega\over 4 \pi}\right) \l... ...BB}\over10^5~\textrm{K}}\right)^4 \left({R\over10^{15}~\textrm{cm}}\right)\cdot$     (28)

We further assume that initially there are no other photons or electrons present (except maybe in very small numbers) and that there is no external electron injection. Since the Bethe-Heitler pair production has a threshold condition $\gamma x\ge 1+{m_{\rm e}/m_{\rm p}}$ (corresponding to head-on collisions) it follows that, in the case where $y=\gamma_{\rm p,max}(kT_{\rm BB}/m_{\rm e}c^2)\ll 1$, there will be negligible pair production. Therefore, for all practical purposes, the solution of the proton equation will still be given by Eq. (25). However, for $y\sim1$, the proton-photon reaction rate is substantial and cannot be neglected as a proton loss mechanism. Moreover, the produced electron/positron pairs provide an injection term for the electron equation and lose energy mainly by inverse Compton scattering and/or synchrotron radiation. As a result a photon spectrum is formed. To investigate the properties of this emission, such as its luminosity and spectral shape etc., we must distinguish between two cases.

4.1 Case 1: $\ell {_{\rm p}}\ll \ell {_{\rm BB}}$ and negligible synchrotron losses

In this case, the photons produced by electrons created in the BH process are not important as targets and the resulting photon spectrum is quite simple. It is a single power-law of (number) spectral index -3/2, extending up to an energy $x_{\rm max}$, that is approximately the inverse of the temperature of the black-body field, i.e. $x_{\rm max}\simeq\Theta^{-1}$, where $\Theta=(kT_{\rm BB}/m_{\rm e}c^2)$. The explanation of this spectrum is straight-forward: protons pair-produce on the black-body field and, since they are produced with high energies, the pairs cool on the black-body photons initially by Compton scattering in the Klein-Nishina regime. This produces $\gamma$-rays that are above the threshold for pair production on the black-body photons and, therefore, are re-absorbed. Lower energy pairs, which cool by Compton scattering in the Thomson regime, produce photons which are below the threshold for photon-photon pair production. This naturally produces an electron distribution function $n_{\rm e}\propto\gamma^{-2}$and thus a photon spectrum $n_\gamma\propto x^{-3/2}$. The value of $x_{\rm max}$, therefore, is set by the condition $\tau_{\gamma\gamma}(x_{\rm max})\simeq 1$, where $\tau_{\gamma\gamma}$ is the optical depth for photon-photon pair production on the background black-body field.

Since for the present case there is neither escape of electrons from the system nor any sink of energy, (e.g. synchrotron self-absorption) other than photon escape, the radiated luminosity (or, equivalently, $\ell _{\gamma }$) equals the luminosity injected in pairs once a state steady is achieved, i.e. $\ell_{\gamma}\simeq\ell_{\rm e}^{\rm BH}$, where

 
$\displaystyle \ell_{\rm e}^{\rm BH}={1\over 3}\int {\rm d}\gamma(\gamma-1)Q_{\rm e}^{\rm BH}$     (29)

is the compactness of the created pairs from the Bethe-Heitler pair production. Therefore, the overall photon luminosity depends on the parameter y defined above and, as we show below, also on $\ell_{\rm BB}$and  $\ell_{\rm p}$.

As an illustrative case we take $\ell_{\rm BB}=1\gg\ell_{\rm p}=2.5\times 10^{-3}$. Here also $T_{\rm BB}=10^5$ K, while $\gamma _{\rm p,min}=10^{0.1}$, $\gamma _{\rm p,max}=10^6$. The dotted line in Fig. 3 depicts the electron injection function which shows a broad maximum. The same figure shows the photon spectrum which is obtained from the cooling of these electrons and the ambient black-body field. The dashed line shows the spectrum in the case where the $\gamma\gamma$pair production has been artificially switched off. The spectrum is flat and peaks at high energies. We note that both the electron production function and the unabsorbed photon spectrum extend to about two orders of magnitude above $\gamma_{\rm p,mx}$, an effect that is due to the kinematics of the Bethe-Heitler pair production - see Fig. 3. At lower energies it produces the characteristic -3/2 power-law. The full line shows the final photon spectrum which includes $\gamma\gamma$absorption. It has still the same power-law, however all the details of the electron injection spectrum which were evident in the unabsorbed spectrum have disappeared due to the intense attenuation. Nevertheless the overall luminosity is conserved (as it should be) and as the electromagnetic cascade redistributes the power to lower energies, the flux is increased there. Figure 4 shows the effects of losses on the steady-state proton distribution for these parameters ( $\ell _{\rm BB}=1$) and two higher values of $\ell_{\rm BB}$, compared to the loss-free case.

  \begin{figure} \par\includegraphics[width=8.4cm,clip]{2161fg3.ps} \end{figure} Figure 3: Steady-state photon spectrum resulting from a power-law proton injection and subsequent proton-photon pair production on a black-body photon field in the case where photon-photon pair production (i) has been ignored (dashed line) and (ii) has been taken into account (full line). The dotted line curve depicts the electron/positron distribution function at production. For this particular run the protons were assumed to be injected with a power-law of slope $\beta =2$, between the limits $\gamma _{\rm p,min}=10^{0.1}$ and $\gamma _{\rm p,max}=10^6$. Also the values $\ell_{\rm p}=2.5~\times~ 10^{-3}$ and $t_{\rm p,esc}=t_{\rm cr}$have been assumed. The black-body photon field parameters were $T_{\rm BB}=10^5~$K ( $\Theta =1.7 \times 10^{-5}$) and $\ell _{\rm BB}=1$. Synchrotron losses were neglected.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.4cm,clip]{2161fg4.ps} \end{figure} Figure 4: Proton steady-state spectra for various external black-body photon compactnesses. All cases are taken for the same injection proton parameters ( $\ell_{\rm p}=2.5\times 10^{-3}, ~\gamma_{\rm p,max}=10^6,~t_{\rm p,esc}=1$) and for the same temperature of the external black-body field ( $T_{\rm BB}=10^5~\rm K$) The plotted proton spectra are shown when $\ell _{\rm BB}=0$ (no-loss case, full line), $\ell _{\rm BB}=1$ (dotted line), $\ell _{\rm BB}=10^2$ (short-dashed line) and $\ell _{\rm BB}=10^4$ (long-dashed line).
Open with DEXTER

The efficiency of the BH process, i.e., the ratio of the proton power turned into pairs to the total power injected as protons, is shown in Fig. 5 as a function of the maximum Lorentz factor of injection $\gamma _{\rm p,max}$. The inelasticity of this process is small ( $\xi\sim10^{-3}$), so that high efficiency can only be achieved if a proton interacts many times before escape. This is indeed the case for high black-body compactnesses - the efficiency exceeds $40\%$ for $\ell_{\rm BB}>10^4$ and $\gamma_{\rm p,max}>10^7$.

  \begin{figure} \par\includegraphics[width=7.9cm,clip]{2161fg5.ps} \end{figure} Figure 5: Proton efficiency, i.e. fraction of power lost to pairs to total power injected in protons as a function of the upper cutoff of the proton distribution $\gamma _{\rm p,max}$. The rest of the proton injection parameters are kept constant ( $\ell _{\rm p}=2.5\times 10^{-3}$, $\gamma _{\rm p,min}=10^{0.1}$, $t_{\rm p,esc}=1$), while the external black-body field has temperature $T_{\rm BB}=10^5~\rm K$. and compactnesses ( bottom to top) $\ell_{\rm BB}=.01,~1,~100,~10^4$.
Open with DEXTER

4.2 Case 2: $\ell {_{p}}\ll \ell {_{BB}}$ and non-negligible synchrotron losses

In the more realistic case, where synchrotron losses cannot be neglected, the spectrum of the electrons becomes more complicated, as now the electrons cool by a combination of synchrotron radiation and inverse Compton scattering. Figure 6 shows the obtained spectra in the cases where the magnetic compactness  $\ell_{\rm B}$, defined according to

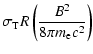$\displaystyle \ell_{\rm B}$ = $\displaystyle \sigma_{\rm T}R \left( {B^2\over {8\pi m_{\rm e}c^2}}\right)$ (30)

is comparable to $\ell_{\rm BB}$. The redistribution of the radiated luminosity to increasingly lower energies is evident, the reason being that, for this particular choice of $T_{\rm BB}$ and B, inverse Compton scattering produces much harder photons than the synchrotron mechanism. Therefore, as  $\ell_{\rm B}$ progressively increases, the peak is shifted towards the lower energies, showing the increasing importance of synchrotron radiation as an electron energy loss/photon emission mechanism. As in Fig. 3, the spectrum continues to be strongly absorbed for photon energies $x>x_{\rm max}\simeq\Theta^{-1}$.
  \begin{figure} \par\includegraphics[width=8cm,clip]{2161fg6.ps} \end{figure} Figure 6: Steady state photon spectra for the same parameters used in Fig. 3 but including synchrotron radiation. The magnetic field used was B=100 G and the magnetic compactnesses were $\ell _{\rm B}=0.01$ (full line), $\ell _{\rm B}=0.1$ (dashed line) and $\ell _{\rm B}=1$. The black-body compactness was $\ell _{\rm BB}=1$.
Open with DEXTER

5 The pair-production/synchrotron instability

5.1 Marginal stability

Kirk & Mastichiadis (1992, henceforth KM92) have shown that ultra-relativistic protons can, under certain conditions, become unstable to various types of radiative instabilities. They showed explicitly the necessary conditions for one of them to occur, namely the Pair-Production/Synchrotron instability (henceforth PPS). To understand the basic idea, assume that protons are confined in a region of characteristic radius R where a magnetic field of strength B is also present. Assume, moreover, that the protons are relativistic and have Lorentz factors such that if they photo-pair produce, the synchrotron photons radiated from the created pairs are sufficiently energetic for the protons to produce more pairs on them. Making the simplifying assumptions that (i) the created pairs have the same Lorentz factors as the protons and (ii) the synchrotron photons are all emitted at the critical frequency, KM92 showed that in order for protons to be able to initiate this loop they should have Lorentz factors above a critical value given by

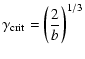$\displaystyle \gamma_{\rm crit}=\left({{2}\over {b}}\right)^{1/3}$     (31)

where $b=B/B_{\rm cr}$ with $B_{\rm cr}$ the critical value of the magnetic field ( $B_{\rm cr}=m_{\rm e}^2 c^3/e\hbar= 4.413 \times 10^{13}~$Gauss). For this loop to be self-sustained it is necessary that at least one of the synchrotron photons should produce a pair before escaping the source and this condition naturally leads to a critical proton number density (see KM92, Eq. (6)).

MK95 presented a numerical simulation of the PPS instability in the case where protons are accelerated from low momenta by a Fermi-type acceleration scheme. Once the protons (assumed to have a density exceeding the critical number density) reached energies above $\gamma_{\rm crit}$, the conditions for the instability loop were complete and the internally produced photons increased, saturating the acceleration, and driving the system to equilibrium. However, the code used by Mastichiadis & Kirk (1995) is limited by the simplifying assumptions mentioned in the previous paragraph. Here we re-examine this problem with the improved version of the code that uses, as described in Sect. 3, the Bethe-Heitler pair-production spectra as given by Monte-Carlo code and the full synchrotron emissivity. The objective is to find an accurate estimate of the critical proton number density above which the PPS instability occurs, i.e., a numerical version of the analytical (but approximate) Fig. 1 of KM92.

  \begin{figure} \par\includegraphics[width=8.45cm,clip]{2161fg7.ps} \end{figure} Figure 7: Plot of the internally produced photon compactness $\ell _{\gamma }$as a function of time for values of $n_{\rm p,0}$ around the critical value $n_{\rm p,0}^{\rm crit}$. In each curve the value of $n_{\rm p,0}$ is increased 2% from its previous value. For these runs $\gamma _{\rm p,max}=10^6$.
Open with DEXTER

To make our results directly comparable with those of the aforementioned figure, we have set the parameters to the values prescribed there. For this we took a source size R=1015 cm, a magnetic field B=103 Gauss and a proton distribution function of the form $n_{\rm p}(\gamma_{\rm p})= n_{\rm p,0}\gamma_{\rm p}^{-\beta}$ with $\beta =2$from the lowest allowed proton energy  $\gamma _{\rm p,min}=10^{0.1}$to a maximum energy  $\gamma _{\rm p,max}$. We note that in this case the proton distribution is held constant throughout each run, i.e. protons do not evolve. For various values of $\gamma _{\rm p,max}$, we run the code for different values of the only remaining free parameter ( $n_{\rm p,0}$). According to KM92, the time evolution of the photon and electron distribution functions is of the form $n_\gamma(t)\propto n_{\rm e}(t)\propto {\rm e}^{st}$with s>0 when the protons are in the unstable regime. Thus in order to verify numerically the existence of the PPS instability we seek a value $n_{\rm p,0}^{\rm crit}$ above which the internally produced electron/positron pairs and photons start increasing with time.

The onset of instability for $\gamma _{\rm p,max}=10^6$ can be seen in Fig. 7 which depicts the photon compactness $l_{\gamma}$as a function of time t (expressed, as always, in units of $t_{\rm cr}$) for various values of $n_{\rm p,0}$ around $n_{\rm p,0}^{\rm crit}$. When the protons are in the stable regime there is some pair production between the protons and the synchrotron photons produced from the initial electron distribution but the system, for times larger than the synchrotron cooling time, settles to a steady-state. Thus for $t>t_{\rm cool}$ we get s=0. However, as can be seen from the figure, as $n_{\rm p,0}$ increases (from bottom to top) the photons start to grow exponentially, with s increasing with increasing $n_{\rm p,0}$. It is worth mentioning that each curve corresponds to a value of $n_{\rm p,0}$ that is larger by only 2% than its previous value; therefore, this figure depicts the rapid onset of the instability.

Figure 8 shows the behaviour of s as a function of the proton normalisation $n_{\rm p,0}$ for three values of $\gamma _{\rm p,max}$. It is evident that once the instability sets in, s is a very sharp function of $n_{\rm p,0}$. Therefore, we find that increasing $n_{\rm p,0}$ approximately by a factor of 2 above its critical value, s becomes greater than one, i.e. the density of photons starts growing on a timescale shorter than the crossing time of the source. This, as we shall see in the next section, has catastrophic consequences for the high energy protons as the spontaneously growing photons make them lose their energies.

  \begin{figure} \par\includegraphics[width=8cm,clip]{2161fg8.ps} \end{figure} Figure 8: Behaviour of the instability growth index s as a function of $n_{\rm p,0}$ for values of $\gamma_{\rm p,max}=10^5,~10^6,~10^7$ ( right to left).
Open with DEXTER

Figure 9 shows the marginal stability curve as is obtained from the present code (in practice we have calculated the values of $n_{\rm p,0}$ which correspond to s=.05. Due to the steep dependence of s on $n_{\rm p,0}$ this value can be considered as very close to the marginal stability one). Note that this curve is in very good agreement with the curve estimated by KM92 (plotted here as a dotted line) for values of $\gamma$close to the threshold, but exceeds it by a factor of about 2 for at high energy. This difference can be attributed to the overestimation of the electron production rate in the BH process as discussed in Sect. 2. For maximum values of the proton Lorentz factor close to $\gamma_{\rm crit}$, all the BH interactions occur close to threshold, so that the assumption used by MK is accurate. (The small difference in the shape of the KM curve and our present result in this energy range can be attributed partly to the kinematics of Bethe-Heitler pair production and partly to the fact that the full expression for the synchrotron emissivity was used.) However, once the upper cut-off of the proton distribution substantially exceeds $\gamma_{\rm crit}$, the effect of pairs injected with $\gamma>\gamma_{\rm p}$ becomes important. These are not taken into account in the approximation used by MK92, but are treated accurately in the simulation-based method used here. It is evident that the basic concept of the feedback loop remains unaltered by our more accurate treatment. The quantitative implications, however, are discussed below.

  \begin{figure} \par\includegraphics[width=8cm,clip]{2161fg9.ps} \end{figure} Figure 9: Plot of the numerically obtained marginal stability as a function of $\gamma _{\rm p,max}$ (full line). The dashed line shows the s=1 locus, while the dotted line depicts the marginal stability results of KM92. Note that the KM92 approximation is reasonably good at low $\gamma _{\rm p,max}$.
Open with DEXTER

5.2 Proton injection

In order to see the effects of the PPS instability when proton losses are taken into account we assume once again (see Sect. 4) that protons are injected in a region of radius R with a power-law (Eq. (24)). However, to make the picture less complicated, we assume that there is no external photon field present. Thus one expects that the proton spectrum will reach an equilibrium state given by the no-loss solution (Eq. (25)). This is indeed true as long as this steady-state solution is below the critical density for the PPS instability, i.e. when $n_{\rm p,0}={Q_{\rm {p,0}}t_{\rm p,esc}}<n_{\rm p,0}^{\rm crit}(\gamma_{\rm p,max})$, with $n_{\rm p,0}$ the normalisation of the protons and $n_{\rm p,0}^{\rm crit}(\gamma_{\rm p,max})$ given from Fig. 9. In this case also there is a very small number of internally produced photons. However, as soon as the condition $n_{\rm p,0}={Q_{\rm {p,0}}t_{\rm p,esc}}>n_{\rm p,0}^{\rm crit}(\gamma_{\rm p,max})$ holds, the criteria for the PPS instability are satisfied. As a result, the photons increase exponentially, protons lose energy due to pair production and the system behaviour depends on the choice of the parameters $Q_{\rm {p,0}}$ and $t_{\rm p,esc}$.

  \begin{figure} \par\includegraphics[width=8cm,clip]{2161fg10.ps} \end{figure} Figure 10: Plot of the evolution of the system in the case where protons are injected with $\beta=2,~\gamma_{\rm p,max}=10^6,~t_{\rm p,esc}=1$, while the combination of the proton injection rate ( $Q_{\rm {p,0}}=0.22$) and $t_{\rm p,esc}$ is such that the steady-state proton distribution in the no-loss case corresponds to an unstable proton distribution. The solid line shows the photon compactness when all processes are taken into account, while the long dashed and dot-dashed lines show the photon compactness when certain processes are omitted (for details see text). The dotted and short dashed lines show the evolution of the first and last proton occupation number bin in the case where all the relevant processes are taken into account.
Open with DEXTER

As a first example, we show in Fig. 10 the case where $\beta=2,~\gamma_{\rm p,max}=10^6,~t_{\rm p,esc}=1$with a proton injection rate of $Q_{\rm {p,0}}=0.22$. The proton compactness parameter, according to Eq. (9), is $\ell_{\rm p}=1710$. The above combination of $Q_{\rm {p,0}}$ and $t_{\rm p,esc}$, according to Fig. 8, corresponds to a feedback loop that causes the photon density to increase with s=0.7. The dotted and short-dashed lines show, respectively, the evolution of the lowest and highest differential density bins of the proton energy. In agreement with the analytical solution of Eq. (5) in the no-loss case, the number of particles in these bins increases very quickly (in about one  $t_{\rm cr}$) to a steady state, which, however, corresponds to an unstable proton configuration. The long-dashed line shows the photon compactness when only synchrotron radiation is taken into account. This increases as $\ell_{\gamma}\propto {\rm e}^{st}$ with s=0.7 until it reaches a steady state. The dot-dashed line shows the effects on the photon compactness caused from the addition of inverse Compton scattering and photon-photon pair production. As these processes are quadratic with respect to the photon and electron/positron number densities they do not affect the slope of the compactness at early stages, i.e. as long as $\ell_{\gamma}\ll 1$. However, at the later stages of evolution these processes become important and, because they are quadratic, they cause the photon compactness to increase even faster and reach saturation sooner. Finally the solid line shows the evolution of the photon compactness when, in addition to the above processes, photon trapping due to the high density of created pairs is taken into account. This leads to higher photon compactnesses as relatively more energy is extracted from the high energy protons. This curve must be considered the "correct'' one as it contains all the relevant processes. On the other hand the photon increase causes the high energy protons (short-dashed line) to lose energy and settle in a new steady state. These losses do not affect naturally the low energy protons (dotted line) which maintain their original steady state.

At the other extreme, one can envisage a case where protons are injected slowly, but have a very long escape time. In this case we take $Q_{\rm {p,0}}=.22 \times 10^{-3}$ and $t_{\rm p,esc}=10^3$ which corresponds to the same no-loss steady state as before. The result is shown in Fig. 11, where quasi-periodic behaviour typical of a relaxation oscillator is apparent. The protons accumulate in the source and, once their density rises above the critical density, the photon density grows rapidly (on the timescale of a few times $t_{\rm cr}$) and deplete the high energy part of the proton spectrum. Once the protons have lost their energy, there is nothing left to sustain the loop and the photons escape from the system. This cycle is repeated as the protons accumulate again in the source. The behaviour of the lowest and highest proton energy bins is also shown (dotted and dashed lines respectively). It is clear that photons and high energy protons are anticorrelated, in the sense that when one population is high, the other is low. These cycles are similar to those found by Stern & Svensson (1991) using Monte-Carlo techniques.

  \begin{figure} \par\includegraphics[width=8.3cm,clip]{2161fg11.ps} \end{figure} Figure 11: Plot of the evolution of the system in the case where a low proton injection rate ( $Q_{\rm {p,0}}=2.2\times 10^{-4}$) combines with a slow protonescape time ( $t_{\rm p,esc}=10^3$) in such a way that the steady-state proton distribution in the no-loss case to correspond to an unstableproton distribution. The rest of the parameters are as in the previous figure. Solid line shows $\ell _{\gamma }$, while dotted and short dashed lines show the evolution of the proton spectrum at $\gamma _{\rm p}=10.^{0.1}$ and $\gamma _{\rm p}=10^6$ respectively.
Open with DEXTER

6 Simultaneous electron and proton injection

As a last case we examine the situation where electrons and protons are injected simultaneously, i.e., both proton and electron kinetic Eqs. (5) and (6) have an external injection term. We assume that both of these terms are in power-law form, so that, in addition to Eq. (24) that describes proton injection, we prescribe electron injection using a similar expression:

 
$\displaystyle Q_{\rm e}^{\rm ext}(\gamma_{\rm e})=Q_{\rm {e,0}} \gamma^{-\beta}H(\gamma_{\rm e}-\gamma_{\rm e,min})H(\gamma_{\rm e,max}-\gamma_{\rm e}).\enspace$     (32)

To lower the number of free parameters we assume that both electrons and protons are injected with the same spectral index $\beta$ and with the same maximum Lorentz factor, i.e. we set arbitrarily $\gamma_{\rm e,max}=\gamma_{\rm p,max}$. Moreover, when solving the relevant kinetic equations, we assume that the two species have equal escape times, i.e., $t_{\rm p,esc}=t_{\rm e,esc}$.

Depending on the particular choice of parameters, high energy electron injection can result in a synchrotron and/or an inverse Compton component (see, for example, Mastichiadis & Kirk 1997). When protons are injected as well, these will interact with the aforementioned photons causing a secondary injection of Bethe-Heitler pairs. This leads to a non-linear situation. To see this, one should compare the compactness of the externally injected electrons $\ell_{\rm e}^{\rm ext}$ (Eq. (10)) with the corresponding compactness of the internally produced pairs via the Bethe-Heitler process $\ell_{\rm e}^{\rm BH}$ (Eq. (29)). As the latter is, in general, a function of both $\ell_{\rm p}$and $\ell_{\rm e}^{\rm ext}$, when $\ell_{\rm e}^{\rm ext}< \ell_{\rm e}^{\rm BH}$ the system operates in the non-linear regime, in the sense that the cooling of the protons occurs mainly on the internally produced photons.

To investigate the effect described above we proceed as follows: we keep the electron injection parameters constant and change only the normalisation of the proton injection rate $Q_{\rm {p,0}}$ in Eq. (24) - or, equivalently, we change the proton compactness parameter $\ell_{\rm p}$ (Eq. (9)). When $\ell_{\rm p}\ll\ell_{\rm e}^{\rm ext}$ the resulting photon spectrum is simply that produced from the cooling of the externally injected electrons. However as we increase $\ell_{\rm p}$, the quantity $\ell_{\rm e}^{\rm BH}$ increases as well and, at some stage, it becomes comparable to $\ell_{\rm e}^{\rm ext}$. Above this point the system enters the nonlinear regime, as the cooling of the protons occurs primarily on its own radiation. Finally, above some critical proton compactness, a loop analogous to the one described in Sect. 5 operates, and the protons convert a substantial fraction of their energy content to electron/positron pairs and radiation. This is depicted in Fig. 12 which shows the evolution of the photons when $\ell_{\rm e}^{\rm ext}$ is kept constant, while $\ell_{\rm p}$ varies. The first curve (dotted line) assumes that no protons are injected. Due to the particular choice of the parameters the primary electrons cool fast and the system quickly reaches a steady state. In the next two cases, the injected proton compactness is $\ell_{\rm p}=200$(long-dashed line) and $\ell_{\rm p}=400$ (short-dashed line) respectively. Again a steady state is quickly reached. However the photon compactness $\ell _{\gamma }$increases as $\ell_{\rm p}$ increases because of the BH pairs created and subsequently cooled. In both of these cases the feedback loop does not operate in the sense that the proton losses remain low - or, equivalently, $\ell_{\gamma}\simeq\ell_{\rm e}^{\rm ext}+\ell_{\rm e}^{\rm BH}\ll\ell_{\rm p}$. However, for the last two cases which are for $\ell_{\rm p}=800$ (full line) and $\ell_{\rm p}=1600$(dot-dash line) the effects of the feedback are evident. In the case of the solid curve, and for the first 300 or so light crossing times, there is a gradual increase of pairs and photons in the system until their numbers are built to a level that allows a catastrophic release of the energy stored in protons. After that, a steady state is reached, but at a level much higher than that of the previous cases: $\ell_{\gamma}\simeq\ell_{\rm e}^{\rm ext}+\ell_{\rm e}^{\rm BH}\simeq\ell_{\rm p}$. It is worth mentioning that this loop operates at a proton compactness which is below the critical threshold obtained in Sect. 5. Therefore, the presence of external electrons helps to initiate the catastrophic proton energy losses at lower proton densities. Finally, the uppermost curve corresponds to a proton injection which is above the critical threshold for the PPS instability and the photons grow very quickly as discussed in Sect. 5 - see also Fig. 10.

The photon spectra corresponding to the steady states obtained in each of these runs are shown in Fig. 13. The bottom curve (dotted line) corresponds to the injection of electrons only whereas the four others are for electron and proton injection, corresponding to the curves of Fig. 12. The extra component due to BH pair production is apparent on the two lower spectra that include protons (long and short-dashed lines). The two uppermost curves correspond to the steady-state spectra when the loop was able to extract most of the proton energy. Due to the resulting high photon compactness the spectra are strongly absorbed at energies above 1 MeV due to photon-photon pair production.

  \begin{figure} \par\includegraphics[width=8.3cm,clip]{2161fg12.ps} \end{figure} Figure 12: Plot of the evolution of the photons in the case where protons and electrons are injected simultaneously with the same slope $\beta =2$ and the same high Lorentz factor cutoff, i.e. $\gamma _{\rm p,max}=\gamma _{\rm e,max}=10^6$ in a region of radius R=1015 cm immersed in a magnetic field of strength B=103 G. The injected electron compactness is $\ell _{\rm e}^{\rm ext}=0.04$ and the evolution of the photons is shown for proton compactnesses ( bottom to top) $\ell _{\rm p}=0$, 200, 400, 800 and 1600. Both species have an escape time equal to $t_{\rm cr}$. All except the highest curve correspond to stable proton distributions in the no-loss case. Nevertheless the solid curve shows a loop that eventually leads to catastrophic proton losses. The uppermost curve (dot-dashed line) corresponds to a proton distribution that is unstable even in the no-loss case. Therefore the photons increase quickly and drive the system to an equilibrium.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{2161fg13.ps} \end{figure} Figure 13: Plot of the photon spectra corresponding to the steady states obtained for the runs shown in Fig. 12. The bottom curve (dotted) shows the spectrum obtained from the cooling of the injected electrons when no protons are injected. As the injected proton compactness increases the photon spectrum is modified due to the presence of the radiation from the created pairs (long and short-dashed curves). Finally when the loop operates the photon spectrum is strongly absorbed above 1 MeV by photon-photon pair creation (solid and dot-dashed curves).
Open with DEXTER

The above findings are summarised in Fig. 14 which shows the photon compactness of the system versus the proton compactness for various injected electron compactnesses. For low values of $\ell_{\rm p}$(i.e. less than 30), the photons of the low-frequency part of the SED produced come almost exclusively from the presence of the electrons, i.e. the protons cannot significantly influence the low-frequency behaviour of the system. We note here that for synchrotron proton blazar model fits to the SED of BL Lac Objects observed at gamma-ray energies (e.g. Mücke et al. 2003) the proton compactness is $\ell_{\rm p}\sim 10^{-3}$-10-2 implying that Bethe-Heitler pair production, and any associated instability, is unimportant in these models. For intermediate values of $\ell_{\rm p}$ (i.e. between 30 and 300) the internally produced Bethe-Heitler pairs make their presence visible in that their cooling increasingly dominates the photon spectrum. Finally at even higher compactnesses the protons become unstable and cool efficiently on their own radiation.

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{2161fg14.ps} \end{figure} Figure 14: Plot of the photon compactness versus the proton compactness for various injected electron compactnesses. The curves correspond to $\ell _{\rm e}^{\rm ext}=1$, 10 and 100 ( from bottom to top). The other parameters are the same as those used in Figs. 12 and 13. The dotted line represents the critical proton compactness in the no-loss case as this was described in Sect. 5.
Open with DEXTER

7 Summary/discussion

In the present paper we have examined some consequences arising from the presence of ultrarelativistic hadrons in compact sources. This was done with the help of a numerical code that was constructed to follow the evolution of the system through the solution of three coupled, time-dependent kinetic equations for protons, electrons and photons respectively. All the relevant basic processes involving electrons and photons in astrophysical pair-plasmas were included. The coupling between the hadronic and the leptonic component was assumed to occur via Bethe-Heitler pair-production. For this process, detailed electron/positron pair-production spectra were obtained with the help of a Monte-Carlo code. These were then incorporated into the kinetic equations which were subsequently solved numerically, revealing effects mainly due to synchrotron and inverse Compton losses.

The choice of the kinetic equation approach allowed us to study various aspects of the behaviour of such a system. Thus we showed that the presence of an external black-body radiation field can extract energy efficiently from the relativistic protons only when the photon compactness is high.

Of special interest are the non-linear cases, i.e., cases in which the protons cool not on a prescribed external photon field, but on the radiation of the internally produced Bethe-Heitler pairs. In the present paper we have verified the existence of the "Pair-Production/Synchrotron'' loop previously studied analytically. We showed that this is a very efficient way of channelling proton energy into electron/positron pairs and radiation. and that the coexistence of relativistic electrons in the system does not stabilise the system but, on the contrary, lowers the critical density threshold, i.e. it facilitates the efficient transfer of energy from the hadronic component to the leptonic/photonic one. This, and the fact that the threshold and critical density conditions can be greatly relaxed if the protons are in relativistic bulk motion, makes this loop a promising candidate for some AGNs (Kazanas & Mastichiadis 1999) and GRBs (Kazanas et al. 2002).

Of the various processes omitted in the present treatment, the most important is that of photo pion-production. This, however, does not affect the results of the present paper because, in the examples shown, the initial conditions were chosen so as to avoid the onset of this process. Other processes involving protons, such as proton synchrotron radiation and proton-proton interactions, etc., are negligible for the parameters of the particular examples given in this paper.

Acknowledgements
A.M. would like to thank R.J.P. for hospitality during his stay in the University of Adelaide. This research was funded in part by a Grant from the Special Funds for Research of the University of Athens. A.M and J.K. acknowledge the EC funding under contract HPRCN-CT-2002-00321 (ENIGMA network). The research of RJP is supported by an Australian Research Council Discovery Grant.

References

 
Copyright ESO 2005