A&A 433, 777-785 (2005)
DOI: 10.1051/0004-6361:20041415
Further evidence for a merger in Abell 2218 from
an XMM-Newton observation
G. W. Pratt - H. Böhringer - A. Finoguenov
MPE Garching, Giessenbachstraße, 85748 Garching, Germany
Received 4 June 2004 / Accepted 17 December 2004
Abstract
The galaxy cluster Abell 2218, at z=0.171, is well-known
for the discrepancy between mass estimates derived from X-ray and
strong lensing analyses. With the present XMM-Newton observation, we are
able to trace the gas density and temperature
profiles out to a radius of
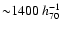 kpc (approximately
the virial radius of the cluster). The overall surface brightness
profile is well fitted over three orders of magnitude with a simple
kpc (approximately
the virial radius of the cluster). The overall surface brightness
profile is well fitted over three orders of magnitude with a simple
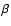 -model with a core radius of
-model with a core radius of
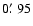 and
and
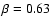 .
The
projected temperature profile declines steeply with radius (by
.
The
projected temperature profile declines steeply with radius (by
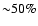 ), and is well described by a polytrope with parameters
t0 =
8.09 keV and
), and is well described by a polytrope with parameters
t0 =
8.09 keV and
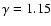 .
The temperature map
shows a pronounced peak in the central arcminute, where the
temperature rises by a factor of two (from
.
The temperature map
shows a pronounced peak in the central arcminute, where the
temperature rises by a factor of two (from 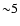 to
to 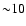 keV). The mass profile, calculated assuming hydrostatic equilibrium
and spherical symmetry, is best fitted with a King approximation
to an isothermal sphere, implying a dark matter distribution with a
central core, in contrast with the cusped cores
found in more obviously relaxed clusters. The X-ray
mass is approximately two times less than the strong lensing mass at
keV). The mass profile, calculated assuming hydrostatic equilibrium
and spherical symmetry, is best fitted with a King approximation
to an isothermal sphere, implying a dark matter distribution with a
central core, in contrast with the cusped cores
found in more obviously relaxed clusters. The X-ray
mass is approximately two times less than the strong lensing mass at
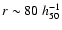 kpc, although the agreement between X-ray and weak
lensing mass measurements at larger radius (
kpc, although the agreement between X-ray and weak
lensing mass measurements at larger radius (
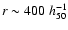 kpc) is slightly better. While the X-ray total mass estimates can vary
by 30 per cent depending on the mass model, all measurements are
significantly lower than the corresponding total mass from optical
measurements. Given the X-ray results indicating considerable
disturbance of the intracluster gas, leading to a probable violation
of the assumption of hydrostatic equilibrium, and the observed
substructure in the optical, suggesting a line-of-sight merger, it is
unlikely that the different mass estimates of this cluster can be
reconciled, at least with standard modelling assumptions.
kpc) is slightly better. While the X-ray total mass estimates can vary
by 30 per cent depending on the mass model, all measurements are
significantly lower than the corresponding total mass from optical
measurements. Given the X-ray results indicating considerable
disturbance of the intracluster gas, leading to a probable violation
of the assumption of hydrostatic equilibrium, and the observed
substructure in the optical, suggesting a line-of-sight merger, it is
unlikely that the different mass estimates of this cluster can be
reconciled, at least with standard modelling assumptions.
Key words: galaxies: clusters: individual:
A2218 - galaxies: intergalactic medium - cosmology:
observations - cosmology: dark matter - X-rays: galaxies: clusters
In what has effectively become the standard scenario for the formation
of structure in the Universe, galaxy clusters are born in the collapse
of initial density fluctuations and grow under the influence of
gravity. They are the nodes of cosmic structure, accumulating mass
through a combination of continuous accretion of smaller subunits
along the filaments between clusters, interrupted by the occasional
violent merger. Cosmological simulations show that, in a given
cosmological volume, the sample of clusters will span the range from
those which are relatively relaxed to those which are clearly in the
midst of a major merger (e.g., Ascasibar et al. 2003), not surprising given the
hierarchical scenario.
Given a sufficiently large sample of galaxy clusters, constraints can
be put on cosmological parameters. For instance, constraints on
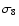 and
and 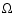 can be found by observing the cluster mass
function and its evolution (Perrenod 1980; see Henry 2004 for
a recent review). Cluster masses can be estimated using traditional
baryonic mass tracers such as the velocity dispersion of the galaxies
(e.g., Girardi et al. 1998), or the X-ray emission of the intracluster
medium (e.g., Reiprich & Böhringer 2002), provided some assumptions are made about
the relationship between the distribution of dark and luminous
matter. For example, the fact that a given cluster is roughly
spherical and in approximate hydrostatic equilibrium is a fundamental
assumption when the total mass is derived from the X-ray data. On the
other hand, gravitational lensing offers another view of the
distribution of matter, allowing the calculation of the projected mass
within a cluster, either from strong lensing at small scales or weak
lensing on larger scales. However, because lensing measures the
projected mass, strong lensing in particular is very sensitive to
additional matter along the line of sight (Wambsganss et al. 2004), and to the
detailed dynamical state of the cluster (Torri et al. 2004). Indeed, it has
been suggested that strong lensing arcs occur predominantly in
clusters which are dynamically more active than typical clusters
(Bartlemann & Steinmetz 1996).
can be found by observing the cluster mass
function and its evolution (Perrenod 1980; see Henry 2004 for
a recent review). Cluster masses can be estimated using traditional
baryonic mass tracers such as the velocity dispersion of the galaxies
(e.g., Girardi et al. 1998), or the X-ray emission of the intracluster
medium (e.g., Reiprich & Böhringer 2002), provided some assumptions are made about
the relationship between the distribution of dark and luminous
matter. For example, the fact that a given cluster is roughly
spherical and in approximate hydrostatic equilibrium is a fundamental
assumption when the total mass is derived from the X-ray data. On the
other hand, gravitational lensing offers another view of the
distribution of matter, allowing the calculation of the projected mass
within a cluster, either from strong lensing at small scales or weak
lensing on larger scales. However, because lensing measures the
projected mass, strong lensing in particular is very sensitive to
additional matter along the line of sight (Wambsganss et al. 2004), and to the
detailed dynamical state of the cluster (Torri et al. 2004). Indeed, it has
been suggested that strong lensing arcs occur predominantly in
clusters which are dynamically more active than typical clusters
(Bartlemann & Steinmetz 1996).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1415f1a.eps}\hspace*{1.3cm}
\includegraphics[width=7.5cm,clip]{1415f1b.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg15.gif) |
Figure 1:
The left panel shows a large-scale XMM/DSS
overlay image. The (log-spaced) contours are from the
adaptively-smoothed, non-background subtracted, EMOS1+EMOS2
[0.5-2.0] keV image. The right panel shows an XMM/HST overlay
image with the same contours. |
| Open with DEXTER |
Cluster mergers release vast amounts of energy into the X-ray emitting
gas of the intracluster medium (ICM), leading to significant
departures from hydrostatic equilibrium. Strong variations are
produced in observable characteristics such as density, and, since
much of the energy is dissipated in shocks, temperature and
entropy. Temperature variations following a merger can survive
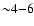 times longer than density substructure, and so the temperature
distribution is a strong diagnostic of the dynamical state of a given
cluster (e.g., Markevitch et al. 1998).
times longer than density substructure, and so the temperature
distribution is a strong diagnostic of the dynamical state of a given
cluster (e.g., Markevitch et al. 1998).
A2218 was one of the first targets for a detailed mass study comparing
X-ray and weak lensing data (Squires et al. 1996), which concluded that
these mass estimates were in agreement (see also
Allen 1998). However, the strong lensing mass (estimated using
the remarkable arcs at a distance of
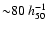 kpc) was not in agreement with the X-ray estimate
(e.g., Miralda-Escudé & Babul 1995). ROSAT studies suggested complicated X-ray
structure near the core (Neumann & Böhringer 1999; Markevitch 1997); recent Chandra
observations have revealed this structure in greater detail
(Machacek et al. 2002). This has given rise to the general conclusion that the
cluster is dynamically active, which is also supported by the presence
of mass substructure in subsequent lensing studies (the latest being
Smith et al. 2004), and indeed substructure in the galaxy distribution
in the optical (Girardi & Mezzetti 2001). The recent Chandra temperature map
of the central regions shows quite strong temperature variations
(Govoni et al. 2004). The cluster also hosts a weak radio halo (Giovannini & Ferretti 2000).
kpc) was not in agreement with the X-ray estimate
(e.g., Miralda-Escudé & Babul 1995). ROSAT studies suggested complicated X-ray
structure near the core (Neumann & Böhringer 1999; Markevitch 1997); recent Chandra
observations have revealed this structure in greater detail
(Machacek et al. 2002). This has given rise to the general conclusion that the
cluster is dynamically active, which is also supported by the presence
of mass substructure in subsequent lensing studies (the latest being
Smith et al. 2004), and indeed substructure in the galaxy distribution
in the optical (Girardi & Mezzetti 2001). The recent Chandra temperature map
of the central regions shows quite strong temperature variations
(Govoni et al. 2004). The cluster also hosts a weak radio halo (Giovannini & Ferretti 2000).
With the present XMM-Newton observations we derive gas density and
temperature profiles out to large radius, generate a large scale
temperature map, and, assuming hydrostatic equilibrium and spherical
symmetry, calculate a mass profile of the cluster. As we will see, the
assumptions inherent in the mass profile calculation are probably
violated, at least in the cluster centre.
The cluster lies at a redshift of z=0.171. In our chosen cosmology
(H0 = 70 km s-1 Mpc-1,
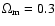 and
and
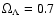 ), 1
), 1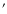 corresponds to
corresponds to
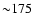 kpc. Errors are quoted at the
kpc. Errors are quoted at the 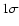 level unless otherwise stated.
level unless otherwise stated.
A2218 was observed for 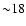 ks on 2002 September 28. The
observation showed no soft proton flares in the high
energy (>10 keV) light curves. There is a slight (
ks on 2002 September 28. The
observation showed no soft proton flares in the high
energy (>10 keV) light curves. There is a slight (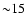 per
cent) increase in the broad-band [0.3-10.0 keV] count rate at the
beginning of the observation, lasting
per
cent) increase in the broad-band [0.3-10.0 keV] count rate at the
beginning of the observation, lasting 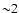 ks. Since the increase
is very weak and of short duration, and has no effect on the derived
normalisation at high energy, we have used the entire observation.
ks. Since the increase
is very weak and of short duration, and has no effect on the derived
normalisation at high energy, we have used the entire observation.
Except where noted, in the following analysis we use EMOS PATTERNs 1-12
and EPN PATTERN 0 events. To correct for vignetting, the photon
weighting method as implemented in the SAS task evigweight was
applied to each event file. The blank-sky event lists of Read & Ponman (2003)
were used as background files, with these event
lists being subjected to the same screening criteria, PATTERN
selection and vignetting correction as the observation event
files.
An XMM/DSS overlay image is shown in Fig. 1. The cluster
exhibits slightly elliptical, symmetric X-ray emission at large
scale. Near the core, the X-ray
emission becomes elongated in the SE-NW direction, which is the same
orientation as the line joining the two brightest cluster galaxies. As
can be seen in the XMM/HST overlay image, the peak of the [0.5-2.0]
keV band X-ray brightness is slightly offset from the cD galaxy. Both
the cD and the [0.5-2.0] keV X-ray peak are offset from the
large-scale centre of symmetry. Since the complicated X-ray morphology
of the central regions has been extensively examined using both ROSAT HRI (Markevitch 1997) and Chandra Machacek et al. (2002), we will
not discuss this further.
3.2 Surface brightness profile
After identification and exclusion of 28 serendipitous sources, an
azimuthally averaged surface brightness profile was generated from
source and background event files of each camera in the 0.3-3.0 keV
band. Events were extracted in circular annuli centred on the emission
peak of the cluster. Background subtraction for each camera was
undertaken as described in Pratt & Arnaud (2002). The EMOS and
EPN profiles are in excellent accord and thus the individual camera
profiles were coadded, and the total profile was then binned to a
S/N ratio of 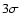 above background. This profile is shown in
Fig. 2. Cluster emission is
detected out to slightly more than
above background. This profile is shown in
Fig. 2. Cluster emission is
detected out to slightly more than
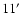 ,
corresponding to
slightly less than 2 Mpc for our chosen cosmology. For comparison, the
ROSAT profile of Cannon et al. (1999) was detected out to
,
corresponding to
slightly less than 2 Mpc for our chosen cosmology. For comparison, the
ROSAT profile of Cannon et al. (1999) was detected out to
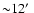 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1415f2.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg28.gif) |
Figure 2:
The combined EPIC 0.3-3.0 keV surface
brightness profile of A2218. The profile is background subtracted
and corrected for vignetting. The solid line is the best fitting
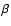 -model. See Table 1 for model
details. -model. See Table 1 for model
details. |
| Open with DEXTER |
3.3 Density profile modelling
In order to calculate the gas density profile, we fitted the surface
brightness profile with analytic models. The fitting process uses
simplex minimisation and takes into account projection effects in the
line of sight. The models we use are convolved with the XMM-Newton PSF and
binned into the same bins as the observed profile. A standard
isothermal 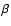 -model is an acceptable fit to these data (
-model is an acceptable fit to these data (
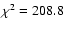 for 168 degrees of freedom), and the values found for
for 168 degrees of freedom), and the values found for 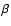 and
and 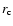 are in good agreement with ROSAT-derived values (e.g.,
Markevitch 1997; Cannon et al. 1999; Birkinshaw & Hughes 1994; Squires et al. 1996). In Fig. 2 the
best-fitting
model is shown compared to the surface brightness profile. In
Table 1 we give the
are in good agreement with ROSAT-derived values (e.g.,
Markevitch 1997; Cannon et al. 1999; Birkinshaw & Hughes 1994; Squires et al. 1996). In Fig. 2 the
best-fitting
model is shown compared to the surface brightness profile. In
Table 1 we give the 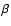 -model parameters for this fit
as well as for surface brightness profiles extracted in
-model parameters for this fit
as well as for surface brightness profiles extracted in
 sectors defined anticlockwise from the positive Y-axis. In all
instances bar the
sectors defined anticlockwise from the positive Y-axis. In all
instances bar the
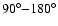 sector, a
sector, a 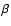 -model is an
adequate fit to the surface brightness. As a further check we
calculated surface brightness profiles centred on the broad-band X-ray
peak found in the Chandra analysis of Machacek et al. (2002). These
profiles yield best-fitting
-model is an
adequate fit to the surface brightness. As a further check we
calculated surface brightness profiles centred on the broad-band X-ray
peak found in the Chandra analysis of Machacek et al. (2002). These
profiles yield best-fitting 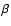 -model parameters
which are in agreement with those in Table 1.
-model parameters
which are in agreement with those in Table 1.
On close examination of Fig. 2, it can be seen that the
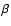 -model is an excellent description of the data over three orders of
magnitude in surface brightness. Related to this is the lack of
evidence for a turnover in the surface brightness at very large radius
(cf., Vikhlinin et al. 1999), although this latter point is
highly sensitive to the exact background subtraction method.
-model is an excellent description of the data over three orders of
magnitude in surface brightness. Related to this is the lack of
evidence for a turnover in the surface brightness at very large radius
(cf., Vikhlinin et al. 1999), although this latter point is
highly sensitive to the exact background subtraction method.
Table 1:
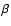 -model fits for various sectors of A2218,
errors are 90 per cent confidence. Sectors are defined
anticlockwise from the positive Y-axis.
-model fits for various sectors of A2218,
errors are 90 per cent confidence. Sectors are defined
anticlockwise from the positive Y-axis.
In the following, the background spectra were normalised using the
count rates in the source-free [10.-12.] keV (EMOS) and [12.-14.] keV
(EPN) bands. The normalisation factors used were 1.09, 1.11 and 1.15 for
EMOS1, EMOS2 and EPN, respectively.
4.1 Global spectrum
We extracted a global spectrum from all events within a circle of
radius
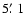 to allow for direct comparison with the Chandra results. We fitted the data using a simple single
temperature absorbed MEKAL model with the redshift fixed at the
average redshift of the cluster (z=0.17).
to allow for direct comparison with the Chandra results. We fitted the data using a simple single
temperature absorbed MEKAL model with the redshift fixed at the
average redshift of the cluster (z=0.17).
It was found that naive fitting of the spectra in the band [0.3-10.0]
keV with the absorption fixed at the galactic level (
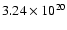 cm-2) produced results where the EPN temperature was
significantly lower than that found by the EMOS. Conversely, if the
absorption was let free, then the EPN absorption was significantly
lower than that found by the EMOS (which was in good agreement with the
galactic value). We thus adopted the ad hoc strategy discussed
in Pratt & Arnaud (2002), fixing the low-energy cutoff at 0.6
keV for the EMOS and 1.0 keV for the EPN, which leads to good agreement
between EPIC temperatures with the absorption fixed at the galactic
value.
cm-2) produced results where the EPN temperature was
significantly lower than that found by the EMOS. Conversely, if the
absorption was let free, then the EPN absorption was significantly
lower than that found by the EMOS (which was in good agreement with the
galactic value). We thus adopted the ad hoc strategy discussed
in Pratt & Arnaud (2002), fixing the low-energy cutoff at 0.6
keV for the EMOS and 1.0 keV for the EPN, which leads to good agreement
between EPIC temperatures with the absorption fixed at the galactic
value.
The global temperature in this case is
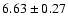 ,
with an
abundance of
,
with an
abundance of
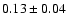 solar (90% confidence), the latter
measured relative to Anders & Grevesse (1989). This is in good
agreement with previously determined values, such as the Ginga
analysis of McHardy et al. (1990), the ASCA analyses of
Mushotzky & Loewenstein (1997), Allen (1998) and Cannon et al. (1999), and the Chandra
analysis of Machacek et al. (2002).
solar (90% confidence), the latter
measured relative to Anders & Grevesse (1989). This is in good
agreement with previously determined values, such as the Ginga
analysis of McHardy et al. (1990), the ASCA analyses of
Mushotzky & Loewenstein (1997), Allen (1998) and Cannon et al. (1999), and the Chandra
analysis of Machacek et al. (2002).
4.2 Radial temperature profile
We then calculated a simple projected radial temperature
profile. After exclusion of point sources, spectra were extracted in
10 annuli centred on the X-ray emission peak and extending to the
radius of maximum detection of the surface brightness profile (i.e.,
0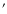 -11
-11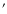 ). The spectra were binned to
). The spectra were binned to 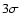 to allow
the use of Gaussian statistics. EPIC spectra were then
simultaneously fitted in the [1.-10.] keV band with a single
temperature MEKAL model with free abundances and the absorption fixed
at the galactic value. We choose a relatively high low-energy cutoff
to avoid problems related to the variation of the soft X-ray
background with position on the sky.
to allow
the use of Gaussian statistics. EPIC spectra were then
simultaneously fitted in the [1.-10.] keV band with a single
temperature MEKAL model with free abundances and the absorption fixed
at the galactic value. We choose a relatively high low-energy cutoff
to avoid problems related to the variation of the soft X-ray
background with position on the sky.
While we have already normalised the background using the count rates
in the source-free high energy bands, background subtraction is
critical in spectroscopic studies at the
lowest surface brightness levels, and can have significant effects on
the radial profile at high radii. We thus re-fitted the spectra with
the background at 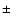 10 per cent of nominal, the variation seen in
the typical quiescent background level. The temperatures of all
annuli agree within the
10 per cent of nominal, the variation seen in
the typical quiescent background level. The temperatures of all
annuli agree within the 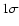 error bars whatever the
normalisation.
error bars whatever the
normalisation.
The projected temperature profile is shown in
Fig. 3. The error bars are the upper and lower limit
temperatures for each annulus taking into account variations of 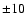 percent in the background normalisation. These uncertainties
are the total systematic plus statistical errors and should be viewed
as very conservative estimates. As expected, the
external annuli exhibit the largest uncertainties; however, the
robustly determined lower limit of the temperature in the final
annulus is 2.3 keV. The temperature profile is in excellent agreement
with that found in the ASCA analysis of
Cannon et al. (1999) and the
more recent Chandra analysis of Markevitch et al. (2000), but
extends to larger radius (albeit with large uncertainties).
percent in the background normalisation. These uncertainties
are the total systematic plus statistical errors and should be viewed
as very conservative estimates. As expected, the
external annuli exhibit the largest uncertainties; however, the
robustly determined lower limit of the temperature in the final
annulus is 2.3 keV. The temperature profile is in excellent agreement
with that found in the ASCA analysis of
Cannon et al. (1999) and the
more recent Chandra analysis of Markevitch et al. (2000), but
extends to larger radius (albeit with large uncertainties).
A polytropic model,
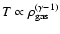 ,
with the gas density described with the
,
with the gas density described with the 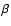 -model discussed
above (Sect. 3.3), is a good description of the projected
temperature profile. The best-fitting values for the central
temperature and polytropic index are
-model discussed
above (Sect. 3.3), is a good description of the projected
temperature profile. The best-fitting values for the central
temperature and polytropic index are
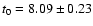 keV and
keV and
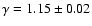 ,
respectively; this model
is also shown in Fig. 3.
,
respectively; this model
is also shown in Fig. 3.
As a consequence of the high temperature, abundance measurements of
this cluster are poorly-constrained, but are consistent with being
flat at the average value (
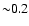 )
out to the detection limit.
)
out to the detection limit.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1415f3.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg53.gif) |
Figure 3:
The projected radial temperature profile of
A2218. Error bars are upper ( lower) limits from fits with
background normalisation at +10 (-10) per cent of
nominal. The solid line is the best fitting
polytropic model to the data. See text for
details. |
| Open with DEXTER |
4.3 Temperature map
We next produced a temperature map using the adaptive binning
technique described in Belsole et al. (2004). A full energy
band image with the sources excised was extracted from each camera,
and the camera images coadded. Starting from the largest spatial scale
(i.e., the entire image), the image was divided into cells. Each cell
is divided by four until a certain threshold criterion is met (for
this map, a total of 1000 counts in the full energy band prior to
background subtraction). Spectra are then extracted from the source
and background event lists with the resulting spatial binning, and
background subtracted. The same absorbed MEKAL model was fitted to
each spectrum in the bands described above (this time with the
abundance fixed to
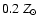 ). The derived uncertainties are
dependent on the temperature. In building the temperature map shown in
Fig. 4, we only used cells with relative errors smaller
than 50 per cent. The
temperature structures in this map are very similar to those in the Chandra map of Govoni et al. (2004).
). The derived uncertainties are
dependent on the temperature. In building the temperature map shown in
Fig. 4, we only used cells with relative errors smaller
than 50 per cent. The
temperature structures in this map are very similar to those in the Chandra map of Govoni et al. (2004).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1415f4.ps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg55.gif) |
Figure 4:
Adaptively-binned temperature map of
A2218. The contours are the same as those in
Fig. 1. |
| Open with DEXTER |
5.1 Deprojection of temperature profile and correction for PSF
effects
In order to have the best estimate of the mass profile it is necessary
to take into account PSF and projection effects on the temperature
profile. Since correction for these effects using simultaneous
spectral fits under XSPEC tends to be unstable (Pratt & Arnaud 2005; Pointecouteau et al. 2004), we
use the method described in Pointecouteau et al. (2005). With the gas density
represented by the best fitting 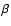 -model (Sect. 3.3), we
adopt a polytropic representation of the projected temperature profile
(Sect. 4.2), and convolve this with a redistribution
matrix which takes into account both PSF and projection effects. The
projected profile was randomly sampled 1000 times within the observed
errors, the gas density profile being allowed to vary within the
uncertainties of the best fitting
-model (Sect. 3.3), we
adopt a polytropic representation of the projected temperature profile
(Sect. 4.2), and convolve this with a redistribution
matrix which takes into account both PSF and projection effects. The
projected profile was randomly sampled 1000 times within the observed
errors, the gas density profile being allowed to vary within the
uncertainties of the best fitting 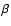 -model. The final deprojected,
PSF-corrected temperature profile and associated
errors were then the mean and standard deviation of the 1000 corrected
values at each point.
-model. The final deprojected,
PSF-corrected temperature profile and associated
errors were then the mean and standard deviation of the 1000 corrected
values at each point.
Fitting a polytropic model to the deprojected, PSF-corrected
temperature profile yields best-fitting values for the central
temperature and polytropic index of
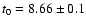 keV and
keV and
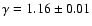 ,
respectively.
,
respectively.
5.2 Total mass profile calculation
Combining the deprojected, PSF-corrected density and temperature
profiles (Sects. 3.3
and 5.1), we can derive a total mass profile under
the assumptions of hydrostatic equilibrium and spherical
symmetry. Given the observed temperature structure, this is probably
not a good assumption (certainly in the inner
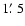 or so), but
it is still
interesting to see if X-ray and lensing mass estimates agree in the
external regions. The mass profile was calculated using the Monte
Carlo method described in Pratt & Arnaud (2003); the resulting
total mass profile is shown in Fig. 5.
or so), but
it is still
interesting to see if X-ray and lensing mass estimates agree in the
external regions. The mass profile was calculated using the Monte
Carlo method described in Pratt & Arnaud (2003); the resulting
total mass profile is shown in Fig. 5.
For easier comparison with previous analyses, particularly results
from ASCA (Cannon et al. 1999) and Chandra (Machacek et al. 2002), we
also show the mass profile obtained when the temperature profile is
assumed isothermal and the gas density is parameterised by a
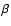 -model. For this we assume a temperature of kT= 6.6keV (Sect. 4.1) and the best fitting
-model. For this we assume a temperature of kT= 6.6keV (Sect. 4.1) and the best fitting 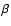 -model in
Sect. 3.3. The mass profile obtained using this method is
slightly different from the one we have derived using spatially
resolved temperature information, being slightly lower in the inner
regions, and higher in the outskirts.
-model in
Sect. 3.3. The mass profile obtained using this method is
slightly different from the one we have derived using spatially
resolved temperature information, being slightly lower in the inner
regions, and higher in the outskirts.
5.3 Mass profile modelling
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1415f5.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg59.gif) |
Figure 5:
The total mass profile of A2218, calculated
from the X-ray data assuming hydrostatic equilibrium and spherical
symmetry. The dashed line is the isothermal 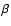 -model mass,
assuming a constant temperature of kT= 6.6 keV
(Sect. 4.1).The solid line is the best fitting
isothermal sphere model (King approximation) for the total mass
profile; also shown (dot-dash line) is the best fitting NFW mass
model to the entire profile (see Table 2 for
details). -model mass,
assuming a constant temperature of kT= 6.6 keV
(Sect. 4.1).The solid line is the best fitting
isothermal sphere model (King approximation) for the total mass
profile; also shown (dot-dash line) is the best fitting NFW mass
model to the entire profile (see Table 2 for
details). |
| Open with DEXTER |
Since the mass profile is defined to very good precision, it is
interesting to compare it with theoretical expectations. We thus tried
fitting the mass profile with functional forms for the dark matter
density, these being the King approximation to an isothermal sphere
(e.g., Sarazin 1986) and the NFW profile (Navarro et al. 1997), given by:
respectively, where we have followed Ettori et al. (2002), in
expressing the normalisation of both mass models through the
concentration parameter, c. The King profile is clearly preferred in
terms of 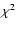 ,
although the removal of the central mass point
leads to an acceptable fit for the NFW mass model (see
Table 2 for details). The best-fitting mass profile
models are compared to the data in Fig. 5.
,
although the removal of the central mass point
leads to an acceptable fit for the NFW mass model (see
Table 2 for details). The best-fitting mass profile
models are compared to the data in Fig. 5.
Table 2:
NFW and King isothermal sphere fits to the total mass
profile of A2218. Errors are 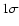 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1415f6.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg76.gif) |
Figure 6:
The entropy profile of A2218. The radius has
been scaled to r200 using the r200-T relation of
Arnaud et al. (2005). The entropy is scaled using the
empirical scaling of Ponman et al. (2003, )math56#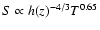 #. The line following the points is the
entropy profile obtained from the best-fitting analytical models
to the deprojected, PSF-corrected gas density and temperature
profiles. The straight line is the mean scaled entropy profile found
by Pratt & Arnaud (2005). #. The line following the points is the
entropy profile obtained from the best-fitting analytical models
to the deprojected, PSF-corrected gas density and temperature
profiles. The straight line is the mean scaled entropy profile found
by Pratt & Arnaud (2005). |
| Open with DEXTER |
It has been known for some time that the central regions of
this cluster show signs of being morphologically disturbed in X-ray
(Markevitch 1997; Neumann & Böhringer 1999; Machacek et al. 2002). The spatially resolved temperature maps from this
work and from Chandra (Govoni et al. 2004) provide further
evidence, if any were needed, that A2218 is undergoing (or has
undergone) a merger. The
centrally-peaked radial temperature profile has been resolved into a
small region of significantly hotter gas in the core. The temperature
varies by a factor of two in the central arcminute. The hottest
parts of the cluster are only approximately spatially coincident with
the weak radio halo (Govoni et al. 2004). Comparing the HST galaxy distribution
(Fig. 1)
and the temperature map (Fig. 4), the hottest region is
spatially coincident with the two main galaxies, and thus with the two
main mass peaks found in lensing analyses, but is offset from the
X-ray surface brightness maximum.
We have also investigated the structure in entropy and pressure
using masks created to resolve the observed fluctuations in (i) the
temperature and surface brightness, and (ii) the entropy and
pressure. Both masks have 16 regions, 8 regions covering the
central
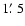 ,
and 8 covering larger scales of
,
and 8 covering larger scales of
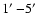 .
The method of mask generation and the calculation of the
deprojected pressure and entropy in each region is described in
Henry et al. (2004). The
fluctuations on these scales are found to be statistically significant
and amount to
.
The method of mask generation and the calculation of the
deprojected pressure and entropy in each region is described in
Henry et al. (2004). The
fluctuations on these scales are found to be statistically significant
and amount to
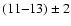 per cent in entropy and
per cent in entropy and 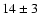 per
cent in pressure, where the two values given for the entropy show the
slight dependence on the mask. Note however that the results obtained
using the two different masks are consistent. The scatter in the
entropy and pressure in the central arcminute is
per
cent in pressure, where the two values given for the entropy show the
slight dependence on the mask. Note however that the results obtained
using the two different masks are consistent. The scatter in the
entropy and pressure in the central arcminute is 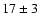 per cent and
per cent and
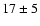 per cent, respectively.
per cent, respectively.
The temperature structure of a cluster has often been used to learn
more about the merger kinematics in interacting clusters
(e.g., Markevitch et al. 1999; Belsole et al. 2005,2004). This is very difficult in the present
case, since, at least in X-ray, the merger geometry is not
obvious. In particular, the X-ray surface
brightness does not show more than one peak and is fairly symmetric at
large radii.
The entropy profile of the cluster shown in Fig. 6 was
calculated using the now-customary entropy definition,
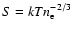 ,
where we have used the best-fitting
,
where we have used the best-fitting 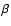 -model for the gas
density (Sect. 3.3) and the deprojected, PSF-corrected
temperature profile (Sect. 5.1). Uncertainties due to gas
density profile modelling are negligible compared to the temperature
measurement errors. The radius has been scaled using the observed
r200-T relation of Arnaud et al. (2005)
-model for the gas
density (Sect. 3.3) and the deprojected, PSF-corrected
temperature profile (Sect. 5.1). Uncertainties due to gas
density profile modelling are negligible compared to the temperature
measurement errors. The radius has been scaled using the observed
r200-T relation of Arnaud et al. (2005)![[*]](/icons/foot_motif.gif) ,
and the entropy has been scaled
using the relation found by Ponman et al. (2003)
,
and the entropy has been scaled
using the relation found by Ponman et al. (2003)![[*]](/icons/foot_motif.gif) . We also show an
analytically-derived profile
obtained using the best fitting analytic description of the
temperature and density data.
. We also show an
analytically-derived profile
obtained using the best fitting analytic description of the
temperature and density data.
It is clear that the entropy profile of A2218 is rather flat in the
inner regions (
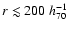 kpc, or
kpc, or
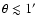 ), where the central entropy levels out to a value of
), where the central entropy levels out to a value of
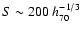 keV cm2 at
20 h70-1 kpc. This
flattening is driven by the large core in the gas density. Because of
this, A2218 was found to be a significant outlier in the sample of
Lloyd-Davies et al. (2000). In fact, the temperature map shows variations of a factor
of two (from
keV cm2 at
20 h70-1 kpc. This
flattening is driven by the large core in the gas density. Because of
this, A2218 was found to be a significant outlier in the sample of
Lloyd-Davies et al. (2000). In fact, the temperature map shows variations of a factor
of two (from 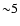 to
to 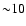 keV) in the central
arcminute. The complex
entropy distribution in the central regions is smoothed out by the use
of annular regions to produce the profile.
keV) in the central
arcminute. The complex
entropy distribution in the central regions is smoothed out by the use
of annular regions to produce the profile.
From an analysis of five clusters, Pratt & Arnaud (2005) found approximately 20 per cent dispersion in the scaled entropy profiles of their
sample. Their mean scaled profile, obtained in the radial range [0.05-0.5] r200 (Eq. (4) of Pratt & Arnaud 2005) is also shown in
Fig. 6. Excluding the inner three points, a power-law
fit to the entropy profile of A2218 yields a slope of
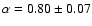 ,
slightly shallower than the mean scaled profile, although
consistent within the
,
slightly shallower than the mean scaled profile, although
consistent within the 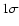 uncertainties.
uncertainties.
It is becoming increasingly clear that the mass profiles of relatively
relaxed, hot clusters are well described by the NFW profile (e.g.,
Lewis et al. 2003; Pointecouteau et al. 2004; Arabadjis et al. 2002; David et al. 2001; Allen et al. 2001; Pratt & Arnaud 2002; Pointecouteau et al. 2005). Such clusters
generally exhibit strongly peaked surface brightness profiles, and
regular density and temperature structure. In cases such as
these, the standard assumptions in the X-ray mass analysis
(hydrostatic equilibrium and spherical symmetry) are more
than likely warranted.
An NFW model is not a good description of the total mass profile of
A2218, particularly in the inner regions, as expected given the
observed density and temperature structure. While exclusion of the
central mass point improves the NFW fit considerably, the best fitting
mass model to the entire profile remains the King model, a consequence
more of the large core in the gas density than the radial temperature
distribution.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1415f7.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg89.gif) |
Figure 7:
The projected mass profile of A2218. Filled
circles with error bars are the XMM data points. The dashed line
is the isothermal 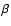 -model mass, assuming a constant temperature
of 6.6 keV. Various other
symbols indicate different lensing mass
estimates. -model mass, assuming a constant temperature
of 6.6 keV. Various other
symbols indicate different lensing mass
estimates. |
| Open with DEXTER |
The considerable disagreement between the masses derived from X-ray
and lensing analyses of this cluster has generated some debate in the
past (e.g., Allen 1998; Miralda-Escudé & Babul 1995). In Fig. 7 we show the
projected mass profile obtained from these XMM-Newton data, converted to
the SCDM (
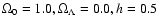 )
cosmology used
in previous analyses. The profile is compared to the masses obtained
from strong lensing (Allen 1998; Loeb & Mao 1994; Kneib et al. 1995), weak lensing
(Smail et al. 1997; Squires et al. 1996) and combined lensing (Smith et al. 2004; AbdelSalam et al. 1998).
)
cosmology used
in previous analyses. The profile is compared to the masses obtained
from strong lensing (Allen 1998; Loeb & Mao 1994; Kneib et al. 1995), weak lensing
(Smail et al. 1997; Squires et al. 1996) and combined lensing (Smith et al. 2004; AbdelSalam et al. 1998).
Despite having a well constrained radial temperature distribution, the
X-ray mass is approximately two times less than the strong lensing
mass at
85 h50-1 kpc. At larger radius, the agreement between
mass estimates is better, although still not perfect. The observed
disagreement in the inner regions would be expected if either (i)
there was a smaller subcluster in the line of sight, or (ii) the
hydrostatic assumption is violated, possibilities we discuss in more
detail below.
Depending on the adopted mass
model, the virial mass, M200, varies by about 30 per cent (see
Table 2).
Arnaud et al. (2005) have recently derived an X-ray M-T relation derived from XMM-Newton observations of 10 clusters in the 2-9 keV range. Since the
methods detailed in the present paper are very
similar to their analysis, it forms an ideal comparison sample.
The total mass, M200, predicted by the M-T relation of
Arnaud et al. (2005), assuming a virial temperature of 6.6 keV
(Sect. 4.1), is
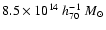 ,
about 25 per cent higher than the
highest mass estimate from mass profile modelling
(Table 2).
,
about 25 per cent higher than the
highest mass estimate from mass profile modelling
(Table 2).
We can also compare the mass estimates from the different X-ray mass
models with the optical virial mass estimates of Girardi & Mezzetti (2001). We note
that the most distant galaxy from the cluster centre in Girardi &
Mezzetti's analysis is only at
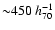 kpc, and so
there is a fair amount of extrapolation needed in their mass
estimate. These authors analyse 43 galaxies and find
kpc, and so
there is a fair amount of extrapolation needed in their mass
estimate. These authors analyse 43 galaxies and find
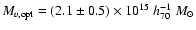 ,
for an
optically-derived virial radius of
2.3 h70-1 Mpc. Our
best-fitting mass models give
,
for an
optically-derived virial radius of
2.3 h70-1 Mpc. Our
best-fitting mass models give
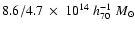 (NFW/King) for the same radius. This is
a very significant mass discrepancy. If there is indeed a line of sight
merger, this will artificially increase the optical galaxy velocity
dispersion if only one component is assumed, leading to a higher
optical mass estimate.
(NFW/King) for the same radius. This is
a very significant mass discrepancy. If there is indeed a line of sight
merger, this will artificially increase the optical galaxy velocity
dispersion if only one component is assumed, leading to a higher
optical mass estimate.
We have undertaken a detailed X-ray analysis of the well-known lensing
cluster A2218. In the inner
regions (
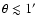 ,
or
,
or
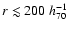 kpc) the X-ray isophotes become elongated and oriented approimately
SW-NE, the same direction as the line joining the two brightest
cluster galaxies (which are also the mass peaks seen in lensing
studies). There is a marked offset between the position of the cD
galaxy and the X-ray brightness peak, as was seen in previous ROSAT
and Chandra studies (Markevitch 1997; Neumann & Böhringer 1999; Machacek et al. 2002). In agreement with
previous Chandra results (Markevitch et al. 2000), we find that the
temperature profile decreases significantly from the centre. With the
present observation, we find that this decrease continues to the
virial radius of the cluster. From an adaptively-binned temperature
map, we find similar temperature structure to that found in the Chandra observation (Govoni et al. 2004). There is a pronounced peak in the
temperature in the inner
kpc) the X-ray isophotes become elongated and oriented approimately
SW-NE, the same direction as the line joining the two brightest
cluster galaxies (which are also the mass peaks seen in lensing
studies). There is a marked offset between the position of the cD
galaxy and the X-ray brightness peak, as was seen in previous ROSAT
and Chandra studies (Markevitch 1997; Neumann & Böhringer 1999; Machacek et al. 2002). In agreement with
previous Chandra results (Markevitch et al. 2000), we find that the
temperature profile decreases significantly from the centre. With the
present observation, we find that this decrease continues to the
virial radius of the cluster. From an adaptively-binned temperature
map, we find similar temperature structure to that found in the Chandra observation (Govoni et al. 2004). There is a pronounced peak in the
temperature in the inner
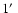 ,
where the temperature rises from
,
where the temperature rises from
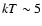 keV to
keV to 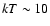 keV. The peak is not correlated with
any obvious surface brightness feature, and is offset from the surface
brightness maximum. The scatter in deprojected entropy and pressure in
the central arcminute is typically
keV. The peak is not correlated with
any obvious surface brightness feature, and is offset from the surface
brightness maximum. The scatter in deprojected entropy and pressure in
the central arcminute is typically
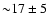 per cent.
per cent.
The mass profile (determined assuming HE and spherical symmetry) is
best fitted with a King mass model, in contrast with the results from
more relaxed clusters. An NFW model is a particularly bad fit in the
central regions. The X-ray mass estimate does not agree with the mass
estimated from strong lensing arcs at
80 h50-1, although the
agreement improves when comparing X-ray and weak lensing masses at
large radii. X-ray total mass estimates dependent on mass profile
fitting can vary by 30 per cent depending on the mass model
used. While the results must be viewed with caution, the total mass
measurement is 20-60 per cent smaller than the mass expected from the
M-T relation. X-ray and lensing mass measurements are
significantly smaller than optical virial mass estimates by more than
a factor of two.
An important clue to the merger geometry in this system comes from
optical observations. The distribution of galaxy velocities in the
optical study of Girardi et al. (1997) strongly indicates substructure in the
line of sight. Given this and the observed X-ray characteristics, it
is likely that A2218 is either an ongoing merger between a main
cluster and a smaller subcluster, or a single cluster in a more
advanced merger state. In either case, the central regions, at least,
of the cluster are unlikely to be in hydrostatic equilibrium. As a
result of this, X-ray mass estimates are highly
uncertain. Discrepancies between X-ray and lensing mass estimates due
to line of sight effects and/or mergers have also been discussed in
Andersson & Madejski (2004, A1698) and Zhang et al. (2004, CL0024+17), and in the case of
A2218 itself, by Machacek et al. (2002), in the context of the Chandra
observation.
Perhaps the most significant result from our analysis is the
calculation of a well-constrained radial temperature profile out
to approximately the virial radius of the cluster. It is unfortunate
in a way that A2218 is so obviously undergoing a merger event. In
other circumstances it would have been an ideal benchmark object for
mass measurements using the various methods in use today.
Acknowledgements
G.W.P. is grateful to J.-L. Sauvageot, M. Arnaud and E. Pointecouteau for
useful discussions. We thank the referee for comments which allowed us
to improve the paper. G.W.P. acknowledges funding from a Marie Curie
Intra-European Fellowship under the FP6 programme (Contract
No. MEIF-CT-2003-500915). A.F. acknowledges support from BMBF/DLR under
grant 50 OR 0207 and partial support from NASA grant NNG04GF686. The
present work is based on observations obtained with XMM-Newton,
an ESA science mission with instruments and contributions directly
funded by ESA Member States and the USA (NASA). This research has made
use of the NASA's Astrophysics Data System Abstract Service; the
SIMBAD database operated at CDS, Strasbourg, France; the High Energy
Astrophysics Science Archive Research Center Online Service, provided
by the NASA/Goddard Space Flight Center and the Digitized Sky Surveys
produced at the Space Telescope Science Institute.
- AbdelSalam, H. M., Saha,
P., & Williams, L. L. R. 1998, AJ, 116, 1541 [NASA ADS] [CrossRef]
- Allen, S. W. 1998, MNRAS,
296, 392 [NASA ADS] [CrossRef] (In the text)
- Allen, S. W., Schmidt, R.
W., & Fabian, A. C. 2001, MNRAS, 328, L37 [NASA ADS] [CrossRef]
- Anders, E., & Grevesse, N.
1989, GeCoA, 53, 197 [NASA ADS] (In the text)
- Andersson, K. E., &
Madejski, G. M. 2004, ApJ, 607, 190 [NASA ADS] [CrossRef] (In the text)
- Arabadjis, J. S., Bautz,
M. W., & Garmire, G. P. 2002, ApJ, 572, 66 [NASA ADS] [CrossRef]
- Arnaud, M., Pointecouteau, E.,
& Pratt, G. W. 2005, A&A, submitted
(In the text)
- Ascasibar, Y., Ypes, G.,
Müller, V., & Gottlöber, S. 2003, MNRAS, 346,
731 [NASA ADS] [CrossRef] (In the text)
- Belsole, E., Pratt,
G. W., Sauvageot, J.-L., & Bourdin, H. 2004, A&A, 415,
821 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Belsole, E.,
Sauvageot, J.-L., Pratt, G. W., & Bourdin, H. 2005, A&A,
430, 385 [EDP Sciences] [NASA ADS] [CrossRef]
- Bartelmann, M., & Steinmetz,
M. 1996, MNRAS, 283, 431 [NASA ADS] (In the text)
- Birkinshaw, M., & Hughes, J.
P. 1994, ApJ, 420, 33 [NASA ADS] [CrossRef]
- Cannon, D. B., Ponman, T.
J., & Hobbs, I. S. 1999, MNRAS, 302, 9 [NASA ADS] [CrossRef] (In the text)
- David, L. P., Nulsen,
P. E. J., McMamara, B. R., et al.001, ApJ, 557, 546
- Ettori, S., De Grandi, S.,
& Molendi, S. 2002, A&A, 391, 841 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Giovannini, G., & Ferretti,
L. 2000, New Astron., 5, 335 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., & Mezzetti, M.
2001, ApJ, 548, 79 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., Fadda,
D., Escalera, E., et al.997, ApJ, 490, 56
(In the text)
- Girardi, M., Giuricin,
G., Mardirossian, F., Mezzetti, M., & Boschin, W. 1998, ApJ,
505, 74 [NASA ADS] [CrossRef] (In the text)
- Govoni, F., Markevitch, M.,
Vikhlinin, A., et al. 2004, ApJ, 605, 695 [NASA ADS] [CrossRef] (In the text)
- Henry, J. P. 2004, ApJ,
609, 603 [NASA ADS] [CrossRef] (In the text)
- Henry, J. P., Finoguenov,
A., & Briel, U. G. 2004, ApJ, 615, 181 [NASA ADS] [CrossRef] (In the text)
- Kneib, J. P., Mellier,
Y., Pello, R., et al. 1995, A&A, 303, 27 [NASA ADS]
- Kneib, J. P., Ellis,
R. S., Smail, I., Couch, W. J., & Sharples, R. M. ApJ, 471,
643
- Lewis, A. D., Buote, D.
A., & Stocke, J. T. 2003, ApJ, 586, 135 [NASA ADS] [CrossRef]
- Lloyd-Davies, E. J., Ponman,
T. J., & Cannon, D. B. 2000, MNRAS, 315, 689 [NASA ADS] [CrossRef] (In the text)
- Loeb, A., & Mao, S. 1994,
ApJ, 435, L109 [NASA ADS] [CrossRef]
- Machacek, M. E., Bautz, M.
W., Canizares, C., & Garmire, G. P. 2002, ApJ, 567, 188 [NASA ADS] [CrossRef] (In the text)
- Markevitch, M. 1997, ApJ,
483, L17 [NASA ADS] [CrossRef]
- Markevitch, M., Forman, W.
R., Sarazin, C. L., & Vikhlinin, A. 1998, ApJ, 503, 77 [NASA ADS] [CrossRef] (In the text)
- Markevitch, M., Sarazin, C.
L., & Vikhlinin, A. 1999, ApJ, 521, 526 [NASA ADS] [CrossRef]
- Markevitch, M.,
Vikhlinin, A., Mazzotta, P., & VanSpeybroeck, L. 2000
[arXiv:astro-ph/0012215]
(In the text)
- McHardy, I. M., Stewart, G.
C., Edge, A. C., et al. 1990, MNRAS, 242, 215 [NASA ADS] (In the text)
- Miralda-Escudé, J., &
Babul, A. 1995, ApJ, 449, 18 [NASA ADS] [CrossRef] (In the text)
- Mushotzky, R. F., &
Loewenstein, M. 1997, ApJ, 481, L63 [NASA ADS] [CrossRef] (In the text)
- Navarro, J. F., Frenk, C.
S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] (In the text)
- Neumann, D., &
Böhringer, H. 1999, ApJ, 512, 630 [NASA ADS] [CrossRef]
- Perrenod, S. C. 1980,
ApJ, 236, 373 [NASA ADS] [CrossRef] (In the text)
- Pointecouteau, E., Arnaud,
M., Kaastra, J., & De Plaa, J. 2004, A&A, 423, 33 [EDP Sciences] [NASA ADS] [CrossRef]
- Pointecouteau, E., Arnaud, M.,
& Pratt, G. W. 2005, A&A, accepted
[arXiv:astro-ph/0501635]
(In the text)
- Ponman, T. J., Sanderson, A.
J. R., & Finoguenov, A. 2003, MNRAS, 343, 331 [NASA ADS] [CrossRef] (In the text)
- Pratt, G. W., & Arnaud,
M. 2002, A&A, 394, 375 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Pratt, G. W., & Arnaud,
M. 2003, A&A, 408, 1 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Pratt, G. W., & Arnaud,
M. 2005, A&A, 429, 791 [EDP Sciences] [NASA ADS] [CrossRef]
- Read, A. M., & Ponman, T. J.
2003, A&A, 409, 395 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Reiprich, T., &
Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] (In the text)
- Sarazin, C. 1986, Rev.
Mod. Phys., 58, 1 [NASA ADS] [CrossRef] (In the text)
- Smail, I., Ellis, R. S.,
Dressler, A., et al. 1997, ApJ, 479, 70 [NASA ADS] [CrossRef]
- Smith, G. P., Kneib,
J.-P., Smail, I., et al. 2004, MNRAS, submitted
[arXiv:astro-ph/0403588]
(In the text)
- Squires, G., Kaiser,
N., Babul, A., et al. 1996, ApJ, 461, 572 [NASA ADS] [CrossRef] (In the text)
- Torri, E., Meneghetti, M.,
Bartlemann, M., et al. 2004, MNRAS, 349, 476 [NASA ADS] [CrossRef] (In the text)
- Vikhlinin, A., Forman, W.,
& Jones, C. 1999, ApJ, 525, 47 [NASA ADS] [CrossRef] (In the text)
- Wambsganss, J., Bode, P.,
& Ostriker, J. P. 2004, ApJ, 606, L93 [NASA ADS] [CrossRef] (In the text)
- Zhang, Y. Y., Böhringer,
H., Mellier, Y., Soucail, G., & Forman, W. 2004, A&A, 429,
85 [EDP Sciences] [NASA ADS] (In the text)
Copyright ESO 2005
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1415f1a.eps}\hspace*{1.3cm}
\includegraphics[width=7.5cm,clip]{1415f1b.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg15.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1415f2.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1415f3.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg53.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1415f4.ps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1415f5.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg59.gif)
![$\displaystyle \delta_c = \frac{200}{3} \frac{c^3}{[\ln~ (1+c) - c/(1+c)]}$](/articles/aa/full/2005/15/aa1415/img61.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1415f6.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1415f7.eps}\end{figure}](/articles/aa/full/2005/15/aa1415/Timg89.gif)