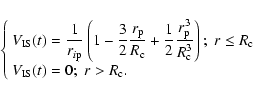 |
(1) |
A&A 433, 1153-1154 (2005)
DOI: 10.1051/0004-6361:20034093e
Erratum
H. Ben Chaouacha1 - N. Ben Nessib1 - S. Sahal Bréchot2
1 - Groupe de Recherche en Physique Atomique et
Astrophysique, Faculté des Sciences de Bizerte, 7021 Zarzouna,
Tunisia
2 -
Laboratoire d'Étude du Rayonnement et de la Matière en Astrophysique, UMR CNRS 8112-LERMA, Observatoire de Paris, Section de Meudon, 92195 Meudon Cedex, France
A&A, 419, 771-776 (2004), DOI: 10.1051/0004-6361:20034093
Abstract
An unfortunate error has been found in the expression
(Eq. (31)) of the ion sphere potential in Ben Chaouacha et al.
(2004, A&A, 419, 771). Corrected expressions are given and the associated
collisional functions are replotted.
Key words: atomic processes - errata, addenda
Due to an unfortunate error, a factor 1/2 is missing in Eq. (31) in Ben Chaouacha et al. (2004). That equation is consequently wrong. The correct expression of the Ion Sphere Potential model is as follows:
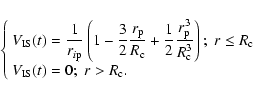 |
(1) |
![\begin{displaymath}%
J_{1\mu}^{{\rm IS}}=\int_{-\infty}^{+\infty}{\rm e}^{i\omeg...
...dehat{{r}_{\rm p}}\right)}{%
R_{\rm c}^{3}}\right] \,{\rm d}t.
\end{displaymath}](/articles/aa/full/2005/15/aa0093-03e/img18.gif) |
(2) |
![\begin{displaymath}%
A_{0}^{{\rm IS}}(z) =\left[ zK_{0}(z)-\left(\frac{3}{2}\rig...
...{2}}-\frac{x_{\rm c}\cos\,(x_{\rm c}z)}{z}\right)
\right] ^{2}
\end{displaymath}](/articles/aa/full/2005/15/aa0093-03e/img19.gif) |
(3) |
![\begin{displaymath}%
A_{\pm }^{{\rm IS}}(z)=\frac{1}{2}\left[ zK_{1}(z)-\left(\f...
...ght)\frac{z^{2}}{z_{\rm c}^{3}}\sin\,(x_{\rm c}z)\right]
^{2}.
\end{displaymath}](/articles/aa/full/2005/15/aa0093-03e/img20.gif) |
(4) |
| |
= |  |
|
 |
|||
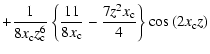 |
(5) |
| |
= | 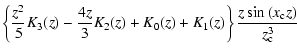 |
|
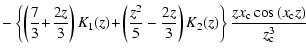 |
(6) |
| |
= | 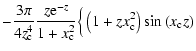 |
|
 |
|||
 |
|||
| (7) |
 |
(8) |
 |
(9) |
| |
= | 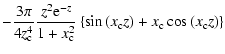 |
|
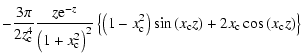 |
|||
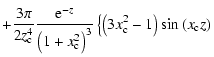 |
|||
| (10) |
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{0093fig1.eps}\end{figure}](/articles/aa/full/2005/15/aa0093-03e/Timg47.gif) |
Figure 1:
Collision functions for the transition probability. Full
lines: non-correlated functions A0(z),
|
| Open with DEXTER | |
These new expressions do not alter the behavior of the collision
functions relative to the Ion Sphere model for the transition
probability and the cross section. In fact the collision functions
plotted in Figs. 1 and 2 differ by less than 10% from the
ones plotted in Ben Chaouacha et al. (2004) for the chosen value
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{0093fig2.eps}\end{figure}](/articles/aa/full/2005/15/aa0093-03e/Timg48.gif) |
Figure 2:
Collision functions for the cross section. Full lines:
non-correlated functions a0(z),
|
| Open with DEXTER | |