A&A 433, 713-715 (2005)
DOI: 10.1051/0004-6361:20042508
Research Note
Monte Carlo simulation of solar p-mode profiles revisited: Bias and uncertainty estimation from one, not many, fits
T. Toutain 1,2 - Y. Elsworth 1 - W. J. Chaplin 1
1 - School of Physics and Astronomy, University of
Birmingham, Edgbaston, Birmingham B15 2TT, UK
2 -
Institute of Theoretical Astrophysics, University of Oslo,
PO Box 1029 Blindern, 0315 Oslo, Norway
Received 9 December 2004 / Accepted 19 January 2005
Abstract
It is quite common in helioseismology to use extensive Monte Carlo
simulations to investigate the bias and associated uncertainties in
fitted p-mode parameters. This can, however, be very time-intensive if
the fitting problem is complicated or large datasets (in time or
resolution) are involved. Here, we show that it is often possible to
reduce significantly the task by taking advantage of the statistical
properties of the p-mode profiles.
Key words: methods: data analysis - methods: statistical - Sun:
helioseismology
Acoustic oscillations of the Sun are being observed more or less continuously, both from
ground-based networks (e.g., BiSON, GONG, ECHO, HiDHN and TON) and space-borne instruments
(the ESA/NASA SOHO satellite). The accumulation of greater numbers of data, and the
increasing quality of them, has brought improvements in both the precision and accuracy with which the p-mode parameters can be determined. Short dataset lengths in the late 1970s meant the p-mode profiles were poorly resolved. By the 1980s, improved resolution
brought improvements in analysis, and observed resonant structures were fitted as combinations of Lorentzian peaks. The basic, symmetric peak model was superseded in the 1990s by formulae modified to take account of the small, but nonetheless significant, fractional asymmetries apparent in the observed profiles. Additional "complications'' in, for example, low-degree "Sun-as-a-star'' data are now also coming to light (e.g., see Chaplin et al. 2004a,b).
Monte Carlo simulations play an important role in testing the development of p-mode parameter extraction (or "fitting'') strategies and allow an assessment of possible bias of the parameters and the robustness of the associated uncertainties returned by the fitting. Fitting strategies evolve by necessity over time as longer, better-quality data throw up new, previously unseen features - like peak asymmetry - that must be properly accounted for if the fitting is to be accurate.
Although very powerful and flexible, a full Monte Carlo approach may be very
time consuming if large datasets or complicated fitting problems are being used or addressed. Here we discuss an approach that, although still based on the Monte Carlo philosophy, takes advantage of the statistical properties of the p-mode profiles to reduce drastically the computational demands involved.
Properties of the p modes are usually extracted by fitting the resonant peaks, in a power spectrum of Doppler velocity or intensity observations, to a suitable model that seeks to describe the underlying profile. Power is distributed about this limit profile according to 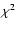 ,
two-degrees-of-freedom statistics (Woodard 1984). This result derives naturally from the fact that the acoustic waves that form the modes are excited randomly by turbulent interactions just beneath the surface of the convection zone (i.e.,
the excitation follows a normal distribution). From this distribution it follows that the likelihood function one must maximize to fit the data takes the form
,
two-degrees-of-freedom statistics (Woodard 1984). This result derives naturally from the fact that the acoustic waves that form the modes are excited randomly by turbulent interactions just beneath the surface of the convection zone (i.e.,
the excitation follows a normal distribution). From this distribution it follows that the likelihood function one must maximize to fit the data takes the form
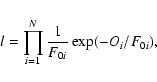 |
(1) |
where O is the profile observed in the spectrum, F0 is the fitted model profile
(the fitted representation of the true, underlying profile) and N is the number
of frequency bins across the range of the profile to be fitted. Rather than maximize
the likelihood
function, it is usual practice to minimize the function
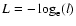 ,
so that
,
so that
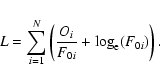 |
(2) |
Uncertainties on the parameters are estimated from the inverse of the Hessian matrix.
A Monte Carlo simulation usually involves generating a large number M of pseudo-observed profiles O(k) (with
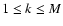 )
from one underlying limit model
)
from one underlying limit model
 .
One then minimizes each Lk to obtain a set of M fitted profiles
F0(k). The
statistical distribution of the fitted parameters that describe these profiles is then analyzed and compared to the parameters used to make the underlying data
.
One then minimizes each Lk to obtain a set of M fitted profiles
F0(k). The
statistical distribution of the fitted parameters that describe these profiles is then analyzed and compared to the parameters used to make the underlying data
 .
.
Let us assume that instead of finding the M profiles
F0(k) of the M corresponding pseudo-observed profiles we instead want to find only one profile F0 which adjusts best to the M profiles at once. That is, we have to minimize
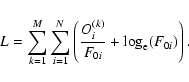 |
(3) |
This gives
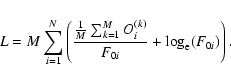 |
(4) |
Dropping the first M, which is not relevant for the minimization, and since
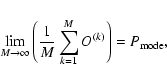 |
(5) |
the ideal case of a Monte Carlo simulation with an infinite number of profiles then implies that the best profile F0 will be uncovered by minimizing
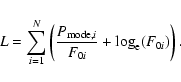 |
(6) |
L is clearly the same as in Eq. (2) when the observed profile, O, is replaced by
 ,
the underlying model used to make the artificial data. "By-passing'' the full Monte Carlo simulation therefore means fitting this underlying limit profile - by the usual maximum-likelihood approach - with a model F0
,
the underlying model used to make the artificial data. "By-passing'' the full Monte Carlo simulation therefore means fitting this underlying limit profile - by the usual maximum-likelihood approach - with a model F0![[*]](/icons/foot_motif.gif) .
.
If we choose F0 to be
 then it is not surprising that the output parameters are those used to make the data. The only new information is the output errors on the parameters, which provide the associated errors when fitting observed profiles with characteristics similar to
then it is not surprising that the output parameters are those used to make the data. The only new information is the output errors on the parameters, which provide the associated errors when fitting observed profiles with characteristics similar to
 .
These errors can be derived analytically
for simple problems (e.g., Libbrecht 1992; Toutain & Appourchaux 1994) but in the more general case this method provides a quick answer.
.
These errors can be derived analytically
for simple problems (e.g., Libbrecht 1992; Toutain & Appourchaux 1994) but in the more general case this method provides a quick answer.
If, on the other hand, we choose F0 to be different from
 we will return an estimate of the bias introduced in the determination of the parameters as a result of using an incorrect model of the underlying profile. A typical application might be to
determine the parameter bias when a Lorentzian profile is fitted to an asymmetric p-mode peak (see Sect. 4).
we will return an estimate of the bias introduced in the determination of the parameters as a result of using an incorrect model of the underlying profile. A typical application might be to
determine the parameter bias when a Lorentzian profile is fitted to an asymmetric p-mode peak (see Sect. 4).
Where the full Monte Carlo approach might involve fitting upward of 1000 or so independent realizations - in order to return a reliable estimate of, and a small error on, the mean fitted parameters - the approach outlined here requires that only one fit be performed. This can be extremely advantageous if the fitting problem is computer time-intensive. However, the single-fit solution also brings with it one clear limitation: the fact that it provides for each parameter a single value (and its associated uncertainty) only. It is therefore not possible to study the distribution of the fitted values to check, for example, that they are distributed normally and not multi-modal or skewed (in which case it would be necessary to re-interpret the output of the minimization). Provided the fitting problem is reasonably well behaved in this regard the single-fit approach is robust and the values returned admit a straight forward interpretation.
4 Example of application of technique
As an example of an application of this method we generated an artificial limit spectrum describing a single radial mode and an additional background term with a white (flat) frequency spectrum. The resonant profile was made from a slightly modified version of the
commonly-used asymmetric formalism of Nigam & Kosovichev (1998). Here, we retained terms linear in the fractional asymmetry parameter 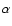 ,
but dropped those in
,
but dropped those in 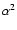 (which, owing to the small magnitude of the asymmetry, do not have a significant impact on the fitting). The underlying limit spectrum,
(which, owing to the small magnitude of the asymmetry, do not have a significant impact on the fitting). The underlying limit spectrum,
 ,
therefore took the form
,
therefore took the form
![\begin{displaymath}%
P_{\rm mode} =\frac{H}{1+4[(\nu -\nu_0)/ \Gamma]^2} \left (1 + 2 \alpha
\frac {\nu -\nu_0} {\Gamma/2} \right ) + n.
\end{displaymath}](/articles/aa/full/2005/14/aa2508/img13.gif) |
(7) |
With reference to the above, the mode was given an underlying central frequency
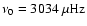 ,
a linewidth
,
a linewidth
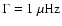 ,
and a fractional peak asymmetry
,
and a fractional peak asymmetry
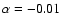 (the height, H, was normalized to unity). The background level n describing the white Gaussian noise source was set to 0.01.
(the height, H, was normalized to unity). The background level n describing the white Gaussian noise source was set to 0.01.
The spectrum was made at a resolution given by 1 yr of contiguous observations. To this we fitted a Lorentzian profile and a flat background term, i.e., the fitting model was
![\begin{displaymath}%
F_0 = \frac{H}{1+4[(\nu -\nu_0)/ \Gamma]^2} + n.
\end{displaymath}](/articles/aa/full/2005/14/aa2508/img17.gif) |
(8) |
In order to establish by how much the estimate of the central frequency of the asymmetric mode was biased by fitting the symmetric model of Eq. (8), we minimized the expression in Eq. (6) to obtain
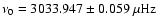 (with the uncertainty coming from the Hessian of the fit). To compare with the usual Monte Carlo approach we applied also a likelihood minimization to 1000 independent realizations of the underlying spectrum
(with the uncertainty coming from the Hessian of the fit). To compare with the usual Monte Carlo approach we applied also a likelihood minimization to 1000 independent realizations of the underlying spectrum
 .
The mean of the fitted central frequencies
was
.
The mean of the fitted central frequencies
was
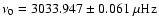 ,
in close agreement with the theoretical expectation from the new approach for both the bias on the central frequency and its standard deviation.
,
in close agreement with the theoretical expectation from the new approach for both the bias on the central frequency and its standard deviation.
We also ran another comparison that simulated a mode with heavier
damping (
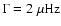 ). This analysis gave estimates for
the frequency of
). This analysis gave estimates for
the frequency of
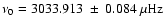 from fitting
Eq. (6), and
from fitting
Eq. (6), and
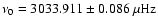 from
the mean of 1000 independent realizations.
from
the mean of 1000 independent realizations.
Though applied to a simple case here this technique could be used for more complex problems, especially those where a long computation time is required.
We have described a technique which could simplify significantly the task of assessing the robustness of fitting codes used to extract estimates of p-mode parameters. It can be applied instead of a full Monte Carlo simulation as a tool to estimatequickly the theoretical expectation for the bias, and standard deviation, in the parameters
given by maximum likelihood fitting.
Acknowledgements
T.T. acknowledges the support of the UK Particle Physics and Astronomy Research Council.
-
Appourchaux, T. 2003, A&A, 412, 903 [EDP Sciences] [NASA ADS] [CrossRef]
- Chaplin W. J.,
Appourchaux T., Elsworth Y., et al. 2004, A&A, 416, 341 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Chaplin W. J.,
Appourchaux T., Elsworth Y., et al. 2004, A&A, 424, 713 [EDP Sciences] [NASA ADS] [CrossRef]
- Libbrecht, K.
1992, ApJ, 387, 712 [NASA ADS] [CrossRef] (In the text)
- Nigam, R., &
Kosovichev A. G. 1998, ApJ, 505, L51 [NASA ADS] [CrossRef] (In the text)
- Toutain, T.,
& Appourchaux, T. 1994, A&A, 289, 649 [NASA ADS] (In the text)
- Woodard, M. 1984,
Thesis, University of California, San Diego
(In the text)
Copyright ESO 2005
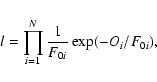
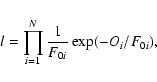
![]() )
from one underlying limit model
)
from one underlying limit model
![]() .
One then minimizes each Lk to obtain a set of M fitted profiles
F0(k). The
statistical distribution of the fitted parameters that describe these profiles is then analyzed and compared to the parameters used to make the underlying data
.
One then minimizes each Lk to obtain a set of M fitted profiles
F0(k). The
statistical distribution of the fitted parameters that describe these profiles is then analyzed and compared to the parameters used to make the underlying data
![]() .
.
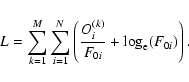
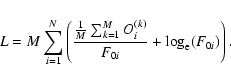
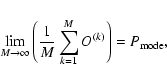
![]() then it is not surprising that the output parameters are those used to make the data. The only new information is the output errors on the parameters, which provide the associated errors when fitting observed profiles with characteristics similar to
then it is not surprising that the output parameters are those used to make the data. The only new information is the output errors on the parameters, which provide the associated errors when fitting observed profiles with characteristics similar to
![]() .
These errors can be derived analytically
for simple problems (e.g., Libbrecht 1992; Toutain & Appourchaux 1994) but in the more general case this method provides a quick answer.
.
These errors can be derived analytically
for simple problems (e.g., Libbrecht 1992; Toutain & Appourchaux 1994) but in the more general case this method provides a quick answer.
![]() we will return an estimate of the bias introduced in the determination of the parameters as a result of using an incorrect model of the underlying profile. A typical application might be to
determine the parameter bias when a Lorentzian profile is fitted to an asymmetric p-mode peak (see Sect. 4).
we will return an estimate of the bias introduced in the determination of the parameters as a result of using an incorrect model of the underlying profile. A typical application might be to
determine the parameter bias when a Lorentzian profile is fitted to an asymmetric p-mode peak (see Sect. 4).
![\begin{displaymath}%
P_{\rm mode} =\frac{H}{1+4[(\nu -\nu_0)/ \Gamma]^2} \left (1 + 2 \alpha
\frac {\nu -\nu_0} {\Gamma/2} \right ) + n.
\end{displaymath}](/articles/aa/full/2005/14/aa2508/img13.gif)
![]() ). This analysis gave estimates for
the frequency of
). This analysis gave estimates for
the frequency of
![]() from fitting
Eq. (6), and
from fitting
Eq. (6), and
![]() from
the mean of 1000 independent realizations.
from
the mean of 1000 independent realizations.