V. Jonauskas![]() ,1 - P. Bogdanovich2 - F. P. Keenan1 - M. E. Foord3 - R. F. Heeter3 - S. J. Rose4 - G. J. Ferland5 - R. Kisielius
,1 - P. Bogdanovich2 - F. P. Keenan1 - M. E. Foord3 - R. F. Heeter3 - S. J. Rose4 - G. J. Ferland5 - R. Kisielius![]() ,1
- P. A. M. van Hoof1 - P. H. Norrington6
,1
- P. A. M. van Hoof1 - P. H. Norrington6
1 - Department of Pure and Applied Physics,
The Queen's University of Belfast,
Belfast BT7 1NN, Northern Ireland, UK
2 - Vilnius University Research
Institute of Theoretical Physics and Astronomy, A. Gostauto 12,
01108 Vilnius, Lithuania
3 - University of California, Lawrence Livermore National Laboratory,
Livermore, CA 94551, USA
4 - Department of Physics, Clarendon Laboratory, Parks Road,
Oxford OX1 3PU, UK
5 - Department of Physics, University of Kentucky, Lexington,
KY 40506, USA
6 - Department of Applied Mathematics and Theoretical Physics,
The Queen's University of Belfast,
Belfast BT7 1NN, Northern Ireland, UK
Received 2 November 2004 / Accepted 3 December 2004
Abstract
Energies of the 700 lowest levels in Fe XX have
been obtained using the multiconfiguration Dirac-Fock method.
Configuration interaction method on the basis
set of transformed radial orbitals with variable parameters taking into
account relativistic corrections in the Breit-Pauli approximation
was used to crosscheck our presented results.
Transition
probabilities, oscillator and line strengths are presented for
electric dipole (E1), electric quadrupole (E2) and magnetic dipole (M1)
transitions among these levels.
The total radiative transition probabilities from each level are also provided.
Results are compared with data compiled by NIST and with other
theoretical work.
Key words: atomic data
The new generation X-ray telescopes on board the space
observatories Chandra and XMM-Newton provide high resolution
spectra of numerous astrophysical sources
that are rich in emission and absorption lines from various iron ions, including
Fe XX
(van der Heyden et al. 2003; Mewe et al. 2003,2001).
For example, the
Fe XX emission line at 12.831 ![]() between the 2p2(1D)3d1 2P3/2 level and the first excited level
of the ground configuration is prominent in the X-ray spectrum of Capella
obtained with LETG spectrometer on Chandra (Mewe et al. 2001).
In addition, several forbidden M1-type transitions among the levels of
the ground configuration 2s22p3 of Fe XX have been identified in
solar spectra obtained by Skylab and SOHO/SUMER spectrographs
(Kucera et al. 2000).
between the 2p2(1D)3d1 2P3/2 level and the first excited level
of the ground configuration is prominent in the X-ray spectrum of Capella
obtained with LETG spectrometer on Chandra (Mewe et al. 2001).
In addition, several forbidden M1-type transitions among the levels of
the ground configuration 2s22p3 of Fe XX have been identified in
solar spectra obtained by Skylab and SOHO/SUMER spectrographs
(Kucera et al. 2000).
Nahar (2004) report the largest calculations of radiative rates for N-like iron to date in the framework of the Iron Project (Hummer et al. 1993), an international project initiated to fulfill a demand for accurate atomic data for the analysis of spectra obtained from satellite-born telescope missions. They employed the SUPERSTRUCTURE (Eissner et al. 1974) and the Breit-Pauli R-matrix (BPRM) code (Berrington et al. 1995), where only one-electron Darwin and mass-velocity as well as spin-orbit operators are included. A total of 1792 bound fine-structure levels were considered, with atomic data for E1-type (electric dipole) transitions obtained using the latter code, and rates for forbidden E2 (electric quadrupole), E3 (electric octupole) as well as M1 (magnetic dipole) transitions calculated with the former one. In addition, Butler & Zeippen (2001) used the BPRM code to generate collisional data among 86 levels of the n=2 and n=3 complexes in Fe XX.
Calculations by Froese Fischer & Tachiev (2004) using the multiconfiguration Hartree-Fock (MCHF) code for C III show good agreement with the results of Nahar (2002) obtained from the BPRM code for allowed transition probabilities. However transition probabilities are larger by a factor of 3-5 for intercombination lines. Hibbert (2003) also observe different results comparing their CIV3 (Hibbert 1975) and MCHF (Froese Fischer & Tachiev 2004) data with the BPRM calculations of Berrington (2001) for some transitions in Na III. The differences in derived results for the various methods in the above papers demonstrate the need to perform calculations for Fe XX using other codes than employed by Nahar (2004). Also, the list of terms for levels presented by Nahar (2004) in their large-scale calculations is insufficient to unambiguously identify levels.
Earlier, Bhatia & Mason (1980) used computer packages
(SUPERSTRUCTURE)
developed
at University College
London (Eissner et al. 1974)
to obtain
radiative rates for transitions within the levels of
the 2s22p3 and 2s12p4 configurations.
Subsequently (Mason & Bhatia 1983), they supplemented their data
by including 2s22p23s1 and 2s22p23d1 configurations.
Later, Merkelis et al. (1997,1999) employed the stationary
second-order many-body perturbation theory approach to
calculate electric dipole, electric quadrupole and magnetic
dipole transition data for the ions of the N I isolectronic
sequence. These data include ions with
![]() but are limited to
configurations 1s22s22p3, 1s22s2p4 and 1s22p5.
Large-scale calculations of oscillator strengths for Fe XX were also
performed under the Opacity Project (The Opacity Project Team 1995,1997),
but the relativistic effects were not included in their data.
but are limited to
configurations 1s22s22p3, 1s22s2p4 and 1s22p5.
Large-scale calculations of oscillator strengths for Fe XX were also
performed under the Opacity Project (The Opacity Project Team 1995,1997),
but the relativistic effects were not included in their data.
The present results for Fe XX continue our series of
calculations, which aim
to provide highly reliable energy levels
and radiative rates for iron ions up to
the n=5 complex
(Jonauskas et al. 2004b,a).
We note that in photoionized plasmas these high-lying levels will not
in general be populated via electron impact (although collisional
redistribution among the levels may play a role), but rather by a range of
processes including recombination and charge transfer
(Savin 2001).
Accurate atomic data for highly excited levels of Fe XX are
needed to properly interpret the high resolution spectra arising from
Chandra and XMM-Newton, which have particularly
large effective areas
in the 6 to 18 ![]() wavelength range, covering Fe XX
lines arising from the
wavelength range, covering Fe XX
lines arising from the ![]() complex.
complex.
Here we report MCDF calculations of level energies, E1, E2 and M1-type radiative transition probabilities, line and oscillator strengths for 700 levels of Fe XX . Calculated results are compared with data compiled by NIST, as well as results obtained by other authors. The agreement between the length and velocity forms of electric transition operators is checked as an additional measure of accuracy. In addition, total transition probabilities are provided, required for calculating branching ratios and the radiative lifetimes of levels.
We perform two sets of calculations. In the first one we use the multiconfiguration Dirac-Fock (MCDF) method employed in the GRASP code of Grant et al. (1980) and Parpia et al. (1996) (http://www.am.qub.ac.uk/DARC). The second one adopts configuration interaction (CI) method on the basis of transformed radial orbitals (TROs) with variable parameters including relativistic effects in the Breit-Pauli approximation (Bogdanovich & Karpuskiene 1999). The latter one refered here as CITRO was used for crosschecking our MCDF result.
In the MCDF method, relativistic orbitals with the
same j but differing m quantum numbers have the same radial
form:
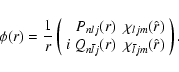 |
(1) |
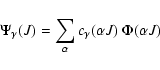 |
(2) |
Intermediate coupling wavefunctions are eigenfunctions of the Dirac-Coulomb-Breit Hamiltonian in the relativistic approximation and the Coulomb-Breit-Pauli Hamiltonian in the nonrelativistic approximation. The relativistic Hamiltonian reduces to a nonrelativistic one, leaving terms up to the square of the fine-structure constant in the expansion for matrix elements.
The Breit operator presented in the Coulomb gauge:
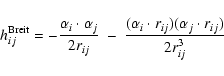 |
(3) |
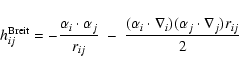 |
(4) |
![$\displaystyle h_{ij}^{\rm trans}=\frac{1}{r_{ij}}\left[ 1-\alpha _{i}\cdot \alp...
...\alpha _{j}\cdot \nabla _{j})~\frac{\cos (\omega r_{ij})-1}{\omega ^{2}}\right]$](/articles/aa/full/2005/14/aa2301/img21.gif) |
(5) |
One-electron excitations from the 2p orbital of the 1s22s22p3, 1s22s12p4 and 1s22p5 configurations up to the 8k orbital, as well as two-electron excitations from orbitals with n=2 to all possible combinations of two electrons in the shells with n=3 were employed to generate one-electron wavefunctions as a basis set for CSFs in the MCDF method. Additionally, to extend the CI basis and obtain higher accuracy, additional 33 configurations are included, namely: 2s23p3, 2p34d2, 2p34f2, 2s22p13p14p1, 2s22p13p15p1, 2s22p13p16p1, 2s22p13p14f1, 2s12p23p14p1, 2s12p23p14d1, 2s12p24p14d1, 2s12p25p14d1, 2s12p23d14d1, 2s12p23s14d1, 2s12p24s14d1, 2s12p25s14d1, 2s22p13p14d1, 2s12p23p14f1, 2s22p13p15s1, 2s12p34f1, 2p33p14p1, 2p33p14f1, 2s22p14f2, 2s12p24f2, 2s23d14f2, 2s24d14f2, 2s22p15f2, 2s12p25f2, 2s12p24d2, 2s13p24d2, 2s22p14d2, 2s23p14d2, 2s23d14d2, 2s23s14d2.
In the nonrelativistic, multiconfiguration Hartree-Fock method, CSFs are obtained
in the LSJ-coupling scheme and form intermediate coupling wavefunctions:
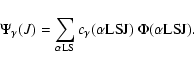 |
(6) |
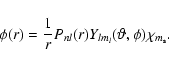 |
(7) |
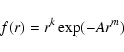 |
(9) |
In the conventional Breit-Pauli (BP) approximation, the Hamiltonian includes mass-correction, one- and two-body Darwin, spin-spin contact, and orbit-orbit terms as well as spin-orbit, spin-other-orbit and spin-spin corrections (Karazija 1996). The former group of operators shifts energies of terms and the latter ones are responsible for the fine-structure splitting. Spin-other-orbit, orbit-orbit, spin-spin, spin-spin contact and two-body Darwin operators are derived from the Breit operator by expanding its matrix elements obtained with two-component relativistic orbitals in orders of the fine-structure constant. Orbit-orbit interaction, due to its complexity (Gaigalas 1999; Badnell 1997; Eissner et al. 1974), leads to a large consumption of computational time, and a small contribution to energies of levels is often omitted in calculations (Froese Fischer & Tachiev 2004). Our CITRO calculations include spin-orbit, spin-other-orbit and spin-spin corrections as well as orbit-orbit corrections within a shell of equivalent electrons. Orbit-orbit interactions between shells are usually smaller than within shells.
In CITRO calculations, we use Hartree-Fock
radial orbitals for electrons with
![]() whose states are presented here. States with
whose states are presented here. States with
![]() and
and
![]() employ TROs. Therefore, the number of radial orbitals used in
calculations with CITRO totals 52. The method presented by
Bogdanovich & Momkauskaite (2004); Bogdanovich et al. (2002)
was adopted to reduce large number of admixed configurations leaving only
configurations with significant influence on the energy of adjusted
configurations. Number of CSFs with odd parity decreases from 249 252 to
132 746 and CSFs with even parity - from 243 104 to 124 217.
Methods used for energy matrix diagonalization are provided by
Bogdanovich et al. (2002).
employ TROs. Therefore, the number of radial orbitals used in
calculations with CITRO totals 52. The method presented by
Bogdanovich & Momkauskaite (2004); Bogdanovich et al. (2002)
was adopted to reduce large number of admixed configurations leaving only
configurations with significant influence on the energy of adjusted
configurations. Number of CSFs with odd parity decreases from 249 252 to
132 746 and CSFs with even parity - from 243 104 to 124 217.
Methods used for energy matrix diagonalization are provided by
Bogdanovich et al. (2002).
We present calculations for the 700 lowest energy levels of Fe XX, and radiative transition characteristics among these. Transition probabilities, oscillator and line strengths for electric dipole, electric quadrupole and magnetic dipole transitions are obtained in the fully relativistic MCDF approach. All 698 levels arising from the 1s22s22p3, 1s22s12p4, 1s22p5, 1s22s22p2nl, 1s22s12p3n'l, and 1s22p43l' (n=3,4,5, n'=3,4, l=0,..,n-1, l'=0,1,2) configurations are taken into account. Binding energies of the two lowest levels from the 1s22s12p35s1 configuration are lower than our chosen cut-off value, which corresponds to the highest level of the 1s22s22p25g1 configuration. Therefore those levels are also included here.
The energies of the above configurations calculated with the fully relativistic GRASP code are listed in Table 1. Indices for the levels in the first column of Table 1 are used in all tables except Table 2, where results obtained with the original CITRO code of Bogdanovich & Karpuskiene (1999) are presented. Energy levels are given in cm-1 relative to the ground state 1s22s22p3 4S3/2, along with the leading percentage compositions (where these exceed 10%) for intermediate wavefunctions. The LSJ-coupling CSFs with largest weights for the intermediate wavefunctions are provided in the second and third columns of the table. Intermediate coupling is strong for some excited levels, so the level assignments for some terms are ambiguous.
In Table 3 our energy levels obtained with the GRASP and CITRO codes are compared with values calculated by Mason & Bhatia (1983) with SUPERSTRUCTURE and Nahar (2004) BPRM results, as well as data compiled by NIST (National Institute for Standards and Technology: www.physics.nist.gov) whose data are commonly used as reference set for atomic results. The energy levels are compared with respect to the ground level energies of the corresponding data sets. The Nahar (2004) values in the Table 3 are obtained with the BPRM code because it is used for E1-type transitions in their calculations. Their calculations with SUPERSTRUCTURE are in better agreement with NIST data than the BPRM results.
Fairly good agreement with NIST energy levels is
obtained using the CITRO code.
The highest deviation from
the NIST energies does not exceed 0.4% and the average deviation is
0.2%.
In addition, the ground state energy of -219 142 254 cm-1
is close to the NIST recommended value of
![]() cm-1.
There is also very good agreement between
Mason & Bhatia (1983) and NIST data sets,
showing an average deviation of only 0.4%.
The highest deviations in the former calculations are
for the excited levels of the ground configuration, but
even then the discrepancy does not exceed 1.6%.
Their scaling parameters for Thomas-Fermi
potential were
cm-1.
There is also very good agreement between
Mason & Bhatia (1983) and NIST data sets,
showing an average deviation of only 0.4%.
The highest deviations in the former calculations are
for the excited levels of the ground configuration, but
even then the discrepancy does not exceed 1.6%.
Their scaling parameters for Thomas-Fermi
potential were
![]() ,
,
![]() and
and
![]() for
all cases.
Mason & Bhatia (1983) includes only the 2s22p3, 2s12p4,
2s22p23s1 and 2s22p23d1 configurations
for their results, while
Nahar (2004) also use the SUPERSTRUCTURE for
forbidden transitions and include 9 configurations. However,
their
results for energy levels are worse than the data of Mason & Bhatia (1983),
while the
latter calculations omitted much of the correlations.
Nahar (2004) does not present values of
the scaling parameters employed in their calculations.
for
all cases.
Mason & Bhatia (1983) includes only the 2s22p3, 2s12p4,
2s22p23s1 and 2s22p23d1 configurations
for their results, while
Nahar (2004) also use the SUPERSTRUCTURE for
forbidden transitions and include 9 configurations. However,
their
results for energy levels are worse than the data of Mason & Bhatia (1983),
while the
latter calculations omitted much of the correlations.
Nahar (2004) does not present values of
the scaling parameters employed in their calculations.
The presented BPRM results of Nahar (2004) show an average discrepancy of 0.5% with NIST values. These authors obtain better agreement with NIST than data provided by Butler & Zeippen (2001) which are not presented in the Table 3. A maximum disagreement of 3.1% is obtained for the second excited level 1s22s22p3 2D5/2. One of the reasons for the discrepancy is that BPRM omits all two-electron corrections originating from the Breit-Pauli operator. In Table 4 we estimate the magnitudes of some corrections missed in their calculations using the Breit-Pauli code (without TROs). The largest discrepancies of energy computed with spin-orbit, spin-other-orbit, spin-spin and orbit-orbit (within a shell) interactions with those that include only spin-orbit corrections is obtained for the same level 1s22s22p3 2D5/2. Spin-other-orbit and orbit-orbit interactions have the largest influence to the shifts of energies compared with spin-spin corrections. Added spin-other-orbit and orbit-orbit corrections shift the level down by a similar amount relative to the ground level. The total shift caused by these corrections leads to 3438 cm-1. The influence of spin-spin interaction on the shift of the levels is smaller, and does not exceed 500 cm-1 for 1s22s12p4 4P3/2.
MCDF results show an average difference of 0.5% from NIST data for the energy levels displayed in Table 3. The largest deviation is for levels of the ground configuration, but it does not exceed 2.2% and is less than 1% for other energies. The total number of CSFs included in the CI basis is 10050, while the CITRO employs 256963 CSFs. After CI functions are supplemented by the above mentioned 33 configurations for the MCDF calculations, the average discrepancy changes from 0.6% to 0.5%. The discrepancy for the first excited level is reduced from 2.6% to 2.2%, and for the second excited level from 2.1% to 1.9%. It indicates that a larger set of CI wavefunctions would be required for our MCDF calculations to achieve higher accuracy.
To ensure the consistency of the spectroscopic dataset for levels presented in Table 1, new LSJ-coupling spectroscopic notations are proposed in Table 5 for the levels with similar contributions to intermediate wavefunctions. We use the same technique as presented in our earlier paper for Fe XIX (Jonauskas et al. 2004b).
Energy levels and intermediate coupling wavefunctions calculated with the configuration interaction method have been employed to derive matrix elements of transition operators, which subsequently are adopted for the calculation of transition probabilities, line and oscillator strengths. Our calculated wavelengths and line strengths using the two methods mentioned above, as well as values obtained by Nahar (2004) are listed in Table 6 along with data provided by NIST. Nahar (2004) use the BPRM code for E1-type transitions and SUPERSTRUCTURE for forbidden transitions, which correspond to those in the table within the n=2 complex. Only the ab initio calculations of Nahar (2004) are presented here, while their transition probabilities and oscillator strengths are corrected by the available transition energies from NIST. It is more expedient to compare calculated line strengths, as these do not explicitly depend on the transition energy and so do not contain errors arising from this quantity.
The CITRO results presented in Table 6 agree well with the wavelengths compiled by NIST, with differences of less than 1%. The largest discrepancies of up to 3.6% are obtained by the SUPERSTRUCTURE calculations of Nahar (2004) that correspond to forbidden transitions. MCDF wavelengths differ from NIST values by 2.4% and 1.9%, respectively, for transitions from the first and second excited levels to the ground state. Shorter wavelengths agree to better than 1% for our and the Nahar (2004) datasets. The agreement of the length and velocity forms (Babushkin and Coulomb gauges in the relativistic approach) is better for levels involving excited states, while weak transitions show the largest discrepancies.
Large discrepancies for line strengths are observed for transitions which include level 2s22p2(1D)3d1 2D5/2 (index 70). Due to strong mixing of the CSFs, the label of the level is ambiguous as the largest weight of the 2s22p2(1D)3d1 2D5/2 configuration state function amounts to less than 50% in both our calculations. NIST data report a weight of 54%, which is similar to our obtained values. On the other hand, agreement for weak transitions is never good due to mixing effects. It is interesting that all three calculations that incorporate different methods show similar discrepancies with the NIST line strengths. Similar discrepancies are also observed in all three calculations for transitions to the ground and second excited levels. Length and velocity forms of transitions from the level agree to better than 4% for both our results, indicating that major correlation effects are included in the intermediate coupling wavefunctions.
Line strengths obtained by Nahar (2004) using the BPRM code show the largest discrepancies with NIST data. In many cases it happens for intercombination spin-changing E1-type transitions. A similar effect was observed by Froese Fischer & Tachiev (2004) in Na III. However, some dipole allowed E1-type transitions of Nahar (2004) also differ by more than a factor of 4 from NIST values. As noted by Hibbert (2003), the large discrepancies can be understood by the fact that the BPRM code uses term-coupling coefficients to introduce relativistic effects, which lead to restrictions on the LSJ mixing coefficients. On the other hand, conventional atomic structure codes deal with the diagonalization of the full Hamiltonian matrix.
Wavelengths, transition probabilities, line and oscillator strengths
obtained with
the GRASP code for electric dipole, quadrupole and magnetic dipole
transitions are presented in Tables 8, 9 and 10.
Ratios between velocity and length forms for electric transitions are also
provided.
The total number of dipole allowed and intercombination E1-type transitions is
71 398, but only
E1-type transitions with
![]() are included in Table 8.
Tables 9 and 10
contain data for forbidden E2-type and M1-type
transitions with
are included in Table 8.
Tables 9 and 10
contain data for forbidden E2-type and M1-type
transitions with
![]() ,
yielding a total of 167 480 radiative rates.
,
yielding a total of 167 480 radiative rates.
The influence of forbidden transitions on the lifetimes of levels is prominent for excited levels of the ground configuration and highly excited 2s12p3(2D) 3d1 2G9/2 level (index 151). It can be seen from Table 7 that level 151 decays primarily through E2-type transitions, which reduces the lifetime of the level by more than a factor of 2. The E2-type transitions make a contribution of more than 10% to the decay of 2p4 (1D) 3d1 2G9/2 (261), 2s22p2 (3P) 3p1 4D7/2 (31), 2s12p3 (3D) 3p1 4F9/2 (107), 2p4 (1D) 3d1 2G7/2 (260), 2s22p2 (3P) 3p1 2S1/2 (25), 2s12p3 (3P) 3d1 4F9/2 (174), 2p4 (3P) 3d1 4F9/2 (245) and 2p4 (3P) 3d1 4D7/2 (241) levels. Most of these levels have large total quantum numbers, limiting the decay routes for strong dipole allowed transitions. Magnetic dipole transitions are responsible for finite lifetimes of excited levels of the ground configuration.
Finally, a comparison between the length and velocity forms of
the electric dipole transitions shows an agreement
of better than 10% for 790 transitions with ![]() ,
and an average deviation of only 6%.
Two forms differ by up to 60% for some of the strong transitions,
but their contributions to the lifetimes of the corresponding levels
is negligible.
For many E2 transitions, the two forms agree to better than 5%.
,
and an average deviation of only 6%.
Two forms differ by up to 60% for some of the strong transitions,
but their contributions to the lifetimes of the corresponding levels
is negligible.
For many E2 transitions, the two forms agree to better than 5%.
Multiconfiguration Dirac-Fock energy levels, as well as electric dipole, electric quadrupole and magnetic dipole transition probabilities, line and oscillator strengths have been computed for nitrogen-like Fe XX. The 700 lowest energy levels are considered. Calculated values have been compared with the data compiled by NIST and other theoretical results. Breit-Pauli energy levels and electric dipole transition characteristics on the basis set of transformed radial orbitals with variable parameters were used to crosscheck our MCDF result.
Leading percentage compositions for intermediate wavefunctions are presented in the basis of LSJ-coupling configuration state functions. Spectroscopic notations of levels identified by the largest weights of CSFs are checked for their completeness. Of the 700 levels, 203 have weights of LSJ-coupling CSFs of less than 50% due to strong mixing.
The 5 major radiative probabilities from each level and the total values obtained in the MCDF approximation have been provided, taking into account forbidden transitions. The largest contributions of forbidden M1-type transitions have been obtained for the lifetimes of fine-structure levels of the ground configuration. The electric quadrupole transitions are mainly noticeable for transitions from levels with large total quantum numbers. Their contributions to the lifetimes of levels exceed 10% for 9 highly excited levels. On the other hand, the 2s12p3(2D)3d1 2G9/2 level decay mainly trough E2-type transition. The influence of M2 and E3-type transitions that are not presented here is negligible.
Good agreement between our set of energy levels and radiative transition characteristics for Fe XX and the available NIST data, as well as our use of a large basis of configuration state functions, allows to conclude that the achieved accuracy of our calculations is higher than those available to date. We hope that our data will be useful in astrophysical and other applications.
Acknowledgements
F.P.K. and S.J.R. are grateful to AWE Aldermaston for the award of William Penney Fellowships. This work was supported by PPARC and EPSRC, and also by NATO Collaborative Linkage Grant CLG.979443. We are also grateful to the Defence Science and Technology Laboratory (dstl) for support under the Joint Grants Scheme. We thank STScI for support through HST-AR-09923.01A.
| Index | CSF |
|
|
|
|
|
| 2 | 2s2 2p3 2D1.5 | 138620 | 140598 | 140903 | 138856 | 141715 |
| 3 | 2s2 2p3 2D2.5 | 176130 | 178989 | 181615 | 175952 | 179537 |
| 4 | 2s2 2p3 2P0.5 | 260270 | 257573 | 264577 | 260471 | 263209 |
| 5 | 2s2 2p3 2P1.5 | 323340 | 319877 | 328554 | 322368 | 325962 |
| 6 | 2s1 2p4 4P2.5 | 752730 | 747101 | 757407 | 750386 | 753649 |
| 7 | 2s1 2p4 4P1.5 | 820820 | 812698 | 824127 | 817703 | 821409 |
| 8 | 2s1 2p4 4P0.5 | 842740 | 834443 | 846184 | 839423 | 843536 |
| 9 | 2s1 2p4 2D1.5 | 1042570 | 1044277 | 1050625 | 1039244 | 1050924 |
| 10 | 2s1 2p4 2D2.5 | 1058360 | 1061216 | 1068073 | 1055467 | 1066222 |
| 11 | 2s1 2p4 2S0.5 | 1195260 | 1195284 | 1205245 | 1192125 | 1205489 |
| 12 | 2s1 2p4 2P1.5 | 1242430 | 1251404 | 1253310 | 1239208 | 1255768 |
| 13 | 2s1 2p4 2P0.5 | 1340040 | 1345312 | 1351305 | 1336259 | 1352396 |
| 14 | 2p5 2P1.5 | 1954520 | 1966690 | 1948441 | 1971784 | |
| 15 | 2p5 2P0.5 | 2062200 | 2076076 | 2055642 | 2079179 | |
| 16 | 2s2 2p2 (3P) 3s1 4P0.5 | 7194000 | 7193289 | 7162927 | 7182452 | 7155228 |
| 17 | 2s2 2p2 (3P) 3s1 4P1.5 | 7255000 | 7256327 | 7229209 | 7247014 | 7221726 |
| 18 | 2s2 2p2 (3P) 3s1 2P0.5 | 7287000 | 7286360 | 7259935 | 7277194 | 7252311 |
| 19 | 2s2 2p2 (3P) 3s1 4P2.5 | 7299000 | 7299603 | 7274815 | 7288611 | 7264310 |
| 20 | 2s2 2p2 (3P) 3s1 2P1.5 | 7331000 | 7330953 | 7306639 | 7320048 | 7296115 |
| 23 | 2s2 2p2 (1D) 3s1 2D2.5 | 7430000 | 7430336 | 7411460 | 7422476 | 7400563 |
| 24 | 2s2 2p2 (1D) 3s1 2D1.5 | 7440000 | 7439775 | 7421293 | 7432236 | 7410643 |
| 33 | 2s2 2p2 (1S) 3s1 2S0.5 | 7554000 | 7551182 | 7545340 | 7555745 | 7530985 |
| 39 | 2s2 2p2 (3P) 3d1 4F1.5 | 7672000 | 7650500 | 7646562 | 7663219 | 7638491 |
| 46 | 2s2 2p2 (3P) 3d1 4F3.5 | 7740000 | 7714100 | 7722324 | 7736076 | 7712951 |
| 47 | 2s2 2p2 (3P) 3d1 4D0.5 | 7752000 | 7721000 | 7727811 | 7743115 | 7720580 |
| 56 | 2s2 2p2 (3P) 3d1 4P2.5 | 7802000 | 7790100 | 7796375 | 7806999 | 7785892 |
| 58 | 2s2 2p2 (3P) 3d1 4P1.5 | 7802000 | 7803000 | 7808139 | 7818763 | 7798298 |
| 61 | 2s2 2p2 (3P) 3d1 2F3.5 | 7820000 | 7818200 | 7830306 | 7839918 | 7819869 |
| 62 | 2s2 2p2 (3P) 3d1 2D1.5 | 7859000 | 7850700 | 7853131 | 7864123 | 7844676 |
| 63 | 2s2 2p2 (3P) 3d1 2D2.5 | 7843000 | 7854500 | 7854097 | 7865251 | 7846514 |
| 69 | 2s2 2p2 (1D) 3d1 2D1.5 | 7919000 | 7909800 | 7925646 | 7933796 | 7915116 |
| 70 | 2s2 2p2 (1D) 3d1 2D2.5 | 7913000 | 7918200 | 7929859 | 7937908 | 7919464 |
| 71 | 2s2 2p2 (1D) 3d1 2P0.5 | 7964000 | 7931300 | 7947242 | 7953974 | 7936656 |
| 72 | 2s2 2p2 (3P) 3d1 2F3.5 | 7935000 | 7944100 | 7950051 | 7958832 | 7941761 |
| 79 | 2s2 2p2 (1D) 3d1 2S0.5 | 7995000 | 7960100 | 7979856 | 7986462 | 7969218 |
| 80 | 2s2 2p2 (3P) 3d1 2D2.5 | 7983000 | 7969000 | 7980602 | 7988008 | 7971406 |
| 82 | 2s2 2p2 (1D) 3d1 2P1.5 | 7967000 | 7966700 | 7984157 | 7989830 | 7974014 |
| 85 | 2s2 2p2 (1S) 3d1 2D2.5 | 8047000 | 8069800 | 8065978 | 8072444 | 8051967 |
| 86 | 2s2 2p2 (1S) 3d1 2D1.5 | 8061000 | 8080900 | 8075722 | 8083172 | 8063693 |
| Index | E1 | E2 | E3 | E4 |
| 2 | 141857 | 143122 | 143444 | 141910 |
| 3 | 182708 | 181082 | 181201 | 179270 |
| 4 | 264047 | 264411 | 264530 | 263975 |
| 5 | 327447 | 326489 | 326519 | 325670 |
| 6 | 755194 | 754560 | 754597 | 754662 |
| 7 | 821273 | 821367 | 821849 | 821936 |
| 8 | 843083 | 844242 | 843812 | 843945 |
| 9 | 1050595 | 1050928 | 1051144 | 1049976 |
| 10 | 1068168 | 1067125 | 1067206 | 1065988 |
| 11 | 1204074 | 1204221 | 1204372 | 1204963 |
| 12 | 1253448 | 1252420 | 1252540 | 1252569 |
| 13 | 1350217 | 1349293 | 1349347 | 1349601 |
| 14 | 1970331 | 1970400 | 1970517 | 1971268 |
| 15 | 2078969 | 2077652 | 2077773 | 2078527 |
| Index | Index | Changed CSF |
| 26 | 22 | 2s2 2p2 (3P) 3p1 4P3/2 |
| 42 | 48 | 2s2 2p2 (3P) 3d1 4D5/2 |
| 72 | 61 | 2s2 2p2 (1D) 3d1 2F7/2 |
| 80 | 63 | 2s2 2p2 (1D) 3d1 2F5/2 |
| 153 | 163 | 2s1 2p3 (1P) 3p1 2P1/2 |
| 180 | 192 | 2s1 2p3 (3S) 3p1 2P3/2 |
| 200 | 209 | 2s1 2p3 (3S) 3d1 2D5/2 |
| 211 | 218 | 2p4 (3P) 3s1 2P3/2 |
| 225 | 228 | 2p4 (3P) 3p1 2P1/2 |
| 250 | 254 | 2p4 (3P) 3d1 2F5/2 |
| 252 | 242 | 2p4 (3P) 3d1 2P1/2 |
| 256 | 243 | 2p4 (3P) 3d1 2D3/2 |
| 277 | 281 | 2s2 2p2 (3P) 4p1 4P3/2 |
| 293 | 309 | 2s2 2p2 (3P) 4f1 2D5/2 |
| 296 | 297 | 2s2 2p2 (3P) 4d1 2P3/2 |
| 300 | 286 | 2s2 2p2 (3P) 4d1 4P5/2 |
| 315 | 295 | 2s2 2p2 (3P) 4f1 4G7/2 |
| 317 | 333 | 2s2 2p2 (3P) 4f1 4D5/2 |
| 400 | 405 | 2s1 2p3 (3D) 4p1 2P3/2 |
| 445 | 479 | 2s1 2p3 (3D) 4f1 4F5/2 |
| 462 | 480 | 2s1 2p3 (3D) 4f1 4P3/2 |
| 488 | 487 | 2s1 2p3 (3P) 4d1 4P3/2 |
| 505 | 522 | 2s1 2p3 (3P) 4f1 4G7/2 |
| 506 | 536 | 2s2 2p2 (3P) 5p1 4P3/2 |
| 525 | 512 | 2s1 2p3 (3P) 4f1 4F5/2 |
| 545 | 571 | 2s2 2p2 (3P) 5f1 2G7/2 |
| 546 | 572 | 2s2 2p2 (3P) 5g1 2F7/2 |
| 547 | 574 | 2s2 2p2 (3P) 5g1 2H9/2 |
| 557 | 530 | 2s2 2p2 (3P) 5d1 2P3/2 |
| 558 | 541 | 2s2 2p2 (3P) 5p1 2S1/2 |
| 578 | 628 | 2s2 2p2 (3P) 5g1 2G7/2 |
| 579 | 618 | 2s2 2p2 (3P) 5f1 2D5/2 |
| 584 | 560 | 2s2 2p2 (3P) 5d1 4D7/2 |
| 588 | 532 | 2s2 2p2 (3P) 5d1 4P5/2 |
| 601 | 576 | 2s1 2p3 (3S) 4f1 2F5/2 |
| 604 | 625 | 2s2 2p2 (3P) 5g1 4G9/2 |
| 609 | 573 | 2s2 2p2 (3P) 5f1 2G9/2 |
| 624 | 605 | 2s2 2p2 (3P) 5g1 4G7/2 |
| 626 | 638 | 2s2 2p2 (3P) 5g1 4F5/2 |
| 631 | 629 | 2s2 2p2 (3P) 5g1 2F5/2 |
| 640 | 634 | 2s1 2p3 (1P) 4p1 2P1/2 |