A&A 433, 467-477 (2005)
DOI: 10.1051/0004-6361:20042007
Ageing analysis of the giant radio galaxy J1343+3758
M. Jamrozy1 - J. Machalski2 - K.-H. Mack3,1 -
U. Klein1
1 - Radioastronomisches Institut der Universität Bonn, Auf dem
Hügel 71, 53121 Bonn, Germany
2 -
Obserwatorium Astronomiczne, Uniwersytet Jagiellonski,
ul. Orla 171, 30244 Kraków, Poland
3 -
Istituto di Radioastronomia, via P. Gobetti 101, 40129 Bologna,
Italy
Received 14 September 2004 / Accepted 22 November 2004
Abstract
Deep 4860 and 8350 MHz observations with the VLA and 100-m Effelsberg telescopes,
supplementing available radio survey maps at the frequencies of 327 MHz (WENSS
survey) and 1400 MHz (NVSS survey), are used to study the synchrotron spectra and
radiative ages of relativistic particles in opposite lobes of the giant
radio galaxy J1343+3758 (Machalski & Jamrozy 2000). The classical spectral ageing
analysis (e.g. Myers & Spangler 1985) with assumption of equipartition magnetic
fields gives a mean separation velocity (
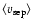 )
of
about 0.16 c and 0.12 c measured with respect to the emitting plasma, and
suggests a maximum particle age of about 48 and 50 Myr in the NE and SW lobes,
respectively. On the contrary, a mean jet-head advance speed
(
)
of
about 0.16 c and 0.12 c measured with respect to the emitting plasma, and
suggests a maximum particle age of about 48 and 50 Myr in the NE and SW lobes,
respectively. On the contrary, a mean jet-head advance speed
(
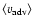 )
in the above lobes, derived from ram-pressure arguments, is about 0.016 c and
0.017 c, respectively. This would imply a substantial backflow of the lobe
material from the hotspot regions towards the radio core,
)
in the above lobes, derived from ram-pressure arguments, is about 0.016 c and
0.017 c, respectively. This would imply a substantial backflow of the lobe
material from the hotspot regions towards the radio core,
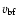 ,
which is
not supported by the available radio maps. A compromise is achieved by assuming
an enhancement of 3 to 5 times the equipartition magnetic field strengths in the
lobes which gives
,
which is
not supported by the available radio maps. A compromise is achieved by assuming
an enhancement of 3 to 5 times the equipartition magnetic field strengths in the
lobes which gives
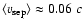 and
and
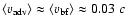 ,
hence a dynamical
age of the source of 204
,
hence a dynamical
age of the source of 204 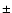 40 Myr. A comparison of the radiative and dynamical ages of the
investigated giant radio galaxy implies that the dynamical age is about 4 times the maximum
synchrotron age of the emitting particles, which supports the conclusion of Blundell & Rawlings
(2000) that the spectral and dynamical ages are comparable only when they
are
40 Myr. A comparison of the radiative and dynamical ages of the
investigated giant radio galaxy implies that the dynamical age is about 4 times the maximum
synchrotron age of the emitting particles, which supports the conclusion of Blundell & Rawlings
(2000) that the spectral and dynamical ages are comparable only when they
are 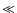 10 Myr, and suggests that for FRII-type sources the discrepancy between these ages
increases with age.
10 Myr, and suggests that for FRII-type sources the discrepancy between these ages
increases with age.
Key words: radio continuum: galaxies - galaxies: active - galaxies: individual: J1343+3758
Reliable determinations of the present (at the observing epoch) age of extended
extragalactic radio sources are crucial for an observational constraint of the
existing analytical models of their dynamical evolution (e.g. Kaiser et al. 1997
(hereafter referred to as KDA); Blundell et al. 1999a). Most of the published studies
about the age of the sample members in selected sets of radio sources have been based
on the analysis of their radio spectra. There is no doubt that the radio continuum
spectra in different parts of a radio source should contain crucial information about
its history. In the classical synchrotron-source theory the observed variations of
these spectra are directly related to the mechanisms of particle energy losses. If high
energy particles with an initial power-law spectrum experienced only synchrotron
losses via the uniform magnetic field in which they were immersed, then a
characteristic frequency break in that spectrum
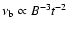 would appear, where t is the time elapsed since the particles were accelerated
to their initial energy distribution (cf. Kardashev 1962; Pacholczyk 1970;
Jaffe & Perola 1973).
would appear, where t is the time elapsed since the particles were accelerated
to their initial energy distribution (cf. Kardashev 1962; Pacholczyk 1970;
Jaffe & Perola 1973).
This simple method was used to estimate the radiative ages and expansion speeds
in large samples of powerful 3CR sources (Myers & Spangler 1985; Alexander & Leahy
1987; Leahy et al. 1989; Carilli et al. 1991; Liu et al. 1992), as well as in samples
of low- and intermediate-luminosity radio galaxies (Klein et al. 1995; Parma et al. 1999).
In the meantime serious criticism of the interpretation of the radio
spectrum variations within a source in terms of particle ageing has been published
in a number of papers (e.g. Rudnick et al. 1994; Jones et al. 1999; Blundell &
Rawlings 2000) envisaging a possibly dominant r
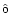 le of the local magnetic field
evolution. Nevertheless, Kaiser (2000) has argued that if the bulk backflow and
energy losses, both radiative and adiabatic, "are self-consistently taken into
account'', the spectral and dynamical ages (the observed linear size of a
source/lobe divided by the speed at which it has expanded to that time) can be
comparable. Blundell & Rawlings (2000) contend that this will be the case only if
these ages are
le of the local magnetic field
evolution. Nevertheless, Kaiser (2000) has argued that if the bulk backflow and
energy losses, both radiative and adiabatic, "are self-consistently taken into
account'', the spectral and dynamical ages (the observed linear size of a
source/lobe divided by the speed at which it has expanded to that time) can be
comparable. Blundell & Rawlings (2000) contend that this will be the case only if
these ages are 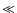 10 Myr.
10 Myr.
The determination of the ages of the largest FRII-type (Fanaroff & Riley 1974) sources
is of special interest. Classical double radio sources with a projected linear size
D exceeding 1 Mpc (for
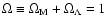 and
H0=50 km s-1 Mpc-1)
and
H0=50 km s-1 Mpc-1)![[*]](/icons/foot_motif.gif) are commonly considered as a somewhat special class of
extragalactic sources. They are characterised by the rapid decrease of their
luminosity with increasing size, which is clearly visible in the low-frequency
luminosity vs. projected linear size (the P-D) diagram, cf. Neeser et al.
(1995); Blundell et al. (1999a). The recent analytical models of the time evolution
of FRII-type sources (KDA; Blundell & Rawlings 1999b) can explain the extreme source
size by the longer lifetimes of the largest sources and effective synchrotron
cooling, adiabatic expansion losses, and inverse Compton scattering of the cosmic
microwave background. However, giants can be exceptionally large also because
their intergalactic environment is less dense than that surrounding smaller sources
(e.g. Mack et al. 1998). The latter suggestion has been supported by the finding that
high-redshift giants studied by Cotter (1998) exist exclusively in low-density environments.
are commonly considered as a somewhat special class of
extragalactic sources. They are characterised by the rapid decrease of their
luminosity with increasing size, which is clearly visible in the low-frequency
luminosity vs. projected linear size (the P-D) diagram, cf. Neeser et al.
(1995); Blundell et al. (1999a). The recent analytical models of the time evolution
of FRII-type sources (KDA; Blundell & Rawlings 1999b) can explain the extreme source
size by the longer lifetimes of the largest sources and effective synchrotron
cooling, adiabatic expansion losses, and inverse Compton scattering of the cosmic
microwave background. However, giants can be exceptionally large also because
their intergalactic environment is less dense than that surrounding smaller sources
(e.g. Mack et al. 1998). The latter suggestion has been supported by the finding that
high-redshift giants studied by Cotter (1998) exist exclusively in low-density environments.
Our recent analysis of the time evolution of giant radio galaxies in view
of the analytical KDA model strongly suggested that
there is not one dominant factor responsible for the huge linear sizes of those sources;
we found that giants are relatively old sources with high enough jet
power that have evolved in a low-density environment (Machalski et al. 2004a).
In this paper we perform the standard ageing analysis for the source J1343+3758,
the third largest FRII-type radio galaxy known after 3C 236 and WNB 2147+816
(Machalski & Jamrozy 2000), following the
previous similar studies of giant sources by Parma et al. (1996),
Mack et al. (1998),
Schoenmakers et al. (1998, 2000) and Lara et al. (2000). This ensures a homogeneous
comparison of the ages determined for giant radio sources. We also estimate the
dynamical age of this source using the approach of Begelman & Cioffi (1989).
In Sect. 2 the observational data used for the spectral ageing analysis are
described, and the non-survey high-frequency 4860 and 8350-MHz maps of J1343+3758
are presented. Its morphological, spectral and polarisation properties are described
in Sect. 3. The spectral ageing analysis and the dynamical considerations are given
and the results are discussed in Sect. 4. Other physical parameters of the investigated
source (the jet power, central core density, pressure of the shocked jet material,
total energy contained in the lobes, and fraction of the jet energy used for the
adiabatic expansion of the source cocoon) are calculated and discussed in Sect. 5.
The summary is given in Sect. 6.
Below we describe the observational data used for the spectral ageing analysis
of the source J1343+3758. For this purpose we incorporate the low-resolution 327
and 1400-MHz maps available from the WENSS (Rengelink et al. 1997) and NVSS
(Condon et al. 1998) sky surveys, respectively, supplemented by our own
high-frequency 4860 and 8350-MHz maps. In these maps J1343+3758 appears as a straightforward
 FRII-type radio source composed of two separate lobes without any
evident bridge connecting them.
FRII-type radio source composed of two separate lobes without any
evident bridge connecting them.
The WENSS map of the total intensity emission at 327 MHz with an angular
resolution of
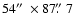 is reproduced in Fig. 1a.
The emission from the south-west (SW) lobe extends almost up to the radio
core region, and is described in more detail in Sect. 3.1.
The total intensity 1400-MHz NVSS map with a resolution of
is reproduced in Fig. 1a.
The emission from the south-west (SW) lobe extends almost up to the radio
core region, and is described in more detail in Sect. 3.1.
The total intensity 1400-MHz NVSS map with a resolution of
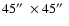 and the electric field E-vectors
superimposed is shown in Fig. 1b.
Figure 1c shows the linearly polarised intensity map with the
vectors of fractional linear polarisation superimposed. The mean fractional polarisation in both
lobes at 1400 MHz is given in Sect. 3.3. A distinct hotspot at the outer edge of the north-east
(NE) lobe is visible on the high-resolution 1400-MHz FIRST (Becker et al. 1995) map. A trace of a
hotspot is also visible in the SW lobe although it is rather dim.
and the electric field E-vectors
superimposed is shown in Fig. 1b.
Figure 1c shows the linearly polarised intensity map with the
vectors of fractional linear polarisation superimposed. The mean fractional polarisation in both
lobes at 1400 MHz is given in Sect. 3.3. A distinct hotspot at the outer edge of the north-east
(NE) lobe is visible on the high-resolution 1400-MHz FIRST (Becker et al. 1995) map. A trace of a
hotspot is also visible in the SW lobe although it is rather dim.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2007f1a.ps}\par\vspace*{3mm}...
...b.ps}\par\vspace*{3mm}
\includegraphics[width=8cm,clip]{2007f1c.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg28.gif) |
Figure 1:
Images of the radio source J1343+3758 at a) 327 and b), c)
1400 MHz from the WENSS and NVSS surveys, respectively.
a) The contours, spaced by factors of 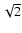 in brightness, are
plotted starting with 9 mJy beam-1.
b) Total intensity contours, spaced by a factor of 2, are plotted
starting with 1 mJy beam-1. Superimposed are electric field E-vectors
with their lengths proportional to the polarised intensity.
c) Linearly polarised intensity contours of 0.8, 1.6, 3.2 mJy beam-1
with the vectors of the fractional linear polarisation superimposed. The scales
of the polarisation vectors are indicated by the bars, and the beam size by the
ellipse in a) and circles in b), c) in the bottom left corners of the
images; "x'' marks the position of the parent galaxy.
in brightness, are
plotted starting with 9 mJy beam-1.
b) Total intensity contours, spaced by a factor of 2, are plotted
starting with 1 mJy beam-1. Superimposed are electric field E-vectors
with their lengths proportional to the polarised intensity.
c) Linearly polarised intensity contours of 0.8, 1.6, 3.2 mJy beam-1
with the vectors of the fractional linear polarisation superimposed. The scales
of the polarisation vectors are indicated by the bars, and the beam size by the
ellipse in a) and circles in b), c) in the bottom left corners of the
images; "x'' marks the position of the parent galaxy. |
| Open with DEXTER |
The observations were carried out with the VLA D-array at two correlator
frequencies of 4835 and 4885 MHz, each with a bandwidth of 50 MHz. The telescope gains
were calibrated using the standard calibration source 3C286 and the flux density scale
of Baars et al. (1977). The source J1324+408 was used as phase calibrator.
The SW lobe was observed in Sept. 30, 2000 with the pointing center at
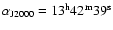 ;
;
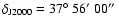 ,
i.e.
,
i.e.
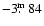 away from the core.
With an integration time of 2
away from the core.
With an integration time of 2  31 min, a rms noise of about 27
31 min, a rms noise of about 27  Jy beam-1 was achieved. The opposite
NE lobe was observed in Feb. 25, 2003 with the pointing center at
Jy beam-1 was achieved. The opposite
NE lobe was observed in Feb. 25, 2003 with the pointing center at
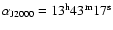 ;
;
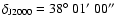 ,
i.e.
,
i.e.
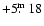 away from the core.
With an integration time of
away from the core.
With an integration time of 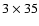 min, the rms noise was about 23
min, the rms noise was about 23 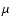 Jy beam-1.
The data were reduced and maps of both lobes produced using the NRAO AIPS software
package. After initial CLEANing of the maps, several self-calibrations were performed to
improve their quality. Then the maps of the NE and SW lobes were corrected for the
primary beam attenuation and convolved to the common resolution of
Jy beam-1.
The data were reduced and maps of both lobes produced using the NRAO AIPS software
package. After initial CLEANing of the maps, several self-calibrations were performed to
improve their quality. Then the maps of the NE and SW lobes were corrected for the
primary beam attenuation and convolved to the common resolution of
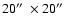 .
Finally, using the AIPS task COMB, the two maps were combined into a single image of
the entire source. This combined 4860-MHz map overlaid on the optical DSS field is shown in
Fig. 2. The contour levels are spaced by a factor of
.
Finally, using the AIPS task COMB, the two maps were combined into a single image of
the entire source. This combined 4860-MHz map overlaid on the optical DSS field is shown in
Fig. 2. The contour levels are spaced by a factor of 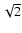 starting with
40
starting with
40 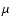 Jy beam-1.
The VLA data can be affected by missing-spacing effects, which implies that the
measured 4860 MHz flux densities in the extended diffuse region of the lobes can
be lower limits.
The flat-spectrum radio core (cf. Table 1) coincides with a
Jy beam-1.
The VLA data can be affected by missing-spacing effects, which implies that the
measured 4860 MHz flux densities in the extended diffuse region of the lobes can
be lower limits.
The flat-spectrum radio core (cf. Table 1) coincides with a
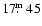 (R-band) galaxy. Its redshift of
(R-band) galaxy. Its redshift of
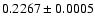 was measured by Machalski
et al. (2001).
was measured by Machalski
et al. (2001).
The second set of high-frequency observations of J1343+3758 has been carried out at
8350 MHz with a broad-band (1100 MHz) receiver in the secondary focus of the
Effelsberg 100-m radio telescope. The system is fed by a single horn with two
opposite circularly polarised feeds providing an angular resolution of
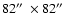 .
The observations were made in two runs of
6.5 h each. The weather conditions were excellent during the measurements on
Aug. 5 and 6, 2003.
.
The observations were made in two runs of
6.5 h each. The weather conditions were excellent during the measurements on
Aug. 5 and 6, 2003.
Pointing and focusing of the antenna, as well as the calibration and polarisation
performance of the receiver were checked by frequent (every two hours) cross-scanning
and mapping of the calibration source 3C 286. Its assumed flux density of 5.225 Jy at
8350 MHz is based on the scale of Baars et al. (1977). The measured mean polarisation
position angle and the mean degree of polarised intensity were
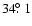 and 11.6%, respectively.
and 11.6%, respectively.
The data reduction was performed using the MPIfR-NOD2 reduction software
(Haslam 1974). Individual one-dimensional scans were first transformed into maps
of the Stokes I, Q, and U signals. Each map was then carefully examined for
interference spikes. The scanning effects were removed and a stack of
individual maps was made with the technique of "basket-weaving'' (Sieber et al.
1979). The final total-power and polarised-intensity maps were produced using the
NRAO-AIPS package. The applied integration time has allowed us to achieve a rms
noise of 0.39 and 0.09 mJy beam-1 in the I map and Q, U maps, respectively.
The Effelsberg 8350-MHz map of the total intensity emission from J1343+3758 is shown
in Fig. 3a. E-vectors of the linearly polarised emission with their
lengths proportional to the polarised intensity (
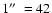
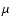 Jy beam-1)
are superimposed on the total-intensity contours.
The contour map of linearly polarised emission with the vectors of the fractional linear
polarisation superimposed is shown in Fig. 3b. At this frequency both lobes
are highly polarised; the degree of polarisation in the NE and SW lobes is given
in Sect. 3.3.
Jy beam-1)
are superimposed on the total-intensity contours.
The contour map of linearly polarised emission with the vectors of the fractional linear
polarisation superimposed is shown in Fig. 3b. At this frequency both lobes
are highly polarised; the degree of polarisation in the NE and SW lobes is given
in Sect. 3.3.
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{2007f2.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg42.gif) |
Figure 2:
VLA D-array map of J1343+3758 at 4860 MHz convolved to the
angular resolution of
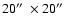 and overlaid on the optical
field from the Digital Sky Survey. The contour levels are spaced by factors of
and overlaid on the optical
field from the Digital Sky Survey. The contour levels are spaced by factors of
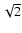 ;
the first contour is 40 ;
the first contour is 40 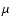 Jy beam-1. The compact 1.16 mJy
radio core coincides with the parent galaxy position. Jy beam-1. The compact 1.16 mJy
radio core coincides with the parent galaxy position. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{2007f3a.ps}\par\vspace*{3mm}
\includegraphics[width=8.3cm,clip]{2007f3b.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg43.gif) |
Figure 3:
The Effelsberg images of the source J1343+3758 at 8350 MHz.
a) Total intensity contours spaced by a factor of 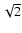 starting with 1.35 mJy beam-1. Superimposed are E-vectors with
their lengths proportional to the polarised intensity.
b) Linearly polarised intensity contours spaced by a factor of
starting with 1.35 mJy beam-1. Superimposed are E-vectors with
their lengths proportional to the polarised intensity.
b) Linearly polarised intensity contours spaced by a factor of
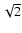 starting with 0.28 mJy beam-1 with the vectors of
the fractional linear polarisation superimposed. Otherwise the layout
is the same as in Fig. 1.
starting with 0.28 mJy beam-1 with the vectors of
the fractional linear polarisation superimposed. Otherwise the layout
is the same as in Fig. 1. |
| Open with DEXTER |
The morphology of J1343+3758 in all of the maps presented above is typical of
an FRII-type radio galaxy, although some features are seen only in the WENSS map.
As mentioned in Sect. 2.1, at 327 MHz the SW-lobe emission seems to extend
back to the compact core region, reaching a separate 15 mJy radio component. As
this component coincides with a faint optical galaxy (
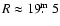 ;
;
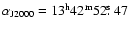 ;
;
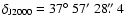 )
and is
)
and is
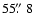 apart
from the radio core and the host galaxy, it is very likely a steep-spectrum
background source.
apart
from the radio core and the host galaxy, it is very likely a steep-spectrum
background source.
The NE lobe consists of two parts: the brighter northern-most region seen in all
four maps and containing the distinct hotspot, and the low-brightness
elongated emission aligned with the source axis and extending half way towards the
core. The latter part is not detected at 8350 MHz. The integrated flux
density of the SW lobe is larger than that of the NE one, so the brighter lobe is
closer to the host galaxy. Such a property has been found in most of the giant
sources in the sample of Machalski et al. (2001). This is expected in the
frame of the pure kinematic model of Longair & Riley (1979): if a source is
intrinsically highly symmetric, its inclination to the observer's line of sight
differs (but slightly) from
 ,
and the luminosity of its lobes
decreases with time. In such a case, the lobe seen as closer to the radio core
ought to be younger and brighter than the farther one. However, in Sects. 4.2
and 4.3 we find that the radiative and dynamical ages of the two lobes are very
similar, so that the projection effects are likely negligible, and the observed
asymmetries must be caused mostly by an inhomogeneity of the intergalactic medium
(IGM). The measured flux densities of J1343+3758 and its components are given in Table 1.
,
and the luminosity of its lobes
decreases with time. In such a case, the lobe seen as closer to the radio core
ought to be younger and brighter than the farther one. However, in Sects. 4.2
and 4.3 we find that the radiative and dynamical ages of the two lobes are very
similar, so that the projection effects are likely negligible, and the observed
asymmetries must be caused mostly by an inhomogeneity of the intergalactic medium
(IGM). The measured flux densities of J1343+3758 and its components are given in Table 1.
Table 1:
The radio flux densities of the source J1343+3758 and its lobes.
An important parameter of the radio morphology is the "axial ratio'' (AR), i.e.
the ratio between the length and the width of the source or its lobes (cf. Leahy
& Williams 1984). A low AR suggests a faster lateral expansion of the
synchrotron emitting blob of plasma; the expansion is likely dependent on the ratio
between the internal pressure in the blob and the pressure of the ambient medium (e.g.
Begelman & Cioffi 1989; KDA). Using the prescription given by
Leahy & Williams (1984), values of AR of 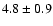 and
and 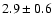 are found for the NE and SW lobes of J1343+3758. These values are similar to
those determined in another sample of giant radio sources by Schoenmakers et al.
(2000) where most of the lobes have
are found for the NE and SW lobes of J1343+3758. These values are similar to
those determined in another sample of giant radio sources by Schoenmakers et al.
(2000) where most of the lobes have
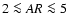 .
.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{2007f4a.ps}\par\vspace*{3mm}
\includegraphics[width=8.5cm,clip]{2007f4b.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg53.gif) |
Figure 4:
a) The map of the spectral index
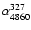 across the radio galaxy; b) this index in 30
across the radio galaxy; b) this index in 30
 wide strips
perpendicular to the source axis vs. strip distance from the core.
wide strips
perpendicular to the source axis vs. strip distance from the core. |
| Open with DEXTER |
We have made spectral index maps of J1343+3758 using the WENSS, NVSS, VLA, and
Effelsberg data. In each case the highest resolution map was convolved to the resolution
of another map. The final gray-scale map of the spectral index between the
frequencies 327 and 4860 MHz is shown in Fig. 4a. The rapid steepening of this index from the
hotspot regions towards the radio core is evident.
The high-resolution FIRST and our VLA maps (cf. Machalski & Jamrozy 2000)
allow us to determine the size and spectral
index of the compact hotspot in the NE lobe. Its Gaussian deconvolved size is
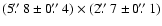 with the position angle
tilted by
with the position angle
tilted by 
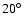 from the source main axis. The spectral index is
from the source main axis. The spectral index is
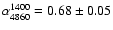 (
(
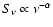 ). The hotspot linear
size is used in the dynamical considerations in Sect. 4.3.
). The hotspot linear
size is used in the dynamical considerations in Sect. 4.3.
The magnetic field vectors found in this giant source follow the general
trend known for FRII-type radio galaxies (Saikia & Salter 1988). The magnetic
field lines are circumferential towards the sources' peripheries and nearly
orthogonal to the source axis in the vicinity of the hotspots.
The lobes of J1343+3758 show high fractional polarisation which increases
significantly in the neighbourhood of the hotspots
(see Figs. 1b and 1c, and Fig. 3).
Integration of the available Stokes Q and U images yields a total fractional
polarisation of 11.4% 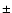 0.5% and 12.3%
0.5% and 12.3% 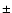 1.0% for the NE lobe, and
10.2%
1.0% for the NE lobe, and
10.2% 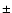 0.4% and 5.3%
0.4% and 5.3% 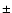 0.7% for the SW lobe at 1400 and 8350 MHz,
respectively. The degrees of polarisation in the SW lobe indicate some
depolarisation at higher frequencies.
0.7% for the SW lobe at 1400 and 8350 MHz,
respectively. The degrees of polarisation in the SW lobe indicate some
depolarisation at higher frequencies.
In order to obtain a Rotation Measure (RM) image of J1343+3758 we convolved
the 1400 MHz polarisation map to the beam of the Effelsberg 8350-MHz image.
Using the AIPS task COMB we calculated the values of the RM in the
regions where the polarised intensity is larger than 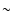
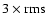 noise
at both frequencies. For the Faraday rotation in a slab with a uniform
field one can write
noise
at both frequencies. For the Faraday rotation in a slab with a uniform
field one can write
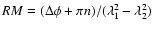 where
where
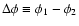 is the rotation of the polarisation
position angle
is the rotation of the polarisation
position angle 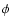 between the two wavelengths
between the two wavelengths
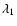 and
and
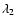 ,
where
,
where
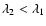 and n is an integer. We find
a mean RM of
and n is an integer. We find
a mean RM of
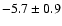 rad m-2 and
rad m-2 and
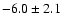 rad m-2 for
the NE and SW lobes, respectively. The RM, however, cannot be determined
reliably from our two-frequency data because of an ambiguity in the value of n.
The similar distributions of the magnetic field position angles and of the RMvalues across the lobes would suggest that a contribution of the radio galaxy to
the observed RM is negligible and that observed Faraday rotation may be of
Galactic origin since the mean Galactic RM at the position of J1343+3758 lies
between -30 rad m-2 and 0 rad m-2 (Simard-Normandin & Kronberg 1980).
However, this has to be checked by additional polarisation measurements at other
frequencies.
rad m-2 for
the NE and SW lobes, respectively. The RM, however, cannot be determined
reliably from our two-frequency data because of an ambiguity in the value of n.
The similar distributions of the magnetic field position angles and of the RMvalues across the lobes would suggest that a contribution of the radio galaxy to
the observed RM is negligible and that observed Faraday rotation may be of
Galactic origin since the mean Galactic RM at the position of J1343+3758 lies
between -30 rad m-2 and 0 rad m-2 (Simard-Normandin & Kronberg 1980).
However, this has to be checked by additional polarisation measurements at other
frequencies.
For the spectral analysis, the maps obtained at the four
different frequencies were convolved to a common angular resolution
determined by the lowest original one, i.e. the resolution of the Effelsberg
map. Then we determined the spectrum at different positions of the source
averaging the four flux densities within 30
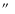 -wide strips orthogonal
to the source axis. In Fig. 4b the spectral index within these strips,
calculated between the frequencies of 327 and 4860 MHz is plotted against
the physical distance from the radio core.
-wide strips orthogonal
to the source axis. In Fig. 4b the spectral index within these strips,
calculated between the frequencies of 327 and 4860 MHz is plotted against
the physical distance from the radio core.
For the three
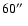 -wide strips covering the NE lobe and the other three covering
the SW lobe, the values of the equipartition energy density (
-wide strips covering the NE lobe and the other three covering
the SW lobe, the values of the equipartition energy density (
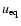 )
and the
corresponding magnetic field strength (
)
and the
corresponding magnetic field strength (
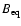 ), calculated with the formula
of Miley (1980), as well as the minimum pressure
), calculated with the formula
of Miley (1980), as well as the minimum pressure
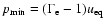 (with
(with
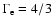 for the relativistic equation of state) are
given in Table 2.
for the relativistic equation of state) are
given in Table 2.
Table 2:
Magnetic field strength, equipartition energy density, and corresponding
minimum pressure in the lobes of J1343+3758 at the given distance from the core.
The mean spectra in the strips given in Table 2 were fitted with the three
models of the synchrotron radiation and inverse-Compton losses: continuum
injection (CI), Kardashev-Pacholczyk (KP), and Jaffe-Perola (JP)
(for a review of these models; see Myers & Spangler (1985)).
Assuming that (i) the minimum-energy conditions apply, (ii) the magnetic field (B)
in each strip of a lobe is constant throughout the emission process, (iii) the particles
are injected into the lobe with a constant power-law energy spectrum with an injection
spectral index
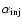 ,
and have spent equal time in each strip of different
magnetic field strength, the radiative (synchrotron) age in the JP model is given by
,
and have spent equal time in each strip of different
magnetic field strength, the radiative (synchrotron) age in the JP model is given by
![\begin{displaymath}\tau_{\rm rad}=50.3\frac{B^{1/2}}{B^{2}+B_{\rm iC}^{2}}
\{\nu_{\rm b}(1+z)\}^{-1/2}\left[10^{6} ~{\rm yr}\right]
\end{displaymath}](/articles/aa/full/2005/14/aa2007/img95.gif) |
(1) |
where
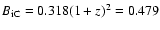 nT is the magnetic field strength
equivalent to the inverse-Compton microwave background, and
nT is the magnetic field strength
equivalent to the inverse-Compton microwave background, and
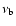 is the characteristic break frequency corresponding to a break in the particle
energy distribution in the emission spectrum. In Eq. (1)
is the characteristic break frequency corresponding to a break in the particle
energy distribution in the emission spectrum. In Eq. (1)
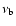 is expressed
in GHz. It is worth emphasising that the true magnetic field strength Bremains one of the most uncertain parameters in the spectral ageing analysis.
is expressed
in GHz. It is worth emphasising that the true magnetic field strength Bremains one of the most uncertain parameters in the spectral ageing analysis.
Using the SYNAGE software (Murgia 1996), the best
fits to the spectra are achieved with the CI model and
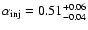 ,
and with the KP model and
,
and with the KP model and
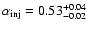 for the NE and SW lobes, respectively.
The JP model with
for the NE and SW lobes, respectively.
The JP model with
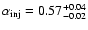 fits quite well
the spectrum of the entire source. The above result is consistent with those
found in different radio galaxies, for example: the young normal-size Cygnus A
(Carilli et al. 1991) and the much older giant 8C 0821+695 (Lara et al. 2000).
We find that the reduced
fits quite well
the spectrum of the entire source. The above result is consistent with those
found in different radio galaxies, for example: the young normal-size Cygnus A
(Carilli et al. 1991) and the much older giant 8C 0821+695 (Lara et al. 2000).
We find that the reduced 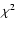 values of the fits with the CI model are
lower than those with the KP and JP ones only in the first two strips closer to
the NE hotspot. Moreover, different synchrotron ages in the NE lobe resulting
from the fits with the above different models, give comparable lobe-material
expansion speeds, thus a comparable dynamical age. Note
that the fits with the KP and JP models are indistinguishable within the frequency
range observed. Thus in the final analysis we use the physically more reasonable JP
model fits in both lobes though the KP model formally fits the data slightly better.
values of the fits with the CI model are
lower than those with the KP and JP ones only in the first two strips closer to
the NE hotspot. Moreover, different synchrotron ages in the NE lobe resulting
from the fits with the above different models, give comparable lobe-material
expansion speeds, thus a comparable dynamical age. Note
that the fits with the KP and JP models are indistinguishable within the frequency
range observed. Thus in the final analysis we use the physically more reasonable JP
model fits in both lobes though the KP model formally fits the data slightly better.
The observed spectra in the strips given in Table 2 and their fits with the JP
model for
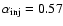 are shown in Fig. 5. The panels a), b), c)
contain the spectra in the NE lobe, and the panels d), e), f) show those in
the SW lobe. The values of the resultant break frequency
are shown in Fig. 5. The panels a), b), c)
contain the spectra in the NE lobe, and the panels d), e), f) show those in
the SW lobe. The values of the resultant break frequency
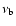 and
and
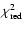 are shown in each panel. An evident excess of the 8350-MHz flux density value seen
in the panels c), d), e) is discussed at the end of Sect. 4.3.
are shown in each panel. An evident excess of the 8350-MHz flux density value seen
in the panels c), d), e) is discussed at the end of Sect. 4.3.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{2007f5.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg101.gif) |
Figure 5:
a)-c) Spectra observed in different strips across the NE lobe
of J1343+3758 fitted with the JP model for
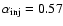 .
d)-f) The same for the SW lobe. The values of the resultant .
d)-f) The same for the SW lobe. The values of the resultant
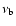 and and
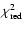 are shown in the top-right corner of each panel, and
the distance of each strip from the radio core is given its bottom-left corner.
are shown in the top-right corner of each panel, and
the distance of each strip from the radio core is given its bottom-left corner. |
| Open with DEXTER |
Following the authors of many previous publications on this topic, in the
first step of our analysis we substitute the "equipartition'' magnetic
field strength (
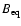 )
for B in Eq. (1). The resultant spectral ages of
particles derived from the data of consecutive strips are given in Col. 4
of Table 3 (indicated as
)
for B in Eq. (1). The resultant spectral ages of
particles derived from the data of consecutive strips are given in Col. 4
of Table 3 (indicated as
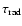 )
and plotted with open circles in
Fig. 6 against the distance from the radio core. The errors in
)
and plotted with open circles in
Fig. 6 against the distance from the radio core. The errors in
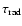 are derived from the uncertainties of
are derived from the uncertainties of
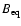 and
and
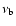 given in
Tables 2 and 3. The uncertainties in
given in
Tables 2 and 3. The uncertainties in
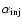 (given in
the text) and
(given in
the text) and
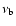 are estimated from the 1-
are estimated from the 1- region of allowance
in the free parameters space in the fits. A weighted least-squares fit to the
first-step ages in Fig. 6 (shown by the solid lines) yields a mean jet-head
separation velocity measured with respect to the lobe emitting plasma,
region of allowance
in the free parameters space in the fits. A weighted least-squares fit to the
first-step ages in Fig. 6 (shown by the solid lines) yields a mean jet-head
separation velocity measured with respect to the lobe emitting plasma,
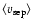 ,
for the NE and SW lobes. The relevant values divided
by the speed of light (indicated as
,
for the NE and SW lobes. The relevant values divided
by the speed of light (indicated as
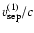 ), and the maximum
synchrotron age,
), and the maximum
synchrotron age,
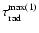 ,
obtained by extrapolation of these
fits up to the core are given in Cols. 5 and 6 of Table 3. These maximum ages are
very similar, their mean value is 48.8
,
obtained by extrapolation of these
fits up to the core are given in Cols. 5 and 6 of Table 3. These maximum ages are
very similar, their mean value is 48.8 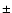 3.9 Myr. The comparable ages of
the lobes would support the presumption that giant radio galaxies are observed at
inclination angles very close to 90
3.9 Myr. The comparable ages of
the lobes would support the presumption that giant radio galaxies are observed at
inclination angles very close to 90
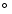 .
If so, the observed asymmetries
in the length, brightness, spectral-index, depolarisation, etc. of the lobes, would
likely be caused by an inhomogeneity of the surrounding intergalactic medium, not by
the effect of projection and light travel time.
.
If so, the observed asymmetries
in the length, brightness, spectral-index, depolarisation, etc. of the lobes, would
likely be caused by an inhomogeneity of the surrounding intergalactic medium, not by
the effect of projection and light travel time.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2007f6.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg107.gif) |
Figure 6:
Radiative age of relativistic particles in the lobes of J1343+3758 vs.
distance from the radio core. Open circles: age corresponding to
the equipartition magnetic field strengths; the filled circles: the age determined
for the enhanced fields (cf. the text). The solid and dashed lines show the weighted
least-squares fits to these ages. The extrapolations of the fits towards the core suggest
maximum spectral ages of particles in both lobes. |
| Open with DEXTER |
Adopting the formalism used by
Lara et al. (2000), we assume that the mean backflow speed (
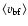 )
is a factor
)
is a factor 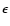 of the mean advance velocity of the jet-head with respect
to the external medium, i.e.
of the mean advance velocity of the jet-head with respect
to the external medium, i.e.
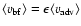 .
In this case the dynamical age of a source is
.
In this case the dynamical age of a source is
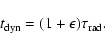 |
(2) |
Taking into account the results of numerical simulations (e.g. Wilson & Scheuer 1983)
indicating that sources with substantial backflow inflate wider lobes, and the arguments
of Alexander & Leahy (1987) for an increase of the ratio
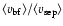 with decreasing source luminosity, one can assume that
the backflow velocity of the emitting plasma down the lobes of J1343+3758 is
comparable to the advance speed of the jet-head because of the low axial ratios
of both lobes (AR<5) and their low luminosities. Thus, if
with decreasing source luminosity, one can assume that
the backflow velocity of the emitting plasma down the lobes of J1343+3758 is
comparable to the advance speed of the jet-head because of the low axial ratios
of both lobes (AR<5) and their low luminosities. Thus, if
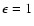 the
dynamical age of our giant radio galaxy would be
the
dynamical age of our giant radio galaxy would be
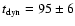 Myr.
Myr.
Under the above assumption, i.e.
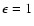 ,
the value of
,
the value of
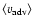 would be at least 0.060 c. However, if there is a constant
acceleration or deceleration of the jet-head advance velocity, the mean velocity
will be related to the present-day velocity,
would be at least 0.060 c. However, if there is a constant
acceleration or deceleration of the jet-head advance velocity, the mean velocity
will be related to the present-day velocity,
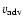 ,
as follows:
,
as follows:
where
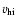 is the initial jet-head velocity, and a is the
acceleration/deceleration. This is important because an independent estimate of
is the initial jet-head velocity, and a is the
acceleration/deceleration. This is important because an independent estimate of
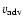 can be made by assuming the balance between the internal pressure at
the jet's head and the ram-pressure of the external ambient medium retreating at
speed
can be made by assuming the balance between the internal pressure at
the jet's head and the ram-pressure of the external ambient medium retreating at
speed
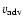 (Scheuer 1974). Moreover, basing ourselves on the result obtained by
Machalski et al. (2004b), we can assume
(Scheuer 1974). Moreover, basing ourselves on the result obtained by
Machalski et al. (2004b), we can assume
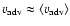 .
In that paper, the authors argue that in the large and old radio sources a jet-head
velocity deceleration is negligible because of the evident departure of their lobes/cocoon
expansion from self-similarity. If so, using the equation (cf. Arnaud et al. 1984)
.
In that paper, the authors argue that in the large and old radio sources a jet-head
velocity deceleration is negligible because of the evident departure of their lobes/cocoon
expansion from self-similarity. If so, using the equation (cf. Arnaud et al. 1984)
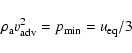 |
(3) |
it is possible to confine a value of
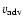 if the external medium density
(
if the external medium density
(
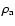 )
can be estimated.
)
can be estimated.
In order to estimate
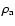 in the hotspot regions of J1343+3758 we
used the results of the dynamical evolution analysis for giant radio galaxies of
Machalski et al. (2004a). In that paper, the time evolution of giant radio galaxies
was analysed on the basis of dynamical evolution of the entire FRII-type
population. Using the analytical evolutionary KDA model, the authors derived a number
of physical parameters for FRII-type radio sources whose ages had been well determined
and published in the literature prior to their analysis.
in the hotspot regions of J1343+3758 we
used the results of the dynamical evolution analysis for giant radio galaxies of
Machalski et al. (2004a). In that paper, the time evolution of giant radio galaxies
was analysed on the basis of dynamical evolution of the entire FRII-type
population. Using the analytical evolutionary KDA model, the authors derived a number
of physical parameters for FRII-type radio sources whose ages had been well determined
and published in the literature prior to their analysis.
Table 3:
Frequency break in the JP model, synchrotron ages and separation speeds
derived in the first and the second steps of the ageing analysis.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2007f7.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg122.gif) |
Figure 7:
a) Model energy density (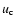 )
in the NE and SW lobes of J1343+3758
vs. the ambient density at their peripheries ( )
in the NE and SW lobes of J1343+3758
vs. the ambient density at their peripheries (
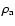 )
for different ages of the
lobes with present values of their observational parameters (cf. the text); b)
model jet power ( )
for different ages of the
lobes with present values of their observational parameters (cf. the text); b)
model jet power (
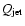 )
vs. the central core density ( )
vs. the central core density (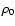 )
for the NE and SW
lobes at different ages. )
for the NE and SW
lobes at different ages. |
| Open with DEXTER |
Summarising, the KDA model assumes that the radio structure is formed by two jets
emanating from the AGN into a surrounding ambient medium in two opposite directions,
then terminates in strong shocks, and finally inflates the source's cocoon. A density
distribution of the unperturbed external gas is approximated by a power-law relation
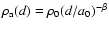 ,
where d is the radial distance from the
core,
,
where d is the radial distance from the
core, 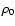 is the density at the core radius a0, and
is the density at the core radius a0, and 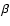 is the exponent
in this distribution. The cocoon expands along the jet axis driven by the hotspot
pressure
is the exponent
in this distribution. The cocoon expands along the jet axis driven by the hotspot
pressure 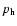 and, in the perpendicular direction, by the cocoon pressure
and, in the perpendicular direction, by the cocoon pressure 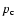 .
The
rate at which energy is transported along each jet,
.
The
rate at which energy is transported along each jet,
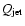 ,
is assumed to be constant
during the source lifetime. The quantitative values of
,
is assumed to be constant
during the source lifetime. The quantitative values of
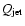 ,
,
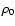 ,
and the cocoon
energy density
,
and the cocoon
energy density 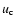 can be derived by fitting them to the observational data: the
monochromatic source luminosity, projected linear size, axial ratio AR, and given age
can be derived by fitting them to the observational data: the
monochromatic source luminosity, projected linear size, axial ratio AR, and given age![[*]](/icons/foot_motif.gif) .
.
Following the approach of Machalski et al. (2004a) and adopting their values of all free
parameters of the KDA model (e.g. a0=10 kpc and 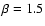 ), we fit the basic
physical parameters of the NE and SW lobes of J1343+3758 for a number of dynamical
ages. Given these parameters, the relation between
), we fit the basic
physical parameters of the NE and SW lobes of J1343+3758 for a number of dynamical
ages. Given these parameters, the relation between 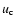 and
and
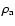 is
determined at the end of each lobe, and
is
determined at the end of each lobe, and
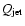 and
and 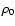 can be specified.
The logarithmic-scale plots of
can be specified.
The logarithmic-scale plots of 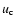 vs.
vs.
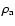 and
and
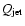 vs.
vs.
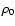 fitted for a number of the lobe ages t*, are shown in Figs. 7a and 7b,
respectively. Note that these plots do not represent a time evolution of the given
parameters; they show their predicted values at different (unknown) age of the lobes
with apparent size, axial ratio, and luminosity.
fitted for a number of the lobe ages t*, are shown in Figs. 7a and 7b,
respectively. Note that these plots do not represent a time evolution of the given
parameters; they show their predicted values at different (unknown) age of the lobes
with apparent size, axial ratio, and luminosity.
Inserting the values of 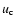 into Eq. (3) instead of
into Eq. (3) instead of
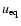 (which may be valid for the unknown present age of the lobe only), we have
(which may be valid for the unknown present age of the lobe only), we have
As both 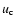 and
and
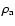 appear to be power-law functions
of t*, we find the following dependence of
appear to be power-law functions
of t*, we find the following dependence of
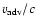 on age t (in Myr):
on age t (in Myr):
for the NE and SW lobes, respectively.
Inserting the first step values of
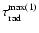 (Col. 6
in Table 3) into the above equations, we find advance speeds of (0.016
(Col. 6
in Table 3) into the above equations, we find advance speeds of (0.016 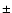 0.003) c
and (0.017
0.003) c
and (0.017 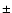 0.005) c for the NE and SW lobes, respectively.
0.005) c for the NE and SW lobes, respectively.
If these were correct, the backflow velocity
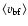 would be a few
times higher than the
would be a few
times higher than the
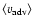 speeds, i.e.
speeds, i.e.  1.
This problem already occurred in the spectral ageing analysis of Cygnus A by
Carilli et al. (1991). In their paper they proposed a "self-consistent''
solution allowing a decrease of the magnetic field strengths which
would increase the jet-head pressure and slow the rate of radiative
losses, and hence would decrease the separation speed of the lobe material.
1.
This problem already occurred in the spectral ageing analysis of Cygnus A by
Carilli et al. (1991). In their paper they proposed a "self-consistent''
solution allowing a decrease of the magnetic field strengths which
would increase the jet-head pressure and slow the rate of radiative
losses, and hence would decrease the separation speed of the lobe material.
A similar solution for the case of J1343+3758 leads to a different conclusion.
Though either decrease or increase of the magnetic field strength with respect to
the equipartition value would raise both the total pressure of the relativistic
particles and of the B-fields according to the relation
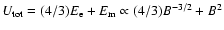 ,
a reduction of
the lobe-material separation speed, in order to match the different velocities
,
a reduction of
the lobe-material separation speed, in order to match the different velocities
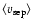 and
and
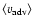 ,
is only possible by
an increase of the magnetic field strength. This is a consequence of
Eq. (1): the maximum amount of time elapsed since the last acceleration of
particles is achieved for
,
is only possible by
an increase of the magnetic field strength. This is a consequence of
Eq. (1): the maximum amount of time elapsed since the last acceleration of
particles is achieved for
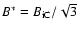 and is a function of redshift.
If the equipartition fields (
and is a function of redshift.
If the equipartition fields (
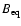 )
are lower than the value of B*,
their increase raises
)
are lower than the value of B*,
their increase raises
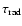 ;
if
;
if
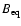 is higher than B*,
its further increase reduces
is higher than B*,
its further increase reduces
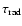 .
Low equipartition magnetic fields
are typical of almost all giant radio sources because of their large volumes and low
luminosities.
.
Low equipartition magnetic fields
are typical of almost all giant radio sources because of their large volumes and low
luminosities.
Therefore in the second step of our analysis, we increase the fields
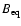 and find that a satisfactory match between
and find that a satisfactory match between
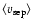 and
and
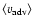 would be achieved if the fields were enhanced by a
factor of 5.5 and 3.4 in the NE and SW lobes, respectively. These enhanced values
(indicated
would be achieved if the fields were enhanced by a
factor of 5.5 and 3.4 in the NE and SW lobes, respectively. These enhanced values
(indicated
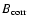 )
are given in Col. 7 of Table 3.
The relevant values of the radiative age of relativistic particles (
)
are given in Col. 7 of Table 3.
The relevant values of the radiative age of relativistic particles (
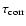 )
vs. the distance from the radio core are given in Col. 8 of Table 3, and plotted
with filled circles in Fig. 6. The weighted least-squares fit to the second-step
ages (shown by the dashed lines in Fig. 6) yields much slower velocities
)
vs. the distance from the radio core are given in Col. 8 of Table 3, and plotted
with filled circles in Fig. 6. The weighted least-squares fit to the second-step
ages (shown by the dashed lines in Fig. 6) yields much slower velocities
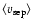 than the corresponding values found in the
first step. These values in units of c, (
than the corresponding values found in the
first step. These values in units of c, (
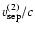 ), and the
maximum radiative age at the core position are given in Cols. 9 and 10 of Table 3.
), and the
maximum radiative age at the core position are given in Cols. 9 and 10 of Table 3.
Now, multiplying the right-hand side of Eq. (3) by the factors of 13.01 and 5.05
(as a result of the
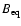 -field enhancement by 5.5 and 3.4), the previous
log(
-field enhancement by 5.5 and 3.4), the previous
log(
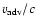 )
- t* relations change into:
)
- t* relations change into:
for the NE and SW lobes, respectively. Inserting the maximum values of particle
ages determined in the second step (Col. 10 of Table 3) into the above relations,
we have
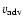 = (0.028
= (0.028 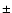 0.007)c and
0.007)c and
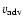 = (0.021
= (0.021 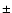 0.013)c
for the NE and SW lobes, respectively.
0.013)c
for the NE and SW lobes, respectively.
Indeed, these speeds are one half of the second step separation velocities
(see Col. 9 of Table 3) as required by the assumption of comparable jet-head
and backflow velocities. Dividing the projected lobe lengths of
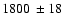 kpc and
1340
kpc and
1340 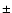 18 kpc by the averaged advance velocities of
18 kpc by the averaged advance velocities of
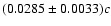 and
and
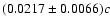 ,
and dynamical ages of 206
,
and dynamical ages of 206 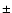 22 and 201
22 and 201 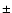 58 Myr,
respectively, for the NE and SW lobes are found. As they are very close to each other,
the mean value of 204
58 Myr,
respectively, for the NE and SW lobes are found. As they are very close to each other,
the mean value of 204 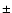 40 Myr seems to be a reliable dynamical age of the radio
galaxy J1343+3758. If correct, its spectral age of about 49 Myr will be only one fourth of
the suggested dynamical age.
40 Myr seems to be a reliable dynamical age of the radio
galaxy J1343+3758. If correct, its spectral age of about 49 Myr will be only one fourth of
the suggested dynamical age.
The spectra in Fig. 5 show an intriguing excess of the 8350 MHz flux-density
in faint parts of the extended diffuse structure of both lobes. It could be
explained by a slight but possible deficit of 4860 MHz flux density due to missing
spacings in the high-frequency VLA observations. We estimate a possible decrease of
that flux at the distance from the core of 1161 and 623 kpc in the NE and SW lobes,
respectively, to be less than 20%.
This would cause about 50% higher values of
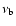 and about 22% lower
values of
and about 22% lower
values of
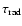 and
and
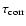 at these distances, resulting in
less than 10% decrease of the
at these distances, resulting in
less than 10% decrease of the
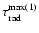 and
and
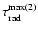 values given in Table 3. However, similar high-frequency
excesses seem to be present in some other giant radio galaxies, e.g. in the southern
lobe of B1358+305 (Parma et al. 1996), in both lobes of 8C 0821+695 (Lara et al.
2000), and possibly in one of the lobes of the giant quasars MCR 0437-244 and
MCR 1025-229 (Ishwara-Chandra & Saikia 1999). More high-frequency and
adequate angular-resolution data are necessary to determine whether such high-frequency
flattening could be real.
values given in Table 3. However, similar high-frequency
excesses seem to be present in some other giant radio galaxies, e.g. in the southern
lobe of B1358+305 (Parma et al. 1996), in both lobes of 8C 0821+695 (Lara et al.
2000), and possibly in one of the lobes of the giant quasars MCR 0437-244 and
MCR 1025-229 (Ishwara-Chandra & Saikia 1999). More high-frequency and
adequate angular-resolution data are necessary to determine whether such high-frequency
flattening could be real.
A multiplication of the left-hand side of Eq. (3) by the jet-head area yields
the ram-pressure force exerted by the ambient medium and balancing the jet thrust.
Begelman & Cioffi (1989) modified the former Scheuer model of an overpressured
cocoon (Model A; Scheuer 1974), admitting fluctuations in the jet direction that
cause the time-averaged momentum flux to be spread over a much wider area
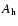 than the instantaneous cross-section of the jet. That modified model
makes it possible to predict the time elapsed from the `birth' of the source to the epoch of
our observations when it reached the observed linear size. This time, i.e.
dynamical age (their Eq. (3)), is
than the instantaneous cross-section of the jet. That modified model
makes it possible to predict the time elapsed from the `birth' of the source to the epoch of
our observations when it reached the observed linear size. This time, i.e.
dynamical age (their Eq. (3)), is
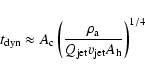 |
(4) |
where
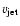 is the jet speed and
is the jet speed and 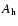 and
and 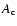 are the cross sectional areas of the bow shock at the end of the lobe and of the
lobe itself measured transversely to the jet axis, respectively. In most
analyses
are the cross sectional areas of the bow shock at the end of the lobe and of the
lobe itself measured transversely to the jet axis, respectively. In most
analyses
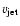 is assumed equal to the speed of light.
is assumed equal to the speed of light.
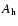 and
and 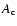 can be determined from the observations. For an independent
estimation of the dynamical age from Eq. (4), the expected values of
can be determined from the observations. For an independent
estimation of the dynamical age from Eq. (4), the expected values of
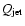 and
and
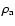 are taken from the statistical correlations found in the sample of
FRII-type radio sources by Machalski et al. (2004a) (cf. Sect. 4.3). They found
that
are taken from the statistical correlations found in the sample of
FRII-type radio sources by Machalski et al. (2004a) (cf. Sect. 4.3). They found
that
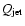 is highly correlated with the source luminosity
is highly correlated with the source luminosity
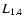 ,
and
,
and
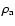 is highly anticorrelated with its linear size D. The partial
correlation
is highly anticorrelated with its linear size D. The partial
correlation
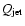 -
-
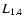 was calculated with taking account of unavoidable
correlations of these two parameters with redshift and source age. A partial
correlation coefficient of +0.901 was found if z and
was calculated with taking account of unavoidable
correlations of these two parameters with redshift and source age. A partial
correlation coefficient of +0.901 was found if z and
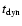 were kept
constant. A partial correlation coefficient of -0.935 in the correlation
were kept
constant. A partial correlation coefficient of -0.935 in the correlation
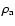 -D was found if
-D was found if 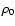 and
and
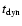 were kept constant.
Given
were kept constant.
Given
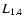 and D, the values of
and D, the values of
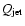 and
and
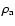 for the
entire giant source can be estimated from:
for the
entire giant source can be estimated from:
For J1343+3758 we have:
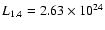 W Hz-1 sr-1
and D=3.14 Mpc, hence
W Hz-1 sr-1
and D=3.14 Mpc, hence
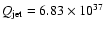 W and
W and
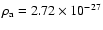 kg m-3 are found from the above statistical
correlations. The largest lateral deconvolved size of the source measured in the maps
is 506
kg m-3 are found from the above statistical
correlations. The largest lateral deconvolved size of the source measured in the maps
is 506 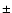 86 kpc, which yields
86 kpc, which yields
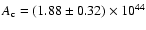 m2. The hotspot
in the NE lobe has the minor Gaussian diameter of
m2. The hotspot
in the NE lobe has the minor Gaussian diameter of
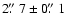 measured in three
maps (cf. Sect. 3.2) yielding
measured in three
maps (cf. Sect. 3.2) yielding
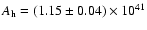 m2. Substitution of
the above values into Eq. (4) with approximation
m2. Substitution of
the above values into Eq. (4) with approximation
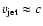 gives
gives
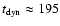 Myr, fully consistent with the value estimated in Sect. 4.3.
Myr, fully consistent with the value estimated in Sect. 4.3.
The main physical parameters for both individual lobes of J1343+3758 derived from
fitting are given in Table 4, and have been used to compare with the relevant quantities
obtained
from the statistics given in Sect. 4.4. The values of
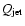 ,
,
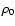 and
and
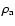 ,
as well as the mean energy density (
,
as well as the mean energy density (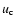 ), total emitted
energy (
), total emitted
energy (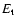 - the product of energy density and the lobe/cocoon volume),
and the ratio of the total energy delivered by the jet and the emitted energy
(
- the product of energy density and the lobe/cocoon volume),
and the ratio of the total energy delivered by the jet and the emitted energy
(
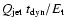 )
derived for the NE and SW lobes at ages
of 206 and 201 Myr, respectively, are given in Table 4. The latter ratio, i.e. the
reciprocal of the efficiency factor by which the kinetic energy of the jets is
converted into electromagnetic radiation, is much higher than
)
derived for the NE and SW lobes at ages
of 206 and 201 Myr, respectively, are given in Table 4. The latter ratio, i.e. the
reciprocal of the efficiency factor by which the kinetic energy of the jets is
converted into electromagnetic radiation, is much higher than  2, a value
usually assumed. The difference between the values of
2, a value
usually assumed. The difference between the values of
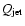 (
(
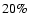 )
and
)
and 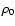 (
(
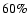 )
found from fitting for
the opposite lobes can be considered as the uncertainties of these values derived from
the model.
)
found from fitting for
the opposite lobes can be considered as the uncertainties of these values derived from
the model.
Table 4:
Main physical parameters of the lobes derived from the analytical model
of KDA (cf. Sect. 4.3) assuming the dynamical age estimate determined in this
paper.
Comparing the values of
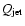 and
and
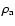 from Table 4 to the corresponding
values derived from the statistical correlations in Sect. 4.4, one can notice that
the jet power and the ambient density required by the dynamical model for the lobes
of J1343+3758 are higher by
from Table 4 to the corresponding
values derived from the statistical correlations in Sect. 4.4, one can notice that
the jet power and the ambient density required by the dynamical model for the lobes
of J1343+3758 are higher by 
 and
and 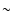
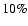 ,
respectively, than the
values suggested by the statistics. However these differences have a marginal
influence on the source dynamical age derived from Eq. (4) where it is proportional
to
,
respectively, than the
values suggested by the statistics. However these differences have a marginal
influence on the source dynamical age derived from Eq. (4) where it is proportional
to
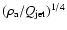 .
Now, the substitution of the
.
Now, the substitution of the
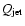 and
and
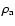 values fitted for the NE lobe (containing the distinct hotspot) into
Eq. (4) gives
values fitted for the NE lobe (containing the distinct hotspot) into
Eq. (4) gives
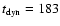 Myr, sufficiently close to the estimate
determined from the "self-consistent'' solution in Sect. 4.3.
Myr, sufficiently close to the estimate
determined from the "self-consistent'' solution in Sect. 4.3.
In this paper the radio properties of the giant radio galaxy J1343+3758 have been analysed.
We present the new high frequency 4860 and 8350 MHz total power and polarisation maps
of this source. Using the flux densities between 151 and 8350 MHz, and
radio maps at 327, 1400, 4860 and 8350 MHz we have studied the synchrotron
spectrum in different parts of its extended lobes, and performed the standard ageing
analysis. The maximum age of the relativistic particles calculated with the assumption
of equipartition magnetic fields is found to be about 50 Myr which is only one fourth of
the estimated dynamical age of the radio structure derived from the ram-pressure
arguments. This result is in agreement with the conclusion of Blundell
& Rawlings (2000) that the spectral and dynamical ages of a FRII-type radio galaxy
are comparable only when these ages are 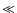 10 Myr and the discrepancy between
them increases with the age of the radio source. We include here also the KDA model
estimates of other physical parameters of J1343+3758, i.e. the jet power, the
central density of the galaxy nucleus, the ambient medium density, the lobe energy
density and the total energy of the source.
10 Myr and the discrepancy between
them increases with the age of the radio source. We include here also the KDA model
estimates of other physical parameters of J1343+3758, i.e. the jet power, the
central density of the galaxy nucleus, the ambient medium density, the lobe energy
density and the total energy of the source.
Acknowledgements
The authors acknowledge the National Radio Astronomy Observatory (NRAO)
which is a facility of the National Science Foundation operated under
cooperative agreement by Associated Universities, Inc. as well as the
Space Telescope Science Institute for the usage of the DSS data base.
This research is partly based on observations performed with the 100-m
telescope of the Max-Planck-Institut für Radioastronomie (MPIfR) at
Effelsberg. M.J. acknowledges the Deutsche Forschungsgemeinschaft
for the award of a postdoctoral fellowship (GRK 787).
- Alexander,
P., & Leahy, J. P. 1987, MNRAS, 225, 1 [NASA ADS] (In the text)
- Arnaud, K. A.,
Fabian, A. C., Eales, S. A., Jones, C., & Forman, W. 1984,
MNRAS, 211, 981 [NASA ADS] (In the text)
- Baars, J. W. M.,
Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A. 1977, A&A,
61, 99 [NASA ADS] (In the text)
- Becker, R. H.,
White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] (FIRST)
(In the text)
- Begelman, M.
C., & Cioffi, D. F. 1989, ApJ, 345, L21 [NASA ADS] [CrossRef] (In the text)
- Blundell, K.
M., Rawlings, S., & Willott, C. J. 1999a, AJ, 117, 766 (In the text)
- Blundell, K.
M., & Rawlings, S. 1999b, Nature, 399, 330 [NASA ADS] [CrossRef]
- Blundell, K.
M., & Rawlings, S. 2000, AJ, 119, 1111 [NASA ADS] [CrossRef] (In the text)
- Carilli, C. L.,
Perley, R. A., Dreher, J. W., & Leahy, J. P. 1991, ApJ, 383,
554 [NASA ADS] [CrossRef] (In the text)
- Condon, J. J.,
Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef]
(NVSS)
(In the text)
- Cotter, G. 1998, in
Observational Cosmology with the New Radio Surveys, ed. M. N.
Bremer, N. Jackson, & I. Perez-Fournon (Kluwer Acad. Publ.),
233
(In the text)
- Fanaroff, B.
L., & Riley, J. M. 1974, MNRAS, 167, 31 [NASA ADS] (In the text)
- Gregory, P. C.,
Scott, W. K., Douglas, K., & Condon, J. J. 1996, ApJS, 103, 427 [NASA ADS] [CrossRef]
(GB6)
- Hales, S. E. G.,
Baldwin, J. E., & Warner, P. J. 1988, MNRAS, 234, 919 [NASA ADS] (6C)
- Haslam, C. G. T.
1974, A&AS, 15, 333 [NASA ADS] (In the text)
-
Ishwara-Chandra, C. H., & Saikia, D. J. 1999, MNRAS, 309,
100 [NASA ADS] [CrossRef] (In the text)
- Jones, T. W., Ryu,
D., & Engel, A. 1999, ApJ, 512, 105 [NASA ADS] [CrossRef] (In the text)
- Jaffe, W. J., &
Perola, G. C. 1973, A&A, 26, 423 [NASA ADS] (In the text)
- Kaiser, C. R.,
Dennett-Thorpe, J., & Alexander, P. 1997, MNRAS, 292, 723 [NASA ADS]
(KDA)
(In the text)
- Kaiser, C. R. 2000,
A&A, 362, 447 [NASA ADS] (In the text)
- Kardashev, N.
S. 1962, SvA, 6, 317 [NASA ADS] (In the text)
- Klein, U., Mack,
K.-H., Gregorini, L., & Parma, P. 1995, A&A, 303, 427 [NASA ADS] (In the text)
- Lara, L., Mack, K.-H.,
Lacy, M., et al. 2000, A&A, 356, 63 [NASA ADS] (In the text)
- Leahy, J. P., &
Williams, A. G. 1984, MNRAS, 210, 929 [NASA ADS] (In the text)
- Leahy, J. P., Muxlow,
T. W. B., & Stephens, P. W. 1989, MNRAS, 239, 401 [NASA ADS] (In the text)
- Liu, R., Pooley, G.,
& Riley, J. M. 1992, MNRAS, 257, 545 [NASA ADS] (In the text)
- Longair, M. S.,
& Riley, J. M. 1979, MNRAS, 188, 625 [NASA ADS] (In the text)
- Machalski,
J., & Jamrozy, M. 2000, A&A, 363, L17 [NASA ADS] (In the text)
- Machalski,
J., Jamrozy, M., & Zola, S. 2001, A&A, 371, 445 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Machalski,
J., Chyzy, K. T., & Jamrozy, M. 2004a, Acta Astr., 54, 249 [NASA ADS] (In the text)
- Machalski,
J., Chyzy, K. T., & Jamrozy, M. 2004b, Acta Astr., 54, 391 [NASA ADS]
- Mack, K.-H., Klein, U.,
O'Dea, C. P., Willis, A. G., & Saripalli, L. 1998, A&A,
329, 431 [NASA ADS] (In the text)
- Miley, G. 1980,
ARA&A, 18, 165 [NASA ADS] (In the text)
- Murgia, M. 1996,
Laurea Thesis, University of Bologna
(In the text)
- Myers, S. T., &
Spangler, S. R. 1985, ApJ, 291, 52 [NASA ADS] [CrossRef] (In the text)
- Neeser, M. J.,
Eales, S. A., Law-Green, J. D., Leahy, J. P., & Rawlings, S.
1995, ApJ, 451, 76 [NASA ADS] [CrossRef] (In the text)
- Pacholczyk,
A. G. 1970, Radio Astrophysics (San Francisco: Freeman)
(In the text)
- Parma, P., de Ruiter,
H. R., Mack, K.-H., et al. 1996, A&A, 311, 49 [NASA ADS] (In the text)
- Parma, P., Murgia,
M., Morganti, R., et al. 1999, A&A, 344, 7 [NASA ADS] (In the text)
- Pooley, D. M.,
Waldram, E. M., & Riley, J. M. 1998, MNRAS, 298, 637 [NASA ADS] [CrossRef]
- Rengelink, R.
B., Tang, Y., de Bruyn, A. G., et al. 1997, A&AS, 124, 259 [NASA ADS]
(WENSS)
(In the text)
- Rudnick, L.,
Katz-Stone, D. M., & Anderson, M. C. 1994, ApJS, 90, 955 [NASA ADS] [CrossRef] (In the text)
- Saikia, D. J.,
& Salter, C. J. 1988, ARA&A, 26, 93 [NASA ADS] (In the text)
- Scheuer, P. A. G.
1974, MNRAS, 166, 513 [NASA ADS] (In the text)
-
Schoenmakers, A. P., Mack, K.-H., Lara, L., et al. 1998, A&A,
336, 455 [NASA ADS] (In the text)
-
Schoenmakers, A. P., Mack, K.-H., de Bruyn, A. G., et al. 2000,
A&AS, 146, 293 [NASA ADS] (In the text)
- Sieber, W., Haslam,
C. G. T., & Salter, C. J. 1979, A&A, 74, 361 [NASA ADS] (In the text)
-
Simard-Normandin, M., & Kronberg, P. P. 1980, ApJ, 242, 74 [NASA ADS] [CrossRef]
- Wilson, M. J.,
& Scheuer, P. A. G. 1983, MNRAS, 205, 449 [NASA ADS] (In the text)
- Zhang, X., Zheng, Y.,
Chen, H., et al. 1997, A&AS, 121, 59 [NASA ADS]
Copyright ESO 2005
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2007f1a.ps}\par\vspace*{3mm}...
...b.ps}\par\vspace*{3mm}
\includegraphics[width=8cm,clip]{2007f1c.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{2007f2.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{2007f3a.ps}\par\vspace*{3mm}
\includegraphics[width=8.3cm,clip]{2007f3b.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg43.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{2007f4a.ps}\par\vspace*{3mm}
\includegraphics[width=8.5cm,clip]{2007f4b.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg53.gif)
![\begin{displaymath}\tau_{\rm rad}=50.3\frac{B^{1/2}}{B^{2}+B_{\rm iC}^{2}}
\{\nu_{\rm b}(1+z)\}^{-1/2}\left[10^{6} ~{\rm yr}\right]
\end{displaymath}](/articles/aa/full/2005/14/aa2007/img95.gif)
![\begin{figure}
\par\includegraphics[width=15cm,clip]{2007f5.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2007f6.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg107.gif)
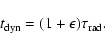
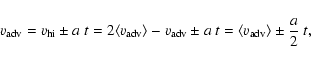
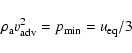
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2007f7.ps}
\end{figure}](/articles/aa/full/2005/14/aa2007/Timg122.gif)
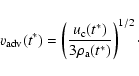
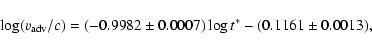
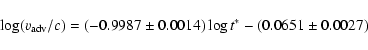
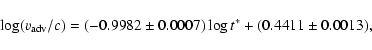
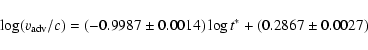
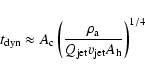
![\begin{displaymath}\log(Q_{\rm jet}[{\rm W}])=0.768\log(L_{\rm 1.4}[{\rm W~Hz^{-1}~sr^{-1}}])+19.08~~\mbox{and}
\end{displaymath}](/articles/aa/full/2005/14/aa2007/img151.gif)
![\begin{displaymath}\log(\rho_{\rm a}[{\rm kg~m^{-3}}])=-1.5\log(D[{\rm Mpc}])-25.82.
\end{displaymath}](/articles/aa/full/2005/14/aa2007/img152.gif)