F. Baudin1 - R. Samadi2,3 - M.-J. Goupil2 - T. Appourchaux4,1
- C. Barban5,![]() - P. Boumier1
- W. J. Chaplin6 - P. Gouttebroze1
- P. Boumier1
- W. J. Chaplin6 - P. Gouttebroze1
1 - Institut d'Astrophysique Spatiale, CNRS/Université Paris XI
UMR 8617, 91405 Orsay Cedex, France
2 - Observatoire de Paris, LESIA, CNRS UMR
8109, 92195 Meudon, France
3 -
Observatório Astronómico UC, FCTUC, Coimbra, Portugal
4 -
European Space Agency, Research and
Science Support Department, Science Payload and Advanced Concept
Office, PO Box 299, 2200Ag Noordwijk, The Netherlands
5 - National
Solar Observatory, 950 N. Cherry Avenue, Tucson AZ 85719, USA
6 -
School of Physics and Astronomy, University of Birmingham, Edgbaston,
Birmingham B15 2TT, UK
Received 4 May 2004 / Accepted 13 November 2004
Abstract
Acoustic rates of excitation of solar p modes can be estimated from observations
in order to place constraints on the modelling of the excitation process and the
layers where it occurs in the star. For several reasons (including a poor signal
to noise ratio and mode overlap), this estimation is difficult. In this work, we
use three completely independent datasets to obtain robust estimates in the
solar case for ![]() modes. We also show that the height in the
solar atmosphere where the modes are observed
must be taken into account. Our three sets of results are shown to be
consistent, particularly in the lower part of the p-mode spectrum (from
1.8 mHz to 2.8 mHz). At higher frequencies, the agreement is not as good,
because of a larger dispersion of the measurements and also because of some
systematic differences which might be due to observation height estimation or to
a systematic influence of the noise.
modes. We also show that the height in the
solar atmosphere where the modes are observed
must be taken into account. Our three sets of results are shown to be
consistent, particularly in the lower part of the p-mode spectrum (from
1.8 mHz to 2.8 mHz). At higher frequencies, the agreement is not as good,
because of a larger dispersion of the measurements and also because of some
systematic differences which might be due to observation height estimation or to
a systematic influence of the noise.
Key words: Sun: oscillation - Sun: helioseismology
Solar seismology has been used for many years to "sound out'' the interior of the Sun through information provided by the acoustic resonances (the so-called p modes). More precisely, the frequencies of these resonances - which are usually extracted by the analysis of power frequency spectra - are governed by the physical conditions inside the Sun, and these can be "inverted'' to infer these conditions (e.g., sound speed, density, rotation). In the last ten years, new ways of analysing the solar oscillations or extracting information from them have been developed, mainly in the field of local seismology (analysing local propagation of acoustic waves). However, globally coherent, or "classical'' seismology, is also developing and giving rise to new results: for example Houdek et al. (2001) have used the width of the resonances to infer convection properties. Nevertheless, the outer layers of the Sun remain poorly described, as well as the convection in these layers.
Seismology can place constraints on the modelling of these layers, and on the convection which excites the acoustic resonances. Among others, Samadi & Goupil (2001) have proposed such a model and compared the acoustic rates thereby predicted (see Sect. 2) with observations (Samadi et al. 2003). They found a good overall agreement when the input data of the theoretical model of stochastic excitation were constrained with a 3-D simulation of the Sun. However, even if the agreement is good for the lower part of the p-mode spectrum, some clear discrepancies remain at higher frequencies, which is unfortunately where the properties are most difficult to measure.
The excitation rate of low-frequency p modes is mainly dominated by inertia. In contrast, the excitation of high-frequency p modes is more sensitive to the nature of the source of excitation (either dynamical via Reynolds stresses or thermal via turbulent entropy fluctuations, see Samadi et al. 2001; Goldreich et al. 1994). The excitation rate at high frequencies also depends on the temporal properties of the turbulence in the outer layers of the star (Samadi et al. 2003). Observational constraints are needed for the modelling of such properties.
The estimation of the power and width of the acoustic resonances is subject to several sources of error. First, there is a large uncertainty in the measurement as the power spectrum of a resonance (or mode) has a large variance because of the stochastic nature of the excitation (see Sect. 6). Moreover, the absolute calibration in amplitude of a Doppler time series is a complex problem (see Sect. 4). Another problem is to know exactly at which height in the solar atmosphere the modes are observed. Oscillations of the photosphere are measured in two ways: photometry in a given wavelength range, or Doppler measurements on a line formed in the photosphere (like the data used in this work). As the density drops rapidly with height in the solar atmosphere, the observed amplitude increases rapidly. Thus, a measurement of power is meaningful only if the altitude to which it corresponds is known. With a proper calibration, comparisons of the absolute power levels of models of mode excitation by convection are possible (whose results are strongly dependent on height; see Sect. 5).
Our aim in this paper is to obtain reliable measurements of the
excitation rate of globally coherent, low-angular degree (or
low-![]() )
modes. To have confidence in the results we have used
three independent datasets (see Sect. 3) covering the
same observation period, and then analysed these with the same method
and software. We have been particularly careful in our extraction of
the parameters at high frequencies (see
Sect. 6). Furthermore, we have also taken into account in
our analysis the observation heights in the solar atmosphere at which
the three datasets were "taken''. As such, we have attempted to make
available to modellers an internally consistent set of results.
)
modes. To have confidence in the results we have used
three independent datasets (see Sect. 3) covering the
same observation period, and then analysed these with the same method
and software. We have been particularly careful in our extraction of
the parameters at high frequencies (see
Sect. 6). Furthermore, we have also taken into account in
our analysis the observation heights in the solar atmosphere at which
the three datasets were "taken''. As such, we have attempted to make
available to modellers an internally consistent set of results.
The rate at which a p mode of frequency ![]() is excited is
expressed as in Goldreich et al. (1994):
is excited is
expressed as in Goldreich et al. (1994):
According to Eqs. (1) and (2),
the excitation rate P can then be related to the seismic data by:
A pulsation code is used to compute the eigenfunctions, ![]() ,
and the
mode mass
,
and the
mode mass
![]() for a calibrated solar model (see
Sect. 2.3). It is important to stress that the radius
for a calibrated solar model (see
Sect. 2.3). It is important to stress that the radius
![]() ,
at which
,
at which
![]() must be evaluated depends on the
spectral line of the corresponding seismic measurement (see
Sect. 5) and therefore on the observation set and
instrument.
must be evaluated depends on the
spectral line of the corresponding seismic measurement (see
Sect. 5) and therefore on the observation set and
instrument.
To a first approximation, the mode profile in the observed power velocity
spectrum,
![]() ,
can reasonably be assumed to be Lorentzian
with a maximum power spectral density, or height,
,
can reasonably be assumed to be Lorentzian
with a maximum power spectral density, or height,
![]() ,
and a
linewidth at half maximum given by
,
and a
linewidth at half maximum given by
![]() .
The mode profile is then written as:
.
The mode profile is then written as:
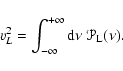 |
(6) |
Once the quantities
![]() and
and ![]() are determined,
one needs to compute the velocity.
The mean square velocity of the mode,
are determined,
one needs to compute the velocity.
The mean square velocity of the mode,
![]() ,
is then:
,
is then:
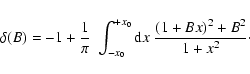 |
(10) |
The solar model we consider is calculated with the CESAM code
(Morel 1997) and appropriate input physics, as described in detail
in Lebreton et al. (1999). In particular, convection is modelled according
to the classical mixing-length theory (Böhm-Vitense 1958, hereafter MLT)
with a mixing-length
![]() ,
where
,
where ![]() is the pressure
scale height and
is the pressure
scale height and
![]() is the mixing-length parameter. In
contrast with Lebreton et al. (1999), the atmosphere is calculated assuming the
Eddington classical gray atmosphere, and microscopic diffusion is
included according to the simplified formalism of Michaud & Proffitt (1993).
The calibration of the solar model in luminosity and radius for an
age of 4.65 Gyr fixes the initial helium content Y=0.2751, the
metallicity Z=0.0196 and the MLT parameter
is the mixing-length parameter. In
contrast with Lebreton et al. (1999), the atmosphere is calculated assuming the
Eddington classical gray atmosphere, and microscopic diffusion is
included according to the simplified formalism of Michaud & Proffitt (1993).
The calibration of the solar model in luminosity and radius for an
age of 4.65 Gyr fixes the initial helium content Y=0.2751, the
metallicity Z=0.0196 and the MLT parameter
![]() .
.
The oscillation eigenfunctions, and hence the mode masses,
![]() ,
in Eq. (4) are next obtained with the
adiabatic pulsation code of Tran Minh & Leon (1995) from the solar model.
,
in Eq. (4) are next obtained with the
adiabatic pulsation code of Tran Minh & Leon (1995) from the solar model.
In order to measure the influence of the treatment of convection and of the atmosphere, we have considered two additional solar models. One solar model assumes Canuto et al. (1996)'s local treatment of convection. The second has its atmosphere calculated assuming Kurucz's model, computed such as to provide a good agreement between synthetic and observed Balmer line profiles.
At fixed ![]() ,
we find that the mode masses depend on the treatment
of convection and on the treatment of the atmosphere but the
associated changes in
,
we find that the mode masses depend on the treatment
of convection and on the treatment of the atmosphere but the
associated changes in
![]() are found to be of the same
order as the observational error bars associated with the excitation
rates. As we are, here, mainly interested in the comparison between
observations from different instruments, the effect of the adopted
physics on
are found to be of the same
order as the observational error bars associated with the excitation
rates. As we are, here, mainly interested in the comparison between
observations from different instruments, the effect of the adopted
physics on
![]() does not influence the results.
does not influence the results.
Three datasets were used in this work, each covering the 805-d period
from 1996 April to 1998 June. This epoch coincides with a period of
low activity on the Sun. The use of several sets allows a direct
comparison, and an assessment of the influence on the results of each
observation method. The three time series come from the instrument
GOLF (Global Oscillation at Low Frequencies, Gabriel et al. 1997) onboard the
satellite SoHO, and from the ground-based networks BiSON (Birmingham
Solar Oscillation Network, Chaplin et al. 1996) and GONG (Global Oscillation
Network Group, Harvey et al. 1996). Each are velocity measurements integrated
over the whole solar disc![]() sensitive to
low-degree modes (mainly
sensitive to
low-degree modes (mainly ![]() = 0, 1 and 2). The analysis has been
performed in the same way for the three sets (i.e., the same fitting
algorithm).
= 0, 1 and 2). The analysis has been
performed in the same way for the three sets (i.e., the same fitting
algorithm).
An obvious difference between the datasets is the "duty cycle'', or fraction of effective time for which observations are available. Interruptions can result from instrumental failures, and also from bad weather for the ground-based networks. Power levels in the Fourier (frequency) spectrum can be corrected to take account of these interruptions through a simple multiplication by the inverse of the duty cycle. However, as shown by Chaplin et al. (2003), this simple correction does not completely remove the bias in the fitted width and height parameters that is caused by the window. In this work, acoustic rates computed from BiSON and GONG spectra were therefore additionally corrected by a constant value of 9% for each 10% change in duty cycle, as indicated by Chaplin et al. (2003).
In addition to this, two aspects play an important role in the comparison of the three datasets. First, the absolute calibration of a Doppler time series is a delicate task. Among the seismic observables, frequencies are very accurately estimated (to some ppm), whereas amplitudes are not. One of the reasons for this is the difficulty in properly deriving the photospheric displacement from the spectro-photometric measurements performed by the instruments. The case of GOLF can be cited as a good example as, because of technical problems, Doppler shifts are estimated from only one wing of the selected atomic lines. However, the task is not much easier for the other two instruments (Hill, Leibacher, private communication). This is detailed in Sect. 4.
The second aspect of the problem of acoustic rate estimation is the height in the solar photosphere to which the observations correspond, as the amplitude of the modes varies with height. This is the old and complex problem of line formation in the solar atmosphere, illustrated by an abundant literature, and detailed in Sect. 5.
GOLF is based on a non-imaging spectrophotometer using the Na I D1 (at 589.6 nm) and D2 lines (at 589.0 nm) to measure the velocity of the photosphere. Because of technical problems (Gabriel et al. 1997), the velocity is derived from intensity measurements in only one wing of the lines (the blue wing for the period used here). The average position of the measurement points in the wing is 108 mÅ from the centre for the D1 line, and 81 and 135 mÅ for the D2 lines. To this must be added the value of the gravitational redshift for the sodium lines: 12.5 mÅ.
As GOLF is space-borne, the interruptions in the observations are very few, and the duty cycle reaches almost 100% over the total duration of the period of observation chosen here.
The BiSON instruments are also non-imaging spectrophotometers, but
they work in the K I line at 769.9 nm. The intensity is measured
in both wings, at typically ![]() 63 mÅ from the centre of the line
(which presents a gravitational redshift of 16 mÅ ).
63 mÅ from the centre of the line
(which presents a gravitational redshift of 16 mÅ ).
Despite the use of six active sites spread widely in longitude, the
network experiences some interruptions yielding a duty cycle of
![]() 74% for the period used here.
74% for the period used here.
The GONG instrument is an imaging Fourier tachometer using
Ni I at 676.8 nm, which measures velocity from the whole line,
as described by Jones (1989). The time series used here is the
![]() dataset (integration over 95% of the solar disc). Again,
there are some gaps in network coverage giving a duty cycle for the
period covered of about
dataset (integration over 95% of the solar disc). Again,
there are some gaps in network coverage giving a duty cycle for the
period covered of about ![]() 82%.
82%.
The sensitivity of each instrument is not exactly the same: first, the
geometrical visibility of the modes must be taken into account to
compare those of different degree ![]() .
The limb-darkening
influences this parameter for the GOLF and BiSON spectrophotometers
(see Appendix in Appourchaux et al. 2000; Christensen-Dalsgaard & Gough 1982), making it
different for each instrument despite the fact that the geometry is
intrinsic to the modes. In addition, GOLF and BiSON have their
sensitivity influenced by the relative velocity of the instrument (due
to the SoHO orbit for GOLF and to Earth orbit and rotation for BiSON,
and to the gravitational redshift for both) and also by the solar
rotation, as described by Christensen-Dalsgaard (1989). The impact of these effects on
visibility gives rise to the so-called "Doppler imaging''. This yields
a
.
The limb-darkening
influences this parameter for the GOLF and BiSON spectrophotometers
(see Appendix in Appourchaux et al. 2000; Christensen-Dalsgaard & Gough 1982), making it
different for each instrument despite the fact that the geometry is
intrinsic to the modes. In addition, GOLF and BiSON have their
sensitivity influenced by the relative velocity of the instrument (due
to the SoHO orbit for GOLF and to Earth orbit and rotation for BiSON,
and to the gravitational redshift for both) and also by the solar
rotation, as described by Christensen-Dalsgaard (1989). The impact of these effects on
visibility gives rise to the so-called "Doppler imaging''. This yields
a
![]() parameter (see Eq. (7)) for each
spectrophotometer, and for each degree
parameter (see Eq. (7)) for each
spectrophotometer, and for each degree ![]() .
Based on
Appourchaux et al. (2000) and Christensen-Dalsgaard (1989) and on the limb-darkening description
of Allen (1991), we have derived this parameter for GOLF and BiSON.
.
Based on
Appourchaux et al. (2000) and Christensen-Dalsgaard (1989) and on the limb-darkening description
of Allen (1991), we have derived this parameter for GOLF and BiSON.
GONG is not a spectrophotometer but a Fourier tachometer. We have
derived
![]() for the modes
for the modes ![]() and 2 from the value for
and 2 from the value for
![]() modes (given by F. Hill, private communication) and from
their geometrical visibility.
modes (given by F. Hill, private communication) and from
their geometrical visibility.
All these values are listed in Table 1.
As mentioned in Sect. 2.1, the mass of the modes is one of the parameters needed to compute the excitation rate. As this mode mass is the mode inertia (an intrinsic characteristic) normalised by the displacement at the height where the wave is observed, this height must be properly estimated to derive correct values of the excitation rate. However, obtaining reliable formation heights of solar lines is a complex problem. In addition, each instrument analyses a well delimited part of the profile of the line, and as from the center of the line to the wings the height of formation varies by hundreds of km, the characteristics of each instrument must be taken into account. For the three relevant spectral lines used here, we have made use of Jones (1989) for GONG, and Bruls & Rutten (1992) for BiSON and GOLF. The work done by Jones is perfectly suited as it takes into account the manner in which GONG measurements are performed. On the other hand, the work of Bruls & Rutten is more general, but provides enough information to estimate the formation height of the K line of BiSON and the Na D1 of GOLF. Unfortunately, this work does not include the neighbouring Na D2 line.
Table 1:
Observational correction
![]() for the different instruments and
modes (see Sect. 4).
for the different instruments and
modes (see Sect. 4).
We have taken these estimates as a first approach and are aware of their limitations. In addition to the missing D2 line, some other aspects are neglected, e.g., integration over the entire solar disc and limb darkening effect. A complete and coherent treatment of the three lines, applied to the specific case of each instrument, is necessary but remains the next step for a future work.
It is not easy to define a formation height since physically it is not
a single altitude in the solar atmosphere, but a range of contributing
altitudes to the radiation of interest. The heights we extract from
the literature must be considered only as estimates of the maximum of
contribution. From Fig. 3 of Jones (1989), we have estimated the
observation height of GONG at
![]() 240 km above the
photosphere. Knowing the average position at which BiSON and GOLF
measurements are made in the wings of K and Na lines, we have set
240 km above the
photosphere. Knowing the average position at which BiSON and GOLF
measurements are made in the wings of K and Na lines, we have set
![]() 280 km from Fig. 10 of Bruls & Rutten (1992), and
280 km from Fig. 10 of Bruls & Rutten (1992), and
![]() 340 km from their Fig. 11. Again, these
estimates have to be taken as approximate, not only for the reasons
already mentioned but also because they result from an average of
different physical cases (the "hot'' and "cool'' models of Bruls &
Rutten). More recently, Georgobiani et al. (2003) also showed that the
definition of height is not trivial when comparing geometrical
height and optical height.
340 km from their Fig. 11. Again, these
estimates have to be taken as approximate, not only for the reasons
already mentioned but also because they result from an average of
different physical cases (the "hot'' and "cool'' models of Bruls &
Rutten). More recently, Georgobiani et al. (2003) also showed that the
definition of height is not trivial when comparing geometrical
height and optical height.
The effect of height formation influences the determined acoustic
rates, via the mode mass, mainly at high frequencies (![]() mHz);
the effect is much weaker at lower frequencies (see
Fig. 1). As such, this makes the interpretation of
the results easier.
mHz);
the effect is much weaker at lower frequencies (see
Fig. 1). As such, this makes the interpretation of
the results easier.
![\begin{figure}
\par\includegraphics[angle=90,width=7.4cm,clip]{1229_fig1.ps}
\par\end{figure}](/articles/aa/full/2005/13/aa1229/Timg57.gif) |
Figure 1:
Mode mass computed for different heights. Because the modes
at higher frequencies are concentrated closer to the surface, the masses
tend to decrease with increasing frequency. The increasing value of
the eigenfunction |
| Open with DEXTER | |
The parameters necessary for the derivation of the acoustic rate are listed in Sect. 2. From the observations, two characteristics of the modes are needed: their width and their height in the power spectrum. They have been obtained by a classical fitting procedure applied in exactly the same manner to the three data sets. The modes are fitted using the asymmetric profile described by Nigam et al. (1998). This slight deformation of the peak is known to have a significant influence on frequency, but omitting it also leads to a bias in the determination of the acoustic rate, as shown in Fig. 2.
![\begin{figure}
\par\includegraphics[angle=90,width=7.4cm,clip]{1229_fig2.ps}\end{figure}](/articles/aa/full/2005/13/aa1229/Timg58.gif) |
Figure 2: Excitation rate computed from Lorentzian profiles and asymmetric profiles, showing a significant bias. |
| Open with DEXTER | |
In the frequency interval from 2 to 3.5 mHz in the three datasets, the
signal to noise ratio (SNR) is good and the fitting procedure extracts
robust estimates of the mode parameters. However, as shown in
Samadi et al. (2003), the high frequencies part (higher than 3.5mHz) of the
spectrum is interesting as observations and models tend to differ
here. It is also the most difficult part of the spectrum to analyse,
first because of the decreasing SNR, and second because of the
increasing width of the modes. This makes the pairs ![]() and
and
![]() overlap. This in turn makes the fitting more difficult as
cross-talk will appear between the modes.
overlap. This in turn makes the fitting more difficult as
cross-talk will appear between the modes.
![\begin{figure}
\par\includegraphics[angle=90,width=7.7cm,clip]{1229_fig3.ps}\end{figure}](/articles/aa/full/2005/13/aa1229/Timg61.gif) |
Figure 3:
Fitted heights for |
| Open with DEXTER | |
To minimize the effect of cross-talk between neighbouring modes, as
well as between the fitted parameters of a single mode, we
modified the fitting strategy at high frequencies. The aim of these
changes was to minimize the number of fitted parameters; these were
tested on the high SNR part of the spectrum and then applied at high
frequencies. The changes applied can be something as simple as imposing the same
amplitude for the ![]() components of a mode (see
Fig. 3), or the same asymmetry for a pair
components of a mode (see
Fig. 3), or the same asymmetry for a pair ![]() or
or ![]() as shown by Thiery et al. (2000). However, at very high frequencies (
as shown by Thiery et al. (2000). However, at very high frequencies (![]() ), some more parameters have to be fixed in order to avoid poor
convergence in the fits.
First, we have chosen to restrict ourselves to the extracted
), some more parameters have to be fixed in order to avoid poor
convergence in the fits.
First, we have chosen to restrict ourselves to the extracted
![]() parameters, as full-disc observations are much
less sensitive to
parameters, as full-disc observations are much
less sensitive to ![]() (see Fig. 4). The comparable
heights of the
(see Fig. 4). The comparable
heights of the ![]() and
and ![]() make this pair much more difficult
to fit. Then,
the strategy chosen here consisted of fixing
the frequency difference in
make this pair much more difficult
to fit. Then,
the strategy chosen here consisted of fixing
the frequency difference in ![]() pairs (leaving the
pairs (leaving the ![]() frequency to be fitted) in addition to fixing the relative height
(from estimates done in the part of the spectrum with good SNR)
of the
frequency to be fitted) in addition to fixing the relative height
(from estimates done in the part of the spectrum with good SNR)
of the ![]() mode compared to that of the nearby
mode compared to that of the nearby ![]() (which is
fitted).
(which is
fitted).
![\begin{figure}
\par\includegraphics[angle=90,width=7.6cm,clip]{1229_fig4.ps}\end{figure}](/articles/aa/full/2005/13/aa1229/Timg64.gif) |
Figure 4: Power spectrum at high frequencies from GOLF data, showing the overlapping pairs of modes. |
| Open with DEXTER | |
An additional way of improving the fitting is to use averaged power spectra. Instead of taking the power spectrum of the whole time series, one divides the series in N subsets, whose N spectra are averaged. It is the averaged spectrum that is then fitted. As the quantity of information is the same in both cases, no improvement should be expected in precision. Nevertheless, as the averaged spectrum has a reduced variance compared to the single (long) spectrum, and despite a poorer frequency resolution because of the shorter subsets, the fitting algorithm works better at high frequencies where the underlying shape of the peaks in the spectrum becomes then more evident. For this work, we averaged N = 20 spectra, each made from contiguous 40.25-d pieces. Uncertainties in the fitted parameters were computed according to Appourchaux (2003).
In order to check the reliability of the fitting, we performed a
"blind'' test using artificial data. The spectrum used is the main
Hare-and-Hounds set of the Fitting at Low Angular-degree Group
(FLAG)![]() . One
of us (WJC) generated the data for the fitter (FB) to analyse, with
the basic underlying mode parameters unknown to the latter. As shown
in Fig. 5, the output of the fitting procedure are in
very good agreement with the input of the simulation, except at very
high frequencies where a tendency to a slight underestimation is visible
(but generally smaller than the error bars). Even if extensive
simulations should be necessary to completely validate the fitting
procedure, we consider that this first test is significant.
. One
of us (WJC) generated the data for the fitter (FB) to analyse, with
the basic underlying mode parameters unknown to the latter. As shown
in Fig. 5, the output of the fitting procedure are in
very good agreement with the input of the simulation, except at very
high frequencies where a tendency to a slight underestimation is visible
(but generally smaller than the error bars). Even if extensive
simulations should be necessary to completely validate the fitting
procedure, we consider that this first test is significant.
![\begin{figure}
\par\includegraphics[angle=90,width=7.4cm,clip]{1229_fig5.ps}\end{figure}](/articles/aa/full/2005/13/aa1229/Timg66.gif) |
Figure 5: Comparison of the excitation rate computed from the fitting procedure applied to a simulated spectrum (solid line) and the input excitation rate used for the simulation (crosses). |
| Open with DEXTER | |
First, we compare the results for the acoustic rate of excitation of the modes, without any correction for the different observation heights in the solar atmosphere. The mode mass used was computed for an observation height of h=0 km. This height is certainly not suited for any of the three instruments, but allows a comparison of the raw results in order to check for a possible bias due to the fitting procedure. Corrected results are shown and discussed in Sect. 7.2.
One can see from Fig. 6 that the independent
measurements from the three helioseismic instruments coincide
reasonably well. The error bars used in Fig. 6 are
1![]() errors. The different measurements agree typically
to within 1 or 2
errors. The different measurements agree typically
to within 1 or 2![]() .
The agreement between the different
datasets is particularly convincing at low frequencies, except for an
almost constant difference: in the range 2-3 mHz, the GOLF rate is
systematically lower than that of BiSON (by about 20% on average),
whereas that of GONG is systematically higher (
.
The agreement between the different
datasets is particularly convincing at low frequencies, except for an
almost constant difference: in the range 2-3 mHz, the GOLF rate is
systematically lower than that of BiSON (by about 20% on average),
whereas that of GONG is systematically higher (![]() 15%). As
mentioned in Sect. 5, mode mass does not make an
important difference in this frequency range. The most likely origin
of this discrepancy is an inaccurate absolute calibration of the three
signals. However, we regard the level of agreement achieved as
more than satisfactory given the complexities and uncertainties
involved in the calibration.
15%). As
mentioned in Sect. 5, mode mass does not make an
important difference in this frequency range. The most likely origin
of this discrepancy is an inaccurate absolute calibration of the three
signals. However, we regard the level of agreement achieved as
more than satisfactory given the complexities and uncertainties
involved in the calibration.
At higher frequencies (
![]() mHz), it is the difficulty in
fitting the mode parameters (see Sect. 6) that is most
problematic. Moreover, the mode mass correction is no longer
negligible at these frequencies. However, despite a larger dispersion
of the results, the GOLF rates are seen to be sytematically higher
than those of BiSON, most of which are in turn higher than those of
GONG. This ordering is different from the one seen at low frequencies,
and in fact reflects that of the observation heights of the three
instruments. It is clearly necessary to correct for this effect.
mHz), it is the difficulty in
fitting the mode parameters (see Sect. 6) that is most
problematic. Moreover, the mode mass correction is no longer
negligible at these frequencies. However, despite a larger dispersion
of the results, the GOLF rates are seen to be sytematically higher
than those of BiSON, most of which are in turn higher than those of
GONG. This ordering is different from the one seen at low frequencies,
and in fact reflects that of the observation heights of the three
instruments. It is clearly necessary to correct for this effect.
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{1229_fig6.ps}\end{figure}](/articles/aa/full/2005/13/aa1229/Timg67.gif) |
Figure 6: Raw (no mass mode correction) acoustic rates for the three instruments. |
| Open with DEXTER | |
The mode masses for the correction applied here were computed using
the observation heights chosen in Sect. 5:
![]() 240 km,
240 km,
![]() km and
km and
![]() 340 km. As expected, the correction does not make a
large difference in the comparison of BiSON and GONG, as their
observation heights are similar. Also foreseeable was
the GOLF results were moved towards those of the other instruments, because of
its higher observation height. However, the GOLF results remain higher
than the others, particularly if one takes into account the apparent
underestimation at low frequencies, which is certainly due to the absolute
calibration as discussed in the next section.
340 km. As expected, the correction does not make a
large difference in the comparison of BiSON and GONG, as their
observation heights are similar. Also foreseeable was
the GOLF results were moved towards those of the other instruments, because of
its higher observation height. However, the GOLF results remain higher
than the others, particularly if one takes into account the apparent
underestimation at low frequencies, which is certainly due to the absolute
calibration as discussed in the next section.
Table 2:
Computed and measured (using GOLF data) parameters for ![]() modes,
including the mode mass correction for acoustic rates.
modes,
including the mode mass correction for acoustic rates.
A first general conclusion that can be drawn from this work is that
the excitation rate of solar p modes can be measured to relatively
good accuracy. We have measured it from three completely independent
datasets and found that the results were in agreement (without the need for
speculative corrections). The discrepancies are of the order of
1![]() (which corresponds to a mean relative error of 22% for GOLF
and 28% for BiSON and GONG) at low frequencies. These discrepancies can
reach a level of 2 or 3
(which corresponds to a mean relative error of 22% for GOLF
and 28% for BiSON and GONG) at low frequencies. These discrepancies can
reach a level of 2 or 3![]() at high frequencies, where the
analysis is particularly difficult.
at high frequencies, where the
analysis is particularly difficult.
The level of agreement achieved has been possible by using a careful
fitting of the data. The model fitted to the observations included an
asymmetry in the peaks, since we found that the use of a Lorentzian
profile yielded a small but systematic error. A strategy was
adopted at high frequencies, where in the fitting of the
![]() pairs we used a fixed frequency difference and a fixed amplitude
ratio. This gave robust fits despite the poor signal to noise ratio
(SNR) and the large width of the peaks. A comparison with simulated
data (the Hare-and-Hounds FLAG spectrum) validated this
approach. However, extensive simulations would be necessary to
estimate, for example, the influence of a poor SNR at high
frequencies.
pairs we used a fixed frequency difference and a fixed amplitude
ratio. This gave robust fits despite the poor signal to noise ratio
(SNR) and the large width of the peaks. A comparison with simulated
data (the Hare-and-Hounds FLAG spectrum) validated this
approach. However, extensive simulations would be necessary to
estimate, for example, the influence of a poor SNR at high
frequencies.
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{1229_fig7.ps}\end{figure}](/articles/aa/full/2005/13/aa1229/Timg71.gif) |
Figure 7: Mode mass corrected acoustic rates for the three instruments. |
| Open with DEXTER | |
The agreement between the results from the three sets allows us to put
constraints on the excitation rate.
The excitation rate can be conveniently expressed as a power law:
![]() (see for example
Goldreich et al. 1994). At low frequencies, the exponent
(see for example
Goldreich et al. 1994). At low frequencies, the exponent ![]() mainly represents the inertia dependence of the excitation. At high frequencies,
the excitation (and so the slope
mainly represents the inertia dependence of the excitation. At high frequencies,
the excitation (and so the slope ![]() )
is strongly dependent on
the adopted description of the turbulence.
The three sets considered here yield similar values of
)
is strongly dependent on
the adopted description of the turbulence.
The three sets considered here yield similar values of
![]() at low frequencies (1.8
at low frequencies (1.8
![]() mHz):
mHz):
![]() for GOLF;
for GOLF;
![]() for BiSON; and
for BiSON; and
![]() for
GONG. At higher frequencies (3.3 mHz
for
GONG. At higher frequencies (3.3 mHz
![]() mHz), the task is
more difficult. First, the raw data (Fig. 6) - which
have a positive, null and negative value for
mHz), the task is
more difficult. First, the raw data (Fig. 6) - which
have a positive, null and negative value for ![]() - show the
necessity of applying a mode mass correction to take account of the
height of observation in the solar atmosphere. After the correction
has been applied (Fig. 7), the three instruments yield
- show the
necessity of applying a mode mass correction to take account of the
height of observation in the solar atmosphere. After the correction
has been applied (Fig. 7), the three instruments yield
![]() values of:
values of:
![]() for GOLF;
for GOLF;
![]() for
BiSON; and
for
BiSON; and
![]() for GONG. This shows that the
mode mass correction brings the GOLF results closer to those of
BiSON and GONG.
for GONG. This shows that the
mode mass correction brings the GOLF results closer to those of
BiSON and GONG.
However, there is still some residual high-frequency discrepancy. This suggests that more work is needed, in particular: (i) on the determination of the observation heights; and (ii) on the influence of the SNR on the measurements at high frequencies. If the Na line used by GOLF were higher than expected in the solar atmosphere, the mode mass correction would be stronger and this might possibly make the GOLF results compatible with those of BiSON and GONG. Calculations based on the same hypothesis for radiative transfer in the solar atmosphere for the three atomic lines used are necessary to determine the three heights consistently. Moreover, these calculations must take into account the instrumental details in each case to allow an accurate determination. On the other hand, it must be noted that because of their lower-fill window functions, the SNR in the BiSON and GONG spectra is lower than for GOLF. The poor SNR in the Fourier spectra at high frequencies might bias the observed excitation rate. Extensive numerical simulations are needed to test the extent of this.
This work must be seen as a first step towards a better understanding of p-mode excitation and an improved description of convection in the outer layers of the Sun. The use of three different datasets shows that the estimation of the excitation rate is not trivial, as several instrument related effects must be taken into account. However, the results from the three instruments show that it is possible to provide reliable estimates. This is necessary to allow fruitful comparisons between models and observations and to obtain information on the excitation process (is it dominated by Reynolds stress or entropy fluctuation?) and on turbulent convection (for instance its dynamical properties such as the degree of correlation in the turbulent convection). This will be the aim of a following paper.
Acknowledgements
We would like to thank Frank Hill, John Leibacher, and Stuart Jefferies for helpful discussions, Yveline Lebreton for the computation of solar models, and Luca Bertello for providing the calibrated GOLF data. RS's work has been supported by Société de Secours des Amis des Sciences (Paris, France) and by Fundacão para a Ciência e a Tecnologia (Portugal) under grant SFRH/BPD/11663/2002. GOLF is the result of the cooperative endeavours of many individuals, to whom we are deeply indebted. SoHO is a mission of international cooperation between ESA and NASA. We thank all those who have been, or are currently, involved in the BiSON project. BiSON is funded by the UK Particle Physics and Astronomy Research Council (PPARC). This work utilizes data obtained by the Global Oscillation Network Group (GONG) Program, managed by the National Solar Observatory, which is operated by AURA, Inc. under a cooperative agreement with the National Science Foundation. The data were acquired by instruments operated by the Big Bear Solar Observatory, High Altitude Observatory, Learmonth Solar Observatory, Udaipur Solar Observatory, Instituto de Astrofísica de Canarias, and Cerro Tololo Interamerican Observatory.