A&A 432, 1151-1155 (2005)
DOI: 10.1051/0004-6361:20042351
K. M. Aggarwal1 - F. P. Keenan1 - S. J. Rose2
1 - Department of Pure and Applied Physics, The Queen's University of Belfast, Belfast BT7 1NN, Northern Ireland, UK
2 -
Department of Physics, Clarendon Laboratory, Parks Road, Oxford OX1 3PU, UK
Received 10 November 2004 / Accepted 29 November 2004
Abstract
Energy levels, radiative rates, collision strengths, and effective collision strengths for all transitions up to and including the n = 5 levels of Al XIII have been computed
in the jj coupling scheme including relativistic effects. All partial waves with angular momentum ![]() have been included, and resonances have been
resolved in a fine energy grid in the threshold region. Collision strengths are tabulated at energies above thresholds in the range
have been included, and resonances have been
resolved in a fine energy grid in the threshold region. Collision strengths are tabulated at energies above thresholds in the range
![]() Ryd, and results
for effective collision strengths, obtained after integrating the collision strengths over a Maxwellian distribution of electron velocities, are tabulated
over a wide temperature range of
Ryd, and results
for effective collision strengths, obtained after integrating the collision strengths over a Maxwellian distribution of electron velocities, are tabulated
over a wide temperature range of
![]() K. The importance of including relativistic effects in a calculation is discussed in comparison
with the earlier available non-relativistic results.
K. The importance of including relativistic effects in a calculation is discussed in comparison
with the earlier available non-relativistic results.
Key words: atomic data - atomic processes
The earlier available atomic data for Al XIII are from our own calculations (Aggarwal et al. 2001), which adopted the R-matrix program (Berrington et al. 1995) to compute
collision strengths (![]() ), and also
included resonances in threshold region to calculate effective collision strengths (
), and also
included resonances in threshold region to calculate effective collision strengths (![]() ). Results were reported for transitions among the
). Results were reported for transitions among the ![]() states, but the
major deficiency of those results is that the calculations were performed in the LS coupling scheme. As a result of this, desired atomic data for fine-structure transitions
are not available. Therefore, in the present work we are performing a fully relativistic calculation in order to report results for fine-structure transitions. Additionally, we
are availing the opportunity to report radiative rates, which are required in any modelling or diagnostic analysis and are not yet available in the literature. Furthermore,
overall improvements are made over the existing (non-relativistic) results by increasing the partial waves range from
states, but the
major deficiency of those results is that the calculations were performed in the LS coupling scheme. As a result of this, desired atomic data for fine-structure transitions
are not available. Therefore, in the present work we are performing a fully relativistic calculation in order to report results for fine-structure transitions. Additionally, we
are availing the opportunity to report radiative rates, which are required in any modelling or diagnostic analysis and are not yet available in the literature. Furthermore,
overall improvements are made over the existing (non-relativistic) results by increasing the partial waves range from ![]() to
to ![]() ,
energy range for
,
energy range for ![]() from 220 Ryd to 300 Ryd, and the temperature range for
from 220 Ryd to 300 Ryd, and the temperature range for ![]() from log
from log
![]() K to 6.8 K.
K to 6.8 K.
The 1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f, 5s, 5p, 5d, 5f and 5g configurations of Al XIII give rise to 25 fine-structure levels, listed in Table 1. To calculate energy levels
and radiative rates, we have used the
GRASP (General purpose Relativistic Atomic Structure Package) code of Dyall et al. (1989). In Table 1 we list the calculated
energies (with and without the inclusion of QED corrections) for these levels. Also included in this table are the experimental energies compiled by NIST
(http://www.physics.nist/gov/PhysRefData). The net effect of including the QED corrections is to lower the energies by ![]() 0.027 Ryd, in general. However, the
agreement between the theoretical and experimental level energies is excellent, both in magnitude and orderings.
0.027 Ryd, in general. However, the
agreement between the theoretical and experimental level energies is excellent, both in magnitude and orderings.
Table 1: Comparison between NIST and our present GRASP energy levels (in Ryd) for Al XIII.
The absorption oscillator strength (fij) and radiative rate Aji (in s-1) for an allowed transition ![]() are related by the following expression:
are related by the following expression:
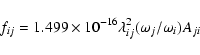 |
(1) |
For the computations of collision strengths ![]() ,
we have adopted the Dirac Atomic R-matrix Code (DARC) of Norrington & Grant (2005). This program
includes relativistic effects in a systematic way, in both the target description and the scattering model. It is based on the jj coupling scheme, and uses the
Dirac-Coulomb Hamiltonian in the R-matrix approach. In our calculations the R-matrix radius has been adopted to be 7.36 au, and 55 continuum orbitals have been included for each channel angular momentum for the expansion of the wavefunction. This allows us to compute
,
we have adopted the Dirac Atomic R-matrix Code (DARC) of Norrington & Grant (2005). This program
includes relativistic effects in a systematic way, in both the target description and the scattering model. It is based on the jj coupling scheme, and uses the
Dirac-Coulomb Hamiltonian in the R-matrix approach. In our calculations the R-matrix radius has been adopted to be 7.36 au, and 55 continuum orbitals have been included for each channel angular momentum for the expansion of the wavefunction. This allows us to compute ![]() up to an energy of
300 Ryd, which will easily permit us to calculate excitation rate coefficients up to a temperature of
up to an energy of
300 Ryd, which will easily permit us to calculate excitation rate coefficients up to a temperature of
![]() K, sufficient for applications to a wide variety of
plasmas. The maximum number of channels for a partial wave is 110, and the corresponding size of the Hamiltonian matrix is 6088. In order to obtain convergence of
K, sufficient for applications to a wide variety of
plasmas. The maximum number of channels for a partial wave is 110, and the corresponding size of the Hamiltonian matrix is 6088. In order to obtain convergence of
![]() for all transitions and at all energies, we have included all partial waves with angular momentum
for all transitions and at all energies, we have included all partial waves with angular momentum ![]() ,
although a higher range would have been
preferable for the convergence of "elastic'' transitions (see Fig. 1 above), which are allowed within the degenerate levels of a state.
,
although a higher range would have been
preferable for the convergence of "elastic'' transitions (see Fig. 1 above), which are allowed within the degenerate levels of a state.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{2351fig1.ps}
\end{figure}](/articles/aa/full/2005/12/aa2351/Timg23.gif) |
Figure 1:
Partial collision strengths for the 2s 2S1/2-2p 2P
|
| Open with DEXTER | |
In Figs. 1-3 we show the variation of ![]() with angular momentum J at four energies of 170, 200, 250 and 300 Ryd, and for three transitions, namely 2-4 (2s 2S1/2-2p 2P
with angular momentum J at four energies of 170, 200, 250 and 300 Ryd, and for three transitions, namely 2-4 (2s 2S1/2-2p 2P
![]() ), 3-7 (2p 2P
), 3-7 (2p 2P
![]() -3d 2D3/2) and 14-22 (4d 2D5/2-5d 2D5/2). The 2-4 is an "elastic'' transition, which
belongs to the degenerate levels of a state. Such transitions converge very slowly, as seen in Fig. 1, mainly because of their small threshold energies. However, 3-7 is an
allowed transition belonging
to different
-3d 2D3/2) and 14-22 (4d 2D5/2-5d 2D5/2). The 2-4 is an "elastic'' transition, which
belongs to the degenerate levels of a state. Such transitions converge very slowly, as seen in Fig. 1, mainly because of their small threshold energies. However, 3-7 is an
allowed transition belonging
to different ![]() levels, but
levels, but ![]() for this (and similar other transitions) have fully converged within the partial waves range of our calculations, at all energies.
Similarly, the convergence of
for this (and similar other transitions) have fully converged within the partial waves range of our calculations, at all energies.
Similarly, the convergence of ![]() with J is slow for some forbidden transitions, such as 14-22, as shown in Fig. 3. However, except for the "elastic'' transitions
discussed above, our values of
with J is slow for some forbidden transitions, such as 14-22, as shown in Fig. 3. However, except for the "elastic'' transitions
discussed above, our values of ![]() have converged for all other transitions, including the allowed ones, and at all energies.
have converged for all other transitions, including the allowed ones, and at all energies.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{2351fig2.ps}
\end{figure}](/articles/aa/full/2005/12/aa2351/Timg25.gif) |
Figure 2:
Partial collision strengths for the 2p 2P
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{2351fig3.ps}
\end{figure}](/articles/aa/full/2005/12/aa2351/Timg26.gif) |
Figure 3: Partial collision strengths for the 4d 2D5/2-5d 2D5/2 transition (14-22) in Al XIII at 4 electron energies of 170 Ryd (circles), 200 Ryd (triangles), 250 Ryd (stars), and 300 Ryd (squares). |
| Open with DEXTER | |
Our results of ![]() for "elastic'' transitions may be underestimated by (over) a factor of two, as can be seen by a comparison with the earlier results of Zygelman &
Dalgarno (1987) for the 2-3 and 2-4 transitions. Since the top-up according to the sum rules of Burgess & Tully (1992) results in the overestimation of the contribution of
higher neglected partial waves for a majority of allowed (and intercombination) transitions, such as 3-7 transition for which
for "elastic'' transitions may be underestimated by (over) a factor of two, as can be seen by a comparison with the earlier results of Zygelman &
Dalgarno (1987) for the 2-3 and 2-4 transitions. Since the top-up according to the sum rules of Burgess & Tully (1992) results in the overestimation of the contribution of
higher neglected partial waves for a majority of allowed (and intercombination) transitions, such as 3-7 transition for which ![]() has converged within the partial waves
range of the calculations as shown in Fig. 2, we have preferred not to apply their sum rule for the elastic transitions. Therefore,
our results for
has converged within the partial waves
range of the calculations as shown in Fig. 2, we have preferred not to apply their sum rule for the elastic transitions. Therefore,
our results for ![]() as well as
as well as ![]() (discussed below in Sect. 4) for "elastic'' transitions are based on the contribution of partial waves with
(discussed below in Sect. 4) for "elastic'' transitions are based on the contribution of partial waves with ![]() ,
and should be applied with caution.
,
and should be applied with caution.
In Table 3 we list our values of ![]() for all transitions at energies above thresholds. In this energy range the values of
for all transitions at energies above thresholds. In this energy range the values of ![]() vary (almost) smoothly, and
results at any energy in the
vary (almost) smoothly, and
results at any energy in the
![]() Ryd range can be easily interpolated. The only other results available in the literature with which to compare are
our earlier calculations (Aggarwal et al. 2001) performed in the LS coupling scheme. The present summed-up results for corresponding LS coupled transitions agree within
10% with our earlier
Ryd range can be easily interpolated. The only other results available in the literature with which to compare are
our earlier calculations (Aggarwal et al. 2001) performed in the LS coupling scheme. The present summed-up results for corresponding LS coupled transitions agree within
10% with our earlier ![]() values, for all transitions and at all energies. This is highly satisfactory, as expected.
values, for all transitions and at all energies. This is highly satisfactory, as expected.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{2351fig4.ps}
\end{figure}](/articles/aa/full/2005/12/aa2351/Timg27.gif) |
Figure 4: Collision strengths for the 1s 2S1/2-2s 2S1/2 transition (1-2) in Al XIII. |
| Open with DEXTER | |
Effective collision strengths ![]() are obtained after integrating
are obtained after integrating ![]() over a Maxwellian distribution of electron velocities, and are very simply related to the
excitation q(i,j) and de-excitation q(j,i) rate coefficients as shown in Eqs. (1)-(3) of our earlier paper (Aggarwal et al. 2001).
In order to account for resonances, we have performed our calculations of
over a Maxwellian distribution of electron velocities, and are very simply related to the
excitation q(i,j) and de-excitation q(j,i) rate coefficients as shown in Eqs. (1)-(3) of our earlier paper (Aggarwal et al. 2001).
In order to account for resonances, we have performed our calculations of ![]() in a fine energy mesh throughout the thresholds region. Close to thresholds (
in a fine energy mesh throughout the thresholds region. Close to thresholds (![]() 0.1 Ryd
above each threshold), the energy mesh is 0.001 Ryd, and is 0.002 Ryd in the remaining region. In total, values of
0.1 Ryd
above each threshold), the energy mesh is 0.001 Ryd, and is 0.002 Ryd in the remaining region. In total, values of ![]() have been computed at over 18 000 energies in the
thresholds region. This fine
energy mesh ensures to a large extent that neither a majority of resonances are omitted, nor a few comparatively large resonances have unreasonably large widths. In Figs. 4-6
we demonstrate our results of
have been computed at over 18 000 energies in the
thresholds region. This fine
energy mesh ensures to a large extent that neither a majority of resonances are omitted, nor a few comparatively large resonances have unreasonably large widths. In Figs. 4-6
we demonstrate our results of ![]() for only three transitions, namely 1-2 (1s 2S1/2-2s 2S1/2), 4-6 (2p 2P
for only three transitions, namely 1-2 (1s 2S1/2-2s 2S1/2), 4-6 (2p 2P
![]() -3s 2S1/2), and
9-11 (3d 2D5/2-4s 2S1/2). These transitions clearly illustrate the density and importance of resonances. It may also be noted here that
although 4-6 is an allowed transition, its resonance structure is quite significant, as seen in Fig. 5.
-3s 2S1/2), and
9-11 (3d 2D5/2-4s 2S1/2). These transitions clearly illustrate the density and importance of resonances. It may also be noted here that
although 4-6 is an allowed transition, its resonance structure is quite significant, as seen in Fig. 5.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{2351fig5.ps}
\end{figure}](/articles/aa/full/2005/12/aa2351/Timg28.gif) |
Figure 5:
Collision strengths for the 2p 2P
|
| Open with DEXTER | |
In Table 4 we list our results of ![]() for all transitions, over a wide temperature range of
for all transitions, over a wide temperature range of
![]() K, which is fully sufficient for applications
in laboratory and astrophysical plasmas, but if required, can be extrapolated up to
K, which is fully sufficient for applications
in laboratory and astrophysical plasmas, but if required, can be extrapolated up to
![]() K without much loss of accuracy.
The only other similar results available in the literature are from our earlier non-relativistic calculations (Aggarwal et al. 2001). For a majority of
transitions, the agreement between the two sets of calculations is within 10% at all temperatures. However, for four LS transitions (with their indices in bold faces),
namely 1-2 (1s 2S-2s 2S), 2-4 (2s 2S-3s 2S), 2-5 (2s 2S-3p 2P
K without much loss of accuracy.
The only other similar results available in the literature are from our earlier non-relativistic calculations (Aggarwal et al. 2001). For a majority of
transitions, the agreement between the two sets of calculations is within 10% at all temperatures. However, for four LS transitions (with their indices in bold faces),
namely 1-2 (1s 2S-2s 2S), 2-4 (2s 2S-3s 2S), 2-5 (2s 2S-3p 2P![]() ), and 6-8 (3d 2D-4p 2P
), and 6-8 (3d 2D-4p 2P![]() ), the present
results are higher by up to
), the present
results are higher by up to ![]() 20% towards the lower end of the temperature range, whereas for the 3-7 (2p 2P
20% towards the lower end of the temperature range, whereas for the 3-7 (2p 2P![]() -4s 2S) transition the discrepancy is
up to 50%. We show the comparison
between the two calculations in Fig. 7 for three transitions, namely 1-2 (1s 2S-2s 2S), 2-4 (2s 2S-3s 2S), and 6-8
(3d 2D-4p 2P
-4s 2S) transition the discrepancy is
up to 50%. We show the comparison
between the two calculations in Fig. 7 for three transitions, namely 1-2 (1s 2S-2s 2S), 2-4 (2s 2S-3s 2S), and 6-8
(3d 2D-4p 2P![]() ). As seen in this figure, the differences between the two calculations are only at lower temperatures, and disappear with increasing
temperature. The differences at lower temperatures are clearly due to the presence (or absence) of resonances in the thresholds region, as the agreement between the two
sets of
). As seen in this figure, the differences between the two calculations are only at lower temperatures, and disappear with increasing
temperature. The differences at lower temperatures are clearly due to the presence (or absence) of resonances in the thresholds region, as the agreement between the two
sets of ![]() at energies above thresholds is highly satisfactory, as discussed in Sect. 3. Furthermore, a fresh look at Fig. 4 makes these differences clearly
understandable. The present Fig. 4 for the 1-2 transition has more (and denser) resonances in comparison to those in Fig. 5 of Aggarwal et al. (2001) for the same transition.
The energy mesh in the present work is finer (
at energies above thresholds is highly satisfactory, as discussed in Sect. 3. Furthermore, a fresh look at Fig. 4 makes these differences clearly
understandable. The present Fig. 4 for the 1-2 transition has more (and denser) resonances in comparison to those in Fig. 5 of Aggarwal et al. (2001) for the same transition.
The energy mesh in the present work is finer (![]() 0.002 Ryd) in comparison to
0.002 Ryd) in comparison to ![]() 0.014 Ryd adopted in our earlier work. In our earlier work, resonances were
resolved at
0.014 Ryd adopted in our earlier work. In our earlier work, resonances were
resolved at ![]() 3800 energies in comparison to over 18 000 energies in the present calculations, in the same energy range. However, test calculations with coarser mesh show
that it has a negligible effect on the determined values of
3800 energies in comparison to over 18 000 energies in the present calculations, in the same energy range. However, test calculations with coarser mesh show
that it has a negligible effect on the determined values of ![]() ,
because energy mesh near thresholds is comparable in both calculations, and only differ at energies
well above the thresholds. The major differences between the two calculations arise because of
the inclusion of fine-structure in the definition of channel coupling, i.e. adoption of the jj coupling scheme, which gives rise to additional resonances. The effect of
these additional resonances (in the present calculations) is more apparent for three other transitions, which we discuss below.
,
because energy mesh near thresholds is comparable in both calculations, and only differ at energies
well above the thresholds. The major differences between the two calculations arise because of
the inclusion of fine-structure in the definition of channel coupling, i.e. adoption of the jj coupling scheme, which gives rise to additional resonances. The effect of
these additional resonances (in the present calculations) is more apparent for three other transitions, which we discuss below.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{2351fig6.ps}
\end{figure}](/articles/aa/full/2005/12/aa2351/Timg31.gif) |
Figure 6: Collision strengths for the 3d 2D5/2-4s 2S1/2 transition (9-11) in Al XIII. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{2351fig7.ps}
\end{figure}](/articles/aa/full/2005/12/aa2351/Timg32.gif) |
Figure 7:
Comparison between present (continuous curve) and earlier (Aggarwal et al. 2001) effective collision strengths for the 1s 2S-2s 2S ( 1-2:
stars and the lowest curve),
2s 2S-3s 2S ( 2-4: squares and the middle curve), and 3d 2D-4p 2P |
| Open with DEXTER | |
For three transitions, namely 3-4 (2p 2P![]() -3s 2S), 5-7 (3p 2P
-3s 2S), 5-7 (3p 2P![]() -4s 2S) and 6-7 (3d 2D-4s 2S), differences between
our present and earlier (Aggarwal et al. 2001)
results of
-4s 2S) and 6-7 (3d 2D-4s 2S), differences between
our present and earlier (Aggarwal et al. 2001)
results of ![]() are up to a factor of three as shown in Fig. 8. At lower temperatures the present results are invariably higher, and merge with the earlier results with
increasing temperature. Since the discrepancy is highest for the 3-4 transition, we discuss this transition in further detail to understand the differences.
A closer look at Fig. 5 for the 4-6 (2p 2P
are up to a factor of three as shown in Fig. 8. At lower temperatures the present results are invariably higher, and merge with the earlier results with
increasing temperature. Since the discrepancy is highest for the 3-4 transition, we discuss this transition in further detail to understand the differences.
A closer look at Fig. 5 for the 4-6 (2p 2P
![]() -3s 2S1/2)
transition clearly shows that resonances are denser (and some of them are higher in magnitude as well), in comparison to those shown in Fig. 9a of Aggarwal et al. (2001) for
the corresponding LStransition. Additionally, very close to the threshold there are a few narrow resonances, which were not there in the earlier work. As a result of these, the present results of
-3s 2S1/2)
transition clearly shows that resonances are denser (and some of them are higher in magnitude as well), in comparison to those shown in Fig. 9a of Aggarwal et al. (2001) for
the corresponding LStransition. Additionally, very close to the threshold there are a few narrow resonances, which were not there in the earlier work. As a result of these, the present results of
![]() are considerably higher towards the lower end of the temperature range. In fact the same conclusion applies to the 5-7 and 6-7 transitions, as can be
seen in Fig. 6 for the 9-11 (3d 2D5/2-4s 2S1/2) transition, which is a part of the 6-7 transition in LS coupling. However, to confirm the effect of
these (few) near threshold resonances, we have performed an exercise by re-calculating values of
are considerably higher towards the lower end of the temperature range. In fact the same conclusion applies to the 5-7 and 6-7 transitions, as can be
seen in Fig. 6 for the 9-11 (3d 2D5/2-4s 2S1/2) transition, which is a part of the 6-7 transition in LS coupling. However, to confirm the effect of
these (few) near threshold resonances, we have performed an exercise by re-calculating values of ![]() without them. The results so obtained are also shown in Fig. 8
as broken lines. As expected, the agreement between the two calculations is excellent (within 5%) at all temperatures. Therefore, inclusion of additional resonances
(arising from the redistribution of levels ordering as shown in Table 1) has affected the values of
without them. The results so obtained are also shown in Fig. 8
as broken lines. As expected, the agreement between the two calculations is excellent (within 5%) at all temperatures. Therefore, inclusion of additional resonances
(arising from the redistribution of levels ordering as shown in Table 1) has affected the values of ![]() for a few transitions, particularly at lower temperatures.
This is a very interesting conclusion, as it emphasizes the importance of relativistic effects in a calculation for a comparatively light ion, such as Al XIII.
for a few transitions, particularly at lower temperatures.
This is a very interesting conclusion, as it emphasizes the importance of relativistic effects in a calculation for a comparatively light ion, such as Al XIII.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{2351fig8.ps}
\end{figure}](/articles/aa/full/2005/12/aa2351/Timg33.gif) |
Figure 8:
Comparison between present (continuous curve) and earlier (Aggarwal et al. 2001) effective collision strengths for the 2p 2P |
| Open with DEXTER | |
In this paper we have reported results for energy levels, radiative rates, collision strengths and effective collision strengths for transitions in Al XIII. Apart from the
inclusion of relativistic effects to calculate our results for fine-structure transitions, a few other improvements have been made over our earlier (non-relativistic) results
(Aggarwal et al. 2001), which are: (i) the partial waves range has been increased from 45 to 60, which improves the convergence of ![]() for allowed transitions, particularly
at higher energies; (ii) the energy range has been increased from 220 to 300 Ryd, which enabled us to increase the temperature range of
for allowed transitions, particularly
at higher energies; (ii) the energy range has been increased from 220 to 300 Ryd, which enabled us to increase the temperature range of ![]() from
from
![]() K to
K to
![]() K; and (iii) the energy mesh is finer in the thresholds region from
K; and (iii) the energy mesh is finer in the thresholds region from ![]() 0.014 Ryd to
0.014 Ryd to ![]() 0.002 Ryd, which has improved the accuracy of
0.002 Ryd, which has improved the accuracy of ![]() results,
particularly at lower temperatures. Additionally, radiative rates have been reported for transitions among the
results,
particularly at lower temperatures. Additionally, radiative rates have been reported for transitions among the ![]() levels of Al XIII, which were not available earlier.
levels of Al XIII, which were not available earlier.
Since our earlier non-relativistic calculations for Al XIII are already available in the literature (Aggarwal et al. 2001), two definite conclusions can be drawn from
the comparison with present
relativistic results. Firstly, relativistic effects are very important, because inclusion of fine-structure in the definition of channel coupling gives rise to additional
resonances, and hence increases the value of ![]() by up to a factor of three, for some of the transitions, particularly at lower temperatures. Secondly, in a
non-relativistic calculation, results for
by up to a factor of three, for some of the transitions, particularly at lower temperatures. Secondly, in a
non-relativistic calculation, results for ![]() and
and ![]() for fine-structure transitions can be derived from the corresponding LS transition, if one of the levels
is non-degenerate, such as 2S and 1D, because of the following statistical relationship:
for fine-structure transitions can be derived from the corresponding LS transition, if one of the levels
is non-degenerate, such as 2S and 1D, because of the following statistical relationship:
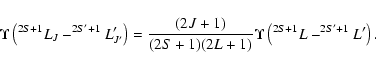 |
(2) |
Finally, the atomic data reported in this paper are probably the best available to date, and we hope the present set of results will be highly useful for diagnostic and
modelling applications. The accuracy of our energy levels and radiative rates are assessed to be better than 1% and 5%, respectively, whereas the corresponding results for
![]() and
and ![]() could easily vary by up to 20% at higher energies and lower temperatures, respectively. Furthermore, our
could easily vary by up to 20% at higher energies and lower temperatures, respectively. Furthermore, our ![]() results for transitions involving
the n = 5 levels may be comparatively less accurate, particularly at lower temperatures, because resonances arising from the
results for transitions involving
the n = 5 levels may be comparatively less accurate, particularly at lower temperatures, because resonances arising from the ![]() levels have not been included
in the present work.
levels have not been included
in the present work.
Acknowledgements
The work reported in this paper has been financed by the EPSRC and PPARC of the United Kingdom. We wish to thank Dr. Patrick Norrington for providing his code prior to publication. FPK and SJR (British Crown Copyright 2004/MoD) are grateful to AWE Aldermaston for the award of William Penney Fellowships. Finally, we thank an anonymous Referee for his useful comments and suggestions.