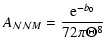A&A 432, 783-795 (2005)
DOI: 10.1051/0004-6361:20041923
Galaxy-galaxy-galaxy lensing: Third-order correlations between
the galaxy and mass distributions in the Universe
P. Schneider -
P. Watts
Institut f. Astrophysik u. Extr. Forschung, Universität Bonn,
Auf dem Hügel 71, 53121 Bonn, Germany
Received 30 August 2004 / Accepted 21 October 2004
Abstract
Galaxy-galaxy lensing (GGL) measures the 2-point cross-correlation between
galaxies and mass in the Universe. In this work we seek to generalise this
effect by considering the third-order correlations between galaxies and mass:
galaxy-galaxy-galaxy lensing. Third-order correlations in the cosmic shear
field have recently been reported in the VIRMOS-DESCART and CTIO surveys.
Such data should also be
ideal for measuring galaxy-galaxy-galaxy lensing. Indeed, the
effects of these higher-order correlations may have already been detected
in recent studies of galaxy-galaxy lensing. Higher-order cross-correlation
functions contain invaluable information about the relationship between
galaxies and their mass environments that GGL studies alone cannot detect.
In this paper we lay out the basic relations for third-order cross
correlations and their projections and introduce a new set of scale
dependent third-order bias parameters. We define three new observables: two
galaxy-shear-shear correlation functions, 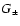 ,
and a
galaxy-galaxy-shear correlation,
,
and a
galaxy-galaxy-shear correlation, 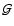 .
We relate these to the
various projected cross-bispectra and give practical estimators for their
measurement. We note that the observational signature of these
correlators is simply the excess shear-shear correlation measured about
foreground galaxies (for
.
We relate these to the
various projected cross-bispectra and give practical estimators for their
measurement. We note that the observational signature of these
correlators is simply the excess shear-shear correlation measured about
foreground galaxies (for 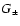 )
and the average tangential shear around
foreground galaxy pairs (for
)
and the average tangential shear around
foreground galaxy pairs (for 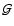 ). These quantities are no more than
second order in the shear and so should be more easily measurable than the
shear 3-point correlation. Finally we derive expressions for the third
order aperture mass statistics in terms of both the cross-bispectra and
the real-space correlation functions. Such statistics provide a very
localized measurement of the bispectra, thus encapsulating
essentially all of the available third-order information, while remaining
easily obtainable from observations of 3-point cross-correlation
functions. In addition we find that utilising aperture statistics has the
further benefit that they measure only the connected part of the third
order correlation.
). These quantities are no more than
second order in the shear and so should be more easily measurable than the
shear 3-point correlation. Finally we derive expressions for the third
order aperture mass statistics in terms of both the cross-bispectra and
the real-space correlation functions. Such statistics provide a very
localized measurement of the bispectra, thus encapsulating
essentially all of the available third-order information, while remaining
easily obtainable from observations of 3-point cross-correlation
functions. In addition we find that utilising aperture statistics has the
further benefit that they measure only the connected part of the third
order correlation.
Key words: gravitational lensing - cosmology: large-scale
structure of the Universe - galaxies: evolution -
galaxies: statistics
1 Introduction
Gravitational lensing offers the possibility of studying the statistical
properties of the mass distribution in the Universe without referring
to the relation between the mass and the luminous tracers, like
galaxies. The weak lensing effect (see Mellier 1999; Bartelmann &
Schneider 2001, hereafter BS01; Refregier 2003; van Waerbeke &
Mellier 2003, for recent reviews)
of the large-scale structure, called
cosmic shear (see, e.g., Blandford et al. 1991; Miralda-Escudé
1991; Kaiser 1992; Jain & Seljak 1997), has been detected by a number
of groups (e.g. van Waerbeke et al. 2000, 2001, 2002; Bacon et al. 2000; Kaiser et al. 2000;
Wittman et al. 2000; Maoli et al. 2001; Refregier et al. 2002; Hämmerle et al. 2002; Brown et al. 2003; Jarvis et al. 2003). Most of these cosmic shear measurements have concentrated on
second-order shear statistics, but quite recently, third-order cosmic shear
measurements have been reported as well (Bernardeau et al. 2002;
Pen et al. 2003; Jarvis et al. 2004).
Weak lensing can also be used for measuring the relation between mass
and galaxies. The measurement of this galaxy-galaxy lensing (GGL) was first
attempted by Tyson et al. (1984), and its first detection was
published by Brainerd et al. (1996). Since then, quite a number of
GGL measurements have been reported, in the HST Medium
Deep Survey (Griffiths et al. 1996), the Hubble Deep Field
(Dell'Antonio & Tyson 1998; Hudson et al. 1998), and more recently,
in the RCS survey by Hoekstra et al. (2001, 2002), the COMBO-17 survey
(Kleinheinrich et al. 2004) and the Sloan Digital Sky Survey (Fischer et al. 2000; McKay et al. 2001; Guzik & Seljak 2002; Sheldon et
al. 2004; Seljak et al. 2004). GGL measures the two-point
correlation function (2PCF) between galaxy positions and shear.
On small scales, GGL measures the lensing effect of the dark halo in
which the luminous galaxy is embedded. It therefore provides a probe of
the density profile of galaxy halos which can be compared to the
predictions of the CDM model. In particular, the properties of dark
matter halos, such as virial mass and concentration, can be studied as
a function of galaxy type (early vs. late), environment (e.g., have
the halos of galaxies in groups and clusters been stripped by the
tidal interactions), and redshift. On scales larger than
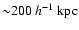 ,
the GGL signal is no longer dominated by the halo
of galaxies, but receives a substantial contribution from the matter in
which galaxies are embedded, namely groups and clusters. From this
signal, one learns about the environments of galaxies. For example,
the density-morphology relation can be traced back directly to the
underlying mass density, instead to the galaxy number density.
,
the GGL signal is no longer dominated by the halo
of galaxies, but receives a substantial contribution from the matter in
which galaxies are embedded, namely groups and clusters. From this
signal, one learns about the environments of galaxies. For example,
the density-morphology relation can be traced back directly to the
underlying mass density, instead to the galaxy number density.
Schneider (1998) pointed out that the correlation between galaxy
positions and shear provides a direct measure of the bias factor of
galaxies; in particular, the scale dependence of the bias factor can
be probed directly (van Waerbeke 1998). Indeed, on scales
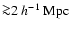 ,
GGL measures a combination of the galaxy-mass
correlation coefficient r and the bias factor b. These two functions
can be obtained individually when the GGL signal is combined with the
cosmic shear signal, as shown by Hoekstra et al. (2002). In fact,
Hoekstra et al. (2002) have measured rand b as a function of scale. Future measurements of
these quantities as a function of scale, redshift and galaxy type,
using the upcoming wide-field imaging surveys, will provide invaluable
input for the interpretation of galaxy redshift samples. In addition,
b and r are functions which depend on the formation and evolution
of galaxies; they can therefore be used as constraints for those
models.
,
GGL measures a combination of the galaxy-mass
correlation coefficient r and the bias factor b. These two functions
can be obtained individually when the GGL signal is combined with the
cosmic shear signal, as shown by Hoekstra et al. (2002). In fact,
Hoekstra et al. (2002) have measured rand b as a function of scale. Future measurements of
these quantities as a function of scale, redshift and galaxy type,
using the upcoming wide-field imaging surveys, will provide invaluable
input for the interpretation of galaxy redshift samples. In addition,
b and r are functions which depend on the formation and evolution
of galaxies; they can therefore be used as constraints for those
models.
As already mentioned, a non-vanishing cosmic shear three-point
correlation function (3PCF) has been detected, and future
surveys will measure it with great precision. These surveys will
certainly also measure higher-order correlations between galaxies
and matter, generalizing the GGL measurements. Although the
detailed physical interpretation of such higher-order cross
correlations remains to be investigated, it is obvious that they
contain valuable
information concerning the relationship between galaxies and their
mass environments beyond that which is measurable in GGL. In
the language of the halo occupation distribution (Berlind &
Weinberg 2002), one can think of these higher-order functions as
probing the moments of an occupation probability P(N|M) that a
halo of virial mass M contains N galaxies of a particular
type. Such information is of crucial importance since it places
powerful constraints upon models of galaxy formation.
We save the detailed interpretation of higher-order cross
correlations for a forthcoming paper, where we explore such themes
in the context of the halo model. In this work we lay out the
basic relations for the third-order galaxy-mass correlations.
After introducing the projected mass and galaxy number densities
in Sect. 2, we define the third-order bias factor and two
third-order correlation coefficients in Sect. 3. The relation
between the projected bispectra and the three-dimensional
bispectra is given in Sect. 4. Practical estimators for the
galaxy-galaxy-shear and the galaxy-shear-shear correlation
functions are provided in Sect. 5. We will argue that these
third-order galaxy-mass correlations have already been measured
and published. In Sect. 6, the relation between the correlation
functions and the cross-bispectra are derived, and a consistency
relation for the two galaxy-shear-shear 3PCFs is obtained that should
be satisfied provided the shear is a pure E-mode field.
In Sect. 7 we define aperture measures of the
projected matter and galaxy densities and consider their
third-order statistics; in particular, on the one
hand they are related to the projected bispectra, on the other hand,
they can be
directly calculated from the respective correlation functions. We
discuss our results in Sect. 8.
Ménard et al. (2003) have considered a different approach to measure
third-order correlations between the mass and the galaxy distribution,
employing the magnification bias of background galaxies. Generalizing an
effect that has been observed at the two-point statistical level, where
correlations between high-redshift QSOs and low redshift galaxies are observed
and which are interpreted as being due to the magnification caused by the
large-scale matter distribution of which the foreground galaxies are biased
tracers (see Dolag & Bartelmann 1997; Bartelmann & Schneider 2001, and
references therein), Ménard et al. (2003) considered the excess of distant QSOs around pairs of foreground
galaxies. For linear deterministic bias of the galaxy distribution, the ratio
of this third-order statistics and the square of the QSO-galaxy correlation
function becomes essentially independent of the bias, as well as of the shape
and amplitude of the power spectrum of density fluctuations. This result is
very similar to the corresponding ratio of third-order cosmic shear statistics
and the square of the shear dispersion (Bernardeau et al. 1997; Schneider et
al. 1998; van Waerbeke et al. 1999).
2 Projection of density and galaxies
The gravitational lensing effect of the inhomogeneous matter distribution in
the Universe is described in terms of an equivalent surface mass density
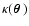 ,
which is obtained by projecting the three-dimensional
density contrast,
,
which is obtained by projecting the three-dimensional
density contrast, 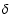 ,
of the matter along the line-of-sight (see
BS01, and references therein). If we
consider sources at comoving distance w, this surface mass density is given by
,
of the matter along the line-of-sight (see
BS01, and references therein). If we
consider sources at comoving distance w, this surface mass density is given by
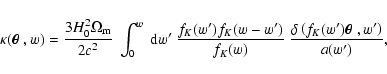 |
(1) |
where fK(w) is the comoving angular-diameter distance corresponding
to comoving distance
w, fK(w)=w for flat Universes,
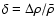 is the
relative density contrast of matter, H0 is the Hubble constant, c the
velocity of light,
a(w)=1/(1+z) is the cosmic scale factor, normalized to
unity today, and
is the
relative density contrast of matter, H0 is the Hubble constant, c the
velocity of light,
a(w)=1/(1+z) is the cosmic scale factor, normalized to
unity today, and
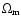 is the density parameter in matter.
For a redshift distribution of ("background'') sources with probability density
is the density parameter in matter.
For a redshift distribution of ("background'') sources with probability density
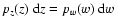 ,
the effective surface mass density becomes
,
the effective surface mass density becomes
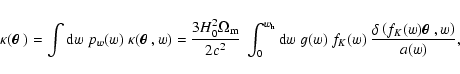 |
(2) |
with
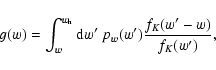 |
(3) |
which is the source-redshift weighted lens efficiency factor
 for a
density fluctuation at distance w. The quantity
for a
density fluctuation at distance w. The quantity
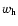 is the comoving horizon distance, obtained from w(a) by letting
is the comoving horizon distance, obtained from w(a) by letting
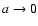 .
The shear, i.e. the projected tidal gravitational field which can be
measured as the expectation value of image ellipticities of the galaxy
population, is obtained from the projected surface mass density
.
The shear, i.e. the projected tidal gravitational field which can be
measured as the expectation value of image ellipticities of the galaxy
population, is obtained from the projected surface mass density 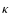 in
the usual way: one defines the deflection potential
in
the usual way: one defines the deflection potential
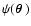 which
satisfies the two-dimensional Poisson equation
which
satisfies the two-dimensional Poisson equation
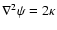 ,
in
terms of which the Cartesian components of the shear read
,
in
terms of which the Cartesian components of the shear read
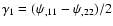 ,
,
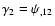 ,
where indices
separated by a comma denote partial derivatives.
,
where indices
separated by a comma denote partial derivatives.
In analogy to the matter density contrast 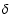 ,
we define the number
density contrast
,
we define the number
density contrast
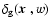 of galaxies as
of galaxies as
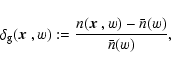 |
(4) |
where
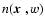 is the number density of galaxies at comoving position
is the number density of galaxies at comoving position
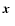 and comoving distance w (the latter providing a parameterization of cosmic
time), and
and comoving distance w (the latter providing a parameterization of cosmic
time), and 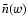 is the mean number density of galaxies at that
epoch. Since the galaxy distribution is discrete, the true number density is
simply a sum of delta-functions. What is meant by n is that the probability
of finding a galaxy in the volume
is the mean number density of galaxies at that
epoch. Since the galaxy distribution is discrete, the true number density is
simply a sum of delta-functions. What is meant by n is that the probability
of finding a galaxy in the volume 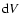 situated
at position
situated
at position
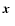 is
is
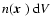 .
We consider now a population
of ("foreground'') galaxies with spatial number density
.
We consider now a population
of ("foreground'') galaxies with spatial number density
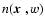 .
The number density of these galaxies on the sky at
.
The number density of these galaxies on the sky at
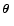 is then
is then
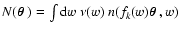 ,
where
,
where 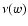 is the
redshift-dependent selection function, describing what fraction of the
galaxies at comoving distance w is included in the sample.
The selection function
is the
redshift-dependent selection function, describing what fraction of the
galaxies at comoving distance w is included in the sample.
The selection function 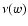 can differ between different types of
foreground galaxies and thus depends on the sample selection.
The mean number
density of these galaxies on the sky is
can differ between different types of
foreground galaxies and thus depends on the sample selection.
The mean number
density of these galaxies on the sky is
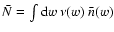 ;
the redshift distribution of these
galaxies, or more precisely, their distribution in comoving distance therefore
is
;
the redshift distribution of these
galaxies, or more precisely, their distribution in comoving distance therefore
is
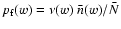 ,
thus relating the
selection function
,
thus relating the
selection function 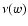 to the redshift distribution. Using the
definition (4), one then finds for the number density of
galaxies
to the redshift distribution. Using the
definition (4), one then finds for the number density of
galaxies
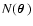 on the sky and their fractional number density contrast
on the sky and their fractional number density contrast
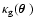 ,
,
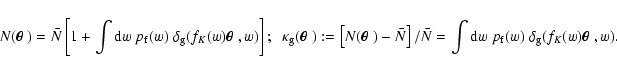 |
(5) |
3 Definition of bias and correlation coefficients
3.1 Second-order statistics
In its simplest form, the relation between the density contrast
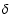 and the fractional number density contrast
and the fractional number density contrast
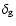 of galaxies is described by the bias factor b, in the form
of galaxies is described by the bias factor b, in the form
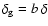 .
This picture of linear deterministic
biasing is most likely too simple a description for the galaxy
distribution, at least on small spatial scales where the density
field is non-linear. Instead, one defines the bias parameter in
terms of the power spectra of the galaxy and matter distribution.
Let
.
This picture of linear deterministic
biasing is most likely too simple a description for the galaxy
distribution, at least on small spatial scales where the density
field is non-linear. Instead, one defines the bias parameter in
terms of the power spectra of the galaxy and matter distribution.
Let
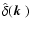 and
and
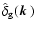 be the
Fourier transforms of the density and galaxy contrast,
respectively; their power spectra
be the
Fourier transforms of the density and galaxy contrast,
respectively; their power spectra
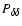 and
and
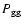 are defined by the correlators
are defined by the correlators
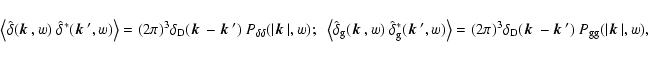 |
(6) |
where
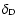 denotes Dirac's delta-"function'', and we have
allowed for an evolution of the power spectra with redshift or
comoving distance w. The occurrence of the delta function is due
to the assumed statistical homogeneity of the random matter and
galaxy fields, and the fact that the power spectra depends only on
the modulus of
denotes Dirac's delta-"function'', and we have
allowed for an evolution of the power spectra with redshift or
comoving distance w. The occurrence of the delta function is due
to the assumed statistical homogeneity of the random matter and
galaxy fields, and the fact that the power spectra depends only on
the modulus of
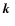 is due to their statistical isotropy. The
bias parameter b(k,w) is defined by the ratio of these two power
spectra,
is due to their statistical isotropy. The
bias parameter b(k,w) is defined by the ratio of these two power
spectra,
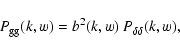 |
(7) |
which agrees with the previous definition in the case of linear
deterministic biasing, but is far more general. In particular, we
allow for a scale- and redshift dependence of b. Next, we define
the cross-power spectrum
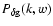 through
through
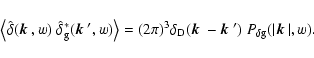 |
(8) |
The cross-power spectrum is related to
the power spectrum of the matter density by
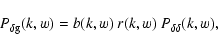 |
(9) |
where we have defined the galaxy-mass correlation coefficient
r(k,w), which can also depend on scale and redshift. In the case
of linear deterministic biasing, 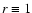 .
.
3.2 Third-order statistics
We now generalize the foregoing definitions to third-order statistics. The
bispectra of the matter and galaxy distributions
are defined through the
triple correlators
| |
|
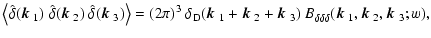 |
|
| |
|
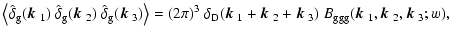 |
(10) |
where the delta function ensures that these triple correlators
vanish unless the three
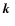 -vectors form a closed triangle -
this property again follows from the statistical homogeneity of
the density fields. Furthermore, statistical isotropy causes the
bispectrum to depend only on the length of two of its
-vectors form a closed triangle -
this property again follows from the statistical homogeneity of
the density fields. Furthermore, statistical isotropy causes the
bispectrum to depend only on the length of two of its
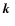 -vectors and the angle they enclose. Finally, parity invariance
of the density fields requires that the bispectra are even
functions of this angle. In a similar spirit to Eq. (8) we can define the cross-bispectra
-vectors and the angle they enclose. Finally, parity invariance
of the density fields requires that the bispectra are even
functions of this angle. In a similar spirit to Eq. (8) we can define the cross-bispectra
| |
|
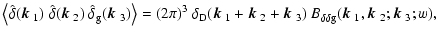 |
|
| |
|
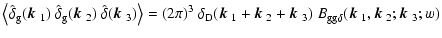 |
(11) |
where we have introduced the notation
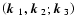 to indicate the symmetry with respect to
interchanging the first two arguments, meaning, e.g., that
to indicate the symmetry with respect to
interchanging the first two arguments, meaning, e.g., that
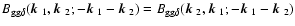
.
In the case of linear deterministic biasing, the various bispectra
would be related through simple relations, e.g.,
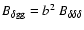 .
However, in the more general
(and realistic) case, these relations are more complex. We define
the third-order bias parameter b3 and the two galaxy-mass
correlation coefficients r1 and r2 through the relations
.
However, in the more general
(and realistic) case, these relations are more complex. We define
the third-order bias parameter b3 and the two galaxy-mass
correlation coefficients r1 and r2 through the relations
The bias and correlation coefficients satisfy the same symmetries as
those of the bispectra. In the case of linear deterministic biasing,
b3=b and r1=1=r2. These higher-order biasing and correlation
parameters depend on the formation and evolution of galaxies and their
relation to the underlying density field; in general, they encapsulate
information concerning the non-Gaussian nature of the bias. As we show
in the next section, the correlation of lensing shear with the
positions of galaxies on the sky provides a direct means for measuring
(integrals of) these higher-order functions.
4 Projected power- and bispectra
The lensing effect and the position of galaxies on the sky are both described
by projections of the density field  and the galaxy field
and the galaxy field
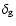 along the line-of-sight, as shown in Sect.2. The
projected fields share the properties of the three-dimensional distributions
as being homogeneous and isotropic random fields; hence, their second- and
third-order properties can as well be described by power and bispectra.
The relation between the power spectra of projected quantities to that of the
three-dimensional distribution is given by Limber's equation in Fourier space,
as has been derived by Kaiser (1992): Let
along the line-of-sight, as shown in Sect.2. The
projected fields share the properties of the three-dimensional distributions
as being homogeneous and isotropic random fields; hence, their second- and
third-order properties can as well be described by power and bispectra.
The relation between the power spectra of projected quantities to that of the
three-dimensional distribution is given by Limber's equation in Fourier space,
as has been derived by Kaiser (1992): Let
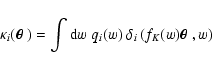 |
(14) |
be projections of the 3D fields 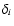 ,
where the qi(w) are weight
functions depending on the comoving distance. Provided these weight functions
do not vary appreciably over comoving scales on which the power spectrum is
significantly different from zero, the (cross) power spectrum reads
,
where the qi(w) are weight
functions depending on the comoving distance. Provided these weight functions
do not vary appreciably over comoving scales on which the power spectrum is
significantly different from zero, the (cross) power spectrum reads
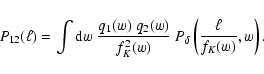 |
(15) |
Hence, the 2D power at
angular scale 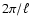 is obtained from the 3D power at
length scale
is obtained from the 3D power at
length scale
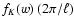 ,
integrated over w.
For the power spectra of the projected mass density
,
integrated over w.
For the power spectra of the projected mass density 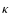 and the galaxies
and the galaxies
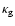 ,
and the cross-power of these two quantities, we therefore
find, by comparing Eqs. (14) and (15) with
Eqs. (2) and (5),
,
and the cross-power of these two quantities, we therefore
find, by comparing Eqs. (14) and (15) with
Eqs. (2) and (5),
where
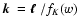 and where we have used the
definition of the bias and galaxy-mass parameters given in
Sect. 3.1. The quantity
and where we have used the
definition of the bias and galaxy-mass parameters given in
Sect. 3.1. The quantity
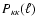 is
the power spectrum probed by second-order cosmic shear
measurements whereas
is
the power spectrum probed by second-order cosmic shear
measurements whereas
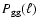 is the power spectrum of
the galaxy distribution [with the selection function specified by
is the power spectrum of
the galaxy distribution [with the selection function specified by
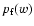 ]
on the sky, i.e., the Fourier transform of the
angular 2PCF of galaxies. The cross-power
]
on the sky, i.e., the Fourier transform of the
angular 2PCF of galaxies. The cross-power
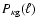 is the quantity that is measured in galaxy-galaxy lensing
observations; see Hoekstra et al. (2002).
is the quantity that is measured in galaxy-galaxy lensing
observations; see Hoekstra et al. (2002).
The bispectrum of the projected quantities Eq. (14) is defined in
terms of the triple correlator
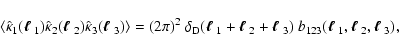 |
(17) |
where the relation between the bispectrum of the projected quantities 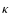 and the 3D bispectrum is given by
and the 3D bispectrum is given by
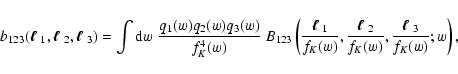 |
(18) |
which is valid under the same conditions required for the validity of
Eq. (15), i.e., the weight functions qi(w) should not vary
appreciably over scales on which the bispectrum is significantly
non-zero. Inserting into this relation the weight functions q appropriate
for the surface mass density 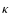 and the projected number density
and the projected number density
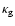 ,
one obtains the bispectra
,
one obtains the bispectra
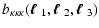 |
= |
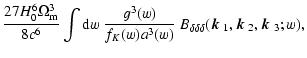 |
(19) |
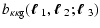 |
= |
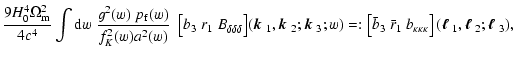 |
(20) |
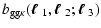 |
= |
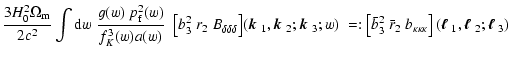 |
(21) |
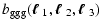 |
= |
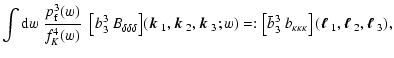 |
(22) |
where again the vectors
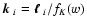 ,
and we have
defined the projected bias factor
,
and we have
defined the projected bias factor 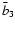 and correlation
coefficients
and correlation
coefficients 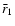 ,
,
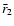 ,
which depend, in addition to the
angular wave vectors
,
which depend, in addition to the
angular wave vectors
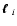 ,
on the redshift distribution of
foreground and background galaxies. The correlations are strongest
if the redshift distribution of the foreground galaxies matches
the most efficient lensing redshift for a given source redshift
distribution - see Hoekstra et al. (2002) for a similar
discussion in the context of second-order galaxy-mass
correlations.
,
on the redshift distribution of
foreground and background galaxies. The correlations are strongest
if the redshift distribution of the foreground galaxies matches
the most efficient lensing redshift for a given source redshift
distribution - see Hoekstra et al. (2002) for a similar
discussion in the context of second-order galaxy-mass
correlations.
The basic observables for the second-order statistics obtained
from observational data are the 2PCFs. Hence, the angular 2PCF of
galaxies
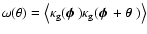 is the Fourier transform
of
is the Fourier transform
of
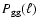 .
The second-order statistics of the
projected matter density are probed by the shear 2PCFs
.
The second-order statistics of the
projected matter density are probed by the shear 2PCFs
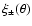 .
They are defined in the following way: let
.
They are defined in the following way: let
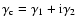 denote the complex shear
in Cartesian coordinates. Given a direction
denote the complex shear
in Cartesian coordinates. Given a direction 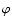 ,
we define the
rotated shear
,
we define the
rotated shear
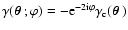 .
This definition implies that
.
This definition implies that
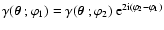 .
The real and imaginary part of
.
The real and imaginary part of
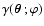 are the tangential and cross component of
the shear relative to the direction
are the tangential and cross component of
the shear relative to the direction  (see, e.g., Crittenden et al. 2002; Schneider et al. 2002). Hence the shear 2PCFs
are written as
(see, e.g., Crittenden et al. 2002; Schneider et al. 2002). Hence the shear 2PCFs
are written as
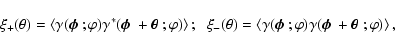 |
(23) |
where the average is over all pairs of points with angular
separation 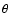 ,
and
,
and 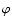 is the polar angle of their
separation vector
is the polar angle of their
separation vector
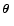 .
The imaginary parts of
.
The imaginary parts of 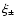 vanish due to parity invariance (e.g., Schneider 2003). For a set
of observed galaxies, the shear in Eq. (23) is replaced by
the image ellipticities, which are an unbiased estimator of the
shear (we neglect here the difference between shear and reduced
shear; see BS01). The shear 2PCFs are related in a simple way to
the power spectrum
vanish due to parity invariance (e.g., Schneider 2003). For a set
of observed galaxies, the shear in Eq. (23) is replaced by
the image ellipticities, which are an unbiased estimator of the
shear (we neglect here the difference between shear and reduced
shear; see BS01). The shear 2PCFs are related in a simple way to
the power spectrum
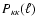 - see Kaiser (1992).
- see Kaiser (1992).
The cross-power is probed by the galaxy-galaxy lensing signal, which
correlates the tangential component of the shear at the location of a
background galaxy with the position of a foreground galaxy. We define this
correlation function as
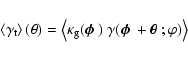 |
(24) |
(e.g., Hoekstra et al. 2002),
where 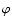 is, as before, the polar angle of the connection vector
is, as before, the polar angle of the connection vector
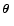 ,
and the imaginary part of Eq. (24) vanishes due to parity
invariance. A practical estimator for
,
and the imaginary part of Eq. (24) vanishes due to parity
invariance. A practical estimator for
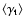 is obtained by
averaging the tangential shear component of the background galaxies in all
foreground-background pairs with separation
is obtained by
averaging the tangential shear component of the background galaxies in all
foreground-background pairs with separation 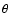 .
.
Similarly, the third-order statistics are best probed from
observing the 3PCFs. The angular 3PCF of galaxies is one of the
standard ways to characterize the non-Gaussian properties of the
galaxy distribution on the sky, and standard methods for
estimating it are known (see, e.g., Peebles 1980). The bispectrum
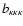 is
probed by the shear 3PCF, as defined in Schneider & Lombardi
(2003; see also Takada & Jain 2003a; Zaldarriaga & Scoccimarro
2003), and its relation to the bispectrum has been derived in
Schneider et al. (2004). We next derive expressions for the
correlation functions related to the cross-bispectra.
is
probed by the shear 3PCF, as defined in Schneider & Lombardi
(2003; see also Takada & Jain 2003a; Zaldarriaga & Scoccimarro
2003), and its relation to the bispectrum has been derived in
Schneider et al. (2004). We next derive expressions for the
correlation functions related to the cross-bispectra.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{g3fig1_xf.eps} \hspace*{3.3cm}
\includegraphics[width=4.5cm,clip]{g3fig2_xf.eps}\end{figure}](/articles/aa/full/2005/12/aa1923/Timg109.gif) |
Figure 1:
Geometry of the galaxy-shear-shear correlation,
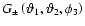 ( left panel), and the galaxy-galaxy-shear
correlation,
( left panel), and the galaxy-galaxy-shear
correlation,
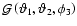 ( right
panel). Note that the sign of the angle
( right
panel). Note that the sign of the angle
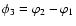 is
important.
is
important.
|
| Open with DEXTER |
5.1 Galaxy-shear-shear correlation
Consider a triplet of points, where two background galaxies are
located at
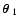 and
and
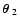 ,
and a foreground
galaxy is located at
,
and a foreground
galaxy is located at
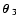 (see Fig. 1, left). We define
the following galaxy-shear-shear 3PCFs
(see Fig. 1, left). We define
the following galaxy-shear-shear 3PCFs
where the separation vectors between the background galaxies and the
foreground galaxy are
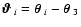 for
i=1,2, and
for
i=1,2, and 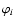 is the polar direction of the separation vector
is the polar direction of the separation vector
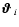 .
These correlation functions depend on the
moduli of the separation vectors
.
These correlation functions depend on the
moduli of the separation vectors
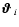 and the angle
and the angle 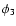 enclosed by them. In order to find a practical estimator for these
cross-correlations, it is useful to consider the modified correlators
enclosed by them. In order to find a practical estimator for these
cross-correlations, it is useful to consider the modified correlators
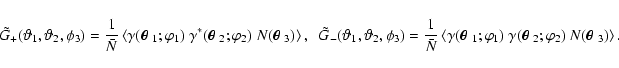 |
(27) |
Using
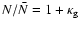 ,
these modified correlators become
,
these modified correlators become
where
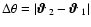 is the separation between
the two background galaxies. The phase factors with which the
shear 2PCFs are multiplied are obtained by rotating the shears
from the direction pointing towards the foreground galaxy to that
of the separation vector of the two background galaxies. If the
polar angle of the latter is denoted by
is the separation between
the two background galaxies. The phase factors with which the
shear 2PCFs are multiplied are obtained by rotating the shears
from the direction pointing towards the foreground galaxy to that
of the separation vector of the two background galaxies. If the
polar angle of the latter is denoted by
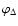 ,
then
,
then
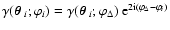 ,
from which the expressions for
the phase factors follow. Hence, the modified galaxy-shear-shear
correlators are given by the sum of the (reduced)
galaxy-shear-shear correlators
,
from which the expressions for
the phase factors follow. Hence, the modified galaxy-shear-shear
correlators are given by the sum of the (reduced)
galaxy-shear-shear correlators 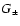 (which is proportional to
the cross-bispectrum
(which is proportional to
the cross-bispectrum
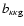 )
plus the 2PCF of
cosmic shear (23), modified by a phase factor that
accounts for the fact that the projection directions of the shear
are
)
plus the 2PCF of
cosmic shear (23), modified by a phase factor that
accounts for the fact that the projection directions of the shear
are 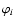 ,
and thus do not correspond to the separation vector between the
background galaxy pair.
,
and thus do not correspond to the separation vector between the
background galaxy pair.
We can obtain practical estimators for these cross 3PCFs, as
follows: first, one defines bins in
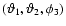 -space.
Then, for each triplet of two background galaxies and one
foreground galaxy whose separation falls inside a given bin, one
adds the product of shears, so that
-space.
Then, for each triplet of two background galaxies and one
foreground galaxy whose separation falls inside a given bin, one
adds the product of shears, so that
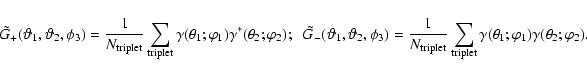 |
(30) |
These estimators can be easily calculated from the catalog of
galaxy positions and ellipticities, e.g., using the method of
Jarvis et al. (2004) for finding triplets. From the estimator
above, the contribution of the shear 2PCF according to Eq. (29) has to be subtracted in order to obtain the
reduced galaxy-shear-shear 3PCF 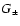 .
Note that observationally
the galaxy-shear-shear correlation is simply the excess of the
shear 2PCF measured around foreground galaxies.
.
Note that observationally
the galaxy-shear-shear correlation is simply the excess of the
shear 2PCF measured around foreground galaxies.
Next we consider the 3PCF between the shear of one background
galaxy and the positions of two foreground galaxies. Let the
former be at position
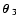 ,
the latter at positions
,
the latter at positions
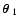 and
and
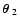 ,
then we define the reduced
galaxy-galaxy-shear correlation function as
,
then we define the reduced
galaxy-galaxy-shear correlation function as
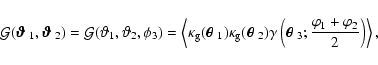 |
(31) |
where, as before,
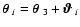 ,
and
,
and 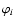 is the polar angle of the vector
is the polar angle of the vector
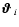 ,
for i=1,2 (see
Fig. 1, right). The shear in Eq. (31) is projected along
the line which bisects the angle between the two foreground
galaxies, as measured from the background galaxy. As before, for
obtaining a practical estimator it is useful to first define a
modified 3PCF,
,
for i=1,2 (see
Fig. 1, right). The shear in Eq. (31) is projected along
the line which bisects the angle between the two foreground
galaxies, as measured from the background galaxy. As before, for
obtaining a practical estimator it is useful to first define a
modified 3PCF,
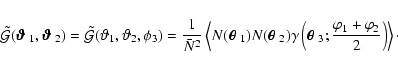 |
(32) |
Using again
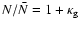 ,
and applying the
transformation law for rotating shears, this can be written as
,
and applying the
transformation law for rotating shears, this can be written as
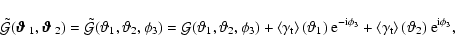 |
(33) |
where the last two terms are the two-point galaxy-shear
correlation functions (24), obtained from rotating the
shear in the direction of the two foreground galaxies. Hence, the
correlator
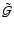 is the sum of the reduced
galaxy-galaxy-shear correlation function plus the two GGL
contributions which would be present even for the case of purely
Gaussian density fields. A practical estimator for
is the sum of the reduced
galaxy-galaxy-shear correlation function plus the two GGL
contributions which would be present even for the case of purely
Gaussian density fields. A practical estimator for
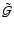 is obtained by finding triplets of galaxies that fall in a given
bin, and then summing over the shears of the background galaxies,
is obtained by finding triplets of galaxies that fall in a given
bin, and then summing over the shears of the background galaxies,
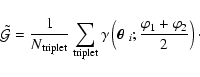 |
(34) |
The signature of the galaxy-galaxy-shear correlation is therefore just
the excess shear measured about pairs of foreground
galaxies.
Note that integral measures
of these three-point cross-correlation functions have probably been measured
already. McKay et al. (2002) have demonstrated in their measurement of GGL
from the SDSS that the GGL signal is stronger, and extends to much larger
separations, for foreground galaxies that are located in regions of high
galaxy density. This detection provides a correlation between the GGL signal
and the number density of galaxies, and therefore an integral over the 3PCF
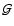 .
Furthermore, the galaxy-shear-shear correlation seems to be in the
cosmic shear analysis of the COMBO-17 fields by Brown et al. (2003), where
they find a stronger-than-average cosmic shear signal in the A901 field, and a
weaker-than-average cosmic shear signal in the CDFS, which is a field
selected because it is rather poor in brighter galaxies.
.
Furthermore, the galaxy-shear-shear correlation seems to be in the
cosmic shear analysis of the COMBO-17 fields by Brown et al. (2003), where
they find a stronger-than-average cosmic shear signal in the A901 field, and a
weaker-than-average cosmic shear signal in the CDFS, which is a field
selected because it is rather poor in brighter galaxies.
The measurement of these galaxy-mass 3PCFs is expected to be
considerably easier than measuring the shear 3PCF itself. Note
that 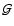 is first order, and
is first order, and 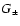 are second order in
the shear. For the same reason that GGL measurements are easier to
obtain than second-order cosmic shear measurements, the former
being just first order in the shear, one therefore expects that
are second order in
the shear. For the same reason that GGL measurements are easier to
obtain than second-order cosmic shear measurements, the former
being just first order in the shear, one therefore expects that
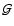 and
and 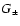 are more straightforward to measure from a
given data set. In particular, every wide-field survey in which
the shear 3PCF can be measured should yield a significant
measurement of these cross-correlation functions.
are more straightforward to measure from a
given data set. In particular, every wide-field survey in which
the shear 3PCF can be measured should yield a significant
measurement of these cross-correlation functions.
6 Relation to the bispectrum
It is relatively straightforward to write the correlation functions
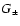 and
and 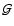 in terms of the (projected) bispectra defined
in Sect. 4. The complex shear is related to the
convergence in Fourier space so that
in terms of the (projected) bispectra defined
in Sect. 4. The complex shear is related to the
convergence in Fourier space so that
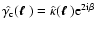 ,
where
,
where 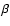 is the
polar angle of the vector
is the
polar angle of the vector
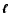 .
Using this, along with the rule
for rotating shears, one can re-write Eq. (25)
as
.
Using this, along with the rule
for rotating shears, one can re-write Eq. (25)
as
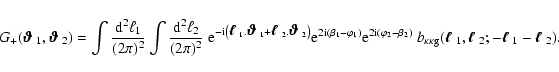 |
(35) |
Similar relations hold for the correlation functions defined by Eqs. (26) and (31). Next we split the angles
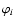 and
and 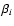 into their mean and their difference, by writing
into their mean and their difference, by writing
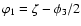 ,
,
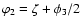 and
and
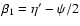 ,
,
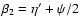 ,
where
,
where 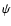 represents the angle
contained by
represents the angle
contained by 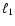 and
and 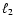 ,
and
,
and 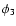 is the same as in
previous sections.
Then, we write
is the same as in
previous sections.
Then, we write
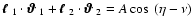 ,
where
,
where
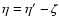 ,
and
,
and
![\begin{displaymath}A^2 = \ell_1^2 \vartheta_1^2 + \ell_2^2 \vartheta_2^2 - 2\ell...
...\vartheta_2\right)^2 {\rm e} ^{-\rm i (\phi_3-\psi)} \right].
\end{displaymath}](/articles/aa/full/2005/12/aa1923/img153.gif) |
(36) |
Splitting up the integrals in Eq. (35) into polar
coordinates in 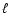 -space, the
-space, the 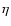 -integral can be performed,
yielding
-integral can be performed,
yielding
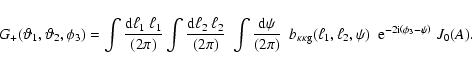 |
(37) |
In a similar manner, we find for G-
and for 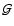
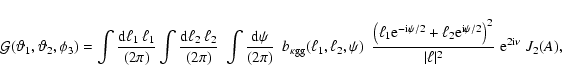 |
(40) |
with
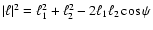 .
The above results link directly the cross-correlation functions in
real space to their equivalent projected bispectra. In a similar
fashion, one may also derive a set of inverse relations, i.e.
expressing the bispectra in terms of Fourier integrals of the
correlation functions, beginning with the definition of the
bispectrum in Eq. (17). The resulting
expressions, which are derived in the same way as above, are
.
The above results link directly the cross-correlation functions in
real space to their equivalent projected bispectra. In a similar
fashion, one may also derive a set of inverse relations, i.e.
expressing the bispectra in terms of Fourier integrals of the
correlation functions, beginning with the definition of the
bispectrum in Eq. (17). The resulting
expressions, which are derived in the same way as above, are
Using the same transformations of the polar angles as before, one more
integration can be carried out, resulting in
In a similar way, we can express the cross-bispectrum
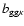 in terms of
in terms of 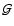 ,
yielding
,
yielding
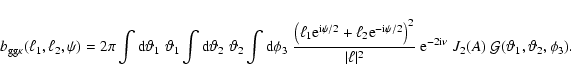 |
(45) |
Using Eq. (35) and replacing the cross-bispectrum in
favour of G-, using Eq. (41), one can express G+ in
terms of G-. Similarly, using Eqs. (39) and (42), we obtain the inverse relation; these read:
Hence, if the shear field is a pure E-mode field, these interrelations
will be satisfied; note that similar equations are valid for the shear
2PCF (Crittenden et al. 2002; Schneider et al. 2002), relating
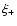 to
to 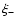 and vice versa.
and vice versa.
7 Aperture statistics
In Sect. 5 we defined 3PCFs for the galaxy-mass
correlations, and gave practical estimators for measuring them.
These 3PCFs were then related to the corresponding bispectra through
Fourier transform relations in Sect. 6. As was demonstrated in
Schneider et al. (2004), the relation between the shear 3PCF and the underlying
projected mass bispectrum is rather complicated and not easy to
evaluate. From Eqs. (37) through (40) we
observe that the same is true for the relation between the
correlation functions considered here and the corresponding
bispectra.
However, we can avoid the use of numerically complicated
transformations between the 3PCF and the bispectra by considering
aperture statistics (Schneider 1996, 1998; van Waerbeke 1998;
Crittenden et al. 2002), in the same way as has been done for the
shear 3PCF (Jarvis et al. 2004; Schneider et al. 2004) and for
the measurement of the second-order bias factor and galaxy-mass
correlation coefficient (Hoekstra et al. 2001, 2002). The main
reason for this is that the third-order aperture statistics on the one hand
provide a very localized measurement of the
corresponding bispectra, and on the other hand can be readily
evaluated from the corresponding 3PCFs. In this section, we apply
the aperture statistics to the galaxy-mass 3PCFs. The aperture
mass is defined as
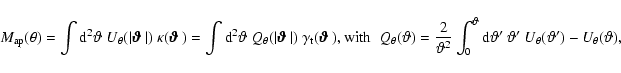 |
(48) |
where 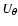 is a weight function of zero total weight, i.e.,
is a weight function of zero total weight, i.e.,
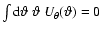 .
The scale of the weight
function is described by
.
The scale of the weight
function is described by 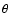 ,
and
,
and
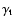 is the
tangential shear component as measured with respect to the
direction towards the center of the aperture. Furthermore, we
define the aperture counts
is the
tangential shear component as measured with respect to the
direction towards the center of the aperture. Furthermore, we
define the aperture counts
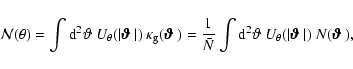 |
(49) |
where the final equality follows because U is a compensated
filter function. We consider here the filter function introduced
by Crittenden et al. (2002), which has also been used by Jarvis
et al. (2004) and Schneider et al. (2004). Writing
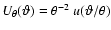 ,
the filter
function reads
,
the filter
function reads
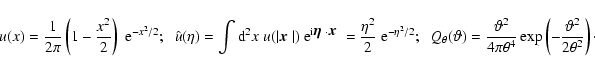 |
(50) |
This choice for 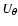 has the disadvantage that the support
of the filter is formally infinite; however, the Gaussian factor
renders the effective range of support finite, since the
filter function becomes extremely small for
has the disadvantage that the support
of the filter is formally infinite; however, the Gaussian factor
renders the effective range of support finite, since the
filter function becomes extremely small for
 .
This disadvantage over other filter functions that have been
employed in cosmic shear studies (Schneider et al. 1998) is more
than compensated by the convenient mathematical properties, of
which we will make extensive use below.
.
This disadvantage over other filter functions that have been
employed in cosmic shear studies (Schneider et al. 1998) is more
than compensated by the convenient mathematical properties, of
which we will make extensive use below.
We can now relate the third-order correlations between the
aperture measures to the corresponding bispectra. Consider first
Replacing the  by their Fourier transforms, carrying out
the
by their Fourier transforms, carrying out
the
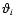 -integrations, making use of Eq. (50) and the
definition of the bispectra, yields
-integrations, making use of Eq. (50) and the
definition of the bispectra, yields
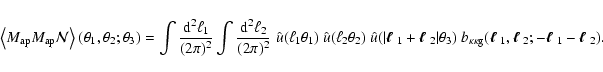 |
(51) |
Similarly, we obtain for the galaxy-galaxy-mass aperture correlator
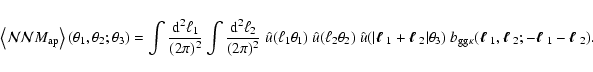 |
(52) |
Since  is a function that has a very narrow peak, the
third-order aperture measures provide very localized information
on the respective bispectra and are thus ideal for probing the
latter. Unless the bispectra have very sharp features, the
third-order aperture measures contain essentially all information
about the bispectra - cf. the corresponding discussion for the
shear 3PCF and their aperture measures in Schneider et al. (2004). We next show how the third-order aperture measures can be
calculated directly in terms of the respective correlation
functions. For that, it is convenient to introduce a complex
aperture shear measure, defined as
is a function that has a very narrow peak, the
third-order aperture measures provide very localized information
on the respective bispectra and are thus ideal for probing the
latter. Unless the bispectra have very sharp features, the
third-order aperture measures contain essentially all information
about the bispectra - cf. the corresponding discussion for the
shear 3PCF and their aperture measures in Schneider et al. (2004). We next show how the third-order aperture measures can be
calculated directly in terms of the respective correlation
functions. For that, it is convenient to introduce a complex
aperture shear measure, defined as
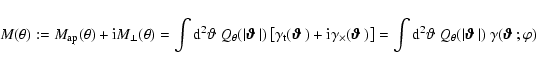 |
(53) |
where 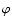 is the polar angle of
is the polar angle of
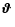 .
If the shear field is entirely due
to the lensing mass distribution,
.
If the shear field is entirely due
to the lensing mass distribution,  vanishes identically (Crittenden et al. 2002). A non-zero value for
vanishes identically (Crittenden et al. 2002). A non-zero value for 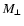 would indicate the presence of
B-mode shear. In fact
would indicate the presence of
B-mode shear. In fact
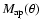 vanishes identically for B-modes, whereas
vanishes identically for B-modes, whereas
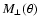 yields zero for a pure E-mode field. Thus, the
aperture measures are ideally suited to separating E- and B-modes of
the shear.
yields zero for a pure E-mode field. Thus, the
aperture measures are ideally suited to separating E- and B-modes of
the shear.
We will now express the third-order aperture measures to the 3PCFs
considered in the previous section. First we find from the
definition (53)
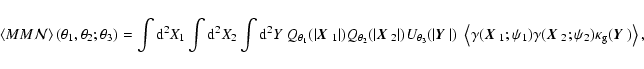 |
(54) |
where 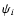 is the polar angle of the vector
is the polar angle of the vector
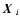 ,
i=1,2. Next we
introduce the separation vectors
,
i=1,2. Next we
introduce the separation vectors
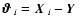 ,
and let
,
and let 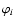 denote their polar angle. Then we apply the transformation
denote their polar angle. Then we apply the transformation
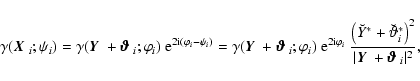 |
(55) |
where we have introduced the notation that a two-dimensional vector
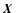 can be written as a complex number
can be written as a complex number
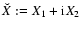 ,
which is
convenient for expressing phases: If
,
which is
convenient for expressing phases: If 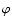 is the polar angle of
is the polar angle of
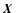 ,
then
,
then
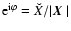 .
Inserting the foregoing expression
into Eq. (54) and using the definition (50) of the
filter functions, one obtains
.
Inserting the foregoing expression
into Eq. (54) and using the definition (50) of the
filter functions, one obtains
The
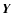 -integration can be performed, and the result, when
multiplied with the phase factors, only depends on the modulus of
the
-integration can be performed, and the result, when
multiplied with the phase factors, only depends on the modulus of
the
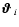 and the angle
and the angle 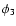 they enclose. Hence,
they enclose. Hence,
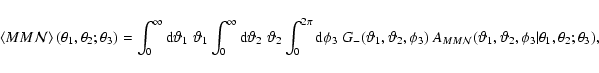 |
(57) |
where the convolution function
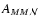 is given in the
appendix. In the same way, we can evaluate
is given in the
appendix. In the same way, we can evaluate
where again the convolution function is given in the appendix. By combining
Eqs. (57) and (58), one finds
The first of these is the expression that is directly related to
the bispectrum
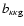 .
The second expression is
expected to vanish if the shear is caused solely by gravitational
lensing. A significant non-zero value of this correlator would
indicate the presence of B-mode shear which is correlated with the
foreground galaxy distribution. The final expression is expected
to be zero because it is not parity-invariant, as all odd-order
statistics in B-mode shear (Schneider 2003); hence, a measured
non-zero value would indicate that the data violate parity
invariance.
.
The second expression is
expected to vanish if the shear is caused solely by gravitational
lensing. A significant non-zero value of this correlator would
indicate the presence of B-mode shear which is correlated with the
foreground galaxy distribution. The final expression is expected
to be zero because it is not parity-invariant, as all odd-order
statistics in B-mode shear (Schneider 2003); hence, a measured
non-zero value would indicate that the data violate parity
invariance.
One may consider how the results defined above would change if the modified
correlators
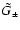 were used in the definition of
were used in the definition of
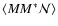 and
and
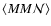 .
Using the fact that
.
Using the fact that
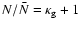 we
find, using Eq. (54), that since U is a compensated filter,
the additional terms arising from two point shear-shear correlations
vanish. Thus we make the following useful assertion that when working with
the aperture mass statistics, one need not subtract the contribution from the
shear 2PCF to compute the reduced three point
statistics.
we
find, using Eq. (54), that since U is a compensated filter,
the additional terms arising from two point shear-shear correlations
vanish. Thus we make the following useful assertion that when working with
the aperture mass statistics, one need not subtract the contribution from the
shear 2PCF to compute the reduced three point
statistics.
Finally, we consider the galaxy-galaxy-mass third-order aperture
statistics
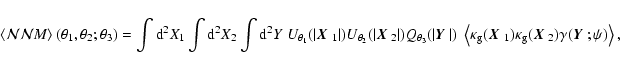 |
(60) |
where 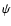 is the polar angle of
is the polar angle of
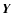 .
Again introducing the separation
vectors
.
Again introducing the separation
vectors
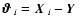 ,
which have polar angles
,
which have polar angles 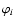 ,
i=1,2,
using the transformation
,
i=1,2,
using the transformation
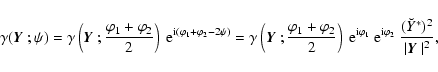 |
(61) |
and inserting the definitions (50) into
Eq. (60) yields
where the convolution function is also derived in the appendix. The real part
of
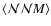 corresponds to the aperture 3PCF that is directly
related to the bispectrum
corresponds to the aperture 3PCF that is directly
related to the bispectrum
 ,
whereas the imaginary part
vanishes due to parity invariance. Finally in this section we note that, as
with the galaxy-mass-mass statistics, the quantity
,
whereas the imaginary part
vanishes due to parity invariance. Finally in this section we note that, as
with the galaxy-mass-mass statistics, the quantity
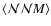 does not change when the definition for
does not change when the definition for
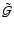 is used in place of
is used in place of  in Eq. (60). Second-order galaxy-galaxy lensing effects are
therefore not important for
the three-point aperture mass statistics.
in Eq. (60). Second-order galaxy-galaxy lensing effects are
therefore not important for
the three-point aperture mass statistics.
In this paper, we have defined third-order galaxy-mass correlation
functions and the corresponding third-order bias factor and
related them to quantities which can be measured directly through
galaxy-galaxy-galaxy lensing. Whereas the underlying physical
quantities are the bispectra of the mass and galaxy distribution,
as well as the cross-bispectra, the observables are the shear as
measured from the ellipticity of background galaxies in relation
to the position of foreground galaxies. We have argued that these
third-order correlations have probably been measured already, and
are almost certainly measurable from data sets existing now; the
ongoing and planned wide-field surveys will obtain precision
measurements of these third-order statistics. The basic
observables are the 3PCFs, as their measurement is not affected by
holes and gaps in the data set which are unavoidable due to the
selection of the survey geometry and masking of bright stars and
galaxies, as well as CCD defects. The 3PCFs are related to the
corresponding bispectra through a very broad and oscillating
filter function (see Schneider et al. 2004, for the case of the
shear 3PCF) and thus do not directly provide information about the
shape of the bispectra. Therefore, we have considered the aperture
statistics, which on the one hand can be calculated readily from
the measured correlation functions, and on the other hand are
related to the bispectra through a narrow filter function, hence
providing localized information on the latter. In fact, unless the
bispectra vary strongly as a function of their angular wave
vectors
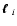 ,
the third-order aperture measures are
expected to contain essentially all information about the
third-order galaxy-mass correlations. Furthermore, the aperture
measures allow one to easily identify the presence of B-modes in
the shear field, as well as unphysical parity-violating
contributions, which can only be due to the observing and data
reduction steps, unless we drop the assumption that the mass
distribution in our Universe is parity invariant.
,
the third-order aperture measures are
expected to contain essentially all information about the
third-order galaxy-mass correlations. Furthermore, the aperture
measures allow one to easily identify the presence of B-modes in
the shear field, as well as unphysical parity-violating
contributions, which can only be due to the observing and data
reduction steps, unless we drop the assumption that the mass
distribution in our Universe is parity invariant.
The convolution functions relating the 3PCFs to the third-order
aperture measures have in principle an infinite support; in practice,
however, the exponential factor implies that the 3PCFs have to be
measured only up to a few times the corresponding filter scales
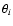 .
Therefore, these convolution functions have
essentially finite support.
.
Therefore, these convolution functions have
essentially finite support.
Nevertheless, in order to calculate the
third-order aperture measures, the corresponding correlation functions
need to be measured to
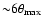 ,
where
,
where
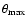 is the largest of the three aperture radii. The largest scale on
which the correlation functions can be measured is determined by the
geometry of the survey. For a large survey with contiguous area, this
scale is limited by the smallness of the signal when entering the
linear regime of structure evolution. In this case, the aperture
measures contain all the information contained in the measured
correlation functions. If the survey consists of independent patches
each of size
is the largest of the three aperture radii. The largest scale on
which the correlation functions can be measured is determined by the
geometry of the survey. For a large survey with contiguous area, this
scale is limited by the smallness of the signal when entering the
linear regime of structure evolution. In this case, the aperture
measures contain all the information contained in the measured
correlation functions. If the survey consists of independent patches
each of size 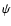 ,
then the correlation functions can be measured
for angular scales up to
,
then the correlation functions can be measured
for angular scales up to
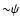 ,
meaning that the aperture measures
are limited to
,
meaning that the aperture measures
are limited to
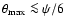 .
In this case, the
measured correlation functions contain more information than the
aperture measures. In a future work, we plan to study these aspects;
note, however, that estimates of the "information content'' are
tedious, since they involve the covariance of third-order statistical
measures, and thus depend, in general, on six variables and have to be
estimated from sixth-order statistics.
.
In this case, the
measured correlation functions contain more information than the
aperture measures. In a future work, we plan to study these aspects;
note, however, that estimates of the "information content'' are
tedious, since they involve the covariance of third-order statistical
measures, and thus depend, in general, on six variables and have to be
estimated from sixth-order statistics.
The correlation function 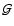 measures the same cross-bispectrum as the
third-order statistics considered by Ménard et al. (2003). In that paper, they
considered the correlation between pairs of foreground galaxies and background
QSOs. Due to the magnification of distant QSOs by the matter in which the
foreground galaxies are embedded, and the steep slope of bright QSO source
counts, such a correlation should be measurable with the large QSO sample
obtained by the Sloan Digital Sky Survey. Instead of magnification, we employ
the shear around galaxy pairs. Which of the two methods is better able to
measure the galaxy-mass bispectrum depends on the available observational
data. For deep wide-field images, the shear method investigated here will be
more efficient, given the sparseness of bright QSOs on the sky.
measures the same cross-bispectrum as the
third-order statistics considered by Ménard et al. (2003). In that paper, they
considered the correlation between pairs of foreground galaxies and background
QSOs. Due to the magnification of distant QSOs by the matter in which the
foreground galaxies are embedded, and the steep slope of bright QSO source
counts, such a correlation should be measurable with the large QSO sample
obtained by the Sloan Digital Sky Survey. Instead of magnification, we employ
the shear around galaxy pairs. Which of the two methods is better able to
measure the galaxy-mass bispectrum depends on the available observational
data. For deep wide-field images, the shear method investigated here will be
more efficient, given the sparseness of bright QSOs on the sky.
As is true for the second-order galaxy-mass correlations, as
measured in GGL, the physical interpretation of the third-order
correlations is not straightforward, but needs to be done in the
frame of a model. On very large scales, we might expect that b3essentially becomes a constant, but that will be difficult to
measure, as on these large scales, the density field is expected to
quickly approach a Gaussian, and thus the bispectrum should be very
small.
A useful analytic description of clustering statistics on all cosmological
scales is given by the halo model (see Cooray & Sheth 2002, for a review).
Within this framework it will be possible to relate the higher-order
cross-correlation functions to the quantities that specify the Halo Occupation
Distribution. As pointed out by Berlind & Weinberg (2002) the HOD
essentially contains all of the information about the statistics of
galaxy clustering that theories of galaxy formation are able to provide; it is
a complete description of the bias. Future empirical determinations of the HOD
using observations of galaxy and mass clustering will enable powerful
constraints to be placed on the development of models for galaxy formation. In
a forthcoming paper we shall explore these concepts in detail, building the
physical interpretation of our third-order galaxy-mass correlations using the
halo model and the HOD.
Acknowledgements
We thank Martin Kilbinger for useful comments on the manuscript.
This work was supported by the German Ministry for
Science and Education (BMBF) through the DLR under the project 50 OR
0106 and by the Deutsche
Forschungsgemeinschaft under the project SCHN 342/3-1.
In this appendix, we derive the convolution functions which relate the
third-order aperture measures to the corresponding 3PCFs. We start by rewriting
the exponent in Eqs. (56), (58) and (62) by
making a translation
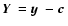 ,
where
,
where
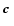 is chosen so
as to remove
linear terms in
is chosen so
as to remove
linear terms in
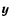 ,
,
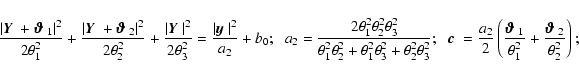 |
(A.1) |
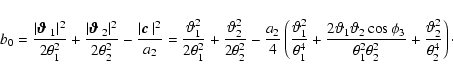 |
(A.2) |
Next, we consider the prefactor of the exponential in
Eq. (56), and change the integration variable from
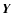 to
to
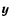 .
For this, we first define
.
For this, we first define
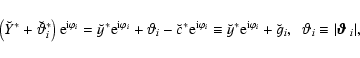 |
(A.3) |
for i=1,2, or more explicitly,
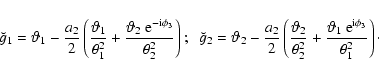 |
(A.4) |
The prefactor of the exponential, when multiplied with the phase
factors, then becomes
where C denotes additional terms which, however, become zero
when the
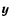 -integration is carried out, since the exponent
depends only on
-integration is carried out, since the exponent
depends only on
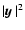 .
The
.
The
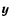 -integration can now
be carried out,
-integration can now
be carried out,
The result depends only on
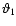 ,
,
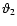 and the angle
and the angle
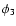 between
between
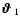 and
and
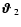 ,
so that an additional
angular integration can be carried out in Eq. (56). We
thus arrive at Eq. (57), with
,
so that an additional
angular integration can be carried out in Eq. (56). We
thus arrive at Eq. (57), with
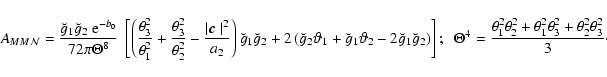 |
(A.6) |
Similar expansions of the prefactors of the exponentials in
Eqs. (58) and (62) can also be
determined using the same definitions as above. Performing the
relevant integrals, we find that the convolution factors for
Eqs. (59) and (63) are then given by
and
where
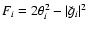 .
.
- Bacon, D. J.,
Refregier, A. R., & Ellis, R. S. 2000, MNRAS, 318, 625 [NASA ADS] (In the text)
- Bartelmann,
M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] (BS01)
(In the text)
- Berlind, A.,
& Weinberg, D. 2002, ApJ, 575, 587 [NASA ADS] [CrossRef] (In the text)
- Bernardeau,
F., van Waerbeke, L., & Mellier, Y. 1997, A&A, 322, 1 [NASA ADS] (In the text)
- Bernardeau,
F., Mellier, Y., & van Waerbeke, L. 2002, A&A, 389,
L28 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Blandford, R.
D., Saust, A. B., Brainerd, T. G., & Villumsen, J. V. 1991,
MNRAS, 251, 600 [NASA ADS] (In the text)
- Brainerd, T.
G., Blandford, R. D., & Smail, I. 1996, ApJ, 466, 623 [NASA ADS] [CrossRef] (In the text)
- Brown, M. L., Taylor,
A. N., Bacon, D. J., et al. 2003, MNRAS, 341, 100 [NASA ADS] [CrossRef] (In the text)
- Cooray, A., &
Sheth, R. 2002, PhR, 372, 1 [NASA ADS] (In the text)
- Crittenden,
R. G., Natarajan, P., Pen, U.-L., & Theuns, T. 2002, ApJ, 568,
20 [NASA ADS] [CrossRef] (In the text)
- Croft, R. A. C.,
& Metzler, C. A. 2001, ApJ, 545, 561 [NASA ADS]
- Dell'Antonio, I. P.,
& Tyson, J. A. 1996, ApJ, 473, L17 [NASA ADS] [CrossRef]
- Dolag, K., &
Bartelmann, M. 1997, MNRAS, 291, 446 [NASA ADS] (In the text)
- Fischer, P.,
McKay, T. A., Sheldon, E., et al. 2000, AJ, 120, 1198 [NASA ADS] [CrossRef] (In the text)
- Griffiths, R.
E., Casertano, S., Im, M., & Ratnatunga, K. U. 1996, MNRAS,
282, 1159 [NASA ADS] (In the text)
- Guzik, J., &
Seljak, U. 2002, MNRAS, 335, 311 [NASA ADS] [CrossRef] (In the text)
- Hoekstra, H.,
Yee, H. K. C., & Gladders, M. D. 2001, ApJ, 558, L11 [NASA ADS] [CrossRef] (In the text)
- Hoekstra, H.,
van Waerbeke, L., Gladders, M. D., Mellier, Y., & Yee, H. K. C.
2002, ApJ, 577, 604 [NASA ADS] [CrossRef] (In the text)
- Hudson, M. J.,
Gwyn, S. D. J., Dahle, H., & Kaiser, N. 1998, ApJ, 503,
531 [NASA ADS] [CrossRef] (In the text)
- Jain, B., & Seljak,
U. 1997, ApJ, 484, 560 [NASA ADS] [CrossRef] (In the text)
- Jarvis, M.,
Bernstein, G. M., Fischer, P., et al. 2003, AJ, 125, 1014 [NASA ADS] [CrossRef] (In the text)
- Jarvis, M.,
Bernstein, G. M., & Jain, B. 2004, MNRAS, 352, 338 [NASA ADS] [CrossRef] (In the text)
- Kaiser, N. 1992,
ApJ, 388, 272 [NASA ADS] [CrossRef] (In the text)
- Kaiser, N., Wilson,
G., & Luppino, G. 2000 [arXiv:astro-ph/0003338]
(In the text)
-
Kleinheinrich, M., Rix, H.-W., Erben, T., et al. 2004, A&A,
submitted (also [arXiv:astro-ph/0404527])
(In the text)
- Maoli, R., van
Waerbeke, L., Mellier, Y., et al. 2001, A&A, 368, 766 [EDP Sciences] [CrossRef] (In the text)
- McKay, T. A.,
Sheldon, E. S., Racusin, J., et al. 2001
[arXiv:astro-ph/0108013]
(In the text)
- Mellier, Y. 1999,
ARA&A, 37, 127 [NASA ADS] (In the text)
- Ménard, B.,
Bartelmann, M., & Mellier, Y. 2003, A&A, 409, 411 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Miralda-Escudé, J. 1991, ApJ, 380, 1 [NASA ADS] [CrossRef] (In the text)
- Peebles, P. J. E.
1980, The large-scale structure of the universe (Princeton
University Press)
(In the text)
- Pen, U.-L., Zhang, T.,
van Waerbeke, L., et al. 2003, ApJ, 592, 664 [NASA ADS] [CrossRef] (In the text)
- Refregier, A.
2003, ARA&A, 41, 645 [NASA ADS] (In the text)
- Refregier,
A., Rhodes, J., & Groth, E. J. 2002, ApJ, 572, L131 [NASA ADS] [CrossRef] (In the text)
- Schneider, P.
1996, MNRAS, 283, 837 [NASA ADS] (In the text)
- Schneider, P.
1998, ApJ, 498, 43 [NASA ADS] [CrossRef] (In the text)
- Schneider, P.
2003, A&A, 408, 829 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Schneider,
P., & Lombardi, M. 2003, A&A, 397, 809 [EDP Sciences] [NASA ADS] [CrossRef]
- Schneider,
P., van Waerbeke, L., Jain, B., & Kruse, G. 1998, MNRAS, 296,
873 [NASA ADS] [CrossRef] (In the text)
- Schneider,
P., van Waerbeke, L., & Mellier, Y. 2002, A&A, 389,
729 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Schneider,
P., Kilbinger, M., & Lombardi, M. 2004, A&A, submitted
(also [arXiv:astro-ph/0308328])
(In the text)
- Seljak, U.,
Makarov, A., Mandelbaum, R., et al. 2004
[arXiv:astro-ph/0406594]
(In the text)
- Sheldon, E. S.,
Johnston, D. E., Frieman, J. A., et al. 2004, AJ, 127, 2544 [NASA ADS] [CrossRef] (In the text)
- Takada, M., &
Jain, B. 2003a, ApJ, 583, L49 [NASA ADS] [CrossRef] (In the text)
- Takada, M., &
Jain, B. 2003b, MNRAS, 344, 857 [NASA ADS] [CrossRef]
- Tyson, J. A., Valdes,
F., Jarvis, J. F., & Mills, Jr., A. P. 1984, ApJ, 281, L59 [NASA ADS] [CrossRef] (In the text)
- van Waerbeke,
L. 1998, A&A, 334, 1 [NASA ADS] (In the text)
- van Waerbeke,
L., & Mellier, Y. 2003 [arXiv:astro-ph/0305089]
(In the text)
- van Waerbeke,
L., Bernardeau, F., & Mellier, Y. 1999, A&A, 243, 15 [NASA ADS] (In the text)
- van Waerbeke,
L., Mellier, Y., Erben, T., et al. 2000, A&A, 358, 30 [NASA ADS] (In the text)
- van Waerbeke,
L., Mellier, Y., Radovich, M., et al. 2001, A&A, 374, 757 [EDP Sciences] [NASA ADS] (In the text)
- van Waerbeke,
L., Mellier, Y., Pello, R., et al. 2002, A&A, 393, 369 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Wittman, D. M.,
Tyson, J. A., Kirkman, D., Dell'Antonio, I., & Bernstein, G.
2000, Nature, 405, 143 [NASA ADS] [CrossRef] (In the text)
-
Zaldarriaga, M., & Scoccimarro, R. 2003, ApJ, 584, 559 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
![]() ,
and a
galaxy-galaxy-shear correlation,
,
and a
galaxy-galaxy-shear correlation, ![]() .
We relate these to the
various projected cross-bispectra and give practical estimators for their
measurement. We note that the observational signature of these
correlators is simply the excess shear-shear correlation measured about
foreground galaxies (for
.
We relate these to the
various projected cross-bispectra and give practical estimators for their
measurement. We note that the observational signature of these
correlators is simply the excess shear-shear correlation measured about
foreground galaxies (for ![]() )
and the average tangential shear around
foreground galaxy pairs (for
)
and the average tangential shear around
foreground galaxy pairs (for ![]() ). These quantities are no more than
second order in the shear and so should be more easily measurable than the
shear 3-point correlation. Finally we derive expressions for the third
order aperture mass statistics in terms of both the cross-bispectra and
the real-space correlation functions. Such statistics provide a very
localized measurement of the bispectra, thus encapsulating
essentially all of the available third-order information, while remaining
easily obtainable from observations of 3-point cross-correlation
functions. In addition we find that utilising aperture statistics has the
further benefit that they measure only the connected part of the third
order correlation.
). These quantities are no more than
second order in the shear and so should be more easily measurable than the
shear 3-point correlation. Finally we derive expressions for the third
order aperture mass statistics in terms of both the cross-bispectra and
the real-space correlation functions. Such statistics provide a very
localized measurement of the bispectra, thus encapsulating
essentially all of the available third-order information, while remaining
easily obtainable from observations of 3-point cross-correlation
functions. In addition we find that utilising aperture statistics has the
further benefit that they measure only the connected part of the third
order correlation.
![]() ,
the GGL signal is no longer dominated by the halo
of galaxies, but receives a substantial contribution from the matter in
which galaxies are embedded, namely groups and clusters. From this
signal, one learns about the environments of galaxies. For example,
the density-morphology relation can be traced back directly to the
underlying mass density, instead to the galaxy number density.
,
the GGL signal is no longer dominated by the halo
of galaxies, but receives a substantial contribution from the matter in
which galaxies are embedded, namely groups and clusters. From this
signal, one learns about the environments of galaxies. For example,
the density-morphology relation can be traced back directly to the
underlying mass density, instead to the galaxy number density.
![]() ,
GGL measures a combination of the galaxy-mass
correlation coefficient r and the bias factor b. These two functions
can be obtained individually when the GGL signal is combined with the
cosmic shear signal, as shown by Hoekstra et al. (2002). In fact,
Hoekstra et al. (2002) have measured rand b as a function of scale. Future measurements of
these quantities as a function of scale, redshift and galaxy type,
using the upcoming wide-field imaging surveys, will provide invaluable
input for the interpretation of galaxy redshift samples. In addition,
b and r are functions which depend on the formation and evolution
of galaxies; they can therefore be used as constraints for those
models.
,
GGL measures a combination of the galaxy-mass
correlation coefficient r and the bias factor b. These two functions
can be obtained individually when the GGL signal is combined with the
cosmic shear signal, as shown by Hoekstra et al. (2002). In fact,
Hoekstra et al. (2002) have measured rand b as a function of scale. Future measurements of
these quantities as a function of scale, redshift and galaxy type,
using the upcoming wide-field imaging surveys, will provide invaluable
input for the interpretation of galaxy redshift samples. In addition,
b and r are functions which depend on the formation and evolution
of galaxies; they can therefore be used as constraints for those
models.
![]() ,
we define the number
density contrast
,
we define the number
density contrast
![]() of galaxies as
of galaxies as
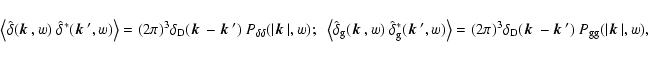
![]() .
However, in the more general
(and realistic) case, these relations are more complex. We define
the third-order bias parameter b3 and the two galaxy-mass
correlation coefficients r1 and r2 through the relations
.
However, in the more general
(and realistic) case, these relations are more complex. We define
the third-order bias parameter b3 and the two galaxy-mass
correlation coefficients r1 and r2 through the relations
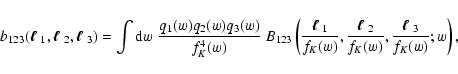
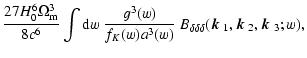
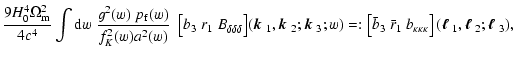
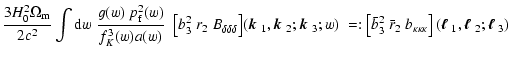
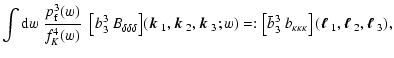
![]() is
probed by the shear 3PCF, as defined in Schneider & Lombardi
(2003; see also Takada & Jain 2003a; Zaldarriaga & Scoccimarro
2003), and its relation to the bispectrum has been derived in
Schneider et al. (2004). We next derive expressions for the
correlation functions related to the cross-bispectra.
is
probed by the shear 3PCF, as defined in Schneider & Lombardi
(2003; see also Takada & Jain 2003a; Zaldarriaga & Scoccimarro
2003), and its relation to the bispectrum has been derived in
Schneider et al. (2004). We next derive expressions for the
correlation functions related to the cross-bispectra.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{g3fig1_xf.eps} \hspace*{3.3cm}
\includegraphics[width=4.5cm,clip]{g3fig2_xf.eps}\end{figure}](/articles/aa/full/2005/12/aa1923/Timg109.gif)
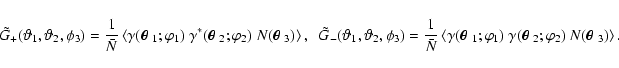
![]() -space.
Then, for each triplet of two background galaxies and one
foreground galaxy whose separation falls inside a given bin, one
adds the product of shears, so that
-space.
Then, for each triplet of two background galaxies and one
foreground galaxy whose separation falls inside a given bin, one
adds the product of shears, so that
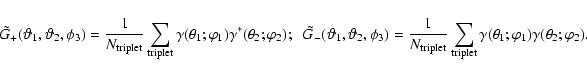
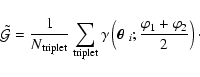
![]() .
Furthermore, the galaxy-shear-shear correlation seems to be in the
cosmic shear analysis of the COMBO-17 fields by Brown et al. (2003), where
they find a stronger-than-average cosmic shear signal in the A901 field, and a
weaker-than-average cosmic shear signal in the CDFS, which is a field
selected because it is rather poor in brighter galaxies.
.
Furthermore, the galaxy-shear-shear correlation seems to be in the
cosmic shear analysis of the COMBO-17 fields by Brown et al. (2003), where
they find a stronger-than-average cosmic shear signal in the A901 field, and a
weaker-than-average cosmic shear signal in the CDFS, which is a field
selected because it is rather poor in brighter galaxies.
![]() is first order, and
is first order, and ![]() are second order in
the shear. For the same reason that GGL measurements are easier to
obtain than second-order cosmic shear measurements, the former
being just first order in the shear, one therefore expects that
are second order in
the shear. For the same reason that GGL measurements are easier to
obtain than second-order cosmic shear measurements, the former
being just first order in the shear, one therefore expects that
![]() and
and ![]() are more straightforward to measure from a
given data set. In particular, every wide-field survey in which
the shear 3PCF can be measured should yield a significant
measurement of these cross-correlation functions.
are more straightforward to measure from a
given data set. In particular, every wide-field survey in which
the shear 3PCF can be measured should yield a significant
measurement of these cross-correlation functions.
![\begin{displaymath}A^2 = \ell_1^2 \vartheta_1^2 + \ell_2^2 \vartheta_2^2 - 2\ell...
...\vartheta_2\right)^2 {\rm e} ^{-\rm i (\phi_3-\psi)} \right].
\end{displaymath}](/articles/aa/full/2005/12/aa1923/img153.gif)
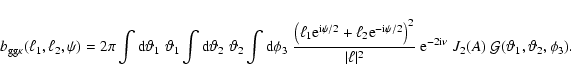
![$\displaystyle {2\over \pi}\int{\rm d}\vartheta\;\vartheta\int{\rm d}\phi\;
{ \l...
...ta\vartheta_2\cos~(\phi_3-\phi) \right]^3 }\;
G_-(\vartheta_1,\vartheta,\phi) ;$](/articles/aa/full/2005/12/aa1923/img171.gif)
![$\displaystyle {2\over \pi}\int{\rm d}\vartheta\;\vartheta\int{\rm d}\phi\;
{ \l...
...ta\vartheta_2\cos~(\phi_3-\phi) \right]^3 }\;
G_+(\vartheta_1,\vartheta,\phi) .$](/articles/aa/full/2005/12/aa1923/img172.gif)
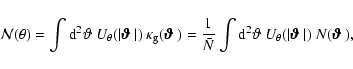
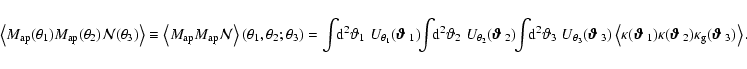
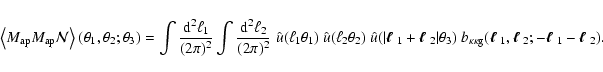
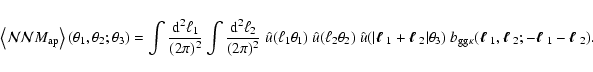
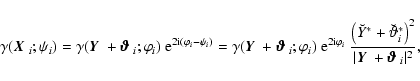
![]() were used in the definition of
were used in the definition of
![]() and
and
![]() .
Using the fact that
.
Using the fact that
![]() we
find, using Eq. (54), that since U is a compensated filter,
the additional terms arising from two point shear-shear correlations
vanish. Thus we make the following useful assertion that when working with
the aperture mass statistics, one need not subtract the contribution from the
shear 2PCF to compute the reduced three point
statistics.
we
find, using Eq. (54), that since U is a compensated filter,
the additional terms arising from two point shear-shear correlations
vanish. Thus we make the following useful assertion that when working with
the aperture mass statistics, one need not subtract the contribution from the
shear 2PCF to compute the reduced three point
statistics.
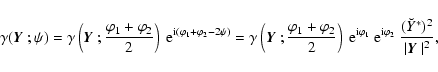
![]() .
Therefore, these convolution functions have
essentially finite support.
.
Therefore, these convolution functions have
essentially finite support.
![]() ,
where
,
where
![]() is the largest of the three aperture radii. The largest scale on
which the correlation functions can be measured is determined by the
geometry of the survey. For a large survey with contiguous area, this
scale is limited by the smallness of the signal when entering the
linear regime of structure evolution. In this case, the aperture
measures contain all the information contained in the measured
correlation functions. If the survey consists of independent patches
each of size
is the largest of the three aperture radii. The largest scale on
which the correlation functions can be measured is determined by the
geometry of the survey. For a large survey with contiguous area, this
scale is limited by the smallness of the signal when entering the
linear regime of structure evolution. In this case, the aperture
measures contain all the information contained in the measured
correlation functions. If the survey consists of independent patches
each of size ![]() ,
then the correlation functions can be measured
for angular scales up to
,
then the correlation functions can be measured
for angular scales up to
![]() ,
meaning that the aperture measures
are limited to
,
meaning that the aperture measures
are limited to
![]() .
In this case, the
measured correlation functions contain more information than the
aperture measures. In a future work, we plan to study these aspects;
note, however, that estimates of the "information content'' are
tedious, since they involve the covariance of third-order statistical
measures, and thus depend, in general, on six variables and have to be
estimated from sixth-order statistics.
.
In this case, the
measured correlation functions contain more information than the
aperture measures. In a future work, we plan to study these aspects;
note, however, that estimates of the "information content'' are
tedious, since they involve the covariance of third-order statistical
measures, and thus depend, in general, on six variables and have to be
estimated from sixth-order statistics.
![]() measures the same cross-bispectrum as the
third-order statistics considered by Ménard et al. (2003). In that paper, they
considered the correlation between pairs of foreground galaxies and background
QSOs. Due to the magnification of distant QSOs by the matter in which the
foreground galaxies are embedded, and the steep slope of bright QSO source
counts, such a correlation should be measurable with the large QSO sample
obtained by the Sloan Digital Sky Survey. Instead of magnification, we employ
the shear around galaxy pairs. Which of the two methods is better able to
measure the galaxy-mass bispectrum depends on the available observational
data. For deep wide-field images, the shear method investigated here will be
more efficient, given the sparseness of bright QSOs on the sky.
measures the same cross-bispectrum as the
third-order statistics considered by Ménard et al. (2003). In that paper, they
considered the correlation between pairs of foreground galaxies and background
QSOs. Due to the magnification of distant QSOs by the matter in which the
foreground galaxies are embedded, and the steep slope of bright QSO source
counts, such a correlation should be measurable with the large QSO sample
obtained by the Sloan Digital Sky Survey. Instead of magnification, we employ
the shear around galaxy pairs. Which of the two methods is better able to
measure the galaxy-mass bispectrum depends on the available observational
data. For deep wide-field images, the shear method investigated here will be
more efficient, given the sparseness of bright QSOs on the sky.
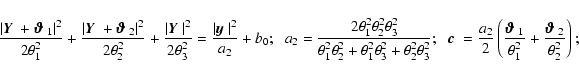
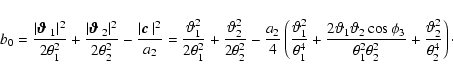
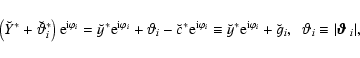
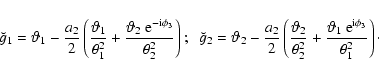
![\begin{displaymath}\int{\rm d}^2 y ~ F'_{MM{\cal N}}~ {\rm e}^{-\vert \mbox{\bol...
...reve{g}_1 \vartheta_2-2\breve{g}_1\breve{g}_2\right) \right].
\end{displaymath}](/articles/aa/full/2005/12/aa1923/img243.gif)
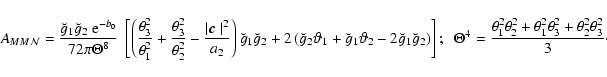
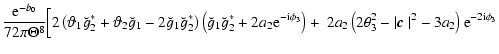
![$\displaystyle \hspace{5cm}
+ ~ 4 \breve{g}_1 \breve{g}^*_2 \left(2\theta_3^2 -\...
...^2}{a_2}\left(2\theta_3^2 -\vert \mbox{\boldmath$c$ } \vert^2 - a_2\right)\Big]$](/articles/aa/full/2005/12/aa1923/img251.gif)