A&A 432, 879-888 (2005)
DOI: 10.1051/0004-6361:20041793
Kinematics of RHB stars to trace the structure of the Galaxy
T. A. Kaempf1 - K. S. de Boer1 - M. Altmann1,2,3
1 - Sternwarte der Universität Bonn, Auf dem Hügel 71, 53121 Bonn,
Germany
2 - Dr. Remeis Sternwarte der Universität Erlangen-Nürnberg, Sternwartstr.
7, 96049 Bamberg, Germany
3 - Departamento de Astronomía de la Universidad de Chile, Camino del
Observatorio 1515, Las Condes, Chile
Received 4 August 2004 / Accepted 16 November 2004
Abstract
Red horizontal-branch (RHB) stars have been selected from the H IPPARCOS catalogue to investigate their kinematics and spatial distribution.
H IPPARCOS parallaxes, literature radial velocities and
H IPPARCOS proper motions, together with models for the gravitational potential of the Milky Way allow
a calculation of the actual velocity vectors and the orbits of the RHB stars.
The velocity characteristics are used to define a halo population sample (HPS)
in the collection of RHBs.
The orbits lead statistically to an overall z-distance probability
distribution, showing that the RHBs exhibit two populations,
a disk one having a scale height of
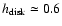 kpc
and a halo one of
kpc
and a halo one of  4 kpc. We have investigated the influence on our results
of parallax accuracy and of a demarcation line
in the HRD between the RHB and the red-giant (RG) star region.
Neither of them show marked effects.
We have performed the orbit analysis using the potential model
of Allen & Santillan as well as of Dehnen & Binney.
The results differ only slightly for the disk population, showing that these
potential models are not a critical part of such orbit investigations.
RHB scale height values are smaller than those found earlier for sdB stars,
most likely because the samples of stars used had different spatial
distributions a priori.
The data do not allow us to specify a trend in the kinematic behaviour of
star types along the horizontal branch.
4 kpc. We have investigated the influence on our results
of parallax accuracy and of a demarcation line
in the HRD between the RHB and the red-giant (RG) star region.
Neither of them show marked effects.
We have performed the orbit analysis using the potential model
of Allen & Santillan as well as of Dehnen & Binney.
The results differ only slightly for the disk population, showing that these
potential models are not a critical part of such orbit investigations.
RHB scale height values are smaller than those found earlier for sdB stars,
most likely because the samples of stars used had different spatial
distributions a priori.
The data do not allow us to specify a trend in the kinematic behaviour of
star types along the horizontal branch.
Key words: astrometry - stars: kinematics - stars: horizontal-branch - Galaxy:
general
1 Introduction
While it is rather simple to study the structure of other stellar systems from
images alone, the true shape of the Milky Way is very hard to determine.
With the help of ever growing galactic surveys one is finally able to
make use of highly accurate positions and motions of thousands of stars.
In conjunction with mass models of the Milky Way, such a wealth of data gives
us the first detailed glimpses of the structure and evolution of our own galaxy.
Choosing a single stellar type, in particular one with well-defined
luminosity, allows us to work with clean samples.
Late main-sequence (MS) stars were used to probe the solar vicinity within
several hundred parsecs, while giants and A type MS stars were observed up to
two kiloparsecs away. For regions of negligible interstellar extinction the stellar density field
was derived from these surveys (e.g. Becker 1940; Elvius 1951;
and Upgren 1963). Results from these studies established the idea of a multi-component galaxy,
consisting of a central bulge, a thin disk, a thick disk (found by
Gilmore & Reid 1983) and an encompassing halo.
Further information on the exact shapes of these components can then be used to
constrain theories of galactic evolution. Models for the formation history of the disk are separated into two families. If the thin disk is formed after the thick disk, one speaks of a
"top down'' scenario. Different examples of this model type are described in
Gilmore (1984), Sandage (1990), Norris & Ryan (1991), and Burkert et al. (1992).
If the thin disk is formed before the thick disk, it is called a
"bottom up'' scenario. Members of this group are the models of Norris (1987), Quinn et al. (1993), Kroupa (2002) and Gilmore & Reid (1983).
A summary of the various models is given by Majewski (1993).
With the astrometry satellite H IPPARCOS, an automated survey of stellar positions with unprecedented accuracy was made possible. Some 120 000 stars were observed for the main mission.
Data were collected in the Hipparcos Catalogue (ESA 1997).
In addition, the satellite provided two-colour photometry for slightly more than
one million stars. The data were reported in the Tycho Catalogue (ESA 1997).
Among the brighter old stars easily identifiable from optical observations
are the RR Lyr stars and blue subdwarf stars. These are stars of the horizontal branch (HB),
consisting of a 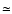 0.5
0.5 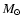 He core surrounded by a hydrogen shell
ranging in mass from negligible to up to about 0.5
He core surrounded by a hydrogen shell
ranging in mass from negligible to up to about 0.5 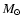 .
From thin to thick shells, the stars are classified as
sdO, sdB, HBB and HBA stars, followed by the RR Lyr stars,
and finally the "massive'', red HB (RHB) stars.
Of these, the sdB and RR Lyr stars are the easiest to spot and characterize.
The former show a simple relation between the line strengths of the Balmer
series and
.
From thin to thick shells, the stars are classified as
sdO, sdB, HBB and HBA stars, followed by the RR Lyr stars,
and finally the "massive'', red HB (RHB) stars.
Of these, the sdB and RR Lyr stars are the easiest to spot and characterize.
The former show a simple relation between the line strengths of the Balmer
series and
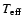 and
and  .
The latter, as variable stars, are identified by their characteristic light curve.
.
The latter, as variable stars, are identified by their characteristic light curve.
Several studies exist dealing with the spatial distribution of sdB stars.
Heber (1986) and Moehler et al. (1990) found vertical distributions
with scale heights of  200 pc, way too small for old stars.
However, Villeneuve et al. (1995b) and Villeneuve et al. (1995a) showed that larger values are
more realistic. In two extensive studies of the kinematics of sdB stars
(de Boer et al. 1997; Altmann et al. 2004)
it could be shown that the sdB stars seen in the solar neighbourhood
are divided in two populations,
a disk one with a scale height of
200 pc, way too small for old stars.
However, Villeneuve et al. (1995b) and Villeneuve et al. (1995a) showed that larger values are
more realistic. In two extensive studies of the kinematics of sdB stars
(de Boer et al. 1997; Altmann et al. 2004)
it could be shown that the sdB stars seen in the solar neighbourhood
are divided in two populations,
a disk one with a scale height of 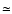 1 kpc and an extended one
chracterized by a scale height of
1 kpc and an extended one
chracterized by a scale height of  7 kpc.
Furthermore, trends were seen in the kinematics of HB star samples.
The cooler Blue HB (BHB) star samples seemed to be more
dominated by the halo population than the sdB star sample (Altmann & de Boer 2000).
7 kpc.
Furthermore, trends were seen in the kinematics of HB star samples.
The cooler Blue HB (BHB) star samples seemed to be more
dominated by the halo population than the sdB star sample (Altmann & de Boer 2000).
In this study we investigate the kinematics and spatial distribution
of the red HB stars. Finding RHBs in a sky field is not without difficulty.
By just looking at colours, one can easily confuse them with MS stars, subgiants, red-clump stars and blue-loop stars. Without knowledge of absolute magnitudes it is therefore not possible to select
RHBs just by colour. Using H IPPARCOS data we are able to resolve this matter.
Moreover, it gives us a rather large sample of RHBs to work with.
To characterize the large scale distribution of stars
of a given type one in principle would need to know the location
of such stars in complete large distance samples.
For our H IPPARCOS RHB stars this is illusionary,
since the sample is complete out to perhaps 100 pc
(see Sect. 3.2.4).
However, the kinematics of the RHB stars also give information
about past and future locations.
We will calculate the galactic orbits (as in de Boer et al. 1997; Altmann et al. 2004)
of the RHB stars and analyze the orbit statistics to arrive at mean spatial distributions.
The organisation of this paper is the following.
We begin with the assembly of our data sample in Sect. 2.
Errors and selection effects of the sample are described in Sect. 3.
The analysis of the orbits of the selected RHBs is given in Sect. 4,
while Sect. 5 compares results using different models for the
galactic potential. We conclude with a final discussion in Sect. 6.
2 Establishing the RHB data sample
Tautvaisiene (1996) and Rose (1985) give observational methods to find RHB stars
through photometriy and spectroscopy.
However, the simplest way to define the state of evolution of stars is given by
their location in the HRD.
Using H IPPARCOS data we created a colour magnitude diagram of stars not listed in
the Catalogue of the Components of Double
and Multiple Stars (Dommanget & Nys 2002), having
(B-V) 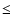 0.025 mag, and relative parallax error smaller than 20%.
The RHB stars could then be selected from the diagram by choosing an appropriate
range in MV and (B-V) by eye (see Fig. 1).
CMDs of globular clusters like 47 Tuc helped choose the proper magnitude and
colour ranges.
We also confirmed that the spectroscopically identified RHB stars
from Behr (2003) mostly fulfil the selection criteria.
0.025 mag, and relative parallax error smaller than 20%.
The RHB stars could then be selected from the diagram by choosing an appropriate
range in MV and (B-V) by eye (see Fig. 1).
CMDs of globular clusters like 47 Tuc helped choose the proper magnitude and
colour ranges.
We also confirmed that the spectroscopically identified RHB stars
from Behr (2003) mostly fulfil the selection criteria.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1793fig1.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg30.gif) |
Figure 1:
CMD of single H IPPARCOS stars with
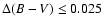 and
and
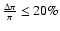 .
The stars inside the window are our selected
RHB candidates. The window borders are: .
The stars inside the window are our selected
RHB candidates. The window borders are:
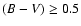 , ,
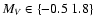 , ,
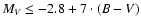 , ,
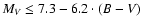 .
The dash-dotted line marks the window separation border of
Sect. 4.4.3 while the dashed line marks the alternative cut-off of
Sect. 4.4.2. .
The dash-dotted line marks the window separation border of
Sect. 4.4.3 while the dashed line marks the alternative cut-off of
Sect. 4.4.2. |
| Open with DEXTER |
Table 1:
Numbers of stars at various selection steps as a function of relative
parallax error. The three BB2k columns show: number of RHB sample stars found,
total number of measurements, number of stars that are fainter than 7.3 mag, the completeness limit of the H IPPARCOS mission.
For more on the complexities of the boundary line toward the giant branch
see Sect. 3.2.2.
Five samples were assembled from stars within this window.
These sets differ in parallax precisions, with each having
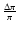 lower than 10%, 15%, 20%, 25%, and 30%, respectively. Thus, with such a criterion, we almost get a volume-complete sample for
spheres with a rather blurry boundary. Effects from this sample definition are discussed in Sect. 4.4.1 for the 10%, 20%, and 30% samples.
Table 1 gives the number of stars in the samples at different
points of the assembly process.
lower than 10%, 15%, 20%, 25%, and 30%, respectively. Thus, with such a criterion, we almost get a volume-complete sample for
spheres with a rather blurry boundary. Effects from this sample definition are discussed in Sect. 4.4.1 for the 10%, 20%, and 30% samples.
Table 1 gives the number of stars in the samples at different
points of the assembly process.
To reconstruct the full spatial motion, radial velocities are required.
H IPPARCOS did not have a dedicated instrument to measure
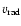 and so
we chose the recent release of the General Catalog of mean radial
velocities by Barbier-Brossat & Figon (2000); (hereafter BB2k).
By cross-checking our candidate RHBs with BB2k we found radial velocities for 35% up to 83% of our HIP stars, depending on the parallax accuracy (Table 1).
This already hints at selection effects that are discussed in
Sect. 3.2.
and so
we chose the recent release of the General Catalog of mean radial
velocities by Barbier-Brossat & Figon (2000); (hereafter BB2k).
By cross-checking our candidate RHBs with BB2k we found radial velocities for 35% up to 83% of our HIP stars, depending on the parallax accuracy (Table 1).
This already hints at selection effects that are discussed in
Sect. 3.2.
3 Error limits and selection effects
3.1 Error limits
Measurement errors for the H IPPARCOS objects vary not only with brightness but also
with celestial position. This is due to the scanning law because certain areas in the sky were
observed more often than others. Therefore, for all HIP stars of
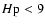 mag (the faintest of our stars has
mag (the faintest of our stars has
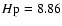 mag) we only cite median precisions.
They are 0.97 mas for the parallaxes and 0.88 mas/yr and 0.74 mas/yr for
mag) we only cite median precisions.
They are 0.97 mas for the parallaxes and 0.88 mas/yr and 0.74 mas/yr for
 =
=
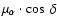 and
and
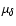 ,
respectively. Systematic errors were estimated to be below 0.1 mas.
,
respectively. Systematic errors were estimated to be below 0.1 mas.
Errors from BB2k depend on the source from which the radial velocity was taken.
Single high resolution spectra, of course, yield better results compared to
big surveys at low resolution.
However, errors are usually below 10
 and never higher than 20
and never higher than 20
 for our samples.
for our samples.
H IPPARCOS proper motion uncertainties for stars of our sample are equal to 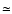 2
2
 .
Therefore the total error in space velocity is dominated by the uncertainty of the radial component.
Thus, we estimate the total error in space velocity to be about 10
.
Therefore the total error in space velocity is dominated by the uncertainty of the radial component.
Thus, we estimate the total error in space velocity to be about 10
 .
.
3.2 Possible selection effects
3.2.1 H IPPARCOS stars and measurement accuracy
H IPPARCOS was an astrometric mission that used a list of objects to be
observed, the H IPPARCOS Input Catalogue (HIC) by Turon et al. (1992).
A magnitude-complete set down to 7.3 mag was assembled, some 52 000 objects.
Any stars fainter than that limit came from individual proposals.
The selection effects so introduced cannot be quantified.
For the number of stars in our sample fainter than 7.3 mag
see Table 1.
H IPPARCOS parallaxes are usually determined at an average precision of 0.8 mas for
high ecliptic latitudes, and around 1.2 mas near the ecliptic.
High accuracy areas for
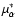 are roughly at
are roughly at
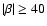
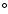 (0.8 mas yr-1, down from 1.3 mas yr-1). For
(0.8 mas yr-1, down from 1.3 mas yr-1). For
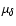 on average the standard error is 0.8 mas yr-1.
No position-dependent colour errors are given in ESA (1997).
on average the standard error is 0.8 mas yr-1.
No position-dependent colour errors are given in ESA (1997).
The mission's 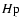 passband was more sensitive to blue light (Fig. 1.3.1 in
ESA 1997). Redder stars, therefore, show a higher uncertainty in their measurements.
Since our stars are usually brighter than V=8 mag, this effect is small and
probably only shows up in the crowded region of the RGB cut-off.
passband was more sensitive to blue light (Fig. 1.3.1 in
ESA 1997). Redder stars, therefore, show a higher uncertainty in their measurements.
Since our stars are usually brighter than V=8 mag, this effect is small and
probably only shows up in the crowded region of the RGB cut-off.
3.2.2 Boundary of RHB and red clump
The definition of our RHB sample in the CMD is a selection effect in its
own right. While the range in luminosity and the boundary on the side of the MS can be easily defined, the separation from the red-giant branch (RGB) is less certain.
In particular, that region of the CMD contains the "Red Clump'',
a region where three main types of stars are found.
First, there are the RG stars evolving upwards in the CMD
(but having an uneven distribution along the RG).
These are mostly contributing to the red part of the Red Clump, and are thus
excluded from our sample. Second, there are the red HB stars distributed horizontally toward the RGB but of which the ones with mass up to 1.5 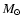 are located above and
somewhat bluer than the reddest end of the HB range (see e.g. Sweigart 1987; Seidel et al. 1987 for the overall shape of the HB).
Finally, the yet more massive blue loop stars may contribute to the
more luminous part of the Red Clump region.
A full discussion of the complexities can be found in Gallart (1998).
are located above and
somewhat bluer than the reddest end of the HB range (see e.g. Sweigart 1987; Seidel et al. 1987 for the overall shape of the HB).
Finally, the yet more massive blue loop stars may contribute to the
more luminous part of the Red Clump region.
A full discussion of the complexities can be found in Gallart (1998).
Since all HB stars have essentially the same life time irrespective
of their mass, the possible presence of younger (and thus more massive)
RHBs cannot be neglected.
Young RHBs exhibit disk kinematics and we may expect the disk population
to be more dominant in our sample.
Effects of the choice of the boundaries in the CMD
(see Fig. 1) will be discussed in Sects. 4.4.2 and 4.4.3.
3.2.3 Radial velocity catalogues
The BB2k data are a compendium of measured radial velocities from various
sources published before December 1990.
By looking at how many of the RHBs compared to the whole HIP stars can be found in the BB2k catalogue, we can estimate how well, compared to
other stellar types, our RHB stars are represented in BB2k.
We limit the search to objects brighter than 7.3 mag in V for completeness
reasons. A total of 15 752 single stars fit this criteria, with 2052 falling in
our RHB window. BB2k lists entries for 9446 (60%) and 1101 (54%) of these categories,
respectively. We conclude that our RHB candidate stars are not significantly undersampled in BB2k.
3.2.4 Overall effects
Considering the properties of the catalogues used and our selection criterion,
we can estimate the volume completeness of our sample.
H IPPARCOS measured all stars down to 7.3 mag.
In conjunction with our lower absolute magnitude limit of 1.8 mag gives (assuming negligible extinction) a completeness radius of 126 pc. The BB2k is not magnitude complete.
Some 1600 RHB candidates with
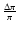
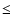 30% and brighter than 7.3 mag are not
listed in BB2k. A merging of the two catalogues thus shrinks the completeness radius.
For
30% and brighter than 7.3 mag are not
listed in BB2k. A merging of the two catalogues thus shrinks the completeness radius.
For
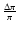
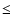 30% the new limiting magnitude is 6.4 mag corresponding to a
distance of 83 pc. In contrast to Altmann et al. (2004), we are not limited towards the bright magnitudes.
Thereby it is certain that all nearby candidate RHBs are included in our sample.
30% the new limiting magnitude is 6.4 mag corresponding to a
distance of 83 pc. In contrast to Altmann et al. (2004), we are not limited towards the bright magnitudes.
Thereby it is certain that all nearby candidate RHBs are included in our sample.
For all objects with 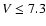 mag we know the HIC to be complete.
Measurement errors of these objects are such that we can confirm the correct
CMD position for 91.3% of our RHB sample. The only other factor of influence is the BB2k, which gives
mag we know the HIC to be complete.
Measurement errors of these objects are such that we can confirm the correct
CMD position for 91.3% of our RHB sample. The only other factor of influence is the BB2k, which gives
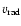 for
for  54% of the selected HIP stars. A total percentage of completeness for these bright stars is then found to be
54% of the selected HIP stars. A total percentage of completeness for these bright stars is then found to be
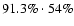
 50%.
For our fainter objects this value decreases to
50%.
For our fainter objects this value decreases to 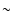 20%
if we assume that the HIC only contains half of all fainter RHBs.
20%
if we assume that the HIC only contains half of all fainter RHBs.
4 The spatial distribution of RHB stars
4.1 Distribution from position and velocity
A histogram of the circular velocity 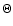 of our sample shows
a high narrow peak located at roughly
of our sample shows
a high narrow peak located at roughly
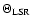 .
These are the thin disk stars. After taking out this group,
the presence of a broader distribution centered around
.
These are the thin disk stars. After taking out this group,
the presence of a broader distribution centered around
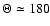
 becomes apparent. It may represent the group often called the thick disk.
Finally, there are stars covering a wide range of values of
becomes apparent. It may represent the group often called the thick disk.
Finally, there are stars covering a wide range of values of
![$\Theta \in
[-100,+340]$](/articles/aa/full/2005/12/aa1793/img47.gif)
 .
These are the halo stars in our sample.
However, we cannot assign an individual star to these groups
and therefore no velocity dispersions were calculated.
.
These are the halo stars in our sample.
However, we cannot assign an individual star to these groups
and therefore no velocity dispersions were calculated.
The separation of the thick and thin disk stars can be seen clearly in a Toomre diagram
(Fig. 2). A large number of objects cluster in the region with
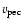
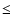 50
50
 .
These are mainly thin disk stars that are moving along with the LSR.
Stars in a range of 50
.
These are mainly thin disk stars that are moving along with the LSR.
Stars in a range of 50 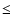
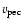
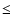 150
150
 are mostly thick disk objects.
They are lagging behind in
are mostly thick disk objects.
They are lagging behind in 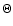 because they are kinematically heated up
compared to thin disk stars. This effect is known as the asymmetric drift of the thick disk (see e.g. Binney & Tremaine 1987).
because they are kinematically heated up
compared to thin disk stars. This effect is known as the asymmetric drift of the thick disk (see e.g. Binney & Tremaine 1987).
All other stars, upwards of
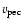 = 150
= 150
 ,
must be halo objects.
Some have large perpendicular velocities, both with prograde and retrograde
orbits. Stars with large peculiar velocities include those staying in the disk but
having highly non-circular orbits.
An example of these is the star with
,
must be halo objects.
Some have large perpendicular velocities, both with prograde and retrograde
orbits. Stars with large peculiar velocities include those staying in the disk but
having highly non-circular orbits.
An example of these is the star with
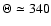
 ,
which
never strays further than 530 pc from the galactic plane.
We make a rough selection of halo objects for further analyses and will refer
to these 25 stars as the Halo Population Sample (HPS).
,
which
never strays further than 530 pc from the galactic plane.
We make a rough selection of halo objects for further analyses and will refer
to these 25 stars as the Halo Population Sample (HPS).
The separation of the populations can be further investigated with the help of
a Bottlinger diagram (Fig. 3). Stars of the above defined HPS are marked by heavier points and show velocities that are very different from the LSR.
Other stars outside of the enlarged frames (Fig. 3, right side) are
most certainly thick disk stars.
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{1793fig2.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg50.gif) |
Figure 2:
The Toomre diagram of our
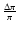 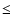 30% sample. The circles show
the peculiar velocity
30% sample. The circles show
the peculiar velocity
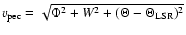 with respect to the LSR. Up to a peculiar velocity of 50 with respect to the LSR. Up to a peculiar velocity of 50
 the sample is
distributed rather evenly. Upwards of these values the stars fall short in
orbital velocity. These objects are halo and thick disk stars.
the sample is
distributed rather evenly. Upwards of these values the stars fall short in
orbital velocity. These objects are halo and thick disk stars. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1793fig3.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg51.gif) |
Figure 3:
The Bottlinger diagram of our
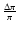 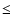 30% sample. The
panels at right show the enlarged regions marked by squares in the left panels.
Heavier points are for the Halo Population Sample (HPS) stars.
The circle symbols denote solar values.
Note the two groups of stars in the more detailed
30% sample. The
panels at right show the enlarged regions marked by squares in the left panels.
Heavier points are for the Halo Population Sample (HPS) stars.
The circle symbols denote solar values.
Note the two groups of stars in the more detailed
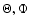 panel. panel. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{1793fig4.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg52.gif) |
Figure 4:
Meridian plots of some of the calculated orbits in a model by
Allen & Santillan (1991). The top row shows
orbits of HPS stars. The middle row shows the orbit of the fastrunner star HIP 98269 ( left) while the other two are thick disk candidates. The bottom row depicts thin disk orbits. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1793fig5.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg53.gif) |
Figure 5:
Logarithmic histograms, that show the complete
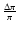 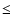 30% sample (gray) and the contribution of our HPS stars (black).
We have added a constant offset for visibility reasons.
The ecc-histogram shows a separation of populations around 0.45.
As expected, the halo stars show much higher eccentricities than the disk
stars. In the nze-histogram the halo stars do not only build the tail of the
distibution, but also account for low values.
The peak on the right side of the diagram includes the stars with
higher normalized z-extent than plotted.
30% sample (gray) and the contribution of our HPS stars (black).
We have added a constant offset for visibility reasons.
The ecc-histogram shows a separation of populations around 0.45.
As expected, the halo stars show much higher eccentricities than the disk
stars. In the nze-histogram the halo stars do not only build the tail of the
distibution, but also account for low values.
The peak on the right side of the diagram includes the stars with
higher normalized z-extent than plotted. |
| Open with DEXTER |
The right half of Fig. 3 shows the values similar to the LSR in more
detail. The
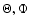 -diagram shows a separation into two groups.
Such structures are well known and have been analysed in various studies.
Several stellar streams were already found in the U,V distribution of H IPPARCOS data.
Skuljan et al. (1999) even associated close star clusters with some of these
streams. We refer to Skuljan et al. (1999) and Nordström et al. (2004) for more on that topic.
-diagram shows a separation into two groups.
Such structures are well known and have been analysed in various studies.
Several stellar streams were already found in the U,V distribution of H IPPARCOS data.
Skuljan et al. (1999) even associated close star clusters with some of these
streams. We refer to Skuljan et al. (1999) and Nordström et al. (2004) for more on that topic.
4.2 Population assignment from orbit data
We have calculated the orbits of our stars based on
the galactic potential model of Allen & Santillan (1991) (hereafter AS)
using an orbit code developed by Odenkirchen & Brosche (1992), and
further adapted for our work (de Boer et al. 1997; Altmann et al. 2004).
Orbits are calculated in steps of 1 Myr over a time span of 10 Gyr
(since we are not modeling the evolution of the Galaxy, this long span,
although physically unrealistic,
is allowed for a good sampling of the shape of wide orbits).
A selected few orbits can be seen in Fig. 4.
Most of the orbits are of a regular box shape.
A few are irregularly shaped, perhaps a result of the close approach of the
star to the galactic center and thus the interaction with the Bulge potential.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1793fig6.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg54.gif) |
Figure 6:
Diagram of 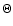 (gray triangles) and
(gray triangles) and
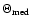 (black
squares) against total kinetic energy and median kinetic energy, respectively.
Filled symbols are stars of the HPS.
The parabolas are isovelocity lines for
(black
squares) against total kinetic energy and median kinetic energy, respectively.
Filled symbols are stars of the HPS.
The parabolas are isovelocity lines for 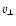 ,
which is
orthogonal to ,
which is
orthogonal to 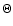 .
Medianised values lie on an almost straight line
pointing from the LSR data point towards lower .
Medianised values lie on an almost straight line
pointing from the LSR data point towards lower
 and
and
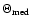 . . |
| Open with DEXTER |
By looking at histograms of the orbit eccentricities and normalized z-extents
(Fig. 5), we qualitatively come to the same conclusions as in
Altmann et al. (2004).
In the ecc-histogram, a separation between a high and low eccentricity
sample can be made with the help of the HPS.
It is roughly at ecc=0.45, above which the halo stars dominate the
distribution.
In the nze-histogram, the stars at nze > 0.3 are clearly of the HPS.
But HPS stars also contribute to the peak at low normalized z-extents,
since our definition of the HPS does not exclude highly eccentric, coplanar orbits.
Figure 6 shows the kinetic energy versus orbital velocity
of our star sample. Both the measured and medianised values are given.
Looking at the median values, one can see that most of the disk stars are
situated along a line pointing from the LSR towards lower
 and
and
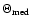 .
A clear gap can be seen at
.
A clear gap can be seen at
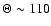
 ,
below which there are only HPS stars.
,
below which there are only HPS stars.
Using the information from Fig. 2 we have separated the HPS stars
from the disk stars, a separation confirmed through the kinematic
representation of Figs. 3, 5, and 6.
However, individual stars of one group may still be included in the other group.
4.3 Spatial distribution from orbit statistics
From the sum of the orbits we obtain the z-probability distribution of
our sample stars, as introduced in de Boer et al. (1997) and further refined in
Altmann et al. (2004). We analysed it for disk and halo populations with a weighted 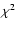 -fit.
The large range in N(z) made a weighting scheme necessary that could take
into account both the disk region and halo region data points.
We chose 1/N(z) as a weight to accomplish that goal.
A simple exponential relation of the form
-fit.
The large range in N(z) made a weighting scheme necessary that could take
into account both the disk region and halo region data points.
We chose 1/N(z) as a weight to accomplish that goal.
A simple exponential relation of the form
 was fitted for each component. where N(0) is the star number density in the local galactic plane and h is the scale height. Both sides of the distribution were used for the calculations.
was fitted for each component. where N(0) is the star number density in the local galactic plane and h is the scale height. Both sides of the distribution were used for the calculations.
Analyses of the orbits showed that the data points with z>8 kpc are from
three stars only. They are HD 126778, HD 175305 and HD 184266.
All the other HPS stars show strongly elliptic orbits close to the galactic plane.
Figure 7 shows the z-probability distribution, as well as the best
fits. First, a two-component fit, representing the disk and the halo, was made.
But in the range of 2-5 kpc the full z-distribution is not very well
approximated (see left half of Fig. 7).
We therefore also made a three component fit. The results give a much better fit to the data than with only two components (right half of Fig. 7).
Assuming that exponential functions apropriately describe the
z-distribution, our data suggests the existence of more than two spatially
distinct stellar groups.
Table 2:
The fit results of the z-probability distribution from
Fig. 7. Scale heights and number densities are
given for each fitted component. For a two-component fit no "thick disk''
values were determined.
![\begin{figure}
\par\includegraphics[angle=270,width=8.3cm,clip]{1793fig7.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg64.gif) |
Figure 7:
The z-probability distribution of our
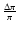  30% stars with
a two-component and a three-component z-distribution exponential fit,
shown in the left and right halves of the diagram, respectively.
Fitted curves are: thin dashed ones the individual population components (see
Sect. 4.3), thick dashed ones are the complete fits.
Note that the three-component fit is a better approximation of the actual
distribution.
30% stars with
a two-component and a three-component z-distribution exponential fit,
shown in the left and right halves of the diagram, respectively.
Fitted curves are: thin dashed ones the individual population components (see
Sect. 4.3), thick dashed ones are the complete fits.
Note that the three-component fit is a better approximation of the actual
distribution. |
| Open with DEXTER |
The results of the fits are given in Table 2.
We note that the scale heights of the halo are derived from only three stellar orbits and are only listed for completeness.
The results obtained are based on what will be called the base-line model.
Below we will explore star selections with different parallax accuracies
or selected with different magnitude and colour limits (as in
Fig. 1). We will also explore (in Sect. 5) the effects of different
models for the mass distribution in the Milky Way on our base-line results.
4.4.1 Samples with 10, 20, 30% parallax accuracy
In Sect. 2 we briefly gave some details on star samples with
different
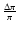 constraints. By analysing the 10% and 20% samples we can derive some information on the spatial distribution of the stellar populations. This implies dealing with smaller samples and thus a deterioration in number statistics.
constraints. By analysing the 10% and 20% samples we can derive some information on the spatial distribution of the stellar populations. This implies dealing with smaller samples and thus a deterioration in number statistics.
Diagrams derived from the current velocities are qualitatively the same for all
the samples. A closer inspection of the Toomre diagram shows that a majority
of our objects are stars with thin disk orbit characteristics and only a minor
fraction is of a halo like type. Disk stars are included in all the samples in a large
enough quantity for analyses. In the U,V-diagram, the bimodality of the data can still be seen, even in the 10% sample. This is due to the fact that the separation is observed for disk stars, and
they are adequately represented in all the percentage sets.
In contrast, only three of the HPS stars have a relative parallax error below 10%.
This low number implies that with these we cannot make a meaningful
analyses for the halo. For
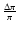
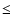 20%, the number of HPS stars is twelve.
20%, the number of HPS stars is twelve.
The orbital data thus confirms the similarity of the composition of the
error-selected samples.
For the disk stars, the histograms are of similar shape
and HPS stars of the 10% and 20% sample are also present with
eccentricities larger than 0.4. We conclude that no kinematical preference can be found in the closer samples.
Even though we have very low numbers of stars for a z-distribution analysis
in the 10% sample (see Table 1), we give rough estimates
on the scale heights. They are 0.12 kpc for the thin disk, 0.34 kpc for the thick
disk and 8 kpc for the halo. Scale heights of the 20% sample are 0.12 kpc, 0.46 kpc, and 9 kpc,
respectively. These results are not different in an essential way from those of
Table 1.
4.4.2 Influences of the RHB-RGB separation line
Another, perhaps critical aspect of our RHB selection from H IPPARCOS data is the
heavily populated location of the window border at the RG branch.
By excluding more of the critical red stars, we can check for influences of
giants and see if our above results still hold.
A new separation was adopted, by shifting the line towards brighter MV by
0.5 mag (see dashed line in Fig. 1).
We thereby excluded almost half of the full
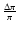
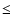 30% sample ending
up with some 1942 H IPPARCOS stars. From these stars, 731 had 789 measurements documented in BB2k (1327 stars in the full sample, see Table 1).
30% sample ending
up with some 1942 H IPPARCOS stars. From these stars, 731 had 789 measurements documented in BB2k (1327 stars in the full sample, see Table 1).
With this new and restricted sample we noted several things.
The velocity histogram shows that some of the stars lagging
behind the disk rotation are now missing.
The histogram of thick disk velocity stars now consists of several peaks.
Stars with thin disk velocities are also less numerous, but the peak is
still very similar in shape.
Looking at the Toomre diagram allows the identification of the "missing''
stars. We found that only 15 of the HPS stars are still included in the
restricted sample, but the relative number of HPS to disk stars stays the same (1.9% compared
to 2.1% for the base-line sample). In addition, a reduction of star numbers in the range of
100

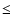
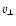
 150
150
 was noticed. The absence of these objects explains new gaps in the ecc-histogram (at ecc=0.35) and
was noticed. The absence of these objects explains new gaps in the ecc-histogram (at ecc=0.35) and 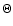 ,
,
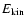 -diagram (at
-diagram (at
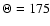
 ). In contrast, the Bottlinger diagram and the histogram of normalized
z-extent are qualitatively the same as with the base-line sample.
). In contrast, the Bottlinger diagram and the histogram of normalized
z-extent are qualitatively the same as with the base-line sample.
Thus, we derived the scale heights for this restriced
sample via a 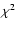 -fit from the z-probability distribution
results for the disks in
-fit from the z-probability distribution
results for the disks in
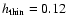 kpc and
kpc and
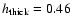 kpc.
For the halo we get
kpc.
For the halo we get
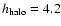 kpc.
kpc.
4.4.3 Non HB stars
In the selection window there is a potential contamination of stars that do not
belong to the HB, such as massive core helium burners or RG stars
(see Sect. 3.2.2).
Core helium burners are more massive than RHB stars and evolve faster.
The probability to find these inside our window is small.
RG stars of solar metallicity found within our selection window are younger
than 1.25 billion years (Yonsei-Yale isochrones by Kim et al. 2002).
Assuming a constant Star Formation Rate (SFR) and an observed RGB
only of solar metallicity, we would
expect that an RGB of
![$\left[\frac{M}{H}\right]$](/articles/aa/full/2005/12/aa1793/img69.gif) = -0.5 dex would lie roughly 0.25 mag to the blue.
RG Stars of that metallicity develop faster by some 50% (derived from
Yonsei-Yale evolutionary tracks by Yi et al. 2003), so this metal-poor
RGB would in the CMD be at two-thirds of the observed RGB's density.
However, the density bluewards of the observed RGB is much lower than that.
Had the SFR in the past been smaller, then the contamination of our sample is
smaller, too. If the SFR had been larger in the past, we would see many more RGs of bluer
colour than actually are seen in the H IPPARCOS CMD. All this shows that a contamination of our RHB sample (if present) comes from young stars and not from old, metal-poor RG stars.
= -0.5 dex would lie roughly 0.25 mag to the blue.
RG Stars of that metallicity develop faster by some 50% (derived from
Yonsei-Yale evolutionary tracks by Yi et al. 2003), so this metal-poor
RGB would in the CMD be at two-thirds of the observed RGB's density.
However, the density bluewards of the observed RGB is much lower than that.
Had the SFR in the past been smaller, then the contamination of our sample is
smaller, too. If the SFR had been larger in the past, we would see many more RGs of bluer
colour than actually are seen in the H IPPARCOS CMD. All this shows that a contamination of our RHB sample (if present) comes from young stars and not from old, metal-poor RG stars.
We check for this contamination of our RHB sample by separating the
selection window in two parts. The Blue Sample is defined as having (B-V) 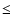 0.85 mag, while the other stars are assigned to the Red Sample (see Fig. 1).
Stars that belong to the bluer sample are certain to be RHBs.
These 99 stars include 6 HPS stars. The Red Sample contains 1228 stars, including 19 HPS stars.
0.85 mag, while the other stars are assigned to the Red Sample (see Fig. 1).
Stars that belong to the bluer sample are certain to be RHBs.
These 99 stars include 6 HPS stars. The Red Sample contains 1228 stars, including 19 HPS stars.
The analyses of the two samples suggest that there are no
significant differences in kinematic behaviour.
The Blue Sample does have a comparatively higher fraction of halo stars,
including the two stars that have orbits reaching out to z>10 kpc.
Scale heights of the Blue Sample are found to be
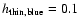 kpc,
kpc,
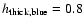 kpc, and
kpc, and
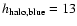 kpc.
For the Red Sample we obtain
kpc.
For the Red Sample we obtain
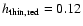 kpc,
kpc,
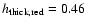 kpc, and
kpc, and
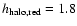 kpc.
The latter value is so low because the far-out moving halo stars are part of the
Blue Sample.
kpc.
The latter value is so low because the far-out moving halo stars are part of the
Blue Sample.
Had our base-line sample been contaminated by stars of non-HB nature, in other words mostly younger stars, then the z-distribution from the various samples should show significant
differences in the thin disk component. This was not observed and we therefore conclude
that we are essentially working with just RHB stars.
5 Effects of galactic mass models
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{1793fig8.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg76.gif) |
Figure 8:
Meridian plots of some of the calculated orbits in the "2b''
potential by Dehnen & Binney (1998). The same stars as in Fig. 4 were used to
allow comparisons. The orbits shown are the ones differing most between the AS and DB potential
models (see Sect. 5). |
| Open with DEXTER |
Several models have been proposed to describe the true gravitational potential
of our galaxy, e.g., by AS, Flynn et al. (1996), Johnston et al. (1995), and
Dehnen & Binney (1998) (hereafter DB). Thusfar we have used the AS model, with
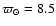 kpc and
kpc and
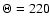
 .
Here we want to compare our results for the orbit statistics with those derived
using one of the DB models. They are using different shapes for the disk and spheroidal potentials.
We traced the orbits of our selected RHB candidates in their
potential called "2b''. It was chosen, because with
.
Here we want to compare our results for the orbit statistics with those derived
using one of the DB models. They are using different shapes for the disk and spheroidal potentials.
We traced the orbits of our selected RHB candidates in their
potential called "2b''. It was chosen, because with
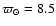 kpc and
kpc and
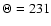
 it is the one most similar to the AS model. Fits to the models yield the following Oort constants:
A=12.95
it is the one most similar to the AS model. Fits to the models yield the following Oort constants:
A=12.95
 kpc-1 B=-12.95
kpc-1 B=-12.95
 kpc-1 for the model by AS
and A=13.8
kpc-1 for the model by AS
and A=13.8
 kpc-1 B=-13.3
kpc-1 B=-13.3
 kpc-1 for the "2b'' model by DB.
To further facilitate comparisons with previous results, we chose the same time
constraints (10 Gyr backwards in 1 Myr steps).
kpc-1 for the "2b'' model by DB.
To further facilitate comparisons with previous results, we chose the same time
constraints (10 Gyr backwards in 1 Myr steps).
In Fig. 8 we provide the meridional plots of the same stars as in
Fig. 4 from the "2b'' potential. The orbits of the first two objects shown appear to have changed considerably in the meridional plot,
but they still retain almost the same eccentricities and normalized z-extents.
For the following two, reaching far out in 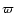 ,
ecc and nze change.
Since these stars stay closer to the galactic center in the "2b'' potential of DB, the ecc decreases, while nze increases. Other orbits for disk stars appear to be largely unchanged on the plotted scales.
,
ecc and nze change.
Since these stars stay closer to the galactic center in the "2b'' potential of DB, the ecc decreases, while nze increases. Other orbits for disk stars appear to be largely unchanged on the plotted scales.
Differences in ecc and nze between the orbits in the AS and DB potentials
for the whole 30% ensemble are given in Fig. 9.
On average, a slight decrease of ecc can be seen in Fig. 9a,
while in normalised z-extent (Fig. 9b) the
disk stars lie slightly above zero, documenting larger values of nze in the
"2b'' potential. A closer look at the data revealed this to be a simultaneous effect of an
increase of
 and decrease of
and decrease of
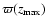 .
These differences arise from the different characteristics of the two potentials.
.
These differences arise from the different characteristics of the two potentials.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1793fig9.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg83.gif) |
Figure 9:
Comparison of the eccentricities a) and normalized z-extents b) of our stars in the potential of Allen & Santillan (AS) and the "2b'' potential of
Dehnen & Binney (DB). The HPS stars are given as filled
symbols, the others as grey open circles. Orbits are less eccentric in the DB
than in the AS potential. In nze there is a large scatter in the differences. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=8.4cm,clip]{1793fi10.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg85.gif) |
Figure 10:
The z-distribution of our
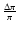 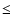 30% RHB sample in the "2b'' potential by DB.
The maximum |Z| values are roughly 18 kpc, which is lower than in a potential
from AS. This flatter distribution of the halo group is reflected in the fit
parameters:
30% RHB sample in the "2b'' potential by DB.
The maximum |Z| values are roughly 18 kpc, which is lower than in a potential
from AS. This flatter distribution of the halo group is reflected in the fit
parameters:
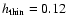 kpc; kpc;
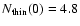 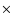 106;
106;
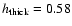 kpc; kpc;
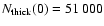 ; ;
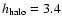 kpc; kpc;
 . . |
| Open with DEXTER |
Medianised values of 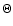 and
and
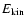 are found to be similar as in
Fig. 6. Again, strong clustering along a roughly straight line is seen, which reaches
from the model's LSR rotational velocity of 231
are found to be similar as in
Fig. 6. Again, strong clustering along a roughly straight line is seen, which reaches
from the model's LSR rotational velocity of 231
 towards lower energies.
The gap in that line around
towards lower energies.
The gap in that line around
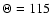
 is also seen, but it
is not as wide as for the AS data.
is also seen, but it
is not as wide as for the AS data.
The z-probability distribution of our RHB candidate stars in the "2b'' potential of DB is given in Fig. 10. Differences to the fit parameter values for the AS potential only
arise for the halo. Its lower scale height and higher number density are, however,
in line with the change in the shape of the orbits (compare Fig. 4
with Fig. 8).
6 Comparing the distribution of RHB stars with other types
The results for the spatial distribution of the RHB stars can be compared with
the distributions found for other stellar types.
In particular a comparison with the distribution of sdBs (Altmann et al. 2004) is of relevance.
6.1 General comparison
In Table 2 we have collected the data from our fit to
the z-probability distributions of the 30% sample. We give values for all three components, the thin disk, thick disk, and halo. While the N(0) values cannot be compared to real midplane densities, their ratios can still be used for this discussion.
For the thin disk, Majewski (1993) gives in his review a lower scale height limit
of 325 pc, a value mostly from successful starcount models.
Recently, Chen et al. (2001) found 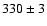 pc, while Du et al. (2003) found
pc, while Du et al. (2003) found
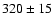 pc. Our value of 120 pc is much smaller than those.
However, there are measurements by Kuijken & Gilmore (1989), Kroupa et al. (1993), and Ojha et al. (1994)
that give 249 pc, 250 pc, and 240 pc, respectively, as scale height for the thin disk.
It is not obvious why all these results differ so much.
Since we are using calculated orbits to determine the scale heights,
instead of just positions, the potential model may also come into play.
pc. Our value of 120 pc is much smaller than those.
However, there are measurements by Kuijken & Gilmore (1989), Kroupa et al. (1993), and Ojha et al. (1994)
that give 249 pc, 250 pc, and 240 pc, respectively, as scale height for the thin disk.
It is not obvious why all these results differ so much.
Since we are using calculated orbits to determine the scale heights,
instead of just positions, the potential model may also come into play.
The review by Majewski (1993) gives thick disk scale heights of 1.3 to 2.5 kpc.
Some more recently published values are 0.58-0.75 kpc (Chen et al. 2001),
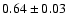 kpc (Du et al. 2003), and 0.8-1.2 kpc (Kerber et al. 2001).
Thus, the scale height of the thick disk is found to be in the range of 0.6 to 2.5 kpc.
Our value of 0.58 kpc for both potentials is at the lower end of the above
range. Since the more recent studies tend to find values of 1 kpc or less,
we think that we are in line with those publications.
kpc (Du et al. 2003), and 0.8-1.2 kpc (Kerber et al. 2001).
Thus, the scale height of the thick disk is found to be in the range of 0.6 to 2.5 kpc.
Our value of 0.58 kpc for both potentials is at the lower end of the above
range. Since the more recent studies tend to find values of 1 kpc or less,
we think that we are in line with those publications.
Midplane thick-to-thin-disk number ratios in the literature are given from as
low as 2% (Gilmore 1984) up to 13% (Chen et al. 2001).
There is, due to the way such data are fitted, an anti-correlation between
density ratio and scale height.
Our ratio of about 1% is lower than the values given above with a
rather low scale height. The ratio of halo to thin disk stars taken from our data is
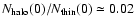 % (
% (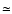 0.04% for the "2b'' potential by Dehnen & Binney 1998). Typically, these values range from 0.05% to 0.4% (see e.g. Chen et al. 2001;
Kerber et al. 2001). These discrepancies are probably due to the small volume in space, from which
we drew our data, the small sphere around the Sun. Other studies are based on selected fields with, in general, more distant stars. These are less likely to include thin disk stars, while thick disk stars are less likely to be included in our sample.
0.04% for the "2b'' potential by Dehnen & Binney 1998). Typically, these values range from 0.05% to 0.4% (see e.g. Chen et al. 2001;
Kerber et al. 2001). These discrepancies are probably due to the small volume in space, from which
we drew our data, the small sphere around the Sun. Other studies are based on selected fields with, in general, more distant stars. These are less likely to include thin disk stars, while thick disk stars are less likely to be included in our sample.
Could this aspect (samples of different distance ranges) explain all the
differences? A comparison between a spherical and conical survey of stellar
populations with the same densities and scale heights gives hints to the answer.
For a sphere the number of disk stars in the volume increases with the observed
distance. This increase is much greater than for a narrow cone that looks away from the
disk. For example, with our fit results from Sect. 4.3 we obtain a ratio of
 % for a sphere with radius 2 kpc, while
the same ratio for the cone of the same length towards a galactic pole is 5.5%.
For a distance of 5 kpc the numbers are 0.33% and 43%, respectively.
This extreme case should emphasise, that even with our very low midplane density
ratio, a conical survey can find a large number of halo stars.
Effects arising from the shape and depth of the surveyed volume are therefore important.
% for a sphere with radius 2 kpc, while
the same ratio for the cone of the same length towards a galactic pole is 5.5%.
For a distance of 5 kpc the numbers are 0.33% and 43%, respectively.
This extreme case should emphasise, that even with our very low midplane density
ratio, a conical survey can find a large number of halo stars.
Effects arising from the shape and depth of the surveyed volume are therefore important.
Another, more fundamental, reason for the different results comes
from the method of analysis. While some other studies explicitly assign the stars to one of the three stellar populations (thin disk, thick disk, halo), we opted not to do so.
Our results are not influenced by errors in such assignments.
Rather, our derived scale heights and number densities are only a result of the
fitting procedure and are dependent of the weights used.
Differences coming from the fit procedure are thus not negligible.
We chose inverse counts as weights, because the fit function approximated the
distribution equally well for both the disk and halo component.
6.2 Are there differences in population along the HB?
In de Boer et al. (1997) the z-probability distribution was introduced as a tool to
determine scale heights of stellar populations.
The latest results on BHB stars involving this method are given in Altmann et al. (2004).
From some 120 sub-dwarf stars, they derived a scale
height of 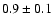 kpc for the thick disk.
Another population with scale height of about 7 kpc was found in the data.
These values are larger than the ones derived from our RHB sample (0.58 kpc and 4.2 kpc) by almost a factor of two.
kpc for the thick disk.
Another population with scale height of about 7 kpc was found in the data.
These values are larger than the ones derived from our RHB sample (0.58 kpc and 4.2 kpc) by almost a factor of two.
For this paper the same orbit calculation tools were used as in Altmann et al. (2004).
Any systematic effects (too restrictive potentials as in Sect. 6.1)
arising from the analyses should therefore be the same for both studies.
But the fitting of the z-distributions was done differently.
We used the whole range in Z to do a weighted fit for three components simultaneously.
However, the values are taken from data of two positionally very different
samples. The RHB sample is located near the sun, while
the sdBs are generally farther away at high galactic latitudes.
Consequently, from the RHBs we find z-distributions that lack a well defined
halo, while for the sdBs a thin disk component was barely seen.
The large difference for the halo scale heights from the RHBs results from this
"undersampling'' in our sample. Another effect of this is that we get the lower midplane halo-to-disk number density ratios mentioned in Sect. 6.1.
A greater number of far-out halo stars could surely be found in the H IPPARCOS and
BB2k data, but we deciced to limit the observed volume by our already
rather large relative parallax error of 30%.
G AIA (Perryman et al. 2001), ESA's future astrometric mission will measure
three-dimensional positions and velocities down to 17.5 mag.
With such a wealth of data, we will be able to derive firmer results on the halo
scale height of RHBs.
The thick disk components from both studies are well represented, showing a
large number of objects. Scale height differences in this population can therefore not be explained
by low number statistics. Again, the selection of the samples influences the results, albeit at a lower level than for the halo component. Whether the scale heights can be explained by an intrinsic difference in kinematics of RHBs compared to sdBs, cannot be decided.
For that we would need to observe the same volume of space.
1)
The position and velocity diagrams (Figs. 2 and 3) show that the RHB sample
is a mix of disk stars (with
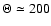
 )
and stars with lower orbital speed and thus larger perpendicular velocity,
establishing the group of the asymmetric drift.
A relatively small subset exhibits velocity and kinetic energy of a nature
typical for the halo.
)
and stars with lower orbital speed and thus larger perpendicular velocity,
establishing the group of the asymmetric drift.
A relatively small subset exhibits velocity and kinetic energy of a nature
typical for the halo.
2)
The orbit shapes indicate a predominance of rather circular orbits.
Again, a small subset exhibits very elliptic orbits in part reaching to
large distances from the disk.
3)
The orbit statistics make clear that only a few of the H IPPARCOS-BB2k
stars reach far into the halo.
This does not imply that stars found to have highly excentric orbits
but staying in the disk are not part of the halo population.
4)
No significant dependence of the thin disk parameters on the volume surveyed was
found. However, the thick disk and halo show varying parameters due to the low number of
objects.
5)
Different models of the distribution of mass in the galaxy do not
produce significant differences in the scale heights of our sample.
6)
The vertical scale height of our RHB star samples and the ones of the earlier
investigated sdB stars are significantly different.
This either points at a different history of the progenitors of these groups
or, given the widely different spatial sampling, demonstrates that source
selection leads to strong biases with
concomittant differences in the resulting average parameters.
7)
The range of thick disk scale heights, as derived from orbits as well as other
methods, is either due to sample selection problems or is
inconsistent with a simple galactic structure.
Acknowledgements
We are grateful to the DLR for supporting TAK and MA under the grants
50QD 0103 and 50QD 0102, as well as FONDAP for support of MA under the grant
1501 0003.
Also, we wish to express our gratitude to Walter Dehnen, who gave us access to
his galactic mass models and software for orbit calculation.
We like to thank Michael Odenkirchen and Michael Geffert for
providing program code used throughout these studies, and Philip Willemsen
for helpful discussions.
For this work the SIMBAD and VIZIER databases at CDS in Strasbourg were
frequently used.
- Allen, C., & Santillan,
A. 1991, RMxA, 22, 255 [NASA ADS] (In the text)
- Altmann, M., & de
Boer, K. S. 2000, A&A, 353, 135 [NASA ADS] (In the text)
- Altmann, M., Edelmann,
H., & de Boer, K. S. 2004, A&A, 414, 181 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Barbier-Brossat, M., &
Figon, P. 2000, A&AS, 142, 217 [NASA ADS] (In the text)
- Becker, F. 1940, Z.
Astrophys., 19, 50 [NASA ADS] (In the text)
- Behr, B. B. 2003,
ApJS, 149, 101 [NASA ADS] [CrossRef] (In the text)
- Binney, J., & Tremaine, S.
1987, Galactic Dynamics (Princeton Univ. Press)
(In the text)
- Burkert, A., Truran,
J. W., & Hensler, G. 1992, ApJ, 391, 651 [NASA ADS] [CrossRef] (In the text)
- Chen, B., Stoughton,
C., Smith, J. A., et al. 2001, ApJ, 553, 184 [NASA ADS] [CrossRef] (In the text)
- de Boer, K. S., Aguilar
Sanchez, Y., Altmann, M., et al. 1997, A&A, 327, 577 [NASA ADS] (In the text)
- Dehnen, W., & Binney,
J. 1998, MNRAS, 294, 429 [NASA ADS] [CrossRef] (In the text)
- Dommanget, J., & Nys,
O. 2002, Observations et Travaux, 54
(In the text)
- Du, C., Zhou, X., Ma, J.,
et al. 2003, A&A, 407, 541 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Elvius, T. 1951,
Stockholms Observ. Annaler, 16, 1 (In the text)
- ESA 1997, The Hipparcos and
Tycho catalogues, Vol. SP-1200 (ESA)
(In the text)
- Flynn, C.,
Sommer-Larsen, J., & Christensen, P. R. 1996, MNRAS, 281,
1027 [NASA ADS] (In the text)
- Gallart, C. 1998,
ApJ, 495, L43 [NASA ADS] [CrossRef] (In the text)
- Gilmore, G. 1984, MNRAS,
207, 223 [NASA ADS] (In the text)
- Gilmore, G., & Reid, N.
1983, MNRAS, 202, 1025 [NASA ADS] (In the text)
- Heber, U. 1986,
A&A, 155, 33 [NASA ADS] (In the text)
- Johnston, K. V.,
Spergel, D. N., & Hernquist, L. 1995, ApJ, 451, 598 [NASA ADS] [CrossRef] (In the text)
- Kerber, L. O.,
Javiel, S. C., & Santiago, B. X. 2001, A&A, 365,
424 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kim, Y., Demarque, P., Yi,
S. K., & Alexander, D. R. 2002, ApJS, 143, 499 [NASA ADS] [CrossRef] (In the text)
- Kroupa, P. 2002, MNRAS,
330, 707 [NASA ADS] [CrossRef] (In the text)
- Kroupa, P., Tout, C. A.,
& Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] (In the text)
- Kuijken, K., &
Gilmore, G. 1989, MNRAS, 239, 605 [NASA ADS] (In the text)
- Majewski, S. R.
1993, ARA&A, 31, 575 [NASA ADS] (In the text)
- Moehler, S., de
Boer, K. S., & Heber, U. 1990, A&A, 239, 265 [NASA ADS] (In the text)
- Nordström, B.,
Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Norris, J. 1987, ApJ,
314, L39 [NASA ADS] [CrossRef] (In the text)
- Norris, J. E., &
Ryan, S. G. 1991, ApJ, 380, 403 [NASA ADS] [CrossRef] (In the text)
- Odenkirchen, M., &
Brosche, P. 1992, AN, 313, 69 [NASA ADS] (In the text)
- Ojha, D. K.,
Bienayme, O., Robin, A. C., & Mohan, V. 1994, A&A,
284, 810 [NASA ADS] (In the text)
- Perryman,
M. A. C., de Boer, K. S., Gilmore, G., et al.
2001, A&A, 369, 339 [EDP Sciences] [NASA ADS] (In the text)
- Quinn, P. J.,
Hernquist, L., & Fullagar, D. P. 1993, ApJ, 403, 74 [NASA ADS] [CrossRef] (In the text)
- Rose, J. A. 1985,
AJ, 90, 787 [NASA ADS] [CrossRef] (In the text)
- Sandage, A. 1990, JRASC,
84, 70 [NASA ADS] (In the text)
- Seidel, E.,
Demarque, P., & Weinberg, D. 1987, ApJS, 63, 917 [NASA ADS] [CrossRef] (In the text)
- Skuljan, J.,
Hearnshaw, J. B., & Cottrell, P. L. 1999, MNRAS, 308,
731 [NASA ADS] [CrossRef] (In the text)
- Sweigart,
A. V. 1987, ApJS, 65, 95 [NASA ADS] [CrossRef] (In the text)
- Tautvaisiene, G. 1996,
Baltic Astronomy, 5, 503 [NASA ADS] (In the text)
- Turon, C., Crézé,
M., Egret, D., et al. 1992, The HIPPARCOS input catalogue, ESA
SP-1136
(In the text)
- Upgren, A. R. 1962,
AJ, 67, 37 [NASA ADS] [CrossRef]
- Upgren, A. R. 1963,
AJ, 68, 194 [NASA ADS] [CrossRef] (In the text)
-
Villeneuve, B., Wesemael, F., & Fontaine, G. 1995a, ApJ, 450,
851 [NASA ADS] [CrossRef] (In the text)
-
Villeneuve, B., Wesemael, F., Fontaine, G., Carignan, C., &
Green, R. F. 1995b, ApJ, 446, 646 [NASA ADS] [CrossRef] (In the text)
- Yi, S. K., Kim, Y.,
& Demarque, P. 2003, ApJS, 144, 259 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1793fig1.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{1793fig2.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg50.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1793fig3.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg51.gif)
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{1793fig4.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg52.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1793fig6.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg54.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.3cm,clip]{1793fig7.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{1793fig8.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1793fig9.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg83.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.4cm,clip]{1793fi10.ps}
\end{figure}](/articles/aa/full/2005/12/aa1793/Timg85.gif)