A&A 432, 1049-1056 (2005)
DOI: 10.1051/0004-6361:20041675
F. Lepreti 1 - H. Isliker 1 - K. Petraki 1,2 - L. Vlahos 1
1 - Department of Physics, Aristotle University of Thessaloniki,
54124 Thessaloniki, Greece
2 -
Department of Physics and Astronomy, UCLA, Los Angeles,
California 90095, USA
Received 16 July 2004 / Accepted 8 November 2004
Abstract
We propose a model for the acceleration of charged particles in
interplanetary space that appear during quiet time periods, that is,
not associated with solar activity events like intense flares or
coronal mass ejections. The interaction
of charged particles with modeled turbulent electromagnetic fields,
which mimic the fields observed in the interplanetary medium,
is studied.
The turbulence is modeled by means of a dynamical system,
the Gledzer-Ohkitani-Yamada (GOY) shell model,
which describes the gross features
of the Navier-Stokes equations. The GOY model is used to build
a 3D velocity field, which in turn is used to numerically solve the
ideal magneto-hydrodynamic (MHD) induction equation,
while the electric field is calculated from the ideal Ohm's law.
Particle acceleration in such an environment is investigated by
test particle simulations, and the resulting energy distributions
are discussed and compared to observations of suprathermal electrons
and ions during quiet periods in interplanetary space.
Key words: acceleration of particles - turbulence - Sun: solar wind - interplanetary medium
The observations of high energy, suprathermal particle populations in interplanetary space reveal the presence of a rich variety of physical characteristics and processes (see Reames 1999, for a review). The information recovered from time profiles of particle fluxes, energy spectra, element abundances, ionization states, etc., is essential in determining many properties of the sources and of the mechanisms of particle acceleration. The remarkable heterogeneity found in the detected energetic particle events is related, in large part, to the existence of different sources of acceleration in interplanetary space. Suprathermal populations can be produced by solar flares, collisionless shock waves driven by Coronal Mass Ejections (CMEs), Corotating Interaction Regions (CIRs), or the heliospheric termination shock.
For many years, the attention of researchers has been focused on suprathermal particles with energies above a few hundred keV, due to the fact that the spacecraft instruments lacked the sensitivity needed to investigate the energy range from the solar wind thermal plasma up to a few hundred keV. In recent years, however, with the launch of the Ulysses, Advanced Composition Explorer (ACE), and WIND spacecrafts, this gap has been filled and observations of "quiet time'' suprathermal particles, that is, not associated with the abrupt energization events mentioned above, have become available.
The electron spectrum, measured between
![]() 5 eV and
5 eV and ![]() 100 keV by the 3D Plasma and Energetic
Particles Experiment (Lin et al. 1995) on the WIND spacecraft during
a quiet period, has been
investigated by Lin (1998). A Maxwellian core
dominates the spectrum from
100 keV by the 3D Plasma and Energetic
Particles Experiment (Lin et al. 1995) on the WIND spacecraft during
a quiet period, has been
investigated by Lin (1998). A Maxwellian core
dominates the spectrum from ![]() 5 eV to
5 eV to ![]() 50 eV, while a
hotter population, the so-called solar wind halo (Feldman et al. 1975),
takes over in the range between
50 eV, while a
hotter population, the so-called solar wind halo (Feldman et al. 1975),
takes over in the range between ![]() 100 eV
to
100 eV
to ![]() 1 keV, due to the escape of coronal thermal electrons with temperature
of
1 keV, due to the escape of coronal thermal electrons with temperature
of ![]() 106 K. However, these WIND observations have made possible
the identification of a third, much harder component, which has been denoted
the "super-halo'', with energies
from
106 K. However, these WIND observations have made possible
the identification of a third, much harder component, which has been denoted
the "super-halo'', with energies
from ![]() 2 keV up to
2 keV up to ![]() 100 keV and an approximate power law
shape with exponent
100 keV and an approximate power law
shape with exponent ![]() 2.5. The angular distribution of these
"super-halo'' electrons is nearly isotropic. According to Lin (1998),
this high energy population is not solar in origin,
since this would imply a continuous production and escape of
electrons with such energies from the Sun.
It has been suggested (Lin 1998) that the "super-halo'' tail is due to
acceleration by CIRs beyond 1 AU, but clear evidence for correlations
with CIRs or solar active regions have not yet been found.
2.5. The angular distribution of these
"super-halo'' electrons is nearly isotropic. According to Lin (1998),
this high energy population is not solar in origin,
since this would imply a continuous production and escape of
electrons with such energies from the Sun.
It has been suggested (Lin 1998) that the "super-halo'' tail is due to
acceleration by CIRs beyond 1 AU, but clear evidence for correlations
with CIRs or solar active regions have not yet been found.
The velocity distributions of solar wind ions from 0.6 to 100 keV/e,
measured using the
Solar Wind Ion Composition Spectrometer (SWICS) instruments
on Ulysses and ACE (Gloeckler et al. 1995,1992), have been
studied in Gloeckler (1999), Gloeckler et al. (2000), and
Gloeckler (2003). One of the most important findings of these
works is that the speed distributions of H+, He+ and He++ ions
show well developed, approximate power law tails during quiet time
periods, that is, far from shocks, CIR compressions and other disturbances.
This indicates the presence of a population of highly suprathermal ions
at all times. The power law exponents of these tails, which extend
over the whole measurement range, are between ![]() 5 and
5 and ![]() 5.5in the slow, in-ecliptic solar wind, and
5.5in the slow, in-ecliptic solar wind, and ![]() 8 in the super-quiet
fast wind coming from polar coronal holes. Comparing ACE observations at
8 in the super-quiet
fast wind coming from polar coronal holes. Comparing ACE observations at
![]() 1 AU to Ulysses observations at
1 AU to Ulysses observations at ![]() 5 AU, the authors
also found that the tails are continuously regenerated
in the out-flowing solar wind, overcoming the cooling related to
the wind expansion. The main question arising from these observations
is how these ubiquitous suprathermal ions are produced in the quiet
solar wind when there are no shocks, CIRs or other
disturbances observed locally. le Roux et al. (2001) suggested that
pickup ions might be accelerated by large-scale turbulent electric
fields directed along the background magnetic field. In order to
explore this possibility, they presented a numerical model for
gyrotropic, pitch-angle dependent pickup ion transport between
the Sun and the Earth based on standard kinetic theory for
charged particles. The ion kinetic transport equation used in
their model includes a Gaussian random value
representation of the large-scale field-aligned electric field
fluctuations averaged over the characteristic length and time
scales of MHD turbulence in the low-latitude solar wind.
The authors choose the standard deviation of these electric fields
by requiring the reproduction of observed accelerated pickup
ion spectra and in this way they were able to obtain a qualitative
agreement of the results of their model with the suprathermal
He+ spectra in the slow low-latitude solar wind, observed at
5 AU, the authors
also found that the tails are continuously regenerated
in the out-flowing solar wind, overcoming the cooling related to
the wind expansion. The main question arising from these observations
is how these ubiquitous suprathermal ions are produced in the quiet
solar wind when there are no shocks, CIRs or other
disturbances observed locally. le Roux et al. (2001) suggested that
pickup ions might be accelerated by large-scale turbulent electric
fields directed along the background magnetic field. In order to
explore this possibility, they presented a numerical model for
gyrotropic, pitch-angle dependent pickup ion transport between
the Sun and the Earth based on standard kinetic theory for
charged particles. The ion kinetic transport equation used in
their model includes a Gaussian random value
representation of the large-scale field-aligned electric field
fluctuations averaged over the characteristic length and time
scales of MHD turbulence in the low-latitude solar wind.
The authors choose the standard deviation of these electric fields
by requiring the reproduction of observed accelerated pickup
ion spectra and in this way they were able to obtain a qualitative
agreement of the results of their model with the suprathermal
He+ spectra in the slow low-latitude solar wind, observed at ![]() 1 AU.
1 AU.
Kirsch & Mall (2003) recently presented an analysis of interplanetary
suprathermal ions, based on
measurements performed with the SMS experiment (Gloeckler et al. 1995)
on the WIND spacecraft, in the range 0.5-225 keV/e.
The authors investigated particle bursts in which
high energy protons in the range 5-100 keV are observed in association
with distinct decreases of the magnetic field magnitude.
They considered only events not associated with
shocks, CIRs, and magnetospheric disturbances. As a consequence
of the observed magnetic field behaviour, they suggest that
these bursts could be the result of a local reconnection process, or,
alternatively, they propose that inductive electric fields
(i.e.
![]() )
could be a possible explanation for the observed particle acceleration.
)
could be a possible explanation for the observed particle acceleration.
Here, we investigate with a new approach the possibility that the high energy particles observed in the interplanetary space during quiet time periods are due to a process of stochastic acceleration in the turbulent electromagnetic fields present in the heliospheric plasma. Recently, the stochastic acceleration process in turbulent electromagnetic fields has been investigated with numerical experiments in which test particle simulations are performed in field configurations that are obtained from the solution of the magneto-hydrodynamic (MHD) equations (Nodes et al. 2003; Dmitruk et al. 2003). The authors suggest that these simulations could potentially be applied to astrophysical problems. As an alternative approach, other authors have studied the motion of test particles in electromagnetic fields built up by means of suitable models for particular applications, like the Earth's magnetotail (Veltri et al. 1998) or the solar corona (Arzner & Vlahos 2004). With respect to other approaches, test particle simulations offer the possibility to describe some peculiar features of particle acceleration in turbulent fields, especially the possibility for particles to be trapped, possibly in or around strong, coherent electric field regions, leading to effective acceleration even for low initial energies (Dmitruk et al. 2003; Ambrosiano et al. 1988).
In the present paper, we present a model for stochastic, quiet time particle acceleration in the interplanetary space, based on turbulent electromagnetic fields constructed by means of the so-called Gledzer-Ohkitani-Yamada (GOY) shell model (Yamada & Ohkitani 1987; Gledzer 1973), which mimics the nonlinear dynamics of fluid turbulence. The use of such a simplified description of turbulence implies that we can describe only some basic features of the nonlinear interactions occurring in turbulent fluids, with the advantage that we can simulate turbulent electromagnetic field configurations without the computational difficulty of solving the full MHD equations. The magnetic field is determined through the MHD induction equation, assuming weak magnetic fields so that the back reaction onto the plasma can be neglected. The electric field is given by Ohm's law. In this framework, we perform test particle simulations, concentrating mainly on the energetics of the injected particles, i.e. electrons and ions.
A basic description of the model is given in Sect. 2. In Sect. 3, we present the numerical simulations performed and the results obtained from them. Discussions and conclusions are given in Sect. 4.
The model describes the acceleration of charged test
particles in turbulent electromagnetic fields, as obtained
from a dynamical system model of turbulence. In general, the
macroscopic description of a plasma is given by the
magneto-hydrodynamic (MHD) equations (see e.g. Boyd & Sanderson 2003).
Here, we consider particle acceleration events
occurring in regions of the interplanetary space
where the magnetic field is weak, so that we can
restrict ourselves to weakly magnetized plasmas, which implies that the
temporal evolution of the plasma is governed by the velocity field.
In order to build up the velocity field configurations,
we use the so-called GOY shell model, through which it is possible
to generate a turbulent, incompressible
3D velocity field
![]() ,
as will be explained in Sect. 2.1.
,
as will be explained in Sect. 2.1.
The velocity field is used to obtain numerical solutions
of the MHD induction equation for a perfectly conducting plasma, namely
To investigate the acceleration of test particles in the
electromagnetic fields generated as described above, we consider the
relativistic equations of motions of a charged particle in an external
electromagnetic field:
The 3D, time-dependent velocity field
![]() is constructed by means of the so-called GOY shell
model for turbulence. Shell models (see Bohr et al. 2000, for a complete
review) are dynamical systems designed to represent in a
simplified way the spectral form of the equations which describe
turbulent fluids. They were originally proposed by
Obukhov (1971), Desnyansky & Novikov (1974), and Gledzer (1973) for hydrodynamic
turbulence. The GOY shell model (Yamada & Ohkitani 1987; Gledzer 1973) has been extensively
investigated, both analitically and numerically
(Biferale et al. 1995; Yamada & Ohkitani 1987; Jensen et al. 1991). In the following, we describe some
basic characteristics of the GOY model.
is constructed by means of the so-called GOY shell
model for turbulence. Shell models (see Bohr et al. 2000, for a complete
review) are dynamical systems designed to represent in a
simplified way the spectral form of the equations which describe
turbulent fluids. They were originally proposed by
Obukhov (1971), Desnyansky & Novikov (1974), and Gledzer (1973) for hydrodynamic
turbulence. The GOY shell model (Yamada & Ohkitani 1987; Gledzer 1973) has been extensively
investigated, both analitically and numerically
(Biferale et al. 1995; Yamada & Ohkitani 1987; Jensen et al. 1991). In the following, we describe some
basic characteristics of the GOY model.
The main idea of the GOY shell model is to mimic the Navier-Stokes
equations by a dynamical
system in which the velocity field fluctuations at different
length scales are represented by scalar variables un(t).
To this aim, the Fourier space is divided into N shells, with the
associated wave number denoted by kn, where the shell index n is
discrete. The scalar, complex
variable un(t) is associated with the nth shell, and the nonlinear
dynamics of turbulent fluids are modeled by quadratic couplings
among nearest and next nearest neighbour shells, following the assumption
that the nonlinear interactions are local in the k space. The coefficients
of the nonlinear terms are determined by imposing the conservation of the ideal
invariants of the Navier-Stokes equations. The equations of evolution of the
dynamical variables un(t) are (Bohr et al. 2000)
The parameter ![]() stands for the kinematic viscosity, while
stands for the kinematic viscosity, while
![]() is
a stochastic forcing term acting on the shell m, one of the first shells,
providing a constant average energy flux into the system (
is
a stochastic forcing term acting on the shell m, one of the first shells,
providing a constant average energy flux into the system (
![]() is the Kronecker symbol). The wave numbers are chosen to follow the relation
is the Kronecker symbol). The wave numbers are chosen to follow the relation
One of the main advantages of shell models over numerical
simulations of the Navier-Stokes equations is that they can be
investigated at much higher Reynolds numbers. They provide a good
description of the scaling properties of fully developed turbulence
in the inertial range, even if, being scalar models, they do not include information about the spatial structures of turbulence. From the scalar variables un(t) we can generate
an incompressible velocity field
![]() in the real 3D space by applying a simple numerical algorithm (Bohr et al. 2000).
The dynamical variables un(t) of the shell model are supposed to
represent the coefficients of a Fourier expansion with wave vectors
in the real 3D space by applying a simple numerical algorithm (Bohr et al. 2000).
The dynamical variables un(t) of the shell model are supposed to
represent the coefficients of a Fourier expansion with wave vectors
![]() in a shell of
radius
in a shell of
radius
![]() .
We introduce a set of vectors
.
We introduce a set of vectors
![]() :
:
In order to satisfy the incompressibility constraint
![]() ,
the vectors
,
the vectors
![]() and the coefficients Cn(j) must satisfy the condition
and the coefficients Cn(j) must satisfy the condition
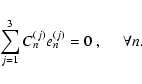 |
(10) |
![\begin{figure}
\par\includegraphics[width=14.4cm,clip]{1675fig1.eps}\end{figure}](/articles/aa/full/2005/12/aa1675/Timg44.gif) |
Figure 1:
3D visualization of the magnetic field intensity
|
| Open with DEXTER | |
The numerical investigation consists of two main steps: 1) the calculation of the magnetic and electric fields from Eqs. (1) and (2), in which the velocity field given by Eq. (9) is used; 2) test particle simulations through the numerical solutions of Eqs. (3) and (5).
The GOY shell model equations Eq. (6) are solved by using a 4th order
Runge-Kutta integration algorithm, using N=22 shells. The kinematic
viscosity in the shell model is assumed to be
![]() .
Once the shell model has reached a statistically stationary state,
we start the numerical integration of the MHD induction equation
(Eq. (1)), by using the Wilson upwind scheme (Hawley et al. 1984),
imposing free outflow boundary conditions and
using the velocity field
.
Once the shell model has reached a statistically stationary state,
we start the numerical integration of the MHD induction equation
(Eq. (1)), by using the Wilson upwind scheme (Hawley et al. 1984),
imposing free outflow boundary conditions and
using the velocity field
![]() from Eq. (9).
The initial magnetic field
from Eq. (9).
The initial magnetic field
![]() is given by a random perturbation constructed through a sum
of Fourier modes
is given by a random perturbation constructed through a sum
of Fourier modes
![]() ,
with Gaussian distributed amplitudes
,
with Gaussian distributed amplitudes
![]() ,
random phases
,
random phases
![]() and with the constraint
and with the constraint
![]() imposed, as it follows
from
imposed, as it follows
from
![]() .
The size of the grid is 643.
The evolution of the system is followed over a time interval
.
The size of the grid is 643.
The evolution of the system is followed over a time interval
![]() ,
where
,
where
![]() is a typical eddy turnover time,
given by
is a typical eddy turnover time,
given by
![]() ,
L being the size of the simulation
domain and
,
L being the size of the simulation
domain and
![]() the rms velocity. The condition that the kinetic
energy density is much smaller than the magnetic energy density is
checked during the time evolution. We also monitor the value of
the rms velocity. The condition that the kinetic
energy density is much smaller than the magnetic energy density is
checked during the time evolution. We also monitor the value of
![]() ,
evaluated through a standard finite differences scheme, and verify that it does not vary
significantly with respect to the initial value, which can
be considered zero within the numerical error.
,
evaluated through a standard finite differences scheme, and verify that it does not vary
significantly with respect to the initial value, which can
be considered zero within the numerical error.
The equations are solved in non-dimensional form, and suitable
rescaling factors are applied to describe quiet time periods in
interplanetary space. The applied forcing term leads to
an rms velocity field intensity of
![]()
![]() 107 cm s-1.
This value is slightly larger that the rms velocity estimates
obtained from a 30 year dataset of solar wind observations,
which gave values around 7
107 cm s-1.
This value is slightly larger that the rms velocity estimates
obtained from a 30 year dataset of solar wind observations,
which gave values around 7 ![]() 106 cm s-1 (Breech et al. 2003).
This means that in our simulations we are assuming a slightly enhanced
turbulence level with respect to the average.
The linear size of the simulation box is assumed to be
L = 2.2
106 cm s-1 (Breech et al. 2003).
This means that in our simulations we are assuming a slightly enhanced
turbulence level with respect to the average.
The linear size of the simulation box is assumed to be
L = 2.2 ![]() 1010 cm. The rms value of the magnetic field intensity,
after the rescaling, is
1010 cm. The rms value of the magnetic field intensity,
after the rescaling, is
![]()
![]() 10-5 G,
while the rescaled rms value of the electric field intensity is
10-5 G,
while the rescaled rms value of the electric field intensity is
![]()
![]() 10-8 statvolt cm-1.
These values are slightly larger than the rms values obtained
from long time datasets of solar wind observations.
10-8 statvolt cm-1.
These values are slightly larger than the rms values obtained
from long time datasets of solar wind observations.
To illustrate the 3D structure of the magnetic and electric
fields, in Fig. 1 we present a 3D visualization of the
regions where the magnetic field and electric field intensities exceed
the thresholds
![]()
![]() 10-4 G and
10-4 G and
![]()
![]() 10-7 statvolt cm-1, respectively.
10-7 statvolt cm-1, respectively.
In Fig. 2 we present the Probability Density Functions (PDFs) of the three electric field components, collected at a fixed time from the entire simulation box. In order to compare the different PDFs, the variables are first translated to zero mean and then normalized to their standard deviation, so that all the PDFs have zero mean and unit standard deviation. As it can be seen, these PDFs are not Gaussian, they exhibit clear exponential tails. This result is in qualitative agreement with the one-point PDFs of the observed interplanetary induced electric fields (IEF) presented in Breech et al. (2003). In a more recent work (Sorriso-Valvo et al. 2004), it has been shown that the statistical properties of the IEF depend on the wind velocity, an effect that we do not model here (see discussion in Sect. 4).
In this subsection, we present some results obtained from test particle
simulations of electrons and ions in the electromagnetic field
configurations generated as described in the previous subsection.
Specifically, the magnetic and electric field configurations obtained at
the time
![]() during the evolution of Eq. (1) are used.
The particle motion Eqs. (3) and (5) are solved with
a 4th order Runge-Kutta, adaptive step-size scheme. The magnetic and
electric field configurations are kept constant during the time we monitor
the particles, assuming a much slower evolution time for the fluid
velocity field than for the test particles.
Since the magnetic and the electric
fields are given only at a discrete set of points, both fields
are interpolated with a local, 3D linear interpolation to provide the field
values in between grid-points, wherever they are needed for the integration
scheme. The initial time step used for the integration is set to
during the evolution of Eq. (1) are used.
The particle motion Eqs. (3) and (5) are solved with
a 4th order Runge-Kutta, adaptive step-size scheme. The magnetic and
electric field configurations are kept constant during the time we monitor
the particles, assuming a much slower evolution time for the fluid
velocity field than for the test particles.
Since the magnetic and the electric
fields are given only at a discrete set of points, both fields
are interpolated with a local, 3D linear interpolation to provide the field
values in between grid-points, wherever they are needed for the integration
scheme. The initial time step used for the integration is set to
![]() ,
where
,
where ![]() is the gyration period of the particles at the starting point.
is the gyration period of the particles at the starting point.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1675fig2.eps}\end{figure}](/articles/aa/full/2005/12/aa1675/Timg62.gif) |
Figure 2: PDFs of the three components of the electric field: the solid, dashed, and dot-dashed lines represent the PDFs of Ex, Ey, and Ez respectively. |
| Open with DEXTER | |
The charged test particles are injected at random
positions within the simulation box, with velocities extracted from
the tail of a Maxwellian distribution with temperature T = 1.15 ![]() 105 K
(corresponding to
105 K
(corresponding to ![]() 10 eV), which represents
a typical value in the interplanetary space at 1 AU from the Sun.
The threshold velocity used to select only the particles in the tail
of the Maxwellian is
10 eV), which represents
a typical value in the interplanetary space at 1 AU from the Sun.
The threshold velocity used to select only the particles in the tail
of the Maxwellian is
![]() ,
where
,
where
![]() is the thermal
velocity. The choice to use only the tail of the initial Maxwellian
distribution is due to the fact that we do not model the collisional
processes occurring in the interplanetary space plasma, so we assume
that only the high energy part of the distribution participates
in the acceleration process.
If a particle leaves the simulation box before the end of its
tracing time interval, it is reinjected into the box at a random point
on the surface opposite to the one through which it had left.
The maximum tracing time interval used in this work is t = 300 s,
which is much smaller
than the typical collision times for electrons and ions with velocities
larger than twice the thermal velocity (see e.g. Montgomery 1983),
so that we can neglect collisional effects.
is the thermal
velocity. The choice to use only the tail of the initial Maxwellian
distribution is due to the fact that we do not model the collisional
processes occurring in the interplanetary space plasma, so we assume
that only the high energy part of the distribution participates
in the acceleration process.
If a particle leaves the simulation box before the end of its
tracing time interval, it is reinjected into the box at a random point
on the surface opposite to the one through which it had left.
The maximum tracing time interval used in this work is t = 300 s,
which is much smaller
than the typical collision times for electrons and ions with velocities
larger than twice the thermal velocity (see e.g. Montgomery 1983),
so that we can neglect collisional effects.
In Fig. 3, a sample trajectory of a typical test electron is
shown.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1675fig3.eps}\end{figure}](/articles/aa/full/2005/12/aa1675/Timg65.gif) |
Figure 3: Trajectory of a test electron. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1675fig4.eps}\end{figure}](/articles/aa/full/2005/12/aa1675/Timg66.gif) |
Figure 4:
Part of the time evolution of the kinetic energy of a test electron
( upper panel),
the associated electric field intensity along the trajectory ( middle panel),
and the cosine of the angle |
| Open with DEXTER | |
In Fig. 5, a sample trajectory of a test proton is
shown.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{1675fig5.eps}\end{figure}](/articles/aa/full/2005/12/aa1675/Timg67.gif) |
Figure 5: Trajectory of a test proton. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{1675fig6.eps}\end{figure}](/articles/aa/full/2005/12/aa1675/Timg68.gif) |
Figure 6:
Part of the time evolution of the kinetic energy of a test proton
( upper panel), the associated electric field intensity along the trajectory ( middle panel), and the cosine of the angle |
| Open with DEXTER | |
In Fig. 7, we report the kinetic energy PDFs of 104 test electrons at
the initial time t=0 s, and at three successive times t=1 s,
t=30 s, and t=300 s respectively.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1675fig7.eps}\end{figure}](/articles/aa/full/2005/12/aa1675/Timg69.gif) |
Figure 7: Kinetic energy probability density function of 104 test electrons at the initial time t=0 (dotted curve), and after t=1 s (dashed curve), t=30 s (dot-dashed curve), t=300 s (solid curve). |
| Open with DEXTER | |
In Fig. 8, we report the kinetic energy PDFs of 104 test protons at the same times as for the electrons.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1675fig8.eps}\end{figure}](/articles/aa/full/2005/12/aa1675/Timg70.gif) |
Figure 8: Kinetic energy probability density function of 104 test protons at the initial time t=0 (dotted curve), and after t=1 s (dashed curve), t=30 s (dot-dashed curve), t=300 s (solid curve). |
| Open with DEXTER | |
Since observations are also available for other ions, and in particular
for He ions, we also investigated the kinetic energy PDF of He+ ions.
The time evolution of this PDF, shown in Fig. 9, is
quite similar to the proton case. For t=1 s, the tail of the PDF extends to lower energies than for the protons, again being a power-law shape that persists until t=30 s.
For t=300 s, energies up to ![]() 100 keV are reached, with
a narrow and steep tail that is difficult to classify.
100 keV are reached, with
a narrow and steep tail that is difficult to classify.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1675fig9.eps}\end{figure}](/articles/aa/full/2005/12/aa1675/Timg71.gif) |
Figure 9: Kinetic energy probability density function of 104 test He+ ions at the initial time t=0 (dotted curve), and after t=1 s (dashed curve), t=30 s (dot-dashed curve), t=300 s (solid curve). |
| Open with DEXTER | |
In this paper, we have presented a model for turbulent
particle acceleration based on a dynamical system description of
turbulence. The aim of the model is to describe long lasting
particle acceleration processes occurring in the turbulent
interplanetary space during quiet time periods,
which lead to the appearance of suprathermal
tails at all times in the energy distributions of electrons and
ions (extending up to ![]() 100 keV).
100 keV).
The acceleration process has been investigated by performing test particle numerical simulations in the electromagnetic fields obtained by numerically solving the ideal MHD induction equation, which is driven by the velocity field that is calculated using a dynamical system model (the so-called GOY shell model) of turbulence. This approach implies that the magnetic fields are supposed to be weak, or that the magnetic energy density is much smaller than the kinetic energy density of the flow.
The PDFs of the electric field components have been shown to be non-Gaussian, exhibiting exponential tails. The presence of roughly exponential tails in the one-point PDFs of the interplanetary induced electric fields (IEF) has been recently shown based on data analysis performed on 30 years of measurements that were acquired by different spacecrafts (Breech et al. 2003). However, more recently (Sorriso-Valvo et al. 2004), it has been shown that using homogeneous datasets with respect to wind velocity and solar activity, that is, considering short datasets and separating the data according to slow and fast wind streams, the exponential tails are recovered only in the radial components of the electric field, that is, the component along the Sun-Earth direction, which coincides with the mean wind direction. Our model is obviously not able to reproduce in detail these statistical properties of the observed IEF, since we do not take into account some basic features of the solar wind structure, e.g. its mean bulk velocity, mean magnetic field structure, etc. In other words, we consider only the effect of field fluctuations related to the presence of turbulence.
With our approach, we have been able to obtain basic physical insights into the process of particle acceleration due to turbulent electric fields in weakly magnetized plasmas, and to investigate the possibility that this mechanism plays a role in the acceleration of charged particles to suprathermal energies in interplanetary space during quiet periods. The trajectories obtained from the simulations indicate that the particles alternately visit regions in which they are trapped for some time, due to the effects of turbulence, and other regions where long "jumps'' are observed. The observed motion of the test particles suggests that a Fokker-Planck description of the diffusion process underlying the particle acceleration is not sufficient to achieve a complete characterization of the problem. This is one of the main reasons why a test particle approach is adequate in studying such situations.
We found that, starting from an initial thermal population, both in the case
of electrons and ions, the initial Maxwellian energy distributions evolve
in time, giving rise to
power-law tails for shorter times, which become very steep and narrow
for the longest time we monitor the particles, so that it is
difficult to discriminate between exponential and power-law distributions.
At the maximum time we allow, the particles reach
energies up to ![]() 100 keV. The fact that our model is able to reproduce
the observed energies suggests that
a stochastic acceleration mechanism resulting from the turbulence
that is developed
in the interplanetary space can be at the origin of the ubiquitous
suprathermal tails observed during quiet time periods, even if
the detailed shape of the observed distributions,
which exhibit approximate power law tails, is not very well
recovered by our model.
100 keV. The fact that our model is able to reproduce
the observed energies suggests that
a stochastic acceleration mechanism resulting from the turbulence
that is developed
in the interplanetary space can be at the origin of the ubiquitous
suprathermal tails observed during quiet time periods, even if
the detailed shape of the observed distributions,
which exhibit approximate power law tails, is not very well
recovered by our model.
The difficulty in reproducing the observations in detail at this stage is related to some limitations of our model in its current form. Our main simplifying assumptions are: (1) We have assumed that the magnetic energy density is much smaller than the kinetic energy density of the fluid. This assumption is often not fulfilled in the interplanetary space, due to the presence of a strong Alfvenic component in the solar wind turbulence (see e.g. Tu & Marsch 1995; Goldstein et al. 1995). (2) The detailed properties of intermittency in solar wind turbulence (see e.g. Burlaga 1991; Carbone et al. 1995; Marsch & Liu 1993; Burlaga 1992) are not included in the model, and this could have an effect especially on the high energy part of the kinetic energy PDFs. (3) The resistivity, which modifies the small-scale structure of the electric field, is treated as a constant, not taking its possible dynamic evolution into account (see Arzner & Vlahos 2004; Dmitruk et al. 2003). (4) The large scale magnetic field structure, which was not included in the present study, but which nevertheless would be interesting to be investigated, will have a less deciding influence on the energetics.
In order to overcome the limitation (1), a dynamical system for MHD turbulence must be considered, instead of a hydrodynamical model, whereas for the limitation (2), a more appropriate description of intermittency should be introduced in the reconstruction of the 3D fields from the 1D scalar fields that are yielded by the shell models. The presented results suggest that on modifying our model in this way, better compatibility with the observations can be reached.
Acknowledgements
This work was partially supported by the Research Training Network (RTN) "Theory, Observation, and Simulation of Turbulence in Space Plasmas'', funded by the European Commission (contract No. HPRN-CT-2001-00310).