A&A 432, 411-422 (2005)
DOI: 10.1051/0004-6361:20041907

The dynamical structure of isotropic spherical galaxies with a central black hole

M. Baes1,2 - H. Dejonghe1 - P. Buyle1


1 - Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281-S9, 9000 Gent, Belgium
2 - European Southern Observatory, Casilla 19001, Santiago, Chile

Received 26 August 2004 / Accepted 2 November 2004

Abstract
We discuss the kinematical structure of a two-parameter family of isotropic models with a central black hole. The family contains the slope of the central density cusp and the relative black hole mass as parameters. Most of the basic kinematical quantities of these models can be expressed analytically. This family contains three distinct models where also the distribution function, differential energy distribution and spatial LOSVDs can be expressed completely analytically. Each of these models shows a drastically different behaviour of the distribution function. Although the effect of a black hole on the distribution function is very strong, in particular for models with a shallow density cusp, the differential energy distribution is only marginally affected. We discuss in detail the effects of a central black hole on the LOSVDs. The projected velocity dispersion increases with black hole mass at small projected radii, but the effect of a black hole on the shape of the LOSVDs (characterized by the h4 parameter) is less straightforward to interpret. Too much reliance on the wings of the LOSVDs and the value of the h4 parameter to determine black hole masses might hence be dangerous.

Key words: black hole physics - galaxies: kinematics and dynamics - galaxies: structure

1 Introduction

During the past decade, various observational discoveries have changed our view on galactic nuclei rather drastically. Firstly, galactic nuclei are generally observed to have a cuspy density distribution at small radii, with densities behaving as $\rho(r)\propto r^{-\gamma}$. The observed cusp slopes are far from uniform and range from zero to more than 2 (Lauer et al. 1995; Gebhardt et al. 1996; Ravindranath et al. 2001; Seigar et al. 2002; Genzel et al. 2003; Scarlata et al. 2004). Secondly, high-resolution imaging has revealed that a substantial fraction of the galactic nuclei in both spiral and elliptical galaxies show small-scale structure, in the form of bars, mini-spirals or dust lanes (Phillips et al. 1996; Malkan et al. 1998; Carollo et al. 1998; Tran et al. 2001; Martini et al. 2003). Thirdly, there is now enough credible evidence that (nearly) all nearby galaxies harbor a supermassive black hole in their centre. Intriguingly, the masses of these putative black holes are tightly coupled to large-scale parameters of the host galaxies (Kormendy & Richstone 1995; Ferrarese & Merritt 2000; Gebhardt et al. 2000; Graham et al. 2001; McLure & Dunlop 2002; Ferrarese 2002; Baes et al. 2003a; Marconi & Hunt 2003). Clearly, these various aspects are not isolated features, they all play part in the processes that shape galactic nuclei and galaxies in general. Unfortunately, we still know little about the formation processes and evolutionary scenarios of galactic nuclei and their black holes. For example, it is still unclear when and how supermassive black hole are being fuelled and what the mutual influence is between black holes and the central density cusps in galactic nuclei. Various relevant processes probably play at scales which are beyond (or at the limit of) the current observational capabilities. In order to increase our understanding, more detailed theoretical modelling, for example using N-body of SPH simulations, is necessary.

As a starting point or general framework for such studies, one needs a set of reference models which are simple enough and still can present a wide enough variety in structural characteristics. Because of the observed cuspy nature of galaxy centers, well explored models such as the Plummer model (Plummer 1911; Dejonghe 1987) and the isochrone sphere (Hénon 1959, 1960) are less suitable. Scale free models are a useful alternative. Such models have a density profile that decreases as $r^{-\gamma}$, and they include the singular isothermal sphere as a special case. Because of the simplicity of these models, their dynamical structure can be easily studied, even in axisymmetric or triaxial generalizations (e.g. Toomre 1982; Evans 1994; Qian et al. 1995; de Bruijne et al. 1996; Evans et al. 1997; Jalali & de Zeeuw 2001). Unfortunately, scale free models always have an infinite total mass, with the mass diverging in the centre for  $\gamma\geq3$ and at large radii for  $\gamma\leq3$.

A set of models that does not suffer from this disadvantage is the family of $\gamma $-models, introduced independently by Dehnen (1993) and Tremaine et al. (1994). These models have a central  $r^{-\gamma}$density cusp ($\gamma<3$) and the density falls at r-4 at large radii, such that the total mass is always finite. Special cases are the well-known Hernquist and Jaffe models (Hernquist 1990; Jaffe 1984). Many interesting dynamical properties such as the intrinsic and projected velocity dispersions, the distribution function and the differential energy distribution can be calculated analytically for the $\gamma $-models, under the assumption of a self-consistent isotropic dynamical structure. Extensions towards an anisotropic distribution functions or flattened geometry have been presented (e.g. Dehnen & Gerhard 1994; Hiotelis 1994; Carollo et al. 1995; Zhenglu 2000; Baes et al. 2002a; Zhenglu & Moss 2002).

As supermassive black holes appear to the present in nearly all galactic nuclei, it would be very interesting to extend the family of $\gamma $-models with a central black hole. In principle this is quite straightforward: one just has to add an extra contribution from the black hole to the stellar potential and re-calculate the dynamical properties with this new potential. In fact, Tremaine et al. (1994) consider the case where a central black hole is present in the $\gamma $-models. They present analytical expressions for the velocity dispersions and discuss the effect of a black hole on the distribution function. Unfortunately, they do not seek for analytical expressions for the distribution function and they leave some of the most interesting kinematical properties such as the differential energy distribution and the LOSVDs undiscussed. Ciotti (1996) provides a first attempt to construct completely analytical dynamical models for galaxies with a central black hole. Extending the work by Carollo et al. (1995), he considers a set of Hernquist models embedded in a dark matter halo. Setting the dark halo radius to zero reduces this halo to a central black hole. He demonstrates that many of the interesting dynamical quantities, including the distribution function and the differential energy distribution, can be calculated analytically (albeit as rather complicated functions involving Jacobian functions). Baes & Dejonghe (2004) present a one-parameter family with a steep $\gamma=\frac{5}{2}$ cusp slope and the black hole mass as a parameter. Almost all interesting properties of this family of models can be written in terms of elementary functions.

In this paper, we present a detailed analysis of a two-parameter family of spherical isotropic dynamical models based on the $\gamma $-models. The family contains as parameters the slope of the central density cusp $\gamma $ and the ratio $\mu$ of the central black hole mass to the total mass of the system. The parameter space covered by these models goes from weakly cusped models to very centrally concentrated models with an infinite stellar potential well, and from self-consistent models without black hole to systems where the dynamical structure is completely dominated by the central black hole. In Sect. 2 we define the models. In Sect. 3 we derive some basic properties, most of which can be calculated completely analytically. In Sect. 4 we discuss the energy budget of the models and look at the virial theorem. In Sect. 5 we derive expressions for and discuss the distribution function and the differential energy distribution. In Sect. 6 we study the LOSVDs of the models in our family and discuss the observational signature of a black hole. In the last section we summarize the results, and in the Appendices we present some mathematical expressions which might be useful for people who wish to use these models as input for further theoretical studies.

2 Definition of the models

The $\gamma $-models have a luminosity density

 \begin{displaymath}% \rho(r) = \frac{3-\gamma}{4\pi}~ \frac{1}{r^\gamma(1+r)^{4-\gamma}}\cdot \end{displaymath} (1)

The parameter $\gamma $ determines the density slope of the system at small radii; it can assume values between 0 and 3. All models have a luminosity density that behaves as r-4 at large radii, such that the total luminosity is finite.

The gravitational potential of the models we consider is the sum of two contributions: the stellar mass and a central black hole. We introduce the parameter $\mu$ as the relative importance of the black hole mass to the total mass in the system, such that $\mu$ can only assume values between 0 and 1. Note that the convention we use is similar to the one adopted by Baes & Dejonghe (2004), but different from the convention used in e.g. Tremaine et al. (1994) and Zhao (1996). In these papers, $\mu$ denotes the black hole mass relative to the stellar mass and the normalization is such that the stellar mass is set to unity. We prefer to set the total mass of the galaxy equal to unity however, because all models then have the same behaviour at large radii.

In the limit $\mu=0$ there is no black hole and we recover the self-consistent $\gamma $-models described in detail by Dehnen (1993) and Tremaine et al. (1994). The potential reduces to the stellar potential

 \begin{displaymath}% \Psi(r) \rightarrow \Psi_*(r) = \frac{1}{2-\gamma} \left[1-\left(\frac{r}{1+r}\right)^{2-\gamma}\right]. \end{displaymath} (2)

This expression is not valid for $\gamma=2$, the Jaffe model. If we take the limit $\gamma\rightarrow2$ in the previous expression we obtain the Jaffe potential $\Psi_*(r) = \ln(1+1/r)$. This special case divides the family of $\gamma $-models in two classes: self-consistent $\gamma $-models with $\gamma<2$ have a finite potential well with depth $\Psi_0=1/(2-\gamma)$, whereas the stellar potential well is infinitely deep for the models with $2\leq\gamma<3$.

The other extreme case on the range of possible black hole masses is $\mu =1$, corresponding to systems where the entire mass resides within the central black hole. In this case, the total gravitational potential reduces to a Kepler potential,

 \begin{displaymath}% \Psi(r) \rightarrow \Psi_\bullet(r) = \frac{1}{r}\cdot \end{displaymath} (3)

Although these systems where the dynamics are dominated by a central black hole do not form a realistic representation of real galaxies, they are useful in order to investigate the maximal effect of a black hole on the dynamical properties of the $\gamma $-models.

The general case $0<\mu<1$ is intermediate between these two extreme cases. We can write the cumulative mass function and the potential of the $\gamma $-models as

  
    $\displaystyle M(r) = (1-\mu) \left(\frac{r}{1+r}\right)^{3-\gamma} + \mu,$ (4)
    $\displaystyle \Psi(r) = \frac{1-\mu}{2-\gamma} \left[1-\left(\frac{r}{1+r}\right)^{2-\gamma}\right] + \frac{\mu}{r}.$ (5)

The two Eqs. (1) and (5) form a two-parameter family of potential-density pairs. Each pair of parameters ($\gamma $, $\mu$) completely defines a dynamical model. The study of these models as a function of the parameters $\gamma $ and $\mu$ is the goal of this paper.

3 Basic properties

3.1 The surface brightness

The surface brightness profile of a $\gamma $-model can be found by projecting the luminosity density on the plane of the sky,

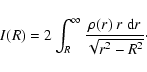\begin{displaymath}% I(R) = 2\int_R^\infty \frac{\rho(r)~r~{{\rm d}}r}{\sqrt{r^2-R^2}}\cdot \end{displaymath} (6)

At large radii, the surface brightness falls as R-3. In the central regions, models with $\gamma<1$ have a finite central surface brightness (in spite of the divergence of the luminosity density), whereas models with $\gamma>1$ have a surface brightness profile that diverges as $R^{1-\gamma}$. The surface brightness can be evaluated analytically for all integer and half-integer values of $\gamma $. Analytical expressions and other photometric quantities such as the cumulative surface brightness and the half-light radius can be found in Hernquist (1990), Dehnen (1993), Tremaine et al. (1994) and Baes & Dejonghe (2004).

3.2 The velocity dispersion

For a spherical isotropic system, the intrinsic velocity dispersion profile can be found using the solution of the lowest-order Jeans equation (Dejonghe 1986; Binney & Tremaine 1987),

 \begin{displaymath}% \sigma^2(r) = \frac{1}{\rho(r)}\int_r^\infty \frac{M(r)~\rho(r)~{{\rm d}}r}{r^2}\cdot \end{displaymath} (7)

After substitution of the general cumulative mass function (4) and some algebra, we obtain the expression

 \begin{displaymath}% \rho(r)\sigma^2(r) = (1-\mu)W_\gamma(r) + 2\mu~W_{\frac{3+\gamma}{2}}(r), \end{displaymath} (8)

where the function $W_\gamma(r)$ is defined as

 \begin{displaymath}% W_\gamma(r) = \frac{3-\gamma}{4\pi} \int_r^\infty \frac{r^{1-2\gamma}{{\rm d}}r}{(1+r)^{7-2\gamma}}\cdot \end{displaymath} (9)

From Eq. (8) we see that $W_\gamma(r)$ is nothing but the velocity dispersion  $\rho(r)\sigma_*^2(r)$ of the self-consistent $\gamma $-model, which can be evaluated in terms of elementary functions for all values of $\gamma $ (see Appendix A).

3.3 The projected velocity dispersion

The projected velocity dispersion profile  $\sigma _{{\rm p}}(R)$ can be found by projecting the intrinsic dispersion on the plane of the sky,

 \begin{displaymath}% \sigma_{{\rm p}}^2(R) = \frac{2}{I(R)} \int_R^\infty \frac{\rho(r)\sigma^2(r)~r~{{\rm d}}r}{\sqrt{r^2-R^2}}\cdot \end{displaymath} (10)

This expression can be written in a form very similar to Eq. (8),

 \begin{displaymath}% I(R)\sigma_{{\rm p}}^2(R) = (1-\mu)Y_\gamma(R) + 2\mu~Y_{\frac{3+\gamma}{2}}(R), \end{displaymath} (11)

with (Tremaine et al. 1994)

 \begin{displaymath}% Y_\gamma(R) = \frac{3-\gamma}{2\pi} \int_R^\infty \frac{r^{1-2\gamma}~\sqrt{r^2-R^2}~{{\rm d}}r}{(1+r)^{7-2\gamma}}\cdot \end{displaymath} (12)

The function $Y_\gamma(R)$ represents the projected velocity dispersion  $I(R)\sigma^2_{{{\rm p}},*}(r)$ of the self-consistent $\gamma $-model. It can be expressed analytically for all integer and half-integer values of $\gamma $, and has to be calculated numerically for the other values of $\gamma $. A useful transformation for the numerical calculation of the integral can be found in Appendix B of Dehnen (1993).

4 The energy budget and the virial theorem

The (scalar) virial theorem states that any steady-state system satisfies the relation

2K = U, (13)

where K is the total kinetic energy and U=-W is the total (binding) potential energy of the system. It is easy to verify that the $\gamma $-models without a central black hole satisfy the virial theorem. For a self-consistent spherical system the total potential and kinetic energy can be found as

 \begin{displaymath}% U_* = 2\pi\int_0^\infty \rho(r)~\Psi_*(r)~r^2~{{\rm d}}r. \end{displaymath} (14)


  
                          K* = $\displaystyle 6\pi\int_0^\infty \rho(r)\sigma_*^2(r)~r^2~{{\rm d}}r$ (15)
  = $\displaystyle 2\pi\int_0^\infty \rho(r)~M_*(r)~r~{{\rm d}}r,$ (16)

where the second expression for the kinetic energy is derived by substituting Eq. (7) into the first expression and partial integration. Through substitution of the expressions (1), (2) and (4) into these formulae, one finds that the self-consistent $\gamma $-models have an infinite energy budget for $\gamma\geq\frac{5}{2}$, whereas for $\gamma<\frac{5}{2}$ we obtain (Tremaine et al. 1994)

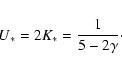\begin{displaymath}% U_* = 2K_* = \frac{1}{5-2\gamma}\cdot \end{displaymath} (17)

For systems with a central black hole, the total kinetic energy can still be calculated using Eq. (15) or (16), with the contribution of the black hole taken into account in the dispersion or the cumulative mass distribution. The total potential energy, however, cannot be found by just replacing the stellar potential by the total potential, as the expression (14) is derived under the assumption that the system is self-consistent. The correct expression for the potential energy consists of an internal and an external contribution (Binney & Tremaine 1987, problem 8.2),

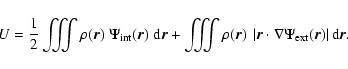\begin{displaymath}% U = \frac{1}{2} \iiint \rho({{\vec r}})~\Psi_{{\rm int... ...\Psi_{{\rm ext}}({{\vec r}})\right\vert {{\rm d}}{{\vec r}}. \end{displaymath} (18)

In our present case, the external potential is the gravitational potential from the central black hole, such that these formulae reduce to

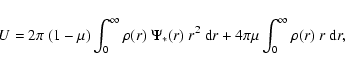\begin{displaymath}% U = 2\pi~(1-\mu) \int_0^\infty \rho(r)~\Psi_*(r)~r^2~{{\rm d}}r + 4\pi\mu \int_0^\infty \rho(r)~r~{{\rm d}}r, \end{displaymath} (19)

or equivalently,

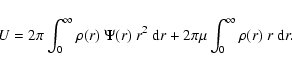\begin{displaymath}% U = 2\pi\int_0^\infty \rho(r)~\Psi(r)~r^2~{{\rm d}}r + 2\pi\mu\int_0^\infty \rho(r)~r~{{\rm d}}r. \end{displaymath} (20)

Comparing this expression to the equivalent formula (14) of the self-consistent models, we notice that the black hole mass adds an extra contribution to the potential energy apart from its contribution to the potential of the system. Using the expressions (1), (5) and (4), one finds that the total energy budget is infinite for  $\gamma\geq2$, whereas for $\gamma<2$ we obtain

\begin{displaymath}% U = 2K = \frac{1}{5-2\gamma} \left[1 + \mu\left(\frac{3-\gamma}{2-\gamma}\right)\right]\cdot \end{displaymath} (21)

The virial theorem is thus satisfied.

5 The distribution function and the differential energy distribution

All the kinematical information on a given system is contained in the distribution function  $f({{\vec r}},{{\vec v}})$, which represents the number density of stars in six-dimensional phase space. For spherical isotropic systems, the distribution function depends only on the binding energy ${\mathcal{E}}= \Psi(r)-v^2/2$. The key to calculating the distribution function $f({\mathcal{E}})$ of isotropic spherical models is the augmented density $\tilde\rho(\Psi)$, i.e. the luminosity density written as a function of the potential. The Eddington formula specifies how the distribution function can be calculated from the augmented density,

  
                                 $\displaystyle % f({\mathcal{E}})$ = $\displaystyle \frac{1}{\sqrt{8}\pi^2}~ \frac{{{\rm d}}}{{{\rm d}}{\mathcal{E}}}... ...}}\tilde{\rho}}{{{\rm d}}\Psi}~ \frac{{{\rm d}}\Psi}{\sqrt{{\mathcal{E}}-\Psi}}$ (22)
  = $\displaystyle \frac{1}{\sqrt{8}\pi^2} \int_0^{\mathcal{E}}\frac{{{\rm d}}^2\til... ...{E}}}~\pi^2} \left(\frac{{{\rm d}}\tilde{\rho}}{{{\rm d}}\Psi}\right)_{\Psi=0}.$ (23)

The distribution function obviously is an important characteristic of the dynamical structure of galaxies. However, it is not straightforward to physically interpret the meaning of the distribution function when expressed as a function of binding energy. A more natural diagnostic quantity is the differential energy distribution (DED) ${\mathcal{N}}({\mathcal{E}})$, which describes the number of stars per unit binding energy. For isotropic systems, the DED is simply the product of the distribution function  $f({\mathcal{E}})$ and the density-of-states function  $g({\mathcal{E}})$, defined as the phase space volume accessible for a star with binding energy  ${\mathcal{E}}$. This function can be calculated as

 \begin{displaymath}% g({\mathcal{E}}) = 16\sqrt{2}~\pi^2 \int_{{\mathcal{E}}}... ...d}}\Psi}\right\vert~ \sqrt{\Psi-{\mathcal{E}}}~{{\rm d}}\Psi, \end{displaymath} (24)

and depends only on the potential of the system, not on the density profile (Binney & Tremaine 1987).

5.1 Models without a central black hole ${(\mu =0)}$

For $\gamma $-models without a black hole, we can calculate the distribution function  $f_*({\mathcal{E}})$ directly by substituting Eqs. (1) and (2) into the Eddington relation (22). We obtain the expression

 \begin{displaymath}% f_*({\mathcal{E}}) = \frac{3-\gamma}{16\sqrt{2}\pi^3}~ \... ...t+\gamma]~{{\rm d}}\Psi_*} {t^2~\sqrt{{\mathcal{E}}-\Psi_*}}, \end{displaymath} (25)

where $t\equiv t(\Psi_*)$ is defined as

 \begin{displaymath}% t(\Psi_*) = \left\{ \begin{array}{ll} [1-(2-\gamma)~\Ps... ...}^{-\Psi_*} & \quad {\rm if} \;\gamma=2. \end{array}\right. \end{displaymath} (26)

This integral can generally be expressed in terms of hypergeometric functions,
 
                                  $\displaystyle % f_*({\mathcal{E}})$ = $\displaystyle \frac{3-\gamma}{\sqrt{8}~\pi^3}~ \sqrt{{\mathcal{E}}} \Bigl[ (4-\... ...1 \left( 1,\frac{-\gamma}{2-\gamma};\frac{3}{2};(2-\gamma){\mathcal{E}} \right)$  
    $\displaystyle -2~(3-\gamma)~ {}_2F_1 \left( 1,\frac{1-\gamma}{2-\gamma};\frac{3}{2};(2-\gamma){\mathcal{E}} \right)$  
    $\displaystyle +2~(1-\gamma)~ {}_2F_1\left( 1,\frac{3-\gamma}{2-\gamma};\frac{3}{2};(2-\gamma){\mathcal{E}} \right)$  
    $\displaystyle +\gamma~ {}_2F_1\left( 1,\frac{4-\gamma}{2-\gamma};\frac{3}{2};(2-\gamma){\mathcal{E}} \right) \Bigr].$ (27)

For $\gamma=2\pm1/n$ with n a natural number, the distribution function can be written as a combination of elementary functions. In particular, the self-consistent $\gamma $-models with ${\gamma =1}$, $\frac{3}{2}$and  $\frac{5}{2}$ have fairly simple distribution functions (Hernquist 1990; Dehnen 1993; Tremaine et al. 1994; Baes & Dejonghe 2004). The $\gamma=2$ model is a particular case: its distribution function can be expressed most conveniently in terms of the error function and Dawson's integral (Jaffe 1983).

The calculation of $g({\mathcal{E}})$ is also straightforward for the self-consistent $\gamma $-models. Substituting the potential (5) in Eq. (24) one immediately obtains (Dehnen 1993)

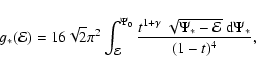\begin{displaymath}% g_*({\mathcal{E}}) = 16\sqrt{2}\pi^2 \int_{{\mathcal{E}}... ...amma}~\sqrt{\Psi_*-{\mathcal{E}}}~{{\rm d}}\Psi_*} {(1-t)^4}, \end{displaymath} (28)

with $t\equiv t(\Psi_*)$ as in Eq. (26). The integral in this equation is quite similar to the integral in Eq. (25). A closed expression for  $g_*({\mathcal{E}})$ for general $\gamma $ in terms of hypergeometric functions cannot be obtained, but the integral can be expressed analytically for all $\gamma=2\pm1/n$ with n a natural number. Examples of such closed expressions can be found in Dehnen (1993) and Baes & Dejonghe (2004).

5.2 Models dominated by a central black hole ${(\mu =1)}$

For models where the potential is completely dominated by the central black hole, the distribution function can also be calculated by a straightforward application of Eddington's formula. The result can generally be expressed in terms of hypergeometric functions,

 
                              $\displaystyle % f_\bullet({\mathcal{E}})$ = $\displaystyle \frac{4\sqrt{2}(3-\gamma)}{315\pi^3} {\mathcal{E}}^{5/2} \Bigl[ 63~ {}_2F_1 \left(3,6-\gamma;\frac{7}{2};-{\mathcal{E}}\right)$  
    $\displaystyle -36(1-\gamma)~{\mathcal{E}}~ {}_2F_1 \left(3,6-\gamma;\frac{9}{2};-{\mathcal{E}}\right)$  
    $\displaystyle -4\gamma(1-\gamma)~{\mathcal{E}}^2 {}_2F_1 \left(3,6-\gamma;\frac{11}{2};-{\mathcal{E}}\right) \Bigr].$ (29)

For half-integer or integer values of $\gamma $, the distribution function can be written in terms of elementary functions. In the central regions of the galaxy ( ${\mathcal{E}}\rightarrow\infty$), this distribution function has the asymptotic behaviour

 \begin{displaymath}% f_\bullet({\mathcal{E}}) \sim \frac{3-\gamma}{2(2\pi)^{5/... ...+1)}{\Gamma(\gamma-\frac{1}{2})}~ {\mathcal{E}}^{\gamma-3/2}. \end{displaymath} (30)

It is interesting to compare these results with those obtained by de Bruijne et al. (1996). They consider a set of axisymmetric cuspy densities in a spherical potential and present two different analytical families of three-integral distribution functions. For the special case of isotropic spherical galaxies dominated by a black hole potential ( $q=\delta=1$ and $\beta=0$) the expression (30) is recovered, after correction for the different normalization conventions.

Since the density-of-states function only depends on the potential of the system, we recover the simple and well-known expression $g_\bullet({\mathcal{E}}) = \sqrt{2}\pi^3~{\mathcal{E}}^{-5/2}$, independent of $\gamma $.

A particularly interesting case is the model with $\gamma=\frac{1}{2}$. This model has a simple distribution function and differential energy distribution,

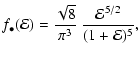    $\displaystyle f_\bullet({\mathcal{E}}) = \frac{\sqrt{8}}{\pi^3}~ \frac{{\mathcal{E}}^{5/2}}{(1+{\mathcal{E}})^5},$ (31)
    $\displaystyle {\mathcal{N}}_\bullet({\mathcal{E}}) = \frac{4}{(1+{\mathcal{E}})^5}\cdot$ (32)

For $\gamma $-models with a central black hole, this model is the one with the smallest possible cusp slope. Indeed, $\gamma $-models with $\gamma<\frac{1}{2}$ cannot support a central black hole when they have an isotropic dynamical structure, because stars at each binding energy level will induce a r-1/2 cusp at small radii (Tremaine et al. 1994).

5.3 The general case ${(0<\mu <1)}$

For the general case, a direct calculation of the augmented density is not the best way to calculate the distribution function. Instead, we use an approach based on the analysis of Ciotti (1996), who showed a convenient way to calculate the distribution function of a set of two-component models. If we invert the relation (2) to $r=r(\Psi_*)$, and substitute it into the expression (5), we obtain

 \begin{displaymath}% \Psi = \omega(\Psi_*) \equiv (1-\mu)~\Psi_* + \frac{\mu~(1-t)}{t}, \end{displaymath} (33)

with $t\equiv t(\Psi_*)$ as in expression (26). The relation (33) links the stellar potential $\Psi_*$ at a given position in the system to the total potential $\Psi$. We can also regard it more generally as the definition of a mapping function $\omega$, which maps the interval  $[0,\Psi_0]$ onto the positive real axis. It is a monotonically increasing function, and therefore the inverse function  $\omega^{-1}$ exists. Transforming the Eddington formula (22) to an integration with respect to the stellar potential we obtain

 \begin{displaymath}% f({\mathcal{E}}) = \frac{1}{\sqrt{8}\pi^2}~ \left[\frac{... ...d}}{\mathcal{Q}}}{{{\rm d}}{\mathcal{E}}_*} ({\mathcal{E}}_*) \end{displaymath} (34a)

with ${\mathcal{E}}_*=\omega^{-1}({\mathcal{E}})$ and ${\mathcal{Q}}$ a function defined by the integral

 \begin{displaymath}% {\mathcal{Q}}(x) = \int_0^x \frac{{{\rm d}}\tilde\rho}{{... ... \frac{{{\rm d}}\Psi_*}{\sqrt{\omega(x)-\omega(\Psi_*)}}\cdot \end{displaymath} (34b)

This expression is similar to the formula used by Ciotti (1996) to calculate the distribution function of his two-component Hernquist models. Whether this integration can be performed analytically depends on the complexity of both factors of the integrand. It appears that this integration can be performed analytically (only) for the models with ${\gamma =1}$, $\frac{3}{2}$ and  $\frac{5}{2}$. For these three models, both the augmented density  $\tilde\rho(\Psi_*)$ and the mapping function  $\omega(\Psi_*)$ are rational functions. For ${\gamma =1}$ and $\gamma=\frac{3}{2}$, the factor under the square root can be reduced to a cubic polynomial, while for $\gamma=\frac{5}{2}$it can be reduced to a quadratic polynomial in $\Psi_*$. As a result, the function  ${\mathcal{Q}}(x)$ and the distribution function can be expressed by means of elliptic integrals for the former two models, and completely in terms of elementary functions for the latter model. More details can be found in Appendix B.

For other values of $\gamma $ (including $\gamma=2$), an analytical evaluation of the integral (34b) is not possible, and the distribution function has to be calculated numerically. For this goal, the expression (34a) is not particularly useful, because it involves a differentiation of a numerically determined function. A more convenient formula for numerical integration can be obtained by using the alternative form (23) of the Eddington equation. The second term in this expression vanishes for all $\gamma $-models, because $\tilde\rho(\Psi) \propto \Psi^4$ at large radii. If we do the substitution  $\Psi\rightarrow\Psi_*$ in this last equation, we obtain

 \begin{displaymath}% f({\mathcal{E}}) = \frac{1}{\sqrt{8}\pi^2} \int_0^{{\mat... ...d}}\Psi_*}{\sqrt{\omega({\mathcal{E}}_*)-\omega(\Psi_*)}}\cdot \end{displaymath} (35)

Combined with a numerical solution of the equation ${\mathcal{E}}_*=\omega^{-1}({\mathcal{E}})$, this formula makes it possible to evaluate the distribution function numerically using standard quadrature techniques.

In order to calculate the density-of-states function for $\gamma $-models with a black hole, we can apply the same technique as for the calculation of the distribution function. If we rewrite Eq. (24) as an integral with the stellar potential as the integration variable, we obtain

 \begin{displaymath}% g({\mathcal{E}}) = 16\sqrt{2}~\pi^2 \int_{{\mathcal{E}}_... ...qrt{\omega(\Psi_*)-\omega({\mathcal{E}}_*)}~ {{\rm d}}\Psi_*. \end{displaymath} (36)

This integral shows many similarities with the integral in the expression (34b), and the prospects to find an analytical solution are very similar. One can demonstrate that the density-of-states function can be written in terms of elliptic integrals for ${\gamma =1}$ and $\gamma=\frac{3}{2}$, and completely in terms of elementary functions for $\gamma=\frac{5}{2}$. For all other values of $\gamma $, including the Jaffe model, the density-of-states function cannot be expressed analytically.

5.4 Asymptotic expansions


  \begin{figure} \par\includegraphics[angle=-90,width=15.65cm,clip]{1907fig1.eps}\end{figure} Figure 1: The distribution function ( top row) and differential energy distribution ( bottom row) for $\gamma $-models without and with a central black hole. The value of $\gamma $ is indicated in each panel. The black curves correspond to the self-consistent models, the colored curves correspond to models with various black hole masses: $\mu =0.001$ (yellow), $\mu =0.01$ (green), $\mu =0.1$ (cyan) and $\mu =1$(red).
Open with DEXTER

We can get a better insight into the behaviour of the distribution function and the DED of the $\gamma $-models with a central black hole by studying the asymptotic behaviour. In the limit ${\mathcal{E}}\rightarrow0$, i.e. in the outer regions of the system, a black hole has no effect on the dynamics of the $\gamma $-models, as the asymptotic expansion of the potential  $\Psi\rightarrow r^{-1}$ is independent of $\mu$. The behaviour of the distribution function and the DED in the low binding-energy limit is

 
    $\displaystyle f({\mathcal{E}}) \sim \frac{4\sqrt{2}(3-\gamma)}{5\pi^3}~{\mathcal{E}}^{5/2},$ (37)
    $\displaystyle {\mathcal{N}}({\mathcal{E}}) \sim \frac{8(3-\gamma)}{5}\cdot$ (38)

More interesting is the asymptotic behaviour of the distribution function and the differential energy distribution in the high binding-energy limit. To find asymptotic expansions for the self-consistent $\gamma $-models, we must separately consider the models with a modest and those with a strong central density cusp. The self-consistent $\gamma $-models with a modest density cusp $\gamma<2$have a finite potential well $\Psi_0=(2-\gamma)^{-1}$, and after some algebra one finds that in the limit ${\mathcal{E}}\rightarrow\Psi_0$,
  
    $\displaystyle f_*({\mathcal{E}}) \sim \frac{\sqrt{2}}{8\pi^{5/2}}~ \frac{\gamma... ...gamma}{2-\gamma}\right)}~ (\Psi_0-{\mathcal{E}})^{-\frac{6-\gamma}{4-2\gamma}},$ (39)
    $\displaystyle {\mathcal{N}}_*({\mathcal{E}}) \sim \frac{2\gamma~(3-\gamma)}{(2-... ...ac{12-3\gamma}{4-2\gamma}\right)}~ (\Psi_0-{\mathcal{E}})^{\frac{1}{2-\gamma}}.$ (40)

The self-consistent models with a central density cusp slope $\gamma>2$ have an infinitely deep potential well, and for these models one finds in the limit ${\mathcal{E}}\rightarrow\infty$
  
    $\displaystyle f_*({\mathcal{E}}) \sim \frac{\sqrt{2}}{8\pi^{5/2}}~ \gamma~(3-\g... ...\frac{2+\gamma}{2\gamma-4}\right)}~ {\mathcal{E}}^{\frac{6-\gamma}{2\gamma-4}},$ (41)
    $\displaystyle {\mathcal{N}}_*({\mathcal{E}}) \sim \frac{2\gamma~(3-\gamma)}{(\g... ...ma\left(\frac{\gamma+1}{\gamma-2}\right)}~ {\mathcal{E}}^{-\frac{1}{\gamma-2}}.$ (42)

Finally, for the Jaffe model $\gamma=2$, the model that separates these two classes, the expansion in the limit ${\mathcal{E}}\rightarrow\infty$reads
    $\displaystyle f_*({\mathcal{E}}) \sim \frac{1}{4\pi^{5/2}}~{{\rm e}}^{2{\mathcal{E}}},$ (43)
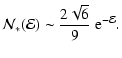    $\displaystyle {\mathcal{N}}_*({\mathcal{E}}) \sim \frac{2\sqrt{6}}{9}~{{\rm e}}^{-{\mathcal{E}}}.$ (44)

When the $\gamma $-models contain a black hole, the potential well is infinitely deep for all values of the cusp slope $\gamma $. The asymptotic behaviour of the distribution function and the differential energy distribution changes to
  
    $\displaystyle f({\mathcal{E}}) \sim \frac{3-\gamma}{2(2\pi)^{5/2}}~ \frac{\Gamm... ...amma+1)}{\Gamma(\gamma-\frac{1}{2})}~ \mu^{-\gamma}~{\mathcal{E}}^{\gamma-3/2},$ (45)
    $\displaystyle {\mathcal{N}}({\mathcal{E}}) \sim \frac{\sqrt{\pi}~(3-\gamma)}{8}... ...gamma+1)}{\Gamma(\gamma-\frac{1}{2})}~ \mu^{3-\gamma}~{\mathcal{E}}^{\gamma-4}.$ (46)

These expressions are valid for all models with a central black hole $(0<\mu\leq1)$ and for all values of $\gamma>\frac{1}{2}$. For the limiting case $\gamma=\frac{1}{2}$, the leading terms from Eqs. (45) and (46) vanish and the asymptotic expansion for ${\mathcal{E}}\rightarrow\infty$ reads
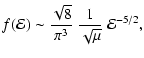    $\displaystyle f({\mathcal{E}}) \sim \frac{\sqrt{8}}{\pi^3}~\frac{1}{\sqrt{\mu}}~{\mathcal{E}}^{-5/2},$ (47)
    $\displaystyle {\mathcal{N}}({\mathcal{E}}) \sim 4\mu^{5/2}~{\mathcal{E}}^{-5}.$ (48)

5.5 Discussion

In the top panels of Fig. 1 we plot the distribution function of various $\gamma $-models with various black hole masses. A black hole drastically changes the behaviour of the distribution function, particularly for the models with a shallow cusp slope $(\gamma<2)$ which have a finite stellar potential well. For these models, the self-consistent distribution function is a strongly increasing function of energy, which diverges for ${\mathcal{E}}\rightarrow\Psi_0$ according to formula (39). When a central black hole is present in these model, stars of all binding energies populate the galaxy. The behaviour of the distribution function in this new territory depends on the cusp slope, as prescribed by the asymptotic expression (45). For models with $\gamma<\frac{3}{2}$, the distribution function decreases as a function of binding energy in the neighborhood of the black hole. The distribution function of such models thus has two regimes: it converges to zero both in the low and high binding energy limit and has a maximal value at binding energies around the depth of the stellar potential well. The larger the black hole mass, the larger the value of the binding energy where the distribution function becomes maximal and the smoother the transition between the two regimes. For the $\gamma=\frac{3}{2}$ model, the distribution function becomes asymptotically flat in the high binding energy limit. For models with a steeper cusp slope, the distribution function is a monotonically increasing function of binding energy, and the differences between a model without and with black hole become less pronounced. In particular for models with $\gamma\geq2$ the presence of a black hole does not drastically change the behaviour of the distribution function. Both without and with a central black hole the distribution function is a monotonically increasing function of binding energy, diverging in the high energy limit. Equations (41) and (45) show that the slope of the distribution function in the high energy limit changes from $(6-\gamma)/(2\gamma-4)$ to  $\gamma-\frac{3}{2}$ when a black hole is present.

In the bottom row of Fig. 1 we plot the differential energy distribution  ${\mathcal{N}}({\mathcal{E}})$ for the same models as in the top row. For all models, ${\mathcal{N}}({\mathcal{E}})$ converges to a finite value $8(3-\gamma)/5$ in the low binding energies limit. Typically, ${\mathcal{N}}({\mathcal{E}})$ is hardly affected for low binding energies, where it is a decreasing function of increasing black hole mass. Only at high binding energies does the effect of a black hole become visible, in particular for models with a shallow density cusp. The differential energy distribution  ${\mathcal{N}}_*({\mathcal{E}})$ of the models without black hole suddenly drops to zero when  ${\mathcal{E}}$ approaches the depth of the potential well, in spite of the divergence of the distribution function (see Eq. (40)). In the presence of a black hole, where stars can populate orbits with arbitrarily high binding energies, ${\mathcal{N}}({\mathcal{E}})$ smoothly decreases as ${\mathcal{E}}^{\gamma-4}$ in the high energy limit. For $\gamma $-models with a steeper cusp slope, in particular the models with an infinitely deep stellar potential well, the effect on the differential energy distribution is weaker.

Although the effect of a black hole on the shape of the distribution function is severe, it thus appears that the effect on the differential energy distribution is rather modest, even for the models with a finite stellar potential well. In the energy region that was off limits for the self-consistent models, ${\mathcal{N}}({\mathcal{E}})$ assumes very low values. Although the addition of a black hole opens up a huge range for possible binding energies, the number of stars that actually populate these orbits is thus fairly small. This can be quantified by calculating the mean binding energy  $\langle{\mathcal{E}}\rangle$ of stars in the models. The mean binding energy is defined as

 \begin{displaymath}% \langle{\mathcal{E}}\rangle = \int_0^\infty {\mathcal{N}}({\mathcal{E}})~{\mathcal{E}}~{{\rm d}}{\mathcal{E}}. \end{displaymath} (49)

A more straightforward way to calculate the mean binding energy is through the formula
                            $\displaystyle % \langle{\mathcal{E}}\rangle$ = $\displaystyle \iiint {{\rm d}}{{\vec r}} \iiint f({{\vec r}},{{\vec v}}) \left[\Psi(r)-\frac{1}{2}{{\vec v}}^2\right] {{\rm d}}{{\vec v}}$ (50)
  = $\displaystyle 4\pi\int_0^\infty \rho(r) \left[\Psi(r)-\frac{3}{2}\sigma^2(r)\right] r^2~{{\rm d}}r.$ (51)

Using similar algebra as in Sect. 4, we find

\begin{displaymath}% \langle{\mathcal{E}}\rangle = \frac{3}{4(5-2\gamma)} \left[1+\mu\left(\frac{4-\gamma}{3(2-\gamma)}\right)\right]\cdot \end{displaymath} (52)

Numerical integration of Eq. (49) for a selection of models gives identical results. For a Hernquist model (${\gamma =1}$), the ratio $\langle{\mathcal{E}}\rangle/\langle{\mathcal{E}}\rangle_*$ equals $1+\mu$, so the mean binding energy for a model with $\mu =0.001$ is only 0.1% larger than the mean binding energy of the self-consistent model.

Another characteristic that can be used to quantify the importance of a central black hole on the energy distribution is the fraction $\theta$ of stars on orbits with a binding energy larger than the potential well of the corresponding self-consistent model,

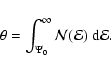\begin{displaymath}% \theta = \int_{\Psi_0}^\infty {\mathcal{N}}({\mathcal{E}})~{{\rm d}}{\mathcal{E}}. \end{displaymath} (53)

For a ${\gamma =1}$ model with black hole masses $\mu =0.001$ and $\mu =0.01$, numerical integration yields $\theta=1.63$ $\times$ 10-4and $\theta=1.81$ $\times$ 10-3 respectively.

These numbers clearly demonstrate that the effect of a black hole on the global energy distribution is actually quite small, although the distribution function when represented as a function of the binding energy is affected in a very significant way.

6 The LOSVD

The LOSVD (also called line profile or velocity profile) $\phi_{{\rm p}}(R,v_\parallel)$ is the distribution of line-of-sight velocities at a given projected radius R. From an observer's point of view, this is definitely one of the most important kinematical quantities of a galaxy model, because a LOSVD contains all kinematic information that can be obtained from a galaxy at a given line of sight and LOSVDs are in principle directly observable.


  \begin{figure} \par\includegraphics[angle=-90,width=15.55cm,clip]{1907fig2.eps}\end{figure} Figure 2: The observed LOSVDs for $\gamma $-models without and with a central black hole. The top panels are the LOSVDs at a projected radius R=1, the middle panels correspond to R=0.1 and the bottom panels are the LOSVDs at R=0.01. The value of $\gamma $ is indicated each panel and the colour code is the same as in Fig. 1.
Open with DEXTER

6.1 Calculation of the LOSVDs

The LOSVD can be found through the formula

 \begin{displaymath}% \phi_{{\rm p}}(R,v_\parallel) = \frac{2}{I(R)} \int_R^\i... ...c{\rho(r)~\phi(r,v_\parallel)~r~{{\rm d}} r}{\sqrt{r^2-R^2}}, \end{displaymath} (54)

where the function $\phi(r,v_\parallel)$ represents the spatial LOSVD. In general, the spatial LOSVD $\phi({{\vec r}},{{\vec k}},v_\parallel)$describes the distribution of line-of-sight velocities at a position  ${{\vec r}}$ in an arbitrary direction  ${{\vec k}}$. It can be found by integrating the distribution function over the two velocity components perpendicular to  ${{\vec k}}$ and normalizing the resulting distribution

 \begin{displaymath}% \phi({{\vec r}},{{\vec k}},v_\parallel) = \frac{1}{\rho(r)} \iint f({{\vec r}},{{\vec v}})~ {{\rm d}}{{\vec v}}_\perp. \end{displaymath} (55)

For general anisotropic systems, these integrations are usually very cumbersome, and an analytical evaluation of the spatial LOSVD can only be obtained for a limited number of models (e.g. Carollo et al. 1995; Baes & Dejonghe 2002b). For isotropic models, however, the spatial LOSVD is independent of the direction  ${{\vec k}}$ and can be written as  $\phi(r,v_\parallel)$. The expression (55) can then be transformed to

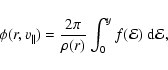\begin{displaymath}% \phi(r,v_\parallel) = \frac{2\pi}{\rho(r)} \int_0^y f({\mathcal{E}})~{{\rm d}}{\mathcal{E}}, \end{displaymath} (56)

where $y = \Psi(r)-v_\parallel^2/2$. If we substitute the Eddington formula (22) into this equation, we obtain

 \begin{displaymath}% \phi(r,v_\parallel) = \frac{1}{\sqrt{2}\pi~\rho(r)} \int... ...e\rho}{{{\rm d}}\Psi}~\frac{{{\rm d}}\Psi}{\sqrt{y-\Psi}}\cdot \end{displaymath} (57)

Comparing this expression with the Eddington formula (22), we see that the spatial LOSVD of an isotropic dynamical model can be calculated analytically if the same is true for the distribution function. In fact, the spatial LOSVD is obtained almost automatically during the calculation of the distribution function. This means that the spatial LOSVD of the self-consistent $\gamma $-models can generally be expressed in terms of hypergeometric functions, and in terms of elementary functions for $\gamma=2\pm1/n$with n a natural number. The spatial LOSVD of the black-hole-dominated $\gamma $-models can also be expressed in terms of hypergeometric functions, and in terms of standard functions for integer and half-integer values of $\gamma $. To calculate the spatial LOSVD for the $\gamma $-models with a black hole, we use a similar method as for the calculation of the distribution function. Changing the integration variable from $\Psi$ to $\Psi_*$ in Eq. (57) we find

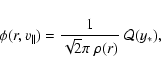\begin{displaymath}% \phi(r,v_\parallel) = \frac{1}{\sqrt{2}\pi~\rho(r)}~ {\mathcal{Q}}(y_*), \end{displaymath} (58)

with $y_*=\omega^{-1}(y)$ and the function  ${\mathcal{Q}}$ defined in Eq. (34b). For the models with ${\gamma =1}$, $\gamma=\frac{3}{2}$ and $\gamma=\frac{5}{2}$, both the inverse of the mapping function $\omega$ and the function  ${\mathcal{Q}}$ can be expressed analytically, such that the spatial LOSVD can be written completely in analytical form (including elliptic integrals for the ${\gamma =1}$ and $\gamma=\frac{3}{2}$ models). For the other values of $\gamma $, both of these operations must be done numerically.


  \begin{figure} \par\includegraphics[angle=-90,width=15.65cm,clip]{1907fig3.eps}\end{figure} Figure 3: The moments of the LOSVDs for $\gamma $-models without and with a central black hole. The top row shows the projected dispersion profile  $\sigma _{{\rm p}}(R)$, the bottom row shows the Gauss-Hermite shape parameter h4(R). The value of $\gamma $ is indicated in each panel and the colour code is the same as in Fig. 1.
Open with DEXTER

Summarizing, the calculation of the LOSVDs requires only one single quadrature for all self-consistent and black hole dominated models, and for the $\gamma $-models with a black hole if ${\gamma =1}$, $\gamma=\frac{3}{2}$ or $\gamma=\frac{5}{2}$. For the remaining $\gamma $-models containing a central black hole, the calculation of the LOSVDs requires a double quadrature. We calculated the LOSVDs with the Monte Carlo integration routines built into the SKIRT code (Baes et al. 2003b).

6.2 Discussion

In Fig. 2 we plot a number of LOSVDs for a set of $\gamma $-models for various values of the black hole mass $\mu$. As expected, the influence of a (realistic) black hole is negligible at large projected radii. At gradually smaller projected radii the influence of a black hole becomes more important. The signature of the presence of the black hole is primarily a broadening of the LOSVD. The degree of the broadening depends on the black hole fraction and on the central slope.

A quantitative investigation of the effects of a black hole on the LOSVDs is more easy when we study the moments of the LOSVDs. The first and second-order moments of the LOSVDs are nothing but the mean rotation and the projected dispersion. Rather than the true higher-order moments, one usually utilizes the coefficients hi from a Gauss-Hermite expansion to further characterize the shape of the LOSVDs (Gerhard 1993; van der Marel & Franx 1993). In Fig. 3 we plot the projected velocity dispersion profile and the h4 profile for a set of $\gamma $-models without and with black holes of various masses (all odd moments are zero).

The projected dispersion profile of models with a shallow central density slope are most sensitive to a black hole. As a result of the presence of a black hole, the stars in the very centre of the galaxy will obtain large velocities, including velocities which are not possible in the finite central potential wells of the self-consistent models. This causes a dramatic increase in the velocity dispersion at small radii, resulting in the usual R-1/2 divergence. Note that this divergence is maintained in spite of the smoothing effect of the projection along the line of sight: the projected dispersion is a weighted integral of the intrinsic dispersion along the line of sight, such that the projected dispersion at small projected radii contains a significant contribution from stars at large radii.

The projected dispersion profile for models with a steep cusp slope is much less affected by a central black hole. Even without a black hole, these models already have steep stellar potential wells where stars can obtain arbitrarily high velocities. The limit case is the (degenerate) model with $\gamma\rightarrow3$, where the self-consistent potential is already a point potential, and the addition of a black hole does not alter the kinematical structure of the galaxy at all.

The effect of a black hole on the h4 shape parameter of the LOSVD is less straightforward to interpret. For the models with a shallow cusp, the central black hole does significantly affect the h4 profile, but there is no clear trend with increasing black hole mass. For the models with a steep density cusp, the effect of a black hole on the h4 profile is negligible. This trend, or rather the non-existence of a clear trend, contrasts with the signature of a dark matter halo on the observed kinematics at large radii. In elliptical galaxies, which lack a ubiquitous and straightforward tracer population such as the H I gas in spiral galaxies, the stellar kinematics are one of the most important tracers for dark matter. The most obvious signature of dark matter on the stellar kinematics is the behaviour of the projected velocity dispersion at large radii: dark matter causes the $\sigma_{{\rm p}}$ profile to remain flat or to decrease more slowly than expected from the photometry alone (Saglia et al. 1992, 1993). This observational signature suffers from a mass-anisotropy degeneracy, however: a tangential stellar orbital structure can cause a similar signature (Gerhard 1993). The key to discriminate between these possibilities is the behaviour of the h4 profile. Carollo et al. (1995) studied in some detail the effect of a dark matter halo on the h4 shape parameter. They found that, both for isotropic and radially anisotropic models, the h4 parameter increases at large projected radii due to the presence of a dark matter halo. On the other hand, a tangential orbital structure causes a negative h4 profile at large radii. The measurement of the projected dispersion and the h4 profile at large radii would therefore in principle suffice to constrain the dark matter content in ellipticals (Rix et al. 1997; Gerhard et al. 1998; Kronawitter et al. 2000), although systematic effects caused by dust, non-sphericity etc. might further complicate this issue (Baes & Dejonghe 2001; Sanchis et al. 2004). There is apparently no analogy for this situation for the detection of black holes in galactic nuclei: as the signature of a central black hole on the h4 profile does not follow a clear trend, the projected velocity dispersion is by far the most obvious observational signature by which a black hole can be detected in non-rotating stellar nuclei.

7 Discussion and conclusion

Galactic nuclei observed in real galaxies show a variety of structure, with central density cusps ranging from flat cores to steep cusps. The main goal of this paper was to construct simple dynamical models for spherical systems with a central black hole, reflecting the variety of central structure observed in real galactic nuclei. We have performed a detailed study of a two-parameter family of dynamical models based on the family of $\gamma $-models introduced by Dehnen (1993) and Tremaine et al. (1994). The family contains as parameters the slope of the central density cusp $\gamma $ and the ratio $\mu$ of the central black hole mass to the total mass of the system. By varying these parameters, we have been able to study a very wide range of models, going from weakly cusped models to very centrally concentrated models with an infinite stellar potential well, and ranging from self-consistent models without black hole to systems where the dynamical structure is completely dominated by the central black hole. We have only considered models with an isotropic dynamical structure, which do not cover the range of orbital structure observed in real galactic nuclei. It is possible to generalize the isotropic models presented in this paper to anisotropic models with a constant anisotropy or with an Osipkov-Merritt type distribution function (Osipkov 1979; Merritt 1985). For such models, the calculation of the most important dynamical properties is not much more demanding than for isotropic models. The construction of general anisotropic dynamical models is much more complicated, however, and falls beyond the scope of this paper.

For this two-parameter family of isotropic dynamical models, we have calculated the most important kinematical quantities, such as the intrinsic and projected velocity dispersions, the total energy budget, the distribution function, the differential energy distribution and the LOSVDs. Many of these quantities could be calculated completely analytically for all values of $\gamma $ and $\mu$. For the models without black hole and the black hole dominated models, the distribution function, the differential energy distribution and the spatial LOSVDs can be calculated completely analytically. The same is true for three distinct $\gamma $-models with a central black hole - these three models each form an analytical one-parameter family with the central black hole mass as an explicit parameter. Although these three models differ only by the slope of the central density profile, their kinematical properties are very different. We therefore believe that the set of $\gamma $-models discussed in this paper, and in particular the three completely analytical models, answer the need for dynamical models which are on the one hand relatively simple and on the other hand reflect the range of central structure observed in the nuclei of real galaxies.

As most of the kinematics can be calculated completely analytically, the presented models make it possible to investigate the effect of a central black hole on the kinematics of galactic nuclei. In general, the effect of a black hole depends on the central density cusp (the parameter $\gamma $). Models with a steep density cusp are least affected by the presence of a black hole. They already have a steep and infinitely deep potential well and a strong central density concentration, and the kinematical effect of a black hole is quite marginal. The distribution function remains a monotonically increasing function of binding energy; only the slope in the high-energy limit is altered by the presence of a black hole. Models with a shallow central density cusp on the other hand are more strongly affected by the presence of a black hole. They have a less concentrated density profile and therefore only a finite central potential well. The influence of a black hole on the distribution function can be important. For example, models with $\gamma<\frac{3}{2}$ have distribution functions which tend to zero both in the low and high binding energies regime. The differential energy distribution, which gives a better physical insight in the orbital structure of the system, is less affected by the presence of a black hole. For realistic black hole masses, the shift in the mean binding energy of the stars or the fraction of stars on orbits with binding energies exceeding the depth of the stellar potential well is marginal. Nevertheless, the different behaviour of the distribution function is important, as it bears direct consequences for the stability of the $\gamma $-models with a black hole. A monotonically rising distribution function as a function of binding energy is a sufficient condition for stability against radial and non-radial perturbations. This means that the $\gamma $-models with a black hole with $\gamma\geq\frac{3}{2}$ are stable. The models with a shallower cusp slope have a decreasing distribution function in the high binding energy limit, and their stability is hence uncertain. This interesting issue can only be investigated in a detailed N-body or linear mode analysis studies.

Finally, we can wonder whether these three models are unique or whether other simple dynamical models could easily be found for which most of the kinematical properties can be expressed analytically. It is rather straightforward to construct models with a black hole in which the (intrinsic and/or projected) velocity dispersions can be expressed analytically, as the velocity dispersion is just a linear function of the black hole mass. The construction of models where more complicated dynamical properties such as the distribution function and the spatial LOSVDs can be expressed analytically is more difficult. A direct integration of the Eddington equation does not seem the most obvious way to proceed [however, see Baes & Dejonghe (2004) for a case where this is doable]. A more promising path is the idea of mapping the total potential onto the stellar potential, proposed by Ciotti (1996) and adapted by us in the present paper. Nevertheless, the conditions on the mapping function in order to allow an analytical evaluation of the distribution function are quite stringent, and they probably do not apply for a large set of models. Out of the range of $\gamma $-models, we found that only three different models satisfy these conditions. We also searched for other models in the large family of the so-called $(\alpha,\beta,\gamma)$-models (Zhao 1996), an extension of the $\gamma $-models, but no other models satisfied the necessary conditions.

Acknowledgements
The main part of this work was done when M.B. was a Postdoctoral Fellow of the Fund for Scientific Research Flanders (FWO). The numerical calculations were performed using the SKIRT cluster at the Universiteit Gent, for which M.B. obtained an FWO research grant. The FWO is kindly acknowledged for the financial support. The referee, Tim de Zeeuw, is acknowledged for helpful suggestions.

Appendix A: The function W${_\gamma }$(r)

The function $W_\gamma(r)$ is defined in Eq. (9) as

 \begin{displaymath}% W_\gamma(r) = \frac{3-\gamma}{4\pi} \int_r^\infty \frac{r^{1-2\gamma}{{\rm d}}r}{(1+r)^{7-2\gamma}}, \end{displaymath} (A.1)

where it is assumed that r is a real number and the parameter $\gamma $ assumes values between 0 and 3. Formally, it can conveniently be expressed in terms of the incomplete Beta function or the hypergeometric function. It can also be written completely in terms of elementary functions. If $\gamma $ is not equal to 1, $\frac{3}{2}$, 2 or  $\frac{5}{2}$, we obtain an algebraic expression

\begin{displaymath}% W_\gamma(r) = \frac{3-\gamma}{4\pi} \sum_{j=0}^4 \left( ... ... \left[1-\left(\frac{r}{1+r}\right)^{2+j-2\gamma}\right]\cdot \end{displaymath} (A.2)

For the four special values of $\gamma $, we can obtain a closed expression for $W_\gamma(r)$ through direct integration of Eq. (A.1) or through application of the reduction formulae of hypergeometric functions. The results are
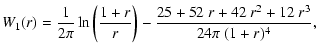    $\displaystyle W_1(r) = \frac{1}{2\pi}\ln\left(\frac{1+r}{r}\right) - \frac{25+52~r+42~r^2+12~r^3}{24\pi~(1+r)^4},$ (A.3)
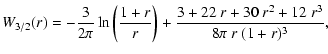    $\displaystyle W_{3/2}(r) = -\frac{3}{2\pi}\ln\left(\frac{1+r}{r}\right) + \frac{3+22~r+30~r^2+12~r^3}{8\pi~r~(1+r)^3},$ (A.4)
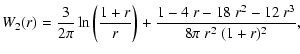    $\displaystyle W_2(r) = \frac{3}{2\pi}\ln\left(\frac{1+r}{r}\right) + \frac{1-4~r-18~r^2-12~r^3}{8\pi~r^2~(1+r)^2},$ (A.5)
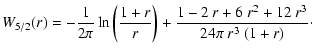    $\displaystyle W_{5/2}(r) = -\frac{1}{2\pi}\ln\left(\frac{1+r}{r}\right) + \frac{1-2~r+6~r^2+12~r^3}{24\pi~r^3~(1+r)}\cdot$ (A.6)

Appendix B: The function ${\mathcal{Q}}$(x) for some selected models

B.1 The ${\gamma =1}$ model

For the Hernquist model we find a simple augmented density,

 \begin{displaymath}% \tilde\rho(\Psi_*) = \frac{1}{2\pi}~\frac{\Psi_*^4}{1-\Psi_*}, \end{displaymath} (B.1)

and for the mapping function we find

 \begin{displaymath}% \omega(\Psi_*) = \Psi_*\left(1+\frac{\mu\Psi_*}{1-\Psi_*}\right)\cdot \end{displaymath} (B.2)

If we substitute the expressions (B.1) and (B.2) into Eq. (34b), we obtain

 \begin{displaymath}% {\mathcal{Q}}(x) = \frac{1}{2\pi\sqrt{1-\mu}} \int_0^x ... ...m d}}\Psi_*} {\sqrt{(x-\Psi_*)~(1-\Psi_*)^3~(\zeta-\Psi_*)}}, \end{displaymath} (B.3)

where $\zeta = 1+\mu/(1-\mu)(1-x)$. The integrand in this expression is basically the combination of a rational function and the square root of a cubic polynomial. The function  ${\mathcal{Q}}$ (and hence the distribution function) can therefore be expressed completely in terms of elliptic integrals. An explicit form requires a reduction of this elliptic integral to a combination of the standard elliptic integrals. For the Hernquist model, one finds that the distribution can be written as

\begin{displaymath}% f({\mathcal{E}}) = A_1+A_2\mathbb{F}(\phi,k)+A_3\mathbb{E}(\phi,k), \end{displaymath} (B.4)

where Ai are algebraic functions of ${\mathcal{E}}$ and $\mu$, $\mathbb{F}$and  $\mathbb{E}$ are Legendre's incomplete elliptic integrals of the first and second kind, and the arguments of the elliptic integrals are
    $\displaystyle \phi = \arcsin\sqrt{{\mathcal{E}}},$ (B.5)
    $\displaystyle k = \left[1+\frac{(1-\mu)(1-{\mathcal{E}})^2}{\mu}\right]^{-1/2}\cdot$ (B.6)

For the calculation of the density-of-states function, similar formulae apply. Practically, it is easiest to use a symbolic mathematical package such as Maple or Mathematica. These packages return an explicit form for most elliptic integrals, and the expressions can be converted immediately to Fortran or C code using internal conversion routines.

B.2 The $\gamma=\frac{3}{2}$ model

For $\gamma=\frac{3}{2}$ we obtain

  
    $\displaystyle \tilde\rho(\Psi_*) = \frac{3}{256\pi}~\frac{(4-\Psi_*)^4\Psi_*^4}{(2-\Psi_*)^3},$ (B.7)
    $\displaystyle \omega(\Psi_*) = \Psi_*\left[1+\frac{\mu~\Psi_*~(3-\Psi_*)}{(2-\Psi_*)^2}\right]\cdot$ (B.8)

Substitution of Eqs. (B.7) and (B.8) into formula (34b) yields
 
$\displaystyle % {\mathcal{Q}}(x) = \frac{3}{256\pi\sqrt{1-\mu}} \int_0^x \frac{... ...d}}\Psi_*} {(2-\Psi_*)^3~ \sqrt{(x-\Psi_*)~(\zeta_--\Psi_*)~(\zeta_+-\Psi_*)}},$     (B.9)

where the roots of the cubic polynomial under the square root are

 \begin{displaymath}% \zeta_\pm = 2 + \frac{2\mu}{(1-\mu)~(2-x)^2} \left[1\pm\sqrt{1-\frac{(1-\mu)~(2-x)^3}{\mu}}\right]\cdot \end{displaymath} (B.10)

Since the integrand of ${\mathcal{Q}}$ is the product of a rational function and the square root of a cubic polynomial, the integral can be written in terms of elliptic integrals.

B.3 The $\gamma=\frac{5}{2}$ model

The $\gamma=\frac{5}{2}$ model has an augmented density very similar to that of the $\gamma=\frac{3}{2}$ model,

 \begin{displaymath}% \tilde\rho(\Psi_*) = \frac{1}{256\pi}~\frac{(4+\Psi_*)^4\Psi_*^4}{(2+\Psi_*)^3}\cdot \end{displaymath} (B.11)

The mapping function $\omega(\Psi_*)$ is very simple

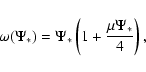\begin{displaymath}% \omega(\Psi_*) = \Psi_*\left(1+\frac{\mu\Psi_*}{4}\right), \end{displaymath} (B.12)

and substitution of these expressions into Eq. (34b) gives
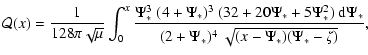$\displaystyle % {\mathcal{Q}}(x) = \frac{1}{128\pi\sqrt{\mu}} \int_0^x \frac{\P... ...i_*+5\Psi_*^2)~{{\rm d}}\Psi_*} {(2+\Psi_*)^4~\sqrt{(x-\Psi_*)(\Psi_*-\zeta)}},$     (B.13)

where $\zeta=-(x+4/\mu)$. As the integrand in this expression is the product of a rational function and the square root of a quadratic polynomial, the function  ${\mathcal{Q}}$ (and the distribution function) can be expressed completely in terms of elementary functions. Explicit expressions for the distribution function, as well as for the density-of-states function, in terms of elementary functions can be found in Baes & Dejonghe (2004).

References

 
Copyright ESO 2005