A&A 432, 731-736 (2005)
DOI: 10.1051/0004-6361:20041855
N. J. Wilson - K. L. Bell - C. E. Hudson
Department of Applied Mathematics and Theoretical Physics, The Queen's University of Belfast, Belfast BT7 1NN, Northern Ireland
Received 18 August 2004 / Accepted 8 November 2004
Abstract
We extend a previous calculation of effective collision
strengths for electron impact excitation of the boron-like ion C II. The earlier work was restricted to the excitation
within the 2s22p ground configuration and the sixteen
2s22p-2s2p2 fine-structure transitions whilst the present
paper considers all fine-structure transitions among the levels
arising from the lowest 16 LS states. The collisional cross
sections are computed in the multichannel close-coupling
R-matrix approximation, in which sophisticated
configuration-interaction wave functions are used to represent the
target states. The 16 states included have the following basis
configurations: the 2s22p ground state, four 2s2p2 states,
three 2p3 states, one 2s2p3s state as well as the
2s23
![]() and 2s24
and 2s24
![]() states. The 16 LStarget states correspond to 30 fine-structure levels and lead to a
total of 435 fine-structure transitions. In this paper we tabulate
effective collision strengths, obtained by averaging the electron
collision strengths over a Maxwellian distribution of velocities,
for electron temperatures in the range given by
states. The 16 LStarget states correspond to 30 fine-structure levels and lead to a
total of 435 fine-structure transitions. In this paper we tabulate
effective collision strengths, obtained by averaging the electron
collision strengths over a Maxwellian distribution of velocities,
for electron temperatures in the range given by
![]() (K) = 3.0-5.5,
suitable for most astrophysical applications and
laboratory plasma diagnostics. Significant differences from a
previous calculation are noted and comparisons are made with some recent experimental data.
(K) = 3.0-5.5,
suitable for most astrophysical applications and
laboratory plasma diagnostics. Significant differences from a
previous calculation are noted and comparisons are made with some recent experimental data.
Key words: atomic processes - line: formation - methods: analytical
Table 1:
LS energies relative to the 2s22p 2P![]() ground state of C II. Also noted is how the LS states split into J-levels and assignments of level indices to
the target states are given. The observed values are the experimental energy
levels compiled by NIST.
ground state of C II. Also noted is how the LS states split into J-levels and assignments of level indices to
the target states are given. The observed values are the experimental energy
levels compiled by NIST.
Recently, a 16-state R-matrix calculation has been
performed for C II by two of the present authors (Wilson &
Bell 2002). In this work, the excitation within the
2s22p ground configuration and the sixteen 2s22p-2s2p2fine-structure transitions were considered. However emission lines
due to other excitations, such as the
2s2p2 2S-2s23p 2P![]() transition occur in
planetary nebulae (Vassiliadis et al. 1998) and in
laboratory plasmas (Arad et al. 2000). Since these lines
were not considered by Wilson & Bell (2002), and given
the likelihood that collision strength data are required for other
transitions, it is clearly desirable that a comprehensive
tabulation of accurate collision strength data is available for
use in application.
transition occur in
planetary nebulae (Vassiliadis et al. 1998) and in
laboratory plasmas (Arad et al. 2000). Since these lines
were not considered by Wilson & Bell (2002), and given
the likelihood that collision strength data are required for other
transitions, it is clearly desirable that a comprehensive
tabulation of accurate collision strength data is available for
use in application.
A brief review of earlier theoretical calculations, generally
focusing on a limited number of transitions was given in Wilson &
Bell (2002) and will not be repeated here. However, it is
useful to compare with previous work, and for this purpose we will
consider the effective collision strengths of Blum & Pradhan
(1992), who performed a 10-state R-matrix
calculation, resulting in data at a number of temperatures for 153
fine-structure transitions. We also compare with the crossed beams experimental results of Williams et al. (1998) and the merged beams results of Smith et al. (1996) for the 2s22p 2P![]() -2s2p2 2D excitation.
-2s2p2 2D excitation.
Improved computing capabilities now enable larger calculations to be undertaken and so the aim of this paper is to present Maxwellian-averaged collision strengths for the 435 J-resolved fine-structure transitions arising from the inclusion of 16 LStarget states in the calculation at a number of temperatures of interest to astrophysicists and plasma physicists. The increased number of target states leads to additional channel-coupling effects manifesting themselves in the cross sections obtained as resonances. Care has been taken in the present work to fully delineate these resonances, since they can lead to a considerable enhancement of the collision rates. As a consequence, a large amount of accurate new collisional atomic data becomes available for the C II ion. The range of temperatures considered is appropriate for many astrophysical applications, including the study of gaseous nebulae as well as solar and laboratory type plasmas.
We employ the multi-channel R-matrix method as described by Berrington et
al. (1987) to compute the collision strengths
![]() for electron impact
excitation of C II. The relationship between
for electron impact
excitation of C II. The relationship between
![]() and the
excitation cross section
and the
excitation cross section
![]() for an initial state i and a final
state f can be expressed by the equation
for an initial state i and a final
state f can be expressed by the equation
Pnl (r) = 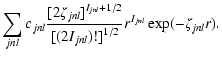 |
(2) |
A useful test of the accuracy of the wavefunctions employed is a comparison of
computed energy levels with available experimental data. In Table 1, we compare
the present target state energies (in rydbergs) for C II relative to the
2s22p 2P![]() ground state with the critically evaluated data from
the NIST database
at http://www.physics.nist.gov averaged in accordance with their
statistical weights. The agreement between the present theory and observed
values is excellent and we thus conclude that the wavefunctions employed are of
sufficient accuracy for the R-matrix collision strength calculation. In
Table 1 we also present the number of J levels into which each of the 16 LS target
states is split together with the 30 values of J and the assignment to each J level
of an index (1 to 30).
ground state with the critically evaluated data from
the NIST database
at http://www.physics.nist.gov averaged in accordance with their
statistical weights. The agreement between the present theory and observed
values is excellent and we thus conclude that the wavefunctions employed are of
sufficient accuracy for the R-matrix collision strength calculation. In
Table 1 we also present the number of J levels into which each of the 16 LS target
states is split together with the 30 values of J and the assignment to each J level
of an index (1 to 30).
Using these target state wavefunctions, the procedure outlined by Burke & Robb (1975) is used for the expansion of the ion-plus-electron (or (N+1)-electron) system. The R-matrix radius is taken to be 28.8 atomic units and a zero logarithmic derivative is imposed at this boundary. For each orbital angular momentum, 40 Schmidt-orthogonalized continuum orbitals were included, ensuring that a converged collision strength was obtained for the energy range considered. The correct positioning of resonances relative to the target states included in the calculation was ensured by adjusting our theoretical energies to the NIST values, prior to diagonalization of the Hamiltonian matrix. The energy levels for the two highest LS states included in this calculation were adjusted to their arithmetic mean, 1.53839 Ry, since the energy order of these close-lying states differs from that in the NIST database.
We included all partial waves with ![]() for both even and
odd parities and doublet, quartet and sextet multiplicities. This
ensured that the collision strengths for the optically forbidden
transitions had converged. For dipole-allowed transitions,
however, it was necessary to consider the effect of higher partial
waves with L>12 because they have a significant effect upon the
collision strengths. We assume the partial collision strengths
form a geometric series expansion, with a geometric scaling factor
given by the ratio of two adjacent terms. This "topping-up''
procedure has been used successfully in similar calculations of
Bell & Ramsbottom (2000), and Ramsbottom et al.
(2001).
for both even and
odd parities and doublet, quartet and sextet multiplicities. This
ensured that the collision strengths for the optically forbidden
transitions had converged. For dipole-allowed transitions,
however, it was necessary to consider the effect of higher partial
waves with L>12 because they have a significant effect upon the
collision strengths. We assume the partial collision strengths
form a geometric series expansion, with a geometric scaling factor
given by the ratio of two adjacent terms. This "topping-up''
procedure has been used successfully in similar calculations of
Bell & Ramsbottom (2000), and Ramsbottom et al.
(2001).
For small energy intervals between fine-structure levels, it is possible to recouple the matrices obtained from non-relativistic calculations in LS coupling to obtain collision strengths between these levels. Above all the thresholds the effects of intermediate coupling in the target can be included by using this method. The present work utilizes the program of Saraph (1978) to undertake this recoupling procedure. Further details of the coupling scheme are provided by Bell & Ramsbottom (2000).
Effective collision strengths
![]() for a particular
electron temperature
for a particular
electron temperature ![]() (in Kelvin) were obtained by averaging
the collision strengths
(in Kelvin) were obtained by averaging
the collision strengths
![]() over a Maxwellian
distribution of velocities, so that
over a Maxwellian
distribution of velocities, so that
The collision strengths presented in this work have been
evaluated for a very fine mesh of incident impact energies, at
energy intervals typically less than 0.0002 rydbergs across the
energy range considered (0 to 10 Ry). This ensured that the
autoionizing resonances which converge to the target state
thresholds were fully delineated. Those resonances located at
energies lower than the highest threshold considered in this work
(2s24f 2F![]() )
are physically meaningful; however at
higher energies (i.e. above 1.53839 Ry) pseudo-resonances appear.
These arise from the inclusion of pseudo-orbitals in the
wavefunction expansion (Burke et al. 1981). At higher
temperatures the high-impact energy region is much more important
and so it is necessary to properly average over the
pseudo-resonances to prevent distortion of the correct results in
the calculation of the effective collision strengths.
)
are physically meaningful; however at
higher energies (i.e. above 1.53839 Ry) pseudo-resonances appear.
These arise from the inclusion of pseudo-orbitals in the
wavefunction expansion (Burke et al. 1981). At higher
temperatures the high-impact energy region is much more important
and so it is necessary to properly average over the
pseudo-resonances to prevent distortion of the correct results in
the calculation of the effective collision strengths.
In Fig. 1 we present the collision strength as a function of incident electron energy relative to the ground state in rydbergs for the 2s2p2 4P1/2-2s2p2 2D5/2fine-structure forbidden transition. It is evident from this figure that a large number of autoionizing resonances are present in the collision strength. The number of resonances increases as additional target states are included, since this leads to further channel-coupling effects. These resonances play a crucial role in the magnitude of Maxwellian-averaged collision strengths, normally resulting in a significant enhancement in the effective collision strength. It is therefore important that these resonances are considered carefully. The use of a suitably fine mesh of energies ensures that all resonances are fully resolved.
![\begin{figure}
\par {\includegraphics[width=8.8cm,clip]{1855fig1.eps} }
\end{figure}](/articles/aa/full/2005/11/aa1855/Timg24.gif) |
Figure 1: Collision strength as a function of incident electron energy in rydbergs for the 2s2p2 4P1/2-2s2p2 2D5/2 fine-structure forbidden transition. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.8cm,clip]{1855fig2.eps} }
\end{figure}](/articles/aa/full/2005/11/aa1855/Timg25.gif) |
Figure 2: Present effective collision strength as a function of log (T) where T is the electron temperature in kelvin for the 2s2p2 4P1/2-2s2p2 2D5/2 fine-structure forbidden transition (solid line) compared with the results of Blum & Pradhan (1992) (dashed line). |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.8cm,clip]{1855fig3.eps} }
\end{figure}](/articles/aa/full/2005/11/aa1855/Timg26.gif) |
Figure 3:
Collision strength as a function of incident electron energy
in rydbergs for the 2s2p2 2D3/2-2s23p 2P
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.8cm,clip]{1855fig4.eps} }
\end{figure}](/articles/aa/full/2005/11/aa1855/Timg27.gif) |
Figure 4:
The effective collision strength as a function of log (T)
where T is the electron temperature in kelvin for the
2s2p2 2D3/2-2s23p 2P
|
| Open with DEXTER | |
In Fig. 2, the effective collision strength for the 2s2p2 4P1/2-2s2p2 2D5/2 transition from the present calculation is plotted as a function of the decimal logarithm of the electron temperature in kelvin and compared with the previous 10-state calculation of Blum & Pradhan (1992) at a range of temperatures for which a comparison is possible. The present results are higher than those of Blum & Pradhan (1992) by a factor of about 50% at 1000 K, decreasing towards higher temperatures before becoming larger again. The reason for the enhancement in this calculation is the presence of additional resonances and a careful consideration of all resonances as discussed earlier.
In Fig. 3 we show the collision strength as a function of
incident electron energy relative to the ground state in rydbergs
for the 2s2p2 2D3/2-2s23p 2P
![]() fine-structure allowed transition. As for the forbidden transition
considered in Figs. 1 and 2, many resonant features, converging to
the thresholds included in the calculation, can be observed in the
collision strength spectrum. The corresponding effective collision
strength from the present calculation for the
2s2p2 2D3/2-2s23p 2P
fine-structure allowed transition. As for the forbidden transition
considered in Figs. 1 and 2, many resonant features, converging to
the thresholds included in the calculation, can be observed in the
collision strength spectrum. The corresponding effective collision
strength from the present calculation for the
2s2p2 2D3/2-2s23p 2P
![]() transition is
shown as the solid line in Fig. 4. As in Fig. 2, we compare our
results with the calculation of Blum & Pradhan (1992). For
this allowed transition, the effective collision strengths for the
two calculations are in very close agreement at lower
temperatures. However at higher temperatures the present results
are many times higher than the results of Blum & Pradhan
(1992).
transition is
shown as the solid line in Fig. 4. As in Fig. 2, we compare our
results with the calculation of Blum & Pradhan (1992). For
this allowed transition, the effective collision strengths for the
two calculations are in very close agreement at lower
temperatures. However at higher temperatures the present results
are many times higher than the results of Blum & Pradhan
(1992).
One point, from Figs. 2 and 4, that must be commented on, is that, although there is an abundance of resonance structure in the collision strengths (Figs. 1 and 3), the corresponding effective collision strengths remain relatively flat until the high temperature extremity. This can be explained by considering the nature of Eq. (3) where we note that the exponential term controls how much of the collision strength is picked up when performing the integration.
This exponential term depends on the electron temperature ![]() and its effect is easy to see through the following illustration. Consider an electron temperature of
and its effect is easy to see through the following illustration. Consider an electron temperature of
![]() i.e. 1000 K. The exponential term falls off to 10% of its maximum within a energy of 0.015 Ry above threshold. However, at
i.e. 1000 K. The exponential term falls off to 10% of its maximum within a energy of 0.015 Ry above threshold. However, at
![]() i.e. 10 000 K, falling off to 10% occurs after 0.15 Ry above threshold. Thus higher temperatures allow for significant contributions to be picked up by the integral at energies further from threshold, i.e. more of the resonance structure can be picked up leading to an enhanced effective collision strength.
i.e. 10 000 K, falling off to 10% occurs after 0.15 Ry above threshold. Thus higher temperatures allow for significant contributions to be picked up by the integral at energies further from threshold, i.e. more of the resonance structure can be picked up leading to an enhanced effective collision strength.
In Figs. 2 and 4, the apparent flatness of the effective collision strengths at low temperatures occurs because at these lower temperatures only a small energy region of the collision strength is significant and it isn't until higher temperatures that the contributions from the higher energy resonances begin to become significant. The effective collision strength in Fig. 2 is very flat until very high temperatures, which can be understood by looking at the associated collision strength in Fig. 1. Here we see that close to threshold there are very few resonances e.g looking 0.1 Ry above threshold, we find are only two resonances in Fig. 1. Thus, it is not until the highest temperatures that a change in the effective collision strength occurs due to the contribution from resonances at energies beyond 0.1 Ry above threshold.
The effective collision strength in Fig. 4 starts to increase more rapidly and at an earlier temperature than that in Fig. 2. This is due to more resonant structure occurring at energies closer to threshold in Fig. 3 than for the previous transition in Fig. 1. (The contrast between the two collision strengths in the energy region less than 0.1 Ry in highly illustrative of this point.)
We also note that the values of Blum & Pradhan (1992) shown in Figs. 2 and 4 remain flat over the entire temperature range and show no increase with temperature. This is because in the current calculation the resonance structure is much more well resolved and defined.
![\begin{figure}
\par {\includegraphics[width=8.8cm,clip]{1855fig5.eps} }
\end{figure}](/articles/aa/full/2005/11/aa1855/Timg30.gif) |
Figure 5:
Comparison of the current collision strength (solid line) with experimental data for the 2s22p 2P |
| Open with DEXTER | |
In Fig. 5 we display the collision strength for the transition between two LS levels 2s22p 2P![]() -2s2p2 2D and compare with experimental data. Data from two experiments have been noted: the crossed beams experiment of Williams et al. (1998) and the merged beams experiment of Smith et al. (1996). Both these experiments measure the excitation cross section, and so to make comparison with the current data we have converted the cross sections to collision strengths by applying Eq. (1).
-2s2p2 2D and compare with experimental data. Data from two experiments have been noted: the crossed beams experiment of Williams et al. (1998) and the merged beams experiment of Smith et al. (1996). Both these experiments measure the excitation cross section, and so to make comparison with the current data we have converted the cross sections to collision strengths by applying Eq. (1).
The experiment of Williams et al. (1998) studies the near threshold excitation of the 2s22p 2P![]() -2s2p2 2D transition and so comparison can only be made over a small incident electron energy range. The data of Smith et al. (1996) were taken over a larger range of energies and so here we have more values with which to compare. For both sets of experimental values in the immediate threshold region (
-2s2p2 2D transition and so comparison can only be made over a small incident electron energy range. The data of Smith et al. (1996) were taken over a larger range of energies and so here we have more values with which to compare. For both sets of experimental values in the immediate threshold region (![]() 0.68-0.75 Ry) we find that the calculated collision strength is much higher. However, once we go beyond 0.75 Ry, we find that the agreement with the experimental data becomes quite good. In fact we find that in this region there are perhaps only 2 experimental points that do not catch the calculated collision strength within the range of their error bars. This would suggest that at the very least the collision strength for this transition is known to better than 20% over this energy region. Unfortunately these appear to be the only experimental data available for this ion.
0.68-0.75 Ry) we find that the calculated collision strength is much higher. However, once we go beyond 0.75 Ry, we find that the agreement with the experimental data becomes quite good. In fact we find that in this region there are perhaps only 2 experimental points that do not catch the calculated collision strength within the range of their error bars. This would suggest that at the very least the collision strength for this transition is known to better than 20% over this energy region. Unfortunately these appear to be the only experimental data available for this ion.
The inclusion of the 16 LS target states leads to 30 J levels
and a total of 435 transitions. In Table 2 (available at the CDS) we present the
non-zero effective collision strengths for all transitions for a
range of electron temperatures [
![]() (K) = 3.0-5.5] suitable for
application in plasma and astronomical diagnostics.
Table 2 contains the following information: Col. 1 lists the transitions between fine-structure levels indicated as initial-final according to the J-index assigned to each fine-structure level in Table 1. For example, 2-8 denotes the transition 2s22p 2P
(K) = 3.0-5.5] suitable for
application in plasma and astronomical diagnostics.
Table 2 contains the following information: Col. 1 lists the transitions between fine-structure levels indicated as initial-final according to the J-index assigned to each fine-structure level in Table 1. For example, 2-8 denotes the transition 2s22p 2P
![]() -2s2p
2 S1/2. The remaining 11 columns list the effective collision strengths for each transition at the following logarithmic electron temperatures
-2s2p
2 S1/2. The remaining 11 columns list the effective collision strengths for each transition at the following logarithmic electron temperatures
![]() (K) = 3.00, 3.25, 3.50, 3.75, 4.00, 4.25, 4.50, 4.75, 5.00, 5.25, 5.50. A superscript indicates the power of 10 with which the number must be multiplied i.e., a-n=
(K) = 3.00, 3.25, 3.50, 3.75, 4.00, 4.25, 4.50, 4.75, 5.00, 5.25, 5.50. A superscript indicates the power of 10 with which the number must be multiplied i.e., a-n=
![]() .
For some of the transitions noted in Table 2, the agreement between this calculation and the
data obtained by Blum & Pradhan (1992) is good (see for
example those transitions considered in Wilson & Bell
2002). However, as can for example be observed in Figs. 2 and 4, for other transitions significant differences are noted.
.
For some of the transitions noted in Table 2, the agreement between this calculation and the
data obtained by Blum & Pradhan (1992) is good (see for
example those transitions considered in Wilson & Bell
2002). However, as can for example be observed in Figs. 2 and 4, for other transitions significant differences are noted.
It is difficult to predict the overall accuracy of these results. However we note that we have employed sophisticated configuration-interaction wavefunctions which are in excellent agreement with experiment and have carefully considered resonant phenomena in this work. Experience from similar calculations and in particular the application of those data indicate that the effective collision strength data may be accurate to approximately 10% for transitions not involving the higher-lying states. In practice the accuracy can only truly be assessed through the application of these data to plasma models or through still more sophisticated calculations.
In this paper we extend a previous calculation of effective
collision strengths for electron impact excitation of the
C II ion. These astrophysically important atomic data are
evaluated for a large range of electron temperatures, (
![]() (K) = 3.0-5.5) and for all transitions among the lowest 16 LSstates of C II, corresponding to 30 fine-structure levels
and 435 individual transitions. We believe that the present
results are the most accurate currently available. Significant
differences between the present results and the previous work of
Blum & Pradhan (1992) for some transitions are observed;
for other transitions the comparison is much more favourable.
(K) = 3.0-5.5) and for all transitions among the lowest 16 LSstates of C II, corresponding to 30 fine-structure levels
and 435 individual transitions. We believe that the present
results are the most accurate currently available. Significant
differences between the present results and the previous work of
Blum & Pradhan (1992) for some transitions are observed;
for other transitions the comparison is much more favourable.
It is expected that the present effective collision strengths will have a typical accuracy of 10-20%, particularly for those transitions between the well-represented low-lying levels. Such an accuracy is given due to the sophisticated nature of the calculation where care has been taken to included such effects as correlation, configuration-interaction and top-up of the partial waves for the allowed transitions. It should be noted, however, that uncertainties for some of the transitions between the highest lying levels of C II may be significantly larger. It is clear that either merged or crossed beams experiments are capable of producing data for comparison with theoretical values. The authors would encourage the production of such data.
Acknowledgements
The calculations were carried out using the MIRACLE supercomputer at the HiPerSPACE Computing Centre, UCL, which is funded by the UK Particle Physics and Astronomy Research Council. The work presented in this paper has also been supported by PPARC through a Rolling Grant.