A&A 432, 699-704 (2005)
DOI: 10.1051/0004-6361:20041366
M. D. Ding 1 - H. Li 2 - C. Fang 1
1 - Department of Astronomy, Nanjing University, Nanjing 210093, PR China
2 -
Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210008,
PR China
Received 28 May 2004 / Accepted 1 November 2004
Abstract
We explore the formation of the He I 10 830 Å line in a flaring atmosphere,
with special attention to the nonthermal effects of an electron beam.
Using non-LTE calculations we obtain the line profiles from different
model atmospheres. Without the nonthermal effects, the line changes
from weak absorption in a cool atmosphere to emission in a hot and
condensed atmosphere, as expected. However, the presence of an
electron beam can significantly change the line strength, producing
much stronger absorption and emission in these two cases.
We find that in the nonthermal case, the collisional ionization of
He I followed by recombinations becomes an important process
in populating the triplet levels corresponding to the He I 10 830 Å line.
These results suggest that the He I 10 830 Å line is also a potential
diagnostic tool for nonthermal effects in solar or stellar flares.
Key words: line: profiles - Sun: atmosphere - Sun: flares - stars: atmospheres
Although the He I 10 830 Å line is much weaker than some
chromospheric lines such as H![]() or Ca II H and K, it remains an
important line in the spectroscopy of solar active phenomena. The formation
of this line in the solar atmosphere has been studied by many authors
(e.g., Milkey et al. 1973; Shine et al. 1975; Fontenla et al. 1993; Andretta
& Jones 1997, hereafter AJ97; Labrosse & Gouttebroze 2001). The He I 10 830 Å line involves two triplet levels with several distinguishing features. The
lower level of this line (
or Ca II H and K, it remains an
important line in the spectroscopy of solar active phenomena. The formation
of this line in the solar atmosphere has been studied by many authors
(e.g., Milkey et al. 1973; Shine et al. 1975; Fontenla et al. 1993; Andretta
& Jones 1997, hereafter AJ97; Labrosse & Gouttebroze 2001). The He I 10 830 Å line involves two triplet levels with several distinguishing features. The
lower level of this line (
![]() )
is a metastable level which is
about 20 eV above the ground state (
)
is a metastable level which is
about 20 eV above the ground state (
![]() ). Therefore, electric
dipole transition is forbidden between them. In order to produce enough
populations at the metastable level, two distinct mechanisms have been
proposed, namely, the photoionization-recombination mechanism (PRM) and
the collisional mechanism (CM). The former assumes that the EUV radiation
coming back from the corona leads to an overionization of He I
in the chromosphere (
). Therefore, electric
dipole transition is forbidden between them. In order to produce enough
populations at the metastable level, two distinct mechanisms have been
proposed, namely, the photoionization-recombination mechanism (PRM) and
the collisional mechanism (CM). The former assumes that the EUV radiation
coming back from the corona leads to an overionization of He I
in the chromosphere (
![]() K), followed by a recombination to
excited levels. Direct collisional excitation from the ground state
occurs in a relatively hotter material (
K), followed by a recombination to
excited levels. Direct collisional excitation from the ground state
occurs in a relatively hotter material (
![]() K). These two
mechanisms are usually difficult to distinguish in the formation of the
He I 10 830 Å line (Sasselov & Lester 1994). A detailed discussion on
their application to the solar atmosphere can be found in AJ97. On the
other hand, the upper level of the line (
K). These two
mechanisms are usually difficult to distinguish in the formation of the
He I 10 830 Å line (Sasselov & Lester 1994). A detailed discussion on
their application to the solar atmosphere can be found in AJ97. On the
other hand, the upper level of the line (
![]() )
is J-splitting, so that the line is a multiplet with components at
10 830.341, 10 830.250, and 10 829.081 Å, respectively. The first two
components blend together while the third is usually distinguishable.
)
is J-splitting, so that the line is a multiplet with components at
10 830.341, 10 830.250, and 10 829.081 Å, respectively. The first two
components blend together while the third is usually distinguishable.
In the solar disk, the He I 10 830 Å line appears as a weak absorption line in the continuum background. Its absorption depth increases with increasing coronal EUV irradiation (e.g., Avrett et al. 1994; AJ97). Only at the site of a very strong flare does the line turn to emission. This needs the atmosphere to be highly heated and condensed, as reflected in the semi-empirical model F2 proposed by Machado et al. (1980).
Considering the specific features of the He I 10 830 Å line and its potential role in the spectroscopy of solar flares (e.g., Li et al. 1996; You et al. 1998), we need to know how the line changes with different physical conditions in a flaring atmosphere. When a flare occurs, the flaring atmosphere is heated to a higher temperature; at the same time, some chromospheric material is driven to flow into the corona (chromospheric evaporation), thus making the chromosphere more condensed. This process can be visually seen from the change in semi-empirical models, e.g., from the quiet-Sun model VAL-C (Vernazza et al. 1981) to flare models F1 and F2 (Machado et al. 1980). On the other hand, it is known that flares are usually heated by energetic electrons. The impact on the atmosphere by a beam of nonthermal electrons not only produces direct heating, but also changes the line and continuum emission through nonthermal ionization and excitation of neutral atoms. Studies have shown that the hydrogen Lyman lines (Hénoux et al. 1995), the Balmer and Ca II lines (Fang et al. 1993), the EUV continuum (Ding & Schleicher 1997), the optical continuum (Ding et al. 2003), and even the SOHO/MDI Ni I 6768 Å line (Ding et al. 2002) can be changed by the nonthermal effects to an extent that is of course different from case to case. However, it is still unknown how the He I 10 830 Å line responds to the bombardment of a nonthermal electron beam. In this paper, we study this issue by making non-LTE calculations of model atmospheres. We introduce the basic computational method in Sect. 2, present the results in Sect. 3, and give our conclusion in Sect. 4.
The model atom for He I adopted here consists of the five lowest
levels (with principal quantum number ![]() )
plus the ground state of
He II. The level energies are from Martin (1987). There are only
three permitted radiative transitions between these levels (Fig. 1), the
oscillator strengths of which are given by Kono & Hattori (1984). Line
broadening data are from Griem (1974) and Dimitrijevic & Sahal-Bréchot
(1984). The collisional excitation rates, collisional ionization rates,
and photoionization cross-sections are computed according to Benson
& Kulander (1972), Mihalas & Stone (1968), and Fernley et al. (1987).
)
plus the ground state of
He II. The level energies are from Martin (1987). There are only
three permitted radiative transitions between these levels (Fig. 1), the
oscillator strengths of which are given by Kono & Hattori (1984). Line
broadening data are from Griem (1974) and Dimitrijevic & Sahal-Bréchot
(1984). The collisional excitation rates, collisional ionization rates,
and photoionization cross-sections are computed according to Benson
& Kulander (1972), Mihalas & Stone (1968), and Fernley et al. (1987).
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1366fig1.eps}
\end{figure}](/articles/aa/full/2005/11/aa1366/Timg9.gif) |
Figure 1: Schematic diagram showing the atomic model of He I comprising the five lowest bound levels plus continuum. |
| Open with DEXTER | |
As was done in AJ97, we do not consider the fine structure of the
![]() state when solving the rate equations. The occupation
number at this state is finally distributed to each sublevel according
to its statistical weight in order to compute the emergent He I 10 830 Å line.
This simplification is valid when collisional
transitions between sublevels are so frequent as to maintain such a
distribution. Radiative transitions may violate this distribution only
when the multiplet components show quite different intensities.
This could happen in the solar atmosphere where the multiplet
components are formed at different depths. However, as will be
demonstrated below, the He I 10 830 Å line is mostly formed in a relatively
dense medium, which guarantees enough collisions between sublevels
to make the simplification still viable.
state when solving the rate equations. The occupation
number at this state is finally distributed to each sublevel according
to its statistical weight in order to compute the emergent He I 10 830 Å line.
This simplification is valid when collisional
transitions between sublevels are so frequent as to maintain such a
distribution. Radiative transitions may violate this distribution only
when the multiplet components show quite different intensities.
This could happen in the solar atmosphere where the multiplet
components are formed at different depths. However, as will be
demonstrated below, the He I 10 830 Å line is mostly formed in a relatively
dense medium, which guarantees enough collisions between sublevels
to make the simplification still viable.
We select three model atmospheres: the quiet-Sun model, VAL-C (Vernazza et al. 1981), and the flare models, F1 and F2 (Machado et al. 1980), to represent different events or different heating status of the flaring atmosphere. Also, we introduce a nonthermal electron beam bombarding the atmosphere in association with the flare impulsive heating.
As was discussed in Fang et al. (1993), the electron beam can
cause nonthermal excitation and ionization of the neutral atoms.
Therefore, the statistical equilibrium equation becomes
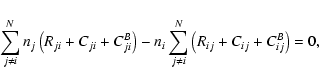 |
(1) |
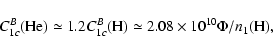 |
(2) |
The nonthermal excitation rates of He I can be estimated in
the same way. However, we lack reliable data for cross-sections of
collisional excitation by ![]() 30 keV electrons.
A comparison between the cross-section of collisional ionization
and that of collisional excitation to the triplet levels of He I
by
30 keV electrons.
A comparison between the cross-section of collisional ionization
and that of collisional excitation to the triplet levels of He I
by ![]() 3 keV electrons reveals that the latter is four times
smaller than the former. If this applies to the case of
deka keV electrons, the effect of nonthermal excitation
should be much smaller than the effect of nonthermal ionization. This
has been confirmed by test computations. Therefore, in the following
computations, we only consider the effect of nonthermal ionization.
3 keV electrons reveals that the latter is four times
smaller than the former. If this applies to the case of
deka keV electrons, the effect of nonthermal excitation
should be much smaller than the effect of nonthermal ionization. This
has been confirmed by test computations. Therefore, in the following
computations, we only consider the effect of nonthermal ionization.
We then solve the coupled equations of statistical equilibrium and
radiative transfer, together with the hydrostatic equilibrium
equation, for model atmospheres. The three lines at 584, 10 830, and 20 581 Å and the five continua are all treated with
detailed radiative transfer equations. Therefore, the non-local
effects are taken into account consistently.
![\begin{figure}
\par\includegraphics[width=13.8cm,clip]{1366fig2.eps}
\end{figure}](/articles/aa/full/2005/11/aa1366/Timg17.gif) |
Figure 2: Line profiles of He I 10 830 Å depending on the atmospheric models and the effect of a nonthermal electron beam. From left to right, the three panels refer to three atmospheric models: VAL-C (Vernazza et al. 1981), F1 and F2 (Machado et al. 1980). The solid lines refer to the case without an electron beam, while the dashed and dotted lines refer to the cases with electron beams whose energy fluxes are 109 and 1010 erg cm-2 s-1, respectively. The profiles are computed at solar disk center and normalized to the nearby continuum. |
| Open with DEXTER | |
As is well known, the He I 10 830 Å line is very sensitive to the coronal EUV irradiation. In our calculations, we use the semi-empirical models VAL-C for the quiet-Sun, F1 for a weak flare, and F2 for a strong flare. The EUV irradiations computed from these models are quite different and have been consistently incorporated in the calculations of the He I 10 830 Å line. However, the EUV irradiation during flares should change rapidly and exerts a great influence on the line profile. Generally speaking, the effect of an enhanced coronal irradiation is to strengthen the He I 10 830 Å line owing to an enhanced PRM. In some sense, this effect cannot be easily distinguished from the effect of nonthermal electrons. In the present work, we restrict our attention to the role of nonthermal electrons. A combination of both factors will be studied in a future work.
The model atom for He I adopted here is rather simple with only five bound levels. Including more bound levels can yield more quantitatively accurate results. We postulate that recombinations to other bound levels can reduce somewhat the populations at the triplet levels and thus the strength of the He I 10 830 Å line. However, the results on the nonthermal effects drawn below are qualitatively valid, considering that our purpose is not to reproduce exactly the observed line profiles, but only to show the role of nonthermal electrons.
We make non-LTE calculations for the three model atmospheres
mentioned above with and without a nonthermal electron beam.
The line profiles are plotted in Fig. 2. We notice that, if
there is no nonthermal electron beam, the He I 10 830 Å line
appears in very weak absorption in the quiet-Sun model, then the line
depth increases in the F1 model and it finally changes to an emission
line in the F2 model. The effect of the nonthermal electron beam
is, however, quite obvious in changing the line strength.
In the quiet-Sun model, the presence of an electron beam can result in
a rather strong absorption profile, in contrast to the weak absorption
one in the case of no electron beam. In the F1 model, the profile
changes from absorption to emission, depending on the energy flux
of the electron beam. In the F2 model, the profile is always in
emission; however, the electron beam can make the profile much
stronger.
![\begin{figure}
\par\includegraphics[width=14.2cm,clip]{1366fig3.eps}
\end{figure}](/articles/aa/full/2005/11/aa1366/Timg18.gif) |
Figure 3:
Line source function and optical depth at 10 830.341 Å (the center of the strongest component of
the He I 10 830 Å line) in different atmospheric models and for different cases
of nonthermal electron beams. The quantities of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{1366fig4.eps}
\end{figure}](/articles/aa/full/2005/11/aa1366/Timg19.gif) |
Figure 4: Transitions to the triplet levels corresponding to the He I 10 830 Å line through three different processes: the photoionization-recombination mechanism (PRM, solid lines), the collisional mechanism (CM, dashed lines), and the collisional ionization-recombination mechanism (CRM, dotted lines). The upper panels show the case without an electron beam, while the lower panels are for the case with an electron beam of energy flux 109 erg cm-2 s-1. |
| Open with DEXTER | |
The above results can be explained by checking the formation process of the He I 10 830 Å line. For this purpose, we plot in Fig. 3 the line source function and the optical depth at line center (referring to the center of the strongest component) for all the above cases. We first discuss the case of no electron beam. As was indicated by Avrett et al. (1994), the He I 10 830 Å line is optically thin in the chromosphere of the quiet-Sun region which produces only a weak absorption in the line. Changing from the quiet-Sun to the flare models, the chromospheric contribution to the line increases. The reason is that, on one hand, a flaring atmosphere produces an enhanced EUV irradiation responsible for the photoionization of He I and, on the other hand, the heated and condensed material results in more collisional excitations. Therefore, both the PRM and CM work more effectively than in the quiet atmosphere, leading to an overpopulation of the triplet levels corresponding to the He I 10 830 Å line.
However, if we introduce an electron beam, the optical depth of
the chromosphere is drastically enhanced. Even in
the quiet-Sun model, the electron beam can make the chromosphere
very opaque. This is by virtue the result of nonthermal
ionization of He I. We call this the collisional
ionization-recombination mechanism, abbreviated as CRM.
In order to show more clearly how the nonthermal electron beam
influences the different transition processes to populate the
triplet levels (levels 2 and 4) corresponding to the He I 10 830 Å line,
we calculate the total transition rates from the PRM, CM and CRM,
respectively, which are expressed as
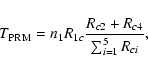 |
(3) |
| (4) |
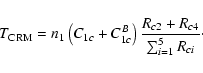 |
(5) |
On the other hand, the line source function also changes but in a slightly different manner. In the hot and condensed model (F2), the line source function mostly increases with height; but in the cool model (VAL-C), it may drop at the top of the chromosphere. Such a difference can be explained in terms of the two-level atom approximation, that is, the line source function is expressed as a linear combination of the mean radiative intensity and the local Planck function. In the VAL-C model, the mass density is relatively low and the line is almost radiation-dominated; thus the source function decreases towards upper layers of the chromosphere owing to efficient photon escaping. In the F2 model, the mass density is higher and the chromosphere becomes much more opaque, especially in the nonthermal case; therefore the source function keeps rising with height in the upper chromospheric layers. The change of the formation height and the source function for the He I 10 830 Å line in different models and in different thermal/nonthermal cases accounts for the computational results described above.
Note the specific shape of the line profile
obtained for the F1 model in the case of a relatively strong
electron beam with energy flux being 1010 erg cm-2 s-1.
The blue (10 829.081 Å) component and the red
(10 830.250 and 10 830.341 Å) component both exhibit a central
reversal; the central reversal in the red component is more
pronounced, which makes the red component even less strong than
the blue component. These features are of
course caused by the opacity effects and the drop of
the line source function at the top layers
in the F1 atmosphere (see Fig. 3). Moreover, the profiles shown
in Fig. 2 have not been convolved with a macro-turbulent velocity.
If we convolve the computed profiles with a Gaussian
macro-velocity of ![]() 10 km s-1, as was usually done,
they will more likely match the observed ones.
10 km s-1, as was usually done,
they will more likely match the observed ones.
AJ97 investigated in detail the influence of the transition region structure, the coronal pressure (the column mass atop the atmosphere), and the coronal irradiation on the He I 10 830 Å line. In our computations, changing models from VAL-C to F1 and then to F2 reflects the effect of increasing the coronal pressure and the coronal irradiation. We find that the change of the profiles in the case without nonthermal effects, shown as solid lines in Fig. 2, is qualitatively consistent with the results revealed by AJ97.
There are currently not many spectroscopic observations of flares in the He I 10 830 Å line. Some previous observations have shown that the He I 10 830 Å line appears either in emission or in absorption in flare regions (e.g., Tandberg-Hanssen 1967; Harvey & Recely 1984; Li et al. 1996). In general, the former occurs preferentially in major flares while the latter in small flares. It has been reported, however, that the line can also go into emission in some small flares (Rust & Bridges 1975; Penn & Kuhn 1995). These observational results are not surprising if considering the different nonthermal effects in each event. To check our computational results presented above, we need time-dependent spectroscopic observations for a flare.
Observations have indicated that nonthermal electrons are usually accelerated during the impulsive phase of solar flares. The flaring atmosphere is heated by the impact of nonthermal electrons and/or by heat conduction. Our computational results imply that whether the He I 10 830 Å line is in absorption or in emission depends on the heating status of the flaring atmosphere and the strength of the electron beam. Therefore, we propose the following scenario for the evolution of the He I 10 830 Å line during a solar flare. At first, when the flare originally occurs, nonthermal electrons begin to be accelerated and to bombard the lower atmosphere which has not been heated substantially; the He I 10 830 Å line changes from weak absorption to strong absorption. With the flare development, the chromosphere becomes gradually heated and condensed, the line then turns from absorption to emission; the emission increases if the electron beam keeps working. We note that, if there is no nonthermal effect, the line profiles from the three model atmospheres also show a similar variation behavior with, however, much less amplitude of absorption and emission in the above two cases. Therefore, we think that a strong absorption at the early phase and a strong emission at the maximum phase can be regarded as evidence of nonthermal effects. The He I 10 830 Å line can be used as a diagnostic tool for nonthermal effects if combined with other lines and hard X-ray observations.
The purpose of this paper is to investigate the formation and properties of the He I 10 830 Å line in a flaring atmosphere. We obtain the line profiles with non-LTE calculations for different model atmospheres with and without nonthermal effects by an electron beam. As expected, if the nonthermal effects are not included, the line is very weak in absorption in a cool atmosphere while it turns to emission in a hot and condensed atmosphere. However, the presence of an electron beam can significantly change the line strength, producing much stronger absorption and emission in these two cases. By analyzing in detail the transition processes between the atomic levels of He I, we find that in the nonthermal case the collisional ionizations of He I are greatly enhanced. Therefore, in addition to the other two processes previously known (i.e., the photoionization-recombination and the collisional excitation), the collisional ionization followed by recombinations can act as an important agent in populating the triplet levels corresponding to the He I 10 830 Å line. With nonthermal effects, the chromosphere usually becomes optically thick in this line. These results suggest that the He I 10 830 Å line is rather sensitive to nonthermal effects. In particular, we suggest that a strong absorption at an early time and a strong emission at the maximum time during a flare could be regarded as a signature of nonthermal effects. This line is therefore a potential diagnostic tool for nonthermal effects in solar and stellar flares. Since the nonthermal effects usually work together with some other effects like an enhanced EUV irradiation and a high coronal pressure (AJ97), multi-line spectroscopy is required for discrimination between them.
Acknowledgements
We are grateful to the referee for valuable comments that helped improve the paper. This work was supported by NKBRSF under grant G20000784, by NSFC under grants 10025315, 10221001, and 10333040, and by a grant from TRAPOYT.