A&A 432, 181-187 (2005)
DOI: 10.1051/0004-6361:20041631

Hysteresis in spectral state transitions - a challenge for theoretical modeling

E. Meyer-Hofmeister - B. F. Liu - F. Meyer

Max-Planck-Institut für Astrophysik, Karl-Schwarzschildstr. 1, 85740 Garching, Germany

Received 9 July 2004 / Accepted 20 October 2004

Abstract
Many low-mass X-ray binaries show both hard and soft spectral states. For several sources the transitions between these states have been observed, mostly from the soft to the hard state during a luminosity decrease. In a few cases also the transition from the hard to the soft state was observed, coincident with an increase of the luminosity. Surprisingly this luminosity was not the same as the one during a following change back to the hard state. The values differed by a factor of about 3 to 5. We present a model for this hysteresis in the light curves of low-mass X-ray binaries (sources with neutron stars or black holes). We show that the different amount of Compton cooling or heating acting on the accretion disk corona at the time of the transition causes this switch in the accretion mode at different mass accretion rates and therefore different luminosities. The inner disk during the soft state provides a certain amount of Compton cooling which is either not present or much less if the inner region is filled with a hot advection-dominated accretion flow (ADAF) that radiates a hard spectrum.

Key words: accretion, accretion disks - black hole physics - X-rays: binaries - stars: neutron

1 Introduction

One of the most fascinating features found in X-ray binary observations are the changes between a soft and a hard spectrum. Transitions between the two spectral states were observed for both neutron star and black hole systems (Tanaka & Shibazaki 1996). For the neutron star 1608-522 Mitsuda et al. (1989) already observed the change from a soft to a hard state. One of the early observed spectral transitions in black hole binaries was found for GRS 1124-684, Nova Mus, (Ebisawa et al. 1994) Esin et al. (1997) modeled this spectral difference using the concept of an inner advection-dominated accretion flow (ADAF). The soft and hard spectral states are then understood as originating from accretion via a disk which reaches inward to the compact object in the soft state, or an advection-dominated hot coronal flow/ADAF in the inner part and accretion via a disk only in the outer regions in the hard state.

This scheme of advection-dominated accretion introduced to model the very low luminosities observed (for a review and references therein see Narayan et al. 1998) was further improved in correspondence to the growing body of observations at different wavelengths (Di Matteo et al. 2000, for a review see Narayan 2002). The basic picture is clear, but the physics of the hot coronal gas is complex and assumptions are unavoidable. Having the two modes of accretion in mind an even more demanding question is what determines the location in the disk where the mode of accretion changes from disk accretion to the ADAF.

To study the change between the different accretion modes, low mass X-ray binaries (LMXBs) that contain a neutron star or a black hole primary (reviews by Tanaka & Shibazaki 1996; Chen et al. 1997; McClintock & Remillard 2004) are suitable objects. The mass overflow rates from the companion star are low, and the disk becomes ionized and an outburst occurs only after mass has accumulated for a long time.

Distinct from these sources are the persistently bright high mass X-ray binaries (HMXBs) with a high mass $\ge$ $ 10 ~M_\odot$companion star, mostly an O or Be star (review by Charles & Coe 2004). These sources are wind accretors. Their luminosities vary much less, but seems for at least the three sources, Cyg X-1, LMC X-1, and LMC X-3 to be in the range which allows transitions.

There is a special feature in the appearance of the transition of spectral states: the hard-soft transition does not occur at the same luminosity as the soft-hard transition. The latter seems to happen at a luminosity lower by a factor of about 5 as far as can be seen from the observations. The aim of our paper is to give an explanation for this peculiar "hysteresis''.

In Sect. 2 we put together the relevant observations. Section 3 summarizes the theoretical work on spectral state transitions. In Sect. 4 we present our computational results. The Compton effect that photons from the central light source have on the coronal electrons depends on the spectrum of the radiation from the innermost region and is different in the two cases, where either a disk exists when the transition from the soft to the hard spectrum occurs or a vertically extended hot flow when the transition from the hard to the soft spectrum occurs. We show that this naturally leads to different transition luminosities. In Sect. 5 we show that this effect explains the hysteresis in the spectral transition luminosity. In Sect. 6 we critically discuss previous suggestions for the cause of the hysteresis. Conclusions follow in Sect. 7.

2 Hysteresis in lightcurves of X-ray binaries - observations

Spectral state transitions are observed in three groups of sources: in HMXBs, in black hole and in neutron star LMXBs. For Cyg X-1, the best known HMXB, mostly in the hard state, a rich documentation is available. In this system no hysteresis is observed (see Sect. 6.2). For the other persistent source, LMC X-3, mostly in the soft state, a hard state occurred in 1998 (Wilms et al. 2001). The X-ray novae have very rare outbursts so that the chance to observe the hard to soft transition during the rise to a new outburst is low.

Maccarone (2003) searched for observations of soft to hard transitions. For his sample of 4 transient black hole X-ray sources, 2 persistent black hole binaries and 3 neutron star binaries he finds transition luminosities in a narrow range of a few percent of the Eddington luminosity. Kalemci et al. (2003) analyze the PCA/RXTE data from all galactic black hole transients observed with RXTE between 1996 and 2001 that made a state transition during outburst decay. But the number of sources where we can compare the luminosity for both transitions is small.

2.1 Observations of individual sources

A hysteresis in the spectral state transition was observed in the following sources:

Aql X-1:
For Aql X-1, the only neutron star LMXB considered here, fortunately a full outburst cycle has been observed. The luminosity at the hard-soft transition was found to be about 5 times higher than the soft-hard transition luminosity (Maccarone & Coppi 2003), 4.2 to $5.5\times 10^{36}~\rm {erg/s}$ in the rise of the outburst and 6.1- $7.5 \times 10^{35}~\rm {erg/s}$ in the decline.

GX 339-4:
This was the system (together with GS 1124-683) for which a hysteresis effect was first pointed out by Miyamoto et al. (1995). The difference in flux of a factor of 100 was deduced from combining results for GX 339-4 (outburst 1988, 1991) and for GS 1124-683. The difference in luminosity might vary from outburst to outburst, but data of the recent outbursts yield much lower differences in luminosity between the spectral changes hard-soft and soft-hard. Hard-state and soft-state observations in 1997 and 1999 were discussed by Nowak et al. (2002, see also references therein). They report a transition back to the hard state at a luminosity lower by about a factor of 3 than that of the brightest hard state observation.

Zdziarski et al. (2004) show that this system had about 15 outbursts from 1987 to 2004. For two recent outbursts the state transitions could be observed in both directions. In both cases the hard-soft transition occurred at a higher flux level than the corresponding soft-hard transition. In the second, better observed, outburst, the luminosity difference for the two transitions is found to be about a factor of 5 in the 1.5-5 keV flux (for details see Zdziarski et al. 2004).

GS 1124-683, Nova Muscae
The data for GS 1124-683, mentioned above show that the soft-hard transition occurs at a luminosity much lower than the maximum (1-37 keV) of the X-ray flux. It is not clear when the hard-soft transition happened.

XTE J1650-500:
Rossi et al. (2004) presented results for the outburst of 2001/2002 and found that the state transitions occurred at different luminosity levels, with a lower luminosity at the soft to hard transition. The difference is about a factor 5 as shown in the hardness-intensity diagram (Rossi et al. 2004, Fig. 2).

XTE J1550-564:
Kubota & Done (2004) discuss the outburst of the microquasar XTE J1550-564 in 1998. The luminosity rise during the outburst was very fast and the spectral change from hard to soft was at a luminosity clearly higher than the one at which the source finally changed back to the hard state, perhaps by a factor around 10. The evolution of XTE J1550-564 during its outburst in 2000 was reported by Rodriguez et al. (2003). The spectral index versus the 2-200 keV flux plotted over the outburst shows a hysteresis of a factor of three.

Other sources:
There are further sources where a hysteresis is suspected: 1E 1740.7-2942 and GRS 1758-258 (Smith et al. 2002) and GRS 1915+105 (Klein-Wolt et al. 2002).

2.2 Definition of "hysteresis''

In our investigation we now use the term "hysteresis'' for the feature that the luminosity at the transition from hard to soft spectral state at the rise of one particular outburst is higher than the luminosity at the reverse transition from soft to hard spectral state in the decrease of the same outburst.

3 The change to a hot coronal flow/ADAF at the inner radius of the thin disk

Historically, different suggestions have been advanced to explain the accretion modes and the change of the spectrum. In early work, Shapiro et al. (SLE) (1976) suggested a hot optically thin flow which however is thermally unstable. This is also the case for the ADAF-SLE solutions constructed by Igumenshchev et al. (1998). ADAF-type two-temperature solutions were first described by Ichimaru (1977) in order to understand the two different spectral states observed for Cyg X-1. He attributed the transition to the energy budget of the plasma near the outer boundary of the disk, the balance between plasma heating by viscous dissipation and radiative loss, and thereby analytically derived a critical mass flow rate for the spectral transition. Meyer & Meyer-Hofmeister (1994) proposed a model for a corona above a geometrically thin standard accretion disk around compact objects, taking into account the interaction of the two flows. In an apparently very different approach Honma (1996) considered the effect of a turbulent diffusive heat flux outwards from a hot and mainly non-radiative advection-dominated inner region to an outer cool accretion disk. In spite of a very different geometry and simplification Honma's model captures the same physical effect as the one by Meyer & Meyer-Hofmeister (1994). For a discussion see Meyer et al. (2000a).

In connection with the application to X-ray binaries Narayan & Yi (1995) suggested that, whenever the accreting gas has a choice between a thin disk and an ADAF, the ADAF configuration is chosen ("strong ADAF principle''). This prescription makes it possible to derive a relation between mass flow rate and disk truncation radius (compare Fig. 8 in Narayan et al. 1998).

In a new systematic analysis Done & Gierlinski (2004) use all data now available from Galactic binary systems to investigate the change of spectra as a function of the accretion rate, and conclude that the major hard-soft spectral transition is driven by a changing inner radius of the accretion disk. In this picture one key feature is missing: what determines the location of this inner radius?

The model proposed by Meyer & Meyer-Hofmeister (1994) was originally worked out to understand the X-rays observed in cataclysmic variables. But the evaporation process is even more important in disks around neutron stars and black holes (Meyer et al. 2000a,b). The corona is fed by matter of the thin disk which evaporates from the cool layers underneath. This establishes a coronal mass flow which diminishes the mass flow rate in the thin disk. In the inner region evaporation becomes so efficient that at low accretion rates all matter flows via the corona and proceeds towards the black hole as a purely coronal vertically extended accretion flow. Very similar to this model is the investigation of the vertical structure of the corona by Rózanska & Czerny (2000); for a discussion of differences in the results see Meyer-Hofmeister & Meyer (2001).

4 Computational results

4.1 The equilibrium between cool disk and hot corona

In order to derive the coronal structure we take the standard equations of viscous hydrodynamics. For the results presented here we used the one-zone model approximation (Meyer et al. 2000a) in a modified version which takes into account different ion and electron temperature and the effect of Compton cooling and heating of coronal electrons by photons from the central area in the soft state (Liu et al. 2002, the Compton effect now taken for hard and soft state, see below). The five ordinary differential equations describing the coronal flows above a disk are: (1) the equation of continuity, (2) the z-component of momentum equation, (3) and (4) the energy equations for ions and electrons and (5) the equation for the thermal conduction for a fully ionized plasma. These five equations have been written up in the paper of Liu et al. (2002) as Eqs. (2)-(4), (6) and (8). The boundary conditions are also taken as in Liu et al. (2002), Eqs. (13) and (14). The lower boundary condition determines the temperature and the relation between pressure and heat flux density at the bottom of the corona and derives from a standard relation between temperature and thermal flux in the very steep temperature profile (see Shmeleva & Syrovatskii 1973; Liu et al. 1995). The upper boundary (free boundary) mirrors the requirement of no thermal heat input from outside and no artificial confinement at the top (i.e. allows for wind loss). We determine the five dependent variables: pressure, ion and electron temperature, heat flux density and the vertical velocity vz as functions of height above the midplane at a given distance R. These vertical structure solutions yield the mass evaporation rate.

Compared to Eqs. (4) and (6) of Liu et al. (2002) we introduced a factor of 1.5 in the term for the sidewise advection of energy, which now reads $\frac{3}{R}\rho_i v_R u_i$ for ions and correspondingly for electrons. This takes into account the difference of the specific energy between the mass flows entering and leaving the "one zone'' due to its radial dependence (cf. Meyer-Hofmeister & Meyer 2003, Sect. 2).

For equipartition field strength, synchrotron cooling in the temperature ranges of T=108.7 K, where radiation losses are important in coronal models presented here, is less than 1/10 of the cooling by bremsstrahlung and is neglegible. For higher values of magnetic to gas thermal energy density it might however become important.

4.2 Parameters chosen for the computations

We take a black hole mass of $6~M_\odot$. As claimed before (Liu et al. 2002), the results are actually mass-independent as long as Compton heating by high-energy photons can be neglected. For the viscosity parameter we take $\alpha=0.3$ (for the influence of $\alpha$ on the evaporation efficiency see Meyer-Hofmeister & Meyer 2001 and Liu et al. 2002, for its use in modeling of X-ray binary spectra Esin et al. 1997, for applications to accretion disk evolution Meyer-Hofmeister & Meyer 1999).

4.3 The effect of Compton cooling and heating

The Compton cooling/heating rate per unit volume is the sum of Compton cooling and heating (inverse Compton and Compton effect).

 \begin{displaymath} q_{\rm Comp}={4k T_{\rm e}-h\bar{\nu} \over m_{\rm e} c^2}n_{\rm e}\sigma_{\rm T} cu, \end{displaymath} (1)

with k the Boltzmann constant, $T_{\rm e}$ electron temperature, $h\bar{\nu}$mean photon energy, $m_{\rm e}$ electron mass, c velocity of light, $n_{\rm e}$ electron particle density, $\sigma_{\rm T}$ Thomson cross section and u the energy density of the photon field. For coronal electrons above a thin disk, the photon field is composed of photons from the central source and those from the disk underneath. In our case the former are dominant and hence the contribution of the latter can be neglected here. The Compton cooling by photons of the secondary stars is generally negligible. Even in the case of Cyg X-1 with its supergiant companion their energy flux density at the central disk corona is less than 10-3 of the irradiating X-ray flux density.

In the soft state where the disk reaches inward to the last stable orbit the flux from the central region seen by the corona at distance R is

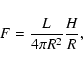\begin{displaymath}F={L\over 4\pi R^2}{H\over R}, \end{displaymath} (2)

where L is the luminosity of the central source, which translates into a central mass accretion rate $\dot M$ by $L=\eta \dot Mc^2$. We use $\eta=0.1$. The factor H/R is the ratio of coronal height to distance. It takes into account that the coronal electrons only see the central radiating disk projected on their line of sight. We take the factor as 1/2, typical for the bulk of the coronal electrons. For the hard spectral state we treat the inner hot ADAF region as an external source of hard photons. We take a lower efficiency of light production $\eta=0.05$. The radiation comes from an inner vertically extended optically thin region and the factor H/R has to be replaced by one. To a corona far away from the central source all photons come from nearly the same direction and thus uc=F. For given mass accretion rate and radius the Compton cooling/heating rate (Eq. (1)) is then a function of coronal temperature and density. $q_{\rm Comp}>0$means Compton cooling and $q_{\rm Comp}<0$ means heating.

For the investigation of coronal structure and evaporation rate in the soft spectral state the mean photon energy is much less than the electron energy, $h\bar{\nu}\ll 4kT_{\rm e}$. For the hard spectral state we use a hard state spectrum of 100 keV mean photon energy. Zdziarski & Gierlinski (2004) found in their analysis a range of 100 to 200 keV to be characteristic for the hard state in black hole binaries.

4.3.1 The Compton effect in the soft and the hard spectral state
In the soft state, Compton cooling leads to lower temperatures and lower densities in the corona, and therefore yields a lower mass flow rate in the corona and a lower evaporation rate than without Comptonizing irradiation. Figure 1 displays three different aspects: first, the effect of Compton cooling on the evaporation in the soft state for different central luminosities, i.e. mass accretion rates ( $\dot M_{\rm {Edd}}=L_{\rm {Edd}}/0.1c^2$ with $L_{\rm {Edd}}=4 \pi GMc/\kappa$, $\kappa$ electron scattering opacity). The sequence of dash-dotted, solid, dashed and dotted lines shows that a higher central luminosity, i.e. a higher central accretion rate leads to stronger Compton cooling of the corona and results in less evaporation. The distance where evaporation is maximal then moves outwards because the effect of Compton cooling decreases with increasing distance from the source.

Further, Fig. 1 makes it possible to study the thin disk truncation. For $\dot M/\dot M_{\rm Edd}=0.01$, mass evaporation (dotted lines) is very weak. Such a mass flow rate is higher than the maximal evaporation rate, $ \dot M/\dot M_{\rm {Edd}} \ge 10^{-2.86}$, so that the gas accretes to the center through the thin optically thick disk. With $\dot M/\dot M_{\rm Edd}$ decreased, e.g. $\dot M/\dot M_{\rm Edd}=0.006$, soft radiation and Compton cooling decrease, and the evaporation rate increases (dashed line). Also for this mass flow rate the disk would not be truncated since evaporation cannot deplete the inner disk region. In both these cases the disk reaches inward to the last stable orbit with a soft multi-temperature black body spectrum. When $\dot M/\dot M_{\rm Edd}$ decreases to 0.005, the evaporation rate nearly reaches the same value (solid line). The supply of accreting gas to the inner disk and hence the supply of soft photons is stopped. The inner disk is finally depleted by accretion and evaporation, the accretion changes from the disk-dominated to the RIAF/ADAF-dominated mode, and the spectrum becomes hard.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1631fig1.ps}\end{figure} Figure 1: Determination of the accretion rate at spectral transition in soft and hard state. (1) Soft state: sequence of 4 curved lines: dash-dotted, solid, dashed and dotted line: evaporation rates without, and with Compton effect from a soft disk spectrum for central accretion rates $\dot M/\dot M_{\rm Edd}= 0.005,0.006, 0.01$ respectively. Horizontal lines: accretion rates taken for the Compton effect. Comparison with the evaporation rate maximum shows: for 0.01 and 0.006 the evaporation rate is low enough to allow disk accretion to continue inward, the spectrum is soft; for 0.005  $\dot M/\dot M_{\rm Edd}$ this rate and the maximal evaporation rate become approximately equal, i.e. evaporation begins to deplete the disk, the transition to the hard state is triggered. (2) Hard state: solid line in the upper right diagram: evaporation rate for the Compton effect of a hard spectrum of 100 keV mean photon energy for $\dot M/\dot M_{\rm Edd}=0.028$: only one curve is drawn, evaporation for the rate of hard-soft transition.
Open with DEXTER

Finally in Fig. 1 the result from a hard state irradiation is shown (100 keV mean photon energy and central ADAF region luminosity for $\dot M/\dot M_{\rm Edd}=0.028$). This accretion rate was determined such that it is the same as the maximal value of the evaporation rate. At a slightly higher accretion rate an inner disk forms, initializing the spectral transition to the soft state.

What accounts for the difference between soft and hard state irradiation? The soft state photon energy is very low compared to that of the electrons in the corona, and irradiation always means cooling. In the hard state the photon energy becomes comparable to the electron energy and as the latter decreases with increasing distance from the central source initial cooling turns into effective heating with the resulting high evaporation rate.

5 The hysteresis in the spectral transitions

Let us discuss what the computational results mean for a full outburst cycle in a black hole or neutron star binary. In quiescence the mass accretion rate is very low, evaporation cuts off the inner disk region, inside advection-dominated accretion is dominant. When the outburst begins the mass accretion rate $\dot M$rises, the disk truncation radius moves inward, always to the location where the increased accretion rate and the local evaporation rate are equal, following the evaporation rate - truncation radius relation for the hard spectral state. This relation however peaks at $\dot M \approx 2.8\times 10^{-2}\; \dot M_{\rm {Edd}}$ (upper right solid line in Fig. 1). When $\dot M$surpasses this value, no disk cut-off is possible anymore, the disk starts to diffuse inwards to the last stable orbit, and soft photons from this inner disk reach the corona. From then on we have the coronal structure corresponding to the soft state.

When the outburst declines again the accretion rate drops. As a consequence Compton cooling weakens and evaporation increases until at $\dot M/\dot M_{\rm {Edd}}\approx 5 \times 10^{-3}$ the mass flow in the disk and evaporation become equal, the soft-hard transition is triggered and accretion in the inner region takes the form of a purely coronal flow with a hard spectrum which will remain during the whole quiescence.

The important feature in such an outburst cycle is that the spectral transitions are triggered at different accretion rates depending on from which spectral state the transition occurs. In our example the accretion rate at the hard-soft transition thus is a factor of 5 to 6 higher than the one at the inverse soft-hard transition. If the efficiency of hard state light production is not much smaller than the factor $\frac{1}{2}$ assumed here this gives a significant hysteresis in the transition luminosities as observed.

In Fig. 2 we show the computed truncation radius at different times during an outburst cycle: a decrease of $R_{\rm {in}}/R_{\rm S}$ during rise to outburst until the hard-soft transition is reached, a constant value $R_{\rm {in}}=3R_{\rm S}$ as long as the accretion rate is high (maybe very high), and a change back to a large value during the soft-hard transition, followed by further increase. At each moment of time the truncation radius belongs to the appropriate local evaporation rate. For that value the correct Compton effect consistent with the particular accretion rate always has to be included.

Note that the detailed value derived for the hysteresis amplitude depends on the choice of the parameters used to describe the complex real situation by a one-zone model.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1631fig2.ps}\end{figure} Figure 2: The hysteresis in the truncation radius: the arrows show how the disk inner radius changes with mass accretion rate during an outburst cycle (starting from the upper left corner of the figure). In quiescence the spectrum is hard. After onset of the outburst the increasing mass accretion rate yields a decreasing truncation radius. When $\dot M/\dot M_{\rm Edd}$ has reached the critical value for the hard-soft state transition the disk extends inward to the last stable orbit. During the further rise to outburst maximum and the following decline the system stays in the soft state ( $R_{\rm {in}}=3R_{\rm S}$, horizontal line in the diagram), until the accretion rate drops to the rate at which the soft-hard transition occurs and the disk becomes truncated again. For even smaller rates the disk truncation moves outward. Due to the effect of Compton cooling, the rates for the two spectral state transitions are different, see text.
Open with DEXTER

6 Discussion

6.1 Other suggestions to explain the hysteresis

We list here suggestions by different authors as well as an additional possibility. The first three possible scenarios were outlined in the investigation of Maccarone & Coppi (2003).

(1) The state transition luminosity from an adiabatic accretion flow to a thin disc is higher than the transition luminosity from a thin disc to an adiabatic flow because interactions are more efficient in the thin disc where the mean particle separation is smaller. - In standard theory the ADAF state would have to change to the thin disk accretion state when the optically thin flow ceases to exist because radiative cooling overcomes viscous heating. This boundary is defined by the "strong ADAF principle''. For the opposite transition however there is no such limit: a cool disk can exist for very low accretion rates even if it becomes optically thin. This holds as long as corona-disk interaction is left out.

(2) During the rapid luminosity rise, a geometrically thin accretion flow is not stable, so the geometrically thick flow persists because the system is out of equilibrium. - In our picture an increasing mass flow rate in the disk (in X-ray transients caused by a disk instability) shifts the inner edge of the thin disk inward towards the black hole or neutron star. These inner disk regions are radiation-pressure-dominated. Recently Gierlinski & Done (2004) discussed the issue whether the disks in X-ray binaries are unstable. They find that multi-temperature black body spectra are a good fit to the observations and that no variability in the lightcurves is found which would indicate an instability. Then instability should not be the cause of the hysteresis.

(3) A time lag is present in the soft-hard transition because the disk must be evacuated or evaporated. - In our picture the change from disk accretion to a hot coronal flow will start where the evaporation rate first exceeds the mass flow rate in the thin disk. A ring-shaped disk region becomes evaporated and the gas in the remaining inner thin disk can disappear by flowing inward in the thin disk or evaporating to a hot flow. At present it is not clear how fast such a left-over inner disk region disappears completely (see also our discussion of the situation in Cyg X-1 in the next section). The diffusive depletion time of a disk at the distance where the transition occurs is generally short but the situation is complex because of corona-disk interaction, and requires more detailed investigation.

(4) Zdziarsky & Gierlinski (2004) note that observations indicate that in a certain range of $L/L_{\rm {Edd}}$ both a hot accretion flow or thin disk accretion seem possible, and suggest this might be responsible for the hysteresis in the long-time light curves of black hole binaries. - This is true but by itself does not explain how the hysteresis comes about and how big it is.

(5) An argument which we want to add here for clarification concerns the fact that the efficiency of light production is different for the two modes of accretion. In our theoretical investigation we derive a certain mass flow rate for which the spectral state transition occurs. If the efficiency is lower in the optically thin advection-dominated mode than in the optically thick disk accretion we expect a luminosity increase at the time of the hard-soft transition and a decrease at the reverse transition. If one attributes the newly reached higher or lower luminosity to the state transition this would be higher for the hard-soft transition and lower for the soft-hard transition, a difference in luminosity in the same sense as the observed hysteresis. How large is this luminosity difference? Observation for Cyg X-1 show only a small difference between the two states. Czerny & Rózanska (2004) derive an accretion efficiency as a function of the distance from the black hole. In this evaluation the viscosity also enters. If from their investigation we take the values closest to our model for the spectral state transition we find a factor of about two between the efficiencies in disk accretion and in the hot flow. Also, the observed luminosity from disk accretion is reduced if we see the source at a high inclination angle. A difference of a factor of two would not be sufficient to explain the observed hysteresis.

Summarizing the ideas discussed above we can conclude that the suggestions are either not promising for explaining the hysteresis or at present there is not yet a quantitative result (suggestion 3).

6.2 The case of Cygnus X-1

Cyg X-1 is one of the best studied black hole X-ray binaries. Most of the time the system is in a hard spectral state. A soft spectral state was observed in 1994, 1996 and 2000-2002. During the first observed soft state the source was not observed at lower energies (Cui et al. 1997). In the following transitions hard and soft band fluxes were observed. From the light curve of the 1996 state transition obtained from the ASM and BATSE data Zdziarski & Gierlinski (2004, Fig. 5) conclude that there is no noticeable hysteresis in Cyg X-1 (see also Zdziarski et al. 2002).

The light curve of Cyg X-1 shows quite large fluctuations in the flux on the time scale of the state transition itself. In Cyg X-1 with only moderate differences in the mean mass accretion rate, the fluctuations in the flux might be more important than in X-ray transients with rapidly changing accretion rates. Then the effect of different Compton heating and cooling might be washed out by backward and forward transitions.

7 Conclusions

Our investigation is aimed at understanding the mysterious hysteresis in the light curve of X-ray binaries and to evaluate quantitative results for the difference in luminosity at the hard to soft and the soft to hard spectral transitions. This hysteresis was found in the observations of several X-ray binaries. We have shown that this is a natural outcome of the different Compton effects that photons from the central light source have on the coronal electrons and thereby on the coronal structure in the hard and the soft state and therefore on the evaporation rate.

Most observations concern black hole systems. For our results we have determined the Compton effect in the hard spectral state for a spectrum of 100 keV mean photon energy (Zdziarski & Gierlinski 2004). For different systems peaks of the hard spectra are also found at lower energies, e.g. at 20-30 keV for the very bright black hole candidate system Cyg X-3 (Szostek & Zdziarski 2004). For neutron star systems whose hard spectra typically display about equal energy contributions over the full range from 3 to 100 keV (Gilfanov et al. 1998) the mean photon energy is also lower, around 20 keV. In view of the clear hysteresis shown by Aql X-1 it will be interesting to investigate those cases as well and derive a value for the expected hysteresis.

One may note that our model not only explains the observed hysteresis but also yields a quantitative estimate that agrees with the observations. At the same time this result further confirms the picture of the evaporation model: the interaction of a cool disk and a corona above with a maximal evaporation efficiency determining the spectral transition.

Acknowledgements
B. F. Liu thanks the Alexander-von-Humboldt Foundation for the award of a research fellowship during which this investigation was performed.

References

 
Copyright ESO 2005