E. Piconcelli - E. Jimenez-Bailón - M. Guainazzi - N. Schartel - P. M. Rodríguez-Pascual - M. Santos-Lleó
XMM-Newton Science Operation Center (ESAC), Apartado 50727, 28080 Madrid, Spain
Received 8 July 2004 / Accepted 26 October 2004
Abstract
We present results of a systematic analysis of the XMM-Newton spectra of 40 quasars (QSOs) (![]() )
from the Palomar-Green (PG) Bright
Quasar Survey sample (MB<-23). The sample includes 35 radio-quiet
quasars (RQQs) and 5 radio-loud quasars (RLQs). The analysis of the
spectra above 2 keV reveals that the hard X-ray continuum emission
can be modeled with a power law component with
)
from the Palomar-Green (PG) Bright
Quasar Survey sample (MB<-23). The sample includes 35 radio-quiet
quasars (RQQs) and 5 radio-loud quasars (RLQs). The analysis of the
spectra above 2 keV reveals that the hard X-ray continuum emission
can be modeled with a power law component with
![]() and
and
![]() for
the RQQs and RLQs, respectively. Below 2 keV, a strong, broad
excess is present in most QSO spectra. This feature has been fitted
with four different models assuming several physical scenarios.
All tested models (blackbody, multicolor blackbody,
bremsstrahlung and power law) satisfactorily fitted the majority of
the spectra. However, none of them is able to provide an adequate
parameterization for the soft excess emission in all QSOs,
indicating the absence of a universal shape for this spectral
feature.
An additional cold absorption component was required only in three
sources. On the other hand, as recently pointed out by Porquet et al. (2004) for a smaller sample of PG QSOs,
warm absorber features are present in 50% of the QSO spectra in contrast with their rare occurrence
(
for
the RQQs and RLQs, respectively. Below 2 keV, a strong, broad
excess is present in most QSO spectra. This feature has been fitted
with four different models assuming several physical scenarios.
All tested models (blackbody, multicolor blackbody,
bremsstrahlung and power law) satisfactorily fitted the majority of
the spectra. However, none of them is able to provide an adequate
parameterization for the soft excess emission in all QSOs,
indicating the absence of a universal shape for this spectral
feature.
An additional cold absorption component was required only in three
sources. On the other hand, as recently pointed out by Porquet et al. (2004) for a smaller sample of PG QSOs,
warm absorber features are present in 50% of the QSO spectra in contrast with their rare occurrence
(![]() 5-10%) in previous studies. The XMM-Newton view of
optically selected bright QSOs therefore suggests that there are
no significant differences in the X-ray spectral properties
compared with those of the low-luminosity Seyfert 1 galaxies.
Properties of the Fe K
5-10%) in previous studies. The XMM-Newton view of
optically selected bright QSOs therefore suggests that there are
no significant differences in the X-ray spectral properties
compared with those of the low-luminosity Seyfert 1 galaxies.
Properties of the Fe K![]() emission lines are presented in a
companion paper.
emission lines are presented in a
companion paper.
Key words: galaxies: active - galaxies: nuclei - galaxies quasars: general - X-rays: galaxies
Quasars (QSOs) emit a large amount of their emission in the X-ray band, where luminosities can reach 1046-47 erg s-1 (Zamorani et al. 1981). Variability studies indicate that the X-rays originated in a region very close to the central object, probably an accreting supermassive black hole. Therefore, the analysis of the emission in this energy range provides strong constraints for models of the mechanism powering the QSOs. X-ray emission properties of QSOs have been largely studied during the last decades. Different samples of QSOs have been analyzed with previous X-ray satellites such as Einstein (Zamorani et al. 1981), EXOSAT (Comastri et al. 1992), Ginga (Lawson & Turner 1997), ASCA (Cappi et al. 1997; George et al. 2000; Reeves & Turner 2000), ROSAT (Schartel et al. 1997; Laor et al. 1997) and BeppoSAX (Mineo et al. 2000).
From these studies it emerges that the typical spectrum of a QSO in the
hard (>2 keV) band is dominated by a power law-like emission with a photon index
![]() .
For Seyfert galaxies, the most popular physical scenario
(Haardt & Maraschi 1991) explains this hard spectral component as the emission
originating in a hot corona placed above the accretion disk which
comptonizes the UV-soft X-ray thermal emission from the disk and
up-scatters it into the hard X-ray band. Part of the continuum
emission is then reprocessed in the disk and/or in other nuclear
physical components (i.e. the molecular torus, clouds) producing the
typical reflection spectrum (George & Fabian 1991). The most
striking feature in the reflection spectrum is the fluorescent Fe
K
.
For Seyfert galaxies, the most popular physical scenario
(Haardt & Maraschi 1991) explains this hard spectral component as the emission
originating in a hot corona placed above the accretion disk which
comptonizes the UV-soft X-ray thermal emission from the disk and
up-scatters it into the hard X-ray band. Part of the continuum
emission is then reprocessed in the disk and/or in other nuclear
physical components (i.e. the molecular torus, clouds) producing the
typical reflection spectrum (George & Fabian 1991). The most
striking feature in the reflection spectrum is the fluorescent Fe
K![]() emission line around 6.4 keV. This scenario has been extended to the QSOs,
although the observational evidence for a reflection component in their X-ray spectra is poor.
Signatures of the presence of large amounts of
ionized and/or cold gas were also detected in the soft X-ray portion of
QSO spectra (Cappi et al. 1997; George et al. 1997). It has also been reported that a fraction of QSOs present a gradual upturn in the
emission emerging below 2-3 keV, the so-called soft excess (Comastri et al. 1992), whose nature is still debated.
emission line around 6.4 keV. This scenario has been extended to the QSOs,
although the observational evidence for a reflection component in their X-ray spectra is poor.
Signatures of the presence of large amounts of
ionized and/or cold gas were also detected in the soft X-ray portion of
QSO spectra (Cappi et al. 1997; George et al. 1997). It has also been reported that a fraction of QSOs present a gradual upturn in the
emission emerging below 2-3 keV, the so-called soft excess (Comastri et al. 1992), whose nature is still debated.
Systematic analysis of QSOs with high spectral resolution provide a very useful tool for investigating their nature. In this paper we analyze a sample of QSOs observed with XMM-Newton, which provides the highest throughput and sensitivity to date. We investigate the spectral characteristics of the objects in the sample and search for common features in order to elucidate the physical mechanisms responsible for the X-ray emission. The sample includes both radio loud and radio quiet quasars (RLQs and RQQs, respectively). The classification is based on the strength of the radio emission relative to the optical. Many studies show systematic differences in the spectral properties in the X-ray band of both types of objects, such as for instance the slope of the power law (Laor et al. 1997; Reeves & Turner 2000) which is evidence for a possible difference in the physical processes that give rise to the X-ray emission. Therefore the chosen sample provides useful information about possible differences between RLQs and RQQs. Results based on XMM-Newton observations of a smaller subsample of PG QSOs have recently been presented by Porquet et al. (2004; P04 hereafter). Thanks to the larger number of objects, our survey makes it possible to obtain a complete description of the X-ray spectral properties of optically selected QSOs based on a sounder statistical ground.
Table 1: The sample.
In Sect. 2 we present the general characteristics of the objects included in the sample, as well as the XMM-Newton observations and the reduction technique. We performed a systematic analysis of all objects assuming several physical scenarios for the emission of the QSO. The corresponding results are presented in Sect. 3, which also includes a detailed analysis of the most peculiar objects. In Sect. 4 we discuss observational constraints obtained by this study to the physical scenario for the X-ray emission/absorption mechanisms at work in QSOs and we also compare them with previous similar works. Finally, the main results of this study are summarized in Sect. 5.
The raw data from the EPIC instruments were processed using the standard Science Analysis System (SAS)
v5.4.1 (Loiseau 2003) to produce the linearized event files for pn, MOS1 and MOS2.
Only events with single and double patterns for the pn (
![]() )
and single, double, triple and quadruple events for the
MOS (
)
and single, double, triple and quadruple events for the
MOS (
![]() ), were used for the spectral analysis. The subsequent event selection was
performed taking into account the most updated calibration files at
the time of the reduction (September 2003). All known flickering and
bad pixels were removed. Furthermore, periods of background flaring in
the EPIC data were excluded using the method described in Piconcelli
et al. (2004). Useful exposure times after cleaning are listed in
Table 2 for each camera together with the date and the
revolution of each reduced observation. In the case of 0844+349,
1244+026 and 1440+356, the pn observations are affected by
pile-up, and therefore only the MOS spectra were used for the
analysis. On the other hand, for 1226+023 and 1501+106 only
pn data were analyzed because of the impossibility to select a background region since the MOS
observations were carried out in small window mode. Source
spectra were extracted from circular regions centered on the peak of
the X-ray counts. Backgrounds were estimated in a source-free circle of equal
radius close to the source on the same CCD. Appropriate response and
ancillary files for both the pn and the
MOS cameras were created using respectively the RMFGEN and ARFGEN tools in the
), were used for the spectral analysis. The subsequent event selection was
performed taking into account the most updated calibration files at
the time of the reduction (September 2003). All known flickering and
bad pixels were removed. Furthermore, periods of background flaring in
the EPIC data were excluded using the method described in Piconcelli
et al. (2004). Useful exposure times after cleaning are listed in
Table 2 for each camera together with the date and the
revolution of each reduced observation. In the case of 0844+349,
1244+026 and 1440+356, the pn observations are affected by
pile-up, and therefore only the MOS spectra were used for the
analysis. On the other hand, for 1226+023 and 1501+106 only
pn data were analyzed because of the impossibility to select a background region since the MOS
observations were carried out in small window mode. Source
spectra were extracted from circular regions centered on the peak of
the X-ray counts. Backgrounds were estimated in a source-free circle of equal
radius close to the source on the same CCD. Appropriate response and
ancillary files for both the pn and the
MOS cameras were created using respectively the RMFGEN and ARFGEN tools in the
![]() software.
As the difference between the MOS1 and MOS2 response matrices is a few percent,
we created a combined MOS spectrum and
response matrix. The background-subtracted spectra for the pn and combined
MOS cameras were then simultaneously fitted. According to the current calibration uncertainties
we performed the spectral analysis in the 0.3-12 keV band for
pn and in the 0.6-10 keV band for the MOS cameras.
software.
As the difference between the MOS1 and MOS2 response matrices is a few percent,
we created a combined MOS spectrum and
response matrix. The background-subtracted spectra for the pn and combined
MOS cameras were then simultaneously fitted. According to the current calibration uncertainties
we performed the spectral analysis in the 0.3-12 keV band for
pn and in the 0.6-10 keV band for the MOS cameras.
The source spectra were grouped such that each spectral bin contains
at least 35 (or more in the case of the brightest sources)
counts in order to apply the modified ![]() minimization
technique and they were analyzed using XSPEC v.11.2 (Arnaud 1996).
Galactic absorption (see Table 1) is implicitly included in all the spectral
models presented hereafter. The photoelectric absorption cross
sections of Morrison & McCammon (1983) and the solar abundances of
Anders & Grevesse (1989) were used. The quoted errors refer to the
90% confidence level for one interesting parameter
(i.e.
minimization
technique and they were analyzed using XSPEC v.11.2 (Arnaud 1996).
Galactic absorption (see Table 1) is implicitly included in all the spectral
models presented hereafter. The photoelectric absorption cross
sections of Morrison & McCammon (1983) and the solar abundances of
Anders & Grevesse (1989) were used. The quoted errors refer to the
90% confidence level for one interesting parameter
(i.e.
![]() ;
Avni 1976). Throughout this paper we
assume a flat
;
Avni 1976). Throughout this paper we
assume a flat ![]() CDM cosmology with (
CDM cosmology with (
![]() ,
,
![]() , 0.7) and a Hubble constant of 70 km s-1 Mpc-1 (Bennett et al. 2003). All fit parameters are
given in the quasar rest frame.
, 0.7) and a Hubble constant of 70 km s-1 Mpc-1 (Bennett et al. 2003). All fit parameters are
given in the quasar rest frame.
A simple redshifted power law model was fitted to the hard X-ray
band, excluding the data below 2 keV where additional spectral
components like soft excess and absorbing features can heavily modify
the primary source continuum. This fit turned out to be acceptable for most
sources, with only five objects (i.e. 1211+143, 1226+023,
1411+442, 1630+377 and 2214+139) yielding an associated
![]() > 1.2. Some of
these sources show a very flat spectrum with
> 1.2. Some of
these sources show a very flat spectrum with
![]() which suggests the presence of intrinsic
absorption obscuring the primary continuum. The resulting best-fit
parameters are displayed in Table 3. Using the maximum
likelihood technique (see Maccacaro et al. 1988), we have calculated the
best simultaneous estimate of the average photon index of
which suggests the presence of intrinsic
absorption obscuring the primary continuum. The resulting best-fit
parameters are displayed in Table 3. Using the maximum
likelihood technique (see Maccacaro et al. 1988), we have calculated the
best simultaneous estimate of the average photon index of
![]() and the intrinsic spread
and the intrinsic spread
![]() .
Figure 1 shows the
68%, 90% and 99% confidence contours for the two parameters together
with the best-fit values obtained, i.e.
.
Figure 1 shows the
68%, 90% and 99% confidence contours for the two parameters together
with the best-fit values obtained, i.e.
![]() and
and
![]() (errors have been calculated using the
68% contour level).
(errors have been calculated using the
68% contour level).
![\begin{figure}
\par\includegraphics[angle=90,width=7cm,clip]{1621f1.ps}
\end{figure}](/articles/aa/full/2005/10/aa1621/Timg44.gif) |
Figure 1:
Confidence contours for the simultaneous determination of the
photon index
|
| Open with DEXTER | |
Although the quality of the fit in the 2-12 keV band is good for most
quasars, the residuals show an excess around 6 keV which suggests iron fluorescence emission.
A detailed analysis of the Fe K![]() emission line is deferred to a second paper (see Jimenez-Bailon et al. 2004, Paper II hereafter).
emission line is deferred to a second paper (see Jimenez-Bailon et al. 2004, Paper II hereafter).
The extrapolation of the power law to energies lower than 2 keV clearly revealed the presence of large deviations in all but one (i.e. 1206+459) spectra, with the most common residual feature being a smooth excess of soft X-ray flux. On the other hand, a handful of objects (i.e. 1001+054, 1114+445, 1115+080 and 2214+139) exhibit a deep and sharp deficit in the 0.5-2 keV band likely due to complex absorption.
The 0.3-12 keV spectrum of each source was fitted with a single
power law model (PL) in order to provide an overall indication of the
X-ray broad-band spectral shape (
![]() and
dispersion of
and
dispersion of
![]() ).
The vast majority of
).
The vast majority of
![]() values associated with this
parameterization show that it yields a very poor description of the
EPIC data (see Table 4 for the
results).
This is clearly a evident consequence of the inclusion in the fit of the 0.3-2 keV range, which is dominated by the emission of the steeper "soft
excess'' component.
Therefore, we fitted more complex models
accounting for the soft excess (Sect. 3.2) and the
absorption features (Sect. 3.4) if present in the spectrum.
The presence of iron emission lines is investigated in Paper II.
values associated with this
parameterization show that it yields a very poor description of the
EPIC data (see Table 4 for the
results).
This is clearly a evident consequence of the inclusion in the fit of the 0.3-2 keV range, which is dominated by the emission of the steeper "soft
excess'' component.
Therefore, we fitted more complex models
accounting for the soft excess (Sect. 3.2) and the
absorption features (Sect. 3.4) if present in the spectrum.
The presence of iron emission lines is investigated in Paper II.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1621f2a.eps}\includegraphi...
...m,clip]{1621f2c.eps}\includegraphics[width=6.5cm,clip]{1621f2d.eps}
\end{figure}](/articles/aa/full/2005/10/aa1621/Timg47.gif) |
Figure 2: The ratios (data/model) resulting from fitting a power law to the 2-12 keV EPIC data ( pn data in black, MOS in red) and extrapolating to lower energies in the case of the QSO ( from top left) a) 1307+085 (z = 0.155): the soft excess emission in this source proves to be best fitted with a blackbody (i.e. model A; see Table 10); b) 1226+023 ( z = 0.158): note that the excess is broader than in 1307+085 (the two QSOs have a similar z) which requires two blackbodies (i.e. model E; see Table 10) to be parametrized; c) 1352+183 (z = 0.158) for which model C (i.e. bremsstrahlung + power law) gives the best fit. Bottom right: d) the ratio resulted fitting with model A the EPIC data of 1440+356 (z = 0.079). Note the large residuals at high energies. This QSO is best fitted with a double power law model (i.e. model D; see Table 10). |
| Open with DEXTER | |
Furthermore, photoelectric absorption edges were added to the fits
whenever appropriate. We
included these additional components by
the F-test criterion at a significance level ![]() 95%.
For the high-z QSO 1206+459, whose emission did not show any deviation from a simple
power law continuum, we did not perform any further spectral fits.
Eight sources (i.e. 0050+124, 1001+054, 1114+445, 1115+080, 1226+023, 1404+226,
1411+442, and 2214+139) exhibited spectra more complex than a
two-component continuum (plus absorption edge) and
yielded a
95%.
For the high-z QSO 1206+459, whose emission did not show any deviation from a simple
power law continuum, we did not perform any further spectral fits.
Eight sources (i.e. 0050+124, 1001+054, 1114+445, 1115+080, 1226+023, 1404+226,
1411+442, and 2214+139) exhibited spectra more complex than a
two-component continuum (plus absorption edge) and
yielded a
![]()
![]() 1.2 for each of the tested models. They are not listed in the relative tables, but rather they
are individually discussed in Sect. 3.4.
1.2 for each of the tested models. They are not listed in the relative tables, but rather they
are individually discussed in Sect. 3.4.
The best-fitting parameters resulting from the application of model A, B, C and D are shown in Table 5-8, respectively.
All objects for which we tested these models showed a
statistically significant improvement in the goodness of fit upon the
addition of a spectral component accounting for the soft excess.
Using the maximum likelihood technique,
we derived the best simultaneous estimate of the mean value and the intrinsic
dispersion of the relevant parameter (i.e.
![]() ,
,
![]() ,
,
![]() and
and
![]() )
of each tested model.
Figure 3 shows such best fit values as well as the corresponding 68%, 90% and 99% confidence contour levels. Finally, Table 9 lists the same values with the relative
uncertainties given at the 68% confidence level for two relevant parameters.
)
of each tested model.
Figure 3 shows such best fit values as well as the corresponding 68%, 90% and 99% confidence contour levels. Finally, Table 9 lists the same values with the relative
uncertainties given at the 68% confidence level for two relevant parameters.
![\begin{figure}
\par\includegraphics[angle=90,width=6cm,clip]{1621f3a.ps}\include...
...p]{1621f3c.ps}\includegraphics[angle=90,width=6cm,clip]{1621f3d.ps}
\end{figure}](/articles/aa/full/2005/10/aa1621/Timg57.gif) |
Figure 3:
Mean value and intrinsic dispersion of
the relevant parameters of soft excess in models A (
|
| Open with DEXTER | |
In this section we present the results of an analysis of the subsample of
objects included in the Laor et al. (1997) study (marked with L in
Table 1). Laor et al. (1997) analyzed the
ROSAT observations of 23 quasars
from the Bright Quasar Survey with z < 0.4 and
![]() cm-2. We performed the
analysis of 21 out of the 23 objects observed by Laor et al. (1997):
there are no publicly available observations yet in the XMM-Newton archive for 1425+267
and 1543+489. The selection criteria for the Laor et al. (1997)
sample only consider optical properties of the QSOs. Therefore the
complete subsample is unbiased in terms of X-ray properties, and it is
representative of the low-redshift, optically selected QSO population.
Taking into account the results for the spectral analysis performed for
the whole sample of quasars, we calculated the mean values of the
relevant parameters of the models considered for the analysis: hard band power law and models
A, B, C and D. Table 9
shows the mean values and the dispersion of each parameter estimated
using the maximum likelihood technique. Figure 4
shows the plots for the 68%, 90% and 99% confidence contours and
the mean value and dispersion found for each spectral parameter. All
the mean values of the different parameters found for the Laor
subsample are fully compatible within the errors with the results for
the whole sample.
cm-2. We performed the
analysis of 21 out of the 23 objects observed by Laor et al. (1997):
there are no publicly available observations yet in the XMM-Newton archive for 1425+267
and 1543+489. The selection criteria for the Laor et al. (1997)
sample only consider optical properties of the QSOs. Therefore the
complete subsample is unbiased in terms of X-ray properties, and it is
representative of the low-redshift, optically selected QSO population.
Taking into account the results for the spectral analysis performed for
the whole sample of quasars, we calculated the mean values of the
relevant parameters of the models considered for the analysis: hard band power law and models
A, B, C and D. Table 9
shows the mean values and the dispersion of each parameter estimated
using the maximum likelihood technique. Figure 4
shows the plots for the 68%, 90% and 99% confidence contours and
the mean value and dispersion found for each spectral parameter. All
the mean values of the different parameters found for the Laor
subsample are fully compatible within the errors with the results for
the whole sample.
The models tested to account for the soft excess can explain
successfully the spectra of 30 out of the 40 sources. The spectra of
the remaining nine sources have been analyzed separately (see below) while
none of the two component models improved the quality of the fit for 1206+459 likely because of
the low signal-to-noise ratio of its spectrum.
Even though
the four models considered to explain the soft excess provided good
fits (
![]() )
for the majority of the sources, we found
that for half of the sources, more complex parameterizations were required. Table 10 lists the best fit model
as well as the resulting values of the spectral parameters for each
quasar in the sample.
)
for the majority of the sources, we found
that for half of the sources, more complex parameterizations were required. Table 10 lists the best fit model
as well as the resulting values of the spectral parameters for each
quasar in the sample.
In the following we report on those sources for which
the best fit model to the X-ray emission is more complex than a two-component parameterization.
A consistent fraction of the QSOs in the sample, i.e. 13 out of 40,
required two thermal components to match their broad soft excess.
Such sources have been fitted by the models labeled E and H in
Table 10.
In model E, both thermal components are modeled with a blackbody model. The mean temperatures obtained
through the maximum likelihood method are
![]() keV for the lower,
and
keV for the lower,
and
![]() keV for higher temperature, while the dispersions
are
keV for higher temperature, while the dispersions
are
![]() and
and
![]() ,
respectively.
On the other hand, only one source, i.e. 1411+442, required a blackbody plus a
Raymond-Smith plasma (i.e. Model H in Table 10) to account for its soft excess (see below for further
details on this source).
,
respectively.
On the other hand, only one source, i.e. 1411+442, required a blackbody plus a
Raymond-Smith plasma (i.e. Model H in Table 10) to account for its soft excess (see below for further
details on this source).
Table 9: Dispersion and mean value of the relevant parameters of the models tested for the sample and the Laor et al. (1997) subsample. See Sects. 3.2 and 3.3 for details. The mean values of the kT in models A, B and C are given in units of keV.
Spectral features due to absorption edges were reported in 16 quasars.
The majority of them were found in the range 0.7-0.8 keV: most these
features are probably due to He-like oxygen and/or a blend of M-shell
iron inner shell transitions (the so-called unresolved transition
array or UTA; Behar et al. 2001). In three QSOs, i.e.
1115+080, 1211+143, 1226+023, an edge was detected around
7.1-7.4 keV, implying reprocessing in ionized iron material.
Interestingly, the spectrum of 1211+143 shows three absorption
edges, which are located, respectively, at
0.775+0.011-0.005,
0.967+0.010-0.009 and
7.25+0.14-0.09 keV. Since
these absorption features are indicative of the presence of a warm
absorber along the line-of-sight, we attempted a further fit using
the model ABSORI in XSPEC (Done et al. 1992) to account for the
ionized absorbing plasma in all the sources showing absorption edges.
However, such parameterization did not significantly improve the
goodness-of-fit statistic of any source expect for 1001+054, 1114+445, 1404+226 and
2214+139
(see below for more details on these sources), leaving the
resulting gas parameters (i.e. T,
![]() and
and ![]()
![]() ) basically unconstrained. The most
likely explanation for this result is the relatively limited photon
statistics affecting the
EPIC spectrum of these QSOs, which did not allow a more detailed
description of the warm absorber than in terms of one (or more)
edge(s).
) basically unconstrained. The most
likely explanation for this result is the relatively limited photon
statistics affecting the
EPIC spectrum of these QSOs, which did not allow a more detailed
description of the warm absorber than in terms of one (or more)
edge(s).
Finally, in the following we report more details on the spectral
analysis of the eight most peculiar sources in our sample, for which
model A, B, C, and D gave an associate
![]()
![]() 1.2 (see
Sect. 3.2).
1.2 (see
Sect. 3.2).
0050+124 (I Zw 1). The XMM-Newton spectrum shows a complex soft X-ray
emission dominated by cold absorption. The observed data are best
explained by a power law,
![]() ,
accounting for the
hard band and a double blackbody component,
,
accounting for the
hard band and a double blackbody component,
![]() keV
and
kT2=0.19+0.03-0.02 keV. Our analysis reveals the presence of
cold absorption modeled by the ZWABS model in XSPEC,
keV
and
kT2=0.19+0.03-0.02 keV. Our analysis reveals the presence of
cold absorption modeled by the ZWABS model in XSPEC,
![]() =
=
![]() cm-2, and an absorption edge
located at
0.65+0.01-0.02 keV.
These results are in agreement with a previous
XMM-Newton data analysis by Gallo et al. (2004).
cm-2, and an absorption edge
located at
0.65+0.01-0.02 keV.
These results are in agreement with a previous
XMM-Newton data analysis by Gallo et al. (2004).
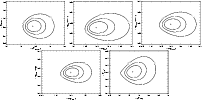 |
Figure 4: Mean value and intrinsic dispersion of the relevant parameters for tested models applied to the Laor et al. (1997) quasars together with 68%, 90% and 99% confidence contours derived with the maximum likelihood method. |
| Open with DEXTER | |
1114+445. An HST spectrum of this quasar revealed strong
UV absorption lines (Mathur et al. 1998). In the X-ray band the
presence of optically thin partially ionized material was detected
(Laor et al. 1997; George et al. 1998). By applying a power law model
to the 2-12 keV data we obtained a flat photon index (
![]() ). Extrapolation down to lower energies shows a broad
absorbing feature in the range 0.5-1 keV. The broad band X-ray
continuum of this QSO is well described by a power law with
). Extrapolation down to lower energies shows a broad
absorbing feature in the range 0.5-1 keV. The broad band X-ray
continuum of this QSO is well described by a power law with
![]() modified by two ionized absorption components (ABSORI in XSPEC) plus a blackbody component accounting for the soft
excess (see Table 10 for the best fit parameters). The
presence of the second "warm'' component yielded an improvement in
the fit at >99.9% confidence level (e.g. Fig. 5).
XMM-Newton has therefore clearly revealed, for the first time in this QSO, a multi-zone ionized absorber similar to what we found for
2214+139 (see below; Piconcelli et al. 2004). We also reported
the presence of a significant (
modified by two ionized absorption components (ABSORI in XSPEC) plus a blackbody component accounting for the soft
excess (see Table 10 for the best fit parameters). The
presence of the second "warm'' component yielded an improvement in
the fit at >99.9% confidence level (e.g. Fig. 5).
XMM-Newton has therefore clearly revealed, for the first time in this QSO, a multi-zone ionized absorber similar to what we found for
2214+139 (see below; Piconcelli et al. 2004). We also reported
the presence of a significant (
![]() )
fluorescence iron
emission line with a narrow profile at 6.45
+0.02-0.08 keV
(e.g. Paper II). On the other hand, we did not find
any evidence of a Fe K-shell absorption edge as detected at
)
fluorescence iron
emission line with a narrow profile at 6.45
+0.02-0.08 keV
(e.g. Paper II). On the other hand, we did not find
any evidence of a Fe K-shell absorption edge as detected at ![]() 7.25 keV with a
7.25 keV with a
![]() in the ASCA spectrum
by George et al. (1998). Our results agree with those recently
published by Ashton et al. (2004) from an independent analysis of the
same XMM-Newton data. They also detected a two-phase warm absorber even if
they found a best fit value of the ionization parameter for the
hotter-phase component of the warm absorber larger than ours (and,
consequently, also a larger column density).
in the ASCA spectrum
by George et al. (1998). Our results agree with those recently
published by Ashton et al. (2004) from an independent analysis of the
same XMM-Newton data. They also detected a two-phase warm absorber even if
they found a best fit value of the ionization parameter for the
hotter-phase component of the warm absorber larger than ours (and,
consequently, also a larger column density).
1115+080. XMM-Newton data of this BAL quasar have also been analyzed by
Chartas et al. (2003). This study revealed an absorbed
soft energy spectrum. Even though
Chartas et al. (2003) suggested that the soft spectrum is best fitted by an
ionized absorber, our study found that a neutral absorption model
cannot be ruled out. Our analysis indicates that the
best fit model for the observed spectrum consists of a power
law modified by cold absorption and two absorption edges at
7.1+0.3-0.4 keV
and ![]() keV (see Table 10 for further
details). Taking into account the Chartas et al. (2003) results, we have tried to
explain the soft energy absorption by an ionized absorber using the
ABSORI model in XSPEC. The value found for the ionization
parameter (
keV (see Table 10 for further
details). Taking into account the Chartas et al. (2003) results, we have tried to
explain the soft energy absorption by an ionized absorber using the
ABSORI model in XSPEC. The value found for the ionization
parameter (![]() )
is extremely low and therefore the model does not
differ from the neutral absorption one.
)
is extremely low and therefore the model does not
differ from the neutral absorption one.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1621f5a.eps}\includegraphics[width=7cm,clip]{1621f5b.eps}
\end{figure}](/articles/aa/full/2005/10/aa1621/Timg101.gif) |
Figure 5:
The ratios between the EPIC data ( pn data in black, MOS in red) and a fit with single warm absorber model for 1114+445 ( left) and 2214+139 ( right):
the large residuals below 1 keV strongly suggest the presence of a complex "multi-component'' warm absorber. Note also the residuals around 5-6 keV which indicate Fe K |
| Open with DEXTER | |
Table 11: Fluxes and absorption-corrected luminosities calculated assuming the best fit model. The last two columns list the ratio between the strength of the soft excess and the high energy power law component in the 0.5-2 and 0.5-10 keV band, respectively.
1226+023 (3C 273) The main feature in the pn spectrum of this well-known radio-loud QSO is the broad soft excess. A simple two-component model indeed fails to adequately describe its 0.3-12 keV emission (see Sect 3.2 and Fig. 2). Our best fit includes two blackbody components (with
1404+226. This narrow line QSO was observed by ROSAT and ASCA. Ulrich et al. (1999)
reported a very steep soft X-ray continuum, and
evidence of a complex ionized absorber. In particular, a peculiar absorption
feature around 1 keV led these authors to claim deviations from
solar abundances in this source.
Our results confirm the spectral complexity of 1404+226: we have found a
best fit model consisting of a blackbody with
kT
= 0.144+0.002-0.003 keV and a steep (
![]() )
power law modified by ionized absorption. For
the gas we derive a column density
)
power law modified by ionized absorption. For
the gas we derive a column density ![]()
![]() cm-2 and
an ionization parameter
cm-2 and
an ionization parameter
![]() erg cm-2 s-1. No evidence of
elemental abundances different from solar values has been found.
Finally, no significant fluorescence iron emission line has been detected.
erg cm-2 s-1. No evidence of
elemental abundances different from solar values has been found.
Finally, no significant fluorescence iron emission line has been detected.
1411+442. This BAL QSO is X-ray faint (
![]() erg cm-2 s-1). The 2-10 keV spectrum is extremely flat
with a
erg cm-2 s-1). The 2-10 keV spectrum is extremely flat
with a
![]() and a clear excess around 6 keV.
The addition of a line with a narrow Gaussian profile to parameterize
the Fe K
and a clear excess around 6 keV.
The addition of a line with a narrow Gaussian profile to parameterize
the Fe K![]() emission feature produced a very significant (at 99.8% confidence level) improvement in the fit. The centroid
(
emission feature produced a very significant (at 99.8% confidence level) improvement in the fit. The centroid
(
![]() keV) and narrowness of the
line suggest a likely origin from neutral material located far away
from the innermost regions of the accretion disk.
keV) and narrowness of the
line suggest a likely origin from neutral material located far away
from the innermost regions of the accretion disk.
The best fit model requires a power law with partial-covering
(ZPCF in XSPEC) and a Raymond-Smith plasma component (the
latter significant at >99.9% confidence level). For the absorbing gas
we obtained a column density ![]()
![]() cm-2 and a covering fraction of 96%.
The plasma temperature and the photon index of the power law were found to be
cm-2 and a covering fraction of 96%.
The plasma temperature and the photon index of the power law were found to be
![]() keV and
keV and
![]() ,
respectively.
,
respectively.
The limited statistics did not allow us to test more complex fitting models aimed, for instance, at checking the presence of a warm absorber in this source, as observed in other AGNs with prominent absorption lines in the UV spectrum (e.g. Crenshaw et al. 2003; Monier et al. 2001; Piconcelli et al. 2004). This EPIC observation has also been analyzed by Brinkmann et al. (2004a) who reported results consistent with ours.
2214+139 (MKN 304). Our analysis matches well with previous results
based on Einstein and ROSAT observations,
which reported a very flat continuum for this source, and suggested
the likely existence of heavy absorption.
The XMM-Newton data reveal a complex spectrum, dominated by strong
obscuration due to ionized gas (see Fig. 5). With an ![]()
![]() 1023 cm-2,
it is one of the ionized absorbers with the highest column density seen so
far by XMM-Newton and Chandra.
A two-component warm gas provides an excellent description
of this absorbing plasma. From the spectral analysis we derived
1023 cm-2,
it is one of the ionized absorbers with the highest column density seen so
far by XMM-Newton and Chandra.
A two-component warm gas provides an excellent description
of this absorbing plasma. From the spectral analysis we derived
![]() =
89.3
+13.9-12.0 erg cm-2 s-1 and
=
89.3
+13.9-12.0 erg cm-2 s-1 and
![]() erg cm-2 s-1 for the hot
(i.e. with
erg cm-2 s-1 for the hot
(i.e. with
![]() K) and the cold (i.e. with
K) and the cold (i.e. with
![]() K) component, respectively.
In addition to a narrow Fe K
K) component, respectively.
In addition to a narrow Fe K![]() emission line at
emission line at ![]() 6.4 keV, another emission line feature was
significantly detected at 0.57 keV, likely due to the helium-like
oxygen triplet (perhaps originating in the warm absorber itself). We also reported
the presence of a weak soft excess component which can be interpreted
as partial covering or scattered emission from the ionized outflowing plasma.
For the complete and detailed presentation and discussion of these results
see Piconcelli et al. (2004).
6.4 keV, another emission line feature was
significantly detected at 0.57 keV, likely due to the helium-like
oxygen triplet (perhaps originating in the warm absorber itself). We also reported
the presence of a weak soft excess component which can be interpreted
as partial covering or scattered emission from the ionized outflowing plasma.
For the complete and detailed presentation and discussion of these results
see Piconcelli et al. (2004).
Fluxes in the soft (0.5-2 keV) and hard (2-10 keV)
energy band assuming the best fit model for each quasar as in Table 10 are listed in
Table 11, together with the corresponding luminosities
corrected for both the Galactic absorption and (if present) the additional intrinsic warm/neutral
absorber column densities. The hard (soft) X-ray fluxes range from ![]() 0.1(0.1) to
0.1(0.1) to ![]() 80(45
80(45
![]() erg cm-2 s-1. With a 0.5-10 keV X-ray luminosity of
erg cm-2 s-1. With a 0.5-10 keV X-ray luminosity of ![]() 1043 erg s-1, 1001+054 is the faintest
object in the sample. The most luminous quasar in the hard (soft) band
is 1226+023 (1407+265) with a luminosity
of
1043 erg s-1, 1001+054 is the faintest
object in the sample. The most luminous quasar in the hard (soft) band
is 1226+023 (1407+265) with a luminosity
of ![]()
![]() erg s-1.
In the last two columns of Table 11 the ratios between the strength of the soft
excess and the high energy power law component in the 0.5-2 and 0.5-10 keV band are listed.
erg s-1.
In the last two columns of Table 11 the ratios between the strength of the soft
excess and the high energy power law component in the 0.5-2 and 0.5-10 keV band are listed.
Table 12:
Spearman-rank correlations among spectral parameters of the
soft excess tested models and X-ray parameters (luminosity and
![]() ). The displayed values are
(
). The displayed values are
(![]() ,
,
![]() ), where
), where ![]() is the rank correlation coefficient and
is the rank correlation coefficient and ![]() is the
significance probability. The significant (i.e. >95%) correlations
are marked in boldface (see text for details).
is the
significance probability. The significant (i.e. >95%) correlations
are marked in boldface (see text for details).
Table 13:
Spearman-rank correlations among X-ray observables and
the radio-loudness parameter ![]() ,
the redshift, the FWHM of the H
,
the redshift, the FWHM of the H![]() emission line, the black hole mass
emission line, the black hole mass
![]() and the accretion rate
and the accretion rate
![]() with respect to the Eddington rate. The displayed values are
(
with respect to the Eddington rate. The displayed values are
(![]() ,
,
![]() ), where
), where ![]() is the rank correlation coefficient and
is the rank correlation coefficient and
![]() is the significance probability. The significant (i.e. >95%)
correlations are marked in boldface (see text for details).
is the significance probability. The significant (i.e. >95%)
correlations are marked in boldface (see text for details).
We performed Spearman-rank correlation tests. This test calculates
how well a linear equation describes the relationship between two
variables by means of the rank correlation coefficient (![]() )
and the
probability (
)
and the
probability (![]() ). Positive(negative) values of
). Positive(negative) values of ![]() indicate that
the two quantities are (anti-)correlated, while
indicate that
the two quantities are (anti-)correlated, while ![]() gives the
significance level of such a correlation. In particular, we checked
the type and strength of the relationship among the representative
parameter of each model (i.e.
gives the
significance level of such a correlation. In particular, we checked
the type and strength of the relationship among the representative
parameter of each model (i.e.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
see Sect. 3.2) and
;
see Sect. 3.2) and
![]() ,
,
![]() ,
,
![]() and
and
![]() and
and
![]() (see
Tables 11 and 3). The corresponding results are listed in
Table 12.
(see
Tables 11 and 3). The corresponding results are listed in
Table 12.
This study reveals that none of the 20 pairs of parameters are
significantly (i.e. >99%) correlated.
Nevertheless, we found marginal hints of a non-trivial correlation for five of them, i.e.
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
Some of these correlations appear to be driven by the higher luminosity QSOs, L2-10 > 1045 erg s-1.
For those relationships with
.
Some of these correlations appear to be driven by the higher luminosity QSOs, L2-10 > 1045 erg s-1.
For those relationships with
![]() ,
we also performed a linear regression
fit to the data which, contrary to the Spearman-rank correlation test,
takes also into account the uncertainties associated to the measurements.
The values of
,
we also performed a linear regression
fit to the data which, contrary to the Spearman-rank correlation test,
takes also into account the uncertainties associated to the measurements.
The values of ![]() obtained for each fit revealed that
the probability that the two quantities are linearly correlated
is lower than 50%.
obtained for each fit revealed that
the probability that the two quantities are linearly correlated
is lower than 50%.
We also investigated by the Spearman-rank test the possible
correlations among the most representative X-ray observables inferred
from our analysis (i.e.
![]() ,
,
![]() ,
,
![]() and
and
![]() )
and some QSO physical characteristics, such as the
radio-loudness parameter
)
and some QSO physical characteristics, such as the
radio-loudness parameter ![]() ,
the redshift, the FWHM of the
H
,
the redshift, the FWHM of the
H![]() emission line, the black hole mass
emission line, the black hole mass
![]() ,
and the
accretion rate
,
and the
accretion rate ![]() relative to the Eddington
limit
relative to the Eddington
limit![]() (i.e.
(i.e.
![]() /
/
![]() ). The
results of the correlation analysis are presented in
Table 13. We report significant and
strong anticorrelations between the spectral indices
). The
results of the correlation analysis are presented in
Table 13. We report significant and
strong anticorrelations between the spectral indices
![]() and
and
![]() and
the H
and
the H![]() FWHM, confirming these well-known relationships found for
both QSO-like (Reeves & Turner 2000; P04; Laor et al. 1997) and Seyfert-like AGNs
(Brandt et al. 1997). As already obtained for a smaller
sample of PG QSOs by P04, the hard band slope also appears to
anticorrelate with the black hole mass and to correlate with the fractional accretion rate
FWHM, confirming these well-known relationships found for
both QSO-like (Reeves & Turner 2000; P04; Laor et al. 1997) and Seyfert-like AGNs
(Brandt et al. 1997). As already obtained for a smaller
sample of PG QSOs by P04, the hard band slope also appears to
anticorrelate with the black hole mass and to correlate with the fractional accretion rate ![]() .
The latter, furthermore, has been found to be inversely
linked with the
.
The latter, furthermore, has been found to be inversely
linked with the
![]() with a significance of
with a significance of
![]() ,
i.e. larger than in P04.
PG QSOs with small
,
i.e. larger than in P04.
PG QSOs with small
![]() tend to be less X-ray luminous. Laor (2000) pointed out
that nearly all the PG RLQs with
tend to be less X-ray luminous. Laor (2000) pointed out
that nearly all the PG RLQs with
![]() are radio-loud and
this could have caused a bias in our correlation analysis.
The (anti-)correlations between (
are radio-loud and
this could have caused a bias in our correlation analysis.
The (anti-)correlations between (
![]() )
)
![]() and
and
![]() still hold
when RLQs are excluded.
An interesting discovery yielded
by the present analysis is the very significant (
still hold
when RLQs are excluded.
An interesting discovery yielded
by the present analysis is the very significant (
![]() )
anticorrelation between the radio-loudness
)
anticorrelation between the radio-loudness ![]() and
and
![]() ,
i.e. the ratio between the strength of the soft
excess and the high energy power law component in the 0.5-10 keV
band. This seems to indicate that the soft excess emission in
RLQs is less prominent than in RQQs. However, a larger number of
objects with
,
i.e. the ratio between the strength of the soft
excess and the high energy power law component in the 0.5-10 keV
band. This seems to indicate that the soft excess emission in
RLQs is less prominent than in RQQs. However, a larger number of
objects with
![]() (i.e. radio-loud) is needed to
confirm the robustness of this relationship. Finally, no correlation
among the three X-ray observables and redshift was detected apart from
the trivial case (
(i.e. radio-loud) is needed to
confirm the robustness of this relationship. Finally, no correlation
among the three X-ray observables and redshift was detected apart from
the trivial case (
![]() ,
z) which is due to selection
effects. Figure 6 shows the plots corresponding to the very significant (i.e. at >99% confidence
level) non-trivial correlations found in our analysis.
,
z) which is due to selection
effects. Figure 6 shows the plots corresponding to the very significant (i.e. at >99% confidence
level) non-trivial correlations found in our analysis.
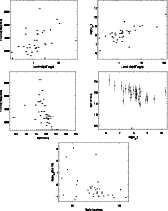 |
Figure 6:
Significant (i.e. at >99% confidence
level) correlations found among X-ray observables and QSO physical
properties (See Table 13 and text for
details). From top-left to bottom: a) FWHM(H |
| Open with DEXTER | |
In Sect. 3.1 we presented the results for the power law fit in
the high energy (2-12 keV) band for all the QSO. The ![]() analysis
shows that the fits are acceptable, i.e.
analysis
shows that the fits are acceptable, i.e.
![]() ,
in all but four
cases, i.e. 1411+442 (
,
in all but four
cases, i.e. 1411+442 (
![]() ); 1440+356
(
); 1440+356
(
![]() ); 1630+377 (
); 1630+377 (
![]() ); 2214+139
(
); 2214+139
(
![]() ). Except for 1630+377, absorption was
significantly detected in all these QSOs, being the most probable
cause for the poor quality of the fit. In the case of 1630+377, the
presence of an intense iron line could be responsible for the large
). Except for 1630+377, absorption was
significantly detected in all these QSOs, being the most probable
cause for the poor quality of the fit. In the case of 1630+377, the
presence of an intense iron line could be responsible for the large
![]() .
.
The mean value found for the index of the power law was
![]() and shows a significant
spread,
and shows a significant
spread,
![]() .
The mean photon index is in
good agreement with the results found from observations with
previous satellites. Reeves & Turner (2000) and
George et al. (2000) reported an average
.
The mean photon index is in
good agreement with the results found from observations with
previous satellites. Reeves & Turner (2000) and
George et al. (2000) reported an average
![]() and
and
![]() observing,
respectively, 27 and 26 RQQs with ASCA (we compare
observing,
respectively, 27 and 26 RQQs with ASCA (we compare
![]() with results from RQQ samples since RQQs
represent
with results from RQQ samples since RQQs
represent ![]() 90% of our objects). A higher value (but consistent with
ours within the statistical uncertainties) was derived
from BeppoSAX data of 10 QSOs, i.e.
90% of our objects). A higher value (but consistent with
ours within the statistical uncertainties) was derived
from BeppoSAX data of 10 QSOs, i.e.
![]() (Mineo et al. 2000). It has been observed in several studies
(Zamorani et al. 1981; Reeves & Turner 2000) that RLQs have flatter
spectral indices that RQQs. Our results confirm this trend with
these mean values for the photon indices:
(Mineo et al. 2000). It has been observed in several studies
(Zamorani et al. 1981; Reeves & Turner 2000) that RLQs have flatter
spectral indices that RQQs. Our results confirm this trend with
these mean values for the photon indices:
![]() and
and
![]() .
The
possible flatness of the spectral index for RLQs is consistent with a
different process being responsible for the emission in the two types
of QSO. While in RQQs the X-ray emission is thought to be associated
with Compton up-scattering of soft photons originating in the
accretion disk by hot electrons with a thermal distribution
probably located in a corona above the accretion disk (Haardt &
Maraschi 1993; Reeves & Turner 2000), in RLQs the effect of the
relativistic jet could play an important role in the X-ray emission
(Ghisellini et al. 1985; Reeves & Turner 2000). Even though
our results also show that the spectral index in RLQs is
flatter than in RQQs, a study of a large sample of RLQs observed with
ASCA (Sambruna et al. 1999) showed that if one compares RLQs and RQQs
which match in X-ray luminosity, there is no clear evidence of a
difference in the spectral slope of these two types of QSOs.
.
The
possible flatness of the spectral index for RLQs is consistent with a
different process being responsible for the emission in the two types
of QSO. While in RQQs the X-ray emission is thought to be associated
with Compton up-scattering of soft photons originating in the
accretion disk by hot electrons with a thermal distribution
probably located in a corona above the accretion disk (Haardt &
Maraschi 1993; Reeves & Turner 2000), in RLQs the effect of the
relativistic jet could play an important role in the X-ray emission
(Ghisellini et al. 1985; Reeves & Turner 2000). Even though
our results also show that the spectral index in RLQs is
flatter than in RQQs, a study of a large sample of RLQs observed with
ASCA (Sambruna et al. 1999) showed that if one compares RLQs and RQQs
which match in X-ray luminosity, there is no clear evidence of a
difference in the spectral slope of these two types of QSOs.
We note that our mean
![]() (see Table 9) is similar to that found by Laor et al. (1997), i.e.
(see Table 9) is similar to that found by Laor et al. (1997), i.e.
![]() .
Therefore
XMM-Newton EPIC results for the overall spectral shape of the QSOs appear to be
consistent with those from ROSAT PSPC and ASCA GIS/SIS
observations.
.
Therefore
XMM-Newton EPIC results for the overall spectral shape of the QSOs appear to be
consistent with those from ROSAT PSPC and ASCA GIS/SIS
observations.
Finally, a very significant (
![]() )
(anti-) correlation between
(
)
(anti-) correlation between
(
![]() )
)
![]() and the black hole mass was
found (e.g. P04 and Sect. 3.7). Moreover, both
these relationships still hold if only RQQs are considered. This
points to the possibility that the black hole mass could play a major
role in the definition of the hard X-ray properties in a
QSO. Interestingly, a similar suggestion is reported by Laor (2000)
who found a clear bimodality in the radio-loudness distribution as
a function of the
and the black hole mass was
found (e.g. P04 and Sect. 3.7). Moreover, both
these relationships still hold if only RQQs are considered. This
points to the possibility that the black hole mass could play a major
role in the definition of the hard X-ray properties in a
QSO. Interestingly, a similar suggestion is reported by Laor (2000)
who found a clear bimodality in the radio-loudness distribution as
a function of the
![]() in the PG sample. These results can
provide new insights in the ultimate driver of
the AGN activity.
in the PG sample. These results can
provide new insights in the ultimate driver of
the AGN activity.
The systematic modeling of the 0.3-12 keV emission by different two-component continua presented in Sect. 3.2 allows us to draw useful conclusions on the physical nature of the soft excess.
Note the ubiquity of such a soft excess component: we
detected a low-energy X-ray turn-up in 37 out of 40 QSOs![]() . Previous studies based on ASCA
(George et al. 2000; Reeves & Turner 2000) and BeppoSAX (Mineo
et al. 2000) QSO samples reported the detection of an excess of
emission with respect to the high energy power law below 1-1.5 keV
in
. Previous studies based on ASCA
(George et al. 2000; Reeves & Turner 2000) and BeppoSAX (Mineo
et al. 2000) QSO samples reported the detection of an excess of
emission with respect to the high energy power law below 1-1.5 keV
in ![]() 50-60% of the objects. However, as pointed out by these
authors, one should bear in mind the limited statistics (in the
case of some BeppoSAX exposures) and the limited bandpass
(0.6-10 keV in the case of ASCA) affecting these observations.
50-60% of the objects. However, as pointed out by these
authors, one should bear in mind the limited statistics (in the
case of some BeppoSAX exposures) and the limited bandpass
(0.6-10 keV in the case of ASCA) affecting these observations.
All the models applied to account for the soft excess component (i.e. blackbody, multicolor blackbody, bremsstrahlung and a power law) provided a statistically acceptable description of the broad-band X-ray spectrum for the majority of QSOs. In the following we discuss our results in the light of the physical scenario assumed in each tested model.
To first order approximation, the emission from a standard
optically-thick accretion disk can be modeled by a blackbody or a
multicolor blackbody components. The
![]() values obtained by
the application of these two models reveal that these
parameterizations give a fair representation of the EPIC QSO
spectra (e.g. Tables 5 and 6). Nevertheless, the
observed values of
values obtained by
the application of these two models reveal that these
parameterizations give a fair representation of the EPIC QSO
spectra (e.g. Tables 5 and 6). Nevertheless, the
observed values of
![]() and
and
![]() keV exceed
the maximal temperature for an accretion disk (e.g. Frank et al. 1992, for a review) which is
keV exceed
the maximal temperature for an accretion disk (e.g. Frank et al. 1992, for a review) which is
![]() eV for a
black hole mass of 10
eV for a
black hole mass of 10
![]() accreting at the
Eddington rate. Furthermore,
accreting at the
Eddington rate. Furthermore,
![]() is an upper limit to
the disk temperature since the accretion could be sub-Eddington
and/or outer parts of the disk would likely be cooler. Hence, the
mean values shown in Table 9 for the
temperatures of a blackbody (
is an upper limit to
the disk temperature since the accretion could be sub-Eddington
and/or outer parts of the disk would likely be cooler. Hence, the
mean values shown in Table 9 for the
temperatures of a blackbody (
![]() )
and a multicolor
blackbody (
)
and a multicolor
blackbody (
![]() )
argue that these models must be considered
just as phenomenological and not as physically consistent
models. Such an "optically-thick'' scenario is even more critical
in those quasars with a double blackbody component as the best fit for
the soft excess. In fact, they show a soft energy feature too broad
to be fitted by a single temperature blackbody and,
consequently, the second blackbody component usually has an
unrealistic
)
argue that these models must be considered
just as phenomenological and not as physically consistent
models. Such an "optically-thick'' scenario is even more critical
in those quasars with a double blackbody component as the best fit for
the soft excess. In fact, they show a soft energy feature too broad
to be fitted by a single temperature blackbody and,
consequently, the second blackbody component usually has an
unrealistic
![]() keV.
keV.
The soft X-ray emission of starburst regions (SBRs) is known to be
dominated by the emission from a one- or multi-component hot
diffuse plasma at temperatures in the range of
![]() keV
(Ptak et al. 1999; Read & Ponman 2001; Strickland & Stevens 2000).
This thermal emission can be represented by a bremsstrahlung model.
We found that this model is an appropriate fit
(
keV
(Ptak et al. 1999; Read & Ponman 2001; Strickland & Stevens 2000).
This thermal emission can be represented by a bremsstrahlung model.
We found that this model is an appropriate fit
(
![]() )
to the soft excess emission of an important
fraction of the objects in the sample (i.e. 28 out of 37 QSOs),
and is the best fit model for 8 sources. The mean temperature for
the bremsstrahlung model obtained for the 28 objects of our
sample,
)
to the soft excess emission of an important
fraction of the objects in the sample (i.e. 28 out of 37 QSOs),
and is the best fit model for 8 sources. The mean temperature for
the bremsstrahlung model obtained for the 28 objects of our
sample,
![]() keV, is compatible with typical
values in SBRs. The diffuse gas associated to the soft X-ray
emission of the SBRs typically has abundances in the range
0.05-0.3 Z
keV, is compatible with typical
values in SBRs. The diffuse gas associated to the soft X-ray
emission of the SBRs typically has abundances in the range
0.05-0.3 Z![]() (Ptak et al. 1999; Read & Ponman 2001).
However, the bremsstrahlung model does not include any emission
lines and therefore it is not possible to measure the abundances of
the diffuse gas and test if they are compatible with the typical
ones measured in SBRs. In order to determine these abundances, we
fitted the spectra of the eight sources for which the bremsstrahlung
model is the best fit for their soft excess emission with
the MEKAL model (Mewe et al. 1986) leaving the abundances as
a free parameter. The resulting values of the abundances were in all
cases consistent with zero with upper limits in the range
0.011-0.15 Z
(Ptak et al. 1999; Read & Ponman 2001).
However, the bremsstrahlung model does not include any emission
lines and therefore it is not possible to measure the abundances of
the diffuse gas and test if they are compatible with the typical
ones measured in SBRs. In order to determine these abundances, we
fitted the spectra of the eight sources for which the bremsstrahlung
model is the best fit for their soft excess emission with
the MEKAL model (Mewe et al. 1986) leaving the abundances as
a free parameter. The resulting values of the abundances were in all
cases consistent with zero with upper limits in the range
0.011-0.15 Z![]() .
Except for two objects, 1634+706 with
.
Except for two objects, 1634+706 with
![]()
![]() and 2303+029 with
and 2303+029 with
![]()
![]() ,
the abundances
are therefore lower than the typical values observed in SBRs.
Moreover, in the soft band, the X-ray luminosities of SBRs vary in
the range of
1038-41 erg s-1 (Ptak et al. 1999; Read & Ponman
2001) while the luminosities associated to the optically thin soft
X-ray component for these 8 QSOs are in all cases above
,
the abundances
are therefore lower than the typical values observed in SBRs.
Moreover, in the soft band, the X-ray luminosities of SBRs vary in
the range of
1038-41 erg s-1 (Ptak et al. 1999; Read & Ponman
2001) while the luminosities associated to the optically thin soft
X-ray component for these 8 QSOs are in all cases above
![]() erg s-1, and, therefore, two orders of magnitude
larger than the typical SBRs values, even considering extreme cases such as
Ultra-Luminous Infrared Galaxies (Franceschini et al. 2003).
Hence,
on the basis of the abundances and luminosities inferred for our QSOs,
it is very unlikely that the bremsstrahlung emission could be
associated to powerful emission from a starburst region.
erg s-1, and, therefore, two orders of magnitude
larger than the typical SBRs values, even considering extreme cases such as
Ultra-Luminous Infrared Galaxies (Franceschini et al. 2003).
Hence,
on the basis of the abundances and luminosities inferred for our QSOs,
it is very unlikely that the bremsstrahlung emission could be
associated to powerful emission from a starburst region.
Even if (at the moment) quite speculative, another possible physical
interpretation for the bremsstrahlung model is the emission from a
transition layer between the accretion disk and the corona, as
proposed by Nayakshin et al. (2000). These authors indeed suggested
that in the case of sources with SED dominated by the UV thermal disk
emission (such as the present PG QSOs) bremsstrahlung emission from such a
layer could significantly contribute to the soft X-ray emission in
AGNs and also a plasma temperature of ![]() 0.4 keV should be
observed.
0.4 keV should be
observed.
Alternatively, the bremsstrahlung model can be interpreted, in a similar way as the blackbody and multicolor blackbody models, as a purely mathematical parametrization of the QSO continuum (e.g. Fiore et al. 1995).
The power law is also, obviously, just a functional form to describe
the true soft excess emission, without any underlying specific
physical scenario. For six QSOs in the sample the power law
model gave the best fit. Notably, two QSOs (i.e.
0804+761 and 1440+356) show a particularly flat slope of the high energy power
law (
![]() and
and
![]() ,
respectively, but note
the large errors). Furthermore both
,
respectively, but note
the large errors). Furthermore both
![]() are very
marginally (or not) consistent with the
are very
marginally (or not) consistent with the
![]() measured
for these QSOs, suggesting the presence of a hard tail
instead of a soft excess. Such a hard X-ray feature could also be
related to a strong reflection component (or/and a peculiar
variability behavior) which cannot be constrained due to
limited EPIC bandpass. However, such a scenario seems to be
unlikely for these QSOs because of the lack of a strong iron line in
their spectra (not detected in 1440+356 and with an
measured
for these QSOs, suggesting the presence of a hard tail
instead of a soft excess. Such a hard X-ray feature could also be
related to a strong reflection component (or/and a peculiar
variability behavior) which cannot be constrained due to
limited EPIC bandpass. However, such a scenario seems to be
unlikely for these QSOs because of the lack of a strong iron line in
their spectra (not detected in 1440+356 and with an ![]() eV
in 0804+76; see Paper II). Interestingly both these QSOs are
classified as Narrow Line Quasars (Osterbrock & Pogge 1985), a
class of objects that usually show extreme flux variations,
steep X-ray slopes and very strong soft excess extending up to
eV
in 0804+76; see Paper II). Interestingly both these QSOs are
classified as Narrow Line Quasars (Osterbrock & Pogge 1985), a
class of objects that usually show extreme flux variations,
steep X-ray slopes and very strong soft excess extending up to ![]() 3 keV in some cases (e.g. O'Brien et al. 2001). This also seems
the case for 1440+356 where such a spectral component
dominates the broad band X-ray luminosity (e.g.
Table 11).
3 keV in some cases (e.g. O'Brien et al. 2001). This also seems
the case for 1440+356 where such a spectral component
dominates the broad band X-ray luminosity (e.g.
Table 11).
Comptonization of thermal disk emission has been suggested as a likely
physical origin of the soft excess in the X-ray spectra of type 1
AGNs. The electron population responsible for the up-scattering is
thought to have a lower temperature (typically from 0.1 to few keVs)
than the population producing the observed hard X-ray emission
(approximatively a power law in the 2-10 keV band) with a
![]() keV (Perola et al. 2002). The exact location of such an
electron population is still an open issue: a warm skin on the disk
surface (Rozanska 1999), a transition between a cold and a hot disk
(Magdziarz et al. 1998), or a single hybrid non-thermal/thermal
plasma (Vaughan et al. 2002 and reference therein) are the most viable
candidates. Interestingly, this soft X-ray component would contain
the bulk of the bolometric luminosity of the source.
keV (Perola et al. 2002). The exact location of such an
electron population is still an open issue: a warm skin on the disk
surface (Rozanska 1999), a transition between a cold and a hot disk
(Magdziarz et al. 1998), or a single hybrid non-thermal/thermal
plasma (Vaughan et al. 2002 and reference therein) are the most viable
candidates. Interestingly, this soft X-ray component would contain
the bulk of the bolometric luminosity of the source.
According to this scenario, recent studies (P04; Gierlinski & Done
2004) indeed modeled the soft X-ray excess of PG QSOs by a "cool''
Compton-scattering medium. This fit successfully reproduces the QSO spectral shape. However, the typical value found for the electron
temperature is
![]() a few hundred eVs, with a very small range
of variation through the broad distribution in luminosity and
black hole mass within the sample.
As pointed out by different authors (Brinkmann et al. 2004b; Page et al. 2004b; P04) the major problem with the Comptonization fit is the
limited bandpass of XMM-Newton that does not allow to adequately constrain
either the blackbody emission from the disk or the exponential
cut-off at high energy. So a plausible explanation for the observed
narrow range of
a few hundred eVs, with a very small range
of variation through the broad distribution in luminosity and
black hole mass within the sample.
As pointed out by different authors (Brinkmann et al. 2004b; Page et al. 2004b; P04) the major problem with the Comptonization fit is the
limited bandpass of XMM-Newton that does not allow to adequately constrain
either the blackbody emission from the disk or the exponential
cut-off at high energy. So a plausible explanation for the observed
narrow range of
![]() values is an observational bias due to the
lack of sensitivity below 0.3 keV in the EPIC data. Furthermore, as
pointed out by P04, the inferred values of
values is an observational bias due to the
lack of sensitivity below 0.3 keV in the EPIC data. Furthermore, as
pointed out by P04, the inferred values of
![]() imply an extreme
compactness of the Comptonizing region, i.e. 0.1 gravitational radii
(
imply an extreme
compactness of the Comptonizing region, i.e. 0.1 gravitational radii
(![]() 1012 cm). This size is difficult to explain even in a
scenario where the hard X-ray continuum is thought to be produced in
discrete magnetic flares (instead of an extended corona) above the
accretion disk (e.g. Merloni & Fabian 2002, for a review).
Nevertheless, Comptonization seems the most realistic interpretation
of the soft excess in QSOs. Unfortunately, the
spectral capabilities of Chandra and XMM-Newton are not sufficient
to disentangle the well-known degeneracy between the
1012 cm). This size is difficult to explain even in a
scenario where the hard X-ray continuum is thought to be produced in
discrete magnetic flares (instead of an extended corona) above the
accretion disk (e.g. Merloni & Fabian 2002, for a review).
Nevertheless, Comptonization seems the most realistic interpretation
of the soft excess in QSOs. Unfortunately, the
spectral capabilities of Chandra and XMM-Newton are not sufficient
to disentangle the well-known degeneracy between the
![]() and the
optical depth of the scattering plasma (e.g. Vaughan et al. 2002;
Brinkmann et al. 2004b). EUV to very hard X-rays (i.e. a few hundred keV) broad band observations can help to solve
this issue.
and the
optical depth of the scattering plasma (e.g. Vaughan et al. 2002;
Brinkmann et al. 2004b). EUV to very hard X-rays (i.e. a few hundred keV) broad band observations can help to solve
this issue.
Gierlinski & Done (2004) suggested interpreting the soft excess
in RQQs as an artifact of unmodeled relativistically smeared
partially ionized absorption because strong O and Fe absorption features at 0.7-0.9 keV can lead to an apparent upward
curvature below these energies, mimicking the presence of a true soft
excess component. This scenario predicts a very steep (
![]() )
intrinsic continuum slope in the hard X-ray band (i.e. >10 keV) for RQQs. However, such large values of the intrinsic photon index
(i.e. corrected for both reflection and absorption) have
not been observed neither by BeppoSAX or Ginga
observations (e.g. Mineo et al. 2000; and Lawson & Turner 1997,
respectively). Nonetheless, even if not in such a dramatic way, broad
"warm'' absorption features due to atomic transitions could have some effect
on the estimate of the real slope of the primary
continuum emission. More sensitive high-energy spectroscopic
studies carried out in the near future with Astro-E2 or Constellation-X will make a definitive test of this hypothesis possible.
)
intrinsic continuum slope in the hard X-ray band (i.e. >10 keV) for RQQs. However, such large values of the intrinsic photon index
(i.e. corrected for both reflection and absorption) have
not been observed neither by BeppoSAX or Ginga
observations (e.g. Mineo et al. 2000; and Lawson & Turner 1997,
respectively). Nonetheless, even if not in such a dramatic way, broad
"warm'' absorption features due to atomic transitions could have some effect
on the estimate of the real slope of the primary
continuum emission. More sensitive high-energy spectroscopic
studies carried out in the near future with Astro-E2 or Constellation-X will make a definitive test of this hypothesis possible.
On the basis of RGS observations Branduardi-Raymond et al. (2001) proposed to explain the observed soft excess in the Seyfert
galaxies MKN 766 and MCG-6-30-15 in terms of strong relativistically
broadened recombination H-like emission lines of O, N and C. However,
as pointed out by Pounds & Reeves (2002), all the objects for which
this interpretation seems to be feasible have a low X-ray luminosity
(i.e.
![]() erg s-1) and their soft excess component
emerges very sharply below
erg s-1) and their soft excess component
emerges very sharply below ![]() 0.7 keV from the extrapolation of
the 2-10 keV power law. On the contrary, all the soft excesses
observed in PG QSOs turn up smoothly below
0.7 keV from the extrapolation of
the 2-10 keV power law. On the contrary, all the soft excesses
observed in PG QSOs turn up smoothly below ![]() 2 keV. So this soft
X-ray broad emission lines scenario seems to fail for the sources
(which all have
2 keV. So this soft
X-ray broad emission lines scenario seems to fail for the sources
(which all have
![]() erg s-1) in our sample.
erg s-1) in our sample.
Finally, the finding of an anticorrelation between ![]() and
and
![]() (see Table 13) seems to
support the hypothesis that the soft excess in radio-loud QSOs is
due to an X-ray emission component originating in the jets.
(see Table 13) seems to
support the hypothesis that the soft excess in radio-loud QSOs is
due to an X-ray emission component originating in the jets.
In order to study the presence of a cold absorber in QSOs, we have
added a neutral absorption component to the different models tested.
The analysis reveals that the majority of the spectra does not
require this component, and that the equivalent hydrogen column is
negligible in comparison with the Galactic one. Only three
sources, all of them RQQs, show the presence of a cold
absorber, i.e. 0050+124, 1115+080 and 1411+442. The
former two have columns of ![]()
![]() cm-2, likely
associated to their host galaxies. The strongest absorption
was found for 1411+442,
cm-2, likely
associated to their host galaxies. The strongest absorption
was found for 1411+442, ![]() =
=
![]() cm-2, although because of the low statistic of the data it is
not possible to confirm if this feature originates from cold
absorption or is indeed related to a warm absorber. The rarity of
intrinsic neutral absorption observed here is in agreement with
previous studies of optically-selected QSOs (Laor et al. 1997; Mineo
et al. 2000) and, in general, with the findings of recent
wide-angle deep XMM-Newton surveys (e.g. Barcons et al. 2002;
Piconcelli et al. 2003; Caccianiga et al. 2004)
which reported a small fraction of
broad line AGNs with a significant cold absorption component in excess
of the Galactic value.
cm-2, although because of the low statistic of the data it is
not possible to confirm if this feature originates from cold
absorption or is indeed related to a warm absorber. The rarity of
intrinsic neutral absorption observed here is in agreement with
previous studies of optically-selected QSOs (Laor et al. 1997; Mineo
et al. 2000) and, in general, with the findings of recent
wide-angle deep XMM-Newton surveys (e.g. Barcons et al. 2002;
Piconcelli et al. 2003; Caccianiga et al. 2004)
which reported a small fraction of
broad line AGNs with a significant cold absorption component in excess
of the Galactic value.
Therefore, we can conclude that for PG QSOs there is a good correlation between optical spectral type and X-ray absorption properties, in agreement with the predictions of the AGN Unification Models.
Warm (i.e. partially ionized) absorbers in active galaxies
are revealed by the presence of absorption edges in their soft X-ray
spectra (Pan et al. 1990). In particular, OVII (0.739 keV) and OVIII (0.871 keV) absorption edges were the typical
signatures of such ionized gas detected in ROSAT and ASCA
low-resolution observations. Notably, Reynolds (1997) found a warm
absorber in ![]() 50% of the well studied Seyfert galaxies.
50% of the well studied Seyfert galaxies.
The study of this spectral component took a remarkable step forward owing to the higher resolution (R> 100) of the grating spectrometers on-board XMM-Newton and Chandra. H- and He-like absorption lines of cosmically abundant elements such as C, O, Ne, Mg and Si are the most numerous and strongest features observed in the soft X-ray spectra of bright Seyfert 1 galaxies. The presence between 0.73 and 0.77 keV of the unresolved transition array (UTA, e.g. Behar et al. 2001) of iron M-shell ions is also particularly common. The X-ray absorption lines are typically blueshifted by a few hundred km s-1 and show complex profiles due to a wealth of kinematic components. The ionized material is therefore in an outflow and it generally shows multiple ionization states (Kaastra et al. 2000; Collinge et al. 2001; Piconcelli et al. 2004).
On the contrary, the properties of the warm absorber in QSOs are
poorly known so far. Nonetheless, it is widely accepted that the
presence of ionized absorbing gas in such high luminosity AGNs is not
as common as in Seyfert galaxies. Laor et al. (1997) indeed detected
it in ![]() 5% of the optically selected QSO population, and, on
the basis of a large ASCA sample, Reeves & Turner (2000) and
George et al. (2000) both confirmed the rare occurrence in their
spectra of opacity due to ionized gas along the line of sight. Bearing
in mind the limited statistics, George et al. (2000) did not find,
however, significant differences in the physical parameters of the
warm absorber (i.e. ionization state and column density) in low and
high luminosity AGNs.
5% of the optically selected QSO population, and, on
the basis of a large ASCA sample, Reeves & Turner (2000) and
George et al. (2000) both confirmed the rare occurrence in their
spectra of opacity due to ionized gas along the line of sight. Bearing
in mind the limited statistics, George et al. (2000) did not find,
however, significant differences in the physical parameters of the
warm absorber (i.e. ionization state and column density) in low and
high luminosity AGNs.
The scenario emerging from our analysis is completely different. In fact, we significantly detect absorption features due to ionized gas in the spectra of 18 out 40 QSOs, i.e. the 45% of the sample. This fraction is similar to what is found for Seyfert galaxies. The detection rate of warm absorbers appears therefore to be independent of the X-ray luminosity. This confirms the recent result of P04 based on a smaller sample of 21 QSOs observed by XMM-Newton, and puts it on a sounder statistical ground.
As reported in Sect. 3.4 most of these absorption
features are observed in the range 0.7-0.8 keV: this suggests
that they are likely due to the He-like O edge and/or the blend of
M-shell Fe lines (UTA). In the case of the edges found in the
high-energy portion of the spectrum around 7 keV (as in 1115+080,
1211+143 and 1226+023), the energy of these features is still
consistent with an origin in "neutral'' material (i.e. FeI-V). So an
alternative explanation in terms of reflection from the optically
thick accretion disk cannot be ruled out. The edge detected at ![]() 9 keV in 1115+08 would imply an ionization state higher than FeXXVI, so the possible origin of this feature in an ionized outflow
(with a velocity of 0.34c to account for the observed blueshift) as
proposed by Chartas et al. (2003) seems to be the most reasonable.
9 keV in 1115+08 would imply an ionization state higher than FeXXVI, so the possible origin of this feature in an ionized outflow
(with a velocity of 0.34c to account for the observed blueshift) as
proposed by Chartas et al. (2003) seems to be the most reasonable.
Because of the strength of the absorption features in their spectra, for 4 objects (i.e. 1001+054, 1114+445, 1404+226 and 2214+139) we could apply the ABSORI model in the fit and, consequently, derive some physical parameters of the warm absorber in these sources (see Table 10). For 2214+139 and the BAL QSO 1001+054 the inferred column densities of the ionized gas are larger than 1023 cm-2, i.e. among the highest seen by XMM-Newton and Chandra so far. Even more interesting are the results we report for 1114+445 and 2214+139. Their XMM-Newton spectra indeed show for the first time evidence for a multi-zone warm absorber in both QSOs.
These findings agree with the recent results obtained for Seyfert galaxies which claim a multiphase outflowing plasma as origin of the warm absorber. Unfortunately, because of the EPIC spectral resolution, we cannot draw any conclusion on the ionization structure (i.e. discrete or continuous) of the ionized wind.
All the QSOs in our sample classified as "Soft X-ray Weak'' QSOs
(SXWQs) by Brandt et al. (2000) (namely 1001+054,
1411+442 and 2214+139) have been found to be heavily absorbed.
This finding supports the hypothesis that the observed soft X-ray
"weakness'' of SXWQs is likely due to the presence of absorbing
matter along the line of sight instead of an "intrinsic'' weakness due
to a different SED and/or emission/accretion mechanisms at work in
SXWQs with respect to "normal'' QSOs. Furthermore, all SXWQs
analyzed here also show prominent absorption lines in the UV and in 2
out of 3 SXWQs the absorption occurs in an ionized gas![]() .
These results support the idea of a possible physical connection between UV and X-ray absorbers (Crenshaw et al. 2003).
.
These results support the idea of a possible physical connection between UV and X-ray absorbers (Crenshaw et al. 2003).
We have presented the results of the spectral analysis of 40 QSOs
EPIC spectra observed by XMM-Newton. These objects represent ![]() 45%
of the complete PG QSOs sample. The main findings of our study are:
45%
of the complete PG QSOs sample. The main findings of our study are:
Acknowledgements
The authors wish to thank the referee, Dr. James Reeves, for the prompt and encouraging report and the useful comments, which have significantly improved the paper. We also would to thank the XMM-Newton SOC science support team members at ESAC. This paper is based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and the USA (NASA). This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
Table 2: Journal of observations.
Table 3: Spectral fitting results. I: power law model applied to the hard band (2-12 keV). 1001+054 is excluded due to the very poor statistics in this energy range.
Table 4: Spectral fitting results. II: power law model (model PL) applied to the 0.3-12 keV band.
Table 5: Spectral fitting results. III: power law plus blackbody model for the soft excess component (model A).
Table 6: Spectral fitting results. IV: power law plus multi-color blackbody model for the soft excess component (model B).
Table 7: Spectral fitting results. V: power law plus bremsstrahlung model for the soft excess (model C).
Table 8: Spectral fitting results. VI: double power law (model D).
Table 10:
Spectral fitting results. VII: best fit model. A: bb; B: diskbb; C:
brems; D: power law; E: double bb; F: absori; G: double absori + bb; H: partial-covering
(cold)+raymond-smith; I: partial-covering(warm)+emission line;
J: absori+bb; PL: simple power law. Models with * include an
additional cold absorption component. All but one (i.e. model PL) models
also include a power law component. For the results concerning the Fe K![]() line see Paper II.
line see Paper II.