A&A 432, 117-138 (2005)
DOI: 10.1051/0004-6361:20041114
On the lifetime of metastable states in self-gravitating systems
P. H. Chavanis
Laboratoire de Physique Théorique, Université Paul
Sabatier, 118 route de Narbonne, 31062 Toulouse, France
Received 17 April 2004 / Accepted 3 November 2004
Abstract
We discuss the physical basis of the statistical
mechanics of self-gravitating systems. We show the correspondance
between statistical mechanics methods based on the evaluation of
the density of states and partition function and thermodynamical
methods based on the optimization of a thermodynamical potential
(entropy or free energy). We address the question of the
thermodynamic limit of self-gravitating systems, the justification
of the mean-field approximation, the validity of the saddle point
approximation near the transition point, the lifetime of metastable
states and the fluctuations in isothermal spheres. In particular,
we emphasize the tremendously long lifetime of metastable states of
self-gravitating systems which increases exponentially with the
number of particles N except in the vicinity of the critical
point. More specifically, using an adaptation of the Kramers
formula justified by a kinetic theory, we show that the lifetime of
a metastable state scales as
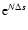 in microcanonical
ensemble and
in microcanonical
ensemble and
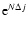 in canonical ensemble, where
in canonical ensemble, where 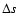 and
and 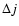 are the barriers of entropy and free energy
are the barriers of entropy and free energy
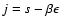 per particle respectively. The physical
caloric curve must take these metastable states (local entropy
maxima) into account. As a result, it becomes multi-valued and
leads to microcanonical phase transitions and "dinosaur's necks''
(Chavanis 2002b, [arXiv:astroph/0205426]; Chavanis & Rieutord 2003, A&A, 412, 1). The consideration of
metastable states answers the critics raised by D.H.E. Gross
[cond-mat/0307535/0403582].
per particle respectively. The physical
caloric curve must take these metastable states (local entropy
maxima) into account. As a result, it becomes multi-valued and
leads to microcanonical phase transitions and "dinosaur's necks''
(Chavanis 2002b, [arXiv:astroph/0205426]; Chavanis & Rieutord 2003, A&A, 412, 1). The consideration of
metastable states answers the critics raised by D.H.E. Gross
[cond-mat/0307535/0403582].
Key words: gravitation - stellar dynamics - globular clusters: general - methods: miscellaneous
1 Introduction
The statistical mechanics of self-gravitating systems has a long
history starting with the seminal papers of Antonov (1962) and
Lynden-Bell & Wood (1968). A statistical mechanics approach is
particularly relevant to describe the late stages of "small'' groups
of stars (
 ), such as globular clusters, which evolve
under the influence of stellar encounters ("collisional''
relaxation). Apart from astrophysical applications, the statistical
mechanics of stellar systems is of great interest in physics because
it differs in many respects from that of more familiar systems with
short-range interactions (Padmanabhan 1990; Chavanis 2002c). In
particular, for systems with long-range interactions, the
thermodynamical ensembles are not equivalent, negative specific heats
are allowed in the microcanonical ensemble (but not in the canonical
ensemble) and metastable equilibrium states can have tremendously long
lifetimes making them of considerable interest.
), such as globular clusters, which evolve
under the influence of stellar encounters ("collisional''
relaxation). Apart from astrophysical applications, the statistical
mechanics of stellar systems is of great interest in physics because
it differs in many respects from that of more familiar systems with
short-range interactions (Padmanabhan 1990; Chavanis 2002c). In
particular, for systems with long-range interactions, the
thermodynamical ensembles are not equivalent, negative specific heats
are allowed in the microcanonical ensemble (but not in the canonical
ensemble) and metastable equilibrium states can have tremendously long
lifetimes making them of considerable interest.
Two types of approaches have been developed to determine the
statistical equilibrium state of a self-gravitating system. In the
thermodynamical approach, one determines the most probable
distribution of particles by maximizing the Boltzmann entropy at fixed
mass and energy in the microcanonical ensemble or by minimizing the
free energy F=E-TS at fixed mass and temperature in the canonical
ensemble (Lynden-Bell & Wood 1968; Katz 1978; Chavanis 2002a). This
approach is the simplest and the most illuminating. In addition, it is
directly related to kinetic theories (based on the Landau or on the
Fokker-Planck equation) for which the Boltzmann entropy (or the
Boltzmann free energy) plays the role of a Lyapunov functional and
satisfies a H-theorem. Alternatively, in the statistical
mechanics approach, one starts from the density of states or
partition function, transforms it into a functional integral and uses
a saddle point approximation valid in a properly defined thermodynamic
limit (Horwitz & Katz 1978; de Vega & Sanchez 2002; Katz 2003).
In the first part of this paper, we discuss the connexion between
these two procedures. We remain at a heuristic level, stressing more
the physical ideas than the mathematical formalism. In
Sect. 2, we introduce the entropy by a combinatorial
analysis. In order to regularize the problem at short distances, we
consider either the case of self-gravitating fermions or the case of
self-gravitating particles with a soften potential. We also discuss
the thermodynamic limit of the classical and quantum self-gravitating
gas. In Sect. 3, we show the relation between the
density of states g(E) and the entropy functional S[f] and between
the partition function 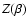 and the free energy functional
and the free energy functional
![$J[f]=S[f]-\beta E[f]$](/articles/aa/full/2005/10/aa1114/img31.gif) .
In the thermodynamic limit, the saddle point
approximation amounts to maximizing the entropy at fixed mass and
energy (microcanonical ensemble) or to minimizing the free energy at
fixed mass and temperature (canonical ensemble). In
Sect. 4, we discuss the notion of canonical and
microcanonical phase transitions in self-gravitating systems. We
perform the (standard) horizontal and (less standard) vertical Maxwell
constructions and discuss the validity of the saddle point
approximation near the transition point for finite N systems. These
results (e.g., microcanonical first order phase transitions) are
relatively new in statistical mechanics and still subject to
controversy (Gross 2003, 2004). Therefore, we provide a relatively
detailed discussion of these issues.
.
In the thermodynamic limit, the saddle point
approximation amounts to maximizing the entropy at fixed mass and
energy (microcanonical ensemble) or to minimizing the free energy at
fixed mass and temperature (canonical ensemble). In
Sect. 4, we discuss the notion of canonical and
microcanonical phase transitions in self-gravitating systems. We
perform the (standard) horizontal and (less standard) vertical Maxwell
constructions and discuss the validity of the saddle point
approximation near the transition point for finite N systems. These
results (e.g., microcanonical first order phase transitions) are
relatively new in statistical mechanics and still subject to
controversy (Gross 2003, 2004). Therefore, we provide a relatively
detailed discussion of these issues.
In the second part of the paper, we emphasize the importance of
metastable states in astrophysics and show how they can be taken
into account in the statistical approach. In Sect. 5, we use the Kramers formula to estimate the lifetime of a metastable state. We show that the lifetime of a
metastable state scales as
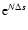 in microcanonical
ensemble and
in microcanonical
ensemble and
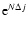 in canonical ensemble, where
in canonical ensemble, where 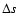 and
and 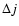 are the barriers of entropy and free energy
are the barriers of entropy and free energy
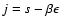 per particle respectively. Therefore, the
typical lifetime of a metastable state scales as
per particle respectively. Therefore, the
typical lifetime of a metastable state scales as
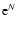 except in
the vicinity of the critical point
except in
the vicinity of the critical point 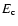 (Antonov energy) or
(Antonov energy) or 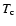 (Emden-Jeans temperature). We explicitly compute the barriers of
entropy and free energy close to the critical point for classical
self-gravitating particles (stars). The very long lifetime of
metastable states, scaling as
(Emden-Jeans temperature). We explicitly compute the barriers of
entropy and free energy close to the critical point for classical
self-gravitating particles (stars). The very long lifetime of
metastable states, scaling as
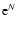 ,
was pointed out by Chavanis
& Rieutord (2003) and the difficulty of a stellar system to overcome
the entropic barrier and collapse was qualitatively discussed in
Chavanis & Sommeria (1998). We here improve these arguments by
developing a theory of fluctuations in isothermal spheres, following
the approach of Katz & Okamoto (2000). We also determine how
finite N effects affect the collapse temperature and the
collapse energy. Finally, in Sect. 6, we derive
a Fokker-Planck equation for the evolution of the distribution of
energies P(E,t) in the canonical ensemble and make contact with
the standard Kramers problem. We determine the typical lifetime of
a metastable state by calculating the escape time accross a
barrier of free energy.
,
was pointed out by Chavanis
& Rieutord (2003) and the difficulty of a stellar system to overcome
the entropic barrier and collapse was qualitatively discussed in
Chavanis & Sommeria (1998). We here improve these arguments by
developing a theory of fluctuations in isothermal spheres, following
the approach of Katz & Okamoto (2000). We also determine how
finite N effects affect the collapse temperature and the
collapse energy. Finally, in Sect. 6, we derive
a Fokker-Planck equation for the evolution of the distribution of
energies P(E,t) in the canonical ensemble and make contact with
the standard Kramers problem. We determine the typical lifetime of
a metastable state by calculating the escape time accross a
barrier of free energy.
2 The most probable distribution
2.1 The Fermi-Dirac distribution
We consider a system of N particles confined within a spherical box
of radius R and interacting via Newtonian gravity. Let
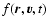 denote the distribution function of the system, i.e.
denote the distribution function of the system, i.e.
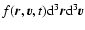 gives the mass of particles whose position and velocity are in the cell
gives the mass of particles whose position and velocity are in the cell
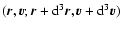 at time t. The
integral of f over the velocity determines the spatial density
at time t. The
integral of f over the velocity determines the spatial density
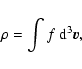 |
(1) |
and the total mass of the configuration is given by
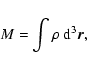 |
(2) |
where the integral extends over the entire domain. On the other hand,
in the meanfield approximation, the total energy of the system can be
expressed as
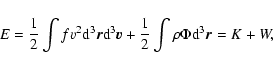 |
(3) |
where K is the kinetic energy and W the potential energy. The
meanfield expression of the potential energy is obtained from the
exact expression
| W |
= |
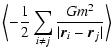 |
|
| |
= |
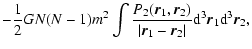 |
(4) |
by approximating the two-body distribution function
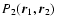 by the product of two one-body distribution
functions
by the product of two one-body distribution
functions
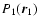
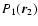 and using
and using
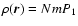 .
For self-gravitating systems, this
mean-field approximation is exact in a proper thermodynamic limit
.
For self-gravitating systems, this
mean-field approximation is exact in a proper thermodynamic limit
 with
with
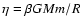 and
and
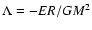 fixed (see Appendix A). The
gravitational potential
fixed (see Appendix A). The
gravitational potential
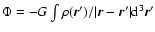 is solution of the
Newton-Poisson equation
is solution of the
Newton-Poisson equation
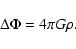 |
(5) |
In order to regularize the problem at short distances, we shall invoke
quantum mechanics and use the Pauli exclusion principle. The Pauli
exclusion principle is a fundamental concept in physics and it has
also applications in astrophysics, e.g. in white dwarf and neutron
stars. Therefore, it can be considered as a physically relevant
small-scale regularization for compact objects (e.g., Chavanis
2002d). We wish to determine the most probable distribution of
self-gravitating fermions at statistical equilibrium. To that purpose,
we divide the individual phase space
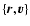 into a very large number of microcells with size (h/m)3 where his the Planck constant (the mass m of the particles arises because
we use
into a very large number of microcells with size (h/m)3 where his the Planck constant (the mass m of the particles arises because
we use  instead of
instead of  as a phase space coordinate). A
microcell is occupied either by 0 or 1 fermion (or g=2s+1fermions if we account for the spin). We shall now group these
microcells into macrocells each of which contains many microcells but
remains nevertheless small compared to the phase-space extension of
the whole system. We call
as a phase space coordinate). A
microcell is occupied either by 0 or 1 fermion (or g=2s+1fermions if we account for the spin). We shall now group these
microcells into macrocells each of which contains many microcells but
remains nevertheless small compared to the phase-space extension of
the whole system. We call 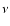 the number of microcells in a
macrocell. Consider the configuration
the number of microcells in a
macrocell. Consider the configuration
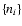 where
there are n1 fermions in the 1st macrocell, n2 in the
2nd macrocell etc., each occupying one of the
where
there are n1 fermions in the 1st macrocell, n2 in the
2nd macrocell etc., each occupying one of the 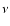 microcells with no cohabitation. The number of ways of assigning a microcell to the first element of a macrocell is
microcells with no cohabitation. The number of ways of assigning a microcell to the first element of a macrocell is 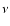 ,
to the second
,
to the second
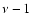 etc. Since the particles are indistinguishable, the number
of ways of assigning microcells to all ni particles in a macrocell
is thus
etc. Since the particles are indistinguishable, the number
of ways of assigning microcells to all ni particles in a macrocell
is thus
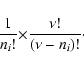 |
(6) |
To obtain the number of microstates corresponding to the macrostate
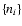 defined by the number of fermions ni in each macrocell (irrespective of their precise position in the cell), we need to take the product of terms such as Eq. (6) over all
macrocells. Thus, the number of microstates corresponding to the
macrostate
defined by the number of fermions ni in each macrocell (irrespective of their precise position in the cell), we need to take the product of terms such as Eq. (6) over all
macrocells. Thus, the number of microstates corresponding to the
macrostate
 ,
i.e. the probability of the state
,
i.e. the probability of the state
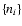 ,
is
,
is
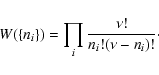 |
(7) |
This is the Fermi-Dirac statistics. As is customary, we define the
entropy of the state
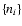 by
by
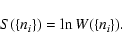 |
(8) |
It is convenient here to return to a representation in terms of
the distribution function giving the phase-space density in the
ith macrocell
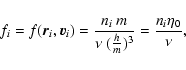 |
(9) |
where we have defined
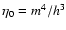 ,
which represents the
maximum value of f due to Pauli's exclusion principle. Now,
using the Stirling formula, we have
,
which represents the
maximum value of f due to Pauli's exclusion principle. Now,
using the Stirling formula, we have
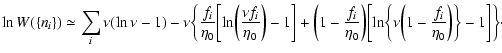 |
|
|
(10) |
Passing to the continuum limit
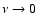 ,
we obtain the
usual expression of the Fermi-Dirac entropy
,
we obtain the
usual expression of the Fermi-Dirac entropy
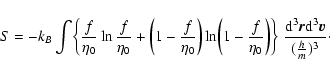 |
(11) |
If we take into account the spin of the particles, the above
expression remains valid but the maximum value of the distribution
function is now
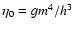 ,
where g=2s+1 is the
spin multiplicity of the quantum states (the phase space element
has also to be multiplied by g). In the non-degenerate (or
classical) limit
,
where g=2s+1 is the
spin multiplicity of the quantum states (the phase space element
has also to be multiplied by g). In the non-degenerate (or
classical) limit
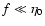 ,
the Fermi-Dirac entropy (11) reduces to the Boltzmann entropy
,
the Fermi-Dirac entropy (11) reduces to the Boltzmann entropy
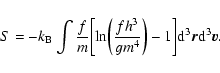 |
(12) |
Now that the entropy has been precisely justified, the statistical
equilibrium state (most probable state) of self-gravitating
fermions is obtained by maximizing the Fermi-Dirac entropy (11) at
fixed mass (2) and energy (3):
![\begin{displaymath}%
{\rm Max}\quad S[f]\quad \vert \quad E[f]=E,\ M[f]=M.
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img69.gif) |
(13) |
Introducing Lagrange multipliers 1/T (inverse temperature) and 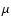 (chemical potential)
to satisfy these constraints, and writing the variational
principle in the form
(chemical potential)
to satisfy these constraints, and writing the variational
principle in the form
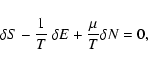 |
(14) |
we find that the critical points of entropy
correspond to the Fermi-Dirac distribution
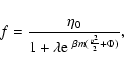 |
(15) |
where
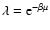 is a strictly positive constant
(inverse fugacity) and
is a strictly positive constant
(inverse fugacity) and
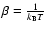 is the inverse
temperature. Clearly, the
distribution function satisfies
is the inverse
temperature. Clearly, the
distribution function satisfies
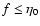 ,
which is a
consequence of Pauli's exclusion principle.
,
which is a
consequence of Pauli's exclusion principle.
So far, we have assumed that the system is isolated so that the energy
is conserved. If now the system is in contact with a thermal bath
(e.g., a radiation background) fixing the temperature, the statistical
equilibrium state minimizes the free energy F=E-TS, or maximizes the
Massieu function
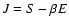 ,
at fixed mass and temperature:
,
at fixed mass and temperature:
![\begin{displaymath}%
{\rm Max}\quad J[f]\quad \vert\quad M[f]=M.
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img76.gif) |
(16) |
Introducing Lagrange multipliers and
writing the variational principle in the form
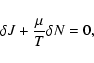 |
(17) |
we find that the critical points of free energy are again given
by the Fermi-Dirac distribution (15). Therefore, the critical
points (first variations) of the variational problems (13) and (16) are the same. However, the stability of the system (regarding the second variations) can be different in microcanonical and canonical ensembles (see, e.g., Chavanis 2002b). When this happens, we
speak of a situation of ensemble inequivalence. The stability of
the system can be determined by a graphical construction, by simply
plotting the series of equilibria 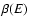 and using the turning
point method of Katz (1978, 2003). Inequivalence of statistical
ensembles occurs when the series of equilibria presents turning points
or bifurcations.
and using the turning
point method of Katz (1978, 2003). Inequivalence of statistical
ensembles occurs when the series of equilibria presents turning points
or bifurcations.
2.2 Classical particles with soften gravitational potential
We now consider a system of classical self-gravitating particles, like
stars in globular clusters. In order to make the problem of
statistical mechanics well-posed mathematically (see below), we
introduce a soften potential of the form
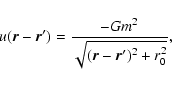 |
(18) |
where r0 is the soften radius. As we shall see, the soften radius r0 plays a role similar to the inverse of 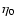 ,
the maximum phase space density, in the case of self-gravitating fermions. As said previously, this soften radius is introduced in order to pose the
problem correctly. However, we shall argue in the sequel that this small-scale cut-off is irrelevant for the structure of stellar systems.
,
the maximum phase space density, in the case of self-gravitating fermions. As said previously, this soften radius is introduced in order to pose the
problem correctly. However, we shall argue in the sequel that this small-scale cut-off is irrelevant for the structure of stellar systems.
We wish to determine the most probable distribution of stars at
statistical equilibrium (Ogorodnikov 1965). To that purpose, we divide
the individual phase space
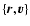 into a
very large number of microcells with size (h/m)3 where h is a
constant with dimension of angular momentum. Of course, quantum
mechanics is not relevant for stellar systems so that h should not
be confused with the Planck constant in the present context. For
classical systems, a microcell can be occupied by an arbitrary number
of particles. Adapting the counting analysis of Sect. 2.1 to
the present context, the number of microstates corresponding to the
macrostate
into a
very large number of microcells with size (h/m)3 where h is a
constant with dimension of angular momentum. Of course, quantum
mechanics is not relevant for stellar systems so that h should not
be confused with the Planck constant in the present context. For
classical systems, a microcell can be occupied by an arbitrary number
of particles. Adapting the counting analysis of Sect. 2.1 to
the present context, the number of microstates corresponding to the
macrostate
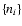 ,
i.e. its probability, is
,
i.e. its probability, is
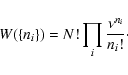 |
(19) |
This is the Maxwell-Boltzmann statistics. If we define the
entropy of the state
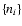 by
by
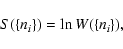 |
(20) |
and take the continuum limit, we obtain the
usual expression of the Boltzmann entropy
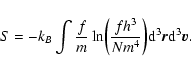 |
(21) |
Note that it differs from the expression (12) obtained from
the Fermi-Dirac entropy. This is of course related to the Gibbs
paradox in standard thermodynamics (Huang 1963). In the absence of
self-gravity, Eq. (21) reduces to the awkward expression
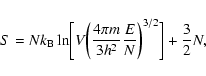 |
(22) |
which is clearly non-extensive. By constrast, Eq. (12) leads to the
Sackur-Tetrode formula
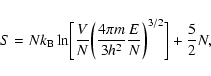 |
(23) |
which is extensive. As is well-known, the origin of this discrepency
is due to the indiscernability of the particles and to the presence of
the factor N! in the Maxwell statistics (19). For a molecular
gas, the Gibbs paradox is usualy solved by invoking quantum
mechanics. For a system of stars, one cannot use this argument. We
shall consider that the stars are discernable and use the
expression (21) for the entropy. However, this choice does not
affect the structure of the equilibrium state as we shall see in
the sequel.
The most probable distribution of stars at statistical equilibrium is
now obtained by maximizing the Boltzmann entropy (21) at fixed
mass and energy. This yields the Maxwell-Boltzmann distribution
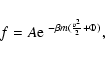 |
(24) |
where 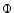 is related to the density
is related to the density 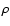 by
by
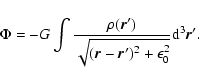 |
(25) |
The microcanonical ensemble is the correct description of stellar
systems which form an isolated Hamiltonian system in a first
approximation. We can also consider the case of self-gravitating
systems in contact with a thermal bath of non-gravitational origin
which imposes its temperature T. For such systems, the correct
description is the canonical ensemble and the statistical equilibrium
state is obtained by minimizing the Boltzmann free energy F=E-TS at
fixed mass. The canonical ensemble is also the correct description of
a gas of self-gravitating Brownian particles (Chavanis et al. 2002). In this model, the friction and the stochastic fluctuations can mimick the influence of an external medium (thermostat) to which the
system of origin is coupled.
2.3 Thermodynamic limit of self-gravitating systems
We introduce dimensionless variables such that
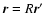 ,
,
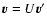 and
f=(M/R3U3)f' where R is the box
radius, M is the mass of the system and
and
f=(M/R3U3)f' where R is the box
radius, M is the mass of the system and
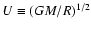 is a
typical velocity obtained by a Virial type argument (or dimensional
analysis). For self-gravitating fermions, the entropy (11) can
be expressed as
is a
typical velocity obtained by a Virial type argument (or dimensional
analysis). For self-gravitating fermions, the entropy (11) can
be expressed as
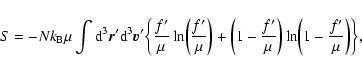 |
(26) |
where
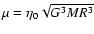 is the degeneracy parameter (Chavanis
& Sommeria 1998). Writing
is the degeneracy parameter (Chavanis
& Sommeria 1998). Writing
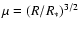 with
R*=h2/GM1/3m8/3, we note that
the degeneracy parameter is the ratio, to the power 3/2, of the
system's radius divided by the radius R* of a "white dwarf
star'' (i.e. a completely degenerate ball of fermions)
with mass M. The classical limit corresponds to
with
R*=h2/GM1/3m8/3, we note that
the degeneracy parameter is the ratio, to the power 3/2, of the
system's radius divided by the radius R* of a "white dwarf
star'' (i.e. a completely degenerate ball of fermions)
with mass M. The classical limit corresponds to
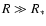 ,
i.e.
,
i.e.
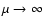 .
The conservation of mass is equivalent to
.
The conservation of mass is equivalent to
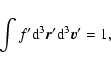 |
(27) |
and the conservation of energy is equivalent to
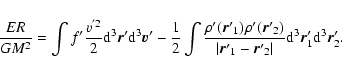 |
(28) |
Finally, the Massieu function can be written
![\begin{displaymath}%
J=N(s[f']+\eta \Lambda[f']),
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img100.gif) |
(29) |
where s=S/N,
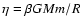 and
and
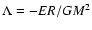 .
We define
the thermodynamic limit as
.
We define
the thermodynamic limit as
 such that
such that
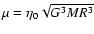 ,
,
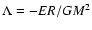 and
and
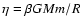 are fixed. Coming back to physical quantities, it makes sense
to fix h, m and G. Then, we have the scalings
are fixed. Coming back to physical quantities, it makes sense
to fix h, m and G. Then, we have the scalings
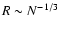 ,
,
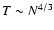 ,
,
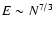 ,
,
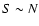 and
and 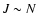 as
as
 (the free energy F scales as N7/3). This
is the quantum thermodynamic limit (QTL) for the self-gravitating gas
(Chavanis 2002b; Chavanis & Rieutord 2003). This thermodynamic limit
is relevant for compact objects with small radii
(the free energy F scales as N7/3). This
is the quantum thermodynamic limit (QTL) for the self-gravitating gas
(Chavanis 2002b; Chavanis & Rieutord 2003). This thermodynamic limit
is relevant for compact objects with small radii
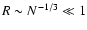 such as white dwarfs, neutron stars, fermion balls etc. The usual
thermodynamic limit
such as white dwarfs, neutron stars, fermion balls etc. The usual
thermodynamic limit
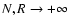 with N/R3 constant
is clearly not relevant for inhomogeneous systems whose energy is
non-additive (Padmanabhan 1990).
with N/R3 constant
is clearly not relevant for inhomogeneous systems whose energy is
non-additive (Padmanabhan 1990).
For classical particles with soften potential, the entropy (21)
can be expressed as
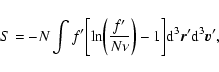 |
(30) |
where
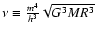 is the
counterpart of the degeneracy parameter. For classical
particles, we see that it does not play any fundamental role in
determining the structure of the system since it just appears as
an additional constant term (independent on f) in the entropy.
If we only consider the part of entropy that depends on the distribution function, we get
is the
counterpart of the degeneracy parameter. For classical
particles, we see that it does not play any fundamental role in
determining the structure of the system since it just appears as
an additional constant term (independent on f) in the entropy.
If we only consider the part of entropy that depends on the distribution function, we get
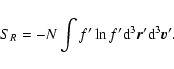 |
(31) |
This is the relevant part of the entropy functional considered by
Antonov (1962) and Lynden-Bell & Wood (1968). We can therefore write
S[f]=SR[f]+SI where SI is the constant part (irrelevant). The
conservation of mass is equivalent to Eq. (27) and the
conservation of energy is equivalent to
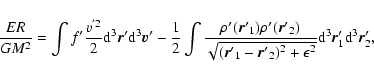 |
(32) |
where
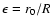 .
As before, the Massieu function is given by
Eq. (29). We define the thermodynamic limit as
.
As before, the Massieu function is given by
Eq. (29). We define the thermodynamic limit as
 such that
such that
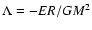 ,
,
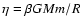 and
and
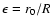 are fixed. Coming back to physical quantities, it
makes sense to fix r0, m and G. Then, we have the scalings
(Chavanis & Rieutord 2003)
are fixed. Coming back to physical quantities, it
makes sense to fix r0, m and G. Then, we have the scalings
(Chavanis & Rieutord 2003) 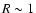 ,
,
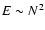 ,
,
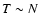 ,
,
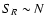 and
and
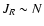 as
as
 (the free
energy FR scales as N2). These scalings imply that
(the free
energy FR scales as N2). These scalings imply that
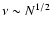 (if we fix h). Therefore, the (irrelevant) constant part of
the entropy per particle diverges logarithmically as
(if we fix h). Therefore, the (irrelevant) constant part of
the entropy per particle diverges logarithmically as
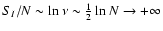 .
This does not seem to be a
crucial problem since this diverging term does not depend on f and
therefore does not affects the structure of the equilibrium state.
However, in a strict sense, there is no thermodynamic limit for
classical self-gravitating particles with soften potential. This
contrasts with the case of self-gravitating fermions that possess a
rigorous thermodynamic limit (QTL).
.
This does not seem to be a
crucial problem since this diverging term does not depend on f and
therefore does not affects the structure of the equilibrium state.
However, in a strict sense, there is no thermodynamic limit for
classical self-gravitating particles with soften potential. This
contrasts with the case of self-gravitating fermions that possess a
rigorous thermodynamic limit (QTL).
Let us finally consider the case of classical self-gravitating
particles without small-scale cut-off. The entropy is given by the
Boltzmann formula (21). When r0=0, we know that the
Boltzmann entropy has no global maximum at fixed mass and energy
(Antonov 1962). However, for sufficiently high energies, it has local
entropy maxima that describe metastable gaseous states. The
thermodynamic limit in that context corresponds to
 such that
such that
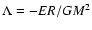 and
and
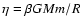 are of
order unity. If we fix m, G and T, we have the scalings
are of
order unity. If we fix m, G and T, we have the scalings 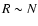 ,
,
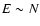 ,
,
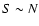 ,
,
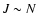 and
and 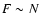 as
as
 .
This is the classical thermodynamic limit (CTL), or dilute
limit, for the self-gravitating gas (de Vega & Sanchez
2002). Physically, it describes metastable gaseous states that
are not affected by the small-scale cut-off (Chavanis & Rieutord
2003). As we shall see, these metastable states have considerably long
lifetimes so that this thermodynamic limit is relevant for classical
objects with large radii
.
This is the classical thermodynamic limit (CTL), or dilute
limit, for the self-gravitating gas (de Vega & Sanchez
2002). Physically, it describes metastable gaseous states that
are not affected by the small-scale cut-off (Chavanis & Rieutord
2003). As we shall see, these metastable states have considerably long
lifetimes so that this thermodynamic limit is relevant for classical
objects with large radii
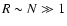 such as globular clusters.
such as globular clusters.
3 Connexion with statistical mechanics
3.1 Series of equilibria and metastable states
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{le5.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg124.gif) |
Figure 1:
Series of equilibria for self-gravitating fermions with small cut-off/large 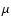 /large system size R. It has a Z-shape structure (dinosaur's neck). There can be several values of inverse temperature /large system size R. It has a Z-shape structure (dinosaur's neck). There can be several values of inverse temperature 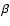 for a given energy E. They correspond to local maxima (LEM), global maxima (GEM) or saddle points (SP) of entropy S[f]. Similar remarks apply in the canonical ensemble where the role of (E, S) and (
for a given energy E. They correspond to local maxima (LEM), global maxima (GEM) or saddle points (SP) of entropy S[f]. Similar remarks apply in the canonical ensemble where the role of (E, S) and (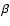 , J) is reversed. , J) is reversed. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{felP.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg125.gif) |
Figure 2:
Series of equilibria for self-gravitating fermions with large cut-off/small 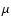 /small system size R. It has a N-shape structure. There is only one value of inverse temperature /small system size R. It has a N-shape structure. There is only one value of inverse temperature 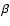 for a given energy E in the microcanonical ensemble. It
corresponds to a global maximum of entropy (GEM). By contrast, there
are several values of energy E for a given
for a given energy E in the microcanonical ensemble. It
corresponds to a global maximum of entropy (GEM). By contrast, there
are several values of energy E for a given 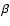 in the canonical
ensemble. They correspond to local maxima (LFEM), global maxima (GFEM)
or saddle points (SP) of free energy J[f].
in the canonical
ensemble. They correspond to local maxima (LFEM), global maxima (GFEM)
or saddle points (SP) of free energy J[f]. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{etalambdaP.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg126.gif) |
Figure 3:
Series of equilibria for self-gravitating classical particles without small-scale cut-off. There exists only local entropy maxima (metastable state) or unstable saddle points of entropy in MCE. Similar remarks hold in CE for the free energy. |
| Open with DEXTER |
The critical points of entropy S[f] at fixed E and M (i.e., the
distribution functions
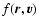 which cancel the first
order variations of S at fixed E, M) form a series of equilibria
parameterized, for example, by the density contrast
which cancel the first
order variations of S at fixed E, M) form a series of equilibria
parameterized, for example, by the density contrast
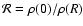 between the center and the edge of the system (see
Chavanis 2002b). At each point in the series of equilibria corresponds
a temperature
between the center and the edge of the system (see
Chavanis 2002b). At each point in the series of equilibria corresponds
a temperature 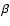 and an energy E. In this approach,
and an energy E. In this approach, 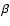 is
the Lagrange multiplier associated with the conservation of energy in
the variational problem (14). It has also the interpretation
of a kinetic temperature in the Fermi-Dirac distribution (15). We can thus plot
is
the Lagrange multiplier associated with the conservation of energy in
the variational problem (14). It has also the interpretation
of a kinetic temperature in the Fermi-Dirac distribution (15). We can thus plot 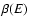 along the series of
equilibria. The form of this "caloric curve'' depends on the value of
the degeneracy parameter
along the series of
equilibria. The form of this "caloric curve'' depends on the value of
the degeneracy parameter 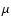 in the case of fermions (Chavanis
2002b) and on the soften radius
in the case of fermions (Chavanis
2002b) and on the soften radius 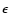 for regularized classical
systems (Chavanis & Ispolatov 2002). It also depends on the dimension
of space D (Sire & Chavanis 2002; Chavanis 2004a). In D=3, the
caloric curve has a Z-shape (see Fig. 1) for small cut-off
and a N-shape (see Fig. 2) for large cut-off (for no
cut-off, we recover the well-known spiral of Fig. 3).
There can be several values of temperature
for regularized classical
systems (Chavanis & Ispolatov 2002). It also depends on the dimension
of space D (Sire & Chavanis 2002; Chavanis 2004a). In D=3, the
caloric curve has a Z-shape (see Fig. 1) for small cut-off
and a N-shape (see Fig. 2) for large cut-off (for no
cut-off, we recover the well-known spiral of Fig. 3).
There can be several values of temperature 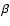 for the same energy E because the variational problem (13) can have several
solutions: a local entropy maximum (metastable state), a global
entropy maximum, and one or several saddle points. We must represent
all these solutions on the caloric curve because local entropy maxima
(metastable states) are in general more physical than global entropy
maxima for the timescales achieved in astrophysics. Indeed, the system
can remain frozen in a metastable gaseous phase for a very long
time. This is the case, in particular, for globular clusters and for
the gaseous phase of fermionic matter (at high energy and high
temperature). The time required for a system placed in a metastable
gaseous state to collapse is in general tremendously long and
increases exponentially with the number N of particles. Thus,
for the same energy E because the variational problem (13) can have several
solutions: a local entropy maximum (metastable state), a global
entropy maximum, and one or several saddle points. We must represent
all these solutions on the caloric curve because local entropy maxima
(metastable states) are in general more physical than global entropy
maxima for the timescales achieved in astrophysics. Indeed, the system
can remain frozen in a metastable gaseous phase for a very long
time. This is the case, in particular, for globular clusters and for
the gaseous phase of fermionic matter (at high energy and high
temperature). The time required for a system placed in a metastable
gaseous state to collapse is in general tremendously long and
increases exponentially with the number N of particles. Thus,
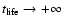 in the thermodynamic limit
in the thermodynamic limit
 .
The robustness of metastable states is due to the long-range
nature of the gravitational potential. Therefore, at high temperatures
and high energies, the global entropy maximum is not physically
relevant. Condensed objects (e.g., planets, stars, white dwarfs,
fermion balls,...) only form below a critical energy
.
The robustness of metastable states is due to the long-range
nature of the gravitational potential. Therefore, at high temperatures
and high energies, the global entropy maximum is not physically
relevant. Condensed objects (e.g., planets, stars, white dwarfs,
fermion balls,...) only form below a critical energy 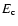 (Antonov
energy) or below a critical temperature
(Antonov
energy) or below a critical temperature 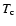 (Jeans temperature),
when the gaseous metastable phase ceases to exist. The point where the
metastable phase disappears is called a spinodal point.
(Jeans temperature),
when the gaseous metastable phase ceases to exist. The point where the
metastable phase disappears is called a spinodal point.
3.2 Microcanonical ensemble
Let us explain things differently so as to make a closer contact with
statistical mechanics. In statistical mechanics, one usually starts
with the density of states
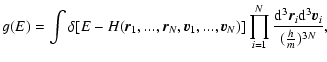 |
|
|
(33) |
where H is the Hamiltonian. For our system
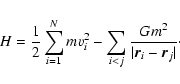 |
(34) |
The density of states is the normalization factor of the N-body microcanonical distribution
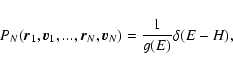 |
(35) |
stating that all accessible microstates are equiprobable.
Introducing the probability
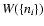 of the state
of the state
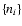 ,
we can rewrite the density of states in the
form
,
we can rewrite the density of states in the
form
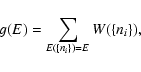 |
(36) |
where the sum runs over all macrostates with energy E.
Introducing the entropy 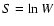 of the state
of the state
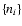 and taking the continuum limit, the density of states
can be expressed formally as
and taking the continuum limit, the density of states
can be expressed formally as
![\begin{displaymath}%
g(E)=\int {\cal D}f {\rm e}^{S[f]}\delta (E-E[f])\delta (M-M[f]),
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img137.gif) |
(37) |
where the sum runs over all distribution functions and S[f] is the
Fermi-Dirac entropy (11) if the particles are fermions and the
Boltzmann entropy (21) for classical particles (in that case,
the gravitational potential must be regularized otherwise the density
of states (33) diverges). The probability of the distribution
function
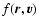 is proportional to
is proportional to
![${\rm e}^{S[f]}$](/articles/aa/full/2005/10/aa1114/img138.gif) .
We now
define the microcanonical entropy by
.
We now
define the microcanonical entropy by
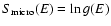 and the
microcanonical temperature by
and the
microcanonical temperature by
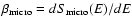 .
By
definition, the caloric curve
.
By
definition, the caloric curve
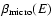 is uni-valued (Gross
2003). In the thermodynamic limit defined in Sect. 2.3, the
entropy S[f] scales as
is uni-valued (Gross
2003). In the thermodynamic limit defined in Sect. 2.3, the
entropy S[f] scales as  N, that is
S[f]=Ns[f] where
N, that is
S[f]=Ns[f] where 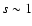 is the entropy per particle. Therefore, for
is the entropy per particle. Therefore, for
 ,
the integral in Eq. (37) is dominated by the state
,
the integral in Eq. (37) is dominated by the state
 which is the global maximum of S[f] at
fixed M and E (rigorously speaking, we should work with the
dimensionless quantities defined in Sect. 2.3 to get rid of
the
which is the global maximum of S[f] at
fixed M and E (rigorously speaking, we should work with the
dimensionless quantities defined in Sect. 2.3 to get rid of
the
 dependence). Then,
dependence). Then,
![$g(E)\simeq
{\rm e}^{S[f_{{\rm global}}]}$](/articles/aa/full/2005/10/aa1114/img144.gif) ,
,
![$S_{{\rm micro}}\simeq S[f_{{\rm global}}]$](/articles/aa/full/2005/10/aa1114/img145.gif) and
and
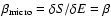 .
However, this approach fails
to take into account metastable states (local maxima of S[f] at
fixed M and E), which are of considerable interest in
astrophysics. Indeed, equilibrium statistical mechanics tells nothing
about timescales; a kinetic theory is required in that case. As
explained above, these metastable states can persist for very long
times. They correspond to the observed "diluted'' structures in the
universe (e.g., globular clusters). Therefore, the caloric curve
.
However, this approach fails
to take into account metastable states (local maxima of S[f] at
fixed M and E), which are of considerable interest in
astrophysics. Indeed, equilibrium statistical mechanics tells nothing
about timescales; a kinetic theory is required in that case. As
explained above, these metastable states can persist for very long
times. They correspond to the observed "diluted'' structures in the
universe (e.g., globular clusters). Therefore, the caloric curve
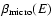 does not describe the system adequately. The series
of equilibria
does not describe the system adequately. The series
of equilibria 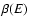 contain more information as they show local
and global entropy maxima (as well as unstable saddle points). The
curve
contain more information as they show local
and global entropy maxima (as well as unstable saddle points). The
curve
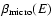 can be deduced from
can be deduced from 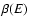 by keeping
only global entropy maxima (see Fig. 4). If we adopt this
procedure, we find that the system exhibits a first order microcanonical phase transition (provided that the system size
by keeping
only global entropy maxima (see Fig. 4). If we adopt this
procedure, we find that the system exhibits a first order microcanonical phase transition (provided that the system size 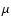 is sufficiently large) at a transition energy
is sufficiently large) at a transition energy
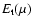 where the
gaseous phase and the condensed phase have the same entropy (see Chavanis
2002b). In the strict thermodynamic limit
where the
gaseous phase and the condensed phase have the same entropy (see Chavanis
2002b). In the strict thermodynamic limit
 ,
this
phase transition is marked by a discontinuity of temperature. In fact,
for finite N systems, the saddle point approximation
,
this
phase transition is marked by a discontinuity of temperature. In fact,
for finite N systems, the saddle point approximation
![$g(E)\simeq
{\rm e}^{S[f_{{\rm global}}]}$](/articles/aa/full/2005/10/aa1114/img144.gif) breaks down near the transition energy (Chavanis &
Ispolatov 2002). This is because the contribution of the local entropy
maximum in the functional integral (37) becomes more and more
important as we approach
breaks down near the transition energy (Chavanis &
Ispolatov 2002). This is because the contribution of the local entropy
maximum in the functional integral (37) becomes more and more
important as we approach 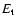 .
For the saddle point approximation
to be valid, the number of particles must scale as
.
For the saddle point approximation
to be valid, the number of particles must scale as
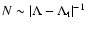 for
for
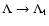 (see Sect. 4.2). Thus, for large but finite N, the
temperature variation is sharp but remains continuous at the
transition. We again emphasize that, due to the existence of
metastable states, this phase transition may not be physically
relevant. The true phase transition (gravothermal catastrophe) will
rather take place at, or near, the spinodal point
(see Sect. 4.2). Thus, for large but finite N, the
temperature variation is sharp but remains continuous at the
transition. We again emphasize that, due to the existence of
metastable states, this phase transition may not be physically
relevant. The true phase transition (gravothermal catastrophe) will
rather take place at, or near, the spinodal point 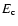 (Antonov
energy) where the metastable branch disappears. Estimating the
lifetime of a metastable state by the Kramers formula
(Antonov
energy) where the metastable branch disappears. Estimating the
lifetime of a metastable state by the Kramers formula
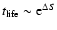 ,
where
,
where 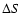 is the height of the entropic barrier
(difference of entropy between the local maximum and the saddle
point), we find that
is the height of the entropic barrier
(difference of entropy between the local maximum and the saddle
point), we find that
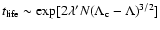 with
with
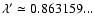 (see Sect. 5). Except
in the vicinity of the critical point
(see Sect. 5). Except
in the vicinity of the critical point
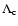 ,
the lifetime of a
gaseous metastable state is enormous as it increases exponentially
with the number of particles. Thus, metastable states have a
considerable interest in astrophysics.
,
the lifetime of a
gaseous metastable state is enormous as it increases exponentially
with the number of particles. Thus, metastable states have a
considerable interest in astrophysics.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{caloric.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg155.gif) |
Figure 4:
Strict microcanonical caloric curve for
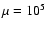 (the control parameter is the energy E). This figure is obtained from Fig. 1 by keeping only global entropy maxima. It corresponds therefore to the true caloric curve
(the control parameter is the energy E). This figure is obtained from Fig. 1 by keeping only global entropy maxima. It corresponds therefore to the true caloric curve
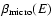 which is univalued (Gross 2003). For
which is univalued (Gross 2003). For
 ,
there is a discontinuity of temperature at the transition energy ,
there is a discontinuity of temperature at the transition energy
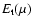 .
For finite N systems, this discontinuity is smoothed out. Although this caloric curve is correct in a strict sense, it is not physical because it ignores metastable states that have an infinite lifetime in the thermodynamic limit. The physical caloric curve is obtained from Fig. 1 by discarding the unstable saddle points of entropy that form the intermediate branch (see Fig. 5). .
For finite N systems, this discontinuity is smoothed out. Although this caloric curve is correct in a strict sense, it is not physical because it ignores metastable states that have an infinite lifetime in the thermodynamic limit. The physical caloric curve is obtained from Fig. 1 by discarding the unstable saddle points of entropy that form the intermediate branch (see Fig. 5). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{el5phys.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg156.gif) |
Figure 5:
Physical microcanonical caloric curve for
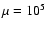 (the control parameter is the energy E). This figure displays stable and metastable equilibrium states. The metastable states have infinite lifetime in the thermodynamic limit so they are physically relevant. The first order microcanonical phase transition of Fig. 4 does not take place in practice. Due to the existence of metastable states, the system displays a microcanonical hysteretic cycle marked by a "collapse'' and an "explosion'' at the spinodal points where the branch of metastable states disapears (Chavanis & Rieutord 2003).
(the control parameter is the energy E). This figure displays stable and metastable equilibrium states. The metastable states have infinite lifetime in the thermodynamic limit so they are physically relevant. The first order microcanonical phase transition of Fig. 4 does not take place in practice. Due to the existence of metastable states, the system displays a microcanonical hysteretic cycle marked by a "collapse'' and an "explosion'' at the spinodal points where the branch of metastable states disapears (Chavanis & Rieutord 2003). |
| Open with DEXTER |
If we now consider the case of classical particles (
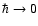 or
or
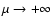 ), the transition energy
), the transition energy
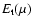 is
rejected to
is
rejected to 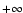 so that the whole branch of gaseous states is
metastable. This "no cut-off'' limit is relevant to classical objects
such as globular clusters or to the interstellar medium because, for
these systems, the size of the particles (stars and atoms) clearly
does not matter. In that case, the series of equilibria
so that the whole branch of gaseous states is
metastable. This "no cut-off'' limit is relevant to classical objects
such as globular clusters or to the interstellar medium because, for
these systems, the size of the particles (stars and atoms) clearly
does not matter. In that case, the series of equilibria 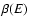 forms a spiral (see Fig. 3) indicating the existence of
one local entropy maximum and one (or several) saddle points of
entropy for a given energy (Lynden-Bell & Wood 1968). This spiral is
the limiting form, for
forms a spiral (see Fig. 3) indicating the existence of
one local entropy maximum and one (or several) saddle points of
entropy for a given energy (Lynden-Bell & Wood 1968). This spiral is
the limiting form, for
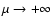 ,
of the fermionic
caloric curve (see Fig. 11 in Chavanis 2002b). In this limit, the
branch of "collapsed'' states (condensed phase) coincides with the
x-axis where
,
of the fermionic
caloric curve (see Fig. 11 in Chavanis 2002b). In this limit, the
branch of "collapsed'' states (condensed phase) coincides with the
x-axis where 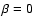 .
It corresponds to configurations made of two particles in contact (
.
It corresponds to configurations made of two particles in contact (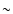 binary star) surrounded by a hot halo with
binary star) surrounded by a hot halo with
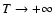 .
This "binary+halo'' configuration has an
infinite entropy so, in a sense, it is the most probable configuration
in the microcanonical ensemble (see Appendix A of Sire & Chavanis
2002). However, for sufficiently large energies (above the Antonov
point), these configurations must be discarded "by hands'' because
they are reached for inaccessibly large times. Therefore, for
classical particles, the physical caloric curve
.
This "binary+halo'' configuration has an
infinite entropy so, in a sense, it is the most probable configuration
in the microcanonical ensemble (see Appendix A of Sire & Chavanis
2002). However, for sufficiently large energies (above the Antonov
point), these configurations must be discarded "by hands'' because
they are reached for inaccessibly large times. Therefore, for
classical particles, the physical caloric curve
 is obtained by taking
is obtained by taking
![$g(E)\simeq {\rm e}^{S[f_{{\rm local}}]}$](/articles/aa/full/2005/10/aa1114/img162.gif) and
and
![$S_{{\rm physical}}\simeq S[f_{{\rm local}}]$](/articles/aa/full/2005/10/aa1114/img163.gif) where
where
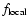 is the local
entropy maximum at fixed mass and energy (Chavanis 2003).
is the local
entropy maximum at fixed mass and energy (Chavanis 2003).
3.3 Canonical ensemble
In the canonical ensemble, the object of fundamental importance is the
partition function
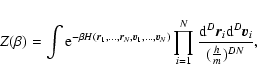 |
(38) |
which is the normalization of the N-body canonical distribution
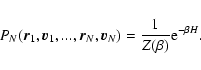 |
(39) |
The partition function can be rewritten
where
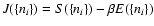 is the "free energy'' of the macrostate
is the "free energy'' of the macrostate
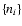 and the sum runs over all macrostates (in the
present context,
and the sum runs over all macrostates (in the
present context,
![$J[f]=S[f]-\beta E[f]$](/articles/aa/full/2005/10/aa1114/img31.gif) is a more natural functional
than the usual free energy
F[f]=E[f]-TS[f]). Taking the continuum
limit, the partition function can be expressed formally as
is a more natural functional
than the usual free energy
F[f]=E[f]-TS[f]). Taking the continuum
limit, the partition function can be expressed formally as
![\begin{displaymath}%
Z(\beta)=\int {\cal D}f {\rm e}^{J[f]}\delta (M-M[f]),
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img171.gif) |
(41) |
where the sum runs over all distribution functions and J[f] is the Fermi-Dirac free energy if the
particles are fermions and the Boltzmann free energy for classical
particles (in that case, the gravitational potential must be
regularized otherwise the partition function (38)
diverges). Note that Eq. (41) can also be obtained from the exact formula
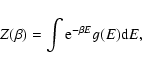 |
(42) |
by substituting Eq. (37) for g(E) and carrying out the
integration over E. We now define the canonical free energy by
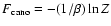 .
The average energy of the system at
temperature T can be written
.
The average energy of the system at
temperature T can be written
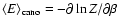 .
By definition, the caloric curve
.
By definition, the caloric curve
 is uni-valued. In the thermodynamic limit
defined in Sect. 2.3, the free energy J[f] scales as
is uni-valued. In the thermodynamic limit
defined in Sect. 2.3, the free energy J[f] scales as 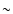 N. Therefore, for
N. Therefore, for
 ,
the integral in
Eq. (41) is dominated by the state
,
the integral in
Eq. (41) is dominated by the state
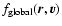 which is the global maximum of J[f] at fixed M. Then,
which is the global maximum of J[f] at fixed M. Then,
![$Z(\beta)\simeq {\rm e}^{J[f_{{\rm global}}]}$](/articles/aa/full/2005/10/aa1114/img176.gif) ,
,
![$F_{{\rm cano}}\simeq
-(1/\beta)J[f_{{\rm global}}]=E[f_{{\rm global}}]-TS[f_{{\rm global}}]$](/articles/aa/full/2005/10/aa1114/img177.gif) and
and
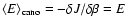 .
Metastable states (local
maxima of J[f] at fixed M) can be taken into account by plotting
the full curve
.
Metastable states (local
maxima of J[f] at fixed M) can be taken into account by plotting
the full curve 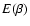 .
It is obtained from
.
It is obtained from 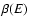 defined in
Sect. 3.1 by simply reversing the graph since the critical
points of the variational problems (13) and (16) are
the same (see Sect. 2.1). The curve
defined in
Sect. 3.1 by simply reversing the graph since the critical
points of the variational problems (13) and (16) are
the same (see Sect. 2.1). The curve
 can be deduced from
can be deduced from 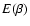 by keeping only
global maxima of free energy J (see Fig. 6). If we adopt
this procedure, we find that the system exhibits a first order canonical phase transition at a transition temperature
by keeping only
global maxima of free energy J (see Fig. 6). If we adopt
this procedure, we find that the system exhibits a first order canonical phase transition at a transition temperature
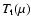 where the gaseous phase and the condensed phase have the same free
energy (see Chavanis 2002b). This phase transition is marked by a
discontinuity of energy (latent heat). In fact, the saddle point
approximation
where the gaseous phase and the condensed phase have the same free
energy (see Chavanis 2002b). This phase transition is marked by a
discontinuity of energy (latent heat). In fact, the saddle point
approximation
![$Z(\beta)\simeq {\rm e}^{J[f_{{\rm global}}]}$](/articles/aa/full/2005/10/aa1114/img176.gif) breaks down near the
transition temperature. For large but finite N, the energy variation
is sharp but remains continuous at the transition. For the
saddle point approximation to be valid, the number of particles must
scale as
breaks down near the
transition temperature. For large but finite N, the energy variation
is sharp but remains continuous at the transition. For the
saddle point approximation to be valid, the number of particles must
scale as
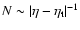 for
for
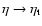 (see Sect. 4.2). We again emphasize that, due to the existence
of metastable states, this phase transition may not be relevant and
that the physical phase transition (isothermal collapse) takes place
at, or near, the spinodal point
(see Sect. 4.2). We again emphasize that, due to the existence
of metastable states, this phase transition may not be relevant and
that the physical phase transition (isothermal collapse) takes place
at, or near, the spinodal point 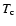 (Jeans temperature) where the
metastable branch disappears (see Fig. 8). Estimating the
lifetime of a metastable state by the Kramers formula
(Jeans temperature) where the
metastable branch disappears (see Fig. 8). Estimating the
lifetime of a metastable state by the Kramers formula
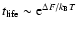 ,
where
,
where 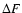 is the height of the potential
barrier (difference of free energy between the local maximum and the
saddle point), we find that
is the height of the potential
barrier (difference of free energy between the local maximum and the
saddle point), we find that
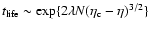 with
with
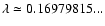 (see
Sect. 5). Except in the vicinity of the critical
point
(see
Sect. 5). Except in the vicinity of the critical
point
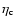 ,
the lifetime of a gaseous metastable state is
enormous as it increases exponentially with the number of
particles. Metastable states are therefore highly robust. For
classical objects (
,
the lifetime of a gaseous metastable state is
enormous as it increases exponentially with the number of
particles. Metastable states are therefore highly robust. For
classical objects (
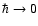 ), the transition temperature
), the transition temperature
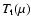 is rejected to
is rejected to 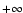 so that the whole branch of
gaseous states is metastable. In that case, the series of equilibria
so that the whole branch of
gaseous states is metastable. In that case, the series of equilibria 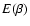 forms a spiral (see Fig. 3) indicating the
existence of one local minimum of free energy F and one (or several)
saddle points of free energy for a given temperature. In the classical
limit, the branch of "collapsed'' states (condensed phase) is
rejected to
forms a spiral (see Fig. 3) indicating the
existence of one local minimum of free energy F and one (or several)
saddle points of free energy for a given temperature. In the classical
limit, the branch of "collapsed'' states (condensed phase) is
rejected to
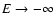 .
It corresponds to configurations
where all the particles have collapsed at r=0. This "Dirac peak''
configuration has an infinite free energy
.
It corresponds to configurations
where all the particles have collapsed at r=0. This "Dirac peak''
configuration has an infinite free energy 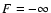 (due to the
infinite binding energy) so, in a sense, it is the most probable
configuration in the canonical ensemble (see Appendix B of Sire &
Chavanis 2002). This differs from the global entropy maximum made of a
binary star surrounded by a hot halo in the microcanonical ensemble.
For sufficiently large temperatures (above the Emden-Jeans
point), these configurations must be discarded "by hands'' because
they are reached for inaccessibly large times. Therefore, for
classical particles, the physical caloric curve
(due to the
infinite binding energy) so, in a sense, it is the most probable
configuration in the canonical ensemble (see Appendix B of Sire &
Chavanis 2002). This differs from the global entropy maximum made of a
binary star surrounded by a hot halo in the microcanonical ensemble.
For sufficiently large temperatures (above the Emden-Jeans
point), these configurations must be discarded "by hands'' because
they are reached for inaccessibly large times. Therefore, for
classical particles, the physical caloric curve
 is obtained by taking
is obtained by taking
![$Z(\beta)\simeq {\rm e}^{J[f_{{\rm local}}]}$](/articles/aa/full/2005/10/aa1114/img189.gif) and
and
![$J_{{\rm physical}}\simeq J[f_{{\rm local}}]$](/articles/aa/full/2005/10/aa1114/img190.gif) where
where
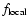 is the local
maximum of free energy J at fixed mass and temperature (Chavanis 2003).
is the local
maximum of free energy J at fixed mass and temperature (Chavanis 2003).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{caloricCan.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg191.gif) |
Figure 6:
Strict canonical caloric curve for
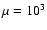 (the control parameter is
the inverse temperature
(the control parameter is
the inverse temperature 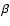 ). This figure is obtained from Fig. 2
by keeping only global maxima of free energy J. It corresponds therefore
to the true canonical caloric curve which is univalued and
does not display negative specific heats contrary to the
corresponding microcanonical caloric curve (see Fig. 7).
For ). This figure is obtained from Fig. 2
by keeping only global maxima of free energy J. It corresponds therefore
to the true canonical caloric curve which is univalued and
does not display negative specific heats contrary to the
corresponding microcanonical caloric curve (see Fig. 7).
For
 ,
there is a discontinuity of energy (latent heat) at the transition temperature ,
there is a discontinuity of energy (latent heat) at the transition temperature
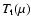 .
For finite N systems, this discontinuity is smoothed-out. Although this canonical caloric curve is correct in a strict sense, it is not physical because it ignores metastable states that have an infinite lifetime in the thermodynamic limit .
For finite N systems, this discontinuity is smoothed-out. Although this canonical caloric curve is correct in a strict sense, it is not physical because it ignores metastable states that have an infinite lifetime in the thermodynamic limit
 .
The physical canonical caloric curve is obtained from Fig. 2 by discarding the unstable saddle points of free energy that form the intermediate branch with negative specific heats (see Fig. 8). .
The physical canonical caloric curve is obtained from Fig. 2 by discarding the unstable saddle points of free energy that form the intermediate branch with negative specific heats (see Fig. 8). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{el3micro.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg192.gif) |
Figure 7:
Microcanonical caloric curve for the same cut-off/degeneracy parameter 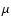 /system's radius R as Fig. 6 (the control parameter is the energy E). It has a N-shape structure and displays a stable region with negative specific heats. All the equilibria are global maxima of entropy. In the canonical ensemble the region of negative specific heats is replaced by a phase transition (see Fig. 6). The curves of Figs. 6 and 7 are similar to those obtained by Padmanabhan (1990) with his toy model consisting in N=2 stars in gravitational interaction. /system's radius R as Fig. 6 (the control parameter is the energy E). It has a N-shape structure and displays a stable region with negative specific heats. All the equilibria are global maxima of entropy. In the canonical ensemble the region of negative specific heats is replaced by a phase transition (see Fig. 6). The curves of Figs. 6 and 7 are similar to those obtained by Padmanabhan (1990) with his toy model consisting in N=2 stars in gravitational interaction. |
| Open with DEXTER |
3.4 Grand canonical ensemble
In the grand canonical ensemble, the partition function is
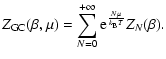 |
|
|
(43) |
Using Eq. (41), we get
where
![$G[f]=J[f]+\beta \mu N[f]$](/articles/aa/full/2005/10/aa1114/img197.gif) is the grand potential. Of course,
the expression (41) for ZN is correct only for
is the grand potential. Of course,
the expression (41) for ZN is correct only for 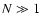 .
However, the contribution of small N terms in the grand
partition function (43) is expected to be weak so that
Eq. (44) provides a good approximation of the series. Now, the
grand potential G[f] scales as
.
However, the contribution of small N terms in the grand
partition function (43) is expected to be weak so that
Eq. (44) provides a good approximation of the series. Now, the
grand potential G[f] scales as 
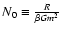 .
Therefore, in the thermodynamic limit
.
Therefore, in the thermodynamic limit
 with fixed
with fixed 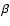 ,
G (gravitational constant) and m, the
partition function
,
G (gravitational constant) and m, the
partition function
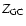 is dominated by the distribution f which
maximizes the grand potential G[f] at fixed
is dominated by the distribution f which
maximizes the grand potential G[f] at fixed 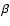 and
and 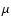 .
This
problem has been considered for classical particles in
D=3 (Chavanis 2003). We shall reserve for a future work the study of
self-gravitating fermions in the grand canonical ensemble.
.
This
problem has been considered for classical particles in
D=3 (Chavanis 2003). We shall reserve for a future work the study of
self-gravitating fermions in the grand canonical ensemble.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{el3phys.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg202.gif) |
Figure 8:
Physical canonical caloric curve for
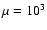 (the control parameter is the inverse temperature
(the control parameter is the inverse temperature 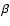 ). This figure displays stable and metastable equilibrium states. The metastable states have infinite lifetime in the thermodynamic limit so they are physically relevant. The first order canonical phase transition of Fig. 6 does not take place in practice. Due to the existence of metastable states the system displays a canonical hysteretic cycle marked by a "collapse'' and an "explosion'' at the spinodal points where the branch of metastable states disapears (Chavanis & Rieutord 2003). ). This figure displays stable and metastable equilibrium states. The metastable states have infinite lifetime in the thermodynamic limit so they are physically relevant. The first order canonical phase transition of Fig. 6 does not take place in practice. Due to the existence of metastable states the system displays a canonical hysteretic cycle marked by a "collapse'' and an "explosion'' at the spinodal points where the branch of metastable states disapears (Chavanis & Rieutord 2003). |
| Open with DEXTER |
4 First order microcanonical and canonical phase transitions
4.1 Maxwell constructions and critical points
The deformation of the caloric curve when we vary the degeneracy
parameter 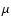 / system size R is represented in
Figs. 9 and 10. Similar curves are obtained for a hard
sphere gas or a soften potential (Chavanis & Ispolatov 2002) instead
of fermions. In that case,
/ system size R is represented in
Figs. 9 and 10. Similar curves are obtained for a hard
sphere gas or a soften potential (Chavanis & Ispolatov 2002) instead
of fermions. In that case, 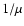 plays the
role of the cut-off radius a or soften radius r0.
plays the
role of the cut-off radius a or soften radius r0.
For
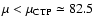 ,
the curve
,
the curve 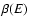 defining the
series of equilibria is monotonic, so there is no phase
transition. For
defining the
series of equilibria is monotonic, so there is no phase
transition. For
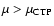 ,
the curve
,
the curve 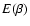 is multivalued
so that a canonical first order phase transition is expected. The
temperature of transition in the canonical ensemble can be obtained by
a Maxwell construction as for the familiar Van der Waals gas. The
equal area Maxwell condition
A1=A2 (see
Fig. 9) can be expressed as
is multivalued
so that a canonical first order phase transition is expected. The
temperature of transition in the canonical ensemble can be obtained by
a Maxwell construction as for the familiar Van der Waals gas. The
equal area Maxwell condition
A1=A2 (see
Fig. 9) can be expressed as
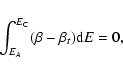 |
(45) |
where EA is the energy of the gaseous phase and 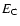 the
energy of the condensed phase at the transition temperature
the
energy of the condensed phase at the transition temperature 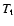 .
Since
.
Since
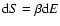 ,
one has
,
one has
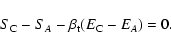 |
(46) |
Introducing the free energy
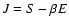 ,
we verify that
the Maxwell construction is equivalent to the equality of the free
energy of the two phases at the transition:
,
we verify that
the Maxwell construction is equivalent to the equality of the free
energy of the two phases at the transition:
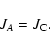 |
(47) |
If we keep only global maxima of free energy (in the canonical ensemble) as in
Fig. 6, the winding branch has to be replaced by a
horizontal plateau. We see in Fig. 9 that the extent
of the plateau decreases as 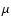 decreases (dashed line). At the canonical
critical point
decreases (dashed line). At the canonical
critical point
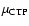 ,
the plateau disappears and the curve
presents an inflexion point.
,
the plateau disappears and the curve
presents an inflexion point.
For
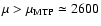 ,
the curve
,
the curve 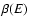 is multivalued so
that a microcanonical first order phase transition is expected to
occur (in addition to the canonical first order phase transition
described previously). The energy of transition can be obtained by a
vertical Maxwell construction. The equal area Maxwell condition
A1=A2 (see Fig. 10) can be expressed as
is multivalued so
that a microcanonical first order phase transition is expected to
occur (in addition to the canonical first order phase transition
described previously). The energy of transition can be obtained by a
vertical Maxwell construction. The equal area Maxwell condition
A1=A2 (see Fig. 10) can be expressed as
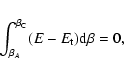 |
(48) |
where TA and 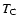 are the temperatures of
the two phases at the transition energy
are the temperatures of
the two phases at the transition energy 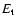 .
Since
.
Since
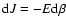 ,
one has
,
one has
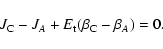 |
(49) |
Thus, the Maxwell construction is equivalent to the equality of the
entropy of the two phases at the transition:
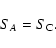 |
(50) |
If we keep only global maxima of entropy (in the microcanonical
ensemble) as in Fig. 4, the winding branch has to be
replaced by a vertical plateau. We see that the extent of the plateau
decreases as 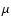 decreases (dashed line). At the microcanonical
critical point
decreases (dashed line). At the microcanonical
critical point
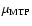 ,
the plateau disappears and the curve
presents an inflexion point.
,
the plateau disappears and the curve
presents an inflexion point.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{tricritiqueP.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg220.gif) |
Figure 9:
Horizontal Maxwell plateau associated with a canonical first order phase transition. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{tricritiquemicroP.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg221.gif) |
Figure 10:
Vertical Maxwell plateau associated with a microcanonical first order phase transition. |
| Open with DEXTER |
Therefore, for
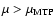 ,
we expect a microcanonical and a
canonical first order phase transition, for
,
we expect a microcanonical and a
canonical first order phase transition, for
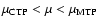 only a canonical first order phase transition and for
only a canonical first order phase transition and for
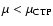 no phase transition at all. We emphasize, however, that due to the
presence of long-lived metastable states, the first order phase
transitions and the plateaux are not relevant for the timescales of
interest (see Sect. 3). Only the zeroth order phase
transitions (gravothermal catastrophe and isothermal collapse) marked
by a discontinuity of entropy or free energy are physically relevant.
no phase transition at all. We emphasize, however, that due to the
presence of long-lived metastable states, the first order phase
transitions and the plateaux are not relevant for the timescales of
interest (see Sect. 3). Only the zeroth order phase
transitions (gravothermal catastrophe and isothermal collapse) marked
by a discontinuity of entropy or free energy are physically relevant.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{EbetaJMU1e3.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg225.gif) |
Figure 11:
Caloric curve of the self-gravitating Fermi gas with
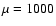 .
In the canonical ensemble, the temperature of
transition is determined by a Maxwell construction. For .
In the canonical ensemble, the temperature of
transition is determined by a Maxwell construction. For
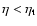 (
(
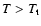 ), the gaseous states are global maxima
of free energy J[f] and the condensed states local maxima (see
the dashed curve). The situation is reversed for ), the gaseous states are global maxima
of free energy J[f] and the condensed states local maxima (see
the dashed curve). The situation is reversed for
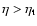 ( (
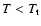 ). ). |
| Open with DEXTER |
4.2 Validity of the saddle point approximation near the transition point
In this section, we discuss the validity of the saddle point
approximation near the transition point. In the canonical
ensemble, the partition function can be written
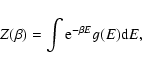 |
(51) |
where g(E) is the density of states with energy E. Introducing the entropy
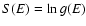 ,
we can rewrite the partition function as
,
we can rewrite the partition function as
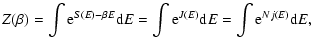 |
|
|
(52) |
where
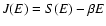 is the "free energy''. As explained in
Sect. 3, the equilibrium states correspond to maxima
of J. The condition J'(E)=0, leading to
is the "free energy''. As explained in
Sect. 3, the equilibrium states correspond to maxima
of J. The condition J'(E)=0, leading to
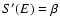 ,
determines
a series of equilibria
,
determines
a series of equilibria 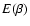 .
We shall consider the case where
the series of equilibria
.
We shall consider the case where
the series of equilibria 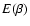 has the N-shape structure of
Fig. 11. The transition temperature
has the N-shape structure of
Fig. 11. The transition temperature
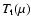 is
determined by a Maxwell construction (see Sect. 4.1). From Eq. (52), the distribution of energies at temperature T is given by
is
determined by a Maxwell construction (see Sect. 4.1). From Eq. (52), the distribution of energies at temperature T is given by
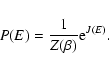 |
(53) |
It has a bimodal structure as shown in Fig. 12. The energies
where P(E) is maximum (denoted E1 and E2) correspond to
the stable (GFEM) and metastable (LFEM) states in Fig. 11. The energy
where P(E) is minimum (denoted E*) corresponds to the unstable
states (SP) in Fig. 11. For
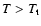 ,
gaseous
configurations (high energies) are more probable than condensed
configurations (low energies). This is the opposite for
,
gaseous
configurations (high energies) are more probable than condensed
configurations (low energies). This is the opposite for
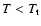 .
Note that the notion of "more probable'' is delicate since
the system can remain blocked in a metastable ("less probable'')
state for very long time, making that state the physically most relevant
state.
.
Note that the notion of "more probable'' is delicate since
the system can remain blocked in a metastable ("less probable'')
state for very long time, making that state the physically most relevant
state.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{ProbE.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg231.gif) |
Figure 12:
Distribution of energies
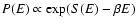 in the canonical ensemble for different values of
temperature (here
in the canonical ensemble for different values of
temperature (here 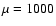 ). The entropy S(E) has been calculated
in the mean-field approximation, using Eq. (66). The
distribution of energies has a bimodal structure characteristic of a
first order canonical phase transition. For ). The entropy S(E) has been calculated
in the mean-field approximation, using Eq. (66). The
distribution of energies has a bimodal structure characteristic of a
first order canonical phase transition. For
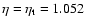 ,
the
two phases have the same probability. For ,
the
two phases have the same probability. For
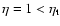 ,
the
gaseous phase (high energies) is the "most probable'' and for ,
the
gaseous phase (high energies) is the "most probable'' and for
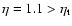 ,
the condensed phase (low energies) is the "most
probable'' in a strict sense. ,
the condensed phase (low energies) is the "most
probable'' in a strict sense. |
| Open with DEXTER |
For
 ,
the partition function can be
approximated by
,
the partition function can be
approximated by
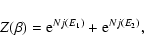 |
(54) |
where E1 and E2 are the energies at which J(E) is
maximum. We now wish to obtain the strict caloric curve
 defined in Sect. 3. When T is not too close from the transition temperature
defined in Sect. 3. When T is not too close from the transition temperature 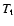 and
and
 ,
we need just keep the contribution of the global maximum of free energy as explained previously. To investigate
the situation close to the transition temperature, we rewrite the
partition function (54) as
,
we need just keep the contribution of the global maximum of free energy as explained previously. To investigate
the situation close to the transition temperature, we rewrite the
partition function (54) as
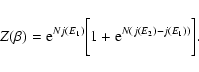 |
(55) |
Now, close to the transition point, we have
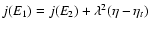 ,
where
,
where 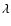 is a
constant of order unity depending on
is a
constant of order unity depending on 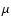 (see
Fig. 11, dashed line). Therefore,
(see
Fig. 11, dashed line). Therefore,
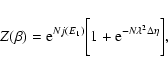 |
(56) |
where
 .
Thus, the saddle point
approximation is valid for
.
Thus, the saddle point
approximation is valid for
 .
This requires
increasing large values of N as we approach the transition
temperature
.
This requires
increasing large values of N as we approach the transition
temperature 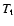 .
.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{entropie.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg239.gif) |
Figure 13:
Caloric curve of the self-gravitating Fermi gas with
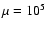 .
In the microcanonical ensemble, the energy of
transition is determined by a Maxwell construction. For .
In the microcanonical ensemble, the energy of
transition is determined by a Maxwell construction. For
 ,
the gaseous states are global
maxima of entropy S[f] and the condensed states are local maxima
(see the dashed curve). The situation is reversed for ,
the gaseous states are global
maxima of entropy S[f] and the condensed states are local maxima
(see the dashed curve). The situation is reversed for
 . .
|
| Open with DEXTER |
In the microcanonical ensemble, the density of states can be
written
![\begin{displaymath}%
g(E)=\int {\cal D}f {\rm e}^{S[f]}\delta (E-E[f])\delta (M-M[f]).
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img240.gif) |
(57) |
We shall consider the case where the series of equilibria 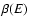 has the S-shape structure of Fig. 13. The transition
energy
has the S-shape structure of Fig. 13. The transition
energy
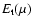 is determined by a Maxwell construction (see Sect. 4.1). For
is determined by a Maxwell construction (see Sect. 4.1). For
 ,
the density of states can be approximated
by
,
the density of states can be approximated
by
![\begin{displaymath}%
g(E)={\rm e}^{Ns[f_{1}]}+{\rm e}^{Ns[f_{2}]},
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img241.gif) |
(58) |
where f1 and f2 are the distribution functions
corresponding to the global and local maxima of entropy (we shall
denote by f* the distribution function corresponding to the
saddle point of entropy). The corresponding temperatures 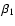 ,
,
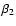 and
and 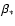 form the series of
equilibria
form the series of
equilibria 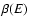 in Fig. 13. We now wish to
obtain the strict caloric curve
in Fig. 13. We now wish to
obtain the strict caloric curve
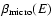 defined in Sect. 3.
When E is not too close from the transition energy
defined in Sect. 3.
When E is not too close from the transition energy 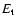 and
and
 ,
we need just keep the contribution of the
global maximum of entropy. To investigate the situation close to the
transition energy, we rewrite the density of states (58) as
,
we need just keep the contribution of the
global maximum of entropy. To investigate the situation close to the
transition energy, we rewrite the density of states (58) as
![\begin{displaymath}%
g(E)={\rm e}^{Ns[f_{1}]}\biggl\lbrack
1+{\rm e}^{N(s[f_{2}]-s[f_{1}])}\biggr\rbrack.
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img245.gif) |
(59) |
Now, close to the transition point, we have
![$s[f_1]=s[f_2]+\lambda'^{2}(\Lambda-\Lambda_{\rm t})$](/articles/aa/full/2005/10/aa1114/img246.gif) ,
where
,
where 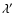 is
a constant of order unity depending on
is
a constant of order unity depending on 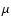 (see
Fig. 13). Therefore,
(see
Fig. 13). Therefore,
![\begin{displaymath}%
g(E)={\rm e}^{Ns[f_{1}]}\biggl\lbrack
1+{\rm e}^{-N\lambda^2\Delta\Lambda}\biggr\rbrack,
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img248.gif) |
(60) |
where
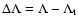 .
Thus, the saddle point
approximation is valid for
.
Thus, the saddle point
approximation is valid for
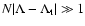 .
This
requires increasing large values of N as we approach the
transition point
.
This
requires increasing large values of N as we approach the
transition point 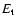 .
.
4.3 Comparison with other works
To conclude this section, we shall briefly compare our results with
those of previous works. A complementary discussion is given in
Chavanis (2002b).
The statistical mechanics of the classical self-gravitating gas
( ,
no small scale cut-off) has been first considered by
Antonov (1962), Lynden-Bell & Wood (1968) and Katz (1978) by using
thermodynamical potentials. Lynden-Bell & Wood (1968) realized the
importance of negative specific heats as a driving mechanism for the
gravothermal catastrophe. The paradox posed by the negative heat
capacity in statistical mechanics was solved by Thirring (1970) in
terms of ensemble inequivalence and further discussed by Lynden-Bell
& Lynden-Bell (1977) with the aid of a toy model. The occurence of
negative heat capacities in the reverse gradient isotherms of all first order phase transitions was demonstrated by Lynden-Bell
(1999). These results have been reviewed by Padmanabhan (1990) and
complements have been given by de Vega
& Sanchez (2002) and Chavanis (2002a, 2003).
,
no small scale cut-off) has been first considered by
Antonov (1962), Lynden-Bell & Wood (1968) and Katz (1978) by using
thermodynamical potentials. Lynden-Bell & Wood (1968) realized the
importance of negative specific heats as a driving mechanism for the
gravothermal catastrophe. The paradox posed by the negative heat
capacity in statistical mechanics was solved by Thirring (1970) in
terms of ensemble inequivalence and further discussed by Lynden-Bell
& Lynden-Bell (1977) with the aid of a toy model. The occurence of
negative heat capacities in the reverse gradient isotherms of all first order phase transitions was demonstrated by Lynden-Bell
(1999). These results have been reviewed by Padmanabhan (1990) and
complements have been given by de Vega
& Sanchez (2002) and Chavanis (2002a, 2003).
The hard sphere problem was explored by Aronson & Hansen (1972) who
gave an account of the phase transitions which had been suggested but
not demonstrated for that system. A similar discussion has been given
by Hertel & Thirring (1971) for self-gravitating fermions. These
authors consider a large small-scale cut-off (or a small system size)
and discuss first order phase transitions and Maxwell constructions in
the canonical ensemble. This corresponds to
Fig. 9. The distinction between the Emden-Jeans point 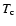 and the transition point
and the transition point
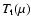 was emphasized by
Kiessling (1989) and Stahl et al. (1994). They argued that the
instability should take place at the transition point (where the free
energies of the two phases coincide), i.e. at a higher temperature
than the Emden-Jeans temperature:
was emphasized by
Kiessling (1989) and Stahl et al. (1994). They argued that the
instability should take place at the transition point (where the free
energies of the two phases coincide), i.e. at a higher temperature
than the Emden-Jeans temperature:
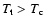 .
This is however not
the case in practice because of the long lifetime of metastable states
that we discuss here. The Emden-Jeans point
.
This is however not
the case in practice because of the long lifetime of metastable states
that we discuss here. The Emden-Jeans point 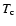 ,
which really
corresponds to Jeans instability threshold for box confined systems
(see Chavanis 2002a) is the most physically relevant collapse point.
,
which really
corresponds to Jeans instability threshold for box confined systems
(see Chavanis 2002a) is the most physically relevant collapse point.
Stahl et al. (1994) considered the case of a low small-scale cut-off
and discussed first order phase transitions in the microcanonical ensemble (see also Youngkins & Miller 2000). However,
they did not give the caloric curves 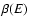 and the vertical
Maxwell constructions corresponding to
Fig. 10. These curves are important to settle the
thermodynamical stability of the system using the standard turning
point argument (Katz 1978, 2003). Chavanis
& Sommeria (1998) gave the series of equilibria of Fermi-Dirac
spheres but did not discuss the nature of phase transitions in
detail. A more complete discussion was given by Chavanis (2002b) for
self-gravitating fermions and by Chavanis & Ispolatov (2002) for a
soften potential. The phase diagrams in the
and the vertical
Maxwell constructions corresponding to
Fig. 10. These curves are important to settle the
thermodynamical stability of the system using the standard turning
point argument (Katz 1978, 2003). Chavanis
& Sommeria (1998) gave the series of equilibria of Fermi-Dirac
spheres but did not discuss the nature of phase transitions in
detail. A more complete discussion was given by Chavanis (2002b) for
self-gravitating fermions and by Chavanis & Ispolatov (2002) for a
soften potential. The phase diagrams in the 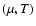 and
and 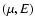 planes were given by Chavanis & Rieutord (2003). These studies show
how the series of equilibria depend on the "effective'' cut-off
parameter
planes were given by Chavanis & Rieutord (2003). These studies show
how the series of equilibria depend on the "effective'' cut-off
parameter 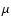 ,
leading to Z-shape and N-shape curves. Therefore,
they make the bridge between the classical spiral of Lynden-Bell &
Wood (no cut-off) and the N-shape caloric curve studied by Aronson
& Hansen (large cut-off).
,
leading to Z-shape and N-shape curves. Therefore,
they make the bridge between the classical spiral of Lynden-Bell &
Wood (no cut-off) and the N-shape caloric curve studied by Aronson
& Hansen (large cut-off).
The effect of the dimension of space D on the gravitational phase
transitions has been studied by Sire & Chavanis (2002) and Chavanis
(2004a). Finally, gravitational phase transitions in rotating systems
have been discussed by Votyakov et al. (2002) for a model on a lattice
with a large spacing and by Chavanis & Rieutord (2003) for
fermions. Dynamical models of gravitational phase transitions have
been considered by Ispolatov & Karttunen (2003) in the
microcanonical ensemble (by using molecular dynamics simulations) and
by Chavanis et al. (2002) in the canonical ensemble (by introducing a model of
self-gravitating Brownian particles). More recent simulations have been performed in the case of self-gravitating Brownian fermions (Chavanis et al. 2004).
5 The persistence of metastable states
5.1 Typical lifetime of a metastable state
In this section, we estimate the lifetime of a metastable state by
using an adaptation of the Kramers formula (Risken 1989). We start
first by the canonical ensemble. Close to the critical temperature  ,
see Fig. 11, the free energy F[f] has one global minimum
,
see Fig. 11, the free energy F[f] has one global minimum
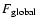 (stable GFEM), one local minimum
(stable GFEM), one local minimum
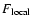 (metastable LFEM) and one saddle point
(metastable LFEM) and one saddle point
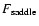 (unstable SP). We call
(unstable SP). We call
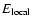 the energy of the metastable
equilibrium state and
the energy of the metastable
equilibrium state and
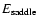 the energy of the unstable saddle
point. For a system initially prepared at
the energy of the unstable saddle
point. For a system initially prepared at
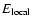 ,
the probability
of the energy E is
,
the probability
of the energy E is
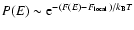 .
Now, if
the energy fluctuations drive the system past
.
Now, if
the energy fluctuations drive the system past
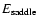 ,
it will
collapse. Therefore, the lifetime of the metastable state can be
estimated by
,
it will
collapse. Therefore, the lifetime of the metastable state can be
estimated by
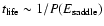 or
or
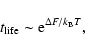 |
(61) |
where
 is the barrier of potential appropriate to our problem. Noting that
is the barrier of potential appropriate to our problem. Noting that
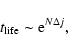 |
(62) |
we conclude that, except in the vicinity of the critical point  ,
the lifetime of a metastable state scales as
,
the lifetime of a metastable state scales as
 .
Therefore, metastable states (LFEM) are extremely robust in astrophysics and cannot be neglected, even if there exists states with
lower free energy (GFEM). To investigate the situation close to the
critical point
.
Therefore, metastable states (LFEM) are extremely robust in astrophysics and cannot be neglected, even if there exists states with
lower free energy (GFEM). To investigate the situation close to the
critical point 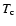 ,
we shall calculate the barrier of potential
,
we shall calculate the barrier of potential 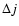 for the classical self-gravitating gas (
for the classical self-gravitating gas (
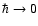 ). To that purpose, we use the results derived in a preceding paper (Chavanis 2002a).
). To that purpose, we use the results derived in a preceding paper (Chavanis 2002a).
We recall that the series of equilibria is parameterized by
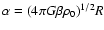 ,
where
,
where 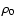 is the central
density. Introducing the Milne variables
is the central
density. Introducing the Milne variables
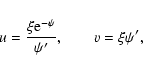 |
(63) |
and noting
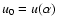 and
and
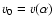 their values at the edge of the confining box, the thermodynamical parameters of the self-gravitating
gas are given by
their values at the edge of the confining box, the thermodynamical parameters of the self-gravitating
gas are given by
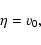 |
(64) |
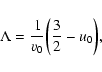 |
(65) |
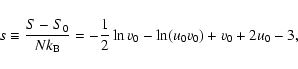 |
(66) |
where
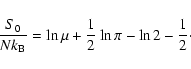 |
(67) |
The free energy per particle
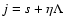 is
is
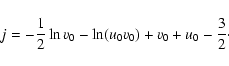 |
(68) |
We now expand the Milne variables close to the critical point
 .
Recalling that
.
Recalling that
 ,
,
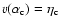 and
and
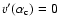 ,
we get
,
we get
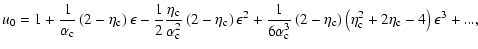 |
|
|
(69) |
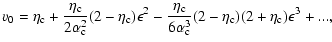 |
|
|
(70) |
where
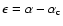 .
We also recall that
.
We also recall that
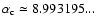 and
and
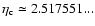 Substituting Eqs. (69) and (70) in Eq. (68), we find that
Substituting Eqs. (69) and (70) in Eq. (68), we find that
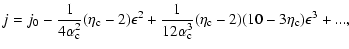 |
|
|
(71) |
where
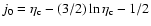 .
On the other hand, recalling that
.
On the other hand, recalling that
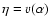 ,
we get
,
we get
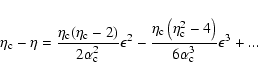 |
(72) |
Eliminating 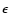 from the foregoing relations, we finally obtain
from the foregoing relations, we finally obtain
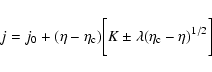 |
(73) |
with
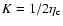 and
and
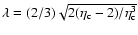 .
We note that
.
We note that
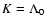 where
where
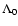 is the normalized energy at the
critical temperature (this comes from the fact that
is the normalized energy at the
critical temperature (this comes from the fact that
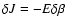 ). Equation (73) reproduces the cusp at
). Equation (73) reproduces the cusp at
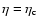 formed by the curve
formed by the curve 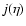 in
Fig. 11. Since
in
Fig. 11. Since
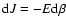 ,
,
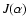 and
and
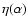 are extrema at the same points in the series of equilibria, which is at the origin of the cusp. From Eq. (73), the barrier of free energy near the critical point
are extrema at the same points in the series of equilibria, which is at the origin of the cusp. From Eq. (73), the barrier of free energy near the critical point
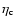 is given by
is given by
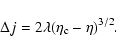 |
(74) |
Accordingly, the lifetime of the metastable state scales as
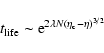 |
(75) |
with
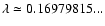 Metastable states are therefore robust if
Metastable states are therefore robust if
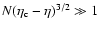 .
Note that if we had estimated the
lifetime of the metastable state by
.
Note that if we had estimated the
lifetime of the metastable state by
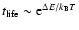 ,
we would have obtained
,
we would have obtained
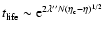 with
with
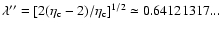 We see that entropic
effects modify the power of
We see that entropic
effects modify the power of
 in the expression of the
metastable state lifetime. Returning to Eq. (75), the
temperature of collapse
in the expression of the
metastable state lifetime. Returning to Eq. (75), the
temperature of collapse 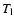 taking into account finite N effects can be
estimated by
taking into account finite N effects can be
estimated by
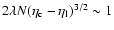 .
This leads to
.
This leads to
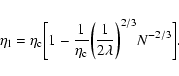 |
(76) |
A numerical application gives
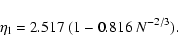 |
(77) |
In the microcanonical ensemble, the lifetime of a metastable state can be estimated by
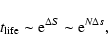 |
(78) |
where 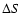 is the entropic barrier. By performing a study
similar to the previous one close to the turning point of energy
is the entropic barrier. By performing a study
similar to the previous one close to the turning point of energy
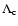 (see Fig. 13), we find that
(see Fig. 13), we find that
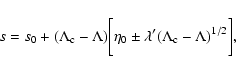 |
(79) |
with
s0=-0.192962...,
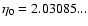 and
and
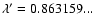 Therefore,
Therefore,
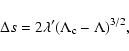 |
(80) |
and
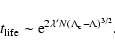 |
(81) |
The energy of collapse 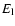 taking into account finite N effects can be estimated by
taking into account finite N effects can be estimated by
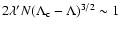 .
This leads to
.
This leads to
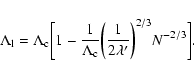 |
(82) |
A numerical application gives
 |
(83) |
This corresponds to a density contrast
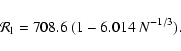 |
(84) |
These results are similar to those found by Katz & Okamoto (2000) by
analyzing the microcanonical fluctuations of isothermal spheres. In
particular, the scaling with N is the same. In the following
section, we apply their theory of fluctuations to the canonical
ensemble and show the relation with the preceding approach.
5.2 Canonical fluctuations in isothermal spheres
The canonical partition function can be written
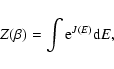 |
(85) |
where
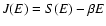 .
As before, we shall consider the situation where J(E) has two maxima (stable) and one minimum (unstable). This corresponds to the caloric curve of Fig. 11. We shall
be interested here by the metastable state, i.e. the local
maximum of J(E). Thus, we eliminate "by hands'' the contribution of
the global maximum in the integral. Expanding J(E) around the local
maximum up to second order, we obtain
.
As before, we shall consider the situation where J(E) has two maxima (stable) and one minimum (unstable). This corresponds to the caloric curve of Fig. 11. We shall
be interested here by the metastable state, i.e. the local
maximum of J(E). Thus, we eliminate "by hands'' the contribution of
the global maximum in the integral. Expanding J(E) around the local
maximum up to second order, we obtain
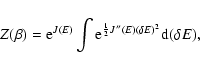 |
(86) |
where E now refers to the energy of the metastable state and 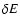 is a fluctuation around equilibrium. According to the foregoing equation,
the probability of the fluctuation
is a fluctuation around equilibrium. According to the foregoing equation,
the probability of the fluctuation 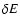 is given by
is given by
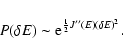 |
(87) |
Noting that
J''(E)=S''(E) and recalling that
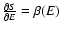 at equilibrium, we can rewrite the foregoing expression as
at equilibrium, we can rewrite the foregoing expression as
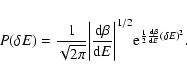 |
(88) |
This formula shows that only equilibrium states with positive specific heats
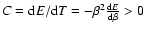 are stable in the canonical ensemble. The variance of the fluctuations of energy is given by
the usual formula
are stable in the canonical ensemble. The variance of the fluctuations of energy is given by
the usual formula
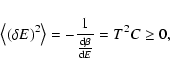 |
(89) |
which can also be directly derived from the exact N-body
distribution function (39) in a classical way. These results
are valid on the whole gaseous branch of Fig. 11. If we
now examine the situation close to the critical point (
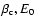 )
where
)
where
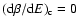 ,
we have to first order
,
we have to first order
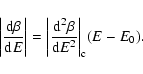 |
(90) |
We note E' the energy of the unstable saddle point of free energy J at temperature T. Close to the critical point (
 )
we can approximate the caloric curve
)
we can approximate the caloric curve  by a parabole. Thus, E' is related to E, the energy of the local maximum of free energy J at temperature T, by
by a parabole. Thus, E' is related to E, the energy of the local maximum of free energy J at temperature T, by
Using the criterion of Katz & Okamoto (2000), adapted to the
canonical ensemble, we define the temperature of collapse as the
temperature  at which the typical fluctuations of energy
at which the typical fluctuations of energy
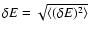 are of the same order
as the difference E-E'. Indeed, as we approach the critical point (
are of the same order
as the difference E-E'. Indeed, as we approach the critical point (
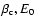 )
the fluctuations of energy become so important
(since the specific heat diverges) that the system can overcome the
barrier of potential played by the saddle point of free energy and collapse
(eventually reaching the global maximum of J). Thus, for finite N systems, gravitational collapse can occur before the ending (
)
the fluctuations of energy become so important
(since the specific heat diverges) that the system can overcome the
barrier of potential played by the saddle point of free energy and collapse
(eventually reaching the global maximum of J). Thus, for finite N systems, gravitational collapse can occur before the ending (
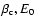 )
of the metastable branch (spinodal
point). According to the preceding criterion, the temperature of
collapse is determined by the condition
)
of the metastable branch (spinodal
point). According to the preceding criterion, the temperature of
collapse is determined by the condition
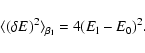 |
(92) |
Using Eqs. (89) and (90), we obtain
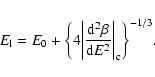 |
(93) |
It is more logical to write this criterion in terms of the temperature  .
Close to the critical point, we have
.
Close to the critical point, we have
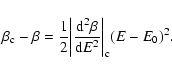 |
(94) |
Thus, using Eq. (93), we get
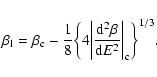 |
(95) |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{collN.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg337.gif) |
Figure 14:
Caloric curve showing metastable states (local
maxima of J) and unstable equilibria (saddle points of J) in
the canonical ensemble for classical particles (
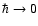 ). As we approach the critical temperature ). As we approach the critical temperature
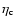 ,
the
fluctuations of energy increase considerably allowing the system
to collapse before the end of the metastable branch (spinodal
point). The temperature of collapse ,
the
fluctuations of energy increase considerably allowing the system
to collapse before the end of the metastable branch (spinodal
point). The temperature of collapse 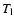 is the temperature
at which the typical fluctuations of energy are of the same order
as the energy difference
is the temperature
at which the typical fluctuations of energy are of the same order
as the energy difference
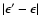 . . |
| Open with DEXTER |
We can obtain more explicit results in the case of classical
isothermal spheres (see Fig. 14). Introducing the
usual dimensionless parameters
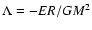 and
and
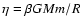 ,
the foregoing relation can be rewritten
,
the foregoing relation can be rewritten
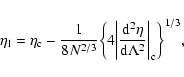 |
(96) |
Now, we have (see Chavanis 2002a)
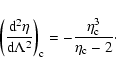 |
(97) |
Therefore, the temperature of collapse for finite N systems is given by
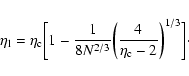 |
(98) |
A numerical application gives
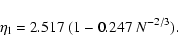 |
(99) |
This estimate can be compared with Eq. (77) which has the
same scaling with N. Of course, we should not give too much credit
on the numerical factor in front of N-2/3 since the criterion for determining  is
essentially phenomenological. The corresponding energy
is
essentially phenomenological. The corresponding energy
 can be deduced from Eq. (94) and is given by
can be deduced from Eq. (94) and is given by
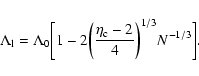 |
(100) |
It may also be of interest to determine the corresponding density
contrast
 .
To that purpose, we start from the
formula (see Chavanis 2002a)
.
To that purpose, we start from the
formula (see Chavanis 2002a)
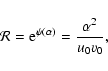 |
(101) |
and we use the expansion (69) and (70) of the Milne
variables. This yields
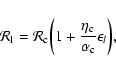 |
(102) |
where
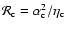 .
Now,
.
Now,
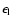 is determined by Eqs. (72) and (98) yielding
is determined by Eqs. (72) and (98) yielding
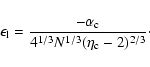 |
(103) |
Substituting this result in Eq. (102) we finally obtain
 |
(104) |
or, with numerical values,
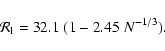 |
(105) |
The above theory thus predicts that, for finite N systems, the
collapse should take place slightly before the canonical spinodal
point
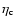 due to the enhancement of energy fluctuations as we
approach this critical point.
Similar conclusions can be obtained by
developing a theory of hydrodynamic fluctuations showing that the
density fluctuations become large before the point of ordinary
instability is reached (Monaghan 1978). The Monte Carlo simulations of
de Vega & Sanchez (2002) in the canonical ensemble (with N=2000particles) reveal that the collapse indeed takes place before the
critical point. However, the collapse occurs apparently at the point
where the isothermal compressibility
due to the enhancement of energy fluctuations as we
approach this critical point.
Similar conclusions can be obtained by
developing a theory of hydrodynamic fluctuations showing that the
density fluctuations become large before the point of ordinary
instability is reached (Monaghan 1978). The Monte Carlo simulations of
de Vega & Sanchez (2002) in the canonical ensemble (with N=2000particles) reveal that the collapse indeed takes place before the
critical point. However, the collapse occurs apparently at the point
where the isothermal compressibility
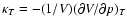 diverges. This corresponds to an inverse normalized
temperature
diverges. This corresponds to an inverse normalized
temperature
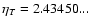 It is sensibly smaller than the
value obtained from Eq. (99) with N=2000. The same
discrepency with the prediction of Katz & Okamoto (2000) is found in
the microcanonical ensemble by de Vega & Sanchez (2002). These
results seem to indicate that the higher collapse temperature and
energy found in Monte Carlo simulations are not due to finite N effects. They seem to be independent on N and correspond to other critical points that do not coincide with the spinodal point. We intend to perform independent Monte Carlo simulations to check these
results.
It is sensibly smaller than the
value obtained from Eq. (99) with N=2000. The same
discrepency with the prediction of Katz & Okamoto (2000) is found in
the microcanonical ensemble by de Vega & Sanchez (2002). These
results seem to indicate that the higher collapse temperature and
energy found in Monte Carlo simulations are not due to finite N effects. They seem to be independent on N and correspond to other critical points that do not coincide with the spinodal point. We intend to perform independent Monte Carlo simulations to check these
results.
5.3 General expression of the potential barrier
We can use the preceding approach to obtain a simple approximate
expression of the potential barrier close to the critical point
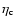 .
Consider a system at fixed temperature T and denote by E its equilibrium energy such that J'(E)=0 (we
consider here that E is the energy of the metastable state).
For a fluctuation
.
Consider a system at fixed temperature T and denote by E its equilibrium energy such that J'(E)=0 (we
consider here that E is the energy of the metastable state).
For a fluctuation
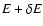 ,
we have seen that the variation of
free energy
,
we have seen that the variation of
free energy
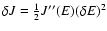 can be
expressed as
can be
expressed as
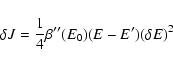 |
(106) |
where we have assumed that E is close to the critical point E0and, as before, E' is the energy of the minimum of J at
temperature T. We can use this expression to estimate the potential
barrier
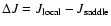 .
Thus, setting
.
Thus, setting
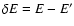 ,
we get
,
we get
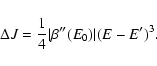 |
(107) |
Using Eq. (94) to express this relation in terms of the
temperature, we finally obtain
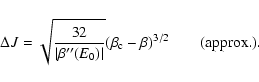 |
(108) |
This is an estimate, because the curve J(E) is not just a parabole
between E and E' as it has been assumed to get Eq. (106)
from Eq. (91). Using Eq. (97), this approximate
expression can be written
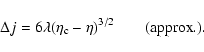 |
(109) |
It differs from the exact expression (74) by a factor 3.
Noting that
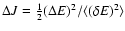 ,
according to Eqs. (88) and (89), the
criterion (92) of Katz & Okamoto (2000) discussed previously is
equivalent to
,
according to Eqs. (88) and (89), the
criterion (92) of Katz & Okamoto (2000) discussed previously is
equivalent to
 .
Alternatively, writing
.
Alternatively, writing
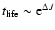 ,
the criterion that we have used to get Eq. (76)
corresponds to
,
the criterion that we have used to get Eq. (76)
corresponds to
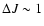 .
Therefore, on a qualitative point of
view, the approaches of Sects. 5.1 and 5.2 are
equivalent. They slightly differ on the details (definition of
collapse temperature, estimate of
.
Therefore, on a qualitative point of
view, the approaches of Sects. 5.1 and 5.2 are
equivalent. They slightly differ on the details (definition of
collapse temperature, estimate of 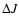 )
explaining why
Eqs. (77) and (99) are not exactly the same.
)
explaining why
Eqs. (77) and (99) are not exactly the same.
We can also try to calculate 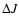 by working directly on the
series of equilibria
by working directly on the
series of equilibria 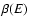 .
Taking E as a control parameter, we
have
.
Taking E as a control parameter, we
have
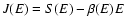 .
Noting that
.
Noting that
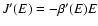 ,
,
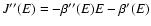 and
and
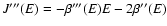 ,
and expanding J(E) close to the
critical point where
,
and expanding J(E) close to the
critical point where
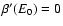 ,
we get
,
we get
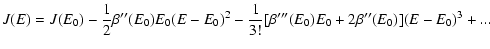 |
|
|
(110) |
Using the relation
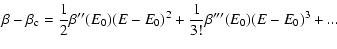 |
|
|
(111) |
between the temperature and the energy close to the critical
point, we find that
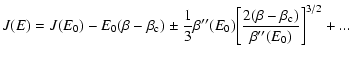 |
|
|
(112) |
Therefore, close to the critical point, the barrier of free energy is
exactly given by
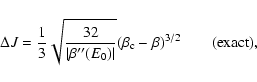 |
(113) |
which returns Eq. (74).
We can use the same type of approach in the microcanonical
ensemble to obtain a simple expression of the
entropic barrier close to the critical point
 .
Consider a system at fixed energy E and denote by
.
Consider a system at fixed energy E and denote by  its
equilibrium temperature (we consider here that
its
equilibrium temperature (we consider here that  is the temperature of the metastable
state). For a fluctuation
is the temperature of the metastable
state). For a fluctuation
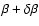 ,
the variation of
entropy can be expressed as (see Katz & Okamoto 2000 for details)
,
the variation of
entropy can be expressed as (see Katz & Okamoto 2000 for details)
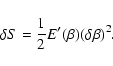 |
(114) |
Assuming that 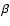 is close to the critical point
is close to the critical point 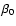 ,
and using arguments similar to those developed previously, we get
,
and using arguments similar to those developed previously, we get
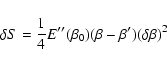 |
(115) |
where  is the inverse temperature of the saddle point of
entropy. We can use this expression to estimate the entropic barrier
is the inverse temperature of the saddle point of
entropy. We can use this expression to estimate the entropic barrier
 .
Thus, setting
.
Thus, setting
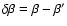 ,
we find that
,
we find that
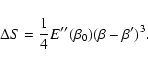 |
(116) |
Using
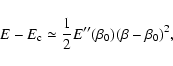 |
(117) |
to express the temperature as a function of the energy close to
the critical point, we finally obtain
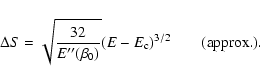 |
(118) |
We note that Eqs. (108) and (118) are symmetrical
provided that we interchange E and 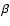 .
Evaluating numerically
.
Evaluating numerically
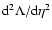 at the critical point
at the critical point
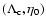 ,
this approximate expression can be written
,
this approximate expression can be written
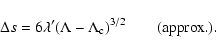 |
(119) |
It differs from the exact expression (80) by a factor 3.
We can also try to calculate  directly from the series of
equilibria
directly from the series of
equilibria 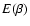 .
Taking
.
Taking 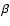 as a control parameter, we have
as a control parameter, we have
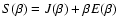 and we recall that
and we recall that
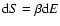 and
and
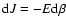 .
Thus
.
Thus
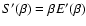 ,
,
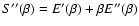 and
and
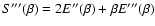 .
Expanding
.
Expanding 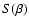 close to the critical point where
close to the critical point where
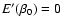 ,
we get
,
we get
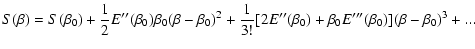 |
|
|
(120) |
Using the relation
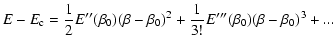 |
|
|
(121) |
between the energy and the temperature close to the critical
point, we find that
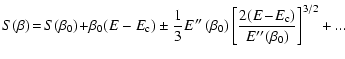 |
|
|
(122) |
Therefore, close to the critical point, the barrier of entropy is
exactly given by
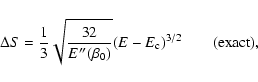 |
(123) |
which returns Eq. (80).
6 Relation to the Kramers problem
6.1 The Fokker-Planck equation
In the preceding section, we have used the Kramers formula to estimate
the lifetime of metastable states in self-gravitating systems. We
would like now to justify this formula from first principles. In
order to determine the lifetime of a metastable state, we need to
introduce a dynamical model. In the canonical ensemble, we can
consider a system of self-gravitating Brownian particles (Chavanis et al. 2002) described by the stochastic equations
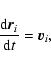 |
(124) |
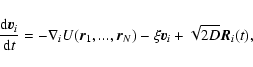 |
(125) |
where
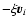 is a friction force and
is a friction force and
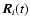 is a
white noise satisfying
is a
white noise satisfying
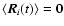 and
and
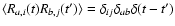 ,
where a,b=1,2,3 refer to the coordinates of space and
i,j=1,...,Nto the particles. The particles interact via the gravitational
potential
,
where a,b=1,2,3 refer to the coordinates of space and
i,j=1,...,Nto the particles. The particles interact via the gravitational
potential
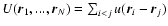 where
where
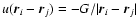 .
The inverse temperature
.
The inverse temperature 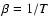 is related to the
diffusion coefficient through the Einstein relation
is related to the
diffusion coefficient through the Einstein relation
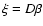 .
.
Using standard stochastic processes, we can derive the N-body
Fokker-Planck equation (see Chavanis 2004b)
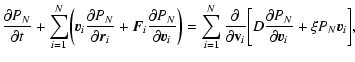 |
|
|
(126) |
where
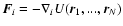 is the gravitational force acting on particle i and
is the gravitational force acting on particle i and
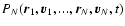 is the N-body distribution function. Its stationary states correspond to the canonical distribution
is the N-body distribution function. Its stationary states correspond to the canonical distribution
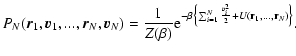 |
|
|
(127) |
If we implement a mean-field approximation (see Chavanis 2004b), we can
show that the distribution function
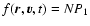 is
solution of the Kramers-Poisson system. However, this is not the
approach that we shall consider here.
is
solution of the Kramers-Poisson system. However, this is not the
approach that we shall consider here.
We wish to obtain the time evolution of the distribution of energies P(E,t). To that purpose, we shall follow a method similar to that developed by Kramers (1940) in his investigation of the escape of Brownian particles over a potential barrier. The difference is that we
work here in a 6N dimensional phase space. Assuming that
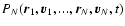 depends only on
energy
depends only on
energy
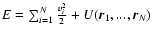 and time t, and averaging the Fokker-Planck Eq. (126) on the hypersurface of energy E, we show in Appendix B that
and time t, and averaging the Fokker-Planck Eq. (126) on the hypersurface of energy E, we show in Appendix B that
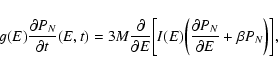 |
(128) |
where g(E) is the density of states and I(E) is the phase space hypervolume with energy less than E (thus
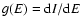 ). Now, the distribution of energies is given by
). Now, the distribution of energies is given by
|
P(E,t)=PN(E,t)g(E).
|
(129) |
At equilibrium, using Eq. (127), we have
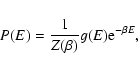 |
(130) |
which returns Eq. (53). Out of equilibrium, substituting
Eqs. (129) into (128) and simplifying the resulting
expressions, we finally obtain
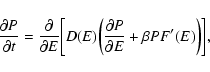 |
(131) |
where
D(E)=3M I(E)/g(E) and
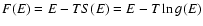 is the free
energy. This is similar to the Fokker-Planck equation describing the
stochastic motion of a particle in a potential where
the energy E plays the role of the position x and where the free
energy F(E) plays the role of the potential U(x). In the
following, we shall assume that the free energy F(E) has a local
minimum at EA (metastable), a local maximum at EB (unstable)
and a global minimum at
is the free
energy. This is similar to the Fokker-Planck equation describing the
stochastic motion of a particle in a potential where
the energy E plays the role of the position x and where the free
energy F(E) plays the role of the potential U(x). In the
following, we shall assume that the free energy F(E) has a local
minimum at EA (metastable), a local maximum at EB (unstable)
and a global minimum at 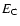 .
A typical situation is illustrated in
Fig. 15. We shall prepare a large number
.
A typical situation is illustrated in
Fig. 15. We shall prepare a large number
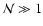 of systems close to the energy EA with the canonical distribution (130).
Thus,
of systems close to the energy EA with the canonical distribution (130).
Thus,
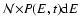 gives the number of
systems with energy between E and
gives the number of
systems with energy between E and
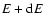 at time t. As time goes
on, a fraction of these systems reaches the energy EB and
undergoes gravitational collapse towards
at time t. As time goes
on, a fraction of these systems reaches the energy EB and
undergoes gravitational collapse towards 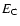 .
Therefore, we adopt
the boundary condition
.
Therefore, we adopt
the boundary condition
Our aim, now, is to estimate the current of diffusion past EB and the typical lifetime of metastable states.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{EsMU10e3.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg423.gif) |
Figure 15:
Illustration of the barrier of free energy corresponding to
Fig. 12. Point A corresponds to the gaseous
metastable state and point B is the unstable solution creating a
barrier for reaching the condensed state C. |
| Open with DEXTER |
6.2 The stationary solutions
The stationary solutions of Eq. (131) are of the form
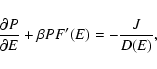 |
(133) |
where J<0 is the current of diffusion in energy space. Using the boundary condition (132), the solution of Eq. (133) reads
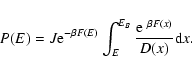 |
(134) |
The current of diffusion can therefore be expressed as
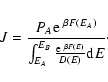 |
(135) |
To estimate the probability PA, we shall approximate the curve F(E) close to A by a parabole. We thus make the expansion
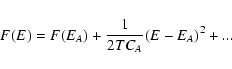 |
(136) |
where we have used
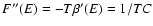 where
where
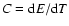 is the
specific heat. Therefore,
is the
specific heat. Therefore,
On the other hand, the integral in Eq. (135) is dominated by the value of the integrand close to B. Making the same quadratic expansion as in Eq. (136), we get
where we recall that CB<0 for the unstable solution. We thus obtain
the expression of the current
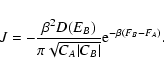 |
(139) |
This expression involving the barrier of
free energy 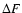 ,
is similar to the one obtained by Kramers (1940) in his
classical study. In our case, the parameters have a thermodynamical
interpretation while Kramers considers a dynamical system in a
potential U(x).
,
is similar to the one obtained by Kramers (1940) in his
classical study. In our case, the parameters have a thermodynamical
interpretation while Kramers considers a dynamical system in a
potential U(x).
6.3 The escape time
The preceding approach assumes that the population of systems that are
introduced at A is continuously renewed so as to counterbalance the
population of systems that are lost at B and maintain a stationary
regime. We shall now relax this simplifying assumption and look for
decaying solutions of Eq. (131) of the form
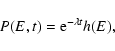 |
(140) |
where h(E) satisfies the differential equation
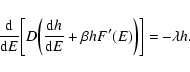 |
(141) |
Assuming that close to EA the system is at equilibrium, the foregoing equation can be integrated into
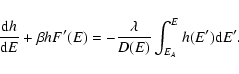 |
(142) |
In usual situations, the eigenvalue 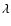 is expected to be small
as it corresponds to the inverse lifetime of the metastable states. We
thus consider the perturbative expansion of h in powers of
is expected to be small
as it corresponds to the inverse lifetime of the metastable states. We
thus consider the perturbative expansion of h in powers of 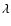 and write
and write
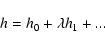 |
(143) |
Substituting this expansion in Eq. (142) and identifying terms of equal order, we obtain the differential equations
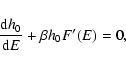 |
(144) |
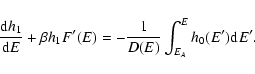 |
(145) |
The first equation integrates into
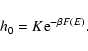 |
(146) |
Substituting this result in Eq. (145), we get
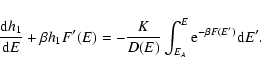 |
(147) |
The solution of this first order differential equation can be written
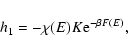 |
(148) |
where the function 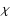 is defined by
is defined by
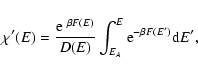 |
(149) |
with
 .
Therefore, in the approximation
.
Therefore, in the approximation
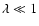 ,
the solution of Eq. (131) is
,
the solution of Eq. (131) is
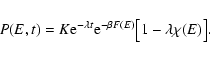 |
(150) |
The eigenvalue 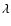 is determined by the boundary condition (132) yielding
is determined by the boundary condition (132) yielding
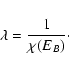 |
(151) |
Therefore, the lifetime of the metastable state is given by
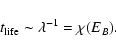 |
(152) |
We can now try to simplify this expression. First, we approximate Eq. (149) by
After integrating and setting E=EB, we obtain
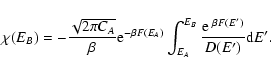 |
(154) |
With the additional approximation
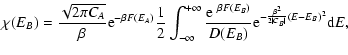 |
|
|
(155) |
we finally get
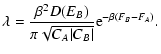 |
|
|
(156) |
Therefore, the lifetime of a metastable state behaves as
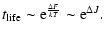 |
|
|
(157) |
We note that the expression of 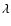 is similar to the expression (139) obtained for the current J. The connexion is the
following. In the non-stationary case, the current of diffusion at EB is
is similar to the expression (139) obtained for the current J. The connexion is the
following. In the non-stationary case, the current of diffusion at EB is
Hence, normalizing the current by the exponential decay of the density probability, we get
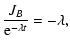 |
|
|
(159) |
which is equivalent to Eq. (139).
In the preceding analysis, we have worked in the canonical ensemble
because the Brownian model (124) and (125) is easier to study
than the N-stars Hamiltonian model, while exhibiting qualitatively
the same phenomena (phase transitions, metastable states etc.). We
expect to have symmetric expressions in the microcanonical ensemble
with the correspondance
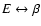 and
and
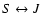 .
This study is left for a future work.
.
This study is left for a future work.
7 Conclusion
In this paper, we have completed previous investigations concerning
the statistical mechanics of self-gravitating systems in
microcanonical and canonical ensembles. The microcanonical ensemble is
the proper description of isolated Hamiltonian systems such as
globular clusters (Binney & Tremaine 1987). The canonical ensemble is
relevant for systems in contact with a heat bath of non-gravitational
origin. It is also the proper description of stochastically forced
systems such as self-gravitating Brownian particles (Chavanis et al. 2002). We have justified the mean-field approximation, in a proper thermodynamic limit
 with
with
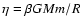 and
and
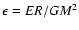 fixed, from the equilibrium BBGKY hierarchy
(Appendix A). In this thermodynamic limit, the equilibrium state is determined by a maximization problem: the maximization of entropy at
fixed mass and energy in the microcanonical ensemble and the
minimization of free energy at fixed mass and temperature in the
canonical ensemble. This determines the most probable
macroscopic distribution of particles at equilibrium. This can also be
seen as a saddle point approximation in the functional integral
formulation of the density of states and partition function. The
probability of the distribution function is given by a Cramer formula
fixed, from the equilibrium BBGKY hierarchy
(Appendix A). In this thermodynamic limit, the equilibrium state is determined by a maximization problem: the maximization of entropy at
fixed mass and energy in the microcanonical ensemble and the
minimization of free energy at fixed mass and temperature in the
canonical ensemble. This determines the most probable
macroscopic distribution of particles at equilibrium. This can also be
seen as a saddle point approximation in the functional integral
formulation of the density of states and partition function. The
probability of the distribution function is given by a Cramer formula
![${\cal P}[f]\sim {\rm e}^{Ns[f]}$](/articles/aa/full/2005/10/aa1114/img467.gif) or
or
![${\cal P}[f]\sim {\rm e}^{Nj[f]}$](/articles/aa/full/2005/10/aa1114/img468.gif) ,
which
constitutes a result of Large Deviations (for a regularized
gravitational potential). We have shown that the saddle point
approximation is less and less accurate close to the transition point
since the condition
,
which
constitutes a result of Large Deviations (for a regularized
gravitational potential). We have shown that the saddle point
approximation is less and less accurate close to the transition point
since the condition
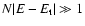 (in microcanonical ensemble) or
(in microcanonical ensemble) or
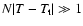 (in canonical ensemble) must be satisfied.
(in canonical ensemble) must be satisfied.
We have also argued that the lifetime of metastable states (local
entropy maxima) scales as
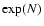 due to the long-range nature
of the interaction. Therefore, the importance of these metastable
states is considerable and they cannot be simply ignored. Metastable
states are in fact stable and they correspond to observed
structures in the universe such as globular clusters. The preceding
estimate must, however, be revised close to the critical point. By
solving a Fokker-Planck equation, we have shown that the lifetime of
metastable states is given by the Kramers formula involving the
barrier of entropy or free energy. These barriers have been calculated
exactly close to the Antonov energy
due to the long-range nature
of the interaction. Therefore, the importance of these metastable
states is considerable and they cannot be simply ignored. Metastable
states are in fact stable and they correspond to observed
structures in the universe such as globular clusters. The preceding
estimate must, however, be revised close to the critical point. By
solving a Fokker-Planck equation, we have shown that the lifetime of
metastable states is given by the Kramers formula involving the
barrier of entropy or free energy. These barriers have been calculated
exactly close to the Antonov energy 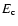 (in microcanonical
ensemble) and close to the Jeans-Emden temperature
(in microcanonical
ensemble) and close to the Jeans-Emden temperature 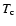 (in
canonical ensemble). We have obtained the estimates
(in
canonical ensemble). We have obtained the estimates
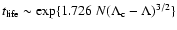 (in microcanonical ensemble) and
(in microcanonical ensemble) and
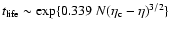 (in canonical ensemble) so that the
lifetime decreases as we approach
(in canonical ensemble) so that the
lifetime decreases as we approach  or
or  .
This implies that
the collapse will take place slightly above
.
This implies that
the collapse will take place slightly above  or
or 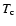 at an
energy
at an
energy
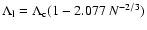 or temperature
or temperature
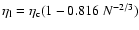 .
Similar conclusions have been
reached by Katz & Okamoto (2000). Yet, these predictions do not seem
to be consistent with the Monte Carlo simulations of de Vega &
Sanchez (2002), although they find that the collapse indeed takes
place slightly before the critical point. Independent simulations are
under preparation to check that point. In a recent work (Chavanis
2004b; and Appendix A), we have shown that the mean-field approximation
becomes inaccurate close to the critical point. This may be a reason
for the discrepency between the theory of fluctuations exposed here
and the numerical simulations of de Vega & Sanchez (2002).
.
Similar conclusions have been
reached by Katz & Okamoto (2000). Yet, these predictions do not seem
to be consistent with the Monte Carlo simulations of de Vega &
Sanchez (2002), although they find that the collapse indeed takes
place slightly before the critical point. Independent simulations are
under preparation to check that point. In a recent work (Chavanis
2004b; and Appendix A), we have shown that the mean-field approximation
becomes inaccurate close to the critical point. This may be a reason
for the discrepency between the theory of fluctuations exposed here
and the numerical simulations of de Vega & Sanchez (2002).
Finally, a part of our discussion was devoted to answer the critics
raised by Gross (2003, 2004) in recent comments. This author argues
that the microcanonical entropy
 and the microcanonical
temperature
and the microcanonical
temperature
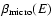 must be single valued. This is true in
a strict sense, but the problem is richer than that because of the
existence of long-lived metastable states. Therefore, the physical caloric curve/series of equilibria
must be single valued. This is true in
a strict sense, but the problem is richer than that because of the
existence of long-lived metastable states. Therefore, the physical caloric curve/series of equilibria 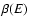 is
multi-valued and leads to "dinosaur's necks'' and special
"microcanonical phase transitions'' (Chavanis 2002b). This is
specific to systems with long-range interactions in view of the long
lifetime of metastable states (local entropy maxima). These results
have stimulated a general classification of phase transitions by
Bouchet & Barré (2005). Microcanonical phase transitions (as in
Fig. 1) have not been fully appreciated by Gross and his
collaborators because their studies (e.g., Votyakov et al. 2002)
consider a large small-scale cut-off for which the caloric curve
looks like Fig. 2 and is univalued. If these authors reduce
their small-scale cut-offs, they will see "dinosaurs'' appear!
is
multi-valued and leads to "dinosaur's necks'' and special
"microcanonical phase transitions'' (Chavanis 2002b). This is
specific to systems with long-range interactions in view of the long
lifetime of metastable states (local entropy maxima). These results
have stimulated a general classification of phase transitions by
Bouchet & Barré (2005). Microcanonical phase transitions (as in
Fig. 1) have not been fully appreciated by Gross and his
collaborators because their studies (e.g., Votyakov et al. 2002)
consider a large small-scale cut-off for which the caloric curve
looks like Fig. 2 and is univalued. If these authors reduce
their small-scale cut-offs, they will see "dinosaurs'' appear!
On a mathematical point of view, the statistical mechanics of the
classical self-gravitating gas ( )
poses problem because the
density of states diverges even if the system is enclosed within a
box, due to the formation of binaries. Our approach suggests the
following procedure to rigorously carry out a statistical mechanics:
first, introduce a soften potential with small-scale cut-off
)
poses problem because the
density of states diverges even if the system is enclosed within a
box, due to the formation of binaries. Our approach suggests the
following procedure to rigorously carry out a statistical mechanics:
first, introduce a soften potential with small-scale cut-off
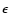 .
We can then perform the statistical mechanics
properly. Keep only the metastable states defined as local
maxima of entropy. For
.
We can then perform the statistical mechanics
properly. Keep only the metastable states defined as local
maxima of entropy. For
 ,
they are physically
relevant since they have infinite lifetime. Finally, take the limit
,
they are physically
relevant since they have infinite lifetime. Finally, take the limit
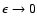 (the structure of the gaseous metastable
states is independent on the cut-off for
(the structure of the gaseous metastable
states is independent on the cut-off for
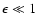 ). We note
that the order of the limits
). We note
that the order of the limits
 and
and
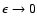 is not interchangeable. It should be
made clear that these metastable states exist only in "boxes'', or
for truncated isothermal systems, at less than the Antonov critical
radius (this concerns about
is not interchangeable. It should be
made clear that these metastable states exist only in "boxes'', or
for truncated isothermal systems, at less than the Antonov critical
radius (this concerns about  of tidally truncated globular
clusters). Now, real star clusters do not leave in boxes so it is
always the evolution beyond the Antonov point (core collapse) that
matters eventually especially as the mass segregation decreases the
Antonov radius. This ultimate evolution leads to the formation of
binaries.
of tidally truncated globular
clusters). Now, real star clusters do not leave in boxes so it is
always the evolution beyond the Antonov point (core collapse) that
matters eventually especially as the mass segregation decreases the
Antonov radius. This ultimate evolution leads to the formation of
binaries.
Acknowledgements
I am grateful to J. Katz for stimulating
discussions. I also thank the referee for additional comments. While
this paper was in course of redaction, I became aware of a preprint by
Antoni et al. [cond-mat/0401177] (Europhys. Lett., 66, 645 (2004))
where similar arguments about the lifetime of metastable states for a
toy model with long-range interactions have been developed
independently.
Appendix A: Justification of the mean-field approximation
from the equilibrium BBGKY hierarchy
In this Appendix, we show that the mean-field approximation is
exact for self-gravitating systems in a properly defined
thermodynamic limit
 with
with
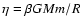 and
and
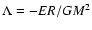 fixed. In the canonical
ensemble, the equilibrium N-body distribution function is given by
fixed. In the canonical
ensemble, the equilibrium N-body distribution function is given by
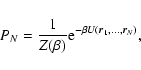 |
(A.1) |
where we only consider the configurational part (the velocity part,
which is just a product of Maxwellians, is trivial). Here,
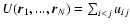 where
where
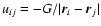 is the gravitational potential (rigorously
speaking, we must use a soften potential in order to regularize the
partition function). Taking the derivative of Eq. (A.1) with
respect to
is the gravitational potential (rigorously
speaking, we must use a soften potential in order to regularize the
partition function). Taking the derivative of Eq. (A.1) with
respect to
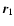 ,
we get
,
we get
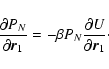 |
(A.2) |
From this relation we can obtain the full equilibrium BBGKY hierarchy
for the reduced distribution functions (Chavanis 2004b). Restricting
ourselves to the one and two-body distribution functions
 |
(A.3) |
with j=1,2, we find
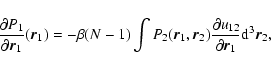 |
(A.4) |
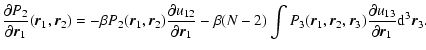 |
|
|
(A.5) |
As is well-known, each equation of the hierarchy involves the next
order distribution function. We now decompose the two-body and
three-body distribution functions in the suggestive forms
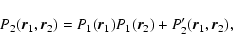 |
(A.6) |
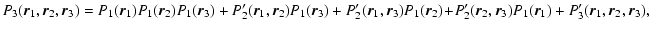 |
|
|
(A.7) |
where Pn' are the cumulants. We shall consider the thermodynamic
limit
 with fixed
with fixed
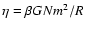 .
In
this limit, it can be shown that the non trivial correlations P'nare of order
N-(n-1). Here, we shall just establish this result
for the two-body distribution function P'2. Substituting the
decompositions (A.6) and (A.7) in Eqs. (A.4) and (A.5) and assuming that P'3, of order N-2, is negligible (this corresponds to the Kirkwood approximation in plasma physics) the equation for the two-body distribution function becomes
after simplification
.
In
this limit, it can be shown that the non trivial correlations P'nare of order
N-(n-1). Here, we shall just establish this result
for the two-body distribution function P'2. Substituting the
decompositions (A.6) and (A.7) in Eqs. (A.4) and (A.5) and assuming that P'3, of order N-2, is negligible (this corresponds to the Kirkwood approximation in plasma physics) the equation for the two-body distribution function becomes
after simplification
We thus find that
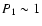 and
and
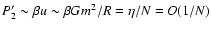 .
Therefore, in the limit
.
Therefore, in the limit
 ,
the two-body distribution
function is the product of two one-body distribution functions:
,
the two-body distribution
function is the product of two one-body distribution functions:
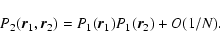 |
(A.9) |
This justifies the exactness of the mean-field approximation for
self-gravitating systems. Note that 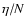 can be identified as the
gravitational version of the "plasma parameter''. This is similar to
the remark of Lundgren & Pointin (1977) for the point vortex
gas. Now, plugging this result in Eq. (A.4), we find that, for
can be identified as the
gravitational version of the "plasma parameter''. This is similar to
the remark of Lundgren & Pointin (1977) for the point vortex
gas. Now, plugging this result in Eq. (A.4), we find that, for
 ,
,
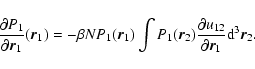 |
(A.10) |
Integrating with respect to
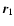 and introducing the mean density
and introducing the mean density
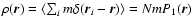 ,
we obtain the Boltzmann
distribution
,
we obtain the Boltzmann
distribution
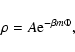 |
(A.11) |
where
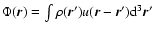 is the self-consistent gravitational potential. Adding the gaussian velocity factor, we obtain the Maxwell-Boltzmann distribution
is the self-consistent gravitational potential. Adding the gaussian velocity factor, we obtain the Maxwell-Boltzmann distribution
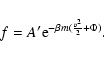 |
(A.12) |
As we have seen in Sect. 2, the distribution function (A.12) can also be obtained by minimizing the Boltzmann free
energy
![$F_{\rm B}[f]$](/articles/aa/full/2005/10/aa1114/img502.gif) at fixed mass M and temperature T. This method
provides a condition of thermodynamical stability
at fixed mass M and temperature T. This method
provides a condition of thermodynamical stability
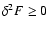 ,
which is not captured by the equilibrium BBGKY hierarchy; it just
yields critical points of free energy. To get the condition of
stability, we need to consider time-dependent solutions and kinetic
equations, i.e. the non-equilibrium BBGKY hierarchy. Indeed, the
thermodynamical stability is related to the dynamical stability with
respect to the Fokker-Planck equation (Chavanis 2004c).
,
which is not captured by the equilibrium BBGKY hierarchy; it just
yields critical points of free energy. To get the condition of
stability, we need to consider time-dependent solutions and kinetic
equations, i.e. the non-equilibrium BBGKY hierarchy. Indeed, the
thermodynamical stability is related to the dynamical stability with
respect to the Fokker-Planck equation (Chavanis 2004c).
The equation for the two-body distribution function (A.8) is
complicated because the one-body distribution function is spatially
inhomogeneous. It may be of interest, however, to advocate the Jeans
swindle and consider, formally, the case of an infinite homogeneous
self-gravitating system (this can be made rigorous in a cosmological
context; see Kandrup 1983). Making the drastic approximation
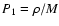 where
where 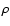 is a constant, Eq. (A.8) simplifies into
is a constant, Eq. (A.8) simplifies into
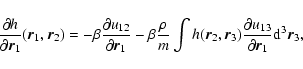 |
(A.13) |
where the second term in the right hand side of Eq. (A.8), of order
1/N2, has been neglected. The correlation function h is defined by
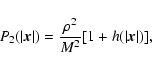 |
(A.14) |
where
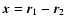 .
Taking the divergence of
Eq. (A.13) and using
.
Taking the divergence of
Eq. (A.13) and using
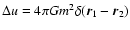 ,
we obtain
,
we obtain
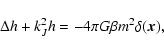 |
(A.15) |
where
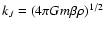 is the inverse of the Jeans
length. This equation is easily integrated to yield
is the inverse of the Jeans
length. This equation is easily integrated to yield
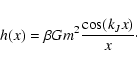 |
(A.16) |
This is the counterpart of the Debye-Hückel result in the
gravitational case (Kandrup 1983). We emphasize that the above results
are valid for other systems with long-range interactions (Chavanis
2004b). In particular, for the HMF model for which a homogeneous
phase rigorously exists, we find by the same method that
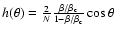 ,
where
,
where
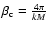 is the
critical inverse temperature. In particular, the correlation function
diverges close to the critical point where the homogeneous phase
becomes unstable, so that the mean-field approximation ceases to be
valid. We expect a similar behavior for inhomogenous
self-gravitating systems close to
is the
critical inverse temperature. In particular, the correlation function
diverges close to the critical point where the homogeneous phase
becomes unstable, so that the mean-field approximation ceases to be
valid. We expect a similar behavior for inhomogenous
self-gravitating systems close to 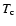 .
.
Considering now an isolated Hamiltonian system, the N-body
microcanonical distribution function is given by
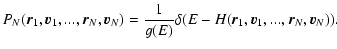 |
|
|
(A.17) |
From this expression it is easy to write the equilibrium BBGKY hierarchy (Chavanis 2004b). The first two equations of this hierarchy are
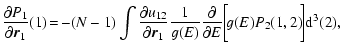 |
|
|
(A.18) |
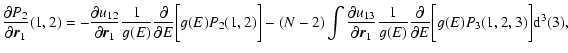 |
|
|
(A.19) |
where we have written
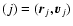 .
Now,
.
Now,
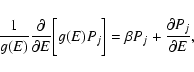 |
(A.20) |
where
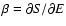 and
and
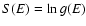 .
The ratio of
.
The ratio of
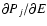 on
on
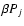 is of order
is of order
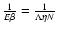 .
Therefore, in the thermodynamic limit
.
Therefore, in the thermodynamic limit
 with
with 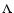 ,
,
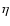 fixed, the second term
in the r.h.s. of Eq. (A.20) is always negligible with respect to
the first. To leading order in N, we obtain the same
equations as in the canonical ensemble.
Therefore, the mean-field approximation is exact and leads to the
Boltzmann distribution (A.11). Observing that
fixed, the second term
in the r.h.s. of Eq. (A.20) is always negligible with respect to
the first. To leading order in N, we obtain the same
equations as in the canonical ensemble.
Therefore, the mean-field approximation is exact and leads to the
Boltzmann distribution (A.11). Observing that
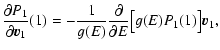 |
|
|
(A.21) |
and taking the
 limit, we find that
limit, we find that
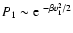 .
Combined with Eq. (A.11), this leads to
the Maxwell-Boltzmann distribution (A.12). Therefore, the
equilibrium BBGKY hierarchy in the microcanonical ensemble leads to
the same result (A.12) as in the canonical ensemble. As indicated
previously, the inequivalence of ensembles will appear by considering
the non-equilibrium BBGKY hierarchy. The thermodynamical stability in
the microcanonical ensemble is connected to the dynamical stability
with respect to the Landau equation (see Chavanis 2004c) which can be
deduced from the non-equilibrium BBGKY hierarchy (Balescu 1963) to
order 1/N.
.
Combined with Eq. (A.11), this leads to
the Maxwell-Boltzmann distribution (A.12). Therefore, the
equilibrium BBGKY hierarchy in the microcanonical ensemble leads to
the same result (A.12) as in the canonical ensemble. As indicated
previously, the inequivalence of ensembles will appear by considering
the non-equilibrium BBGKY hierarchy. The thermodynamical stability in
the microcanonical ensemble is connected to the dynamical stability
with respect to the Landau equation (see Chavanis 2004c) which can be
deduced from the non-equilibrium BBGKY hierarchy (Balescu 1963) to
order 1/N.
Appendix B: Derivation of Eq. (128)
The phase space hypervolume with energy less than E is defined by
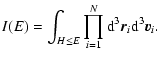 |
|
|
(B.1) |
Integrating over the velocities and using the fact that the kinetic term in the Hamiltonian is quadratic, a standard calculation yields
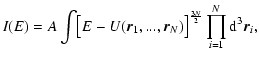 |
|
|
(B.2) |
where
A=(2/m)3N/2V3N and Vn is the volume of a unit-hypersphere in a space of dimension n. The density of states
 is therefore given by
is therefore given by
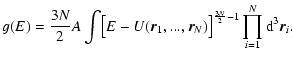 |
|
|
(B.3) |
Assuming now that
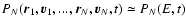 ,
and substituting this ansatz in the
N-body Fokker-Planck equation Eq. (126), we obtain after
simplification
,
and substituting this ansatz in the
N-body Fokker-Planck equation Eq. (126), we obtain after
simplification
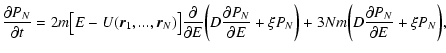 |
|
|
(B.4) |
where the term in bracket is
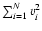 .
We note that
PN=PN(E,t) is not an exact solution of (126), as
expected. To get rid of the dependence in
.
We note that
PN=PN(E,t) is not an exact solution of (126), as
expected. To get rid of the dependence in
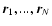 ,
we shall average Eq. (B.4) over the hypersurface of
energy E using
,
we shall average Eq. (B.4) over the hypersurface of
energy E using
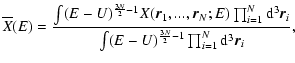 |
|
|
(B.5) |
according to Eq. (B.3). This gives
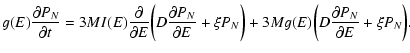 |
|
|
(B.6) |
Using
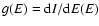 ,
we can put this equation in the form (128).
,
we can put this equation in the form (128).
Appendix C: Rotating self-gravitating systems
In this Appendix, we briefly consider the case of rotating
self-gravitating systems. Introducing dimensionless variables as
in Sect. 2.3, the conservation of angular momentum is
equivalent to
![${\setbox 0=\hbox{$\lambda$ }\kern-.025em\copy0\kern-\wd0
\kern-0.05em\copy0\ker...
...copy0\kern-\wd0
\kern-0.05em\copy0\kern-\wd0\kern-.025em\raise.0233em\box0}[f']$](/articles/aa/full/2005/10/aa1114/img537.gif) with
with
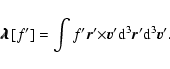 |
(C.1) |
Now, repeating the argumentation of Sect. 3, the
density of states
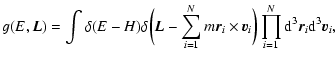 |
|
|
(C.2) |
can be written formally as
![$\displaystyle %
g(E,{\vec L})=\int {\cal D}f \ {\rm e}^{S[f]}
\delta(E-E[f])
\delta(M-M[f])\delta({\vec L}-{\vec L}[f]).$](/articles/aa/full/2005/10/aa1114/img540.gif) |
|
|
(C.3) |
Similarly, the partition function
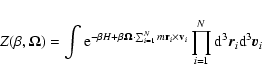 |
(C.4) |
can be written as
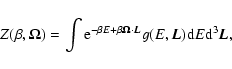 |
(C.5) |
or
![\begin{displaymath}%
Z(\beta,{\bf\Omega})=\int {\cal D}f \ {\rm e}^{J[f]}\delta(M-M[f]),
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img543.gif) |
(C.6) |
where
![$J[f]=S[f]-\beta E[f]+\beta {\setbox 0=\hbox{$\Omega$ }\kern-.025em\copy0\kern-\wd0
\kern-0.05em\copy0\kern-\wd0\kern-.025em\raise.0233em\box0}\cdot {\vec L}[f]$](/articles/aa/full/2005/10/aa1114/img544.gif) is the
free energy. In order to apply the saddle point approximation, we
just need to impose that
is the
free energy. In order to apply the saddle point approximation, we
just need to impose that
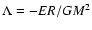 ,
,
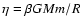 ,
,
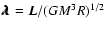 and
and
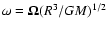 remain of order unity in the
limit
remain of order unity in the
limit
 (in the case of self-gravitating
fermions, we also need to impose that
(in the case of self-gravitating
fermions, we also need to impose that
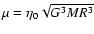 is
fixed and in the case of a soften potential that
is
fixed and in the case of a soften potential that
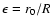 is
fixed). This defines the thermodynamic limit for rotating
self-gravitating systems. The corresponding scalings are given in
Chavanis & Rieutord (2003). In particular,
is
fixed). This defines the thermodynamic limit for rotating
self-gravitating systems. The corresponding scalings are given in
Chavanis & Rieutord (2003). In particular, 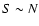 and
and 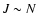 .
Therefore, in the
.
Therefore, in the
 limit, we have to maximize
S[f] at fixed E, M and
limit, we have to maximize
S[f] at fixed E, M and 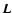 in the microcanonical ensemble
and we have to maximize
in the microcanonical ensemble
and we have to maximize
![$J[f]=S[f]-\beta E[f]+\beta\ {\bf\Omega}\cdot
{\vec L}[f]$](/articles/aa/full/2005/10/aa1114/img549.gif) at fixed
at fixed 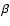 ,
M and
,
M and
 in the canonical
ensemble. Computation of rotating self-gravitating systems in relation
with statistical mechanics have been performed by Votyakov et al. (2002) for a classical gas on a lattice with a large spacing and by Chavanis & Rieutord (2003) for fermions with arbitrary degree of degeneracy.
in the canonical
ensemble. Computation of rotating self-gravitating systems in relation
with statistical mechanics have been performed by Votyakov et al. (2002) for a classical gas on a lattice with a large spacing and by Chavanis & Rieutord (2003) for fermions with arbitrary degree of degeneracy.
- Antonov, V. A. 1962,
Vest. Leningr. Gos. Univ., 7, 135 (In the text)
- Aronson, E. B., & Hansen,
C. J. 1972, ApJ, 177, 145 [NASA ADS] [CrossRef] (In the text)
- Balescu, R. 1963,
Statistical Mechanics of Charged Particles (New-York:
Interscience)
(In the text)
- Bouchet, F., & Barré,
J. 2005, J. Stat. Phys., submitted [cond-mat/0303307]
(In the text)
- Chavanis, P. H. 2002a, A&A,
381, 340 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Chavanis, P. H. 2002b, PRE, 65,
056123 [NASA ADS] [MathSciNet] (In the text)
- Chavanis, P. H.
2002c, Statistical mechanics of two-dimensional vortices and
stellar systems, in Dynamics and thermodynamics of systems with
long range interactions, ed. T. Dauxois, S. Ruffo, E. Arimondo,
& M. Wilkens, Lect. Notes Phys., 602 (Springer)
[cond-mat/0212223]
(In the text)
- Chavanis, P. H. 2002d, The
self-gravitating Fermi gas, in Proceedings of the Fourth
International Heidelberg Conference on Dark Matter in Astro and
Particle Physics, ed. Klapdor-Kleingrothaus (New-York: Springer)
[arXiv:astro-ph/0205426]
(In the text)
- Chavanis, P. H. 2003,
A&A, 401, 15 [EDP Sciences] [NASA ADS] (In the text)
- Chavanis, P. H. 2004a, PRE,
69, 066126 [NASA ADS] (In the text)
- Chavanis, P. H. 2004b
[arXiv:cond-mat/0409641]
(In the text)
- Chavanis, P. H. 2004c, Physica
A, 332, 89 [NASA ADS] [MathSciNet] (In the text)
- Chavanis, P. H.,
& Ispolatov, I. 2002, PRE, 66, 036109 [NASA ADS] (In the text)
- Chavanis, P. H.,
& Rieutord, M. 2003, A&A, 412, 1 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Chavanis, P. H., Ribot,
M., Rosier, C., & Sire, C. 2004 (Banach Center Publications),
in press [cond-mat/0407386]
(In the text)
- Chavanis, P. H., Rosier, C.,
& Sire, C. 2002, PRE, 66, 036105 [NASA ADS] (In the text)
- Chavanis, P. H., &
Sommeria, J. 1998, MNRAS, 296, 569 [NASA ADS] [CrossRef] (In the text)
- de Vega, H. J., & Sanchez,
N. 2002, Nucl. Phys. B, 625, 409 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Gross, D. H. E. 2003
[cond-mat/0307535]
(In the text)
- Gross, D. H. E. 2004
[cond-mat/0403582]
(In the text)
- Hertel, P., &
Thirring, W. 1971, in Quanten und Felder, ed. H. P. Dürr
(Vieweg: Braunschweig)
(In the text)
- Horwitz, G., &
Katz, J. 1978, ApJ, 222, 941 [NASA ADS] [CrossRef] (In the text)
- Huang, K. 1963,
Statistical mechanics (John Wiley)
(In the text)
- Ispolatov, I., &
Karttunen, M. 2003, PRE, 68, 036117 [NASA ADS] (In the text)
- Kandrup, H. 1983,
Astrophy. Space. Sci., 89, 143 [NASA ADS] [MathSciNet] (In the text)
- Katz, J. 1978, MNRAS, 183,
765 [NASA ADS] (In the text)
- Katz, J. 2003, Found.
Phys., 33, 223 [CrossRef] [MathSciNet] (In the text)
- Katz, J., & Okamoto, I.
2000, MNRAS, 317, 163 [NASA ADS] [CrossRef] (In the text)
- Kiessling, M. K. H. 1989, J.
Stat. Phys., 55, 203 [CrossRef] [MathSciNet] (In the text)
- Kramers, H. A. 1940,
Physica, 7, 284 [CrossRef] [MathSciNet] (In the text)
- Lundgren, T. S., & Pointin,
Y. B. 1977, J. Stat. Phys., 17, 323 [CrossRef] (In the text)
- Lynden-Bell, D. 1999, Physica
A, 263, 293 [NASA ADS] (In the text)
- Lynden-Bell, D., &
Lynden-Bell, R. M. 1977, MNRAS, 181, 405 [NASA ADS] (In the text)
- Lynden-Bell, D., & Wood,
R. 1968, MNRAS, 138, 495 [NASA ADS] (In the text)
- Monaghan, J. J.
1978, MNRAS, 184, 25 [NASA ADS] (In the text)
- Ogorodnikov, K. F. 1965,
Dynamics of stellar systems (Pergamon)
(In the text)
- Padmanabhan, T. 1990,
Phys. Rep., 188, 285 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Risken, H. 1989, The
Fokker-Planck equation (Springer)
(In the text)
- Sire, C., & Chavanis, P.
H. 2002, PRE, 66, 046133 [NASA ADS] (In the text)
- Stahl, B., Kiessling, M.
K. H., & Schindler, K. 1994, Planet. Space Sci., 43, 271 [NASA ADS] (In the text)
- Thirring, W. 1970,
Z. Phys., 235, 339 (In the text)
- Votyakov, E. V., De
Martino, A., & Gross, D. H. E. 2002, Eur. Phys. J. B, 29,
593 [EDP Sciences] [NASA ADS] (In the text)
- Youngkins, V., & Miller, B.
2000, PRE, 62, 4583 [NASA ADS] (In the text)
Copyright ESO 2005
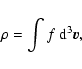
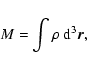
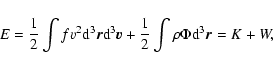
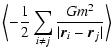
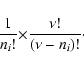
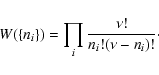
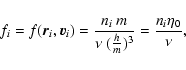
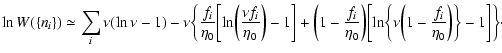
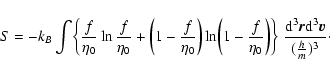
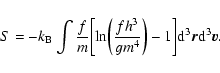
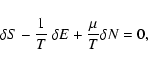
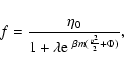
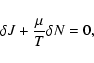
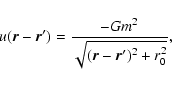
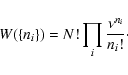
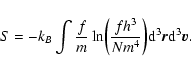
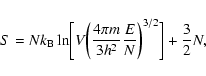
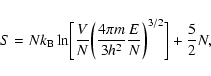
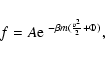
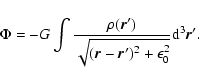
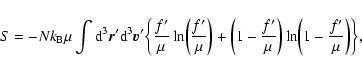
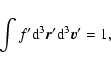
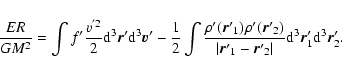
![\begin{displaymath}%
J=N(s[f']+\eta \Lambda[f']),
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img100.gif)
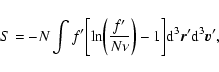
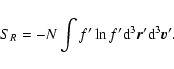
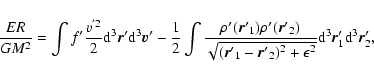
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{le5.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg124.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{felP.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg125.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{etalambdaP.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg126.gif)
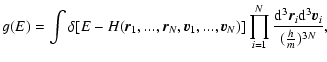
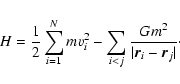
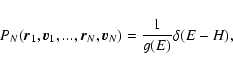
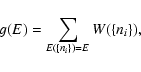
![\begin{displaymath}%
g(E)=\int {\cal D}f {\rm e}^{S[f]}\delta (E-E[f])\delta (M-M[f]),
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img137.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{caloric.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg155.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{el5phys.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg156.gif)
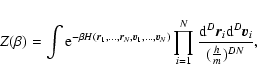
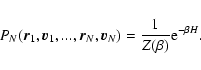
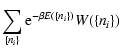
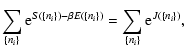
![\begin{displaymath}%
Z(\beta)=\int {\cal D}f {\rm e}^{J[f]}\delta (M-M[f]),
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img171.gif)
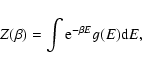
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{caloricCan.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg191.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{el3micro.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg192.gif)
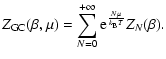
![$\displaystyle \sum_{N=0}^{+\infty}\int {\cal D}f {\rm e}^{J[f]}{\rm e}^{N\mu\over k_{\rm B}T}\delta (N-N[f])$](/articles/aa/full/2005/10/aa1114/img195.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{el3phys.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg202.gif)
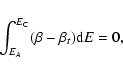
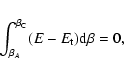
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{tricritiqueP.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg220.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{tricritiquemicroP.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg221.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{EbetaJMU1e3.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg225.gif)
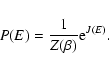
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{ProbE.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg231.gif)
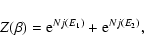
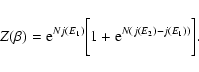
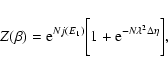
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{entropie.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg239.gif)
![\begin{displaymath}%
g(E)=\int {\cal D}f {\rm e}^{S[f]}\delta (E-E[f])\delta (M-M[f]).
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img240.gif)
![\begin{displaymath}%
g(E)={\rm e}^{Ns[f_{1}]}+{\rm e}^{Ns[f_{2}]},
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img241.gif)
![\begin{displaymath}%
g(E)={\rm e}^{Ns[f_{1}]}\biggl\lbrack
1+{\rm e}^{N(s[f_{2}]-s[f_{1}])}\biggr\rbrack.
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img245.gif)
![\begin{displaymath}%
g(E)={\rm e}^{Ns[f_{1}]}\biggl\lbrack
1+{\rm e}^{-N\lambda^2\Delta\Lambda}\biggr\rbrack,
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img248.gif)
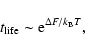
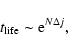
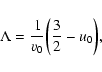
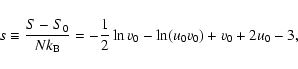
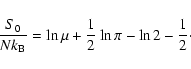
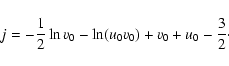
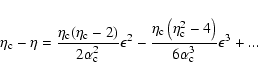
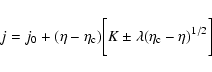
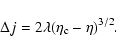
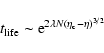
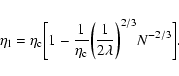
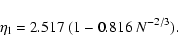
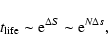
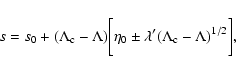
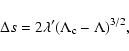
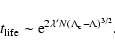
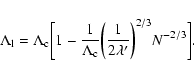

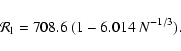
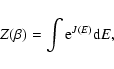
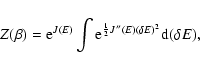
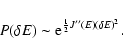
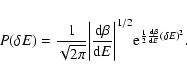
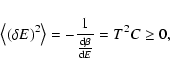
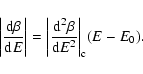
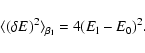
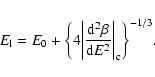
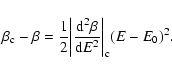
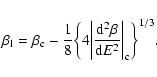
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{collN.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg337.gif)
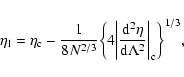
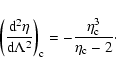
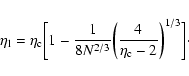
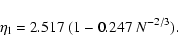
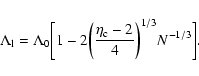
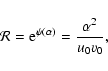
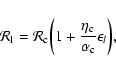
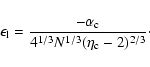
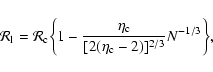
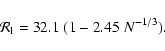
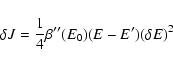
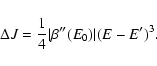
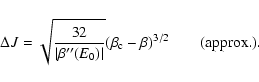
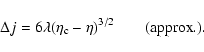
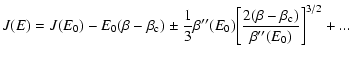
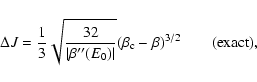
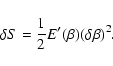
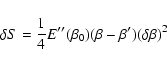
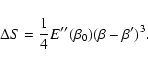
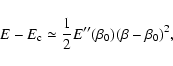
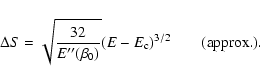
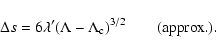
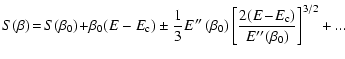
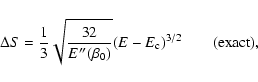
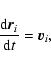
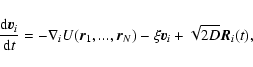
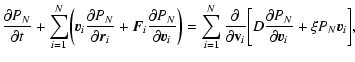
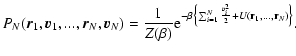
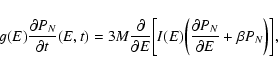
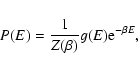
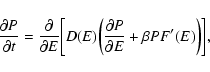
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{EsMU10e3.eps}\end{figure}](/articles/aa/full/2005/10/aa1114/Timg423.gif)
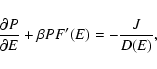
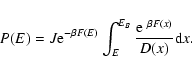
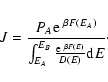
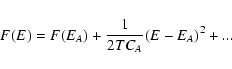
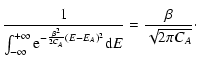
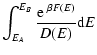
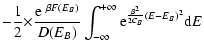
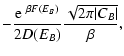
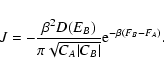
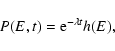
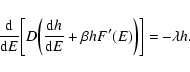
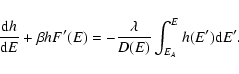
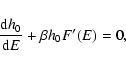
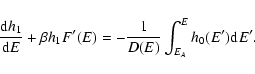
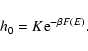
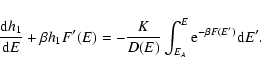
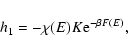
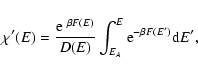
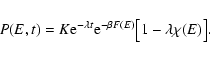
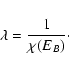
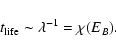
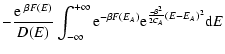
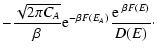
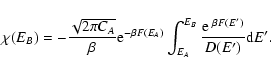
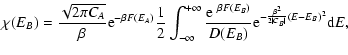
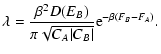
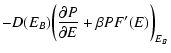
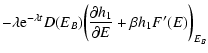
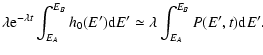
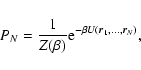
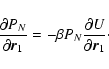

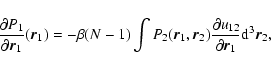
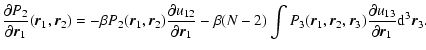
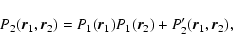
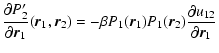
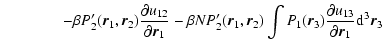
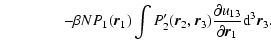
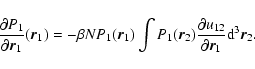
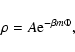
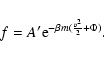
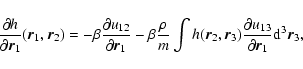
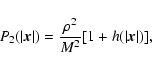
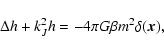
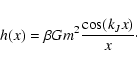
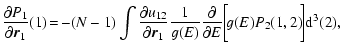
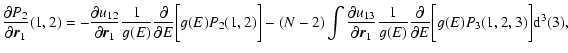
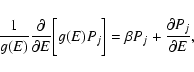
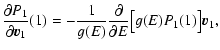
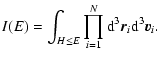
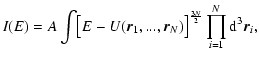
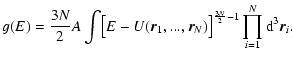
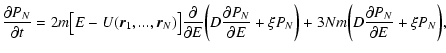
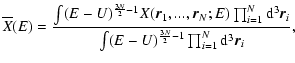
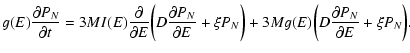
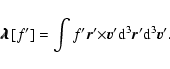
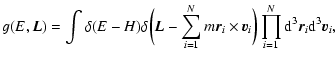
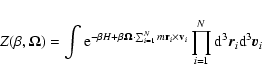
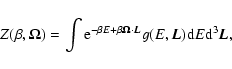
![\begin{displaymath}%
Z(\beta,{\bf\Omega})=\int {\cal D}f \ {\rm e}^{J[f]}\delta(M-M[f]),
\end{displaymath}](/articles/aa/full/2005/10/aa1114/img543.gif)