A&A 431, 831-846 (2005)
DOI: 10.1051/0004-6361:20041831
A supermassive binary black hole in the quasar 3C 345
A. P. Lobanov1 - J. Roland2
1 - Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, Bonn 53121, Germany
2 -
Institut d'Astrophysique, 98 bis bd. Arago,
75014 Paris, France
Received 11 August 2004 / Accepted 16 October 2004
Abstract
Radio loud active galactic nuclei present a remarkable
variety of signs indicating the presence of periodical processes
possibly originating in binary systems of supermassive black holes,
in which orbital motion and precession are ultimately responsible
for the observed broad-band emission variations, as well as for the
morphological and kinematic properties of the radio emission on
parsec scales. This scenario, applied to the quasar 3C 345, explains the observed variations of radio and optical
emission from the quasar, and reproduces the structural variations
observed in the parsec-scale jet of this object. The binary system
in 3C 345 is described by two equal-mass black holes with masses of
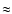 7.1
7.1 
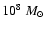 separated by
separated by 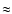 0.33 pc and orbiting with a period
0.33 pc and orbiting with a period 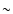 480 yr. The orbital motion induces a precession of the accretion disk around the primary black hole, with a period of
480 yr. The orbital motion induces a precession of the accretion disk around the primary black hole, with a period of 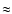 2570 yr. The jet plasma is
described by a magnetized, relativistic electron-positron beam
propagating inside a wider and slower electron-proton jet. The
combination of Alfvén wave perturbations of the beam, the orbital
motion of the binary system and the precession of the accretion disk
reproduces the variability of the optical flux and evolution of the
radio structure in 3C 345. The timescale of quasi-periodic flaring
activity in 3C 345 is consistent with typical disk instability
timescales. The present model cannot rule out a small-mass orbiter
crossing the accretion disk and causing quasi-periodic flares.
2570 yr. The jet plasma is
described by a magnetized, relativistic electron-positron beam
propagating inside a wider and slower electron-proton jet. The
combination of Alfvén wave perturbations of the beam, the orbital
motion of the binary system and the precession of the accretion disk
reproduces the variability of the optical flux and evolution of the
radio structure in 3C 345. The timescale of quasi-periodic flaring
activity in 3C 345 is consistent with typical disk instability
timescales. The present model cannot rule out a small-mass orbiter
crossing the accretion disk and causing quasi-periodic flares.
Key words: galaxies: individual: 3C 345 -
galaxies: nuclei - galaxies: jets - radio continuum: galaxies
1 Introduction
Most of the radio loud active galactic nuclei (AGN) exhibit emission
and structural variability over the entire
electromagnetic spectrum, on timescales ranging from several hours to
several years and on linear scales of from several astronomical units to
several hundreds of parsecs. In AGN with prominent relativistic jets,
this variability appears to be related to the observed morphology and
kinematics of the jet plasma on parsec scales (e.g., Zensus et al.
2002; Jorstad et al. 2001). In a number of radio-loud
AGN, enhanced emission regions (components) embedded in the jet
move at superluminal speeds along helical trajectories (Zensus et al. 1995, 1996; Zensus 1997), and the ejection of such components is often associated with optical and/or
 -ray outbursts.
-ray outbursts.
In a growing number of cases, explanation of the observed nuclear
variability and structural changes in parsec-scale jets is linked to
the presence of supermassive binary black hole (BBH) systems in the
centers of radio loud AGN. The BBH model was originally formulated by
Begelman et al. (1980), and it was studied
subsequently in a number of works (e.g., Polnarev & Rees 1994;
Makino & Ebisuzaki 1996; Makino 1997; Ivanov et al. 1999). The BBH model postulates that an accretion disk (AD) exists around at least one of the two black
holes (typically, around the more massive one), and the resulting
variability and structural changes are determined by the dynamic
properties of the disk itself and the BBH-AD system (this
includes the disk and black hole precession, orbital motion, passages
of the secondary component through the AD).
The most celebrated examples of successful application of the BBH model include OJ 287 (Sillanpää et al. 1988; Valtaoja et al. 2000), 3C 273 and
M 87 (Kaastra & Roos 1992), 1928+738
(Roos et al. 1993), Mrk 501 (Rieger &
Mannheim 2000) and PKS 0420-014 (Britzen et al.
2001). The epochs and structure of major outbursts in
OJ 287 have been suggested to result from passages of the
secondary black hole of a binary pair in OJ 287 through the
accretion disk around the primary during the orbit (Lehto & Valtonen
1996). The component ejection epochs are correlated with the
optical outbursts, and the component trajectories show evidence for a
helical morphology of the jet in OJ 287 (Vicente et al. 1996). Several jet components observed in 3C 345 also move along distinct helical paths (Steffen et al. 1995; Lobanov 1996, hereafter L96). Lobanov &
Zensus (1999, hereafter LZ99) have shown that shocks are not
likely to play a significant role in the dynamics and emission of
parsec-scale regions in 3C 345. Recently, the presence of
binary black hole systems (albeit with extremely short precession
periods and small orbital separations) has been suggested for 3C 279
(Abraham & Carrara 1998), 3C 273 (Abraham & Romero
1999) and 3C 345 (Caproni & Abraham 2004),
from the observed periodic variations of the component ejection angle.
The observed helical trajectories of jet components are a strong
indication of precession or perturbation of the jet flow. The
dynamics and emission of such perturbed outflows have been explained
in the framework of the two-fluid model (Sol et al. 1989; Hanasz & Sol 1996) describing the structure and emission of the jet in terms of an ultra-relativistic
electron-positron (
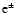 )
beam with
)
beam with
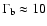 surrounded by a slower, electron-proton (
surrounded by a slower, electron-proton (
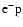 )
jet moving at a
speed
)
jet moving at a
speed
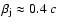 .
.
Observational evidence for the two-fluid model is reviewed in Roland
& Hetem (1996). The presence of two fluids in extragalactic
outflows was first inferred in the large-scale jet of Cygnus A
(Roland et al. 1988). The two-fluid model is
supported by 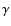 -ray observations of MeV sources (Roland &
Hermsen 1995; Skibo et al. 1997) and
polarized structures in the compact radio jet of 1055+018
(Attridge et al. 1999). The X-ray and
-ray observations of MeV sources (Roland &
Hermsen 1995; Skibo et al. 1997) and
polarized structures in the compact radio jet of 1055+018
(Attridge et al. 1999). The X-ray and
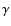 -ray observed in Cen A may be formed by the
-ray observed in Cen A may be formed by the
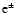 beams (Marcowith et al. 1995, 1998). Direct detections of fast and slow jet speeds
have been reported for Cen A (Tingay et al. 1998)
and M 87 (Biretta et al. 1999).
Subluminal speeds, possibly related to the
beams (Marcowith et al. 1995, 1998). Direct detections of fast and slow jet speeds
have been reported for Cen A (Tingay et al. 1998)
and M 87 (Biretta et al. 1999).
Subluminal speeds, possibly related to the
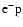 plasma, have been
observed in the double-sided jets in 3C 338 (Feretti et al.
1993). The two-fluid scenario has been used to explain the
morphology and velocity field in the large-scale jet in
3C 31 (Laing & Bridle 2002, 2004).
plasma, have been
observed in the double-sided jets in 3C 338 (Feretti et al.
1993). The two-fluid scenario has been used to explain the
morphology and velocity field in the large-scale jet in
3C 31 (Laing & Bridle 2002, 2004).
Orbital motion and disk precession in the BBH-AD system perturb (but
not disrupt) the
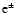 beam, which leads to the complex
variability and kinematic patterns observed in the compact jets. On
scales of up to several hundreds of parsecs, the
beam, which leads to the complex
variability and kinematic patterns observed in the compact jets. On
scales of up to several hundreds of parsecs, the
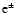 beam is not
disrupted by Langmuir turbulence (Sol et al. 1989) and Alfvén and whistler waves (Pelletier & Sol 1992; Achatz & Schlickeiser 1993). No strong
Kelvin-Helmholtz instability should form on these scales, despite the
significant transverse stratification of the outflow (Hanasz & Sol
1996). Kinematic and emission properties of perturbed beams
have been calculated (Roland et al. 1994; Desringe
& Fraix-Burnet 1997), and it has been shown that the observed
variability and non-linear trajectories of jet components may indeed
be caused by a perturbed
beam is not
disrupted by Langmuir turbulence (Sol et al. 1989) and Alfvén and whistler waves (Pelletier & Sol 1992; Achatz & Schlickeiser 1993). No strong
Kelvin-Helmholtz instability should form on these scales, despite the
significant transverse stratification of the outflow (Hanasz & Sol
1996). Kinematic and emission properties of perturbed beams
have been calculated (Roland et al. 1994; Desringe
& Fraix-Burnet 1997), and it has been shown that the observed
variability and non-linear trajectories of jet components may indeed
be caused by a perturbed
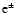 plasma. In a more general
approach, solutions for the restricted three-body problem (Laskar
1990; Laskar & Robutel 1995) have been applied for
deriving the parameters of the perturbed beam and precessing accretion
disk in the BBH system in the quasar PKS 0420-014 (Britzen
et al. 2001).
plasma. In a more general
approach, solutions for the restricted three-body problem (Laskar
1990; Laskar & Robutel 1995) have been applied for
deriving the parameters of the perturbed beam and precessing accretion
disk in the BBH system in the quasar PKS 0420-014 (Britzen
et al. 2001).
In this paper, the dynamics of the BBH-AD system and the two-fluid
model are combined together in order to construct a single framework
for explaining optical flaring activity, kinematic properties and
internal structure of the compact parsec-scale jets. The combined
model is developed to describe the quasar 3C 345 . It is
presented in Sect. 2. Section 3 provides
an overview of the basic properties of the optical and radio emission from
3C 345. In Sects. 4-5, the
model is applied to describe the evolution of the optical emission and
radio jet in 3C 345 after a strong flare in 1992 that
resulted in the appearance of a new superluminal jet component C7.
Throughout the paper, the Hubble constant
H0=70 h km s-1 Mpc-1, deceleration parameter q0=0.5, and negative definition of the spectral index,
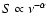 are used. For 3C 345 (z=0.595, Hewitt & Burbidge 1993), the adopted
cosmological parameters correspond to a luminosity distance
are used. For 3C 345 (z=0.595, Hewitt & Burbidge 1993), the adopted
cosmological parameters correspond to a luminosity distance
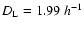 Gpc. The corresponding linear scale is
3.79 h-1 pc mas-1. A proper motion of 1 mas/year
translates into an apparent speed of
19.7 h-1c. Subscripts "b'',
"j'', "c'', and "m'' are introduced to identify quantities related
to the beam, jet, moving plasma condensation, and magnetic field,
respectively.
Gpc. The corresponding linear scale is
3.79 h-1 pc mas-1. A proper motion of 1 mas/year
translates into an apparent speed of
19.7 h-1c. Subscripts "b'',
"j'', "c'', and "m'' are introduced to identify quantities related
to the beam, jet, moving plasma condensation, and magnetic field,
respectively.
2 The binary black hole model
The binary black hole model provides a general formalism for
calculating the emission and kinematics of an outflow originating from
a BBH-AD system. The two-fluid description of the outflow is
adopted (Fig. 1), with the following assumptions:
- 1.
- The outflow consists of an
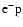 plasma (hereafter the jet) moving at mildly relativistic speed
plasma (hereafter the jet) moving at mildly relativistic speed
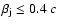 and an
and an
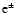 plasma (hereafter the beam) moving at
highly relativistic speed (with corresponding Lorentz factors
plasma (hereafter the beam) moving at
highly relativistic speed (with corresponding Lorentz factors
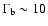 ). Both beam and jet may be transversely
stratified.
). Both beam and jet may be transversely
stratified.
- 2.
- The magnetic field lines are parallel to the flow in the
beam and the mixing layer, and the field is toroidal in the jet
(Fig. 1). The energy densities of the beam, jet
and magnetic field are related as follows:
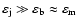 .
The magnetic field lines are perturbed, and the perturbation
propagates downstream at the Alfvén speed,
.
The magnetic field lines are perturbed, and the perturbation
propagates downstream at the Alfvén speed, 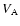 .
.
In the two-fluid model, the
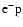 jet carries most of the mass and
kinetic power released on kiloparsec scales (large scale jets,
extended lobes, hot spots). The
jet carries most of the mass and
kinetic power released on kiloparsec scales (large scale jets,
extended lobes, hot spots). The
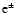 beam propagates in a
channel inside the jet, and it is mainly responsible for the formation
of superluminal jet components observed on parsec scales. The beam
interior is assumed to be homogeneous, ensuring that the beam rotation
does not affect the observed evolution. Assuming a pressure
equilibrium between the beam and the jet, a typical size of the beam
is
beam propagates in a
channel inside the jet, and it is mainly responsible for the formation
of superluminal jet components observed on parsec scales. The beam
interior is assumed to be homogeneous, ensuring that the beam rotation
does not affect the observed evolution. Assuming a pressure
equilibrium between the beam and the jet, a typical size of the beam
is
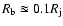 ,
which is of the order
of 0.1 pc (Pelletier & Roland 1989). For AGN at distances of
the order of 1 Gpc, this translates into an angular dimension of
,
which is of the order
of 0.1 pc (Pelletier & Roland 1989). For AGN at distances of
the order of 1 Gpc, this translates into an angular dimension of 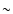 30 microarcseconds, and the beam remains transversely unresolved for very long baseline interferometry (VLBI) observations at
centimeter wavelengths.
30 microarcseconds, and the beam remains transversely unresolved for very long baseline interferometry (VLBI) observations at
centimeter wavelengths.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{1831fg01.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg59.gif) |
Figure 1:
Two-fluid model for relativistic outflows. A fast,
relativistic
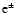 beam is surrounded by a slower, possibly
thermal, beam is surrounded by a slower, possibly
thermal,
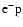 outflow, with a mixing layer forming between the
beam and the jet. The magnetic field, B, is parallel to the flow
in the beam and in the mixing layer, and the field is toroidal in the
jet. The magnetic lines are perturbed and the perturbation
propagates outwards at the Alfvén speed, outflow, with a mixing layer forming between the
beam and the jet. The magnetic field, B, is parallel to the flow
in the beam and in the mixing layer, and the field is toroidal in the
jet. The magnetic lines are perturbed and the perturbation
propagates outwards at the Alfvén speed, 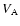 . . |
| Open with DEXTER |
The basic geometry of the model is illustrated in Fig. 2.
Two black holes M1 and M2 orbit each other in the plane (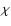 O
O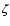 ). The center of the mass of the binary system is in O. An accretion disk around the black hole M1 is inclined at an angle
). The center of the mass of the binary system is in O. An accretion disk around the black hole M1 is inclined at an angle
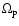 with respect to the orbital plane. The angle
with respect to the orbital plane. The angle
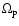 is
the opening half-angle of the precession cone. The disk precesses
around the
is
the opening half-angle of the precession cone. The disk precesses
around the
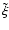 axis, which is parallel to the
axis, which is parallel to the 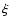 -axis. The
momentary direction of the beam axis is then given by the vector
-axis. The
momentary direction of the beam axis is then given by the vector
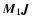 .
The line of sight makes an angle
.
The line of sight makes an angle 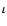 with the precession axis.
with the precession axis.
![\begin{figure}
\par\includegraphics[width=7.75cm,clip]{1831fg02.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg63.gif) |
Figure 2:
Geometry of the BBH model. M1 and M2 denote the locations of
two black holes orbiting around each other in the plane (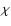 O O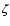 ).
The coordinate system is referenced to the center of mass of the
binary system (O). The accretion disk around the black hole M1 inclined at an angle ).
The coordinate system is referenced to the center of mass of the
binary system (O). The accretion disk around the black hole M1 inclined at an angle
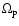 with respect to the orbital plane,
such that the
with respect to the orbital plane,
such that the
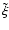 axis (parallel to the axis (parallel to the 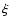 axis) is the
precession axis. The momentary direction of the beam axis is given by
the vector axis) is the
precession axis. The momentary direction of the beam axis is given by
the vector
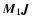 . . |
| Open with DEXTER |
The beam exists inside the jet for as long as its density
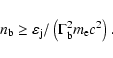 |
(1) |
For a typical parsec-scale jet, this implies
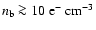 .
The beam moves along magnetic field lines in the
.
The beam moves along magnetic field lines in the
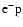 jet if the magnetic field is larger than the critical value
jet if the magnetic field is larger than the critical value
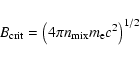 |
(2) |
where
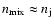 is the density of the
plasma in the beam-jet mixing layer (Pelletier et al. 1988). The magnetic field in the jet rapidly becomes toroidal (Pelletier & Roland 1990). The beam is not disrupted by
Kelvin-Helmholtz perturbations if the magnetic field is larger than
is the density of the
plasma in the beam-jet mixing layer (Pelletier et al. 1988). The magnetic field in the jet rapidly becomes toroidal (Pelletier & Roland 1990). The beam is not disrupted by
Kelvin-Helmholtz perturbations if the magnetic field is larger than
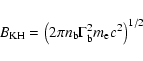 |
(3) |
(Pelletier & Roland 1989). A typical density ratio in parsec-scale jets is
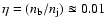 ,
which implies
,
which implies
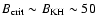 mG. Sol et al. (1989) have demonstrated that the beam does not suffer from inverse Compton and synchrotron losses on parsec scales.
Relativistic bremsstrahlung, ionization and annihilation losses are
also insignificant on these scales. Diffusion by turbulent Alfvén
waves is not expected for beams with
mG. Sol et al. (1989) have demonstrated that the beam does not suffer from inverse Compton and synchrotron losses on parsec scales.
Relativistic bremsstrahlung, ionization and annihilation losses are
also insignificant on these scales. Diffusion by turbulent Alfvén
waves is not expected for beams with
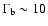 .
.
The relativistic plasma injected into the beam in the vicinity of the black
hole M1 moves at a speed characterized by the bulk Lorentz factor
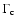 .
The condensation follows the magnetic field lines. The perturbation of the magnetic field propagates at the Alfvén speed
.
The condensation follows the magnetic field lines. The perturbation of the magnetic field propagates at the Alfvén speed
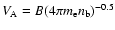 .
For highly energetic beams, the classical density
.
For highly energetic beams, the classical density
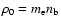 is substituted with the enthalpy
is substituted with the enthalpy
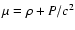 ,
where P is the pressure,
,
where P is the pressure,
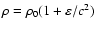 is the relativistic
density and
is the relativistic
density and
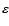 is the specific internal energy. Taking into
account relativistic corrections, and recalling that the enthalpy becomes
is the specific internal energy. Taking into
account relativistic corrections, and recalling that the enthalpy becomes
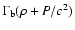 in a plasma moving at a bulk speed
in a plasma moving at a bulk speed
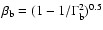 ,
the resulting phase
speed of the Alfvén perturbation with respect to the beam plasma is
,
the resulting phase
speed of the Alfvén perturbation with respect to the beam plasma is
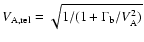 .
Thus, for a typical
.
Thus, for a typical
 beam propagating at
beam propagating at
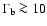 inside a jet with
inside a jet with
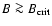 ,
the relativistic Alfvén speed is
,
the relativistic Alfvén speed is  0.1 c.
0.1 c.
The observed trajectory of the beam is affected primarily by the
orbital motion in the BBH system and the precession of the AD around
the primary BH. The jet structure on parsec scales is
mainly determined by the precession. The orbital motion introduces a
small ( 0.1 mas) oscillation of the footpoint of the jet, and it
is not immediately detectable in VLBI images with a typical resolution
of
0.1 mas) oscillation of the footpoint of the jet, and it
is not immediately detectable in VLBI images with a typical resolution
of  1 mas. Consider first the effect of the precession of the accretion disk. The coordinates of the component moving in the perturbed beam are given by
1 mas. Consider first the effect of the precession of the accretion disk. The coordinates of the component moving in the perturbed beam are given by
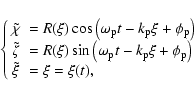 |
(4) |
where 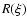 is the perturbation amplitude,
is the perturbation amplitude,
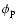 is the
initial precession phase,
is the
initial precession phase, 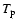 is the precession period,
is the precession period,
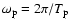 and
and
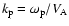 .
The time t is measured in the rest frame of the beam. The tilde in
.
The time t is measured in the rest frame of the beam. The tilde in
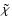 and
and
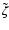 indicates that the
orbital motion has not yet been taken into account (here the axes
indicates that the
orbital motion has not yet been taken into account (here the axes
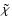 and
and
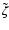 are assumed to be parallel to the axes
are assumed to be parallel to the axes 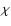 and
and 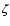 ,
respectively; see Fig. 2). Obviously,
,
respectively; see Fig. 2). Obviously,
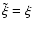 ,
and the tilde can be omitted in all
expression with
,
and the tilde can be omitted in all
expression with 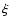 .
The
.
The 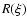 can be chosen to be
can be chosen to be
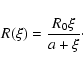 |
(5) |
Here,
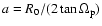 ,
and R0 is the maximum amplitude of the perturbation.
,
and R0 is the maximum amplitude of the perturbation.
The form of the function 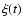 depends on the evolution of
the speed
depends on the evolution of
the speed
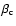 of the plasma condensation injected into
the perturbed beam. From Eq. (4), the components of
of the plasma condensation injected into
the perturbed beam. From Eq. (4), the components of
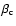 are:
are:
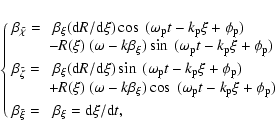 |
(6) |
so that
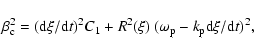 |
(7) |
where
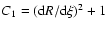 ,
and remembering that
,
and remembering that
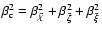 .
Equation (7) is a quadratic equation with
respect to
.
Equation (7) is a quadratic equation with
respect to
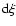 /
/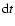 ,
and it can be written in the form of
,
and it can be written in the form of
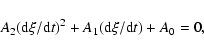 |
(8) |
with
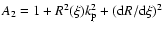 ,
,
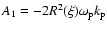 and
and
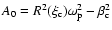 .
The component speed
.
The component speed
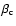 can be conveniently expressed as a function of
can be conveniently expressed as a function of 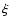 or
or 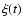 (it can also be viewed constant, in the simplest case). The jet side solution of Eq. (7) can be obtained for the
time
(it can also be viewed constant, in the simplest case). The jet side solution of Eq. (7) can be obtained for the
time 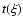 in the rest frame of the beam, under the condition of
initial acceleration of the beam (
in the rest frame of the beam, under the condition of
initial acceleration of the beam (
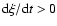 ,
for
,
for
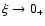 ). The formal solution of Eq. (8) is
). The formal solution of Eq. (8) is
![$\displaystyle %
\frac{{\rm d} \xi}{{\rm d} t} = \frac{1}{A_2} \biggl\{ R^2(\xi)...
... p}\right)\left(1 +
\frac{{\rm d} R}{{\rm d} \xi}\right) \right]^{1/2}\biggl\},$](/articles/aa/full/2005/09/aa1831/img108.gif) |
|
|
(9) |
and 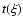 is then given by
is then given by
![\begin{displaymath}%
t(\xi) = t_0 + \int^{\xi}_{\xi_{0}} \frac{A_2}{k_{\rm p}\om...
... c} - \omega^2_{\rm p} R^2(\xi) C_1\right]^{1/2}} {\rm d} \xi.
\end{displaymath}](/articles/aa/full/2005/09/aa1831/img109.gif) |
(10) |
In general, both
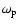 and
and 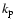 can also vary. Their variations
should then be given with respect to
can also vary. Their variations
should then be given with respect to 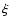 ,
in order to preserve
the solution given by Eq. (10). Numerical methods should be used
otherwise. The solution determined by Eq. (10) can
be found for all
,
in order to preserve
the solution given by Eq. (10). Numerical methods should be used
otherwise. The solution determined by Eq. (10) can
be found for all 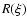 not exceeding the limit of
not exceeding the limit of
![\begin{displaymath}%
R(\xi) \le \beta_{\rm c} \left[ \omega^2_{\rm p} - k^2_{\rm p}
\beta^2_{\rm c} \cos^2\psi(\xi)\right]^{-1/2}.
\end{displaymath}](/articles/aa/full/2005/09/aa1831/img112.gif) |
(11) |
The beam pitch angle
 in
Eq. (11) is measured "locally'' (as opposed to the
"global'' pitch angle
in
Eq. (11) is measured "locally'' (as opposed to the
"global'' pitch angle
![$\psi_{\rm g}(\xi) = \arctan~[R(\xi_{\rm c})/\xi]$](/articles/aa/full/2005/09/aa1831/img114.gif) ), and it
describes the evolution of the amplitude of the beam perturbation. For
a jet with constant beam pitch angle (
), and it
describes the evolution of the amplitude of the beam perturbation. For
a jet with constant beam pitch angle (
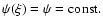 ), the
inequality 11 can be rewritten as:
), the
inequality 11 can be rewritten as:
![\begin{displaymath}%
\xi \le \beta_{\rm c} \left[ \omega^2_{\rm p} \tan^2\psi - k^2_{\rm p} \beta^2_{\rm c} \sin^2\psi
\right]^{-1/2}.
\end{displaymath}](/articles/aa/full/2005/09/aa1831/img116.gif) |
(12) |
The speed
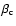 and the local pitch angle
and the local pitch angle 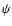 should satisfy the condition:
should satisfy the condition:
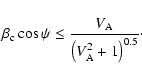 |
(13) |
If inequalities (11)-(13) are satisfied, the
solution provided by Eq. (10) can be used to represent
the form of the function 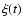 and describing the kinematics of the beam.
and describing the kinematics of the beam.
The trajectory of a superluminal feature travelling in the perturbed
beam is modified also by the orbital motion of the two black holes in
the binary system. This motion can be taken into account by solving
the restricted three-body problem for the BBH-AD system (Laskar
1990; Laskar & Robutel 1995). The orbital plane is
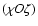 ,
and the coordinate system is centered at the mass
center of the system. The orbit is given by
,
and the coordinate system is centered at the mass
center of the system. The orbit is given by
![$
r=p/[1+e~\cos\varphi(t)]$](/articles/aa/full/2005/09/aa1831/img120.gif) ,
where
,
where 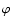 is the true anomaly, pis the semi-latus rectum and e is the numerical eccentricity of the
orbit. The resulting coordinates (
is the true anomaly, pis the semi-latus rectum and e is the numerical eccentricity of the
orbit. The resulting coordinates (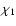 ,
,
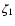 )
of the black
hole M1 are given by
)
of the black
hole M1 are given by
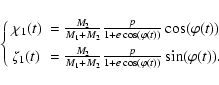 |
(14) |
The beam trajectory can be reconstructed from Eqs. (4) and (14), which gives
![\begin{displaymath}%
\left\{
\begin{array}{ll}
\chi & =\tilde{\chi} + \chi_{1}(t...
...(t)
+ \phi_{\rm o}) \\ [2mm]
\xi & =\xi(t)
\end{array}\right.
\end{displaymath}](/articles/aa/full/2005/09/aa1831/img125.gif) |
(15) |
where
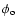 is the initial orbital phase,
is the initial orbital phase,
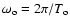 ,
,
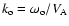 ,
and
,
and 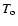 is the orbital period. This system of equations describes completely the kinematics of the perturbed beam. Similarly to the
solution obtained for Eq. (8),
is the orbital period. This system of equations describes completely the kinematics of the perturbed beam. Similarly to the
solution obtained for Eq. (8), 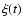 can now be determined by forming
can now be determined by forming
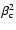 from the coordinate
offsets given by Eq. (15) and solving for
from the coordinate
offsets given by Eq. (15) and solving for
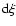 /
/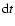 ,
so that (for the jet side solution)
,
so that (for the jet side solution)
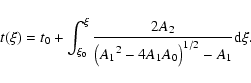 |
(16) |
The coefficients A0, A1, and A2 are given explicitly in
Appendix II in Britzen et al. (2001).
The strongest effect on the form of the beam trajectory is produced by
three model parameters: the beam speed
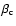 ,
the Alfvén
speed
,
the Alfvén
speed 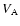 ,
and the precession period
,
and the precession period 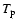 .
The orbital
period in the BBH system affects only the position of the footpoint of
the jet. Since VLBI measurements are made with respect to the
footpoint position,
.
The orbital
period in the BBH system affects only the position of the footpoint of
the jet. Since VLBI measurements are made with respect to the
footpoint position, 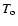 would not have an effect on fitting
the observed trajectories of the jet components (the orbital period is
constrained by the variability of the optical emission). It is
easy to see that the remaining parameters (R0,
would not have an effect on fitting
the observed trajectories of the jet components (the orbital period is
constrained by the variability of the optical emission). It is
easy to see that the remaining parameters (R0,
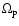 ,
,
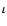 and
and 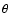 )
describe only the orientation and shape of the overall
envelope within which the perturbed beam is evolving.
The
)
describe only the orientation and shape of the overall
envelope within which the perturbed beam is evolving.
The 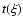 solutions described by Eqs. (10) and (16) can degenerate or become non-unique with respect
to
solutions described by Eqs. (10) and (16) can degenerate or become non-unique with respect
to
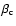 ,
,
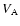 ,
,
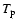 ,
if these parameters are
correlated. The combinations of
,
if these parameters are
correlated. The combinations of
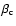 ,
,
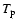 and
and 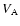 describing the same beam trajectory must not depend on the
rest frame time t or beam location
describing the same beam trajectory must not depend on the
rest frame time t or beam location 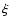 .
However, the solution given by Eq. (10)
implies that the beam trajectory would remain the same if
.
However, the solution given by Eq. (10)
implies that the beam trajectory would remain the same if
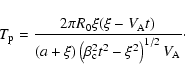 |
(17) |
Obviously, Eq. (17) depends on both t and 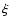 .
The
dependence vanishes only when
.
The
dependence vanishes only when
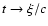 .
The precession
period then becomes a complex number, and the resulting combination of
the parameters does not describe a physically meaningful situation.
This implies that the model does not become degenerate or non-unique with
respect to
.
The precession
period then becomes a complex number, and the resulting combination of
the parameters does not describe a physically meaningful situation.
This implies that the model does not become degenerate or non-unique with
respect to
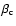 ,
,
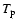 and
and 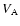 ,
and each physically
possible combination of these parameters describes a unique beam trajectory.
,
and each physically
possible combination of these parameters describes a unique beam trajectory.
The model introduces two new properties in the description of the
BBH-AD system: 1) the Lorentz factor of the relativistic beam is time
variable; 2) the initial perturbation of the magnetic lines in the
beam dissipates on a timescale
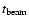 .
These modifications
are introduced in order to accommodate for the kinematic properties of
the jet in 3C 345 in which the curvature of component trajectories
decreases at larger distances, and accelerated motions are strongly implied
by the observed trajectories and apparent speeds of several jet
components (LZ99). The beam accelerates from
.
These modifications
are introduced in order to accommodate for the kinematic properties of
the jet in 3C 345 in which the curvature of component trajectories
decreases at larger distances, and accelerated motions are strongly implied
by the observed trajectories and apparent speeds of several jet
components (LZ99). The beam accelerates from
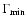 to
to
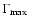 over a rest frame time interval
over a rest frame time interval
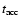 ,
and
,
and
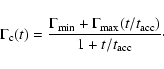 |
(18) |
The perturbation dissipates at a characteristic time
 .
The amplitude of the perturbation given by Eq. (5) is modified by an attenuation term (characteristic
damping time of the perturbation), so that
.
The amplitude of the perturbation given by Eq. (5) is modified by an attenuation term (characteristic
damping time of the perturbation), so that
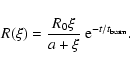 |
(19) |
The model takes account of an arbitrary source orientation, by
introducing a position angle,
 of the
of the 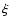 -axis in the
picture plane of the observer.
-axis in the
picture plane of the observer.
Corrections for the relativistic motion of the beam must be made, in
order to enable calculations of physical quantities in the observer's
frame. This requires a knowledge of the angle 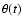 between the
instantaneous velocity vector of the component and the line of sight (LOS). Since the observed angular size of the BBH orbit is small (
between the
instantaneous velocity vector of the component and the line of sight (LOS). Since the observed angular size of the BBH orbit is small ( 1 milliarcsecond), the LOS can be assumed to lie in the plane parallel to
1 milliarcsecond), the LOS can be assumed to lie in the plane parallel to
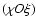 ,
making an angle
,
making an angle 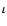 with the
with the 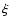 axis. In this case,
axis. In this case,
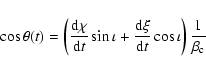 |
(20) |
in the observer's frame (Camenzind & Krockenberger 1992), with the resulting Doppler
beaming factor
![$\delta_{\rm c}(t)=\{\Gamma_{\rm c}[1-\beta_{\rm c}\cos\theta(t)]\}^{-1}$](/articles/aa/full/2005/09/aa1831/img144.gif) The observed flux density of the moving component is
The observed flux density of the moving component is
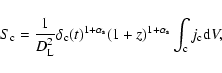 |
(21) |
where z and 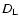 are the redshift and luminosity distance of
the source,
are the redshift and luminosity distance of
the source, 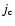 is the emissivity of the component and
is the emissivity of the component and
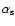 is the synchrotron spectral index. The shortening of time in the observer's frame is given by
is the synchrotron spectral index. The shortening of time in the observer's frame is given by
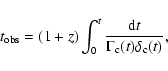 |
(22) |
and the component travels over the distance
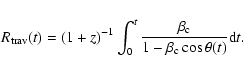 |
(23) |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1831fg03.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg151.gif) |
Figure 3:
Optical and radio variability of 3C 345. Shown are the epochs of
spectral flares (LZ99) that have resulted in appearances of
new superluminal components in the jet. The radio data are from the
Michigan monitoring program (Aller et al. 2003). The optical data are from Kinman et al. (1968); Smyth & Wolstencroft (1970); Lü
(1972); McGimsey et al. (1975); Pollock et al.
(1979); Angione et al. (1981); Kidger
(1988) Webb et al. (1988); Kidger & de Diego
(1990); Vio et al. (1991); Schramm et al.
(1993); Babadzhanyants et al. (1995);
Belokon' & Babadzhanyants (1999). All optical data
have been converted into the B magnitude scale. |
| Open with DEXTER |
3 The quasar 3C 345
The 16m quasar 3C 345 exhibits remarkable structural and
emission variability on parsec scales around a compact unresolved
radio core. The total radio flux density of 3C 345 has been
monitored at 5, 8, and 15 GHz (Aller et al. 2003), and at 22 and 37 GHz (Teräsranta et al. 1998). The source has also been monitored with the Green Bank
Interferometer at 2.7 and 8.1 GHz (Waltman et al. 1991).
The observed variability of the optical emission is possibly
quasi-periodic with a period of 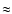 1560 days (Babadzhanyants &
Belokon' 1984; Kidger 1989), although it has been suggested that the
light curve may originate from a non-linear and non-stationary
stochastic process (Vio et al. 1991). A strong optical flare
observed in 3C 345 in 1991-92 (Schramm et al. 1993; Babadzhanyants et al. 1995) was connected with the appearance of a new
superluminal jet component, C7 (L96). LZ99 report possible 3.5-4 year
quasi-periodicity manifested by spectral flares of the radio emission
and appearances of new jet components. Historical optical and 8 GHz radio lightcurves are shown in Fig. 3 together with the epochs of the spectral flares and component ejections.
1560 days (Babadzhanyants &
Belokon' 1984; Kidger 1989), although it has been suggested that the
light curve may originate from a non-linear and non-stationary
stochastic process (Vio et al. 1991). A strong optical flare
observed in 3C 345 in 1991-92 (Schramm et al. 1993; Babadzhanyants et al. 1995) was connected with the appearance of a new
superluminal jet component, C7 (L96). LZ99 report possible 3.5-4 year
quasi-periodicity manifested by spectral flares of the radio emission
and appearances of new jet components. Historical optical and 8 GHz radio lightcurves are shown in Fig. 3 together with the epochs of the spectral flares and component ejections.
The evolution of the parsec-scale jet of 3C 345 has been studied
extensively with the VLBI: see Unwin et al. (1983),
Biretta et al. (1986), Zensus et al. (1995, hereafter ZCU95), L96,
Ros et al. (2000, hereafter
R00), Klare (2003). The relativistic jet model
(Blandford & Rees 1978) has been applied to explain the
emission and kinematic changes observed in the parsec-scale
structures. Using the X-ray data to constrain the jet kinematics,
ZCU95 and Unwin et al. (1994) derive physical
conditions in the jet from a model that combines the inhomogeneous jet
model of Königl (1981) for the core with homogeneous
synchrotron spheres for the moving jet components (Cohen
1985). The evolution of the core flux density is well
represented by a sequence of flare-type events developing in a
partially opaque, quasi-steady jet (LZ99). Spectral properties
of the parsec-scale emission have been studied in several works
(L96; Lobanov et al. 1997; Lobanov
1998b). Unwin et al. (1997) have analyzed a
correlation between the X-ray variability and parsec-scale radio
structure of 3C 345.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1831fg04.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg152.gif) |
Figure 4:
Parsec-scale jet in 3C 345 at 5 and 15 GHz. Contours are
drawn at -1, 1, 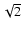 ,
2, ... of the lowest contour (2.5 mJy/beam,
in both images). Curved lines mark the trajectories of superluminal
features C1-C7 identified in the jet. The component trajectories are polynomial fits to the position measurements from the 1979-1998 VLBI monitoring data (ZCU95; L96;
R00). The positions of C7 measured at 22 GHz are shown in the inset. ,
2, ... of the lowest contour (2.5 mJy/beam,
in both images). Curved lines mark the trajectories of superluminal
features C1-C7 identified in the jet. The component trajectories are polynomial fits to the position measurements from the 1979-1998 VLBI monitoring data (ZCU95; L96;
R00). The positions of C7 measured at 22 GHz are shown in the inset. |
| Open with DEXTER |
Figure 4 shows VLBI images of the jet in 3C 345 at 5
and 15 GHz, with the trajectories of eight superluminal components
identified and monitored in the jet in 1979-1999. The morphology of
3C 345 is typical for a core dominated source: a bright and compact
core responsible for 50-70% of the total emission, and a compact
jet that contains several enhanced emission regions (jet components)
moving at apparent speeds of up to
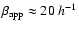 .
.
The compact jet in 3C 345 extends over 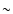 25 mas, which
corresponds to a projected distance of
25 mas, which
corresponds to a projected distance of 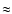 95
95
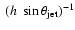 pc
(
pc
(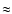 800 h-1 pc, assuming the most likely viewing angle of
the jet
800 h-1 pc, assuming the most likely viewing angle of
the jet
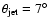 ). The jet has two twists at separations of
). The jet has two twists at separations of  1 and
1 and  5 mas. The twists appear to
retain their positions in the jet over the entire duration of the VLBI
monitoring. Such stability of the twists suggests that they are
likely to reflect the three-dimensional structure of the jet. The
unchanging positions of the twists are also consistent with the
similarities of the apparent trajectories of the jet components at separations
5 mas. The twists appear to
retain their positions in the jet over the entire duration of the VLBI
monitoring. Such stability of the twists suggests that they are
likely to reflect the three-dimensional structure of the jet. The
unchanging positions of the twists are also consistent with the
similarities of the apparent trajectories of the jet components at separations
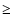 1 mas (Fig. 4). The two-dimensional
trajectories observed in several jet components follow similar,
overlapping tracks, and outline a continuous picture of a curved jet.
The separation of 20 mas from the core can mark a transition point
from compact jet to large-scale jet. At this separation, the jet
finally turns to the direction
1 mas (Fig. 4). The two-dimensional
trajectories observed in several jet components follow similar,
overlapping tracks, and outline a continuous picture of a curved jet.
The separation of 20 mas from the core can mark a transition point
from compact jet to large-scale jet. At this separation, the jet
finally turns to the direction
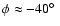 observed in the
large-scale jet of 3C 345 (Kolgaard et al. 1989).
observed in the
large-scale jet of 3C 345 (Kolgaard et al. 1989).
The measured positions of the component C7 (Fig. 4)
provide an accurate account of the jet kinematics within  2 mas
distance from the core. The large amount and good quality of the data
at 22 GHz are sufficient for determining the component trajectory
without using measurements made at lower frequencies. The total of 18
VLBI observations of 3C 345 at 22 GHz are combined for the
epochs between 1989 and 1998 (L96; R00; Klare
2003). For several of these observations, new model fits have
been made for the purpose of obtaining consistent error estimates for
the positions and flux densities of C7. Table 1 presents
the resulting database of the positions and flux densities of C7 at 22 GHz.
2 mas
distance from the core. The large amount and good quality of the data
at 22 GHz are sufficient for determining the component trajectory
without using measurements made at lower frequencies. The total of 18
VLBI observations of 3C 345 at 22 GHz are combined for the
epochs between 1989 and 1998 (L96; R00; Klare
2003). For several of these observations, new model fits have
been made for the purpose of obtaining consistent error estimates for
the positions and flux densities of C7. Table 1 presents
the resulting database of the positions and flux densities of C7 at 22 GHz.
C7 was first reliably detected in 1991.5 at 22 GHz
at a core separation of
 as (L96)
Reports of earlier detections in 1989.2 at 100 GHz (Bååth et al. 1992) and 22 GHz (L96) are inconclusive because of the likely confusion and blending with the nearby component C6 and the core itself.
as (L96)
Reports of earlier detections in 1989.2 at 100 GHz (Bååth et al. 1992) and 22 GHz (L96) are inconclusive because of the likely confusion and blending with the nearby component C6 and the core itself.
Table 1:
Positions and flux densities of C7 at 22 GHz.
Following the procedure established in ZCU95 and L96,
polynomial functions are fitted to the component coordinate offsets x(t) and y(t) from the core position which is fixed at the point (0, 0). From the polynomial fits, the proper motion
![$\mu (t) =
[({\rm d} x/{\rm d} t)^2 + ({\rm d} y/{\rm d} t)^2]^{1/2}$](/articles/aa/full/2005/09/aa1831/img220.gif) ,
apparent speed
,
apparent speed
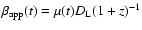 and apparent distance
and apparent distance
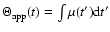 travelled by the component along its
two-dimensional path can be recovered. For the purpose of comparison
to the previous work of L96 and Lobanov & Zensus (1996), the
detection reported for the epoch 1989.25 is included in the polynomial
fitting, but all results for the epochs before 1991 should be viewed as only tentative.
travelled by the component along its
two-dimensional path can be recovered. For the purpose of comparison
to the previous work of L96 and Lobanov & Zensus (1996), the
detection reported for the epoch 1989.25 is included in the polynomial
fitting, but all results for the epochs before 1991 should be viewed as only tentative.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1831fg05.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg223.gif) |
Figure 5:
Kinematic properties of the jet determined from the observed
trajectory of C7. In all panels, the solid line represents a model
with
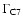 increasing linearly with time from
increasing linearly with time from
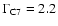 in 1990 to
in 1990 to
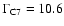 in 1998. The
lower boundary of the shaded area corresponds to
in 1998. The
lower boundary of the shaded area corresponds to
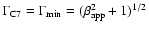 ,
the upper boundary
is drawn for ,
the upper boundary
is drawn for
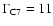 .
Arrows indicate the direction of
increasing .
Arrows indicate the direction of
increasing
 from
from
 to 11.
Individual panels show: a) Measured apparent speed
to 11.
Individual panels show: a) Measured apparent speed
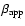 (dashed line) and evolution of the Lorentz factor
(dashed line) and evolution of the Lorentz factor
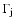 .
b) Angle between the velocity vector of C7 and the line of sight. c) Doppler factor. d) Distance travelled by C7 in the rest
frame of the jet. The derived .
b) Angle between the velocity vector of C7 and the line of sight. c) Doppler factor. d) Distance travelled by C7 in the rest
frame of the jet. The derived
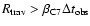 because of the time contraction in the observer's frame
of reference.
because of the time contraction in the observer's frame
of reference. |
| Open with DEXTER |
Kinematic properties of C7 are presented in Fig. 5. The
apparent speed
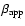 of C7 increased from
of C7 increased from  2 c in 1989 to
2 c in 1989 to
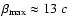 in 1997 (the decrease of
in 1997 (the decrease of
 after 1997 is an artifact of the
polynomial fit). The component reached the minimum apparent speed of
after 1997 is an artifact of the
polynomial fit). The component reached the minimum apparent speed of
 in 1990.5. Such large changes
of
in 1990.5. Such large changes
of
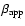 indicate that C7 has moved along a
substantially curved three-dimensional path, with the bulk Lorentz factor most likely changing with time. If the Lorentz factor is constant, then
indicate that C7 has moved along a
substantially curved three-dimensional path, with the bulk Lorentz factor most likely changing with time. If the Lorentz factor is constant, then
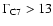 (to satisfy the observed
(to satisfy the observed
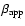 ). If
). If
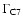 varies, the lower boundary of the variations is given by the minimum Lorentz factor
varies, the lower boundary of the variations is given by the minimum Lorentz factor
![$\Gamma_{{\rm
min}} = [\beta_{{\rm app}}^2(t) + 1]^{1/2}$](/articles/aa/full/2005/09/aa1831/img227.gif) ,
which describes the
motion with the least kinetic power. In Fig. 5,
,
which describes the
motion with the least kinetic power. In Fig. 5,
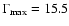 is set, and the kinematic parameters of C7
are described for all allowed variations of
is set, and the kinematic parameters of C7
are described for all allowed variations of
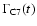 (
(
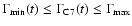 ). As seen in Fig. 5, neither of
the two boundaries provides a satisfactory description of the
component kinematics. The case
). As seen in Fig. 5, neither of
the two boundaries provides a satisfactory description of the
component kinematics. The case
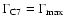 results in uncomfortably small
results in uncomfortably small
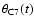 and disproportionally large travelled distance
and disproportionally large travelled distance
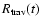 .
With
.
With
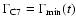 ,
the resulting
variations of
,
the resulting
variations of
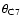 exceed
exceed
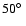 ,
which is difficult to explain. A plausible evolution of the rest
frame speed of C7 can be described by a linear increase of the Lorentz
factor from
,
which is difficult to explain. A plausible evolution of the rest
frame speed of C7 can be described by a linear increase of the Lorentz
factor from
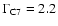 in 1989 to
in 1989 to
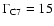 in 1998. In this case, none of the kinematic parameters change
drastically in the course of the component evolution:
in 1998. In this case, none of the kinematic parameters change
drastically in the course of the component evolution:
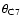 varies within
varies within 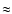
 ,
and
,
and
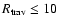 pc. This indicates that the motion of C7 is likely to be accelerated during the initial stages of its evolution, at distances of
pc. This indicates that the motion of C7 is likely to be accelerated during the initial stages of its evolution, at distances of  2 mas from the core. At such distances, acceleration of the
component rest frame speeds has also been reported in several other
jet components in 3C 345 (Lobanov & Zensus 1996,
LZ99). Consequently, this must be a general property of the jet
plasma on these spatial scales, and it should be taken into account in
the modelling of the jet kinematics.
2 mas from the core. At such distances, acceleration of the
component rest frame speeds has also been reported in several other
jet components in 3C 345 (Lobanov & Zensus 1996,
LZ99). Consequently, this must be a general property of the jet
plasma on these spatial scales, and it should be taken into account in
the modelling of the jet kinematics.
The observed consistency of the two-dimensional component tracks
plotted in Fig. 4 suggests that all jet
components in 3C 345 travel along similar trajectories.
There is however a substantial amount of evidence for global evolution
of the entire jet. In Fig. 6, the apparent
accelerations,
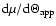 ,
of the components are
plotted against the respective component origin epochs taken from
L96. The apparent accelerations show a steady increase,
following the order of component succession, which is a strong
indication for long-term changes in the jet. While it is conceivable
that the younger components are intrinsically faster, this would
require the presence of a non-stationary process affecting
significantly the particle acceleration in the nuclear regions of
3C 345. The more likely explanation of the observed
long-term trend of the component accelerations is precession of the
jet axis. In this case, variations of the component ejection angle
alone are sufficient to explain the observed trend: the components
ejected at angles closer to
,
of the components are
plotted against the respective component origin epochs taken from
L96. The apparent accelerations show a steady increase,
following the order of component succession, which is a strong
indication for long-term changes in the jet. While it is conceivable
that the younger components are intrinsically faster, this would
require the presence of a non-stationary process affecting
significantly the particle acceleration in the nuclear regions of
3C 345. The more likely explanation of the observed
long-term trend of the component accelerations is precession of the
jet axis. In this case, variations of the component ejection angle
alone are sufficient to explain the observed trend: the components
ejected at angles closer to
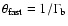 would have higher
would have higher
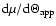 .
In the course of the precession, the ejection angle would
change steadily, and the measured
.
In the course of the precession, the ejection angle would
change steadily, and the measured
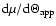 should show sinusoidal variations. The rather large errors in the measured
should show sinusoidal variations. The rather large errors in the measured
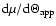 in Fig. 6 allow only a very rough estimate of the precession period
in Fig. 6 allow only a very rough estimate of the precession period
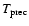 ,
which should be in the range of 850-3670 years, to be made.
,
which should be in the range of 850-3670 years, to be made.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1831fg06.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg243.gif) |
Figure 6:
Apparent acceleration
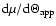 of the component proper motions, plotted versus the component epochs
of origin. The origin epochs are obtained by back-extrapolating the
observed trajectories of the jet components (L96). The shaded area
cover the range of precession periods which would reproduce the
observed trend of
of the component proper motions, plotted versus the component epochs
of origin. The origin epochs are obtained by back-extrapolating the
observed trajectories of the jet components (L96). The shaded area
cover the range of precession periods which would reproduce the
observed trend of
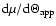 . . |
| Open with DEXTER |
Periodic changes are also evident in the variations of the jet
position angle measured at 22 GHz for successive jet components as
they reach a 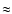 0.5 mas separation from the core. The resulting
position angles are plotted in Fig. 7. The position
angle varies with a period of
0.5 mas separation from the core. The resulting
position angles are plotted in Fig. 7. The position
angle varies with a period of
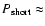 9.5 years and
an amplitude of
9.5 years and
an amplitude of
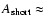 20
20
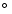 .
A longer term
trend is suggested by the slope in the linear regression of the
position angle data, which implies a rate of change in the position
angle of
.
A longer term
trend is suggested by the slope in the linear regression of the
position angle data, which implies a rate of change in the position
angle of 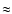 0.4
0.4
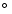 /year. The time coverage of the data is
too short to provide an accurate estimate of the period of the long
term variations. A formal fit constrains the period to within a range
of 300-3000 years, with a mean value of
/year. The time coverage of the data is
too short to provide an accurate estimate of the period of the long
term variations. A formal fit constrains the period to within a range
of 300-3000 years, with a mean value of
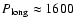 years and an amplitude of
years and an amplitude of
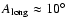 .
The
shaded area in Fig. 7 represents a combined fit to
the data by the two periods. The estimate of
.
The
shaded area in Fig. 7 represents a combined fit to
the data by the two periods. The estimate of
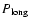 obtained from the change in position angle falls within the range of
periods implied by
obtained from the change in position angle falls within the range of
periods implied by
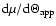 ,
and it can therefore be associated with the precession. The nature of
the short-term changes of the jet position is unclear, but they could
be related to the rotation of the accretion disc or the jet itself or
to the orbital motion in the BBH system.
,
and it can therefore be associated with the precession. The nature of
the short-term changes of the jet position is unclear, but they could
be related to the rotation of the accretion disc or the jet itself or
to the orbital motion in the BBH system.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1831fg07.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg249.gif) |
Figure 7:
Position angle of different jet components measured at
22 GHz at 0.5 mas separation from the core. Short-term variations, with a
period of 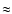 9.5 years, are evident. A linear regression
(dotted line) suggests the presence of a long-term trend, with a
annual change rate of 0.4 9.5 years, are evident. A linear regression
(dotted line) suggests the presence of a long-term trend, with a
annual change rate of 0.4 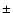 0.3
0.3
 /year. The shaded area shows
the best fit by the two periodical processes combined, with the
estimated periods /year. The shaded area shows
the best fit by the two periodical processes combined, with the
estimated periods
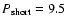  0.1 years and
0.1 years and
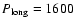 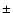 1300 years. The solid line represents the trend in the
position angle due to the long-term periodicity.
1300 years. The solid line represents the trend in the
position angle due to the long-term periodicity. |
| Open with DEXTER |
4 Application of the BBH model
The BBH model applies a single model framework to explain the
emission and kinematic properties of the jet in the optical and radio
regimes. The evolution of superluminal features observed in the radio
jet is explained by a precession of the accretion disk around the
primary black hole M1, and the characteristic shape of the optical
light curve is produced by the orbital motion of the black hole M1.
The different characteristic timescales and amplitudes of changes in
the radio and optical regimes imply a complex composition of the
emitting material. The optical emission of 3C 345 during the strong
flare in 1990-93 varied by 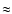 2.5 mag, with a typical
timescale of
2.5 mag, with a typical
timescale of 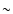 0.6 yr for individual sub-flare events (see
Fig. 15). The radio emission of the jet component C7
associated with that flare showed only a single rise and decay
event, changing by a factor of
0.6 yr for individual sub-flare events (see
Fig. 15). The radio emission of the jet component C7
associated with that flare showed only a single rise and decay
event, changing by a factor of 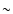 15 on a timescale of
15 on a timescale of 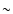 6 years. This difference in the behavior of the optical and radio variability can be reconciled by assuming that the
relativistic
6 years. This difference in the behavior of the optical and radio variability can be reconciled by assuming that the
relativistic
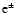 plasma responsible for the optical emission is injected into
the beam during a time
plasma responsible for the optical emission is injected into
the beam during a time
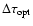 which is much
shorter than the injection timescale
which is much
shorter than the injection timescale
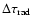 for the
plasma responsible for the radio emission. For C7, the plasma
responsible for the optical emission is modelled by a point-like
component and the plasma responsible for the radio
emission is modelled by a temporally extended
component, so that
for the
plasma responsible for the radio emission. For C7, the plasma
responsible for the optical emission is modelled by a point-like
component and the plasma responsible for the radio
emission is modelled by a temporally extended
component, so that
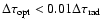 .
In the BBH frame, the
radio component emits over a period of
.
In the BBH frame, the
radio component emits over a period of 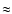 1.9 yr, with
component ejections occurring approximately every 4 years. A general
sketch of the composition of a flare is shown in Fig. 8.
1.9 yr, with
component ejections occurring approximately every 4 years. A general
sketch of the composition of a flare is shown in Fig. 8.
The application of the model consists of two parts. In the first
part, the observed trajectory and flux density of the jet component C7
are reconstructed, using the precession of the accretion disk around
the black hole M1, and solving formally the problem defined by
Eq. (8). In the second part, the optical light
curve of 3C 345 is calculated from the orbital properties of the
BBH system provided by the solution of Eq. (16).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1831fg08.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg250.gif) |
Figure 8:
Composition of a nuclear flare. The flare begins with an
injection of highly energetic particles emitting optical synchrotron
radiation. The timescale of the injection
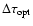 is comparable to the synchrotron loss time of the optically emitting
plasma. Rapid energy losses and injection of radio emitting plasma on
the timescale is comparable to the synchrotron loss time of the optically emitting
plasma. Rapid energy losses and injection of radio emitting plasma on
the timescale
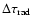 lead to progressively decreasing
mean energy of the plasma and subsequent propagation of the flare to
radio wavelengths. The optically emitting plasma is represented in the
model by a point-like component injected into the beam, while the radio
emitting plasma is temporally resolved, with the
resulting
lead to progressively decreasing
mean energy of the plasma and subsequent propagation of the flare to
radio wavelengths. The optically emitting plasma is represented in the
model by a point-like component injected into the beam, while the radio
emitting plasma is temporally resolved, with the
resulting
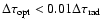 . . |
| Open with DEXTER |
Basic geometrical parameters of the system are recovered by fitting
the precession model to the observed two-dimensional path of C7. These include
-
-
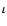 - viewing angle of the jet axis (Fig. 2);
- viewing angle of the jet axis (Fig. 2);
-
-
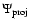 - position angle of the jet axis in the
plane of the sky;
- position angle of the jet axis in the
plane of the sky;
-
-
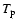 - precession period;
- precession period;
-
-
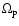 - opening half-angle of the precession cone;
- opening half-angle of the precession cone;
-
-
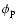 - initial phase of the precession;
- initial phase of the precession;
-
- R0 - maximum amplitude of the perturbation;
-
-
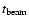 - characteristic dampening time of the perturbed
beam.
- characteristic dampening time of the perturbed
beam.
It should be stressed that none of the parameters listed above depend
on the velocity of the moving component. However, the shape of the
path depends on the Alfvén speed 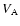 of the magnetic field
perturbation. This speed is determined by fitting simultaneously the
geometry of the component path and the orbital motion in the binary
system.
of the magnetic field
perturbation. This speed is determined by fitting simultaneously the
geometry of the component path and the orbital motion in the binary
system.
The velocity of the jet component is constrained by fitting the coordinate
offsets, x(t) and y(t), of the component from the position of the
radio core. In 3C 345, the apparent motion of all jet components is non-linear and
shows accelerations and decelerations (ZCU95; L96; LZ99). To account for
this, a variable Lorentz factor must be introduced, using
Eq. (18). With a variable Lorentz factor, the x(t) and y(t) offsets are fitted simultaneously, and a three-dimensional trajectory of the component is recovered.
This procedure yields the following parameters:
-
-
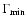 - initial Lorentz factor of the component;
- initial Lorentz factor of the component;
-
-
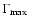 - final Lorentz factor of the component,
after the acceleration;
- final Lorentz factor of the component,
after the acceleration;
-
-
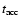 - characteristic acceleration time.
- characteristic acceleration time.
In addition to the geometrical and kinematic factors, the flux density
evolution in the optical and radio regimes is characterized by the
synchrotron energy loss timescales
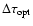 and
and
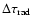 and by the duration
and by the duration
 during which the relativistic plasma
responsible for the flare remains optically thick in the radio
regime. The radio lightcurve of C7 constrains uniquely the viewing
angle of the jet. The information contained in the radio lightcurve is
fundamental for determining the duration of the radio emitting stage,
during which the relativistic plasma
responsible for the flare remains optically thick in the radio
regime. The radio lightcurve of C7 constrains uniquely the viewing
angle of the jet. The information contained in the radio lightcurve is
fundamental for determining the duration of the radio emitting stage,
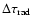 ,
of the flare and ensuring the consistency
between the precession fit and the BBH fit.
,
of the flare and ensuring the consistency
between the precession fit and the BBH fit.
The main effect of the BBH system is the orbital motion of both black
holes around the center of mass of the system. This motion explains
the observed optical light curve, the fine structure of the parsec-scale jet,
and peculiarities of component motions around the general trajectory
determined by the precession. The fit by the BBH system yields the
following parameters:
-
- M1 - mass of the primary black hole containing the
accretion disk;
-
- M2 - mass of the secondary black hole;
-
-
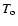 - orbital period in the BBH system;
- orbital period in the BBH system;
-
- e - eccentricity of the orbit;
-
-
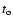 - injection epoch of a new jet component;
- injection epoch of a new jet component;
-
-
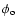 - initial orbital phase at the injection epoch.
- initial orbital phase at the injection epoch.
4.4 Consistency between the precession and BBH fits
The BBH model, which is obtained by fitting a
point-like component to reproduce the observed optical lightcurve,
must be consistent with the results derived from the precession fit.
In other words, the evolution of the extended, radio emitting, component
determined from fitting the BBH model must reproduce the
trajectory and kinematic properties of the radio emitting plasma
obtained from the precession fit.
Consistency between the fits by the precession and orbital motion is
ensured under the following five conditions which connect the formal
fitting with the specific properties of the two-fluid model:
- 1.
- The characteristic Lorentz factor obtained from fitting the
optical light curve by the BBH model must be larger than the
corresponding Lorentz factor obtained from fitting the trajectory of C7 by the precession model. This is simply due to the fact that the
rest frame trajectory in the BBH model is longer than the trajectory
in the precession model (see Fig. 14, implying that
the component has to move faster in the BBH model to
reproduce the same observed two-dimensional trajectory.
- 2.
- The optical component is assumed to be temporarily
unresolved, but not the radio component. This
condition is required to explain the differences in the emission
variations observed in the optical and radio regimes.
- 3.
- The ejection epoch of the optical component precedes that of
the radio component. This condition reflects the nuclear flare
structure assumed (Fig. 8).
- 4.
- For a given mass M1 of the primary black hole, the
combination of the mass of the secondary M2, orbital period
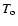 and acceleration time
and acceleration time
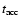 must reconcile satisfactorily the rest frame time derived from the precession model with the rest frame time obtained from the BBH model (see
Fig. 9).
must reconcile satisfactorily the rest frame time derived from the precession model with the rest frame time obtained from the BBH model (see
Fig. 9).
- 5.
- A single value of the Alfvén speed must reproduce the observed
shape of the component trajectory obtained from the precession fit and
satisfy the orbital period obtained from the BBH fit.
These five conditions ensure that the kinematic and flux density
variations of the radio component recovered from the BBH and
precession fits are consistent, and thus the BBH scenario explains
the radio and optical components simultaneously.
5 Properties of the BBH system in 3C 345
The best fit parameters of the precessing jet and the BBH system in
3C 345 determined using the model developed in Sect. 2
and the fitting method described in Sect. 4 are
presented in Table 2. The procedural steps through
which the fit was obtained are summarized below.
Table 2:
Precession, orbital and flare properties of the BBH system in
3C 345.
5.1 Geometrical and precession properties
The position angle of the jet axis in the plane of the sky is determined directly from the VLBI images of 3C 345, which yields
The injection epoch 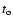 does not have to coincide with the
epoch of first detection of C7, since the temporal and linear scales
for plasma acceleration may be comparable to, or even larger than, the
smallest angular scale at which the component becomes detectable in
VLBI images. The most accurate estimate of the epoch of origin of C7 is provided by the
onset of the radio flux increase (see Fig. 3), which yields
does not have to coincide with the
epoch of first detection of C7, since the temporal and linear scales
for plasma acceleration may be comparable to, or even larger than, the
smallest angular scale at which the component becomes detectable in
VLBI images. The most accurate estimate of the epoch of origin of C7 is provided by the
onset of the radio flux increase (see Fig. 3), which yields
This value indeed provides the best fit for both the optical
lightcurve and the evolution of C7.
The jet viewing angle, 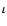 ,
opening half-angle of the precession cone
,
opening half-angle of the precession cone
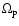 ,
and initial precession phase,
,
and initial precession phase,
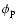 ,
are obtained by fitting the observed two-dimensional path of C7. This fit constrains uniquely the initial precession phase at
,
are obtained by fitting the observed two-dimensional path of C7. This fit constrains uniquely the initial precession phase at 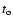
For fitting the jet viewing angle, an initial guess is provided by the
best fit values (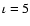 -8
-8
 obtained from modelling the
kinematic (ZCU95), spectral (LZ99) and opacity (Lobanov
1998a) properties of the compact jet in 3C 345. A family of
solutions across the
obtained from modelling the
kinematic (ZCU95), spectral (LZ99) and opacity (Lobanov
1998a) properties of the compact jet in 3C 345. A family of
solutions across the 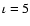 -
-
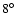 interval is presented in
Table 3, together with corresponding
interval is presented in
Table 3, together with corresponding 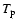 and
and
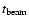 calculated for
calculated for
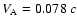 .
(note that determination of
.
(note that determination of 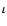 and
and
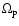 does not
depend on the knowledge of
does not
depend on the knowledge of 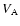 ). The best fit to the
observed path of C7 is provided by
). The best fit to the
observed path of C7 is provided by
At this stage, the maximum perturbation amplitude, R0, and the
timescale,
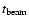 of damping the perturbed beam can be
constrained. An initial guess for R0 (0.5-0.8 pc) is
provided by the largest deviation of the positions of C7 from a
straight line defined by
of damping the perturbed beam can be
constrained. An initial guess for R0 (0.5-0.8 pc) is
provided by the largest deviation of the positions of C7 from a
straight line defined by
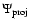 .
The best fit for the observed path of C7 is obtained with
.
The best fit for the observed path of C7 is obtained with
Table 3:
Precession solutions for 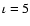 -
-
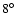 .
.
The fit for 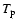 depends on the Alfvén speed
depends on the Alfvén speed 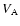 in
the jet. For each value
in
the jet. For each value 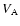 an appropriate
an appropriate 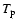 can be
found from the precession fit that would reproduce exactly the same
two-dimensional trajectory. This family of solutions is given in
Table 4. The value of
can be
found from the precession fit that would reproduce exactly the same
two-dimensional trajectory. This family of solutions is given in
Table 4. The value of 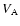 is constrained
after a similar family of solutions is obtained for the BBH fit to the
optical light curve. A unique solution for
is constrained
after a similar family of solutions is obtained for the BBH fit to the
optical light curve. A unique solution for 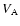 is then found
by reconciling the values of
is then found
by reconciling the values of 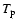 and
and 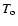 obtained from
the BBH and precession fits.
obtained from
the BBH and precession fits.
Table 4:
Precession solutions for
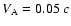 -0.15 c.
-0.15 c.
After the two-dimensional path of C7 has been fitted by the geometrical
and precession parameters, the precession model is applied to fit the
trajectory and flux density evolution of C7, which yields
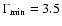 ,
,
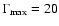 and
and
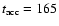 yr. These parameters are independent from the choice of
yr. These parameters are independent from the choice of  .
It should also be noted that the Lorentz factors derived above are
related to the radio emitting plasma. The optically emitting plasma
may have a different range of Lorentz factors.
.
It should also be noted that the Lorentz factors derived above are
related to the radio emitting plasma. The optically emitting plasma
may have a different range of Lorentz factors.
5.3 Consistency between the radio and optical fits
In order to ensure consistency between the precession and BBH fits,
and to bootstrap together the fit of the trajectory and kinematics
of C7 and the fit of the optical light curve, two general model classes
are considered for describing the properties of the radio and
optically emitting plasmas, in terms of the minimum (or initial)
Lorentz factors of the two plasmas (these scenarios are based on the
consistency conditions described in Sect. 4.4):
Model 1:
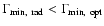 ,
,
Model 2:
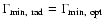 .
.
In both cases, the radio emitting plasma is injected immediately after the optically
emitting plasma (as illustrated in Fig. 8).
For model 1,
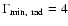 and
and
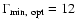 are chosen from the precession fit (note that this
corresponds to injection speeds of
are chosen from the precession fit (note that this
corresponds to injection speeds of
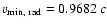 and
and
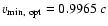 ). For model 2,
). For model 2,
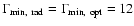 is assumed.
Both scenarios fit well the optical light curve, but model 1
reproduces better the kinematics of C7, particularly at the beginning
of the component evolution.
is assumed.
Both scenarios fit well the optical light curve, but model 1
reproduces better the kinematics of C7, particularly at the beginning
of the component evolution.
Figure 9 compares the rest frame time obtained from the precession fit and the BBH fit by the two models. The injection epoch
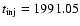 obtained
from the precession fit is recovered by model 1, but cannot be
reproduced by model 2.
obtained
from the precession fit is recovered by model 1, but cannot be
reproduced by model 2.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1831fg09.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg283.gif) |
Figure 9:
Rest frame time recovered from the precession fit (describing
the trajectory of the VLBI component) and the BBH models 1 and 2
(describing the optical variability) under the consistency
constraints discussed in Sect. 4.4. The injection
epoch
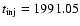 (for which
(for which
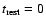 is required
by the precession fit) is reproduced by the BBH model 1 and cannot
be recovered from the BBH model 2. The agreement between the
precession fit and model 1 ensures that the BBH scenario provides
a single framework for describing simultaneously the observed
trajectory and flux density changes of C7 and the observed
variability of the optical emission of 3C 345.
is required
by the precession fit) is reproduced by the BBH model 1 and cannot
be recovered from the BBH model 2. The agreement between the
precession fit and model 1 ensures that the BBH scenario provides
a single framework for describing simultaneously the observed
trajectory and flux density changes of C7 and the observed
variability of the optical emission of 3C 345. |
| Open with DEXTER |
For the earliest epochs of the evolution of C7, model 2 does not
reproduce satisfactorily the separations of C7 from the core
(Fig. 10) and the flux density changes
(Fig. 11). The discrepancy between the fits by the
precession model and model 2 is particularly visible in the
speed evolution obtained from the precession and BBH fits
(Fig. 12). Model 1 is therefore a
better counterpart to the precession fit described in
Sect. 5.1.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1831fg10.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg284.gif) |
Figure 10:
Evolution of the separation of the jet component C7 from the core.
The fit by the precession model is consistent with the fit by
BBH model 1. BBH model 2 fails to reproduce the earliest
position measurements of C7. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.25cm,clip]{1831fg11.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg285.gif) |
Figure 11:
Radio flux density of C7 at 22 GHz. The fits by
the precession model and BBH model 1 are consistent. BBH
model 2 cannot reproduce the onset of the radio emission. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{1831fg12.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg286.gif) |
Figure 12:
Apparent speed evolution of the jet component C7 recovered
from the precession and BBH fits. The fit by BBH model 1 is
consistent with the fit by the precession, while BBH model 2
cannot be reconciled with the precession fit at all. |
| Open with DEXTER |
Figure 13 compares the precession and the BBH model 1
fits to the observed two-dimensional path of C7. The agreement between
the fits is excellent. The two fits differ by less than 0.02 mas
(Fig. 14). This deviation is caused by the orbital motion
of the black hole ejecting the jet, which is not accounted for in the
precession fit.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{1831fg13.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg287.gif) |
Figure 13:
Two-dimensional path of C7. The precession fit and the fit by BBH model 1 are presented. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1831fg14.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg288.gif) |
Figure 14:
Two-dimensional path of C7 within 1 mas of the nucleus.
The difference between the precession and BBH model 1 fit is
due to the orbital motion of the black hole ejecting the jet. |
| Open with DEXTER |
Fitting the optical light curve constrains the orbital period 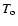 ,
orbital eccentricity and initial orbital phase
,
orbital eccentricity and initial orbital phase
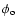 in the BBH system, under the conditions of consistency described in Sect. 5.3. The fit to the optical curve requires
a nearly circular orbit (e < 0.1), constrains uniquely the initial orbital phase
in the BBH system, under the conditions of consistency described in Sect. 5.3. The fit to the optical curve requires
a nearly circular orbit (e < 0.1), constrains uniquely the initial orbital phase
and produces a family of solutions for 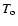 depending on the value of
depending on the value of 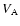 .
These solutions are presented in Table 5 for
the same range of
.
These solutions are presented in Table 5 for
the same range of 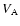 as in Table 4. The fit
to the optical light curve is shown in Fig. 15.
It does not depend on the actual value of
as in Table 4. The fit
to the optical light curve is shown in Fig. 15.
It does not depend on the actual value of 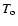 because
because
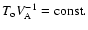 ,
and thus the same shape of the
lightcurve can be reproduced by a number of combinations of
,
and thus the same shape of the
lightcurve can be reproduced by a number of combinations of 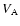 and
and 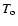 .
.
Table 5:
Orbital period solutions for
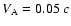 -0.15 c.
-0.15 c.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{1831fg15.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg292.gif) |
Figure 15:
Optical variability in 3C 345 in 1990-93. Solid lines show the
fits by the BBH model. Individual peaks result from the orbital motion in the BBH system. |
| Open with DEXTER |
In order to reconcile the two families of 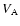 -dependent
solutions (the precession solutions in Table 4 and
the orbital period solutions in Table 5), the value of
the Alfvén speed must be constrained. The periodic changes of the
position angle of component ejection plotted in
Fig. 7 can be used for this purpose. The Alfvén wave perturbations, propagating at
-dependent
solutions (the precession solutions in Table 4 and
the orbital period solutions in Table 5), the value of
the Alfvén speed must be constrained. The periodic changes of the
position angle of component ejection plotted in
Fig. 7 can be used for this purpose. The Alfvén wave perturbations, propagating at
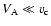 cannot account for such a short period. The observed period
cannot account for such a short period. The observed period
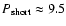 yr must therefore reflect perturbations of the
magnetic field caused by the orbital motion in the BBH system. In this
case,
yr must therefore reflect perturbations of the
magnetic field caused by the orbital motion in the BBH system. In this
case,
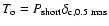 ,
where
,
where
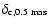 is the Doppler factor of the beam plasma measured at the same location (0.5 mas from the nucleus) at
which the oscillations of the ejection angle are registered. The
kinematic fit yields
is the Doppler factor of the beam plasma measured at the same location (0.5 mas from the nucleus) at
which the oscillations of the ejection angle are registered. The
kinematic fit yields
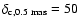 ,
which results in the orbital period
,
which results in the orbital period
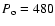 yr. The corresponding value of the Alfvén speed is then
yr. The corresponding value of the Alfvén speed is then
It should be noted that the Doppler factor
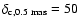 is similar to the Doppler factors implied by the observed statistics of superluminal motions near blazar cores (Jorstad et al. 2001a).
is similar to the Doppler factors implied by the observed statistics of superluminal motions near blazar cores (Jorstad et al. 2001a).
With the Alfvén speed determined, the masses of the black holes can
now be estimated from 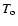 and
and 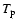 .
Since the orbital
separation
.
Since the orbital
separation
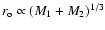 ,
a family of
solutions can be produced that satisfy
,
a family of
solutions can be produced that satisfy
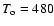 yr,
yr,
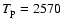 yr and reproduce the observed optical lightcurve of
3C 345 and radio properties of C7 (the shapes of the optical and
radio lightcurves depend on the mass ratio
yr and reproduce the observed optical lightcurve of
3C 345 and radio properties of C7 (the shapes of the optical and
radio lightcurves depend on the mass ratio
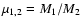 ). The
resulting solutions are presented in Table 6 for five
selected values of M1.
). The
resulting solutions are presented in Table 6 for five
selected values of M1.
In order to identify an acceptable solution for the black hole masses,
stability conditions of the accretion disk must be considered. The
rotational timescale of a precessing accretion disk in a binary system is
given by a characteristic period (Laskar & Robutel 1995)
The disk in a BBH system will be stable over timescales comparable
with the typical timescales of existence of a powerful radio source in
AGN,
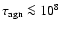 yr, if two conditions are satisfied:
yr, if two conditions are satisfied:
- 1.
-
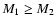 ,
where M1 is the mass of the black hole
surrounded by the accretion disk.
,
where M1 is the mass of the black hole
surrounded by the accretion disk.
- 2.
-
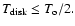
These conditions restrict the mass of the primary black hole to a
range
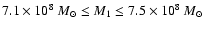 .
The lower limit corresponds to
.
The lower limit corresponds to
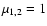 ,
and the
upper limit corresponds to
,
and the
upper limit corresponds to
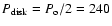 yr. The acceptable range of M1 is very narrow, and any
value within this range can be adopted. Since
yr. The acceptable range of M1 is very narrow, and any
value within this range can be adopted. Since 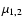 does not
change significantly over the acceptable range of M1 (
does not
change significantly over the acceptable range of M1 (
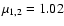 for
for
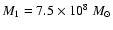 ),
),
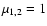 can be adopted
for the binary black hole mass solution, yielding
can be adopted
for the binary black hole mass solution, yielding
listed in Tables 2 and 6.
Table 6:
Black hole mass solutions for
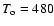 yr.
yr.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1831fg16.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg316.gif) |
Figure 16:
Range of acceptable solutions for the mass M1 of the primary
black hole in 3C 345. The acceptable solutions exist within the range
7.1 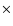
 .
Asterisks mark the solution for .
Asterisks mark the solution for
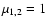 ,
for which
M1 =
M2 = 7.1 ,
for which
M1 =
M2 = 7.1 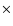
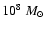 .
Shaded areas cover the values of M1, .
Shaded areas cover the values of M1, 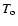 and
and 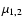 for which the accretion disk cannot remain stable
over the typical timescale of existence of a powerful radio source in AGN,
for which the accretion disk cannot remain stable
over the typical timescale of existence of a powerful radio source in AGN,
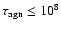 yr. yr. |
| Open with DEXTER |
6 Discussion
The BBH model applied to the quasar 3C 345 ties together, within a
single framework, the variability of the optical flux and the
evolution of the superluminal feature C7 resulted from a powerful flare
that occurred in 1991. The model reconstructs the physical conditions
in the plasma ejected into the jet during the flare, and the dynamic
properties of the binary system of supermassive black holes.
The binary black hole scenario was previously applied to 3C 345 by
Caproni & Abraham (2004) who attributed variations of the ejection
angle (similar to those plotted in Fig. 7) to
precession of the accretion disk. This approach yielded an
uncomfortably short precession period of
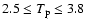 yr, very high black hole masses (M1 = 4-5
yr, very high black hole masses (M1 = 4-5 
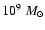 ,
M2 = 3-4
,
M2 = 3-4 
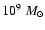 ), and extremely small orbital separation
), and extremely small orbital separation
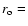 0.017-0.024 pc, which is
0.017-0.024 pc, which is 
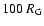 of the primary black hole. In such a
tight binary, the effective accretion radius of the secondary,
of the primary black hole. In such a
tight binary, the effective accretion radius of the secondary,
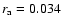 -0.050 pc, is larger than the orbital separation, and
it is very difficult to maintain the accretion disk intact. Indeed, it
can be shown (Ivanov et al. 1998) that the mass loss
rate
-0.050 pc, is larger than the orbital separation, and
it is very difficult to maintain the accretion disk intact. Indeed, it
can be shown (Ivanov et al. 1998) that the mass loss
rate 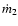 due to a shock that is formed after each passage of
the secondary through the accretion disk may be very large, and for
the BBH parameters of Caproni & Abraham (2004), it can reach
due to a shock that is formed after each passage of
the secondary through the accretion disk may be very large, and for
the BBH parameters of Caproni & Abraham (2004), it can reach
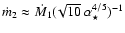 ,
where
,
where  is the rate of accretion on the primary black hole
and
is the rate of accretion on the primary black hole
and
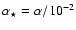 is the disc viscosity.
For weak accretion rates or small disk viscosity,
is the disc viscosity.
For weak accretion rates or small disk viscosity, 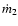 can even
become larger than
can even
become larger than 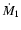 ,
which would most likely lead to a
subsequent destruction of the accretion disk.
,
which would most likely lead to a
subsequent destruction of the accretion disk.
Another argument against associating the ejection angle variability
with the disk precession is presented by the observed long-term
kinematic changes in the jet. The apparent accelerations plotted in
Fig. 6 and the long-term trend present in the
ejection angle changes plotted in Fig. 7 indicate
the presence of a periodic process on timescales of  2000 yr. This observed periodicity, though very difficult to establish, agrees well with the precession period recovered by fitting
the BBH model to the trajectory and flux evolution of C7.
2000 yr. This observed periodicity, though very difficult to establish, agrees well with the precession period recovered by fitting
the BBH model to the trajectory and flux evolution of C7.
The trajectory of C7 (and indeed the trajectories of several other
superluminal features monitored closely in the jet of 3C 345; Lobanov
& Zensus 1996; L96; LZ99) is clearly
non-ballistic on timescales spanning almost 10 years in the observer's
frame (and more than 100 years in the comoving frame). This is a clear
observational argument against a very short precession period in
3C 345. The model developed in this paper attributes non-ballistic
trajectories of the jet features to Alfvén perturbations of the
magnetic field, possibly modulated by the orbital motion in the system.
![\begin{figure}
\par\includegraphics[width=7.75cm,clip]{1831fg17.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg328.gif) |
Figure 17:
Characteristic timescales of disk activity in 3C 345,
compared to the quasi-period of the nuclear flares and to the
orbital and characteristic disk rotation periods). The
disk thermal instability operates at 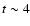 yr at distances of yr at distances of 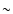
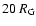 .
The mechanical (sound wave) instability reaches the
same timescale at .
The mechanical (sound wave) instability reaches the
same timescale at 
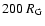 ,
where it becomes comparable
with the orbital and drift (accretion rate variations) timescales of
the disk. A combination of these effects may cause the flare
activity observed in 3C 345. ,
where it becomes comparable
with the orbital and drift (accretion rate variations) timescales of
the disk. A combination of these effects may cause the flare
activity observed in 3C 345. |
| Open with DEXTER |
The sum of the black hole masses (
M1,2 = 1.4 
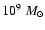 )
estimated in our model agrees well with the mass
)
estimated in our model agrees well with the mass
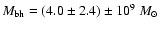 obtained
from measurements of nuclear opacity and magnetic field strength in
3C 345 (Lobanov 1998a). Gu et al. (2001)
report a higher value of
obtained
from measurements of nuclear opacity and magnetic field strength in
3C 345 (Lobanov 1998a). Gu et al. (2001)
report a higher value of
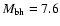
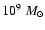 for 3C 345, from the properties of the broad line region. This estimate, however, depend strongly on the monochromatic luminosity (
for 3C 345, from the properties of the broad line region. This estimate, however, depend strongly on the monochromatic luminosity (
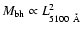 )
for
which the errors can be as large as 30% even for the nearby objects
(Kaspi et al. 2000). This error could be even larger for weaker
objects (3C 345 is about 100 times weaker in the optical than an
average object from the sample of Kaspi et al. 2000), and
overestimating
)
for
which the errors can be as large as 30% even for the nearby objects
(Kaspi et al. 2000). This error could be even larger for weaker
objects (3C 345 is about 100 times weaker in the optical than an
average object from the sample of Kaspi et al. 2000), and
overestimating
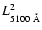 by only 50% would be bring
the
by only 50% would be bring
the
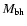 down to a value similar to the one derived in
this paper.
down to a value similar to the one derived in
this paper.
Finally, let us consider the periodicity of the flares and component
ejections in 3C 345. A  4 yr period of the flaring activity
is inferred from the observed variability of the radio nucleus
(LZ99), and it is related with the ejections of superluminal
features (see Fig. 3). Since this period is much
shorter than
4 yr period of the flaring activity
is inferred from the observed variability of the radio nucleus
(LZ99), and it is related with the ejections of superluminal
features (see Fig. 3). Since this period is much
shorter than
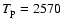 yr,
yr,
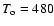 yr and
yr and
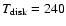 yr obtained in our model, there should be some
other periodic process affecting the accretion disk on timescales of
yr obtained in our model, there should be some
other periodic process affecting the accretion disk on timescales of
 4 yr. Figure 17 shows four different
characteristic disk timescales in 3C 345, for the black hole and
disk parameters determined in Sect. 4. These
timescales can be compared to the periodicity of the nuclear
flares. It appears that several processes occurring in the disk at
radial distances of 20-200
4 yr. Figure 17 shows four different
characteristic disk timescales in 3C 345, for the black hole and
disk parameters determined in Sect. 4. These
timescales can be compared to the periodicity of the nuclear
flares. It appears that several processes occurring in the disk at
radial distances of 20-200  may have similar
characteristic timescales. Thermal instability at
may have similar
characteristic timescales. Thermal instability at 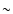
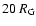 and mechanical (sound wave) instability at
and mechanical (sound wave) instability at 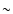
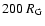 will develop at timescales of
will develop at timescales of 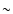 4 yr. In addition to
this, the orbital and drift (accretion rate variation) timescales
approach
4 yr. In addition to
this, the orbital and drift (accretion rate variation) timescales
approach 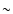 4 yr at
4 yr at 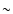
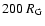 .
A combination of
these effects can cause the observed flare activity.
.
A combination of
these effects can cause the observed flare activity.
Another possible explanation for the observed flares is an
intermediate or stellar mass black hole or even a neutron star
orbiting the primary black hole at
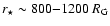 at a large angle with respect to the
accretion disk plane. Close approaches to, or even passages
through, the accretion disk should lead to formation of shock waves
in the disk (Ivanov et al. 1998; Subr
& Karas 1999), which in turn would cause an increase in the
accretion rate resulting in a nuclear flare and injection of a dense
plasma cloud into the jet.
at a large angle with respect to the
accretion disk plane. Close approaches to, or even passages
through, the accretion disk should lead to formation of shock waves
in the disk (Ivanov et al. 1998; Subr
& Karas 1999), which in turn would cause an increase in the
accretion rate resulting in a nuclear flare and injection of a dense
plasma cloud into the jet.
The periodicity of the flares may also be caused by a turbulence in the jet. Formation of a
turbulent layer close to the beam-jet boundary can enhance the pair
creation rate in the beam, which would be observed as the appearance,
and propagation, of a bright feature embedded in the flow.
The model developed in this paper explains the variability of the
optical flux and the kinematic and emission properties of the feature C7 observed in the relativistic jet of 3C 345 after a strong
nuclear flare. The dynamic properties of the system are described in
the framework of the orbital motion in a binary system of supermassive
black holes and the precession of an accretion disk around the primary
black hole. The emission and physical properties of relativistic
plasma produced during the flare are treated within the two-fluid
approach postulating a highly relativistic
 beam propagating
inside an
beam propagating
inside an
 jet. The
jet. The
 jet transports a major
fraction of the kinetic power associated with the outflow from the
nucleus of 3C 345, stabilizes
the
jet transports a major
fraction of the kinetic power associated with the outflow from the
nucleus of 3C 345, stabilizes
the
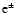 beam against plasma instabilities and shields it from
interaction with the external medium.
beam against plasma instabilities and shields it from
interaction with the external medium.
Determination of the properties of the jet and the binary system in
3C 345 is a difficult process involving two major steps. First, the
precession characteristics of the accretion disk are determined by
fitting the kinematic and flux density evolution of C7. This yields a
precession period
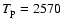 yr, which is in a good
agreement with the periodicities inferred from the changes of
kinematic properties of individual jet components and variations of
the ejecting position angle in 3C 345.
yr, which is in a good
agreement with the periodicities inferred from the changes of
kinematic properties of individual jet components and variations of
the ejecting position angle in 3C 345.
In the second step, the orbital and physical properties of the binary system are recovered
by fitting the observed optical variability. This yields an orbital
period of
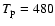 .
The consistency between
the two fits is ensured by requiring the fit to the optical light
curve to reproduce also the kinematic and flux density evolution of C7. The consistency argument constrains the properties of radio and optically emitting plasma, with
.
The consistency between
the two fits is ensured by requiring the fit to the optical light
curve to reproduce also the kinematic and flux density evolution of C7. The consistency argument constrains the properties of radio and optically emitting plasma, with
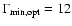 and
and
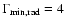 .
.
After ensuring consistency between the two fits, they are combined in
order to constrain the Alfvén speed
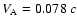 ,
and
make it popsible to recover the physical properties of the system. In
the last step, the conditions of disk stability are employed to
determine the individual masses of the binary companions. This
procedure yields
M1 = M2 = 7.1
,
and
make it popsible to recover the physical properties of the system. In
the last step, the conditions of disk stability are employed to
determine the individual masses of the binary companions. This
procedure yields
M1 = M2 = 7.1 
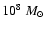 .
Finally, the model offers an explanation for the observed 4-year quasi
periodicity of nuclear flares in 3C 345. This
quasi-periodicity arises naturally from the characteristic timescales
of the accretion disk surrounding the primary black hole. The overall
success that the model has in explaining a variety of the
observational properties in 3C 345 argues in favor of this
explanation.
.
Finally, the model offers an explanation for the observed 4-year quasi
periodicity of nuclear flares in 3C 345. This
quasi-periodicity arises naturally from the characteristic timescales
of the accretion disk surrounding the primary black hole. The overall
success that the model has in explaining a variety of the
observational properties in 3C 345 argues in favor of this
explanation.
- Abraham, Z., & Carrara,
E. A. 1998, ApJ, 496, 172 [NASA ADS] [CrossRef] (In the text)
- Abraham, Z., & Romero,
G. E. 1999, A&A, 344, 61 [NASA ADS] (In the text)
- Achatz, U., &
Schlickeiser, R. 1993, A&A, 274, 165 [NASA ADS] (In the text)
- Aller, M. F., Aller,
H. D., & Hughes, P. A. 2003, ApJ, 586, 33 [NASA ADS] (In the text)
- Angione, R. J., Moore, E. P.,
Roosen, R. G., & Sievers, J. 1981, AJ, 86, 653 [NASA ADS]
- Attridge, J. M., Roberts,
D. H., & Wardle, J. F. C. 1999, ApJ, 518, 87 [NASA ADS] (In the text)
- Bååth, L. B. Rogers, A.
E. E., Inoue, M., et al. 1992, A&A, 257, 31 [NASA ADS]
- Babadzhanyants, M. K.,
& Belokon', E. T. 1984, Astrophys., 20, 461 [NASA ADS]
- Babadzhanyants, M. K.,
Belokon', E. T., & Gamm, N. G. 1995, Astron. Rep., 39, 393 [NASA ADS] (In the text)
- Belokon, E. T., &
Babadzhanyants, M. K. 1999, Astron. Lett., 25, 781 [NASA ADS] (In the text)
- Begelman, M. C.,
Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [NASA ADS] (In the text)
- Biretta, J. A., Moore, R.
L., & Cohen, M. H. 1986, ApJ, 308, 93 [NASA ADS] (In the text)
- Biretta, J. A., Sparks,
W. B., & Macchetto, F. 1999, ApJ, 520, 621 [NASA ADS] [CrossRef] (In the text)
- Blandford, R. D., &
Rees, M. J. 1978, in Pittsburgh Conf. BL Lac Objects, ed. A. M.
Wolfe (Pittsburgh: University of Pittsburgh), 328
(In the text)
- Britzen, S., Roland, J., Laskar,
J., et al. 2001, A&A, 374, 784 [EDP Sciences] [NASA ADS]
- Caproni, A., & Abraham,
Z. 2004, ApJ, 602, 625 [NASA ADS] (In the text)
- Camenzind, M., &
Krockenberger, M. 1992, A&A, 255, 59 [NASA ADS] (In the text)
- Cohen, M. H. 1985, in
Extragalactic Energetic Sources, ed. V. K. Kapahi (Bangalore:
Indian Academy of Sciences), 1
(In the text)
- Despringre, V., &
Fraix-Burnet, D. 1997, A&A, 320, 26 [NASA ADS] (In the text)
- Feretti, L., Comoretto, G.,
Giovannini, G., et al. 1993, ApJ, 408, 446 [NASA ADS]
- Gu, M., Cao, X., &
Jiang, D. R. 2001, MNRAS, 1111
(In the text)
- Hanasz, M., & Sol, H.
1996, A&A, 315, 355 [NASA ADS] (In the text)
- Hewitt, A., & Burbidge,
G. 1993, ApJS, 87, 451 [NASA ADS] (In the text)
- Ivanov, P. B.,
Igumenshchev, I. V., & Novikov, I. D. 1998, ApJ, 507, 131 [NASA ADS] (In the text)
- Ivanov, P. B.,
Papaloizou, J. C. B., & Polnarev, A. G. 1999, MNRAS, 307,
79 [NASA ADS] [CrossRef] (In the text)
- Jorstad, S. G., Marscher, A. P.,
Mattox, J. R., et al. 2001, ApJ, 556, 738 [NASA ADS]
- Jorstad, S. G., Marscher, A. P.,
Mattox, J. R., et al. 2001, ApJS, 134, 181 [NASA ADS] [CrossRef]
- Kaastra, J. S., & Roos,
N. 1992, A&A, 254, 96 [NASA ADS] (In the text)
- Kaspi, S., Smith, P. S., Netzer,
H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef]
- Kidger, M. R. 1988, PASP,
100, 1248 [NASA ADS] (In the text)
- Kidger, M. R. 1989,
A&A, 226, 9 [NASA ADS]
- Kidger, M. R., & de
Diego, J. A. 1990, A&A, 227, L25 [NASA ADS] (In the text)
- Kinman, T. D., Lamla, E., Ciurla,
T., Harlan, E., & Wirtanen, C. A. 1968, ApJ, 152, 357 [NASA ADS]
- Klare, J. 2003, Ph.D.
Thesis, University of Bonn, Germany
(In the text)
- Kolgaard, R. I., Wardle,
J. F., & Roberts, D. H. 1989, ApJ, 97, 1550 [NASA ADS] (In the text)
- Königl, A. 1981,
ApJ, 243, 700 [NASA ADS] (In the text)
- Laing, R., & Bridle, A.
H. 2002, MNRAS, 336, 1161 [NASA ADS] [CrossRef] (In the text)
- Laing, R., & Bridle, A.
H. 2004, MNRAS, 348, 1459 [NASA ADS] (In the text)
- Laskar, J. 1990, in
Méthodes Modernes de la Mécanique Céleste, ed. D.
Benest, & C. Froeschlé, 89
(In the text)
- Laskar, J., & Robutel,
P. 1995, Celestial Mechanics, 62, 193 [NASA ADS] (In the text)
- Lehto, H. J., &
Valtonen, M. J. 1996, ApJ, 460, 270 [NASA ADS] (In the text)
- Leppänen, K. J.,
Zensus, J. A., & Diamond, P. J. 1995, AJ, 110, 2479 [NASA ADS] [CrossRef]
- Lobanov, A. P. 1996, Ph.D.
Thesis, NMIMT, Socorro, USA (L96)
(In the text)
- Lobanov, A. P. 1998a,
A&A, 330, 79 [NASA ADS] (In the text)
- Lobanov, A. P. 1998b,
A&AS, 133, 261 [NASA ADS] (In the text)
- Lobanov, A. P., &
Zensus, J. A. 1996, in Energy Transport in Radio Galaxies and
Quasars, ed. P. E. Hardee, J. A. Zensus, & A. H. Bridle (San
Francisco: ASP), ASP Conf. Ser., 100, 124
(In the text)
- Lobanov, A. P., &
Zensus, J. A. 1999, ApJ, 521, 509 [NASA ADS] (LZ99)
(In the text)
- Lobanov, A. P., Carrara,
E., & Zensus, J. A. 1997, Vistas Astron., 41, 253 [NASA ADS] (In the text)
- Lü, P. K. 1972, AJ,
77, 829 [NASA ADS] (In the text)
- Makino, J. 1997, ApJ,
478, 58 [NASA ADS] (In the text)
- Makino, J., &
Ebisuzaki, T. 1996, ApJ, 465, 527 [NASA ADS] (In the text)
- Marcowith, A., Henri, G.,
& Pelletier, G. 1995, MNRAS, 277, 681 [NASA ADS] (In the text)
- Marcowith, A., Henri, G.,
& Renaud, N. 1998, A&A, 331, L57 [NASA ADS] (In the text)
- McGimsey, B. Q., Smith, A. G.,
Scott, R. L., et al. 1975, AJ, 80, 895 [NASA ADS] [CrossRef]
- Pelletier, G., Sol, H.,
& Asseo, E. 1988, Phys. Rev. A, 38, 2552 [NASA ADS] (In the text)
- Pelletier, G., &
Roland, J. 1989, A&A, 224, 24 [NASA ADS] (In the text)
- Pelletier, G., &
Roland, J. 1990, in Parsec-Scale Jets, ed. J. A. Zensus, & T.
J. Pearson (Cambridge: Cambridge University Press), 323
(In the text)
- Pelletier, G., & Sol,
H. 1992, MNRAS, 254, 635 [NASA ADS] (In the text)
- Pollock, J. T., Pica, A. J., Smith,
A. G., et al. 1979, AJ, 84, 1658 [NASA ADS]
- Polnarev, A. G., &
Rees, M. J. 1994, A&A, 283, 301 [NASA ADS] (In the text)
- Rieger, F. M., &
Mannheim, K. 2000, A&A, 359, 948 [NASA ADS] (In the text)
- Roland, J., & Hermsen,
W. 1995, A&A, 297, L9 [NASA ADS] (In the text)
- Roland, J., & Hetem, A.
1996, in Cygnus A: Study of a radio galaxy, ed. C. L. Carilli,
& D. E. Harris (Cambridge: Cambridge University Press),
126
(In the text)
- Roland, J., Peletier, G.,
& Muxlow, T. 1988, A&A, 207, 16 [NASA ADS] (In the text)
- Roland, J., Teyssier, R.,
& Roos, N. 1994, A&A, 290, 357 [NASA ADS] (In the text)
- Roos, N., Kaastra, J. S.,
& Hummel, C. A. 1993, ApJ, 409, 130 [NASA ADS] [CrossRef] (In the text)
- Ros, E., Zensus, J. A., &
Lobanov, A. P. 2000, A&A, 354, 55 [NASA ADS] (R00)
(In the text)
- Sillanpää, A.,
Haarala, S., & Valtonen, M. J. 1988, ApJ, 325, 628 [NASA ADS] [CrossRef] (In the text)
- Schramm, K.-J., Borgeest, U.,
Camenzind, M., et al. 1993, A&A, 278, 391 [NASA ADS]
- Skibo, J. G., Dermer, C.
D., & Schlickeiser, R. 1997, ApJ, 483, 56 [NASA ADS] (In the text)
- Smyth, M. J., &
Wolstencroft, R. D. 1970, A&AS, 8, 471 (In the text)
- Sol, H., Pelletier, G.,
& Asseo, E. 1989, MNRAS, 237, 411 [NASA ADS] (In the text)
- Steffen, W., Zensus, J. A.,
Krichbaum, T. P., Witzel, A., & Qian, S. J. 1995, A&A, 302,
335 [NASA ADS]
- Subr, L., & Karas, V.
1999, A&A, 352, 452 [NASA ADS] (In the text)
- Teräsranta, H., Tornikoski,
M., Mujunen, A., et al. 1998, A&AS, 132, 305 [NASA ADS]
- Tingay, S. J., Jauncey, D. L.,
Reynolds, J. E., et al. 1998, AJ, 115, 960 [NASA ADS]
- Valtaoja, E., Teräsranta, H.,
Tornikoski, M., et al. 2000, ApJ, 531, 744 [NASA ADS]
- Vicente, L., Charlot, P.,
& Sol, H. 1996, A&A, 312, 727 [NASA ADS] (In the text)
- Vio, R., Cristiani, S., Lessi, O.,
& Salvadori, L. 1991, ApJ, 380, 351 [NASA ADS]
- Unwin, S. C., Cohen, M. H.,
Pearson, T. J., et al. 1983, ApJ, 271, 536 [NASA ADS]
- Unwin, S. C., Wehrle, A. E., Urry,
C. M., et al. 1994, ApJ, 432, 103 [NASA ADS]
- Unwin, S. C., Wehrle, A. E.,
Lobanov, A. P., et al. 1997, ApJ, 480, 596 [NASA ADS]
- Waltman, E. B., Fiedler, R. L.,
Johnston, K. J., et al. 1991, ApJS, 77, 379 [NASA ADS]
- Webb, J. R., Smith, A. G., Leacock,
R. J., et al. 1988, AJ, 95, 374 [NASA ADS] [CrossRef]
- Zensus, J. A. 1997,
ARA&A, 35, 607 [NASA ADS] (In the text)
- Zensus, J. A., Krichbaum,
T. P., & Lobanov, A. P. 1995, Proc. Natl. Acad. Sci. USA, 92,
11348 [NASA ADS] (In the text)
- Zensus, J. A., Krichbaum,
T. P., & Lobanov, A. P. 1996, Rev. Mod. Astron., 9, 241 [NASA ADS] (In the text)
- Zensus, J. A., Cohen, M.
H., & Unwin, S. C. 1995, ApJ, 443, 35 [NASA ADS] (ZCU95)
(In the text)
- Zensus, J. A., Ros, E.,
Kellermann, K. I., et al. 2002, AJ, 124, 662 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{1831fg01.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg59.gif)
![\begin{figure}
\par\includegraphics[width=7.75cm,clip]{1831fg02.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg63.gif)
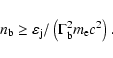
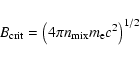
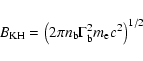
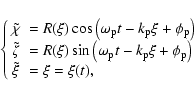
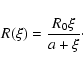
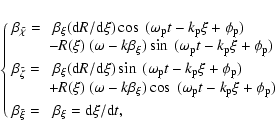
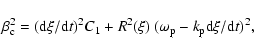
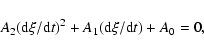
![$\displaystyle %
\frac{{\rm d} \xi}{{\rm d} t} = \frac{1}{A_2} \biggl\{ R^2(\xi)...
... p}\right)\left(1 +
\frac{{\rm d} R}{{\rm d} \xi}\right) \right]^{1/2}\biggl\},$](/articles/aa/full/2005/09/aa1831/img108.gif)
![\begin{displaymath}%
t(\xi) = t_0 + \int^{\xi}_{\xi_{0}} \frac{A_2}{k_{\rm p}\om...
... c} - \omega^2_{\rm p} R^2(\xi) C_1\right]^{1/2}} {\rm d} \xi.
\end{displaymath}](/articles/aa/full/2005/09/aa1831/img109.gif)
![\begin{displaymath}%
R(\xi) \le \beta_{\rm c} \left[ \omega^2_{\rm p} - k^2_{\rm p}
\beta^2_{\rm c} \cos^2\psi(\xi)\right]^{-1/2}.
\end{displaymath}](/articles/aa/full/2005/09/aa1831/img112.gif)
![\begin{displaymath}%
\xi \le \beta_{\rm c} \left[ \omega^2_{\rm p} \tan^2\psi - k^2_{\rm p} \beta^2_{\rm c} \sin^2\psi
\right]^{-1/2}.
\end{displaymath}](/articles/aa/full/2005/09/aa1831/img116.gif)
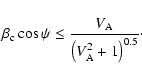
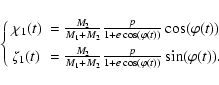
![\begin{displaymath}%
\left\{
\begin{array}{ll}
\chi & =\tilde{\chi} + \chi_{1}(t...
...(t)
+ \phi_{\rm o}) \\ [2mm]
\xi & =\xi(t)
\end{array}\right.
\end{displaymath}](/articles/aa/full/2005/09/aa1831/img125.gif)
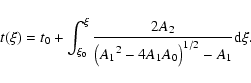
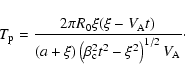
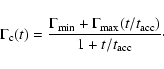
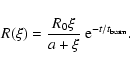
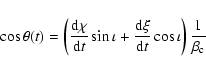
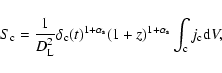
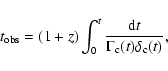
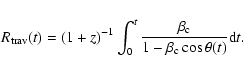
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1831fg03.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg151.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1831fg04.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg152.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1831fg05.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg223.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1831fg06.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg243.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1831fg07.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg249.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1831fg08.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg250.gif)
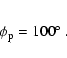
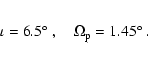
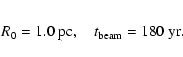
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1831fg09.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg283.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1831fg10.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg284.gif)
![\begin{figure}
\par\includegraphics[width=7.25cm,clip]{1831fg11.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg285.gif)
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{1831fg12.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg286.gif)
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{1831fg13.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg287.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1831fg14.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg288.gif)
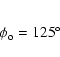
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{1831fg15.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg292.gif)
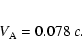
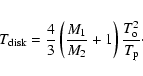
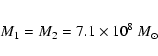
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1831fg16.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg316.gif)
![\begin{figure}
\par\includegraphics[width=7.75cm,clip]{1831fg17.eps}\end{figure}](/articles/aa/full/2005/09/aa1831/Timg328.gif)