- ...
always
![[*]](/icons/foot_motif.gif)
- This approximation can fail in a catastrophic way if
there is a close approach by some of the VAs in between the observations
and the prediction.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... orbits
![[*]](/icons/foot_motif.gif)
- Väisälä's method to compute some
"Väisälä'' orbit from two observations should not be confused with
Väisälä's method to solve Gauss' problem of the orbit from three
observations, although of course the two algorithms are related.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... symmetric
![[*]](/icons/foot_motif.gif)
- But not necessarily
diagonal (Carpino et al. 2003).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
continuation
![[*]](/icons/foot_motif.gif)
- Our two impact monitoring systems, CLOMON2 and
Sentry, use different conventions for the orientation of the LOV.
Thus, in comparing the outputs of CLOMON2 and Sentry, it is necessary
to check whether the orientation of the LOV is the same.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... examples
![[*]](/icons/foot_motif.gif)
- The
eigenvalues of the covariance matrix are given with the orbital
elements in the NEODyS and AstDyS information systems.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... convergence
![[*]](/icons/foot_motif.gif)
- In a numerical
procedure, convergence is defined as having the last iteration with a
small enough correction; in this context, the following properties are
satisfied only approximately.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Runge-Kutta
![[*]](/icons/foot_motif.gif)
- In
fact, we use a second order implicit Runge-Kutta-Gauss.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
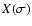
![[*]](/icons/foot_motif.gif)
- It would be possible to use an
interpolation procedure also with the parameter
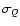 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... failed
![[*]](/icons/foot_motif.gif)
- Unless some
other preliminary orbit algorithm is available.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
orbit
![[*]](/icons/foot_motif.gif)
- In this case, the covariance provides information on
the uncertainty but it is not possible to define formally a confidence
region because the minimum value of the cost function is not known
(and may not exist).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
service
![[*]](/icons/foot_motif.gif)
- http://hamilton.dm.unipi.it/astdys/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ridiculous
![[*]](/icons/foot_motif.gif)
- The only
one-nighters for which a comparatively accurate orbit can be computed
are some Near Earth Asteroids, in particular the ones with very high
proper motion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... successfully
![[*]](/icons/foot_motif.gif)
- We have so far
proposed, by using this algorithm, more than 4000 orbit identifications published by the MPC.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... it
![[*]](/icons/foot_motif.gif)
- The
LOV algorithms are available in the free software
OrbFit at http://newton.dm.unipi.it/orbfit/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.