A&A 431, 451-464 (2005)
DOI: 10.1051/0004-6361:20041324
Numerical simulations of expanding supershells in dwarf irregular
galaxies
II. Formation of giant HI rings
E. I. Vorobyov1,2 - Shantanu Basu2
1 - Institute of Physics, Stachki 194, Rostov-on-Don, Russia
2 -
Department of Physics and Astronomy, University of Western Ontario, London,
Ontario N6A 3K7, Canada
Received 19 May 2004 / Accepted 14 October 2004
Abstract
We perform numerical hydrodynamic modeling of various physical
processes that can form an HI ring as is observed in Holmberg I (Ho I).
Three energetic mechanisms are considered: multiple
supernova explosions (SNe), a hypernova explosion associated with a gamma
ray burst (GRB), and the vertical impact of a high
velocity cloud (HVC). The total released energy has an upper limit of
 1054 erg. We find that multiple SNe are in general more effective
in producing shells that break out of the disk
than a hypernova explosion of the same total energy.
As a consequence, multiple SNe form rings with a high ring-to-center
contrast
1054 erg. We find that multiple SNe are in general more effective
in producing shells that break out of the disk
than a hypernova explosion of the same total energy.
As a consequence, multiple SNe form rings with a high ring-to-center
contrast
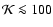 in the HI column density, whereas
single hypernova explosions form rings with
in the HI column density, whereas
single hypernova explosions form rings with
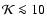 .
Only multiple SNe can reproduce both
the size (diameter
.
Only multiple SNe can reproduce both
the size (diameter  1.7 kpc) and the ring-to-center contrast (
1.7 kpc) and the ring-to-center contrast (
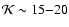 )
of the HI ring in Ho I. High velocity clouds create HI rings
that are much smaller in size (
)
of the HI ring in Ho I. High velocity clouds create HI rings
that are much smaller in size (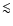 0.8 kpc) and contrast (
0.8 kpc) and contrast (
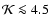 )
than seen in Ho I. We construct model position-velocity (pV) diagrams and find that they
can be used to distinguish among different HI ring formation mechanisms.
The observed pV-diagrams of Ho I (Ott et al. 2001) are best
reproduced by multiple SNe. We conclude that the giant HI ring in
Ho I is most probably formed by multiple SNe. We also find that the appearance
of the SNe-driven shell in the integrated HI image depends on
the inclination angle of the galaxy. In nearly face-on galaxies, the integrated
HI image shows a ring of roughly constant HI column density
surrounding a deep central depression, whereas
in considerably inclined galaxies (
)
than seen in Ho I. We construct model position-velocity (pV) diagrams and find that they
can be used to distinguish among different HI ring formation mechanisms.
The observed pV-diagrams of Ho I (Ott et al. 2001) are best
reproduced by multiple SNe. We conclude that the giant HI ring in
Ho I is most probably formed by multiple SNe. We also find that the appearance
of the SNe-driven shell in the integrated HI image depends on
the inclination angle of the galaxy. In nearly face-on galaxies, the integrated
HI image shows a ring of roughly constant HI column density
surrounding a deep central depression, whereas
in considerably inclined galaxies (
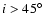 )
the HI image is characterized
by two kidney-shaped density enhancements and a mild central depression.
)
the HI image is characterized
by two kidney-shaped density enhancements and a mild central depression.
Key words: galaxies: dwarf - ISM: bubbles
There are a few nearby low-mass dwarf irregular galaxies (dIrr's) such as
Holmberg I (Tully et al. 1978;
Ott et al. 2001), M 81 dwA (Sargent et al. 1983; Westpfahl & Puche 1993), Sagittarius DIG (Young & Lo 1997), Sextans A (Skillman et al.
1988; Stewart 1998), the HI morphology of
which is totally dominated by a single ring structure of size comparable
to or bigger than their optical extent.
The integrated HI image of these dIrr's shows a central HI hole surrounded
by a denser HI ring.
The contrast in the azimuthally averaged HI column density between the central hole
and the ring varies from  3-4 in Sextans A and M 81 dwA to
3-4 in Sextans A and M 81 dwA to  15-20 in Holmberg I.
HI rings that do not dominate the overall HI extent of a
galaxy, yet occupy a considerable region (kpc scale),
have also been found in other dIrr's such as DDO 47 (shell 13, according to Walter
& Brinks 2001) and Holmberg II (shell 21, according to
Puche et al. 1992).
15-20 in Holmberg I.
HI rings that do not dominate the overall HI extent of a
galaxy, yet occupy a considerable region (kpc scale),
have also been found in other dIrr's such as DDO 47 (shell 13, according to Walter
& Brinks 2001) and Holmberg II (shell 21, according to
Puche et al. 1992).
There are a number of scenarios that could create HI holes in galactic disks
(see Sánchez-Salcedo
2002), which can loosely be divided into two groups comprising
the energetic and non-energetic mechanisms.
The energetic mechanisms assume a deposition of vast amount of energy into
the interstellar medium and include multiple supernova explosions
(Mac Low & McCray 1988; De Young & Heckman 1994;
Mac Low & Ferrara 1999; Silich et al. 2001),
impact of high velocity clouds (Tenorio-Tagle et al. 1987; Comerón
& Torra 1992; Rand & Stone 1996),
and gamma ray bursts (Efremov et al. 1998; Loeb & Perna 1998).
The non-energetic mechanisms include a combined action of thermal and gravitational
instabilities in the gas disk (Wada et al. 2000), turbulent clearing
(Elmegreen 1997; Walter & Brinks 1999), and
ultra-violet erosion of the HI disk (Vorobyov & Shchekinov 2004).
It appears however very unlikely that a central HI depression surrounded by
a denser HI ring with size comparable to the galaxy's optical extent
could be produced by a non-energetic mechanism.
Indeed, Vorobyov et al. (2004) have recently shown that the HI ring-like
morphology of Holmberg I (Ho I) can be produced by multiple supernova explosions (SNe).
In this paper, we consider two other energetic mechanisms of HI ring formation,
namely the impact of high velocity clouds (HVCs) and gamma ray bursts (GRBs),
and show that they cannot explain the formation of the observed giant HI ring
in Ho I. We generate the position-velocity diagrams and show that they can be used
to distinguish between the rings created by different energetic mechanisms.
We find that the appearance of HI rings created by multiple SNe
is sensitive to the inclination angle of the galaxy. In considerably inclined
galaxies, the HI ring would rather appear as two kidney-shaped density
enhancements similar to those observed in Sectans A.
The paper is organized as follows. In Sect. 2 the numerical hydrodynamic
model for simulating multiple SNe, GRBs, and the impact
of HVCs is formulated. A comparative study of multiple SNe
and GRBs of the same total energy is performed in Sect. 4. The
collision of HVCs with the galactic gas disk is considered in Sect. 5.
The main results are summarized in Sect. 7.
2 Numerical model
Our model galaxy consists of a rotating gas disk, stellar disk, and a
spherically symmetric dark matter halo.
The density profile of the stellar component is chosen as:
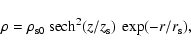 |
(1) |
where
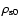 is the stellar density in the center of the galaxy, and
is the stellar density in the center of the galaxy, and 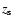 and
and 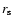 are the vertical scale height and radial scale length of the stellar component, respectively.
We assume that the density profile of the dark matter (DM) halo can be approximated
by a modified isothermal sphere (Binney & Tremaine 1987)
are the vertical scale height and radial scale length of the stellar component, respectively.
We assume that the density profile of the dark matter (DM) halo can be approximated
by a modified isothermal sphere (Binney & Tremaine 1987)
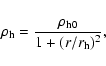 |
(2) |
where the central density
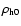 and the characteristic scale length
and the characteristic scale length 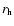 were given by Mac Low & Ferrara (1999) and Silich & Tenorio-Tagle (2001)
based on the study of the dark-to-visible mass ratios by Persic et al. (1996):
were given by Mac Low & Ferrara (1999) and Silich & Tenorio-Tagle (2001)
based on the study of the dark-to-visible mass ratios by Persic et al. (1996):
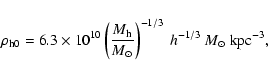 |
(3) |
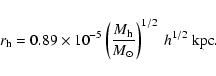 |
(4) |
Here, h is the Hubble constant in units of 100 km s-1 Mpc-1 and 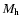 is the total halo mass. We adopt h=0.65 throughout the paper.
is the total halo mass. We adopt h=0.65 throughout the paper.
Our model galaxy is meant to represent Ho I and we use the observations
of Ott et al. (2001) to constrain the parameters of our model.
We note that 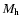 in Eqs. (3) and (4) is, in
fact, the total mass of the halo. We vary
in Eqs. (3) and (4) is, in
fact, the total mass of the halo. We vary 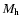 until the actual halo
mass confined within the HI diameter of Ho I
(5.8 kpc, Ott et al. 2001) agrees with the observed value,
until the actual halo
mass confined within the HI diameter of Ho I
(5.8 kpc, Ott et al. 2001) agrees with the observed value,
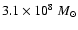 .
This fit yields a value of
.
This fit yields a value of
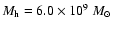 for Ho I.
Once the total halo mass is fixed, we derive the parameters of the halo
density distribution using Eqs. (3) and (4), which
are further used to compute the gravitational potential of the halo
as described in Vorobyov et al. (2004).
We have adopted a value of
for Ho I.
Once the total halo mass is fixed, we derive the parameters of the halo
density distribution using Eqs. (3) and (4), which
are further used to compute the gravitational potential of the halo
as described in Vorobyov et al. (2004).
We have adopted a value of
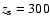 pc, which is typical
for dwarf irregular galaxies.
The radial scale length
pc, which is typical
for dwarf irregular galaxies.
The radial scale length
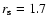 kpc of the stellar disk is estimated from the
kpc of the stellar disk is estimated from the 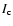 -band radial surface brightness profile of Ho I.
With
-band radial surface brightness profile of Ho I.
With 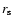 and
and 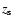 being
fixed, the stellar density
being
fixed, the stellar density
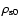 in Eq. (1) is varied so as to
obtain the measured luminous stellar mass of
in Eq. (1) is varied so as to
obtain the measured luminous stellar mass of
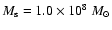 .
This results in
.
This results in
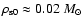 pc-3.
The adopted parameters of the stellar disk are further used
to compute the stellar gravitational potential by solving the Poisson equation.
pc-3.
The adopted parameters of the stellar disk are further used
to compute the stellar gravitational potential by solving the Poisson equation.
Once the stellar and DM halo gravitational potentials are fixed,
we obtain the initial gas density distribution by solving the steady-state momentum equation
as described in Vorobyov et al. (2004). We set the gas velocity dispersion
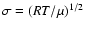 to be 9 km s-1 (Ott et al. 2001).
We vary the rotation curve until
the initial gas surface density distribution becomes exponential, which
is in agreement with observations of the HI radial distribution in many
dIrr's (Taylor et al. 1994).
The observed rotation curve (RC) of Ho I is known to the accuracy
of the inclination angle, which in turn is poorly determined (Ott et al. 2001)
due to Ho I's small inclination. We have chosen the initial
RC in our model so that the initial radial gas surface
density distribution well reproduces the observed profile at r>1 kpc,
i.e. at radii which are not affected by the
subsequent ring expansion. We do not expect our initial RC to
match the currently observed RC, since the latter
is already affected by ring formation. Furthermore,
accurately modeling the observed RC
(for an assumed inclination angle) requires non-axisymmetric simulations,
since the dynamical center of Ho I is
to be 9 km s-1 (Ott et al. 2001).
We vary the rotation curve until
the initial gas surface density distribution becomes exponential, which
is in agreement with observations of the HI radial distribution in many
dIrr's (Taylor et al. 1994).
The observed rotation curve (RC) of Ho I is known to the accuracy
of the inclination angle, which in turn is poorly determined (Ott et al. 2001)
due to Ho I's small inclination. We have chosen the initial
RC in our model so that the initial radial gas surface
density distribution well reproduces the observed profile at r>1 kpc,
i.e. at radii which are not affected by the
subsequent ring expansion. We do not expect our initial RC to
match the currently observed RC, since the latter
is already affected by ring formation. Furthermore,
accurately modeling the observed RC
(for an assumed inclination angle) requires non-axisymmetric simulations,
since the dynamical center of Ho I is  0.7 kpc
offset from the morphological center of the ring.
This offset may complicate the shape of the observed RC,
because it is measured around the dynamical center. This task is beyond
the scope of our paper.
The resulting radial gas surface density
profile, as well as the Gaussian vertical scale height h of the gas distribution
and initial gas rotation curve, are plotted in Fig. 1 by the solid,
dotted, and dashed lines, respectively.
The total gas mass
within the computational domain is
0.7 kpc
offset from the morphological center of the ring.
This offset may complicate the shape of the observed RC,
because it is measured around the dynamical center. This task is beyond
the scope of our paper.
The resulting radial gas surface density
profile, as well as the Gaussian vertical scale height h of the gas distribution
and initial gas rotation curve, are plotted in Fig. 1 by the solid,
dotted, and dashed lines, respectively.
The total gas mass
within the computational domain is
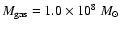 ,
of which
,
of which 
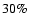 is contributed by He (
is contributed by He (
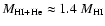 ,
,
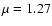 ,
Brinks 1990). This value of
,
Brinks 1990). This value of
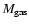 roughly agrees with that
obtained by Ott et al. (2001).
roughly agrees with that
obtained by Ott et al. (2001).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1324fig1.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg45.gif) |
Figure 1:
The equilibrium radial distribution of gas surface density
(the solid line), the initial rotation curve (the dashed line), and
the Gaussian vertical scale height of gas distribution (the dotted
line). |
| Open with DEXTER |
A usual set of hydrodynamical equations in cylindrical coordinates (with the assumption of axial symmetry)
is solved using the method of finite-differences with a time-explicit, operator-split solution procedure as
used in the ZEUS-2D code described in detail in Stone & Norman (1992).
The computational domain spans the range of
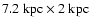 in the vertical and horizontal directions, respectively, with a resolution of 5 pc.
We have implemented the optically thin cooling curve given
in Wada & Norman (2001) for a metallicity of one tenth of solar, which is typical for dIrr's.
The cooling processes taken into account are:
(1) recombination of H, He, C, O, N, Si, and Fe;
(2) collisional excitation of HI, CI-IV, and OI-IV;
(3) hydrogen and helium bremsstrahlung;
(4) vibrational and rotational excitation of
in the vertical and horizontal directions, respectively, with a resolution of 5 pc.
We have implemented the optically thin cooling curve given
in Wada & Norman (2001) for a metallicity of one tenth of solar, which is typical for dIrr's.
The cooling processes taken into account are:
(1) recombination of H, He, C, O, N, Si, and Fe;
(2) collisional excitation of HI, CI-IV, and OI-IV;
(3) hydrogen and helium bremsstrahlung;
(4) vibrational and rotational excitation of 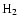 ;
(5) atomic and molecular cooling due to fine-structure emission of C, C+,
and O, and rotational line emission of CO and
;
(5) atomic and molecular cooling due to fine-structure emission of C, C+,
and O, and rotational line emission of CO and 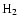 .
We use an empirical heating function tuned to balance the cooling in
the background atmosphere so that it maintains the gas in hydrostatic
and thermal equilibrium; it may be thought of as a crude model for
the stellar energy input. However, heating is prohibited at
.
We use an empirical heating function tuned to balance the cooling in
the background atmosphere so that it maintains the gas in hydrostatic
and thermal equilibrium; it may be thought of as a crude model for
the stellar energy input. However, heating is prohibited at
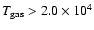 K
to avoid the effects of spurious heating of a bubble's interior
by the time-independent heating function. This
is physically justified since most of the heating in the warm interstellar medium
comes from the photoelectric heating of polycyclic aromatic hydrocarbon molecules
(PAHs) and small grains, which will be either evaporated or highly ionized in the bubble filled with
hot supernova ejecta.
Cooling and heating are treated numerically at the end of the time integration
step using an implicit update to the energy equation. The implicit equation
for energy density is solved by Newton-Raphson iteration, supplemented by a bisection algorithm for
occasional zones where the Newton-Raphson method does not converge. In order to monitor accuracy,
the total change in the internal energy density in one time step is kept below
K
to avoid the effects of spurious heating of a bubble's interior
by the time-independent heating function. This
is physically justified since most of the heating in the warm interstellar medium
comes from the photoelectric heating of polycyclic aromatic hydrocarbon molecules
(PAHs) and small grains, which will be either evaporated or highly ionized in the bubble filled with
hot supernova ejecta.
Cooling and heating are treated numerically at the end of the time integration
step using an implicit update to the energy equation. The implicit equation
for energy density is solved by Newton-Raphson iteration, supplemented by a bisection algorithm for
occasional zones where the Newton-Raphson method does not converge. In order to monitor accuracy,
the total change in the internal energy density in one time step is kept below 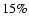 .
If this condition is not met, the time step is reduced and a solution
is again sought. In the following we give a brief description on the mechanisms of energy
injection used in our numerical simulation.
.
If this condition is not met, the time step is reduced and a solution
is again sought. In the following we give a brief description on the mechanisms of energy
injection used in our numerical simulation.
Here, we briefly review possible mechanisms of HI ring
formation as observed in Ho I.
Consecutive supernova explosions. The origin of the giant HI rings in dIrr's is traditionally thought to lie in the
combined effect of stellar winds and supernova explosions produced by young
stellar associations (see e.g. Ott et al. 2001).
In our simulations, the energy of supernova explosions is released in the form of thermal energy
in the central region with a radius of 30 pc filled with the hot (
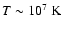 )
and rarified (
)
and rarified (
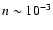 cm-3) gas, which is presumably formed
by the previous action of stellar winds.
We use a constant wind approximation, i.e. at each time step we add energy
to the source region at a rate of
cm-3) gas, which is presumably formed
by the previous action of stellar winds.
We use a constant wind approximation, i.e. at each time step we add energy
to the source region at a rate of 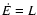 ,
where L is the mechanical
luminosity defined as the total released energy of SNe divided by the duration of the energy
input phase. We choose the energy input phase to last for 30 Myr,
which corresponds roughly to the difference in the lifetimes of the most and
least massive stars capable of producing SNe in a cluster of simultaneously
born stars. Since in the present simulations we deal with large stellar
clusters with hundreds of supernovae, the release of the energy of SNe
in the form of thermal energy is justified (Mac Low & McCray 1988).
,
where L is the mechanical
luminosity defined as the total released energy of SNe divided by the duration of the energy
input phase. We choose the energy input phase to last for 30 Myr,
which corresponds roughly to the difference in the lifetimes of the most and
least massive stars capable of producing SNe in a cluster of simultaneously
born stars. Since in the present simulations we deal with large stellar
clusters with hundreds of supernovae, the release of the energy of SNe
in the form of thermal energy is justified (Mac Low & McCray 1988).
Gamma ray bursts. The consecutive SN explosions may not be the only mechanism
that could release
1053-1054 erg of energy,
enough to form giant HI rings.
Another mechanism has been suggested by Efremov et al. (1998)
and Loeb & Perna (1998), who argued that the GRB
explosions are powerful enough to make kpc-size shells in the interstellar
media of spiral and irregular galaxies. Although the physics of
GRBs is still poorly understood, the general picture emerging is that they are
highly energetic events (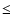 1054 erg, see e.g. Paczynski 1998)
that release energy in a short period of time (of the order of a few seconds).
Consequently, we model the GRB explosion (hereafter, "hypernova'' according
to Paczynski 1998) by an instantaneous release of
thermal energy within a sphere of 30 pc, filled with hot (
1054 erg, see e.g. Paczynski 1998)
that release energy in a short period of time (of the order of a few seconds).
Consequently, we model the GRB explosion (hereafter, "hypernova'' according
to Paczynski 1998) by an instantaneous release of
thermal energy within a sphere of 30 pc, filled with hot (
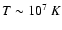 )
and rarified (
)
and rarified (
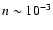 cm-3) gas. We have also
explored the injection of hypernova energy in the form of kinetic energy
and found that it does not noticeably influence the dynamics of the hypernova-driven shell.
cm-3) gas. We have also
explored the injection of hypernova energy in the form of kinetic energy
and found that it does not noticeably influence the dynamics of the hypernova-driven shell.
Impact of high velocity clouds. Another possible mechanism that could
create HI holes in the galactic disks was proposed
by Tenorio-Tagle et al. (1987), who argued that the infall of high velocity clouds
could deposit 1052 to 1054 erg per collision.
The numerical simulations of Tenorio-Tagle et al. (1987) have indeed
shown that HVCs are capable of forming the giant curved arcs and cavities
in the Galactic disk (see also Rand & Stone (1996)
for numerical simulations of HVC impact in NGC 4631). Most
previous numerical simulations have been concerned with the infall of HVCs
in massive galaxies, because their collisional cross section is much larger
than that of dwarf irregulars. Moreover, the gas disks in dwarf irregulars
are in general thicker than those of massive spiral galaxies, which would
make it more difficult for an HVC to penetrate the disk.
In summary, the formation of a giant HI hole
surrounded by a denser HI ring (as is observed in Ho I and other dwarf irregulars)
by the infall of HVCs is not obvious and requires further investigation.
Taking into account the diameter of the HI ring in Ho I ( 1.7 kpc),
we consider the most energetic HVCs,
which cover a velocity range
1.7 kpc),
we consider the most energetic HVCs,
which cover a velocity range
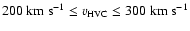 and have HI column density
and have HI column density
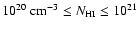 cm-3.
In our simulations the kinetic energies of HVCs range from
cm-3.
In our simulations the kinetic energies of HVCs range from
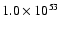 to
to
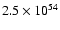 erg, which corresponds to a variation in HVC masses of
erg, which corresponds to a variation in HVC masses of
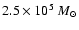 to
to
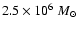 .
Such massive and energetic HVCs most probably have an extragalactic origin.
.
Such massive and energetic HVCs most probably have an extragalactic origin.
4 Supernova explosions versus gamma ray bursts
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1324fig2.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg61.gif) |
Figure 2:
Temporal evolution of the gas volume density distribution
after the release of
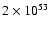 erg of thermal energy at z=0,r=0 pc.
The upper panels correspond to 200 consecutive SN explosions over
30 Myr, while the lower panels show the impact of a single hypernova
of the same total energy of erg of thermal energy at z=0,r=0 pc.
The upper panels correspond to 200 consecutive SN explosions over
30 Myr, while the lower panels show the impact of a single hypernova
of the same total energy of
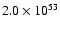 erg. The scale bar is in gm cm-3. erg. The scale bar is in gm cm-3. |
| Open with DEXTER |
We start by showing in Fig. 2 the temporal evolution of the distribution
of the gas volume density produced by 200 consecutive
SNe (the upper panels) and by a hypernova explosion of the same total
energy of
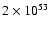 erg (the lower panels).
The overall gas dynamics is similar
in both cases. However, there are minor differences seen not only in the dynamics
of the hot gas but also in the shape of the blown-up shell.
In the case of a hypernova explosion, there is no "blowout'' observed
(i.e. the shell breaking out of the disk and pumping the hot gas into the
intergalactic medium).
The hot gas is always confined inside the shell in the early expansion
phase and it cools down at later times t>40 Myr due to the radiative cooling.
As a result, the shell collapses at t=45 Myr,
creating a mildly compressed central core, the gas density of which
is however below the Jeans limit.
In the case of multiple SNe, part of the hot gas is lifted to a higher altitude
of
erg (the lower panels).
The overall gas dynamics is similar
in both cases. However, there are minor differences seen not only in the dynamics
of the hot gas but also in the shape of the blown-up shell.
In the case of a hypernova explosion, there is no "blowout'' observed
(i.e. the shell breaking out of the disk and pumping the hot gas into the
intergalactic medium).
The hot gas is always confined inside the shell in the early expansion
phase and it cools down at later times t>40 Myr due to the radiative cooling.
As a result, the shell collapses at t=45 Myr,
creating a mildly compressed central core, the gas density of which
is however below the Jeans limit.
In the case of multiple SNe, part of the hot gas is lifted to a higher altitude
of 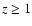 kpc due to a buoyancy effect developing at
kpc due to a buoyancy effect developing at
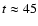 Myr.
It is also seen that in the early expansion phase the shell is on average
thicker in the case of the hypernova explosion than in the case of multiple
SN explosions. Since the numerical modeling of Vorobyov et al. (2004) suggested
that the shell in Ho I has already blown out of the disk, we do not consider
further the energy release of
Myr.
It is also seen that in the early expansion phase the shell is on average
thicker in the case of the hypernova explosion than in the case of multiple
SN explosions. Since the numerical modeling of Vorobyov et al. (2004) suggested
that the shell in Ho I has already blown out of the disk, we do not consider
further the energy release of
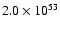 erg.
erg.
The difference in the shell dynamics between the multiple SN and hypernova
becomes pronounced as one considers
more energetic explosions. For instance, Fig. 3 shows the distribution
of the gas volume density produced by 500 consecutive
SN explosions (the upper panels) and by a single hypernova explosion of the
same total energy
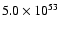 erg (the lower panels). Now, the dynamics of the SN-driven
shell shows a clear blowout phase at
erg (the lower panels). Now, the dynamics of the SN-driven
shell shows a clear blowout phase at
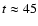 Myr after the beginning
of the energy input phase. On the contrary, the hypernova-driven shell
never breaks out of the disk, though its energy is equal to the total energy
released by multiple supernovae. This difference remains for presumably
an upper limit energy release of 1054 erg that a stellar cluster could produce in
Holmberg I. As seen in the
upper panels of Fig. 4, the shell dynamics governed by
1000 consecutive SN explosions exhibits a violent blowout, whereas
that governed by a hypernova of the same total energy of 1054 erg shows
almost no sign of blowout. This is in good agreement with the previous
model of Efremov et al. (1999), who
used a thin shell approximation to study the evolution of shells formed
by a single hypernova and multiple SNe. These authors
have also found that an abrupt energy input creates shells that do not
blow out to the galactic halo for energies
Myr after the beginning
of the energy input phase. On the contrary, the hypernova-driven shell
never breaks out of the disk, though its energy is equal to the total energy
released by multiple supernovae. This difference remains for presumably
an upper limit energy release of 1054 erg that a stellar cluster could produce in
Holmberg I. As seen in the
upper panels of Fig. 4, the shell dynamics governed by
1000 consecutive SN explosions exhibits a violent blowout, whereas
that governed by a hypernova of the same total energy of 1054 erg shows
almost no sign of blowout. This is in good agreement with the previous
model of Efremov et al. (1999), who
used a thin shell approximation to study the evolution of shells formed
by a single hypernova and multiple SNe. These authors
have also found that an abrupt energy input creates shells that do not
blow out to the galactic halo for energies 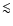 1054 erg.
Noticeably, the
final fate of the gas distribution is similar in all cases: the hot bubble fills
in and the gas disk mostly recovers its pre-explosion appearance after
1054 erg.
Noticeably, the
final fate of the gas distribution is similar in all cases: the hot bubble fills
in and the gas disk mostly recovers its pre-explosion appearance after 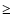 160 Myr with
a slightly more centrally condensed radial gas distribution.
160 Myr with
a slightly more centrally condensed radial gas distribution.
The occurrence of the blowout in the case of multiple supernova explosions
and its absence in the case of a hypernova explosion can
be understood if one considers the dynamics of the hot gas filling
the shell interior.
In Fig. 5 we plot the gas volume density distribution and
velocity field produced by 500 consecutive SN explosions
(the left panel) and a hypernova of the same total energy of
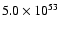 erg (the right
panel). An obvious difference is seen: the hot gas ejected
by multiple SNe forms a "vortex'' that acts to de-stabilize the swept-up shell
of cold material via a Kelvin-Helmholtz instability. The shell loses its
smooth elliptical form and develops "ripples'' at its tops. The dynamical
pressure of the hot gas (note that its velocity is much higher
than in the case of a hypernova explosion) accelerates
the "rippled'' shell. As a consequence, the shell shows a strong Rayleigh-Taylor
instability via the development of a characteristic "spike-and-bubble'' morphology,
as is seen in the left panel of Fig. 5.
erg (the right
panel). An obvious difference is seen: the hot gas ejected
by multiple SNe forms a "vortex'' that acts to de-stabilize the swept-up shell
of cold material via a Kelvin-Helmholtz instability. The shell loses its
smooth elliptical form and develops "ripples'' at its tops. The dynamical
pressure of the hot gas (note that its velocity is much higher
than in the case of a hypernova explosion) accelerates
the "rippled'' shell. As a consequence, the shell shows a strong Rayleigh-Taylor
instability via the development of a characteristic "spike-and-bubble'' morphology,
as is seen in the left panel of Fig. 5.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1324fig5.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg67.gif) |
Figure 5:
The vertical cut through the distribution of the gas volume
density produced by 500 consecutive SNe at t=27 Myr ( the left panel) and single
hypernova of the same total energy of
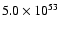 erg
( the right panel). The gas velocity field is shown by the arrows. erg
( the right panel). The gas velocity field is shown by the arrows. |
| Open with DEXTER |
In the case of a hypernova explosion of the same total energy, the gas velocity
field plotted in the right panel of Fig. 5 lacks any circular motion
inside the shell.
The smooth elliptical shell of cold material
of roughly the same size as in the case of multiple SNe expands
at roughly the sound speed.
The shell has already started losing its pressure support (as implied by the
thickening of the shell walls) due to radiative cooling of its hot interior.
As a consequence, the decelerating shell does not
develop a Rayleigh-Taylor instability and the blowout phase is not observed.
We note here that a hypernova-driven shell expands out to a certain radius
faster than a shell created by multiple SNe with the same total energy, as reported by
Efremov et al. (1999).
Our numerical simulations have shown that the difference in the dynamics of
shells produced by multiple SNe and a single
hypernova of the same total energy intensifies as one considers
more flattened gas systems.
The maximum difference is found in the strongly vertically
stratified gas distributions assumed for massive spiral galaxies.
The vortex forms since the shell becomes elongated in the vertical
direction. Consider the simplified situation of hot gas ejected radially
by SNe which is reflected from the cold dense walls of the elliptical shell.
The gas will not be reflected along the local normal direction to the shell
unless it is moving along z=0 or r=0. In general, a tangential
component of the velocity of hot gas 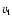 (with respect
to the shell's walls) is generated. It is always directed upwards
for gas above the midplane and downwards for gas below the midplane.
Let us consider the upper hemisphere.
The occurrence of
(with respect
to the shell's walls) is generated. It is always directed upwards
for gas above the midplane and downwards for gas below the midplane.
Let us consider the upper hemisphere.
The occurrence of
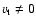 near the shell walls and the
axial symmetry of the shell makes the hot gas
(streaming upwards along the shell walls) accumulate
at the top of the shell, because it cannot pass through the symmetry axis.
Both the growing pressure of this hot gas (due to its negligible cooling)
and the downward pull of the z-component of the galactic
gravitational field lead to a downward flow
along the axis of symmetry.
This completes the circle and generates a vortex structure as seen in
the left panel of Fig. 5.
The development of such vortices is also seen in the axially symmetric numerical
simulations of Recchi et al. (2001). However, a strong non-axisymmetry
of the SNe-driven shell may complicate the formation of the vortex.
near the shell walls and the
axial symmetry of the shell makes the hot gas
(streaming upwards along the shell walls) accumulate
at the top of the shell, because it cannot pass through the symmetry axis.
Both the growing pressure of this hot gas (due to its negligible cooling)
and the downward pull of the z-component of the galactic
gravitational field lead to a downward flow
along the axis of symmetry.
This completes the circle and generates a vortex structure as seen in
the left panel of Fig. 5.
The development of such vortices is also seen in the axially symmetric numerical
simulations of Recchi et al. (2001). However, a strong non-axisymmetry
of the SNe-driven shell may complicate the formation of the vortex.
The driving force for the vortex is a continuous or
quasi-continuous release of energy by SNe of a stellar cluster or a group
of closely located stellar clusters.
This is also the reason why vortices do not form in a shell created
by a single hypernova explosion. We have found that the vortex develops
even when the number of SNe is quite moderate ( 20) and the release
of energy is discrete.
The length scale of the vortex is approximately equal to the shell's
semi-minor axis and time scale is limited by the duration of energy
input from SNe, i.e.
20) and the release
of energy is discrete.
The length scale of the vortex is approximately equal to the shell's
semi-minor axis and time scale is limited by the duration of energy
input from SNe, i.e. 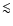 30 Myr.
In general, at least two vortices can co-exist within a single shell: one
in the upper hemisphere and the other in the lower hemisphere of the shell.
30 Myr.
In general, at least two vortices can co-exist within a single shell: one
in the upper hemisphere and the other in the lower hemisphere of the shell.
Hypernovae tend to form complete shells. Such shells would appear in nearly face-on
dwarf galaxies as HI rings
with a low ring-to-center contrast in the HI column density.
For instance, in Fig. 6 we plot the contrast in the HI column density between
the ring and the central depression,
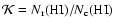 ,
as a
function of the ring radius R obtained for three different energy inputs.
The ring column density
,
as a
function of the ring radius R obtained for three different energy inputs.
The ring column density
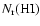 is computed by azimuthally
averaging
is computed by azimuthally
averaging 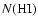 around the ring.
An inclination angle (i.e. the angle between the rotation axis of the
galaxy and the line of sight) of
around the ring.
An inclination angle (i.e. the angle between the rotation axis of the
galaxy and the line of sight) of
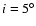 is assumed, which is appropriate
for a nearly face-on galaxy.
The solid lines give
the contrast
is assumed, which is appropriate
for a nearly face-on galaxy.
The solid lines give
the contrast 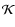 for the multiple SN explosions, whereas the dashed
lines do that for the hypernova explosion. As is seen, the ring-to-center
contrast
for the multiple SN explosions, whereas the dashed
lines do that for the hypernova explosion. As is seen, the ring-to-center
contrast 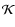 produced by the hypernova explosion never exceeds 10 even
for the upper limit energy of
hypernova explosions of 1054 erg. On the other hand, multiple SNe
can form HI rings with a much higher ring-to-center contrast
produced by the hypernova explosion never exceeds 10 even
for the upper limit energy of
hypernova explosions of 1054 erg. On the other hand, multiple SNe
can form HI rings with a much higher ring-to-center contrast
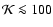 .
The latter takes place when the SN-driven shell is in the blowout phase.
Note that the difference
in
.
The latter takes place when the SN-driven shell is in the blowout phase.
Note that the difference
in 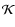 between the HI rings produced by multiple SNe and those produced
by hypernovae
smears out if the total released energy is
between the HI rings produced by multiple SNe and those produced
by hypernovae
smears out if the total released energy is 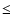
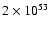 erg.
erg.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1324fig6.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg73.gif) |
Figure 6:
The contrast in the HI column density between the ring and
the central depression
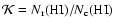 as a function of the ring radius. The solid
lines show the contrast
as a function of the ring radius. The solid
lines show the contrast 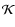 produced by multiple SNe, whereas
the dashed lines show that produced by a single hypernova of the same
total energy. An inclination angle of
produced by multiple SNe, whereas
the dashed lines show that produced by a single hypernova of the same
total energy. An inclination angle of 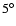 is assumed.
The energy input
is indicated in the right upper corner of each panel. The dashed-dotted
and dotted lines in the lower panel give the contrast
is assumed.
The energy input
is indicated in the right upper corner of each panel. The dashed-dotted
and dotted lines in the lower panel give the contrast 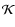 for
an inclination angle of
for
an inclination angle of 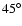 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1324fig7.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg74.gif) |
Figure 7:
The pV-diagrams of the shell created by 500 consecutive
SNe. The pV-cuts are taken along the major axis of the model galaxy
viewed at an angle of 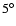 .
The evolutionary time of the shell
is indicated in the right upper corner. The quantity .
The evolutionary time of the shell
is indicated in the right upper corner. The quantity
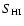 is plotted in all model pV-diagrams.
is plotted in all model pV-diagrams. |
| Open with DEXTER |
4.1 PV-diagrams
The position-velocity (pV) diagram is a powerful tool to search for coherent structures
in the interstellar medium.
In this section we compute model pV-diagrams in order to determine
their utility for distinguishing between the SN-driven shells and those produced by a
hypernova explosion of the same total energy.
The HI flux density
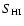 is obtained using the following conversion
formula (Binney & Merrifield 1998):
is obtained using the following conversion
formula (Binney & Merrifield 1998):
![\begin{displaymath}{M_{\rm HI} \over \triangle v} = 2.35 \times 10^5~\left( {D \...
...
\right) \ \ \left[{M_{\odot} \over {\rm km\: s^{-1}}}\right],
\end{displaymath}](/articles/aa/full/2005/08/aa1324/img75.gif) |
(5) |
where for the distance D we take 3.5 Mpc, appropriate for Holmberg I.
The position-velocity cuts are taken along the major axis of the projected shell.
The width of the cuts is 30 pc. We tried twice wider cuts (60 pc), but found little
difference in the appearance of the resulting pV-diagrams as compared to
those obtained with narrower cuts. The gas is assumed to be thermalized when
constructing the model pV-diagrams, i.e. a Maxwellian velocity distribution
is assumed for the gas in each computational cell,
with the scale determined by the local gas temperature (see Mashchenko
& Silich 1995).
No attempt was made to include the effects of turbulence.
The model galaxy is assumed to have an inclination angle of 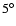 .
The position-velocity cuts along the minor axis of the projected shell have similar
appearance for such low inclination angles.
.
The position-velocity cuts along the minor axis of the projected shell have similar
appearance for such low inclination angles.
Figure 7 shows the model
pV-diagrams of the shell produced by 500 consecutive SNe. The quantity
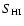 is plotted in all model pV-diagrams.
Two bright blobs elongated in the vertical direction are apparent in each pV-diagram.
They represent the dense
walls of the shell expanding in the plane of the galaxy, i.e. perpendicular to
the line of sight at the adopted inclination angle of
is plotted in all model pV-diagrams.
Two bright blobs elongated in the vertical direction are apparent in each pV-diagram.
They represent the dense
walls of the shell expanding in the plane of the galaxy, i.e. perpendicular to
the line of sight at the adopted inclination angle of 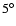 .
If the shell has not yet broken out of the disk (t=9 and 18 Myr),
these two blobs appear to close at their tops and form a complete
elliptical ring. The relative amplitude
of
.
If the shell has not yet broken out of the disk (t=9 and 18 Myr),
these two blobs appear to close at their tops and form a complete
elliptical ring. The relative amplitude
of
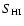 around the ring is however varying by roughly an order
of magnitude, reflecting the difference in the HI column density along
the major axis of the projected shell -
there is much less gas on the approaching and receding sides of the shell
than on those expanding perpendicular to the line of sight.
around the ring is however varying by roughly an order
of magnitude, reflecting the difference in the HI column density along
the major axis of the projected shell -
there is much less gas on the approaching and receding sides of the shell
than on those expanding perpendicular to the line of sight.
The elliptical ring is virtually absent in the later expansion phase at t=36 and
45 Myr when the shell has already broken out of the disk (the lower frames
in Fig. 7).
Instead, the pV-diagrams are totally dominated by two high-intensity blobs. A
few smaller patches seen between the blobs
represent the dense, cold clouds fragmented off the shell and pushed by
the dynamical pressure of the hot gas to a higher altitude of 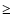 1 kpc.
The thickening of the shell after the blowout
is also noticeable in the lower frames of Fig. 7.
The same tendency is found in the pV-diagrams of the shell created by 1000 consecutive SNe. The complete ring is seen
only in the very early phase of the shell expansion at t=9 Myr and is virtually
absent after the blowout at t=27, 45, and 54 Myr.
1 kpc.
The thickening of the shell after the blowout
is also noticeable in the lower frames of Fig. 7.
The same tendency is found in the pV-diagrams of the shell created by 1000 consecutive SNe. The complete ring is seen
only in the very early phase of the shell expansion at t=9 Myr and is virtually
absent after the blowout at t=27, 45, and 54 Myr.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1324fig8.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg76.gif) |
Figure 8:
The pV-diagrams of the shell produced by a single hypernova
of the total energy of
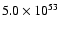 erg. The pV-cuts are
taken along the major axis of the model galaxy viewed at an inclination angle
of erg. The pV-cuts are
taken along the major axis of the model galaxy viewed at an inclination angle
of 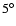 . . |
| Open with DEXTER |
Figure 8 shows the pV-diagrams
of the shell produced by a hypernova of total energy
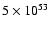 erg.
The position-velocity cuts are taken along the major axis of the projected
shell at four different evolutionary times: t=9, 18, 27, and 36 Myr, i.e., before it
has expanded out to its maximum size (t=9 and 18 Myr) and after it has started to collapse
due to the radiative cooling of the shell interior. An inclination angle
erg.
The position-velocity cuts are taken along the major axis of the projected
shell at four different evolutionary times: t=9, 18, 27, and 36 Myr, i.e., before it
has expanded out to its maximum size (t=9 and 18 Myr) and after it has started to collapse
due to the radiative cooling of the shell interior. An inclination angle
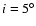 is assumed. The elliptical hole surrounded by a ring of higher
HI flux density
is assumed. The elliptical hole surrounded by a ring of higher
HI flux density
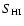 is clearly visible in those pV-diagrams.
The HI flux
is clearly visible in those pV-diagrams.
The HI flux
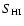 from the ring is
from the ring is 
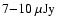 ,
which
should, in principle, be detectable.
Hypernova explosions tend to form complete shells that are clearly visible
in the pV-diagrams.
This characteristic feature of a hypernova-driven shell
is also present when one considers very energetic explosions.
For instance, Fig. 9
shows the pV-diagrams of the shell produced by a hypernova of the total energy
of 1054 erg. The elliptical hole surrounded by the ring is clearly seen
even when the shell has already started to collapse at t=45 Myr, as implied
by the presence of a vertical bar at zero radial offset
(see the lower right panel in Fig. 9).
Note the size of the shell in Figs. 8 and 9.
It is twice the local Gaussian scale height h, which is
,
which
should, in principle, be detectable.
Hypernova explosions tend to form complete shells that are clearly visible
in the pV-diagrams.
This characteristic feature of a hypernova-driven shell
is also present when one considers very energetic explosions.
For instance, Fig. 9
shows the pV-diagrams of the shell produced by a hypernova of the total energy
of 1054 erg. The elliptical hole surrounded by the ring is clearly seen
even when the shell has already started to collapse at t=45 Myr, as implied
by the presence of a vertical bar at zero radial offset
(see the lower right panel in Fig. 9).
Note the size of the shell in Figs. 8 and 9.
It is twice the local Gaussian scale height h, which is  350 pc at
a galactocentric radius of 0.5 kpc in our model galaxy.
350 pc at
a galactocentric radius of 0.5 kpc in our model galaxy.
The comparison of Fig. 7-9 indicates that
the SNe-driven shell in its late expansion phase (when its radius
exceeds 1.5 h) may be distinguished from that produced by the single hypernova explosion
based on its appearance in the pV-diagrams.
The pV-diagrams of the hypernova-driven shell show the characteristic elliptical
ring in virtually any evolutionary phase of the shell, whereas
the pV-diagrams of the SN-driven shell do that only in the early expansion
phase, well before the blowout.
The present numerical simulations
(see also Vorobyov & Shchekinov 2004) show that the SN-driven shell breaks out of the disk
when its radius exceeds  1.5 h.
As a consequence of the blowout, the SN-driven shell transforms into an
open cylinder and the pV-diagrams show two parallel blobs representing
the walls of the expanding cylindrical shell.
On the contrary, the hypernova-driven shell appears to
survive the expansion even when its radius exceeds 2.0 h. As a result,
the characteristic elliptical ring representing the complete expanding
shell is clearly seen in the pV-diagrams.
Thus, if the pV-diagrams show an elliptical hole surrounded by a denser
ring, the radius of which is
greater than 1.5 h (as in the lower frames of Figs. 8 and 9), this may indirectly point to a hypernova origin of the shell.
1.5 h.
As a consequence of the blowout, the SN-driven shell transforms into an
open cylinder and the pV-diagrams show two parallel blobs representing
the walls of the expanding cylindrical shell.
On the contrary, the hypernova-driven shell appears to
survive the expansion even when its radius exceeds 2.0 h. As a result,
the characteristic elliptical ring representing the complete expanding
shell is clearly seen in the pV-diagrams.
Thus, if the pV-diagrams show an elliptical hole surrounded by a denser
ring, the radius of which is
greater than 1.5 h (as in the lower frames of Figs. 8 and 9), this may indirectly point to a hypernova origin of the shell.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1324fig9.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg78.gif) |
Figure 9:
The same as Fig. 8, but for a single hypernova
of the total energy of 1054 erg. |
| Open with DEXTER |
The model pV-diagrams considered in Sect. 4.1 were constructed under
the assumption that the model galaxy is viewed nearly face-on, namely at an inclination
angle of 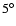 .
In this section we study how a higher inclination angle could influence the appearance
of the SN- and hypernova-driven shells in the pV-diagrams. Figure 10
shows the model pV-diagrams of the shell created by 1000 consecutive SNe.
The pV-diagrams are constructed at three different evolutionary times t=9, 27, and 45 Myr after the beginning of the energy injection phase. The left
and right panels in Fig. 10 are the position-velocity cuts along the minor and
major axes of the projected shell, respectively. An inclination
angle of
.
In this section we study how a higher inclination angle could influence the appearance
of the SN- and hypernova-driven shells in the pV-diagrams. Figure 10
shows the model pV-diagrams of the shell created by 1000 consecutive SNe.
The pV-diagrams are constructed at three different evolutionary times t=9, 27, and 45 Myr after the beginning of the energy injection phase. The left
and right panels in Fig. 10 are the position-velocity cuts along the minor and
major axes of the projected shell, respectively. An inclination
angle of
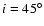 is adopted. The characteristic hole surrounded by a
ring of higher HI flux density (see Sect. 4.1)
is barely seen even in the very early expansion phase at t=9 Myr due
to the projection smearing at higher inclination angles.
In the later expansion phase at t=45 Myr
the pV-cuts taken along the major axis show two elongated
blobs, the morphological centers of which are symmetrically displaced by
is adopted. The characteristic hole surrounded by a
ring of higher HI flux density (see Sect. 4.1)
is barely seen even in the very early expansion phase at t=9 Myr due
to the projection smearing at higher inclination angles.
In the later expansion phase at t=45 Myr
the pV-cuts taken along the major axis show two elongated
blobs, the morphological centers of which are symmetrically displaced by
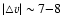 km s-1with respect to v=0 km s-1. The displacement is
defined as
km s-1with respect to v=0 km s-1. The displacement is
defined as
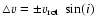 ,
where
,
where
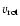 is the
rotation velocity of the SN-driven shell. The positive and negative
is the
rotation velocity of the SN-driven shell. The positive and negative
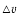 correspond to
the receding and approaching parts of the shell, respectively.
It is important to note here that similar pV-diagrams
are obtained for Ho I by Ott et al. (2001, see their Fig. 8).
A large displacement between the blobs with respect to the systemic
velocity of
correspond to
the receding and approaching parts of the shell, respectively.
It is important to note here that similar pV-diagrams
are obtained for Ho I by Ott et al. (2001, see their Fig. 8).
A large displacement between the blobs with respect to the systemic
velocity of
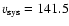 km s-1is clearly seen in the pV-cut taken along the major axis of Ho I.
However, we found it difficult to estimate the value of
km s-1is clearly seen in the pV-cut taken along the major axis of Ho I.
However, we found it difficult to estimate the value of
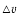 from the
observed pV-diagram shown in Fig. 8 of Ott et al. (2001) due to its considerable
asymmetry (caused probably by an off-center location
of the stellar cluster responsible for the creation of the shell).
The modeled value of
from the
observed pV-diagram shown in Fig. 8 of Ott et al. (2001) due to its considerable
asymmetry (caused probably by an off-center location
of the stellar cluster responsible for the creation of the shell).
The modeled value of
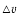 depends also on the adopted rotation curve
of Ho I, which is poorly known (Ott et al. 2001).
Therefore, it is problematic to obtain the inclination angle of Ho I
by comparing the modeled and observed
depends also on the adopted rotation curve
of Ho I, which is poorly known (Ott et al. 2001).
Therefore, it is problematic to obtain the inclination angle of Ho I
by comparing the modeled and observed
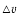 .
Nevertheless, we conclude that Ho I is viewed at an inclination
angle considerably higher than
.
Nevertheless, we conclude that Ho I is viewed at an inclination
angle considerably higher than 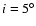 ,
because the modeled pV-cuts of Fig. 7 obtained
for an inclination angle of only
,
because the modeled pV-cuts of Fig. 7 obtained
for an inclination angle of only 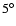 do not show a noticeable
displacement.
do not show a noticeable
displacement.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1324fg10.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg85.gif) |
Figure 10:
The pV-diagrams of the shell created by 1000 consecutive
SNe. The pV-cuts are taken along the minor ( the left panels) and
the major ( the right panels) axis of the model galaxy viewed at an
angle of 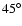 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1324fg11.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg86.gif) |
Figure 11:
The same as in Fig. 10, but for a single hypernova
of the same total energy of 1054 erg. The pV-cuts taken along
the minor axis of the hypernova-driven shell show the characteristic
S-shaped structure due to an expansion in the vertical direction. |
| Open with DEXTER |
The pV-diagrams of the shell created by a single hypernova
explosion of the total energy 1054 erg are shown in Fig. 11.
The left panels give the pV-cuts along the minor axis of the projected
shell, whereas the right panels do those along the major axis.
The pV-diagrams of the shell created by a single hypernova explosion are
noticeably different from those created by multiple SNe. The hypernova-driven
shell does not break out of the disk even when its radius exceeds 2.0 h.
As a consequence, the shell preserves its elliptical form and
the characteristic elliptical hole surrounded by the ring
of a higher HI flux intensity is apparent in the pV-cuts taken along the major
axis (the right panels in Fig. 11) at t=9 and 27 Myr after the explosion.
The elliptical ring dissolves at 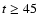 Myr due to the projection effect
(note that in nearly face-on galaxies the elliptical
ring can still be resolved at that phase). In that later phase, the hypernova-driven shell can
barely be distinguished from that created by multiple SNe based on the
appearance in the pV-diagrams taken along the major axis of the projected
shell. Fortunately, the pV-cuts taken along the minor axis
of the hypernova-driven shell show the characteristic S-shaped structure.
The pV-cuts along the minor axis are sensitive only to the expansion/contraction
motion of the shell. As is seen in the lower panels of Fig. 4, the hypernova-driven
shell at t=27-45 Myr expands in the vertical direction, but shows the lack of expansion or contraction
motion in the galactic plane (except for the very late phase when the shell
has already started to collapse).
As a result, the shell seen in the pV-diagrams as the elliptical ring
transforms into the S-shaped structure in the later expansion phase.
Note that neither elliptical rings nor S-shaped structures are seen in
the observed pV-diagrams of Ho I plotted in Fig. 8 of Ott et al. (2001).
Myr due to the projection effect
(note that in nearly face-on galaxies the elliptical
ring can still be resolved at that phase). In that later phase, the hypernova-driven shell can
barely be distinguished from that created by multiple SNe based on the
appearance in the pV-diagrams taken along the major axis of the projected
shell. Fortunately, the pV-cuts taken along the minor axis
of the hypernova-driven shell show the characteristic S-shaped structure.
The pV-cuts along the minor axis are sensitive only to the expansion/contraction
motion of the shell. As is seen in the lower panels of Fig. 4, the hypernova-driven
shell at t=27-45 Myr expands in the vertical direction, but shows the lack of expansion or contraction
motion in the galactic plane (except for the very late phase when the shell
has already started to collapse).
As a result, the shell seen in the pV-diagrams as the elliptical ring
transforms into the S-shaped structure in the later expansion phase.
Note that neither elliptical rings nor S-shaped structures are seen in
the observed pV-diagrams of Ho I plotted in Fig. 8 of Ott et al. (2001).
As was demonstrated in Fig. 6, the HI rings created by
multiple SNe have a much
higher contrast in the HI column
density between the ring and central depression,
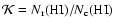 ,
than those created by a single hypernova
explosion of the same total energy.
However, a higher inclination may considerably reduce the value of
,
than those created by a single hypernova
explosion of the same total energy.
However, a higher inclination may considerably reduce the value of 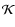 due to the projection smearing effect. For instance, the dotted-dashed line in Fig. 6 shows the
contrast
due to the projection smearing effect. For instance, the dotted-dashed line in Fig. 6 shows the
contrast 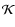 as a function of the ring radius R produced by 1000 consecutive SNe,
whereas the dotted
line does that for the hypernova of the same total energy. An inclination
angle of
as a function of the ring radius R produced by 1000 consecutive SNe,
whereas the dotted
line does that for the hypernova of the same total energy. An inclination
angle of 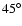 is assumed. The ring-to-center contrast in
is assumed. The ring-to-center contrast in 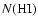 produced by both multiple
SNe and hypernova stays around
produced by both multiple
SNe and hypernova stays around
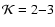 .
The only exception is
seen when the SN-driven shell expands out to
.
The only exception is
seen when the SN-driven shell expands out to
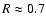 kpc and breaks
out of the disk. Then, the ring-to-center contrast reaches a maximum value of
kpc and breaks
out of the disk. Then, the ring-to-center contrast reaches a maximum value of
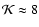 .
It is instructive to compare the ring-to-center contrast and size of HI rings produced
in our simulations (by both multiple SNe and single hypernovae) with the observed
contrast
.
It is instructive to compare the ring-to-center contrast and size of HI rings produced
in our simulations (by both multiple SNe and single hypernovae) with the observed
contrast 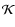 and size of the HI ring in Ho I. Figure 12 shows
the observed HI map of Ho I as obtained by Ott et al. (2001). The
diameter of the ring is
and size of the HI ring in Ho I. Figure 12 shows
the observed HI map of Ho I as obtained by Ott et al. (2001). The
diameter of the ring is  1.7 kpc and the ring-to-center contrast
is
1.7 kpc and the ring-to-center contrast
is
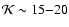 .
Our simulations show (see Fig. 6) that
both multiple SNe and single hypernovae may form rings of up to 2 kpc in diameter.
However, single hypernovae fail to produce rings with the observed contrast
of
.
Our simulations show (see Fig. 6) that
both multiple SNe and single hypernovae may form rings of up to 2 kpc in diameter.
However, single hypernovae fail to produce rings with the observed contrast
of
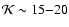 .
This is true even in the most favorable case of near
zero inclination angle.
Taking into account that both the observations
of Ott et al. and numerical modeling of Vorobyov et al. (2004) set
the lower limit on the inclination angle of Ho I as
.
This is true even in the most favorable case of near
zero inclination angle.
Taking into account that both the observations
of Ott et al. and numerical modeling of Vorobyov et al. (2004) set
the lower limit on the inclination angle of Ho I as
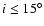 ,
the
formation of the HI ring with such a high contrast
,
the
formation of the HI ring with such a high contrast
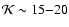 by means of
a hypernova explosion seems highly problematic. Apparently, only
multiple SNe can produce HI rings with such a high ring-to-center contrast
by means of
a hypernova explosion seems highly problematic. Apparently, only
multiple SNe can produce HI rings with such a high ring-to-center contrast 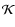 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1324fg12.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg93.gif) |
Figure 12:
Integrated HI emission of Ho I. In the bottom left
corner we show the half-power beam (8
 2 2  7.0
7.0
 ).
The grayscale represents the HI column density.
The data have been obtained from the Very Large Array observations
(Ott et al. 2001). ).
The grayscale represents the HI column density.
The data have been obtained from the Very Large Array observations
(Ott et al. 2001). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1324fg13.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg94.gif) |
Figure 13:
The integrated HI image of the ring produced by 500 consecutive
SNe. The inclination angle is indicated in the right upper corner.
The scale bar is in cm-2. The origin of narrow rings is an assumption
of axisymmetry in our numerical simulations. |
| Open with DEXTER |
The integrated HI image of the shell created by multiple
SNe appears in nearly face-on galaxies as
a ring of elevated HI density surrounding the central depression.
For instance, the left upper panel in Fig. 13 shows the integrated HI image
of the shell created by 500 consecutive SNe. The HI image is taken at t=45 Myr after the beginning
of the energy input phase, when the shell has already broken out of the
disk. An inclination angle of 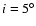 is assumed. As is obviously seen,
the blown-out shell in nearly face-on galaxies appears
as a ring with a high ring-to-center HI column density contrast (
is assumed. As is obviously seen,
the blown-out shell in nearly face-on galaxies appears
as a ring with a high ring-to-center HI column density contrast ( 25-30).
There is little azimuthal variation in the HI column density around the
ring.
However, the integrated HI image of the blownout shell observed in substantially
inclined galaxies shows a considerable variation in the HI column density around the
ring. For instance, at
higher inclination angles of
25-30).
There is little azimuthal variation in the HI column density around the
ring.
However, the integrated HI image of the blownout shell observed in substantially
inclined galaxies shows a considerable variation in the HI column density around the
ring. For instance, at
higher inclination angles of 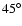 and
and 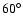 the relative amplitude
of azimuthal variations
in
the relative amplitude
of azimuthal variations
in
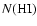 around the ring is
around the ring is 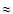 2 and
2 and 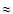 3, respectively.
In this case, the integrated HI image is dominated by two kidney-shaped
density enhancements and shows a mild central minimum.
It is interesting to note that the Sextans A and M 81 dwA
dwarf irregular galaxies have a somewhat similar HI distribution (see Skillman et al. 1988; Stewart 1998). In
the case of Sextans A, the relative amplitude of azimuthal variations in
the HI column density around the ring
is
3, respectively.
In this case, the integrated HI image is dominated by two kidney-shaped
density enhancements and shows a mild central minimum.
It is interesting to note that the Sextans A and M 81 dwA
dwarf irregular galaxies have a somewhat similar HI distribution (see Skillman et al. 1988; Stewart 1998). In
the case of Sextans A, the relative amplitude of azimuthal variations in
the HI column density around the ring
is 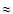 2.5-3 (according to Skillman et al. 1988) and the inclination angle
determined from the outer HI contours is
2.5-3 (according to Skillman et al. 1988) and the inclination angle
determined from the outer HI contours is
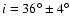 (assuming
the circular symmetry).
Note that the narrow ring-shaped structures seen in Fig. 13 are in fact the dense fragments
of a broken-up shell, which appear as rings rather than dense clumps due
to the axisymmetric nature of our numerical simulations.
In edge-on galaxies, the integrated HI image would resemble a "dumbbell'',
as shown in the right lower panel of Fig. 13.
The absence of noticeable azimuthal variations in HI column density
around the HI ring in Fig. 12 suggests that
Ho I is viewed at an inclination angle considerably smaller than
(assuming
the circular symmetry).
Note that the narrow ring-shaped structures seen in Fig. 13 are in fact the dense fragments
of a broken-up shell, which appear as rings rather than dense clumps due
to the axisymmetric nature of our numerical simulations.
In edge-on galaxies, the integrated HI image would resemble a "dumbbell'',
as shown in the right lower panel of Fig. 13.
The absence of noticeable azimuthal variations in HI column density
around the HI ring in Fig. 12 suggests that
Ho I is viewed at an inclination angle considerably smaller than
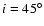 .
This is in agreement with previous estimates by Ott
et al. (2001) and Vorobyov et al. (2004), who found that Ho I
has an inclination angle of
.
This is in agreement with previous estimates by Ott
et al. (2001) and Vorobyov et al. (2004), who found that Ho I
has an inclination angle of 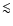
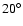 .
.
4.3 Off-plane explosions
A general assumption made in the above simulations of both SN-driven
and hypernova-driven shells was that the energy is released exactly in
the midplane of the model gas disk. However, taking into account the considerable
thickness of the gas disks in dIrr's, the occurrence of a hypernova or massive
stellar cluster at a position moderately offset with respect to
the galactic midplane, appears plausible. In this section we investigate how
the off-plane explosions may influence the appearance of the shells in
the pV-diagrams.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1324fg14.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg100.gif) |
Figure 14:
Off-plane explosions. Temporal evolution of the gas volume density distribution
after the release of
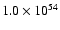 erg of thermal energy at r=0,z=100 pc.
The upper panels correspond to 1000 consecutive SN explosions over
30 Myr, while the lower panels show the impact of a single hypernova
of the same total energy of 1054 erg. The scale bar is in gm cm-3. erg of thermal energy at r=0,z=100 pc.
The upper panels correspond to 1000 consecutive SN explosions over
30 Myr, while the lower panels show the impact of a single hypernova
of the same total energy of 1054 erg. The scale bar is in gm cm-3. |
| Open with DEXTER |
If the stellar cluster is located at a moderate height of z=100 pc ( 1/3 h) above the midplane of the galaxy, the temporal evolution of the gas volume density
is found to be similar to that obtained
in Sect. 4 for the midplane stellar cluster.
For instance, the upper panels in Fig. 14
show five temporal snapshots
of the gas volume density distribution created by the energy release of
1000 consecutive SNe. A more intensive blowout takes place in the upper
part of the galaxy where the stellar cluster is nested.
However, the pV-diagrams and ring-to-center contrast in HI column
density
1/3 h) above the midplane of the galaxy, the temporal evolution of the gas volume density
is found to be similar to that obtained
in Sect. 4 for the midplane stellar cluster.
For instance, the upper panels in Fig. 14
show five temporal snapshots
of the gas volume density distribution created by the energy release of
1000 consecutive SNe. A more intensive blowout takes place in the upper
part of the galaxy where the stellar cluster is nested.
However, the pV-diagrams and ring-to-center contrast in HI column
density 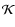 are only slightly affected by this mild asymmetry.
are only slightly affected by this mild asymmetry.
The temporal evolution of the shell created by a single hypernova
that is moderately offset with respect to the midplane of the galaxy produces
some noticeable differences. The lower panels in Fig. 14
give five temporal snapshots of the gas volume density distribution created
by the hypernova of total energy 1054 erg that is placed 100 pc above
the midplane of the galactic gas disk. The egg-like shell is formed after
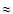 15 Myr, the upper part of which retains a relatively smooth appearance
for several tens of Myr before it breaks due to a Rayleigh-Taylor instability
and dissolves at
15 Myr, the upper part of which retains a relatively smooth appearance
for several tens of Myr before it breaks due to a Rayleigh-Taylor instability
and dissolves at 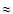 70-80 Myr after the explosion.
Note that in the case of multiple SNe such smooth kpc-sized
arcs of dense material are never formed in our numerical simulations. Instead,
inspection of Figs. 2-4, and 14 indicates
that multiple SNe tend to produce patchy filaments and dense clumps of
a few hundred parsecs in size (except for the very late phase when the
shell has already collapsed). Indeed, a Rayleigh-Taylor instability, the
effect of which is strengthened
by the preceding Kelvin-Helmholtz instability, efficiently fragments the
SN-driven shell when the latter breaks out of the gas disk. Longer fragmentation
times of hypernova-driven shells as compared to fragmentation times of
shells created by multiple SNe were also found in the model of Efremov et al. (1999).
It is interesting to mention in this context the W4 HII
region in the Perseus arm of the outer Galaxy. Dennison et al. (1997)
have observed a highly elongated shell of
70-80 Myr after the explosion.
Note that in the case of multiple SNe such smooth kpc-sized
arcs of dense material are never formed in our numerical simulations. Instead,
inspection of Figs. 2-4, and 14 indicates
that multiple SNe tend to produce patchy filaments and dense clumps of
a few hundred parsecs in size (except for the very late phase when the
shell has already collapsed). Indeed, a Rayleigh-Taylor instability, the
effect of which is strengthened
by the preceding Kelvin-Helmholtz instability, efficiently fragments the
SN-driven shell when the latter breaks out of the gas disk. Longer fragmentation
times of hypernova-driven shells as compared to fragmentation times of
shells created by multiple SNe were also found in the model of Efremov et al. (1999).
It is interesting to mention in this context the W4 HII
region in the Perseus arm of the outer Galaxy. Dennison et al. (1997)
have observed a highly elongated shell of
 emission, the base
of which is located near the W4 HII region. The
emission, the base
of which is located near the W4 HII region. The
 shell appears
to close far above the Galactic plane and is interpreted by Basu et al.
(1999)
to be the dense ionized wall of swept-up gas surrounding a bubble of hot
rarefied gas created by the stellar winds from the massive stars.
However, the apparent smooth appearance of the
shell appears
to close far above the Galactic plane and is interpreted by Basu et al.
(1999)
to be the dense ionized wall of swept-up gas surrounding a bubble of hot
rarefied gas created by the stellar winds from the massive stars.
However, the apparent smooth appearance of the
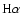 shell implies
that the Rayleigh-Taylor instability is suppressed there, possibly due
to the stabilizing effect of a swept-up tangential magnetic field in the
shell (Komljenovic et al. 1999).
An alternative explanation may involve a shell formed by a hypernova explosion.
In that case, the characteristic growth time of a Rayleigh-Taylor instability in the expanding shell
is much longer than in the case of multiple SNe, and the shell may survive
for a longer time and expand to a higher altitude.
shell implies
that the Rayleigh-Taylor instability is suppressed there, possibly due
to the stabilizing effect of a swept-up tangential magnetic field in the
shell (Komljenovic et al. 1999).
An alternative explanation may involve a shell formed by a hypernova explosion.
In that case, the characteristic growth time of a Rayleigh-Taylor instability in the expanding shell
is much longer than in the case of multiple SNe, and the shell may survive
for a longer time and expand to a higher altitude.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1324fg15.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg102.gif) |
Figure 15:
Off-plane explosion. The pV-diagrams of the shell created by a single hypernova
of the total energy of 1054 erg. The pV-cuts are taken along the major
axis of the model galaxy viewed at an
inclination angle of 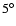 . . |
| Open with DEXTER |
Off-plane hypernova explosions may leave noticeable signatures in the pV-diagrams.
While the upper part of the egg-like shell is thin and contains a small fraction
of the total gas mass, the lower part of the shell accumulates a larger amount
of gas mass and becomes clearly visible in the pV-diagrams. Figure 15
shows the pV-cuts taken along the major axis of the
shell created by a single hypernova of the total energy of 1054 erg,
which is placed 100 pc above the midplane of the galaxy.
An inclination angle of 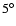 is adopted. The bottom of the egg-like shell
appears in the pV-diagrams as a bright arc connecting two vertical blobs.
The latter are the walls of the shell expanding in the horizontal direction.
The top of the shell is clearly visible only in the very early expansion
phase at
is adopted. The bottom of the egg-like shell
appears in the pV-diagrams as a bright arc connecting two vertical blobs.
The latter are the walls of the shell expanding in the horizontal direction.
The top of the shell is clearly visible only in the very early expansion
phase at 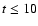 Myr. However, it could be seen in
Myr. However, it could be seen in
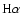 emission,
if a powerful ionizing source is located inside the shell, as might be
the case for the W4 HII region discussed above.
emission,
if a powerful ionizing source is located inside the shell, as might be
the case for the W4 HII region discussed above.
5 High velocity clouds
In this section we numerically study the vertical impact of high velocity clouds
as a potential mechanism of the giant HI ring formation in Ho I.
The numerical simulations of multiple SNe in Sect. 4
have shown that it requires
>
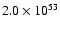 erg of released energy to form HI rings with
HI ring-to-center contrast
erg of released energy to form HI rings with
HI ring-to-center contrast
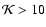 .
Hence, we consider only very energetic HVCs that could
potentially deposit a comparable amount of kinetic energy to the interstellar
medium. We have performed a parameter study assuming that HVCs cover a range of velocities
.
Hence, we consider only very energetic HVCs that could
potentially deposit a comparable amount of kinetic energy to the interstellar
medium. We have performed a parameter study assuming that HVCs cover a range of velocities
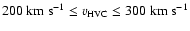 and masses
and masses
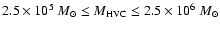 .
Thus, the kinetic energies of HVCs range from
.
Thus, the kinetic energies of HVCs range from
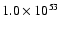 to
to
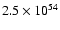 erg. Clouds are assumed to have a constant density
and be either spherical or cylindrical in shape. The initial position of
the cloud center is 3.2 kpc above the midplane.
erg. Clouds are assumed to have a constant density
and be either spherical or cylindrical in shape. The initial position of
the cloud center is 3.2 kpc above the midplane.
Figure 16 shows the temporal evolution of the distribution of the
gas volume density produced by the impact of a cloud of
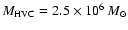 and
and
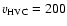 km s-1.
The total kinetic energy of the cloud is thus equal to
km s-1.
The total kinetic energy of the cloud is thus equal to
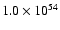 erg. The maximum column density
erg. The maximum column density
 of the cloud measured along its diameter
is
of the cloud measured along its diameter
is
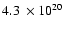 cm-2. The impinging HVC creates a hot
rarified bubble by pushing matter toward the galactic plane.
The bubble does not form a complete sphere and fills out
cm-2. The impinging HVC creates a hot
rarified bubble by pushing matter toward the galactic plane.
The bubble does not form a complete sphere and fills out
 40 Myr after the onset of the collision. The HVC continues
to push the gas along its way and eventually breaks through the disk. At
this stage (
40 Myr after the onset of the collision. The HVC continues
to push the gas along its way and eventually breaks through the disk. At
this stage (
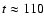 Myr), the initial
shape of the HVC is completely lost due to a combined action of Rayleigh-Taylor
and thermal instabilities.
The HVC emerges above the galactic plane as a complicated network of dense filaments,
clumps, and arcs.
The formation of dense filaments and clumps was also reported in numerical
simulations by Franco et al. (1988).
It takes another 70 Myr for this remnant to fall back onto the disk and
create another bubble, though less prominent than the first one.
Myr), the initial
shape of the HVC is completely lost due to a combined action of Rayleigh-Taylor
and thermal instabilities.
The HVC emerges above the galactic plane as a complicated network of dense filaments,
clumps, and arcs.
The formation of dense filaments and clumps was also reported in numerical
simulations by Franco et al. (1988).
It takes another 70 Myr for this remnant to fall back onto the disk and
create another bubble, though less prominent than the first one.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1324fg16.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg109.gif) |
Figure 16:
The distribution of the gas volume density created by the
collision of a cloud of
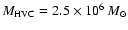 and
and
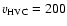 km s-1 with the galactic
gas disk. km s-1 with the galactic
gas disk. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1324fg17.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg110.gif) |
Figure 17:
The integrated HI image of the gas volume density distribution
shown in Fig. 16. An inclination angle of 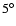 is adopted.
The scale bar is in cm-2.
is adopted.
The scale bar is in cm-2. |
| Open with DEXTER |
Although the kinetic energy of the impinging cloud is high (1054 erg)
and the cloud produces a considerable disturbance in the gas disk of the
target galaxy, we have found that it is rather ineffective in creating giant HI
rings similar to that observed in Ho I.
The HVC pushes the matter mostly in the vertical direction so that the HI image of a
nearly face-on galaxy does not show a considerable radial variation
in the HI column density within the impact region. Indeed, Fig. 17
shows the integrated HI image of the gas volume density distribution shown
in Fig. 16. An inclination angle of 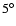 is assumed.
The formation of a ring-like structure is only seen in the late collision
phase (
is assumed.
The formation of a ring-like structure is only seen in the late collision
phase (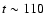 Myr), when the cloud has plunged through the gas disk
and pushed a considerable fraction of the disk gas to an altitude
Myr), when the cloud has plunged through the gas disk
and pushed a considerable fraction of the disk gas to an altitude  kpc.
Most of the gas constituting this remnant retains
the orbital momentum it had before the collision.
Since the horizontal gravity is much less at
kpc.
Most of the gas constituting this remnant retains
the orbital momentum it had before the collision.
Since the horizontal gravity is much less at  kpc than in
the plane of the galaxy, the lifted gas starts spiraling away on ballistic
orbits and it can be observed in nearly face-on galaxies as a dense HI ring surrounding the central
depression (see the left lower panel in Fig. 17). The maximum size of such an HI ring (diameter
kpc than in
the plane of the galaxy, the lifted gas starts spiraling away on ballistic
orbits and it can be observed in nearly face-on galaxies as a dense HI ring surrounding the central
depression (see the left lower panel in Fig. 17). The maximum size of such an HI ring (diameter
 0.8 kpc) is at least twice smaller than that found in our numerical simulations of
multiple SNe
and hypernova explosions of the same total energy. Note that the
diameter of the HI ring in Ho I is
0.8 kpc) is at least twice smaller than that found in our numerical simulations of
multiple SNe
and hypernova explosions of the same total energy. Note that the
diameter of the HI ring in Ho I is  1.7 kpc. We find that most of the HI rings formed
by the impact of HVCs have diameters less than 0.5 kpc. The HVCs of a smaller
size and higher HI column density, but the same kinetic energy,
tend to form smaller rings. The size of the HI ring depends weakly on the shape of the cloud.
HVCs with the total kinetic energy below
1.7 kpc. We find that most of the HI rings formed
by the impact of HVCs have diameters less than 0.5 kpc. The HVCs of a smaller
size and higher HI column density, but the same kinetic energy,
tend to form smaller rings. The size of the HI ring depends weakly on the shape of the cloud.
HVCs with the total kinetic energy below
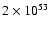 do not form
noticeable HI rings. HI rings with a diameter
of
do not form
noticeable HI rings. HI rings with a diameter
of  0.8 kpc are never formed in our simulations for the considered
upper limit of HVC kinetic energy,
0.8 kpc are never formed in our simulations for the considered
upper limit of HVC kinetic energy,
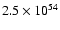 erg.
erg.
A more dramatic difference between the HI rings formed by the vertical
impact of
HVCs and those created by multiple SNe is seen in the values of  .
As is obviously seen from Fig. 6,
1000 consecutive SNe can create rings with
.
As is obviously seen from Fig. 6,
1000 consecutive SNe can create rings with 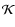 as high as 100, whereas
Fig. 17 indicates that the impact of a cloud of the same kinetic
energy generates the ring with
as high as 100, whereas
Fig. 17 indicates that the impact of a cloud of the same kinetic
energy generates the ring with
 .
Note that
.
Note that  in Holmberg I is
in Holmberg I is  15-20 (Ott et al. 2001).
The same tendency is found for other values of released energy: multiple
SNe produce rings with roughly 20-30 times
higher values of
15-20 (Ott et al. 2001).
The same tendency is found for other values of released energy: multiple
SNe produce rings with roughly 20-30 times
higher values of  than
does the impact of a cloud of the same total energy. On the other
hand, hypernova explosions form rings with
than
does the impact of a cloud of the same total energy. On the other
hand, hypernova explosions form rings with 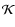 roughly a factor of 2 higher
than those created by the clouds of the same kinetic energy.
The difference in
roughly a factor of 2 higher
than those created by the clouds of the same kinetic energy.
The difference in 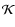 between the rings formed by the three mechanisms
considered above is smeared out as one considers higher inclination angles
of
between the rings formed by the three mechanisms
considered above is smeared out as one considers higher inclination angles
of
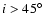 .
.
The impact of HVCs should leave prominent features in the pV-diagrams,
which could be used to distinguish between the rings formed by the impact
of HVCs and those formed by multiple SN and hypernova explosions. Indeed,
Fig. 18 shows the pV-cuts taken along the major axis of the
galaxy experiencing the collision with a cloud of
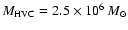 and
and
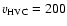 km s-1An inclination angle of
km s-1An inclination angle of 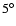 is adopted.
The open bubble produced by the impinging cloud is clearly seen in the
upper left panel of Fig. 18. The bubble starts filling out after t=45 Myr.
However, the cloud is still clearly visible in the pV-diagrams at that
time as a dense irregular clump moving towards the observer. The velocity of the cloud
noticeably decreases during the passage from
is adopted.
The open bubble produced by the impinging cloud is clearly seen in the
upper left panel of Fig. 18. The bubble starts filling out after t=45 Myr.
However, the cloud is still clearly visible in the pV-diagrams at that
time as a dense irregular clump moving towards the observer. The velocity of the cloud
noticeably decreases during the passage from
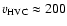 km s-1 at
the onset of collision to
km s-1 at
the onset of collision to
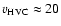 km s-1at the time when the cloud emerges on the other side of the gas disk.
The pV-diagram at this time (t=110 Myr) is dominated by two bright and compact clumps,
which represent the cold dense gas compressed and pushed by the cloud to
an altitude of
km s-1at the time when the cloud emerges on the other side of the gas disk.
The pV-diagram at this time (t=110 Myr) is dominated by two bright and compact clumps,
which represent the cold dense gas compressed and pushed by the cloud to
an altitude of
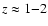 kpc. The depression
in the HI flux seen in the pV-diagram near the galactic center is due to the HI
ring formation discussed above. Note that these two clumps are noticeably different in
shape from those observed in the pV-diagrams of the shells formed by multiple
SN and hypernova explosions (see Figs. 7-9).
The second bubble formed by the remnant falling back onto the disk is clearly
seen in the lower right panel of Fig. 18.
kpc. The depression
in the HI flux seen in the pV-diagram near the galactic center is due to the HI
ring formation discussed above. Note that these two clumps are noticeably different in
shape from those observed in the pV-diagrams of the shells formed by multiple
SN and hypernova explosions (see Figs. 7-9).
The second bubble formed by the remnant falling back onto the disk is clearly
seen in the lower right panel of Fig. 18.
It is obviously seen that neither the pV-diagrams nor the size and/or ring-to-center
contrast 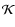 obtained in the simulations of the vertical collision of HVCs with
the galactic disk can account for what is actually
observed in Ho I. We thus conclude that multiple SN explosions
remain the most plausible explanation for the origin of the giant
HI ring morphology in Ho I.
obtained in the simulations of the vertical collision of HVCs with
the galactic disk can account for what is actually
observed in Ho I. We thus conclude that multiple SN explosions
remain the most plausible explanation for the origin of the giant
HI ring morphology in Ho I.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{1324fg18.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg117.gif) |
Figure 18:
The pV-diagrams of the gas volume density distribution shown
in Fig. 16. The pV-cuts are taken along the major axis of
the projected galaxy. An inclination angle of 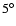 is assumed.
is assumed. |
| Open with DEXTER |
If SNe are the origin of HI rings surrounding HI holes, the presence
of a remnant stellar cluster is expected. Such stellar clusters are not always observed within HI
rings or holes. For instance, Rhode et al. (1999) found that
several HI holes in the dwarf irregular galaxy Holmberg II lack any stellar
cluster counterparts. However, in the case of Holmberg I, the B-band
magnitude as well as the U-B color of the optical emission from the giant HI hole indicates that a stellar cluster of 
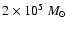 may be present there (Vorobyov et al. 2004).
may be present there (Vorobyov et al. 2004).
The high density clumps produced in our simulations due to the fragmentation of
SNe-driven shells are usually not self-gravitating. The masses of these clumps
are slightly below the Jeans mass
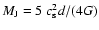 ,
where d is the size of the clump. This expression is derived
from the virial theorem assuming spherical clumps. This is consistent with
a low H
,
where d is the size of the clump. This expression is derived
from the virial theorem assuming spherical clumps. This is consistent with
a low H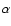 luminosity of Ho I:
luminosity of Ho I:
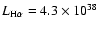 erg s-1 (Miller & Hodge 1996). This also implies that
SNe alone have difficulty in producing self-gravitating clumps in dwarf
irregular galaxies, and probably
an external agent such as ram pressure or the collision of two or more SNe-driven
shells is needed to induce star formation. In massive disk galaxies, radiative
cooling is usually more efficient than in dwarf irregulars due to a
higher metallicity. Therefore, dense
clumps are more likely to become Jeans unstable.
On the other hand, the most energetic HVC's with kinetic energy
erg s-1 (Miller & Hodge 1996). This also implies that
SNe alone have difficulty in producing self-gravitating clumps in dwarf
irregular galaxies, and probably
an external agent such as ram pressure or the collision of two or more SNe-driven
shells is needed to induce star formation. In massive disk galaxies, radiative
cooling is usually more efficient than in dwarf irregulars due to a
higher metallicity. Therefore, dense
clumps are more likely to become Jeans unstable.
On the other hand, the most energetic HVC's with kinetic energy
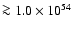 erg
can indeed produce dense clumps that are Jeans unstable. However, such energies
are rather exceptional and hence this mechanism cannot account for most star formation
in dwarf irregulars.
erg
can indeed produce dense clumps that are Jeans unstable. However, such energies
are rather exceptional and hence this mechanism cannot account for most star formation
in dwarf irregulars.
There are a few assumptions inherent to the model that need further discussion.
The interstellar medium distribution in Ho I. The solution of the
steady state momentum equation in Sect. 2 produces a smooth initial gas distribution,
which may be only a first order approximation to the more realistic inhomogeneous
interstellar medium of dwarf irregulars. The influence of the deviations
from a smooth ISM distribution in the gas disk on the formation and evolution
of HI shells deserves a separate detailed study. We expect here
that the effect of small scale inhomogeneities with sizes much smaller than
that of the HI shell should be cancelled out as the shell forms. Conversely,
large scale inhomogeneities with sizes comparable to that of the HI shell
could influence its shape and evolution, making it easier/harder to break
out of the disk. In particular, large scale inhomogeneities may reduce the
smooth appearance of hypernova-driven shells discussed in Sect. 4.3.
However, considering the size of the HI ring in Ho I ( 1.7 kpc), we do not expect
inhomogeneities of such a scale to be present in the initial gas distribution
of this galaxy.
1.7 kpc), we do not expect
inhomogeneities of such a scale to be present in the initial gas distribution
of this galaxy.
The vertical scale height of the stellar disk and gas velocity dispersion.
The actual value of the vertical scale height 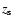 of the
stellar disk is difficult to estimate, since Ho I has a low inclination
angle. We have adopted a value of
of the
stellar disk is difficult to estimate, since Ho I has a low inclination
angle. We have adopted a value of
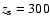 pc, which is typical
for dwarf irregular galaxies. A moderate variation
pc, which is typical
for dwarf irregular galaxies. A moderate variation  100 pc in the value of
100 pc in the value of 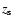 has a minor influence on the gas distribution and, hence, on our main results.
The HI velocity dispersion of Ho I is measured by Ott et al. (2001,
see their Fig. 10).
A moderate value
has a minor influence on the gas distribution and, hence, on our main results.
The HI velocity dispersion of Ho I is measured by Ott et al. (2001,
see their Fig. 10).
A moderate value
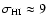 km s-1 is found for most of Ho I
disk, which is typical for gas-rich, quiet dwarf galaxies (Stil 1999)
and is used in our numerical simulations.
A small portion of gas disk in the northwestern part of Ho I has,
however, a slightly higher value of
km s-1 is found for most of Ho I
disk, which is typical for gas-rich, quiet dwarf galaxies (Stil 1999)
and is used in our numerical simulations.
A small portion of gas disk in the northwestern part of Ho I has,
however, a slightly higher value of
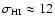 km s-1.
Such a variation in
km s-1.
Such a variation in
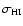 is not expected to influence our main results.
On the other hand, the measured
is not expected to influence our main results.
On the other hand, the measured
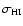 represents the cold component of the gas
disk only. If a massive hot gas component is present in Ho I, the
velocity dispersion
represents the cold component of the gas
disk only. If a massive hot gas component is present in Ho I, the
velocity dispersion
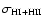 of the mixture of hot
and cold gas components may be
significantly greater. An increased gas velocity dispersion makes the gas disk
thicker. For instance, for an adopted value of
of the mixture of hot
and cold gas components may be
significantly greater. An increased gas velocity dispersion makes the gas disk
thicker. For instance, for an adopted value of
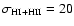 km s-1,
the Gaussian scale height of the model gas disk h becomes roughly three times
larger than that shown by the dotted line in Fig. 1.
However,
km s-1,
the Gaussian scale height of the model gas disk h becomes roughly three times
larger than that shown by the dotted line in Fig. 1.
However, 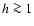 kpc is not expected in Ho I,
because a SN-driven shell with radius
kpc is not expected in Ho I,
because a SN-driven shell with radius
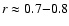 kpc would not
blow out of the disk.
Therefore, we would not observe such a high column density contrast
(
kpc would not
blow out of the disk.
Therefore, we would not observe such a high column density contrast
(
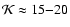 )
between the HI ring and the central depression.
Furthermore, Ho I is a quiet dwarf galaxy
with an average star formation rate of only
)
between the HI ring and the central depression.
Furthermore, Ho I is a quiet dwarf galaxy
with an average star formation rate of only
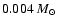 yr-1 (Miller
& Hodge 1996)
and we do not expect a large amount of hot gas
to be present there. Hence, we conclude that the integrated
gas velocity dispersion of Ho I is not expected to deviate much from the
adopted value of
yr-1 (Miller
& Hodge 1996)
and we do not expect a large amount of hot gas
to be present there. Hence, we conclude that the integrated
gas velocity dispersion of Ho I is not expected to deviate much from the
adopted value of 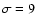 km s-1.
km s-1.
Internal structure and geometry of HVCs. The shape of HVCs (i.e.
spherical or cylindrical) is found
to have a very minor influence on our results, which is in agreement with
many previous studies of HVC collisions with a gas disk (e.g. Comeron &
Torra 1992). The assumption of an initially homogeneous cloud is
certainly an idealized case, since the observations show that
HVCs are very clumpy and hierarchically structured (e.g. Wakker & Schwarz
1991). It may be that the remnant of the initially homogeneous cloud
that emerges at the other side of the galactic plane at
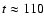 Myr in
Fig. 16 is a better example of an HVC prior to the collision.
Inhomogeneous structure further reduces the ability of an HVC to produce
large HI rings.
Myr in
Fig. 16 is a better example of an HVC prior to the collision.
Inhomogeneous structure further reduces the ability of an HVC to produce
large HI rings.
7 Conclusions
We have numerically studied the formation of a giant HI ring as is observed
in the Holmberg I dwarf irregular galaxy (Ott et al. 2001).
The following three energetic mechanisms with the total released energy
of  1054 erg have been considered: multiple SNe, a
hypernova explosion associated with a gamma ray burst, and the vertical
impact of an HVC.
The shells created by those mechanisms are seen in the integrated HI image
of a nearly face-on galaxy as the HI rings of various sizes and ring-to-center
contrasts
1054 erg have been considered: multiple SNe, a
hypernova explosion associated with a gamma ray burst, and the vertical
impact of an HVC.
The shells created by those mechanisms are seen in the integrated HI image
of a nearly face-on galaxy as the HI rings of various sizes and ring-to-center
contrasts  in the HI column density.
We find the following differences among the HI rings formed by those mechanisms:
in the HI column density.
We find the following differences among the HI rings formed by those mechanisms:
- Multiple SNe form rings with the highest ring-to-center contrast
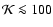 .
A single hypernova
and an HVC form rings with much smaller values
of
.
A single hypernova
and an HVC form rings with much smaller values
of
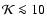 and
and
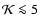 ,
respectively.
This is due to the difference in the dynamics of the shells produced by
multiple SNe and those created by a hypernova: multiple SNe are
much more effective in producing blowout due to a combined action of
Kelvin-Helmholtz and Rayleigh-Taylor instabilities
than are single hypernovae of the same total energy.
The vertical impact of an HVC is found to be ineffective in evacuating the gas in the
radial direction and hence in creating HI rings with a high ring-to-center
contrast. It is important to note that the difference in
,
respectively.
This is due to the difference in the dynamics of the shells produced by
multiple SNe and those created by a hypernova: multiple SNe are
much more effective in producing blowout due to a combined action of
Kelvin-Helmholtz and Rayleigh-Taylor instabilities
than are single hypernovae of the same total energy.
The vertical impact of an HVC is found to be ineffective in evacuating the gas in the
radial direction and hence in creating HI rings with a high ring-to-center
contrast. It is important to note that the difference in 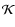 found among the
three energetic mechanisms
smears out at an inclination angle
found among the
three energetic mechanisms
smears out at an inclination angle
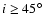 due to the projection effect.
due to the projection effect.
- Both multiple SNe and a hypernova can account for the
observed size of the HI ring in Ho I (diameter
 1.7 kpc).
The maximum size of the ring that an HVC is found
to form in our numerical simulations is
1.7 kpc).
The maximum size of the ring that an HVC is found
to form in our numerical simulations is  0.8 kpc.
We thus conclude that only multiple SNe can reproduce both
the size (diameter
0.8 kpc.
We thus conclude that only multiple SNe can reproduce both
the size (diameter  1.7 kpc) and the ring-to-center contrast in
the HI column density (
1.7 kpc) and the ring-to-center contrast in
the HI column density (
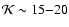 ) of the HI ring in Ho I.
) of the HI ring in Ho I.
We construct the model position-velocity diagrams and find that they can be used to distinguish
between HI rings produced by different energetic mechanisms.
The model pV-diagrams of the blownout shell produced by multiple SNe
are similar to those observed in Ho I and show two symmetrically displaced,
elongated blobs representing the walls of the shell.
On the other hand, the model pV-diagrams of
the shell created by a hypernova explosion show a characteristic
elliptical ring-like structure, which is not seen in the observed pV-diagrams of Ho I.
The impact of HVCs leaves prominent features in the model pV-diagrams that
are also not found in the observed pV-diagrams of Ho I.
Those features include dense irregular clumps and a void representing the impinging
cloud and the bubble formed by the impact.
We thus conclude that multiple SNe
appear to be the most plausible energetic mechanism
of the HI ring formation in Ho I.
Our numerical simulations indicate that the appearance of the SN-driven
shell in dwarf irregulars may depend on the inclination of the galaxy.
In nearly face-on galaxies the blownout shell appears in the integrated
HI image as an HI ring with a deep central minimum. There is little azimuthal variation
in the HI column density around the ring.
The integrated HI image of the blownout shell in considerably inclined galaxies
(
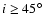 )
is instead dominated by two
kidney-shaped enhancements and shows a mild central minimum, which is similar to what
is found in Sectans A and M 81 dwA (Skillman et al. 1988; Stewart 1998).
In nearly edge-on galaxies the integrated HI image of the blownout shell
resembles a "dumbbell''.
)
is instead dominated by two
kidney-shaped enhancements and shows a mild central minimum, which is similar to what
is found in Sectans A and M 81 dwA (Skillman et al. 1988; Stewart 1998).
In nearly edge-on galaxies the integrated HI image of the blownout shell
resembles a "dumbbell''.
The offplane explosion of a hypernova creates the egg-like shell
that can preserve its shape for a considerably longer time than the
shell created by multiple SNe of the same total energy.
This may explain the smooth appearance of the highly elongated H shell
observed by Dennison et al. (1997) in the W4 HII region of the Perseus arm.
shell
observed by Dennison et al. (1997) in the W4 HII region of the Perseus arm.
Acknowledgements
The authors are thankful to the referee, Prof. J. Palous,
for valuable suggestions and comments that helped improve the manuscript.
This work was supported by the NATO Science Fellowship Program administered
by the Natural Sciences and Engineering Research Council (NSERC) of Canada.
E.V. is grateful to the staff of the Department of Physics and Astronomy,
University of Western Ontario for their hospitality.
- Basu, S., Johnstone, D.,
& Martin, P. G. 1999, ApJ, 516, 843 [NASA ADS] [CrossRef] (In the text)
- Binney, J., & Merrifield,
M. 1998, in Galactic Astronomy, ed. P. Ostriker, & D. N.
Spergel (Princeton University Press), 442
(In the text)
- Binney, J., &
Tremaine, S. 1987, Galactic Dynamics (Princeton: Princeton Univ.
Press)
(In the text)
- Brinks, E. 1990, in The
Interstellar Medium of Galaxies, ed. H. Thronson, & J. Shull
(Dordrecht: Kluwer), 39
(In the text)
- Comerón, F.,
& Torra, J. 1992, A&A, 261, 94 [NASA ADS] (In the text)
- Dennison, B.,
Topasna, G. A., & Simonetti, J. H. 1997, ApJ, 474, L31 [NASA ADS] [CrossRef] (In the text)
- De Young, D., &
Heckman, T. M. 1994, ApJ, 431, 598 [NASA ADS] [CrossRef] (In the text)
- Efremov, Yu. N.,
Elmegreen, B. G., & Hodge, P. W. 1998, ApJ, 501, L163 [NASA ADS] [CrossRef] (In the text)
- Efremov, Yu. N.,
Ehlerová, S., & Palous, J. 1999, A&A, 350, 457 [NASA ADS] (In the text)
- Elmegreen, B. G.
1997, ApJ, 477, 196 [NASA ADS] [CrossRef] (In the text)
- Franco, J.,
Tenorio-Tagle, G., Bodenheimer, P., Rózyczka, & Mirabel,
I. F. 1988, ApJ, 333, 826 [NASA ADS] [CrossRef] (In the text)
- Komljenovic, P. T., Basu, S.,
& Johnstone, D. 1999, in New Perspectives on the Interstellar
Medium, ed. A. R. Taylor, T. L. Landecker, & G. Joncas (San
Francisco: ASP), ASP Conf. Ser., 168, 299
(In the text)
- Loeb, A., & Perna, R. 1998,
ApJ, 503, L35 [NASA ADS] [CrossRef] (In the text)
- Mac Low, M.-M., &
Ferrara, A. 1999, ApJ, 513, 142 [NASA ADS] [CrossRef] (In the text)
- Mac Low, M.-M., &
McCray, R. 1988, ApJ, 324, 776 [NASA ADS] [CrossRef] (In the text)
- Mashchenko, S. Ya., &
Silich, S. A. 1995, AZh, 72, 660 [NASA ADS] (In the text)
- Miller, B. W., &
Hodge, P. 1996, ApJ, 458, 467 [NASA ADS] [CrossRef] (In the text)
- Ott, J., Walter, F., Brinks,
E., et al. 2001, AJ, 122, 3070 [NASA ADS] [CrossRef] (In the text)
- Paczynski, B. 1998, ApJ, 494,
45 [NASA ADS] [CrossRef] (In the text)
- Persic, M., Salucci,
P., & Stel, F. 1996, MNRAS, 281, 27 [NASA ADS] (In the text)
- Puche, D., Westpfahl, D.,
Brinks, E., & Roy, J.-R. 1992, AJ, 103, 1841 [NASA ADS] [CrossRef] (In the text)
- Rand, R. J., & Stone,
J. M. 1996, AJ, 111, 190 [NASA ADS] [CrossRef] (In the text)
- Rhode, K. L., Saltzer, J.
J., Westpfahl, D. J., & Radice, L. A. 1999, AJ, 118, 323 [NASA ADS] [CrossRef] (In the text)
- Recchi, S., Matteucci,
F., & D'Ercole, A. 2001, MNRAS, 322, 800 [NASA ADS] [CrossRef] (In the text)
- Sánchez-Salcedo, F. J.
2002, Rev. Mex. Astron. Astrofís., 38, 39 [NASA ADS] (In the text)
- Sargent, E. L. W.,
Sancisi, R., & Lo, K. Y. 1983, ApJ, 265, 711 [NASA ADS] [CrossRef] (In the text)
- Silich, S., &
Tenorio-Tagle, G. 2001, ApJ, 552, 91 [NASA ADS] [CrossRef] (In the text)
- Stone, J. M., & Norman, M.
L. 1992, ApJS, 80, 753 [NASA ADS] [CrossRef] (In the text)
- Young, L. M., & Lo,
K. Y. 1997, ApJ, 490, 710 [NASA ADS] [CrossRef] (In the text)
- Skillman, E. D.,
Terlevich, R., Teuben, P. J., & van Woerden, H. 1988, A&A,
198, 33 [NASA ADS] (In the text)
- Stewart, S. 1998,
Ph.D. Thesis, The University of Alabama
(In the text)
- Stil, J. A. 1999, Ph.D.
Thesis, Univ. Leiden
(In the text)
- Taylor, C., Brinks, E.,
Pogge, R. W., & Skillman, E. D. 1994, AJ, 107, 971 [NASA ADS] [CrossRef] (In the text)
- Tenorio-Tagle, G., Franco, J.,
Bodenheimer, P., & Rózyczka, M. 1987, A&A, 179,
219 [NASA ADS] (In the text)
- Tully, R. B., Bottinelli,
L., Fisher, J. R., et al. 1978, A&A, 63, 37 [NASA ADS] (In the text)
- Vorobyov, E. I., Klein, U.,
Shchekinov, Yu. A., & Ott, J. 2004, A&A, 413, 939 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Vorobyov, E. I., &
Shchekinov, Yu. A. 2004, A&A, 416, 499 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Wada, K., & Norman, C.
2001, ApJ, 547, 172 [NASA ADS] [CrossRef] (In the text)
- Wada, K., Spaans, M.,
& Kim, S. 2000, ApJ, 540, 797 [NASA ADS] [CrossRef] (In the text)
- Wakker, B. P., &
Schwarz, U. J. 1991, A&A, 250, 484 [NASA ADS] (In the text)
- Walter, F., &
Brinks, E. 1999, AJ, 118, 273 [NASA ADS] [CrossRef] (In the text)
- Walter, F., &
Brinks, E. 2001, AJ, 121, 3026 [NASA ADS] [CrossRef] (In the text)
- Weaver, R., McCray, R.,
Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [NASA ADS] [CrossRef]
- Westpfahl, D.,
& Puche, D. 1993, in ESO Conf. Workshop Proc. 49, Dwarf
Galaxies, ed. G. Meylan, & P. Prugniel (Garching: ESO),
295
(In the text)
Copyright ESO 2005
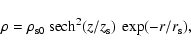
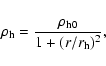
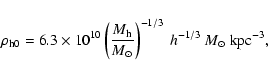
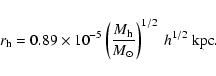
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1324fig1.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg45.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1324fig2.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg61.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1324fig3.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg65.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1324fig4.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg66.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1324fig5.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg67.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1324fig6.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg73.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1324fig7.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg74.gif)
![\begin{displaymath}{M_{\rm HI} \over \triangle v} = 2.35 \times 10^5~\left( {D \...
...
\right) \ \ \left[{M_{\odot} \over {\rm km\: s^{-1}}}\right],
\end{displaymath}](/articles/aa/full/2005/08/aa1324/img75.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1324fig8.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1324fig9.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg78.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1324fg10.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg85.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1324fg11.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1324fg12.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg93.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1324fg13.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg94.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1324fg14.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1324fg15.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg102.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1324fg16.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg109.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1324fg17.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg110.gif)
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{1324fg18.eps}
\end{figure}](/articles/aa/full/2005/08/aa1324/Timg117.gif)